Structural Insights into Hearing Loss Genetics from Polarizable Protein Repacking

Abstract

Hearing loss is associated with ∼8100 mutations in 152 genes, and within the coding regions of these genes are over 60,000 missense variants. The majority of these variants are classified as “variants of uncertain significance” to reflect our inability to ascribe a phenotypic effect to the observed amino acid change. A promising source of pathogenicity information is biophysical simulation, although input protein structures often contain defects because of limitations in experimental data and/or only distant homology to a template. Here, we combine the polarizable atomic multipole optimized energetics for biomolecular applications force field, many-body optimization theory, and graphical processing unit acceleration to repack all deafness-associated proteins and thereby improve average structure MolProbity score from 2.2 to 1.0. We then used these optimized wild-type models to create over 60,000 structures for missense variants in the Deafness Variation Database, which are being incorporated into the Deafness Variation Database to inform deafness pathogenicity prediction. Finally, this work demonstrates that advanced polarizable atomic multipole force fields are efficient enough to repack the entire human proteome.

Significance

We are interrogating the genetics of deafness using a targeted sequencing panel (called OtoSCOPE) that includes 152 deafness-associated genes. OtoSCOPE enables us to identify an average of 545 variants per patient, which are curated in the deafness-specific database we purpose built called the Deafness Variation Database (http://deafnessvariationdatabase.org). To inform the interpretation of missense variants from a structural biology perspective, we describe new, to our knowledge, algorithms for repacking protein structures. Our approach, implemented in the publicly available software Force Field X (https://ffx.biochem.uiowa.edu), is used to generate 473 wild-type structures for OtoSCOPE genes. These protein models have been integrated into the Deafness Variation Database to inform classification of missense variants and form the foundation for downstream analyses of protein-protein binding and folding stability.

Introduction

As the most common human sensory deficit, deafness impacts an estimated 360 million people globally (World Health Organization data, http://www.who.int/pbd/deafness/estimates/en/index.html). Its cause is multifactorial, and with recent advances in the application of targeted genetic sequencing technology to clinical medicine, our understanding of genetic contributions to deafness has greatly advanced. The use of deafness-specific gene panels has changed the clinical paradigm in the evaluation of the deaf patient and is laying the foundation for personalized gene therapy to treat hearing loss.

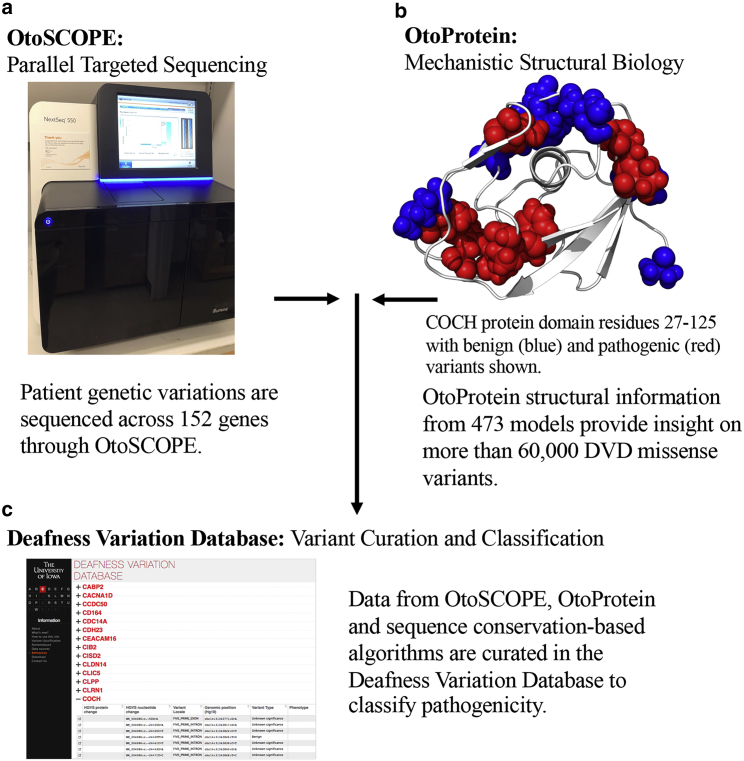
The targeted genetic sequencing panel developed by our group, which we refer to as OtoSCOPE, includes 152 deafness-associated genes (1, 2). Its use enables us to identify an average of 545 variants per patient, which are curated in the publicly available deafness-specific database we purpose built called the Deafness Variation Database (DVD, Fig. 1; Table S1; http://deafnessvariationdatabase.org) (3, 4). The DVD collates data from major public databases and uses criteria recommended by the American College of Medical Genetics and Genomics to classify every genetic variant as benign (B), likely benign (LB), variant of uncertain significance (VUS), likely pathogenic (LP), or pathogenic (P) based on collected evidence and curation by experts in genetic hearing loss. Of the ∼800,000 variants in the genes included on OtoSCOPE that are listed in the DVD, more than 60,000 missense variations exist. Of these variants, ∼4000 are LP/pathogenic, ∼38,000 are VUSs, and ∼18,000 are LB/B.

Figure 1.

Incorporating structural biophysics into variant classification. (a) OtoSCOPE sequencing technology discovers 545 variants per patient on average, 71 of which are nonsynonymous coding, splice site, or indel variants. (b) Protein structural coverage for OtoScope genes is an important step toward identifying the molecular causation of disease-causing variants along with classifying VUSs. (c) Variants collected through OtoSCOPE sequencing are curated in the Deafness Variation Database (DVD). For each variant, the DVD combines minor allele frequency, experimental results, pathogenicity predictions from sequence conservation-based classifiers, and now, insights from protein structures (i.e., OtoProtein, described in this work). The pathogenicity for nearly 80% of the variants in the DVD remains unknown, which means they are placed into the variant of uncertain significance (VUS) category. To see this figure in color, go online.

Many of the missense variations labeled as VUSs will ultimately be classified as LP/pathogenic, but we are currently relegated to classifying them as VUSs as a reflection of our inability to predict the phenotypic consequences of most genetic variations. We often lack variant-specific wet-lab-based functional evidence (5), and insights derived from atomic resolution simulations must continue to mature to reliably make meaningful genotype-phenotype correlations.

Atomic resolution simulation techniques such as molecular dynamics (MD) provide a promising first-principles approach for computationally predicting the potential impact of missense variants. However, its success is dependent, in part, on accurate protein structures. These structures are typically determined from an experimental method (i.e., x-ray crystallography, NMR, cryo-electron microscopy, etc.) or from homology modeling. The latter leverages existing protein structure(s) as a template from which to create the model of a homologous amino acid sequence. Homology modeling is most reliable when homologous sequences have at least 30% sequence identity, which typically indicates protein fold is conserved (6, 7). To complement and enhance models available in databases such as ModBase (8) and SwissProt (9), dramatic improvements are possible by global optimization (i.e., repacking) of amino acid side chains using more advanced molecular physics than was originally available (or could be computationally afforded) at the time of their creation.

For example, most protein structures found in both the Protein Data Bank (10) and homology modeling databases (8, 9) are based on refinement with pairwise potential energy functions (i.e., force fields) such as the fixed-charge Amber (11, 12), CHARMM (13, 14), and OPLS-AA (15, 16) models (17). Over the past decade, more accurate polarizable force fields have emerged that overcome limitations in previous generation pairwise models (18), including both the Atomic Multipole Optimized Energetics for Biomolecular Applications (AMOEBA) force field (19, 20) and the CHARMM Drude (21) model. Structural optimization with these state-of-the-art energy functions, when used with continuum representations of solvation (22, 23, 24), can compensate for limitations in experimental data and improve homology models. However, multiple challenges must be overcome to realize the benefits of polarizable atomic multipole force fields, including mitigating their increased computational expense and overcoming the loss of convenient pairwise approximations that are widespread in structural biology software such as Modeler (25), Phenix (26), and Rosetta (27).

Our decision to use the AMOEBA force field for this work is based on a series of previous structural refinement studies performed over the last decade (28, 29, 30, 31, 32, 33, 34, 35) that systematically demonstrate both improved agreement to x-ray and neutron diffraction data (i.e., lower R/R_free) and improved MolProbity metrics (36, 37) compared to fixed-charge force fields. MolProbity identifies high-energy atomic clashes, unfavorable side-chain conformations, and polypeptide backbone conformations inconsistent with low-energy secondary structure. The algorithm is widely used by crystallographers to aid refinement of models by reporting structural features that are known to be unphysical. Lower MolProbity scores are consistent with higher-quality x-ray diffraction data (i.e., a score of 1.0 is calibrated to reflect 1.0 Å resolution data). For example, AMOEBA-assisted x-ray refinement on ultra-high-resolution (0.43–0.59 Å) peptide crystals (28) and high-resolution (0.65–0.89 Å) lysozyme, trypsin, and DNA data sets (29) demonstrated lower R/R_free values compared to conventional refinement using force fields without advanced electrostatics. Work on joint x-ray/neutron data sets for B-form DNA and Z-form DNA (31) demonstrated that AMOEBA-assisted refinement outperformed a variant of OPLS-AA in terms of both lower R/R_free values and improved water hydrogen bonding networks. Finally, more recent work on a series of proliferating cell nuclear antigen structures thoroughly compared AMOEBA-assisted x-ray refinement to OPLS-AA/L, including rotamer repacking in both cases, and AMOEBA again outperformed OPLS-AA/L in terms of both lower R/R_free and improved MolProbity scores (35).

Building on the promising refinement results from these previous studies, here we use refinement with AMOEBA to generate a family of deafness-related protein structures called OtoProtein. Our approach combines the AMOEBA potential energy function (19, 20), many-body optimization theory (35), and GPU acceleration (38, 39) to optimize all available deafness-associated protein models. To assess the resulting structures objectively, we evaluated overall quality with the MolProbity (36, 37) algorithm. Correcting rotamer outliers often improves other metrics and permits further relaxation of the structure with local minimization, resulting in more realistic, lower-energy structures for downstream analysis (e.g., MD, alchemical free-energy simulations, or feature extraction for bioinformatics analysis).

As described in the Results, our mean postoptimization MolProbity score is consistent with near-atomic resolution. The structures have been integrated with the DVD to provide insight into the biophysical impacts of deafness-related genetic variations, which aids in predicting variant effect and pathogenicity. Our polarizable protein repacking algorithm is freely available in the open source software Force Field X (FFX, http://ffx.biochem.uiowa.edu) and may be useful to others in the community that are integrating structural biophysics into variant classification.

Materials and Methods

Many-body energy expansion parallelization across GPUs

Generation and assessment of OtoProtein structures, as depicted in Fig. 1, will now be described in detail. Under a many-body potential, the total energy of a protein E(r) can be defined to arbitrary precision using the expansion

$$E\left(\text{r}\right)=E_{env}+\sum _i{E}_{self}\left(r_i\right)+\sum _i\sum _{j>i}{E}_2\left(r_i,r_j\right)+\sum _i\sum _{j>i}\sum _{k>j}{E}_3\left(r_i,r_j,r_k\right)+\dots ,$$ (1)

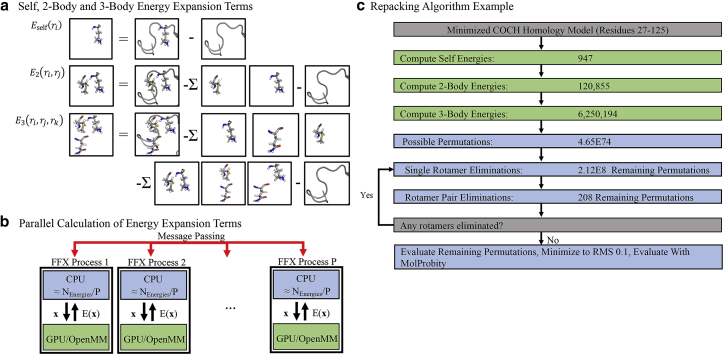
where E_env is the energy of the environment (i.e., the protein backbone and residues that are not being optimized); E_self(r_i) is the self-energy of residue i that includes its intramolecular bonded energy terms and nonbonded interactions with the backbone; E₂(r_i, r_j) is the two-body nonbonded interaction energy between residues i and j with other residues turned off; and E₃(r_i, r_j, r_k) is the three-body nonbonded interaction energy between residues i, j, and k with other residues turned off. The self, two-body, and three-body energy terms are calculated as follows, where E_BB/SC is the total energy of the backbone with the side chain(s) of the selected residue(s) included (shown graphically in Fig. 2 a).

$$E_{self}\left(r_i\right)=E_{BB/SC}\left(r_i\right)-E_{env}$$ (2)

$$E_2\left(r_i,r_j\right)=E_{BB/SC}\left(r_i,r_j\right)-E_{self}\left(r_i\right)-E_{self}\left(r_j\right)-E_{env}$$ (3)

$$E_3\left(r_i,r_j,r_k\right)=E_{BB/SC}\left(r_i,r_j,r_k\right)-E_{self}\left(r_i\right)-E_{self}\left(r_j\right)-E_{self}\left(r_k\right)-E_2\left(r_i,r_j\right)-E_2\left(r_i,r_k\right)-E_2\left(r_j,r_k\right)-E_{env}$$ (4)

Figure 2.

Overview of the protein repacking algorithm. (a) Depictions of rotamer self, two-body, and three-body energy terms are given. (b) Parallel computation of energy terms across processes and GPUs is shown. Processes (blue boxes) are each assigned a group of self-energies to calculate, where $N_{self}=\sum _{i=1}^{N_{residues}}{n}_i$ is the sum of rotamers across all residues to give N_self/P evaluations per process. Processes compute energy values by sending a conformation x to a GPU (green box) for evaluation using the OpenMM application programming interface, followed by return of the energy E(x) and its communication to all processes using the Java message-passing interface (red arrows). The two-body and three-body energies are parallelized in a similar fashion. (c) The number of side-chain energies and conformational permutations for a 98-residue COCH protein domain are shown as an example. After all energy terms have been calculated (green rectangles), the combinatorial side-chain conformational space is reduced using many-body Goldstein rotamer and rotamer pair elimination criteria (see Materials and Methods) to achieve a tractable number of permutations to evaluate. Before eliminations, 4.65 × 10⁷⁴ side-chain permutations exist, but only 208 permutations remain to be evaluated after eliminations. To see this figure in color, go online.

Individual energy evaluations are calculated on graphical processing units (GPUs) via the CUDA kernels of OpenMM (39), and the evaluations are distributed over many GPUs, potentially over multiple nodes, using the PJ library (Fig. 2 b; (40)). Side-chain rotamer conformations that are not part of the optimum structure can be rigorously eliminated using mathematical expressions (Fig. 2 c; (35, 41, 42)).

Computing the self, two-body, and three-body energy terms as a function of rotamer conformation is computationally expensive. To address this challenge, our FFX program utilizes two complementary parallelization approaches, including 1) use of the Parallel Java (PJ) (40) message-passing interface library to distribute terms among multiple processes and 2) use of the OpenMM application programming interface (39) to perform force-field-energy evaluations on NVIDIA GPUs (Nvidia, Santa Clara, CA) via CUDA kernels. FFX uses PJ to divide each shared memory node of a multiple node compute cluster into one or more processes (Fig. 2 b). Energy terms are then assigned to processes, evaluated, and globally communicated across all processes using PJ message passing, with synchronization steps between calculation of the self, two-body, and three-body energy terms (i.e., two-body terms depend on self-terms as shown in Eq. 3, and thus must be calculated after self-energies are completed and before three-body energies). The FFX-OpenMM interface (based on Java Native Access wrappers to the OpenMM C++ application programming interface) is used to offload energy evaluations from FFX, which executes on central processing units (CPUs), to OpenMM on a GPU. Once all energy terms are calculated, side-chain rotamers and rotamer pairs are eliminated by lower-energy alternatives based on rigorous mathematical inequalities that have been described for pairwise force fields (e.g., dead-end elimination (41) and Goldstein elimination (42)) and more recently generalized to include three-body terms for use with many-body force fields (35) such as the polarizable AMOEBA model (20, 30). The many-body Goldstein criteria for rotamer elimination (35), truncated at three-body terms, is given by

$$E_{self}\left(r_i^{\alpha }\right)-E_{self}\left(r_i^{\beta }\right)+\sum _{j\text{'}}\underset{\gamma }{\min }\left\{E_2\left(r_i^{\alpha },r_j^{\gamma }\right)-E_2\left(r_i^{\beta },r_j^{\gamma }\right)+\sum _{k\text{'}}\underset{\delta }{\min }\left[E_3\left(r_i^{\alpha },r_j^{\gamma },r_k^{\delta }\right)-E_3\left(r_i^{\beta },r_j^{\gamma },r_k^{\delta }\right)\dots \right]\right\}>0$$ (5)

and, if satisfied, indicates rotamer α of residue i is eliminated by rotamer β (the ellipses signify the presence of further higher-order terms). The expression for rotamer pair elimination is given by

$$E_{pair}\left(r_i^{\alpha },r_j^{\beta }\right)-E_{pair}\left(r_i^{\gamma },r_j^{\delta }\right)+\sum _{k^{\text{'}}}\underset{\epsilon }{\min }\left\{E_2\left(r_i^{\alpha },r_k^{\epsilon }\right)+E_2\left(r_j^{\beta },r_k^{\epsilon }\right)+E_3\left(r_i^{\alpha },r_j^{\beta },r_k^{\epsilon }\right)-E_2\left(r_i^{\gamma },r_k^{\epsilon }\right)-E_2\left(r_j^{\delta },r_k^{\epsilon }\right)-E_3\left(r_i^{\gamma },r_j^{\delta },r_k^{\epsilon }\right)+\sum _{l^{\text{'}}}\underset{\eta }{\min }\left[E_3\left(r_i^{\alpha },r_k^{\epsilon },r_l^{\eta }\right)+E_3\left(r_j^{\beta },r_k^{\epsilon },r_l^{\eta }\right)-E_3\left(r_i^{\gamma },r_k^{\epsilon },r_l^{\eta }\right)-E_3\left(r_i^{\delta },r_k^{\epsilon },r_l^{\eta }\right)+\dots \right]\right\}>0$$ (6)

and, if satisfied, indicates that the rotamer pair $\left(r_i^{\alpha },r_j^{\beta }\right)$ for residues i and j is eliminated by rotamer pair $\left(r_i^{\gamma },r_j^{\delta }\right)$.

Four approximations to rigorous use of the many-body Goldstein inequalities given above were explored, each of which is summarized here and described more fully in the Results. First, it was determined that the expansion could be truncated at pairwise terms because of damping of three-body and higher-order terms by the generalized Kirkwood implicit solvent. However, in the absence of implicit solvent, previous work demonstrated that inclusion of three-body terms is sometimes necessary (35). The second approximation was a distance cutoff; if the closest rotamers for a residue pair or triple are more than 2 Å apart, the interaction energy is set to 0. Third, pruning was utilized to remove rotamers with self-energies 25 kcal/mol or more above the lowest self-energy of a residue before calculation of two-body energies. This criterion is based on the heuristic observation that rotamers with such an unfavorable self-energy (e.g., due to an atomic clash with backbone atoms) are not found in well-packed structures. However, for structures with significant backbone flaws, this approximation must be used with care because it can incorrectly eliminate the “least bad” rotamer that is actually part of the global minimal conformation. Our final approximation involved imposing a three-dimensional grid over the protein, followed by optimization within each subdomain (cube) of the grid, rather than including all protein residues simultaneously. Although the repacking algorithm is a provable global optimizer within a single subdomain of the grid, it is not for the protein grid as a whole because coordinated changes between subdomains are neglected.

The OtoProtein Structure Database

Comparative protein modeling provides a means to predict the structure of a protein whose atomic coordinates have not been solved experimentally by crystallography, NMR, etc. (43). Many human genes implicated in hearing loss have not been studied experimentally, so computational approaches are necessary to generate high-quality protein structures. Comparative protein modeling begins from an experimental structure for an evolutionarily related protein, which is used as a template for the target sequence (10, 44). The percent sequence identity between the homologs provides an estimate of model reliability (45). Comparative protein models are conducive to the study of protein function, dynamics, and interactions with other molecules such as ligands, DNA, RNA, or other proteins. Homology models can also be used to study missense variants, providing a promising basis for understanding the role of protein phenotypes in heterogenic diseases like hearing loss.

However, comparative protein models from leading databases often include defects directly related to approximations in the methods used for their generation (e.g., pairwise force fields, local rather than global optimization, etc.). We sought to improve comparative protein models from SwissProt (44) and ModBase (8) for 152 genes included in the OtoSCOPE platform. Although using homology models based on a sequence identity of 30% or greater generally gives confidence that the protein backbone fold has been evolutionarily conserved (45), this work includes all publicly available models (the average sequence identity was 41.7% for all 473 structural models). Both SwissProt and ModBase strive to provide structural coverage for the largest portion of the human proteome possible; however, this limits their ability to explore the use of advanced many-body force fields. Here, we show that use of the polarizable AMOEBA force field in tandem with global optimization of amino acid side chains (35) can significantly improve the quality of SwissProt or ModBase structures as assessed by tools like MolProbity (36, 37). High-quality protein structural models, in turn, provide optimal starting points for downstream MD simulations that can be used to analyze missense variations (i.e., calculation of folding and/or binding free-energy differences). The parallelized repacking algorithm described here demonstrates that it is now feasible to refine large databases of homology models using advanced polarizable atomic multipole force fields.

All homology models were refined using the 2018 AMOEBA protein force field (20, 46) with generalized Kirkwood implicit solvent (23). The input homology models were first locally optimized using the low-memory Broyden-Fletcher-Goldfarb-Shanno algorithm to a root mean square (RMS) gradient convergence criterion of 0.8 kcal/mol/Å. The rationale for minimizing with a relatively loose convergence criterion before rotamer optimization was to relax the backbone conformation without excessively favoring the starting conformation over alternative rotamers. Locally optimizing to a tighter convergence criterion before side-chain optimization resulted in higher-energy, less favorable structures because of overstabilizing starting rotamers. Next, the side-chain repacking algorithm was applied, followed by a final local low-memory Broyden-Fletcher-Goldfarb-Shanno minimization to an RMS gradient convergence criterion of 0.1 kcal/mol/Å. The resulting protein structures and original homology models were then evaluated and compared using both the MolProbity assessment tool and AMOEBA/GK energies. These optimized wild-type structures were used as input for creating more than 60,000 variant structures for missense variations in the DVD. For each missense variant in the DVD with structural coverage available in the wild-type OtoProtein data set, the corresponding structure(s) were mutated. We then locally repacked all residues within 2 Å of the missense variant (i.e., based on Eq. 7 below) to correct any atomic clashes introduced by the variant amino acid. Many proteins in our data set have more than one homology model available, often covering similar residue ranges. For each missense variant, a locally repacked structure was created for every available wild-type model, which yielded multiple structures for many missense variants in our data set.

Results

Polarizable protein repacking algorithm using GPUs

To benefit fully from the emergence of polarizable force fields in the context of protein structure prediction and repacking, the theory that underlies established algorithms must be revisited to incorporate many-body electronic polarization and to optimize performance across GPUs. We examined four approximations to our many-body protein repacking algorithm to enhance efficiency while maintaining structural quality. The approximations are illustrated using a 98-residue COCH protein (residues 27–125), which was chosen based on its high sequence identity to an experimental NMR template (98% identity) and modest size. Previous work showed that truncating the energy expansion at three-body terms resulted in accurate side-chain positions being identified in the context of real-space x-ray refinement (35). However, when using the native environment approximation (47) in combination with the AMOEBA/GK implicit solvent (23), we found that the contribution of energy terms within the energy expansion decays quickly. The magnitude of each term in Eq. 1 dampens significantly enough that truncation at two-body terms is sufficiently accurate for repacking in implicit solvent (Table 1). This damping manifests as smaller two-body and three-body contributions when GK is enabled (Table S2). In fact, the magnitude of three-body interactions is reduced to such an extent that they generally do not affect side-chain rotamer eliminations (whereas our prior crystal refinement work did not employ an implicit solvation model). Truncation at two-body energy terms results in a nearly 52× speed-up (Table S3) as compared to the original rotamer optimization protocol (35) without any rotamer changes compared to including three-body terms. In future work, we plan to additionally optimize the protonation states of all titratable residues, which will necessitate a fresh appraisal of the impact of three-body energies because of the formal charge of residues changing.

Table 1.

Adjustable Repacking Parameters Are Examined in the Context of Computational Expense and Structural Quality

Truncation of the Energy Expansion at Either Two-Body or Three-Body Terms
Expansion Truncation	Relative Energy	Time	Speed-Up	–
Two-body∗	0.0	847	51.7×	–
Three-body	0.0	43,850	1.0×	–
Based on Truncation at Two-Body terms, Residue Distance Cutoffs from 1 to 6 Å Are Evaluated
Residue Cutoff (Å)	Relative Energy	Time	Speed-op	Overall
1	32.6	137	5.9×	320.0×
2∗	0.2	304	2.7×	144.2×
3	0.0	420	1.9×	104.4×
6	0.0	813	1.0×	53.9×
Based on Truncation at Two-Body Energy Terms and a 2 Å Residue Cutoff, Pruning Thresholds Are Evaluated
Pruning Threshold	Relative Energy	Time	Speed-Up	Overall
5	0.2	43	7.1×	1019.8×
15	0.2	113	2.7×	388.1×
25∗	0.2	142	2.1×	308.8×
No pruning	0.0	304	1.0×	144.2×
Based on Truncation at Two-Body Energy Terms, a 2 Å Residue Cutoff, and 25 kcal/mol Pruning Threshold, Cube Edge Lengths from 10 to 30 Å Are Evaluated for Cube Optimization
Cube Size (Å)	Relative Energy	Time	Speed-Up	Overall
10∗	0.2	40	3.6×	1096.3×
20	0.9	94	1.5×	466.5×
30	0.2	142	1.0×	308.8×

All tests used residues 27–125 of isoform 1 of the COCH protein. All relative potential energies (in kcal/mol) are compared to the global rotamer minimum of the COCH protein as calculated when using no approximations. Times are wall clock times in seconds using a node with four GPUs. The individual and overall speed-ups for each approximation are given. Criteria for evaluating residue distance cutoffs are described in the main text.

^∗The recommended choice for use with AMOEBA and the GK implicit solvent for each adjustable parameter.

The second approximation applies a distance-based cutoff between residues, which results in the interaction energy of two or more side chains being set to 0 if the minimal atomic distance between rotamer permutations is above a defined cutoff. The minimal distance d_min between two residues i and j is calculated using the expression

$$d_{min}\left(i,j\right)=\underset{\left\{\alpha =\mathrm{1..}{n}_i,\beta =\mathrm{1..}{n}_j\right\}}{\min }\left[dist\left(r_i^{\alpha },r_j^{\beta }\right)\right],$$ (7)

where the min operation is over the set of all rotamer permutations (i.e., residues i and j have n_i and n_j rotamers, respectively, to give n_i × n_j permutations), and the distance function (dist) returns the minimal pairwise atomic distance given rotamer conformations $r_i^{\alpha }$and $r_j^{\beta }$. We tested a range of cutoffs and found that 2 Å, when combined with truncation at two-body energies, provides a 144.2× speed-up compared to the original protocol while only increasing the energy relative to the global minimum by 0.2 kcal/mol (i.e., two solvent-exposed side chains had different conformations) (Table 1). Although 2 Å appears to be an overly aggressive cutoff at first glance, evidence from our data set of protein models (Table S4) shows structures still closely approach the global rotamer minimum. We emphasize that AMOEBA/GK force-field energetics are still evaluated with a typical 12 Å pairwise atomic cutoff, whereas the 2 Å residue cutoff is applied only in the context of using Eq. 7 to define interacting residues of the many-body energy expansion (see Figs. S1 and S2 for examples of applying Eq. 7).

The third approximation prunes rotamers and/or rotamer pairs if their conformation is higher than the lowest energy alternative plus a threshold

$$E_{self}\left(r_i^{\alpha }\right)>E_{self}\left(r_i^{\beta }\right)+threshold.$$ (8)

A pruning threshold of 25 kcal/mol results in further speed-up without compromising the quality of output structures (Table 1). Although pruning inequalities are not rigorous, unlike the mathematically proven Goldstein eliminations (see Materials and Methods), they obviate calculating many pair energies to yield over a 3× speed-up. Pruning did not result in any additional changes to rotamer conformations as compared to the global minimum found when using a two-body expansion and cutoff of 2 Å.

The final approximation uses a series of cube-shaped domains defined by imposing a three-dimensional grid over the protein, followed by sequential optimization of each cube of the grid. This approximation is especially useful for large protein domains that have an intractable number of energetically closely spaced permutations even after application of elimination criteria. By varying cube size and cube overlap, we determined that a cube edge length of 10 Å with no overlap optimized performance without degrading quality (Table 1). Cube optimization results in no additional change in energy relative to the global minimum found when using a two-body expansion and residue cutoff of 2 Å (note that a 30 Å cube contains the whole COCH domain and is a global optimization). Combining all four optimal approximations results in a total speed-up of ∼3 orders of magnitude.

We next implemented a parallelization approach that combines PJ with GPU acceleration. As the number of nodes is increased, our PJ message-passing parallelization algorithm achieved a near-linear speed-up (Tables 2 and S5). Offloading energy evaluations to OpenMM on a single node equipped with a GPU (two Intel Xeon E5-2680v4 CPUs (Intel, Santa Clara, CA) and one NVIDIA GTX 1080 TI GPU [Nvidia]) resulted in a 11.5-fold speed-up compared to using the same node with no GPU (i.e., a single GPU was 11.5× faster than parallelization over all 28 Intel CPU cores) on the COCH protein domain. Testing parallelization on a larger protein domain such as ACTG1 residues 6–375 demonstrated greater speed-ups relative to the smaller COCH domain (e.g., a 189.3× speed-up for ACTG1 using 16 GPUs, compared to 128.0× for COCH). Our original CPU parallelized Java implementation of the algorithm with no approximations (COCH protein domain run on two Intel Xeon E5-2680v4 CPUs (Intel), three-body expansion, 6 Å cutoff, and no pruning) required calculation of over 6 million energy terms and consumed 16.5 compute days on a node. By combining algorithm approximations, parallelization across four processes on one node (i.e., PJ message passing) and GPU acceleration (1 GPU per process, four GPUs total), our algorithm executes the 20,232 AMOEBA/GK energy terms in only 142 s.

Table 2.

Energy Evaluation Timings for Global Side-Chain Optimization of ACTG1 Residues 6–375 and COCH Residues 27–125 Using a Varying Number of GPUs

Number of Nodes	Number of GPUs	Time for Energies (sec)	Speed-Up (Relative to Using All CPU Cores)
		ACTG1	COCH	ACTG1	COCH
1	0 (CPUs only)	33,126	5505	1.0×	1.0×
1	1	2576	479	12.9×	11.5×
1	2	1277	251	25.9×	21.9×
1	4	656	142	50.5×	38.8×
2	8	336	76	98.6×	72.4×
4	16	175	43	189.3×	128.0×

Each node contains two Intel Xeon E5-2680v4 CPUs and four NVIDIA GTX 1080 TI GPUs.

Comparison of Amber99sb/GB and AMOEBA/GK protein repacking

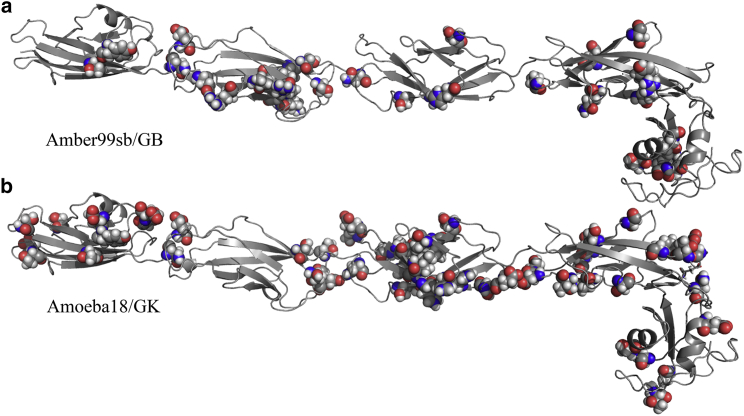
In ongoing work, we are performing AMOEBA free-energy simulations of DVD variants to provide insights into their pathogenic mechanisms. To illustrate the impact of optimizing structures using AMOEBA/GK compared to Amber99sb/generalized born (GB) before MD simulations, we optimized a model of CDH23 containing residues 887–1408 in both the Amber99sb/GB and AMOEBA/GK force fields. We chose to analyze CDH23 887–1408 because of its prevalence in hearing loss; CDH23 has more than 2000 missense variants in the DVD. Optimizing the CDH23 model with Amber99sb/GB resulted in 31 side chains changing from their original conformation, whereas optimizing with AMOEBA/GK resulted in 54 rotamer changes (Fig. 3). The extensive discrepancies between CDH23 conformations that result from repacking under AMOEBA/GK and Amber99sb/GB are consistent with our extensive prior structural refinement comparisons (28, 29, 30, 31, 32, 33, 34, 35). Thus, because our focus is on using AMOEBA for downstream free-energy simulations, further Amber99sb/GB repacking was not justified.

Figure 3.

CDH23 residues 887–1408 optimized using (a) Amber99sb/GB and (b) AMOEBA/GK. Side chains with changes in conformation relative to the original homology model are shown as space-filling spheres. When optimized with the fixed-charge Amber99sb/GB force field, 31 side-chain rotamers changed conformation, whereas repacking with AMOEBA/GK resulted in 54 side-chain rotamers changing. To see this figure in color, go online.

The OtoProtein Structure Database

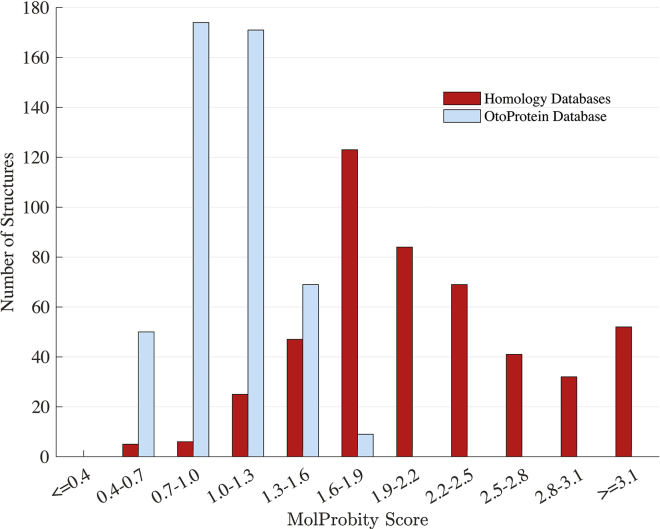
We applied our accelerated repacking algorithm to a set of 473 deafness-associated protein models. For both starting homology models and refined structures, quality was assessed using the heuristic MolProbity algorithm, which examines steric clashes, poor side-chain rotamers, and amino acid backbone favorability (e.g., ϕ/ψ dihedral angle combinations). The MolProbity score is calibrated to predict the quality of x-ray diffraction data that is expected to have produced the assessed structure (i.e., a MolProbity score of 1.5 corresponds to an expected x-ray resolution of 1.5 Å, where lower values indicate higher quality). On average, we reduced steric clashes per 1000 atoms from 25.1 to 0.03, decreased Ramachandran outliers from 2.03 to 0.94%, and decreased the percentage of poor side-chain rotamers from 2.3 to 1.6% (Table 3). Overall, the repacking protocol improved the mean MolProbity score from 2.16 to 1.04, demonstrating that our structures are consistent with protein structural models near-atomic resolution (Fig. 4). The average AMOEBA force-field energy for the data set when locally optimized to RMS gradient convergence criteria of 0.8 kcal/mol/Å was −15,342 kcal/mol. After global side-chain optimization, the average AMOEBA energy for the data set was reduced to −16,287 kcal/mol, a reduction of 945 kcal/mol from the structures that were minimized to an RMS gradient criterion of 0.8 kcal/mol/Å without rotamer optimization. Although local minimization without rotamer optimization dramatically reduces atomic clashes, the number of poor rotamers increased from 2.3 to 2.9% and motivates the need for side-chain repacking. The overall repacking procedure required just 71 GPU days for all 473 OtoProtein structures. The complete list of statistics for each model is available in Table S6. Based on these results, GPU-accelerated repacking with the polarizable AMOEBA force field could potentially be used to improve the quality of large protein structure databases with only a modest investment in hardware.

Table 3.

Average Refinement Statistics for the OtoProtein Structure Database

Database	Clash Score	Poor Rotamers	Ramachandran Favored	Ramachandran Outliers	MolProbity Score
Homology	25.09	2.33%	91.95%	2.03	2.16
Minimization	2.75	2.92%	91.85%	1.87	1.66
OtoProtein	0.03	1.60%	93.48%	0.94	1.04

The data set contains 473 structures.

Figure 4.

Histogram of MolProbity scores for the OtoProtein Structure Database before and after optimization. Before optimization (red), the 473 structures have an average MolProbity score of 2.16, whereas after optimization (blue), the data set has an average MolProbity score of 1.04 (i.e., approaching the quality expected of atomic resolution x-ray structures). To see this figure in color, go online.

To assess the impact of our optimization algorithm as a function of protein features, we compared both final MolProbity score and MolProbity improvement (i.e., the change in MolProbity score due to refinement) with sequence identity to the homology template using linear regression (Figs. S3 and S4). With R² values of only 0.0035 and 0.0256, respectively, neither the MolProbity score nor MolProbity improvement were strongly correlated with sequence identity to the homology model. Similarly, neither MolProbity score nor MolProbity improvement were strongly correlated with the number of residues in the protein structure based on R² values of only 0.0119 and 0.0449, respectively (Figs. S5 and S6). We conclude that the favorable improvements afforded by the repacking approach described here are largely independent of both sequence identity to the homology model and protein size.

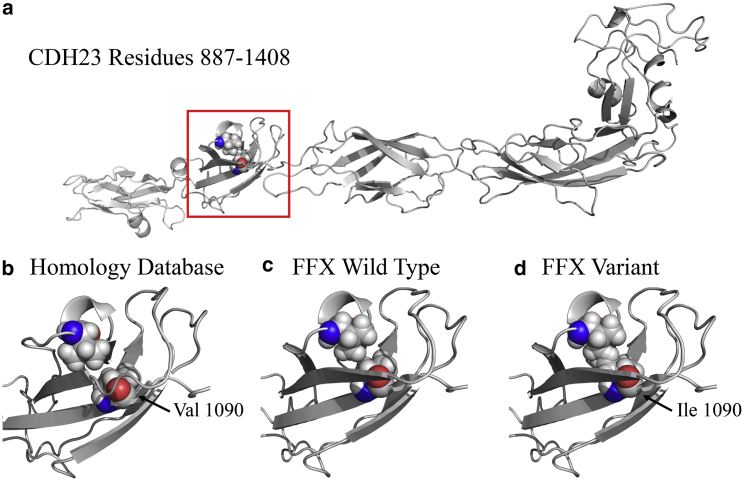
We demonstrate the impact of repacking protein models on variant interpretation through modeling of a pathogenic variant that causes Usher syndrome. Buried in a domain of the CDH23 structure shown in Fig. 3 is valine residue 1090, which causes Usher syndrome when mutated to isoleucine (Fig. 5 a). In the unrefined model of CDH23, a neighboring valine (position 1039) is oriented away from residue 1090 (Fig. 5 b). Optimization using the repacking approach presented here results in the β sheets surrounding Val1090 lengthening and the Val1039 rotamer closely approaching Val1090 (Fig. 5 c). When isoleucine is introduced at position 1090 in the unoptimized structure, Ile1090 and Val1039 do not clash, and accommodation of the variant appears possible. However, when Ile1090 is introduced in the AMOEBA/GK repacked structure, Val1039 and Ile1090 clash, indicating that the variant (known to be pathogenic) is consistent with destabilization of the CDH23 fold. Despite the qualitative nature of this analysis, it illustrates that without repacking, downstream variant free-energy simulations based on homology models will generally need to reach longer timescales to accommodate structural relaxations.

Figure 5.

CDH23 structure showing the pathogenic DVD variant Val 1090 Ile. (a) The wild-type CDH23 model for residues 887–1408 is shown, with Val 1090 highlighted by a red box. (b) Shown in spacefill format are Val 1039 and Val 1090. (c) After AMOEBA/GK repacking, the conformation of Val 1039 changes relative to the variant. (d) A clash is present between Val 1039 and the Ile 1090 variant, which is consistent with altered folding stability and classification as disease causing. This example illustrates that without repacking, downstream free-energy simulation timescales must (in general) increase to allow relaxation of nonoptimal side-chain conformations. To see this figure in color, go online.

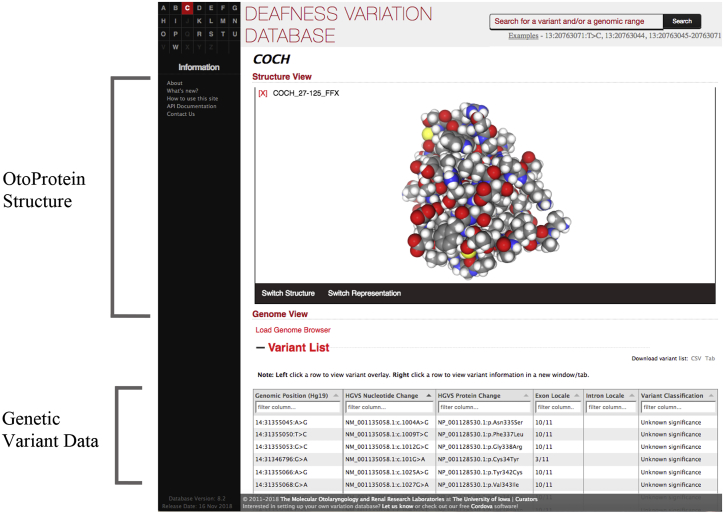
The OtoProtein Structure Database has been incorporated into the DVD to provide public availability of the models in combination with the exhaustive DVD genetic information. The combination of OtoProtein structural information with existing DVD data (e.g., minor allele frequency, pathogenicity assessment, etc.) provides a powerful platform for the auditory research community. For example, it is now possible to visualize clustering of pathogenic variations in specific domains of a protein and to examine structural features that correlate with pathogenicity (Fig. 6). Additionally, more than 60,000 variant-specific structures are available publicly (https://github.com/mrkeeney/deafness-variant-structures) and are currently being incorporated into the DVD.

Figure 6.

Incorporation of OtoProtein structures into the DVD. All models developed with the GPU-accelerated AMOEBA/GK protein repacking algorithm are publicly available in the DVD, where they can be viewed in combination with genomic and variant data. To see this figure in color, go online.

Discussion

Structural coverage of the human proteome has increased rapidly since the early 1990s, with ∼40% of the human proteome now having comparative models based on templates with a sequence identity of at least 30% (9). Here, we applied a GPU-accelerated polarizable protein repacking algorithm to the deafness-associated proteome defined by homology models of any sequence identity (average sequence identity of the data set is 41.7%). We found that 38.8% of the deafness-associated proteome could be modeled structurally, comparable to structural coverage of the entire human proteome. The 473 structural models we collected and optimized span 145 deafness-associated genes. These structures had an initial average MolProbity score of 2.16, but after repacking, the average score improved to approximately atomic resolution at 1.04. These calculations required just 71 GPU days. In addition to covering nearly 40% of OtoSCOPE with atomic resolution structural models, our OtoProtein database provides structural coverage for 22,809 of the 61,971 missense variations in the DVD (16,203 are VUSs, 1931 are LP/pathogenic, and 4675 are B/LB). These models are publicly available in the DVD through the NGL protein viewer (48). When integrated with information on patient missense variations available through the DVD, the OtoProtein database represents a unique tool for understanding deafness genetics from a structural perspective. Building on the OtoProtein structural platform, we have created more than 60,000 models of DVD missense variations, which are publicly available. Future work will simulate these missense variations to quantify thermodynamic free-energy differences and thereby provide insight into how they disrupt protein folding and/or alter protein-protein interactions.

The GPU-accelerated protein repacking algorithm is freely available to the research community through the FFX program, which may be useful to refine other structural data sets outside of the deafness domain. The algorithm is designed for use with advanced polarizable force fields and features an energy expansion up to three-body interactions. Computational speed is achieved using an architecture based on parallelization across an arbitrary number of compute nodes and GPUs and, together with algorithm optimizations, provides multiple orders of magnitude speed-up without compromising structural quality. Although polarizable repacking algorithms were previously not efficient enough to apply to large-scale data sets, this work opens the door to their application to all protein structures in the human proteome. For example, the Swiss Model Repository (SMR) lists 45,083 homology models with an average residue length of 232 amino acids (9). Structures of this size (i.e., ∼230 residues) require only ∼260 s to repack using our algorithm on a node with four GPUs (e.g., repacking our DSSP 88–318 model of 230 residues took 262 s of wall clock time). Based on the average model size in the SMR, we estimate that repacking all SMR human proteins would require only ∼140 days on a node equipped with four GPUs (i.e., ∼2 weeks on our compute cluster, which has 10 such nodes).

A limitation of this repacking algorithm is its reliance on existing homology models to serve as initial coordinates. Although we have demonstrated this improves the quality of existing structural models, it does not provide coverage of proteins through ab initio or de novo techniques. This limitation is the subject of ongoing work based on GPU-accelerated biased sampling methods, which we are using to expand structural coverage of the OtoSCOPE proteome. Despite this limitation, the OtoProtein structural information is already being used to gain insight into the protein phenotype of missense variants associated with deafness.

Author Contributions

Conceived the theory, M.R.T., J.M.L., and M.J.S.; performed the experiments, M.R.T., J.M.L., G.Q., C.E.O’C., and W.T.A.T.; analyzed the data, M.R.T., J.M.L., R.J.H.S., and M.J.S.; contributed code/tools/structures, M.R.T., J.M.L., G.Q., C.E.O’C., R.J.M., H.V.B., W.T.A.T., T.A.B., T.L.C., and M.J.S.; wrote the manuscript, M.R.T., J.M.L., W.T.A.T., T.A.B., T.L.C., R.J.H.S., and M.J.S.

Editor: Alan Grossfield.