Cancer classification and pathway discovery using nonnegative matrix factorization

Abstract

Objectives

Extracting genetic information from a full range of sequencing data is important for understanding disease. We propose a novel method to effectively explore the landscape of genetic mutations and aggregate them to predict cancer type.

Design

We applied non-smooth non-negative matrix factorization (nsNMF) and support vector machine (SVM) to utilize the full range of sequencing data, aiming to better aggregate genetic mutations and improve their power to predict disease type. More specifically, we introduce a novel classifier to distinguish cancer types using somatic mutations obtained from whole-exome sequencing data. Mutations were identified from multiple cancers and scored using SIFT, PP2, and CADD, and collapsed at the individual gene level. nsNMF was then applied to reduce dimensionality and obtain coefficient and basis matrices. A feature matrix was derived from the obtained matrices to train a classifier for cancer type classification with the SVM model.

Results

We have demonstrated that the classifier was able to distinguish four cancer types with reasonable accuracy. In five-fold cross-validations using mutation counts as features, the average prediction accuracy was 80% (SEM=0.1%), significantly outperforming baselines and outperforming models using mutation scores as features.

Conclusion

Using the factor matrices derived from the nsNMF, we identified multiple genes and pathways that are significantly associated with each cancer type. This study presents a generic and complete pipeline to study the associations between somatic mutations and cancers. The proposed method can be adapted to other studies for disease status classification and pathway discovery.

Graphical abstract

1. BACKGROUND AND SIGNIFICANCE

Personalized medicine is becoming increasingly popular in cancer where genetic profiles of tumors can be used to guide clinical decisions such as treatment options and preventive measures [1]. The development of massively parallel, high throughput DNA sequencing technology has enabled the cataloging of somatic mutations in cancer, making genomic data increasingly accessible. Understanding the association between genetics and disease is important for understanding the underlying pathophysiology. In cancer, many molecular and genomic studies have identified somatic mutations within genes associated with cancer initiation, progression, and treatment responses [2–4].

The majority of sequencing studies have focused on the identification of individual driver genes [5]. However, driver mutations are often highly heterogeneous between cancer genomes, even within the same type of cancer [6]. Furthermore, studies have observed cancer to be highly complex, often resulting from multiple interacting mutations and related pathways [7, 8]. While many methods attempt to address the complex mutational heterogeneity in cancer, it still remains a challenge due to limited study-power and lack of complete knowledge regarding gene and pathway interaction [9–13]. Despite the fact that mutations in many genes have been identified in cancer, it is not yet understood how these genes cumulatively interact in the development and progression of cancer. It has been a challenge to study these mutations and their interactions together due to large-scale complexity.

It is important to consider methods that can encompass the full scope of genes. When genes and mutations are studied together, novel biological interactions and pathways can be identified to further provide biological and clinical insights. Many groups have previously utilized feature selection methods for removing irrelevant and redundant information to deal with complexity problems. Vector Quantization (VQ) [14] and Principle Component Analysis (PCA) [15] have been widely used for feature selection. More recently, attention has been drawn to non-negative matrix factorization (NMF). In a face recognition study, Lee et al. suggested NMF could outperform VQ and PCA for feature recognition [16]. In addition, the non-negative constraint of NMF is important because non-negativity is more realistic, easier to interpret, and prevalent in real world applications. In particular, NMF has been applied to disease subtype studies using gene expression data [17, 18] and sequencing data [19–21]. With the aim to uncover the genetic complexity behind cancer development, and to identify mutations that directly affect processes involved with oncogenesis, we propose a framework utilizing NMF.

In our proposed framework, NMF was applied to discover latent factors from somatic mutations. The discovered latent factors were used to train an SVM model for cancer type classification. The NMFSVM combination was rigorously evaluated and compared to different baselines. Association studies were performed between the factor matrices derived from NMF and cancer type using penalized logistical regressions. Major factors associated with each cancer type were investigated, and significant genes were identified for investigation in pathway discovery analysis. In addition to this proposed framework serving as a disease type classifier, it can also be utilized to elucidate novel biological interactions and pathways for disease. The details of the study are reported below.

2. MATERIAL AND METHODS

2.1. MUTATION PROFILES

As a pilot study, four prevalent cancers were retrieved from The Cancer Genome Atlas (TCGA), including Glioblastoma Multiforme (GBM), Breast invasive carcinoma (BRCA), Lung Squamous Cell Carcinoma (LUSC), and Prostate Adenocarcinoma (PRAD). Somatic mutations were identified from 2,431 tumors (Table 1). SnpEFF [22] and ANNOVAR [23] were used to annotate 245,88 missense mutations and 57,319 nonsense mutations in the study cohort. Each mutation was functionally scored for being potentially deleterious using SIFT [25], PolyPhen2 (PP2) [26], and CADD [24] scores. In genes containing multiple mutations, SIFT, PP2, and CADD scores, as well as mutational frequency were collapsed and studied as a single variable separately, known as gene burden [24]. Predicted pathogenicity scores (SIFT, PP2, and CADD) were calculated for each mutation within a gene and collapsed as a sum to calculate the gene burden for a specific gene. Namely, gene burden represents a gene’s total predictive pathogenicity based on mutation data. Thus, gene burden was used to represent the damage level of a gene from multiple perspectives. A workflow is illustrated to show the methods used in this study (Figure 1).

Table 1:

The number of samples in each cancer type and the corresponding number of somatic mutations. Mutations annotated with moderate effects are missense mutations or in-frame shift mutations. Mutations annotated as high effects are nonsense mutations. Numbers in parenthesis are standard deviations.

	Cancer	Sample Size	Somatic Moderate	Somatic High
BRCA	Breast Invasive Carcinoma	1,044	68 (11)	20 (5)
LUSC	Lung Squamous Cell Carcinoma	497	214 (15)	44 (3)
PRAD	Prostate Adenocarcinoma	497	34 (19)	8 (3)
GBM	Glioblastoma Multiforme	393	133 (55)	27 (9)

Figure 1:

Workflow of the study. Orange boxes are the data or processes; green boxes are the tools used; blue boxes are the results of the study.

2.2. GENE PRE-SELECTION

Prior to modeling, we evaluated whether a subset of representative genes could be derived without information lost to achieve a more balanced sample feature ratio and reduce noise. The collapsed score in each gene was used as an input variable while the cancer type was used as the output variable. Multinomial logistic regression was fit, and a P-value that yields the null hypothesis of corresponding coefficient being zero was used as an indicator for the pre-selection. The selection criterion for this initial screening was set with a P-value less than or equal to a cutoff. In order to reduce noise and to prevent model overfitting, we tested the model using multiple cutoff thresholds of 0.05, 0.1, 0.2, 0.5, and 1. We compared the results derived from each threshold and selected the most reasonable cutoff based on prediction accuracy and number of features.

2.3. APPLYING NMF TO DISCOVER LATENT FACTORS OF SOMANTIC MUTATIONS

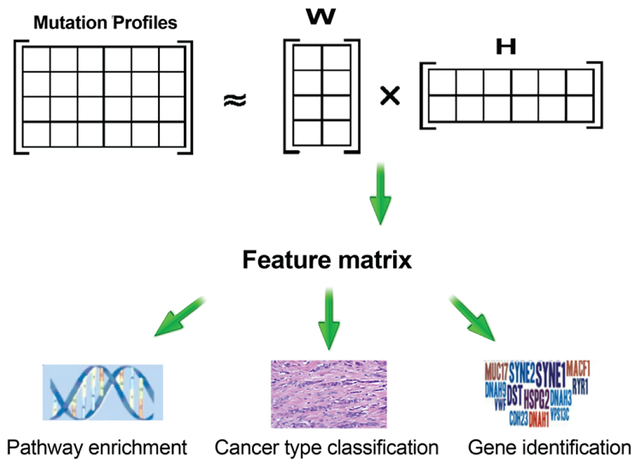
Genes passing the selection threshold were used as inputs for the NMF study. Assume there were N subjects and M selected genes. The data were represented by a matrix A_Score of size. M × N The columns of A_Score represents the collapsed score of the M genes in the N subjects. The matrix A_Score was then decomposed using NMF. The purpose of this study was to find a set of intrinsic patterns that are likely to distinguish cancer types. To perform NMF, the matrix A_Score was factored into two low-rank matrices W and H. Mathematically, A_Score is approximated by A_Score ≈ WH.Matrix A_Score is the approximate linear combinations of the column vectors in matrix W and the coefficients supplied by columns in matrix H. Matrix W has size M × K, with each of the K columns representing a group of weighted genes and w_ij corresponding to the weight of gene i in group j. K denotes the number of factors and is a given input. Matrix H has size K × N, where each of the N columns denotes the feature coefficients for each subject. Entry h_ij is the value of feature i in sample j. The decomposition is achieved by iteratively updating the matrix W and H to minimize a divergence objective [16, 25]. Specifically, for the purpose of sparseness, we used non-smooth Nonnegative Matrix Factorization (nsNMF) [26]. More specifically, the application of nsNMF led to a high degree of sparseness by adding a positive symmetric matrix in the objective function. We achieved modest to high degree of sparseness in both the W (average 51% sparseness) and H matrix (average 85% sparseness).. Each analysis was repeated ten times to address the local optima problem.

2.3. CLASSIFIER TRAINING

Matrix H has size K × N, where each of the N columns denotes the feature coefficients for the corresponding subject. To retain the information from both W and H matrices, a new matrix F was generated by multiplying the transposed matrix A_Score with matrix W. Specifically, an entry in matrix F was computed as $f_{ij}={\sum }_{x=1}^m{A}_{ix}^{\text{T}}*W_{xj}.$ Matrix F has size N × K, with each of the K columns representing the coefficient for each subject. Since A_Score ≈WH, matrix F can be approximated by a kernel matrix (W ×H)^T × W. Subsequently, columns in matrix F were utilized as features to train the classifier. Support vector machine (SVM) was used for the training, where each column corresponds to one predictor in the model. The Radial Basis Function (RBF) kernel was used, with parameters of gamma and C set to default. This trained SVM model was a cancer type classifier.

2.4. FACTOR NUMBER SELECTION

Note that before factorization, the number of factors K need to be pre-defined. Typically, the number of factors K is chosen so that (N + M) ×K < N × M [16]. Selection of K is critical because it determines the number of patterns to be found. Numerous studies have presented different methods for factor number selection: The factor number K can be determined based on different metrics composing of a cophenetic correlation coefficient [18, 26], variation of sum of squares [27], or maximum information reservation [28]. In our study, the most important feature for the classifier is the ability to identify intrinsic patterns that best distinguish cancer types accurately. To achieve this, a numerical screening test was conducted to screen through the different number of factors for best prediction performance. The screened factor numbers ranged from 2 to 15. Multi-class prediction accuracy in each classification was obtained as a performance measurement. Five-fold cross-validation was conducted using multiple different factor numbers. The factor number with the best performance in the cross-validation was chosen. Each experiment was replicated ten times with different initial seeds. Prediction accuracy, precision, recall, and f-measure were used as performance evaluation matrices.

2.5. EVALUATION

To set up baselines for comparison, the mutation frequency and the collapsed scores were used as independent predictors to fit SVM models and penalized logistic regression models were used to predict cancer types. All somatic mutations were also used as predictive variables for cancer classification using the SVM and penalized logistical regression model. A number of models have been developed for cancer classification utilizing somatic mutation profiles, including variations of CADD scores [29], logistical regression on L1-regularised terms [30], and SVM-RFE [30]. In this study, we compared the performances between our proposed model and these reported methods for cancer classification. All studies were replicated ten times with different initial seeds and significance tests were performed for evaluations. P-values were obtained for the evaluations.

2.6. PATHWAY STUDY

The feature matrix F was obtained by multiplying a transposed matrix A_Score with matrix W, with size N × K, where each K columns represents the coefficient for each subject. To determine the association level of each factor with each cancer type, elastic net regression models were fitted using the cancer type as the output variable and each of the columns in the F matrix as input variables. To differentially discover pathways for a cancer type, subjects with the cancer type of interest were treated as cases and the remaining subjects as controls. The regulation parameter λ was selected using ten-fold cross-validation. Association effects for each feature were represented by the beta value and the vector was denoted as $\widehat{\beta }$. We selected the factor corresponding to the largest $\widehat{\beta }$, and denote the factor as a cancer-relevant factor. After selecting the factor, we utilized the matrix W to rank genes. The weights in the matrix W are composed of genes with different weights. We assume genes with the largest coefficients cumulatively and linearly interact with each other and are associated with cancer development. For each cancer, we repeated the experiment and selected the top genes in each factor for enrichment analysis and presented the top significant pathways (adjusted P-value < .05). To ensure stable results, we analyzed the top 100, 200, 300, 400, 500, and 600 genes for pathway analysis and determined 300 genes started yielding stable results as illustrated with BRCA (Table S2).

3. EXPERIMENT RESULTS

After collapsing mutations’ numbers and scores in each gene, a matrix A_Score was formed with the 2,431 subjects as rows. Entry A_ij denotes the j_th gene’s collapsed score for the i_th subject. For gene pre-selection, we screened the p_value of 0.05, 0.1, 0.2, 0.5, and 1 as cutoffs. For each cutoff, prediction accuracy was used as the performance measurement. The experiment was repeated using the Number (collapsed number of mutations), SIFT (collapsed sift scores), PP2 (collapsed PP2 score), and CADD (collapsed CADD scores) matrices. Factor numbers ranged from 2 to 15 (Figure 2). The Number matrix was found to result in better performance than the other matrices. Using the Number matrix, the performance derived from the cutoff of 1 is significantly better than the cutoff of 0.05 (P-value=0.001), 0.1 (P-value=0.01), and 0.2 (P-value=0.04), but not significantly different from the cutoff of 0.5 (P-value=0.61). Balancing the number of features to be included for computation and accuracy, we selected the cutoff of 0.5 for gene pre-selection. Following gene pre-selection, 11,949, 12,753, 17,702, and 11,734 genes were retained for subsequent analysis for the Number, SIFT, PP2, and CADD matrix, respectively.

Figure 2:

The accuracy of cancer type classification using different P-value cutoffs. (A) Sum of the count of mutations (B) Sum of the SIFT scores (C) Sum of the PP2 scores (D) Sum of the CADD scores.

We then compared these four matrices: Number, SIFT, PP2, and CADD. The number of factors K ranged from 2 to 15, a range within the constraint of the rule (N+M)K<NM. For each factor number K, nsNMF was applied to the matrices, and a corresponding classifier was trained. The performances derived from the Number matrix outperformed the other matrices significantly (p<0.01 for all comparisons) (Figure 3). The precision, recall, and f-measures were derived and similar patterns and trends were observed. Based on performance, the matrix Number was used for subsequent analyses. Using Number matrix, the maximum accuracy was 80.0% (Standard Error of the Mean SEM=0.1%) when the factor number equaled 12 (Figure 3). The accuracy was found to become stable when factor number was larger than 12. To prevent potential overfitting, we chose a factor of 12 for our analysis.

Figure 3:

The accuracy of cancer type predictions using different numbers of factors from the matrices of Number (blue), SIFT (red), PP2 (green), and CADD (purple) scores.

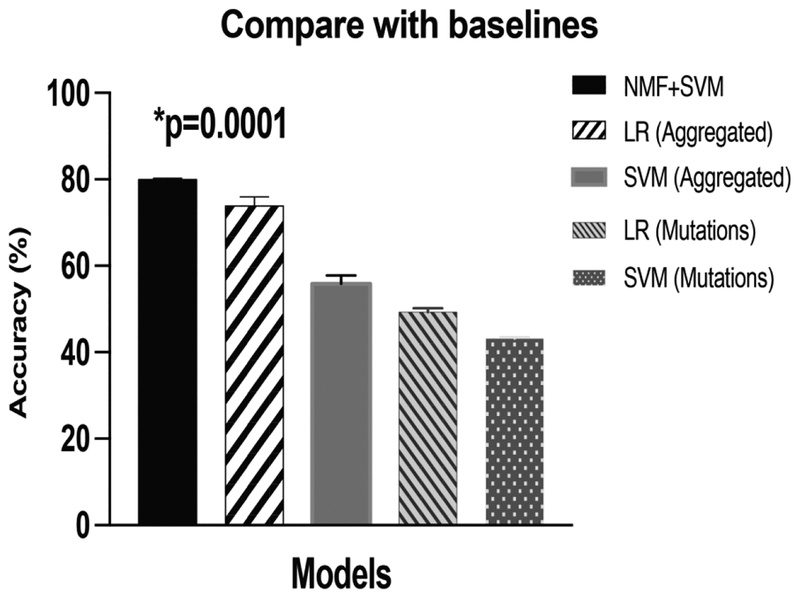
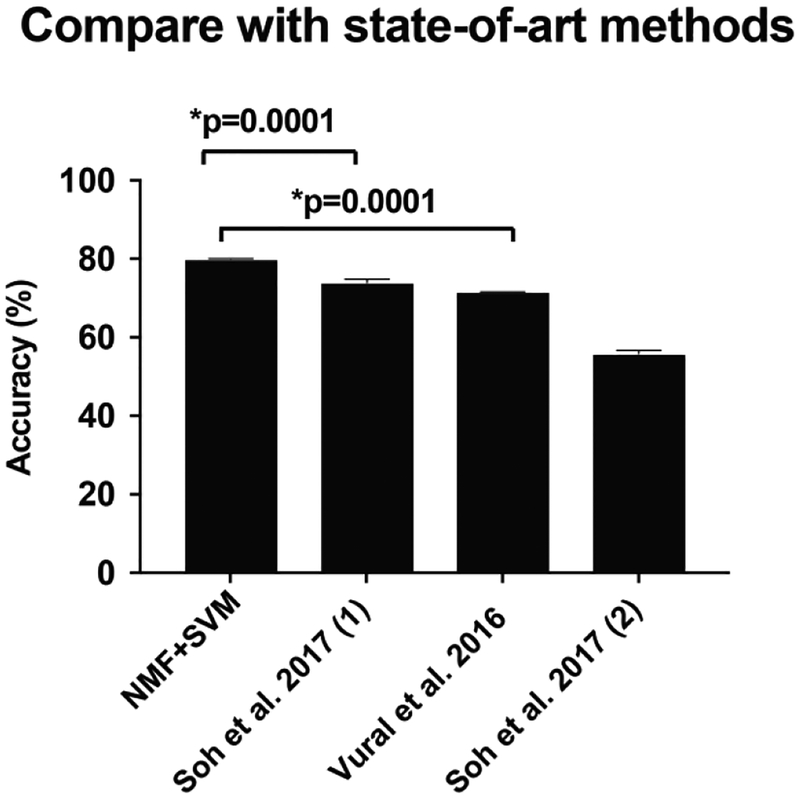
The performance of our proposed model (80.0%, SEM=0.1%) significantly outperformed the other four baselines (Figure 4). The P-value using the Student’s t-test was 0.0001 comparing our proposed model to the second-ranked model (73.9% (SEM=0.8%), which applies penalized logistical regression with the aggregated Number matrix. In the baselines, aggregating the mutations in a gene has improved the performance significantly as well (p<0.01 in both comparisons). A comparison of our proposed model with previously applied methods for cancer classification was conducted. We found that our method achieved significantly improved performance (Figure 5) compared to methods that utilize variations of CADD scores (71.6%) [29], logistical regression on L1-regularised term (74.0%) [31], and SVM-RFE (55.9%) [31].

Figure 4:

Comparison of our proposed model (nsNMF+SVM) with baselines. LR is penalized logistical regression. SVM is support vector machine. Aggregated are the matrices to sum mutations together in the same gene. Mutations are the model that utilizes every single mutation as an input variable.

Figure 5:

Comparison of our proposed model (nsNMF+SVM) with the state-of-the-art methods.

Using regularized logistic regression, we assessed each gene’s association effect with each cancer type. The association score was defined as the sum of feature weights multiplied by the coefficient of each gene. A high score indicates the significant role of a mutated gene in the disease. The genes for each cancer type were identified and sorted by association score (Table S1). The top 300 genes associated with each cancer type were derived and analyzed for pathway enrichment. Interestingly, distinct biological processes were found to be significantly associated (p <0.05) with each type of cancer. Microtubule processes, axon guidance, cell morphogenesis, and synaptic transmission were found to be associated with BRCA, GBM, PRAD, and LUSC, respectively (Table 2). Additional pathways associated with each cancer type can be found in Table S2. Many of these pathways are known to be associated with their corresponding cancer type. For instance, a majority of breast cancer drugs involve targeting microtubules [32]. In glioblastoma, axon guidance is known to play a role in glioma progression [33]. To confirm the robustness of our findings, we performed and evaluated pathway enrichment and discovery using multiple methods [34–38]. We also discovered axon guidance from the Reactome pathway database [37] and synaptic transmission in the KEGG pathway database [38]. Together, these results corrobarated the relevant pathway discovered by our method.

Table 2:

Biological processes most associated with each cancer type.

GO Term	Cancer
Microtubule-based process	BRCA
Axon guidance	GBM
Morphogenesis of a polarized epithelium	PRAD
Chemical synaptic transmission	LUSC

4. DISCUSSION

We have proposed a novel method to fully use and understand somatic mutations to classify the cancer type and derive relevant genes and pathways. In this study, we applied nsNMF and SVM to train a classifier to distinguish and classify a tumor type as Glioblastoma Multiforme (GBM), Breast Invasive Carcinoma (BRCA), Lung Squamous Cell Carcinoma (LUSC), and Prostate Adenocarcinoma (PRAD). Products of the basis matrix and coefficient matrix derived from nsNMF were both retained to construct the feature matrix. Subsequently, the constructed features were used as input variables to train the classifier. We compared functional scores using CADD, SIFT, and PP2, and counted mutation number and found that counted mutation number yielded the best performance (accuracy=80.0% with SEM=0.1%). Finally, regularized logistic regression was applied to study each gene’s association effect with cancer type. Using the associated features, we derived relevant genes and pathways for each cancer.

When training the classifier, we used an alternative method by multiplying the matrix A_Score with matrix to obtain the feature matrix F. Information from the basis component W was retained, providing information about weights in each gene group. This information was then used as features to train the classifier. Another benefit of this alternative method is the ease of us at the testing stage. With the trained W matrix, we only need to multiply the testing A_Score matrix in order to get the test feature matrix. In addition to improving cancer type classification, each gene’s association effect with the cancers was of interest and also studied. The p-value for gene pre-selection was to limit the number of features to be included. One of the challenges for genomics studies are the large number of genes accompanied by the small sample sizes, resulting in a wide and flat matrix, henceforth impact the performance of matrix decomposition. In this study, we utilized a p-value cutoff to pre-select genes but try to only introduce a minimum amount of influence on model performance. Therefore, we have tested multiple p-values and selected the cutoff of 0.5, in which we observed non-significant differences in model performances compared to the no-selection scenario. Genes that were filtered are those with only one or two mutations and only appeared in one or two subjects in the cohort. Removing these genes has a minimum amount of influence and has the potential to remove noises for model training. In our study, if we tune NMF+SVM (our model), we can get even better results. But our purpose is to focus on assessing improvements from NMF. In addition, with the default parameters for NMF + SVM, our model still outperformed the state-of-the-art methods that are parameter-tuned.

The development of high throughput sequencing technology has enabled the cataloging of large-scale mutation information. Somatic mutations are relatively stable and lead to the initiation and progression of many sporadic cancers. Hence in this study, we utilized mutations in protein-coding genes as input data. We acknowledge that non-protein-coding genes, including mutations in intronic areas [39, 40], long non-coding RNAs [41], mi-RNAs [42] are also important for cancer development. In future work, we will incorporate these multiple dimensions of genetics data to increase the model performance. Traditionally, mutations derived from sequence data were examined as a single variable using the regression models [30, 43]. Unfortunately, the large number of variables limit the power of such studies. To reduce the number of variables, studies have proposed to aggregate mutations at the gene level as an input in a regression model [24, 44, 45]. In other studies, mutations in a gene have also been proposed to be studied in a matrix as an input for a kernel test [46, 47]. In this study, we proposed using a framework which utilizes a regression model to pre-select deleterious genes, nsNMF to decompose the matrix, SVM to train a classifier, and then penalized regression to derive relevant genes. Following the careful tuning of parameters and models, we have proved that this is an effective model to classify cancers, derive relevant genes, and identify associated pathways.

5. CONCLUSION

To fully understand a disease, studying mutations using a full range of genes together is of critical importance. Complex traits are modified by multiple genes and multiple mutations together [48]. Traditionally, NMF has been applied to study gene expression [18, 28]. In this study, we proposed using somatic mutations for cancer classification. Furthermore, we proposed generating the feature matrix by integrating both the basis matrix W and the coefficient matrix H. Moreover, we developed a novel method to derive effect scores from the feature matrix. Using this method, we obtained the association score of each gene with a particular cancer type enabling relevant pathway discovery. The discovered effect scores have a high potential to help us better understand the genetic pathophysiology behind cancer.

In this study, we proposed a novel strategy to study the genetic landscape of multiple cancers. In the future, we will use tensor factorization to integrate known pathways to guide the grouping of mutational variants [49] and use external cohorts to validate the proposed model. Furthermore, this generic process only requires the input of somatic mutations and a disease type of interest, without much domain specific knowledge. This strategy has the potential to be easily adapted and applied to other diseases as well.

Highlights.

A novel method to effectively explore the landscape of genetic mutations nsNMF and SVM to utilize the full range of sequencing data

A generic pipeline to study the associations between somatic mutations and cancers Can be adapted to other studies for disease status classification and pathway discovery