Volumetric and shear processes in crystalline rock approaching faulting

Significance

The dynamics of brittle deformation prior to macroscopic instability is critical to faulting events. This study provides direct high-resolution information on this process obtained using X-ray microtomography and digital volume correlation analysis of evolving microfractures and deformation fields in laboratory fracturing experiments. Brittle failure results from the dynamic coupling between microfracture growth, opening, shear, coalescence, and closing. The evolving microfracture volume and size distributions increase as powers of the differential stress, as the differential stress approached the failure level. The results highlight the key roles that seismic and aseismic off-fault cracking play in the preparation process leading to large brittle shear rupture events.

Abstract

Understanding the approach to faulting in continental rocks is critical for identifying processes leading to fracturing in geomaterials and the preparation process of large earthquakes. In situ dynamic X-ray imaging and digital volume correlation analysis of a crystalline rock core, under a constant confining pressure of 25 MPa, are used to elucidate the initiation, growth, and coalescence of microfractures leading to macroscopic failure as the axial compressive stress is increased. Following an initial elastic deformation, microfractures develop in the solid, and with increasing differential stress, the damage pervades the rock volume. The creation of new microfractures is accompanied by propagation, opening, and closing of existing microfractures, leading to the emergence of damage indices that increase as powers of the differential stress when approaching failure. A strong spatial correlation is observed between microscale zones with large positive and negative volumetric strains, microscale zones with shears of opposite senses, and microscale zones with high volumetric and shear strains. These correlations are attributed to microfracture interactions mediated by the heterogeneous stress field. The rock fails macroscopically as the microfractures coalesce and form a geometrically complex 3D volume that spans the rock sample. At the onset of failure, more than 70% of the damage volume is connected in a large fracture cluster that evolves into a fault zone. In the context of crustal faulting dynamics, these results suggest that evolving rock damage around existing locked or future main faults influences the localization process that culminates in large brittle rupture events.

Understanding the route to failure in crystalline rocks is fundamental for developing improved quantitative frameworks for the behavior of faults, the evolution of permeability in the continental crust, and the fracturing of geomaterials. High-resolution earthquake catalogs show abundant microseismicity in the volumes surrounding major faults (1, 2). The interaction between seismicity along faults and in the surrounding rock volume is critical for understanding the spatiotemporal evolution of earthquakes in active areas (3, 4). Laboratory experiments demonstrate that microfracture generation produces macroscopic dilation of rocks before macroscopic shear failure occurs (5–7) and controls the transition from distributed damage to shear localization (8–12). After an initial damage phase of random microfracturing, large fractures and faults nucleate within an array of microfractures oriented more or less parallel to the direction of maximum principle stress. This array is inclined at about 30° relative to the direction of the maximum principle stress (10) and acts as a precursor of the fault formation. The fault and array grow in concert with new microfractures acting as the fault process zone. A model for faulting, based on failure of an array of beams, separated from each other by an array of fractures inclined at about 30° relative to the direction of the maximum principle stress, is presented in ref. 10, but it is not clear whether the array is formed by coalescence of multiple smaller arrays or by the growth of a single array. It is also not clear whether the faults that form within the array propagate from a single nucleation site or propagate from multiple nucleation sites and coalesce.

Determination of the spatial distribution of acoustic emissions in rocks indicates that microfractures initially nucleate and grow at apparently random locations (8, 9) rather than within the future fault zone. However, uncertainties in the locations of acoustic emission sources and inability to monitor aseismic strain release (i.e., failure processes that do not emit acoustic waves) have prevented a more complete quantification of the evolving inelastic strain before failure from these data. In other words, the strain localization processes leading to macroscopic rock failure remain unclear since the experimentalist cannot see how the fracture pattern evolves inside the progressively deformed sample.

Recent analysis of time-lapse 3D X-ray tomograms (13) demonstrated that the total volume of the microfractures, rate of damage growth, and size of the largest microfracture cluster all increase as powers of ${\mathrm{\Delta }}_D$, where ${\mathrm{\Delta }}_D=\left({\sigma }_D^f-{\sigma }_D\right)/{\sigma }_D^f$ is a normalized stress parameter that measures the difference between the differential stress at failure ${\sigma }_D^f$ and the evolving differential stress ${\sigma }_D={\sigma }_1-{\sigma }_3$, where ${\sigma }_1$ and ${\sigma }_3$ are the largest and smallest compressive principle stress values, respectively (a list of symbols is provided in SI Appendix, Table S1). This behavior suggests that fracture growth within low-porosity crystalline rocks under compressional loading is a critical phenomenon, in which acceleration of damage accumulation precedes system-size failure (13, 14). However, in this previous study (13), the precise change in volume due to fracture growth, analogous to microseismicity in the crust, could not be extracted and studied in detail. The present study overcomes this limitation.

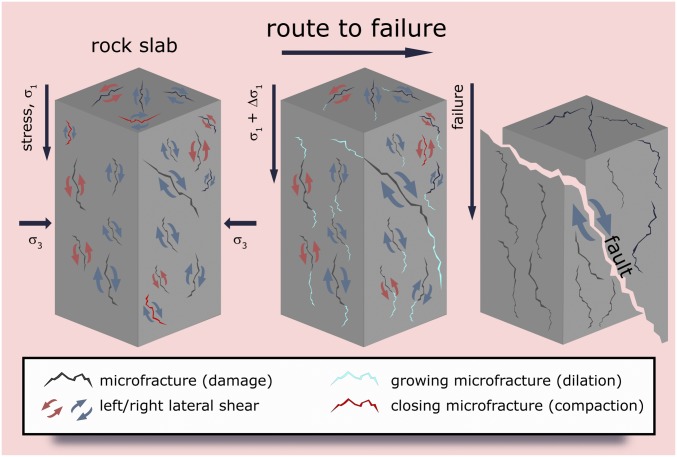
Here we present results of an investigation of the evolving microfractures in a brittle crystalline rock representative of the continental crust during the approach to macroscopic failure. This situation applies to the generation of faulting in pristine rocks (5–8) and to the relocalization of deformation in noncreeping faults that have been partially healed during the interseismic period (15–17). The results are obtained by in situ imaging of microfractures during triaxial compression with dynamic X-ray tomography. A combination of direct time-lapse imaging and digital volume correlation analysis is used to track damage accumulation from the onset of loading to macroscopic failure. The digital volume correlation analysis demonstrates that inelastic strain accumulated as dilatant and contractive damage events as well as left-lateral and right-lateral shear events (Fig. 1). These 4 expressions of damage pervade the volume and interact with each other throughout the deformation, beyond the linear elastic regime. Following macroscopic yielding, strain begins to localize and become increasingly asymmetric as dilation and 1 sense of shear become dominant. These results quantify how 1) macroscopic volumetric strain arises from a competition between microscale dilation and compaction, 2) microscopic deformation outside the future fault zone influences the localization of strain into this zone, and 3) the coalescence of the largest microfracture cluster with surrounding smaller fractures triggers macroscopic shear failure.

Fig. 1.

The route to failure in crystalline rock. Under a state of differential stress $\left({\sigma }_1-{\sigma }_3\right)$, damage accumulates in the form of microfractures that may open, close, and slip in a right-lateral or left-lateral sense. As failure is approached, one slip mode becomes dominant, right-lateral on this sketch, leading to macroscopic faulting.

In Situ Imaging of the Failure of Crystalline Rock and Measurement of Strain Evolution

A centimeter-scale sample of quartz-rich crystalline monzonite rock (13) was deformed under 25 MPa confining pressure and a temperature of 24 °C in the HADES triaxial apparatus (18, 19) installed on X-ray microtomography beamline ID19 at the European Synchrotron Radiation Facility. The experimental conditions are relevant for brittle deformation of rocks at depth up to 2 to 3 km, where rock failure envelopes predict dilatancy and faulting (20). This enabled time-lapse imaging of the sample during compressive deformation. Seventy-seven 3D tomograms were acquired as the differential stress was increased (Materials and Methods), with a spatial resolution of 6.5 μm. The last tomogram was acquired at 99.993% of the failure differential stress, allowing detailed characterization of the system-size faulting process. The loading history and the strain measurements are shown in SI Appendix, Fig. S1. The sample contained around 2,000 grains (10 × 10 × 20 grains), which is a representative volume of the whole rock. Its centimeter-scale dimensions were similar to the dimension of the fault nucleation zone in granite identified using acoustic emissions (21).

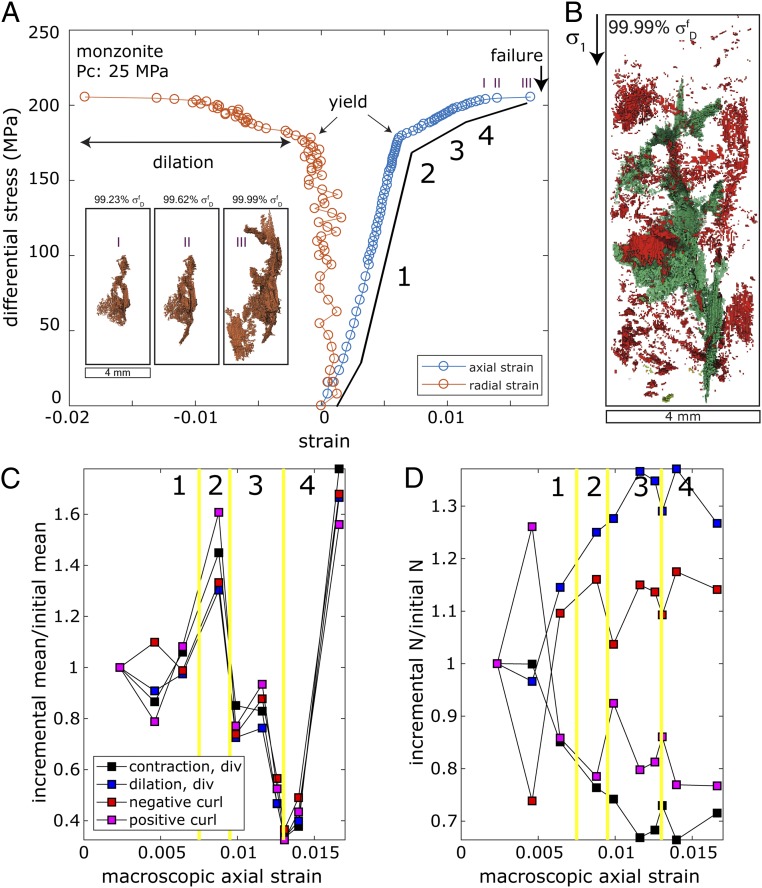
The axial strain versus differential stress relationship (Fig. 2A and Movie S1) shows behavior characteristic of crystalline rocks (e.g., ref. 22). At low differential stresses (40 to 178 MPa), the quasi-linear relationship between macroscopic strain and differential stress is indicative of an elastic regime, with small variations in the slope at stresses below 40 MPa, which we attribute to closing of voids initially present in the rock. Beyond the yield point at 178 MPa, defined here as a deviation of 3% of the experimental volumetric strain from the linear trend in the elastic regime (5), microfractures accumulate progressively in the rock, leading to macroscopic radial dilation, until failure occurs via shear fault development through the growth of the largest microfracture cluster and coalescence with smaller clusters (Fig. 2 A and B).

Fig. 2.

Evolution of damage before failure. (A) Variation of axial and radial strains as the differential stress was increased. A 3D X-ray tomography dataset was acquired under the stress and strain conditions indicated by each circle. The axial strain versus stress curve is divided into 4 stages: 1, elastic; 2, yield; 3, volumetric damage; and 4, localization before failure. (Inset) Evolution of the largest microfracture cluster in the last 3 tomography images (labeled I, II, and III) at 99.23, 99.62, and 99.99% of the failure differential stress, ${\sigma }_D^f$. (B) A 3D view of the accumulated damage at the onset of failure. The largest microfracture cluster (green) is surrounded by microfractures with smaller volumes (red) that pervade the entire rock volume. (C) Relative variation of mean incremental divergence and mean incremental magnitudes of positive and negative curl of the displacement field as failure was approached. (D) Relative variation of the number of subvolumes with divergence and incremental curl magnitudes above/below ±0.5 as failure was approached. Digital volume correlation analysis was used to calculate 10 displacement fields from 11 3D tomograms acquired as the differential stress was increased, and the x coordinate of each of the 10 sets of 4 data points indicates the macroscopic axial strain when the second of each pair of tomograms used in each digital volume correlation analysis was acquired. In C, the mean values of the divergence or curl calculated by digital volume correlation analysis divided by the mean value calculated for the first pair of tomograms are shown. In D, the number of subvolumes above a threshold value used in the digital volume correlation calculation normalized by the same value for the first pair of tomograms are shown.

The 3D digital volume correlation software TomoWarp2 (23) was used to characterize incremental displacement and strain during deformation. Digital volume correlation analysis provides a discretized displacement field from which a discretized displacement gradient field can be calculated. TomoWarp2 calculates translations and rotations between two 3D datasets, following the same procedure as in reference (19). This digital volume correlation technique produces 3D displacement fields from which the divergence, $\nabla \cdot \mathrm{\Delta }\mathbf{u}$, and curl, $\nabla \times \mathrm{\Delta }\mathbf{u}$, of the incremental displacement fields, $\mathrm{\Delta }\mathbf{u}$, are calculated (Figs. 2 C and D and 3 and Movie S2). These fields reveal the magnitude of local dilatancy (positive divergence), compaction (negative divergence), left-lateral shear (negative curl), and right-lateral shear (positive curl).

Fig. 3.

Spatial correlation between dilation and compaction. The divergence field of the incremental displacement vector field caused by the 0.8 MPa differential stress increase just before failure (calculated by digital volume correlation analysis of the last 2 tomograms before failure). (Left) A 2D planar cut along the axis of the cylindrical specimen and (Right) 3D view showing the volumes of high positive and high negative divergence (red indicates divergence > 0.5, and blue indicates divergence < −0.5). The $\nabla \cdot \mathrm{\Delta }\mathbf{u}$ = ±0.5 isosurfaces show the combination of compaction and dilation in the sample and the spatial distribution of these quantities.

In brittle rocks such as quartz-rich monzonite, large strain cannot occur without fracturing, and we attribute large magnitudes of $\nabla \times \mathrm{\Delta }\mathbf{u}$ on the scale of the node spacing used in the digital volume correlation analysis to shear displacement along microfractures. These microfractures may have apertures that are not sufficiently large to produce X-ray attenuation coefficient contrasts that are larger than the noise level, and some of them may remain undetected through segmentation. Some elastic deformation of mineral grains or aggregates of mineral grains may occur without microfracturing, but because of the high stiffness of the mineral grains and the brittleness of the bonding between them this is not expected to contribute significantly to $\nabla \times \mathrm{\Delta }\mathit{u}$ on the scale of the digital volume correlation analysis node spacing. Similarly, the opening and closing of microfractures and other voids is expected to be the dominant contribution to volumetric strain on the digital volume correlation analysis node spacing scale. Because of the very low initial porosity of the sample, most of the volumetric compaction occurred in regions that contained voids that were previously dilated and then collapsed.

If the displacements on opposite sides of a microfracture, which cannot always be detected directly in X-ray tomograms, are measured, an effective discretized simple shear strain proportional to d/Δ_n can be determined, where d is the shear displacement and Δ_n is the node spacing used in the digital volume correlation analysis. For continuous displacement fields, $\nabla \times \mathrm{\Delta }\mathbf{u}$ measures the magnitude and sense of the simple shear strain, and consequently, high magnitudes of $\nabla \times \mathrm{\Delta }\mathbf{u}$ highlight sites of localized shear displacement. We calculated 3D incremental displacement fields between 10 pairs of 3D tomograms at regular intervals of axial strain that encompassed the experiment (Fig. 2 C and D and Movie S2). The windows used to perform the digital volume correlations had a cubic shape with 4 faces parallel to the main compressive stress σ₁ and 2 faces perpendicular to it. Following tests performed in a previous study (19), we used a correlation window size of 10 voxels (65 μm) and node spacing size of 20 voxels (130 μm).

Dynamics of Strain Evolution

The digital volume correlation analysis provides quantitative information about cumulative and incremental strain localization. Time series of 3D divergence and curl fields enable quantitative assessment of evolving volumetric and simple shear components of the incremental strain fields (Fig. 2 C and D and Movie S2). We tracked populations of the increments in positive (dilatational) and negative (contractive) volumetric strain (divergence) and negative (left-lateral) and positive (right-lateral) shear strain (curl) as the differential stress was increased. The results revealed the evolving spatial distribution of left-lateral and right-lateral slip as well as dilation and compaction produced by microfracture development and the final localization of damage onto a sample-spanning fault. The mean magnitudes of the dilation and contraction, and left- and right-lateral shear events, paralleled each other as the differential stress was increased (Fig. 2C).

The varying means of the positive and negative incremental $\nabla \cdot \mathrm{\Delta }\mathbf{u}$ and $\nabla \times \mathrm{\Delta }\mathbf{u}$ populations (Fig. 2C), and the volume of material experiencing high absolute values (>0.5) of each of the 4 displacement field measures (Fig. 2D), can be used to distinguish between 4 phases of evolving deformation and damage preceding macroscopic shear failure: 1) small changes in the mean values of the divergence and curl of the incremental displacement field, corresponding to the initial linear elastic regime; 2) a 30% increase in the volume of rock experiencing divergence and left-lateral curl following the macroscopic yield point (Fig. 2D); 3) a 10% increase of these values from 178 to 190 MPa differential stress (Fig. 2D); and 4) a 400% increase of divergence and left-lateral curl in the final 15 MPa preceding failure at 205.5 MPa (Fig. 2C), while the volume of material experiencing these large strain field modes ($\nabla \cdot \mathrm{\Delta }\mathbf{u}$ and $\nabla \times \mathrm{\Delta }\mathbf{u}$) remained essentially constant during this last phase (Fig. 2D).

The observed variations of means and volume of material experiencing these large-magnitude strain field components indicate that the path toward failure was dominated by the accumulation of compaction, dilation, left-lateral shear, and right-lateral shear and interactions between them, consistent with previous observations and models (10, 24, 25). The macroscopic dilation of the sample was due to a combination of compaction in the direction parallel to the direction of the largest compressive stress and the concomitant increase in the cross-sectional area in the perpendicular plane, with a total volume increase of 2.1% at the onset of failure. Fig. 3 demonstrates that both dilation and compaction were distributed throughout the rock specimen immediately preceding macroscopic failure. This spatial representation of the compacting and dilating volumes above the 95th percentile of the strain populations further shows that regions of high compaction and high dilation were spatially correlated with each other and with the regions of high positive and negative curl (Movie S2). This correlation suggests that regions of high volumetric strain and high shear strain share a common origin, which we attribute to the nucleation, growth, opening, and closing of microfractures and the coupling between them. The postfailure tomogram shows that a higher number of microfractures formed inside grains and propagated across grain boundaries, rather than developing along grain boundaries, in contrast with the behavior observed in Carrara marble (26). The fractures were oriented preferentially toward the direction of the largest compressive stress which is consistent with other studies of similar crystalline rocks (10, 11). Macroscopic shear failure occurred via shear fracture formation that produced a gouge layer with intense grain comminution within a quasi-tabular zone with some variation in thickness (13). This development is similar to field observations of fault zones that contain a gouge layer surrounded by a damage zone (27).

Segmentation of the tomograms into rock matrix and voids (pores and microfractures) provides the volume fraction of voids as a function of increasing differential stress (SI Appendix, Fig. S2). We quantify microfracture growth with a damage index, $D_{\varphi }=\frac{\varphi -{\varphi }_i}{1-{\varphi }_i}$, where ${\varphi }_i$ is the initial void fraction of the sample under the initial confining pressure preceding axial loading $\left({\varphi }_i=0.1\%\right)$ and $\varphi$ is the void fraction measured at a given differential stress (13). The damage index is measured as a function of the normalized deviation of the differential stress from the differential stress at failure ${\mathrm{\Delta }}_D=\left(\frac{{\sigma }_D^f-{\sigma }_D}{{\sigma }_D^f}\right)$, where ${\sigma }_D^f$ is the differential stress at which failure occurred and ${\sigma }_D$ is the differential stress when each tomogram was acquired. As failure was approached, the total volume of microfractures, the volume of the largest microfracture cluster, and the number of detected microfractures all increased (SI Appendix, Fig. S2A). During the final 3 differential stress increments, the largest microfracture cluster increased in size (Fig. 2A, Inset) until it spanned the entire volume (Fig. 2B) and evolved later into the main fault. The volume fraction of microfractures in the specimen at the onset of failure was 1.4%, and the largest microfracture cluster contained 71% of this volume. The generated fault zone was a geometrically complex 3D volume that differs greatly from the concept of fault initiation on a surface that plays a key role in various models, such as those using frictional failure criteria.

Power Law Statistics of Microfracture Growth Events

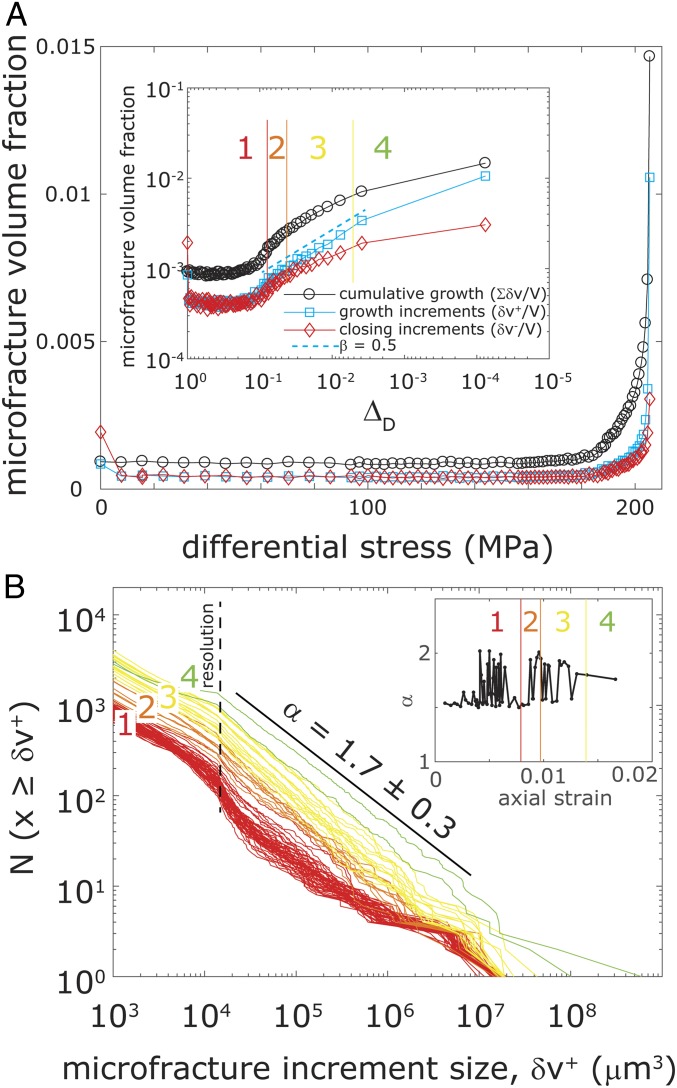
An increase in microfracture nucleation and growth as failure approached has been observed in previous studies (9, 10, 13). However, the detailed geometry and evolution was challenging to quantify because previous studies only characterized the postfailure sample (10, 11, 22) or because they used acoustic emissions, which are not sensitive to all deformation events and do not accurately determine fracture geometries (8, 9, 28). X-ray microtomography coupled with digital volume correlation analysis allows the total strain (seismic plus aseismic) to be measured. We extracted the change in volume of each microfracture and the volume of each new microfracture that developed between successive tomograms and studied their statistics (Fig. 4). This analysis required tracking of each individual microfracture in space and time and recognition of the geometry of new fractures that opened and preexisting fractures that closed. A maximum likelihood method (29) was used to determine how well the microfracture volume increments of growth, $\delta v^{+}$, can be fit by a power law, with an exponent β ∼ 0.5 (Fig. 4A, Inset). This power law behavior breaks down for the last tomogram before failure because of the onset of sliding on the future slip surface, indicating that the largest damage cluster has reached a length close to the size of the sample.

Fig. 4.

Evolution of microfractures toward failure. (A) The total cumulative normalized volume of microfractures (black curve), ${\displaystyle \sum \delta v/V}=\left(\left|{\displaystyle \sum \delta v^{+}}\right|-\left|{\displaystyle \sum \delta v^{-}}\right|\right)/V$, is due to the accumulation of positive volume increments, $\delta v^{+}$, due to microfracture growth (light blue microfractures in Fig. 1) and negative volume increments, $\delta v^{-}$, as some microfractures may close (red microfractures in Fig. 1). Here $V$ is the sample volume. The black curve is equal to the cumulative sum of the light blue curve (positive increments) and red (negative increments) curve. (Inset) The same data plotted versus ${\mathrm{\Delta }}_D=\left(\frac{{\sigma }_D^f-{\sigma }_D}{{\sigma }_D^f}\right)$, where ${\sigma }_D^f$ is the differential stress at failure. β = 0.5 is the power law exponent of the damage increment growth until very close to failure. This power law breaks down for the last increment because of system size effect. (B) Complementary cumulative distribution of microfracture volume growth increments, $\delta v^{+}$, and power law behavior with α = 1.7 ± 0.3 (SD). The red, orange, yellow, and green colors indicate stages 1 through 4 of the macroscopic strain–differential stress behavior shown in Fig. 2. (Inset) The evolution of α toward failure.

The detected volume of fractures is linked to the potential seismic energy release because earthquake potency (moment/rigidity) depends on the volume of rock around a fault that sustains inelastic deformation (30). In analogy to the Gutenberg–Richter frequency–size distribution of earthquakes, we refer to the power law exponent of the frequency–volume distributions of the fractures as the a-value. The distribution of microfracture volume increments is characterized by a constant α value of 1.7 ± 0.3 with 95% confidence. The total number of microfractures increased as failure was approached (SI Appendix, Fig. S2), indicating that the property analogous to earthquake productivity (a-value) also increased. These results are consistent with numerical simulations of evolving seismicity and stress along a strongly heterogeneous fault (31).

Implications for Failure in Continental Rocks and Earthquakes Dynamics

Experiments suggest that in crystalline rocks under confinement, macroscopic dilation occurs through the development of microfractures dominated by tensile cracks (5, 7, 8). The nonlinear shape of the failure envelope suggests that fault localization under compression corresponds to an instability that may be described by continuum models (32). By construction, these mechanical models do not take into account the development of damage and so cannot predict its evolution toward system-size failure. Dilatant behavior highlights the limitations and simplifications of failure criteria that do not consider the effect of volume increase on the evolution of mechanical properties during deformation (33). Dilatancy may cause rock stiffness to decrease and pore fluid pressure to vary compared with commonly used constant volume models. Mohr–Coulomb and Griffith failure theories depend on only a small number of parameters. They describe failure as a scale-independent macroscopic process that is independent of local strain dissipation. Furthermore, they do not take into account processes that occur before failure, how they influence the failure stress, and the dynamics and geometry of large-scale strain localization. These results motivated the development of numerical and mechanical models of rock failure that include damage development preceding macroscopic failure (e.g., refs. 14, 34–36). These models reproduce the dilatant behavior of rocks and the growth of microfractures until their concentration is large enough to enable the development of a macroscopic fault. They also predict the existence of power law behavior, a characteristic of critical phenomena (13, 14), consistent with our experimental observations.

Experiments that detect and quantify energy releasing events before failure, such as those using acoustic emissions (8, 9, 37) or direct visualization of microfractures by X-ray tomography (13), have documented complex behavior between initial yielding and final failure. Such observations cannot be readily reconciled with the Griffith or Mohr–Coulomb failure criteria but can be interpreted in terms of damage mechanics frameworks that describe the acceleration and localization of acoustic emissions before rock failure (9, 37). Damage models that account for the long-range interactions between brittle failure events (14, 35, 37) predict the acceleration of the rate of damage as the stress increases at a constant rate approaching failure, as observed in experiments (13, 28, 37). Such models make several predictions, including the amount of dilatancy, localization, and power law increases in the rate of damage accumulation and the size of the largest microfracture cluster when failure is approached; Renard et al. (13) observed all these predictions experimentally. Our results (Figs. 3 and 4) enable measurements of not only the total damage (i.e., the total volume of all of the fractures as was done in ref. 13) but also the change in volume of each individual microfracture (and the volumes of any new microfractures that formed), as well as the local changes in left-lateral and right-lateral shear for each differential stress increment. This provides 3D maps of the components (dilation, contraction, left-lateral shear, and right-lateral shear) of the incremental damage and how the components of the incremental damage changed with loading. The power law distribution of the increment damage volumes shows an exponent of β ∼ 0.5 (Fig. 4A), and the increase of the incremental damage volumes approaching failure exhibits another power law with an exponent of α ∼ 1.7 (Fig. 4B). Both exponents are in agreement with a 2D numerical damage model (35) that predicts power law exponents of β ∼ 0.4 and α ∼ 1.8.

The results of the present study quantify how macroscopic failure occurs through spatially asymmetric events (Fig. 1) that exhibit power law scaling as failure is approached and how these events pervade the specimen before failure. Crystalline rocks sustain brittle deformation in the seismogenic zone up to about 20 km depth. However, larger stresses, increased temperature, and the presence of fluids may activate additional deformation mechanisms such as subcritical crack growth or pressure solution creep. Therefore, extrapolation of our results to such depths should be done with caution. The spanning of a partially healed fault by the largest damage cluster could explain the occurrence of geochemical signals before earthquakes (38) because new long-range fluid flow pathways connected in 3 dimensions may be formed. The data presented here demonstrate that macroscopic dilation and compaction are coupled processes and that local dilation and compaction are spatially correlated and act in concert (Figs. 2 and 3). This correlation may arise because local dilation or compaction alters the stress field, particularly in neighboring volumes. For example, the growth and concomitant opening of a microfracture with diameter L primarily influences a volume of the order of L³ surrounding the microfracture, as well as the long-range stress field. The resulting volume of influence produces both tensile stress shielding (an increase in compressive stress) and tensile stress amplification (a decrease in compressive stress) that affect the opening, closing, nucleation, and propagation of neighboring microfractures and pore volumes. When the entire volume (i.e., the core specimen in these experiments) has experienced a certain amount of pervasive damage, additional inelastic deformation drives localization (stage 4 in Fig. 2). These cooperative interactions lead to power law distributions of microfracture growth events at every increase of stress (Fig. 4).

Our data at the microscale quantify how failure depends on asymmetric damage development within the future failure zone and in the surrounding rock. Fig. 2D shows that when $n_f$ microfractures open in response to an increment of strain caused by an increment in the differential stress, $\mathrm{\Delta }{\sigma }_D$, close to failure, around $0.5n_f$ microfractures close, and $0.9n_f$ left-lateral shear events and $0.6n_f$ right-lateral shear displacement events occur. In the brittle crust, a balance between volume increasing/decreasing events and between left-/right-lateral shear events may occur in the form of conjugate microseismicity and faulting or distributed deformation near complex fault geometries, as well as in the surrounding volume (26, 39). High-resolution earthquake catalogs in well-instrumented areas show that ongoing seismicity can occur in zones with width of the order of 10 km around major faults (1, 3). While the largest events occur on the main faults, off-fault seismicity and aseismic processes of the type documented in this study can play key roles in the localization or relocalization of faulting in geomaterials.

Materials and Methods

The experiment was performed at 24 °C on a dry cylindrical monzonite specimen of 10 mm length and 4 mm diameter, using a procedure similar to that of Renard et al. (13). The interfaces between the rock sample and the pistons of the rig were not lubricated. To capture snapshots of deformation, the experiment was conducted by increasing the differential stress (the difference between the axial stress, ${\sigma }_1$, and the confining pressure, ${\sigma }_3$) in steps of 8 MPa far from failure (1 to 140 MPa), then steps of 3 MPa (100 to 160 MPa), steps of 1.5 MPa (160 to 190 MPa), and steps of 0.75 MPa as failure at 205.5 MPa was approached (SI Appendix, Fig. S1). This enabled the changes in deformation and damage to be determined in sufficient detail as failure was approached and deformation and damage increased more rapidly with increasing differential stress. We acquired X-ray radiographs at a constant stress after each stress increment. Acquisition of the 2D radiographs required to construct a 3D data set took about 1.5 min. We did not find evidence for significant changes in structure during data acquisition, such as blurring of the distinct edges between void space and grains in the tomograms that would have indicated time-dependent subcritical crack growth in the specimen. A jacket made of Viton fluoropolymer elastomer encased the rock sample, and pressurized silicone oil applied the confining pressure of 25 MPa to this jacket. A series of 77 data sets of 1,600 radiographs were acquired at a voxel size of 6.5 μm, corresponding to the spatial resolution of the images. From the 2D radiographs, 3D volumes of the specimen were reconstructed in 16-bit grayscale following the same procedure as in ref. 19. The details of strain measurements are given in SI Appendix. The tomography data are available in ref. 40.

Microfracture shapes and sizes (Figs. 2 A and B and 4 and SI Appendix, Fig. S2) were imaged and extracted from the tomograms by applying the segmentation procedure described in ref. 12. Every segmented microfracture was identified in each tomogram, and its volume was calculated. Then, by comparing each pair of successive tomograms, the difference between the microfractures in these 2 volumes was extracted to determine the microfracture growth increments (schematically represented in light blue in Fig. 1) and decrements (shown in red in Fig. 1). The contributions of the microfracture volume increments and decrements to the total microfracture volume and the size distribution of the volume increments are shown in (Fig. 4 and SI Appendix, Fig. S2).