Mechanical and kinetic factors drive sorting of F-actin cross-linkers on bundles

Significance

The actin cytoskeleton plays a crucial role in cell division, motion, and internal transport. The main component is F-actin, a semiflexible polymer formed of actin monomers. For a cell to regulate and accomplish the tasks of the cytoskeleton, F-actin polymers are organized into structures by actin-binding proteins. Among these cross-linkers are proteins that join F-actin into a network with structural rigidity and can form tight, rigid bundles. Different cross-linkers perform diverse functions in cells, but how they are sorted to their functional locations is not well understood. In this work, we show how physical and chemical characteristics of the system, including nonequilibrium factors such as actin polymerization, help organize and localize cytoskeletal components.

Abstract

In cells, actin-binding proteins (ABPs) sort to different regions to establish F-actin networks with diverse functions, including filopodia used for cell migration and contractile rings required for cell division. Recent experimental work uncovered a competition-based mechanism that may facilitate spatial localization of ABPs: binding of a short cross-linker protein to 2 actin filaments promotes the binding of other short cross-linkers and inhibits the binding of longer cross-linkers (and vice versa). We hypothesize this sorting arises because F-actin is semiflexible and cannot bend over short distances. We develop a mathematical theory and lattice models encompassing the most important physical parameters for this process and use coarse-grained simulations with explicit cross-linkers to characterize and test our predictions. Our theory and data predict an explicit dependence of cross-linker separation on bundle polymerization rate. We perform experiments that confirm this dependence, but with an unexpected cross-over in dominance of one cross-linker at high growth rates to the other at slow growth rates, and we investigate the origin of this cross-over with further simulations. The nonequilibrium mechanism that we describe can allow cells to organize molecular material to drive biological processes, and our results can guide the choice and design of cross-linkers for engineered protein-based materials.

Networks formed from filamentous actin polymers (F-actin) perform diverse mechanical tasks throughout cells, such as enabling migration (1, 2), adhesion (3), mechanosensing (4), and division (5). F-actin is formed into networks by cross-linkers, actin-binding proteins (ABPs) that link multiple filaments. To form distinct F-actin geometries and accomplish specific cellular mechanisms, cross-linkers with diverse kinetic and mechanical properties must be segregated to different locations in the cell (6). For example, the actin cross-linker fimbrin is used to bundle branched F-actin at the leading edge of migrating cells so that they can harness energy from actin polymerization to generate protrusive forces (1, 7).

The kinetics of ABPs, as well as their mechanical properties, can play subtle roles in cellular processes. For example, we previously showed that having optimal kinetics of binding ($k_{\mathrm{on}},k_{\mathrm{off}}$), in addition to an optimal binding affinity ($K_d=k_{\mathrm{off}}/k_{\mathrm{on}}$) for the cross-linker $\alpha$-actinin is crucial for proper contractile ring formation and constriction during cell division (8). Many ABPs may be involved in one single cellular mechanism; for example, the cytokinetic ring of fission yeast employs formins to assemble F-actin, the cross-linker $\alpha$-actinin to connect F-actin into antiparallel bundles, and myosins to contract the bundles and ultimately divide the cell (9–11). How these cross-linkers interact is not well understood.

Regulating the spatial and temporal organization of ABPs in a crowded cellular environment is understandably complex, and determining the mechanisms involved is an active area of research. Some of this regulation may require explicit signaling pathways; for example, generation of branched networks by the Arp2/3 complex can be activated by upstream activation of a Rho GTPase (12, 13). In addition to these signaling-based mechanisms, emerging data detail many passive mechanisms by which competition between different components for the same substrate can allow self-regulation and localization of ABPs in the actin cytoskeleton (14–17). We recently showed that $\alpha$-actinin and fascin, 2 F-actin cross-linkers that are primarily found separated into different F-actin networks within cells, can self-sort in a simplified in vitro reconstitution of a branched Arp2/3 complex-nucleated network, and even sort to different domains when 2 filaments bundle (Fig. 1A) (16). An outstanding challenge is to determine which of the biochemical characteristics of actin, fascin, and $\alpha$-actinin yield sorting.

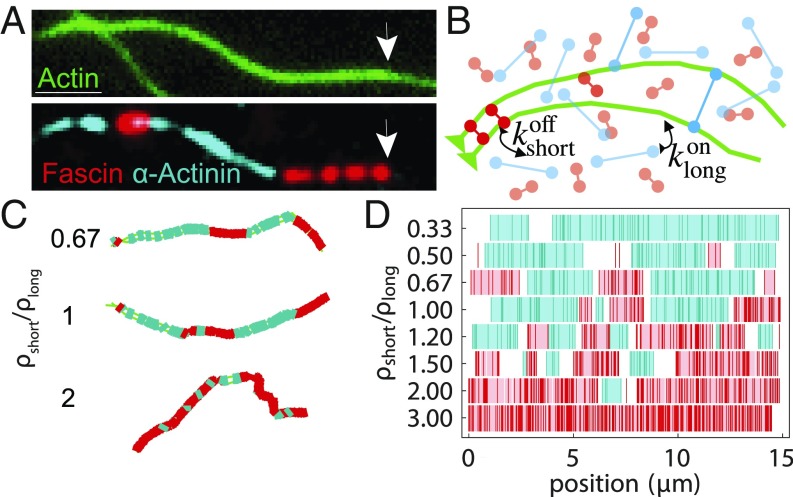
Fig. 1.

Cross-linker segregation in experiment and simulations. (A) Experimental 3-color TIRF microscopy image showing 2 cross-linkers, fascin (red), and $\alpha$-actinin (cyan) in domains on a 2-filament actin bundle (green; arrows indicate polymerizing barbed end). (Scale bar: $2\mathrm{\mu }\mathrm{\text{m}}$.) Adapted from ref. 16. (B) Schematic of AFINES simulation: 2 filaments (green bead spring chains) are combined with 2 populations of cross-linkers, short (red) and long (cyan) that are represented as Hookean springs, which can dynamically bind and unbind from filaments. (C) Bundles formed in AFINES simulations by two 15-$\mathrm{\mu }$m filaments mixed with long cross-linkers ($l_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}=300$ nm; cyan) and short cross-linkers ($l_{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}=200$ nm; red). (D) Domain calculations for different density ratios. Cyan (red) lines show discretized position of long (short) cross-linkers, light blue (pink) regions show extracted domains, and white regions are gaps. See SI Appendix, Table S1 for the list of parameter values for all AFINES simulations in this paper and https://github.com/Simfreed/AFINES for AFINES software and inputs (39).

An important difference between fascin and $\alpha$-actinin is their size; fascin is small ($\sim$8 nm), forming tight bundles composed of narrowly spaced actin filaments, while $\alpha$-actinin is larger ($\sim$35 nm) and hence makes more widely spaced bundles (16, 18, 19). Additionally, filaments in $\alpha$-actinin bundles have mixed polarity, whereas fascin bundles filaments such that their fast-growing barbed ends all face the same direction (20, 21). Therefore, the structures observed in our previous work (e.g., Fig. 1A) are parallel 2-filament bundles in which the spacing between filaments alternates between ∼8 and 35 nm (16). For transitions in bundle spacing, the actin filaments must bend significantly over length scales shorter than their persistence length $L_p=17\mathrm{\mu }\mathrm{\text{m}}$ (22), which is energetically unfavorable. Since we observe domains in experiment, the energetic cost of bending must be compensated for by favorable effects, such as the benefit of binding more cross-linkers and the entropy gained by mixing them.

In this work, we use these observations to develop a theoretical model that enables investigating the full range of mechanical and kinetic cross-linker properties that may lead to domain formation in F-actin bundles. We first test this model in equilibrium systems with constant-length actin filaments using coarse-grained simulations and examine how the lengths of cross-linkers and the flexibility of F-actin affect cross-linker segregation. For nonequilibrium systems with growing filaments, our theoretical analysis predicts that actin polymerization and bundling affinity work together to determine the size of domains. We refine this prediction based on results from in vitro experiments as well as coarse-grained simulations and conclude that in addition to bundling affinity, the affinity of cross-linkers for single filaments can determine which protein will have longer domains on growing bundles. Thus, our theoretical models explain our experimental observations and elucidate passive mechanisms for cross-linker sorting in both equilibrium and nonequilibrium environments.

Results and Discussion

A Simulation Framework for Actin and Cross-Linkers Exhibits Domain Formation.

Throughout this work, we use AFINES (Active Filament Network Simulation), a coarse-grained molecular dynamics simulation framework built specifically for actin and ABP assemblies, to investigate the mechanical properties of actin filaments and cross-linkers that yield domain formation (schematic in Fig. 1B; model details in SI Appendix, section A) (23, 24). Actin filaments are modeled as polar worm-like chains (represented as beads connected by springs). In this work, we have added the ability for filaments to grow from their barbed end by increasing the rest length of the barbed-end spring at a constant rate and adding a bead when that rest length is above a threshold (as done, e.g., in refs. 25 and 26). We have also added the ability for filaments to repel each other via a harmonic excluded volume interaction. Cross-linkers are modeled as Hookean springs with 2 ends (heads) that stochastically bind and unbind from actin filaments via a Monte Carlo (MC) procedure that preserves detailed balance. In this work, we include an additional harmonic energy cost giving a preference for filaments and cross-linkers to be perpendicular, necessary to represent rigid cross-linkers. The simulation proceeds in 2D via Brownian dynamics, without volume exclusion between the cross-linkers, to enable efficient sampling.

With this minimal mechanical-kinetic parameterization, our model exhibits segregation of different length cross-linkers on F-actin bundles, similar to experiment (Fig. 1C). By discretizing the position of the cross-linkers doubly bound to actin filaments, and interpolating gaps between nearby cross-linkers (SI Appendix, section B), we can define domain boundaries in a manner consistent with experimental resolution (Fig. 1D). Thus, we can use AFINES to explore how filament and cross-linker characteristics affect domain formation.

Energetic Cost of Actin Filament Bending Modulates Domain Formation.

In our previous work, we modeled domain formation as a 1D process by which new cross-linkers are added to the barbed end of a growing 2-filament bundle and do not unbind (16), similar to models used for studying self-assembly of binary materials out of equilibrium (27, 28). These assumptions were motivated by our experimental observations that bundling occurred at approximately the same rate as actin filament polymerization, and domain boundaries, once formed, remained fixed for the duration of the experiment (16). In that 1D model, a cross-linker of the same type as the cross-linker at the barbed end binds at a rate of ${\mu }_{\mathrm{on}}^{\mathrm{same}}$, while a cross-linker of a different type binds at a lower rate, ${\mu }_{\mathrm{on}}^{\mathrm{diff}}={\mu }_{\mathrm{on}}^{\mathrm{same}}{e}^{-ϵ/k_{B}T}$, where $k_B$ is Boltzmann’s constant, $T$ is temperature, and $ϵ$ is an energetic penalty incurred by switching cross-linker type. This competition generates a cooperative benefit to having large domains of each single component. We found that a kinetic barrier height of $ϵ=4.8\hspace{0.17em}{k}_{B}T$ yielded domain lengths in good agreement with our experimental results (16). This barrier corresponds to a rate of switching domains that is 120-fold lower than continuing the same domain.

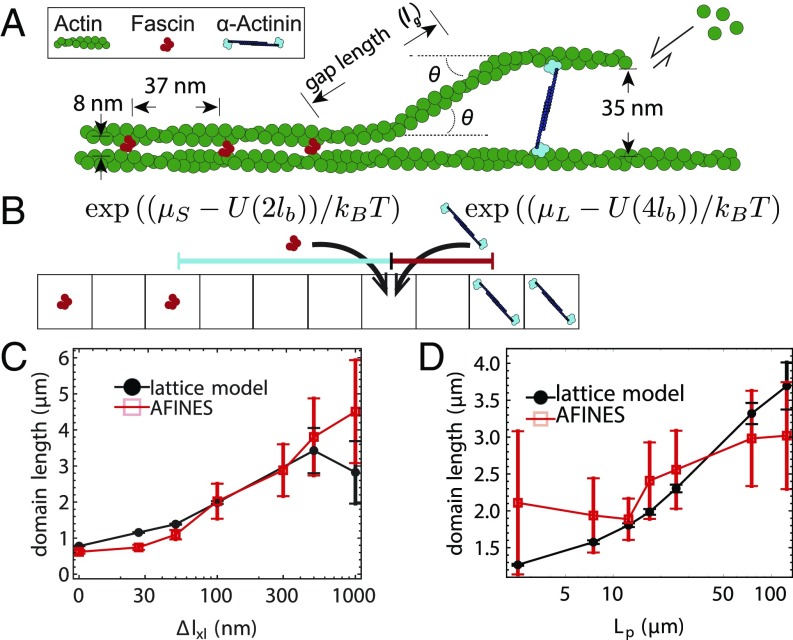
However, fitting that model did not make any connection to the underlying hypothesis that this energetic penalty is due to the cost of bending actin. To derive a similar model from first principles, we estimate the cost of bending actin such that, e.g., an $\alpha$-actinin can be inserted with a gap length of $l_g$ along the filament from a fascin domain. As shown in Fig. 2A, the filament must bend twice at an angle $\theta$ for the filament bundle to switch domains (this geometry, where one filament is straight and the other is bent, is based on cryoelectron microscopy images of domain switches in ref. 16). In the absence of filament fluctuations, we estimate $\theta \approx \arcsin \left(\mathrm{\Delta }{l}_{xl}/l_g\right)$, where $\mathrm{\Delta }{l}_{xl}$ is the difference in length between the 2 cross-linkers. Since the energetic cost of bending an angle $\theta$ over a distance $l_g$ for a worm-like chain is $k_{B}T{L}_p{\theta }^2/2l_g$ (23, 29), the total energy cost to bend a filament twice is

$$U\left(l_g\right)=\frac{k_{B}T{L}_p}{l_g}{\arcsin }^2\left(\frac{\mathrm{\Delta }{l}_{xl}}{l_g}\right).$$ [1]

Fig. 2.

Effect of cross-linker and filament mechanics on domain length. (A) Schematic of a 2-filament bundle transitioning from a tight fascin bundle to a wider-spaced $\alpha$-actinin bundle in an idealized geometry. The filament bends twice at an angle $\theta$, leaving a gap of length $l_g$, defined along the contour of actin rather than between cross-linker centers so that the bending energy in the lattice model and AFINES have the same functional form. (B) Lattice model example, in which there is initially a gap of length $6l_b$ indicated by the black dashed line and the indicated lattice site is empty. If that lattice site switches to a short cross-linker, the gap will reduce to $2l_b$ (red solid line), whereas if it switches to a long cross-linker, the gap will reduce to $4l_b$ (cyan solid line), yielding energy changes ($\mathrm{\Delta }{U}_{\mathrm{l}\mathrm{a}\mathrm{t}}$). (C) Domain lengths from AFINES and lattice model as a function of cross-linker length difference ($\mathrm{\Delta }{l}_{xl}$), with $L_p=17\hspace{0.17em}\mathrm{\mu }$m, $l_{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}=200$ nm, and $l_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}$ varying. (D) Same as C, but varying filament persistence length ($L_p$) while $l_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}=300$ nm. In C and D, domain lengths are averaged over the last 100 s of a 2,000-s simulation, and 40 simulations; error bars are SEM. In D, filament repulsion ($k_{\mathrm{e}\mathrm{x}\mathrm{v}}=0.08$ pN$\mathrm{\mu }{\mathrm{m}}^2$) is also used to prohibit filaments from crossing each other, which occurred at low $L_p$.

Eq. 1 indicates that increasing the magnitude of mechanical parameters, the persistence length of filaments or the difference in length between cross-linkers, will increase the energy required to switch domain type on a filament bundle. The higher switching energy would decrease the likelihood of switching domains and therefore increase domain lengths. While these mechanical characteristics are difficult to modulate experimentally, they are explicit parameters in AFINES, allowing us to directly test Eq. 1 in simulation by exploring a range of cross-linker sizes and filament persistence lengths.

To quantitatively compare the results of our simulations with the predictions from Eq. 1, we use an equilibrium 1D lattice model (Fig. 2B) introducing the gap energy (Eq. 1) into an MC simulation of a “bundle” of fixed length. The lattice contains a constant number of binding sites, $N=L_0/l_b=405$, where $L_0=15\hspace{0.17em}\mathrm{\mu }\mathrm{\text{m}}$ is the filament length and $l_b=37$ nm is the binding site spacing. Each lattice site can be in 1 of 3 states: empty, populated by a short cross-linker (S), or populated by a long cross-linker (L) (Fig. 2B). The energy of the lattice is given by

$$U_{\mathrm{l}\mathrm{a}\mathrm{t}}=-\left(N_S{\mu }_S+N_L{\mu }_L\right)+\sum _{g\in \mathrm{g}\mathrm{a}\mathrm{p}\mathrm{s}}U\left(l_g\right),$$ [2]

where $N_{S\left(L\right)}$ is the number of short (long) cross-linkers, ${\mu }_{S\left(L\right)}$ are their chemical potentials (set to $-2k_{B}T$ by the procedure described in SI Appendix, section C), $U\left(l_g\right)$ uses Eq. 1, and “gaps” is the set of all empty lattice patches between short and long cross-linkers. In the MC procedure, we compute the final state of the lattice using the Metropolis algorithm: iteratively, we switch a randomly chosen site to a randomly chosen new state with probability $min\left(1,\exp \left(-\mathrm{\Delta }{U}_{\mathrm{l}\mathrm{a}\mathrm{t}}/k_{B}T\right)\right)$, where $\mathrm{\Delta }{U}_{\mathrm{l}\mathrm{a}\mathrm{t}}$ is the energy cost incurred by switching (Fig. 2B) (30, 31).

Having parameterized our lattice model to match 1 set of AFINES simulations, we proceeded to systematically vary the 2 quantities that we predict to have a major impact on domain size: $\mathrm{\Delta }{l}_{xl}$ and $L_p$. First, we find that for length differences larger than 30 nm, domain length increases with $\mathrm{\Delta }{l}_{xl}$ (Fig. 2C). Similarly, increasing the filament persistence length yields an increase in domain length (Fig. 2D), and also in the rate of bundling (Movie S3). Our results from the lattice simulation conform well with the AFINES simulations (Fig. 2 C and D), indicating that the mechanical model for cross-linker segregation is a good predictor for domain length in an equilibrium environment. In summary, the primary driving forces controlling domain size in equilibrium are 1) the energetic cost of bending the actin, 2) the energy gain from binding, and 3) the entropy of mixing cross-linkers.

Model Predicts Dependence of Cross-Linker Domain Size on F-Actin Polymerization Rate.

Up to this point, we have confirmed a previous hypothesis that cooperativity and competition between binding of cross-linkers can arise due to the mechanical rigidity of filaments. A key difference between the experiments showing cross-linker domain formation and our coarse-grained and lattice model simulations is that those experiments were done under conditions where the actin is polymerizing (16). We hypothesized that polymerization could have an influence on the sizes of gaps between cross-linkers and, in turn, affect the size of the domains.

To generate a quantitative prediction for the effect of polymerization on competition, we introduced growth into the lattice model of Fig. 2B. Since the experiments on this system are in the regime of very slow cross-linker unbinding, we can efficiently solve this model using kinetic MC (KMC). As in our simpler lattice model of ref. 16, there is only one free parameter, ${\mu }_{\mathrm{o}\mathrm{n}}$, the bundling rate of the cross-linkers at equal concentration.

To perform KMC, the rates of all possible events (binding of either cross-linker to empty sites, plus growth to add an additional empty site) are computed, and then one event is selected randomly from this list weighted by the probability of that event occurring (31). As can be seen in Fig. 3A, the rates of binding to an empty site at the barbed end depend exponentially on the cost of bending actin in Eq. 1. Fig. 3B shows how the probability of switching from one cross-linker type to the other depends on the distance away (gap length) from the current bundle. Interestingly, because the physiological cross-linker length difference is small, equal site-binding probability is reached after only 20 binding sites ($\sim 0.7\hspace{0.17em}\mathrm{\mu }\mathrm{\text{m}}$), much less than the persistence length of a filament (Fig. 3B).

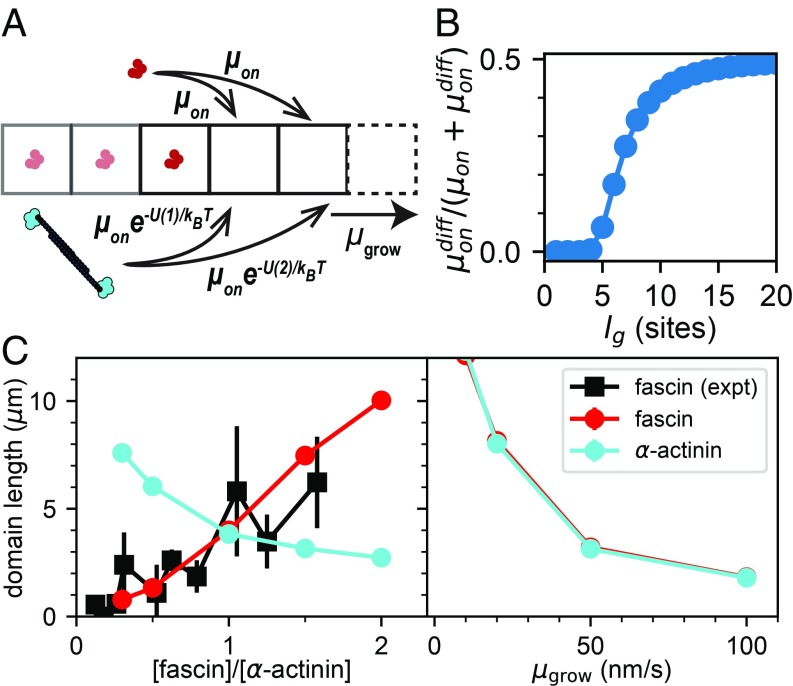
Fig. 3.

Polymerization rate of actin tunes competition between cross-linkers. (A) Numerical model for testing effect of filament growth on domain formation. New cross-linker binding sites are added at a rate ${\mu }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$, and cross-linkers are added via KMC at a rate governed by Eq. 1. (B) Likelihood of adding the other (“diff”) cross-linker at the barbed end at a given number of binding sites from the interface governed by Eq. 1, with equal bundling rates for both cross-linkers, and ${\mu }_{\mathrm{on}}^{\mathrm{diff}}={\mu }_{\mathrm{on}}{e}^{-U\left(l_g\right)/k_{B}T}$. (C, Left) domain size from the KMC model and experimental data from ref. 16 (${\mu }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}=40$ nm/s as in those experiments, with ${\mu }_{\mathrm{on}}^{\alpha -\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}}=0.2$/site/s). (C, Right) Effect of varying ${\mu }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$ while both cross-linkers have the same bundling rate, ${\mu }_{\mathrm{o}\mathrm{n}}=0.2$/site/s. Here, the maximum filament length is 15 $\mathrm{\mu }$m, $L_p=17\mathrm{\mu }$m, $\mathrm{\Delta }{l}_{xl}=27$ nm (corresponding to the difference in length between fascin and $\alpha$-actinin), and each data point is an average over 1,000 simulations (SEM error bars are smaller than the points).

We find that a bundling rate of ${\mu }_{\mathrm{o}\mathrm{n}}=0.2$/site/s produces domains the same size as those in experiments with equal concentration of cross-linkers at a growth rate of ${\mu }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}=40$ nm/s (corresponding to the approximate growth rate in ref. 16). Under these conditions, the bundle is zipped at approximately the same rate as the actin polymerizes (SI Appendix, Fig. S3 A and B), as observed in experiments. By changing the on rate of one of the cross-linkers, we can simulate changing the concentration, and see in Fig. 3C that the cooperative behavior of this model agrees very well with data from ref. 16.

Having developed a model that matched our previous experimental data, we can now return to our question of how polymerization rate affects domain formation. We find that slowing actin polymerization can dramatically increase the size of domains (Fig. 3C). This makes sense within the context of Eq. 1 and Fig. 3B—slow polymerization yields short gap lengths, and switching cross-linkers over short gap lengths has a high energetic cost. Hence, slowing polymerization effectively increases the cooperative benefit of adding the same cross-linker, reminiscent of how changing deposition rate can affect the amount of defects in a nonequilibrium materials growth process (27). Moreover, the magnitude of competition between cross-linkers only depends on the ratio of ${\mu }_{\mathrm{o}\mathrm{n}}/{\mu }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$ and approximately equals our previously calculated value (SI Appendix, Fig. S3C) (16).

Experiments Confirm Fascin and $\alpha$-Actinin Domain Lengths Depend on Actin Polymerization Rate.

To test the prediction that polymerization rate affects the amount of competition between cross-linkers, we performed new in vitro experiments in which we added monomeric actin to a mixture of fascin, and $\alpha$-actinin, at 2 different actin concentrations, $0.75\hspace{0.17em}\mathrm{\mu }$M and $1.5\hspace{0.17em}\mathrm{\mu }$M (Fig. 4A). The results (Fig. 4B) showed that, indeed, polymerization affects the size of observed domains. While our theoretical model predicts that domain sizes of both increase under slower actin polymerization conditions (Fig. 3C), we were surprised to see that only the $\alpha$-actinin domain size increased, out-competing fascin in this case. This suggests that the specific kinetics of binding and unbinding can play an additional role, and that it is possible to have a system where one cross-linker is predominant on fast-growing bundles, and the other on slowly growing bundles.

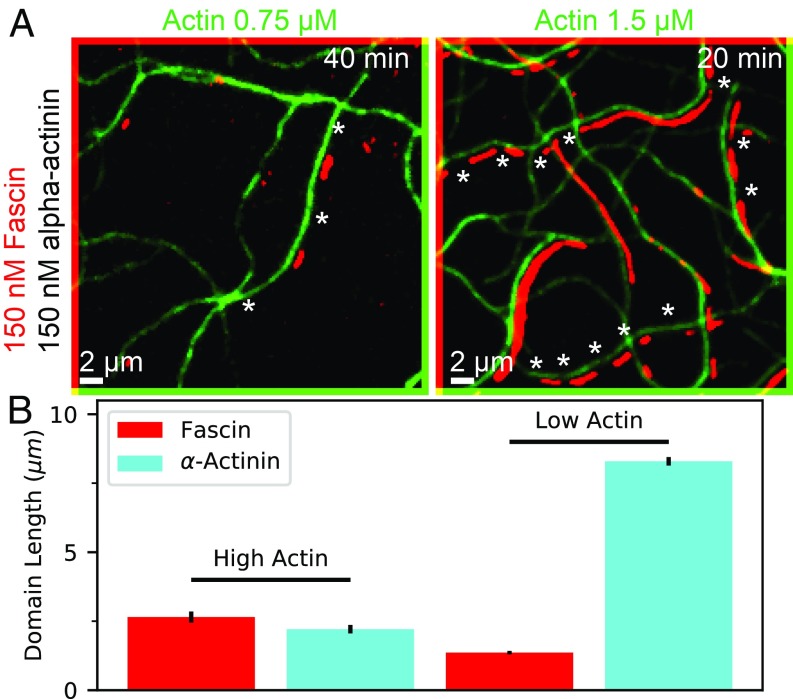
Fig. 4.

TIRF microscopy experiments show effect of polymerization on cross-linker domain formation. (A) Two-color TIRF microscopy image of actin filaments combined with fascin (labeled) and $\alpha$-actinin (unlabeled) at 2 different actin concentrations (images diagonally offset by 2 pixels in each direction for clarity). Measured actin polymerization rates are $46.99\pm 3.62$ nm/s and $22.15\pm 3.78$ nm/s at high and low actin concentrations, respectively. $\alpha$-Actinin domains are inferred from regions with double actin fluorescence but no fascin (examples shown with stars). Full field of view is shown in Movies S4 and S5. Experiments using labeled $\alpha$-actinin and labeled fascin conform with these results but are harder to quantify (ref. 16 and SI Appendix, Fig. S4). (B) Domain length for fascin and $\alpha$-actinin for both conditions, averaged over 2 replicates each; error bars are SEM over replicates.

In our previous work, we showed that both cross-linkers have similar bundling ability under these conditions, and fascin and $\alpha$-actinin dissociated from actin bundles at nearly equal rates (16). Their affinity to a single actin filament is, however, different; we observe coating of single filaments by $\alpha$-actinin, while we do not see significant residence of fascin on single filaments (Movies S4 and S5). This may be due to the size and flexibility of $\alpha$-actinin, which allows it to bind to single filaments with both binding domains (19, 20). Given the surprising difference between our experimental results and theoretical predictions, we wanted to see whether we can observe this switch in dominance from one cross-linker to the other in our more detailed AFINES model and whether changing the binding rate to single filaments effects that cross-over.

Simulation Elucidates Relationship between Filament Growth and Binding Kinetics.

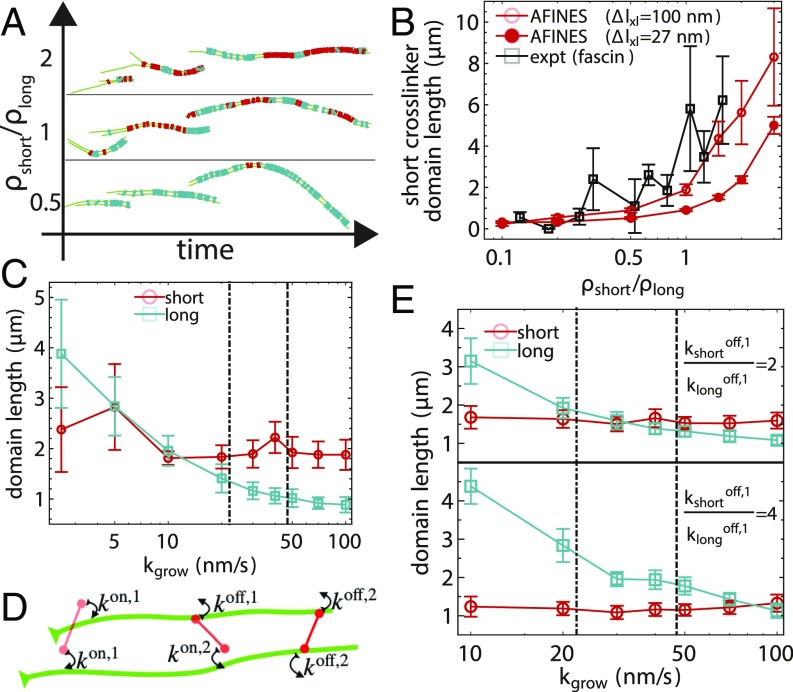
Before investigating the role of filament growth and binding kinetics on domain formation using AFINES, we first benchmark our simulations of growing filaments interacting with short and long cross-linkers (Fig. 5A) against known experimental results. Despite many simplifications in AFINES that could reduce the observed amount of cross-linker bundling cooperativity (including a lack of discrete binding sites, a lack of torsional freedom of the filaments, and a lack of excluded volume between cross-linkers), we are able to obtain similar domain lengths to experiment with similar actin growth rates (40 nm/s), a short cross-linker length of $l_{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}=200$ nm and long cross-linker length of $l_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}=300$ nm (Fig. 5B). While it would be ideal to use cross-linkers that are the same length as in experiment, we found that the spring constants required to maintain constant cross-linker length and promote perpendicular binding to actin filaments become too large for efficient numerical integration when the cross-linkers are their actual sizes. Using the same length difference between cross-linkers as in experiment (27 nm), but with larger lengths, yields the same characteristic highly cooperative domain length growth but with shorter domain sizes (Fig. 5B); thus, we conclude that our AFINES model sufficiently accounts for the key underlying physical principles for sorting.

Fig. 5.

Competition between binding kinetics and polymerization in simulation. (A) AFINES trajectories of 2 filaments growing and forming cross-linker domains with a constant density of long (cyan) cross-linker (${\rho }_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}=0.25\mathrm{\mu }{\mathrm{\text{m}}}^{-2}$) and varying the density of short (red) cross-linker. (B) Domain length of the shorter cross-linker as a function of density ratio for simulations, compared with experiments (16). In simulations, filaments are initially 1 $\mathrm{\mu }$m long and grow to a maximum length of 15 $\mathrm{\mu }$m at a rate of $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}=40\hspace{0.17em}\mathrm{n}\mathrm{m}/\mathrm{s},l_{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}=200$ nm, and $l_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}=227$ nm (filled circles) or 300 nm (unfilled circles). (C) Domain lengths of both cross-linkers as a function of filament growth rate in simulations of bundling. Dot-dashed and dashed lines show experimental growth rates at low and high actin concentrations from Fig. 4, respectively. (D) Schematic showing definition of cross-linker head binding constants (SI Appendix, Eq. 4). (E) Similar to C but while varying the dissociation constant of the short cross-linker from single filaments $k_{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}^{\mathrm{off},1}$. In B, C, and E, domain lengths are averaged over the 100 s after the filament reached its maximum length ($15\hspace{0.17em}\mathrm{\mu }\mathrm{\text{m}}$) and 40 simulations; error bars are SEM.

Therefore, we can now use our AFINES model with $\mathrm{\Delta }{l}_{xl}=100$ nm to systematically study the effects of filament growth on domain length. We find (Fig. 5C) that while the domain length of the longer cross-linker decreases with increasing growth rate (as expected from the lattice model prediction in Fig. 3C), the domain length of the shorter cross-linker is much less sensitive to $k_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}}$ (reasons for this difference between short and long cross-linkers and that AFINES domains are shorter than those in experiment and KMC simulations are discussed in SI Appendix, section D). Interestingly, we observe a cross-over similar to that seen experimentally, although it occurs at a much lower growth rate ($\sim 3$ nm/s).

As noted previously, there is evidence that the single-filament affinities of the 2 cross-linkers are different, and we thus sought to determine whether this could account for the shift in the cross-over to a lower growth rate. To do so, we modified AFINES such that a cross-linker head may have one dissociation rate constant when bound to a single filament ($k^{\mathrm{off},1}$) and another when both heads are bound ($k^{\mathrm{off},2}$), as shown in Fig. 5D (SI Appendix, Eq. 4). In Fig. 5E, we show that increasing the ratio $k_{\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{t}}^{\mathrm{off},1}/k_{\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}}^{\mathrm{off},1}$ (causing the long cross-linkers to have higher affinity for single filaments) shifts the filament growth rate at which the cross-over takes place, up to and beyond that at which this behavior is observed experimentally (i.e., Fig. 4B).

These results are a clear demonstration of how the kinetics of cross-linker binding, and not only bundle affinity, are important for cross-linker segregation under nonequilibrium (polymerizing) conditions. From these data, we speculate that having a longer residence time on single filaments gives a cross-linker an advantage in slow-growth conditions, as that cross-linker is positioned to bundle when fluctuations cause the filaments to have the correct spacing. This is a purely kinetic effect, as domain sizes eventually equalize when observing the filaments at much longer times (SI Appendix, Fig. S5), as expected from the fact that cross-linkers were parameterized to have equivalent bundling affinity.

Conclusions and Outlook

Mechanical properties of F-actin and ABPs are important for cytoskeletal function; for example, filopodia rely on the rigidity of F-actin bundles, while actomyosin contractility depends on actin filament buckling (32–34). Here, we show a context in which these mechanical properties, such as cross-linker length and filament bending rigidity, are also important for cytoskeletal self-organization. We predict that bundling proteins with larger length differences than $\alpha$-actinin and fascin (27 nm) and polymers with larger persistence lengths than actin filaments ($17\hspace{0.17em}\mathrm{\mu }\mathrm{\text{m}}$) will have even more capacity to sort cross-linkers. Engineered cross-linkers with tunable lengths (for example, made from DNA) may enable controlled experiments (35).

We also demonstrated that the sorting of 2 cross-linkers can be controlled by nonequilibrium factors, such as actin polymerization, and depends on the rates of binding and unbinding. The magnitude of these kinetic effects on sorting may be constrained on nonequilibrium statistical mechanical principles (27, 28), and our simulation framework may provide ways of testing those prior theories if dissipation is properly monitored as in ref. 36.

A possible limitation to our experiments is that the domain sizes we observe may be impacted by interactions between proteins and the coverslip, which seems to affect the dynamics of cross-linkers in domains. Coarse-grained simulations do not have this limitation and indeed exhibit domain flux, domain merging, and domain splitting, motivating future experiments on a passivated or lipid surface, where cross-linkers are expected to be able to unbind from the bundle.

Future modeling can expand on this work by incorporating further molecular details of actin filaments and cross-linkers. For example, we do not account for excluded volume between cross-linkers, a simplification that greatly accelerates our simulations but which can lead to occasional configurations with unphysical overlaps. Moreover, in reality, actin filaments have a helical structure, and cross-linker binding at discrete sites requires aligning of the helical pitches. Additionally, the need for torsional strain on the actin may affect the binding length scale and spacing between cross-linkers of the same type. It may be possible to incorporate these structural characteristics using other simulation frameworks (25, 37, 38).

In this work, we have focused on the origin of sorting behavior in 2-filament bundles previously observed in experiments. In cells, the concentrations of actin and cross-linkers are more than 10-fold higher than what can be used for studies using reconstituted proteins (although the ratio of cross-linkers to actin used is more physiological), and polymerization and cross-linking are regulated by many ABPs (21). Because the actin polymerization rate in cells is much higher and widely varying, we expect that kinetics play an even larger role in sorting. In addition, actin filaments inside of cells are actively kept much shorter than in our in vitro experiments and are on the same length scale or shorter than the cross-linker domains we measure in both experiment and simulation; therefore, mechanisms we observe producing domains on 2-filament bundles likely can produce a complete sorting of cross-linkers onto separate bundles in cells. Once sorted networks are formed, we expect the physical principles and kinetic effects studied in this work help maintain the local concentration and molecular composition of a particular actin network by excluding dissimilar cross-linkers, but it remains less clear which physical or regulatory factors and associated molecular mechanisms set up the initial localization of cross-linkers to different parts of the cell. Thus, simulations and experiments of cellular environments are necessary to determine if the specific mechanical and kinetic sorting principles studied here are sufficient to produce distinct actin network architectures.

Materials and Methods

Instructions and code for running and analyzing all simulations are available at the AFINES github page, https://github.com/Simfreed/AFINES (23, 24, 39). Full details of the AFINES simulation model, a table with simulation parameters used for each calculation, and movies corresponding to Figs. 1, 2, and 5 are available (Movies S1–S3, S6, and S7).

Total Internal Reflection Fluorescence Microscopy Experiments.

Actin was purified from rabbit muscle acetone powder and labeled on surface lysines with Alexa488-succinimidylester (Life Technologies), as described in refs. 40 and 41. Human $\alpha$-actinin-4, human fascin 1 were purified and labeled with Cy5-monomaleimide (GE Healthcare) or TMR-6-maleimide (Life Technologies), as described previously (16). Actin filament bundle lengths were measured using the ImageJ software (42). Additional experimental images can be found in SI Appendix, Fig. S4, and total internal reflection fluorescence (TIRF) movies are provided in Movies S4 and S5.