Compressive mechanical properties of rat and pig optic nerve head

Abstract

Glaucoma is the leading cause of irreversible blindness worldwide. Elevated intraocular pressure (IOP), the primary risk factor for glaucoma, is thought to induce abnormally high strains in optic nerve head (ONH) tissues, which ultimately result in retinal ganglion cell damage and vision loss. The mechanisms by which excessive deformations result in vision loss remain incompletely understood. The ability of computational and in vitro models of the ONH to provide insight into these mechanisms, in many cases, depends on our ability to replicate the physiological environment, which in turn requires knowledge of tissue biomechanical properties. The majority of mechanical data published to date regarding the ONH has been obtained from tensile testing, yet compression has been shown to be the main mode of deformation in the ONH under elevated IOP. We have thus tested pig and rat ONH tissue using unconfined cyclic compression. The material constants C₁, obtained from fitting the stress vs. strain data with a neo-Hookean material model, were 428 [367, 488] Pa and 64 [53, 76] Pa (mean [95% Confidence Interval]) for pig and rat optic nerve head, respectively. Additionally, we investigated the effects of strain rate and tissue storage on C1 values. These data will inform future efforts to understand and replicate the in vivo biomechanical environment of the ONH.

1. Introduction

Glaucoma is the leading cause of irreversible blindness worldwide, anticipated to affect approximately 111.8 million people by 2040 (Tham et al., 2014). Glaucoma is an optic neuropathy that results in visual field loss due to the progressive damage and loss of retinal ganglion cells (RGCs). Elevated intraocular pressure (IOP) is the primary risk factor for glaucoma, and although vision loss can occur at any level of IOP (Leske et al., 2003), all clinically available glaucoma treatments aim to slow the progression of vision loss by lowering IOP. Thus, biomechanics are thought to play an important role in RGC loss in glaucoma. Specifically, under elevated IOP, optic nerve head (ONH) tissues experience abnormally high deformations, which in turn may cause abnormal remodeling of the lamina cribrosa and other load-bearing tissues, direct RGC axonal damage, restriction of blood flow and nutrient supply within the ONH, and pathologic changes in ONH astrocyte phenotype (Burgoyne et al., 2005).

In order to understand how tissue mechanical properties and anatomy influence mechanical strains under IOP, and the corresponding cellular response to those strains, relevant in vitro, animal, and computational models must be developed and characterized. Towards this end, it is essential to quantify the mechanical properties of healthy ONH tissue, which can be used for multiple purposes, such as modeling the overall ONH response to pressure changes, and for creating model systems to mimic ONH biomechanics in vitro. Both pigs (Ruiz-Ederra et al., 2005) and rats (2018) are routinely used as experimental animal models of glaucoma. However, few direct measurements of pig and rat ONH material properties have been reported. Furthermore, the majority of these reported values have been from uniaxial tensile tests, while compression is the predominant mode of deformation of the ONH under elevated IOP (Sigal et al., 2007). We have thus tested pig and rat ONH samples in unconfined compression at several strain rates, and herein report material property values obtained from fitting the stress vs. strain data with a neo-Hookean material model. Here we define the optic nerve head to be comprised of all tissue contained within the scleral canal, extending anterior-posteriorly from the vitro-retinal interface to the posterior sclera.

2. Materials and Methods

2.1. Sample sourcing and preparation

A schematic of the ONH dissection procedure is shown in Figure 1.

Figure 1:

Schematic of sample preparation process for rat (top) and pig (bottom) ONH samples

Pig:

Pig eyes were collected from a local slaughterhouse (Holifield Farms Inc., Covington, GA), and tested on the days of collection. Extraocular tissue was removed by dissection and the optic nerve was cut flush with the sclera. While viewing under the dissecting microscope, a thin section including the ONH was cut perpendicular to the ONH using a gentle sawing motion with a razor blade. The first tissue slice was discarded, with a second slice (approximately 0.5 to 1.0 mm thick) used for testing. This slice was assumed to contain the lamina cribrosa because it had a different appearance than the pure white appearance of the retrolaminar optic nerve. Specifically, it showed a darker marbling pattern that appeared consistent on both sides of the sample. The tissue slice was placed on a cutting mat and a cylindrical sample was cut from the optic nerve region with a 1.0 mm diameter biopsy punch. All samples were kept on ice in phosphate buffered saline (PBS) until testing.

Rat:

ONH samples were obtained from 5 male Sprague Dawley rats, age 5-6 months. After euthanasia by CO2, the eyes were proptosed with forceps, enucleated using curved scissors, and placed in PBS on ice. The optic nerve was cut flush with the back of the eye using microscissors, and a 2 mm square region containing the ONH and peripapillary sclera was excised. By cutting the nerve off flush with the sclera, we ensured that the final sample contained only the glial lamina (Downs et al., 2007; Tehrani et al., 2014). The ONH tissue was then dissected using a microblade (prepared from a razor blade using a blade breaker) to cut away the sclera and optic nerve sheath. One ONH sample was obtained per eye, and all samples were kept on ice in PBS until testing.

2.2. Mechanical Testing and Analysis

Samples were tested in unconfined compression. The boundary conditions on the optic nerve head in situ are relatively complex. Thus, neither unconfined nor confined compression testing in the laboratory can perfectly represent the in vivo loading conditions. We selected unconfined compression as this is a well-accepted testing method which is replicable in a laboratory environment, and which has similarities to the situation in situ. Mechanical testing was performed with a MicroSquisher (CellScale; Hamilton, ON) mechanical testing system. All tests were performed in PBS between 35 and 37 °C.

In all cases, cylindrical samples were prepared such that compression was applied along the nerve axis. ONH samples were loaded into the Microsquisher and first subjected to a 50 μN (pig) or 3 μN (rat) preload. Under magnification in the MicroSquisher interface, sample thickness was observed to be uniform before the application of a preload. Samples were compressed to reach the preload value over the course of 120s. The loading platen was subsequently withdrawn to return to 0 μN over another 120s, and finally the preload was reapplied over a third 120s window. These preloads were empirically chosen to ensure full contact of the sample with the loading platen. After the application of the preload, both porcine and rat ONH samples were subjected to 5 cycles of unconfined compression to 15 % compressive deformation over 180 s (5% per minute) or 22.5 s (40% per minute).

In stress and strain calculations, porcine samples were all taken to have a 1 mm diameter, equal to that of the biopsy punch used to cut the sample, and the thickness of each sample was measured in the MicroSquisher interface. Rat ONH samples were imaged with a microscope after testing of all samples had been completed, and the cross-sectional area was computed in ImageJ (Fiji). As neural tissue has been shown to demonstrate hyper-elastic behavior (Franceschini et al., 2006), the first Piola-Kirchoff stress vs. Green-Lagrange strain curve from the loading phase of each cycle was fit with the analytical solution for uniaxial unconfined compression of an incompressible neo-Hookean solid: $\frac{H}{\pi R_0^2}=2C_1\left(\frac{1+\Lambda +{\Lambda }^2}{{\Lambda }^2}\right)(1-\Lambda )$, where H is the applied load, R₀ is the starting radius of the sample, C₁ is a material constant, and Λ is the compression ratio (Humphrey, 2002). Friction between the sample and compression plates was assumed to be negligible, as no barreling of the samples was observed at peak strains.

2.3. Statistical Analysis

Throughout the manuscript, values are expressed as the mean [95% confidence interval]. Values of the neo-Hookean fitting parameter C₁ shown in Figure 1 were compared across cycle and species using a 2-factor ANOVA and Sidak multiple comparisons tests in GraphPad Prism v7.02. The normal distribution of data in each group of Figure 2 was verified with the Shapiro-Wilk tests, p ≥ 0.22. The effect of strain rate (Figure 2) and tissue storage on cycle 5, steady-state C₁ values were evaluated using paired and unpaired 1-tailed Student’s t-tests, respectively.

Figure 2:

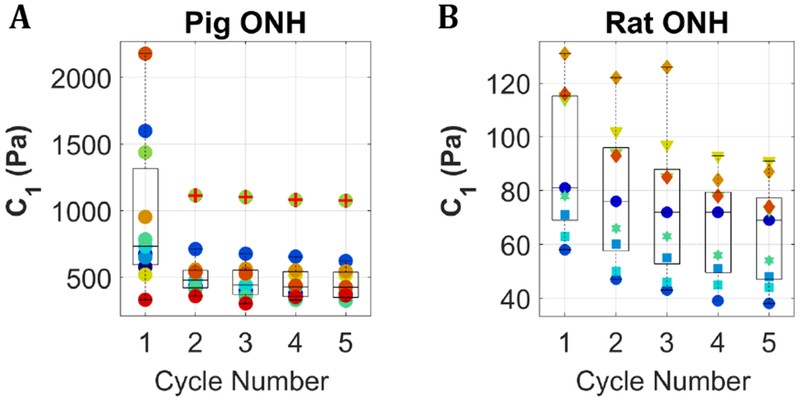
C₁ values for pig and rat optic nerve head samples subjected to cyclic unconfined compression at a 5%/minute strain rate. Colors correspond to individual samples. (A) shows 11 samples. Pig eyes were obtained from a slaughterhouse as a mixed lot on three separate days, thus we can only be certain these samples came from ≥ 7 pigs. (B) shows 9 samples from 5 rats. Different marker shapes correspond to different animals. The central line in each box marks the median, and the box edges mark the 25th and 75th percentiles. Whiskers cover the range of all data points not considered outliers. One sample in the pig data set (panel A) had a consistently high C₁ value and was identified as an outlier in cycles 2–5; this is denoted with a red plus sign over the green point markers.

3. Results

The material constant C1 in the neo-Hookean hyperelastic model, obtained from fitting the loading portion of 5 sequential cycles at 5% per minute to 15% compressive deformation, was used to describe the compressive mechanical properties of pig and rat ONH (Figure 1). Across all samples shown in Figure 1, both rat and pig, the average percent decrease in C₁ between cycle 4 and cycle 5 was 2.4%. Samples with a decrease in C₁ from cycles 4 to 5 of greater than 10% were assumed to have not reached equilibrium and were not included in subsequent analysis; this resulted in the removal of 3 porcine samples. Comparison of C₁ across all cycles showed no significant difference between cycles 2-5 for pig ONH (p ≥ 0.99) and no significant difference between any cycles for the rat ONH (p ≥ 1.0), indicating converged mechanical behavior under the applied loading conditions by cycle 5. The mean [95% confidence interval] C₁ values, excluding a single outlier in the pig data set, were 428 [367, 488] Pa and 64 [53, 76] Pa for pig and rat ONHs, respectively. Pig and rat equilibrium C₁ values were significantly different for all cycles, p ≤ 0.0007. The magnitudes of the 95% confidence intervals were 28% and 36% of the mean C₁ values for pig and rat, respectively.

A subset of the samples represented in Figure 1 was also subjected to five cycles of compressive loading to 15% strain at a higher loading rate of 40% per minute (Figure 2). Mean pig ONH C1 values increased from 464 [394, 535] Pa to 725 [446, 1004] Pa at the higher strain rate, although this increase was not statistically significant (p = 0.110). Rat ONH C₁ values increased significantly from 81 [74, 89] Pa to 121 [105, 137] Pa (p = 0.027).

Finally, we evaluated additional porcine ONH samples 24-36 hours after slaughter (data not shown), as it has been suggested that storage for up to 3 days at 4 °C does not significantly affect scleral mechanical properties (Girard et al., 2007). We observed a decrease in mean C₁ values of 29% and 25%, at 5%/min and 40%/min strain rates, as compared to samples tested within 12 hours of slaughter. This difference was statistically significant at the 5%/min strain rate (p = 0.022), but not at 40%/min (p = 0.151).

4. Discussion

We observed significantly higher ONH stiffness in pigs than in rats. This difference was expected, since pigs, like primates, have a collagenous lamina cribrosa (LC), while rats have a non-collagenous glial lamina. The magnitude of the C1 values we report for both pig and rat ONH are much lower than previously reported values for the ONH, which was also expected, since most previous reports were based on tensile testing. We evaluated ONH samples under compression in the anterior-posterior direction; while the in situ deformations are complex this mode of deformation is seen to have the largest magnitude in situ (Coudrillier et al., 2016).

At 15% compression, our porcine C1 value of 428 [367, 488] Pa at the 5%/min strain rate corresponds to a Young’s modulus of approximately 3.05 kPa. Spoerl et al. reported a relatively high modulus of 17.1 MPa for porcine LC, calculated as the tangent tensile modulus at 20% strain. According to their measurements porcine LC was stiffer than the 11.8-15.6 MPa they reported for human LC (Spoerl et al., 2005). Stiffnesses from 140 to 380 kPa have been used (Sigal et al., 2004) and determined (Edwards and Good, 2001) in mathematical models of the human LC. Braunsmann et al. measured a Young’s modulus of 17.2 kPa for human LC, as measured by AFM indentation, which is both closer in testing method and value to our finding (Braunsmann et al., 2012).

At 15% compression, our rat C1 value of 64 [53, 76]at the 5%/min strain rate corresponds to a Young’s modulus of approximately 456 Pa. Terai et al report a surprisingly high tangent modulus of 8.77 MPa at 5% strain (Terai et al., 2012). This is higher than the modulus they report for the peripapillary sclera, calling these findings into question.

In the rat ONH we also observed a significant, 1.5 fold increase in C₁ values under increased strain rates. This same trend was observed in the porcine ONH, yet the increase was not significant. In vivo, ocular tissues are exposed to quasi-static loading resulting from “steady” IOP, as well as oscillatory loading resulting from cyclic variation in IOP with the cardiac cycle (“the ocular pulse”), which occurs at approximately 1 Hz in pigs and humans, up to approximately 5 Hz in rats. The typical fluctuations in IOP are up to 4 mmHg, which correspond to 0.5% to 3% macroscopic compressive strains in pigs (Coudrillier et al., 2016), varying between animals and with the baseline IOP about which the fluctuation is imposed. These oscillatory strains in the ONH correspond to strain rates of c. 60 - 360 %/min in the pig and 300 - 1800%/min in the rat. We chose a high strain rate of 40%/min as this was the fastest strain rate we could reliably apply with the MicroSquisher. Thus, our results indicated that strain rate dependence of ONH material properties is highly relevant in the rat (the effect would likely be more exaggerated at physiological high strain rates); this should be taken into account when developing materials and experimental paradigms for rat-derived cell culture or computational models. Strain rate dependence of material properties in the pig may also reach significant levels at higher physiological strain rates.

The values reported here will provide useful information for modeling and experiments going forward, particularly as compression has been shown to be the main mode of deformation in the ONH (Sigal et al., 2007). Furthermore, neo-Hookean material models are readily available in most commercial finite element packages; reporting these model parameters will facilitate the incorporation of our findings into finite element models of the ONH. Accounting for the differences we measured in compressive mechanical properties between the porcine lamina cribrosa and the rat glial lamina may be important in the development of animal-specific computational models. Furthermore, knowledge of physiological compressive material properties for the pig and rat ONH will enhance our ability to develop in vitro platforms to study astrocyte (Mulvihill et al., 2018) and RGC mechanobiology in mechanical environments relevant to specific cell lines.

Figure 3:

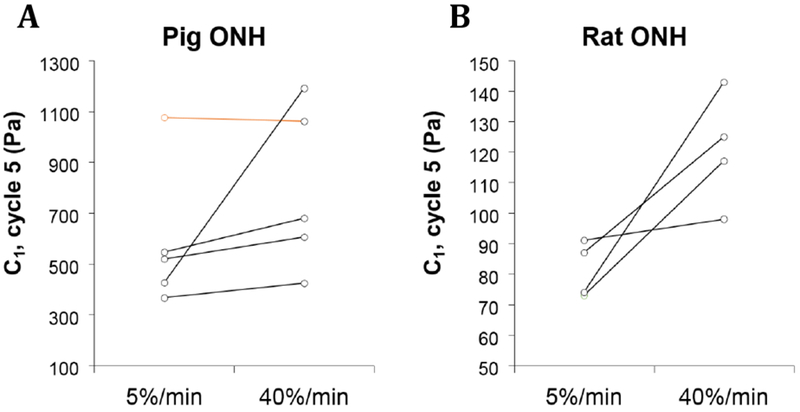
C₁ values for a subset of pig (A) and rat (B) samples that were tested at both 5%/min and 40%/min strain rates. The sample identified as an outlier in the larger porcine 5%/min data set (Figure 1) is indicated in orange.