Unidirectional brain to muscle connectivity reveals motor cortex control of leg muscles during stereotyped walking

Abstract

In lower mammals, locomotion seems to be mainly regulated by subcortical and spinal networks. On the contrary, recent evidence suggests that in humans the motor cortex is also significantly engaged during complex locomotion tasks. However, a detailed understanding of cortical contribution to locomotion is still lacking especially during stereotyped activities. Here, we show that cortical motor areas finely control leg muscle activation during treadmill stereotyped walking. Using a novel technique based on a combination of Reliable Independent Component Analysis, source localization and effective connectivity, and by combining electroencephalographic (EEG) and electromyographic (EMG) recordings in able-bodied adults we were able to examine for the first time cortical activation patterns and cortico-muscular connectivity including information flow direction. Results not only provided evidence of cortical activity associated with locomotion, but demonstrated significant causal unidirectional drive from contralateral motor cortex to muscles in the swing leg. These insights overturn the traditional view that human cortex has a limited role in the control of stereotyped locomotion, and suggest useful hypotheses concerning mechanisms underlying gait under other conditions.

One sentence summary:

Motor cortex proactively drives contralateral swing leg muscles during treadmill walking, counter to the traditional view of stereotyped human locomotion.

1. Introduction

Walking is a complex task that requires the coordinated and flexible activation of several muscles to meet ever-changing environmental challenges. Gait control involves integration of sensory signals and consequent adjustments in descending supraspinal motor commands and spinal neuronal circuits (Grillner, 2011). Basic locomotor patterns are mainly generated by spinal interneuronal networks that integrate descending signals with peripheral afferent signals to achieve specific locomotion schemes (Brooks, 1986; Takakusaki, 2013). Sensory afferent information contributes to corrective reflexes following sudden perturbations and may be used to adapt and update gait patterns (Nielsen, 2003).

Several research groups showed in animal models strong involvement of the cerebellum the motor cortex and the pyramidal tract of the corticospinal tract in visually-guided locomotion and precision stepping (Drew et al., 2008; Drew and Marigold, 2015; Rossignol, 2010). Other groups (Armstrong, 1988; Brown, 1911; Grillner, 1985; Jordan, 1998; Lundberg, 1979; Rossignol, 2000) have provided evidence that cortical activity is not necessary for generating the basic stereotyped locomotion patterns of most lower animals. In fact, even in the absence of any supraspinal input to the spinal cord, spinal networks have the capacity of generating the basic locomotor rhythmicity in chronic spinalized animals.

While it is known that the cortex proactively controls voluntary and precise movements and is involved only in “high-level” motor planning (e.g., gait initiation, addressing obstacles, etc.), its involvement in stereotyped tasks is only hypothesized, because of the limits of available techniques (Beloozerova and Sirota, 2003; Drew and Marigold, 2015; Gossard et al., 2011; Marple-Horvat and Criado, 1999).

Imaging studies based on near-infrared spectroscopy (NIRS) demonstrated that walking is bilaterally associated with activity in primary sensorimotor cortices and supplementary motor areas (Miyai et al., 2001). Studies based on functional magnetic resonance imaging (fMRI) have also supported the involvement of supraspinal structures during walking-related motor imagery tasks (Cunnington et al., 2002, 2005). These techniques lack however of the necessary high dynamic (NIRS) and portability (fMRI) required to detect intra-stride changes in brain activity during ambulation.

Electroencephalography (EEG) is the only non-invasive brain imaging modality that has the potential to achieve the required temporal resolution (Makeig et al., 2009; Menicucci et al., 2014). So far, studies using high-density EEG combined with independent component analysis (ICA) and source localization techniques have shown that electrocortical dynamics, particularly in the sensorimotor cortex, exhibits intra-stride patterns of activation and deactivation (Cevallos et al., 2015; Chéron et al., 2012; Gramann et al., 2011; Gwin et al., 2011; Severens et al., 2012). However, there are conflicting pieces of evidence as to how compromising gait-related movement artifact is to ICA analysis of neural data (Snyder et al., 2015). In particular (Nathan and Contreras-Vidal, 2015a), suggest negligible motion artifacts during walking, while (Castermans et al., 2014) raise doubts on the cortical origin of time-frequency data, time-locked to the gait cycle. In fact, gait-locked artifacts overlap in time and frequency with brain activity. Other authors such as (Kline et al., 2015) and (Oliveira et al., 2016) studied the role of artifacts on artificially-generated brain activity using head phantoms. This latest work, suggests that ICs extracted from moving heads could reliably represent the content of a stationary condition, however the stereotyped nature of movement artifacts has not been proven yet.

Very recently, Kline et al. (2016). showed within-stride modulation of cortico-cortical connectivity. However, more conclusive evidence of cortical control would require the application of a methodology similar to the one used in animal experiments, where functional connectivity between recordings of individual or populations of brain cells and motor output, has been demonstrated during motion (Halliday et al., 1995; Lemon, 1993). A similar approach has been used to reveal frequency-coherent activity between localized recordings from the motor cortex and the EMG generated during human treadmill walking (Petersen et al., 2012), but such cortico-muscular functional connectivity is not informative of the existence of a causal relationship between brain regions and muscles.

The aim is that of defining new methodological approaches to verify the existence of a true brain-to muscle link during this task. We present a methodology (see Materials and Methods) that extends gait-related time-frequency methods and enabled us to analyze simultaneous EEG and EMG recordings. We were able, by highlighting the existence of strong gait phase locked, uni-directional cortico-muscular effective connectivity, to provide evidence for the first time that cortical motor areas are responsible for temporally-precise control of leg muscle activity during stereotyped treadmill walking.

2. Materials and methods

2.1. Summary

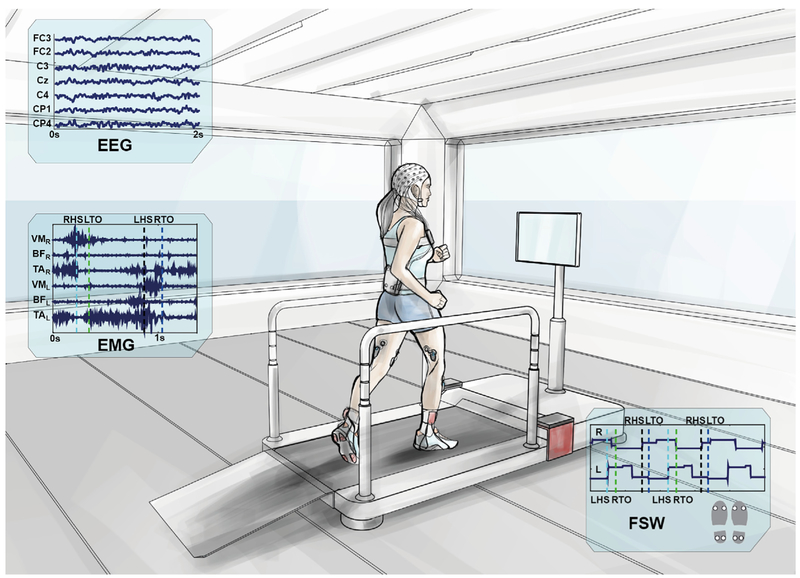
To investigate the neural correlates of gait, the experimental set-up shown in Fig. 1 was used to simultaneously record 64-channel EEG signals and 6 lower-limb EMG signals (Tibialis Anterior – TA, Biceps Femoris – BF, Vastus Medialis – VM, bilaterally) from eleven able-bodied subjects (mean age 30 ± 4 years) who walked on a treadmill at 3.5 km/h in two 10-min time blocks. Four footswitches enabled identification of the gait phase of each leg. The full EEG and EMG datasets (collected during rest and walking conditions) were first time-aligned, and merged. In the pre-processing phase we used Artifact Subspace Rejection (ASR) (Kothe and Jung, 2015) and reliable Independent Component Analysis (ICA) (Artoni et al., 2014) to decompose continuous EEG data into maximally-independent processes. Independent Components (ICs) representing muscle, ocular and other artifacts were removed from the data. We then epoched the EEG and band-pass filtered the EMG time-locked to each gait cycle and visually inspected them for prominent artifacts. Underlying brain source signals were determined by processing scalp EEG data using source localization functions in the eConnectome Matlab toolbox (He et al., 2011). Several regions of interest (ROIs) were defined according to Broadmann Areas near the motor cortex and effective connectivity or ROIs with each muscle was estimated using the Directed Transfer Function (DTF) method. Finally, we used ROIs data to decode EMG envelopes and we confirmed the hypothesis of data stationarity during walking via multiple model ICA (AMICA) (Palmer et al., 2007b).

Fig. 1. Experimental setup.

A participant walking on the treadmill. The amplifiers for EEG and EMG recordings are fixed nearby. Cables departing from the EEG cap are securely fastened to the subject's waist and connected via the Acticap Control Box to the EEG amplifiers via a 2-m custom-made cable, fastened to the hand rails to minimize cable movements. EMG electrodes (Tibialis Anterior – TA, Biceps Femoris – BF, Vastus Medialis – VM) are pre-amplified and wirelessly connected to the BTS free EMG 300 amplifier. Four footswitches (FSW) were attached to the shoe soles, two on the forefoot and two on the heel and synchronized to the EMG as they were connected wirelessly the same amplifier (BTS). EEG and EMG synchronization was performed via an external synchronization trigger. Line noise and EEG-EMG interference was checked before each recording session and artifacts were minimized: subjects fixed their gaze to the screen in front of them throughout the walking task and were asked to relax. Distractors were minimized as ambient lighting was kept constant during the experiment and across sessions, operators were outside the subject's field of view and the room was kept quiet. Subjects (mean age 30 ± 4 years old) walked on the treadmill at 3.5 km/h in two 10-min time blocks after a 5-min resting state period. Acclimation to the experimental condition was achieved by a preliminary 3-min walking. EEG and EMG data were recorded continuously and were then synchronized, time-aligned, merged and segmented offline for further analysis.

Signals recording (Fig. 1).

EEG signals were recorded using a 64-channel EEG amplifier (SD MRI, Micromed S. p.A, Italy) sampling at 2048 Hz/channel and a custom signal pre-amplifying active electrode cap (actiCAP, Brain Products GmbH, Germany). The montage was chosen in accordance with the 5% International 10/20 System (Oostenveld and Praamstra, 2001). Careful scalp preparation ensured electrode impedance was below 20 kΩ in at least 95% of derivations, both at the beginning and the end of the recordings. EMG electrodes were placed according to SENIAM guidelines (www.seniam.org) on 3 muscles of each leg, namely Tibialis Anterior (TA), Vastus Medialis (VM) and Biceps Femoris (BF), which were simultaneously recorded with a wireless EMG system (BTS Free EMG 300) at a sampling rate of 1000 Hz. A common trigger was sent both to EMG and EEG acquisition systems multiple times at the beginning and end of each session to enable robust, minimum jitter in offline synchronization of both devices.

EMG data were resampled and aligned to the EEG before further preprocessing. Throughout the analysis, to avoid misalignment artifacts, EEG and EMG data were treated as a single multivariate data series. Four footswitches (two under the heel and two under the toes for redundancy), were wirelessly connected to the EMG system, recorded with the same sampling frequency (1000 Hz). These data were used to segment the gait events (Right/Left Heel Strike – LHS/RHS and Right/Left Toe Off – LTO/RTO). All recorded events were carefully inspected and data pertaining to improperly-segmented gait cycles were removed.

Special precautions (Fig. 1).

EEG artifacts in general can be classified as physiological or non-physiological. The former include e.g., ocular movement artifacts (eye blinks, lateral and vertical eye movement), muscle (e.g. jaw clenching, neck muscle contraction), heart. The latter include e.g., line noise, electrode detachment, cable movement interference etc. The walking task increases the influence of artifacts by introducing eye bounce (i.e. eye stabilization while fixing a point), cable movements, increased neck and facial muscle activation, increased non-stationarity of line noise interference (as the subject moves into space) and electrode/gel coupling shifts. The difficulty in removing Mobi artifacts is mainly due to the coupling of eye bounce, neck muscle contractions and mechanical artifacts to the walking task itself. While there is no definite way to exclude artifact interference as yet, during the recording sessions particular precautions were taken so as to avoid movement artifacts and other confounding effects as far as possible.

As shown in Fig. 1, the Acticap Control Box (ACB) receiving the cables departing from the EEG cap was securely fastened to the subject's waist. The ACB was connected to the EEG amplifier via a 2-m cable, which was fastened to the hand rails of the treadmill thus minimizing cable movements. The use of active pre-amplified electrodes also helped minimizing cable movement interference. Before each session, we confirmed the lack of any EEG-EMG interference and that the experimental set-up was clear of recording-impairing line noise. This was done by visual inspection of real time data before acquisition and by checking the effect of notch filters in the Micromed recording interface.

A preliminary 3-min walking period allowed acclimation to experimental conditions. Subjects were asked to fix their gaze to a point at eye level in front of them, and were asked to relax throughout the experiment and to avoid, as far as possible, turning or bobbing their head while walking. This helped minimize artifacts arising at the EEG electrode-gel-skin interface. To avoid confounding effects, ambient lighting was kept constant throughout the experiment and ambient noise was minimized. The recording equipment and operators were kept out of the subject's field of view.

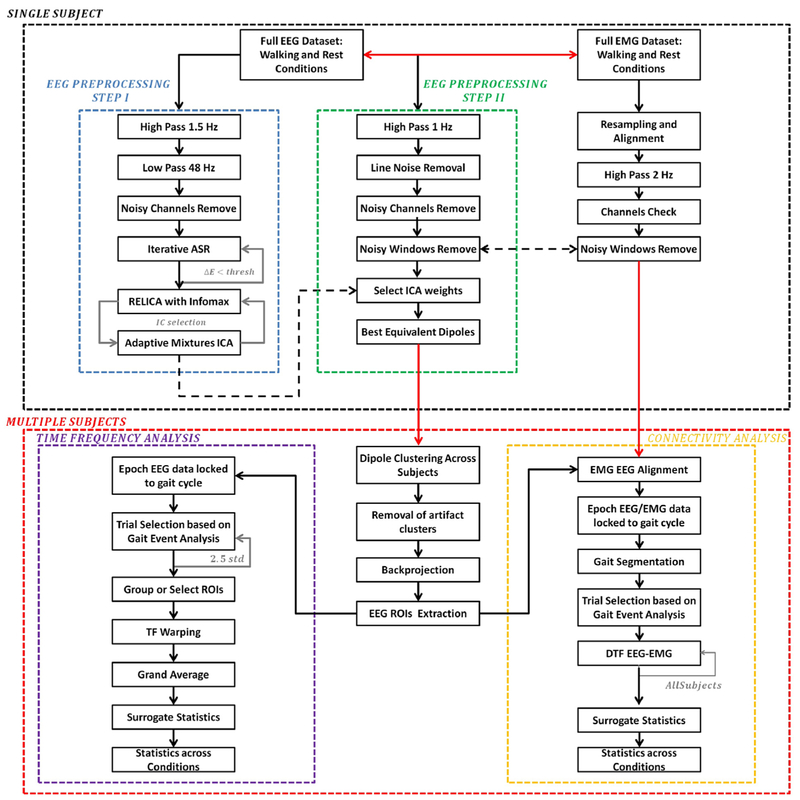
EEG processing outline (Fig. 2).

Fig. 2. Schematic showing the EEG and EMG processing steps.

Analyses were performed first at a single subject level (black dotted box) and results were combined to a multiple-subjects level. Single-subject EEG data went through two EEG preprocessing stages, namely Step I (blue box) and Step II (green box). The first is more aggressive and it is specific to maximize extracted ICs reliability. ICs are applied to data processed according to the second preprocessing step, more conservative, with the aim of retaining the maximum amount of information to be used in subsequent time-frequency and connectivity analyses. EEG and EMG synchronization was maintained throughout the whole preprocessing. Data were further cleaned at group level by removing artifact dipole clusters. Source-level data were extracted and put through a time/frequency analysis processing step (violet box). Epoched EEG trials, locked to the gait cycle were selected based on gait events, grouped according to several regions of interest (ROIs), warped and averaged across subjects. Connectivity analysis was finally performed on joint aligned EEG/EMG data (yellow box).

EEG data recorded during walking, even given the experimental precautions described above, are generally prone to movement and other artifacts (Kline et al., 2015). We therefore devised a two-step data pre-processing procedure to minimize the chance that final results were affected by movement artifact. Fig. 2 shows the outline of data pre-processing and analysis steps. Data were analyzed using Matlab (Mathworks Natick, MA, USA) scripts based on the EEGLAB toolbox (Delorme and Makeig, 2004); EEG signals were decomposed into maximally-independent processes via extended-infomax Independent Component Analysis (ICA) (Makeig et al., 1996). Within the first stage (EEG Preprocessing Step I, green box in Fig. 2), dipolarity (Delorme et al., 2012) and reliability (Artoni et al., 2014) of independent components (ICs) extracted were maximized. The ICA decomposition of this first analysis was then reapplied to the second preprocessing stage (EEG Preprocessing Step II, red box in Fig. 2).

EEG Preprocessing Step I (Figs. 2 and 3).

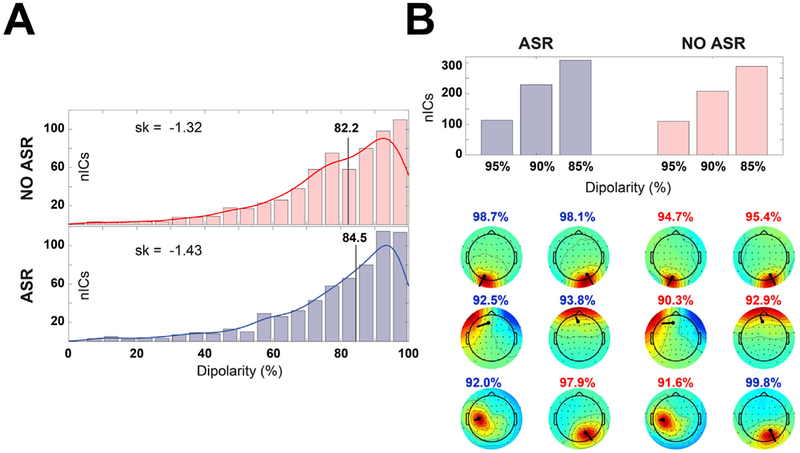
Fig. 3. ASR effect on ICA decomposition.

(A) Distribution of IC dipolarity without (top panel) and with (bottom panel) ASR preprocessing. The vertical line represents the median of the distribution, the skewness is reported on the left. (B) Number of quasi dipolar (dipolarity = 95%) and dipolar (dipolarity = 85%, 90%) ICs extracted with and without ASR preprocessing (top panel). The bottom panel shows a comparison of select IC scalp maps extracted with (left) and without (right) ASR from a representative participant (muscle artifacts – first row; ocular artifacts – second row; brain ICs – third row). IC dipolarity is represented in blue/red whether is higher/lower than the corresponding ASR or NO-ASR value.

The EEG data were first high-pass filtered using a zero-phase 1.5-Hz cutoff, 24th-order Chebyshev type II filter and low-pass filtered using a zero-phase 48-Hz, 71st-order Chebyshev type II filter to remove slow drifts and high frequency noise respectively. The data were then resampled to 512 Hz. Corrupted channels with prolonged prominent artifacts (e.g. flat line, frequent detachments, excessive line noise etc.), when any, were removed by visual inspection (Wagner et al., 2014). Remaining channels were channel-average re-referenced. Next, artifact subspace reconstruction (ASR) (Kothe and Jung, 2015) was used to remove high-amplitude artifacts from the EEG recorded during walking. ASR was calibrated on the data collected during the rest (quiet standing) condition, and applied to data collected during walking. ASR uses a short-time Principal Component Analysis (PCA) of the “calibration” data to identify a nominal-variance subspace. Principal Components (PCs) in new data windows are then classified into nominal variance PCs (EEG-like) or high variance PCs (artifacts) based on a user-defined threshold (default 3–5 standard deviations). The threshold for the ith PC depends on the mean variance in calibration EEG data along its direction. The identified high variance subspace in new data (walking task) is then removed and reconstructed from the nominal-variance subspace. ASR may also remove useful brain activity along with artifacts. To minimize this risk we iterated the ASR artifact removal procedure several times using a 500-ms sliding window and a lax (20 standard deviations) threshold that preserves EEG-like components while ensuring the removal of outliers and extreme mechanical artifacts. It is reasonable to assume in fact that movement-related true brain activity does not have variance greater than 20 standard deviations with respect to mean resting brain activity variance in any principal direction.

After each iteration we noted the L1-norm of the difference between the original and processed data (μ), normalized by dividing by the L1-norm of the original data. The iterative procedure was stopped at iteration i when $\frac{{\mu }_i-{\mu }_{i-1}}{{\mu }_{i-1}}$ < 5%.

This procedure was similar to the REMOV method (Artoni et al., 2012a) and reduced the impact of outliers. Finally, by visual inspection we identified epochs containing high-amplitude artifact, prominent high-frequency neck muscle activity, and other irregular artifacts and removed them. As with any calibration-statistics-based artifact-removal method, ASR may remove useful brain activity along with artifacts or alter the data in unpredictable ways. For this reason, ASR was only used as a preprocessing step in the “EEG Preprocessing Step 1” phase to maximize the reliability of the ICA decomposition that is then applied on more conservatively (non-ASR) processed data.

Remaining EEG data were submitted to ICA decomposition with an AMICA (Palmer et al., 2007b) core and GPU-processed infomax RELICA (Artoni et al., 2014) resampling. Within AMICA, data whose likelihood under the AMICA-derived model was more than five standard deviations from median likelihood were removed. This procedure was applied five times at five-iteration intervals beginning after the first five AMICA iterations. The maximum number of iterations was set to 6000. Given a multivariate data series X (n_channels, t) ICA computes an unmixing matrix W such that sources S = WX are maximally independent. Rows of W represent the weights applied to each channel to obtain the corresponding sources S. The i^th column of A represents the weight of the i^th IC on each EEG channel and can be represented as a “Scalp Map” (see Fig. 4), which can be given as input to a source localization algorithm (e.g., dipfit function in the EEGLAB toolbox). In (Delorme et al., 2012), of 22 blind source separation approaches AMICA was shown to a) remove the most mutual dependence between channel pairs in high-density EEG data sets, and b) to separate the EEG data into the most ICs whose scalp projections (scalp maps) fit closely to a brain-based equivalent dipole, consistent with generation by spatially coherent local field activity across a small patch of cortex.

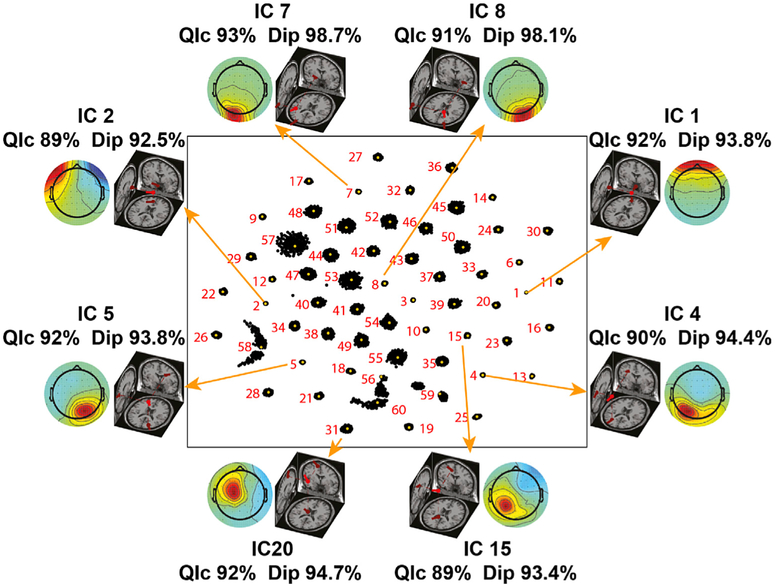
Fig. 4. Representative reliable ICs.

Scalp maps and respective equivalent dipole locations of eight reliable independent components identified using RELICA in the data of a representative participant. Each IC is connected by an arrow to its relative cluster. Each dot represents a particular IC of one (out of 150) ICA run. The more compact the cluster the higher the stability of a IC to small variations in the original data (bootstrapping). IC1 and IC2 account for vertical and lateral eye movement artifacts and IC7 and IC8 account for left and right neck muscle activity respectively. The high quality index (QIc) values for these ICs (respectively 92%, 89%, 93%, 91%) is consistent with the relative compactness of their RELICA IC clusters, and their high dopolarity is ascribed to the short electrode-source distance and power of such artifacts. Artifactual (non-brain) components with high dipolarity (Dip>90%) and replicability quality index (QIc>85%), and with equivalent dipole locations outside the brain volume such as these were removed from the data before proceeding with further analyses. IC4, IC5, IC15, and IC20, instead, represent meaningful, brain-based central, left, and right mu rhythm processes with high dipolarity and QIc. This 2D representation of the IC space enables also to detect possible ICA decomposition artifacts, i.e., components that might not have been successfully separated, by their “mustache”-like distribution (e.g. IC56).

Dipolarity (i.e. IC scalp map variance explained by the best-fitting equivalent dipole – see (Artoni et al., 2014)) for details on how to compute it – was used as benchmark to test the effect of ASR on the ICA decomposition. We replicated the ICA decomposition with and without ASR correction. We compared the median and skewness of the dipolarity distribution across all subjects (Fig. 3, Panel A) and the number of ICs respectively with 85%, 90% and 95% dipolarity (i.e., “quasi-dipolar” (Delorme et al., 2012)). We also compared the dipolarity of select meaningful ICs for a representative participant (Fig. 3, Panel B). ICs with ASR preprocessing exhibited slightly higher dipolarity than ICs without ASR preprocessing (median 84.5 Vs 82.2; skewness −1.43 Vs −1.32).

In order to benchmark the stability of ICs, EEG data were resampled 150 times using the RELICA framework (Artoni et al., 2014) with point-by-point resampling (Artoni et al., 2012b). Within RELICA, ICs were extracted using a GPU-based implementation of Infomax ICA (Bell and Sejnowski, 1995), CUDAICA (Raimondo et al., 2012), whose relative speed on CUDA-enabled workstations made 150 bootstrap repetitions feasible. ICs were then clustered (within subjects, across repetitions) according to their mutual similarity as in (Artoni et al., 2014) into a number of clusters equal to the number of scalp channels. Within the RELICA approach original continuous EEG data are point-by-point resampled 150 times before performing each time a ICA decomposition. The idea behind this approach is that a reliable component (i.e., not a result of algorithm instability, noise, mechanical artifacts) should be both stable (very similar in every decomposition) and dipolar (fitted by an equivalent dipole with low residual variance). ICs within each of the 150 decompositions are pooled together and clustered according to their mutual similarity defined as the matrix of absolute values of the correlation coefficients between IC time courses (Fig. 4). Obviously, the compactness of the cluster is a measure of the stability of the component. Ideally, a perfect cluster, i.e., collapsed onto just one point, would indicate a component is identical in every decomposition.

ICA decompositions in which more than 10% of the ICs were not separated by this procedure into different clusters were excluded to prevent non-converging ICA runs from skewing the decomposition. Clustering was then performed again on the remaining ICs as explained in (Artoni et al., 2014). Within RELICA ICs extracted could be associated with a quality index (based on their cluster size) that allowed determination of their reliability. In particular, the disposition of the dots in Fig. 4 can indicate which ICs were not extracted properly. For example, the IC58 cluster is elongated and split so it may reflect two similar components active in portions of the data. The IC56 cluster is also elongated and the centroid is at the edge of the cluster, and IC57 cluster is widely spread out compared to other clusters (e.g. IC1, IC4, IC5). A “mustache”-like RELICA distribution (e.g. IC56) does not allow a selection of a representative centroid of the cluster. These particular clusters might be the result of a combination of different components that were not successfully separated by ICA, given the limitation of the number of sources extracted to the number of channels available. Else they might arise through decomposition artifact (perhaps through a convergence issue). Therefore, these ICs were not removed from the data outright but held out from further analysis (e.g., from clustering of ICs across subjects).

Due to the time-consuming nature of the AMICA decomposition RELICA was applied using Infomax as core ICA algorithm. To combine the advantages of RELICA with the accuracy of AMICA decompositions (Delorme et al., 2012) we paired RELICA to AMICA ICs based on the absolute value of the correlation coefficients between their time courses. This enabled to associate Infomax-RELICA quality results to AMICA ICs and use the latter in next analyses.

EEG Preprocessing Step II (Figs. 2 and 4).

More conservative preprocessing (see Green box in Fig. 2) was performed to minimize the removal of brain activity while maximizing the quality of the ICA decomposition. Raw data were high-pass filtered with a zero-phase, 1.0-Hz, 24th-order filter before removing line components with a custom 50-Hz comb notch filter with no real poles that maintains frequency content at low (<1.5 Hz) frequencies (Menicucci et al., 2014). Epochs containing high-amplitude artifact potentials, high-frequency muscle noise, and other irregular artifacts were removed from the continuous data by visual inspection while maintaining the alignment with the EMG signals. No ASR procedure was performed to preserve EEG activity. The ICA weights found in EEG Pre-processing Step I were reapplied to the Step II dataset. Electrode positions were aligned to the standard MNI brain template (Montreal Neurological Institute Quebec, Canada). Only dipolar ICs (accounting for at least 82% of the variance of a given IC scalp projection map) were considered. To prevent unreliable ICs from obfuscating across-subject source-level analyses, only stable ICs as per RELICA (quality index > 82%) were used in further analyses. The retained ICs for each subject were categorized as brain or non-brain based on the Tailarach coordinates of their (best-fitting) equivalent dipole and their time-frequency transforms and power spectra.

EMG preprocessing (Fig. 2).

EMG data were filtered with a 2-Hz high-pass filter (24th order, Chebyshev type II). The EMG channel signals were checked for large drifts, discontinuities, and flatline periods. Artifacts arising through, e.g., electrode displacement, loss of scalp contact, etc., were removed by visual inspection. Artifact-laden EMG epochs were removed also from the EEG dataset.

Group level analysis (Fig. 5).

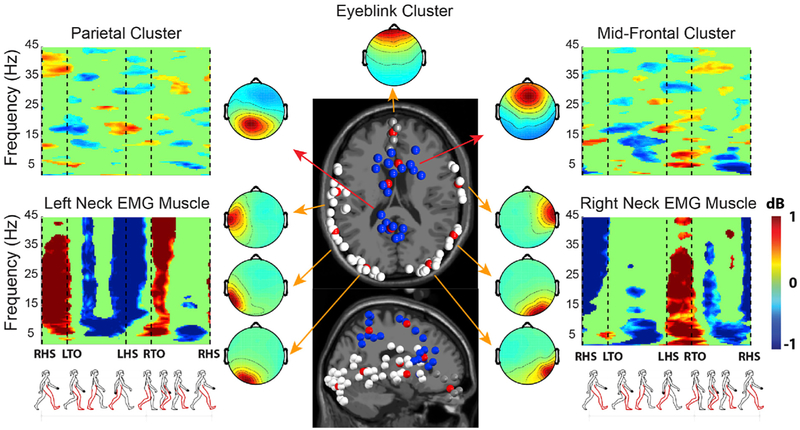
Fig. 5. Artifact and brain IC clusters.

Cluster-mean time/frequency power ratios (in dB) relative to the mean gait cycle spectrum, cluster-mean dipole locations (red balls) and cluster-mean scalp maps for several independent component (IC) clusters (neck muscles, ocular, mid-frontal and superior parietal). Grand-average time-frequency amplitude ratio to the mean gait cycle spectrum plots (ERSP), are masked for significance (p < 0.05); non-significant deviations are shown in green. Note the gait-appropriate EMG patterns (left neck muscles active during beginning and end of the left leg swing phase, right neck muscles during the right leg swing phase). Muscle artifacts show the typical widespread activity localized over many inferior scalp areas. This summary representation allows to correctly identifying artifact clusters and group together functionally-similar IC processes on the basis of multiple measures in the time and frequency domains, thus decreasing the chance of mistaking a non-brain artifact IC for a brain IC.

ICs for each subject found to be reliably present (as above) were clustered across subjects by EEGLAB routines (Delorme and Makeig, 2004) using IC distance vectors combining differences in dipole location, power spectral density (1–45 Hz), Event-Related Spectral Perturbations (ERSPs), and the scalp projection pattern (scalp map) for each IC. Given the high dimensionality of time-frequency features yielded by ERSP images, the dimensionality of the resulting joint vector was reduced to fifteen principal components by principal component analysis (PCA), which explained 95% of the features variance. Vectors were clustered using a k-means (k = 15) algorithm implemented in EEGLAB. Components further than three standard deviations from any of the resulting cluster centers (Outlier ICs) were relegated to a separate “outlier” cluster. The compactness of the group IC clusters, a measure of their inter-subject reliability, can be used in conjunction with the RELICA approach to assess within-subject reliability (Artoni et al., 2014).

Time-Frequency Analysis (Figs. 5 and 6).

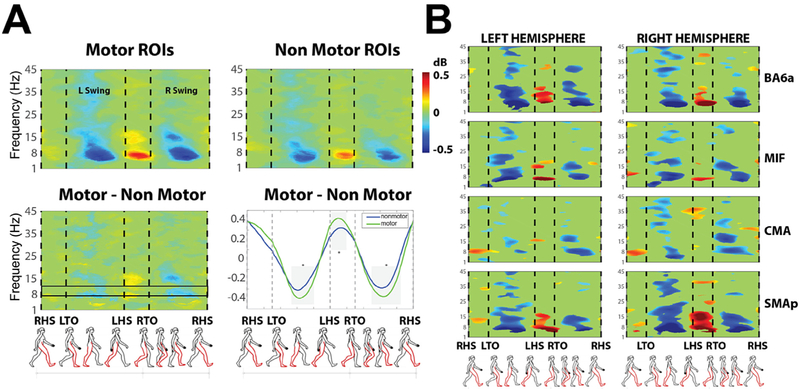
Fig. 6. Time-frequency analysis.

(A) Gait cycle event-related spectral perturbations (ERSPs) for independent component (IC) processes in Motor-related and Non motor-related ROI groups. The (Motor minus Non-Motor) difference is shown in the bottom left panel. Motor ROIs are: ventral premotor cortex (BA6), dorsal premotor cortex (BA6a), supplementary motor (SMAp), cingulate motor cortex (CMA), primary motor cortex divided into foot area (MIF), lip area (MIL), hand area (MIH). Non-motor ROIs are: parietal cortex associative area (BA5), occipital lobe, visuo-motor coordination (BA7), frontal cortex (BA8), prefrontal cortex (BA9_46), occipital cortex (BA19), and the hand representation in the primary sensory cortex (SIH). Results are averaged over all steps after time-warping the spectrograms to 4 gait cycle events: Right Heel Strike (RHS), Left Toe Off (LTO), Left Heel Strike (LHS), Right Toe Off (RTO). Plots are masked for significance (p < 0.05); non-significant values are shown in green. (Bottom right panel) Normalized spectral power in the 8–12 Hz μ rhythm band (highlighted with a black box in the bottom left panel). (B) Gait cycle ERSPs for several motor-related ROIs (BA6a, MIF, CMA, SMAp) in the left (1st column) and right (2nd column) hemispheres.

ERSPs are generally calculated by computing trial-mean power spectra within a sliding latency window and then normalizing the resulting spectrogram by dividing by a mean baseline period spectrum and converting to log scale (dB) (Makeig, 1993). To generate gait cycle ERSPs or each subject and IC single-trial spectrograms were computed and then time-warped using linear interpolation, to align the time points for the right and left heel strikes across epochs as in (Gwin et al., 2011).

Source Imaging (Fig. 7).

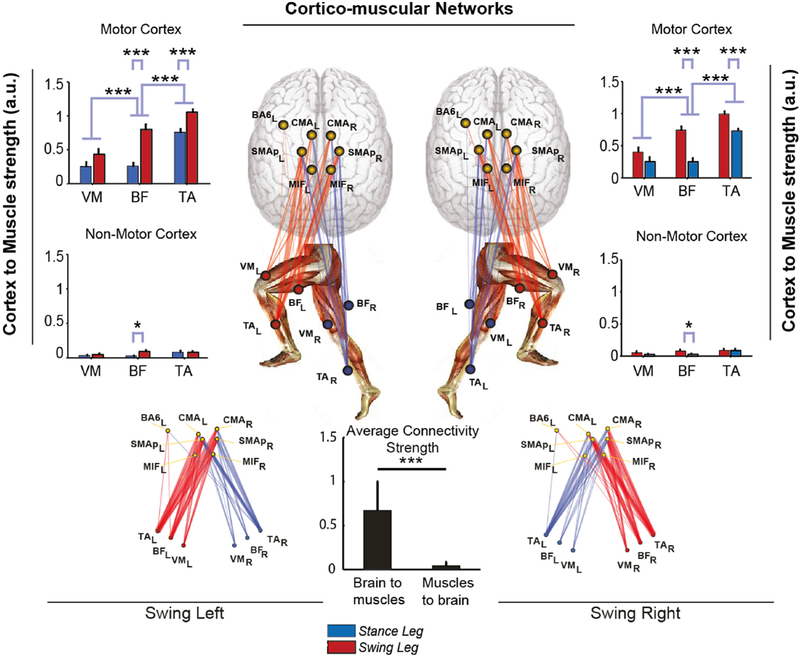
Fig. 7. Cortico-muscular connectivity.

Sum of connectivity strengths between ICs localized to cortical ROIs and recorded leg muscles In the Swing phase of left and right legs, respectively, during V_Tr = 3.5 km/h treadmill walking. Connectivity strengths are shown separately for Motor-related and Non-Motor related ROIs. (Center) Graphs showing brain-to-muscle effective connectivity networks in the Swing phase for each leg. Brain and muscle connections are shown in red and blue, red indicating the leg not contacting, and blue, the leg contacting the ground in the gait phase considered. Thicknesses of the connection lines are proportional to connectivity strength. Links with strengths ≤ 5% of the maximum network connectivity value are not shown. (Center Bottom) Average strength of brain-to-muscle vs. muscle-to-brain connections. Here data are pooled from both legs and swing phases. *p < 0.05; **p < 0.01; ***p < 0.001. Brain-to-muscle connectivity is significantly stronger than muscle-to-brain connectivity. Motor areas ROIs (especially cingulate motor cortex, posterior supplementary motor area, and primary foot motor cortex) have stronger causal influence on lower limb muscle signals than non-motor areas ROIs, also more pronounced in the swing leg and strongest to the Tibialis Anterior – TA, followed by the Biceps Femoris – BF, and Vastus Medialis – VM.

Underlying brain source signals were determined by processing IC-reconstructed scalp EEG data using source localization functions in the eConnectome Matlab toolbox (He et al., 2011) (Else, the analysis may be continued wholly at the level of the source signals identified by ICA). Relevant steps are explained in (He et al., 2011) and reported here for convenience. A cortical current density (CCD) source model was used to solve the inverse problem from the artifact-pruned and retained IC-reconstructed scalp EEG to cortical source distribution using the minimum norm estimate (MNE) with the aid of a boundary element method (BEM) forward head model (Hämäläinen and Sarvas, 1989; He et al., 1987) and Tikhonov regularization (Hansen, 2007). A high-resolution cortical surface consisting of 41,136 triangles, segmented and reconstructed for visualization from MRI images of the Montreal Neurological Institute (MNI) brain using the Curry software (NeuroScan, North Carolina, USA) was used. A source space was formed from this cortical surface down-sampled to 7850 voxel dipole locations, constrained to the gray matter with orientations perpendicular to the containing cortical surface voxel. The scalp surface, skull surface and brain surface, segmented and reconstructed from the MNI brain, are provided by the toolbox. The scalp surface, which consists of 2054 triangular voxels, forms the sensor space. This approach enables comparison of source localizations across subjects in an atlas-based coordinate system that can be used in most EEG studies in which subject MR head images are not available (Darvas et al., 2006; Valdés-Hernández et al., 2009).

With the pre-computed high-resolution lead field matrix (2054 × 7850) relating all the scalp surface voxels to the source voxels, a specific lead field matrix for a user-defined electrode montage (standard 10–20 System in this case) can be constructed as a subset of the precomputed lead field matrix and then used to solve an inverse problem. The solution of the inverse problem yields estimates of continuous time courses for cortical sources. Cortical regions of interest (ROI) can be defined according to Brodmann areas. Thirteen ROIs were defined for each cortical hemisphere: parietal cortex, associative area (BA5), ventral premotor cortex (BA6), dorsal premotor cortex (BA6a), occipital lobe, visuo-motor coordination (BA7), frontal cortex (BA8), prefrontal cortex (BA9_46), occipital cortex (BA19), supplementary motor (SMAp), cingulate motor cortex (CMA), primary motor cortex, BA4, divided into foot area (MIF), lip area (MIL), hand area (MIH), and the primary somatosensory cortex, BA3, hand representation area (SIH). Each ROI source signal was computed by averaging estimated cortical source activities across the source space ROI voxels. It is important to point out though that estimating the actual precision of source localization is currently an open research field (Akalin Acar et al., 2016). Even when inverse source solutions are estimated (either as cortical patches or their equivalent dipoles) using an electrical head model incorporating individual (or template) head tissue geometries and generally assumed conductivity values, the resulting inverse source localization should be interpreted “probabilistically” (Bigdely-Shamlo et al., 2013), with the spatial confidence boundaries (of, in general, a cm or more) difficult to estimate. In the case of distributed cortical surface estimates, the size of the estimated source patch, in particular, may be highly method-dependent.

Directed Transfer Function (Fig. 7).

The Directed Transfer Function (DTF) is a frequency-domain estimator of causal interaction based on the multivariate autoregressive (MVAR) modeling. Quasi-stationary epochs of signals X(t) from twenty-six ROI sources and six EMG channels (EMG sources) were first modeled as the following MVAR process:

$$\sum _{k=0}^p\overline{\Lambda }(k)\mathit{X}(t-k)=\mathit{E}(t),$$

where X(t) is the vector of N source signals (N = 32) recorded in time t, E(t) is a vector of a multivariate zero-mean uncorrelated white noise process; $\overline{\Lambda }(0)=\mathit{I}$ and $\overline{\Lambda }(k)=\mathit{I}-\Lambda (k)$, where Λ (1), Λ (2), …, and Λ (p) are the N × N matrices of model coefficients. The ARfit package (Neumaier and Schneider, 2001) was used in the DTF computation function for the estimation of multivariate autoregressive models. The model order p was determined using the Schwarz Bayesian Criterion (SBC) (Schwarz, 1978). In the frequency domain:

$$\overline{\Lambda }(f)\mathit{X}(f)=\mathit{E}(f),\text{where}\overline{\Lambda }(f)=\sum _{k=0}^p{\overline{\Lambda }}_k{e}^{-j2\pi kf\Delta t}$$

which can be rewritten as:

$$\mathit{X}(f)={\overline{\Lambda }}^{-1}(f)\mathit{E}(f)=H(f)\mathit{E}(f)$$

where H(f) is the inverse of the frequency-transformed coefficient matrix, $\overline{\Lambda }(f)$. From H(f) the full frequency DTF (ffDTF) describing the directional causality from source j to source i can be defined as:

$$c_{ij}^2(f)=\frac{\mid H_{ij}(f){\mid }^2}{{\sum }_f{\sum }_{k=1}^N\mid H_{ik}(f){\mid }^2}$$

where N is the total number of sources. Summation over the whole frequency range of interest, 1–45 Hz, assured that the denominator of this expression did not change with frequency.

Statistical Assessment of Connectivity (Fig. 7).

A nonparametric method based on surrogate data was used to assess the significance of the estimated connectivity measures (Ding et al., 2007; Palus and Hoyer, 1998; Theiler et al., 1992). In this method, the original time series are transformed to the Fourier space, in which the phases are randomly shuffled without changing the magnitude. The surrogate data in the Fourier space are then transformed back to the time domain. This process of phase shuffling preserves the spectral structure of the time series, which is suited for DTF analysis, as both are measures of frequency-specific causal interactions. After shuffling, the connectivity estimation was applied to the surrogate data. The shuffling and connectivity estimation procedures were repeated 100 times, yielding a distribution of the DTF values under the null hypothesis that no connectivity exists. Connectivity estimates were then assessed based on this empirical distribution and of a given significance level, here α = 0.05 (Ding et al., 2007).

Network Measures of Brain-Muscle Connectivity (Fig. 7).

We analyzed cortico-muscular linkage defined by thirty-two nodes (twenty-six EEG ROIs and six EMG sources) and all the links between pairs of nodes (ffDTF measures of effective connectivity, averaged across frequencies and signal epochs). The ffDTF analysis were performed on brief windows (left and right swing gait cycle phases respectively) of ROI source signals and corresponding EMG preprocessed data (see section “EMG preprocessing” in materials and methods section). To measure to what extent the cortical source nodes influenced the muscle nodes, the degree of each muscular node can be calculated (Rubinov and Sporns, 2010) for binary networks, (i.e., networks with binary links representing presence or absence of connection) as the number of links connected to that node. For networks with weighted links giving information about connection strengths (weighted networks), a variant of the node degree can be used, i.e. the node strength, defined as the weighted sum of links connected to that node. The weights are the connection strengths (ffDTF measures) of the involved node pairs. Individual strength values therefore reflect the relative effectivity (effective connectivity) of nodes in the network. For each muscle (TA, BF, and VM), the strength was thus defined as:

$$s_{\mathit{muscle}}=\sum _{j=1}^M{c}_{\mathrm{muscle},j}^2$$

where M is the number of cortical nodes, e.g. the twenty-six EEG ROIs. It is important to note that residual correlation between EEG ROIs (i.e. volume conduction) can lead to biased connectivity values. We feel this issue can affect the results only to a small extent: the node strengths for the different muscles could have been all slightly inflated by these residual correlations, still not affecting the comparisons we made across muscles and legs. This issue however is very relevant when investigating connectivity maps within the brain e.g. studying the causal influence of a brain area over another. In this case it would be possible to (i) perform connectivity analysis at IC-level (Delorme et al., 2011); (ii) use the imaginary part of the cross-spectra (Nolte et al., 2004) then to use the sPCA and MOCA methods for identifying compound systems and for separate sources within each of these systems (Marzetti et al., 2008); (iii) use “lagged connectivity” (lagged phase synchronization - LPS) between pairs of brain sources capable of minimizing non-cerebral artifacts (Canuet et al., 2011; Di Lorenzo et al., 2015; Pascual-Marqui et al., 2011).

Decoding (Fig. 8).

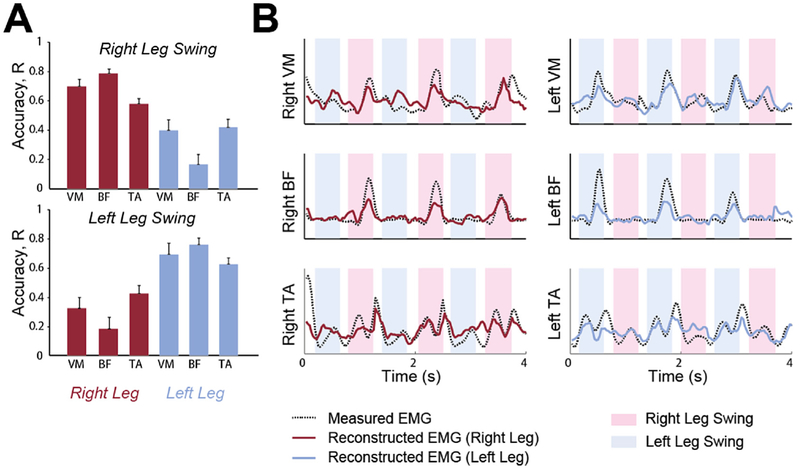
Fig. 8. EMG decoding.

(A) (Left) Decoding accuracy (Pearson's correlation coefficient, R ± SEM across all subjects) of EMG envelopes for activities recorded from the Tibialis Anterior (TA), Vastus Medialis (VM), Biceps Femoris (BF) muscles of the right leg (red bars) and left leg (blue bars) in the swing phase of the right leg (Top) and left leg (Bottom), respectively (B) (Right) Example of EMG envelope reconstruction (Red line, right leg; Blue line, left leg) superimposed on the actual EMG envelope (Black dotted line). Blue- and pink-shaded regions indicate left and right leg swing phases, respectively.

Continuous ROI source signals were used to predict EMG activity using support vector machine (SVM) models (Chang and Lin, 2011) written in Matlab. The SVM (Boser et al., 1992) finds optimal hyperplanes separating different groups of data points. The hyperplanes are completely determined by the computed support vectors (Cortes and Vapnik, 1995). Computational issues and mathematical details can be found in (Burges, 1998) and (Cristianini and Shawe-Taylor, 2000). To predict EMG envelopes of leg muscles from brain source activities, a nonlinear regression problem was solved (as in (Rigosa et al., 2015)). EEG and EMG data underwent different processing steps with respect to connectivity analysis. First, continuous walking EEG data were filtered between 1 and 16 Hz. Aligned continuous EMG data were high-pass filtered at 10 Hz, rectified and then low-pass filtered below 4 Hz. This dataset was used in a 5-times-repeated random sub-sampling validation of the model prediction. At each repetition, 70% of the total record length was used for SVM training. Once trained, each model was used to predict the remaining 30% of test data. At each time point t, the motor ROIs up to a delay of 0.5s were used as input to the classifier and each of the six leg muscles was used as output. For each subject, the mean accuracy Pearson's correlation coefficient, R, between predicted and actual EMG was evaluated across the five realizations of random sub--samplings to determine confidence bounds. The prediction results for each leg muscle are presented as the average accuracy ± SEM across all subjects.

Source stationarity analysis by multiple-model ICA (Fig. 9).

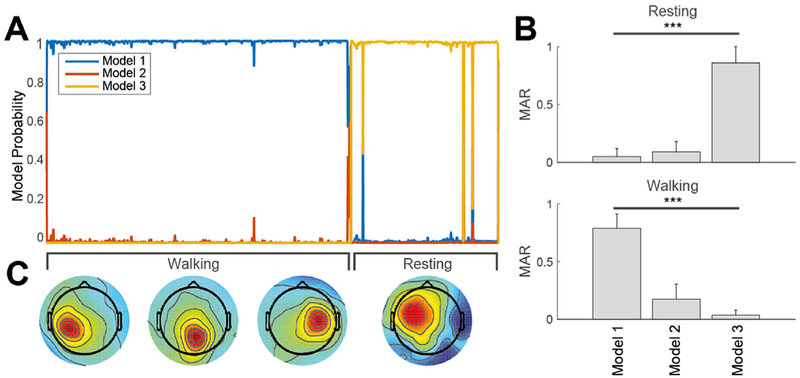
Fig. 9. Adaptive mixtures modeling of gait.

(A) (Left) Smoothed probability of three Adaptive Mixture ICA Models found by AMICA decomposition of concatenated data during the walk and rest conditions for one subject. Models 1 and 3 are active respectively during the walk and rest conditions. (B) (Right) Model Activity Rate (MAR) of the three models during resting and during walking. (C) (Bottom) Three representative components only present in Model 1 (walking), and a component only in Model 3 (resting). This representation demonstrates stationarity of resting and walking phases and the necessity of two separate models to explain the data.

Finally the hypothesis of data stationarity underlining the whole analysis hitherto described was demonstrated by means of multiple-model Adaptive Mixture Independent Component Analysis (AMICA) (Palmer et al., 2007a), which can be viewed as a generalization of the Infomax algorithm (Makeig et al., 1996) supporting a multiple mixture approach (Lee et al., 1999). For each subject, the EEG data recorded during the rest condition were concatenated to those collected during walking and were then submitted to the EEG Pre-processing I procedure. Three-model AMICA was computed, including removal of outlier data points (with likelihood exceeding 5 standard deviations) performed 5 times with a 5-iteration interval beginning after 5 initial iterations. The maximum number of iterations was set to 2000. The number of data samples satisfied an empirical rule for determining the feasibility of computing three-model AMICA. The 2-s smoothed and normalized log-likelihood for each resulting model was then computed through the data. Each model can be viewed in itself as a whole ICA decomposition, active on a particular portion of data. Here each model is given a probability over time depending on how well that particular decomposition explains the data at a certain time-point. AMICA in other words is an extension of the current ICA paradigm and enables to account for structural changes in the data. Its application to the Mobi framework is highly relevant as it enables to test the hypothesis of data stationarity during walking.

3. Results

In this work we adopted several methods to minimize the influence on the results of artifacts in phase with the fundamental stepping frequency, which can mimic time-locked brain activation (Castermans et al., 2014; Kline et al., 2015). In summary, experimental setup precautions enabled to minimize cable movement interference, electrode detachment and non-stationarities. Artifact Subspace Removal (ASR) (Kothe and Jung, 2015) and Reliable Independent Component Analysis (RELICA) (Artoni et al., 2014) helped remove gait locked and non-locked ocular and neck muscle activity from the data. Data epochs with jaw clenching, swallowing, noise bursts and other non-stereotyped artifacts were removed by visual inspection. Source localization (Delorme and Makeig, 2004), and effective connectivity (Kaminski and Blinowska, 1991) between brain and muscles served as indirect evidence of negligible influence of possible remaining movement artifacts (see also Discussions and Materials and methods). Fig. 4 shows eight stable and highly dipolar Independent Components (ICs) identified by applying the decomposition procedure presented in this work (see Materials and Methods) to data from a representative subject.

IC1 and IC2 account for vertical and lateral eye movement artifacts respectively, as shown by the Tailarach coordinates of their equivalent dipoles. IC7 and IC8 account for left and right neck muscle activity respectively. Their high dipolarity can be ascribed to the relatively high power of neck muscle artifact and the small distance between the electrodes and the actual source (the insertion of the neck muscle into the tendon), the high stability measure was made possible by the highly stereotyped muscle activity pattern involved in cyclic gait. The high quality index (QIc) values for these ICs (respectively 92%, 89%, 93%, 91%) is consistent with the relative compactness of the RELICA IC clusters, ensuring that removing these ICs from the data would not inadvertently also remove useful brain activity. Conversely, IC4, IC5, IC15, and IC20 represent meaningful, brain-based central, left, and right mu rhythm processes with high dipolarity and QIc. As reliable ICs need to be both dipolar and stable to input data resampling, the probability of them to be contaminated by non-stereotyped movement artifacts is low. Only reliable ICs were used at group level (clusters).

Fig. 5 shows the grand average time-frequency amplitude ratio to the mean gait cycle spectrum (ERSP), and the equivalent dipoles and average scalp maps for several independent component clusters (neck muscles, ocular, frontal and central brain source clusters).

ERSP plots are masked for significance (p > 0.05, colored green) with respect to the full gait cycle baseline. Posterior and anterior cingulate IC clusters exhibit alternating ERD and ERS within the gait cycle, with stronger ERD at alpha and mu frequencies during the swing phase. The muscle artifact (scalp EMG) clusters reflect the “distributed” nature of EMG activity (various muscles generate non-stereotyped widespread activity localized over many inferior scalp areas). Group-level analysis enables better identification of common patterns between ICs and easier recognition of non-brain artifact components in several categories (eyes, muscles, line noise). Group analysis (selection of ICs at the subject group level instead of the individual subject level, as in RELICA) allows grouping together functionally similar IC processes based on multiple measures in the time and frequency domains, thus decreasing the chance of mistaking a non-brain artifact IC for a brain IC. Once so identified, neck muscle and eye movement-related IC clusters were removed and remaining ICs back-projected to the original scalp channel space (IC-reconstructed scalp EEG), thus under favorable circumstances removing most non-brain physiological artifacts from the data (see also Methods).

EEG processing allowed us to find significant (0.5 dB) modulations in gait-locked spectral power perturbation in β (18–30 Hz), μ (8–12 Hz), and γ (30–45 Hz) frequency bands in brain motor areas which were stronger than gait-locked spectral perturbations in non-motor areas (Fig. 6). Grand-average ERSP for Regions of Interest (ROIs) localized to motor and non-motor areas respectively, masked for significant difference (p < 0.05) from the whole-gait-cycle baseline are shown in Fig. 6A. Activations were significantly stronger (p < 0.001) during the single support gait phase (Heel Strike to Toe Off) than in the double support phase (Toe Off to Heel Strike). ERSPs for the premotor cortex (BA6a), foot motor (MIF), supplementary motor (SMAp), and cingulate motor (CMA) areas of the Left and Right hemispheres, in particular, exhibited significant desynchronization and synchronization in μ and β frequency bands respectively during single and double foot support phases (Fig. 6B). However, ERSP measures for cortical motor ROIs did not differ significantly from ERSP measures for non-motor areas.

We also studied cortical involvement in gait by measuring effective connectivity by Directed Transfer Function (DTF) (Kaminski and Blinowska, 1991) between motor/non-motor cortical ROIs and leg muscle signals in the swing phase. Brain-to-muscle connectivity was significantly stronger than muscle-to-brain connectivity (p < 0.001, Fig. 7). Motor ROIs had stronger causal influence on lower limb muscle signals than non-motor ROIs (p < 0.001). Connectivity of cortical motor sources to Tibialis Anterior and Biceps Femoris was more pronounced in the swing leg (p < 0.001). For both legs, connectivity was strongest to the Tibialis Anterior, followed by the Biceps Femoris, and Vastus Medialis; all these differences significant (p < 0.001). The cortical areas with maximal influence on lower limb muscle signals were cingulate motor cortex, posterior supplementary motor area, and primary foot motor cortex. Premotor areas (BA6) exhibited weaker influence.

Finally, we investigated whether the higher connectivity found between EEG source signals in cortical motor areas and swing leg muscle EMG activations also lead to better performances when predicting EMG activity of the swing leg from EEG signals, compared to the stance leg. Results demonstrated that EMG activity envelopes can be reconstructed from the EEG source signals more accurately in the swing leg (p < 0.001). However, decoding accuracy was highest for BF (R = 0.78 ± 0.04, mean ± SEM) than for the other muscles (R = 0.70 on average), suggesting for a non-linear relationship between muscle node strength and EMG predictability (Fig. 8).

Evidence for data stationarity, which is the underlying hypothesis of the whole analysis, is presented in Fig. 9. It shows the varying smoothed probabilities of three competitively trained Adaptive Mixture ICA (AMICA) models for data of a representative subject. The first model best fits the data in the resting condition; the third model best explains the walking data. The model activity rate (MAR) may be defined as the ratio between the number of time points at which the model has highest probability to the total number of time points in the considered condition. Here, the grand average MAR for the three models (right panel in Fig. 9) shows that Models 1 and 3 are significantly (p < 0.001) pertinent respectively to walking and rest respectively. Since the MAR for Model-2 is significantly lower (p < 0.001) than either other model in the rest and walk conditions, it can be concluded that two ICA models best explain the walking and resting data.

4. Discussion

Here we show for the first time that the human motor cortex proactively controls contralateral leg muscles during walking even in stereotyped steady-state treadmill walking conditions. We demonstrate a unidirectional brain-to-muscle connectivity for proximal and distal muscles, rhythmically related to stride phases. This finding demonstrates a “fine” control of leg muscles during stereotyped treadmill locomotion by a network of areas in the motor cortex known to be involved in non-stereotyped movement (e.g. precision stepping) and movement planning.

Several fMRI (Cunnington et al., 2002, 2005) and SPECT (Fukuyama et al., 1997) studies have shown that significant and widespread activation occurs in premotor (BA6), cingulate motor (CMA), supplementary motor (SMA) and motor (MI) cortices during preparation and planning of self-paced movements. fNIRS studies in healthy people demonstrated in these areas a significant increase of O₂Hb levels occurs during treadmill walking (Miyai et al., 2001). O₂Hb levels were also found to be influenced by gait parameters (e.g., speed, stride-time variability) and by cognitive load during the task (Kurz et al., 2012). Invasive tract-tracing studies in non-human primates have shown that not only neurons in MI, but also those in higher motor areas such as BA6, SMA, and CMA have direct corticospinal connections to the alpha-motor neurons in the anterior horn of the spinal cord (Dum and Strick, 2002). These studies suggest a possible involvement of these areas during voluntary upper limb movements and performance of various motor behaviors, including gait. However, technical shortcomings intrinsic to fMRI and SPECT (non-portability), fNIRS (low spatial resolution, inter-subject variability of the hemodynamic response and especially slow dynamics), and invasive techniques (unsuitable for use with healthy subjects), make it impossible to exhaustively investigate the occurrence of gait-phase-dependent modulation of cortico-muscular control using these techniques.

BA6, SMA and CMA areas, in other words form a network involved in non-stereotyped movements (Drew et al., 2008). Thanks to the novel approach used here, based on the analysis of effective connectivity, we were also able to determine the causal contributions of these and other cortical regions to walking. During gait, local field activities in BA6a, CMA, MIF, and SMAp selectively exercise causal influence specific to the swing leg, most prominent in contralateral SMAp and CMA (p < 0.001). SMA is known to play a role in the period immediately preceding the start of gait (Mihara et al., 2007) and in demanding tasks such as backward walking (Kurz et al., 2012). We now show that SMA is also part of a complex network in the motor cortex that includes all the main motor and premotor areas that rhythmically modulate in different and specific ways both the distal and proximal muscle activations that effect walking.

The stronger cortico-muscular connectivity was observed in distal muscles of the swing leg. This suggests that ankle dorsiflexion and correct foot placement due to TA activation might require fine, direct supraspinal control more than other phases of gait. It has been long believed that the control of the stance period of walking is complex, requiring dynamic postural adjustments, sensorimotor integration and supraspinal control in order to maintain the upright posture in dynamic, challenging conditions (Day and Cole, 2002; Ernst and Banks, 2002; Fetsch et al., 2009). Our result is not in disagreement with this assumption, as the information flow direction (provided by our analysis) removes the afferent sensory component of the neural signaling and therefore considers only the direct contribute of specific motor areas to muscle activation. On the other hand, previous EMG studies examining reciprocal inhibition during gait already described the swing phase to be a critical event requiring supraspinal control (Lavoie et al., 1997) and TMS studies with lower limb muscles MEP recording found that the corticospinal tract is closely linked with the distal muscles controlling ankle flexion/extension during stepping (Schubert et al., 1999) and in particular with TA in the swing phase of the gait cycle (Capaday et al., 1999; Knikou et al., 2013; Takahashi et al., 2014). This is also compatible with previous works showing that in infants (Dominici et al., 2011) and elders (Stelmach and Hömberg, 1993) proximal muscle activity during walking exceeds distal muscle activity, whereas at intervening ages the reverse is true. From a methodological perspective, our results were achieved thanks to the development and use of novel processing algorithms that enabled us to (i) simultaneously analyze EEG and EMG signals, (ii) determine gait-phase dependent modulation of cortical control over leg muscles and (iii) test the directionality of the information flow to minimize the effects arising from sensory inputs and motion artifacts.

Notwithstanding its limitations (e.g., limited spatial resolution, inter-subject variability, high sensitivity to artifacts), the EEG is a suitable option for imaging brain activity during walking because of its high temporal resolution and ease of use. Several authors (Gramann et al., 2014; Gwin et al., 2011; Kline et al., 2016; Sipp et al., 2013; Wagner et al., 2012) have shown cortical activation during human steady-state walking in the time-frequency domain locked to the gait cycle. These results also triggered a debate over the presence of movement artifacts, time-locked to the gait cycle and therefore not removable by averaging, their relevance to the EEG data analysis (Snyder et al., 2015) and ultimately the validity of the presented findings. It is important to point out that for this reason, direct proof of complete removal of gait-locked artifacts cannot be given. This is currently a limitation that afflicts every work in the field that does not investigate a cognitive task timed independently to the gait events (Castermans et al., 2014). Several authors have investigated motion artifacts using phantom heads and accelerometers and found that accelerometer data did not correlate well with movement data recorded by electrodes placed on the simulated scalp, mainly due to the complexity and non-stationarity of the artifact itself (Kline et al., 2015; Oliveira et al., 2016). In fact the whole field is awaiting a hardware EEG cap able to subtract movement artifacts at electrode level as suggested by (Kline et al., 2015). Notwithstanding this, several precautions could be taken and indirect evidence excludes significant residual artifact contamination. On top of experimental set up precautions (see materials and methods) here we employed an iterative conservative ASR approach to homogenize the data before applying ICA. Non-stationary movement artifacts may, in particular, impair the effectiveness of the ICA decomposition, which adds to the difficulty of identifying reliable ICs and clustering them across subjects (Artoni et al., 2014). In EEG preprocessing step 2 we did not use ASR as it may result in unexpected results when paired with ERSP or connectivity measures. Instead we removed by visual inspection non-stereotyped artifacts such as jaw clenching, swallowing and outliers as in (Wagner et al., 2014). We then used RELICA to demonstrate that negligible brain activity was removed in the process. The AMICA/RELICA and two-step artifact removal procedure used in this work (see methods and Fig. 2) allowed reliable artifact ICs that were both stable and dipolar, and therefore not resulting from inadequate IC convergence, to be removed from the data – thus ensuring the selectivity of the artifact removal process. In fact we were able to retain more than 15 highly reliable brain-originated ICs per dataset. The high total number of quasi-dipolar ICs (more than 100) extracted both with and without ASR (see Fig. 3) is indirect proof of both negligible influence of residual movement artifacts and the successful extraction of meaningful brain activity. Also, the multiple-model AMICA decomposition showed that walking, in contrast to resting, introduces stable changes in effective brain EEG sources found by AMICA that were not active during standing (Fig. 8), thus validating the hypothesis of data stationarity underlying analyses combining the two conditions. This result, incidentally, supports the assertion that ICs extracted from moving heads can reliably represent the content of a stationary condition (Oliveira et al., 2016). While it is not possible to exclude residual artifact contamination in time frequency plots completely, band-specific significant ERSP plots, as opposed to wide-band ones (as in (Castermans et al.,2014)) have been considered by several authors (Gramann et al., 2014; Gwin et al., 2011; Wagner et al., 2012, 2014) as indirect evidence of “negligible motion artifacts in scalp EEG during treadmill walking” (Nathan and Contreras-Vidal, 2015b). Finally, the strong directional brain to muscle connectivity serves as another indirect proof of this. It stands to reason in fact that gait-locked movement artifacts, both on EEG and EMG would be equally bi-directionally correlated.

Our time-frequency decompositions found widespread modulations of cortical effective source signals time locked to the gait cycle (Fig. 6), including significant alpha/mu band desynchronization in the single-support phase, stronger for sources in motor than in non-motor areas and strongest for sources in dorsal premotor cortex (BA6a), and in cingulate motor (CMA), foot motor (MIF), and supplementary motor (SMAp) areas. Our results demonstrate the involvement of these brain regions and are in agreement with previous results in literature (Cevallos et al., 2015; Chéron et al., 2012; Gramann et al., 2014; Gwin et al., 2011; Kline et al., 2016; Severens et al., 2012). For instance (Cevallos et al., 2015) showed gait-locked ERSP in the alpha frequency range (9–12 Hz) during walking and persistence of beta ERS (15–20 Hz) during walking imagination, which is consistent with our results. On a methodological note, small residual artifact contamination may however impair the capability of ERSP analysis to show subtle differences e.g. in contralateral predominance that may otherwise be shown with connectivity analysis.

Although the RELICA (Fig. 4) and IC cluster analyses (Fig. 5) show the reliability of the method and the presence of highly dipolar gait-modulated ICs, the analysis of EEG activity alone as in (Gramann et al., 2011; Gwin et al., 2011; Lau et al., 2012), leaves doubt regarding the actual contributions of cognitive circuits (e.g., supporting attentional control (Pfurtscheller et al., 1997)) to gait activity.

Conclusive evidence of cortical control during gait requires in fact the estimation of cortico-muscular functional connectivity. Following this direction, Petersen et al. (2012). have shown frequency-coherent activity between a single EEG channel (Cz) and muscle (TA) but can't exclude sensory information involvement as they do not account either for directionality nor for the presence of a network of areas. Kline et al. (2016) recently demonstrated within-stride cortico-cortical connectivity modulation. Cortico-cortical connectivity however cannot demonstrate the existence of a true causal relationship between cortical field activities and EMG signals.

TA, BF and VM were chosen because of their relevance during the whole gait cycle, both in stance and swing phases (Perry and Burnfield, 2010) and because they are representative of proximal and distal muscular activity of lower limbs. In particular, TA plays an important role in providing ankle dorsiflexion capabilities during the swing phase and providing supplementary support during the stance phase of the leg. For this reason, TA was the muscle of choice of (Petersen et al., 2012) to provide evidence of the possibility of decoding muscle activity using the Cz channel. VM, and to a lesser extent BF, are important contributors to the axial joint force in during stance (Sasaki and Neptune, 2010). Recording three muscles only is a limitation of this work. However, using the cortico-muscular connectivity measures described here, further studies including more muscles might also shed light on how the human nervous system coordinates a large number of muscles (e.g. muscle synergies) to accomplish functional tasks.

By computing cortico-muscular effective connectivity after multi-step ICA-based artifact removal we were able to show, in summary, that in humans the motor cortex plays a significant role, not only during complex and novel motor planning (e.g., gait initiation, addressing obstacles, etc.) but also in control of major leg muscles supporting stereotyped treadmill locomotion. This definitely suggests that while in quadrupedal animals spinal central pattern generators are mainly responsible for the coordination of rhythmic limb behaviors (Brown, 1914; Duysens and Van de Crommert, 1998; Grillner, 1975; Juvin et al., 2005; Marder and Calabrese, 1996; Rossignol et al., 2006), in humans both spinal and motor control intervene. The results counter the traditional view of human stereotyped locomotion as an automated process, forcing reconsideration of gait as a complex process requiring supraspinal control even during stereotyped walking.

The methodological framework developed and exploited in this study could pave the way for new and more effective gait rehabilitation approaches in clinical settings (elderly and subjects with neurological disorders). In fact it was recently shown (Capogrosso et al., 2016) that cortical signals can be used to trigger epidural spinal stimulation to restore locomotion after incomplete lesion. Our results show that EEG signals could be used to implement the same kind of cortical control in human patients, e.g. to develop more efficient ecological “brain-body” neuroprostheses to restore locomotion (Ethier et al., 2012), thus opening up exciting opportunities to the field.