Inference of Population Structure from Time-Series Genotype Data

Abstract

Sequencing ancient DNA can offer direct probing of population history. Yet, such data are commonly analyzed with standard tools that assume DNA samples are all contemporary. We present DyStruct, a model and inference algorithm for inferring shared ancestry from temporally sampled genotype data. DyStruct explicitly incorporates temporal dynamics by modeling individuals as mixtures of unobserved populations whose allele frequencies drift over time. We develop an efficient inference algorithm for our model using stochastic variational inference. On simulated data, we show that DyStruct outperforms the current state of the art when individuals are sampled over time. Using a dataset of 296 modern and 80 ancient samples, we demonstrate DyStruct is able to capture a well-supported admixture event of steppe ancestry into modern Europe. We further apply DyStruct to a genome-wide dataset of 2,067 modern and 262 ancient samples used to study the origin of farming in the Near East. We show that DyStruct provides new insight into population history when compared with alternate approaches, within feasible run time.

Introduction

The widespread availability of ancient DNA—DNA extracted from the remains of people who lived thousands of years ago—has revolutionized our understanding of human history.¹ There are now more than 1,300 sequenced genomes from ancient humans in the published literature,² with the amount of data generated doubling faster than it can be published.³ Detailed investigation of ancient DNA datasets has had profound impact on our understanding of the movement of people, technology, and genes throughout history:^{4, 5, 6} we now know that people thousands of years ago were genetically as different from each other as modern humans across the globe are today, and that migration and admixture were commonplace.⁷ Moreover, the genetic distribution of global populations today are not necessarily representative of the people who lived there in the past.⁸

The newfound complexity in human history, punctuated by numerous migrations and mergers, necessitates the development of computational tools to investigate the relationships between people over time. A typical workflow for the analysis of ancient DNA datasets proceeds in two steps. First, samples are grouped into genetically similar units deemed populations. Second, the ancestral relationships between (ancient and modern) populations are identified. In the first step, one ubiquitous approach uses model-based clustering methods^{9, 10} in conjunction with principal component analysis (PCA¹¹) or multi-dimensional scaling,¹² and a grouping is chosen in a way that is parsimonious between results. Often, groups of samples arise naturally out of the data, and these exploratory analyses can be suggestive of historical relationships. In the second step, expert domain knowledge (e.g., cultural affiliations among artifacts, archaeological evidence) is combined with results from the first step to generate hypotheses regarding the relationships between populations. These hypotheses can be formally tested using simulations, f- and D-statistics,^{13, 14, 15} or fitting admixture graphs.¹⁴

Ancient DNA, however, poses several challenges to traditional analysis pipelines. In contrast with data from modern individuals—where all individuals are sampled at approximately the same time—ancient DNA datasets contain individuals from multiple periods in history. This is potentially problematic when methods implicitly assume all sampled individuals are contemporary. For instance, popular model-based clustering approaches such as structure⁹ and its modern extensions ADMIXTURE¹⁰ and fastSTRUCTURE¹⁶ assume that allele frequencies in populations remain fixed. Ancient DNA datasets clearly violate this assumption because frequencies randomly fluctuate over time due to genetic drift. Moreover, such ancestry approaches suffer from conceptual issues as the interpretation of fixed allele frequencies inferred from time-series data is unclear. Accurately assessing the genetic relationship between ancient samples is crucial because sampled individuals are not chosen through careful study design, but rather by the chance process of bone sample survival in a condition that facilitates extraction of usable DNA.⁸ Thus, there is a need for methods and tools whose assumptions more closely match the specifications of the data.

To address these issues, we present DyStruct (Dynamic Structure): a model-based clustering method to infer shared ancestry from time-series genotype data.¹⁷ DyStruct builds on model-based clustering approaches pioneered by structure-like models and extends them to time-series data by leveraging the close connection between population structure models in population genetics and latent Dirichlet allocation (LDA) in natural language processing.¹⁸ This connection has been long appreciated,¹⁹ with multiple inference methods originally associated with LDA driving methodological advances in population genetics.^{16, 20} DyStruct uses two key methodological developments from this literature. First, LDA has previously been extended to time-series data using dynamic topic models.²¹ Second, the efficient inference algorithm introduced by teraSTRUCTURE²⁰ facilitates the development of more sophisticated population structure models by allowing subsampling of loci along the genome. This significantly reduces the computational cost per iteration, allowing less efficient but more expressive model development while maintaining reasonable run times. Using simulations, we show that DyStruct outperforms the current state of the art in the presence of genetic drift. We further present results on two real datasets: one analyzed by Haak et al.⁵ to investigate the migration of people from the Pontic-Caspian steppe into Europe, and one analyzed by Lazaridis et al.²² to study the genetic makeup of early farmers in the Near East.

Material and Methods

Model Overview

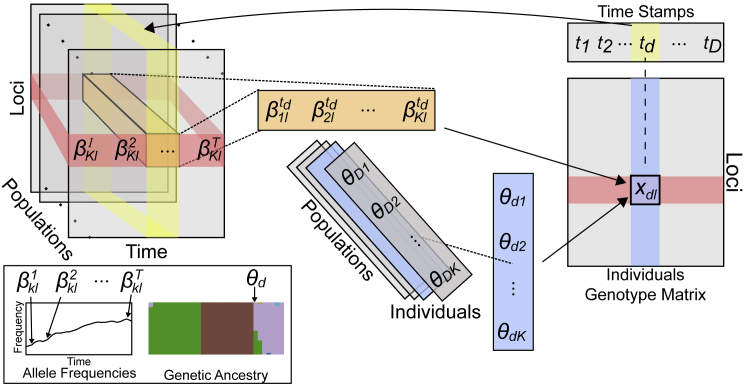
Figure 1 gives a schematic overview of our model. DyStruct infers shared ancestry among individuals by modeling individuals as mixtures of latent populations whose allele frequencies drift independently over time. The input to DyStruct is an individual by genotype matrix, a proposed number of ancestral populations with population sizes, and the time in generations that each sampled individual was alive. Pseudo-haploid ancient samples are automatically detected and explicitly modeled in DyStruct. Individuals are grouped into unique time stamps by generation time. DyStruct uses time-stamped genotypes to estimate both allele frequencies at each time stamp across loci and populations and also the genetic ancestry for each individual. Conceptually, the assumed sampling process for individuals at a particular time point is the same as ADMIXTURE. However, we relax the assumption of fixed allele frequencies by allowing distinct allele frequencies across time points. During parameter inference, changes in allele frequencies are regularized by effective population size to leverage information across time. As we demonstrate below, our model performs well even when the true effective population size is unknown.

Figure 1.

Schematic of DyStruct’s Model

K populations are modeled as collections of allele frequencies at L loci that drift over T time points (left). Each ${\beta }_{kl}^t$ gives the frequency of allele l in population k at time point t. Each individual d of D total individuals is associated with an ancestry vector, ${\mathit{\theta }}_{\mathit{d}}=\left({\mathit{\theta }}_{\mathit{d}1},{\mathit{\theta }}_{\mathit{d}2},\dots ,{\mathit{\theta }}_{\mathit{d}K}\right)$ (middle), giving the proportion of that individual’s genome inherited from each population, and time stamp t_d. Genotypes at a locus l (red) in an individual d (blue), x_dl, are determined by the individual’s ancestry proportions and the allele frequencies across populations when that individual was alive (yellow). Notation matches that of the Material and Methods section.

As the number of time points increases, so does the number of inferred parameters and time complexity of the inference procedure. To counteract this effect, we developed an efficient inference algorithm using stochastic optimization. Briefly, our algorithm iteratively updates allele frequencies and ancestry estimates by sampling loci across the genome in a process motivated by Gopalan et al.,²⁰ which we extended to our model. At each iteration, a random locus is selected. That locus is used to update the estimated allele frequencies across populations given genotyped individuals and their previous ancestry estimates. Then, the ancestry estimates are updated by taking a weighted average of an estimate from the selected locus alone and the previous estimate. This procedure is repeated until parameter estimates converge. To incorporate missing data, a common feature of ancient DNA datasets, allele frequencies at a locus are updated based only on observed genotypes, and ancestry estimates updated only for individuals with nonmissing data at that locus. Using stochastic optimization, as opposed to batch optimization, reduced the run-time of our algorithm from potentially weeks on modern-scale datasets (>200,000 loci and >2,000 individuals) to approximately 24–48 h, while using less than 2 Gb of memory in all experiments.

Time-Series Model

Suppose we have D individuals genotyped at L loci. Each individual d = 1,…,D is associated with a time stamp $t_d\in \left\{\mathrm{1,2},\dots ,T\right\}$, where T is the total number of time points. Let g_t be the total time in number of generations since the first time point t₁ (with g₁ = 0). The genotypes of each individual d are given by the vector ${\mathit{x}}_{\mathit{d}}=\left(x_{d1},x_{d2},\dots ,x_{dL}\right)$, where x_dl denotes the number of reference alleles observed at locus l for that individual.

We assume each sampled individual is a mixture of K unobserved populations. Let the vector ${\mathit{\theta }}_{\mathit{d}}=\left({\mathit{\theta }}_{\mathit{d}1},{\mathit{\theta }}_{\mathit{d}2},\dots ,{\mathit{\theta }}_{\mathit{d}\mathit{K}}\right)$ give the proportion of the genome individual d inherits from each population k; hence ${\sum }_{k=1}^K{\theta }_{dk}=1$. Denote the allele frequency of the reference allele at locus l in population k at time point t by ${\beta }_{kl}^t$. With this notation, we assume the following generative model:

$${\mathit{\theta }}_{\mathit{d}}\sim \mathrm{Dirichlet}\left({\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_{\mathit{K}}\right)\mathrm{for}\mathit{d}=1,\dots ,\mathit{D}.$$ (Equation 1)

$${\beta }_{kl}^t|{\beta }_{kl}^{t-1}\sim \text{Normal}\left({\beta }_{kl}^{t-1},\frac{g_t-g_{t-1}}{12N_k}\right)\text{for }l=\mathrm{1...}L\text{ and }K=\mathrm{1...}K$$ (Equation 2)

$$x_{dl}|{\beta }_{1:K,l}^{t_d},{\mathit{\theta }}_d\sim \text{Binomial}\left(n_d,\sum _{k=1}^K{\theta }_{dk}{\beta }_{kl}^{t_d}\right)\text{for }d=\mathrm{1...}D\text{ and }l=\mathrm{1...}L$$ (Equation 3)

with initial allele frequencies ${\beta }_{kl}^0$ and effective population sizes N_k treated as parameters. The ${\beta }_{kl}^t$ are estimated from data, while N_k are treated as known and fixed. Ancient DNA samples are typically pseudo-haploid, as low sequencing depth makes it difficult to call full diploid genotypes. We explicitly model pseudo-haploid individuals by setting the sample size parameter of the binomial as either n_d = 2 or n_d = 1 depending on whether an individual is diploid or pseudo-haploid.

Note that the variance for drift is different than the variance obtained under Wright-Fisher or using a diffusion approximation. Traditionally, the variance of ${\beta }_{kl}^t|{\beta }_{kl}^{t-1}$ is

$$\text{Var}\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1}\right)=\frac{{\beta }_{kl}^{t-1}\left(1-{\beta }_{kl}^{t-1}\right)\left(g_t-g_{t-1}\right)}{2N_k}\text{.}$$

However, the appearance of allele frequencies in the variance leads to difficulties in deriving an inference algorithm. We approximate the variance by taking the average variance over possibly allele frequencies:

$$\text{Var}\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1}\right)\approx \frac{g_t-g_{t-1}}{12N_k}={\int }_0^1\frac{{\beta }_{kl}^{t-1}\left(1-{\beta }_{kl}^{t-1}\right)\left(g_t-g_{t-1}\right)}{2N_k}d{\beta }_{kl}^{t-1}\text{.}$$

Intuitively, this is similar to assuming a uniform prior over ${\beta }_{kl}^{t-1}$ in the variance and taking the expectation.

Inference

We infer parameters through the posterior distribution. As the posterior distribution under our model is not available in closed form, we use stochastic variational inference²³ to learn an approximation to the posterior distribution $p\left({\mathit{\theta }}_{\mathbf{1}:\mathit{D}},{\mathit{\beta }}_{\mathbf{1}:\mathit{K},\mathbf{1}:\mathit{L}}^{\mathbf{1}:\mathit{T}}|{\mathit{x}}_{\mathbf{1}:\mathit{D},\mathbf{1}:\mathit{L}}\right)\approx q\left({\mathit{\theta }}_{\mathbf{1}:\mathit{D}},{\mathit{\beta }}_{\mathbf{1}:\mathit{K},\mathbf{1}:\mathit{L}}^{\mathbf{1}:\mathit{T}}\right)$. Briefly, variational inference approximates an intractable posterior distribution $p\left(\cdot |X\right)$ by a tractable distribution $q\left(\cdot ;\mathit{\rho }\right)$ indexed by variational parameters $\mathit{\rho }$. The $\mathit{\rho }$ are then optimized to minimize the Kullback-Leibler (KL) divergence, a measure of dissimilarity between two distributions, between the true and approximate posterior. Performance of variational inference depends in part on how well the approximate posterior can capture the true posterior. Intuitively, this means the approximated posterior should be close in form to the true posterior.

We use variational Kalman filtering²¹ to construct an approximate posterior for the ${\beta }_{kl}^t$ that captures the temporal dependencies in our model. The variational approximation takes the form

$$q\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1}\right)=\text{Normal}\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1},\frac{g_t-g_{t-1}}{12N_k}\right)$$

$$q\left({\hat{\beta }}_{kl}^t|{\beta }_{kl}^t,;\nu \right)=\text{Normal}\left({\hat{\beta }}_{kl}^t|{\beta }_{kl}^t,{\nu }^2\right)$$

where ${\hat{\beta }}_{kl}^t$ are additional pseudo-observations that are treated as variational parameters. Following Blei and Lafferty,²¹ we fixed the parameter ${\nu }^2$ and set it to a fixed value ${\nu }^2=0.001$ for all experiments. Given the pseudo-observations, standard Kalman filtering and smoothing equations²⁴ can be applied to compute the marginal posterior

$$q\left({\beta }_{kl}^t|{\hat{\beta }}_{kl}^1,\dots ,{\hat{\beta }}_{kl}^T\right),$$

which is used as an approximation for the true posterior on allele frequencies. The variational approximation for the ancestry vectors is

$$q\left({\mathit{\theta }}_{\mathit{d}};{\hat{\mathit{\theta }}}_{\mathit{d}}\right)=\text{Dirichlet}\left({\mathit{\theta }}_{\mathit{d}}|{\hat{\mathit{\theta }}}_{\mathit{d}}\right).$$

Taken altogether, the variational posterior is given by

$$q\left({\mathit{\theta }}_{\mathbf{1}:\mathit{D}},{\mathit{\beta }}_{\mathbf{1}:\mathit{K},\mathbf{1}:\mathit{L}}^{\mathbf{1}:\mathit{T}}\right)=\prod _{d=1}^{D}q\left({\mathit{\theta }}_{\mathit{d}};{\hat{\mathit{\theta }}}_{\mathit{d}}\right)\prod _{k=1}^K\prod _{l=1}^L\prod _{t=1}^{T}q\left({\beta }_{kl}^t|{\hat{\beta }}_{kl}^1,\dots ,{\hat{\beta }}_{kl}^T\right)\text{.}$$ (Equation 4)

The variational objective function is

$$\mathcal{L}\left({\mathit{\beta }}_{1:K,1:L}^0,{\hat{\mathit{\beta }}}_{1:K,1:L}^{1:T}{\hat{\mathit{\theta }}}_{1:D},{\mathit{x}}_{1:D,1:L}\right)={\mathbb{E}}_q\left[\log p\left({\mathit{\beta }}_{1:K,1:L}^{1:T},{\mathit{\theta }}_{1:D},{\mathit{x}}_{1:D,1:L}\right)\right]-{\mathbb{E}}_q\left[\text{log}q\left({\mathit{\theta }}_{1:D},{\mathit{\beta }}_{1:K,1:L}^{1:T}\right)\right].$$

Optimizing $\mathcal{L}$ with respect to ${\beta }_{kl}^0$ gives maximum likelihood estimates of the model parameters. Optimizing $\mathcal{L}$ with respect to the variational parameters ${\hat{\beta }}_{kl}^t$ and ${\hat{\mathit{\theta }}}_{\mathit{d}}$ gives an approximate posterior close to the true posterior.

We adapt the stochastic variational inference algorithm derived by Gopalan et al.²⁰ for use with our time-series model to optimize $\mathcal{L}$. This allows us to iteratively update the variational parameters ${\hat{\mathit{\theta }}}_{\mathit{d}}$ by subsampling loci along the genome (see Appendix A for more details). Parameter estimates are updated until convergence. After convergence, point estimates for ${\mathit{\theta }}_{\mathit{d}}$ are obtained by taking the expectation under the posterior. For a Dirichlet random variable, this is

$${\theta }_{dk}^{\text{∗}}:={\mathbb{E}}_q\left[{\theta }_{dk}\right]=\frac{{\hat{\theta }}_{dk}}{{\sum }_{k\text{'}=1}^K{\hat{\theta }}_{dk\text{'}}}.$$ (Equation 5)

Note that the ${\hat{\mathit{\theta }}}_{\mathit{d}}$ are parameters of a Dirichlet distribution and do not necessarily sum to 1.

Model Choice (K)

We use a held-out dataset to compare across runs and different values of K. This dataset is constructed by randomly selecting entries in the genotype matrix, which are treated as missing during parameter inference. We compute the log likelihood of the held-out genotypes conditioned on the current point estimates of ${\beta }_{kl}^t$ and ${\mathit{\theta }}_{\mathit{d}}$, which we denote the “conditional log likelihood.” Formally, suppose we have selected a held-out set of individual-locus pairs $\mathcal{H}\subset \left\{\left(d,l\right):d=1,\dots D;l=1,\dots L\right\}$. After convergence, we evaluate the conditional log likelihood on the held-out set,

$${\mathcal{L}}_{\mathcal{H}}:=\sum _{\left(d,l\right)\in \mathcal{H}}\text{log}p\left(x_{dl}|{\mathit{\theta }}_{\mathit{d}},{\beta }_{kl}^{t_d}\right)=\sum _{\left(d,l\right)\in \mathcal{H}}\text{log}\left(\text{Binomial}\left(x_{dl}|n_d,\sum _{k=1}^K{\theta }_{dk}{\beta }_{kl}^{t_d}\right)\right).$$

The best-supported model is the one that achieves the greatest conditional log likelihood. We note that the conditional log likelihood here is equivalent to the log likelihood ADMIXTURE if we treat the samples at each time point separately. We choose this for our model evaluation procedure because it does not depend on choice of population size or number of time points, both of which influence the variational objective.

In-Model Simulations

In-model simulations were performed with 10,000 loci simulated under a discrete time Wright-Fisher model. Specifically, given an allele frequency at time t (p^t), the allele frequency at time t + 1 (p^t+1) was determined by

$$\begin{array}{l}{X}^t\sim \text{Binomial}\left(2N,p^t\right)\\ p^{t+1}=\frac{X^t}{2N}\end{array}$$

Initial frequencies were drawn from an Uniform(0.2,0.8) distribution. For admixed individuals we used the following model:

$${\mathit{\theta }}_{\mathit{d}}\sim \text{Dirichlet}\left(\frac{1}{K}{1}_K\right)\text{ for individuals }d=1,\dots D$$ (Equation 6)

$$x_{dl}\sim \text{Binomial}\left(2,\sum _{k=1}^K{\theta }_{dk}{p}_k^{t_d}\right)\text{for loci }l=1,\dots ,L.$$

We defined two simulation scenarios to investigate model performance. In the “mixture” scenario, all samples were admixed. That is, we drew admixture proportions ${\mathit{\theta }}_{\mathit{d}}$ according to Equation 6. In the “merger” scenario, ancient samples were unadmixed and modern samples were admixed. For unadmixed individuals, we set ${\mathit{\theta }}_{\mathit{d}}$ to an indicator vector denoting that individual’s population and sampled genotypes as above. For admixed samples, we again drew admixture vectors according to Equation 6. We note that this is equivalent to sampling from an admixed population at the time of admixture.

We generated 100 individuals from each time point. All simulations used an effective population size of N = 2,500 for all populations.

Data Sparsity and Pseudo-haploid Samples

Ancient DNA datasets contain sparse, pseudo-haploid, ancient samples, where the sample size of ancient samples is small compared to the sample size of modern samples. To evaluate model performance under these conditions, we simulated 2 populations at 5 time points spanning 400 generations with N = 2,500 for both the mixture and merger scenarios. At each ancient time point, we simulated 20 pseudo-haploid samples and simulated 300 modern samples at the final time point. For ancient samples we varied the percentage of missing data from 0% to 90%, selecting loci uniformly at random without replacement, while modern samples had full data.

Choosing K

We evaluated our ability to infer the correct value of K under both the mixture and merger scenarios, simulating 100 individuals at each of 5 time points spanning 400 generations with N = 2,500. For the mixture scenario, we simulated K = 4 and ran DyStruct from K = 2,…,6. For the merger scenario, we simulated K = 3 and ran DyStruct from K = 2,…,5. For both scenarios, we constructed a hold-out set of 5,000 genotypes.

Out-of-Model Simulations

Coalescent simulations were performed using msprime.²⁵ In the coalescent merger scenario, we simulated two populations that split 3,000 generations ago and merged 200 generations ago. The population size before the merger was set to 2N = 2,500 and after the merger to 2N = 5,000. We simulated 10,000 independent gene genealogies with a mutation rate parameter of 10⁻⁸ per generation. To convert haploid gene genealogies to diploid genealogies, we combined random pairs of gene genealogies. 50 diploid individuals were sampled from each population 10 generations before the merge (210 generations back in time), and 100 diploid individuals were sampled from the modern admixed population. We varied the contributions from each ancient population by adjusting the probabilities that a lineage in the modern population had an ancestor in one of the ancient populations. This procedure is analogous to adjusting the mixture proportions in the modern population. The mixture proportions we explored were .125–.875, .25–.75, .375–.625, and .50–.50.

In the coalescent split scenario, we simulated three modern populations descended from a single ancestral population. We simulated two population splits, one 3,000 generations ago and the other 1,500 generations ago. We used a fixed population size of 2N = 5,000 for all populations. In contrast with the above, we simulated a 10 megabase region with a recombination rate of 10⁻⁸ per generation and a mutation rate of 2 × 10⁻⁸ per generation, and we selected 10,000 evenly spaced gene genealogies for each sampled individual. 100 individuals were sampled from each modern population. 50 ancient individuals were sampled from the population that underwent the second split 50 generations prior.

Choosing K

We ran DyStruct using K = 2, 3 on the coalescent merger scenario and K = 2, 3, 4 on the coalescent split scenario, using a hold-out set of 5,000 genotypes.

Real Datasets

We downloaded the real dataset analyzed by Haak et al.⁵ and ran DyStruct and ADMIXTURE with K = 2,…,5 on two separate subsets of the data: one of 80 ancient samples and 296 modern West Eurasians, and another of the same 80 ancient samples and 17 modern Oceanians (see Figure 6 for sample labels and subsets). The ancient samples included newly reported individuals sampled by Haak et al.,⁵ other ancient samples from the literature,^{26, 27, 28, 29} and modern samples from the Human Origins panel.^{4, 14} After LD pruning (see below), 149,104 loci remained for analysis in the West Eurasian dataset and 174,984 remained for analysis in the Oceanian dataset. We set N = 10,000 for DyStruct. To evaluate model fit across K (see Model Choice (K)), we used a hold-out set of 7,455 genotypes for the West Eurasian dataset and a hold-out set of 8,749 genotypes for the Oceanian dataset, equivalent to approximately 5% of the total number of loci in each dataset.

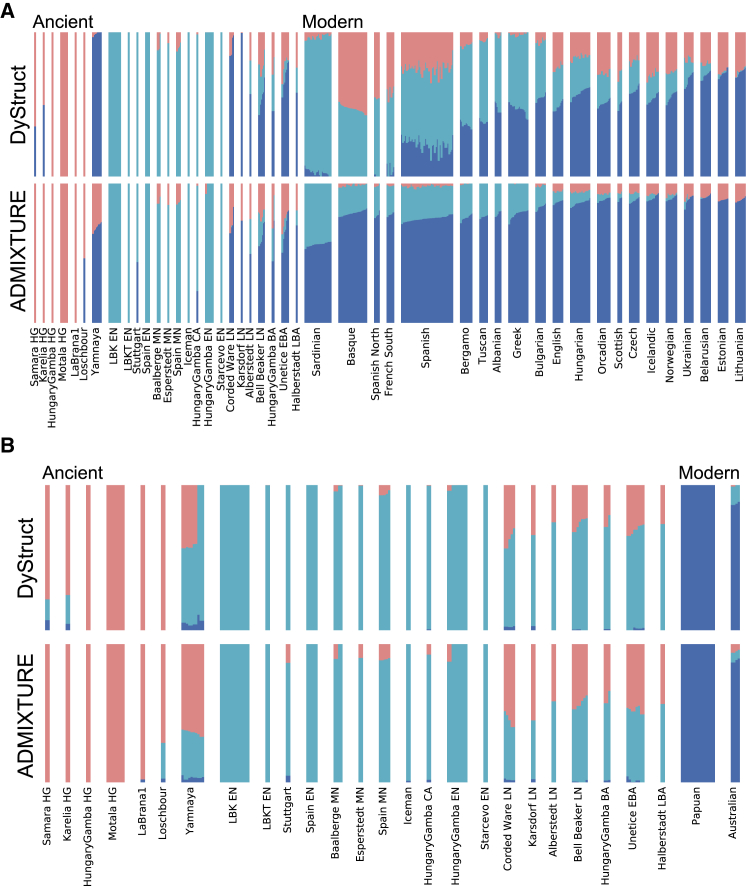
Figure 6.

DyStruct and ADMIXTURE’s Ancestry Estimates on Ancient Samples and a Subset of Modern Europeans and Two Modern Oceanian Populations

(A) Modern samples are ordered by approximately increasing steppe ancestry (blue) from DyStruct’s estimates. DyStruct (top) identifies three ancient clusters: hunter-gatherers (red), Yamnaya steppe (blue), and early farmers (teal). Modern European populations appear as mixtures of these three groups, with modern Sardinians and individuals from the Iberian Peninsula sharing the least amount of steppe ancestry. In ADMIXTURE (bottom), the Yamnaya appear as a mixture of hunter-gatherers and a blue component without a clear interpretation. Hunter-gatherer ancestry is absent from many modern samples, and all modern populations appear to have more steppe ancestry than inferred by DyStruct.

(B) DyStruct correctly identifies when modern samples do not share ancestry with ancient ones. When there is no shared ancestry between ancient and modern populations, and thus little shared ancestry across time, DyStruct and ADMIXTURE’s estimates are similar. Both models identify two clusters of ancient samples: hunter-gatherers (red) and early farmers (teal). Yamnaya share ancestry with both ancient groups.

We also downloaded and analyzed the real dataset analyzed by Lazaridis et al.,²² which included individuals from the Human Origins panel, newly reported ancient samples, and other ancient samples from the literature.^{4, 5, 30, 31, 32, 33, 34} The final dataset consisted of 2,067 modern and 262 ancient individuals. After LD pruning (see below), 293,130 loci remained for analysis. We ran ADMIXTURE and DyStruct from K = 2,…,14. DyStruct was run using N = 10,000 for all populations. To evaluate model fit across K (see Model Choice (K)), we used a hold-out set of 14,657 genotypes, about 5% the number of observed loci .

For all datasets, we first LD pruned loci using Plink v1.07³⁵ with the options --indep-pairwise 200 25 0.4 . Generation times were computed by taking the midpoint of carbon date estimates, or culture date estimates, and converted to generation times assuming a 25-year generation time. Generation times were binned using the script bin_sample_times.py, which constructs a sliding window of 50 generations and merges all generation times within a window to the mean of times in each bin. After preprocessing, there were 7 time points spanning 324 generations for the West Eurasian and Oceanian datasets from Haak et al.⁵ and 10 time points spanning 519 generations for the Lazaridis et al.²² dataset.

PCA was performed using the smartpca program¹¹ on the publicly available subset of 860 modern West Eurasians analyzed by Lazaridis et al.,²² using the options lsqproject: YES and numoutlieriter: 0. Ancient samples were projected onto the principle components of the modern Eurasians.

Results

In-Model Simulations

We first evaluated DyStruct using synthetic data simulated under a discrete-time Wright-Fisher model for two historical scenarios. In the “mixture” scenario, individuals were modeled as mixtures of populations whose allele frequencies drifted independently over time. In the “merger” scenario, older ancient individuals were drawn unadmixed from ancient populations that merged at the last time point to form an admixed modern population. Individuals were also sampled from the admixed modern population. As the merger scenario is reflective of realistic dynamics between ancient and modern populations, we were particularly interested in our model’s ability to detect when modern admixed individuals share ancestry with ancient unadmixed ones. We varied the density of samples in time and number of populations and ran DyStruct under several effective population sizes as the true population size for each population is likely unknown at runtime. For all simulations, we also ran ADMIXTURE and Ohana.³⁶ We compared model performance by computing the root-mean-square-error (RMSE) between the ground truth ancestry estimates and those provided by each respective model.

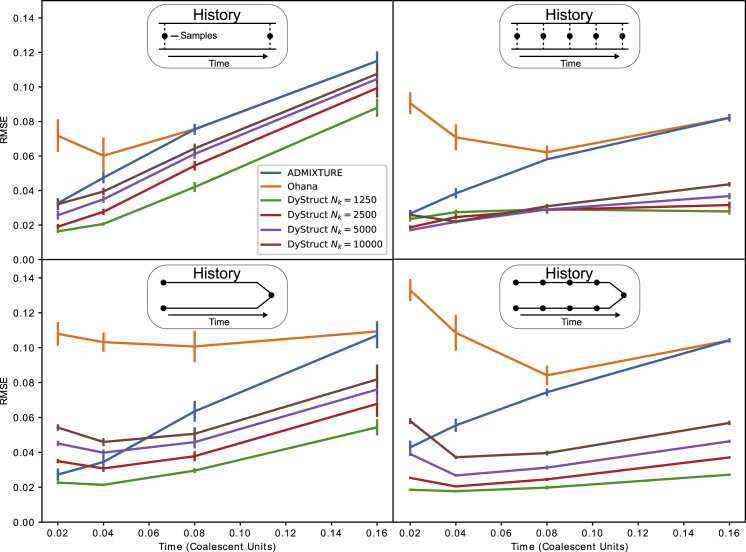
Figure 2 displays DyStruct, ADMIXTURE, and Ohana’s performance on simulations using two ancestral populations with N = 2,500. DyStruct outperformed Ohana across all our simulations. ADMIXTURE outperformed Ohana on 9 of the 16 simulations we performed and had similar RMSE on the remaining simulations. When the true effective size is provided as input to DyStruct (input is denoted by N_k), it outperformed ADMIXTURE across all but one simulation scenario where there was little genetic drift. Notably, even when the incorrect population size is provided to DyStruct, it outperformed ADMIXTURE on the majority of simulations. With N_k = 5,000, DyStruct’s mean RMSE was lower than ADMIXTURE’s on 14 out of 16 simulation scenarios; with N_k = 10,000, it was lower on 11 out of the 16 simulation scenarios. When an under-estimate of the true population size was provided (N_k = 1,250), DyStruct outperformed ADMIXTURE across on all simulations. However, we found that setting N_k lower than this made DyStruct susceptible to local optima when genetic drift was the largest under the denser sampling scheme (simulation time = 0.16 coalescent units; Figure S1). Because ADMIXTURE performed better than Ohana, we choose to focus on comparing DyStruct to ADMIXTURE for the remainder of our analysis.

Figure 2.

Performance of DyStruct, ADMIXTURE, and Ohana on Simulated Data for Two Historical Scenarios and Two Sampling Schemes

Top: individuals are mixtures of two ancestral populations (the “mixture” scenario). Bottom: ancient individuals are sampled solely from one of two ancestral populations that merge at present, and modern samples from the present-day admixed population (the “merger” scenario). Models were compared by computing the root-mean-square-error (RMSE) on ancestry estimates between the simulated ground truth and the output from both models. Diagrams above each plot show the historical scenario simulated, and black circles denote approximately when individuals are sampled. The x axis displays total simulation time between the first and last sample (1 coalescent unit = 2N generations for simulated N = 2,500). The y axis gives the mean RMSE across models (vertical lines denote 1 standard error estimated from 10 replicates). DyStruct was run with varying population sizes to explore model performance when the true size is unknown. DyStruct’s ancestry estimates improve when individuals are more densely sampled in time, while ADMIXTURE’s remain similar. Both models outperform Ohana.

As expected, DyStruct’s ancestry estimates significantly improved with denser sampling over time (Figure 2, right). When individuals were sampled at 5 time points opposed to 2, DyStruct’s RMSE substantially improved across all scenarios. DyStruct’s mean RMSE appeared more stable across time when denser sampling for the mixture scenario, while ADMIXTURE’s mean RMSE increased over time. When sampling more populations, as opposed to more time points, DyStruct and ADMIXTURE’s performance were similar to the two population case (Figure S2).

Choosing K

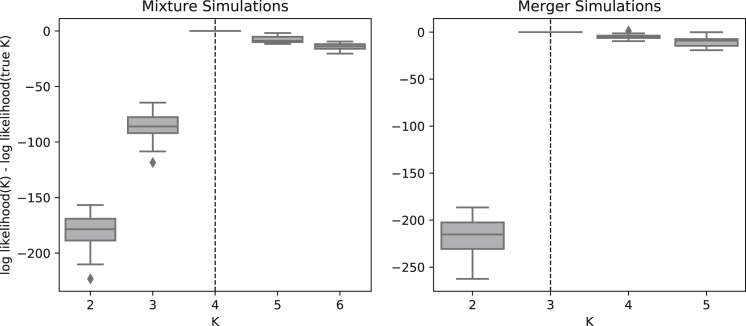
We next investigated DyStruct’s ability to identify the correct number of ancestral populations (K) in our simulations. For each simulation, we held out a set of 5,000 genotypes, and computed the log-likelihood on the hold out set conditioned on estimated model parameters (see Material and Methods). The value of K with the highest log-likelihood was chosen as the best-supported model.

Under the mixture scenario, we performed 10 simulations with K = 4, and ran DyStruct from K = 2,…,6. The best-supported model across all 10 simulations was K = 4 (Figure 3A). Under the merger scenario, we performed 10 simulations with K = 3, and ran DyStruct from K = 2,…,5. The best supported model was K = 3 in 9 out of 10 of our simulations (Figure 3B). Across both sets of simulations, we observed an increase in log-likelihood up to the true value of K, and afterward the held-out log-likelihood leveled off.

Figure 3.

Model Performance for Choosing K under Two In-model Simulation Scenarios

Boxplots of the difference in the conditional log likelihood from the log likelihood of the true K. The conditional log likelihood was computed on 5,000 held out genotypes (y axis) across 10 for different choices of K (x axis). The highest log likelihood is chosen as the “true” K. For the mixture scenario, the correct K (dashed vertical line) is identified 10 out of 10 times. For the merger scenario, the correct K is identified 9 out of 10 times.

Data Sparsity and Pseudo-haploid Samples

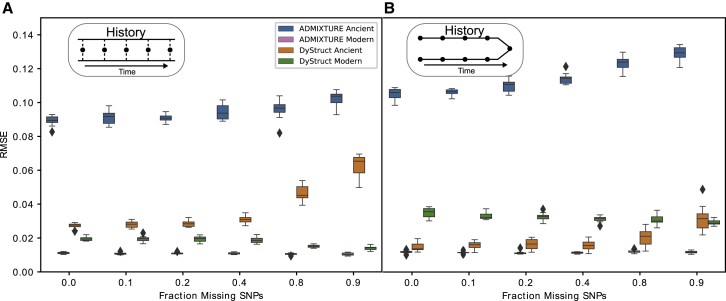
Ancient DNA samples often have low sequencing coverage and low sequencing depth. In practice, samples are often represented as pseudo-haploid—where only a single allele is observed instead of a genotype, and encoded by a 0 or 2—and have a significant amount of missing data. Furthermore, ancient DNA datasets are unbalanced in that substantially more modern samples are sequenced than ancient ones. We thus evaluated DyStruct’s robustness to sparse, pseudo-haploid, and unbalanced datasets. For both the mixture and merger scenarios, we simulated ancient pseudo-haploid individuals, varying the amount of missing data, and using an approximately 3.75 times larger set of modern samples, reflecting the balance of samples in the Haak et al.⁵ dataset (consisting of ancient samples and modern Europeans, see Entry of Steppe Ancestry into Europe).

Figure 4 displays the RMSE on ancient and modern samples for DyStruct and ADMIXTURE. Notably, ADMIXTURE’s RMSE on ancient samples (median RMSE range 0.089–0.10 on the mixture scenario; 0.11–0.13 on the merger scenario) is significantly higher than on modern ones (median RMSE range 0.010–0.011 on the mixture scenario; 0.011–0.012 on the merger scenario). In contrast, under the mixture scenario, DyStruct’s RMSE on ancient samples (median RMSE range 0.028–0.065) was only slightly higher than modern samples (median RMSE range 0.020–0.023). We observed an increase of ∼0.038 in median RMSE from the lowest to the highest amount of missing data. The effect was most apparent at the greatest degrees of missingness (80% missing and 90%_, respectively). Under the merger scenario, the RMSE on ancient samples was lower (median RMSE range 0.014–0.031) than on modern samples (median RMSE range 0.028–0.036), in contrast with the results of the mixture scenario. This is likely because ancient samples in the merger scenario only have a single ancestral component which DyStruct is accurately able to detect. We also observed a small increase in RMSE at high levels of missing data (an increase in median RMSE of 0.018 between from the best to the worst RMSE). Nonetheless, the DyStruct outperformed ADMIXTURE on ancient samples for all explored simulation parameters. ADMIXTURE had a lower RMSE on modern samples than DyStruct, but the difference was slight; the greatest difference in median RMSE across scenarios was 0.024. Taken altogether, our results suggest that DyStruct accurately estimates ancestry components on pseudo-haploid data with varying degrees of missingness.

Figure 4.

DyStruct and ADMIXTURE’s Performance on Sparse Pseudo-haploid Samples

Boxplots of root mean square error (y axis) between the ground truth ancestry and model estimates for ancient and modern samples. The fraction of missing SNPs varied across ancient samples (x axis), while modern samples had full data. Ancient samples are psuedo-haploid, where only a single allele is observed at each locus and encoded by 0 or 2. DyStruct’s ancestry estimates on ancient samples are more accurate than ADMIXTURE across degrees of missing data.

Out-of-Model Simulations

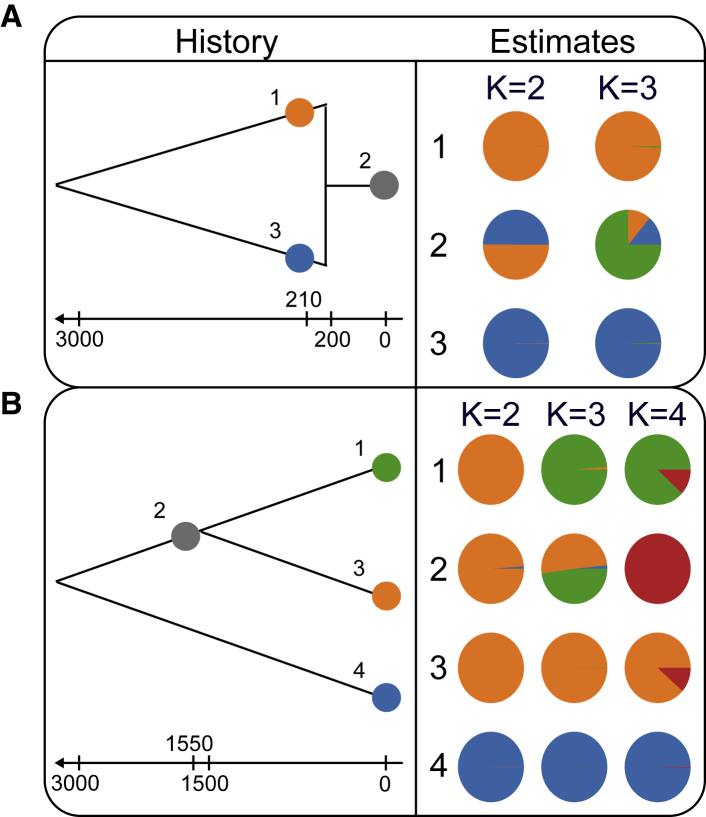
We next tested DyStruct using coalescent simulations. DyStruct assumes that populations are independent over time without population splits or mergers. Thus, coalescent simulations allow us evaluate how DyStruct performs when its modeling assumptions are violated. We performed coalescent simulations under a population merger scenario and a population split scenario, and we sampled individuals from various points along the population phylogeny. For the “coalescent merger” scenario, we simulated two populations that split approximately 3,000 generations in the past (approximately the time of the human out-of-Africa migration) that subsequently mixed 200 generations ago (approximately the time of the entry of steppe ancestry into Europe) to form a single modern population. We varied the contribution of each ancestral population by adjusting the probability that a lineage in the modern population has an ancestor in one of the ancestral populations (see Material and Methods). For the “coalescent split,” we simulated three modern populations that split from a single ancestral population approximately 3,000 generations ago. Two of the modern population subsequently split 1,500 generations ago. We then ran DyStruct on the sampled individuals, varying K, and qualitatively compared ancestry estimates to the true underlying population history because coalescent simulations do not provide per sample ancestry estimates for a quantitative evaluation. In principle, one could count the number of coalescent events in each population for the coalescent merger scenario for comparison. However, this is more complicated for the coalescent split scenario because not all lineages will coalesce before each population split, and thus multiple lineages from different populations remain in all ancestral populations.

Figure 5 displays DyStruct’s mean ancestry estimates for each K, averaging across samples then across simulation replicates, for the coalescent merger scenario with 50% mixing proportions and the coalescent split scenario. For the coalescent merger scenario, DyStruct was able to detect that the modern population is a mixture of the two sampled ancestral populations. At K = 2, the modern population appears as a mixture of the two ancestral populations. Ancient samples from each population are assigned to distinct ancestry components, while the modern samples appear as mixtures of the two ancient populations. At K = 3, assignment for the ancient samples remains the same, while the modern population inherits approximately 25% of its ancestry from the ancient population and the remainder from a novel cluster. Results were qualitatively similar to ADMIXTURE, but the fraction of shared ancestry between ancient and modern samples at K = 3 was much lower (Figure S3). When adjusting the contribution of the ancient populations to the modern, the results remain similar (Figures S4 and S5). At K = 2, estimated mixture proportions closely reflect simulated mixture proportions, with a slight overrepresentation of the major contributing population (Figures S4 and S5).

Figure 5.

DyStruct’s Performance on Coalescent Simulations

Diagrams on the left depict the historical scenario simulated. Colored circles denote where in the population phylogeny individuals were sampled. Arrows and notches below each diagram give the generation time of sampled individuals and historical events. Pie charts on the right give the mean ancestry estimates for each population across 10 replicates.

(A) At K = 2, DyStruct can accurately detect the contribution of the ancient populations to the modern one. Ancient samples are assigned nearly a single ancestry component (color), while modern samples appear as admixed between ancient populations. At K = 3, DyStruct assigns a new cluster to the modern population, but still identifies shared ancestry from its ancestral contributors.

(B) At K = 2, DyStruct identifies the oldest split in the phylogeny. At K = 3, DyStruct splits the ancient population by clusters corresponding to its two descendants. At K = 4, the ancient population gets its own cluster, but DyStruct still identifies shared ancestry between it and its two descendant populations.

Under the coalescent split scenario, DyStruct identifies a contribution from the ancestral population into its modern descendants across all K. At K = 2, DyStruct clusters populations by the oldest split, placing the ancestral population and its descendants in a single cluster. At K = 3, DyStruct assigns modern samples from each population to their own clusters, while the ancient samples appear as a mixture of its two modern descendants. We note that by forcing the four sampled populations into three clusters, it is necessary to identify one (or more) of the populations as admixed. In some cases, one of the modern populations appeared as admixed in addition to the ancestral population (Figure S6). At K = 4, the ancient population receives its own cluster. Notably, its modern descendants appear admixed between their own clusters and the ancestral cluster. This pattern does not appear in ADMIXTURE (Figures S3 and S7), which gives each sampled population their own independent clusters. Thus, ADMIXTURE does not identify a contribution of the ancient population to its descendants at K = 4.

In all cases, the reported means were representative of our simulation replicates as a whole (Figures S4, S6, S8, and S9), as the standard deviation in ancestry estimates across replicates was low.

Choosing K

We further investigated our model fit procedure to identify the best K for both the coalescent merger and coalescent split scenarios. While there is technically no correct K for these scenarios, we wanted to examine how different population relationships changed support for different K. For the coalescent merger scenario, difference in log likelihood for K = 2 and K = 3 was slight (Figure S10), suggesting both are equally well supported, and possibly that we are at the plateau observed in the in-model simulations. With a 50-50 contribution from both populations, the scenario presented in Figure 5, the best supported K was K = 3 in 9 of the 10 simulations. For a 37.5-62.5 split, K = 3 was the best supported K in all 10 simulations. For a 25-75 split, K = 3 was the best supported in 8 out of 10 simulations. For a 12.5-87.5 split, K = 3 was the best supported in 6 out of 10 simulations. Under the coalescent split scenario, K = 4 was best supported in 9 out of 10 simulations, K = 3 was best supported in the remaining simulation, and none of the simulations supported K = 2 (Figure S11).

Entry of Steppe Ancestry into Europe

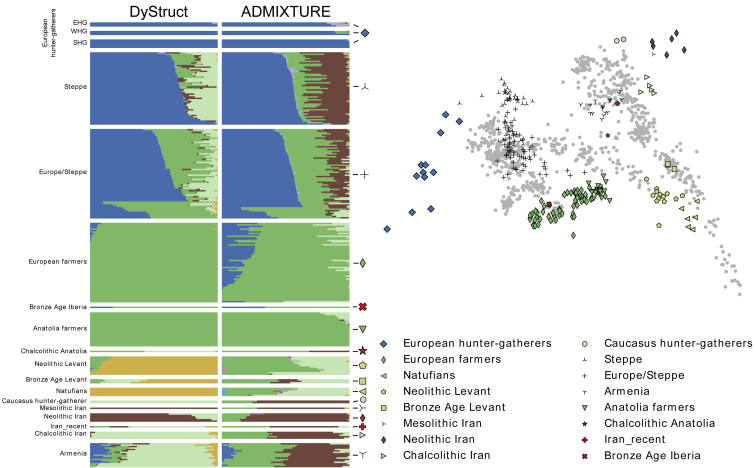
To explore performance on real data, we investigated a dataset of ancient and modern humans studied by Haak et al.⁵ In their analysis, the authors used ancient DNA from early farmers, Yamnaya steppe herders, hunter-gatherers, and later ancient samples to study the movement of early peoples into Europe. Reasoning that movement of genes can mirror movement of people, culture, and technology, the authors compared ancient and modern people to investigate the source of Indo-European languages. The authors detected a migration event from the steppe into Europe around 4,500 years ago and found strong support for a model of modern Europeans as a mixture of three ancestral groups: early farmers, steppe, and hunter-gatherers. Their results suggested the steppe as a likely origin of Indo-European languages.

We applied DyStruct and ADMIXTURE to two subsets of their data. First, as a positive control we wanted to see whether our model could detect ancient admixture in modern Europe. We ran both models with K = 3 on a subset of hunter-gatherers, Yamnaya steppe herders, early farmers, later ancient samples, along with a subset of modern Europeans analyzed by Haak et al.⁵ (Figure 6A). We chose K = 3 because it corresponded to the three populations identified by the authors of the study. Interestingly, DyStruct identifies hunter-gatherers (red), Yamnaya steppe (blue), and early farmers (teal) as distinct clusters (with the exception of the eastern hunter-gatherers Samara and Karelia), while in ADMIXTURE the Yamnaya appear admixed between hunter-gatherers and a blue ancestry component. Hence, DyStruct gives distinct cluster to the three contributing populations identified by Haak et al.⁵ Ancestry estimates on modern populations substantially differ as well. Notably, DyStruct assigns majority farmer ancestry and little steppe ancestry to modern Sardinians and modern populations from the Iberian Peninsula, consistent with Haak et al.⁵ and Olalde et al.⁶ who found that little steppe ancestry penetrated this far south in Europe. In ADMIXTURE, both these groups appear to have substantial portions of the blue ancestry, which roughly corresponds to the steppe group. In practice this indicates that interpreting the blue component as steppe ancestry would lead to an incorrect conclusion.

Notably, DyStruct and ADMIXTURE differ in how they identify the relationship between eastern hunter-gatherers (Samara and Karelia) and the Yamnaya, who are known to share ancestry.¹ DyStruct assigns the Yamnaya their own cluster, and identifies the eastern hunter-gatherers as admixed between the hunter-gatherer cluster and the steppe cluster. ADMIXTURE identifies Yamnaya as a mixture between all hunter-gatherers and the blue ancestry component. Interestingly, at K = 4 ADMIXTURE does cluster the Yamnaya into their own group and identifies shared ancestry between the Yamnaya at the eastern hunter-gatherers (Figure S12). However, it does so at the expense of eliminating their contribution into modern populations—the largest ancestry component in all modern samples does not correspond to any of the three ancient populations.

We additionally compared model fit and results for different values of K (Figures S12 and S13). At K = 2, the best supported K according to our model choice procedure (Figure S11), DyStruct and ADMIXTURE identify two clusters: hunter-gatherers and European farmers. The Yamnaya in DyStruct cluster completely with the hunter-gatherer group, but appear admixed in ADMIXTURE, and their contribution to modern populations differ. At K = 4 and K = 5, DyStruct and ADMIXTURE identify different relationships between samples (Figure S12). At K = 4, DyStruct splits the modern Basque population into its own cluster and clusters the Yamnaya and hunter-gatherers together, while ADMIXTURE identifies a new cluster mostly associated with the modern samples. Interestingly, both models split the Neolithic samples into two clusters for higher K, but at different values of K (K = 4 for DyStruct and K = 5 for ADMIXTURE).

As a negative control, we tested that both models correctly identify distinct modern populations that do not share ancestry with ancient samples. To this end, we ran DyStruct and ADMIXTURE with K = 3 on the same set of ancient samples, but included two modern Oceanian populations instead of modern Europeans (Figure 6B). Encouragingly, DyStruct assigns modern Oceanian populations to their own cluster (blue). Two ancient clusters are identified: hunter-gatherers (red) and early farmers (teal). The Yamnaya appear to share ancestry with both these clusters, the majority of which comes from the hunter-gatherer group. As expected, when there is little shared ancestry over time, both DyStruct and ADMIXTURE produce similar results.

We again compared model fit and results for different values of K (Figures S14 and S15). At K = 2, again the best supported K (Figure S13), both DyStruct and ADMIXTURE split ancient and modern samples into their own groups. At K = 4, ADMIXTURE breaks the Yamnaya into their own cluster, and at K = 5 ADMIXTURE separates Papuan’s from Australians. In contrast, at K = 4 DyStruct separates Papauns from Australians and splits the Neolithic group at K = 5.

Origin of Farming in the Near East

We next conducted a larger experiment using 2,067 modern individuals from the Human Origins dataset, along with 262 ancient individuals, analyzed by Lazaridis et al.²² In their study, the authors used genomic data from ancient samples to investigate the origin of farming in the Near East. One question the authors asked was whether farming technology entered the Near East due to population replacement, similar in spirit to the findings of Haak et al.,⁵ or whether farming technology was adopted by the people already living in these areas. The authors found genetic continuity between early hunter-gatherers in Iran and the Levant the later farmers occupying these regions, suggesting that farming technology entered these areas without substantially displacing the people already there.

We ran both Dystruct and ADMIXTURE from K = 2,…,14 for ancient and modern samples combined, and compared the results (Figures S16 and S17). To better understand how each model captures the genetic relationships between sampled ancient individuals, we also performed a PCA by projecting ancient samples onto the principal components of 860 modern West Eurasians, motivated by the analysis performed by Lazaridis et al.²² Figure 7 displays the PCA (right) and results on ancient samples for K = 10 (left). We chose K = 10 because it highlights the difference in conclusions drawn from DyStruct and ADMIXTURE. The best supported K was K = 12 (Figure S18). We emphasize that no single K can capture all genetic relationships between ancient and modern populations because any K forces a complex population history into a small number of ancestral components. Thus, it is important to systematically investigate each value of K in turn, not only the one best supported by the model.

Figure 7.

Model Comparison between DyStruct, ADMIXTURE, and PCA on samples analyzed from Europe and the Near East

Left: DyStruct and ADMIXTURE’s ancestry estimates on ancient samples when run with K = 10 on 2,329 ancient and modern samples analyzed. Within population samples are ordered by major contributing cluster. Right: Projection of ancient samples onto the principal components of 860 modern West Eurasians. DyStruct identifies five clusters consistent with PCA: European hunter-gatherers (dark blue), Anatolian/European farmers (dark green), Natufians/Neolithic Levant (dark yellow), Caucasus hunter-gatherers (light green), and Neolithic Iran (brown). In ADMIXTURE, Neolithic Levant, and European farmers appear admixed.

DyStruct identifies five clusters consistent with the PCA: European hunter-gatherers (dark blue in Figure 7), Anatolian/European farmers (dark green), Natufians/Neolithic Levant (dark yellow), and Mesolithic/Neolithic Iran (brown), and Caucasus hunter-gatherer (light green). Notably, early hunter-gatherers in the Levant (the Natufians) cluster with later Neolithic samples in the region, and Mesolithic hunter-gatherers in Iran cluster with Neolithic Iran, reflecting genetic continuity in these regions. In addition, early farmers from Anatolia cluster with later European farmers. This is consistent with the conclusions of Lazaridis et al.,²² who found the later samples were genetically similar to their earlier counterparts. In ADMIXTURE, European farmers appear admixed. In addition, ADMIXTURE does not break out Natufians and Levatine farmers into their own group, and they instead appear admixed between the Anatolian farmer component and a light green component.

We note that Lazaridis et al.²² find genetic continuity between Caucasus hunter-gatherers and Neolithic Iran. In addition, they find support for a model of Chalcolithic Iran as a mixture of Neolithic Iran, Caucasus hunter-gatherers, and Levatine farmers. This pattern is partially lost in DyStruct at K = 10, but it is more apparent at different values of K. For instance, at K = 12 Caucasus hunter-gathers, Mesolithic/Neolithic Iran, and Chalcolothic Iran all have the same ancestral components at different ancestry proportions. This again highlights the importance of considering results across K. Indeed, results on ancient samples highlight several important distinctions between DyStruct and ADMIXTURE (Figure S16). For instance, at K = 4, DyStruct breaks Mesolithic Iran (Iran_HotuIIIb) and Neolithic Iran into their own clusters. At K = 5, DyStruct identifies two major clusters among ancient samples: European hunter-gatherers/steppe (dark blue in Figure S16) and early farmers (dark green). In contrast, at K = 5, ADMIXTURE clusters hunter-gatherers (dark green), but the remaining samples appear admixed between the hunter-gatherer group and a dark green component. Each of these provide information about the genetic relationship among samples and suggest hypotheses to test with downstream analysis.

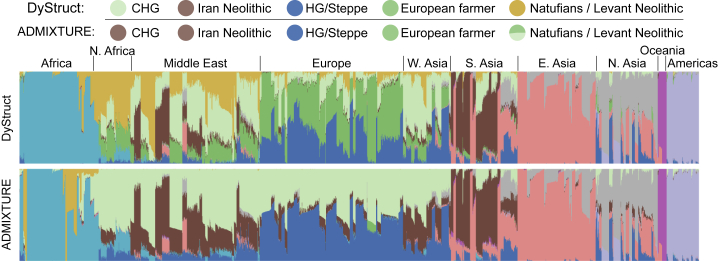
Figure 8 displays DyStruct and ADMIXTURE’s ancestry estimates on modern samples for K = 10. There are several notable differences between the two models. In DyStruct, modern European populations have substantial shared ancestry with earlier European farmers. This pattern is not apparent in ADMIXTURE. In addition, DyStruct identifies a genetic contribution from the Caucasus hunter-gatherer to populations across North African, the Middle East, Europe, and Asia, while ADMIXTURE does not. Interestingly, DyStruct identifies shared ancestry between the Neolithic Iran group, Neolithic Levant group, and modern populations in North Africa and the Middle East, possibly reflecting a known back-migration from Eurasia into North Africa.²² The contribution of the Neolithic Levant group is not as obvious in ADMIXTURE because these samples appear admixed between a dark green component shared with European farmers and a light green component. On modern populations with no ancient contributions, both models report similar results.

Figure 8.

Estimates on Modern Samples in the Human Origins Dataset for DyStruct and ADMIXTURE at K = 10

Ancient populations identified by DyStruct appear as circles above the plot. Ancestry estimates for the contribution of European farmers and the steppe appear substantially different between the two models. Moreover, the unambiguous cluster assignment for Neolithic Iran and Neolithic Levant facilitate their interpretation as ancient contributors to modern populations. Populations with no contribution from ancient samples are correctly identified, and estimates obtained by both models on these samples are similar.

Run Time

We investigated the run time of DyStruct using the subset of ancient samples and modern Europeans from Haak et al.⁵ and Lazaridis et al.²² datasets (Table 1). Because Dystruct needs to infer more parameters than ADMIXTURE (allele frequencies per time point), longer run-time is unavoidable. On the smaller dataset from Haak et al.,⁵ DyStruct ran in less than 4.5 h for each K = 2,3,4,5. On the largest dataset, DyStruct took longer to run, but still maintained a reasonable runtime and is thus feasible for practice purposes.

Table 1.

Running Time Comparison between Dystruct and ADMIXTURE

Dataset	K	DyStruct Run Time (hr)	ADMIXTURE Run Time (hr)
Haak Europe	2	2.32	0.16
Haak Europe	3	3.15	0.30
Haak Europe	4	3.53	0.38
Haak Europe	5	4.32	0.66
Lazaridis	4	30.3	1.87
Lazaridis	6	36.52	3.54
Lazaridis	8	35.88	2.38
Lazaridis	10	42.55	2.99

Running time in hours for DyStruct and ADMIXTURE on ancient samples and modern Europeans from Haak et al.⁵ (376 samples; 149,104 loci; 7 time points) and ancient and modern samples from Lazaridis et al.²² (2,329 samples; 293,130 loci; 10 time points). Each program was run on a multicore machine, setting the number threads to K.

Discussion

We have presented DyStruct, a model and inference algorithm for inferring shared genetic ancestry between ancient and modern samples. By explicitly incorporating temporal dynamics, DyStruct places emphasis on explaining later samples as mixtures of earlier populations, leading to results that are suggestive of underlying population histories. Thus, DyStruct’s utility is in suggesting hypotheses of historical relationships among populations. Indeed, we showed on synthetic data that DyStruct outperforms ADMIXTURE when individuals are sampled over time, and we showed on real data that both models suggest different historical relationships. Encouragingly, when later samples do not share ancestry with earlier ones, the results of both models are comparable.

There are several limitations to our approach. We assumed (1) a fixed number of populations, (2) that populations evolved independently, and (3) that the rate of drift (equivalently the effective population size) was constant across all populations. We investigated the effect of each of these assumptions using simulations. Using coalescent simulations, we demonstrated that when the number of populations is not fixed (1) and populations not independent (2), DyStruct is able to detect meaningful historical relationships among samples. Using Wright-Fisher simulations, we demonstrated that estimated parameters by DyStruct do not substantially change even when the effective population size provided to DyStruct is an order of magnitude off (3). Indeed, DyStruct outperformed ADMIXTURE when given the “incorrect” effective population size. This suggests that none of these limitations severely impact model performance.

We demonstrated using simulations that ancestry estimates by our model are robust to choice of effective population size (N_e). Nonetheless, N_e is required as input to DyStruct and needs to be specified. Estimates of the ancestral effective population size of humans at neutral loci using nucleotide diversity are consistent across studies. The standard reference³⁷ puts N_e = 10,000, while more recent estimates based on a 10 kb noncoding region on chromosome 22,³⁸ and 49 approximately independent 1 kb noncoding segments³⁹ put N_e at 10,000 and 10,400, respectively. While these estimates ignore recent population expansion and population substructure, they are reasonable estimates for input to DyStruct, where the results do not substantially depend on N_e. We therefore recommend running DyStruct with N_e = 10,000 on humans and estimating N_e using nucleotide diversity and coalescent theory for other study systems (e.g., see Charlesworth⁴⁰).

A fundamental limitation of all population structure models is the assumption that there exists some fixed number of discrete clusters. This problem is exacerbated when individuals are sampled over time from populations from complex histories. We noted in our coalescent simulations that there is no clear choice for the correct number of clusters. For instance, in the coalescent merger simulations one could argue that either K = 2 or K = 3 is correct, or that K = 2, K = 3, or K = 4 is correct for the coalescent split simulations. This ambiguity is reflected in the difficulty of our model choice procedure, and more generally any model choice procedure, in consistently picking the same K. Indeed, Pritchard et al.⁹ argued that any choice of K may not reflect “real” populations and that value of the best-supported K itself may not be biologically interesting, and they emphasize the utility of population structure models as exploratory tools. Indeed, they emphasize exploring results across K.⁴¹ This is the view we adopt here. We argue that there is no substitute for carefully examining results across K, synthesizing domain knowledge and results from other exploratory tools to generate testable hypotheses for downstream analysis. The measure of any exploratory tool is the ability to generate hypotheses that are likely to be validated by more fine-grained analysis.

We found that DyStruct was suggestive of historical relationships supported by the literature. On the dataset analyzed by Haak et al.,⁵ DyStruct models modern Europeans as mixtures of ancient hunter-gatherers, steppe herders, and early farmers. This was consistent with the conclusions of the authors of that study. Notably, DyStruct detected this relationship in an unsupervised manor, without having to preassign samples to populations. However, we observed DyStruct and ADMIXTURE sometimes “oversplit” ancient samples. This was apparent at K = 4 for DyStruct and K = 5 for ADMIXTURE on dataset of ancient samples and modern Europeans, where European farmers were split into two separate groups. On the dataset analyzed by Lazaridis et al.,²² DyStruct identified two novel clusters when compared to ADMIXTURE: a cluster of early hunter-gatherers in the Levant with later farmers in the area, and a cluster corresponding to Caucasus hunter-gatherers. This was consistent with our PCA and the conclusions by Lazaridis et al.²² Moreover, by assigning different clusters and mixture proportions to ancient samples, DyStruct was better able to identify their contributions to modern populations. For instance, the contribution of earlier European farmers to modern European populations was absent across much of our results from ADMIXTURE.

Our results on real data suggest that DyStruct tends to assign a single ancestral component to ancient samples when it can better explain their contribution to modern ones. As a consequence, admixture within ancient samples is sometimes missed in favor of ancient admixture into modern populations. In practice this means that admixture within ancient samples will be more apparent at lower K where there are fewer ancestral components, with DyStruct successively splitting off ancient clusters with increasing K. Nonetheless, a major benefit of assigning ancient samples to singular clusters is that the clusters have clear interpretations as populations whose relationship can be further investigated using more fine-grained tools. In this way, DyStruct is ideal for the types of exploratory analysis necessary for clustering samples into populations and suggesting hypotheses of population histories. Furthermore, that some genetic relationships will be omitted is not a limitation unique to DyStruct. All population structure models will miss genetic relationships because they reduce complex historical relationships to a small number of ancestral components.

It is interesting that despite DyStruct’s limitations, it appears to accurately describe population relationships on real data. Because of ubiquitous migration in human history, the relationship between populations is complex, with new populations formed from mergers of multiple ancestral populations. It is possible that DyStruct is capturing an approximation to this reality, one that tree-based approaches are inadequate to detect. Future work should explore this possibility, focusing on extending DyStruct’s model to more sophisticated historical relationships. In this way, DyStruct is a first step toward model-based approaches that capture the complexity in human history.

Declaration of Interests

The authors declare no competing interests.

Published: June 27, 2019

Appendix A: Variational Inference for DyStruct

Here we derive a variational inference algorithm to approximate the posterior distribution under DyStruct’s model. For clarity, we first derive a variational inference algorithm using coordinate ascent, then show how the coordinate ascent procedure can be modified for stochastic optimization.

Computing the ELBO

The ELBO—the objective function in variational inference—is given by

$$L={\mathbb{E}}_q\left[\text{log}p\left({\mathit{\beta }}_{1:K,1:L}^{1:T},{\mathit{\theta }}_{1:D},{\mathit{x}}_{1:D,1:L}\right)\right]-{\mathbb{E}}_q\left[\text{log}q\left({\mathit{\beta }}_{1:K,1:L}^{1:T},{\mathit{\theta }}_{1:D}\right)\right]$$

$$=\sum _{t=1}^T\sum _{k=1}^K\sum _{l=1}^L{\mathbb{E}}_q\left[\text{log}p\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1}\right)\right]$$ (Equation A1)

$$+\sum _{d=1}^D{\mathbb{E}}_q\left[\text{log}p\left({\mathit{\theta }}_{\mathit{d}}\right)\right]$$ (Equation A2)

$$+\sum _{d=1}^D\sum _{l=1}^L{\mathbb{E}}_q\left[\text{log}p\left(x_{dl}|t_d,{\mathit{\theta }}_{\mathit{d}},{\mathit{\beta }}_{\mathbf{1}:\mathit{K},\mathit{l}}\right)\right]$$ (Equation A3)

$$-\sum _{k=1}^K\sum _{l=1}^L{\mathbb{E}}_q\left[\text{log}q\left({\mathit{\beta }}_{\mathit{k}\mathit{l}}^{\mathbf{1}:\mathit{T}}|{\hat{\mathit{\beta }}}_{\mathit{k}\mathit{l}}^{\mathbf{1}:\mathit{T}}\right)\right]$$ (Equation A4)

$$-\sum _{d=1}^D{\mathbb{E}}_q\left[\text{log}q\left({\mathit{\theta }}_{\mathit{d}}|{\hat{\mathit{\theta }}}_{\mathit{d}}\right)\right]\text{.}$$ (Equation A5)

It is optimized with respect to the variational parameters $\left\{{\hat{\mathit{\theta }}}_{\mathit{1}:\mathit{D}},{\hat{\mathit{\beta }}}_{\mathit{1}:\mathit{K},\mathit{1}:\mathit{L}}^{\mathit{1}:\mathit{T}}\right\}$. As written, the ELBO does not have a closed form due to the log sum terms that appear in Equation A3:

$${\mathbb{E}}_q\left[\text{log}p\left(x_{dl}|t_d,{\mathit{\theta }}_{\mathit{d}},{\mathit{\beta }}_{\mathbf{1}:\mathit{K},\mathit{l}}\right)\right]={\mathbb{E}}_q\left[\text{logBinomial}\left(2,\sum _k{\beta }_{kl}^{t_d}{\theta }_{dk}\right)\right]$$

$$=x_{dl}{\mathbb{E}}_q\left[\text{log}\left(\sum _k{\theta }_{dk}{\beta }_{kl}^{t_d}\right)\right]+\left(n_d-x_{dl}\right){\mathbb{E}}_q\left[\text{log}\left(1-\sum _k{\theta }_{dk}{\beta }_{kl}^{t_d}\right)\right]$$

where n_d = 1 if individual d is pseudo-haploid and n_d = 2 if individual d is diploid. Following Gopalan et al.,²⁰ we optimize a surrogate lower bound by introducing auxiliary variational parameters ${\mathit{\varphi }}_{\mathit{d}\mathit{l}}=\left({\mathit{\varphi }}_{\mathit{d}\mathit{l}1},\dots ,{\mathit{\varphi }}_{\mathit{d}\mathit{l}K}\right)$ and ${\mathit{\zeta }}_{\mathit{d}\mathit{l}}=\left({\mathit{\zeta }}_{\mathit{d}\mathit{l}1},\dots ,{\mathit{\zeta }}_{\mathit{d}\mathit{l}K}\right)$ whose vector components sums to 1. An application of Jensen’s inequality shows

$$\text{log}\left(\sum _k{\theta }_{dk}{\beta }_{kl}^{t_d}\right)\ge \sum _k{\varphi }_{dlk}\text{log}\left(\frac{{\theta }_{dk}{\beta }_{kl}^{t_d}}{{\varphi }_{dlk}}\right)$$

$$\text{log}\left(1-\sum _k{\theta }_{dk}{\beta }_{kl}^{t_d}\right)\ge \sum _k{\zeta }_{dlk}\text{log}\left(\frac{{\theta }_{dk}\left(1-{\beta }_{kl}^{t_d}\right)}{{\zeta }_{dlk}}\right).$$

Hence, we still maintain a lower bound on the log likelihood. The auxiliary parameters are optimized to provide a tight lower bound. Fixing all other parameters, the constrained optimization problem can be solved using an application of Lagrange multipliers:

$${\varphi }_{dlk}\propto \text{exp}\left\{{\mathbb{E}}_q\left[\text{log}{\theta }_{dk}\right]+{\mathbb{E}}_q\left[\text{log}{\beta }_{kl}^{t_d}\right]\right\}$$ (Equation A6)

$${\zeta }_{dlk}\propto \text{exp}\left\{{\mathbb{E}}_q\left[\text{log}{\theta }_{dk}\right]+{\mathbb{E}}_q\left[\text{log}\left(1-{\beta }_{kl}^{t_d}\right)\right]\right\}.$$ (Equation A7)

The first term in both equations is an expectation of a sufficient statistic and therefore has a closed form, ${\mathbb{E}}_q\left[\text{log}{\theta }_{dk}\right]=\text{Ψ}\left({\hat{\theta }}_{dk}\right)-\text{Ψ}\left(\sum _k{\hat{\theta }}_{dk}\right)$_, where $\text{Ψ}$ is the Digamma function. The two expectations in the second terms can be approximated by taking second-order Taylor expansion. Let ${\tilde{m}}_{kl}^t$ be the mean of ${\beta }_{kl}^t$ and let ${\tilde{v}}_{kl}^t$ be the variance. Taylor expanding around ${\tilde{m}}_{kl}^t$ and $1-{\tilde{m}}_{kl}^t$_, respectively, gives us

$${\mathbb{E}}_q\left[\text{log}{\beta }_{kl}^t\right]\approx \text{log}{\tilde{m}}_{kl}^t-\frac{{\tilde{v}}_{kl}^t}{2{\left({\tilde{m}}_{kl}^t\right)}^2}$$

$${\mathbb{E}}_q\left[\text{log}\left(1-{\beta }_{kl}^t\right)\right]\approx \text{log}\left(1-{\tilde{m}}_{kl}^t\right).$$

Optimizing ${\hat{\theta }}_d$

Note that the $q\left({\mathit{\theta }}_{\mathit{d}}|{\hat{\mathit{\theta }}}_{\mathit{d}}\right)$ satisfy the mean field assumption: the ${\mathit{\theta }}_{\mathit{d}}$ in the variational posterior are independent. Therefore they have optimal coordinate ascent updates of the form⁴²

$$q^{\text{∗}}\left({\mathit{\theta }}_{\mathit{d}}\right)\propto \text{exp}\left\{{\mathbb{E}}_q\left[\text{log}p\left({\mathit{\theta }}_{\mathit{d}}|{\beta }_{kl}^{t_d},{\mathit{x}}_{\mathit{d},\mathbf{1}:\mathit{L}}\right)\right]\right\}$$

where we have used several conditional independencies to simplify the complete conditional of ${\mathit{\theta }}_{\mathit{d}}$. Using the surrogate lower bound on the ELBO, we can compute $q^{\text{∗}}\left({\mathit{\theta }}_{\mathit{d}}\right)$ in closed form,

$${\hat{\theta }}_{dk}={\alpha }_k+\sum _{l=1}^L{x}_{dl}{\varphi }_{dlk}+\left(n_d-x_{dl}\right){\zeta }_{dlk},$$ (Equation A8)

matching the expression in Gopalan et al.²⁰

Optimizing ${\hat{\beta }}_{kl}^t$

We optimize the variational parameters of the state space model, ${\hat{\beta }}_{kl}^t$_, using variational Kalman filtering.²¹ Recall that we approximate the posterior distribution on allele frequencies by introducing pseudo-observations ${\hat{\theta }}_{kl}^t$. The variational state space model is

$$q\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1};\nu \right)=\text{Normal}\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1},\frac{g_t-g_{t-1}}{12N_k}\right)$$

$$q\left({\hat{\beta }}_{kl}^t|{\beta }_{kl}^t\right)=\text{Normal}\left({\hat{\beta }}_{kl}^t|{\beta }_{kl},{\nu }^2\right).$$

In variational Kalman filtering, the variational distribution for each ${\beta }_{kl}^t$ is its marginal posterior given the ${\hat{\beta }}_{kl}^{1:T}$. That is

$$q\left({\beta }_{kl}^t|{\hat{\beta }}_{kl}^1,{\hat{\beta }}_{kl}^2,\dots ,{\hat{\beta }}_{kl}^T\right)=\text{Normal}\left({\beta }_{kl}^t|{\tilde{m}}_{kl}^t,{\tilde{v}}_{kl}^t\right).$$

Specifically, because we have a Gaussian state space with Gaussian observations in the variational posterior, we know the marginal posterior of ${\beta }_{kl}^t$. Furthermore, the mean ${\tilde{m}}_{kl}^t$ and variance ${\tilde{m}}_{kl}^t$ can be computed using a forward recurrence (Kalman filtering) then backward recurrence (Kalman smoothing). Following the notation in Blei and Lafferty,²¹ the forward (filtered) means and variances are given by

$$m_{kl}^t=\frac{{\nu }^2}{v_{kl}^{t-1}+{\left({\sigma }_k^t\right)}^2+{\nu }^2}{m}_{kl}^{t-1}+\left(1-\frac{{\nu }^2}{v_{kl}^{t-1}+{\left({\sigma }_k^t\right)}^2+{\nu }^2}\right){\hat{\beta }}_{kl}^t$$

$$v_{kl}^t=\left(\frac{{\nu }^2}{v_{kl}^{t-1}+{\left({\sigma }_k^t\right)}^2+{\nu }^2}\right)\left(v_{kl}^{t-1}+{\left({\sigma }_k^t\right)}^2\right)$$

where ${\left({\sigma }_k^t\right)}^2:=\frac{g_t-g_{t-1}}{12N_k}$. The initial conditions are $m_{kl}^0={\beta }_{kl}^0$. The marginal (smoothed) means and variances are

$${\tilde{m}}_{kl}^t=\left(\frac{{\left({\sigma }_k^t\right)}^2}{v_{kl}^t+{\left({\sigma }_k^t\right)}^2}\right)m_{kl}^t+\left(1-\frac{{\left({\sigma }_k^t\right)}^2}{v_{kl}^t+{\left({\sigma }_k^t\right)}^2}\right){\tilde{m}}_{kl}^{t+1}$$

$${\tilde{v}}_{kl}^t=v_{kl}^t+{\left(\frac{v_{kl}^t}{v_{kl}^t+{\left({\sigma }_k^t\right)}^2}\right)}^2\left({\tilde{v}}_{kl}^{t+1}-v_{kl}^t-{\left({\sigma }_k^{t+1}\right)}^2\right)$$

with initial conditions ${\tilde{m}}_{kl}^T=m_{kl}^T$ and ${\tilde{v}}_{kl}^T=v_{kl}^T$.

The variational parameters ${\hat{\beta }}_{kl}^T$ are optimized with respect to the ELBO, hence we need the partial derivatives of the marginal means ${\tilde{m}}_{kl}^t$ with respect to ${\hat{\beta }}_{kl}^t$. These can be obtained using the forward-backward recurrence as in Blei and Lafferty.²¹ We will show the recurrence for initial frequencies ${\beta }_{kl}^t$, which are not maximized in Blei and Lafferty,²¹ and note that the other partial derivatives can be obtained similarly. The recurrence is

$$\frac{\partial m_{kl}^t}{\partial {\beta }_{kl}^0}=\left(\frac{{\nu }^2}{v_{kl}^{t-1}+{\left({\sigma }_k^t\right)}^2+{\nu }^2}\right)\frac{\partial m_{kl}^{t-1}}{{\beta }_{kl}^0}$$

$$\frac{\partial {\tilde{m}}_{kl}^t}{{\beta }_{kl}^0}=\left(\frac{{\left({\sigma }_k^t\right)}^2}{v_{kl}^t+{\left({\sigma }_k^t\right)}^2}\right)\frac{\partial m_{kl}^t}{\partial {\beta }_{kl}^0}+\left(1-\frac{{\left({\sigma }_k^t\right)}^2}{v_{kl}^t+{\left({\sigma }_k^t\right)}^2}\right)\frac{\partial {\tilde{m}}_{kl}^{t+1}}{{\beta }_{kl}^0}.$$

We optimize the ${\hat{\beta }}_{kl}$ with respect to a single locus in a single population at time using a conjugate gradient algorithm, constraining the parameters to lie in the interval (0,1). The terms in the ELBO with respect to locus l in population k are

$$L_{\text{∗}}=\sum _{t=1}^T{\mathbb{E}}_q\left[\text{log}p\left({\beta }_{kl}^t|{\beta }_{kl}^{t-1}]\right)\right]-{\mathbb{E}}_q\left[\text{log}q\left({\beta }_{kl}^t|{\tilde{m}}_{kl}^t,{\tilde{v}}_{kl}^t\right)\right]+\sum _{t=1}^T\sum _{d:t_d=t}{\mathbb{E}}_q\left[\text{log}p\left(x_{dl}|t_d,{\beta }_{kl}^{t_d},{\mathit{\theta }}_{\mathit{d}}\right)\right]$$

$$\ge -\frac{T}{2}\text{log}2\pi -\frac{1}{2}\sum _{t=1}^T\text{log}{\left({\sigma }_k^t\right)}^2-\frac{1}{2}\sum _{t=1}^T\frac{1}{{\left({\sigma }_k^t\right)}^2}{\mathbb{E}}_q\left[{\left({\beta }_{kl}^t-{\beta }_{kl}^{t-1}\right)}^2\right]+\frac{T}{2}\text{log}2\pi +\frac{T}{2}+\frac{1}{2}\sum _{t=1}^T\text{log}{\tilde{v}}_{kl}^t$$

$$+\sum _{t=1}^T\sum _{d:t_d=t}{x}_{dl}{\varphi }_{dlk}\left(\text{log}{\tilde{m}}_{kl}^{t_d}-\frac{{\tilde{v}}_{kl}^{t_d}}{2{\left({\tilde{m}}_{kl}^{t_d}\right)}^2}\right)+\left(n_d-x_{dl}\right){\zeta }_{dlk}\text{log}\left(1-{\tilde{m}}_{kl}^{t_d}\right)=\frac{T}{2}-\frac{1}{2}\sum _{t=1}^T\left(\text{log}{\left({\sigma }_k^t\right)}^2-\text{log}{\tilde{v}}_{kl}^t\right)-\frac{1}{2}\sum _{t=1}^T\frac{1}{{\left({\sigma }_k^t\right)}^2}{\left({\tilde{m}}_{kl}^t-{\tilde{m}}_{kl}^{t-1}\right)}^2-\frac{{\tilde{v}}_{kl}^t}{{\left({\sigma }_k^t\right)}^2}-\frac{{\tilde{v}}_{kl}^{t-1}}{{\left({\sigma }_k^t\right)}^2}+\sum _{t=1}^T\sum _{d:t_d=t}{x}_{dl}{\varphi }_{dlk}\left(\text{log}{\tilde{m}}_{kl}^{t_d}-\frac{{\tilde{v}}_{kl}^{t_d}}{2{\left({\tilde{m}}_{kl}^{t_d}\right)}^2}\right)+\left(n_d-x_{dl}\right){\zeta }_{dlk}\text{log}\left(1-{\tilde{m}}_{kl}^{t_d}\right),$$

where we define ${\tilde{v}}_{kl}^0=0$, ${\left({\sigma }_k^0\right)}^2=1$, and $m_{kl}^0={\tilde{m}}_{kl}^0={\beta }_{kl}^0$ for notational convenience. The inequality follows from using the auxiliary lower bound. Taking partial derivatives with respect to the pseudo-outputs gives us

$$\frac{\partial L_{\text{∗}}}{\partial {\hat{\beta }}_{kl}^s}=-\sum _{t=1}^T\frac{1}{{\left({\sigma }_k^t\right)}^2}\left({\tilde{m}}_{kl}^t-{\tilde{m}}_{kl}^{t-1}\right)\left(\frac{\partial {\tilde{m}}_{kl}^t}{\partial {\hat{\beta }}_{kl}^s}-\frac{\partial {\tilde{m}}_{kl}^{t-1}}{\partial {\hat{\beta }}_{kl}^s}\right)+\frac{\partial {\tilde{m}}_{kl}^t}{\partial {\hat{\beta }}_{kl}^s}\sum _{d:t_d=t}{x}_{dl}{\varphi }_{dlk}\left(\frac{1}{{\tilde{m}}_{kl}^{t_d}}+\frac{{\tilde{v}}_k^{t_d}}{{\left({\tilde{m}}_{kl}^{t_d}\right)}^3}\right)+\left(n_d-x_{dl}\right){\zeta }_{dlk}\frac{1}{\left({\tilde{m}}_{kl}^{t_d}-1\right)}$$

The full algorithm iterates between optimizing the local parameters, ${\varphi }_{dlk}$, and ${\zeta }_{dlk}$ using Equations A6 and A7, and updating the ${\hat{\mathit{\beta }}}_{\mathit{k}\mathit{l}}^{\mathit{1}:\mathit{T}}$ numerically, then updating global parameters ${\hat{\mathit{\theta }}}_{\mathit{d}}$ according to Equation A8. The procedure is repeated until convergence.

Inference Algorithm

We can perform stochastic variational inference through a slight modification to the coordinate ascent algorithm presented above.²³, ⁴² Stochastic variational inference computes noisy estimates of the optimal global parameters by stochastically subsampling data points and using the optimal local parameters to update the global parameters. The optimal global parameters are a weighted average of the previous global parameters, with the newly computed global parameters. Following Gopalan et al.,²⁰ the n + 1 stochastic variational inference update for the global parameters ${\hat{\mathit{\theta }}}_{\mathit{d}}$ is

$${\hat{\theta }}_{dk}^{n+1}={\alpha }_k+\left(1-{\mathit{\epsilon }}_n\right){\hat{\theta }}_{dk}^n+{\mathit{\epsilon }}_{n}L\left(x_{dl}{\varphi }_{dlk}+\left(n_d-x_{dl}\right){\zeta }_{dlk}\right)$$ (Equation A9)

where ${\mathit{\epsilon }}_n$ is the step size for iteration n and L is the number of loci. Provided the step size meets certain criteria, the algorithm is guaranteed to converge. See Hoffman et al.²³ or Blei et al.⁴² for more details.

Algorithm 1. DyStruct’s inference algorithm

• 1:Input: Genotypes ${\mathit{x}}_{\mathit{1}:\mathit{D},\mathit{1}:\mathit{L}}$; Sample Times t_d; Population Size N_k = N for all populations.
• 2:while ${\hat{\mathit{\theta }}}_{\mathit{d}}$ have not converged
• 3:Pick $l\sim \text{Uniform}\left(1,L\right)$
• 4:while ${\mathit{\varphi }}_{\mathit{d}\mathit{l}}$ and ${\mathit{\zeta }}_{\mathit{d}\mathit{l}}$ have not converged
• 5:Update auxiliary parameters ${\mathit{\varphi }}_{\mathit{d}\mathit{l}}$ and ${\mathit{\zeta }}_{\mathit{d}\mathit{l}}$ for d = 1,2,…,D according to Equations A6 and A7.
• 6:Update allele frequency parameters ${\hat{\mathit{\beta }}}_{\mathit{k}\mathit{l}}^{\mathit{1}:\mathit{T}}$ for k = 1,2,…,K using the numerical optimization routine described in the section Optimizing ${\hat{\beta }}_{kl}^t$.
• 7:end while
• 8:Update global parameters ${\hat{\mathit{\theta }}}_{\mathit{d}}$ for d = 1,2,…,D according to Equation A9
• 9:end while

Extensions to Missing Data

The above algorithm holds only for complete data. A small modification is required for missing data, where not every sample has an observed genotype at every locus. Rather than a single global step size ${\mathit{\epsilon }}_t$, we maintain a step size for every individual ${\mathit{\epsilon }}_{m_d}$ where m_d is the number of iterations for individual d. When a locus is subsampled, we update global ancestry estimates only for individuals with observed genotypes at that locus, and the step size for those individuals. We further replace the parameter L with L_d, the number of loci for each observed in each individual.

Pseudo-haploid Detection

In pseudo-haploid samples only one allele of a genotype is observed. For use in traditional analysis pipelines that require genotype data, genotypes for pseudo-haploid samples are coded by 0 if the reference allele is observed or 2 if the nonreference allele is observed. DyStruct detects pseudo-haploid samples by scanning observed genotype data for heterozygous genotypes. Presence of a heterozygous genotype indicates that a sample is not pseudo-haploid, while absence of heterozygous genotypes across observed loci indicates a sample is pseudo-haploid with high probability (for a modest number of loci). For example, given a diploid sample, the probability that no heterozygous genotypes are observed out of L loci is ${\prod }_{l=1}^{L}1-2{\beta }_l\left(1-{\beta }_l\right)$ (${\beta }_l$ is the allele frequency at locus l). Even if all nonreference alleles are rare, say ${\beta }_l=0.01$ (which implies most genotypes are homozygous) at L = 1,000 the probability that no heterozygous genotype is observed is ${\left[1-2\left(0.01\right)\left(0.99\right)\right]}^{1000}=2.06\times {10}^{-9}$. Thus, on realistic sized datasets (i.e., L > 10,000), diploid samples are extremely unlikely to be mislabeled.

Convergence to Local Optima

We observed on real data that DyStruct was sometimes susceptible to local optima. Through experimentation we found that trying multiple initializations (5), running DyStruct over the data once for each initialization, and picking the run with the largest objective function alleviated this problem. While the first epoch through the data is the most expensive because it requires convergence of parameters from scratch, this strategy still incurred less additional computational cost compared to re-running DyStruct 5 times. DyStruct thus uses multiple initializations by default, which can optionally be disabled.

Web Resources

• Code to replicate experiments, https://github.com/tyjo/dystruct-experiments

• DyStruct, https://github.com/tyjo/dystruct

• Real dataset analyzed by Haak et al.,⁵ https://reich.hms.harvard.edu/sites/reich.hms.harvard.edu/files/inline-files/Haak2015PublicData.tar.gz

• Real dataset analyzed by Lazaridis et al.,²² https://reich.hms.harvard.edu/sites/reich.hms.harvard.edu/files/inline-files/NearEastPublic.tar.gz