EQUATION-BASED MODELS OF DYNAMIC BIOLOGICAL SYSTEMS

Abstract

The purpose of this review is to introduce differential equations as a simulation tool in the biological and clinical sciences. This modeling technique is very mature and has been a preferred tool of physiologists and bioengineers, and of quantitative scientists in general, to describe and predict the behavior of complex interacting systems. However, this methodology has not been widely used within clinical medicine, due to a lack of familiarity with highly quantitative methods, and a greater acquaintance with statistical modeling approaches based on inference and empirical data analysis. We will describe various aspects of equation-based modeling, including underlying assumptions, strengths and weaknesses, and provide specific examples of simple models. We conclude that the usefulness of quantitative modeling, including equation-based models, is ultimately linked to the quality and abundance of observation obtained on the system being modeled. Equation-based modeling, though potentially an integrative approach, is complementary to and extends the potential of traditional statistically-based approaches to inference.

Introduction

The science of predicting the time evolution of complex systems and the derivation of rules that will dictate, given the state of a system now, the state of the system at some future time are integral parts of many fields of scientific enquiry, such as physics, atmospheric science, mathematics and engineering. Such rules can be represented through several mathematical formalisms. Although clinical scientists have developed a degree of familiarity with statistical approaches, alternative modeling approaches may present distinct advantages depending on the hypotheses under investigation and the nature of the predictions to be examined.

The purpose of this communication is to provide a non-technical review of a well-established modeling platform, namely differential equations, that harnesses the powerful tools of calculus to analyze the time-dependent behavior of dynamical systems. A salient advantage of using differential equations as a mathematical platform for models comprised of a large number of interacting components where there exist some a priori knowledge as to the nature of those interactions is that simulation and analysis can predict what may follow as time evolves or as the characteristics of particular system components are varied. This mathematical tool is particularly helpful in the case where these predictions are not already obvious to clinical or biological researchers, or where particular outcomes are expected, but the mechanisms underlying outcomes cannot be directly intuited.

Differential equations have been used abundantly by modelers from quantitative fields. Yet, the modeling framework that they provide is largely unknown to basic and clinical scientists. We will briefly describe this framework, provide examples relevant to critical care, and discuss its strengths and weaknesses.

Dynamical systems

A dynamical system is composed of components interacting through a set of explicit rules. The interactions encapsulated in these rules dictate how the states of the components evolve in time, and so the notion of time evolution is key when thinking about such a system. As an example, if one were to consider a set of chemical species mixed in a confined space, the components are the chemical species, the rules are the possible chemical reactions and the rates at which they occur, and the states of the components relate to their concentrations over time. Differential equations provide a language for the expression of such evolution rules. Many primary or calculated useful physiologic quantities, such as cardiac output and vascular resistance, are related in a static fashion. In other words, one can relate these quantities by means of algebraic equations of varying complexity. The equations resulting from drawing an analogy between electrical circuits and the circulation have led to additional appealing concepts in critical care, such as peripheral vascular resistance, vascular capacitance, and airway resistance. However, the clinician is clearly aware that these quantities change over time as the “system” adapts to changing external and internal conditions such as fluid shifts, local concentration of effectors, or drug dose. This paper will concentrate on differential equations as a tool for describing, and making predictions about, such temporal changes, as has long been recognized by scientists of the physical and biological sciences.

Difference and differential equations

Difference equations and iterative maps occur naturally in mathematical biology. An important problem is how the population size of a given species, for example dividing cells or bacteria, varies from one time point to another time point. Let x_n be the population of a species at time n and x_n+1 the population at time n +1. The change in population size during the interval between these times is given by the following growth equation, also known as the logistic map:

$$x_{n+1}=r{x}_n\left(1-x_n\right),$$

where x₀ represents the initial population at time 0, r is a positive number corresponding to an overall growth rate, and the last negative term represents increased competition as the population grows (over limited shared resources for example).

Models composed of such equations, which treat time as evolving in discrete steps, are similar to the cellular automata or agent-based models, in which the rules of the biology are included in the mapping.¹ There is no obstacle to including several interacting variables, or even values from multiple different time steps, within a difference equation. While the principle is simple, the resulting simulations are often not intuitive, giving rise to interesting emergent behaviors. The natural extension of difference equations is to consider the case where the time steps become infinitely small. In this limit, the left hand side of the prediction equation consists of not the value of a variable at the next time step, but rather the velocity at which the variable evolves. Continuous logistic growth, for example, is described by the extension of the discrete logistic map, given by the following ordinary differential equation:

$$\frac{dx(t)}{dt}=rx(t)(1-x(t)),$$

where x(t) denotes population size at time t, the derivative dx(t) / dt the rate of change of x(t) and t itself can be any positive number. The use of discrete time in modeling reproduction is correct for ecology models wherein new organisms are born in synchrony. A discrete model becomes less appropriate when no natural time step exists at the population level, such as bacterial division, where division time varies across the population.

As an example, let us consider the modeling of a host-parasitoid as a system of two difference-equations. The system

$$\begin{gathered} H_{n+1}=\lambda H_{n}f\left(H_n,P_n\right), \\ {P}_{n+1}=c{H}_n\left(1-f\left(H_n,P_n\right)\right), \end{gathered}$$

is derived by letting H_n represent the density of host species in generation n, P_n the density of parasitoids in generation n, f = f (H_n, P_n ) the fraction of hosts not parasitized (1-f is therefore the fraction of hosts parasitized), λ the host reproductive rate, and c the average number of viable eggs laid by a parasitoid on a single host. These equations outline a general framework for host-parasitoid models. Assuming that parasitoids search for hosts independently and randomly and that their searching efficiency is constant, one derives, using the Poisson probability distribution, a specific expression for $f\left(H_n,P_n\right)=p(0)=e^{-a{P}_n}$.

The host reproductive rate λ is assumed to depend on H_n to avoid diverging oscillations. With the choice λ(H_n ) = exp(r(1 – H_n / K)), which is obtained by assuming that in the absence of parasitoids, the host population grows to some limited density, the system has one steady-state $(\overline{H},\overline{P})$. The stability depends on the parameter r and the quantity $\overline{H}/K$. For fixed values of $\overline{H}/K=0.4$ and small values of r, the steady-state is stable. Any initial value spirals in towards the steady-state and will eventually reach it. Beyond a critical r value, the steady-state becomes unstable and stable oscillatory behavior becomes possible. Therefore, dependent on the host reproductive rate r, the model predicts different dynamical behavior in the host-parasitoid system. This agrees with the behavior of many host-parasitoid systems observed in nature². The extend to which such analyses can be applied to the dynamics of human infections is unclear, but recurrent infections are well described clinically.

Ordinary differential equations

Many of the best known computational models for biological processes that evolve continuously in time are expressed as sets of coupled ordinary differential equations (ODEs). ODEs are of the form: $\frac{d{x}_i}{dt}=F\left(x_1,\dots ,x_n,{\lambda }_1,\dots ,{\lambda }_p,t\right)$, i =1,...,n, and describe how individual system variables x_i evolve over time. F is a function of some subset of the variables in the model. Systems where F is free of an explicit dependence on the independent variable, typically time, are called autonomous. The function F and the parameter vector λ= (λ₁,...,λ_p ) encode some simplified version of the biology of the system being modeled. For example, this typically includes information with regard to the presence of specific interactions among components of the system and the relative strength of those interactions, quantified by model parameters. These models are based on the premise that the system involved is “well-mixed” and that there are sufficiently many components (e.g. proteins, cells, small molecules) so that their numbers can be regarded as continuous quantities. Although many of these assumptions are not strictly true within very small spatial domains, such as individual cell, ODE models have provided a great deal of insight into the behavior of complex, interacting systems. Numerical methods and software tools for solving ODEs are mature, very reliable, often freely available, and easily implemented on personal computers. Furthermore, ODE models are amenable to formal mathematical analysis. While it may not be possible to write down formulas that express the solutions to differential equations as explicit functions of time, this computational framework allows one to determine a good approximation of the possible qualitative behaviors that the system can manifest, depending on particular choices of initial conditions and model parameter values.

Qualitative behaviors of autonomous ODE systems may include convergence to equilibrium points or steady states, which are states at which all variables remain constant, periodic oscillations, as well as many more complicated time courses. A more technical description of the qualitative behaviors of autonomous ODE systems can be found in Appendix A. For a fixed parameter set, a system of ODEs may have more than one possible equilibrium, each of which may be stable (in a variety of mathematically defined ways) or unstable. To every stable equilibrium corresponds a basin of attraction, which refers to the set of initial conditions that will ultimately evolve to this equilibrium. These basins can change with changes in parameters; indeed, equilibria and other interesting solutions can be born or cease to exist as parameters vary.

For example, the logistic ODE described above has two equilibria which are stable or unstable dependent on the parameter r. For r<0 the equilibrium x=0 is stable and the equilibrium x=1 is unstable. But if r is increased and the system is considered for r>0 the equilibrium x=0 becomes unstable and the equilibrium x=1 becomes stable. That means every solution of the logistic ODE converges to 0 for r<0 and to 1 for r>0 independent from the initial conditions and the system changes its stability behavior at r=0. This characteristic change in a system’s behavior is called a bifurcation. Correspondingly, one can a priori segment the parameter space into regions with qualitatively different equilibrium structures.

As another example, the viral kinetics of influenza A during infection within an individual can be modeled using a simple 3-dimensional ODE System^3,4, which incorporates viral growth, target cell limitation and the interferon response:

$$\begin{gathered} \frac{dT(t)}{dt}=-\beta T(t)V(t), \\ \frac{dI(t)}{dt}=\beta T(t)V(t)-\delta I(t), \\ \frac{dV(t)}{dt}=pI(t)-cV(t), \end{gathered}$$

where T(t) is the number of uninfected target cells, I(t) is the number of infected cells, and V(t) is the infectious viral titer (or total number of free viral particles or concentration of viral particles per unit volume of tissue) at time t. It is assumed in this model that infection is initiated by introduction of virus into the upper respiratory tract at a concentration equivalent to V₀ viral particles per unit volume of tissue. Susceptible cells become infected by virus at rate βT(t)V(t), where β is the rate constant quantifying the probability that the interaction between a healthy cell and a viral particle results in infection of the cell. Infected cells, I(t), increase viral titers at an average rate of p per cell and die at a rate of δ per unit time, where $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\delta $}\right.$ is the average life span of an infected cell. Free virus is cleared at a rate of c per unit time. The effects of immune responses are not explicitly described in this simple model, but they are implicitly included in the death rate of infected cells (δ) and the clearance rate of virus (c). Such simple systems may still admit complex solutions and several equilibria, depending on the choice of parameters. Evolved versions of such models provide specific predictions regarding infection dynamics, treatment strategies and therefore, when sufficiently validated, could be of potential use in disease diagnosis and optimizing therapy in individual patients.^5,6.

We often focus on using autonomous differential equations for modeling biological or physiological systems, because we want to understand the general behavior of the given system under some form of equilibrium or steady conditions. After this initial analysis, we are interested in how the system behaves when it is subjected to a time-dependent event or intervention, representing, for example, discretionary manipulations such as sequential insults, therapeutic interventions, or time-dependent changes in the properties of the system. For instance, in the context of the acute inflammatory response, Day et al. used a 4-dimensional non-autonomous system of differential equations to describe a time-dependent disturbance consisting of repeated endotoxin administration, as had been given previously in a variety of experiments.⁷ Similarly, we have simulated the impact of the timing and duration of an antitumor necrosis factor antibody in sepsis⁸, and of various vaccine and antibiotic combinations in anthrax infection.⁹

How to model systems with spatial structure

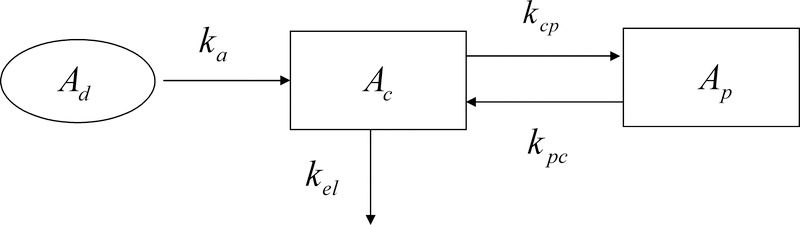
When spatial structure plays an important role in the behavior of a system, ODEs may still provide a useful modeling tool if the system can be considered as a collection of interacting “well-mixed” compartments. A key aspect of the modeling process is the characterization of the transfer of information from one compartment to the next, such as occurs via molecular diffusion across membranes or cellular trafficking between tissues. As long as the factors driving inter-compartmental exchange can be reasonably modeled mathematically, ODEs remain a viable and relatively simple option for characterizing spatially structured systems. As an example, pharmacokinetic models are routinely used to guide drug dosing and predict elimination in various clinical situations.^10,11 A representative pharmacokinetic model is depicted in figure 1 where drug is administered in a depot compartment and diffuses following concentration gradients to a central and a peripheral compartment. A_d(t) represents the amount of drug in the depot compartment, A_c(t) the amount of drug in the central compartment and A_p(t) the amount of drug in the peripheral compartment. The rate constant k_cp describes the diffusion of the drug from the central compartment into the peripheral compartment and k_pc the diffusion from the peripheral into the central compartment, while k_el is the elimination constant and k_a is the infusion rate of the drug. The differential equations that describe the transport of drug across compartments and drug elimination, assuming first order kinetics in each of the compartments, are:

$$\begin{gathered} \frac{d{A}_d(t)}{dt}=-k_a{A}_d(t), \\ \frac{d{A}_c(t)}{dt}=k_a{A}_d(t)+k_{pc}{A}_p(t)-k_{cp}{A}_c(t)-k_{el}{A}_c(t), \\ \frac{d{A}_p(t)}{dt}=k_{cp}{A}_c(t)-k_{pc}{A}_p(t). \end{gathered}$$

Fig. 1.

A pharmacokinetic model. Drug is administered in a depot compartment and diffuses following concentration gradients to a central and peripheral compartment.

Such systems of equations are providing researchers and clinicians with valuable insight in drug dosing, monitoring and design.^12,13

In some settings, the particular geometry of a system is crucial in dictating behavior. For example, the geometry of a nerve axon needs not to be considered for an approximate analysis of action potential propagation, but this geometry is key in determining the precise influence of gradual changes in axon width on propagation characteristics. Similarly, the geometric properties of the arterial tree dictates how stress, pressure waves and flow propagates within the arterial system^14,15, and detailed modeling of the pulmonary structure has prove useful in understanding air flow, pulmonary pressures and drug deposition within the bronchial tree.^16,17 Other examples of relevance to acute care include clot growth¹⁸ and alveolar gas exchange (Figure 2).¹⁹ ODEs provide an insufficient description when continuous aspects of geometry are important or the “well-mixed” assumption is obviously at odds with the nature of the system at hand. The mathematical formalism appropriate to model these systems is that of partial differential equations (PDEs).

Fig. 2.

Alveolar gas exchange. The mathematical formalism appropriate to model this system is that of partial diferential equtions (PDEs).

PDEs and ODEs are often complementary modeling tools and may co-exist in analysis of the same system, especially when one is attempting to include several scales of description. PDEs are much more computationally demanding than ODEs, with simulations of PDEs often requiring a larger computing platform than personal computers. As with ODEs, formal mathematical theory has been developed for many types of PDEs. Unfortunately, this theory is more complicated, and often farther removed from insights about the dynamic structure of the underlying system than is the theory for ODEs. Many of the PDEs relevant to detailed biological modeling are too complex for analytical treatment and therefore the output that can be feasibly obtained from such models is limited to numerical simulations. However, mathematical theory may be useful in selecting appropriate numerical simulation methods and may facilitate accuracy and efficiency of simulations, even when this theory cannot give any direct information about possible model behavior.

A fundamental example of a PDE is the classical diffusion equation, which describes the density fluctuations in a diffusing quantity. It is also used in population genetics to describe the “diffusion” of alleles in a population. It is given in the form

$$\frac{\partial \varphi }{\partial t}=\nabla \cdot D(\varphi )\nabla \varphi (\overrightarrow{r},t),$$

where $\varphi (\overrightarrow{r},t)$ is the density of the diffusing material (such as a molecular species) as a function of space and time, $\overrightarrow{r}$ is the spatial coordinate, t is time, ∂ϕ/ ∂t is the rate of change (partial time derivative) of the density at $\overrightarrow{r}$, D is the collective diffusion coefficient, and the symbol ∇ represents a vector differential operator with respect to space, a generalization of the common derivative. If the diffusion coefficient depends on the density then the equation is nonlinear. If D is a constant, then the equation reduces to the following linear equation:

$$\frac{\partial \varphi }{\partial t}=D{\nabla }^2\varphi (\overrightarrow{r},t).$$

Another example of a system of PDE’s with important biological relevance is given by the classical model of chemotaxis. A widely studied chemotactic phenomenon is that exhibited by the slime mold Dictyostelium discoideum, in which single-cell amoebae move towards regions of high concentrations of cyclic-AMP that is produced by the amoebae themselves. Interesting wave-like movement and spatial patterning are observed experimentally in this context.

A general reaction diffusion-chemotaxis equation is given by

$$\frac{\partial n}{\partial t}=f(n)-\nabla \cdot n\chi (a)\nabla a+\nabla \cdot D\nabla n,$$

where a(x, t) is the attractant concentration, n(x,t) the number of cells, D the diffusion coefficient of the cells, f(n) represents the growth term for the cells and χ(a) is a function of the attractant concentration. Since the attractant a(x, t) is a chemical, it also diffuses, and its behavior is typically modeled by

$$\frac{\partial a}{\partial t}=g(a,n)+\nabla \cdot D_a\nabla a,$$

where D_a is the diffusion coefficient of a and g(a,n) is the kinetics/source term, which may depend on n and a. In the slime mold model of Keller and Segel²⁰, g(a, n) = h×n – k ×a, where h and k are positive constants. Here h×n represents the spontaneous production of the attractant and is proportional to the number of amoebae n, while −k × a represents decay of attractant activity: there is an exponential decay if the attractant is not produced by the cells. When f (n) = 0 and the chemotactic term χ(a) is a positive constant χ₀, one obtains the following nonlinear system

$$\begin{gathered} \frac{\partial n}{\partial t}=D\frac{{\partial }^{2}n}{\partial x^2}-{\chi }_0\frac{\partial }{\partial x}\left(n\frac{\partial a}{\partial x}\right), \\ \frac{\partial a}{\partial t}=hn-ka+D_a\frac{{\partial }^{2}a}{\partial x^2}. \end{gathered}$$

Analysis of this model suggests that the initiation of slime mold aggregation can be viewed as an instability in the spatially uniform and temporally constant state. Extensions of this work showed that, through a sequence of stability changes, such reaction-diffusion models can exhibit an impressive sequence of morphogenetic behavior such as pulse relaying, spiral waves, target patterns, cell streaming and sorting, slug locomotion, and tissue buckling.²¹ Such phenomena are common in biology. In particular spiral waves are of considerable practical importance in a variety of medical situations, particularly in cardiology and neurobiology.

How to model uncertainty

ODEs and PDEs are deterministic models. A given set of initial and/or boundary conditions will always lead the same outcome in these models. However, there exists some degree of noise, or stochasticity, due to unaccounted effects such as temperature fluctuation, variability in molecular interactions, and a wide variety of other factors, in all physical systems. Mathematically, external noise refers to fluctuations created in an otherwise deterministic system by the application of a random force, whose stochastic properties are supposed to be known. Some dynamical systems, by the nature of the interactions that are described, are very robust to noise, while others are much more sensitive. In addition to these structural considerations, the number of cells or molecules in a system also contributes to the importance of stochastic effects in sculpting its behavior. The smaller the scale of description, the greater the potential impact of noise. In situations where the inclusion of noise in a model is appropriate, and where the nature of this noise is reasonably well understood, stochastic differential equations (SDE) provide a mathematical framework for doing so. Due to the importance of stochasticity in the outcomes of many cellular processes, there has been a great deal of interest in applying stochastic simulation methods in simulating processes involving small number of molecules.^22,23,24,25 Most of these methods rely on the Gillespie algorithm^26,27, which yields an exact simulation of a stochastic reaction process. There are extensions of the original algorithm which provide the core for a number of recent simulation tools.²⁸

As an example, consider a simulation of the auto-regulatory network of a single gene,²⁹ where x(t) represents the concentration (or number) of mRNA molecules and y(t) the concentration (or number) of protein molecules at time t. The rate equations of x(t) and y(t) describe the evolution of the mean values of the concentrations (or numbers) of mRNA and protein molecules. The dynamics of the system can be expressed as

$$\begin{gathered} \frac{dx(t)}{dt}=-\gamma x(t)+ky(t)+k_0+\omega (t), \\ \frac{dy(t)}{dt}=k^{\prime }x(t)-{\gamma }^{\prime }y(t)+\xi (t), \end{gathered}$$

where the parameters γ and γ′ represent the decay rates of the mRNA and protein molecules, respectively, k’ represents the translation rate of the protein, k₀ denotes the fundamental transcription rate of mRNA molecules when y = 0, and the parameter k = 0, > 0, < 0 corresponds to absence of feedback regulation, positive feedback and negative feedback, respectively. In the simplest case, the fluctuations are introduced by Gaussian white-noise sources ω(t) and ξ(t). This system will differ in behavior from the noise-free system ( (ω,ξ) = (0,0) ) in that, even when the system is close to an equilibrium state of the deterministic dynamics, there is a finite probability at any given time that the system will spontaneously transition to the basin of attraction of a different stable equilibrium, because of the stochastic influences. This is of great biological and clinical significance, since such stochastic phenomena may explain why, in a large population of similar cells (or individuals), one may see different states of activation (or disease severity) despite similar initial conditions. An SDE model might explain such observations, while the equivalent ODE would be contrived to “choose” an expected outcome for the “average” cell or individual. This will result in the SDE system having a qualitatively different behavior than the corresponding ODEs. For example, the coupled reaction system, A+ 2X ↔ 3X and A ↔ X, with suitable reaction constants, has 3 steady equilibria, 2 stable and one unstable. ODE modeling of this problem will result in a behavior that depends on initial conditions, leading to one of the two steady state solutions. Regardless of initial conditions, the solution of the SDE system flips back and forth between the two steady states (Figure 3). Similar methods can be applied to spatial systems, leading to stochastic PDEs (SPDE).

Fig. 3.

Solution of the SDE system, which describes the couple reaction, A + 2X ↔ X and A ↔ X, with suitable reaction constants. If flips back and forth between 2 stable steady states independent of initial conditions.

In contrast to the deterministic behavior of a whole population, the dynamics of single individuals within a biological population is usually stochastic. Therefore, one uses stochastic processes to model single individual behavior and SDEs or SPDEs to model a whole population with stochastic influences, like the autoregulatory network of a single gene described above. For instance, single ion channel recordings are modeled by using stochastic processes.³⁰ The ionic current through an individual ionic channel of a cell membrane cannot be represented as evolving deterministically,due to stochastic changes in channel states; thus, models of small numbers of channels should be stochastic in nature. While the ensemble average over many experiments on small numbers of channels is deterministic and reproduces the same properties that are seen in macroscopic, population-level measurements., Single-channel recordings contain more information, about variance and other statistical properties, than does the ensemble average.

To describe a channel with n possible states (open, closed, inactivated, etc.), a stochastic variable S(t) ∈1,2,...,n is defined, such that S(t)=i if the channel is in state i at time t. Further, if k_ij (independent of time) is the rate constant for transitions from state i to state j, then the probability that the channel changes from state i to state j in the time interval (t,t+dt) is k_ij dt. We write

$$P\left[S\right(t+dt)=j|S\left(t\right)=i]=k_{ij}dt.$$

Here, P[x | y] is the probability of x given y. The probability that the channel does not change state in the time interval (t, t+dt) is given by

$$P\left[S\right(t+dt)=i|S\left(t\right)=i]=1-K_{i}dt,$$

where $K_i=\sum _{j=1,j\ne i}^n{k}_{ij}$. The probability that the channel stays in state i for time t is given by

$$P\left[M_i(t)|S(0)=i\right]=e^{-K_{i}t}.$$

Since the work of Hodgkin and Huxley³¹, the traditional view of a NA⁺ channel has been that it activates quickly and inactivates slowly. However, single-channel analysis has shown that this interpretation of macroscopic data is not always correct. It turns out that the rate of inactivation of some mammalian NA⁺ channels is faster than the rate of activation.³² Although this reversal of activation and inactivation rates is not correct for all NA⁺ channels in all species, the result overturned some traditional ideas of how NA⁺ channels work.

More recently, alternative methods have been used to represent biological uncertainty. The basis idea is to associate with a given, given the uncertainty in mechanisms and variability of the data, an ensemble of models.^33,8,34 Models included in the ensemble vary both in their structure and parameters. Expected behavior is then expressed statistically, much like a more conventional stochastic model. Yet, the stochasticity included in ensemble modeling is better characterized.

Strengths and pitfalls of equation-based models

Differential equations, as a modeling approach, have enormous appeal. They 1) provide an intuitive means to translate mechanistic concepts into a mathematical framework, 2) can be analyzed using a large body of existing techniques, 3) can be numerically simulated easily and inexpensively on a desktop computer, 4) provide both qualitative and quantitative predictions, and 5) allow for the systematic incorporation of higher levels of complexity and uncertainty (Figure 4). Furthermore, this modeling framework integrates existing knowledge embodied within the structure of the model, yet admits the flexibility of being data-driven and stochastic. Critics are entirely justified in pointing out that equation-based models usually depend on a large number of parameters that quantify biological interaction, and that specifying these parameters is a difficult task (see below). However, these parameters are explicit. Therefore, knowledge gaps are readily identified, unlike alternative modeling approaches. Further, the speed of computation of differential equation-based models allows for massive experimentation with parameters that may not be determined experimentally, leading to the development of hypotheses on the roles of individual parameters, reflecting the presence and relative importance of biological processes or interactions, that can drive subsequent experimental investigations.^35,36

Fig. 4.

Differential equations, as a modeling approach, allow for the systematic incorporation of higher levels of complexity and uncertainty.

In some cases, biological systems may be so fragmented that the use of differential equations may be impractical. For example, the dissemination of an infectious disease in a city, where health care service points, schools, restaurants, and churches all represent privileged areas of disease transmission, would be difficult to simulate with equation-based models. Realistic simulations must take into account individual behavior and the precise geographic location of each of those areas. In such situations, agent-based models certainly represent a more practical simulation platform than PDEs.^37,38

Calibration and validation of equation-based models

A model is deemed valid if the predictions furnished correspond to empirical data. Less strictly, a model may also be qualitatively valid if it correctly reproduces expected qualitative system behavior under a wide range of conditions. Model calibration is the process of adjusting the model parameters such that the output from the model optimally matches the observed set of data. The process of calibrating a statistical regression model is straightforward, as long as the number of observations is sufficient. However, there are several difficult issues that relate to the calibration and validation of complex non-linear dynamical models, and of equation-based models in particular. First, an equation-based model should display biological fidelity, and thus be structurally valid. In other words, the biology embodied in the equations must be rooted in empirical evidence. This entails the inclusion in the model of specific biological processes and their quantification. The level of detail included in such models depends entirely on the scale of description for which a particular model is intended. Interestingly enough, less detailed models might be more difficult to specify, because individual molecular or cellular species may be replaced by more abstract physiologic functions, which may be difficult to associate with empirical readouts.

Quantifying biological processes and interactions is clearly a formidable challenge to modelers, even when empirical observations exist. For example, models commonly necessitate the quantification of molecular half-lives. Empirical data describing an observed half-life in the circulation may be inaccurate in describing the duration of the biological effect of a particular component. A model describing the proinflammatory effects of lipopolysaccharide on vascular endothelium should use a serum half-life, provided provision is made for recirculation and the processes triggered by endotoxin binding are themselves modeled. However, if the downstream effects of the interaction of a molecule with a target cell receptor are not specifically included in the model, then the modeler needs to include an appropriate estimate of the biological half-life of these downstream processes as well.

This simple example should illustrate the great care that must be taken in ascribing values to parameters, irrespective of the modeling framework adopted. At best, these parameter values should serve as a starting point to further fitting of the model to empirical data, or to known qualitative behaviors in the absence of empirical data. A number of very sophisticated algorithms have been proposed and are commonly used to adjust parameters to produce optimal fits to empirical data.³⁹ The process differs fundamentally from statistical settings, in which there are clear prescriptions as to how to achieve model fits and unique solutions typically exist. Because mechanistic models often include many parameters with unclear biological values, the problem of fitting models to empirical data is high dimensional, computationally intensive, and typically admit many equally well-fitting solutions. Therefore, modelers have typically not produced quantitative model validation, except for biologically simplified systems.⁴⁰ A clear research objective resides in the production of new theoretical and computational methods to conduct quantitative fits and to provide ensembles of candidate models^41,42, together with the congruent development of experimental paradigms that will provide optimal data streams to accomplish this task. Indeed, the range of predictions of a mechanistic model extends well beyond defined sets of experimental conditions or clinical interventions ^24,27. This situation is in sharp contrast to statistical models, which cannot offer predictions beyond the empirical construct under which calibrating observations were gathered.

Conclusions and future directions

Equation-based modeling offers distinct practical advantages as a modeling platform, including potential for inclusion of biological detail, suitability for simulation, and ease of parameter manipulation for predictive purposes, but it is not the preferred approach for simulating the stochastic interactions of small numbers of agents or the dynamics of highly fragmented systems. This modeling platform is one of several tools that will be utilized by interdisciplinary teams of expert modelers, basic scientists, and clinicians. While biological scientists should work to improve experimental designs and the reliability and quantity of empirical evidence available, much theoretical work needs to be done by quantitative scientists to facilitate the analysis of complex systems and to develop improved parameter estimation techniques. The expected output of this work will be an improved translation of basic knowledge into clinical care and prevention approaches, as well as the design of new therapies ^27–29.

Quantitatively predictive mathematical models depend exquisitely on the availability of high quality empirical data. Therefore, hypothesis driven, reductionist investigations, examining and quantifying biological processes in highly controlled environments, remain the key foundation of any effort at gaining insight into complex biology through modeling³⁶. As the scientific community is marshalling an unprecedented effort to encourage, support, fund and implement interdisciplinary translational science, there still exists a deep divide in the peer-reviewed literature between the modeling community and the clinical and basic sciences communities. This divide originates from a critical lack of collaborative efforts, a paucity of standards that would appeal to the scientific communities involved in the interdisciplinary effort³⁶ (such as a lack of understanding by experimentalists of the type of data required for modeling), and, rightly or wrongly, a lack of perceived incremental usefulness of the modeling exercise to clinical translation in general. Thus, an opportunity is missed in that the potential of reductionist science is not optimally exploited by complementary efforts of highly-interactive interdisciplinary teams.

Appendix A

Possible behavior in autonomous systems

Solutions to a one-dimensional autonomous ordinary differential equation cannot oscillate. That is, in an oscillatory solution x(t), there exists some interval of x values through which the solution increases over one time interval and decreases over a different time interval. If x’= f(x) is a one-dimensional ODE, then f (x) takes a fixed value at each x, and such an oscillation is not possible.

Alternatively, in a two-dimensional system

$$\begin{gathered} x^{\prime }=f(x,y), \\ {y}^{\prime }=g(x,y), \end{gathered}$$ (1)

it is possible that for a fixed x, there are y values y₁ ≠ y₂ such that f (x, y₁) < 0 < f (x, y₂),allowing the possibility of oscillations.

In two-dimensional systems of the form (1), there are several classic results that ensure or rule out the existence of periodic oscillatory solutions, satisfying x(t + T ) = x(t), y (t + T ) = y(t) for some fixed T > 0, for all t. There are other, more complex solutions, however, such as chaotic dynamics that can only occur in an autonomous system that includes three or more dimensions.

The classical Hodgkin-Huxley (HH) equations³¹, describing action potential generation in a giant axon extracted from the squid nervous system and treated experimentally in a way that eliminates spatial effects, offer an interesting case study. The original HH model consists of a four-dimensional autonomous system of ODE’s, representing the temporal evolution of variables (v,m,h,n). Here, v denotes the voltage across the cell membrane, while (m,h,n) quantify the degree to which ions can pass through voltage-gated sodium and potassium channels in the membrane.

Because the sodium channel activation variable m responds quickly to changes in voltage, it is often approximated by a function of v. Further, an empirical linear relation, such as h ≈ 0.8 – n, has been observed to hold along typical model solutions⁴³. These approximations have long been used to justify reduction of the HH model to a two-dimensional system in (v, h) or (v, n), which actually reproduces qualitative features of action potentials and even quantitative dependence on applied current rather well.

Nonetheless, recent work has shown that when additional dimensions are restored to the model, chaotic dynamics near the action potential threshold, as well as mixed mode oscillations, consisting of various patterns of alternating small oscillations and large excursions in voltage, can arise^44,45. Such solutions may have important implications for transitions between quiescence and repetitive activity patterns in neurons, as their input levels vary.