Abstract
Objective:
The durability of bioprosthetic heart valve (BHV) devices, commonly made of bovine (BP) and porcine (PP) pericardium tissue, is partly limited by device calcification and tissue degeneration [1], which has been associated with pathological levels of mechanical stress [2-4]. This study investigated the impacts of BP and PP tissues with different thicknesses and tissue mechanical properties in BHV applications.
Methods:
Second Harmonic Generation (SHG) imaging was employed to visualize the collagen fibers on each side of the pericardium. Structural constitutive modeling that incorporates collagen fiber distribution obtained from multiphoton microscopy for each tissue type were derived to characterize the corresponding biaxial mechanical testing data collected in a previous study [5]. The models were verified through finite element (FE) simulations of the biaxial test and implemented in valve closing simulations.
Results:
Smooth side collagen fibers were found to correlate with the mechanical response. BHVs with adult (ABP) and calf (CBP) BP tissues had lower maximum principal stresses than those with PP and fetal (FBP) BP tissues. Collagen fiber orientation along the circumferential axis resulted in lower maximum principal stresses and more uniform and symmetric stress distributions throughout the valve.
Conclusions:
The use of PP and FBP tissue resulted in higher peak stresses than ABP and CBP tissues in the given valve design. Additionally, ensuring collagen fiber orientation along the circumferential axis led to lower maximum stresses felt by the valve leaflets, which could also improve BHV durability.
Keywords: transcatheter heart valves, bovine pericardium, porcine pericardium, finite element analysis, collagen, structural constitutive modeling
1. INTRODUCTION
The leaflets of transcatheter aortic valve replacement (TAVR) devices [6, 7] are often made from bovine (BP) or porcine (PP) pericardium tissues. Since the first TAVR procedure in 2002, a range of different TAVR devices have been introduced [1, 8, 9], differing in design parameters such as biological leaflet materials, stent frame, and leaflet shape. Currently, the Edwards SAPIEN series (Edwards Lifesciences, Irvine, CA), made from BP tissue, along with the Medtronic CoreValve series (Medtronic, Minneapolis, MN), made from PP tissue, are the only transcatheter aortic valves (TAV) approved for commercial use in the US. Since the TAVR procedure is still relatively new with the first Conformite Europeene (CE) Mark of TAVR in 2007, few long-term durability studies are available. Recent data show a TAV lifespan of approximately 8 years, with degeneration not uncommon 10 years post-procedure [10]. Comparatively, surgical bioprosthetic heart valves (BHVs) typically last about 10-15 years [11, 12]. It is well known that the durability of BHVs is limited by device calcification and tissue degeneration [1]. Studies have linked aortic valve (AV) calcification with biomechanical factors such as leaflet stresses, preferentially occurring in coaptation or radial patterns, and indicating that mitigating these stresses may alleviate the occurrence of BHV calcification [2-4].
The design and manufacture of TAVs needs to account for the diameter of the delivery sheath in order to navigate through tortuous, possibly sclerotic, arteries to the heart. The thickness of the pericardium tissues is therefore critical in minimizing the crimped diameter. In a previous study by our group [5], we found that BP and PP tissues of different thicknesses and age presented significant differences in their mechanical properties [5]. Differences in both leaflet thickness and mechanical properties can impact TAV leaflet stresses and may thus also affect device durability [2-4].
Also contributing to their anisotropic material response, it is well known that collagen fiber orientation plays an important role in native valve mechanics [13, 14], i.e., the mechanical anisotropy of native AV leaflets is ensured by the aligned orientation of collagen fibers along the circumferential direction [15, 16]. This collagen fiber orientation provides mechanical support when the valve is closed and reduces the leaflet mechanical stresses, but collagen fiber orientation, density, and crimp are known to differ between the smooth and fibrous sides of the pericardium, giving the fibrous side its “rough” nature. However, the exact contribution of the smooth and rough sides of the pericardial tissues to its mechanical properties is largely unknown.
Many studies have investigated the mechanics of chemically-treated BP and PP tissue and fitted the mechanical response under various loading conditions to phenomenological constitutive models [17-20]. However, few have incorporated experimentally-derived structural parameters such as collagen fiber volume fraction, average fiber orientation in the tissue sample and orientation distribution into the model itself. As a result, it is difficult to extrapolate a quantitative understanding of the link between TAV mechanics and structure from available published data.
To address this gap in the literature, the present study investigated the collagen fiber structure in BP and PP tissues via multi-photon microscopy. BP and PP mechanical responses were described with a novel structural constitutive model that incorporates experimentally-derived collagen fiber distributions. The model was implemented into a finite element (FE) framework, validated via biaxial tensile testing simulations [21], and used in TAV closing simulations for each tissue testing group in order to evaluate their load-bearing performance.
2. METHODS
2.1. Sample Preparation
Biaxial testing data was obtained from Caballero et al. (2017) [5]. Briefly, BP and PP sacs were obtained from Animal Technologies, Inc. (Tyler, TX) and chemically treated. BP sacs were extracted from 10 adult (ABP, average thickness 0.427 ± 0.048 mm), 11 calf (CBP, average thickness 0.327 ± 0.046 mm) and 11 fetal (FBP, average thickness 0.231 ± 0.017 mm) cattle. PP sacs were explanted from 22 6-9-month-old pigs and separated into thick (PPK) and thin (PPN) samples (average thickness: 0.186 ± 0.010 mm and 0.142 ± 0.015 mm, respectively). Samples were selected by visual inspection of homogeneity and fiber orientation. Tissue treatment and fixation were performed in two steps at room temperature. The pericardia were pinned down to maintain surface flatness and immersed in a 0.625% glutaraldehyde for 2 hours, then treated with a crosslinking anti-calcification solution of formaldehyde, ethanol, and Tween 80 (Sigma Aldrich, St. Louis, MO) for 18 hours. Treatment with high concentrations of glutaraldehyde has been shown to provide superior mechanical results and resistance to enzymatic degradation [22]. Treated pericardia were then stored at 4°C in 0.25% glutaraldehyde for a minimum of 48 hours prior to testing. Planar biaxial testing was conducted following the methods detailed by Sacks and Sun (2003)[21].
2.2. Multiphoton Microscopy
To quantify the collagen fiber structure, tested biaxial samples from Caballero et al. (2017) [5] were imaged in the central region (delimited by the graphite markers) using second harmonic generation (SHG) imaging. Tissues were imaged on a Zeiss 710 NLO inverted confocal microscope (Carl Zeiss Microscopy, LLC, Thornwood, NY, USA) equipped with a mode-locked Ti:Sapphire Chameleon Ultra laser (Coherent Inc., Santa Clara, CA) in combination with non-descanned detection (NDD). The laser was set to 800 nm and emission was filtered from 380–430 nm [23]. Samples were kept hydrated with saline solution during imaging to prevent drying artifacts and covered with #1.5 coverslips. SHG was collected from the smooth side of the tissue using a Plan-Apochromat 40x oil immersion objective. Zeiss ZEN software was used to visualize and export image stacks for analysis. Image resolution was set to 0.35 × 0.35 μm2 per pixel at 12-bit pixel depth.
2.3. Estimation of Local Collagen Fiber Distribution
The local preferred fiber direction for each z-stack was estimated using a semiautomatic ImageJ-Matlab in-house code (The Mathworks, Inc., Natick, MA). First, OrientationJ distribution [24], an ImageJ [25] plug-in developed for directional analysis, was used to generate a histogram of local angles between ±90° for each optical slice, where 0° aligned to the X1 axis (preferred collagen fiber axis) and ±90° to the X2 axis (cross-fiber axis) from biaxial testing. The local collagen fiber orientation was evaluated pixel-by-pixel based on the structure tensor [26]. Next, the individual histograms at each slice were combined and normalized to calculate a mean local angular histogram for each tissue sample. Finally, the fiber distribution was fitted to a continuous single Gaussian probability density function, given by
| (1) |
where μ and σ are the mean and standard deviation of the fiber orientation distribution, respectively, and θ is the fiber angle moving counterclockwise from the X1 axis. Parameters μ and σ were determined for each tissue sample through fitting the fiber orientation histogram data in the least squares sense using the lsqcurvefit function in MATLAB. Collagen volume fraction (cf) was also obtained; the number of pixels associated with the collagen fibers in each image of each stack of slices was quantified and expressed as a total ratio of collagen fibers compared to the total number of pixels in the stack.
2.4. Structural Constitutive Modeling
For this study, a structural constitutive model was used to fit the BP and PP experimental data. Due to its composition, chemically-treated pericardium can be considered a fiber-reinforced continuum. Accordingly, the strain energy function W was decomposed into a volumetric part U and deviatoric part , and was further decomposed into distinct contributions from the ground substance (i.e., the matrix) of the tissue, , and the contribution from the fibers, . Thus, the total strain energy function can be described as [27, 28]:
| (2) |
where cf is the fiber volume fraction determined from multiphoton microscopy. The contribution of the matrix was modeled with a modified form of the Neo-Hookean strain energy function [29], given by
| (3) |
where C10 and C01 are material constants that relate to the ground matrix, and is the first invariant of the Cauchy-Green deformation tensor. The contribution of an individual fiber, , was modeled with the following strain energy function presented previously [27]:
| (4) |
where A and B are material constants that relate to the collagen fibers, respectively, and , where is the deviatoric fiber stretch. Given the fourth invariant of the Cauchy-Green deformation tensor, , Equation (4) can be rewritten as
| (5) |
For the entire fiber ensemble following the collagen fiber distribution, R(θ), obtained from multiphoton microscopy, the strain energy function becomes
| (6) |
where R(θ)dθ is the fraction of fibers oriented between θ and θ + dθ and subjected to the normalization constraint . The volumetric contribution can be modeled with the penalty function
| (7) |
where D is a material constant that introduces near incompressibility and J is the volume ratio before and after deformation. For the purpose of this study, chemically-treated BP and PP tissues were assumed to be incompressible, thus J = 1, and the overall tissue strain energy is given by
| (8) |
finally, the Second Piola-Kirchhoff stress was calculated by
| (9) |
where E is the Green Strain tensor. Material parameters C10, C01, A, and B were determined for each biaxial test sample through fitting the stress-strain responses to Equation (9) using the nonlinear least-squares fitting function lsqcurvefit in MATLAB. The experimental data from the seven stress-controlled biaxial test protocols were fitted simultaneously to reduce the effect of multiple collinearities. Each set of model parameters was checked for convexity and ellipticity according to the methods of Sun and Sacks [30], to facilitate FE implementation.
2.5. Simulation of Biaxial Testing.
The biaxial tensile testing of one representative sample in each testing group was simulated using ABAQUS (Simulia, RI) to verify the material model coefficients and FE implementation. A 25 × 25 mm2 biaxial testing sample model was created with plane-stress quadrilateral elements for each testing group. The model thickness was assigned according to the mean experimentally measured thickness for each group. Four evenly spaced (2.5 mm from the edge of the sample, 5 mm apart from each other) tensile nodal forces were applied to all four sides of the model to mimic the experimental test set-up [30]. The material model was implemented using an in-house user defined material subroutine [28], and one representative set of material parameters from each testing group was utilized for the simulations. Stress-strain curves were extracted from the center of the model under equibiaxial loading (similarly to experimental methods [21]) and compared to the experimentally-obtained equibiaxial curves.
2.6. Simulation of Valve Closing
An in silico TAV made up of 3948 large-strain shell elements (S4) was utilized to investigate the impacts of different pericardial tissues on leaflet stress [31, 32]. Leaflet dimensions were maintained constant and tissue thickness was changed according to experimentally obtained values for each testing tissue group. The leaflet tissue mechanical properties were defined by Equation (9) and the corresponding material parameters for each testing group. A uniform transvalvular pressure (120 mmHg) was applied to the aortic side of the leaflets in order to simulate diastolic closure of the valve. The master-slave approach in ABAQUS was utilized to define leaflet-leaflet contact on the ventricular side of the leaflets. Leaflet attachment edges were constrained from movement to mimic attachment to a rigid stent. Peak stresses and strains were recorded and analyzed.
Additionally, the effect of the collagen orientation angle was investigated by re-running the valve closing simulation for a representative ABP sample using a collagen fiber angle of 15°, an angle variation for pericardial samples (see results). Maximum principal stresses and strains were compared.
2.7. Statistical Analysis
All measurements are presented as a mean ± standard deviation. The One-Way Analysis of Variance (ANOVA) test was implemented in SigmaPlot (Systat Software Inc., San Jose, CA). If statistical differences were found (p < 0.05), pairwise multiple comparisons were performed using the Holm–Sidak or the Dunn’s methods. The Student’s t-test was used when two groups were compared. Probability values p < 0.001 were considered to indicate differences with high statistical significance.
3. RESULTS
3.1. Multiphoton Microscopy
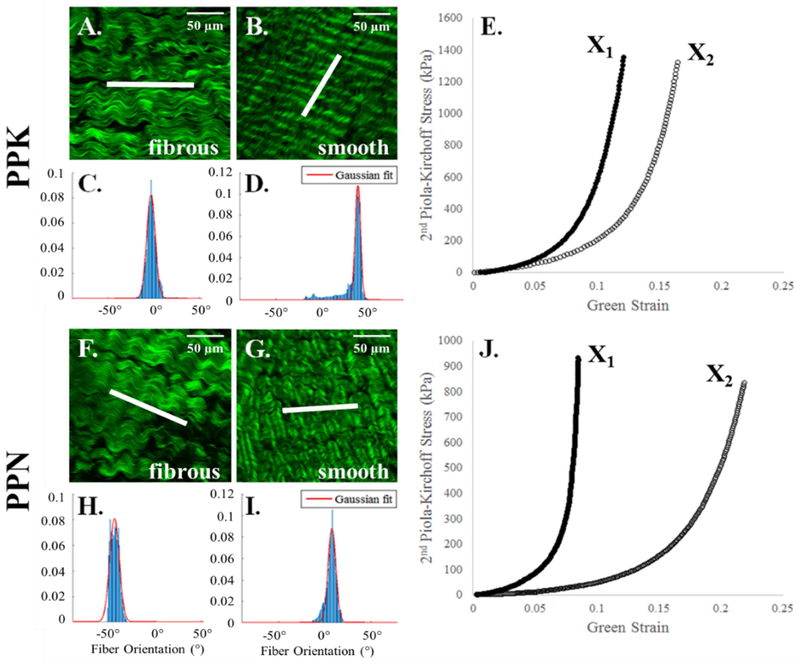
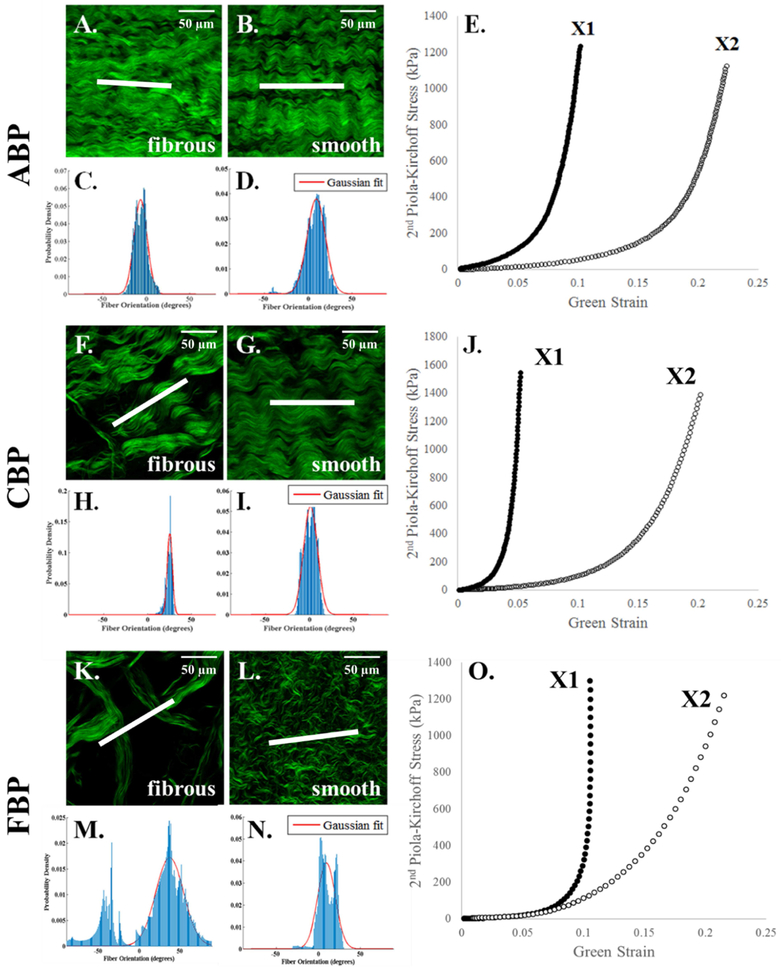
Multiphoton microscopy images suggest that the orientation of the collagen fibers on the smooth side of PP and BP tissues is the main determinant of the sample’s mechanical response. As shown in representative samples in Figure 1B, the smooth side of the PPK sample depicts that collagen fibers are aligned in a slanted fashion, which are reflected in the more isotropic nature of the mechanical response (Figure 1E). Similarly, the alignment of the collagen fibers on the smooth side of the PPN sample (Figure 1G) is reflected in the more anisotropic nature of the mechanical response (Figure 1J). The fibrous side of both samples (Figure 1A, F), however, consist of collagen fibers that do not correspond with the mechanical response, with a fiber orientation peak at approximately 0° for the PPK sample (aligned with X1) and an orientation of approximately 45° for the PPN sample. As in Appendix Figure 1, this phenomenon was also observed in the ABP, CBP, and FBP samples. Additionally, the smooth side of the PP samples shows a shorter crimp period than the BP samples, and the crimp period for all samples is shorter on the smooth than on the fibrous side.
Figure 1.
Representative multiphoton microscopy images and fiber distribution graphs of collagen fibers on the smooth and fibrous sides of PPK (A-E) and PPN (F-J) samples with their respective equibiaxial response. Scale bar shows 50 μm (A, B, F, G, top right). The white line in the center of each image depicts the measured average fiber orientation. The red line depicts the Gaussian fit to the collagen fiber distribution, plotted as probability density vs. fiber orientation (degrees). Fiber orientation values of 0° and ±90° (relative to the horizontal) correspond to alignment with the X1 and X2 axes, respectively.
3.2. Constitutive Modeling of Biaxial Response
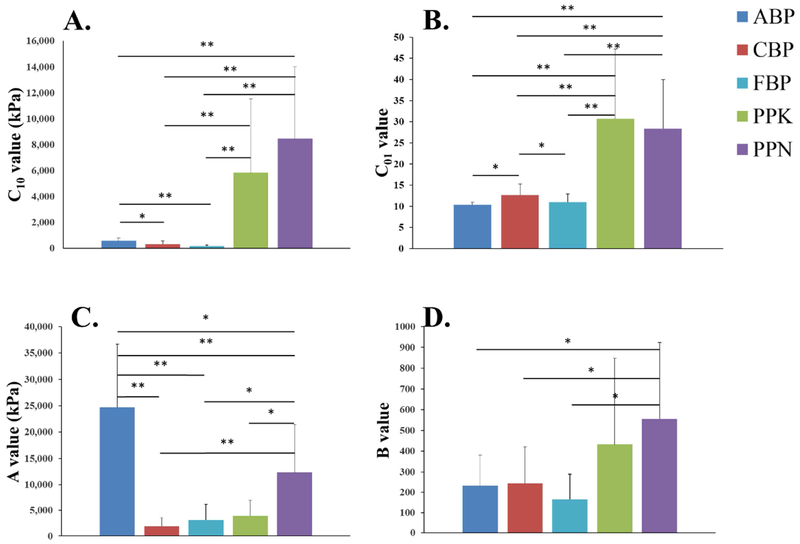
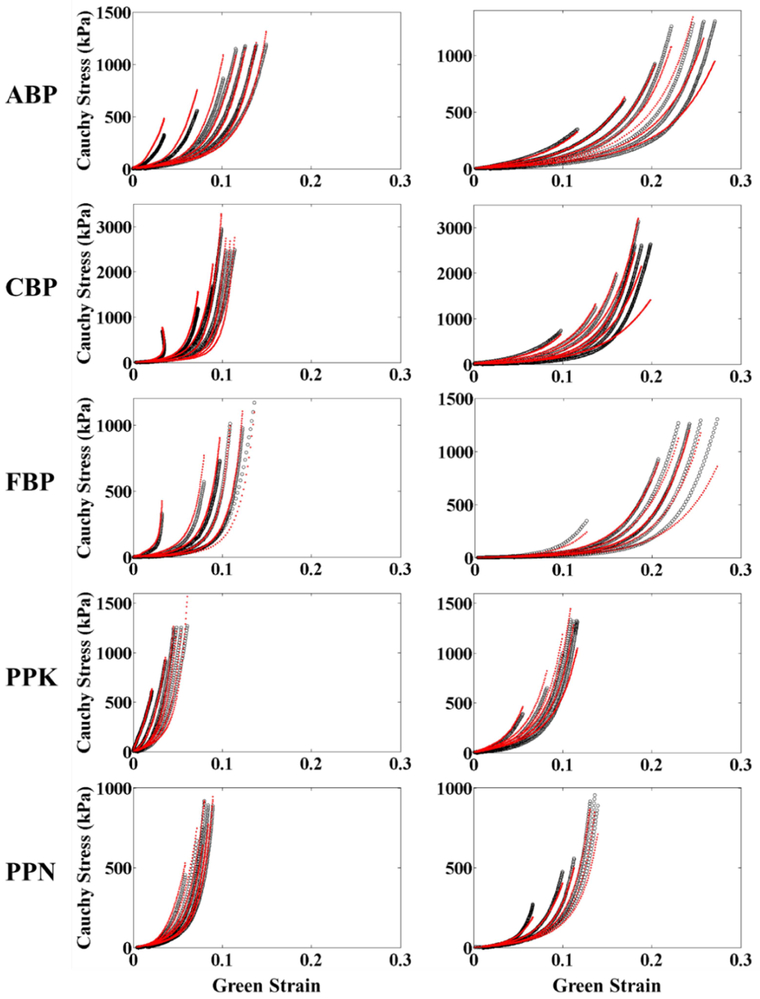
Table 1 shows the average values of the parameters for the Gaussian fiber distribution function Eqn (1), as well as the parameters for the fitting of the biaxial testing results to the strain energy function of Eqn (9). Individual fiber distribution and constitutive model parameters for BP and PP samples are presented in Tables 3 and 4 of the Appendix, respectively. The model was found to accurately capture the tissue mechanical response, with average correlation coefficient values above 0.9 for each tissue group. Representative figures showing the fit of the constitutive model to the biaxial data are shown in Figure 2 of the Appendix.
Table 1.
Average fiber distribution fit and constitutive model parameters for all testing groups.
| ABP | CBP | FBP | PPK | PPN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cf | 0.836 | ± 0.057 | 0.799 | ± 0.099 | 0.802 | ± 0.031 | 0.967 | ± 0.016 | 0.986 | ± 0.100 |
| μ (°) | −2.292 | ± 19.869 | −4.283 | ± 33.617 | 12.752 | ± 27.409 | −10.535 | ± 28.201 | −6.010 | ± 17.181 |
| σ (°) | 7.848 | ± 4.692 | 6.983 | ± 2.148 | 10.393 | ± 1.873 | 4.285 | ± 1.787 | 4.398 | ± 5.286 |
| R2 Gauss | 0.805 | ± 0.162 | 0.846 | ± 0.130 | 0.809 | ± 0.120 | 0.876 | ± 0.069 | 0.845 | ± 0.070 |
| C10 (kPa) | 578.050 | ± 241.308 | 344.233 | ± 227.035 | 169.041 | ± 5698.410 | 5829.662 | ± 5536.346 | 8449.809 | ± 78.430 |
| C01 | 10.379 | ± 0.556 | 12.667 | ± 2.625 | 10.996 | ± 16.450 | 30.722 | ± 11.581 | 28.349 | ± 1.921 |
| A (kPa) | 24702.935 | ± 11957.557 | 1930.649 | ± 1607.324 | 3106.080 | ± 3059.617 | 3925.525 | ± 9121.353 | 12322.629 | ± 3032.719 |
| B | 232.019 | ± 147.962 | 243.955 | ± 177.904 | 163.654 | ± 414.046 | 432.224 | ± 366.976 | 556.208 | ± 124.883 |
| R2 model | 0.937 | ± 0.033 | 0.907 | ± 0.044 | 0.925 | ± 0.039 | 0.932 | ± 0.036 | 0.903 | ± 0.057 |
The model parameter values were compared among the tissue groups. The C10 parameter, which reflects the stiffness of the ground matrix, did not significantly differ when comparing within the PP group, although statistically significant differences were found between the PP and BP groups and within the BP samples (Figure 2A). The PP samples had significantly higher C10 values than the BP samples (p < 0.001 for PPK and PPN vs. ABP, CBP, and FBP). The A parameter, which reflects the collagen fiber stiffness, was found to be significantly smaller for the FBP group than that of ABP (p < 0.001) and PPN (p = 0.029). In addition, the A value for the CBP group was found to be significantly smaller than that of the ABP and PPN groups (p < 0.001, and p = 0.027, respectively). The C01 parameter was found to significantly differ when comparing between species, but not within a species (Figure 2). The PP groups had significantly higher C01 values than the BP groups (p < 0.001 for all cases). This trend was also preserved in the B parameter, but was statistically significant only in comparing PPN and the BP groups (p = 0.040, p = 0.037, and p = 0.008 for PPN vs. ABP, CBP, and FBP, respectively).
Figure 2.
Constitutive model parameters summarized for the PP and BP groups. (*) denotes a statistically significant difference between the groups, p < 0.05. (**) denotes a high level of statistical significance, p < 0.001.
3.3. Model Verification through Biaxial Testing Simulations
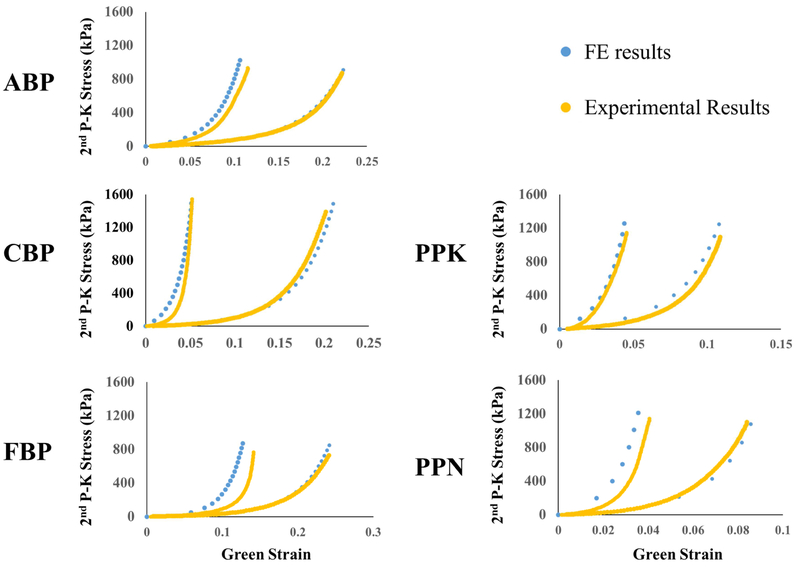
Figure 3 shows the results of the equibiaxial verification simulations compared to the experimentally-obtained mechanical responses. The simulation was able to capture the experimental response well for all representative samples, showing good agreement with experimentally-obtained results.
Figure 3.
Comparison of equibiaxial results obtained through FE simulation (blue) and experimentally (yellow) for a representative sample from each testing group.
3.4. Evaluation of BHV Material by Valve Closing Simulations
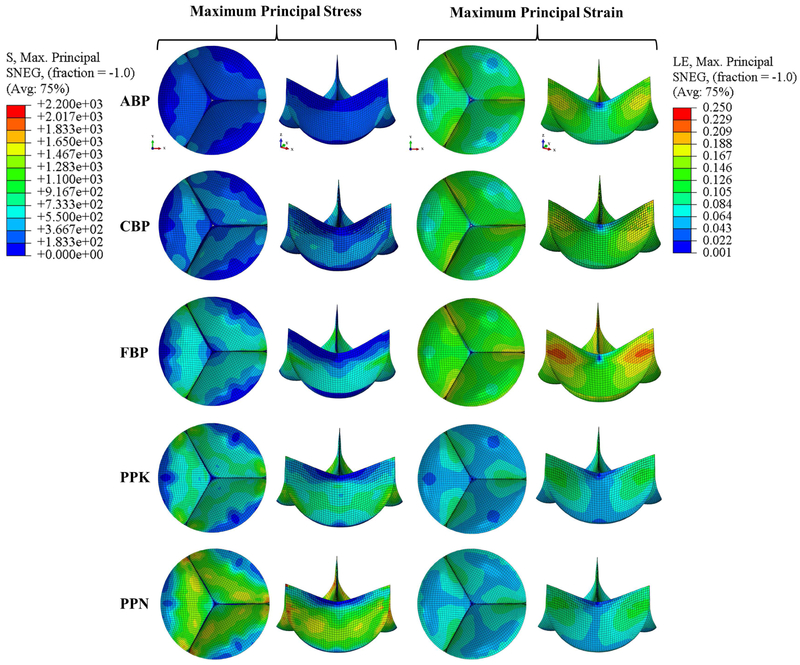
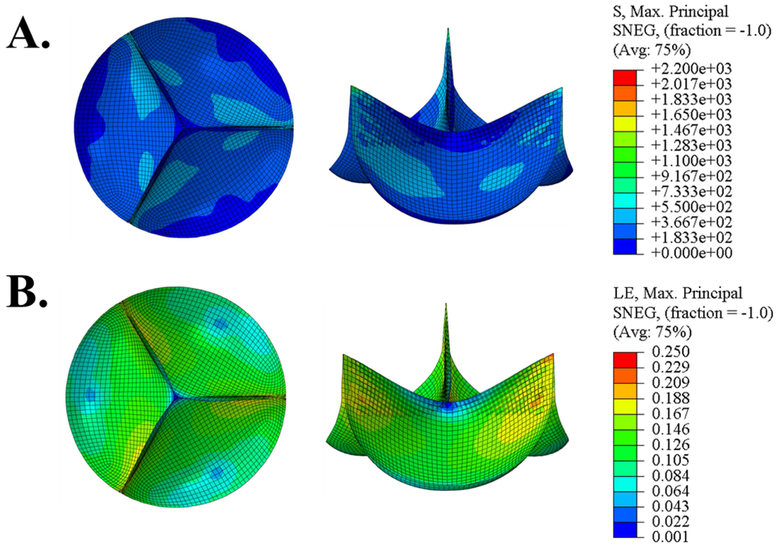
Figure 4 depicts the representative FE valve closing simulation results, which are also summarized in Table 2. It can be seen that the ABP and CBP valves experienced lower peak stresses than the FBP, PPK, and PPN valves. The PPN valve experienced both the highest stresses (followed by FBP, PPK, CBP, and ABP) and lowest strains, while the highest strains were felt by the FBP valve (followed by ABP, PPK, CBP, and PPN).
Figure 4.
Maximum principal stress (kPa) and strain contours in the closed valve configuration using a set of representative parameters for each testing group.
Table 2.
Maximum principal stress and strain values from FE simulations for the representative samples from each testing group.
| Overall Sample | Belly Region | |||
|---|---|---|---|---|
| Max. Principal Stress (kPa) |
Max. Principal Strain (LE) |
Max. Principal Stress (kPa) |
Max. Principal Strain (LE) |
|
| ABP | 502.336 | 0.178 | 434.674 | 0.121 |
| CBP | 912.438 | 0.113 | 740.010 | 0.074 |
| FBP | 1196.970 | 0.215 | 894.273 | 0.142 |
| PPK | 1112.099 | 0.114 | 982.353 | 0.086 |
| PPN | 2173.448 | 0.107 | 1768.880 | 0.084 |
3.5. Impact of Collagen Fiber Orientation
In regards to the average fiber distribution angle, Figure 5 shows the maximum principal stress and strain distribution for a representative ABP sample, with an average fiber distribution angle set to 15° (typical of BP, whose fiber dispersion splay can reach as much as 30° [17]). The sample had higher maximum principal stress and strain values compared to those of the ABP sample with collagen fibers were oriented at just 1.156° to the circumferential axis (587.8 kPa vs. 502.336, and 0.203 vs. 0.178). It was also observed that the 15° sample had un-symmetric stress and strain distributions.
Figure 5.
Maximum principal stress (kPa) and strain contour in the deformed configuration for a representative ABP sample with collagen fibers oriented at θ = 15°.
4. DISCUSSION
This study explored the relationship between the microstructural and mechanical properties of BP and PP tissues. The smooth layer of the pericardium tissue was found to dominate the mechanical response. A structural constitutive model was employed to incorporate collagen fiber distribution into the modeling of mechanical behavior. Unlike phenomenological constitutive models, structural models provide more than just the stress-strain relationship at the tissue scale [27]. By incorporating the orientation of the collagen fibers as well as a statistical dispersion of those fibers, the structural constitutive model can allocate macroscopic stress to different micro-structural components. The constitutive model and model parameters were validated through simulations of the biaxial test experiment, which were able to replicate the experimentally measured tissue responses. Collagen fiber orientation along the circumferential axis was found to decrease the maximum principal stress. In addition, FE simulations of valve closing using BP tissue were found to have lower maximum principal stresses than with PP tissue.
Structure-Function Relationship
One interesting finding of this study is the fact that smooth side fibers are the main contributor to pericardial mechanical response across the testing groups. As shown in Figure 1 and Appendix Figure 1, the smooth side of the sample consists of more packed collagen fibers with a noticeably shorter crimp period; this may contribute to earlier recruitment of collagen fibers and thus result in the dominant mechanical effects from the smooth side collagen fibers. In general, BP tissues had more loosely packed collagen fibers than PP samples, particularly visible in the FBP results. The looser packing and increased crimp period of BP collagen fibers may contribute to their increased extensibility.
The structural model used in this study highlights the impact of the collagen fiber architecture in the mechanical behavior of pericardium. Although the structural model parameters have a direct physical meaning, physical interpretations within the context of the assumptions of the constitutive model must be made with caution. Previous efforts have been targeted towards structural constitutive models in order to characterize the mechanical behavior of cardiac tissue [17-20]. A study by Fan and Sacks [17] developed a similar model accounting for the collagen fiber orientation and distribution. The study primarily focused on the change in fiber crimp and orientation as a result of recruitment, with a significant role played by the ground matrix. Although it was not implemented into the BHV setting, the model was incorporated into simulations of mitral valve closure [18], whose microstructural architecture and geometry are quite different from those of BP and PP tissue. Similarly, they found that mapping collagen fiber orientation and dispersion with experimentally-obtained material properties improves accuracy of the model’s predictive capabilities. Our model also has ability to account for local collagen fiber orientation, which provides a powerful tool for the understanding of collagen fiber contributions to the mechanical response.
BP and PP BHV Mechanics
This study investigated the use of BP and PP tissue in a BHV model under identical design and loading conditions. Due to mechanical testing, tissue treatment, and parameter extraction methods widely varying between studies, a thorough comparison of the data obtained from this study to previously-published results is difficult. Using ABP and CBP tissues resulted in lower peak stresses (500-900 kPa) than the other tissue types investigated in this study, with the ABP tissue showing stresses also lower than CBP. The higher TAV closing stresses of CBP tissue compared to ABP tissue could be due to 1) higher ABP thickness, or 2) better alignment of collagen fibers in the circumferential direction for the ABP valve. Nonetheless, the BP stress values are on par with, or considerably lower than those found by other studies, and fall comfortably in the region of recoverable elastic deformation for ABP and CBP tissues (see Figure 3), as compared to the significantly higher peak stress values for FBP, PPK, and PPN tissues.
A study by Li and Sun [31] investigating the use of BP and PP leaflets in BHV simulations found peak stress values of 916 kPa for adult BP and 1566 kPa for PP tissue of 0.25 mm thickness using the Fung-type model. Increasing tissue thickness was also found to reduce the peak stresses, which may contribute to the lower stress values for BP and higher values for PP presented herein. Another study by Li and Sun [33] looking to optimize the configuration of found peak stresses of 868 kPa for ABP tissue with 0.24 mm thickness in circular TAV configurations. Others have reported higher values [34]. In comparison, Mizoguchi et al. have shown the Edwards SAPIEN 3 (which uses BP tissue) to have peak a principal stress of 3.05 MPa at systolic pressure [35].
Implications for BHV Manufacturing
Studies have shown that the anisotropic nature of heart valve leaflets is important for proper physiological function, as well as to ensure valve durability [31, 33, 36]. As also found in this study, collagen fiber alignment along the circumferential axis was shown to aid in more uniform and symmetric distribution of stress and strain throughout the leaflets, corroborating previous results [31, 33]. It was further found in this study that the smooth side of the tissue dominates the mechanical response, possibly owing to the shorter crimp period of collagen fibers on the smooth side (Figure 1, Appendix Figure 1). When the tissue is stretched, the fibers with the shorter crimp period will get recruited first and dominate the mechanical response.
As a result, collagen fiber alignment for BHV manufacturing should be based on the smooth side fibers. While SHG-imaging visualization of collagen fibers may be a costly undertaking, it will give manufacturers better control of the mechanical properties of BHV components, and thus better control of valve performance and durability. An additionally significant implication based on these findings concerns the “trimming” of BP and PP tissues for BHV manufacturing in order to achieve a desired tissue thickness [37, 38]. Such trimming efforts should aim to preserve the smooth side collagen fibers in order to also preserve the mechanical properties of BP and PP tissues.
Moreover, the mechanical results presented in this study indicate that the use of FBP or PP tissue in BHV and TAVR devices may require optimized valve design and assembly in order to minimize mechanical stresses and improve device durability. Further studies investigating the impact of these mechanical property differences on BHV function are warranted.
Limitations
It should be noted that results from this study only reflect the mechanics and collagen microstructure architecture for BP and PP tissues treated at 0.625% glutaraldehyde. A larger sample size would allow for a more complete investigation of the effects of variation in tissue mechanical properties on peak valve stresses, as well as provide more statistical power in data analysis. Additionally, the fiber orientation integral was evaluated using the rectangle rule—other methods such as Gauss quadrature may achieve higher numerical accuracy and efficiency for simulating heart valve function. Moreover, as this study employed only one valve design in just the valve closing scenario, further analysis is required in order to understand the effects of valve configuration on the peak stresses and strains. Future studies incorporating these aspects would prove beneficial.
5. CONCLUSION
This study investigated and compared the relationship between the mechanical and microstructural properties of BP and PP tissues. SHG imaging was employed to visualize the collagen fibers on the smooth and fibrous sides of the BP and PP tissues, finding that the smooth side fibers better correlate with the mechanical behavior of the tissues. A structural constitutive model incorporating the orientation of collagen fibers was implemented in order to describe the mechanical behavior of BP and PP tissues. The model was also implemented into a FE framework and tested with equibiaxial FE simulations and found to correspond well to the experimental data reported in Part I of this study. FE simulations of TAV closing showed ABP and CBP samples to have lower maximum principal stresses than the other testing groups, as well as lower maximum principal stresses in the belly region of the valve leaflets given identical valve design. Additionally, the effects of fiber orientation were compared, indicating that collagen fiber alignment away from the circumferential axis results in greater maximum principal stresses and strains. Taken together, these results support the need for collagen fiber alignment along the circumferential axis to lower perceived stresses and possibly achieve greater BHV durability.
6. ACKNOWLEDGMENTS
This work was funded in part by HL127570 grant. Fatiesa Sulejmani is also supported by the Georgia Institute of Technology-Emory University-Peking University Global Biomedical Engineering Research and Education Fellowship. Andres Caballero is in part supported by a Fulbright-Colciencias fellowship.
8. APPENDIX
Figure 1.
Representative multiphoton microscopy images and fiber distribution graphs of collagen fibers on the smooth and fibrous sides of ABP (A-E), CBP (F-J), and FBP (K-O) samples with their respective equibiaxial protocols. Scale bar shows 50 μm (top right, panels A, B, F, G, K, L). The red line depicts the Gaussian fit to the collagen fiber distribution, plotted as probability density vs. fiber orientation (degrees). Fiber orientation values of 0° and ±90° correspond to alignment with the X1 and X2 axes, respectively.
Figure 2.
Representative biaxial experimental protocols for each testing group (black) fit according to the structural constitutive model (red).
Table 3.
Individual fiber distribution and constitutive model parameters for BP samples.
| Fiber distribution parameters | r2 | Material parameters | r2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| cf | μ | σ | C10 (kPa) | C01 | A (kPa) | B | |||
| ABP | 0.882 | 9.577 | 12.069 | 0.891 | 576.573 | 11.289 | 25152.893 | 132.172 | 0.920 |
| 0.781 | −15.855 | 7.770 | 0.856 | 464.566 | 10.070 | 34591.312 | 97.827 | 0.937 | |
| 0.955 | −17.771 | 3.154 | 0.929 | 3026.284 | 12.559 | 2491.033 | 469.815 | 0.972 | |
| 0.811 | 1.036 | 2.490 | 0.915 | 283.986 | 10.215 | 21654.944 | 132.619 | 0.969 | |
| 0.800 | −23.286 | 12.659 | 0.623 | 737.877 | 10.683 | 1000.001 | 345.611 | 0.948 | |
| 0.809 | −15.537 | 6.756 | 0.531 | 243.848 | 9.712 | 9833.498 | 118.007 | 0.963 | |
| 0.893 | 26.509 | 4.229 | 0.929 | 773.393 | 9.838 | 1000.000 | 316.697 | 0.940 | |
| 0.845 | −26.167 | 3.287 | 0.923 | 572.154 | 10.983 | 2774.587 | 170.449 | 0.886 | |
| 0.807 | 23.189 | 15.997 | 0.567 | 1013.199 | 10.241 | 41868.236 | 446.126 | 0.880 | |
| 0.777 | 15.385 | 10.067 | 0.882 | 536.852 | 7.081 | 15116.729 | 90.863 | 0.956 | |
| CBP | 0.903 | −3.711 | 18.348 | 0.458 | 809.997 | 11.099 | 26841.671 | 130.173 | 0.907 |
| 0.820 | 58.062 | 4.630 | 0.936 | 358.139 | 10.351 | 1000.000 | 1.000 | 0.812 | |
| 0.954 | 3.432 | 11.370 | 0.883 | 2454.407 | 16.216 | 2653.374 | 495.543 | 0.945 | |
| 0.667 | 16.060 | 6.664 | 0.885 | 277.411 | 12.436 | 1000.001 | 263.032 | 0.910 | |
| 0.758 | −69.998 | 7.608 | 0.893 | 323.023 | 9.826 | 1000.001 | 93.631 | 0.883 | |
| 0.704 | −35.263 | 4.615 | 0.899 | 168.856 | 11.451 | 2236.527 | 188.608 | 0.914 | |
| 0.905 | −38.916 | 7.212 | 0.874 | 1710.722 | 9.077 | 5555.288 | 51.550 | 0.845 | |
| 0.876 | 1.499 | 9.086 | 0.866 | 611.878 | 15.839 | 111890.484 | 450.986 | 0.932 | |
| 0.712 | 3.076 | 5.202 | 0.886 | 194.872 | 16.467 | 136708.480 | 492.834 | 0.944 | |
| 0.789 | 7.726 | 7.921 | 0.877 | 107.484 | 13.897 | 1000.000 | 177.501 | 0.939 | |
| 0.704 | 10.916 | 5.527 | 0.853 | 246.438 | 12.684 | 1000.001 | 338.649 | 0.945 | |
| FBP | 0.831 | 0.728 | 9.704 | 0.886 | 122.431 | 11.348 | 4914.684 | 158.255 | 0.953 |
| 0.993 | −4.374 | 6.727 | 0.929 | 3880.317 | 8.104 | 1513.338 | 78.700 | 0.946 | |
| 0.712 | 26.175 | 14.210 | 0.562 | 142.815 | 11.271 | 16329.509 | 289.482 | 0.964 | |
| 0.927 | 3.301 | 7.670 | 0.787 | 276.556 | 14.337 | 1000.000 | 331.230 | 0.971 | |
| 0.839 | 25.183 | 9.468 | 0.881 | 100.000 | 10.561 | 1564.736 | 353.285 | 0.894 | |
| 0.765 | 35.862 | 15.781 | 0.725 | 208.373 | 8.578 | 1000.000 | 1.000 | 0.847 | |
| 0.652 | 21.423 | 5.939 | 0.895 | 100.000 | 10.181 | 1000.000 | 120.002 | 0.871 | |
| 0.836 | −18.565 | 21.245 | 0.920 | 143.623 | 9.841 | 3146.496 | 66.868 | 0.923 | |
| 0.733 | 34.137 | 1.955 | 0.938 | 171.228 | 13.082 | 1000.000 | 1.000 | 0.918 | |
| 0.720 | 7.400 | 9.314 | 0.880 | 100.000 | 10.522 | 8229.837 | 168.703 | 0.933 | |
| 0.811 | 8.999 | 12.312 | 0.735 | 325.387 | 13.130 | 7732.126 | 231.669 | 0.949 | |
Table 4.
Individual fiber distribution and constitutive model parameters for PP samples.
| Fiber distribution parameters | r2 | Material parameters | r2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Cf | μ | σ | C10 (kPa) | C01 | A (kPa) | B | |||
| PPK | 0.968 | −3.536 | 5.296 | 0.914 | 1952.486 | 19.643 | 1432.034 | 610.173 | 0.965 |
| 0.985 | −39.370 | 2.488 | 0.935 | 17397.377 | 66.327 | 5677.281 | 1.006 | 0.896 | |
| 0.963 | −28.711 | 6.183 | 0.793 | 2313.762 | 44.535 | 7486.456 | 525.213 | 0.919 | |
| 0.993 | −11.365 | 5.924 | 0.884 | 773.568 | 22.885 | 7169.870 | 533.619 | 0.966 | |
| 0.928 | −39.063 | 2.216 | 0.892 | 36100.822 | 26.113 | 1000.000 | 1.000 | 0.925 | |
| 0.910 | −0.620 | 1.866 | 0.944 | 2641.407 | 31.778 | 120873.160 | 475.617 | 0.978 | |
| 0.997 | 2.947 | 6.600 | 0.782 | 7656.069 | 45.008 | 65951.960 | 932.212 | 0.904 | |
| 0.923 | 26.141 | 6.084 | 0.811 | 191834.467 | 11.684 | 1000.002 | 104.404 | 0.933 | |
| 0.987 | −15.104 | 4.732 | 0.788 | 10452.462 | 35.406 | 138799.806 | 1283.854 | 0.988 | |
| 0.999 | −46.876 | 1.969 | 0.934 | 3450.169 | 24.041 | 1000.000 | 1.000 | 0.895 | |
| 0.987 | 39.670 | 3.776 | 0.955 | 425642.876 | 10.525 | 6638.560 | 286.366 | 0.889 | |
| 0.966 | 45.104 | 2.360 | 0.945 | 2776.134 | 16.456 | 1000.000 | 1.000 | 0.828 | |
| PPN | 0.999 | −44.456 | 6.088 | 0.853 | 196860.178 | 14.165 | 24891.035 | 18.445 | 0.867 |
| 0.944 | 7.170 | 13.327 | 0.688 | 491350.406 | 38.141 | 844209.576 | 650.117 | 0.917 | |
| 0.999 | −14.330 | 5.102 | 0.874 | 44241.073 | 32.117 | 145723.660 | 931.442 | 0.908 | |
| 0.999 | 4.427 | 8.012 | 0.841 | 13417.777 | 48.244 | 97183.440 | 839.156 | 0.966 | |
| 0.988 | −9.153 | 5.139 | 0.899 | 54593.702 | 35.206 | 15542.340 | 407.049 | 0.939 | |
| 0.984 | −18.197 | 2.916 | 0.912 | 4506.786 | 25.949 | 19670.100 | 1947.067 | 0.953 | |
| 0.997 | −52.142 | 2.607 | 0.923 | 16338.814 | 9.750 | 1000.004 | 89.368 | 0.935 | |
| 0.986 | −24.039 | 5.095 | 0.810 | 7012.061 | 16.341 | 12345.343 | 763.219 | 0.963 | |
| 0.997 | 35.153 | 2.760 | 0.842 | 2210.530 | 30.063 | 18078.301 | 1011.671 | 0.917 | |
| 0.994 | 42.855 | 1.993 | 0.759 | 5417.058 | 36.277 | 17376.536 | 2818.761 | 0.867 | |
| 0.975 | −8.219 | 3.783 | 0.822 | 3857.386 | 18.146 | 1000.001 | 295.408 | 0.810 | |
| 0.972 | 8.812 | 4.880 | 0.921 | 14838.057 | 35.792 | 1000.000 | 1.000 | 0.793 | |
Footnotes
CONFLICT OF INTEREST
Dr. Wei Sun is a co-founder and serves as the Chief Scientific Advisor of Dura Biotech. He has received compensation and owns equity in the company.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
8. REFERENCES
- 1.Pibarot P and Dumesnil JG, Prosthetic heart valves: selection of the optimal prosthesis and long-term management. Circulation, 2009. 119(7): p. 1034–1048. [DOI] [PubMed] [Google Scholar]
- 2.Thubrikar MJ, Aouad J, and Nolan SP, Patterns of calcific deposits in operatively excised stenotic or purely regurgitant aortic valves and their relation to mechanical stress. The American journal of cardiology, 1986. 58(3): p. 304–308. [DOI] [PubMed] [Google Scholar]
- 3.Leopold JA, Cellular mechanisms of aortic valve calcification. Circulation: Cardiovascular Interventions, 2012. 5(4): p. 605–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bäck M, et al. , Biomechanical factors in the biology of aortic wall and aortic valve diseases. Cardiovascular research, 2013. 99(2): p. 232–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Caballero A, et al. , Evaluation of transcatheter heart valve biomaterials: biomechanical characterization of bovine and porcine pericardium. Journal of the mechanical behavior of biomedical materials, 2017. 75: p. 486–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Patrick PH, TAVR and SAVR: current treatment of aortic stenosis. Clinical Medicine Insights: Cardiology, 2012. 6: p. CMC. S7540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Burrage M, et al. , Transcatheter aortic valve replacement is associated with comparable clinical outcomes to open aortic valve surgery but with a reduced length of in-patient hospital stay: A systematic review and meta-analysis of randomised trials. Heart, Lung and Circulation, 2017. 26(3): p. 285–295. [DOI] [PubMed] [Google Scholar]
- 8.Grover FL, et al. , 2016 annual report of the Society of Thoracic Surgeons/American College of Cardiology transcatheter valve therapy registry. Journal of the American College of Cardiology, 2017. 69(10): p. 1215–1230. [DOI] [PubMed] [Google Scholar]
- 9.Cribier AG, The odyssey of TAVRfrom concept to clinical reality. Texas Heart Institute journal, 2014. 41(2): p. 125–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dvir D, et al. , First look at long-term durability of transcatheter heart valves: assessment of valve function up to 10 years after implantation. Eur J Cardiothorac Surg, 2016. [Google Scholar]
- 11.Foroutan F, et al. , Prognosis after surgical replacement with a bioprosthetic aortic valve in patients with severe symptomatic aortic stenosis: systematic review of observational studies. Bmj, 2016. 354: p. i5065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Glaser N, et al. , Aortic valve replacement with mechanical vs. biological prostheses in patients aged 50–69 years. European heart journal, 2015. 37(34): p. 2658–2667. [DOI] [PubMed] [Google Scholar]
- 13.De Hart J, et al. , Collagen fibers reduce stresses and stabilize motion of aortic valve leaflets during systole. Journal of biomechanics, 2004. 37(3): p. 303–311. [DOI] [PubMed] [Google Scholar]
- 14.Sauren A, et al. , Aortic valve histology and its relation with mechanics—preliminary report. Journal of biomechanics, 1980. 13(2): p. 97–104. [DOI] [PubMed] [Google Scholar]
- 15.Billiar KL and Sacks MS, Biaxial mechanical properties of the natural and glutaraldehyde treated aortic valve cusp—part I: experimental results. Journal of biomechanical engineering, 2000. 122(1): p. 23–30. [DOI] [PubMed] [Google Scholar]
- 16.Mega M, et al. , Imaging analysis of collagen fiber networks in cusps of porcine aortic valves: effect of their local distribution and alignment on valve functionality. Computer methods in biomechanics and biomedical engineering, 2016. 19(9): p. 1002–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fan R and Sacks MS, Simulation of planar soft tissues using a structural constitutive model: finite element implementation and validation. Journal of biomechanics, 2014. 47(9): p. 2043–2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee C-H, et al. , On the effects of leaflet microstructure and constitutive model on the closing behavior of the mitral valve. Biomechanics and modeling in mechanobiology, 2015. 14(6): p. 1281–1302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sacks MS, Zhang W, and Wognum S, A novel fibre-ensemble level constitutive model for exogenous cross-linked collagenous tissues. Interface focus, 2016. 6(1): p. 20150090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang W, et al. , A meso-scale layer-specific structural constitutive model of the mitral heart valve leaflets. Acta biomaterialia, 2016. 32: p. 238–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sacks MS and Sun W, Multiaxial mechanical behavior of biological materials. Annual review of biomedical engineering, 2003. 5(1): p. 251–284. [DOI] [PubMed] [Google Scholar]
- 22.Lee C, et al. , Effects of glutaraldehyde concentration and fixation time on material characteristics and calcification of bovine pericardium: implications for the optimal method of fixation of autologous pericardium used for cardiovascular surgery. Interactive cardiovascular and thoracic surgery, 2016. 24(3): p. 402–406. [DOI] [PubMed] [Google Scholar]
- 23.Wan W, Dixon JB, and Gleason RL Jr, Constitutive modeling of mouse carotid arteries using experimentally measured microstructural parameters. Biophysical journal, 2012. 102(12): p. 2916–2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rezakhaniha R, et al. , Experimental investigation of collagen waviness and orientation in the arterial adventitia using confocal laser scanning microscopy. Biomechanics and modeling in mechanobiology, 2012. 11(3–4): p. 461–473. [DOI] [PubMed] [Google Scholar]
- 25.Schneider CA, Rasband WS, and Eliceiri KW, NIH Image to ImageJ: 25 years of image analysis. Nature methods, 2012. 9(7): p. 671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jahne B, Spatio-temporal image processing: Theory and scientific applications. 1993: Springer-Verlag New York, Inc. [Google Scholar]
- 27.Sun W, Chaikof EL, and Levenston ME. Development and finite element implementation of a nearly incompressible structural constitutive model for artery substitute design. in ASME 2008 Summer Bioengineering Conference 2008. American Society of Mechanical Engineers. [Google Scholar]
- 28.Liu H and Sun W, Numerical Approximation of Elasticity Tensor Associated With Green-Naghdi Rate. Journal of biomechanical engineering, 2017. 139(8): p. 081007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wang Q, Sirois E, and Sun W, Patient-specific modeling of biomechanical interaction in transcatheter aortic valve deployment. Journal of biomechanics, 2012. 45(11): p. 1965–1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sun W and Sacks MS, Finite element implementation of a generalized Fung-elastic constitutive model for planar soft tissues. Biomechanics and modeling in mechanobiology, 2005. 4(2-3): p. 190–199. [DOI] [PubMed] [Google Scholar]
- 31.Li K and Sun W, Simulated thin pericardial bioprosthetic valve leaflet deformation under static pressure-only loading conditions: implications for percutaneous valves. Annals of biomedical engineering, 2010. 38(8): p. 2690–2701. [DOI] [PubMed] [Google Scholar]
- 32.Sun W, Li K, and Sirois E, Simulated elliptical bioprosthetic valve deformation: implications for asymmetric transcatheter valve deployment. Journal of biomechanics, 2010. 43(16): p. 3085–3090. [DOI] [PubMed] [Google Scholar]
- 33.Li K and Sun W, Simulated transcatheter aortic valve deformation: A parametric study on the impact of leaflet geometry on valve peak stress. International journal for numerical methods in biomedical engineering, 2017. 33(3): p. e02814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gunning PS, Vaughan TJ, and McNamara LM, Simulation of self expanding transcatheter aortic valve in a realistic aortic root: implications of deployment geometry on leaflet deformation. Annals of biomedical engineering, 2014. 42(9): p. 1989–2001. [DOI] [PubMed] [Google Scholar]
- 35.Mizoguchi T, et al. , TCT-741 Leaflet Stresses of Sapien 3 Transcatheter Aortic Valve: Implications for Durability. Journal of the American College of Cardiology, 2016. 68(18 Supplement): p. B299–B300. [Google Scholar]
- 36.Merryman WD, et al. , The effects of cellular contraction on aortic valve leaflet flexural stiffness. Journal of biomechanics, 2006. 39(1): p. 88–96. [DOI] [PubMed] [Google Scholar]
- 37.Paniagua D, et al. , Percutaneously implantable replacement heart valve device and method of making same. 2003, Google Patents. [Google Scholar]
- 38.Tian B and Davidson J, Biological tissue for surgical implantation. 2008, Google Patents. [Google Scholar]