Abstract
Walking is characterized by repetitive limb movements associated with highly structured patterns of muscle activity. The causal relationships between the muscle activities and hindlimb segments of walking are difficult to decipher. This study investigated these particular relationships and clarified whether they are correlated with speed to further understand the neuromuscular control pattern. Four adult female rhesus monkeys (Macaca mulatta) were selected to record gait parameters while walking on a bipedal treadmill at speeds of 0.2, 0.8, 1.4, and 2.0 km/h. We recorded 3 ipsilateral hindlimb muscles by surface recording. In this study, we calculated the correlations between electromyography (EMG) and kinematic parameters (24 EMG*17 kinematic parameters). Of the 408 calculated coefficients, 71.6% showed significant linear correlations. Significant linear correlations were found between muscle activity, such as burst amplitudes and the integral of muscle activity, and the corresponding kinematic parameters of each joint. Most of these relationships were speed independent (91.7% of all variables). Through correlation analysis, this study demonstrated a causal association between kinematic and EMG patterns of rhesus monkey locomotion. Individuals have particular musculoskeletal control patterns, and most of the relationships between hindlimb segments and muscles are speed independent. The current findings may enhance our understanding of neuromusculoskeletal control strategies.
Keywords: electromyography, locomotion, neuromuscular control, primate
Introduction
Walking in humans and animals is considered one of the most practiced motor skills and is characterized by repetitive limb movements associated with highly structured patterns of muscle activity [7]. Motor function is the result of muscle contractions that generate interaction forces throughout the skeletal system and the neuronal circuits that control these muscles [23, 38]. In locomotion studies, kinematic, kinetic, and electromyography (EMG) analyses are fundamental for characterizing gait patterns and have provided important information on the neuromusculoskeletal system [18, 43] in mice [21], cats [26], nonhuman primates [30, 31, 46, 47], and humans [2, 11].
Previous studies have examined kinematic and EMG parameters under different conditions to gain insight into the neural organization of locomotion. Numerous studies have shown changes in kinematic and EMG parameters with speed [20, 35]. In studies of human walking, as speed increased, the cycle duration was reduced, which is primarily accomplished by a reduction in the stance duration [19]. The percentage of center of pressure progression decreases in mid-stance and increases in the terminal and pre-swing stances [3], and the average EMG profiles vary predictably [15]. Similar findings have been found in animal studies. Frigon et al. [13] found that phase variations are modulated by speed, which appears to influence the consistency of interlimb coordination during quadrupedal locomotion in healthy adult cats. In studying quadrupedal locomotion of rhesus monkeys, the recruitment patterns of distal muscles in the hindlimb undergo adaptive changes with different speeds [1]. Several studies have investigated motor patterns upon changing external conditions. For instance, Courtine et al. [4, 5] compared straight with curved human walking trajectories to gain insight into the mechanisms underlying the control of asymmetric movements. Luu et al. [25] found that visual feedback can act as a dominant form of feedback in gait modulation by visual distortion during locomotion. All of these investigations considered gait modulation under particular conditions. However, few studies have investigated the relationships between measured output variables, such as the kinematic and kinetic features, and input variables, such as EMG activity. Furthermore, most studies used implanted electrodes for EMG recording [5, 7, 13], which can increase the risk of infection. These relationships are difficult to determine for the following reasons: first, one muscle may affect the kinematics of all segments due to the coordination among body segments, and second, one joint can be controlled by multiple muscles due to coupling between muscles [43].
In this study, we used surface electrodes for EMG recording, described the kinematic and EMG characteristics of gait over a range of treadmill speeds in bipedal stepping monkeys, and analyzed the correlation between EMG and kinematic parameters. The aims of this study were 1) to apply a noninvasive method for investigation of causal associations between hindlimb segments and muscles and 2) to clarify whether they are correlated with speed. We hypothesized that individuals have fixed motor control strategies that remain constant at different speeds. The results explain the relationships between most EMG and kinematic parameters and reveal that most of the parameters have no linear correlation with speed. These findings may be critical for gaining further insight into the mechanisms of neuromusculoskeletal control in primates, including humans, and may contribute to the development of rehabilitation treatments to enhance recovery following neurological diseases.
Materials and Methods
Preparation
Four adult female rhesus monkeys (Macaca mulatta) (age, 5.5 ± 0.4 years; weight, 5.45 ± 0.36 kg) were housed individually in single stainless-steel cages (72 × 61 × 87 cm) at 22–25°C. All procedures that were performed involving animals were conducted in accordance with the ethical standards of the Animal Ethics Committee of Capital Medical University. The monkeys underwent treadmill training with a previously reported training and fixing method one week before data recording [36]. The treadmill speeds were 0.2, 0.8, 1.4, and 2.0 km/h.
Data collection
Kinematics: The kinematics of hindlimb stepping was captured by a six-camera VICON motion system (VICON Motion System Ltd., Oxford, UK ; sampling at 100 Hz). A total of 16 reflective markers (14 mm in diameter) were attached bilaterally to the shaved skin at the anterior superior iliac spine, the posterior superior iliac spine, the distal two thirds of the femur, the knee, the ankle, the heel, and the second metatarsophalangeal (MTP) joint. Using a standard protocol, the locomotion of four monkeys was assessed during steady-state locomotion (at least 10 contiguous steps) at treadmill speeds ranging from 0.2 to 2.3 km/h. Data acquisition has been previously detailed [36].
EMG: Muscle activity was recorded bilaterally for the hindlimb quadriceps muscle group (rectus femoris, RF), the triceps surae (medial gastrocnemius, MG), and the tibialis anterior (TA). Before each locomotor session, the skin was shaved and cleaned with alcohol. Two surface electrodes were placed parallel to the longitudinal axis of the muscle at approximately mid-distance from the two tendinous insertions. EMG signals were amplified by a gain factor of 500 (Myosystem 1400A, Noraxon USA , Inc., Scottsdale, AZ, USA) and collected at a sampling rate of 1,000 Hz.
Data processing
Kinematics: One gait cycle was defined as the time interval between two successive toe-off movements of the right limb. We calculated the cycle duration, the stance duration (paw-contact time), the swing duration (paw in the air), and the duty factor (stance duration/cycle duration) of each gait cycle. The joint angles of the hip, knee, and ankle were calculated based on the coordinate position of each marker. The methods used to calculate gait parameters were previously described [37].
EMG: Raw EMG data were processed with MATLAB (MathWorks, Natick, MA, USA), numerically bandpass filtered (30 to 500 Hz), and full-wave rectified.
The TA cycle duration was defined as the time between the onset points of successive bursts of EMG activity in the TA muscle. The onset of an EMG burst was calculated as the time when the EMG activity remained above the threshold (the mean activity plus 1.5 standard deviations (SD) recorded during a period of 500 ms) when the muscle was least active [7]. We applied a moving average (40-ms width) to the EMG signal to reduce the effects of signal oscillation [7]. The burst duration and the duty factor of each muscle were also calculated. The EMG burst duration was defined as the mean time between the onset and end of several single bursts. We calculated the mean EMG amplitude as the integral of the amplitudes of the rectified EMG envelope divided by the burst duration [33]. The EMG amplitude of each burst was normalized to the mean burst amplitude of the same muscle when walking at 0.2 km/s.
Considering the sharp burst of TA muscle discharge and the time point of TA onset (the TA burst at the end of stance or the beginning of swing), we took the right TA as a reference to measure the onset of bursts in different muscles. We evaluated EMG coupling between the consecutive onsets of muscles, measured as the time between the onsets of activity in successive muscles. The phase relation between two muscles was defined as the time between the consecutive onsets of muscles divided by the TA cycle duration [7].
The percentage of total muscle activity when muscle groups were simultaneously activated was defined as the muscle coactivation index (MCI), which was calculated as follows:MCI = 2 × (EMGmuscleA & EMGmuscleB) / (EMGmuscleA + EMGmuscleB) × 100%,where EMGmuscleA and EMGmuscleB represent the normalized envelopes of muscle EMG. The common EMGmuscleA&EMGmuscleB is the area under the curves that is shared by muscle A and muscle B during an average stride [24]. The MCI reflects the overall coactivation level of the two muscles [41].
Statistical analysis
A total of 320 steps were statistically analyzed in this study (20 gait cycles×4 speeds×4 monkeys). Pearson correlation analysis was performed between gait and EMG parameters. Spearman correlation analysis was performed between speed and all the correlation coefficients between the gait and the EMG parameters. The statistical analysis was conducted with IBM SPSS Statistics version 19.0 (SPSS Inc., IBM Corp., Armonk, NY, USA), and all quantitative data were expressed as means ± SD. P<0.05 was considered statistically significant.
Results
Walking pattern and the effect of speed
Figure 1 shows the graded adjustment of the hindlimb with increasing speed during rhesus bipedal walking. The stick diagrams (Fig. 1A) show the successive hindlimb positions during the swing phases reconstructed from a representative step cycle at each speed. The range of angles increased as the speed was increased for all three hindlimb joints (Fig. 1B). The joint angles exhibited later maximal joint extension, and minimal flexion paralleled the decrease in the duty factor (Fig. 1B). The average EMG activity recorded from the hindlimb muscles is plotted versus the normalized gait cycle duration at each treadmill speed in Fig. 1C. The pattern of hindlimb muscle activity typically showed alternate activation of extensor and flexor muscles during the stance and swing phases of gait.
Fig. 1.
Locomotor patterns of a representative monkey at different treadmill speeds. (A) Typical stick diagrams of the successive hindlimb positions of a monkey during the swing phase for treadmill speeds ranging from 0.2 to 2.0 km/h. (B, C) Time course of hindlimb joint angles (B) and the integrated EMG activity of the selected hindlimb muscles (C) depicting changes during the gait cycle. The mean waveforms recorded during each complete gait cycle (n=20) at each treadmill speed. deg, degree; a.u., arbitrary units; MG, medial gastrocnemius; TA, tibialis anterior; RF, rectus femoris.
Correlation between locomotion kinematics and muscle activity
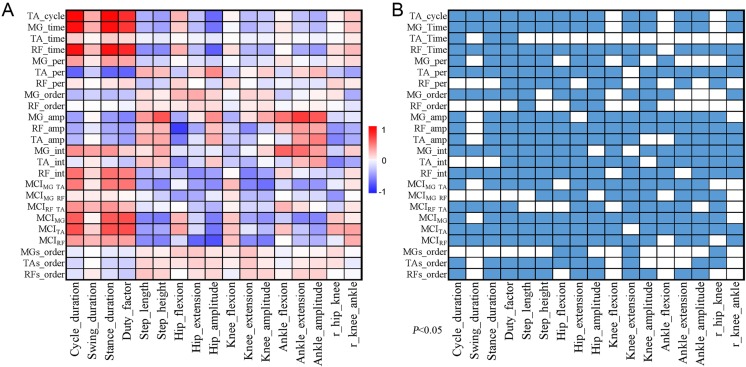
Figure 2 displays the relationship between the representative kinematic and EMG parameters of the hindlimb. The correlation coefficients and P values are listed in Supplementary Table S1 and Supplementary Table S2, respectively (available online). A total of 408 correlation coefficients were calculated in this study (17 kinematic parameters × 24 EMG parameters). Three-fourths of these variables (292/408) showed a significant linear correlation, which revealed close relationships between EMG activity and kinematic parameters (Fig. 2). A significant linear correlation was found between muscle activity, such as burst amplitudes and the integral of muscle activity, and the corresponding kinematic parameters of each joint, such as the amplitude of the joint and the maximum (extension) and minimum (flexion) of the joint. The burst duration of the MG and RF muscles showed significant correlations with stance duration (MG_time vs Stance duration, r=0.940, P=0.000; RF_time vs Stance duration, r=0.931, P=0.000). The burst amplitude and integral of the RF muscle showed linear correlations with the kinematic parameters of the hip and the knee (i.e., RF_amp vs Hip_flexion, r=−0.758, P=0.000; RF_int vs Knee_amplitude, r=−0.367, P=0.000). For the extensor and flexor muscles of the ankle (the MG and TA), the correlation with the kinematic parameters was significant (i.e., MG_amp vs Ankle_extension, r=0.773, P=0.000; TA_int vs r_hip-knee, r=−0.499, P=0.000). For the unilateral hindlimb muscles, Fig. 2 also shows the linear correlations between the MIC and the kinematic parameters of all three hindlimb joints (i.e., MICMG-RF vs Hip_flexion, r=−0.381, P=0.000; MICMG-TA vs Knee_amplitude, r=−0.558, P=0.000). For the homologous hindlimb muscles, the MIC showed linear correlations with stance duration (MICMG vs Stance_duration, r=0.665, P=0.000; MICTA, Stance_duration, r=0.690, P=0.000).
Fig. 2.
Correlation between gait and EMG parameters. (A) Correlation matrix showing robust correlations between kinematic and EMG parameters. Color-coded representation of the r values of the correlation between kinematic parameters and EMG parameters. (B) Matrix of the P values of the linear correlations between the kinematic and EMG parameters (P<0.05, color squares). TA, tibialis anterior; MG, medial gastrocnemius; RF, rectus femoris; MCI, muscle coactivation index.
A few EMG parameters had no significant linear correlation with the kinematic parameters of gait. For example, the burst duration of the TA muscle had no relationship with almost all kinematic parameters (i.e., TA_time vs Step_length, r=−0.057, P=0.312). A similar finding was observed for the burst order of the MG and the RF, which had weak or no correlation with the kinematic parameters (i.e., MG_order vs Step_height, r=0.082, P=0.142; RF_order vs Ankle_extension, r=0.037, P=0.511). The coupling between homologous hindlimb muscles also showed a weak correlation with the kinematic parameters (i.e., MGs_order vs Step_height, r=0.082, P=0.142).
The effect of speed on the relationships between EMG and kinematic parameters
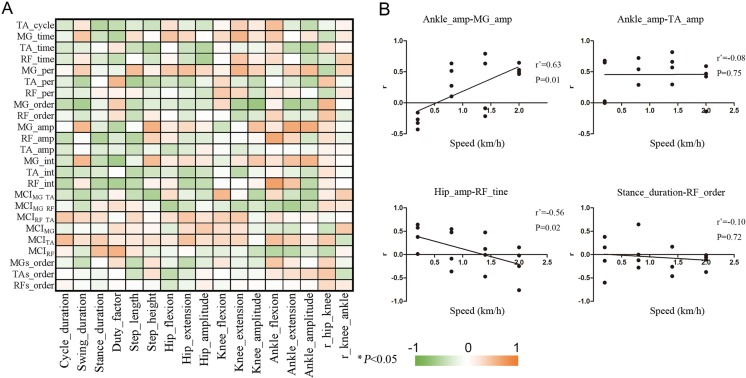
We investigated the relationships between the EMG and kinematic variables across a wide range of speeds. Figure 3A shows that almost all of the relationships had no linear correlation with speed (91.7% of all variables), which revealed the speed-independent relationship between muscle activity and hindlimb segments. The correlation coefficients and P values are listed in Supplementary Table S3 and Supplementary Table S4, respectively (available online). We selected representative relationships between these EMG and kinematic parameters. For example, rAnk_amp-TA_amp (correlation coefficients of the relationship between the amplitude of the ankle and the burst amplitude of the TA muscle) and rStance_duration-RF_order had constant relationships across different speeds (Fig. 3B). However, some of these musculoskeletal relationships still exhibited a speed-dependent control pattern (8.3% of all variables) (Fig. 3A). As speed increased, rAnk_amp-MG_amp and rHip_amp-RF_amp significantly increased and decreased, respectively (Fig. 3B).
Fig. 3.
Correlation between the speed and the r values of the correlation between kinematic and EMG parameters at each speed. (A) Matrix of the linear correlations between the speed and the r values of the correlation between kinematic and EMG parameters at each speed. The bar represents the correlation coefficients of the correlation between speeds and the r values of the correlation between kinematic parameters and EMG parameters. *P<0.05. (B) Linear regression plots demonstrating the correlation between speeds and the correlation coefficients between the kinematic parameters and EMG parameters. Dots represent individual values (n=4 monkeys). Abbreviations are the same as Fig. 2.
Discussion
In the present study, we analyzed gait parameters and associated patterns of hindlimb muscle activity during bipedal treadmill locomotion over a range of speeds in rhesus monkeys and revealed common kinematic and EMG envelope features across strides. We performed a correlation analysis of kinematic and EMG parameters to show the particular relationships between muscles and hindlimb segments. Most of these relationships had no linear correlation with speed, revealing the speed-independent control pattern of gait and specific features of neuromuscular activity control strategies.
Kinematic parameters and muscle activity change at different speeds
Various previous studies have considered the effect of speed on gait patterns, especially in humans [1]. Our results showed that almost every aspect of gait appears to be sensitive to walking speed (spatiotemporal parameters, kinematics, and EMG). Similar observations have been reported in other studies [13, 35]. As speed increases, shorter relative stance durations cause fewer stance-related sensory inputs of limb loading and stretching, which shrinks the burst duration of extensor muscles (the MG and RF) [9]. In addition, the swing phase occupies a greater proportion of the cycle, and swing-related sensory feedback has more time to influence the gait phase, which leads to the later maximal joint extension (Fig. 1B) [12].
Relationship between hindlimb segments and muscles
The central pattern generator (CPG) is usually used to indicate a functional network responsible for generating a rhythm and generates the shape of the pattern of motor bursts of motoneurons for walking, which is a rhythmic movement [6]. The neural network directly controls the muscle activities of hindlimbs to give rise to locomotion. In the current study, we selected representative hindlimb muscles and kinematic parameters related to the hip, knee, and ankle for inclusion in the correlation analysis to show the close relationships between muscle activities and kinematics of the limb (Fig. 2). The linear correlation between one muscle and the kinematics of several joints showed that the muscles and the joints do not have a one-to-one correspondence. During walking, individual muscles not only affect the attached joint but also the functions of other muscles. Indeed, each muscle and joint torque can have an influence on the angle and acceleration of other limb segments that the muscle does not directly act on. Due to the dynamic coupling of limb segments, these influences are essential for the interconnected musculoskeletal system [34].
However, many EMG parameters had no significant linear correlation with the kinematic parameters of gait. For example, the coupling between homologous hindlimb muscles showed a weak correlation with the kinematic parameters. Plotnik et al. [28] found that gait asymmetry was preserved at different speeds, suggesting that left-right antiphase stepping was constant in normal walking. The noncorrelation between several variables may be due to the mechanisms of the planar law and the planar constraint of intersegmental coordination, which reduces the number of effective degrees of freedom requiring control during bipedal walking [10, 27]. Limb movements are remarkably simple in contrast to the patterns of muscle activity, which depend not only on muscle activities but also on gravity and dynamic interaction torques [17]. These factors may influence the musculoskeletal pattern and lead to the noncorrelation between muscle activities and kinematics. A previous study found that while the activation patterns of individual muscles can vary dramatically at various speeds, limb kinematics displayed only limited changes [17].
Speed-independent neuromuscular control pattern
During bipedal walking, each hindlimb contains over 50 muscles that are coordinated. Each muscle has a constant activity pattern in the gait cycle [39]. In practical situations, many muscles share similar activity patterns [42]. Ivanenko et al. [18] identified five basic underlying component waveforms, which account for approximately 90% of the total variance across different muscles during normal walking. The nervous system simplifies muscle control through modularity, using neural patterns to activate muscles [42]. These basic patterns were conserved across subjects with different anthropometrical characteristics (i.e., weight, height, and mass) and locomotion under different speeds, directions of movement, and gravitational loads [14, 21, 45]. Our study found that the correlation coefficients between kinematic and EMG parameters were basically independent of speed (approximately 91.7% of all variables) (Fig. 3A), possibly because the kinematics vary by approximately the same magnitude as the EMG pattern varies with speed. This result implies a constant musculoskeletal relationship across a wide range of speeds, which is consistent with the previous studies mentioned above. Thus, we suggest that a basic musculoskeletal pattern can simplify locomotor control such that the central nervous system (CNS) can regulate movements with fewer changes in the neural strategy for adjusting speed.
Speed-dependent neuromuscular control pattern
However, a small number of these musculoskeletal relationships still exhibit speed-dependent control patterns (only 8.3% of all variables) (Fig. 3A), which may result from walking mechanics at different speeds. When walking slowly, the center of mass remains within the polygon of support formed by the legs on the ground, which is called static stability. As speed increases, the summation of ground reaction force, momentum, and inertia ensure mechanical stability [21]. Energy conversion depends more on the elastic storage in muscles and tendons for progression, which may be one reason behind the changing musculoskeletal relationships with speed. For instance, as speed increased, the correlation coefficients of the relationship between the burst integral of the MG and the amplitude of the ankle increased. In the terminal stance, the fast extensor muscles (the MG) were more heavily recruited at faster speeds to slow the fall of the center of mass in the late stance [16, 32, 33]. This increased correlation may contribute to effective speed regulation.
Potential application
Gait analysis is widely used in clinical research, such as neuromuscular assessments and functional assessments for rehabilitation treatment [29, 40]. Abnormal gait is defined through a comparison of gait patterns and muscle activity between healthy individuals and patients with orthopedic or neurologic pathologies [8, 22]. Clarifying the relationship between EMG activity and kinematic parameters could promote our understanding of musculoskeletal mechanics and the causal relationships between neuromusculoskeletal pathology and abnormal gait in neurological diseases, which have implications in surgical and rehabilitation therapies [44]. In addition, for patients in whom all the data cannot be measured, we can also predict changes in unmeasurable data from all available measured data to provide better treatments.
Limitations
The limitations of this study are as follows. First, due to the use of surface EMG recordings, we could only obtain activity from several superficial muscles. Relating all the details of the kinematics to muscle activity patterns in a rigorous fashion was not possible. Second, to simplify the causal associations between hindlimb segments and muscles, we only performed a linear correlation analysis of kinematic and EMG parameters across a wide range of speeds. Nonlinear patterns were not investigated in this study. Therefore, implanted electrodes for EMG recording will be adopted in the future to analyze nonlinear patterns and to further evaluate the underlying mechanics of motor control.
Conclusion
In conclusion, this study demonstrated a causal associations between kinematic and EMG patterns of rhesus locomotion. Individuals have particular musculoskeletal control patterns, and most of relationships between hindlimb segments and muscles are speed independent. The current findings enhance our understanding of neuromusculoskeletal control strategies and may contribute to improving outcome evaluations and providing advanced treatments for recovery following neurologic disease.
Conflict of Interests
The authors declare that they have no conflicts of interest.
Supplementary Material
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant 31730030), and Ministry of Science and Technology of China (Grants 2017YFC1104001, 2017YFC1104002), and Beijing Science and Technology Program (Grant Z181100001818007), and National Natural Science Foundation of China (Grants 31650001, 31670988, 31320103903), and Beijing Natural Science Foundation Program (Grants KZ201810025030, 7194286), and National Natural Science Foundation of China (Grant 31771053), and China Postdoctoral Science Foundation funded project (Grant 2018M640046), and Fundamental Research Funds for the Central Universities (Grant YWF-19-BJ-J-282).
References
- 1.Andriacchi T.P., Ogle J.A., Galante J.O.1977. Walking speed as a basis for normal and abnormal gait measurements. J. Biomech. 10: 261–268. doi: 10.1016/0021-9290(77)90049-5 [DOI] [PubMed] [Google Scholar]
- 2.Bruijn S.M., van Dien J.H., Meijer O.G., Beek P.J.2009. Is slow walking more stable? J. Biomech. 42: 1506–1512. [Google Scholar]
- 3.Chiu M.C., Wu H.C., Chang L.Y.2013. Gait speed and gender effects on center of pressure progression during normal walking. Gait Posture 37: 43–48. doi: 10.1016/j.gaitpost.2012.05.030 [DOI] [PubMed] [Google Scholar]
- 4.Courtine G., Gerasimenko Y., van den Brand R., Yew A., Musienko P., Zhong H., Song B., Ao Y., Ichiyama R.M., Lavrov I., Roy R.R., Sofroniew M.V., Edgerton V.R.2009. Transformation of nonfunctional spinal circuits into functional states after the loss of brain input. Nat. Neurosci. 12: 1333–1342. doi: 10.1038/nn.2401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Courtine G., Roy R.R., Hodgson J., McKay H., Raven J., Zhong H., Yang H., Tuszynski M.H., Edgerton V.R.2005. Kinematic and EMG determinants in quadrupedal locomotion of a non-human primate (Rhesus). J. Neurophysiol. 93: 3127–3145. doi: 10.1152/jn.01073.2004 [DOI] [PubMed] [Google Scholar]
- 6.Courtine G., Schieppati M.2003. Human walking along a curved path. I. Body trajectory, segment orientation and the effect of vision. Eur. J. Neurosci. 18: 177–190. doi: 10.1046/j.1460-9568.2003.02736.x [DOI] [PubMed] [Google Scholar]
- 7.Courtine G., Schieppati M.2003. Human walking along a curved path. II. Gait features and EMG patterns. Eur. J. Neurosci. 18: 191–205. doi: 10.1046/j.1460-9568.2003.02737.x [DOI] [PubMed] [Google Scholar]
- 8.Deluzio K.J., Wyss U.P., Zee B., Costigan P.A., Sorbie C.1997. Principal component models of knee kinematics and kinetics Normal vs pathological gait patterns. Hum. Mov. Sci. 16: 201–217. doi: 10.1016/S0167-9457(96)00051-6 [DOI] [Google Scholar]
- 9.Duysens J., Clarac F., Cruse H.2000. Load-regulating mechanisms in gait and posture: comparative aspects. Physiol. Rev. 80: 83–133. doi: 10.1152/physrev.2000.80.1.83 [DOI] [PubMed] [Google Scholar]
- 10.Duysens J., Van de Crommert H.W.1998. Neural control of locomotion; The central pattern generator from cats to humans. Gait Posture 7: 131–141. doi: 10.1016/S0966-6362(97)00042-8 [DOI] [PubMed] [Google Scholar]
- 11.England S.A., Granata K.P.2007. The influence of gait speed on local dynamic stability of walking. Gait Posture 25: 172–178. doi: 10.1016/j.gaitpost.2006.03.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Frigon A., D’Angelo G., Thibaudier Y., Hurteau M.F., Telonio A., Kuczynski V., Dambreville C.2014. Speed-dependent modulation of phase variations on a step-by-step basis and its impact on the consistency of interlimb coordination during quadrupedal locomotion in intact adult cats. J. Neurophysiol. 111: 1885–1902. doi: 10.1152/jn.00524.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Frigon A., Gossard J.P.2010. Evidence for specialized rhythm-generating mechanisms in the adult mammalian spinal cord. J. Neurosci. 30: 7061–7071. doi: 10.1523/JNEUROSCI.0450-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gravano S., Ivanenko Y.P., Maccioni G., Macellari V., Poppele R.E., Lacquaniti F.2011. A novel approach to mechanical foot stimulation during human locomotion under body weight support. Hum. Mov. Sci. 30: 352–367. doi: 10.1016/j.humov.2010.01.002 [DOI] [PubMed] [Google Scholar]
- 15.Hof A.L., Elzinga H., Grimmius W., Halbertsma J.P.K.2002. Speed dependence of averaged EMG profiles in walking. Gait Posture 16: 78–86. doi: 10.1016/S0966-6362(01)00206-5 [DOI] [PubMed] [Google Scholar]
- 16.Honeine J.L., Schieppati M., Gagey O., Do M.C.2014. By counteracting gravity, triceps surae sets both kinematics and kinetics of gait. Physiol. Rep. 2: e00229. doi: 10.1002/phy2.229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ivanenko Y.P., Grasso R., Macellari V., Lacquaniti F.2002. Control of foot trajectory in human locomotion: role of ground contact forces in simulated reduced gravity. J. Neurophysiol. 87: 3070–3089. doi: 10.1152/jn.2002.87.6.3070 [DOI] [PubMed] [Google Scholar]
- 18.Ivanenko Y.P., Poppele R.E., Lacquaniti F.2004. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 556: 267–282. doi: 10.1113/jphysiol.2003.057174 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jordan K., Challis J.H., Newell K.M.2007. Walking speed influences on gait cycle variability. Gait Posture 26: 128–134. doi: 10.1016/j.gaitpost.2006.08.010 [DOI] [PubMed] [Google Scholar]
- 20.Kirtley C., Whittle M.W., Jefferson R.J.1985. Influence of walking speed on gait parameters. J. Biomed. Eng. 7: 282–288. doi: 10.1016/0141-5425(85)90055-X [DOI] [PubMed] [Google Scholar]
- 21.Lacquaniti F., Grasso R., Zago M.1999. Motor patterns in walking. News Physiol. Sci. 14: 168–174. [DOI] [PubMed] [Google Scholar]
- 22.Lehmann J.F., de Lateur B.J., Price R.1992. Biomechanics of abnormal gait. Phys. Med. Rehabil. Clin. N. Am. 3: 125–138. doi: 10.1016/S1047-9651(18)30668-5 [DOI] [Google Scholar]
- 23.Lemieux M., Josset N., Roussel M., Couraud S., Bretzner F.2016. Speed-dependent modulation of the locomotor behavior in adult mice reveals attractor and transitional gaits. Front. Neurosci. 10: 42. doi: 10.3389/fnins.2016.00042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lo J., Lo O.Y., Olson E.A., Habtemariam D., Iloputaife I., Gagnon M.M., Manor B., Lipsitz L.A.2017. Functional implications of muscle co-contraction during gait in advanced age. Gait Posture 53: 110–114. doi: 10.1016/j.gaitpost.2017.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Luu T.P., He Y., Brown S., Nakagame S., Contreras-Vidal J.L.2016. Gait adaptation to visual kinematic perturbations using a real-time closed-loop brain-computer interface to a virtual reality avatar. J. Neural Eng. 13: 036006. doi: 10.1088/1741-2560/13/3/036006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Martinez M., Delivet-Mongrain H., Leblond H., Rossignol S.2011. Recovery of hindlimb locomotion after incomplete spinal cord injury in the cat involves spontaneous compensatory changes within the spinal locomotor circuitry. J. Neurophysiol. 106: 1969–1984. doi: 10.1152/jn.00368.2011 [DOI] [PubMed] [Google Scholar]
- 27.Ogihara N., Kikuchi T., Ishiguro Y., Makishima H., Nakatsukasa M.2012. Planar covariation of limb elevation angles during bipedal walking in the Japanese macaque. J. R. Soc. Interface 9: 2181–2190. doi: 10.1098/rsif.2012.0026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Plotnik M., Bartsch R.P., Zeev A., Giladi N., Hausdorff J.M.2013. Effects of walking speed on asymmetry and bilateral coordination of gait. Gait Posture 38: 864–869. doi: 10.1016/j.gaitpost.2013.04.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Plotnik M., Giladi N., Balash Y., Peretz C., Hausdorff J.M.2005. Is freezing of gait in Parkinson’s disease related to asymmetric motor function? Ann. Neurol. 57: 656–663. doi: 10.1002/ana.20452 [DOI] [PubMed] [Google Scholar]
- 30.Rao J.S., Liu Z., Zhao C., Wei R.H., Zhao W., Yang Z.Y., Li X.G.2016. Longitudinal evaluation of functional connectivity variation in the monkey sensorimotor network induced by spinal cord injury. Acta Physiol. (Oxf.) 217: 164–173. doi: 10.1111/apha.12645 [DOI] [PubMed] [Google Scholar]
- 31.Rao J.S., Zhao C., Zhang A., Duan H., Hao P., Wei R.H., Shang J., Zhao W., Liu Z., Yu J., Fan K.S., Tian Z., He Q., Song W., Yang Z., Sun Y.E., Li X.2018. NT3-chitosan enables de novo regeneration and functional recovery in monkeys after spinal cord injury. Proc. Natl. Acad. Sci. USA 115: E5595–E5604. doi: 10.1073/pnas.1804735115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Recktenwald M.R., Hodgson J.A., Roy R.R., Riazanski S., McCall G.E., Kozlovskaya I., Washburn D.A., Fanton J.W., Edgerton V.R.1999. Effects of spaceflight on rhesus quadrupedal locomotion after return to 1G. J. Neurophysiol. 81: 2451–2463. doi: 10.1152/jn.1999.81.5.2451 [DOI] [PubMed] [Google Scholar]
- 33.Roy R.R., Hutchison D.L., Pierotti D.J., Hodgson J.A., Edgerton V.R.1991. EMG patterns of rat ankle extensors and flexors during treadmill locomotion and swimming. J. Appl. Physiol. 70: 2522–2529. doi: 10.1152/jappl.1991.70.6.2522 [DOI] [PubMed] [Google Scholar]
- 34.Sylos-Labini F., Zago M., Guertin P.A., Lacquaniti F., Ivanenko Y.P.2017. Muscle Coordination and Locomotion in Humans. Curr. Pharm. Des. 23: 1821–1833. doi: 10.2174/1381612823666170125160820 [DOI] [PubMed] [Google Scholar]
- 35.Vereecke E.E., D’Août K., Aerts P.2006. Speed modulation in hylobatid bipedalism: a kinematic analysis. J. Hum. Evol. 51: 513–526. doi: 10.1016/j.jhevol.2006.07.005 [DOI] [PubMed] [Google Scholar]
- 36.Wei R.H., Song W., Zhao C., Zhao W., Li L.F., Ji R., Rao J.S., Yang Z.Y., Li X.G.2016. Influence of walking speed on gait parameters of bipedal locomotion in rhesus monkeys. J. Med. Primatol. 45: 304–311. doi: 10.1111/jmp.12235 [DOI] [PubMed] [Google Scholar]
- 37.Wei R.H., Zhao C., Rao J.S., Zhao W., Zhou X., Tian P.Y., Song W., Ji R., Zhang A.F., Yang Z.Y., Li X.G.2018. The kinematic recovery process of rhesus monkeys after spinal cord injury. Exp. Anim. 67: 431–440. doi: 10.1538/expanim.18-0023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wenger N., Moraud E.M., Raspopovic S., Bonizzato M., DiGiovanna J., Musienko P., Morari M., Micera S., Courtine G.2014. Closed-loop neuromodulation of spinal sensorimotor circuits controls refined locomotion after complete spinal cord injury. Sci. Transl. Med. 6: 255ra133. doi: 10.1126/scitranslmed.3008325 [DOI] [PubMed] [Google Scholar]
- 39.Winter D.A.1991. The Biomechanics and Motor Control of Human. Gait Normal, Elderly and Pathological Waterloo Biomechanics Press,Waterloo, Ontario. [Google Scholar]
- 40.Wilson J.L.A.2012. Challenges in dealing with walking speed in knee osteoarthritis gait analyses. Clinl. Biomech. 27: 210–212. doi: 10.1016/j.clinbiomech.2011.09.009 [DOI] [PubMed] [Google Scholar]
- 41.Xiong Q.L., Hou W.S., Xiao N., Chen Y.X., Yao J., Zheng X.L., Liu Y., Wu X.Y.2018. Motor skill development alters kinematics and co-activation between flexors and extensors of limbs in human infant crawling. IEEE Trans. Neural Syst. Rehabil. Eng. 26: 780–787. doi: 10.1109/TNSRE.2017.2785821 [DOI] [PubMed] [Google Scholar]
- 42.Yakovenko S., Mushahwar V., VanderHorst V., Holstege G., Prochazka A.2002. Spatiotemporal activation of lumbosacral motoneurons in the locomotor step cycle. J. Neurophysiol. 87: 1542–1553. doi: 10.1152/jn.00479.2001 [DOI] [PubMed] [Google Scholar]
- 43.Zajac F.E., Neptune R.R., Kautz S.A.2002. Biomechanics and muscle coordination of human walking. Part I: introduction to concepts, power transfer, dynamics and simulations. Gait Posture 16: 215–232. doi: 10.1016/S0966-6362(02)00068-1 [DOI] [PubMed] [Google Scholar]
- 44.Zajac F.E., Neptune R.R., Kautz S.A.2003. Biomechanics and muscle coordination of human walking. Part II: Lessons from dynamical simulations and clinical implications. Gait Posture 17: 1–17. [DOI] [PubMed] [Google Scholar]
- 45.Zelik K.E., La Scaleia V., Ivanenko Y.P., Lacquaniti F.2014. Can modular strategies simplify neural control of multidirectional human locomotion? J. Neurophysiol. 111: 1686–1702. doi: 10.1152/jn.00776.2013 [DOI] [PubMed] [Google Scholar]
- 46.Zhao C., Song W., Rao J.S., Zhao W., Wei R.H., Zhou X., Tian P.Y., Yang Z.Y., Li X.G.2017. Combination of kinematic analyses and diffusion tensor tractrography to evaluate the residual motor functions in spinal cord-hemisected monkeys. J. Med. Primatol. 46: 239–247. doi: 10.1111/jmp.12276 [DOI] [PubMed] [Google Scholar]
- 47.Zhao W., Song W., Rao J.S., Wei R.H., Li L.F., Ji R., Zhao C., Yang Z.Y., Li X.G.2018. Gait division of healthy and spinal cord-injury Rhesus monkeys by one-dimensional toe signals. J. Mech. Med. Biol. 18: 1850017. doi: 10.1142/S0219519418500173 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.