Robust non-rigid motion compensation of free-breathing myocardial perfusion MRI data

Abstract

Kinetic parameter values, such as myocardial perfusion, can be quantified from dynamic contrast enhanced (DCE-) magnetic resonance imaging (MRI) data using tracer-kinetic modelling. However, respiratory motion affects the accuracy of this process. Motion compensation of the image series is difficult due to the rapid local signal enhancement caused by the passing of the gadolinium-based contrast agent. This contrast enhancement invalidates the assumptions of the (global) cost functions traditionally used in intensity-based registrations. The algorithms are unable to distinguish whether the differences in signal intensity between frames are caused by spatial motion artefacts or the local contrast enhancement. In order to address this problem, a fully-automated motion compensation scheme is proposed which consists of two stages. The first of which uses robust principal component analysis (RPCA) to separate the local signal enhancement from the baseline signal, before a refinement stage which uses traditional PCA to construct a synthetic reference series that is free from motion but preserves the signal enhancement. Validation is performed on 18 subjects acquired in free-breathing and 5 clinical subjects acquired with a breath-hold. The validation assesses visual quality, temporal smoothness of tissue curves and the clinically relevant quantitative perfusion values. The expert observers score of visual quality increased by a mean of 1.58/5 after motion compensation and improvement over previously published methods. The proposed motion compensation scheme also leads to the improved quantitative performance of motion compensated free-breathing image series (30% reduction in the coefficient of variation across quantitative perfusion maps, 53% reduction in temporal variations (p<0.001)).

I. Introduction

FIRST-PASS myocardial stress perfusion cardiovascular magnetic resonance (CMR) has become one of the tools of choice for the non-invasive diagnosis of myocardial ischaemia [1]–[3]. In current clinical practice, stress perfusion CMR is assessed visually; however, this requires extensive training and the diagnostic accuracy depends strongly on the operator [4]. As was first suggested more than 20 years ago, it is possible to quantitatively analyse myocardial perfusion in units of ml · min⁻¹ · g⁻¹ using CMR [5], [6] through the application of the indicator-dilution theory [7], [8]. As yet, quantitative analysis of perfusion CMR remains primarily a research tool but its clinical translation would be advantageous as it can be automated [9], [10], enabling accurate and user-independent assessment of myocardial perfusion [6]. Our group has also recently demonstrated the independent prognostic value of quantitative stress perfusion CMR [11].

The fully automated compensation of respiratory motion is a key milestone in the process of the clinical translation of the quantitative analysis as the inter-frame misalignment caused by this respiratory motion can hamper the accuracy of the analysis. In particular, voxel-wise quantification of perfusion is desirable in order to take advantage of the high spatial resolution of MRI and to enable the accurate detection of subendocardial perfusion defects [12]. Such an approach assumes that a voxel represents the same anatomical location in each frame of the image series - i.e. that there is no inter-frame misalignment. When voxel-wise quantification is used, even misalignments as small as one voxel can result in significant errors in the quantitative values.

Current clinical protocols involve acquiring dynamic image series which last 50-90 seconds [13]. Breath-holds can only effectively prevent respiratory motion during a limited time frame of 15-25 seconds, usually during the first-pass of the bolus of contrast agent across the left ventricle (LV) cavity and the LV myocardium. Hence, even when breath-holds are performed, it frequently leads to poor image quality due to the residual motion [14]. This can be worsened by incorrect timing of the breath-hold, resulting in it not coinciding with the passage of the contrast agent in the LV cavity and by the fact that patients with coronary artery disease often struggle to hold their breath properly, especially under the effects of the vasodilator drug.

More recently, some authors [10], [15], [16] have proposed to acquire perfusion images in free-breathing and to apply retrospective motion compensation. This approach has the advantage of being more tolerable for patients and, with good motion compensation, to enable automatically generating accurate voxel-wise perfusion maps without requiring manual segmentation and manual correction of the position of the heart. Furthermore, acquisitions in free-breathing (FB) are more robust when compared to breath-hold (BH) acquisitions when a motion compensation algorithm is used. Shallow free-breathing encourages smooth in-plane motion that aides motion compensation, whereas breath-holds can lead to deep inspiration/expiration and sudden motion both in-plane and through-plane. Additionally, breath-hold scans can also be difficult to retrospectively correct due to the changes in the volumes of the ventricles associated with deep inspiration and expiration [17].

II. Background

The problem of motion compensation can be formulated as an image registration problem. The difficulty in the application of image registration to the motion compensation of myocardial perfusion images is due to the rapidly changing signal intensities caused by the arrival and wash-out of the contrast agent in the region of interest. In the case of nonrigid registrations with vastly different signal intensity profiles, it cannot be guaranteed to not introduce unnatural anatomical deformations [18], [19]. The cost functions that are optimised in the image registrations are global measures [20], they assume that the mapping between tissue and image intensity is constant. This underlying assumption is violated by the local intensity changes. As a result, the cost functions cannot distinguish between the intensity variations that are due to spatial motion artefacts and those that are due to the contrast enhancement. For example, when trying to register a frame with contrast enhancement only in the right ventricle to a frame with contrast enhancement only in the left ventricle, the algorithm will likely try to match the left ventricle to the right ventricle. One possible solution to this problem is to only register successive frames in the image series so that the contrast enhancement should be relatively similar. However, this has the effect of propagating the errors from each registration to every subsequent registration. Also, particularly during the passage of contrast agent from the right ventricle to the left ventricle, the intensity change is fast relative to the temporal sampling rate of the image series, leading to vastly differing contrast between successive frames and the potential for failed registrations.

A. State-of-the-art

Several methods to compensate for motion in myocardial perfusion MRI data already exist. Adluru et al. [21], [22] proposed the use of tracer-kinetic models to create synthetic reference images. However, this work only considered rigid registration with breath-hold acquisitions and the more general applicability of the method is unclear. In particular, the model-fitting is likely to be difficult with free-breathing acquisitions. The method of Melbourne et al. [23] proposed to progressively remove motion in the sequence using principal component analysis (PCA). The original sequence can hence be motion compensated by progressively registering to a motionless synthetic image series reconstructed from only early PCs. This is equivalent to an iterative spatio-temporal denoising. However, this theory breaks down if the acquisition is free-breathing or there is large amounts of motion, such as a deep inspiration, present. This is because the non-random effects of the structured motion biases the PCA decomposition. This results in the motion manifesting itself in the early PCs. Hence, registration to the synthetic PCA-based reference image cannot remove the motion. Wollny et al. [15], [24] built on the work of Milles et al. [25] and proposed to use independent component analysis (ICA) to separate the motion from the image series to create synthetic reference images. However, differentiating between the independent components and hence removing the motion is difficult.

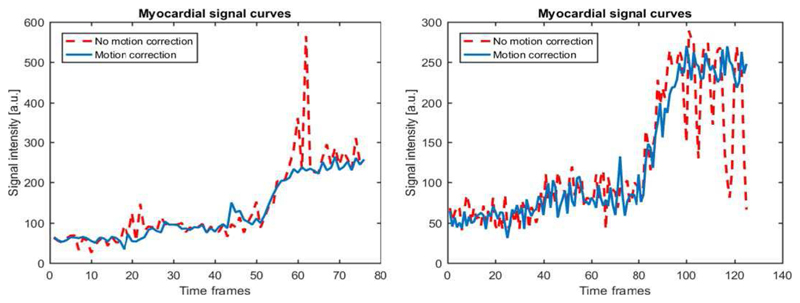
More recently, Benovoy et al. and Xue et al. proposed methods, based on optical flow, that are now components of larger software packages for automated quantitative perfusion analysis [16], [26]. These methods however do not explicitly account for the locally-varying contrast enhancement. As demonstrated in Fig. 1, there can be vastly differing contrast profiles between frames. Lingala et al. [27] proposed deformation corrected compressed sensing (DC-CS) which embeds the motion compensation within an iterative reconstruction scheme. The algorithm iterates a reconstruction step with registration to a spatio-temporal denoised reference. However, it is not clear if it is always possible to create a denoised version with no motion but the same contrast profile as the original image series in this way. The technique also requires many iterations of these steps, the main limitations of doing so are the unwanted smoothing of the images caused by iterative registrations and the time complexity of such an approach. This work will be compared extensively to the method proposed in this paper. The review paper of Pontre et al. [28] compared many of the aforementioned techniques but no clear conclusion was reached.

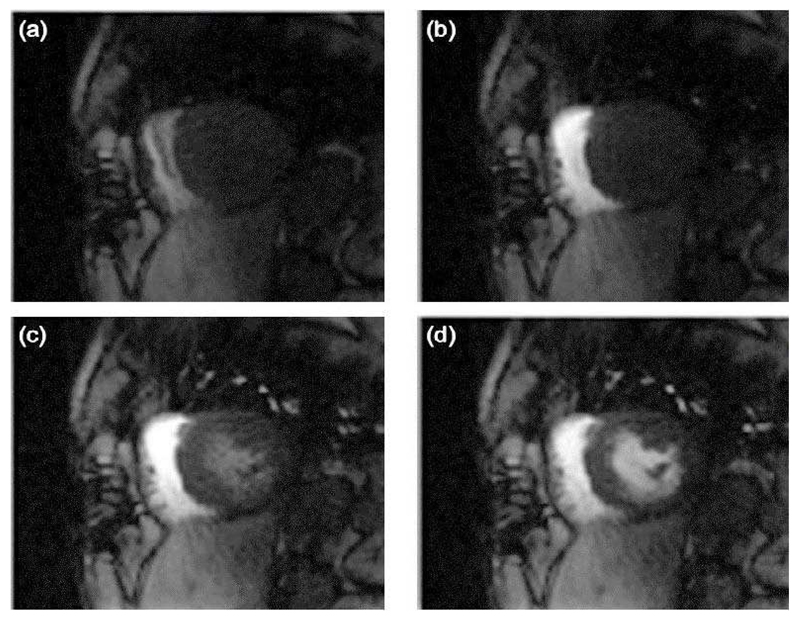
Fig. 1.

Two pairs of successive frames from a myocardial perfusion MRI image series. The first pair ((a) and (b)) are during the arrival of contrast agent in the right ventricle and the second pair ((c) and (d)) are during the arrival of contrast agent in the left ventricle. This serves to show that the contrast profile is not necessary similar between two successive frames.

B. Our Contribution

In this study, we propose a robust fully-automated, image-based approach to the motion compensation of free-breathing perfusion MRI image series using a matrix decomposition technique, robust principal component analysis (RPCA) [29] and non-rigid image registration. This approach is based on the observation that RPCA allows the separation of the dynamic contrast enhancement from the baseline signal in a myocardial perfusion CMR images series. Hence, the deformation fields required to eradicate the respiratory motion can be computed in the absence of the locally-varying contrast enhancement and then applied to the original image series to render it motionless. Hamy et al. [30] demonstrated that RPCA allowed motion compensation of data from liver, small bowel and prostate DCE-MRI. In this work, it is shown that RPCA also facilitates the motion compensation of myocardial perfusion MRI data.

This extension is non-trivial due to the fact the images do not just have one enhancing tissue but rather the enhancing tissue is surrounded by the two more intensely enhancing blood pools. Furthermore, the use of a group-wise registration scheme negates the difficulty of choosing a reference frame. The motion compensation is conducted in a two-stage approach, the first stage uses RPCA, as described above, to account for the bulk motion and the second stage is a refinement stage in which the image series is registered to a separate motionless synthetic image series created using PCA [23] (analogous to the spatio- temporal denoising used in DC-CS). The idea is that such a denoising will be much more efficient after the first bulk motion compensation step. The validation is conducted with its clinical applicability in mind, which is achieved through an assessment of the accuracy of myocardial blood flow quantification and by the scoring of expert readers.

III. Theory

A. RPCA

RPCA is a generalisation of traditional principal component analysis which, as its name suggests, attempts to make the algorithm more robust to corrupt data points [29]. It takes advantage of the fact that, in many applications, the data (M) can be modelled as a combination of a low-rank component (L₀) and a sparse component (S₀) such that: M = L₀ + S₀. Mathematically this can be formulated as the solution of:

$$\text{argmin}{}_{L,S}{\Vert L\Vert }_{\ast }+\lambda {\Vert S\Vert }_1\text{s}.\text{t}.L+S=M$$ (1)

where ||·||∗ is the nuclear norm and is defined as the sum of the singular values of the matrix. λ > 0 is a trade-off parameter that balances the constraint on the rank of L and the sparsity of S. Large values of λ lead to L having higher rank and S being more sparse (λ → ∞ gives L = M and S = 0) and conversely smaller values of λ lead to L having lower rank and S being less sparse (λ → 0 gives L = 0 and S = M). The solution of (1) can be obtained through an augmented Lagrangian multiplier method using an alternating directions approach [31].

B. Motion Compensation

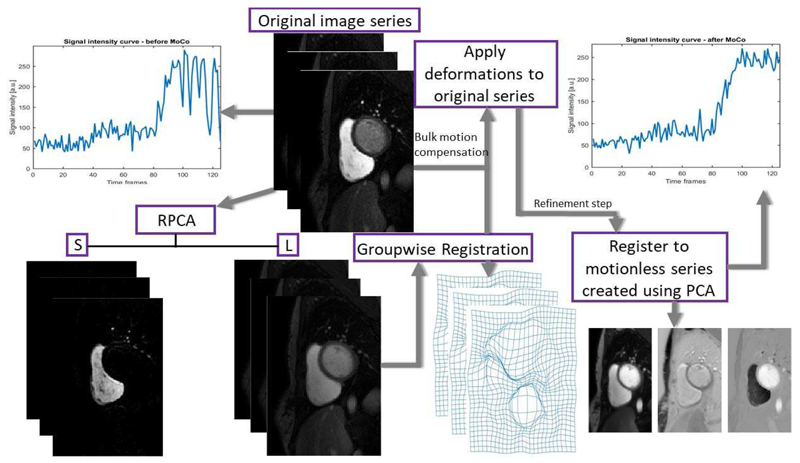
Motion compensation was conducted in two stages, this scheme followed from the observation that it is difficult to optimise the parameters of the image registration algorithms to correct for both large and small deformations simultaneously. In stage 1, it is attempted to correct for the bulk motion caused by the respiration and stage 2 is a refinement step which attempts to account for any remaining fine misalignments. The analysis is performed on image series that have been cropped around the region of interest [32], which vastly reduces the time taken for all processing steps. The full scheme is illustrated in Fig. 2.

Fig. 2.

A flow chart of the proposed motion compensation scheme.

C. Stage 1: bulk motion compensation

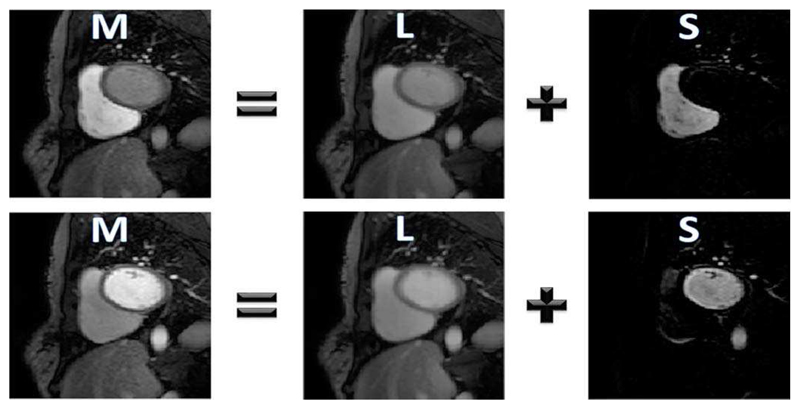
As was shown by Hamy et al. [30], when RPCA is applied to a DCE-MRI image series the low-rank component L well models the baseline signal and the sparse component S captures the contrast enhancement. This decomposition is shown for two example frames in Fig. 3, with videos provided in the supplementary material. With a suitable choice of λ, typically taken to be $\lambda =1/{\sqrt{N}}_p$ where N_p is the number of pixels in an image [29], it is therefore possible to obtain a low-rank image series L which has a similar motion profile as the original image series but without dynamic contrast enhancement. Traditional image registration techniques can be easily applied to this low-rank series as the contrast is similar in each frame. Thereafter, the deformation fields which are computed from L can then be applied to the original image series to eliminate motion.

Fig. 3.

The RPCA based separation of the example images from the original image series (M) into its low-rank (L) and sparse components (S). As discussed, the local signal enhancement is represented in S with no dynamically changing contrast present in L.

Bulk motion is corrected for using a rigid registration scheme which optimises the mutual information cost function [33]. The registration is applied in a group-wise manner, where all frames are registered to the mean frame in an iterative framework, with the mean frame being updated on each iteration (for a total of 3 iterations). This approach performs well as it uses all information at each stage of the registration as opposed to considering only two frames at a time. It also avoids the uncertainties and errors caused by either developing an algorithm to choose a reference frame or doing so in a random manner. The iterative refinement of the reference frame also avoids the complication of registering two frames which are far apart; this could lead to unwanted deformations of the anatomy.

D. Stage 2: refinement

After this first bulk motion compensation, it is observed that the remaining motion appears to be jittery and noiselike. Hence, in the second stage, the frames are registered to a synthetic image series which is created using a PCA decomposition to remove the noise-like motion, as was first proposed by Melbourne et al. [23]. Fig. 4 shows an example frame expressed as a linear combination of the three principal eigen-images, a video of such an example series is provided in the supplementary material. Each frame from the image series resulting from stage one is hence registered to the corresponding frame from the motionless PCA-based synthetic image series. The motion profile for this synthetic image series is shown in Fig. 5. The registrations are performed using freeform deformations [34] which optimises the residual complexity cost function [35] and is performed using a Gaussian image pyramid scheme [36]. This step refines the original motion compensation, and as such is performed on a fine grid of control points (grid spacing (h) of 4 pixels) with relatively weak regularisation (κ = 5). These parameters are similar to the optimal combination for this application found by Wollny et al. [20] (h = 5, κ = 15). As compared to these values, this method uses a finer grid as it is only being used in the second stage and thus only correcting fine misalignments. This work also uses less regularisation as after the first stage the images are already close to being aligned and thus required less protection against local optima. All processing steps were implemented in Matlab (The MathWorks, Natick, MA, USA) using the Medical Image Registration Toolbox for Matlab [37].

Fig. 4.

An example image from the image series which can be expressed as a linear combination of its 3 principal eigen-images.

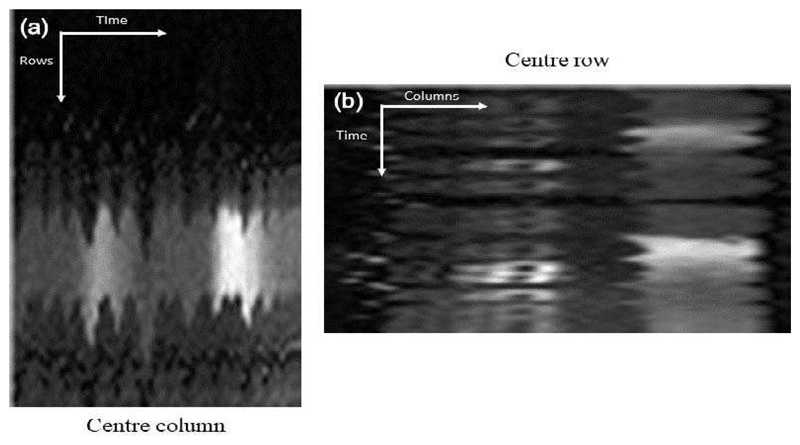
Fig. 5.

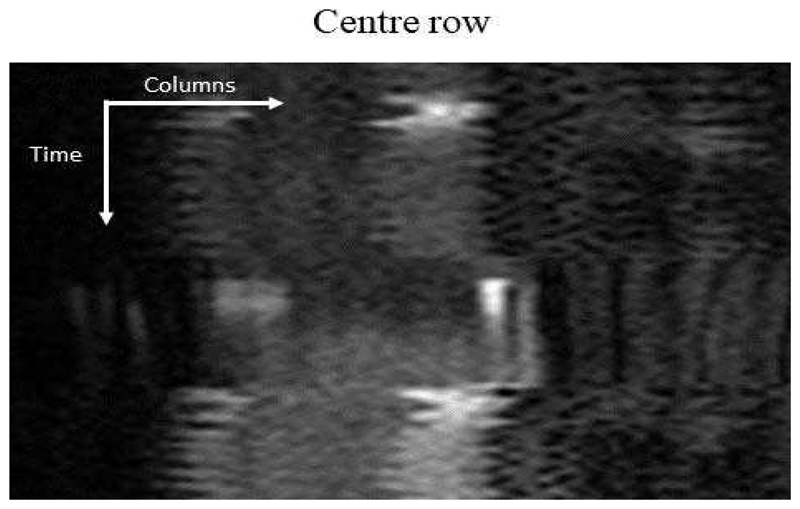
The motion profile of the synthetic reference. This is constructed by taking the centre column (a) and row (b) from each image in the series and stacking them left to right (a) and top to bottom (b). (a) shows the vertical motion (anterior to inferior) and (b) shows the horizontal motion (septal to lateral). This figure indicates a complete absence of motion.

IV. Methods

A. Study population and image acquisition

Dynamic perfusion series were prospectively acquired in patients referred for cardiac MRI at the School of Biomedical Engineering and Imaging Sciences, King’s College London. Image acquisition was carried out at 3.0T (Philips Achieva-TX, Philips Medical Systems) using standard acquisition protocols [13]. Datasets were acquired either in free-breathing or during breath-holds. There was 16 free-breathing rest acquisitions, 2 free-breathing stress acquisitions and 5 breathhold stress acquisitions in total. Images were acquired in 3 short axis views using a turbo field echo gradient echo pulse sequence (typical acquisition parameters TR/TE/flip angle/saturation prepulse delay were 2.5 ms/1.25 ms/15° /100 ms) with a typical spatial resolution of 1.34 × 1.34 × 10 mm. The acquisition of the images was synchronised to the cardiac cycle using a vector electrocardiogram trace. The dynamic image series were acquired during first-pass injection of 0.075 mmol/kg Gadobutrol (Gadovist, Schering, Germany) at 4 ml/s followed by a 20 ml saline flush. A dual bolus contrast agent scheme was used to correct for signal saturation of the AIF, as previously described [38]. All patients consented to the CMR scan and to the inclusion in the study (ethics approval number 15/NS/0030). The study was conducted in accordance with the Declaration of Helsinki.

Image series acquired during a breath-hold can contain significant and sudden motion, whereas images acquired in free-breathing contain a smooth, almost periodic breathing pattern [15] due to the encouraged shallow breathing. The motion profile is visualised for an example free-breathing image series in Fig. 6 which shows the vertical (Fig. 6 (a)) and horizontal (Fig. 6 (b)) motion.

Fig. 6.

The motion profile of a free-breathing image series that was created for the same image series as shown in Fig. 5. The motion is represented as the oscillating pattern and is quite severe in this case. As expected, there is strong vertical motion. There is less horizontal motion but it is still present.

B. Evaluation

The method was evaluated in both a qualitative and quantitative manner. All metrics were computed for 48 individual freebreathing rest image series (16 subjects with 3 slices each), 15 breath-hold stress image series and 6 free-breathing stress image series. All subjects were free from ischaemia and scar. Although quantification of myocardial perfusion is routinely done in research settings, it is likely that visual assessment will remain a part of clinical protocol for the near future. With this in mind, the qualitative facet of the evaluation involved the grading by expert observers. This qualitative assessment compares the original image series to the equivalent image series compensated with both the proposed framework and the DC-CS method [27]. The quantitative assessment involved assessing the temporal smoothness of time-intensity curves while also focusing on the spatial smoothness of the clinically relevant myocardial perfusion values. In the absence of motion, the time-intensity curves should be smooth and the quantitative perfusion maps should be relatively uniform. The quantitative assessment again compares the original image series with the two equivalent motion corrected image series. This follows the recent validation paper of Jansen et al. [39].

The quality of the motion compensation was assessed by two expert observers, blinded to the motion compensation status of the image series, with level III CMR accreditation according to the guidelines of the Society for Cardiovascular Magnetic Resonance (SCMR). The observers (AC and ADMV) viewed the image series and graded each of them on a five point scale. 1=Poor Quality; unnatural deformations, 2=Mediocre Quality; significant motion, 3=Acceptable Quality; some motion, 4=Good Quality; only some unimportant motion, 5=Excellent Quality; no visible motion. The grades from the two observers were deemed to be in agreement if they differed by less than two, otherwise, a consensus grade was reached. The average score from the two observers was then used for assessment.

In the absence of motion, the only change in voxelintensity is the contrast enhancement. These changes should be smooth and slowly-varying. This assumption is violated in the presence of motion as voxels can represent different anatomical features in consecutive frames. To analyse this temporal smoothness, the standard deviation (SD) of the second derivative of the voxel-wise time-intensity curves was computed and the mean value of this was recorded for each slice. Time-intensity curves were smoothed using a Gaussian filter with σ = 1 (time frame) in order to reduce the effect of noise. This smoothing was performed in all cases to ensure fair comparison. Only the part of the curve relating to the first-pass of the contrast agent is assessed.

Myocardial perfusion is quantified through the relationship: C_myo (t) = R_F (t) ∗ C_AIF (t) where R_F, the residue function, is constrained by the Fermi function [5], [6]:

$$R_F(t)=F\cdot \left[\frac{1}{1+\text{exp}[(t-{\tau }_0-{\tau }_d)\cdot k]}\right]\cdot \theta (t-{\tau }_d)$$ (2)

C_AIF (t) is the arterial input function and C_myo (t) is the concentration of contrast agent in the tissue. An estimate of myocardial blood flow F can hence be obtained by deconvolving the observed tissue curve with the AIF.

The fitting is done with a Levenberg-Marquardt nonlinear least square fitting algorithm. θ (t) is the unit step function. The algorithm fits for the variables F, k and τ₀ and uses a predefined τ_d. The fitted value of F is taken as the estimate of myocardial blood flow, whereas k and τ₀ define the shape of the residue function. Signal-intensity curves are converted to concentration of gadolinium by assuming a linear relationship (this can be assumed due to the dual-bolus acquisition) [40].

Since the image series were acquired from healthy patients, relatively uniform perfusion would be expected through-out the myocardium as there is no stress-induced ischaemia and no scarred tissue, based on the late gadolinium enhancement images. However, this will not be the case in the free-breathing acquisitions due to motion artefacts in the time intensity curves, demonstrated in Fig. 7. Image series were therefore quantified with a previously validated in-house software [41], with the aim of showing that it is possible to obtain more homogenous perfusion maps after motion compensation. In order to make this assessment, the SD of each perfusion map was recorded.

Fig. 7.

Voxel-wise time-intensity curves which were extracted from the myocardial segmentation, before and after motion compensation. On the left the motion causes the segmentation of the myocardium to be contaminated by the left ventricle during the upslope of myocardial signal. After motion compensation (right) this effect is corrected and the curves look as expected.

V. Results

A. Qualitative Assessment

The expert observers scored the 69 image series with three different motion compensation statuses (no motion compensation, the DC-CS method and the RPCA-based method proposed in this work), leading to 207 individual scores. The two expert observers assigned identical scores to the image series in 63% of the cases. A difference of more than one point was only observed in 4/207 cases and in all of these cases a consensus score was agreed on. This corresponds to an inter-observer Spearman’s rank correlation coefficient of 0.80.

The mean grades (SD) after averaging the grades from each observer for the rest image series were 2.1 (0.3), 3.71 (0.64), and 4.10 (0.62) for the original free-breathing image series, the DC-CS corrected image series, and the RPCA corrected image series. The equivalent scores for the stress image series were 2.76 (0.53), 3.19 (0.66) and 3.57 (0.66). The Wilcoxon signed rank test showed that there is a significant (Bonferronicorrected) difference between all pairs of populations except the stress DC-CS and stress RPCA corrected images (p=0.07). Although in this case the trend suggests that the RPCA correction works better. This shows that not only does motion compensation improve the image quality of free-breathing image series, but also that our proposed two-step approach gives better results than the previously published method [27]. There are no cases in which the non-motion compensated image series scored higher than an equivalent motion compensated image series. There was a positive difference in the score between the RPCA and DC-CS methods in 48% of the image series with a mean improvement of 0.39. Both observers confirmed that they would be satisfied to report on the free-breathing image series in 100% of the cases. Before and after motion compensation videos are provided in the supplementary materials.

B. Quantitative Assessment

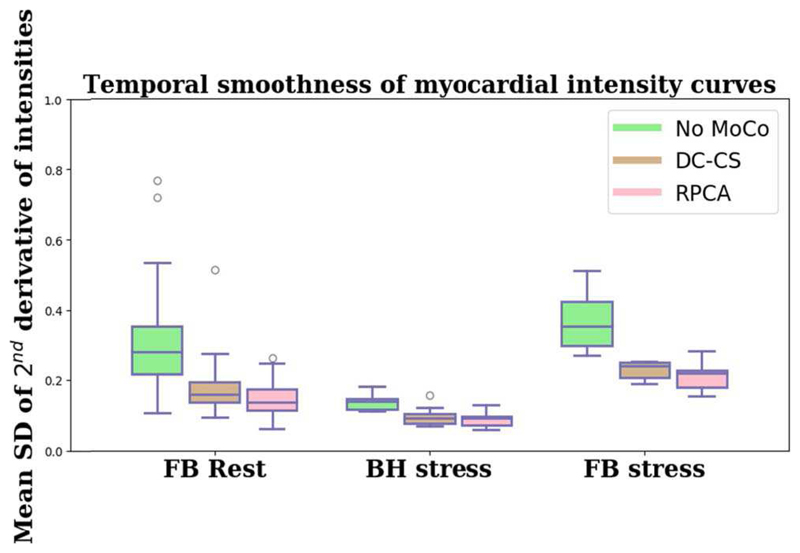
In order to assess the temporal smoothness of the time-intensity curves, the second derivatives of the voxel-wise time-intensity curves are examined. The SD of this is then computed for each curve and the mean value is computed over all curves from an individual slice. The median (interquartile range) values were 0.28 (0.14), 0.16 (0.06) and 0.13 (0.06) at rest and 0.14 (0.14), 0.11 (0.09), and 0.09 (0.08) at stress for the non-motion compensated, DC-CS, and RPCA data respectively. Lower values indicate that the change in intensity between two successive images in the series is smooth and hence indicates a likely reduction in the amount of motion. Fig. 8 shows the distribution of these values. The Wilcoxon signed rank test shows that the values for the RPCA-based method differ significantly from the DC-CS method both at rest (p = 0.013) and at stress (p = 0.024). The two motion compensation schemes are significantly better than no motion compensation both at rest and at stress.

Fig. 8.

The values for the mean standard deviation of the 2^nd derivative of myocardial time-intensity curves. This indicates the temporal smoothness of the image series. The smoother the transition between successive images in the series the less motion that is present.

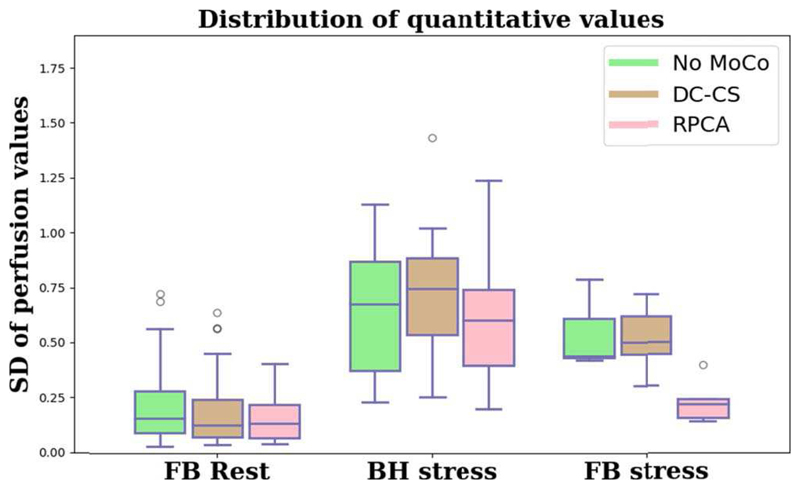
The mean (SD) quantitative perfusion values for the original image series the DC-CS corrected image series, and the RPCA corrected image series are 0.93 (0.33), 0.94 (0.40), and 0.83 (0.26) ml ·min⁻¹ · g⁻¹ at rest and 4.02 (0.91), 4.15 (0.84), and 3.21 (0.73) ml · min⁻¹ · g⁻¹ at stress respectively. As expected the means are very similar and in line with what we would expect to see [42], the reduction in perfusion after motion compensation is due to the lack of artefacts in the intensity curves. However, what is more telling is that at rest the SD accounts for 73%, 53% and 43% of the mean respectively. Due to motion artefacts both the non-motion compensated free-breathing have a higher SD than the motion compensated image series. The median values of the SD of quantitative perfusion value in each slice for the original, DC-CS corrected and RPCA corrected image series are 0.16, 0.13, and 0.14 at rest and 0.61, 0.69 and 0.45 at stress, respectively. The distribution of these values is visualised, in Fig. 9.

Fig. 9.

The values for the standard deviation of perfusion values in each map. Lower standard deviations indicate more homogenous perfusion maps and hence less motion.

The Wilcoxon signed rank test shows that the values for the image series do not differ significantly to those of the two motion compensation schemes, though the trend is clearly visible. The homogeneity of the perfusion maps is improved particularly with the RPCA based method. Furthermore, the homogeneity of the maps at stress for the RPCA corrected image series is significantly improved over the DC-CS corrected image series for both the free-breathing (p=0.001) and breath-hold (p=0.009) image series.

VI. Discussion

In this study, we introduced a novel method for robust and fully-automated, image-based motion compensation of free-breathing perfusion CMR image series. This method was validated both qualitatively and quantitatively. The quality of the motion compensation of both rest and stress free-breathing and stress breath-hold image series was graded by two expert observers in comparison with a previously established method. The quantitative assessment compared free-breathing image series that had subsequently been motion compensated to the original image series and also image series acquired with a breath-hold before and after motion compensation. This evaluation focused on the clinically relevant quantitative perfusion values. The results show an improvement in all metrics for the free-breathing image series that have been motion compensated using the proposed method as compared to the original image series (30% reduction in the coefficient of variation across quantitative perfusion maps, 55% reduction in temporal variations (p<0.001)). The uniformity of the motion compensated free-breathing stress maps is comparable with the breath-hold stress maps. It follows that it may be possible to omit the breath-hold from the clinical protocol, making the procedure easier for both the patient and the scan operator, encouraging smoother respiratory motion which is easier to correct and reducing the potential for large gasps and throughplane motion.

A. Qualitative Assessment

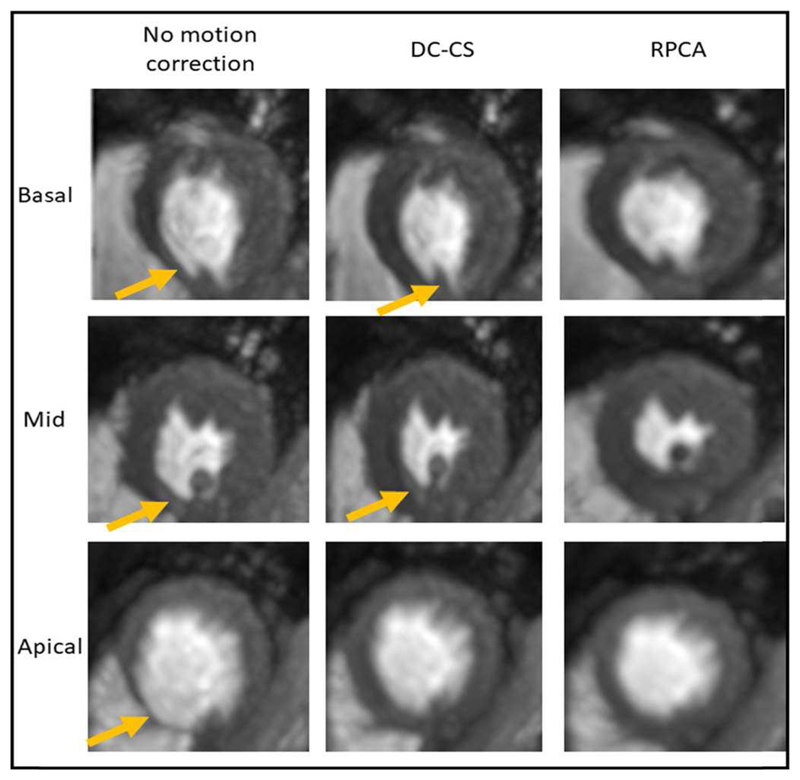
There was a reasonable agreement between observers, with both observers consistently scoring the image series that had been corrected with the RPCA-based method higher than those corrected with DC-CS and those with no motion compensation. Fig. 10 shows the tMIP of each of the three slices for one patient (stress free-breathing) for the three different motion compensation statuses, the increased sharpness of the image series corrected with and the RPCA based approach (column 3) indicates that there is little residual motion remaining.

Fig. 10.

The temporal maximum intensity projection of the three slices from a free-breathing stress acquisition. The increase in sharpness in the RPCA corrected series indicates a lack of motion. The blurring artefacts as a result of motion are shown with yellow arrows.

B. Quantitative Assessment

The temporal variations of the free-breathing (both rest and stress) image series were significantly reduced (by 55%) compared to that of the original image series. This indicates that the motion compensation is indeed enforcing smooth changes between successive images in the series which in turn indicates the eradication of motion. The temporal smoothness of an example free-breathing image series is visualised through its motion profile in Fig. 11. This is the equivalent image series to Fig. 6. In Fig. 12, the deep inspiration and expiration caused by the breath-hold are obvious. After the breath-hold, large amounts of motion can occur due to the subject being out of breath and gasping for air. However, in general, this motion in the BH image series does not significantly affect the clinically relevant quantitative perfusion values. The Fermi deconvolution only uses the part of the time intensity curves that relate to the first-pass of the contrast agent and this is when the breath-hold takes place. However, the BH image series can still produce less uniform perfusion maps in the case of mistiming or failure of the breath-hold.

Fig. 11.

The equivalent motion profile for the same image series as shown in Fig. 6 after motion compensation. The smooth transition between frames indicates the near-total eradication of motion.

Fig. 12.

The equivalent motion profile as shown in Fig. 6 for a breath-hold acquisition. In this image series there is a period of free-breathing followed by a breath-hold during the passage of the main bolus and then another period of free-breathing. The breath-hold is short relative to the passage of the contrast agent, this will impact the tissue curves from the myocardium and subsequently the quantitative perfusion values.

This leads naturally to a comparison of the quantitative perfusion values obtained in each case. As previously remarked, due to the patients’ status there will be no stress-induced ischaemia and therefore relatively uniform perfusion would be expected throughout the myocardium. In the presence of motion this will not be the case due to the motion artefacts in the time intensity curves, which impacts the deconvolution. As such, the mean standard deviation of the quantitative maps is lower after motion compensation with a reduced variability. This effect is more pronounced under stressed conditions. Breath-hold acquisitions are not robust, mistakes by the operator, failed breath-holds by the patient or differences in cardiac output between individuals can adversely impact on the synchronisation of the acquisition. Hence, there can still be significant motion and mistiming during the first-pass of the contrast across the left ventricle and the left ventricular myocardium in the BH image series. At stress, the quantitative maps computed with the motion corrected FB image series are more homogenous than the maps computed with the BH image series.

A further consideration that contributes to the improved uniformity of the motion corrected perfusion maps as compared to the BH perfusion maps is the through-plane motion. The “gasp” or period of deep breathing following a breath-hold can cause significant through-plane motion and cannot be retrospectively compensated for using 2D registrations.

The reported results improve on those obtained with previously established methods [27]. Further to the improved results, the proposed method is beneficial as it is faster (3.5 minutes versus 12 minutes on average). From the point of view of timing, it is potentially advantageous that the motion compensation is achieved in two steps rather than in the many iterations of an iterative procedure.

The bulk compensation step can also deal with structured motion (such as periodic motion and large inspiration) better than the iterative denoising. When compared to directly using the PCA-based approach [23], this approach is deemed to be more applicable to myocardial perfusion imaging. This is because the bulk motion compensation step removes the non-random effects in the data which then allows the successful application of PCA. This leads to better results with both free-breathing and breath-hold data (the clinical standard). Videos which demonstrate the effect of the non-random motion in free-breathing acquisitions on the PCA-based approach are provided in the supplementary material.

The benefits of the proposed approach are that there is no assumptions made on the acquisition system and parameters or even the imaging modality. The resulting motion compensated image series were of higher visual quality. The quantitative information was shown to be preserved after motion compensation, with more robust estimate of myocardial blood flow due to reduced motion artefacts in the signal intensity curves.

C. Limitations

There is a lack of a ground-truth to validate this method. We have attempted to account for this by conducting the evaluation in a multitude of different manners.

To date, the method has only been validated with one set of acquisition parameters. Although we believe there is no reason the acquisition parameters should influence this method, it would be desirable to demonstrate this on further datasets.

Despite the fact this is a 2D compensation for the 3D motion of the heart, image series acquired in the short-axis view with shallow breathing will have predominantly in-plane motion. In our datasets, it is not possible to correct through-plane motion in due to the large slice thickness, large distance between slices and the limited sampling of the left ventricular myocardium.

VII. Conclusion

We have demonstrated the feasibility of a robust fully-automated, image-based approach to the motion compensation of free-breathing perfusion CMR images using the matrix decomposition technique, robust principal component analysis (RPCA) and non-rigid image registration and shown its efficacy using clinical data. With the use of motion compensation algorithms, the evidence presented in this study suggests that a breath-hold protocol for the acquisition of first-pass myocardial perfusion MRI data may be no longer necessary. Motion compensated free-breathing acquisitions led to significantly more uniform quantitative perfusion maps than the original images. The variation of motion corrected free-breathing perfusion maps is equivalent to breath-hold clinical acquisitions. Our method performs well in comparison with the established methods in the literature. Additionally, both expert observers noted that the motion compensated free-breathing image series were all of satisfactory quality for visual assessment. In summary, in addition to the increased convenience of free-breathing acquisition, our motion compensation scheme produces image series of high visual quality and allows the robust quantification of myocardial perfusion.