Crystal structures of DOTMA chelates from Ce³⁺ to Yb³⁺: evidence for a continuum of metal ion hydration states

Abstract

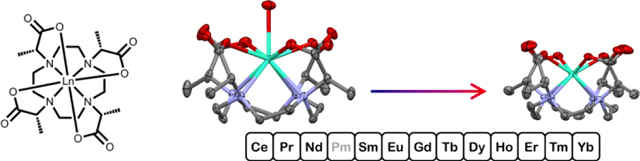
The crystal structures of chelates formed between each stable paramagnetic lanthanide ion and DOTMA are described. A total of 23 individual chelates structures were obtained, in each chelate the coordination geometry around the metal ion is best described as a twisted square antiprism (torsion angle −25.0° – −31.4°). Despite the uniformity of the general coordination geometry provided by the DOTMA ligand, there is a considerable variation in the hydration state of each chelate. The early Ln³⁺ chelates are associated with a single inner sphere water molecule, the Ln-OH₂ interaction is remarkable for being very long. After a clear break at gadolinium the number of chelates in the unit cell that have a water molecule interacting with the Ln³⁺ decreases linearly until at Tm³⁺ no water is found to interact with the metal ion. The Ln-OH₂ distance observed in the chelates of the later Ln³⁺ ions are also extremely long and increase as the ions contract (2.550 – 2.732 Å). No clear break between hydrated and dehydrated chelates is observed, rather this series of chelates appear to represent a continuum of hydration states in which the ligand gradually closes around the metal ion as its ionic radius decreases (with decreased hydration) and the metal drops down into the coordination cage.

Graphical Abstract

Introduction

Octadentate polyaminocarboxylate ligands and their chelates with Ln³⁺ ions are of considerable current interest owing to their existing and potential biomedical application. Uppermost of these is the role of these ligands in the chelation of Gd³⁺ for contrast agents in MRI. There is now increasing concern over the possible chronic toxic effects of residual Gd³⁺ in the aftermath of contrast-enhanced MR exams.^[1] In consequence, it is now commonly accepted that macrocyclic polyamino carboxylate ligands are preferred for this application over their linear counterparts.^[2] Macrocyclic ligands derived from the 12-membered aza-crown cyclen, such as DOTA (Figure 1) are employed in three clinically used contrast agents. The macrocyclic chelate GdDOTA itself was introduced into clinical practice in the late 1980s and has been recognized as one of the safest MRI contrast agents ever since.

Figure 1.

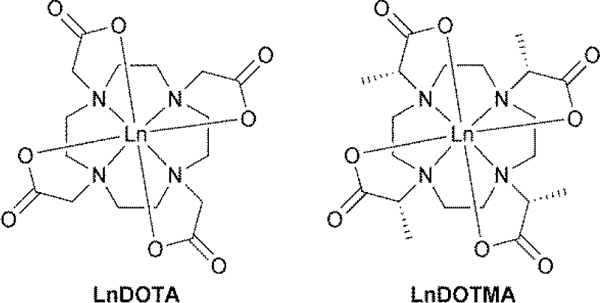
Connectivity structures of the Ln³⁺ chelates of DOTA (1,4,7,10 tetraazacyclododecane-1,4,7,10-tetraacetate, left) and DOTMA (1R,4R,7R,10R- α,α′,α″,α‴- tetramethyl-1,4,7,10 tetraazacyclododecane-1,4,7,10-tetraacetate, right).

The success of DOTA as a ligand for Ln³⁺ ions stems from the pre-organized nature of its coordination cage.^[3] Not only does this preorganization afford chelates of remarkable thermodynamic stability, but the conformational rigidity of the macrocyclic ligand means that the kinetics of metal ion dissociation are very slow.^[4] Although GdDOTA is widely regarded as the gold-standard for safely chelating Ln³⁺ ions in biomedical applications, GdDOTA itself is not a particularly efficacious T₁-shortening agent. The relaxivity (effectiveness) of this chelate is typically between 3 – 5 mM⁻¹s⁻¹ depending on field and temperature.^[5] The low relaxivity of GdDOTA, in common with other low molecular weight paramagnetic chelates, arises because it tumbles rapidly in solution (τ_R < 100 ps). A more effective T₁-shortening agent is generated if the rate of molecular reorientation (1/τ_R) is comparable to the proton Larmor frequency, i.e. significantly slower. But, when tumbling has been appropriately slowed other factors can play a limiting role on relaxivity, foremost among these are the extent of hydration of the Gd³⁺ chelate and the kinetics of water exchange between the bulk and inner coordination sphere.^[6] Water exchange that is either too fast^[7] or too slow^{[3, 8]} will have the effect of limiting relaxivity.^{[2, 9]} For this reason understanding hydration and water exchange – its kinetics and mechanism – has been an area of significant interest as well as controversy in the field of Ln³⁺ coordination chemistry.

The octadentate polyamino carboxylate ligand DOTMA (Figure 1) is a methylated analogue of DOTA that was first reported by Desereux in 1984.^[10] More recently, we have reported some of the important physico-chemical characteristics of GdDOTMA, as well as its crystal structure.^[11] One important finding was that GdDOTMA exhibits much more rapid water exchange kinetics than GdDOTA, an observation that can be attributed to differences in the strength of the metal-water bond. In the crystal GdDOTMA was found to have noticeably longer Gd-OH₂ bond distance (2.50 Å)^[11] than GdDOTA (2.463^[12] or 2.447^[13] Å). The difference in Gd-OH₂ distance can in turn be attributed to the coordination geometry of each chelate: in the crystal GdDOTMA is found to adopt a twisted square antiprism (TSAP) whereas GdDOTA adopts a square antiprism (SAP). The taller coordination cage of the TSAP coordination isomer has the effect of pushing the coordinated water molecule away from the metal, weakening the bond and accelerating the rate of exchange in a dissociative mechanism. This difference in coordination geometry is also maintained in solution where for GdDOTMA the TSAP predominates (3:1)^[11] but for GdDOTA the SAP predominates (7:1).^[14] The SAP/TSAP ratio for both ligands is highly dependent upon the identity of the Ln³⁺ ion chelated with both ligands exhibiting a marked preference for the TSAP isomer when chelating early Ln³⁺ ions.^{[11, 14]} As the Ln³⁺ ions get heavier and smaller the proportion of SAP isomer present in solution increases to a point at which the trend reverses and the proportion of TSAP isomer in solution begins to increase again.^{[11, 14]} For chelates of DOTA this change is pronounced and gives rise to a coordination geometry that is observed in the crystal: both early and late lanthanides exhibiting TSAP geometries but the middle lanthanides appearing as SAP.^[14] These changes in coordination geometry render it impossible to probe the more subtle changes that occur across the Ln³⁺ series for DOTA chelate. Here we report the crystal structures of DOTMA chelates with all of the Ln³⁺ ions from Ce³⁺ to Yb³⁺ (except Pm³⁺). In all cases the LnDOTMA chelate is observed to adopt the TSAP coordination geometry seen in the previously published HoDOTMA and GdDOTMA structures.^{[11, 15]} The Ho³⁺ structure provided some interesting initial insights into hydration and structural changes in DOTA-type chelates owing to the presence of chelates with different hydration states in the unit cell.^[15] Across the Ln³⁺ series the hydration of LnDOTMA changes in unpredicted and interesting ways that provide new and deeper insights into the behaviour of DOTA derivatives during the water exchange process.

Note: Here we do not use the notation TSAP or m (for a 9-coordinate hydrated chelate) and TSAP′ or m′ (for an 8-coordinate dehydrated chelate). The reasons for this will be obvious once the Conclusions section has been reached. Our use of SAP and TSAP describes only the conformation of the DOTA or DOTMA ligand and its coordination to the metal. As we will see, the presence or absence of coordinated water is a more complex concept than can adequately be described by a simple “on/off” or prime notation.

Results and Discussion

Chelate Preparation and Crystallization

In all cases the Ln³⁺ chelate of DOTMA was prepared from a sample of the dihydrochloride salt of the ligand, obtained by previously described procedures.^[11] Chelates were prepared by the previously described method – reaction with the lanthanide oxide;^[11] or by reaction with trichloride salt in aqueous solution at pH 5.5 in a procedure identical that used for a variety of similar chelates.^[16] At the end of the reaction the pH was adjusted to neutral with sodium hydroxide prior to crystallization. Thus, in addition to the anionic chelate and its metallic counter-cation sodium chloride is also present in solution. As previously reported X-ray quality crystals could be grown by slow diffusion of EtOH into an aqueous solution of the chelate.^{[11, 15]} Alternatively X-ray quality crystals were grown by slow evaporation of the aqueous solution of the chelate.^[16]

Some of the structures were affected by merohedral twinning, in light of the similarity in cell constants and with inter-axial angles at or near 90° (see below) this is unsurprising. Appropriate models have been pursued to unravel these complicating features. The hydrated chloride and cation layers have ordered, disordered and partial occupancy waters. Generally, water hydrogens were not located or modeled. Chloride ions are hydrated and found in proximity to and sandwiched between the hydrocarbon corrugation of the macrocycles.

Crystal Packing

LnDOTMA chelates were found to crystalize with one of three metallic counter-ions: sodium (Ce³⁺, Eu³⁺, Gd³⁺, Ho³⁺, Er³⁺, Tm³⁺, Yb³⁺), the corresponding Ln³⁺ ion (Pr³⁺, Nd³⁺, Sm³⁺), or a combination of both sodium and the Ln³⁺ ion (Tb³⁺ and Dy³⁺). Additionally at least one chloride ion is found in the unit cell of every chelate. LnDOTMA chelates have a nominal C₄ symmetry, however, this symmetry is not observed in practice. ErDOTMA exhibits C₂ symmetry in the P2 space group. All other chelates exhibit a pseudo four-fold symmetry, the Ln³⁺ cation and the Cl⁻ anion lie on the pseudo four-fold axis. LnDOTMA chelates are arranged in alternatively oriented sheets (Figure 2). Between the negatively charged faces of two sheets are found hydrated counter cations. The chloride ions and any additional water of hydration are found between the non-polar faces of two sheets.

Figure 2.

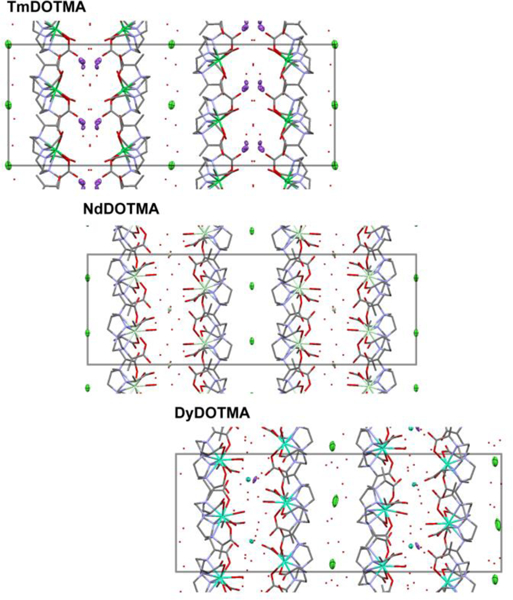
The packing of LnDOTMA chelates with Na⁺ counter cations (Tm³⁺, top), with Ln³⁺ counter cations (Nd³⁺, middle), with mixed counter cations (Dy³⁺, bottom). The dimensions of the unit cell are shown in grey. Hydrogen atoms are omitted for clarity. Counter cations and anions are shown as 50 % ellipsoids (Cl⁻ in green, Na⁺ in purple).

The crystal structures form a family with the most symmetric structure occurring in the orthorhombic space group C 222₁ (#20), with pseudo-tetragonal cell constants (a, b, c) of about 13 × 13 × 38 Å, a cell volume of about 6400 ų and with 8 complexes per cell in general positions. This cell is found for the Pr³⁺, Nd³⁺, Sm³⁺, Eu³⁺, and Tm³⁺ chelates. The symmetry is lowered in mixed cation crystals formed by Tb³⁺ and Dy³⁺ chelates, occurring in the monoclinic system with cell constants as in the parent, space group P 2₁ (#4) (actually P112₁ relative to the parent cell) with Z = 8, and β near 90°; the cell volume remains about 6400 ų. In the lattice of ErDOTMA, the cell is halved (3200 ų) to the monoclinic space group P2 (#3) (actually P112 or P121 with redefined b’ = c/2; c’ = b) relative to the parent cell and chelates lie on a two-fold axis. The two-fold axes are absent in the Ho³⁺ lattice for which a triclinic cell is found, space group P1 (#1), with Z = 4 and c’ = c/2, and volume about 3200 ų. In the Ce³⁺ and Gd³⁺ structures, cell volumes are a quarter of the parent volume (about 1700 ų). Symmetry is reduced to space group P2 (#3) (actually P121 relative to the parent cell) and a’ ≈ b’ ≈ √2/2 a, b, and c’ ≈ c/2, Z = 2. Finally, the Yb³⁺ structure is also triclinic, P1 (#1), with a 1700 ų cell, a’ ≈ b’ ≈ √2/2 a, c’ ≈ c/2, β near 90°, and two independent molecules in the cell.

The Structure of Early LnDOTMA Chelates (Ce³⁺ – Gd³⁺)

Irrespective of the nature of the counter-cation the crystal structures of DOTMA with the early Ln³⁺ ions are all broadly similar. All of the chelates found in each unit cell are identical. The overall form of the chelates with early Ln³⁺ are broadly similar and can be described as a TSAP geometry with a single coordinating water molecule (Figure 3). Each chelate may be described as q = 1 (where q = the hydration number). However, at this juncture it is worth noting that that the Ln-OH₂ distances in these chelates are very long. Although longer Ln-OH₂ distances are expected in TSAP isomers (as noted previously) there is significance to such very long distances, a subject to which we will return.

Figure 3.

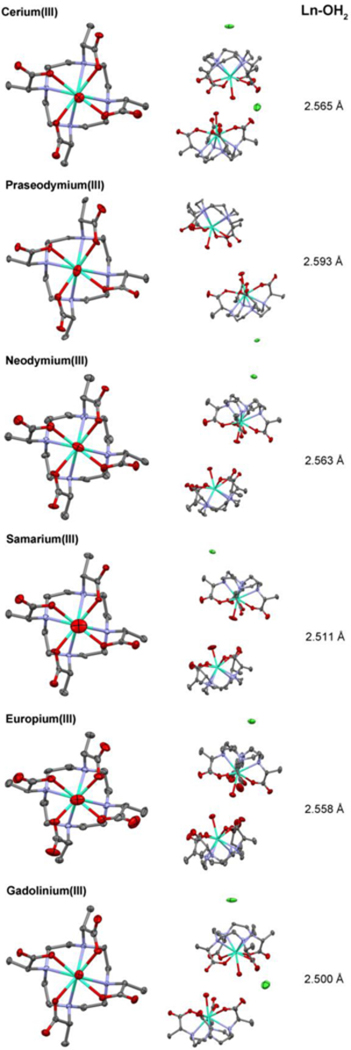
50% Thermal ellipsoids for chelates formed by the early Ln³⁺ ions (Ce³⁺ to Gd³⁺) with DOTMA. Hydrogen atoms, water of crystallization and counter-cations have been omitted for clarity. In each lattice two chelates are oriented O₄-face to O₄-face: this arrangement is shown for each Ln³⁺ (along with the position of additional chloride counter cations).

The conformation of the ligand in each chelate is consistent with the stereochemistry of the ligand. DOTMA is by convention the RRRR- isomer.^[11] The R- configuration at the pendant arms confers a Λ helicity on the pendant arms.^[16–17] The TSAP geometry then defines the overall conformation of the chelate: Λ(λλλλ) in each case. This conformation is also preserved across the chelates of the later lanthanide ions.

The Structure of Late LnDOTMA Chelates (Tb³⁺ – Yb³⁺)

A very clear “break” is observed at gadolinium and the structure of DOTMA chelates with later lanthanides is quite different. Most notably after Gd³⁺ there is a change in the number of unique chelates present in each unit cell. Between Tb³⁺ and Er³⁺ four (or two in the case of Ho³⁺) unique chelates are observed in the repeating unit (Figure 4). A cursory inspection of Figure 4 also indicates a consistent change in hydration number (q) as the metal ion contracts from Tb³⁺ to Tm³⁺. Each of the four unique Tb³⁺ chelates is shown with one water molecule coordinated (q = 1). For Dy³⁺ there are three chelates shown with coordinated water and one shown without water (q = 0). For Ho³⁺ half of the chelates are shown as q = 1 and half as q = 0. One of the four chelates with Er³⁺ is shown with a coordinated water (q = 1), the other three are shown q = 0. Both Tm³⁺ and Yb³⁺ are unambiguously without coordinated water (q = 0).

Figure 4.

50% Thermal ellipsoids of all of the unique LnDOTMA chelates found in the crystal lattice for the late Ln³⁺ ions (Tb³⁺ to Yb³⁺). Hydrogen atoms, water of crystallization and counter-cations have been omitted for clarity. Water molecules coordinated to a metal are shown on the basis of the default settings in the CCDC’s Mercury software.

A superficial analysis would allow that the decreasing ionic radius of the Ln³⁺ ion prevents water from accessing the metal ion to an ever greater extent. This analysis appears in accord with Aime’s explanation of the evolution of the SAP/TSAP ratio across the Ln³⁺ series:^[14] the TSAP isomer of the heaviest lanthanides are proposed to be q = 0. This is used to account for the increased preference of the TSAP isomer in LnDOTA chelates on passing from Ho³⁺ to Lu³⁺, but here the decrease in hydration occurs from Tb³⁺ to Tm³⁺. However, the analysis above is overly simplistic and does not account for other important factors. Firstly, the change in “q” is linear from Tb³⁺ to Tm³⁺, but the change in the average ionic radius would decrease super-linearly over this range (Figure 5). More significantly perhaps is the extraordinarily long Ln-OH₂ distances observed in all of these chelates (Table 1). The images depicted in Figure 4 are generated using the default settings of the CCDC’s Mercury software.^[18] Even though this software shows a bond between metal and water it is questionable whether any of these water molecules can truly be described as “bound”.

Figure 5.

The ionic radius of Ln³⁺ ions depends upon the coordination number of the metal ion (red and blues lines), data taken from Shannon.²⁵ The open circles represent the ionic radius calculated for each Ln³⁺ ion coordinated by DOTMA in this work.

Table 1.

Hydration parameters of LnDOTMA chelates and a comparison of Ln-OH₂ distances formed with the later Ln³⁺ ions in the crystal.

	Tb3+	Dy3+	Ho3+	Er3+	Tm3+	Yb3+
Proportion of chelates hydrated (q = 1 / q = 0)[a]	4/4	3/4	2/4	1/4	0/4	0/4
Observed Ln-OH2 distances / Å	2.592	2.550	2.662	2.732[b]	-	-
	2.617	2.606	2.662	-	-	-
	2.569	2.659	-	-	-	-
	2.628	-	-	-	-	-
Longest capping Ln-OH2 distances / Å (aqua ion)[c]	2.530	2.521	2.528	2.524	2.524	-

^[a]hydration in this case is defined by whether a water molecule is shown as coordinated by the default settings of the Mercury software.

^[b]it is noteworthy that a second chelate has a water molecule 2.902 Å from the metal ion but this is not shown as “bound” by the Mercury software.

^[c]The Ln-O distance of the capping water molecules (the longer of the Ln-OH₂ distances) in nine-coordinate aqua ions found in the CCDC.

It can be stated with certainty that for each metal (Tb³⁺ - Er³⁺) a number of chelates in each unit cell have a water molecule that interacts with the metal ion. But in every case the distance between the Ln³⁺ ion and the water is more than 2.55 Å. Examples of macrocyclic Ln³⁺ chelates in which the Ln-OH₂ distance exceeds 2.55 Å - such as TbDO3AP (Ln-OH₂ = 2.678 Å)^[19] - are rare. Even longer axial coordiation has been observed with other ligands (such as nitrogen),^[20] but the Ln-OH₂ distance in TbDO3AP clearly represents the very limit at which water continues to interact with the Ln³⁺ ion, the water is pushed off entirely in the Dy³⁺ chelate.^[19] A good representation of what represents a long Ln³⁺-OH₂ bond length can be obtained from a survey of the long water bond distances in the 9-coordinate aqua ions in the CCDC. These distances are found to be substantially shorter than Ln³⁺-OH₂ distances found in LnDOTMA chelates between Tb³⁺ and Tm³⁺ (Table 1). There is therefore, no precedent that permits the Ln-OH₂ interactions in LnDOTMA chelates to be called “bonding”. This means that a simple “q = 1 or q = 0” analysis is insufficient to describe hydration in LnDOTMA chelates. Evidently a more nuanced approach is demanded.

Analysis of the Coordination of Ln³⁺ ions by DOTMA

The crystal structures of LnDOTMA chelates present a particular challenge when it comes to analyzing the changes in coordination that occur across the series. Because the lanthanide contraction is highly regular^[21] it is common to examine how the structures and properties of chelate change as a function of Ln³⁺ ion identity. However, there a clear variation from “CN = 9” at the beginning of the series to “CN = 8” at the end. Analysis by Ln³⁺ identity would be inadequate here because the ionic radius of any metal ion is dependent upon the coordination number (CN) of the metal ion, as seen in Figure 5. Furthermore, the long Ln-OH₂ distance observed in the middle of the series creates additional problems for defining how to consider each Ln³⁺ ion. The most accurate picture of the variation across the series is provided by considering the ionic radius of each Ln³⁺ ion individually.

The ionic radius of each Ln³⁺ ion coordinated by DOTMA was estimated in the following manner. The average of the four Ln-O carboxylate and four Ln-N distances for the coordination sphere with DOTMA were determined. The ionic radius of the Ln³⁺ ion is then determined according to the basic principles of Pauling^[22] using Eqn 1. The ionic radii of nitrogen and oxygen were taken to be 1.58 and 1.26 Å, respectively. These values are in good agreement with published values^{[21, 23]} but are chosen specifically to normalize the DOTMA chelate with the shortest Ln-OH₂ distance (Gd³⁺) to a CN of exactly nine.

The results of this exercise are quite striking (Figure 5) – all of the chelates of DOTMA have ionic radii consistent with coordination numbers lower than nine (the exception being Gd³⁺, which was normalized to CN = 9). Except for Tm³⁺ and Yb³⁺ the ionic radii lie close to or between those calculated by Shannon for CN = 9 and CN = 8 chelates.^[21] It is notable that after the gadolinium break there is a general trend from radii corresponding to CN = 9 at Gd³⁺ towards radii corresponding to CN = 8 at Er³⁺. This exercise is particularly valuable since it addresses the question of how the long Ln-OH₂ distances in these chelates should be addressed.

$$I.R{.}^{Ln}=\frac{\left(\left\{Ln-N\right\}-I.R{.}^N\right)+\left(\left\{Ln-O\right\}-I.R{.}^O\right)}{2}$$ (1)

This analytical approach has certain limitations, there are packing effects in the crystal and the carboxylate oxygens atoms interact with counter cations and waters in the lattice differently from chelate to chelate. This means that variation in the oxygen ionic radius is possible and this could account for some of the observed oscillation in coordination number across the early lanthanides in Figure 5 as well as the observation of CNs < 8.

The relationship between CN and ionic radius is linear for Ln³⁺ ions.^[21] The ionic radii in Figure 5 can therefore be used to calculate the CN of each chelate using the values of Shannon^[21] for CN = 9 and CN = 8 complexes.^‡[24] This inevitably affords non-integer CN values, but such an outcome must not be viewed as problematic. It has been common practice to describe the structure of various complexes in terms of fractional coordination numbers.^[25] Furthermore, the work of Parker and co-workers explicitly explains the observation of partial q values in terms of variance in Ln-OH₂ distances.^[26] A fractional CN is but a logical extension to the common observation of fractional q values and long Ln-OH₂ distances, as seen in this crystallographic series.

In solution the Ln-OH₂ distance is expected to be a good indicator of the strength of the interaction of metal ion and water molecule. However, in the crystal it cannot perfectly report on the strength of this interaction. Other interactions between the water and the lattice influence both its position and the extent of its interaction with the metal. Nonetheless, a good linear correlation is observed between the CN derived from the estimated ionic radii and the Ln-OH₂ distance (Figure 6). Given that the ionic radii are not accurately determined (the ionic radii of nitrogen and oxygen may not be identical in each chelate) such good correlation is powerful evidence that it is appropriate to consider the variation in the Ln-OH₂ distance in terms of changes in CN, and therefore also q.^[26a]

Figure 6.

The CN of each Ln³⁺ ion in DOTMA chelates derived from the calculated ionic radius correlates well with the observed Ln-OH₂ distance in that chelate. Data include only structures for which an interacting water molecule is identified by Mercury. Dashed line is a guide to the eye only.

With an appropriate system for describing the chelates in hand, it is now possible to analyze how the structure of these chelates varies across these 23 individual structures. Of particular interest is the way in which the chelate structure changes as a function of variation in Ln³⁺ ion hydration. Lukeš and co-workers were the first to publish the crystal structure of a DOTA-type chelate that included both q = 1 and q = 0 forms in the same coordination geometry.^[27] This structure led to the insight that the position of the metal ion in DOTA-type chelates changes as the water molecule comes and goes in a dissociative exchange process. When water is coordinated to the metal ion the metal sits close to the O₄-coordination plane of the carboxylates. After the water molecule has left the inner coordination sphere, the metal drops down into the ligand cage moving towards the N₄-coordination plane of the cyclen ring. This change in the metal position affects the structure of the chelating ligand, an effect that provided the basis for our own earlier work examining the effect of exchange on hydration.^[28] A number of metrics have been used to describe the changes to the ligand structure associated with change in hydration: the O-Ln-O angle, the area of the O₄ plane, and the d/c ratio. These parameters are ultimately a reflection of the position of the Ln³⁺ within the coordination cage (Figure 7). The effects of changes in hydration on two other parameters of interest have also been examined: α, the torsion angle of the antiprism; and the average N-C-C-N torsion angle of the ethylene bridges of cyclen.

Figure 7.

The relationship between various structural parameters (the d/c ratio (A); the O₄ area and O-Ln-O angle (B); the antiprismatic torsion angle, α, and the average N-C-C-N torsion angle of the cyclen ethylene bridges (C)) as a function of the Ln³⁺ ionic radius, and by extension the hydration state of the chelate. The Tm³⁺ chelate is a clear outlier from the trends in the changes in both α and the N-C-C-N torsion angles because one quartile of the ligand structure adopts a very different conformation from the other three. Data include all 23 structures, dashed lines are a guide to the eye only.

In Figure 7 each of these parameters is plotted as a function of Ln³⁺ ionic radius determined in Figure 5. To some extent the ionic radius here can be considered as surrogate for a change in the hydration state or CN of the Ln³⁺ ion. The range of ionic radii observed across the 23 DOTMA crystal structures (0.212 Å) is significantly larger than the change that would occur during the dissociative water exchange process (0.054 Å for Gd³⁺). This means the structural changes evident in Figure 7 are an exaggeration of the changes that occur during exchange. However, this exaggeration is useful in developing a clearer picture of how the chelate might change during dissociative water exchange and developing an appropriate model for describing hydration.

The d/c ratio directly describes the position of the Ln³⁺ ion relative to the N₄ and O₄ planes. In Figure 7A the d/c ratio is found to decrease linearly as the ionic radius decreases. This is consistent with the observation originally made by Lukeš and co-workers that as the Ln³⁺ ion loses its water of hydration (smaller ionic radius) the metal ion drops down into the coordination cage (smaller d/c ratio). However, these data provide two important additional insights into the movement of the Ln³⁺ ion within the coordination cage. Firstly, this motion is driven not by the change in hydration directly but by the change in ionic radius that is associated with the change in CN during dissociative exchange. The governing role of the ionic radius can be seen by examining the d/c ratio in the crystal structures of other LnDOTA-type chelates (Supporting Information Figure S1). The same trend of decreasing d/c ratio with decreasing ionic radius is observed; however, a clean break is observed between “q = 1” and “q = 0” chelates. This is the second important insight provided by DOTMA: in previously published structures “q = 1” chelates have d/c ratios in excess of 0.66 and “q = 0” chelates d/c ratios less than 0.63. This break appears to create a boundary condition that defines the difference between q = 1 and q = 0. However, in the chelates of DOMTA 9 of the 23 chelates have d/c ratios that span the “break” between 0.660 and 0.635. The change in hydration or ionic radius is not described by a binary “on/off” model, but is represented by a continuum of hydration states. In the crystal this continuum is reflected in an increase in the Ln-OH₂ distance.

Both the O₄ area and the O-Ln-O angle have also been proposed as descriptors of Ln³⁺ ion hydration in DOTA-type chelates. Like the d/c ratio, both of these parameters exhibit a strong linear correlation with the Ln³⁺ ionic radius (Figure 7B). These data are particularly instructive in the case of O-Ln-O angle for which a q = 1/q = 0 boundary condition of 136° has previously been proposed.^[29] However, here again the structures of DOTMA refute the idea of a boundary condition: a continuum of values (notably spanning the previously proposed boundary condition) is observed. Changes in the O₄ area and O-Ln-O angle are also indicative of subtle changes in ligand conformation as the ionic radius (or hydration state) of the Ln³⁺ ion changes. These changes in ligand structure can be described as a type of “breathing motion” in which the four carboxylate oxygen atoms of the O₄ coordination plane close in over the top of the coordination cage as the metal drops down within the coordination cage.

Other changes in the ligand conformation can be observed by examining two torsion angles: α (the torsion angle of the antiprism) and the N-C-C-N torsion angle of the cyclen ethylene bridge (Figure 6C). As the Ln³⁺ ionic radius decreases, the torsion angle of the antiprism (α) decreases slightly. This observation is congruent with the trend observed for the O₄ area. As the O₄ area decreases (with decreasing ionic radius) so the shape of the antiprism must also change: the four carboxylate oxygen atoms close over the top of the coordination cage as the ionic radius decreases, which means that each pendant arm must reach farther around the Ln³⁺ ion. This in turn narrows the torsion angle of the antiprism. There is also a surprising correlation between the N-C-C-N torsion angle and the Ln³⁺ ionic radius. As the Ln³⁺ ion drops down into the coordination cage (decreasing ionic radius), the N-C-C-N torsion angle decreases from about 61.6° (close to an ideal gauche conformation) to a more distorted 57°. This suggests that during dissociative water exchange the macrocyclic ring undergoes a surprising conformational change distorting away from a close to ideal gauche conformation to a flatter conformation as the metal ion moves closer to the ring. This observation may explain why water exchange in nitrobenzyl substituted DOTA chelates is invariably observed to be more rapid than those of the unsubstituted analogues.^{[7b, 30]} In these chelates at least one ethylene bridge is found to be distorted away from a gauche conformation in such a way as would reduce the N-C-C-N torsion angle.^[31] This would place at least part of the macrocyclic ring close to the transition state for dissociative exchange: reducing the energy barrier to exchange, thereby increasing the kinetics of exchange.

Conclusions

The crystal structures of DOTMA with Ln³⁺ ions from Ce³⁺ to Yb³⁺ provide a unique insight into metal ion hydration in DOTA-type chelates. From Ce³⁺ the Ln-OH₂ distance decreases steadily until a “break” at Gd³⁺ (Figure 8) After this “break” the Ln-OH₂ distance increases markedly until eventually the water is displaced from the Ln³⁺ ion altogether. Between Tb³⁺ and Tm³⁺ this displacement is observed as a linear change in the number of chelates in the unit cell that have water molecules interacting with the Ln³⁺ ion centre. The Ln-OH₂ distances are very long for all LnDOTMA chelates, but especially so after the gadolinium break. Such long Ln-OH₂ distances represent a challenge for describing the hydration of metal ions that interact with water at distances longer than reasonable bond lengths. The Ln³⁺ ionic radius is found to be a useful metric that can be estimated from the Ln-N and Ln-O distances and the N and O atomic radii. Because the ionic radius is linearly dependent upon the coordination number this allows the coordination number of the Ln³⁺ ion (and by extension the hydration number, q) to be determined, both of which are frequently found to be fractional in the crystal structures of LnDOTMA. The Ln³⁺ ionic radius correlates very closely with various parameters associated with chelate hydration as well as some associated with the ligand conformation. These correlations present a very clear picture of how the structure of LnDOTMA chelates change with decreasing ionic radius across the Ln³⁺ series. By extension the changes that occur in a chelate as it undergoes dissociative water exchange are reflected in these data. As the water molecule leaves the metal ion decreases in ionic radius and drops down in the ligand coordination cage towards the N₄-plane. This movement of the metal ion causes several changes in the conformation of the ligand, the O₄-plane closes over the top of the increasingly vacant coordination site. It decreases the O₄ area and O-Ln-O angle and causes the torsion angle of the antiprism (α) to decrease slightly as the pendants are forced to reach further over the metal ion. This change also appears to be associated with a flattening of the macrocyclic ring (a decrease in the N-C-C-N torsion angle).

Figure 8.

The Ln-OH₂ distance initially decreases with decreasing Ln³⁺ ionic radius until the “gadolinium break” is reached after which it increases rapidly with decreasing ionic radius until the water is pushed off the chelate completely. Dashed lines are a guide to the eye only.

It is notable that there are no clear breaks in the observed trends that permit hydrated and dehydrated chelates to be differentiated. These 23 chelates present a picture of a continuum of partial hydration states spanning q = 1 to q = 0. The hydration state of the metal chelate is reduced as the Ln-OH₂ distance increases along the axis of the bond. This series of structures affords an insight into the changes that occur during of dissociative exchange. It is worth noting that these structures are not obviously consistent with the results of several modelling studies. For example the interacting water molecule is not found to lean over with increasing Ln-OH₂ distance as it ‘tumbles’ out of the chelate as predicted by Burton and co-workers.^[32] In fact the opposite is observed: the chelates with the longest Ln-OH₂ distance (Ho³⁺ and Er³⁺ are the only two chelates in which the water is perfectly aligned with the centre of the O₄ plane. Nor are these structures consistent with the results of many DFT calculations, for instance Mayer et al.,^[33] in which the Ln-OH₂ distance and the d/c ratios do not correlate properly and the Ln³⁺ ion lies too close to the O₄-plane. The structural changes observed in these structures are, however, consistent with those proposed to account for conformational change observed by ¹H NMR in solution for structurally related chelates.^[28]

Experimental Section

DOTMA and its chelates were prepared, X-ray quality crystals grown and crystal structures determined by previously described methods.^{[11, 15]}

Crystallographic information files have been deposited with the Cambridge Crystallographic Data Centre: 1908883 (Ce³⁺), 1908424 (Pr³⁺) 1908884 (Nd³⁺), 1908885 (Sm³⁺), 1908426 (Eu³⁺), 1908428 (Tb³⁺), 1908427 (Dy³⁺), 1908423 (Er³⁺), 1908425 (Tm³⁺), 190886 (Yb³⁺). Data can be obtained free of charge from www.ccdc.cam.ac.uk/conts/retrieving.html (or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: +44 1223 336033)