From Perception Threshold to Ion Channels—A Computational Study

Abstract

Small-surface-area electrodes have successfully been used to preferentially activate cutaneous nociceptors, unlike conventional large area-electrodes, which preferentially activate large non-nociceptor fibers. Assessments of the strength-duration relationship, threshold electrotonus, and slowly increasing pulse forms have displayed different perception thresholds between large and small surface electrodes, which may indicate different excitability properties of the activated cutaneous nerves. In this study, the origin of the differences in perception thresholds between the two electrodes was investigated. It was hypothesized that different perception thresholds could be explained by the varying distributions of voltage-gated ion channels and by morphological differences between peripheral nerve endings of small and large fibers. A two-part computational model was developed to study activation of peripheral nerve fibers by different cutaneous electrodes. The first part of the model was a finite-element model, which calculated the extracellular field delivered by the cutaneous electrodes. The second part of the model was a detailed multicompartment model of an Aδ-axon as well as an Aβ-axon. The axon models included a wide range of voltage-gated ion channels: Na_TTXs, Na_TTXr, Na_p, K_dr, K_M, K_A, and HCN channel. The computational model reproduced the experimentally assessed perception thresholds for the three protocols, the strength-duration relationship, the threshold electrotonus, and the slowly increasing pulse forms. The results support the hypothesis that voltage-gated ion channel distributions and morphology differences between small and large fibers were sufficient to explain the difference in perception thresholds between the two electrodes. In conclusion, assessments of perception thresholds using the three protocols may be an indirect measurement of the membrane excitability, and computational models may have the possibility to link voltage-gated ion channel activation to perception threshold measurements.

Introduction

The signaling pathway for our everyday perception of pain begins in the periphery through a select group of sensory neurons termed primary afferent nociceptors. Nociceptors are nerve fibers that respond to damaging or potentially damaging stimuli and thus fulfill a protective purpose. In neuropathic conditions, in which the excitability of nociceptors has been shown to be increased, this protective function may be malfunctioning (1). Neuropathic pain has a prevalence rate of 9.8%, which is approximately a third of the adult chronic pain patient group (2, 3). Both diagnosis and treatment of neuropathic pain are today inadequate, and improved diagnostic tools as well as deeper understanding of the pathological mechanisms are needed. Increased excitability of the cell membrane has been identified in several neuropathic pain disorders (1), and several voltage-gated ion channel abnormalities have been observed in patients with neuropathic pain disorders (4). Voltage-gated ion channels are suitable therapeutic targets for analgesic drugs because subtypes of voltage-gated ion channels are selectively expressed in nociceptors (5, 6, 7, 8) and because of their ability to govern the excitability of the nociceptors. Cutaneous electrical stimulation is particularly useful for studying activation of voltage-gated ion channels because the electrical current artificially activates the fibers through bypassing the sensory transduction at the nerve terminal. However, it is difficult to study the excitability of nociceptive fibers to electrical stimulation in isolation without coactivation of larger non-nociceptive fibers because the electrical activation thresholds are lower for larger fibers compared to small fibers. To overcome this obstacle, small surface electrodes (pin electrodes) have been developed (9, 10, 11, 12, 13) that generate a high current density in the epidermis where the small fibers terminate, unlike the large fibers, which terminate in the dermis (14, 15, 16, 17). As a result, the pin electrodes have the potential to preferentially activate nociceptors at low stimulation intensities. Both objective estimations of the latency of evoked potentials (12, 13) and human blink reflexes (10), as well as qualitative measurements of pain perception (9, 18), support that pin electrodes preferentially activate nociceptors. Noninvasive pin electrodes preferentially activate the thinly myelinated Aδ-fibers, and intraepidermal pin electrodes have been reported to preferentially activate unmyelinated C-fibers as well as Aδ-fibers (19).

The excitability of large fibers can be indirectly assessed by measuring the compound action potential, unlike small fibers, for which the compound action potential has a slow velocity and therefore is spread out over time, making it technically difficult to record. Therefore, our group has instead used perception thresholds as an indirect measurement of the excitability. In two recent studies, the perception thresholds for a concentric pin electrode (cathode ∅ = 0.2 mm) versus the conventional large surface-patch electrode (patch electrode, cathode 2 cm²) were compared (18, 20). Both studies showed that perception thresholds differed between the two electrodes, which is a trivial consequence of the difference in electrode/tissue interface area. However, not only did the absolute values differ, but more interestingly, the differences were dependent on the duration and shape of the stimulation current, which might indicate the influence of physiological mechanisms such as voltage-gated ion channels. In the Hennings et al. study (20), two protocols to measure the perception thresholds were used, the strength-duration protocol and the threshold electrotonus protocol. The strength-duration protocol estimates the perception thresholds for different durations of rectangular pulses of the stimulation current. In that study, the strength-duration time constant for the patch electrode was significantly lower than the time constant for the pin electrode. The second protocol, the threshold electrotonus, consists of a rectangular subthreshold prepulse followed by a short 1 ms rectangular pulse. The current of the short pulse is increased until the perception threshold is reached. The threshold electrotonus showed similar threshold reductions to subthreshold prepulses for depolarizing prepulses. However, for long hyperpolarizing prepulses, the pin electrode demonstrated a significant increase in perception threshold compared to the patch electrode. The study by Hugosdottir et al. (18) showed that different shapes of slowly increasing stimulation currents alter the perception thresholds, particularly for long durations (50 ms), but only for the patch electrode. The novelty of these studies is that they support that the perception threshold of cutaneous electrical stimulations can be used to indirectly assess excitability of axonal membranes.

In this study, a computational model has been developed to explain the differences in perception thresholds between the two fiber classes of sensory afferents. The hypothesis is that the main differences in perception threshold between the electrodes originate from the difference in morphology and voltage-gated ion channel distribution of peripheral nerves. For instance, tetrodotoxin (TTX)-resistant sodium currents, both Na_v1.8 (Na_TTXr) and the persistent Na_v1.9 (Na_p), are preferentially expressed in nociceptors (6, 7, 21), and the current density of hyperpolarization-activated cyclic nucleotide-gated channels (HCNs) is significantly positively correlated with the conduction velocity of these fibers (22). The expression and dynamics of potassium channels have also been shown to differ between fiber types (5) particularly the A-type potassium channel (K_A) (5, 8, 23). Therefore, the aim of this study was to investigate whether the difference in perception thresholds between the two electrodes could originate from the voltage-gated ion channel distribution as well as the morphological differences between peripheral nerve endings of large and small fibers.

Materials and Methods

A two-part computational model was developed to study activation of peripheral nerve fibers by cutaneous electrodes (see Fig. 1). The first part of the model is a finite-element model (COMSOL Multiphysics 6.3, Stockholm, Sweden) that calculates the electrical field delivered by a cutaneous electrode. The second part of the model is a detailed multicompartment model (NEURON; Yale, New Haven, CT (24)) of an Aδ-axon as well as an Aβ-axon.

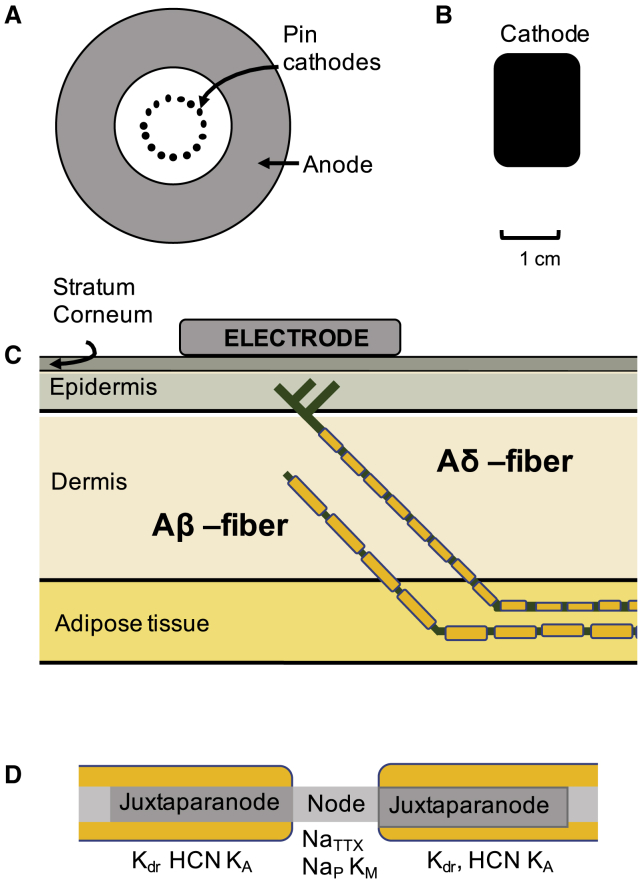
Figure 1.

Computational model design. A two-part computational model has been developed. The first part of the model calculates the electrical field generated by the two electrodes: a pin electrode (A) or a patch electrode (B). The skin model consists of four rectangular skin layers (C). The second part of the model consists of two axon models (Aδ and Aβ) with the spatial location in the skin model illustrated in (C). The morphology of the myelinated axon sections consists of three parts: node of Ranvier, juxtaparanode, and internode (D). The figures are not drawn to scale. To see this figure in color, go online.

Finite-element model for the electrical field

To calculate the electrical field along a nerve fiber, the Mørch et al. model (25) was further developed. The model consists of four rectangular skin layers: stratum corneum, epidermis, dermis, and hypodermis. In each layer, the tissue was modeled as a linear and homogeneous medium. The electrical properties and thicknesses of the different layers were adopted from literature and are listed in Table 1. Both a pin electrode and a patch electrode were implemented in the model. The full size of the model was 15 × 15 cm for the pin model and 20 × 15 cm for the patch model. The pin electrode consisted of 15 steel pin cathodes placed in a circle, and the anode was concentrically placed around the 15 pins (see Fig. 1 A). The pin electrode was designed with the same spatial dimensions as stated in the Lelic et al. study (13). The spatial dimensions for the large-surface-area electrode cathode were 1.5 × 2 cm, and the anode 4.5 × 6 cm. The anode was placed 12 cm from the cathode. The time-dependent solution of the finite-element model was calculated for rectangular pulses of the stimulation current (see Fig. S2). Because there was little effect from the tissue permittivity on the solution, the steady-state solution was used, assuming the system is unchanging with regard to time. The following three boundary conditions were added to the model: the total current through the cathode was set to 1 mA, the total current through the anode was set to −1 mA, and the hypodermis layer was grounded underneath. The steady-state solution of the electrical field was calculated by the Poisson equation:

$$\mathrm{-}\mathit{\Delta }\times \left(\mathit{\sigma \Delta }{\mathrm{V}}_{\mathrm{EF}}\right)=0\mathrm{\sigma -Conductivity}\mathrm{of}\mathrm{the}\mathrm{tissue,}{\mathrm{V}}_{\mathrm{EF}}\mathrm{electrical}\mathrm{potential}$$

Table 1.

The Electrical Properties and Thicknesses of the Different Layers of the Skin

	Electrical Conductivity (S/m)	Relative Electrical Permittivity	Thickness (μm)
Stratum corneum	2 × 10−4 (49)	2 × 103 (49)	20 (50, 51)
Epidermis	H:0.95 (52)	6.1 × 104 (52)	82 (50, 51)
	V:0.15 (52)	2.6 × 104 (52)
Dermis	H:2.57 (52)	2.4 × 105 (52)	1300 (53)
	V:1.62 (52)	9.6 × 104 (52)
Hypodermis	2 × 10−2 (54, 55)	1 × 103 (54, 55)	5000

The iterative nonlinear solver, Automatic Newton, was used with the maximal element size set to 4.2 mm and minimal 0.021 mm. To ensure convergence, both the mesh density and the size of the model were varied (see Fig. S1).

Nerve fiber models

Morphology

To study how the extracellular field is affecting the activation of nerve fibers, two multicompartmental nerve fiber models were developed, one of an Aδ-fiber axon (Ø: 3.5 μm) and another of an Aβ-fiber axon (Ø: 9 μm). In a previous study (26), a novel C-fiber model was developed that was further developed into these two myelinated axon models for the purpose of this study. Because electrical stimulation artificially generates an action potential without activating the sensory receptor terminals, the process of sensory transduction within the sensory terminal was not included in the model. Because the sensory terminal was not included, the Aβ model is terminated by a node of Ranvier. Both ends of the model’s termination conditions were sealed ends. To model a damped propagation of the action potential at the model termination, an additional passive segment was added at the end of the model.

The Aδ-axons lose their myelin when they cross the dermal-epidermal junction (16, 17) and become morphologically indistinguishable from unmyelinated fibers (15). The Aδ model therefore consists of two parts: one myelinated axon located in the deeper tissues and one unmyelinated axon protruding into the epidermis. The morphology of the Aδ-fiber was modeled as a straight line with a 45° angle from the middle of the epidermis to the middle of the hypodermis, where it continues horizontally through the hypodermis. Two side branches were added to the main branch to generate a nerve fiber density of 0.58 fiber endings per millimeter (see Fig. 1 C). The angle between the main branch and side branches was 90°.

The Aβ model has a similar spatial location except that the nerve fiber terminates in the middle of the dermis (see Fig. 1 C). Both nerve fiber models were placed centered underneath the cathode for the patch electrode or underneath one of the pins of the pin electrode. Six additional spatial positions of the nerve fiber model were evaluated. Both models were moved (40 μm) in all three dimensions, generating a total of seven models. The current needed to generate an action potential that propagates to the end model was calculated for each of the seven models.

As the nerve fiber enters the superficial layers of the skin, the length of the intermodal distance decreases, the myelination reduces, and the length of the nodes of Ranvier is increased (15). Therefore, these parameters have been reduced by a factor of two from the morphology measured from fibers in deeper tissues (27, 28). All morphological parameters are listed in Table 2. The electrical field calculated by the finite-element model was added as the extracellular field to the axon models. The number of the compartments were 26,088 for the Aδ model and 27,120 for the Aβ model, and the equations were solved using the variable time step method in NEURON.

Table 2.

Parameters of the Morphology for the Axon Models

	Aδ-Fiber	Aβ-Fiber	Reference
Diameter	3.5 μm	9 μm	N/A
Nodal length	2 μm	2 μm	(15, 27)
Internodal length	400 μm	900 μm	(15, 56)
Juxtaparanodal length	5 μm	5 μm	(57)
Capacitance nodal	1 μF/cm2	1 μF/cm2	(58)
Capacitance myelin	0.012 μF/cm2	0.0071 μF/cm2	(58) C = 1/(myelin sheet + 1)
Resting membrane potential	−60 mV	−60 mV	(59)
Number of myelin sheets	40	70	(15, 28)
Intracellular resistance	130 Ωcm	130 Ωcm	N/A
Branch length	Main: 500 μm	N/A	(15)
	Side branch 1: 49 μm
	Side branch 2: 99 μm
Total model length	5.472 cm	4.994 cm	N/A

Voltage-gated ion channel models

One of the main difficulties in the development of these axon models was to implement the densities of the ion channels. Larger fibers have been thoroughly researched, but for smaller fibers such as nociceptors, it is technically more difficult to perform intracellular recordings by patch-clamp techniques. Therefore, most of the ion channel data is obtained from the dorsal root ganglion soma (DRG) and mainly from the smallest unmyelinated C-fibers. Details regarding the shape of the action potential and the relative influence of the underlying ion channel currents in Aδ-fibers are not known. However, the major sodium current during an action potential in the DRG soma is Na_TTXr (29), most probably driven by the activation of Na_V1.8 channels (6). Therefore, the Na_TTXr current is substantially larger than the Na_TTXs current in the computational model.

The ion channel currents were described by Hodgkin-Huxley-type ion channels. The myelinated fiber section of the Aδ model has the same subtypes of ion channels as the Aβ-fiber model except for the subtypes of the Na_p channel and the K_A channel, which is selectively expressed in nociceptors (8, 21). The HCN maximal conductance was additionally reduced by a factor of two because experimental patch-clamp experiments have estimated that Aδ neuron somas express half the current compared to the larger somas of Aβ neurons (22).

The literature supports large variations of the gating parameters (5), which may be due either to modulatory substances that are missing during patch-clamp experiments or to different compositions of the subtypes of the ion channels. Therefore, the gating parameter voltage dependencies were allowed to be shifted to fulfill the constraints. For the Aβ model, the ion channel dynamics for the delayed rectifier and persistent sodium channels were adopted from Jankelowitz et al.’s model (30). With the original parameters for the delayed rectifier, the channel was activated before the action potential. The delayed rectifier ion channels’ voltage dependence needed to be modified by a depolarizing shift of 40 mV for the channel not be activated before action potential generation, resulting in shifting the V_1/2 to −32 mV, which is consistent with experimental observations (5). In this study, the fast TTX-sensitive currents were denoted as Na_TTXs. and the fast TTX-resistant sodium current as Na_TTXr. The persistent sodium currents are denoted Na_p regardless of their sensitivity to TTX. The Jankelowitz et al. model (30) did not include the slow inactivation gates for Na_TTXs channel (mainly Na_v1.6). Therefore, the ion channel dynamics were implemented from the Watanabe et al. model (31), and the steady-state parameters were shifted 10 mV to generate an action potential that propagated to the proximal end of the axon model and generated depolarization larger than 10 mV. The ion channel dynamics for the M current and HCN were adopted from Tigerholm et al. model (26).

For the Aδ-fiber’s unmyelinated nerve ending, the following three sodium channels were implemented: two TTX-resistant currents (Na_TTXr and Na_p) and the Na_TTXs (mainly Na_v1.7). The steady-state parameters and their time constants for the three sodium channels were taken from the Tigerholm et al. model (26), as were the HCN current and the K_M current dynamics. The model of the K_A was adopted from Watanabe et al. model (31). The channel voltage dependency was modified by a 15 mV hyperpolarizing shift to get the model consistent with the threshold electrotonus measurements of the pin electrode (20). For the Aβ model, steady-state parameters were set to [Vm = -2.4; km = 14.2; Vh = 30.7 and kh = 6.1] (5). The time constants were implemented from the Tigerholm et al. study (26). The parameters for the voltage-gated ion channels are listed in Table 3.

Table 3.

Parameters for the Axon Models

	Model Reference	Spatial Location	Maximal Conductance (S/cm2)
Aδ Model
NaTTXr (Nav1.8)	(26)	Unmyelinated nerve ending	3.03 × 10−2
Nap (Nav1.9)	(26)	Unmyelinated nerve ending and nodes of Ranvier	2.96 × 10−4 (unmyelinated); 1.10 × 10−3 (node)
NaTTXs (Nav1.6)	(31)	Nodes of Ranvier	1.45 × 10−1
NaTTXs (mainly Nav1.7)	(47)	Unmyelinated nerve ending	1.27 × 10−2
Kdr	(30)	Unmyelinated nerve ending and juxtaparanode	1.20 × 10−3 (unmyelinated)
			4.80 × 10−3 (juxtaparanode)
KA	(48)	Unmyelinated nerve ending and juxtaparanode	2.70 × 10−3 (unmyelinated)
			3.00 × 10−3 (juxtaparanode)
KM	(26)	Unmyelinated nerve ending and nodes of Ranvier	2.62 × 10−5 (unmyelinated)
			2.10 × 10−3 (node)
HCN	(26)	Unmyelinated nerve ending and juxtaparanode	3.81 × 10−5 (unmyelinated); 1.52 × 10−4 (juxtaparanode)
Leak channel	(26)	Internode	1.00 × 10−7
Aβ Model
NaTTXs (Nav1.6)	(31)	Nodes of Ranvier	1.45 × 10−1
Nap	(30)	Nodes of Ranvier	2.30 × 10−5
KA	(5)	Juxtaparanode	3.90 × 10−2
KDr	(30)	Juxtaparanode	4.80 × 10−3
HCN	(26)	Juxtaparanode	3.04 × 10−4
KM	(26)	Nodes of Ranvier	2.10 × 10−3
Leak channel	(26)	Internode	1.00 × 10−7

Criteria used to set model parameters

The activation threshold was defined as the stimulation current required to generate an action potential that propagates to the end of the axon model. The maximal conductances for the voltage-gated ion channels were the unknown parameters in the two nerve fiber models. To constrain the model, three criteria were defined:

• 1)The Aδ model should have a lower activation threshold than the Aβ model for the pin electrode.
• 2)The Aβ model should have a lower activation threshold than the Aδ model for the patch electrode.
• 3)Three different protocols measuring the excitability of the membrane have been studied experimentally by recording the perception threshold using the pin and the patch electrode (18, 20). The model should be able to reproduce the differences in perception thresholds between the two electrodes for all three protocols (see Fig. 2). The three protocols are as follows:
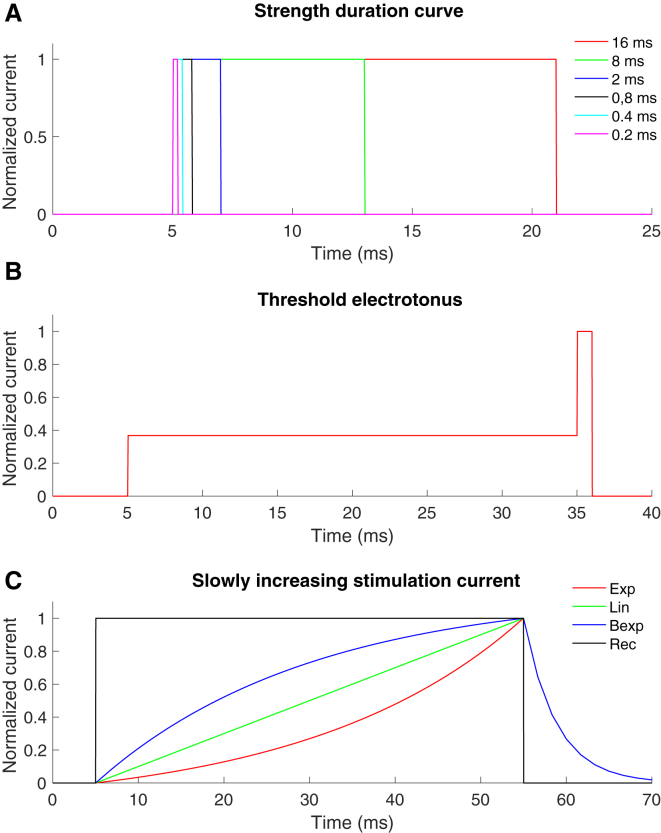
• A.Strength-duration curve, which is measuring the activation thresholds for different durations of rectangular pulses. The strength-duration time constant should be similar to the experimentally obtained values, which for the pin electrode is 1060 ± 690 μs and for the patch electrode 580 ± 160 μs (20). The time constants were estimated as the duration needed to generate an activation threshold of twofold the rheobase (duration 16 ms). To increase the convergence of the axon model, the rise time for the electrical current was set to 0.025 ms.
• B.Threshold electrotonus. First, the activation threshold for a rectangular 1 ms pulse was estimated. Thereafter, a prepulse was applied at a stimulation current corresponding to 20% of the initial activation threshold for the 1 ms pulse (i.e., before the 1 ms pulse was applied). The effect of the prepulse on the activation threshold for a 1 ms pulse was measured. The activation threshold was estimated for both hyperpolarizing and depolarizing prepulses.
• C.Slowly increasing stimulation current. In the Hugossdottir et al. study (18), the perception thresholds were compared for different shapes of slowly increasing stimulation current for the two durations of 5 and 50 ms, respectively. The different shapes and equations are listed in Table 4.

Figure 2.

The normalized time-dependent stimulation currents for the three protocols. (A) The six rectangular pulses used for the strength-duration curve are shown. (B) An example of the subthreshold prepulse used during the threshold electrotonus protocol is shown. (C) The four different shapes of slowly increasing stimulation current used for the slowly increasing stimulation current protocol are shown. To see this figure in color, go online.

Table 4.

The Equation for the Stimulation Current for the Slowly Increasing Stimulation Protocol, see (18)

Pulse Form	Equation for the Stimulation Current	Label
Exponential increase	$I\left(t\right)=\{\begin{array}{cc}\frac{I_s}{e^{\frac{T_S}{\tau }}-1}\left(e^{\frac{t}{\tau }}-1\right),& 0\le t<Ts\\ I_s\times e^{\frac{-t}{{\tau }_{tr}}},& T_s\le t\le T_{tr}\end{array}$	Exp
Linear increase	$I\left(t\right)=\{\begin{array}{cc}\frac{I_s}{T_s}\times t,& 0\le t<Ts\\ I_s\times e^{\frac{-t}{{\tau }_{tr}}},& T_s\le t\le T_{tr}\end{array}$	Lin
Bounded exponential	$I\left(t\right)=\{\begin{array}{cc}\frac{I_s}{1-e^{\frac{-T_S}{\tau }}}\left(1-e^{\frac{-t}{\tau }}\right),& 0\le t<Ts\\ I_s\times e^{\frac{-t}{{\tau }_{tr}}},& T_s\le t\le T_{tr}\end{array}$	ExpB
Rectangular	I(t) = Is(t), 0 ≤ t < TS	Rec

I_s = stimulation current, T_S = stimulation duration, τ = (T_S/2) = time constant. Trailing phase: T_tr = T_S × 1.4 and τ_tr = τ/6.6. See (18).

Results

Activation of nerve fibers by cutaneous electrical stimulation

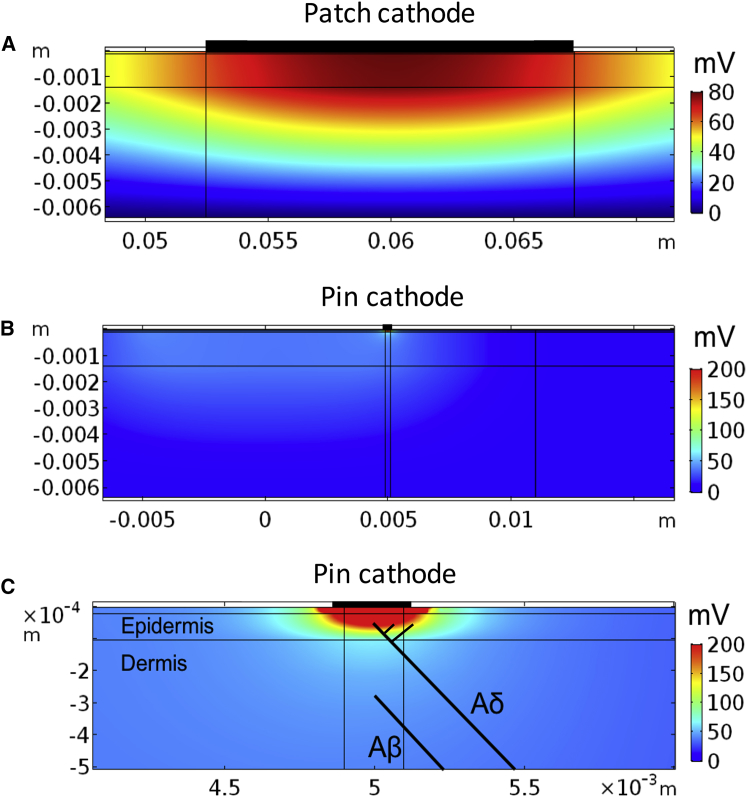
The distinction in spatial location of small and large fiber nerve endings is thought to generate the preferential activation of small fibers by the pin electrode because the pin electrodes have the potential to generate a high electrical current density in the most superficial skin layer (epidermis). To investigate this, the electrical field generated by the two electrodes are depicted in Fig. 3. The pin electrodes generate a local and high electrical current that is highly restricted to the stratum corneum and epidermis, whereas the patch electrode generates a larger spread of the electrical field, resulting in a large depolarizing electrical field also in deep tissues. To investigate how the electrical field from the electrodes is affecting the nerve fibers, we compared the electrical field along two axons, one Aβ and one Aδ, when a constant electrical stimulus of 1 mA was applied through the electrodes (Fig. 4). The pin electrode generated a substantially higher electrical field in the epidermis (0.18 V) compared to the patch electrode (0.08 V). If the electrodes were moved on the surface of the skin, away from the tip of the axon model, the high electrical field in epidermis was largely reduced for the pin electrode, indicating a small region of selective activation of small fibers for the pin electrode (see Fig. S1). The patch electrode was not as sensitive as the pin electrode to movements of the electrode (see Fig. S1).

Figure 3.

The electrical field generated by the two electrodes. A constant 1 mA stimulation current was applied through the electrode, and the electrical field was calculated by the finite-element method. (A) The electrical field generated underneath the cathode of the patch electrode is shown. (B) The electrical field generated underneath one of the pin cathodes is shown. (C) Enlargement of the electrical field generated underneath one of the pin cathodes is shown. The spatial locations of the two axon models are illustrated by the two black lines. Note the spatially localized and the large depolarization generated by the pin electrode in epidermis primarily innervated by nociceptive nerve fibers. To see this figure in color, go online.

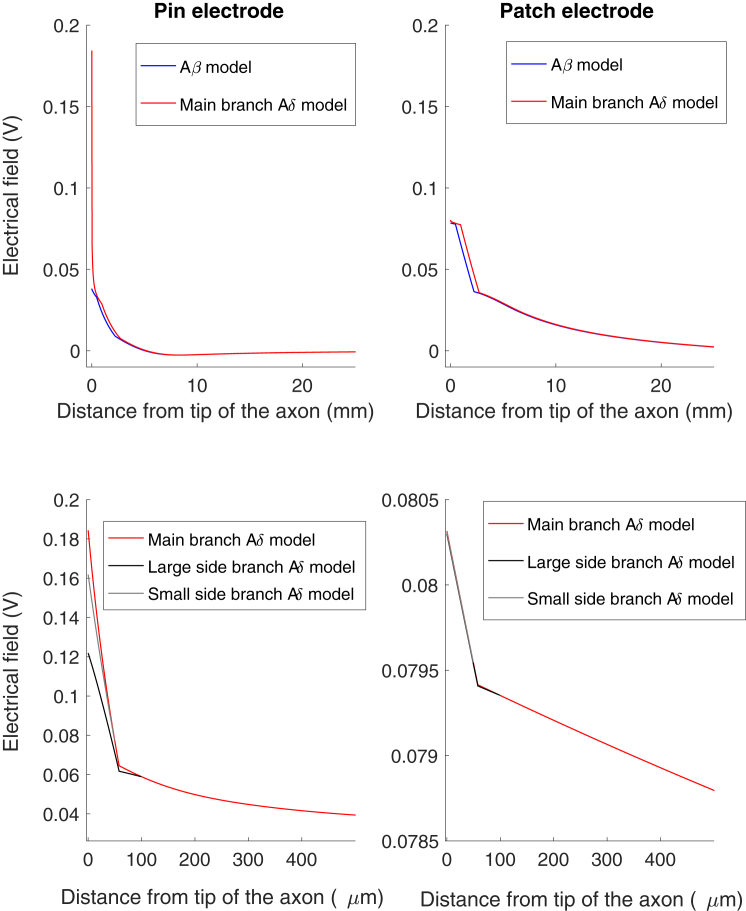
Figure 4.

The electrical field generated by the electrodes along the axons. The figure to the left depicts the pin electrode simulation, and the figure to the right corresponds to the patch electrode stimulation. The figure illustrates the electrical field generated by the two electrodes along the two axon models when a 1 mA continuous pulse was applied through the electrodes. Note the large difference between the electrical fields at the tip of the two axons when the stimulation current was applied through the pin electrode. The lower two figures illustrate the electrical field generated along the branches for the Aδ model. To see this figure in color, go online.

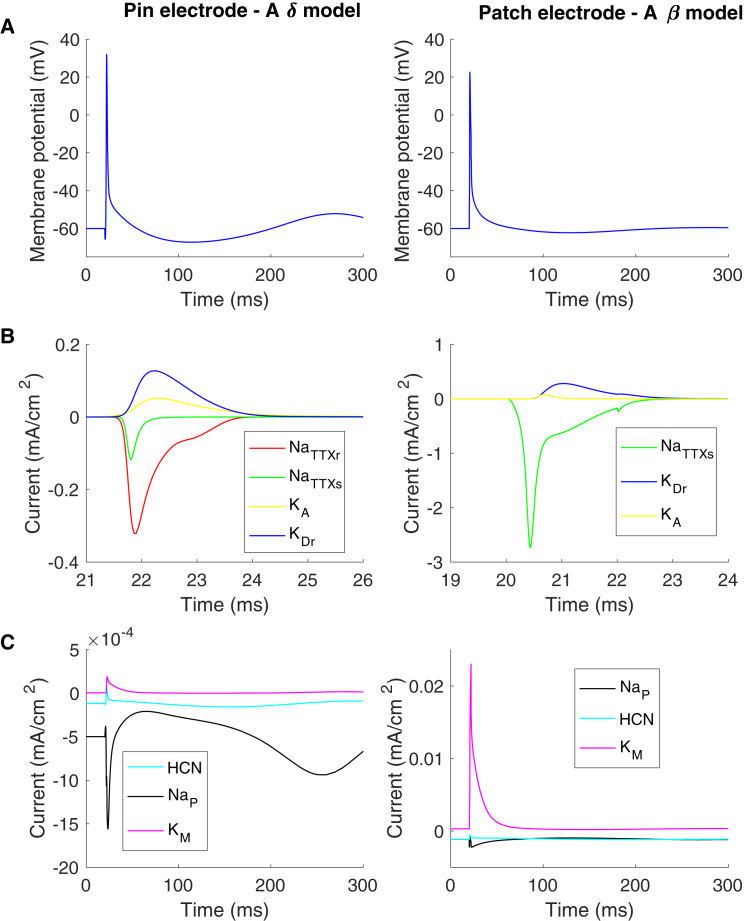
To study the action potential generation, a rectangular pulse with a duration of 2 ms was applied through the electrodes (see Fig. 5), leading to an action potential generated at the tip of the nerves, although, when the Aδ model was activated by the patch electrode, the action potential was generated in deeper tissue layers at the first nodes of Ranvier. In Fig. 5, changes in ion channel currents and membrane potential during an action potential are illustrated.

Figure 5.

Ion channel currents during an action potential. The figures to the left correspond to the simulation with the pin electrode (Aδ model), and the figures to the right correspond to the simulation with the patch electrode (Aβ model). After a single rectangular-pulse-shaped stimulation current (0.4 mA) with a duration of 2 ms, an action potential was generated. (A) Membrane potential and ionic currents recorded at the tip of the axon for both the Aδ and Aβ models are shown. (B) The large ion channel currents are shown. (C) The small ion channel currents are shown. In the Aβ model, the current density for the potassium current is low for both the K_A current and K_Dr current because the combined area of the juxtaparanode is five times larger than the node of Ranvier. To see this figure in color, go online.

The slow ion channels’ densities differ between the two models, particularly the K_M and the persistent sodium channels. For the Aδ model, the persistent sodium is the dominating slow current with a factor of five times higher peak current than the K_M current during an action potential. For the Aβ model, the dominating current is the K_M current, which is a factor of 10 times larger during an action potential (see Fig. 5).

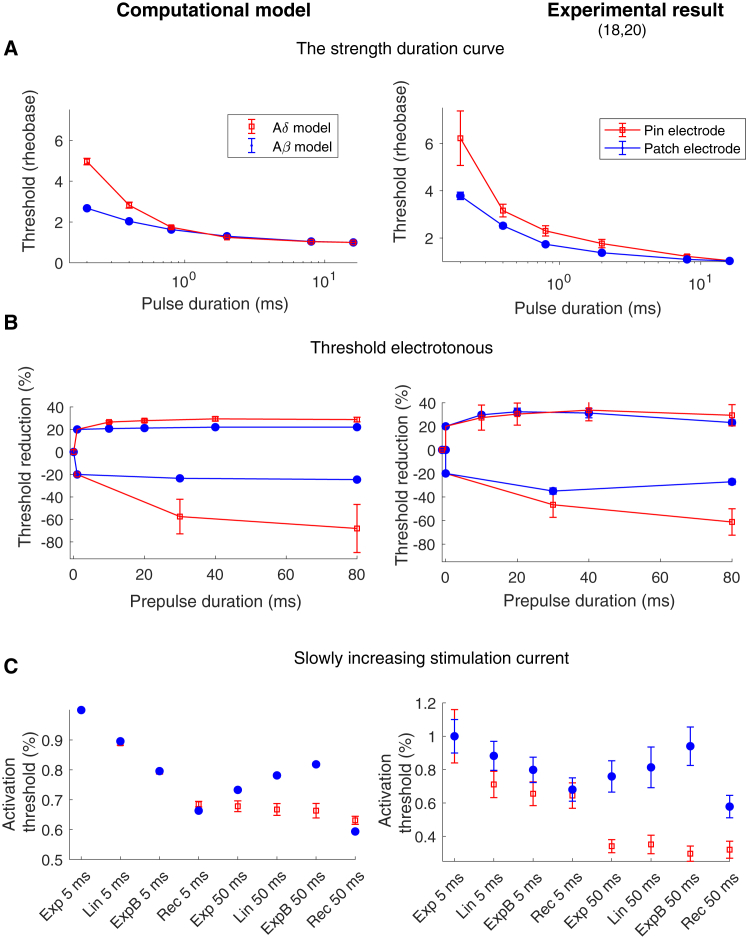
The nerve fiber model’s activation thresholds for the three protocols

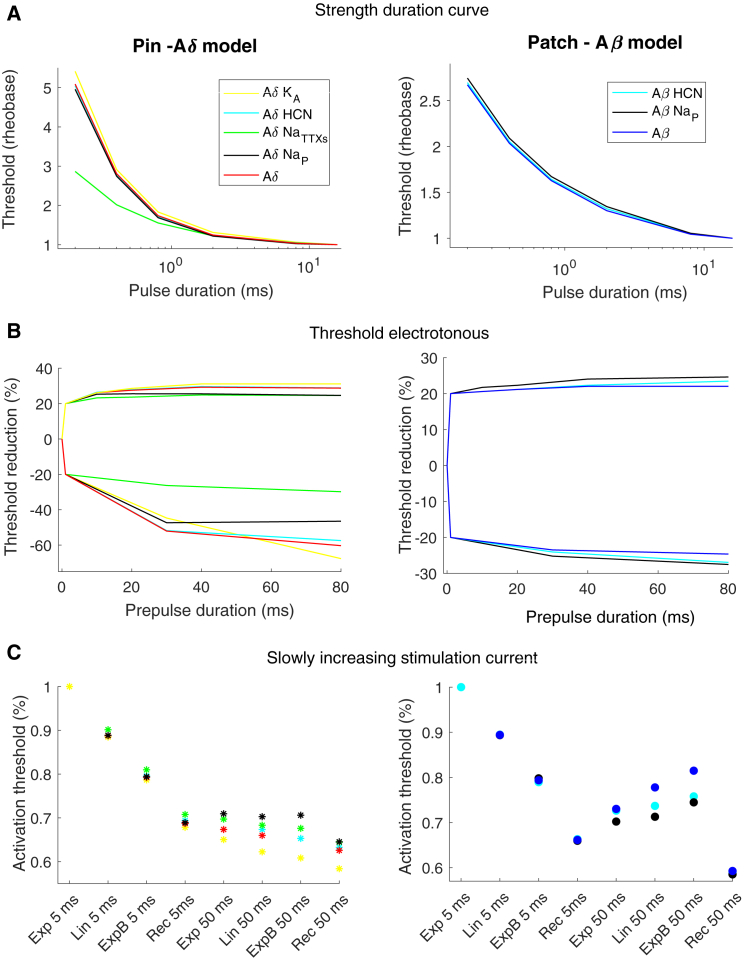
The stimulation current required to generate an action potential for the three different protocols was estimated for all seven spatial positions of the nerve fiber models. If the Aδ model was moved down 40 μm closer to the dermis-epidermis junction, the current needed to activate the fiber model exceeded the value of the Aβ model for the pin electrode. Therefore, this model was not included when the average activation threshold was calculated for the Aδ model. The strength-duration curve protocol measures the activation threshold for different durations of rectangular pulses (see Fig. 6 A). The Aδ model showed a higher increase in activation threshold for shorter pulses compared to the Aβ model. This is consistent with the experimental results showing a significantly higher time constant for the pin electrode (computational model: 633 ± 36 μs, experimental result: 1060 ± 690 μs (20)) than for the patch electrode (computational model: 428 ± 4 μs, experimental result: 580 ± 160 μs (20)). The strength-duration curve is strongly influenced by the fast sodium current which generates the action potential. Subthreshold prepulses are effective to increase the influence of slower ion currents on the activation threshold. In this study, the threshold electrotonus protocol was studied, which examines the excitability changes related to long subthreshold rectangular prepulses (10–80 ms), both depolarizing and hyperpolarizing prepulses. The Aδ model and the Aβ model show similar threshold alterations to subthreshold depolarizing prepulses (see Fig. 6 B). However, for long hyperpolarizing prepulses, the Aδ model had a large increase in the activation threshold compared to the Aβ model. For 80 ms hyperpolarizing prepulses, the activation threshold was increased by 68% in the Aδ model but only by 25% in Aβ model. This result is consistent with experimentally obtained measurements of the perception threshold, in which the only significant difference between the two electrodes’ threshold electrotonus was for long hyperpolarizing prepulses, for which the pin electrode had a significant increase in the perception threshold (61%) compared to the patch electrode (27%) (20).

Figure 6.

The activation threshold for the three protocols. The figures to the left correspond to the average activation thresholds estimated by the computational models, and the figures to the right correspond to experimental data (the data were given from the authors on request (18, 20)). The activation threshold was defined as the stimulation current needed to generate an action potential that propagated to the end of the axon model. The average activation thresholds for different spatial locations are illustrated in the figure to the right. The error bars represent the SD for the computational results and standard error for the experimental results. For abbreviation descriptions for the pulse shapes (Exp, Lin, ExpB and Rec), see Table 4. To see this figure in color, go online.

The last protocol measures the excitability for three different shapes of slowly increasing stimulation pulses: exponential increase (Exp), linear increase (Lin), and bounded exponential increase (ExpB), each with the same durations of either 5 or 50 ms. For the 5 ms duration, both the Aδ model and the Aβ model have a reduced activation threshold when the derivative of the initial phase of the electrical stimulus is high. For the longer 50 ms durations, the threshold is instead increased for the Aβ model from 0.73 (Exp 50 ms) to 0.82 (ExpB 50 ms) (see Fig. 6 C). This is consistent with the experimental study, which measures the perception thresholds for the patch electrode (18). In the experimental study, the patch electrode increased the activation threshold from 0.76 (Exp 50 ms) to 0.94 (ExpB 50 ms) (see Fig. 6 C). For the Aδ model, the activation threshold is not increased for the longer 50 ms duration, which is consistent with the activation threshold measured by the pin electrode (see Fig. 6 C). The rectangular (Rec) pulse was chosen as a control and generated a lower threshold for the 50 ms duration compared to the slowly increasing pulses, which is likewise consistent with experimental observations (18).

Longer-duration electrical stimuli may increase the preferential activation of small fibers

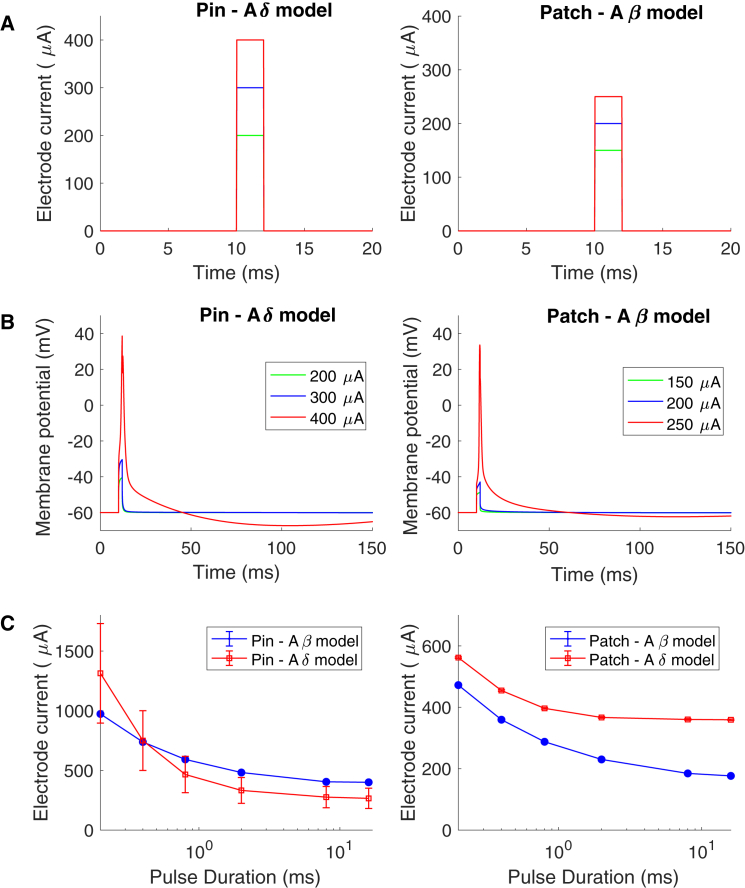
To study how selective the pin electrode is for the strength-duration and the slowly increasing stimulation current protocols, the activation thresholds of the different models were compared. For the strength-duration protocol, the activation thresholds for rectangular pulses with different durations are represented in Fig. 7. The activation threshold is considerably lower for the Aβ model compared to the Aδ model when the patch electrode is activating both axonal models. However, this is not the case for the pin electrode, for which the activation threshold is slightly lower for the Aδ model for pulse durations longer than 0.4 ms. For durations shorter than 0.4 ms, the pin electrode has a higher activation threshold for the Aδ model, which indicates that the selective activation of small fibers is reduced for short durations of rectangular pulses.

Figure 7.

The strength-duration curve for the pin and the patch electrode. (A) The stimulation current through the electrodes is shown. (B) The membrane potential corresponding to an extracellular field alteration when applying the current seen in (A) is shown. through the electrode. The nerve fiber model was placed underneath the electrode in the middle of the epidermis (Aδ model) or the dermis (Aβ model). (C) The average current needed to generate an action potential for different spatial location is illustrated in the figure. The error bars represent the SD. To see this figure in color, go online.

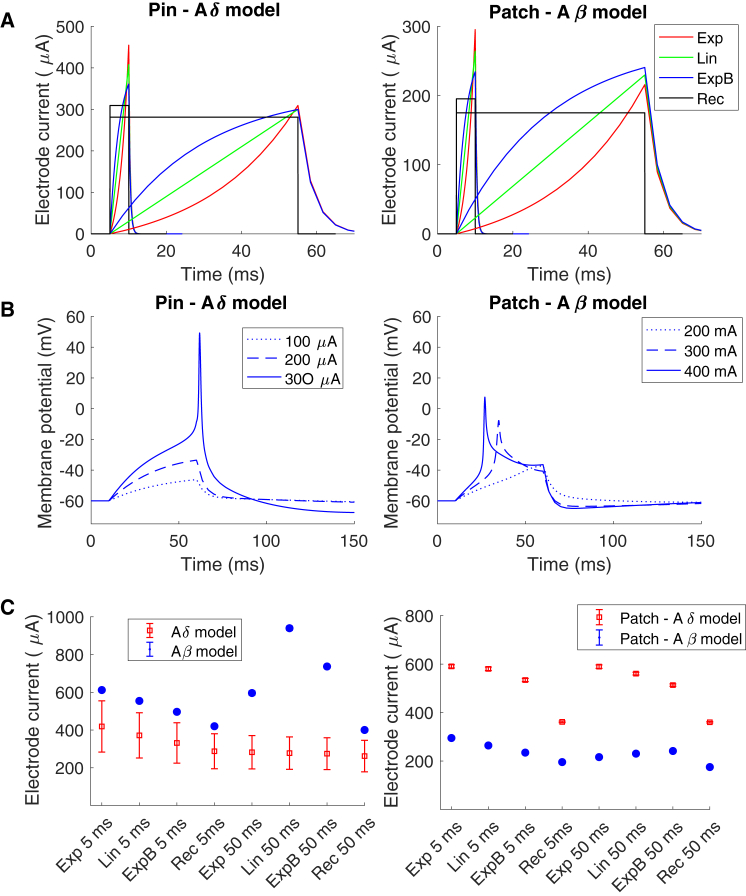
The same behavior can be seen for the slowly increasing stimulation currents, for which the difference in activation thresholds between the two models is larger for long durations compared to short durations for the pin electrode (see Fig. 8 C). The excitability change due to slowly increasing electrical stimuli is different between the two nerve models. The Aδ model becomes more excitable when the membrane potential is increasing slowly, and an action potential can be generated when the cell membrane is depolarized. For the Aβ model, slow depolarization leads to inactivation of sodium channels and to the inability to generate an action potential when the membrane is too depolarized. This can be seen in Fig. 8 B, in which the action potential for the Aβ model is not generated at the maximal depolarization level but instead before, compared to the Aδ model, in which the action potential is generated at the point of maximal depolarization of the cell membrane.

Figure 8.

The effect of slowly increasing electrical stimulation on the preferential activation of small fibers. (A) The stimulation current needed to generate an action potential for different shapes and durations of slowly increasing stimulation current is shown. (B) The membrane potential corresponding to an extracellular field alteration when applying the electrical current with the ExpB shape is shown (see Table 4). The nerve fiber model was placed underneath the electrode in the middle of the epidermis (Aδ model) or the dermis (Aβ model). (C) The average current needed to generate an action potential for different spatial location is illustrated in the figure. The error bars represent the SD. To see this figure in color, go online.

Varying the current densities of the voltage-gated ion channels

The computational model of peripheral nerve endings was sufficient to reproduce the differences in perception thresholds between the two fiber classes. To further study the underlying mechanisms for the differences in perception threshold between the electrodes, the influence of different subtypes of ion channels was studied. The ion channel densities that are selectively expressed in the different classes of fibers were altered: the Na_TTXs channel, the Na_p channel, the K_A channel, and the HCN channel. In small fibers, the action potential is generated by the TTX-resistant current (29), which is not the case in the node of Ranvier, where the dominating sodium current is the Na_TTXs current (32). The Na_TTXr and the Na_TTXs have different dynamics (29) and therefore affect the excitability differently. In Fig. 9, the Na_TTXs current density in the Aδ model was increased until an action potential was generated by the Na_TTXs current. This mainly reduced the activation threshold for short stimulus durations, resulting in a largely reduced time constant for the strength-duration curve (from 628 to 409 μs). Additionally, the strong influence of long hyperpolarizing subthreshold prepulses was reduced in the Aδ model with higher Na_TTXs current density (from 60 to 30%). Moreover, for the Aδ model, both the strength-duration curve and the threshold electrotonus became more similar to the perception threshold recorded for large fibers. For slowly increasing current stimulations, there was a minor change in the Aδ model activation threshold with an increase in the Na_TTXs sensitive current.

Figure 9.

Varying the ion channel current densities. The figures to the left correspond to the activation thresholds estimates by the computational model for the Aδ model when the pin electrode is activating the nerve model. The activation thresholds were calculated when the fiber model was placed underneath the electrode in the middle of the epidermis (Aδ model) or dermis (Aβ model). For the Aδ model, the Na_P and K_A currents were reduced to 10% of their original value. The HCN current and the Na_TTXs current were increased by factors of 2 and 8, respectively. The figures to the right correspond to the activation thresholds estimated by the computational model for the Aβ model when the patch electrode is activating the nerve model. For the Aβ model, the HCN current was reduced to 10% of its original value, and the Na_P density was increased by a factor of 1.5. To see this figure in color, go online.

If instead the Na_p channel’s current density was reduced, the activation threshold for electrotonus and slowly increasing current stimulation was affected, but the activation threshold for the strength-duration curve remained unchanged (see Fig. 9). For instance, the strong effect of hyperpolarizing long prepulses (80 ms) in the Aδ model was reduced from 60 to 46% and became more similar to the Aβ model threshold (25%). Additionally, the low activation threshold for slowly increasing electrical stimulation (ExpB) was increased from 0.65 to 0.71, which is closer to the Aβ model activation threshold (0.81).

When the current density for the subtype of Na_p channels expressed in large fibers was increased in the Aβ model, the activation threshold for long slowly increasing current stimulation was reduced (from 0.81 to 0.74) and became more similar to the Aδ model’s activation threshold (0.65). A reduction of the HCN current density did not influence the activation threshold of the Aβ model considerably.

Discussion

In a previous study, the excitability in an unmyelinated axon model was examined (25), and in this study, the model was further developed into an Aδ model and an Aβ model and included a finite-element model of the skin and two cutaneous electrodes. The origin of the differences in perception thresholds between two electrodes has been studied, and the hypothesis was that the main difference could be explained by different distributions of voltage-gated ion channels and along with differences in morphology between peripheral nerve of small and large fibers. The voltage-gated ion channel densities and morphological differences between the two fiber classes were sufficient to reproduce the main difference in perception threshold between the two electrodes; in particular, the voltage-gated ion channels play a pivotal role.

Computational models of axons and their clinical implications

Even though the field of computational models of central and peripheral nerves arose from Hodgkin’s and Huxley’s squid axon model (33), the number of existing detailed computational models of peripheral small fibers is surprisingly low. Because it is technically difficult to perform intracellular recordings on axons, particularly on thin fibers, there is a lack of data regarding ion channel densities and dynamics. One of the most detailed computational models of a nociceptor is an unmyelinated axon model (26, 34, 35), which was constrained by latency measurements recorded by microneurography. The computational model developed in our study is a combination between the C-fiber model and the Aδ/Aβ model developed in the Mørch et al. study (25). The current computational model combines a computational model of the skin to estimate the extracellular potential with a detailed nerve fiber model with a wide range of voltage-gated ion channels. Existing spaced-clamped models, which lack spatial distribution, have been able to link threshold tracking measurements of compound motor and sensory action potentials to subtypes of voltage-gated ion channels (36, 37, 38, 39, 40). The novelty of our computational model is that it can link perception threshold measurements to voltage-gated ion channel activation in both an Aδ model and an Aβ model. Furthermore, spaced-clamped models of large fibers have been successfully used to identify abnormalities in voltage-gated ion channel densities during pathological conditions (30, 41). Our computational model may be used in a similar fashion. Because perception threshold tracking is a noninvasive and inexpensive method, the model could be a useful tool for understanding the mechanisms of painful peripheral neuropathy, particularly that due to channelopathies. Increased excitability has been identified as an underlying mechanism in many peripheral neuropathies (1). However, the underlying ionic current or passive property alterations resulting in such increased excitability is essentially unknown. For instance, the identification of a specific voltage-gated ion channel or groups of ion channels contributing to the excitability could be used as a powerful diagnostic tool as well as to potentially provide important guidance to the development of novel analgesic drugs. Different subtypes of ion channels affect different aspects of membrane excitability. For instance, slowly activating ion channels mainly affect the excitability when long current simulation is applied, whereas rapidly activating channels have strong influence on excitability of short current stimulations (see Fig. 9). Assuming that a pathological regulation (up or down) of a voltage-gated ion channel has occurred, would it be possible to distinguish which subtypes of ion channels have been altered by an intelligent measure of the perception threshold? By means of example, the three ion channels—the persistent sodium channel, the Na_TTXs channel, and the K_A potassium channel—have all been implicated in peripheral neuropathy (42, 43, 44). If the Na_TTXs current is increased, the activation threshold for small rectangular pulses will be significantly reduced, whereas an increase of the persistent sodium current would mainly affect excitability for slowly increasing pulses or subthreshold prepulses (see Fig. 8). A reduction of the K_A current would mainly affect the excitability for slowly increasing pulses. All three alterations of ion channels should therefore theoretically be possible to identify by perception threshold measurements. This indicates also that computational models may be used as a diagnostic tool to identify ion channelopathies related to small fiber neuropathy.

The mechanism underlying the differences in perception threshold between the electrodes

The excitability in large fibers can be studied by threshold tracking techniques measuring the compound muscle action potential (45). However, the small nociceptive fibers’ compound action potential is technically difficult to assess. Our research group has therefore previously used the perception threshold measurements instead of the compound action potential as an indirect measurement of the excitability in the small fibers (18, 20). The disadvantage of using the perception threshold instead of the compound action potential is the influence of the central nervous system on the measurements, such as habituation, expectation, and attention. Fortunately, the main effect on the perception threshold seems to originate from peripheral nerve mechanisms because excitability protocols such as the threshold electrotonus and strength-duration curve display very similar behavior regardless of whether the measurements relate to the perception threshold or the compound action potential (20, 45). Perception thresholds may therefore be used as an indirect measurement of the membrane excitability of nerve fibers (20). Moreover, the computational model could reproduce the experimentally measured differences in perception thresholds between the two electrodes. When the densities of the ion channels were altered, this had a strong effect on the activation threshold of both models. Interestingly, when the Na_TTXs, which is highly expressed in nodes of Ranvier (32), was increased in the Aδ model, the strength-duration relation chronaxie was reduced from 628 to 409 μs, approaching the value for the Aβ model 428 μs. Also, the large increase of the activation threshold for hyperpolarizing prepulses reduced from 60 to 30%, which is within the range of the experimentally measured value of the patch electrode. This result implicates that the major difference between the strength-duration relationship and the threshold electrotonus of the two electrodes could be explained by the expression of Na_TTXs.

Preferential activation of small nerve fibers by cutaneous electrodes

Preferential activation of small fibers by cutaneous electrodes has been performed by several different types of pin electrodes, all with the common feature of a small cathode (9, 10, 11, 12, 13). Both objective measurements, such as conducting velocity measurements (12, 13, 19) and reflex measurements (10), as well as subjective measurements, such as the quality of the perception (9, 18), support the preferential activation of small fibers by a small area cathode. In our previous computational study (25), the results support that the pin electrode has the potential to generate a high electrical field in the epidermis, where the free nerve endings of small fibers are located. In this study, a more detailed computational model was used, showing that this explanation seems to be valid. Even though the pin electrodes preferentially activate nociceptors, the noninvasive pin electrodes mainly activate Aδ fibers and not C-fibers. The ability to increase the preferential activation of small fibers would be beneficial for studying C-fibers. The results from the computational model predict that the small fibers’ nerve endings need to be located close to the pins of the electrode for the electrode to preferentially activate these fibers. Multiple pins on the electrode may therefore be preferable to increase the amount of small fibers being activated concurrently, which might be needed for the assessment of the perception threshold. Additionally, the results from the model predict that a longer duration of the electrical current, particularly slowly increasing electrical currents, may increase the preferential activation of nociceptors. As long as up to 50 ms durations of slowly increasing electrical input has been proposed to be used to increase the preferential activation of nociceptors (18, 46). The results from our computational models support these experimental results and suggest that the underlying mechanism generating the increase in preferential activation is a selective expression of specific ion channels in nociceptors. To generate the reduced perception threshold of nociceptors for long, slowly increasing electrical stimulus, the model predicted that both the Na_TTXs current as well as the K_M current should be minimally expressed. This result is consistent with the excitability alteration due to long ramp pulses measured in large fibers, for which the reduced excitability for long durations of slowly increasing electrical input is generated by inactivation of sodium channels and the K_M current (45). Small fibers may be less sensitive to depolarization of the membrane because the Na_v1.8, selectively expressed in nociceptors, inactivates at more depolarized membrane potential than the Na_TTXs channels expressed at the node of Ranvier (29).

Limitations of this study

In the finite-element model, several features of the skin were omitted to reduce the computational complexity. For instance, the junctions between the layers were modeled as horizontal planes where the skin layers represented the average features of the skin. The skin is not a homogenous tissue but is innervated by sweat glands and hair cells. For instance, when the electrode is moved over the skin surface, the absolute value of the perception threshold is altered because of, e.g., the proximity to a nerve ending or a sweat gland. The heterogenous composition of the skin and the electrode-skin interface has a strong influence on the absolute value of the perception threshold but less so on the relative difference in perception threshold for electrical stimulation in the range between 0.2 and 50 ms. For such reasons, the normalized perception thresholds were compared to reduce the effect of heterogeneous skin composition. The skin’s dynamic effect on the electrode current is small and has therefore been omitted (Fig. S2).

Even though the computational model includes seven voltage-gated ion channels, the model does not include any calcium channels, which play an important role in regulating the excitability changes in nerve fibers. Finally, the major limitation to this study is the fact that the effect from the central nervous system on the perception threshold was omitted.

Conclusions

Because a computational model of peripheral nerve endings could successfully reproduce the experimental results from recorded perception threshold measurements, the hypothesis that peripheral membrane excitability as well as morphology contributes significantly to the perception threshold was supported.

Additionally, the results from this study indicate that a computational model could have the potential to link perception threshold tracking to the activation of specific ion channel subtypes, for instance, Na_TTXs, Na_TTXr, and Na_p. Furthermore, the two computational models could be used to investigate how to further increase preferential activation of nociceptors by comparing the activation threshold differences.

Author Contributions

J.T., A.H.P., C.D.M., and O.K.A. conceived and designed the research. J.T. carried out all simulations and analyzed the data. J.T., A.H.P., C.D.M., and O.K.A. wrote the article.

Editor: Michael Grabe.