Orbiting of Flagellated Bacteria within a Thin Fluid Film around Micrometer-Sized Particles

Abstract

Bacterial motility under confinement is relevant to both environmental control and the spread of infection. Here, we report observations on Escherichia coli, Enterobacter sp., Pseudomonas aeruginosa, and Bacillus subtilis when they are confined within a thin layer of water around dispersed micrometer-sized particles sprinkled over a semisolid agar gel. In this setting, E. coli and Enterobacteria orbit around the dispersed particles. The liquid layer is shaped like a shallow tent with its height at the center set by the seeding particle, and the meniscus profile set by the strong surface tension of water. The tent-shaped confinement and the left handedness of the flagellar filaments result in exclusively clockwise circular trajectories. The thin fluid layer is resilient because of a balance between evaporation and reinforcement of fluid that permeated out of the agar. The latter is driven by the Laplace pressure caused by the concave meniscus. In short, we explain the physical mechanism of a convenient method to entrap bacteria within localized thin fluid film near a permeable surface.

Significance

This report establishes a physical mechanism for the occurrence of a resilient, tent-shaped layer of liquid that entraps motile bacteria. The mechanism is relevant to practical situations involving bacterial behavior, such as their accumulation at and adhesion to surfaces, biofilm growth, development of bio-microdevices, cleansing hygiene, infection control, etc.

Introduction

Hydrodynamics and confinement dominate bacterial mobility near solid or air-water boundaries, causing flagellated bacteria to move in circular trajectories. A flagellated bacterium propels itself by rotating its flagella relative to its body, which counter-rotates (1). Freely swimming bacterial cells tend to accumulate close to solid surfaces (2, 3, 4), with their residence times within a few micrometers (up to 1–3 μm) from the boundary lasting several seconds (5). The coupling of body rotation and enhancement in the drag force exerted on the part of the cell closer to the solid surface causes the bacterium to move in circular trajectories (6, 7). The handedness of the flagella determines whether the circular trajectory is clockwise or counterclockwise. Escherichia coli, for example, moves forward in clockwise paths when looked at from above (8), propelled by its flagellar filaments with left-handed helical structure; for the same reason, it swims on the right-hand side when prevented to turn by a solid wall on its side (9).

Numerous experimental techniques, including microfluidic devices (10, 11), droplets (12, 13, 14, 15), and vortices (16), have been developed to confine and maneuver motile bacteria. The mode of bacterial motility can also be shaped by confinement. For example, whereas flagellated bacteria swim in liquid, they may move collectively on a solid surface in the form of swarming motility (17, 18, 19, 20). Swarming motility triggers a variety of adhesive mechanisms, including those preceding the growth of biofilms (21, 22, 23). Therefore, the study of bacterial near-surface motility has broad implications, such as in biofouling (24) and infection (25).

This report describes the swimming motility of flagellated bacteria in shallow tents of liquid films seeded by graphite particles or glass beads a few micrometers in diameter. Around these particles sprinkled over the agar surface, one or more bacteria move in persistent circular trajectories for over several minutes. We account for the observed phenomenon with a physics-based model encompassing hydrodynamic analysis, surface tension, evaporation, and porous flow. We also discuss broad implications of the mechanism elucidated by this study.

Materials and Methods

Bacterial strains

Six strains of bacteria were used. Strain HCB33 (wild-type E. coli) was acquired from Howard Berg (Harvard University, Cambridge, MA). Pseudomonas aeruginosa PAO1 was provided by Keiko Tarquinio (Emory University Medical School, Atlanta, GA). Bacillus subtilis 3610 was obtained from Daniel B. Kearns (Indiana University, Bloomington, IN). The remaining three strains were isolated at the Albert Einstein College of Medicine (Bronx, NY). Specifically, H5 is a swarming strain of E. coli from human feces (Committee on Clinical Investigation # 2009-446-006; Institutional Review Board # 2015-4465); SM1 and SM3 are novel strains of swarming Enterobacter sp. isolated from mouse feces (presently undergoing species characterization).

Sample preparation

Bacteria (with the exception of P. aeruginosa) were grown in suspensions of lysogeny broth (LB) medium overnight (∼16 h), and then a 5 μL droplet was taken to inoculate the center of a petri dish containing LB agar gel (LB plus 0.5% agar). Triton X-100 (Sigma-Aldrich, St. Louis, MO) was added (0.1% in volume) to the LB agar as external surfactant for E. coli inoculation to accelerate its colony spread. In particular, it was observed for the H5 strain that with the addition of Triton X-100, the colony spread at a similar rate to what is seen in a typical species of swarming bacteria; it populated the whole petri dish (10 cm in diameter) within a few hours. For the HCB33, the effect of Triton X-100 addition was not as dramatic, and the colony grew only slightly faster compared to when no external surfactant was added to the growth medium. P. aeruginosa was grown overnight in a suspension of tryptic soy broth (TSB), and then, a 5 μL droplet from the culture was inoculated on a petri dish containing TSB agar gel (TSB plus 0.5% agar).

The samples were placed into an incubator with a controlled temperature of 37°C and 50% relative humidity for 3–5 h, depending on the growth rate. In the next step, a droplet containing micrometer-sized particles (graphite or silica beads) was placed at a location close to the swarm front so that the region over which the droplet spread overlapped with the colony, as illustrated in Fig. 1 a. Graphite particles were obtained by scrapping a pencil with a razor blade and then dispersed in deionized water. Silica beads (4.5 μm in diameter; Bangs Laboratories, Fishers, IN) were also diluted in deionized water. After the addition of the water droplet, the petri dish was gently tilted in different directions to guide the droplet to spread away from the bacterial colony. This motion created thin water layers that evaporated within a minute or two on the agar surface. Most bacteria then got stuck on the dried surface, leaving a small number of swimming bacteria trapped in shallow films of water around the dispersed particles.

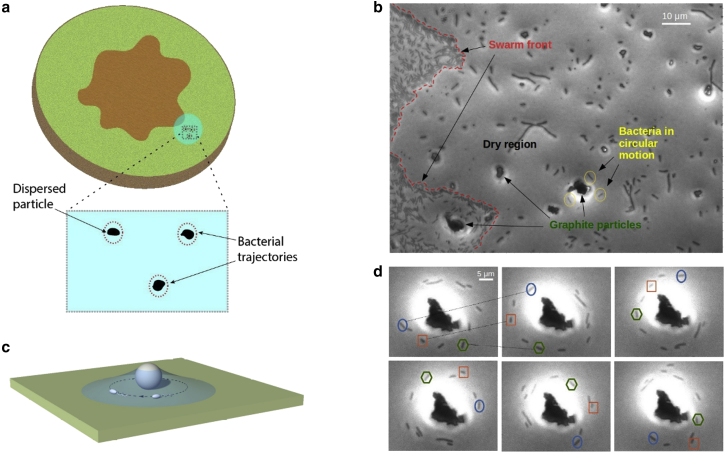
Figure 1.

Circular motion of bacteria around particles on the agar surface. (a) Schematics representing a bacterial swarm (in purple) with a water droplet (containing graphite particles or silica beads) added to a location overlapping the swarm front are shown. A region in the droplet is amplified to illustrate bacterial trajectories around the dispersed particles. (b) Micrograph shows different features following the water droplet evaporation. The swarm front is marked by the red dashed line. Most of the region beyond has dried and is populated by bacteria stuck to the surface, except for those around graphite particles. (c) Shown is an artistic representation of bacterial cells moving around a dispersed particle within a tent-like layer of water around it. (d) Shown is a time lapse following the trajectories of bacterial cells orbiting a graphite particle. Three cells in particular are highlighted with different colors and geometrical contours to aid visual tracing. The sequence goes from left to right, and the pictures shown were taken ∼0.47 s apart. These images were extracted from Video S1. To see this figure in color, go online.

Imaging, measurements, and graphic illustrations

Particles and bacteria on the agar surface were imaged under an upright microscope (Eclipse E800; Nikon, Tokyo, Japan) with a 40× objective lens, coupled to a charge-coupled device camera (Coolsnap EZ; Photometrics, Tucson, AZ). The imaging was controlled by the software MetaMorph (Molecular Devices, San Jose, CA) through which the videos were recorded. The recording rate ranged between 10.72 and 33.88 fps, with lower frame rates chosen for larger imaging areas as needed.

We define a boundary for fluid film around seeding particles as a circular region within which bacteria remain motile. We refer to the radius of this region as the meniscus radius. In practice, the meniscus radius was determined by identifying the five nearest immobilized bacteria around a particle and averaging their distances from the center of the particle. In rare cases, the average was obtained from only three or four distances because the number of immobilized bacteria in the surroundings was lower than five. Thus, our estimate was limited by the optical microscopy images acquired. A full meniscus profile, such as the one obtained with x-ray microscopy in (26), could expand beyond the region defined in this study. Bacterial trajectories and their swimming speeds were calculated using ImageJ from their captured positions in video clips. The numerical calculation applying resistive force theory was implemented in a Python code.

Confocal microscopy was done using an Olympus FV3000 Laser Scanning Microscope (Olympus, Tokyo, Japan) with excitation wavelengths of 488 and 561 nm. The procedure followed a previous publication (27) but was modified because of the peculiarities of our system. To label the agar gel, 0.1 mg/mL solution of Nile red in methanol was mixed in a proportion of 1:100 volume/volume into LB agar in a hot liquid state. Then, 20 μL of the mixture was deposited on a FluoroDish (World Precision Instruments, Sarasota, FL), forming a very thin layer of gel (on the order of 100 μm). Such a thin gel was required for confocal imaging using the inverted microscope so that the gel surface was within the focal depth of a 60× objective lens. In this setting, the transmission lights travel through the gel to enter the objective without being refracted by the large beads sitting on the gel surface. Because of evaporation of fluid in the thin gel, however, there is a limited time window for sample preparation and confocal imaging. Right after the gel was pulled, a mixture of 4.5 μm silica beads and 0.5 μm fluorescent Dragon Green beads (Bangs Laboratories) at a ratio of 1:2000 was added on top of the gel. The smaller beads served as an additional label for tracing the gel surface. The Dragon Green dye was excited by both blue and green lights but more strongly by blue to emit green light. Nile red was mainly excited by green light, emitting red light. It was found to concentrate at the gel surface. Image analysis and processing were done using ImageJ. Adobe Illustrator was used to vectorize images of vertical slices of the data and obtain middle lines through a high-intensity band on these images, locating the gel surface.

To convey physical pictures of bacteria and liquid films, which are invisible under optical microscopy, several figures include illustrations generated using Rhinoceros, a CAD software widely used by architects and designers. Indications are made in respective figure captions where secondary features may have been omitted in those illustrations for the sake of simplicity.

Hydrodynamic model

Lauga et al. developed a model based on resistive force theory to represent bacteria moving close to solid boundaries (28). It models a bacterium as formed by a sphere connected to a helical rod to represent the cell body and flagellar bundle, respectively. The free-swimming organism is subjected to zero net force and torque and is propelled by the rotating flagellar bundle. Body and flagella are characterized by their respective mobility matrices, which appear in the linear system of equations (Eq. 1), given the velocities and rotation rates of the cell body in Eqs. 2 and 3, respectively.

$$\left(A+B\right)X=BY,$$ (1)

where

$$X={\left(Ux,Uy,Uz,\text{Ω}x,\text{Ω}y,\text{Ω}z\right)}^T,$$ (2)

$$Y={\left(\mathrm{0,0,0,0},\omega ,0\right)}^T.$$ (3)

Matrix A is the mobility matrix of the cell body. B is the mobility matrix of the flagella. U_i gives the i-th component of the velocity, and Ω_i gives the i-th component of the rotation rate of the cell body. The rotation rate of the flagella is given by ω. The cell is set to initially align with the y axis without loss of generality. Reference (28) gives the details on how to build the mobility matrices.

The velocities and rotation rates in this model are dependent on the gap distances between the surface and the material parts of the model bacterium. The speed U of the bacterium in circular motion is given by the components along the bottom surface U = (Ux² + Uy²)^1/2, and the radius of curvature R of the cell trajectory is also obtained from the solution of the linear system $R=U/\left|{\mathit{\Omega }}_z\right|$.

Results and Discussion

Circular motion around particles on agar surface

Our experiment starts by adding a tiny droplet of water (2–5 μL) next to a swarming colony, which causes some swarming bacteria to break away into swimming (see Sample preparation; illustrated in Fig. 1 a). This procedure allows us to select actively motile cells, usually seen at the swarm fronts. In a previous study on E. coli (9), the authors also focused on the edge of the swarming colony to select cells transitioning from swarming to swimming motion. We note in our experiment that a number of bacteria leave their pack at the swarm front and disperse over the agar surface (Fig. 1 b). As the droplet of water evaporates, most bacteria get stuck to the surface (in ∼1 min) and cease the swimming motion. However, graphite particles or silica beads settled on the agar surface entrap a layer of water in their surrounding regions, allowing a few bacteria to swim around them, exclusively in clockwise trajectories (Fig. 1, c and d) (Videos S1, S2, and S3). Such an orbiting motion lasts over 10 min during observation, much longer than the time expected for a water film a few micrometers in thickness to disappear due to evaporation, as assessed later in the section.

We observed common orbiting motion among a wild-type strain of E. coli (HCB33) and three recently isolated strains of bacteria, including two novel Enterobacter isolates, SM1 and SM3, and one E. coli isolate, H5 (details in Materials and Methods). For the two E. coli strains, we used 0.5% agar containing added surfactant Triton X-100 (Sigma-Aldrich) of 0.1% vol/vol to facilitate the colony spread, making it easier to select active cells from the colony border. It should be stressed, however, that shallow tents of fluid around the micrometer-sized particles were observed in both cases with or without surfactant added into the agar. Enterobacter sp. readily swarms on the agar gel without additional surfactant, which was the condition for the majority of our experiments. We also experimented with P. aeruginosa (PAO1) and B. subtilis (3610). In these two cases, we also noticed long-lasting water layers around the micrometer-sized particles in which bacteria were motile. For P. aeruginosa, we observed orbiting around the microsized particles, but the motion was less organized (Video S4). The motile cells near the particles tended to go off track from their orbits within a few seconds, possibly due to this species of bacteria frequently reversing flagella motor rotation direction, with a characteristic transit time of 0.56 s (29). B. subtilis, which are longer cells (4–10 μm in length), remained motile within the water meniscus, but they did not orbit persistently. Instead, their maneuvering appeared severely confined by the small regions of the shallow film. These results suggest a common mode of motion of bacteria entrapped around microsized particles on moist surfaces, although the exact trajectories and maneuverability are species dependent. From here on, we focus the remaining report on Enterobacter sp. and E. coli, which reliably form circular trajectories.

Effects of particle size on the radii of meniscus region and bacterial orbits

Small graphite particles (<2.5 μm in size) are usually not surrounded by swimming cells, possibly because they could not retain the water reservoir large enough to entrap bacteria. Large graphite particles (>12 μm in size) retain liquid in a region over 40 μm in radius and thus keep many bacteria swimming in their proximity. Intermediate graphite particles were frequently seen to be surrounded by a few active swimmers and were the ones around which the orbiting of bacteria was most often observed and measured (Fig. 1 d). In cases in which the number of swimmers around a dispersed particle is big (over a dozen, as is commonly seen around large graphite particles or particles immersed in a dense bacterial population), the cells frequently bump into each other, making it difficult to discern individual trajectories. We chose silica beads of uniform size (4.5 μm in diameter) to perform the same experiment and observed equivalent results between the beads (Fig. 2 a) and the graphite particles of comparable size, suggesting that the key parameter is the particle size, not its exact shape nor its chemical nature. The common role of the graphite particles and silica beads is to sustain a tent-shaped water reservoir around them. We also observed that for E. coli (Video S2). They do not tumble as frequently when compared to bacteria grown in bulk liquid, a result reported previously for similar swarming colonies (30).

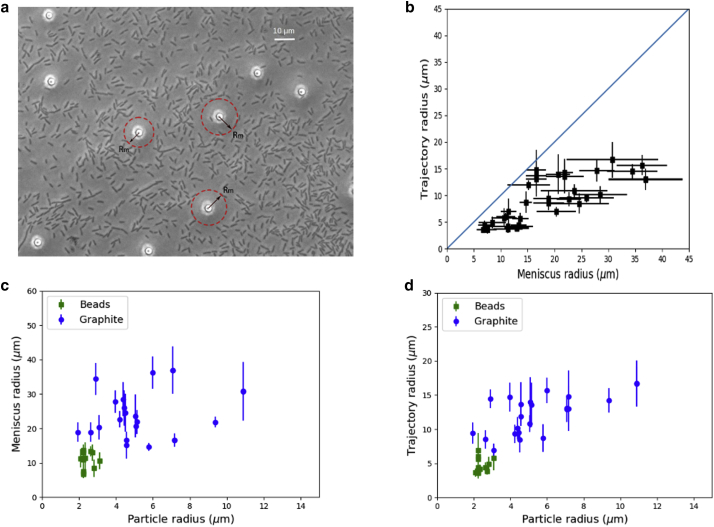
Figure 2.

Image with meniscus of water layer indicated and plots of the measured dependence between meniscus and trajectory radii and particle size. (a) Shown is a micrograph highlighting the meniscus edge of water (radius Rm; defined in Materials and Methods under Imaging, measurements, and graphic illustration) around silica beads. Bacteria outside these circles are stuck in dried regions, whereas a few bacteria within these circles orbit around the beads (Video S2). (b) Shown is the relationship between the cutoff radius of the water meniscus around dispersed particles and the trajectory radius for bacteria orbiting these particles. The blue diagonal line of 45° is a visual guide, which confirms the expected observation that the trajectories are confined within the meniscus. This plot includes orbits around both beads and graphite particles. (c) Shown is the relationship between the size of dispersed particles and the cutoff radius of their surrounding water meniscus. Each data point is an average of five measurements (see Materials and Methods for details on how these measurements were made). (d) Shown is the relationship between the size of dispersed particles (graphite or beads) and the radius of trajectories of orbiting bacteria averaged over three complete orbits around the seeding particle. In (b–d), the error bars represent SD. In (b), the error bars are shown in both the x and y axes. To see this figure in color, go online.

Around the particles where bacteria were observed to orbit, the radii of meniscus and bacterial trajectories both increase with the particle size (Fig. 2, c and d). The general explanation is that bigger particles create taller water tents of larger radii of meniscus, allowing the motile bacteria in the tent to move in larger orbitals. The trajectory radius must always be smaller than the meniscus radius, beyond which cells become immobilized. Accordingly, we see a clear correlation between trajectory radius and meniscus radius, with the latter setting the upper limit for the other radius, as shown in Fig. 2 b. For the silica beads, which are uniform in size, the meniscus and trajectory radii vary within narrow ranges. Graphite particles, which were more variable in size and had irregular shapes, gave rise to a larger variation in meniscus and trajectory radii (Fig. 2, b–d).

Causes for the circular trajectories and hydrodynamic analysis

The orbiting bacteria were observed to be in the same focal plane as the bacterial cells stuck in the nearby dry regions, suggesting the solid confinement imposed by the agar surface to be a key factor for the circular trajectories. Numerous previous studies have shown that bacteria swim in circular trajectories near a solid surface (6, 7, 28). Such a hydrodynamic effect is expected to be strong in this experiment because of close proximity of the cells to the agar surface. Here, however, the trajectories are also subjected to additional constraints imposed by the tent-shaped film, especially the meniscus radius as its boundary cutoff. These constraints appear strong enough to keep the entrapped bacteria swimming persistently in circular trajectories. In contrast, the boundary effects due to graphite particles on the bacterial trajectories may be neglected with the exception of close encounters. In some cases, bacteria were seen to swim within a body length from the center particle or occasionally to even collide with it, but most often orbiting bacteria swam over 8 μm away from the particle, a distance by which the hydrodynamic effect of the graphite boundary becomes negligible (5). These observations reinforce the argument that the circular trajectories are caused by the proximity of the bacteria to the agar surface and the meniscus boundary but not the particle surface.

Measurements on all four strains show a common trend between the speeds of orbiting bacteria and the radii of the curvature of their trajectories. Bacteria swam slower in trajectories of smaller radii, but beyond a certain threshold (∼7 μm), the speed approached an upper limit, between 30 and 50 μm/s, depending on the bacterial strain (Fig. 3 a). These results suggest that graphite particles or beads affect the swimming speed by restricting the bacteria to their close proximity via the tent-shaped liquid film around them. Within smaller trajectories, bacteria cells are more restricted when compared to those that interact only with agar surfaces. Under such conditions, the meniscus may push the cells closer to the agar surface, making them experience more drag and hence slowing them down.

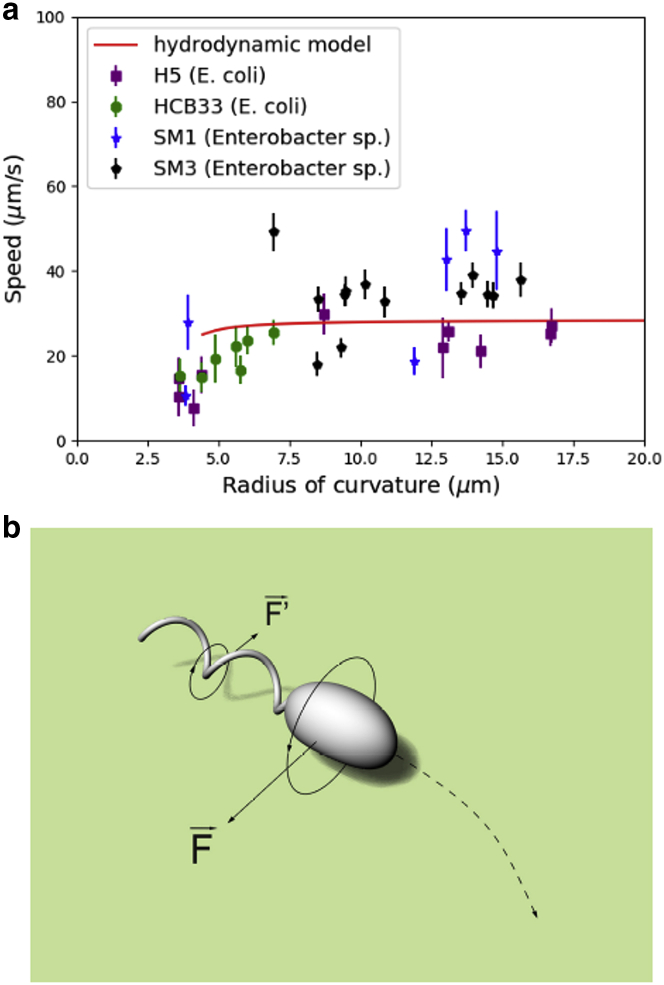
Figure 3.

Measured speed versus radius of trajectory in comparison with numeric predictions by applying a simple hydrodynamic model. (a) Shown is the speed of bacteria with respect to the radius of curvature of trajectories for the four strains tested. The red line is the prediction by applying resistive force theory (with parameters specified in Table S1). The lower end of the line is set by the 5-nm minimal gap chosen between the cell body and the bottom surface in the model. Each data point represents measurements for an individual bacterium. (b) Shown are schematics showing the curvilinear trajectory of a bacterium when it swims close to a solid boundary. The cell body and its flagellar bundle rotate in opposite directions. The larger drag on the cell body at the location facing the surface exerts a lateral force in the opposite direction to that on the flagella (forces indicated in the figure) is shown. The net torque leads to a circular trajectory. To see this figure in color, go online.

We compare the experimental speed profile with predictions based on a hydrodynamic model by Lauga and co-workers (28). Details on its implementation are described under the Hydrodynamic model, with parameters specified in Table S1. Although it is possible to shift the theoretical line in Fig. 3 a by adjusting the parameters for the dimensions of the model bacterium and the flagellar motor rotation speed, the key feature remains the same: the speed initially increases with the radius of curvature but quickly attains an upper value. Bacteria swimming at the lower end values of the radius of curvature moved closer to the seeding particle; hence, they experienced more drag. This drag effect due to the seeding particle is not considered in the hydrodynamic model, which may explain why the data at radii of curvature below 7 μm fall significantly below the model prediction. The theory curve ends at the radius of curvature ∼4 μm, which corresponds to a 5 nm minimal gap set in the model calculation between the cell body and the bottom surface (see Fig. S2). One might argue that the hydrodynamic model is no longer valid with such a small gap. Nevertheless, the consistent trend of the data with the theoretical prediction (Fig. 3 b) supports the notion that whereas the hydrodynamic boundary effect of the bottom surface can account for the circular motion observed in orbiting bacteria, the actual trajectory radius and swimming speed are also affected by other constraints, such as those imposed by the particle surface, air-water interface, and meniscus boundary.

A more rigorous hydrodynamic model should include the air-water interface above the thin film. The boundary condition on the top surface may be modeled as free flow instead of nonslip. In fact, the free flow condition on the upper boundary would result in a circular swimming trajectory of the same handedness as that caused by the solid boundary at the bottom. However, the boundary effect of the air-water interface could also be complicated by increased surface viscosity (31, 32, 33), for instance, because of adsorption of nutrient molecules initially contained in the agar. In light of this uncertainty and our microscopy observation confirming that the bacteria tend to move much closer to the bottom surface, our hydrodynamic model has ignored the air-liquid interface, which is expected to contribute a smaller effect. As a side note, one useful outcome of this model is it confirms, based on the observation that Enterobacter sp. move in the same clockwise direction as E. coli, that both species of bacteria have flagella of left-handed helical structure.

Endurance of the water layer around the seeding particles

One key finding of our study is that graphite or bead particles on the agar surface retain a layer of water around them much longer than expected on a nonpermeable surface. The evaporation of a water layer from a borosilicate glass surface containing microspheres (polystyrene beads of 6 μm diameter) on top has been investigated experimentally using x-ray transmission microscopy (26). The full process lasts ∼12 s, with 96% of the time on a pinning stage when the water film surrounding the bead thins gradually and the last 4% on depinning of the water meniscus around the microsphere in the form of a sudden collapse. In our case, however, the fact that the bottom surface is made by agar gel (> 97.5% water) allows for water to constantly permeate the upper surface. Thus, the meniscus lasts much longer. This observation is explained as a balance between evaporation and additional water being pumped from the agar gel to the layer, as illustrated in Fig. 4. Given the tiny thickness (a few μm) of the water layer, its internal pressure P′ is roughly constant everywhere. The internal pressure within the water layer (P′) is lower than the atmospheric pressure P_o (34). The difference between these two pressures is given by the Young-Laplace equation, P_o − P′ = σ/R, where σ is the water surface tension and 1/R is the meniscus curvature (only significant in the radial direction). Near the top of the agar gel, the pressure is also close to the atmospheric pressure. Hence, a pressure gradient is established between the permeable agar gel and the water layer, giving rise to water being pumped, as expected from Darcy’s law (35). Consequently, even though water is constantly evaporating from the thin layer, it is being replenished by that permeated from the agar gel.

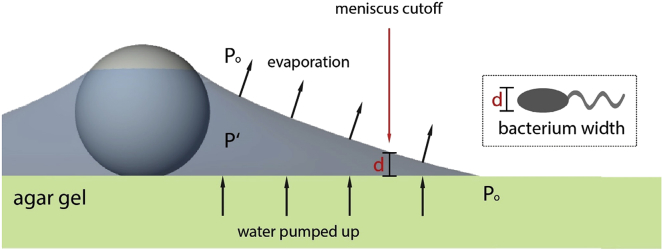
Figure 4.

Schematics illustrating a resilient water layer around a micrometer-sized particle on an agar gel. The internal pressure (P′) within the layer of water is lower than the atmospheric pressure (P_o), which is also roughly the pressure inside the agar gel close to the top surface. This pressure difference pumps water up from the semisolid agar gel, counterbalancing constant evaporation. Hence, the water layer is maintained much longer than on typical nonpermeable solid surfaces. The thickness d corresponds to the width of a bacterial cell, with its location defining a meniscus boundary outside which bacteria get stuck to the agar surface. Note that we have ignored the deformation on the agar surface due to the bead, which is discussed in the text. To see this figure in color, go online.

To quantify the rate of evaporation, we exposed an open agar plate of 10 cm diameter to ambient temperature (22°C) and humidity (40%) and measured ∼0.5 g weight loss per hour. This translates to ∼0.02 μm/s for the rate of water layer thinning. The agar gel of several millimeter thickness can sustain this rate of evaporation for hours when uncovered or days when properly covered. But the same rate of evaporation poses a serious challenge for microscopic imaging, especially for confocal imaging on much thinner gels even in covered plates.

Additionally, we estimated in order of magnitude the radius of curvature of the meniscus at the air-water interface that could sustain a balance between evaporation and water pumping from the gel. The radius of curvature can be calculated by applying Darcy’s law, taking the pressure difference as the ratio of water surface tension to the radius of curvature. We use the meniscus radius as the characteristic length, because the dimensions of the agar gel are much larger, in Darcy’s formula: ΔP = ηLv_z/κ, where ΔP indicates pressure difference, η is the water viscosity, L is a characteristic length, and v_z is the pumping rate along the pressure drop, in our case approximated by the evaporation rate. The permeability coefficient is represented by κ. Not knowing the permeability coefficient of our agar gel, for the order of magnitude, we adopt the reported permeability coefficient for 2% agarose gel, which is 616 nm² (36). The radius of curvature thus estimated is around 83 mm, much larger than the diameter of the tent-like fluid film. This result indicates that even the slightest curvature in the top fluid surface suffices to provide enough pressure difference to maintain the fluid flow required to stably sustain the fluid film.

Confocal imaging of the gel surface deformed by seeding particles

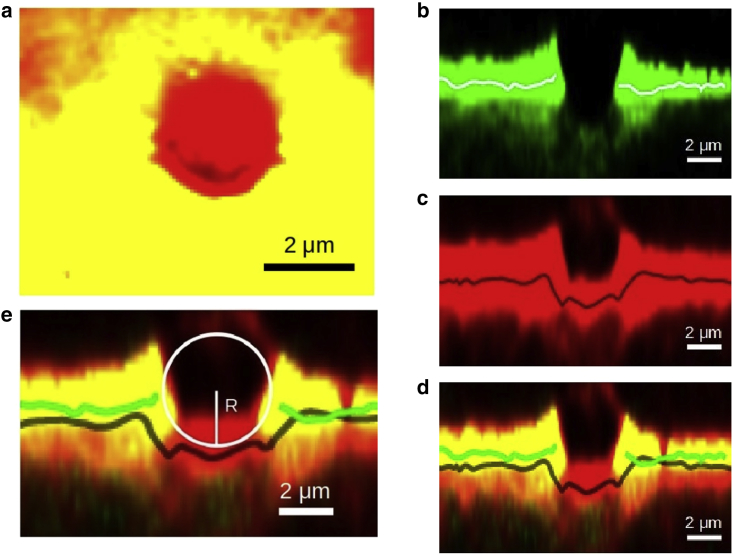
We performed confocal microscopy to evaluate the deformation on the agar gel caused by 4.5 μm silica beads. However, it is technically impractical to do the measurements in the same setup as the bacterial swarms because of the requirement that the gel thickness be not much larger than 100 μm for optimal image acquisition. A consequence of this limitation is that the water meniscus as shown in Fig. 4 lasts under a minute, preventing us from capturing the profile of the thin fluid film even when it was filled with tiny fluorescent beads. Instead, the confocal images were acquired at the moments when the gel had become much drier than that of thicker gels on which the other microscopy experiments were performed. In essence, the images shown in Fig. 5 only help in visualizing the extent of deformation under the silica beads after the liquid film surrounding the large beads has dried.

Figure 5.

Confocal microscopy images illustrating a small but notable compression of a 4.5 μm bead on a 0.5% agar surface. The surface is covered by much smaller beads of 0.5 μm diameter labeled in Dragon Green, which is excited by blue and green lights to emit green and red lights but with green the strongly favored emission. Additionally, the gel is also labeled with Nile red, which is mainly excited by green light, emitting red. (a) Shown is a top down view of a single confocal image slicing through the center of the bead. Yellow light comes from merging green and red channels. The red circular region indicates the presence of the 4.5 μm bead due to the absence of green. This is because the smaller Dragon Green beads were precluded from the site. (b–d) represent an orthogonal cross section of (a) when opening the green channel (b), the red channel (c), and both green and red channels (d). The trend lines in these images indicate the middle line through the bright band. The absence of green light signal in the middle of (b) indicates the absence of Dragon Green beads in that region. The presence of a deformed red region in (c) shows a somewhat compressed surface of the agar gel. (e) shows (d) with an illustrative circle, indicating where the bead sits. To see this figure in color, go online.

Image blurriness poses additional limitations to our analysis. This is a well-known problem for z-resolution of confocal slices, which is partially alleviated by deconvolution. Nevertheless, the trend line going through the middle of the red fluorescent band (Fig. 5 c), highlighting the Nile red-labeled gel surface, indicates the notable deformation below the position of a large bead. The absence of a signal in the green light channel confirms the absence of the smaller Dragon Green beads as the area was covered by only the large bead. The valley of ∼1.3 μm in depth for the line along the red channel gives a rough estimate for the gel deformation due to the 4.5 μm bead. The upward edges around the void of the green channel output indicate that numerous small Dragon Green beads are packed around this region, capturing the history of the meniscus profile, as illustrated in Fig. 4.

Comparison and contrast with a similar recent study

Wakita et al. (37) investigated bacterial motion in a shallow circular pool formed by compression and removal of glass beads 50 μm in diameter close to the edge of a swarming colony of B. subtilis. They identified several types of motion for the bacteria within the circular pools, leaving as an open question the physical mechanism responsible for the resilience of these pools of liquid, which also reportedly lasted for over 10 min. We find our experiment similar to theirs from the point of view of bacteria residing in localized water films on agar gel but rather different in geometric construction of the water film. Whereas in their case, the bacteria become trapped within the pools caused by mechanical compression (or indentation), in our experiment, the motile bacteria are trapped above a flat agar surface but within a thin film of water under a shallow tent. Nevertheless, the thin liquid films in both cases are persistent because they are each connected to a large reservoir of fluid contained in a permeable gel.

We would like to point out that the compression of the gel surface as described in (37) is most likely not due to the weight of the beads but the meniscus surface tension via capillary effect. Specifically, the weight of the titan barium-type (specific density 4.2 g/mL) glass bead 50 μm in diameter is 2.7 nN, so the deformation caused by the bead’s weight on a 0.5% agar gel surface, of Young modulus ∼30 kPa (38), would only be ∼47 nm as estimated based on the model described in (39). In contrast, compression on the gel surface due to the surface tension of meniscus around the bead (i.e., the capillary force) is more significant. We assume roughly a 10 μm radius for the contact circle at the air-water interface around the bead of 50 μm diameter and a 10° angle for the meniscus slope, as illustrated in Fig. 4. The net vertical force integrated over the circle is 0.79 μN, which is nearly 300 times larger than the bead’s weight. The gel deformation under this capillary force amounts to ∼2 μm, comparable to what was observed in (37). This deformation also accounts for our observation that glass beads or graphite particles anchor firmly to the surface once the shallow water tents are established. Performing a similar calculation for the 4.5 μm silica beads used in our experiment, taking into account the corresponding specific density of 2.7 g/mL and integrating over an estimated 1 μm radius for the contact circle at the air-water interface, we obtain an estimated indentation of ∼1.0 μm. Such an indentation is predominantly a result of the force due to the surface tension of water. These estimates confirm that capillary force, not gravity, accounts for significant compression on the agar surface by beads of only a few micrometers in diameter, as shown by confocal imaging (Fig. 5).

Conclusions

In summary, we report a, to our knowledge, novel mechanism by which microsized particles on a moist surface entrap a tent-shaped layer of liquid within which flagellated bacteria swim in circular trajectories. The phenomenon occurs because of strong surface tension at the liquid-air interface and the proximity of the cells to a semipermeable agar gel. Our findings indicate the potential for the persistence of bacteria mobility in thin films of water. The observation that small particles can entrap bacteria under those conditions and allow them to remain viable and motile, even after the liquid film has evaporated from most of the surface area, is significant in certain environmental situations. For instance, this report supports reinforcing proper hygiene habits to prevent bacterial contamination by keeping surfaces dry and clean, ideally free of particles, which might trap bacteria (40).

Author Contributions

G.A., W.C., S.M., and J.X.T. conceived and designed the study. G.A. and W.C. performed the experiments and analysis. S.M. produced and provided the bacteria (SM1, SM3, and H5). G.A. and J.X.T. wrote the article with inputs from all co-authors.

Editor: Julie Biteen.