Integrating single-cell transcriptomic data across different conditions, technologies, and species

Abstract

Computational single-cell RNA-seq (scRNA-seq) methods have been successfully applied to experiments representing a single condition, technology, or species to discover and define cellular phenotypes. However, identifying subpopulations of cells that are present across multiple datasets remains challenging. Here, we introduce an analytical strategy for integrating scRNA-seq datasets based on common sources of variation, enabling the identification of shared populations across datasets and downstream comparative analysis. Implemented in our R toolkit Seurat (http://satijalab.org/seurat/), we use our approach to align scRNA-seq datasets of peripheral blood monocytes (PBMCs) under resting and stimulated conditions, hematopoietic progenitors sequenced using two profiling technologies, and pancreatic cell ‘atlases’ generated from human and mouse islets. In each case, we learn distinct or transitional cell states jointly across datasets, while boosting statistical power through integrated analysis. Our approach facilitates general comparisons of scRNA-seq datasets, potentially deepening our understanding of how distinct cell states respond to perturbation, disease, and evolution.

INTRODUCTION

With recent improvements in cost and throughput^1–3, and the availability of fully commercialized workflows⁴, high-throughput single-cell transcriptomics has become an accessible and powerful tool for unbiased profiling of complex and heterogeneous systems. In concert with novel computational approaches, these datasets can be used for the discovery of cell types and states^5,6, the reconstruction of developmental trajectories and fate decisions^7,8, and to spatially model complex tissues^9,10. Indeed, scRNA-seq is poised to transform our understanding of developmental biology and gene regulation^11–14, and enable systematic reconstruction of cellular taxonomies across the human body^6,15, although substantial computational obstacles remain. In particular, integrated analysis of different scRNA-seq datasets consisting of multiple transcriptomic subpopulations, either to compare heterogeneous tissues across different conditions or to integrate measurements produced by different technologies, remains challenging.

Many powerful methods address individual components of this problem. For example, zero-inflated differential expression tests have been tailored to scRNA-seq data to identify changes within a single cell type^16,17, and clustering approaches^18–23 can detect proportional shifts across conditions if cell types are conserved. However, comparative analysis for scRNA-seq poses a unique challenge, as it is difficult to distinguish between changes in the proportional composition of cell types in a sample and expression changes within a given cell type, and simultaneous analysis of multiple datasets will confound these two disparate effects. Therefore, new methods are needed that can learn jointly between multiple datasets and facilitate comparative analysis downstream. Progress towards this goal is essential for translating the oncoming wealth of single-cell sequencing data into biological insight. An integrated computational framework for joint learning between datasets would allow for robust and insightful comparisons of heterogeneous tissues in health and disease, integration of data from diverse technologies, and comparison of single-cell data from different species.

Here, we present a novel computational strategy for integrated analysis of scRNA-seq datasets, motivated by techniques in computer vision designed for the alignment and integration of imaging datasets^24,25. We demonstrate that multivariate methods designed for ‘manifold alignment’^26,27 can be successfully applied to scRNA-seq data to identify gene–gene correlation patterns that are conserved across datasets and can embed cells in a shared low-dimensional space. We identify and compare 13 aligned PBMC subpopulations under resting and interferon β (IFN-β)–stimulated conditions, align scRNA-seq datasets of complex tissues produced across multiple technologies, and jointly learn shared cell types from droplet-based ‘atlases’ of human and mouse pancreatic tissue. These analyses pose distinct challenges for alignment, but in each case we successfully integrate the datasets and learn deeper biological insight than would be possible from individual analysis. Our approach can be applied to datasets ranging from hundreds to tens of thousands of cells, is compatible with diverse profiling technologies, and is implemented as part of Seurat, an open-source R toolkit for single-cell genomics.

RESULTS

Overview of Seurat alignment workflow

We aimed to develop a diverse integration strategy that could compare scRNA-seq datasets across different conditions, technologies, or species. To be successful in diverse settings, this computational strategy must fulfill the following requirements, as illustrated with a toy example where heterogeneous scRNA-seq datasets are generated in the presence or absence of a drug (Figure 1A). First, subpopulations must be aligned even if each has a unique drug response. This key challenge lies outside of the scope of batch correction methods developed for bulk assays, which assume that confounding variables have uniform effects on all cells in a dataset. Second, the method must allow for changes in cellular density (shifts in subpopulation frequency) between conditions. Third, the method must be robust to changes in feature scale across conditions, allowing either global transcriptional shifts, or differences in normalization strategies between datasets produced with different technologies (i.e. UMI vs. FPKM). Lastly, the process should not be targeted towards defined cell subsets, with no requirement for pre-established sets of markers that can be used to match subpopulations.

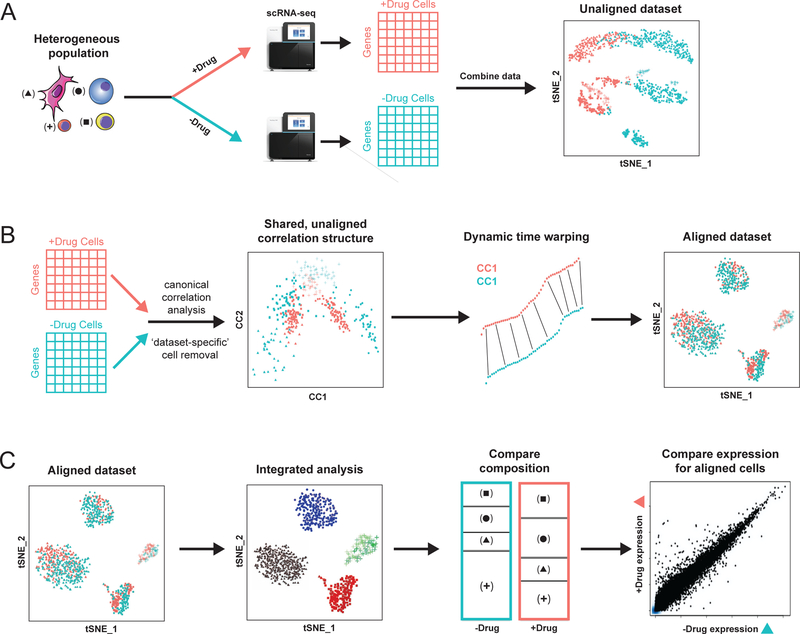
Figure 1. Overview of Seurat alignment of single cell RNA-seq datasets.

(A) Toy example of heterogeneous populations profiled in a case/control study after drug treatment. Cells across four types are plotted with different symbols, while stimulation condition is encoded by color. In a standard workflow, cells often cluster both by cell type and stimulation condition, creating challenges for downstream comparative analysis. (B) The Seurat alignment procedure uses canonical correlation analysis to identify shared correlation structures across datasets, and aligns these dimensions using dynamic time warping. After alignment, cells are embedded in a shared low-dimensional space (visualized here in 2D with tSNE). (C) After alignment, a single integrated clustering can identify conserved cell types across conditions, allowing for comparative analysis to identify shifts in cell type proportion, as well as cell-type specific transcriptional responses to drug treatment.

The Seurat alignment workflow takes as input a list of at least two scRNA-seq datasets, and briefly consists of the following steps (Figure 1B–C; Online Methods). (i) It learns a shared gene correlation structure that is conserved between the datasets using canonical correlation analysis (CCA) (Figure 1B). (ii) As an optional step, it identifies individual cells that cannot be well described by this shared structure. This can help to identify rare populations that may be non-overlapping between the datasets, and can therefore be flagged for further analysis. (iii) It aligns the datasets into a conserved low-dimensional space, using non-linear ‘warping’ algorithms to normalize for differences in feature scale, in a manner that is robust to shifts in population density. (iv) It proceeds with an integrated downstream analysis, for example, identifying discrete subpopulations through clustering, or reconstructing continuous developmental processes (Figure 1C). (v) It performs comparative analysis on aligned subpopulations between the datasets, to identify changes in population density or gene expression (Figure 1C). We describe these steps briefly below, and then apply and validate this strategy on five sets of scRNA-seq experiments from the literature.

Identifying shared correlation structures across datasets

Machine-learning techniques for ‘data fusion’ aim to integrate information from multiple experiments into a consistent representation. For example, CCA aims to find linear combinations of features across datasets that are maximally correlated, identifying shared correlation structures across datasets^28,29. CCA has been used for multi-modal genomic analysis from bulk samples, for example identifying relationships between gene expression and DNA copy number measurements based on the same set of samples³⁰. Here, in contrast to its traditional use in multi-modal analysis^31,32, we apply CCA to identify relationships between single cells from different datasets based on the same set of genes. Effectively, we treat the datasets as multiple measurements of a gene-gene covariance structure, and search for patterns that are common to the datasets. We use CCA for pairwise integration of two datasets, and extend this to multi-set CCA (i.e. Multi-CCA)^33,34 for the integration of multiple datasets. In the description of all methods below, we refer only to CCA for simplicity, but note that each of the individual techniques can extend to Multi-CCA when multiple datasets are included as input (Online Methods).

We employ a variant of CCA, diagonal CCA, to account for cases where there are more cells than genes, and apply this using the single-cell RNA-seq datasets as input. The procedure can consider any gene that is measured across all datasets, though we choose to focus only on genes that exhibit high single cell variation in at least one dataset (Online Methods). CCA identifies sets of canonical ‘basis’ vectors, embedding cells from each dataset in a low-dimensional space, such that the variation along these vectors (gene-level projections) is highly correlated between datasets. We note that CCA is robust to affine transformations in the original data, and is unaffected by linear shifts in gene expression (for example, due to different normalization strategies).

Aligning basis vectors from CCA

CCA returns vectors whose gene-level projections are correlated between datasets, but not necessarily aligned. While linear transformations may be required to correct for global shifts in feature scale or normalization strategy, non-linear shifts may also be needed to correct for shifts in population density. We therefore align the CCA basis vectors between the datasets, resulting in a single, integrated low-dimensional space. Briefly, we represent each basis vector as a ‘metagene’, defined as a weighted expression average of the top genes whose expression exhibits robust correlations with the basis vector (Online Methods). We first linearly transform the ‘metagenes’ to match their 95% reference range (Online Methods), correcting for global differences in feature scale. Next, we determine a mapping between the metagenes using ‘dynamic time warping’, which locally compresses or stretches the vectors during alignment to correct for changes in population density³⁵. We apply this procedure to each pair (or set, for multiple alignment) of basis vectors individually, defining a single, aligned, low-dimensional space representing all datasets. This enables us to perform integrated downstream analyses, including unbiased clustering and the reconstruction of developmental trajectories, as demonstrated below.

Comparative analysis of stimulated and resting PBMCs

We first demonstrate our alignment strategy on a dataset containing many distinct cell types in the presence and absence of perturbation. For example, a recent study examining the effects of interferon stimulation split 14,039 human PBMCs from 8 patients into two groups: one stimulated with interferon-beta (IFN-β) and a culture matched control³⁶. Since all cells contain machinery to respond to IFN-β, stimulation results in a drastic but highly cell-type specific response. Consequently, a traditional joint analysis yields confusing results, as cells tend to cluster both by cell type but also by stimulation condition (Figure 2A). As an alternative to unbiased clustering, a supervised strategy to assign cells to classes based on known markers resulted in a final set of eight clusters³⁶.

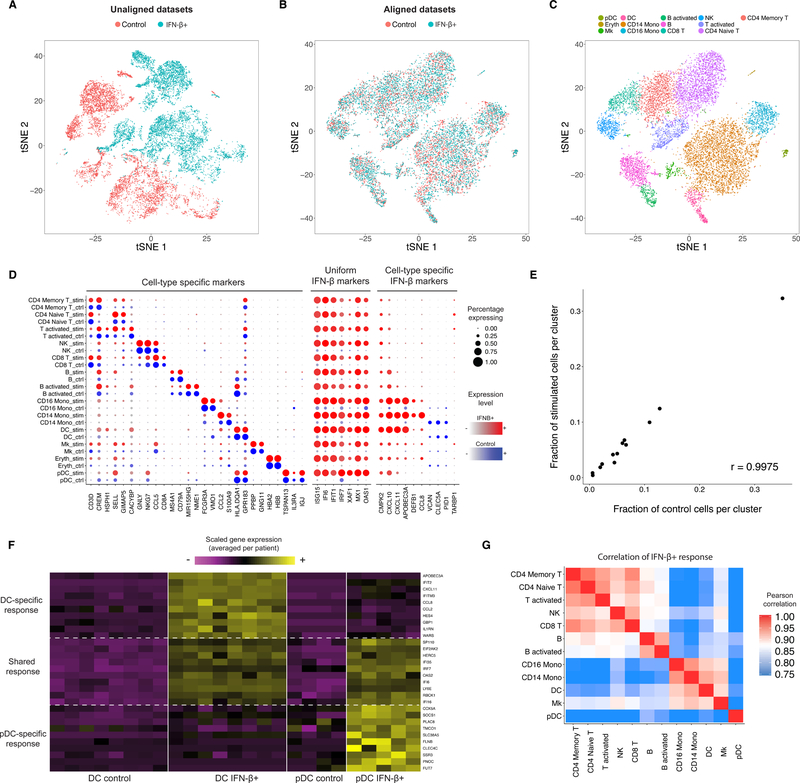
Figure 2. Integrated analysis of resting and stimulated PBMC.

(A-C) tSNE plots of 14,039 human PBMCs split between control and IFN-β-stimulated conditions, prior to (A) and post (B) alignment. After alignment, cells across stimulation conditions group together based on shared cell type, allowing for a single joint clustering (C) to detect 13 immune populations. (D) Integrated analysis reveals markers of cell types (conserved across stimulation conditions), uniform markers of IFN-β response (independent of cell type), and components of the IFN-β response that vary across cell types. The size of each circle reflects the percentage of cells in a cluster where the gene is detected, and the color reflects the average expression level within each cluster. (E) The fraction of cells (median across 8 donors) falling in each cluster (n = 13 clusters) for stimulated and unstimulated cells. (F) Examples of heterogeneous responses to IFN-β between conventional and plasmacytoid dendritic cells (global analysis shown in Supplementary Figure 4B). Each column represents the average expression of single cells within a single patient. Only patient/cluster combinations with at least five cells are shown. (G) Correlation heatmap (n = 430 genes with difference > ln(2) between resting and stimulated) of cell-type specific responses to IFN-β (individual correlations for T and DC subsets shown in Supplementary Figure 4A–B). Cells from myeloid and lymphoid lineages show highly correlated responses, but plasmacytoid dendritic cells exhibit a unique IFN-β response.

In contrast, the Seurat alignment returned a set of canonical correlation vectors that separated PBMC subsets irrespective of stimulation condition. We chose to include 20 vector pairs for downstream analysis (Online Methods), but note that results for this and all examples in the manuscript were robust to the exact choice of this parameter (Supplementary Figure 1). We performed joint graph-based clustering on these aligned vectors and visualized the results with t-Distributed Stochastic Neighbor Embedding (t-SNE) to verify that cells grouped entirely by cell type and were properly aligned across conditions (Figure 2B). Our analysis revealed 13 cell clusters, which included the eight immune subsets described in the original publication, but separated additional populations as well (Figure 2C; Supplementary Data 1). In particular, we were able to separate naïve from memory T cells, plasmacytoid dendritic cells (pDCs) from conventional dendritic cells, and identify an extremely rare (0.4%) population of contaminating erythroblasts. In addition, for T cells and B cells, we discovered activated subpopulations marked by a strong stress response expression signature that is likely an artifact of the culturing process in both conditions (Supplementary Figure 2A–B). We verified the identity of our clusters by examining the expression of canonical cell-type markers (i.e CD3D for T cells, CD79A for B cells), that were conserved across conditions (Figure 2D; Supplementary Figure 3).

Having aligned the datasets, we next sought to compare how PBMCs vary in response to IFN-β. As both conditions were drawn from the same pool of cells, we observed a strikingly similar proportional representation of all clusters in stimulated and control experiments (R=0.997; Figure 2E). However, each cell type exhibited significant changes upon IFN-β stimulation. Applying single cell differential expression tests separately for each cluster, we were able to identify constitutive markers of the IFN-β response induced in all cells (ISG15, IFIT1), as well as components of the IFN-β response that varied across cell types (i.e., CXCL10 was activated primarily in myeloid cells upon stimulation) (Figure 2D). We noted that even canonical cell-type markers such as CD14 were differentially expressed by monocytes (1.98-fold down-regulation; Supplementary Figure 3) in response to stimulation, highlighting the value of our non-targeted analyses in initially classifying cells.

Focusing in on the novel subsets we were able to resolve, we compared the IFN-β response program between naïve and memory CD4+ T cells, and observed nearly identical response signatures (Supplementary Figure 4A). However, while we observed a general correlation between pDC and DC responses, we also saw stark differences that reproduced across patients (Figure 2F). When comparing the IFN-β responses across all cell types, we observed that myeloid and lymphoid cells strongly clustered together, but pDC exhibited a distinct response to IFN-β and clustered separately (Figure 2G; Supplementary Figure 4B).

We externally validated these findings by replicating the setup and stimulation of the original experiment, sorting populations of pDC and DC using standard surface markers (Online Methods), and performing bulk RNA experiments in triplicate on stimulated and control cells. These bulk experiments strongly confirmed our single cell predictions: genes that were differentially regulated by IFN-β stimulation exhibited strikingly similar patterns in both the single cell and bulk datasets, and the bulk samples clustered directly with in silico averaged data from the same cell type (Supplementary Figure 5; Online Methods). Therefore, in a single transcriptome-wide analysis, our alignment procedure sensitively identified shared cell states through integrated clustering, and allowed for the identification of cell-type specific response modules that are likely to play important roles in vivo during immune response to infection.

Strategies to identify non-overlapping populations

In the previous example, identical cell populations were used as input for both populations, and the cell subpopulations should therefore be fully overlapping. We wished to assess how our integration procedure would perform when non-overlapping populations were present in only one of the datasets. This is an important concern both for abundant populations, where absence in one dataset could throw off the integration, but also rare populations, which could blend in with an abundant cluster if unmatched, but may have significant biological importance.

To address this, we performed two ‘in-silico’ experiments, where we artificially removed abundant (CD14+ and CD16+ monocytes; 38%), or rare (erythroblasts; 0.5%) cells from the stimulated dataset only, and repeated the alignment procedure. When we removed abundant populations, we observed negligible effects on the overall clustering and both CD14+ and CD16+ control monocytes were readily identified by visualization and graph-based clustering despite being present in only one dataset (Supplementary Figure 6 A–C).

After removing stimulated erythroblasts, we observed that control erythroblast cells no longer separated in the integrated analysis, while other populations were unaffected (Supplementary Figure 6D). We therefore aimed to design a new test to identify these cells as non-overlapping, so they could be flagged for further exploration downstream. We reasoned that while CCA may struggle to identify canonical correlation vectors that define rare subpopulations present in only one dataset, PCA may be able to separate these cells, as we have previously shown³. Therefore, we quantify how well the low-dimensional space defined by CCA explains each cell’s expression profile, and compare this to PCA, which is performed on each dataset independently (Online Methods). Cells where the percent variance explained is reduced by a user-defined cutoff in CCA compared to PCA are therefore defined by strong sources of variance that are not shared between the datasets. We use a cutoff of 50% for all examples in this manuscript to identify these cells.

This procedure enabled us to sensitively identify a rare group of non-overlapping cells in the control population, all of which could be identified as expressing high levels of HBA1 and HBA2, and corresponded to the erythroblast population whose signal was previously blended into the rest of the data (Supplementary Figure 6E). Notably, this test correctly did not flag similar cells when applied to the original analysis of the full datasets (where the populations were fully overlapping), or in the in silico monocyte removal (where the aligned canonical correlation vectors enabled the identification of both rare and abundant cell states). Taken together, we conclude that our integration procedure is robust to abundant non-overlapping populations, and can also identify rare populations that are present in a single dataset, enabling further characterization.

Integrated analysis of scRNA-seq technologies

We next examined two recent single cell RNA-seq profiles of hematopoietic progenitors from murine bone marrow, but produced with starkly different technologies. Nestorowa et al.³⁷ used the full-length SMART-Seq2 with deep sequencing (6,558 genes/cell) to profile 765 progenitors, while Paul et al.³⁸ applied the 3’ MARS-Seq protocol with shallow sequencing (1,453 genes/cell), to examine 2,686 cells. The distinct differences in amplification, normalization, and coverage pose challenges to integrate these datasets. Additionally, independent analyses from both papers highlighted different aspects of the data; the SMART-Seq2 analysis focused on the broad and continuous trajectories of cells committing to lymphoid, myeloid, erythroid lineages, while the MARS-Seq dataset identified 18 distinct clusters (and one contaminating group of NK cells), representing progenitors of eight distinct hematopoietic lineages. Despite these differences, we asked whether the same distinct progenitor subsets might be found in both datasets through integrated analysis.

Seurat alignment returned canonical correlation vectors that separated distinct progenitor subtypes, revealing populations committed to all eight distinct hematopoietic lineages in both datasets, but successfully identifying the contaminating NK population as ‘non-overlapping’ (Figure 3A–C; Supplementary Figure 7). After alignment, we mapped cells from the SMART-Seq2 dataset onto their closest cluster in the MARS-Seq dataset (Figure 3C–F; Online Methods; Supplementary Data 2). We observed that early megakaryocyte-erythrocyte progenitor cells, identified in the original SMART-Seq2 publication, mapped exclusively onto erythroid and megakaryocytic progenitors in the MARS-Seq data (Clusters C1–7). Similarly, SMART-Seq2 granulocyte-macrophage progenitors mapped onto basophil, eosinophil, dendritic cell, neutrophil, and monocyte progenitors (C11–18). While the MARS-Seq data specifically enriched for myeloid cells, the authors identified populations of very early progenitors that were FLT3+ (C9–10). These cells represent lympho-myeloid component progenitors (lymphoid-primed multi-potent progenitors (LMPP))³⁹, and early lymphoid progenitors from the SMART-Seq2 data mapped exclusively to these clusters. Indeed, after mapping, we observed nearly identical segregation of gene expression markers between SMART-Seq2 and MARS-Seq datasets (Figure 3E–F, Supplementary Figure 8), demonstrating that the biological drivers of alignment were lineage-determining factors. Therefore, Seurat alignment demonstrated that distinct committed progenitor populations were present in the SMART-Seq2 dataset, but were challenging to detect in the original analysis due to reduced cell number.

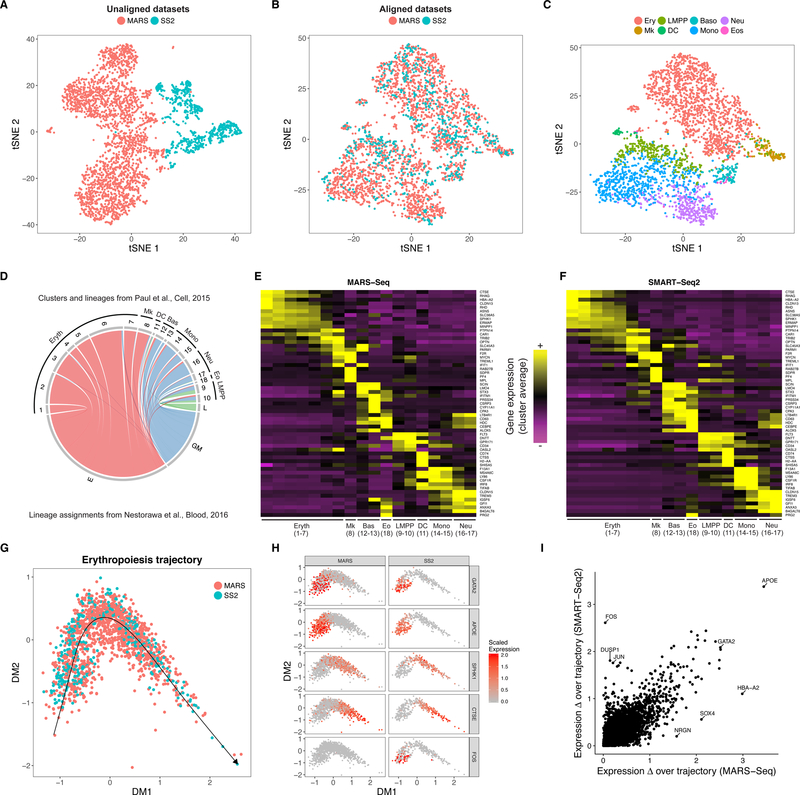
Figure 3. Comparative analysis of mouse hematopoietic progenitors across scRNA-seq technologies.

(A-C) tSNE plots of 3,451 hematopoietic progenitor cells from murine bone marrow sequenced using MARS-seq (2,686) and SMART-Seq2 (765), prior to (A) and post (B-C) alignment. After alignment, cells group together based on shared progenitor type irrespective of sequencing technology. (C-D) Cells from the SMART-Seq2 dataset were mapped onto the closest MARS-Seq cluster and associated lineage (from Paul et al.). (C) tSNE plot of cells colored by assigned lineage. (D) Mapping correspondence between SMART-Seq2 lineage assignments (from Nestorawa et al.) and MARS-Seq clusters. (E-F) Heatmaps showing lineage- specific gene expression patterns in MARS-Seq and SMART-Seq2 datasets. Each column represents average expression after cells are grouped either by the original MARS-Seq cluster assignments (E), or the MARS-Seq cluster they map to (F). (G-H) Integrated diffusion maps of erythroid-committed cells in both datasets reveals an aligned developmental trajectory (G), with conserved ‘pseudo-temporal’ dynamics (H). (I) Scatter plot comparing the range in expression (absolute value) over the developmental trajectory, for each gene, across both datasets.

Lastly, as both datasets identified developmentally heterogeneous populations during erythroid differentiation (broken into 7 stages in the MARS-Seq analysis), we applied diffusion maps to erythroid-committed cells to reconstruct a joint developmental trajectory (Figure 3G). We observed that this developmental path maintained the ‘pseudotemporal’ ordering of cells within both datasets (Supplementary Figure 9) and also aligned the two together, exhibiting nearly identical expression dynamics for canonical differentiation markers (Figure 3H). Extending this analysis globally, we observed that gene expression changes across the trajectory were largely conserved between datasets, particularly for well-characterized effectors of erythropoiesis, yet we also saw technology-specific effects -- for example a strong JUN/FOS response that has previously been associated with cellular stress during scRNA-seq⁴⁰ (Figure 3H–I). Therefore, our procedure can successfully align both discrete and transitioning populations, and enable the identification of gene-expression programs that are conserved or unique to individual datasets.

The ability to pool datasets of the same heterogeneous tissues has the potential to enable similar ‘meta-analyses’ for datasets produced across multiple labs and technologies. To further demonstrate this we include two additional examples (Supplementary Figure 10, 11), demonstrating the integration of human pancreatic islets produced with four plate-based scRNA-seq technologies (CelSeq, CelSeq2, Fluidigm C1, SmartSeq2), and human PBMCs produced with three distinct technologies (10X Genomics 3’ assay, 10X Genomics 5’ assay, and the Illumina/BioRad ddSeq). In the first example, we identify 8 populations of endocrine, exocrine, and stellate cells, clearly defined by cell-type specific markers that were conserved across technologies (Supplementary Figure 10). Notably, we also identified a rare population (1%) of endothelial cells which were present in all datasets, but whose rarity precluded their automated annotation in three of the four original analyses. As each sample was also from a different human donor, the proportion of cell types in each sample was highly variable, but did not confound the integration procedure (Supplementary Figure 10E).

In the second example, pooling the datasets yielded 16,653 PBMCs, allowing us to identify 16 immune populations, including 6 T cell clusters (Supplementary Figure 11A–D), and a rare subpopulation (0.5% frequency) of NK cells. This subpopulation lacked FCGR3A expression but was enriched for XCL1 and GZMK, consistent with highly cytotoxic CD56^bright NK cells⁴¹ (Supplementary Figure 11E). As with previous examples, the rarity of these cells precludes their identification in any individual dataset, and they were not identified in a previous analysis of 68,000 PBMCs⁴. These integrated datasets provide the opportunity to perform ‘meta-analyses’ for differential expression across multiple technologies. As an example of this, we first performed individual ‘within-dataset’ differential expression tests, and then combined the results (Online Methods). Using this approach to identify differential gene expression (DE) between NK cell subsets, we were able to more than triple the number of DE genes detected between these two cell groups (Supplementary Figure 11F), including lowly expressed markers but functionally important chemokines (CCL5), transcriptional regulators (RORA), and surface receptors (FCRL6). Therefore, pooling cells produced by integrating different scRNA-seq technologies not only boosts the statistical power to discover rare cell phenotypes, but also to identify transcriptomic markers of cell state.

Joint learning of cell types across species

As a final example, we tested the ability of Seurat to align heterogeneous populations from the same tissue, but originating from different species. We examined a recent single cell study of both human and mouse pancreatic islets, performed with the inDrop technology¹, that identified islet cell types independently in both species⁴². The study found that cell-type transcriptomes were poorly conserved between human and mouse (avg. correlation between bulk transcriptomes of individual cell types: R=0.42), often finding very few strongly expressed markers that were preserved between species. This widespread divergence poses significant challenges for integration, as structure in the dataset was largely driven by species as well as by individual donor (Figure 4A, Supplementary Figure 12). However, we reasoned that a subset of gene-gene correlations should still be conserved, and therefore aligned all human cells against all mouse cells.

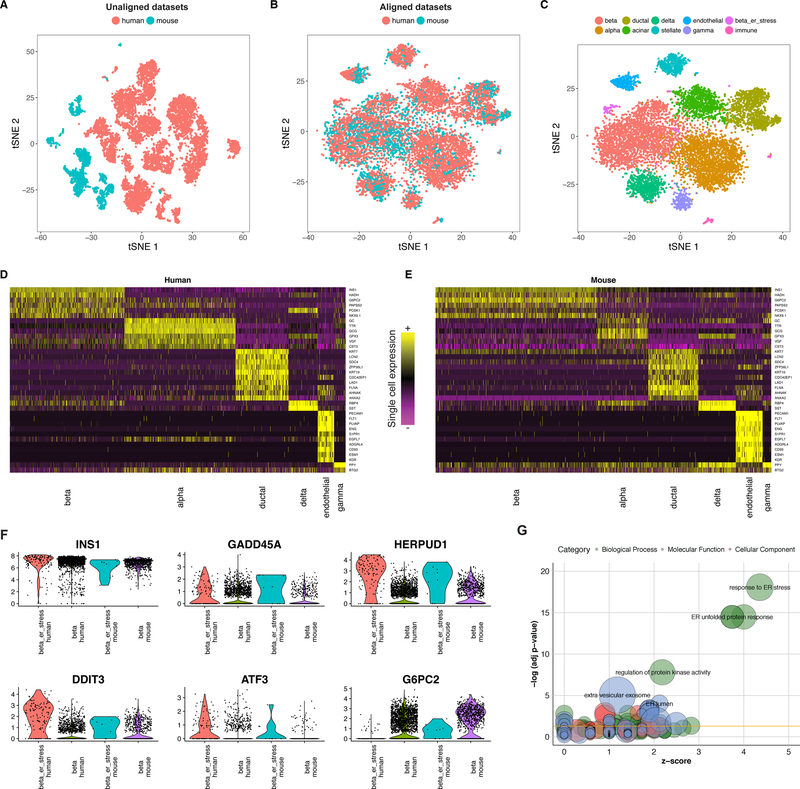
Figure 4. Joint identification of cell types across human and mouse islet scRNA-seq atlases.

(A-C) tSNE plots of 10,191 pancreatic islet cells from human (n = 8,424 cells) and mouse (n = 1,767 cells) donors, prior to (A) and post (B) alignment. After alignment, cells group across species based on shared cell type, allowing for a joint clustering (C) to detect 10 cell populations. (D-E) Unsupervised identification of shared cell-type markers between human and mouse. Single cell expression heatmap for genes identified with joint DE testing across species. (F) Violin plots showing the distribution of gene expression of select genes in the beta cell cluster for human (n = 2,431 cells) and mouse (n = 762 cells) and the stressed beta cell clusters for human (n = 126 cells) and mouse (n = 10 cells). (G) Top n=100 genes up-regulated in the ‘ER-stress’ subpopulation of beta cells in both species are strongly enriched for components of the ER unfolded protein stress response. GO enrichment is visualized using the GOplot R package.

Indeed, Seurat alignment identified canonical correlation vectors that separated cell types, identifying primarily small populations of immune cells (human mast cells and murine B cells) as ‘non-overlapping’ (Figure 4B, Supplementary Figure 12). We next performed a single integrated clustering analysis, identifying 10 clusters, corresponding to alpha, delta, gamma, acinar, stellate, ductal, epithelial, immune, and two subgroups of beta cells (Figure 4C; Supplementary Data 3, Supplementary Figure 9). Our clusters agreed overwhelmingly with the analyses from the independent datasets⁴² (Supplementary Figure 13), though we did observe a low rate (5.8%) of discordant calls, particularly for cells with low UMI counts (Supplementary Figure 14A–B). We were also able to identify a subset of cell type markers that were conserved between human and mouse (Figure 4D–E).

Notably, our procedure identified a rare subpopulation of beta cells in both human and mouse. These cells expressed identical levels of INS, but up-regulated the expression of endoplasmic reticulum (ER) stress genes (HERPUD1; GADD45A) in both species (Figure 4F). A similar signal was observed in a semi-supervised analysis of the human beta cells in the original manuscript⁴², but could not be detected in automated clustering, or an independent analysis of the murine dataset. In contrast, our integrated analyses reveal a conserved set of markers that are strikingly enriched for regulators of ER stress response to unfolded proteins^43,44 (Figure 4G), which has been shown to play an important role in the onset and progression of diabetes. Notably, expression of the transcription factors ATF3 and ATF4 was highly up-regulated in both species, representing factors that have well-established roles in the initiation of stress responses in the pancreas^45,46. Taken together, these results demonstrate that our alignment procedure can identify shared cell states even in the face of significant global transcriptional shifts, driven in this case by millions of years of evolution.

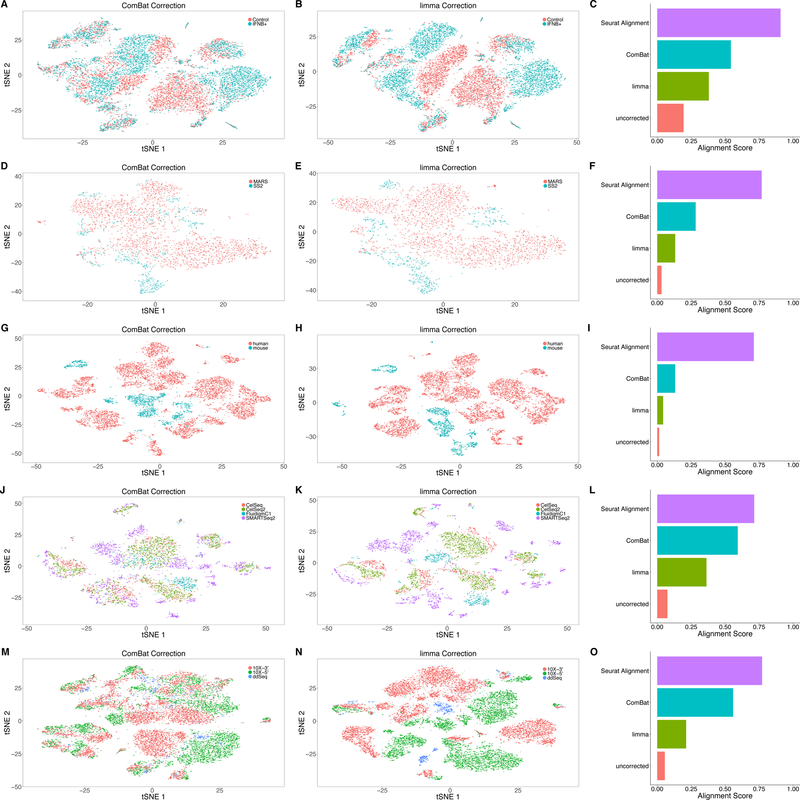
Benchmarking alignment and batch correction techniques

We next compared Seurat’s performance to widely used batch correction tools that have been applied to both bulk⁴⁷ and single cell genomics data⁴⁸. To evaluate each technique, we designed an ‘alignment score’, which examines the local neighborhood of each cell after alignment (Online Methods). When datasets are well aligned, this local neighborhood will consist equally of cells from both datasets, enabling us to quantify the success of each procedure with a score ranging from 0 to 1.

On the five datasets presented here, we benchmarked Seurat’s performance against ComBat⁴⁹ and limma⁵⁰ (Figure 5). In each case, as can be visualized by tSNE or quantified with our alignment score, Seurat’s integration procedure yielded superior results. The differences between these procedures were particularly striking when the transcriptomic differences between datasets (i.e ‘batch effect’) significantly outweighed differences between cell types (‘biology’), as in cross-species integration. However, when we attempted to align datasets from different tissues as a negative control, we observed poor results and low alignment scores, even when cells are not automatically classified as ‘non-overlapping’ (Supplementary Figure 15).

Figure 5. Benchmarking alignment and batch correction methods.

(A, D, G, J, M) tSNE plots for the PBMC dataset (n = 14,039 cells) (A), hematopoietic progenitor cell dataset (n = 3,451 cells) (B), pancreatic islet cell dataset (n = 10,306 cells) (C), multiple human pancreatic islet cell datasets (n = 6,224 cells) (J), and multiple PBMC datasets (n = 16,653 cells) (M) after correction with ComBat and (B, E, H, K, N) with limma. (C, F, I, L, O) Bar plots of the alignment score after correction using the Seurat alignment procedure, ComBat, limma, and after no correction. Seurat alignment outperforms other methods in all five examples. Additional examples of ‘negative controls’ where Seurat fails to align datasets from different tissues are shown in Supplementary Figure 15.

DISCUSSION

We have developed a strategy to integrate scRNA-seq datasets by identifying shared sources of variation, corresponding to subpopulations present in multiple experiments. Implemented in the R toolkit Seurat, our procedure tackles several technical challenges, including the unbiased identification of shared gene–gene correlations across datasets, as well as the alignment of canonical correlation vectors using non-linear ‘warping’ algorithms.

Dataset integration represents a key step in a general framework for case/control studies performed with single-cell resolution. As new datasets are generated, we expect that similar computational analyses will not only be invaluable for characterizing the immune system’s response to vaccination, inflammatory disease, and cancer, but also provide deeper insight into how genetic variation and manipulation affect heterogeneous populations. Similarly, we anticipate that these methods will enable consortia, such as the Human Cell Atlas^15,42,51, which aims to define all human cell types by integrating data generated across diverse single-cell ‘omics’ approaches, to combine datasets produced across many labs and technologies. Recent benchmarking studies of diverse scRNA-seq^52,53 technologies have consistently demonstrated that no single method is uniformly superior, but rather, that each has individual strengths and weaknesses, further highlighting the potential value of data integration.

We demonstrate the ability to align differentiated cell types between human and mouse pancreatic islets, identifying a shared population of beta cells responding to ER protein misfolding stress. These and similar analyses may provide invaluable comparative tools for studies utilizing mouse models of human disease, potentially enabling the identification of human correlates of pathogenic populations discovered in mouse (or vice versa). Furthermore, new datasets will enable the alignment and comparison of developmental trajectories across species, leading to a deeper understanding of how the gene regulatory networks generating cellular diversity are rewired across evolution. As comparative genomics has played a fundamental role in our understanding of the human genome, we believe that cross-species analyses may yield to similar insights towards our understanding of cellular diversity.

Lastly, we note many challenges that future methods will address in extending this work. Although our procedure can robustly integrate multiple datasets with overlapping and non-overlapping populations, future datasets that consist of tens to hundreds batches with dramatically varying sizes and non-overlapping populations will likely require new methods. We also note that examples in this manuscript, including datasets with tens of thousands of cells, run in less than half an hour on a standard laptop computer, but new datasets extending to millions of cells may require advanced computation, subsampling, or newly optimized techniques for integration. Lastly, whereas we focus here on alignment of sequencing-based datasets, the recent invention of spatially resolved or in-situ methods for transcriptomic profiling^54–56 raise the potential for integration with scRNA-seq datasets, including the ability to extend previous efforts to spatially resolve scRNA-seq data^9,10 towards an unsupervised procedure generalizable to any tissue.

ONLINE METHODS

The Seurat alignment procedure is designed to integrate single-cell RNA sequencing data (scRNA-seq) across distinct datasets. Following is an overview of the main steps comprising a typical workflow:

1. Data preprocessing and gene selection

2. Define a shared correlation space with canonical correlation analysis

3. Identify rare non-overlapping subpopulations

4. Align correlated subspaces using dynamic time warping

5. Integrated analysis across datasets (clustering, trajectory building, differential expression)

Below, we describe each of these steps in detail. Additionally, we provide full command lists for the integration of the stimulated and resting immune datasets and for the integration of the four scRNA-seq datasets of human pancreatic islet cells (produced with four different plate-based technologies CelSeq, CelSeq2, Fluidigm C1, SmartSeq2) as supplementary code.

1. Single cell dataset pre-processing

For all single cell analysis, we performed the same initial normalization. Gene expression values for each cell were scaled by the total number of transcripts and multiplied by 10,000. These scaled expression data were then natural-log transformed using log1p before further downstream analyses. After normalization, we calculated scaled expression (z-scores for each gene) for downstream dimensional reduction.

Comparison of stimulated and resting immune cells

We obtained a unique molecular identifier (UMI) count matrix for the Kang et al.³⁶ study from GSE96583. The authors generously provided us with the output of their demuxlet algorithm, which computationally identifies doublets, and assigns individual single cells to one of eight patients. We removed cells with fewer than 500 genes detected, leaving 14,039 single cells in total.

Integrated analysis of scRNA-seq technologies

We obtained a read count matrix for the SMART-Seq2 dataset (Nestorawa et al.)³⁷ under the GEO accession GSE81682, and considered 765 annotated progenitors cells expressing at least 4,000 genes. The authors generously provided lineage annotations for each cell (corresponding to Figure 4 in the original publication, used in our Figure 3). We obtained a batch-corrected UMI count matrix for the MARS-Seq dataset³⁸ from the authors’ online resource (http://compgenomics.weizmann.ac.il/tanay/?page_id=649), where we also obtained the MARS-Seq cluster IDs for each cell. This dataset had been previously filtered to remove cells with less than 500 detected UMI for a total of 2,686 single cells.

Both datasets contain cycling progenitors, and heterogeneity between cell cycle stages for these cells has been previously been shown to confound developmental analyses. Therefore, independently for both datasets, we first assigned a cell cycle score to each cell using the PCA method⁵⁷ on a previously annotated list of cell cycle genes⁵⁸. We then used the ScaleData function in Seurat (using the cell cycle score as latent variable in a linear regression framework) to mitigate this source of variation in the dataset, prior to CCA.

Joint clustering across species

We obtained UMI count matrices for the human and mouse inDrops datasets (Baron et al., 2016)⁴² from GEO accession GSE84133. For both species, we removed cells with less than 500 detected genes to obtain 8,536 and 1,770 single cells respectively. We also regressed out individual-specific effects using ScaleData prior to CCA. We considered all homologous genes with identical gene names between the human and mouse datasets, and allowed the INS human gene to map to the mouse Ins1 and Ins2 genes as in the original manuscript⁴².

Alignment of multiple human pancreas datasets

For the four human pancreas datasets, we obtained count matrices from accession numbers GSE81076 (CelSeq), GSE85241 (CelSeq2), GSE86469 (Fluidigm C1), and E-MTAB-5061 (SMART-Seq2). We filtered cells that expressed less than 1,750 unique genes/cell (CelSeq), or 2,500 genes/cell (CelSeq2/Fluidigm C1/SMART-Seq2). leaving 6,224 cells in total.

Integrated analysis of multiple PBMC datasets across technologies

For the three human PBMC datasets, we obtained gene expression matrices from 10X genomics (https://support.10xgenomics.com/single-cell-gene-expression/datasets/2.1.0/vdj_v1_pbmc_5gex, https://support.10xgenomics.com/single-cell-gene-expression/datasets/2.1.0/pbmc8k). For the ddSeq experiment, PBMCs from a healthy donor were diluted to 2,500 cells/μl and run according to manufacturer’s protocol through 8 ddSeq wells (2 cartridges) with an expected yield of 2,400 cells in total. Sequencing libraries were prepared according to manufacturer’s instructions and sequenced on 2 lanes of a HiSeq 2500 in rapid run mode, with 68 cycles for read 1 (cell barcodes + UMI), 8 cycle sample index and 75 cycle read 2 (transcript). We filtered out those cells with fewer than 750 unique genes, resulting in 16,653 cells in total. Additionally, we observed significant mitochondrial heterogeneity within each dataset, in keeping with previous reports⁵⁹, and regressed out mitochondrial heterogeneity from each dataset prior to running CCA.

Gene set selection

Although the alignment procedure can utilize any gene that is measured with non-zero variance in all datasets, we focused on genes that were highly variable in one or both datasets. We identified these genes by calculating the dispersion (variance to mean ratio) for all genes in each dataset and selected 1,000 genes with the highest dispersion from each. We took the union of these two resulting gene lists as the input genes for CCA. For Multi-CCA, we required that input genes be in the highly variable gene list for at least two datasets.

2. Calculation of canonical correlation vectors

Standard canonical correlation analysis was designed to find projections that maximize correlation between two vectors (datasets or groups). We first describe the two set scenario and then extend this to multiple sets.

Two set canonical correlation

The first step in the alignment utilizes a variation on canonical correlation analysis (CCA) to find projections of both datasets such that the correlation between the two projections is maximized. Formally, CCA finds projection vectors u and v such that the correlation between the two indices u^TX and v^TY is maximized²⁸.

$$ma{x}_{u,v}{u}^T{X}^{T}Yv\text{ subject to} u^T{X}^{T}Xu\le 1, v^T{Y}^{T}Yv\le 1$$ (1)

To apply this in the context of scRNA-seq, let X_g,c be a gene expression matrix of genes g₁, g₂, … , g_n by cells c₁, c₂, … ,c_n and Y_g,d be a gene expression matrix of the same genes g₁, g₂, … , g_n by cells d₁, d₂, … ,d_p In many scRNA-seq experiments, the number of genes of interest that are shared between the two datasets is often much smaller than the total number of cells that were measured (g ≪ c + d). Consequently, the vectors u and v that are returned from CCA as described in equation 1 will not be unique.

One potential solution to this is to regularize or penalize the CCA procedure to promote sparsity. However, this would assign many cells zero loadings in the resulting projections and result in a complete loss of information for a significant proportion of cells. Therefore, we treat the covariance matrix within each dataset as diagonal, a solution that has demonstrated promising results in other high-dimensional problems^60,61. We substitute the identity matrix for X^TX and Y^TY to arrive at equation 2.

$$ma{x}_{u,v}{u}^T{X}^{T}Yv\text{ subject to} {\Vert u\Vert }^2\le 1, {\Vert v\Vert }^2\le 1$$ (2)

To construct our canonical correlation vectors, we standardized X and Y to have a mean of 0 and variance of 1.

$${\forall }_c\sum X\left[,c\right]/g=0,var\left(X\left[,c\right]\right)=1\text{ and }{\forall }_d\sum X\left[,d\right]/g=0,var\left(X\left[,d\right]\right)=1$$

We then are able to solve for the canonical correlation vectors u and v using singular value decomposition (SVD) as follows: Let

$$K=X^{T}Y$$

K can be decomposed using SVD as

$$K=\text{ΓΛ}{\mathrm{\Delta }}^T$$ (3)

where

$$\text{Γ}=({\gamma }_1,\dots ,{\gamma }_k)$$

$$\text{Δ}=({\delta }_1,\dots ,{\delta }_k)$$

$$\text{Λ}=({\lambda }_1^{1/2},\dots ,{\lambda }_k^{1/2})$$

Since we have substituted the identity matrix for X^TX and Y^TY, we can obtain our canonical correlation vectors u and v as the left and right singular vectors from the SVD for i = 1, …,k.

$$u_i={\gamma }_i$$

$$v_i={\delta }_i$$

Since we are interested in only a subset of the canonical correlation vectors, we approximated the singular value decomposition with a partial singular value decomposition using the augmented implicitly restarted Lanczos bidiagonalization algorithm implemented in the irlba R package⁶². This procedure returns a user-defined number (k) of left and right singular vectors which approximate the canonical correlation vectors that project each expression matrix into the maximally correlated subspace.

Multi-set canonical correlation

Two-set canonical correlation analysis can be extended to multi-set analysis (i.e. Multi-CCA), aiming to identify projection vectors that maximize the overall correlation across all datasets. There are several options for how to exactly formulate this optimization problem, for which full descriptions can be found in Kettenring (1971)³³. Here, we’ve chosen to use the same approach as described in Witten and Tibshirani (2009)³⁰.

Formally, if we have N datasets X₁, …, X_N, the goal is to find projection vectors W = w₁, …,w_N that maximize:

$$\underset{w_1.\dots ,w_N}{\text{max}}\sum _{i<j}{w}_i^T{X}_i^T{X}_j{w}_j\hspace{1em}\text{subject to }{w}_n^T{X}_n^T{X}_n{w}_n=1\hspace{1em}\forall n$$

To address cases where there are more cells than genes, as discussed in the previous section, we again make the diagonalizing assumption for the covariance matrix of each dataset. By substituting the identity matrix for each $X_n^T{X}_n$we arrive at

$$\underset{w_1. \dots , w_N}{\text{max}}\sum _{i<j}{w}_i^T{X}_i^T{X}_j{w}_j\hspace{1em}\text{subject to }{\Vert w_n\Vert }^2\le 1\hspace{1em}\forall n$$ (4)

To construct the canonical correlation vectors, we first standardized each X_n such that ∀_c ∑X [,c]/g = 0 , var(X[,c]) = 1. We then are able to solve for the canonical correlation vectors w_n using the following iterative algorithm:

Algorithm 1.

Multi-CCA

procedure MCCA   for all Xn do    [T, Λ, Δ]←SVD(X)    initialize wn ← Δ   for 1, …, # of CCs to compute do    while ||o1 – o2| /o1|< threshold do     o1 ← calculate objective for wn[cc] (4)     for all Xn do      update $w_n\left[cc\right]\leftarrow \frac{(X_n^T\sum _{k\ne n}{X}_k{w}_k\left[cc\right])}{{‖(X_n^T\sum _{k\ne n}{X}_k{w}_k\left[cc\right])‖}_2}$     o2 ← calculate objective for wn[cc] (4)   return W

For computational efficiency, we again use irlba for the initializing singular value decomposition and set a default convergence threshold of 10⁻³ with a maximum of 25 iterations in the while loop.

3. Identification of rare non-overlapping subpopulations

CCA returns vectors that capture sources of variance that are shared between datasets. Therefore, CCA will not pick up sources of variation that are unique to a single dataset, for example, if there is a rare unique population in only one dataset. In contrast, principal component analysis (PCA) would capture this signal when performed individually on each dataset.

We therefore reasoned that we could compare the results of PCA and CCA to identify cells whose expression patterns were not well-explained by a shared correlation structure. In principle, this allows for unsupervised identification of non-overlapping subpopulations, which can be filtered out prior to continuing the alignment procedure. This is of particular importance for rare subpopulations, which if not identified as non-overlapping, could blend into abundant cell states after alignment (Supplementary Figure 6D–E).

Therefore, we quantified how well the low dimensional subspace defined by CCA explains the variance in gene expression as compared to PCA run on each dataset independently. By computing the ratio η of these two measures of variance, we are able to identify cells that have low values for η and may originate from non-overlapping states. In our demonstrated alignment examples, we chose to use the first 20 dimensions from our CCA and PCA calculations when computing η.

To compute this ratio, we first calculate the gene loading matrices A and B for X and Y respectively as

$$A=Xu$$

$$B=Yv$$

We then form orthonormal bases D and E via QR decomposition such that

$$A=DR$$

$$B=ER$$

and project the expression data onto D and E to get $\tilde{X}$and $\tilde{Y}$.

$$\tilde{X}=X^{T}D$$

$$\tilde{Y}=Y^{T}E$$

Next, we reconstruct the data to get $\widehat{X}$ and $\widehat{Y}$

$$\widehat{X}=D{\tilde{X}}^T$$

$$\widehat{Y}=E{Y}^T$$

We then calculate the variance in gene expression σ_CCA for every cell in $\widehat{X}$ and $\widehat{Y}$.

$${\sigma }_{CCA}= \sum _g^{n}var(\widehat{X}\left[g,\right])\hspace{1em}{\sigma }_{CCA}= \sum _g^{n}var(\widehat{Y}\left[g,\right])$$ (5)

Then, we run a principle component analysis on X and Y to produce orthogonal gene loading matrices F and G. Similarly, we can project the expression data onto F and G and reconstruct the data to get $\widehat{X}$ and $\widehat{Y}$.

$$\tilde{X}=X^{T}F$$

$$\tilde{Y}=Y^{T}G$$

$$\widehat{X}=F{\tilde{X}}^T$$

$$\widehat{Y}=G{\tilde{Y}}^T$$

We calculate the variance in gene expression σ_PCA in $\widehat{X}$ and in $\widehat{Y}$ using equation 5. Finally, we define η as the ratio of σ_CCA to σ_PCA to serve as an indicator of how well each cell is defined by shared sources of variance (lower values indicating non-overlapping cells).

$$\eta = \frac{{\sigma }_{CCA}}{{\sigma }_{PCA}}$$ (6)

Empirically, we applied a threshold of 0.5 uniformly in all datasets, where cells with η < 0.5 were considered non-overlapping. We found that this unsupervised procedure robustly identified rare populations that were unique to only dataset. These included terminally differentiated NK cells in the MARS-Seq hematopoietic progenitors, B and T cells in the murine pancreatic islet dataset and mast cells in the human pancreatic islet dataset (Supplementary Figures 7 and 12).

However, identifying a single value for this threshold was challenging for abundant populations that were specific to a single dataset, for example, in our negative control experiments where we aligned datasets that have negligible biological similarity. However, in each of these cases (Supplementary Figure 15), even though we did not initially identify these cells as non-overlapping, our procedure did not artificially align cells from these datasets together. While we anticipate that new methods that can robustly identify non-overlapping subpopulations prior to alignment will be exciting avenues for further development, our examples demonstrate that our method does not artificially align either rare or abundant non-overlapping subpopulations together.

4. Aligning canonical correlation vectors

After CCA, CC vectors are by definition correlated, but not necessarily aligned between datasets. In particular, shifts in feature scale or population densities can drive global differences between CC loadings, and must be corrected for as part of the alignment procedure, as described below.

Gene selection for canonical correlation vector alignment

We first identify genes that drive the shared sources of variation in both datasets by finding those genes whose expression robustly correlates with each projection vector in both datasets. For this, we use the biweight midcorrelation (bicor), a median based similarity metric.

For each canonical correlation vector i, …, k

$$\zeta ={\forall }_g\mathrm{m}\mathrm{i}\mathrm{n}(bicor\left(X\left[g,\right],u_i\right),bicor\left(Y\left[g,\right],v_i\right))$$

We take the genes with the highest ζ values (M) to construct a “metagene”, a weighted linear combination of genes, to use for alignment. In all examples here, we used the top 30 genes to construct the metagene average. However, we note that exact choice of this parameter is robust across a wide range of values. Across all examples in Figures 2–4, we varied this parameter across a range (20–100 genes), and assessed the final alignment score. We observed only minor differences (with an average of less than 2% shift compared to 30 genes).

However, when we continued to reduce this parameter we did begin to observe larger changes in the alignment score (>5% when using less than 10 genes). This is likely due to the fact that when only small numbers of genes are considered, biological stochasticity or technical noise will play a larger role in the pooled metagene. Therefore, the minimum number of genes that are required to have conserved expression patterns between datasets, in order to be correctly aligned, will depend on the scale and sequencing depth of each dataset. Datasets with larger cell number, or deeper sequencing, will be able to pick up on more subtle patterns (with fewer conserved genes), analogous to experimental design considerations for detecting subtle transcriptomic states using unsupervised clustering.

Alignment of two canonical correlation vectors

We define two vectors of metagenes Φ_i and Θ_i where for each cell c in X and each cell d in Y, the metagene is defined as

$${\text{Φ}}_{i,c}= u_{i}X\left[M,c\right]{\text{Θ}}_{\text{i},\text{d}}=v_{i}Y\left[M,d\right]$$ (7)

Each vector of metagenes is then scaled from 0 and 1 to match its 95\% reference range. To do this, we define Q as the quantile function that gives the inverse of the empirical distribution function.

$${\mathrm{\Phi }}_i^{\mathrm{\text{'}}}=\frac{{\mathrm{\Phi }}_i-Q_{{\mathrm{\Phi }}_i}\left(2.5\right)}{Q_{{\mathrm{\Phi }}_i}\left(97.5\right)-Q_{{\mathrm{\Phi }}_i}\left(2.5\right)}{\mathrm{\Theta }}_i^{\mathrm{\text{'}}}=\frac{{\mathrm{\Theta }}_i-Q_{{\mathrm{\Theta }}_i}\left(2.5\right)}{Q_{{\mathrm{\Theta }}_i}\left(97.5\right)-Q_{{\mathrm{\Theta }}_i}\left(2.5\right)}$$

We then look for systematic shifts that still remain after scaling which are largely driven by outliers and linearly shift the metagenes to correct for this. This procedure robustly corrects for differences in feature scale.

$${\mathrm{\Phi }}_i^{\mathrm{\text{'}}}={\mathrm{\Phi }}_i^{\mathrm{\text{'}}}+\underset{z=10,\dots ,90}{\text{min}}\left|Q_{{\mathrm{\Phi }}_i^{\mathrm{\text{'}}}}\left(z\right)-Q_{{\mathrm{\Theta }}_i^{\mathrm{\text{'}}}}\left(z\right)\right|$$

Next, we determine an optimal mapping between the metagenes, using dynamic time warping (DTW) as implemented in the dtw R package⁶³ with default parameters. Traditionally used to find an alignment between two time series³⁵, DTW effectively aligns each cell in the smaller dataset to the cell with the most similar metagene expression in the larger dataset, while maintaining the relative ordering of cells within each dataset. To do this, DTW computes a warping path W that maps elements of X and Y in order to minimize the distance between them.

$$W=w_1,w_2,\dots ,w_k$$

Each w_k corresponds to a point along the warping path that maps an element in X to an element in Y. The minimization problem can then be defined in terms of the cumulative warping distance. We chose to use Euclidean distance as the distance function δ.

$$DTW\left(X, Y\right)= \underset{W}{\text{min}}\left[\sum _{k=1}^p\delta \left(w_k\right)\right]$$ (8)

A key feature of DTW in the alignment procedure is the non-linear warping of each metagene vector. These compressions and stretches correspond to potential shifts in population density across datasets. We then apply an identical warping to the canonical correlation vectors, mapping the CC values from both datasets onto a common aligned scale. We apply this procedure to each pair of basis vectors individually to define a single, aligned, low-dimensional space representing both datasets.

Alignment of multiple canonical correlation vectors

Extending the alignment procedure to multiple datasets follows naturally from the two dataset case. We first choose a reference dataset, which we set by default to be the dataset with the largest number of cells. We then perform repeated pairwise alignments of the canonical correlation vectors to the reference exactly as described for the two-set case above. This procedure warps the canonical correlation vectors for each dataset onto a common aligned space, defined by the “reference” dataset.

CC selection for downstream analysis

Dimensionality reduction, such as PCA, is a commonly applied tool in scRNA-seq analysis to help overcome technical noise and summarize the data in a smaller number of features. Choosing the number of PCs to include for downstream analyses is often performed by plotting the variance explained as a function of the number of principal components, and examining this relationship for saturation. Similarly, here we must decide on the number of aligned canonical correlation vectors to include for downstream analysis. To help guide this parameter choice, we calculated a measure of the correlation strength for each CC vector. Specifically, for each dataset X_n and each CC vector w_n, we examined all genes involved in the construction of the “metagene” (as described above, M = m₁, …,m_g) and calculated the average biweight midcorrelation.

$$\tau = \frac{1}{g}\sum _{i=1}^{g}bicor\left(X_n\left[m_i,\right],w_n\right)$$ (9)

For the reference dataset, we take the average of τ across all pairwise calculations. For each dataset, we plot a LOESS curve of τ (“Shared correlation strength”) as a function of CC vector. Curves for all five examples in this manuscript are shown in Supplementary Figure 1. The saturation point on these curves provides a valuable guide for the number of CCs to include in downstream analyses. Importantly, while the exact saturation point can be subjective, we observe that the global structure of our integrated dataset is robust to the exact choice of this parameter ∓ 5CCs (Supplementary Figure 1).

Calculating an alignment score

While our tSNE plots provide a visual representation of the overlap between datasets after alignments, we sought to develop a quantitative metric to ask how well any group of datasets are aligned. We calculated an alignment score as follows. First, we randomly downsample the datasets to have the same number of cells as the smallest dataset. Then, we construct a nearest-neighbor graph based on the cells’ embedding in some low dimensional space (the aligned CC space after running the alignment procedure). For every cell, we then calculate how many of its k nearest-neighbors belong to the same dataset and average this over all cells to obtain $\overline{x}$. If the datasets are well-aligned, we would expect that each cells’ nearest neighbors would be evenly shared across all datasets. For all of our examples, we chose k to be 1% of the total number of cells. We then normalize by the expected number of same dataset cells and scale to range from 0 to 1.

$$\text{Alignment Score =}1-\frac{\stackrel{-}{x}-\frac{k}{N}}{k-\frac{k}{N}}$$

5. Integrated Analysis Across Datasets

The aligned canonical basis vectors form a shared low-dimensional space that can be used for integrated downstream analyses, for example, clustering or trajectory building. We describe our analyses individually for each dataset below.

Modularity based clustering to identify cell types

To partition cells into clusters, we used the smart local moving (SLM) algorithm for modularity-based clustering⁶⁴. For each of the five of datasets, we computed a cell-cell distance matrix constructed on selected aligned canonical correlation vectors. We constructed a shared-nearest neighbor (SNN) graph based on this distance matrix to use as input to the SLM algorithm, implemented through the FindClusters function in Seurat. To visualize the resulting clusters in two dimensions, we used Barnes-Hut implementation of the t-distributed stochastic neighbor embedding (tSNE) algorithm⁶⁵.

Identification of PBMC subtypes

We chose to use the first 20 aligned canonical correlation vectors to calculate the cell-cell distance matrix and subsequent SNN. We ran FindClusters with a resolution parameter of 0.6, resulting in 13 distinct clusters of cells. These clusters corresponded to CD14+ and CD16+ monocytes, CD4+ memory and naive T cells, CD8+ T cells, B cells, NK cells, dendritic cells, and erythrocyte populations which all showed significant enrichment for canonical cell type markers after running a likelihood-ratio test for differential expression implemented in Seurat as FindAllMarkers. The same 20 CCs were used as input for visualization via tSNE.

To understand global correlations between IFNβ responses for each cell type (Figure 2G), we first placed cells into 26 bins (based on the 13 immune clusters, but also grouped stimulated and resting cells within each cluster separately), and calculated the average expression for each gene within each group. The difference between the average expression of stimulated and resting cells for each cluster represents its transcriptional response to IFNβ stimulation. We then calculated the Pearson correlation of these responses between all pairs of clusters, using 431 genes that exhibited at least a two-fold change in response to stimulation for at least one of the 13 clusters.

Identification of hematopoietic progenitor populations

To identify the hematopoietic progenitor populations present in both the SMART-Seq2 dataset and the MARS-Seq dataset, we used the first 10 aligned canonical correlation vectors as input to calculate the cell-cell distance matrix, SNN, and visualization via tSNE.

We then mapped cells from the SMART-Seq2 dataset to one of the clusters originally identified in the MARS-Seq dataset. In principle, we could simply map each SMART-Seq2 cell to the cluster identity of its nearest neighbor in the MARS-Seq dataset. However, in order to make sure that our mappings were also consistent with the overall structure of the data, we used a two-step procedure.

We first performed a joint clustering on the first 10 aligned CC embeddings using the SLM algorithm via FindClusters with default parameters, revealing 10 clusters (referred to below as ‘joint clusters’). We then calculated the percentage of cells in each MARS-Seq cluster that fell into each of the joint clusters. Let Freq_xy represent the proportion of cells in MARS-Seq cluster x, that fall into joint cluster y.

We next mapped each SMART-Seq cell to the cluster of its closest MARS-Seq neighbor, based on the SNN-defined distance matrix. However, we defined the mapping as discordant if the mapped cluster was present at less than 25 percent frequency in the joint clustering, i.e. Freq_xy < 0.25. In this case, we mapped the SMART-Seq2 cell to its next closest neighbor. Finally, once all cells had been mapped to MARS-Seq clusters, we assigned each cell a lineage identity based on Figure 2 in Paul et al 2015³⁸. These cluster and lineage assignments were used in all downstream analyses.

Identification of pancreatic islet subtypes in human and mouse

We identified conserved populations of islet subtypes by running FindClusters using the first 20 aligned CC embeddings with a resolution parameter of 0.5. This resulted in 10 clusters corresponding to alpha, normal beta, ER stressed beta, delta, gamma, ductal, acinar, stellate, endothelial, and immune cells. The same 20 aligned CCs were used for tSNE visualization. We also observed an 11th cluster of 115 cells that was defined almost entirely by low complexity (median 1,088 genes), which we removed from further analysis (Supplementary Figure 13).

Identification of pancreatic islet subtypes in the four human datasets

In order to identify populations of islet subtypes across the four human pancreas datasets, we ran FindClusters using the first 10 CC embeddings with a resolution parameter of 0.4. This gave 8 distinct clusters corresponding to alpha, beta, ductal, acinar, delta, gamma, stellate, and endothelial populations. The same 10 aligned CCs were used for tSNE visualization.

Identification of PBMC subtypes across three technologies

We chose to use the first 20 aligned canonical correlation vectors as input to FindClusters with a resolution parameter of 1.2. 16 clusters were identified which correspond to CD4+ memory, naive, and regulatory T cells, two CD14+ monocyte populations (HLA low and HLA high), pre-B cells, B cells, CD8+ naive T cells, two populations of CD8+ effector T cells, CD16+ monocytes, conventional dendritic cells, plasmacytoid dendritic cells, megakaryocytes, and two populations of NK cells (CD56^bright and CD56^dim).

Construction of joint erythroid developmental trajectories

We first took a subset of the combined hematopoietic progenitor dataset that included all cells originally assigned to the first seven clusters in the MARS-Seq dataset and cells that mapped to one of those clusters from the SMART-Seq2 dataset. We then built a diffusion map using the first 10 aligned CC embeddings using the diffuse function from the diffusionMap R package (Richards, 2014)⁶⁶ with epsilon parameter set to 9, corresponding to the median distance to the 0.05*n nearest neighbor. Next, we fit a principal curve⁶⁷ through the first two diffusion map coordinates using the principal.curve function from the princurve R package with default parameters⁶⁸. The order of a cell’s projection onto this principal curve represents its predicted progression through erythropoiesis, or “pseudotime” value, as shown in Supplementary Figure 9A–B.

In order to determine the transcriptomic range for each gene across erythropoiesis for the SMART-Seq2 and MARS-Seq datasets, we first calculated the average expression within clusters C1…C7 for each gene, and calculated the range (max-min) of these values. We performed this procedure independently for cells in both datasets, and plotted the values in Figure 3I.

Differential expression testing to detect conserved cell-type markers

To identify cell-type markers that are conserved across datasets, we first performed a joint clustering of the data as described above. Then we conducted differential expression testing on each cell type cluster for each dataset independently using a Wilcoxon rank sum test, requiring a minimum 1.25-fold difference between the two groups of cells and expression in at least 10% of cells in both groups. We used the metap R package to combine p-values using the minimump method. For a detailed review of meta-analysis methods for differential expression, see Tseng, et al. 2012⁶⁹. We visualize the top five markers, ranked by combined p-value, for each cluster in Figure 4D–E.

To identify markers differentially expressed between the beta cell populations, we used the same integrated differential expression procedure, but limited our analysis to only the two beta cell populations. We used the top 100 differentially expressed markers, ranked by integrated p-value, as input for gene ontology enrichment as performed using EnrichR⁷⁰.

Comparison to other batch correction methods

We compared our alignment method to both ComBat⁴⁹ and limma⁵⁰. For each pair of datasets, we first combined the UMI count matrices and scaled and normalized the combined expression matrix. For the ComBat comparisons, we performed batch correction on the scaled and normalized gene expression data using the ComBat function from the sva R package, treating the dataset as the batch. For the limma comparisons, we performed batch correction on the scaled and normalized gene expression data using the removeBatchEffect function from the limma R package, treating the dataset as the batch. All other default parameters were left unchanged for both methods. We then performed a principle component analysis to identify sources of variation that accounted for a majority of the variation in the corrected data. For the PBMC, hematopoietic progenitor, and pancreas datasets we used the first 19, 18 and 21 PCs respectively to visualize with tSNE and to calculate an alignment score. For the two multiple alignment examples of human pancreatic islet cells and PBMCs, we used the first 20 PCs.

Validation of pDC vs DC response to IFNβ

Based on our analysis of the Kang et al. dataset, we observed subsets of genes whose transcriptional response to IFNβ stimulation differed between plasmacytoid and conventional DCs. While these changes were observed at the single cell level, we wished to validate these in bulk experiments. We therefore repeated the original experiment, where PBMCs a healthy human donor (ALLCELLS) were cultured with RPMI medium supplemented with 10% FBS and stimulated for 6 hours with IFNβ (100U/ml, PBL Assay Science), with a subset of cells left unexposed to the stimulation as a control. After stimulation, we sorted pure populations of pDCs (20,000) and cDCs (60,000) based on the following panel of standard antibodies (from BioLegend and BD Pharmingen): CD3 (HIT3a), CD19 (HIB19), CD56 (HCD56), CD14 (HCD14), HLA-DR (LN3), CD11c (Bu15) and CD123 (7G3). pDCs were defined as: CD3− CD19− CD56− CD14− HLA−DR+ CD11c− CD123+. cDCs were defined as: CD3− CD19− CD56− CD14− HLA−DR+ CD11c+. Following sorting, we extracted RNA using TRIzol (Invitrogen) and performed bulk RNA-seq (three technical replicates per sample) using a version of the SMART-Seq2 protocol as previously described^71,72.

A Life Sciences Reporting Summary is available