Atomistic Insights into the Functional Instability of the Second Helix of Fatty Acid Binding Protein

Abstract

Structural dynamics of fatty acid binding proteins (FABPs), which accommodate poorly soluble ligands in the internalized binding cavities, are intimately related to their function. Recently, local unfolding of the α-helical cap in a variant of human intestinal FABP (IFABP) has been shown to correlate with the kinetics of ligand association, shedding light on the nature of the critical conformational reorganization. Yet, the physical origin and mechanism of the functionally relevant transient unfolding remain elusive. Here, we investigate the intrinsic structural instability of the second helix (αII) of IFABP in comparison with other segments of the protein using hydrogen-exchange NMR spectroscopy, microsecond molecular dynamics simulations, and enhanced sampling techniques. Although tertiary interactions positively contribute to the stability of helices in IFABP, the intrinsic unfolding tendency of αII is encoded in its primary sequence and can be described by the Lifson-Roig theory in the absence of tertiary interactions. The unfolding pathway of αII in intact proteins involves an on-pathway intermediate state that is characterized with the fraying of the last helical turn, captured by independent enhanced sampling methods. The simulations in this work, combined with hydrogen-exchange NMR data, provide new, to our knowledge, atomistic insights into the functional local unfolding of FABPs.

Significance

Transient local unfolding of the second helix (αII) of intestinal fatty acid binding protein was recently shown to provide a pathway for ligand entry to the internalized binding site. However, the physical origin and mechanism of this functionally relevant local unfolding remain elusive. Herein, the intrinsic helix instability of αII is investigated using a combined experimental and computational approach. Our results show that the intrinsic tendency for αII to unfold is inherently encoded in its primary sequence and can be described using a statistical mechanical model. An on-pathway folding intermediate of αII in intact proteins has also been identified. Our simulation results, which agree with the hydrogen-exchange data, provide mechanistic insights into the transient unfolding dynamics critical to the protein functions.

Introduction

Belonging to the intracellular lipid binding protein superfamily, fatty acid binding proteins (FABPs) are widely expressed in a variety of tissues and function as chaperones in cells for poorly soluble ligands (1, 2, 3). Despite the diversity of primary sequences (3), a highly conserved tertiary structure that consists of a 10-stranded antiparallel β-barrel structure and two short α-helices (αI and αII) capping one end of the β-barrel is shared among all FABP isoforms (4, 5). This structural form facilitates long-chain fatty acid binding and transport (6), which are associated with a variety of biological processes, such as cell signaling, energy supply, regulatory gene expression (4), and inflammatory and metabolic responses (7). However, a lingering puzzle of the mechanism of the FABP-ligand interactions is how the completely internalized binding site within the β-cage is accessed by ligands from bulk solvent. On the basis of structural and dynamics investigations, a portal region comprised of the helix αII and turns between β-strands C-D and E-F was proposed for ligand entry and exit (8, 9, 10, 11). Early kinetics study of oleate binding to wild-type IFABP revealed a rate-limiting step that is absent in the helixless variant (8), indicating a critical role of the helical region for ligand binding. However, the intrinsic structural reorganization of wild-type IFABP that accounts for this rate-limiting step has not been captured experimentally. In a recent study on a variant of human IFABP in which the helical cap and the β-barrel are covalently linked, transient local unfolding of the helix αII has been observed (6). Importantly, the rate of the transient unfolding (195 s⁻¹) in this closed-cap variant nicely correlates with the maximal ligand association rate (180 s⁻¹) at 13°C, providing strong support for the local unfolding of αII as a critical conformational reorganization required for ligand entry.

All-atom computer simulations represent a powerful method that can provide a wealth of detailed information about protein dynamics and has been previously applied to study the structural dynamics of different FABP isoforms (12, 13, 14, 15, 16, 17). However, transient unfolding of αII as part of the helical cap has not been observed in previous simulations. In addition, previous experimental efforts to probe the intrinsic fast (on the ps–ns timescale) and slow (on the ms timescale) dynamics of wild-type FABPs using relaxation-based NMR experiments failed to capture the unfolding of αII creating the portal for ligand entry (18, 19, 20). The maximal ligand association rate for wild-type IFABP was found to be ∼4 times that of the closed-cap variant (6), indicating that the functionally relevant dynamics in the former may occur on a much faster timescale. In this work, the amide hydrogen-exchange rates of human IFABP were measured, showing that the αII is substantially more unstable than other nonloop regions in intact IFABP and samples an open state with an estimated population of 15%. Long (μs) molecular dynamics (MD) simulations and enhanced sampling methods are employed to investigate the intrinsic instability of α-cap and show that the distinct tendencies of unfolding between αI and αII are inherently encoded in their amino-acid sequences while tertiary contacts stabilize their helical structures in intact proteins. An on-pathway folding intermediate of αII characterized with unfolding of C-terminal helical segments has also been identified. Our simulation results, which agree with the amide hydrogen-exchange data, provide an atomic-level delineation of the transient and functionally relevant unfolding dynamics of IFABP.

Materials and Methods

Hydrogen-exchange NMR spectroscopy

Human intestinal FABP (IFABP) was expressed and purified using the previously described protocol (6, 21). The NMR sample used for the hydrogen-exchange measurement contained 1 mM ¹⁵N-labeled protein, 20 mM sodium phosphate (pH 7.3), 50 mM NaCl, 1 mM EDTA, 95% H₂O, and 5% D₂O. The amide hydrogen-exchange experiments were carried out, using the radiation-damping-based water inversion pulse scheme (22), on a Bruker 800 MHz NMR spectrometer (Bruker, Billerica, MA) equipped with a cryoprobe at 30°C. A series of two-dimensional data sets with mixing times (20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 190, 220, 260, and 300 ms) were recorded for extraction of the residue-specific hydrogen-exchange rates. Each two-dimensional data set consists of 80 × 640 complex points in the ¹⁵N (spectral width of 1743 Hz) and ¹H (spectral width of 11,202 Hz) dimensions, respectively. Each free induction decay was acquired using two scans with an interscan delay of 2 s. A reference spectrum was also acquired with an interscan delay of 10 s. The NMR data were processed using the NMRPipe software package (23).

MD simulations

The crystal structure of human IFABP (Protein Data Bank [PDB]: 3AKM) was used for atomistic simulations in this work. The bound ligand and Mg²⁺ in the crystal structure were removed. The initial conformations of the isolated αI (residues 13–21) and αII helices (residues 24–32) were taken from the human IFABP structure, with the N- and C-termini capped with acetyl and N-methylamide groups, respectively. MD simulations of both the intact protein and isolated helices were performed using the GROMACS-4.5.7 package (24, 25), with the AMBER ff99SBnmr1-ILDN force field (26, 27) and the TIP3P explicit water model (28). Three Cl⁻ ions were added to the system of isolated αII to obtain charge neutrality. The intact IFABP and αI are electronically neutral, and no ions were added. Twin-range cutoff distances for van der Waals interactions were set to 0.8 and 1.0 nm. The short-range electrostatic interactions were cut off at 0.8 nm, and long-range electrostatic interactions were treated using the particle mesh Ewald summation algorithm (29) with an interpolation order of 4. All bonds involving hydrogen atoms were constrained using the LINCS algorithm (30), and a time step of 2 fs was used for leapfrog integration (31). The temperature was kept constant at 300 or 350 K as required in individual simulations by the velocity-rescaling algorithm (32), with a relaxation time of 0.1 ps. Before production runs under the NPT condition, the systems were relaxed by the standard energy minimization and equilibration procedures as described previously (33). Individual simulations on full-length proteins and isolated helices performed in this work are summarized in Table S1.

Well-tempered metadynamics

Well-tempered metadynamics simulation of human IFABP was performed using the PLUMED plugin (34) interfaced with GROMACS at 300 K. The system preparation, except metadynamics parameters, was fully analogous to that of the conventional MD simulations described above. To enhance the sampling of αII unfolding, a pair of collective variables, namely the Cα contacts (N_Cα) and helicity (ψ_α) of αII, were selected, along which the history-dependent bias potential was applied. N_Cα evaluates the number of native contacts between Cα atoms j and k that belong to αII and the rest of the protein, respectively:

$$N_{C\alpha }=\sum _{j,k}\frac{1-{\left(\frac{r_{jk}}{r_0}\right)}^n}{1-{\left(\frac{r_{jk}}{r_0}\right)}^m},$$ (1)

where r₀ = 0.85 nm (35), n = 8, and m = 10. The summation runs over all pairs of Cα atoms (j and k) that are closer than 1.05 nm in the native structure and separated by more than four residues in the primary sequence. The helicity is defined according to the backbone dihedral angle ψ:

$${\mathit{\Psi }}_{\alpha }=\sum _{i=1}^N\frac{1}{2}\left[1+\cos \left({\psi }_i-{\psi }_i^{ref}\right)\right],$$ (2)

where N is the number of residues in αII and ${\psi }_i^{ref}$ is the ψ value of residue i in the starting conformation. The Gaussian bias potential was added every 1 ps, with the initial height of 0.42 kJ/mol and with the widths of 0.531 and 0.041 for N_Cα and ψ_α, respectively. Three independent well-tempered metadynamics simulations were carried out for 0.3, 1.15, and 0.3 μs, with bias factors set to 3, 6, and 15, respectively.

Accelerated MD simulation

Accelerated MD (aMD) simulation (36) was carried out for human IFABP at 300 K, in which a nonnegative boost potential (ΔV(r)) is added to the system potential (V(r)) when V(r) is below a given threshold energy E:

$$\mathit{\Delta }V\left(\mathbf{r}\right)=\frac{{\left(E-V\left(\mathit{r}\right)\right)}^2}{\left(\alpha +E-V\left(\mathit{r}\right)\right)},$$ (3)

where α is the inverse strength boost factor. ΔV(r) = 0 when V(r) is above E. The dual-boost aMD (37, 38) with boost potentials applied to both dihedral potentials and the total potential energy was employed in this work, implemented in AMBER 14 (39). The boost parameters (E_dihed, α_dihed; E_total, α_total) were calculated on the basis of a 100 ns conventional MD simulation of human IFABP, α_dihed = 0.7 kcal mol⁻¹ × N_res, E_dihed = 〈V_dihed〉+ 5α_dihed, α_total = 0.2 kcal mol⁻¹ × N_atoms, E_total = 〈V_total〉+ α_total, where 〈V_total〉and 〈V_dihed〉 are the average total and dihedral potential energies in the 100 ns simulation, respectively. N_atoms and N_res are the numbers of total atoms and protein residues, respectively. Additional details about the system setup are analogous to those of the conventional MD described above and are given in the Supporting Materials and Methods.

Analysis of helix-coil transitions in capped αI and αII peptides

The helix conformation of individual residues of isolated αI and αII in each frame of the MD trajectories is defined according to the backbone dihedral angles (φ, ψ) as follows, −100° < φ < −30° and −67° < ψ < −7°. Equilibrium helix-coil transitions were subsequently analyzed using the statistical mechanical Lifson-Roig (L-R) model (40). A relative statistical weight of 1, v, or w is assigned to a residue in the coil state, at the ends of an uninterrupted sequence of helical conformation, or at the interior of a helical segment that has at least three consecutive residues in the helix conformation, respectively. The partition function (Z) is then given by (41),

$$Z=\left(001\right)\prod _{i=1}^N{\mathbf{M}}_i\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right),$$ (4)

where N is the number of residues of a given peptide, and M_i is a 3 × 3 matrix of conditional probabilities,

$${\mathbf{M}}_i=\left(\begin{array}{ccc}{w}_i& v_i& 0\\ 0& 0& 1\\ v_i& v_i& 1\end{array}\right).$$ (5)

The population (p_LR) of the helix conformation of residue i (with a weight w_i or v_i) can be calculated from the partition function,

$$p_{\text{LR},i}=\raisebox{1ex}{$\partial \ln Z$}\!\left/ \!\raisebox{-1ex}{$\partial \ln w_i$}\right.+\raisebox{1ex}{$\partial \ln Z$}\!\left/ \!\raisebox{-1ex}{$\partial \ln v_i$}\right..$$ (6)

A minimal number of L-R parameters (w or v), assuming common relative weights for all residue types, were used for the analysis of the simulation data, using a Bayesian formalism as described previously (41). Statistical errors of the extracted model parameters were estimated by the SDs of the corresponding values from four segments (2.5 μs each) of the full trajectory (10 μs in total) of each peptide.

Results and Discussion

Low hydrogen-exchange protection of αII in wild-type IFABP

The rate of ligand entry is notably faster in wild-type IFABP than the cap-closed variant (6), and the critical conformational reorganization controlling ligand entry in the former eludes detection by NMR relaxation-dispersion experiments. Amide hydrogen-exchange rates provide an alternative means for qualitative assessment of protein flexibility. With a radiation-damping-based experimental scheme (22), the hydrogen-exchange rates (k_H-EX) of IFABP were previously measured (20). However, it remains unclear whether the exchange occurs through the EX2 limit. In this work, we examined the pH-dependent increase of k_H-EX by raising pH from 7.1 to 7.3. The results of the amide hydrogen-exchange rates at pH 7.3 are summarized in Fig. 1 and Table S2. Except for a few residues with the rates smaller than 0.5 s⁻¹, the hydrogen-exchange rates measured in this work under the condition of pH 7.3 and 30°C are 1.3–1.9 times the rates measured previously under the condition of pH 7.1 and 30°C (20), consistent with the theoretical prediction (1.58 times) of the EX2 model (Fig. S1). Under the EX2 limit, the “open” conformation population of an amide (P_op) could be approximated by k_H-EX/k_rc, where k_rc is the intrinsic hydrogen-exchange rate of an amide in a random coil structure and k_H-EX is the observed exchange rate.

Figure 1.

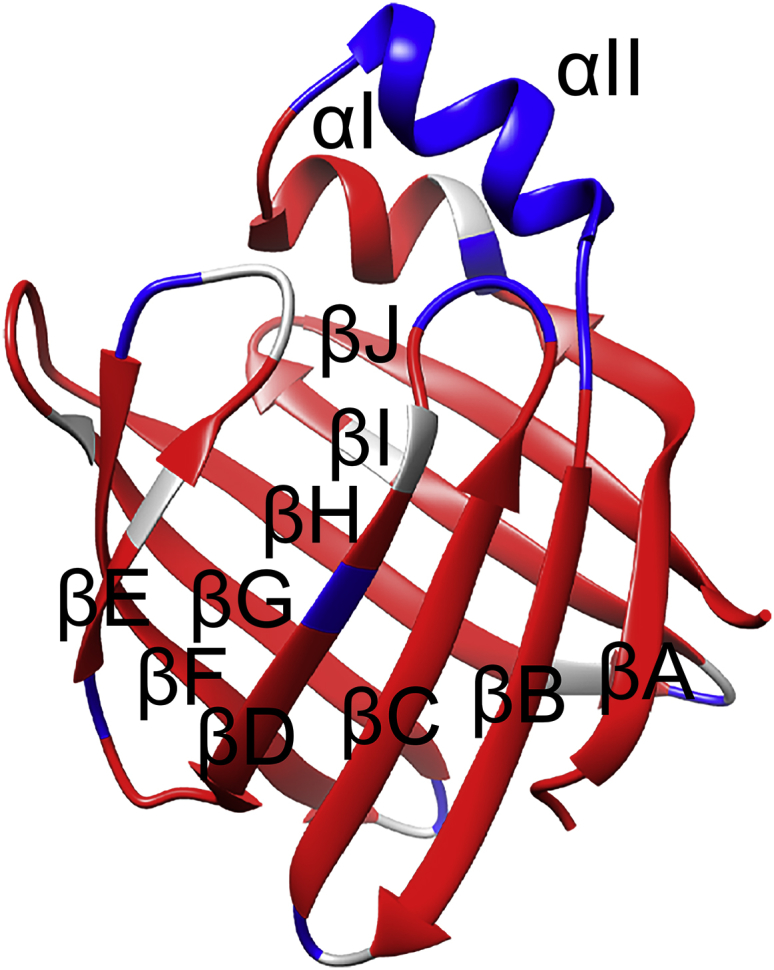
Residues with hydrogen-exchange protection factors larger (smaller) than 30 are colored in red (blue). The residues without available data are shown in gray. To see this figure in color, go online.

Although most of the amides with low protection factors (<150) listed in Table S2 are not involved in hydrogen bonding, the protection factors for residues 28–33 whose amides are involved in H-bonds are in a range of 6–14, indicating that αII (24, 25, 26, 27, 28, 29, 30, 31, 32) in wild-type IFABP populates a relatively large population of “open” species, as is the case in the closed-cap variant (6). On the basis of the P_op values, the population of the “open” state of αII is estimated to be ∼15%.

Transient unfolding of capped αI and αII helices sampled by MD simulations

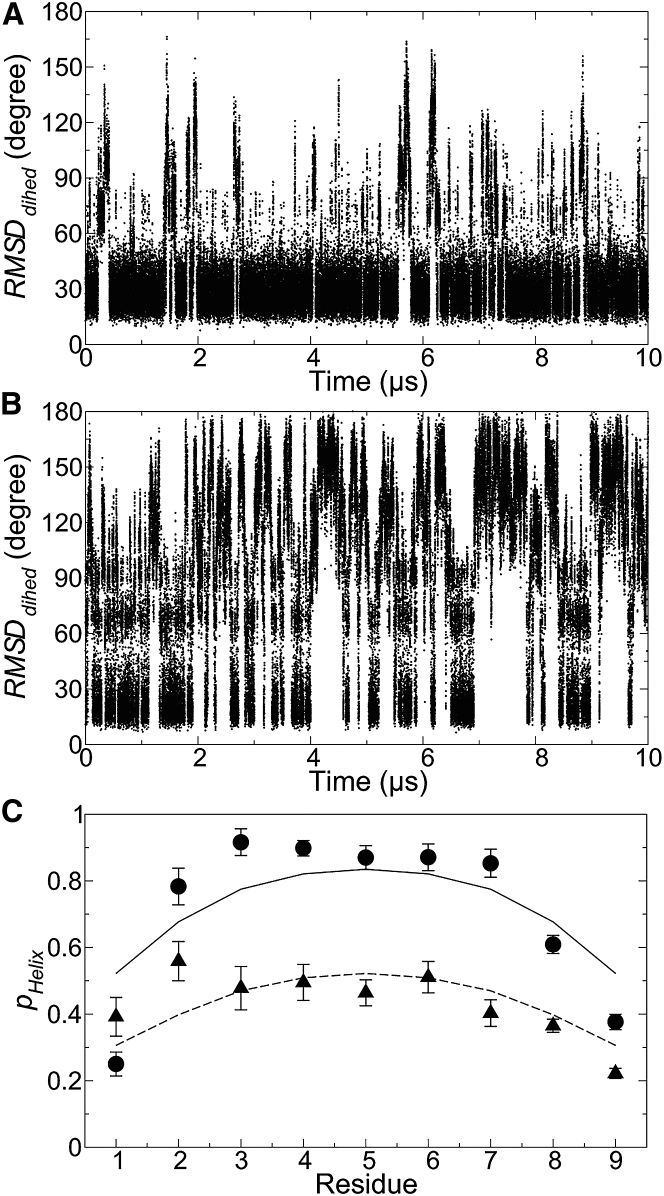
The distinct low protection of αII, as compared with αI and other nonloop regions, prompted us to investigate the differential helix propensities of αI and αII using atomistic simulations that can provide detailed spatiotemporal information unavailable from the experimental data. MD simulations of isolated helical peptides, with amino-acid sequences identical to αI and αII, were therefore carried out at 300 K as described in the Materials and Methods section. As shown in Fig. 2, A and B, reversible partial unfolding and refolding frequently occurred in the 10 μs MD trajectories for both peptides. To evaluate the extent of unfolding, the root mean-square deviations of backbone dihedral angles (RMSD_dihed) were calculated as a function of time for both αI and αII,

$$RMS{D}_{dihed}\left(t\right)=\sqrt{\frac{1}{N}\sum _{i=1}^N\left[{\left({\phi }_i\left(t\right)-{\phi }_i^{ref}\right)}^2+{\left({\psi }_i\left(t\right)-{\psi }_i^{ref}\right)}^2\right]},$$ (7)

where N is the number of residues. ${\phi }_i^{ref}$ and ${\psi }_i^{ref}$ are the backbone dihedral angles of residue i in the initial structure, with −360°, 0, or 360° added to satisfy the requirements $\left|{\phi }_i\left(t\right)-{\phi }_i^{ref}\right|\le 180°$ and $\left|{\psi }_i\left(t\right)-{\psi }_i^{ref}\right|\le 180°$. Although variations of RMSD_dihed values are observed for both peptides, the magnitude and frequency of unfolding are much more pronounced in αII with respect to αI, showing that the functionally relevant instability of αII is encoded in its amino-acid sequence.

Figure 2.

Equilibrium helix-coil transitions in capped αI and αII peptides (with primary sequences of NYDKFMEKM and NIVKRKLAA, respectively). (A and B) RMSD_dihed of isolated αI (A) and αII (B) with respect to the initial conformations in 10 μs MD trajectories is shown. The first and last residues of the peptides were excluded for the calculation. (C) The helix state population of each residue in αI (αII), with simulation data as solid circles (triangles) and predictions from the L-R model as solid (dashed) lines. Minor deviations partly arise from the simple form of the L-R model that assumes a common set of parameters for all amino acids. A more complex L-R model with amino-acid-specific treatment, however, was found to overfit the simulation data.

The equilibrium helix-coil transitions of capped αI and αII peptides were further analyzed using the Lifson-Roig theory (40) for a statistical mechanical description of the ensembles. Fig. 2 C compares the helical state populations of individual residues of αI and αII extracted from the simulations, as well as the corresponding predictions from the L-R model. The results show that the simplest form of the L-R model (with only two parameters, w and v) used here can provide a reasonably good description of the simulation data. The optimal model parameters (w, v) obtained by a Bayesian approach are (2.07 ± 0.12, 0.39 ± 0.02) and (1.43 ± 0.15, 0.24 ± 0.03) for αI and αII, respectively. The relative weights (w, v) in the L-R model can also be interpreted with the more familiar Zimm-Bragg (42) nucleation (σ) and elongation (s) constants (43), σ = v²/(1 + v)⁴ and s = w/(1 + v), giving σ = 0.041 ± 0.002 and s = 1.49 ± 0.07 for αI and σ = 0.024 ± 0.004 and s = 1.15 ± 0.09 for αII. The smaller values of nucleation and elongation constants of αII as compared with αI also evidence that the former is intrinsically more prone to unfold.

Tertiary contacts stabilize α-helices in IFABP

Within intact IFABPs, tertiary interactions between α-helices and the rest of the protein represent a major contribution to the stabilization of α-cap, of which the population of the partially unfolded state is significantly reduced as compared with the isolated peptides. In MD simulations of intact IFABP at 300 K, the helical cap remained folded throughout 1.6 μs simulations (Fig. S2). To observe rare unfolding events of αII in IFABPs, 4 μs MD trajectories of both human and rat IFABPs were subsequently simulated at an elevated temperature (350 K) that speeds up the transitions. Although the overall structure of IFABP remained intact, transient partial unfolding of αII was observed, which is featured with the fraying of the C-terminal region (Fig. 3). The same pattern of transient C-terminal fraying was also observed in the high temperature (350 K) simulation of a homolog protein from the rat species (Fig. S3). The timescale (μs) accessible to the standard MD, nevertheless, is too short for the complete unfolding of αII and for statistical analysis of partial unfolding events.

Figure 3.

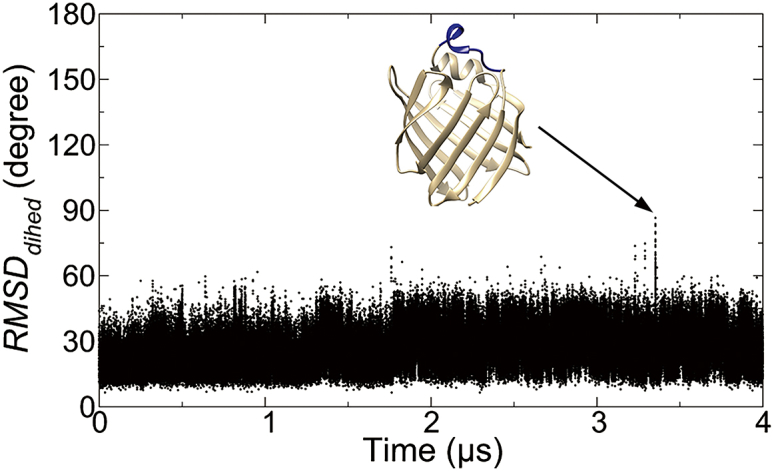
RMSD_dihed of αII (residues 24–32) with respect to the initial conformation in a 4 μs MD simulation of intact human IFABP at 350 K. The inset is the snapshot taken at 3.352 μs. To see this figure in color, go online.

Well-tempered metadynamics simulation of IFABP

The substantially raised free-energy barriers separating the folded and (partially) unfolded states by tertiary interactions in intact IFABPs necessitate the use of a more efficient tool for exploring the highly rugged free-energy surface. For this purpose, well-tempered metadynamics simulation (44) was employed to enhance the sampling of sparsely populated conformational states. In metadynamics, the complexity of protein conformational space is reduced by defining a few collective variables (CVs) providing a coarse-grained description of slow motions. The system evolution in the space of preselected CVs is enhanced by a history-dependent bias potential that is built as a sum of repulsive Gaussians deposited along the trajectory, which could also be used to estimate the free-energy landscape (45).

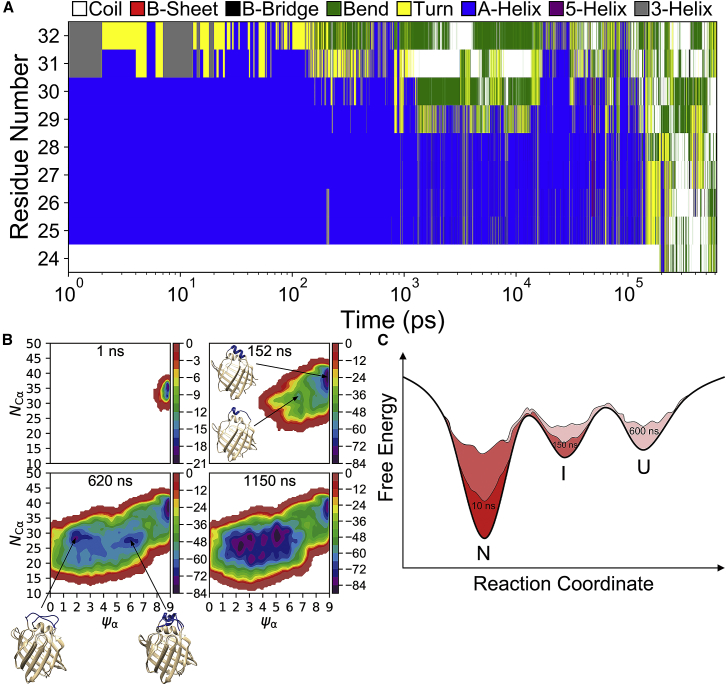
To efficiently explore the unfolding dynamics of αII, the backbone helicity of αII and the number of native Cα-Cα contacts between αII and the rest of the protein were selected as CVs for well-tempered metadynamics simulation in our study. Three independent simulations were performed with bias factors set to 3, 6, and 15, respectively. In each of the independent runs, the accumulated bias potential effectively drove the system out of the native energy basin within 100 ns (Figs. 4 and S5). Before evolving into the fully unfolded state, an intermediate state, which is characterized with the unfolding of the last helical turn (i.e., residues 29–32) of αII, has been identified. The existence of this intermediate is consistent with the transient C-terminal fraying observed in the long MD simulations (Figs. 3 and S3). Despite different efficiencies of energy barrier crossings in the three independent simulations, the same unfolding steps with the intermediate state always sampled before complete unfolding were followed, indicating that this metastable state is an on-pathway folding intermediate connecting the native and unfolded states. Fig. 4 C shows a schematic of the free-energy landscape and the sequential filling of the energy basins of native, intermediate, and unfolded states by the bias potential.

Figure 4.

Well-tempered metadynamics simulation with the bias factor of 6. (A) Time-dependent variation of secondary structures of individual residues of αII is shown. The secondary structures were assigned using the DSSP program (46, 47). The x axis is plotted on a logarithmic scale. (B) Estimated free-energy surfaces (kJ/mol) are shown as a function of CVs at different simulation times. Representative native, partially unfolded, and completely unfolded conformations of αII are shown. (C) A schematic of the free-energy landscape of αII in intact IFABP is given, illustrating a native (N), an on-pathway folding intermediate (I), and an unfolded (U) state and sequential filling of individual minima as a function of time. To see this figure in color, go online.

Complete unfolding of αII was observed and found to be irreversible in all three well-tempered metadynamics simulations. We extended the metadynamics run with the bias factor of 6 up to 1.15 μs; however, a refolding process was not observed after the system evolved to state U. This hysteretic behavior is a typical result of the presence of slow motions not represented by the CVs. The ensemble of the state U includes many non-native interactions among different unfolded conformers that trapped the system in multiple substates of U (Fig. 4 B).

aMD simulation of IFABP

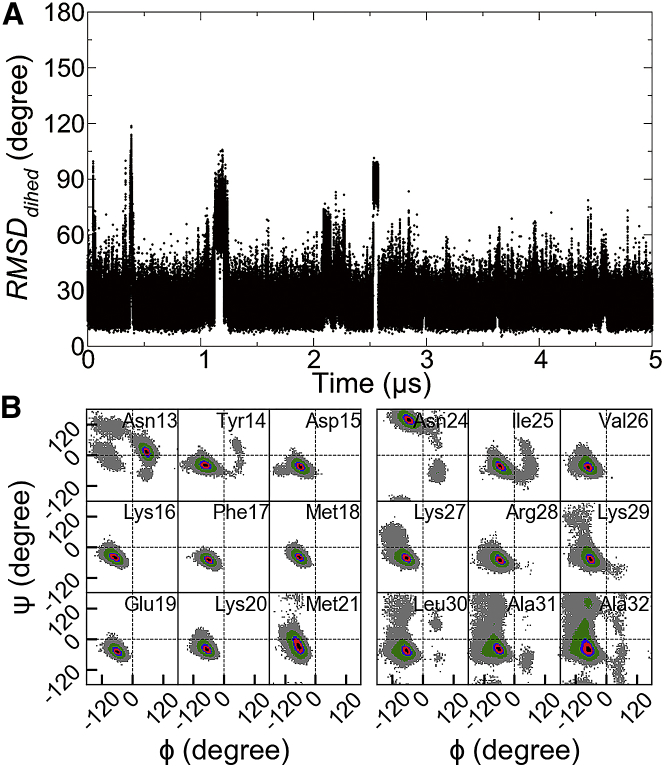
To cross-check the αII unfolding in intact IFABP, we sought an unconstrained simulation technique as an independent verification in a prejudice-free way. aMD that modifies the system potentials below a threshold for efficient crossing of energy barriers (36) provides an alternative means to sample transient unfolding in IFABP without the need for predefining reaction coordinates. In our study, dual-boost aMD, with a non-negative boost potential added to both dihedral and total potential energies, was applied to speed up the conformational transitions in intact IFABP. Although complete unfolding of αII was not observed with the threshold energies (E_total and E_dihed) and boost factors (α_total and α_dihed) used in this study, transient partial unfolding has been repeatedly sampled (Fig. 5 A). Although large statistical noise prevents reweighting of the aMD ensemble, a comparison of backbone dihedral angle distributions of αI and αII sampled in aMD shows a clear distinction of unfolding tendencies (Fig. 5 B). In contrast to the well-maintained secondary structure of αI, most residues of αII underwent transitions, particularly evident in the C-terminal region (residues 29–32). The intrinsic helix instability of αII, especially of its last helical turn, agrees with the results from the metadynamics simulations.

Figure 5.

Transient partial unfolding events sampled by aMD. (A) RMSD_dihed of αII (residues 24–32) with respect to the starting conformation was calculated from the 5 μs aMD simulation of intact IFABP. (B) Ramachandran plots for individual residues of αI (residues 13–21) and αII (residues 24–32) in the aMD simulation are given. The relative density of points per grid (3.6 × 3.6°), with respect to the highest one, is indicated as follows: 0.0 < gray < 0.01; 0.01 ≤ green < 0.2; 0.2 ≤ blue < 0.4; 0.4 ≤ red < 0.8; 0.8 ≤ black ≤ 1. Areas that were not sampled are colored white. To see this figure in color, go online.

Conclusions

In this work, the structural dynamics of IFABP has been investigated by hydrogen-exchange NMR spectroscopy, long MD simulations, and enhanced sampling techniques that provide an atomistic picture of the rare conformational transitions of αII that are functionally linked with the ligand entry and exit processes. Microsecond MD simulations of the helical peptides from IFABP show that the tendency of αII to unfold is inherently encoded in its primary sequence and can be quantitatively described with the Lifson-Roig model. Although tertiary interactions significantly stabilize αII, its higher instability as compared with other nonloop regions is preserved in intact proteins, as shown in both experiments and simulations. An on-pathway folding intermediate of αII in intact IFABP, which is characterized with the fraying of the last helical turn (residues 29–32), has been observed in both well-tempered metadynamics and aMD simulations. It is noted that transitions between the native and the intermediate states occur much more readily than the complete unfolding of αII, which implies a possible mechanism for very fast ligand associations such as the one observed previously in the liver FABP (18), which can be further tested in future experiments and simulations.

Author Contributions

D. Long designed the research. P.C. and D. Liu performed the simulations and analyzed the data. P.X.C. and D.Y. measured the amide hydrogen-exchange rates. P.C., D. Liu, D.Y., and D. Long wrote the manuscript.

Editor: Daniel Raleigh.