Abstract
Behavioral momentum theory (BMT) provides an integrative framework for evaluating the strength of a response when it contacts a disruptor, such as the discontinuation of reinforcement (i.e., extinction). Grounded in Newtonian physics, BMT distinguishes response rate (behavioral velocity) from response strength or persistence (behavioral mass). Behavioral velocity is affected by response-reinforcer contingencies, whereas behavioral mass is affected by stimulus-reinforcer contingencies (Nevin and Wacker 2013). We describe the determiners of behavioral mass, as well as common sources of disruption that are used to measure behavioral mass. Learning activities are embedded throughout this discussion to help readers better understand BMT and its implications for practice across a range of contexts.
Electronic supplementary material
The online version of this article (doi:10.1007/s40614-016-0050-0) contains supplementary material, which is available to authorized users.
Keywords: Behavioral mass, Behavioral momentum theory, Behavioral velocity, Response persistence, Resurgence
In 1687, Sir Isaac Newton published Philosophiae Naturalis Principia Mathematica or Mathematical Principles of Natural Philosophy, wherein he outlined three laws of motion (Newton 1687). Newton’s first and second laws of motion are analogous to the behavior of organisms. For example, Newton’s first law of motion states that an object in motion continues in motion (at a constant velocity) unless acted upon by an external force (i.e., a disruptor). This postulation has implications for behavior. When the environment is static, response rate tends to maintain at a steady state.
Newton’s second law of motion states that the acceleration (or deceleration) of an object is dependent upon two variables: the external force propelling (or disrupting) the object and the mass of the object (i.e., the amount of matter the object contains). When a disruptor is applied to an object in motion, the change in velocity is directly related to the magnitude of the disruptor and inversely related to the object’s mass. That is, large disruptors produce more rapid decreases in an object’s velocity, but objects with greater mass tend to maintain their velocity more so than those with less mass. The momentum of an object is a product of its mass and its velocity and can be thought of as mass in motion—the greater the mass and velocity, the more momentum an object has.
Applying this analogy to behavior suggests that when a disruptor (e.g., extinction, satiation, distraction) is applied to ongoing behavior, the rate at which the behavior will decrease is directly related to the magnitude of the disruptor and inversely related to the behavioral equivalent of mass. Said another way, a larger disruptor will decrease responding more quickly than a smaller one; however, a response with more behavioral mass will persist more in the presence of the disruptor than a response with less mass.
Consider the example of two 8-year-old boys (Adam and Jacob) who engage in aggression when presented with instructional requests in a classroom. The forms of Adam and Jacob’s problem behavior are topographically similar and are both maintained by the same environmental variables. Analogous to Newton’s first law, it is likely that the two boys will continue to be aggressive unless a disruptor (e.g., a treatment intervention) is introduced. The supervising behavior analyst recommends that the teacher implement escape extinction (a source of disruption for responding) for both boys by continuing with academic instructions when problem behavior occurs. For Adam, this intervention works well, and his problem behavior decreases quickly. Unlike Adam, Jacob’s problem behavior continues to occur and appears initially resistant to the intervention. In this case, we might say that Jacob’s problem behavior has more behavioral mass than Adam’s behavior.
Unfortunately, behavioral mass cannot be determined by measuring its current topographical features (or even its function). Many behaviors may look similar across individuals, such as Adam and Jacob’s problem behavior, but behavioral mass (and resistance to treatment) may remain unknown until the response contacts a disruptor. In this paper, we describe the determiners of behavioral mass, as well as common sources of disruption that are used to measure behavioral mass. Learning activities are embedded throughout this discussion to help readers better understand behavioral momentum theory (BMT) and its implications for practice across a range of contexts.
Common Disruptors
One of the most commonly studied sources of disruption for behavior is extinction (e.g., Mace et al. 2010; Nevin et al. 1983; Pritchard et al. 2014; Volkert et al. 2009; Wacker et al. 2011). For example, following effective treatment of problem behavior reinforced by escape from simple manual tasks using functional communication training (FCT) with extinction, Wacker et al. (2011) introduced brief periods of extinction in which task completion and the alternative communication response no longer produced reinforcement. These brief (5 to 15 min) periods of extinction resulted in decreased task completion, fewer alternative communication responses, and increased rates of problem behavior. Following extinction, FCT was reinstated and continued until the individual’s performance improved, at which point extinction was again implemented. This progression continued until the individual’s performance under FCT persisted throughout the extinction period. Some subjects required over 1 year of FCT for treatment effects to maintain during extinction. These results showed not only that periods of extinction may disrupt responding following treatment, but that repeated exposures to FCT can help mitigate the disruptive effects of extinction (for similar findings, see Sweeney and Shahan 2013a).
Researchers have also evaluated the effects of reinforcer satiation as a form of disruption. Nevin et al. (1990) arranged presession access to reinforcement (prefeeding) prior to some sessions in Experiments 1 and 2. Across both experiments, prefeeding disrupted the rates of pigeon’s key pecking in both components of a multiple schedule, and the degree to which responding decreased in each component was dependent on the relative rates of reinforcement obtained in each component. Responding decreased less in the component associated with the relatively dense reinforcement schedule. These results suggest that prior access to “free” or time-based deliveries of a reinforcer may also disrupt responding in applied settings.
Some researchers have evaluated the effects of adding a concurrently available alternative source of reinforcement on behavioral persistence (Lionello-DeNolf et al. 2010). Lionello-DeNolf et al. delivered edible reinforcers according to a multiple schedule of reinforcement for touching shapes on a computer screen. Edibles were provided according to a relatively dense schedule of reinforcement in one component (variable interval [VI] 5 s) and a relatively lean schedule in the other component (VI 15 s). After baseline response rates stabilized, an alternative source of reinforcement (touching a red disk) was made available while the multiple schedule used in baseline continued. Touches to the red disk resulted in access to the same edibles according to VI 6-s schedule. The availability of the alternative source of reinforcement decreased overall response rates with proportionately greater decreases in the component associated with the leaner schedule of reinforcement. Thus, the availability of an alternative source of reinforcement may constitute another type of disruption in applied settings.
Similar to providing an alternative source of reinforcement, Mace et al. (1990) described the use of a concurrent distracting stimulus with two adults who were instructed to sort sets of colored silverware, the colors of which corresponded to two different rates of reinforcement (VI 60 s and VI 240 s). After establishing high rates of silverware sorting across the two contexts, the experimenters turned on a music television (MTV) program in the corner of the therapy room during sorting sessions. Rates of silverware sorting decreased for both adults with the distracting stimulus, with less disruption occurring in the context with the denser reinforcement schedule (VI 60 s). Thus, distraction may constitute another form of disruption that can affect responding in applied settings.
Extinction, satiation, and the presence of concurrently available alternative sources of reinforcement or distracting stimuli are just four types of disruption that have been evaluated experimentally and have shown to alter otherwise stable response rates. There are likely other forms of disruption (perhaps many) that occur in applied settings, and readers may benefit from a better understanding of the predictions of BMT on responding during disruption.
Behavioral Momentum Theory Learning Activities
This tutorial provides hands-on learning activities that attempt to explain some of the complexities of BMT and its predictions of behavior in a user-friendly format, which we hope will complement recently published chapters, discussion papers, and reviews on BMT (Dube et al. 2009; Nevin and Grace 2000; Nevin and Shahan 2011; Nevin and Wacker 2013; Pritchard et al. 2014), while potentially accessing a portion of the behavior-analytic community who may find intimidating the various equations and perhaps difficult-to-understand language associated with BMT. Thus, we designed and embedded within this paper three learning activities to describe how BMT predicts response persistence or resurgence (i.e., the reemergence of a previously reinforced response when a second, alternative response contacts extinction) across three scenarios. In each learning activity, we briefly describe a scenario, provide hypothetical data from each scenario, guide the user through graphing the data, and predict how behavior changes during a disruption. The disruption illustrated in each learning activity is the removal of the reinforcer that previously maintained responding. We selected this form of disruption for demonstration purposes because of its relatively frequent occurrence and its general familiarity. It is important to note, however, that the relative changes in behavior in each context during extinction should be similar with disruptors other than extinction. That is, a behavior with greater behavioral mass should be more persistent in the presence of any disruptor (cf. Lionello-DeNolf et al. 2010).
As you complete the learning activities, you will see that sessions occur in two unique stimulus contexts (contexts 1 and 2). You can think of these contexts as two locations (e.g., a school gymnasium and a math class) or the same location with different stimulus properties (e.g., a homeroom in which different teachers rotate). We will assume that the individual has spent roughly equal amounts of time in both stimulus contexts during each session.
The materials required to complete the learning activities include (a) access to a computer, tablet, or smartphone capable of running Microsoft Excel 2003 or later, (b) a working Internet connection, and (c) a copy (electronic or paper version) of Tables 1, 2, and 3 along with the instructions located below. We designed the learning activities to be completed in conjunction with an Excel file that is available as Supplementary material. The yellow tabs at the bottom left of the opened file indicate the learning activity number, and the final two tabs allow for the reader to view and manipulate the parameters used across the learning activities. Tables 1, 2, and 3 contain the data relevant to learning activities 1 through 3, respectively.1 The learning activities increase in complexity. Therefore, we recommend completing the learning activities in the order they appear.
Table 1.
Data for learning activity 1
| Session | Baseline (high Rate)—context 1 | Baseline (low Rate)—context 2 | Extinction—context 1 | Extinction—context 2 | ||||
|---|---|---|---|---|---|---|---|---|
| Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | |
| 1 | 500 | 120 | – | – | – | – | – | – |
| 2 | – | – | 320 | 20 | – | – | – | – |
| 3 | 480 | 120 | – | – | – | – | – | – |
| 4 | – | – | 340 | 20 | – | – | – | – |
| 5 | 500 | 120 | – | – | – | – | – | – |
| 6 | – | – | 300 | 20 | – | – | – | – |
| 7 | 490 | 120 | – | – | – | – | – | – |
| 8 | – | – | 320 | 20 | – | – | – | – |
| 9 | – | – | – | – | Auto Calc. | (0) | – | – |
| 10 | – | – | – | – | – | – | Auto Calc. | (0) |
| 11 | – | – | – | – | Auto Calc. | (0) | – | – |
| 12 | – | – | – | – | – | – | Auto Calc. | (0) |
| 13 | – | – | – | – | Auto Calc. | (0) | – | – |
| 14 | – | – | – | – | – | – | Auto Calc. | (0) |
| 15 | – | – | – | – | Auto Calc. | (0) | – | – |
| 16 | – | – | – | – | – | – | Auto Calc. | (0) |
| 17 | – | – | – | – | Auto Calc. | (0) | – | – |
| 18 | – | – | – | – | – | – | Auto Calc. | (0) |
| 19 | – | – | – | – | Auto Calc. | (0) | – | – |
| 20 | – | – | – | – | – | – | Auto Calc. | (0) |
| 21 | – | – | – | – | Auto Calc. | (0) | – | – |
| 22 | – | – | – | – | – | – | Auto Calc. | (0) |
| 23 | – | – | – | – | Auto Calc. | (0) | – | – |
| 24 | – | – | – | – | – | – | Auto Calc. | (0) |
Table 2.
Data for learning activity 2
| Session | Baseline—context 1 | Baseline—context 2 | FCT (high rate)—context 1 | FCT (low rate)—context 2 | ||||
|---|---|---|---|---|---|---|---|---|
| Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | |
| 1 | (440) | (60) | – | – | – | – | – | – |
| 2 | – | – | (420) | (60) | – | – | – | – |
| 3 | (420) | (60) | – | – | – | – | – | – |
| 4 | – | – | (405) | (60) | – | – | – | – |
| 5 | (400) | (60) | – | – | – | – | – | – |
| 6 | – | – | (420) | (60) | – | – | – | – |
| 7 | (420) | (60) | – | – | – | – | – | – |
| 8 | – | – | (435) | (60) | – | – | – | – |
| 9 | – | – | – | – | Auto Calc. | 480 | – | – |
| 10 | – | – | – | – | – | – | Auto Calc. | 120 |
| 11 | – | – | – | – | Auto Calc. | 480 | – | – |
| 12 | – | – | – | – | – | – | Auto Calc. | 120 |
| 13 | – | – | – | – | Auto Calc. | 480 | – | – |
| 14 | – | – | – | – | – | – | Auto Calc. | 120 |
| 15 | – | – | – | – | Auto Calc. | 480 | – | – |
| 16 | – | – | – | – | – | – | Auto Calc. | 120 |
| 17 | – | – | – | – | Auto Calc. | 480 | – | – |
| 18 | – | – | – | – | – | – | Auto Calc. | 120 |
| 19 | – | – | – | – | Auto Calc. | 480 | – | – |
| 20 | – | – | – | – | – | – | Auto Calc. | 120 |
| 21 | – | – | – | – | Auto Calc. | 480 | – | – |
| 22 | – | – | – | – | – | – | Auto Calc. | 120 |
| 23 | – | – | – | – | Auto Calc. | 480 | – | – |
| 24 | – | – | – | – | – | – | Auto Calc. | 120 |
Table 3.
Data for learning activity 3
| Session | Baseline—context 1 | Baseline—context 2 | FCT (brief exposure)—context 1 | FCT (extended exposure)—context 2 | ||||
|---|---|---|---|---|---|---|---|---|
| Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | Responses per hour | Reinforcers per hour | |
| 1 | (400) | (60) | – | – | – | – | – | – |
| 2 | – | – | (420) | (60) | – | – | – | – |
| 3 | (440) | (60) | – | – | – | – | – | – |
| 4 | – | – | (400) | (60) | – | – | – | – |
| 5 | (420) | (60) | – | – | – | – | – | – |
| 6 | – | – | (440) | (60) | – | – | – | – |
| 7 | – | – | – | – | Auto Calc. | 240 | – | – |
| 8 | – | – | – | – | – | – | Auto Calc. | 240 |
| 9 | – | – | – | – | – | – | Auto Calc. | 240 |
| 10 | – | – | – | – | – | – | Auto Calc. | 240 |
| 11 | – | – | – | – | Auto Calc. | 240 | – | – |
| 12 | – | – | – | – | – | – | Auto Calc. | 240 |
| 13 | – | – | – | – | – | – | Auto Calc. | 240 |
| 14 | – | – | – | – | – | – | Auto Calc. | 240 |
| 15 | – | – | – | – | Auto Calc. | 240 | – | – |
| 16 | – | – | – | – | – | – | Auto Calc. | 240 |
| 17 | – | – | – | – | – | – | Auto Calc. | 240 |
| 18 | – | – | – | – | – | – | Auto Calc. | 240 |
| 19 | – | – | – | – | Auto Calc. | 240 | – | – |
| 20 | – | – | – | – | – | – | Auto Calc. | 240 |
| 21 | – | – | – | – | – | – | Auto Calc. | 240 |
| 22 | – | – | – | – | – | – | Auto Calc. | 240 |
| 23 | – | – | – | – | Auto Calc. | 240 | – | – |
| 24 | – | – | – | – | – | – | Auto Calc. | 240 |
| 25 | – | – | – | – | – | – | Auto Calc. | 240 |
| 26 | – | – | – | – | – | – | Auto Calc. | 240 |
| 27 | – | – | – | – | Auto Calc. | 240 | – | – |
| 28 | – | – | – | – | – | – | Auto Calc. | 240 |
| 29 | – | – | – | – | – | – | Auto Calc. | 240 |
| 30 | – | – | – | – | – | – | Auto Calc. | 240 |
| 31 | – | – | – | – | Auto Calc. | 240 | – | – |
| 32 | – | – | – | – | – | – | Auto Calc. | 240 |
| 33 | – | – | – | – | – | – | Auto Calc. | 240 |
| 34 | – | – | – | – | – | – | Auto Calc. | 240 |
| 35 | – | – | – | – | Auto Calc. | 240 | – | – |
| 36 | – | – | – | – | – | – | Auto Calc. | 240 |
| 37 | – | – | – | – | – | – | Auto Calc. | 240 |
| 38 | – | – | – | – | – | – | Auto Calc. | 240 |
| 39 | – | – | – | – | Auto Calc. | 240 | – | – |
| 40 | – | – | – | – | – | – | Auto Calc. | 240 |
| 41 | – | – | – | – | – | – | Auto Calc. | 240 |
| 42 | – | – | – | – | – | – | Auto Calc. | 240 |
| 43 | – | – | – | – | Auto Calc. | 240 | – | – |
| 44 | – | – | – | – | – | – | Auto Calc. | 240 |
| 45 | – | – | – | – | – | – | Auto Calc. | 240 |
| 46 | – | – | – | – | – | – | Auto Calc. | 240 |
Learning Activity 1: Baseline Rates of Reinforcement and Persistence
Learning activity 1 provides a simple illustration of how continued responding during extinction is directly attributable to the rate of reinforcement historically delivered in the same stimulus context. In this activity, you will input the data for eight baseline sessions to reveal how high and low rates of reinforcement in baseline change the anticipated response rates when reinforcement is discontinued.
Nevin and Shahan (2011) modeled response patterns during extinction following a history of reinforcement, and their equation is represented here:
| 1 |
In this equation, B t is the response rate at time t in extinction, B o is the baseline response rate, c scales the effects of suspending the reinforcement contingency, d scales the effects of removing reinforcers from the environment, and r is the baseline rate of reinforcement. Thus, the proportion of baseline response rate observed during extinction (B t /B o ) is dependent upon the amount of time (t) extinction has been in place, two separable effects of terminating reinforcement (c and d; Nevin et al. 2001), and the previous baseline reinforcement rate (r). We designed learning activity 1 to illustrate the effects of this last parameter of the equation (i.e., changes in r or the baseline reinforcement rate) on response persistence when extinction begins following a baseline in which two reinforcement schedules operated. In this and all subsequent learning activities, all parameters of the equation are held constant across contexts, except for the parameter of interest. Therefore, in learning activity 1, we modeled the effects of two baseline rates of reinforcement (r) on the persistence of responding during extinction while holding constant the values of all other parameters (i.e., t, c, and d in Eq. 1). For learning activity 1, t = the number of sessions in which extinction has been in place for problem behavior, which changes across the function of the extinction curve (i.e., t = 1 for the first extinction session, t = 2 for the second extinction session, etc.); c = 1; and d = 0.001.
Activity Instructions
In learning activity 1, a high rate of reinforcement (two reinforcers per minute or 120 per hour) is delivered in context 1, whereas context 2 is associated with a low rate of reinforcement (one reinforcer every 3 min or 20 per hour). Table 1 contains the data for learning activity 1. Start by downloading the Excel file titled, “BMT Tutorial Excel File.” Locate and open a “Read Only” copy of the spreadsheet. When the spreadsheet opens, click on the yellow tab labeled, “Learning Activity 1” on the bottom left. Next, you will use Table 1 to graph the baseline data (i.e., responses and reinforcers per hour in contexts 1 and 2) by changing the corresponding light and dark gray cells, respectively. Portions of the data are already entered for you and appear parenthetically in Table 1. Other values will adjust automatically with each data point you enter. The phrase “Auto Calc.” indicates these values.
Using Table 1, start with Session 1 by entering the responses per hour (500) recorded from Baseline (high rate)—context 1 in the same location on the Excel file (cell B3). Press “Enter” on the keyboard, and you will see a data point corresponding to Session 1 appear on the graph below. Next, enter the reinforcers per hour from Session 1 (120) in cell C3. As you input each value, the graphs will update automatically. Repeat this process for Sessions 2 through 8.
The predicted data from the extinction phase (Sessions 9 through 24) will calculate automatically for you. The data legend (located in the extinction phase on the graph) displays the average rate of reinforcement for each baseline context. When finished, the data legend should indicate that 120 reinforcers per hour were delivered in context 1 during baseline and 20 reinforcers per hour in context 2 during baseline. Figure 1 depicts the graphs you will produce if you entered the data correctly.
Fig. 1.
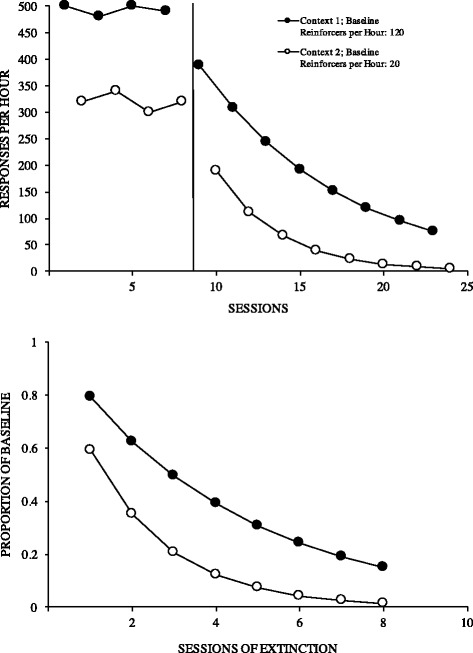
Predicted response rates (top panel) and proportion of baseline responding (bottom panel) during extinction preceded by high (context 1) and low (context 2) rates of reinforcement in baseline
The higher rate of reinforcement delivered in context 1 during baseline (120 reinforcers per hour as compared to 20 per hour in context 2) produced a higher baseline rate of responding but was also associated with greater response persistence when reinforcement was discontinued. Although the baseline response rates differed between contexts, the resulting persistence of behavior during extinction was proportionately greater in context 1. Said another way, the relative decrease in responding observed during extinction was larger in context 2. The bottom panel of Fig. 1 illustrates this finding. In the bottom panel of Fig. 1, we replotted the data from the top panel of Fig. 1 so that baseline differences in responding were equated by dividing each data point during extinction by the average response rate from the corresponding baseline (producing a proportion of baseline). Consistently higher levels of responding are predicted in the context associated with more reinforcement during baseline (context 1), regardless of differences in the baseline response rates. Larger differences in the relative rates of reinforcement in each context would likely lead to larger differences in persistence between contexts (Dube and McIlvane 2001).
Clinical Implications
The results of learning activity 1 suggest that one way to promote response persistence of a socially desirable response (e.g., correct responding on an academic task) would be to increase the rate of reinforcement for that response in the presence of some stimulus prior to the possibility of a disruption (e.g., the child leaving for a summer break, introducing new or more complex tasks, changing the child’s therapist).
How Behavior Obtains Mass
In their behavioral momentum account of response strength, Nevin and Grace (2000) posit that a response’s strength is related to its behavioral mass and that its mass is relatively independent of its rate or velocity. The rate of a response (i.e., its velocity according to BMT) is largely determined by the contingency between the response and its reinforcer (i.e., the schedule of reinforcement). For example, the response-reinforcer contingencies involved in ratio schedules typically produce higher response rates than those involved in interval schedules. Similarly, intermittent reinforcement schedules typically produce higher response rates than does a continuous reinforcement schedule. However, large changes in reinforcement rate can occur under certain conditions without a corresponding change in the rate of a response, and this is the main reason why response rate is not considered a useful measure of response strength (Nevin and Grace 2000). In contrast, in the BMT formulation, the strength of a response results from its behavioral mass, which is primarily a function of the contingency between the discriminative stimulus and the reinforcing consequence (i.e., stimulus-reinforcer pairings; Nevin and Grace 2000).
Nevin and Grace (2000) liken the behavior-strengthening effects of reinforcement to the ways in which physical structures are reinforced. For example, concrete columns in a building are often reinforced with steel rods, which add tensile strength to the columns (and guard against bending forces; Song and Hwang 2004). One could not measure the strengthening effects of the steel rods through observation alone. Rather, the strengthening effects would typically become apparent during a tensile test in which bending forces are systematically applied to the columns. Nevin and Grace suggest that the reinforcement of behavior operates in an analogous manner. That is, the strengthening effects of increases in the rate, amount, or quality of reinforcement may not produce a noticeable change in response rate. Rather, the strengthening effects of increased reinforcement are likely to become apparent only when a disruptor is introduced. Responses that have been strengthened more (due to increased reinforcement) should be more resistant to the disruptor (just as the reinforced concrete is more resistant to the bending forces applied during a tensile test).
Nevin et al. (1990) conducted a study with pigeons that separated the effects of response-reinforcer contingencies (which affect the rate of a response) from stimulus-reinforcer contingencies (which affect the persistence or strength of a response). In Experiment 1, they exposed pigeons to two components that strictly alternated according to a multiple-schedule design, with each component correlated with a distinct discriminative stimulus (red and green). In the green component, the target response always produced reinforcement on a VI 60-s schedule. In the red component, the target response produced reinforcement on a VI 60-s schedule, and additional reinforcers were delivered on a variable-time (VT) 30-s or 15-s schedule. When these schedules were in effect (during baseline), the time-based delivery of additional reinforcers decreased responding in the red component (relative to the green component) because they weakened the response-reinforcer contingency (i.e., more reinforcers were delivered noncontingently than contingently). By contrast, when the delivery of all reinforcers ceased in both the red and green components during extinction, the target response persisted more in the red component (relative to the green component) because during baseline, more reinforcer deliveries were paired with the red stimulus (i.e., more stimulus-reinforcer pairings) relative to the green stimulus.
In Experiment 2, Nevin et al. (1990) showed comparable effects when additional reinforcers were delivered contingent on a concurrently available alternative source of reinforcement (i.e., a second response key). In addition, Mace et al. (2010) replicated and extended the findings of Nevin et al.’s Experiment 2 with a clinical population by showing that problem behavior persisted to a greater extent under extinction when reinforcement was previously delivered following both problem behavior and an alternative response (resulting in more reinforcers) than when reinforcement was previously delivered following only problem behavior (resulting in fewer reinforcers). Together, these experiments show that the delivery of alternative reinforcers either contingently or noncontingently lowers the rate of a response (by weakening the response-reinforcer contingency), but the additional reinforcers also increase the target response’s resistance to a disruptor or its mass (by increasing stimulus-reinforcer pairings).
Learning Activity 2: Rates of Alternative Reinforcement and Resurgence
Learning activity 2 predicts responding when clinicians implement FCT (a common treatment for problem behavior; Tiger et al. 2008) by reinforcing an alternative response and arranging extinction for problem behavior following stable baseline responding in two unique stimulus contexts. The FCT procedures are identical; however, the rate of reinforcement delivered for the alternative response (i.e., the rate of alternative reinforcement) differs across contexts. Following reductions in problem behavior as a result of the FCT procedures, the alternative response is then exposed to extinction (i.e., a disruptor), while problem behavior continues to go unreinforced. Volkert et al. (2009) found that this sequence of conditions can cause resurgence of problem behavior when the alternative communication response contacts extinction (Experiment 1) or a lean reinforcement schedule (Experiment 2) following treatment. Shahan and Sweeney (2011) proposed a quantitative model that describes responding under these specific circumstances. This equation also appears in Nevin and Shahan (2011) and is again re-presented here:
| 2 |
Equation 2 builds on Eq. 1 used in learning activity 1, which described how responding persists when a previously reinforced response contacts extinction. Equation 2 differs from Eq. 1 with the addition of two parameters: one to account for the rate of alternative reinforcement (R a) delivered for the alternative response during FCT and another to scale the disruptive impact on the target response (i.e., problem behavior) of delivering alternative reinforcers (p). This equation predicts that when all other parameters are held constant, delivering a dense rather than a lean schedule of reinforcement for the newly acquired alternative response during FCT will result in quicker reductions in problem behavior, but the added reinforcers in the treatment context will paradoxically increase the degree to which problem behavior would resurge if the alternative response were also to contact extinction. Therefore, for the purposes of learning activity 2, we programmed two different values for R a, but defined and held the following parameters constant across both contexts: r = 60, t = the number of sessions in which extinction has been in place for problem behavior, c = 1, d = 0.001, and p = 0.01.
Activity Instructions
With the Excel file still open, begin by clicking on the yellow tab at the bottom labeled, “Learning Activity 2.” Next, locate and review the information in Table 2. The baseline data for learning activity 2 are already entered for you. Similar to learning activity 1, responding data will be calculated automatically for the FCT and extinction phases. The only data you will enter for learning activity 2 are the rates of alternative reinforcement delivered in each FCT context. During the FCT phase, context 1 is associated with four times the rate of alternative reinforcement (eight reinforcers per minute or 480 per hour) than context 2 (two reinforcers every minute or 120 per hour). Notice, however, that baseline was associated with an equal rate of reinforcement (and similar response rates) across these contexts.
Using Table 2, begin entering the data from Session 9 in the Excel file. Input the reinforcers per hour (480) delivered in FCT (high rate)—context 1 in the Excel file (cell G11). Next, do the same for Session 10 by entering the reinforcers per hour (120) delivered in FCT (low rate)—context 2 (cell I12). The graphs will adjust automatically with each value you enter. Repeat this process for Sessions 11 through 24.
Figure 2 depicts the graphs you will produce if you entered the data correctly. Note that response rates are depicted only for problem behavior. Equal rates of reinforcement were delivered for problem behavior in both baseline contexts, producing similar response rates across contexts. When problem behavior was placed on extinction and a high rate of alternative reinforcement was delivered for an alternative response in context 1 during FCT, problem behavior response rates decreased quicker compared to context 2 in which a low rate of alternative reinforcement was delivered. However, you will notice that when extinction was later arranged for the alternative response while problem behavior continued to result in extinction, responding resurged to a greater extent in context 1 than in context 2, despite showing better treatment effects in the preceding FCT phase. Moreover, the predicted response rates during FCT and extinction were calculated from equal histories of reinforcement (and responding) in baseline. Therefore, the results are similar when the raw responding data from learning activity 2 (Fig. 2, top panel) are expressed as a proportion of baseline (Fig. 2, bottom panel).
Fig. 2.
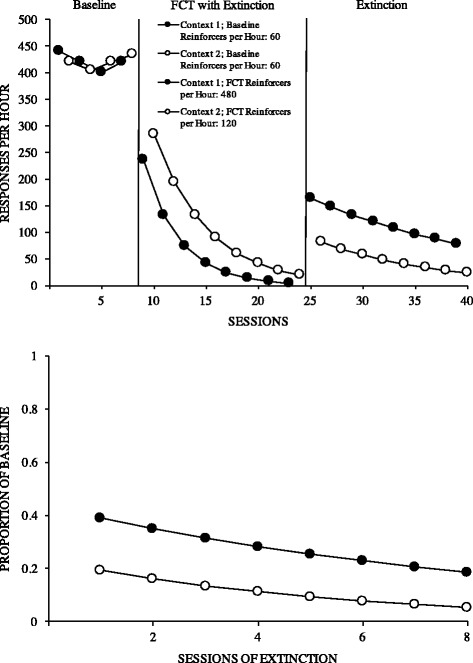
Predicted problem behavior rates during FCT and extinction (top panel) and proportion of baseline responding during extinction (bottom panel) resulting from high (context 1) and low (context 2) rates of reinforcement in FCT
It is important to note that although the results would have differed somewhat with other procedures based on alternative reinforcement (e.g., noncontingent reinforcement; NCR), the general prediction in relative rates of responding during extinction would be similar. That is, BMT predicts that the context associated with the richer history of reinforcement will occasion more responding in the presence of a disruptor, regardless of the type of treatment. Furthermore, these predications should hold irrespective of the function of responding. Sweeney et al. (2014) recently found support for this possibility by demonstrating greater resurgence in pigeons (Experiment 1) and children with intellectual and developmental disabilities (Experiment 2) when differential reinforcement (food or tokens exchangeable for food or drink) included an analog to sensory reinforcement (flashing lights or fireworks with chimes) than when responding resulted only in differential reinforcement.
Clinical Implications
The results from learning activity 2 suggest that one way to mitigate the resurgence of problem behavior is to reduce the rate of alternative reinforcement (e.g., those reinforcers delivered for an alternative response during FCT) before the possibility of a disruptor. Reinforcement-schedule thinning following the identification of an effective intervention for problem behavior is advantageous for multiple reasons (e.g., to achieve a more practical reinforcement schedule for caregivers) and has been the focus of several studies (for a recent review, see Hagopian et al. 2011). However, the results of learning activity 2 suggest an additional consideration for the necessity of reinforcement schedule thinning: leaning the schedule of reinforcement used in a treatment for problem behavior may help offset the possibility of future treatment relapse. Using a different preparation than learning activity 2, Mace et al. (2010) found greater resurgence of problem behavior when extinction followed periods in which FCT procedures were superimposed over existing reinforcement schedules for problem behavior (producing a denser reinforcement schedule) than when extinction followed a phase in which reinforcement was delivered only for problem behavior (a leaner reinforcement schedule). Thinning dense reinforcement schedules used to treat problem behavior may decrease the possibility of treatment relapse in the presence of naturally occurring disruptors (e.g., a decrement in treatment integrity). This possibility was explored recently in a study by Sweeney and Shahan (2013b) who showed that thinning the reinforcement schedule for an alternative response by 10 s daily beginning with VI 10 s and ending with VI 100 s produced lower levels of resurgence in one group of rats relative to another group of rats that experienced a consistent VI 10-s schedule for the alternative response. Additional research on the likelihood of treatment relapse following reinforcement schedule thinning in applied settings seems warranted.
Learning Activity 3: Treatment Durations and Resurgence
As mentioned previously, Wacker et al. (2011) conducted a study in which eight children received FCT with extinction for the treatment of social negatively reinforced problem behavior. These authors extended the BMT literature by focusing on the time parameter (t) from Eq. 2. Consistent with the predictions of BMT, Wacker et al. found that although FCT resulted in rapid reductions in problem behavior, resurgence of problem behavior and general treatment relapse often occurred during probes in which the newly acquired communication response contacted extinction. The most important contribution of this study was that these authors also showed that the disruptive effects of extinction (and potentially other types of disruptors) could be offset by conducting additional FCT with extinction sessions (i.e., by increasing t or the amount of time in which extinction has been in place for problem behavior).
We designed learning activity 3 to build on learning activities 1 and 2 by demonstrating how another parameter from Eq. 2, in this case t, affects resurgence of problem behavior. Similar to learning activities 1 and 2, learning activity 3 allows the reader to set two different values for one parameter (t), while the values of all other parameters remain fixed across contexts. For learning activity 3, r = 60, c = 1, d = 0.001, p = 0.01, and R a = 240.
Following equal rates of reinforcement and problem behavior in two baseline contexts, FCT with extinction begins simultaneously in both contexts, but for unequal durations in learning activity 3. Context 2 is associated with three times the number of FCT sessions than context 1. Therefore, problem behavior will have had the opportunity to contact the extinction component of FCT for three times the number of sessions in context 2 (30 FCT sessions) than in context 1 (10 FCT sessions). When extinction is then arranged for the alternative response while problem behavior continues to result in extinction, BMT predicts that resurgence of problem behavior will be greater in the context in which extinction has remained in place for problem behavior for the briefest amount of time (i.e., context 1).
Activity Instructions
Using the downloaded Excel file, begin by clicking on the yellow tab at the bottom labeled, “Learning Activity 3.” Then, locate and review the information in Table 3. Similar to learning activity 2, you will enter data only from the FCT sessions in learning activity 3. Using Table 3, begin entering the data from Sessions 7 to 46 in the Excel file. You will notice that 240 reinforcers per hour were delivered in every FCT session, regardless of the context in which FCT occurred. Therefore, enter 240 for the 10 FCT sessions that occurred in context 1 (corresponding to the shaded cells in column G) and enter 240 for the 30 FCT sessions that occurred in context 2 (corresponding to the shaded cells in column I). The graphs will adjust automatically with each value you enter.
Figure 3 depicts the graphs you will produce if you entered the data correctly. Note that response rates are depicted for only problem behavior. Additional exposure to FCT with extinction in context 2 produced a more rapid reduction in problem behavior than in context 1. Moreover, when treatment was abruptly terminated by withholding reinforcement for the alternative response while continuing to withhold reinforcement for problem behavior during the extinction phase, problem behavior resurged in only the context with the briefer exposure to treatment (context 2). Linking these predictions to Eq. 2 suggests that conducting additional FCT with extinction sessions increases the time (t) in which extinction has remained in place for problem behavior, thereby decreasing the likelihood of problem behavior resurging when extinction is later arranged for the alternative response. These predictions hold even when baseline response rates in each condition are considered (see Fig. 3, bottom panel).
Fig. 3.
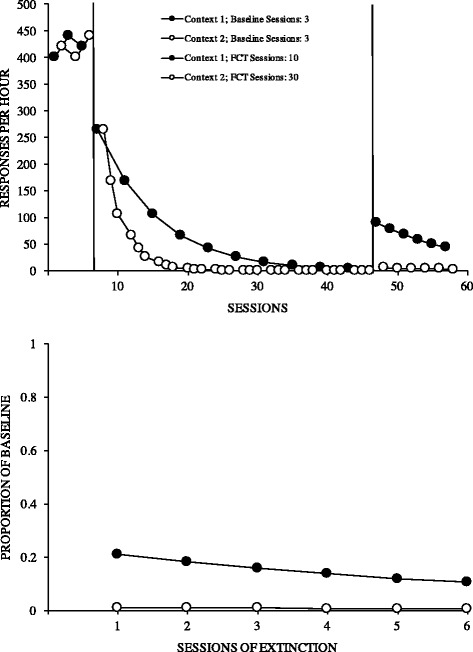
Predicted problem behavior rates during FCT and extinction (top panel) and proportion of baseline responding during extinction (bottom panel) resulting from brief (context 1) and extended (context 2) exposures to FCT
Clinical Implications
The results of learning activity 3, as well as those from Wacker et al. (2011) and Sweeney and Shahan (2013a), suggest that conducting additional treatment sessions in which problem behavior does not produce reinforcement (e.g., FCT with extinction, NCR with extinction) should help minimize the possibility of treatment relapse during extinction and other forms of disruption. Clinicians should consider conducting brief probes of performance under less than ideal conditions (e.g., a lapse in treatment integrity, in a more distracting context, in the presence of other individuals) following stable responding to ensure that the treatment effects are durable. If there is a decrement in performance during these probes, clinicians should consider removing the source of disruption (e.g., by reinstating high levels of treatment integrity, returning to the less distracting context, removing the other individuals) and proceed with treatment as conducted previously. Additional probes could be conducted later once performance returns to a stable level.
Further Manipulation of Parameters Affecting Response Persistence and Resurgence
Learning activities 1–3 guided the reader through manipulating three parameters of two BMT equations: r, R a, and t, respectively. As evidenced by the results of the learning activities, the precise values of these parameters can have rather large impacts on the degree to which responding is predicted to persist or resurge. The remaining two tabs located at the bottom of the Excel file (“Equation 1” and “Equation 2”) allow the reader to manipulate these and the remaining parameters in Eqs. 1 and 2 to evaluate how different conditions (i.e., the values for each of the parameters) affect responding.
For example, learning activities 2 and 3 assumed that FCT was implemented with extinction for problem behavior during treatment. In this situation, parameter c = 1 to indicate that the previous reinforcement schedule in place for problem behavior in baseline was terminated. Had the clinician continued to reinforce problem behavior during treatment (i.e., FCT without extinction), parameters c and dr would be 0. When c = 0, the treatment effects are more delayed than when c = 1. Therefore, whether the contingency for problem behavior is suspended during treatment can produce rather large differences in the anticipated effectiveness of the treatment, regardless the type of treatment (e.g., FCT, NCR). These effects also extend to when extinction is later arranged for both responses because although c = 1 in this final phase in both situations, the amount of time in which extinction has been in place for problem behavior (i.e., the value of t) differs between these situations, with t = 1 for the first session of treatment if c = 1 (i.e., when problem behavior is placed on extinction in treatment) and the value of t increases with each session in which problem behavior goes unreinforced, continuing into the final phase in which both responses are placed on extinction. However, if c = 0 in treatment (i.e., when problem behavior is not placed on extinction), t would not equal 1 until the first session of the final phase, resulting in larger predicted levels of resurgence than had c = 1 and t = 1 in the first session of treatment. The values assigned to parameters d and p have similar effects on predicted responding. We encourage readers to experiment further with these equations and use the Excel spreadsheet to model their own data.
Conclusion
Momentum of responding is a useful outcome in many cases (e.g., Mace and Belfiore 1990), particularly if the goal of intervention is to increase skills and maintain appropriate behavior (e.g., Mace et al. 1988). However, the momentum of a response may have untoward effects when the goal of intervention is to decrease problem behavior such as aggression in a classroom or clinic setting. Thus, the ubiquitous nature of behavioral momentum and its application to both skill acquisition and behavior reduction procedures suggests that an appreciation of BMT may benefit and inform practitioners, students, and researchers. Specifically, variables that promote and diminish behavioral mass require consideration because the momentum of appropriate and problem behavior may determine which one prevails in a given stimulus context. We designed the learning activities in this tutorial to provide readers with a working understanding of the equations of BMT and how the values assigned to the parameters of the models affect response persistence and resurgence. We hope this tutorial provides readers with a better understanding of BMT as a framework from which they may interpret and evaluate applied interventions and procedures, while encouraging future research on the implications of BMT for practice.
Electronic supplementary material
Below is the link to the electronic supplementary material.
(XLSX 109 kb)
Compliance with Ethical Standards
Funding
This work was funded in part by Grant no.1R01HD079113-01 from The National Institute of Child Health and Human Development.
Conflict of Interest
Authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants performed by any of the authors.
Footnotes
Baseline response rates for all learning activities were informed by Nevin’s (1974) Experiment 1 results of pigeon’s rates of key pecking under multiple VI VI schedules of reinforcement. We adjusted these values uniformly to reflect rates of responding characteristic of human performance under similar reinforcement schedules. We used Nevin and Shahan’s (2011) Equations 4 (Learning Activity 1) and 7 (Learning Activities 2 and 3) to model responding during FCT and extinction phases.
References
- Dube WV, McIlvane WJ. Behavioral momentum in computer-presented discriminations in individuals with severe mental retardation. Journal of the Experimental Analysis of Behavior. 2001;75:15–23. doi: 10.1901/jeab.2001.75-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dube WV, Ahearn WH, Lionello-DeNolf K, McIlvane WJ. Behavioral momentum: translational research in intellectual and developmental disabilities. The Behavior Analyst Today. 2009;10:238–253. doi: 10.1037/h0100668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagopian LP, Boelter EW, Jarmolowicz DP. Reinforcement schedule thinning following functional communication training: review and recommendations. Behavior Analysis in Practice. 2011;4:4–16. doi: 10.1007/BF03391770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lionello-DeNolf KM, Dube WV, McIlvane WJ. Evaluation of resistance to change under different disrupter conditions in children with autism and severe intellectual disability. Journal of the Experimental Analysis of Behavior. 2010;93:369–383. doi: 10.1901/jeab.2010.93-369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, Belfiore P. Behavioral momentum in the treatment of escape-motivated stereotypy. Journal of Applied Behavior Analysis. 1990;23:507–514. doi: 10.1901/jaba.1990.23-507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, Hock ML, Lalli JS, West BJ, Belfiore P, Pinter E, Brown DK. Behavioral momentum in the treatment of noncompliance. Journal of Applied Behavior Analysis. 1988;21:123–141. doi: 10.1901/jaba.1988.21-123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, Lalli JS, Shea MC, Lalli EP, West BJ, Roberts M, Nevin JA. The momentum of human behavior in a natural setting. Journal of the Experimental Analysis of Behavior. 1990;54:163–172. doi: 10.1901/jeab.1990.54-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, McComas JJ, Mauro BC, Progar PR, Taylor B, Ervin R, Zangrillo AN. Differential reinforcement of alternative behavior increases resistance to extinction: clinical demonstration, animal modeling, and clinical test of one solution. Journal of the Experimental Analysis of Behavior. 2010;93:349–367. doi: 10.1901/jeab.2010.93-349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA. Response strength in multiple schedules. Journal of the Experimental Analysis of Behavior. 1974;21:389–408. doi: 10.1901/jeab.1974.21-389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Grace RC. Behavioral momentum and the law of effect. Behavioral and Brain Sciences. 2000;23:73–90. doi: 10.1017/S0140525X00002405. [DOI] [PubMed] [Google Scholar]
- Nevin JA, Shahan TA. Behavioral momentum theory: equations and applications. Journal of Applied Behavior Analysis. 2011;44:877–895. doi: 10.1901/jaba.2011.44-877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Wacker DP. Response strength and persistence. In: Madden GJ, Dube WV, Hackenberg TD, Hanley GP, Lattal KA, editors. APA handbook of behavior analysis. Washington: American Psychological Association; 2013. pp. 109–128. [Google Scholar]
- Nevin JA, Mandell C, Atak JR. The analysis of behavioral momentum. Journal of the Experimental Analysis of Behavior. 1983;39:49–59. doi: 10.1901/jeab.1983.39-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Tota ME, Torquato RD, Shull RL. Alternative reinforcement increases resistance to change: Pavlovian or operant contingencies? Journal of the Experimental Analysis of Behavior. 1990;53:359–379. doi: 10.1901/jeab.1990.53-359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, McLean AP, Grace RC. Resistance to extinction: contingency termination and generalization decrement. Animal Learning & Behavior. 2001;29(2):176–191. doi: 10.3758/BF03192826. [DOI] [Google Scholar]
- Newton, I. (1687). Philosophiae naturalis principia mathematica.
- Pritchard D, Hoerger M, Mace FC. Treatment relapse and behavioral momentum theory. Journal of Applied Behavior Analysis. 2014;47:814–833. doi: 10.1002/jaba.163. [DOI] [PubMed] [Google Scholar]
- Shahan TA, Sweeney MM. A model of resurgence based on behavioral momentum theory. Journal of the Experimental Analysis of Behavior. 2011;95:91–108. doi: 10.1901/jeab.2011.95-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song PS, Hwang S. Mechanical properties of high-strength steel fiber-reinforced concrete. Construction and Building Materials. 2004;18(9):669–673. doi: 10.1016/j.conbuildmat.2004.04.027. [DOI] [Google Scholar]
- Sweeney MM, Shahan TA. Behavioral momentum and resurgence: effects of time in extinction and repeated resurgence tests. Learning & Behavior. 2013;41:414–424. doi: 10.3758/s13420-013-0116-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweeney MM, Shahan TA. Effects of high, low, and thinning rates of alternative reinforcement on response elimination and resurgence. Journal of the Experimental Analysis of Behavior. 2013;100:102–116. doi: 10.1002/jeab.26. [DOI] [PubMed] [Google Scholar]
- Sweeney MM, Moore K, Shahan TA, Ahearn WH, Dube WV, Nevin JA. Modeling the effects of sensory reinforcers on behavioral persistence with alternative reinforcement. Journal of the Experimental Analysis of Behavior. 2014;102:252–266. doi: 10.1002/jeab.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiger JH, Hanley GP, Bruzek J. Functional communication training: a review and practical guide. Behavior Analysis in Practice. 2008;1:16–23. doi: 10.1007/BF03391716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkert VM, Lerman DC, Call NA, Trosclair-Lasserre N. An evaluation of resurgence during treatment with functional communication training. Journal of Applied Behavior Analysis. 2009;42:145–160. doi: 10.1901/jaba.2009.42-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wacker DP, Harding JW, Berg WK, Lee JF, Schieltz KM, Padilla YC, Shahan TA. n. Journal of the Experimental Analysis of Behavior. 2011;96:261–282. doi: 10.1901/jeab.2011.96-261. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(XLSX 109 kb)


