The R package beezdemand: Behavioral Economic Easy Demand

Abstract

beezdemand: Behavioral Economic Easy Demand, a novel package for performing behavioral economic analyses, is introduced and evaluated. beezdemand extends the statistical program to facilitate many of the analyses performed in studies of behavioral economic demand. The package supports commonly used options for modeling operant demand and performs data screening, fits models of demand, and calculates numerous measures relevant to applied behavioral economists. The free and open source beezdemand package is compared to commercially available software (i.e., GraphPad Prism™) using peer-reviewed and simulated data. The results of this study indicated that beezdemand provides results consistent with commonly used commercial software but provides a wider range of methods and functionality desirable to behavioral economic researchers. A brief overview of the package is presented, its functionality is demonstrated, and considerations for its use are discussed.

Introduction

Individual choice and decision making are frequently studied topics in the behavioral sciences and various frameworks have been put forward to quantify choice behavior (Baum, 1974; Bickel, DeGrandpre, & Higgins, 1993; Herrnstein, 1961; Kagel, Battalio, & Green, 1995). One approach—behavioral economics—has been increasingly used as a framework for examining choice and decision making under constraint (Hursh, 1991; Hursh & Roma, 2013) and this approach has been especially useful in evaluating how environmental influences and individual differences affect patterns of decision making (Bickel et al., 1993; Bickel, Madden, & Petry, 1998). Under the umbrella term of “behavioral economics,” Consumer Demand Theory (Hursh & Bauman, 1987; Reed, Niileksela, & Kaplan, 2013) has been useful for understanding how individuals come to purchase and consume certain goods over others (e.g., varying prices, the presence of substitutes). In this approach, the emphasis is placed on the relationships between specific commodities and the individual’s demand for them over some domain of cost (Hursh, 1980, 1984).

Behavioral economics has been used effectively to enhance the understanding of drug valuation and the abuse liability of drugs (Bickel, Johnson, Koffarnus, MacKillop, & Murphy, 2014) including nicotine (Bickel, DeGrandpre, Hughes, & Higgins, 1991; Bickel, Odum, & Madden, 1999; Bidwell, MacKillop, Murphy, Tidey, & Colby, 2012; Grace, Kivell, & Laugesen, 2014; Jacobs & Bickel, 1999; Koffarnus, Wilson, & Bickel, 2015b; MacKillop et al., 2012a; MacKillop et al., 2012b; Mackillop et al., 2016; MacKillop et al., 2008; MacKillop & Tidey, 2011; Madden & Kalman, 2010; O'Connor, Bansal-Travers, Carter, & Cummings, 2012; Quisenberry, Koffarnus, Hatz, Epstein, & Bickel, 2015; Wilson, Franck, Koffarnus, & Bickel, 2016), alcohol (Bickel, Marsch, & Carroll, 2000; MacKillop, 2016; MacKillop & Murphy, 2007; Murphy & MacKillop, 2006; O'Connor et al., 2014; Spiga, Martinetti, Meisch, Cowan, & Hursh, 2005), heroin (Greenwald, 2010; Greenwald & Hursh, 2006; Greenwald & Steinmiller, 2009; Jacobs & Bickel, 1999), marijuana (Aston, Metrik, Amlung, Kahler, & MacKillop, 2016; Aston, Metrik, & MacKillop, 2015; Vincent et al., 2017), “bath salts” (Johnson & Johnson, 2014), and cocaine (Bruner & Johnson, 2014; Strickland, Lile, Rush, & Stoops, 2016). Further, behavioral economics has been expanded to examine decision making in domains of health- and nonhealth-related choices (Bickel & Vuchinich, 2000; Epstein, 1995; Epstein, Dearing, Roba, & Finkelstein, 2010; Epstein et al., 2018; Epstein & Saelens, 2000; Jarmolowicz, Reed, Reed, & Bickel, 2016; Reed, Kaplan, Becirevic, Roma, & Hursh, 2016; Roma, Hursh, & Hudja, 2016), consumer behavior (Foxall, Olivera-Castro, Schrezenmaier, & James, 2007; Foxall, Wells, Chang, & Oliveira-Castro, 2010), organizational behavior management (Henley, DiGennaro Reed, Kaplan, & Reed, 2016a; Henley, DiGennaro Reed, Reed, & Kaplan, 2016b), as well as in assessments and treatments for individuals with developmental disabilities (Gilroy, Kaplan, & Leader, 2018a; Reed et al., 2013).

At present, the tools developed to assist researchers in applying models of demand have been derived almost exclusively from the GraphPad Prism^TM (GP; La Jolla, CA, USA; www.graphpad.com) statistical program (Hursh & Roma, 2014; Reed, 2015). Although this software features the nonlinear modeling methods necessary to apply models of operant demand, a heterogeneous range of supplemental software has been developed by applied researchers to provide methods that are not provided by the GP program (e.g., data screening, demand indices). This gap in functionality has naturally led to substantial variability in how demand curve analyses are performed and how results are analyzed (Kaplan et al., 2018). Given this limitation in the tools available to researchers, the beezdemand package (Kaplan, 2018) was developed to provide a robust, comprehensive, and accessible set of methods that can perform the many operations and analytical techniques required when performing demand curve analyses. The purpose of this article is (1) to provide a brief primer of behavioral economic demand, (2) to review the primary functions1 and structure of the beezdemand package, and (3) to validate results of beezdemand against commercial software traditionally used for these purposes (i.e., GP).

The Demand Curve

Behavioral economic demand examines the extent to which an individual will defend its intake (i.e., purchasing, consumption) of a good as the price of that good increases (Hursh, 1978). The demand curve is typically downward sloping, with initial price increases resulting in relatively smaller changes in levels of consumption and relatively larger changes in consumption following greater increases in price (Hursh, Raslear, Bauman, & Black, 1989; Hursh & Roma, 2013). Figure 1 displays a representative demand curve (described below). Several metrics can be obtained from the demand curve, either from the observed data themselves or from derivation via nonlinear regression techniques. Table 1 lists these various metrics along with a brief description of each.

Fig. 1.

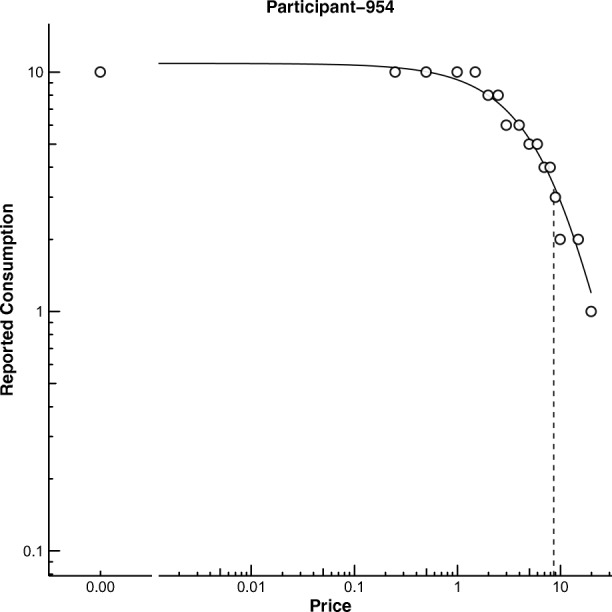
An example plot produced by . Case 954 from the simulated validation dataset. The dashed vertical line corresponds with the point of P_max.

Table 1.

Demand Curve Metrics and Descriptions

Demand Metric	Symbol	Observed or Derived	Description
Intensity	Q 0	Observed/Derived	Level of consumption or likelihood of purchase at low or no costs (e.g., free). Also termed “maximum demand”
k	k	Observed/Derived	The range of consumption in logarithmic units
Alpha	α	Derived	The rate of change in elasticity across the demand curve. Inversely related to value (e.g., smaller values indicate higher demand)
Generalized Essential Value	EV	Derived	Relatively Q0- and k-independent measure of reinforcing value. Larger values indicate higher demand
Breakpoint 1	BP 1	Observed	The highest price in which there is any consumption or likelihood of purchase
Breakpoint 0	BP 0	Observed	First price in which there is no consumption or 0% likelihood of purchase. Fully suppressed responding
Price maximum	P max	Observed/Derived	The price associated with unit elasticity (slope = -1). Indicates the transition from inelastic to elastic.
Output maximum	O max	Observed/Derived	Maximum output or expenditure at price Pmax

Several models have been developed to describe operant demand. The first of these models (i.e., Linear Model) was proposed by Hursh et al. (1989), which takes the form shown in Equation 1.

$$\mathit{lnQ}=\mathit{lnL}+\mathit{bln}\left(P\right)-\mathit{aP}+u$$ 1

In this model, Q is the amount of consumption, P is unit price, L is the intercept or the derived amount of consumption as P approaches zero, b is the initial slope of the demand curve, a is the parameter that represents decreases in consumption as a function of increases in price, and u is the error term (i.e., residuals). Although never explicitly specified in Equation 1, we assume the error term in nonlinear least squares to be normal such that E[u] = 0 and $E\left[u^2\right]={\sigma }_u^2$. Limitations of Equation 1 prompted an alternative method of modeling demand curves, as estimates from Equation 1 may result in unrealistic values (Hursh & Silberberg, 2008). For example, estimates of L may be inflated and estimates of b take on positive values, indicating an initial increase in consumption at low prices. Increases in consumption with increases in price are not to be expected as such patterns would violate the law of demand (Samuelson & Nordhaus, 2009).

The Exponential Model was proposed by Hursh and Silberberg (2008) and describes demand similarly to Equation 1, but improves upon it in several ways. The Exponential Model takes the form shown in Equation 2.

$$\mathit{\text{logQ}}=\mathit{log}{Q}_0+k\left(e^{-\alpha \times \left(Q_0\times C\right)}-1\right)+u$$ 2

In the Exponential Model, Q reflects consumption at each unit price (i.e., C) and Q₀ reflects consumption when the unit price is zero (i.e., free). The parameter Q₀ is also termed the maximum level or “intensity” of demand. The scaling constant k reflects the range of consumption in logarithmic units and contributes to the demand curve’s elasticity by bounding the range of the Equation 2 best-fit function. Considerations for determining scaling constant k are discussed later in this article. As with Equation 1, we assume the error term (u) in nonlinear least squares to be normal such that E[u] = 0 and $E\left[u^2\right]={\sigma }_u^2$. Advantages of the Exponential Model include reducing the measure of essential value to a single parameter, α, and providing more accurate estimates of consumption near a unit price of zero (i.e., Q₀).

Because goods may differ in scalar properties such as magnitude or dose, the Exponential Model accounts for scalar differences by standardizing price in relation to the individual’s intensity of demand, i.e. Q₀ ∙ C (see also Hursh & Winger, 1995). Thus, setting k as a constant and standardizing price in relation to Q₀ isolates changes in elasticity across the demand curve in one rate-constant α. Log transformations are used because elasticity is determined by the slope of the demand curve in log-log coordinates; when data are plotted in log-log coordinates, relative unit changes in consumption can be compared to relative unit changes in price (Hursh, 1980; Lea, 1978). Accordingly, α describes the rate of change of elasticity across the entire demand curve.

With both models, however, consumption values equal to zero are unable to be fitted given the logarithmic transformations of Q. To address concerns associated with consumption values equal to zero, standard practice has been to either omit completely or replace with seemingly arbitrarily small non-zero values (e.g., .1, .01, .001; Kaplan et al., 2018), although differences in these small values are magnified in logarithmic coordinates. Omitting zero values (which are usually at the tail end of the demand curve) gives rise to a statistical issue of missing data that does not occur at random. In an attempt to address this issue, Koffarnus, Franck, Stein, and Bickel (2015a) proposed an alternative formulation of the Exponential Model, wherein individual terms were exponentiated. This rearrangement of terms removed the need to perform logarithmic transformations of Q, allowing consumption values equal to zero to be included in model fitting. The form of the Exponentiated Model is shown in Equation 3.

$$Q=Q_0\times {10}^{\mathrm{k}\left(e^{-\alpha \times \left(Q_0\times C\right)}-1\right)}+u$$ 3

In this model, the parameters included are the same as in the Exponential Model. Although individual terms are exponentiated, the error term (u) is still assumed to be normally distributed (E[u] = 0 and $E\left[u^2\right]={\sigma }_u^2$). Koffarnus et al. (2015a) evaluated both an empirical dataset (Experiment 1) and a simulated dataset (Experiment 2) and the authors suggested that the Exponentiated Model had advantages over the Exponential model when zero values are omitted or replaced with a small, nonzero numbers. However, we note that the empirical and simulated datasets evaluated by Koffarnus et al. (2015a) exemplified the issue of zero values and, as a result, contained a high proportion of zero values. Given the contemporary use of the Exponential and Exponentiated Models over the Linear Model, we focus on the two most recent equations throughout the rest of the article.

Aside from fitted model parameters, other dimensions of the demand curve have proven useful in understanding the extent to which reinforcers maintain responding under varying price constraints. Two of these measures, P_max and O_max, reflect the point of unit elasticity (i.e., where the slope in relative units equals -1) and maximum output, respectively (Hursh, 1980; Lea, 1978). The third measure is breakpoint, defined as either the first price at which the organism does not obtain a reinforcer (BP₀) or the last price at which the organism does earn at least one reinforcer (BP₁; see Katz, 1990). The segment of the demand curve to the left of P_max, characterized by the relatively flat line (i.e., 0 > slope > -1), refers to the inelastic portion of the demand curve, whereas the segment to the right of P_max, characterized by the downward sloping line (i.e., slope < -1), refers to the elastic portion. That is, when the slope is inelastic, one relative unit increase in price is met with less than one relative unit decrease in consumption; when the slope is elastic, one relative unit increase in price results in greater than one relative unit decrease in consumption (Lea, 1978). As mentioned previously, several measures, including Q₀, P_max and O_max, can be determined in two ways (see also Table 1): (1) an estimated or derived value can be obtained based on values derived from the fitted models (Hursh, 2014; Hursh & Roma, 2013) and (2) an observed value can be obtained by visually analyzing the data (Greenwald & Hursh, 2006). Both measures of breakpoint (i.e., BP₀, BP₁) are typically observed.

Whereas the demand curve describes the extent to which consumption changes as a function of unit price, the response output curve, also known as the expenditure curve, describes how overall levels of responding change across a range of prices (Hursh, 1980, 1984; Hursh, Raslear, Shurtleff, Bauman, & Simmons, 1988). The expenditure curve has a ∩ (i.e., inverted ⋃) shape wherein total expenditure increases to a point (i.e., maximum output; O_max) and then declines thereafter (Hursh, 1991). The increase in expenditure is associated with the inelastic portion of the demand curve and the decrease is associated with the elastic portion. Maximum expenditure is typically associated with the point of unit elasticity (i.e., P_max) of the demand curve (Hursh, 1991; Samuelson & Nordhaus, 2009). Total expenditure is calculated by multiplying unit price by the number of reinforcers consumed at that unit price.

beezdemand Package for R

To consolidate existing methods and approaches for applying behavioral economic analyses, we have developed a statistical package to extend the statistical program (R Core Team, 2018). The statistical program is a free and open-source program used to perform many types of statistical analyses and can be extended by peer-reviewed packages. Beezdemand was designed to provide a centralized collection of behavioral economic methods that are openly available, free-of-charge, and subject to peer-review. The latest stable release of beezdemand will always be found on the Comprehensive R Archive Network (CRAN; https://CRAN.R-project.org/package=beezdemand). Among the features included, beezdemand provides methods for easily: obtaining descriptive measures (), detecting nonsystematic data (), detecting and replacing outliers (), determining scaling constants (i.e., k), applying one of several models of behavioral economic demand (), generating standardized figures (), and comparing whether parameter values differ between groups (). In addition to modeling, a range of summary measures, statistical metrics, and graphical illustrations specific to behavioral economic demand analyses are provided. To assist new or infrequent users of , we provide a brief introduction to along with a more thorough description of the functions in the beezdemand package in the supplemental document, “Introduction to R and beezdemand” accessible via the following link https://github.com/brentkaplan/beezdemand/tree/master/pobs (see also the Appendix). We encourage more experienced users of to consult the package vignette. Before displaying the validation results, we briefly describe some of the functions available in the beezdemand package.

The function returns a data frame2 (i.e., table) containing the following descriptive statistics from demand data at each price: mean, median, standard deviation, minimum, and maximum consumption, the proportion of zero values, and number of missing values (not available or NA in nomenclature). This function optionally provides a box-and-whisker plot as well. An example reporting of these measures is provided in Koffarnus et al. (2015a).

The function applies the three criteria proposed by Stein, Koffarnus, Snider, Quisenberry, and Bickel (2015) for identifying nonsystematic purchase task data. This function also reports the number of consumption values equal to or greater than zero. The three criteria include trend (∆Q; i.e., a global reduction in consumption; requiring at least a 0.025 log-unit reduction in consumption per log-unit range in price), bounce (i.e., price-to-price increases in consumption; requiring less than or equal to 10% of prices increments resulting in consumption increasing no more than 25% of initial consumption), and reversals from zero (requiring no instances of two consecutive zeros followed by a nonzero consumption value). This function accepts arguments for each of these criteria in cases where they might be modified.

The function takes a data frame of numerical values (e.g., consumption values, demand metrics), identifies values greater and/or less than 3.29 SDs (Tabachnick & Fidell, 2013), and recodes those values depending on user specification (e.g., one unit higher than the greatest nonoutlying value; i.e., Winsorizing). We have found this to be a common approach in the purchase task literature (Kaplan et al., 2018).

The 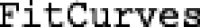function analyzes demand data using one of the three aforementioned models of demand. Demand data can be analyzed at the individual or group level, the scaling constant k can be determined in several ways (e.g., from the observed range of y values, as an individually fitted derived parameter, as a global shared derived parameter), and lower and upper bounds on parameters can be specified. This function returns a data frame of both empirical and derived parameters and can optionally return model objects, the original data used in fitting, and the predicted levels of demand for use in figures. This routine depends on the nlmrt (Nash, 2016) and nls2 (Grothendieck, 2013) packages to fit the demand equations. These two packages support the identification of suitable starting points, which are then supplied to the default optimization function, nls, in the statistical program (R Core Team, 2018). Briefly, the nls function uses an algorithm based on Newton’s method for finding roots. In particular, the Gauss-Newton approach was used with models of operant demand whereby optimization of parameters (i.e., minimizing the sum of squared residuals) is performed using the first derivatives only. The nls function is used at default settings, unless set otherwise, with a maximum of 1,000 iterations.

The 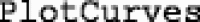function accepts results from 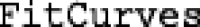and produces figures for each of the participants in the fitted dataset. When aggregate level data are calculated using 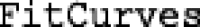, a single figure for those data will be produced. Figures produced by beezdemand are provided in both vector-based (e.g., Portable Document Format) and rasterized formats (e.g., Portable Network Graphic).

Lastly, the function performs an Extra Sum-of-Squares F-test to evaluate if one global parameter (either Q₀ or α) better represents various curves than parameters fitted for each group. Like the 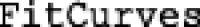function, a data frame object is returned along with fitted model parameters, as desired.

Validation of beezdemand

To evaluate the accuracy, reliability, and precision of this new software package, the results produced by beezdemand were compared to those produced by the GP statistical program. At present, two GP templates are available for download and use in performing demand curve analyses (Hursh & Roma, 2014; Reed, 2015). For the purposes of this study, both statistical tools were compared using the Exponential and Exponentiated models of demand. Comparisons were performed using data from simulations as well as from a peer-reviewed study.

Method

Simulated Study Data

Simulations were constructed to allow for a comparison of both software packages across a wide range of possible demand curve scenarios. Simulated consumption data were derived from the means and standard deviations of group-level responding for 914 participants in an Alcohol Purchase Task (Kaplan & Reed, 2018). From these data, a total of 1,000 hypothetical series of consumption values were simulated across the following prices: $0.00 (free), $0.25, $0.50, $1.00, $1.50, $2.00, $2.50, $3.00, $4.00, $5.00, $6.00, $7.00, $8.00, $9.00, $10.00, $15.00, and $20.00. Simulations were performed using the statistical program and both the simulated data and source code necessary to recreate these simulations have been openly shared and instructions for acquiring these are available in the Appendix. From these simulated values, only series that passed all three of the Stein et al. (2015) criteria for systematic responding were included in the simulated dataset.

Real-World Study Data

Published study data were re-analyzed to evaluate the accuracy and precision of beezdemand in relation to the GP computer program. Data from Kaplan and Reed (2018) were reanalyzed using both programs. In Kaplan and Reed (2018), participants were recruited using the Amazon Mechanical Turk (mTurk;, n.d. platform). The mTurk platform has been used effectively to conduct a range of behavioral economic research (Morris et al., 2017; Roma et al., 2016). A total of 1,104 participants completed a standard form of the Alcohol Purchase Task (APT; Kaplan et al., 2018; Murphy et al., 2013) delivered using the Qualtrics® Research Suite web service. In the APT, participants reported the number of alcoholic drinks they would purchase and consume at a range of prices. All participants completed a standard version of the APT followed by a modified APT framed in terms of a drink special. For the purposes of the present article, we only analyzed responses from the standard APT. The APT included the following prices: $0.00 (free), $0.25, $0.50, $1.00, $1.50, $2.00, $2.50, $3.00, $4.00, $5.00, $6.00, $7.00, $8.00, $9.00, $10.00, $15.00, and $20.00. Using the data from 1,104 participants, the Stein et al. (2015) criteria were applied. Only participants demonstrating systematic consumption (i.e., meeting all three criteria) were included in subsequent analyses, resulting in 914 complete cases. For all other details related to the study, readers are encouraged to consult Kaplan and Reed (2018).

Data Analysis

As noted earlier, the 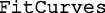function can determine the scaling value k several different ways. We mention these methods because there are currently no agreed upon recommendations for determining k and because values of α are not invariant across different k values. The default method calculates k by taking the difference between the minimum consumption and maximum consumption values across all datasets in logarithmic units and subsequently adds 0.5.3 Adding this amount was originally proposed by Hursh in an early iteration of a Microsoft Excel spreadsheet used to calculate demand metrics. Beezdemand adopts this adjustment for two reasons. First, when fitting Q₀ as a derived parameter, the value may exceed the empirically observed intensity value. Thus, a k value calculated based only on the observed range of data may underestimate the full fitted range of the curve. Second, we have found that values of α (as well as values that rely on α, i.e. approximate P_max) display greater discrepancies when smaller values of k are used compared to larger values of k. An important note is that this method sets k as a constant in Equations 2 and 3 and is not solved for in the fitting process.

As an alternative, k can be specified as a single shared parameter (solved for in the fitting process), whereby k is fit “globally” and other parameters (e.g., Q₀, α) are fit “locally.” In this approach, each dataset will have its own individualized Q₀ and α and all datasets will have a common k value. Whereas all three parameters are optimized for a given sample of data, this approach is more computationally demanding. Finally, k can be determined for each individual dataset as a constant (i.e., observed range of consumption) or as a fitted parameter; however, we do not necessarily recommend these latter two approaches in practice because α varies with changes in k and, as such, α values should not be compared across datasets with differing ks.

For the current analyses, k was calculated separately for the real-world study and simulated validation sets using the default approach just described (the observed range of consumption in logarithmic units and adding 0.5). Thus, the resulting k values were 1.7608 and 5.3116 for the real-world study data and simulated validation set, respectively. Within each dataset, however, the same values were used when fitting both the Exponential and Exponentiated models. Both software programs applied nonlinear model fitting using default settings. Both beezdemand and GP were run on MacOS using version 3.5.1 and GP version 7.0a, respectively.

Results

Simulated Validation Dataset

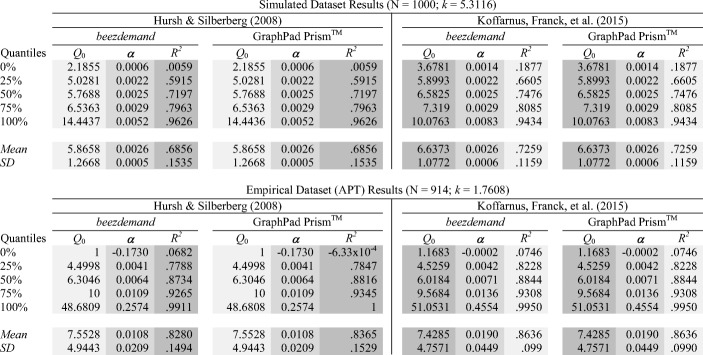
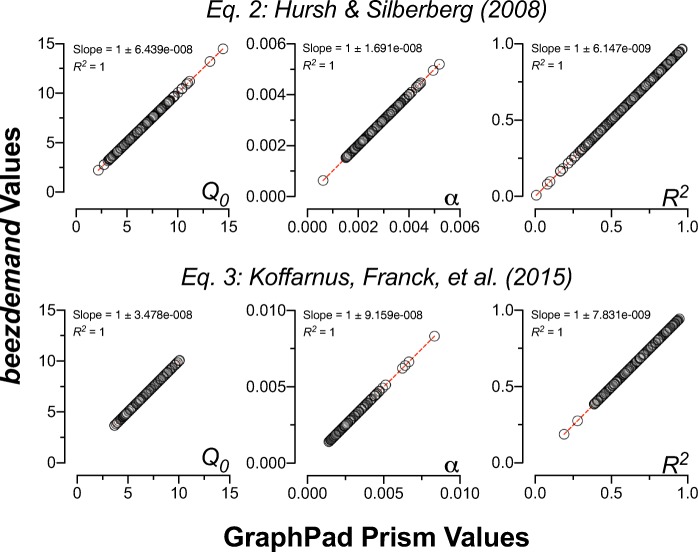
The top half of Table 2 provides a descriptive summary of fitted model parameters from the Exponential and Exponentiated models across the two software packages. In the case of the results from the simulated dataset, there were no discrepancies in the measures obtained from the two software packages (all rs = 1, ps < .0001). Figure 2 displays the high correspondence of results from the simulated validation dataset.

Table 2.

Descriptive Summary of Parameters Obtained Across Datasets, Demand Equations, and Programs

Fig. 2.

Data from the simulated validation dataset. Correspondence in derived parameters from Equations 2 and 3 between beezdemand and GraphPad Prism^TM.

Empirical Validation Dataset

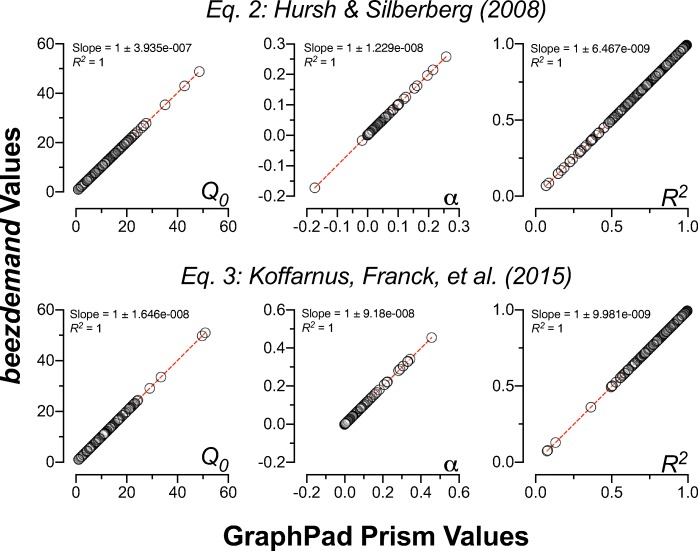
The bottom half of Table 2 displays a descriptive summary of parameters from the Exponential and Exponentiated models across both software packages. As indicated in Table 2, values obtained from both programs were nearly identical up to five significant digits (all rs = 1, ps < .0001). Discrepancies primarily occurred in calculations of R². GraphPad Prism will output R² values of one in cases of a perfect fit (i.e., no degrees of freedom). Beezdemand will output NA (i.e., not available, missing) in extreme circumstances, as those data might warrant further inspection. Figure 3 displays correspondence between the two programs via scatter plots.

Fig. 3.

Data from the empirical validation dataset. Correspondence in derived parameters from Equations 2 and 3 between beezdemand and GraphPad Prism^TM.

Discussion

Behavioral economics is increasingly used as a framework for understanding choice behavior and this framework is used across various disciplines. Researchers from fields of study including health (Bickel & Vuchinich, 2000), addiction (Bickel et al., 2014), nutrition (Epstein et al., 2018), organizational behavior management (Henley et al., 2016a; Wine, Gilroy, & Hantula, 2012), and public policy (Hursh & Roma, 2013) have used the operant demand methodology to better understand various challenges and disorders. However, whereas a wide range of users employ demand-based methodology relatively few peer-reviewed options exist for conducting demand analyses. The purpose of this article was to (1) provide a brief primer of behavioral economic demand, (2) overview the main functions and workflow of the beezdemand package, and (3) validate results of beezdemand against those from a popular commercial software program. The most recent stable release of the package can be installed directly from the Comprehensive R Archive Network (https://CRAN.R-project.org/package=beezdemand).

Beezdemand extends and integrates behavioral economic demand tools into a single, dedicated software package. Whereas screening for systematic data and calculations of advanced demand indices would typically be conducted in standalone spreadsheet software (Hursh & Silberberg, 2008; Kaplan & Reed, 2014; Stein et al., 2015) beezdemand integrates these tools into one package. In addition, the package is especially well-suited to analyze many datasets at one time. In recent years, there has been an increase in the number of studies utilizing crowdsourced platforms such as Amazon Mechanical Turk (Morris et al., 2017; Roma et al., 2016; Snider, Cummings, & Bickel, 2017; Strickland & Stoops, 2018), with which large participant samples can easily be obtained. Given that GP presents with certain limitations (i.e., at the time of this writing, a hard limit of 256 cases), beezdemand provides a true solution for working with large datasets in several ways. First, certain analyses (e.g., sharing one parameter globally while fitting other parameters locally; e.g., shared k), which were unable to be conducted using existing commercial software, can now be accomplished effortlessly when more than 256 cases are present. Second, the suite of functions in beezdemand have been designed to allow for a more consistent workflow. In a basic workflow, data would be examined by 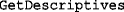, unsystematic cases would be identified by , and data would be fit, evaluated, displayed, and compared using , , , and .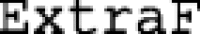

Tools such as beezdemand address a growing need to extend and expand upon tools for behavior economic analyses (see also Gilroy, Franck, & Hantula, 2017; Gilroy, Kaplan, Reed, Koffarnus, & Hantula, 2018b). Beezdemand extends existing solutions while based on an open-source framework, , allowing others to use and modify free of charge. There are numerous advantages of using an open-source programming language such as (e.g., leveraging user-made packages with abilities to directly interact with services such as Amazon Mechanical Turk and Qualtrics® Research Suite), and notwithstanding its rising popularity in academia (Tippmann, 2015) it provides cross-platform compatibility (Macintosh OS, Linux, Windows) and a high degree of customizability. Further, utilizing open-source programming languages helps move science toward enhancing transparency and improving replicability (Open Science Collaboration, 2012). Towards this end, the functions in beezdemand can be used seamlessly within dynamic documents (e.g., knitr, R Markdown; Xie, 2016) to create full, reproducible manuscripts, a benefit of which is the ability to exactly document and recreate the steps used during the import, cleaning, data analysis, and visualization stages of a research project.

With respect to releasing tools under open source terms, work that is transparent and under version control is reflective of an evolving culture of open scholarship. Consistent with the recommendations of the Open Science Collaboration (2012), the specialized methods and analyses featured in beezdemand are released and stored in a public repository (i.e., GitHub) and managed by the open source community (i.e., Comprehensive R Archive Network). Transparency and openness in the development and dissemination of novel methods is important, both for the proper crediting of authors for their work as well as the recognition of those who have contributed to and maintained these resources. Further, centralized features such as issue-tracking also provide means of maintaining and supporting peer-reviewed works in years that follow.

Future Directions

The results from this study indicate that the beezdemand package provides results commensurate with commercial software used in behavioral economic research; however, there are several areas that warrant future consideration. First, beezdemand is entirely written in the programming language and, thus, may present barriers for use among clinicians and researchers not familiar with the software program (see Gilroy et al., 2018b, for alternative open source software providing a Graphical User Interface). Efforts were made, however, to allow beginner users to easily interact with the package and most functions in the package contain details related to their use, as well as example code. In addition, numerous resources exist for new users to learn the programming language (e.g., the Use R! series,n.d.; Swirl, n.d.; StackOverflow, n.d.), thus minimizing barriers to adoption. In efforts to promote adoption, we direct readers unfamiliar with to consult the supplemental document, “Introduction to R and beezdemand” accessible via the link in the Appendix.

Second, beezdemand is predominantly focused on one area of operant behavioral economics. Although the methods evaluated here provide a robust extension to the tools currently available, additional development is necessary to increase the range of analyses provided in this package. For example, future developments will include additional techniques and methods such as normalization procedures (Hursh & Winger, 1995), two-part and mixed-effect modeling (Liao et al., 2013; Yu, Liu, Collins, Vincent, & Epstein, 2014; Zhao et al., 2016), measures of amplitude and persistence (Bidwell et al., 2012; MacKillop et al., 2009), enhanced graphical capabilities, as well as other features. As the behavioral economic field advances and new metrics and approaches are empirically validated, beezdemand will integrate this new knowledge to provide an expansive set of cutting-edge tools. We encourage users to explore the full functionality of the beezdemand package and consider contributing and submitting issues on the package’s GitHub (n.d.) page (https://github.com/brentkaplan/beezdemand).

Appendix

Introduction to R and beezdemand: https://github.com/brentkaplan/beezdemand/tree/master/pobs

Latest stable release package location: https://CRAN.R-project.org/package=beezdemand

Latest development package location: https://github.com/brentkaplan/beezdemand

Simulation script location: https://github.com/brentkaplan/DemandCurveSimulations