The “Reproducibility Crisis:” Might the Methods Used Frequently in Behavior-Analysis Research Help?

Abstract

Mainstream biomedical and behavioral sciences are facing what has been dubbed “the reproducibility crisis.” The crisis is borne out of failures to replicate the results of published research at an average rate of somewhere near 50%. In this paper I make a case that the prime culprit leading to this unsatisfactory state of affairs has been the widespread use of p-values from tests of statistical significance as a criterion for publication. Even though it has been known, and made public, for decades that p-values provide no quantitative information about the likelihood that experimental results are likely to be repeatable, they remain a fundamental criterion for publication. A growing realization among researchers that p-values do not provide information that bears on repeatability may offer an opportunity for wider application of research methods frequently used in the research specialty known as Behavior Analysis, as well as a few other research traditions. These alternative approaches are founded on within- and between-participant replication as integral parts of research designs. The erosion of public confidence in science, which is bolstered by the reproducibility crisis, is a serious threat. Anything that the field of Behavior Analysis can offer as assistance in ameliorating the problem should be welcomed.

What has come to be called the “Replication Crisis” in science was illuminated as a focus of attention among biological/medical scientists in a publication by John Ioannidis titled “Why most published research findings are false,” (Ioannidis, 2005). In the paper, Ioannidis sounded an alarm that published laboratory research findings were being found not to be repeatable when researchers tried to follow them up. In a famous example, C. Glenn Begley (cf. Begley & Ioannidis, 2015), when he took over the laboratory at the corporation Amgen, had scientists attempt to replicate 53 “landmark” studies in cancer research. Forty-seven of those attempts failed. Not long after that Brian Nosek, a noted social psychologist, alerted those interested in Psychology that much research, including some of his own, published in Psychology journals, was not repeatable (Open Science Collaboration, 2015). Obviously, this cannot be good for science, and the problem has become severe enough that lay publications are now reporting on the issue (e.g., Siegfried, 2010; Harris, 2017).

A Root Cause of the Problem

There has been an explosion of papers about the origins of the Replication Crisis. Often suggested as contributing factors are pressure to publish, outright cheating, unconscious bias, data dredging (also known as p-hacking), too-liberal alpha levels in hypothesis testing, and the social safety of accepted procedures (e.g., Barch & Yarkoni, 2013; Branch, 2014; Head, Holman, Lanfear, Kahn, & Jennions, 2015; Świątkowski & Dompnier, 2017). My view is that, although the last in that list is probably important, the others do not contribute much to the problem. For example, eliminating data dredging, which usually violates basic principles of significance testing, would likely have little effect on the repeatability of published work. The same is true for suggestions that the standard for publication be moved from p < .05 to something smaller, like p < .005. Such changes would have little effect, in major part, due to a factor that is interestingly missing from most lists of probable reasons. It is a feature of almost all the work that has been found not to be repeatable. Specifically, a major criterion for publication of the work has been statistical significance, and I argue here that that is an important, maybe even the most important, part of the problem. The usual criterion of p ≤ .05 is generally thought to imply that the failure rate in attempts at replication should be less than 5%, not the more than 50% that has now been reported in several instances (e.g., Open Science Collaboration, 2015). Unfortunately, that assumption is false, with higher rates of replication failure entirely predictable from what a p-value indicates, or more specifically what it clearly does not indicate.

The underlying misconception -- that p-values measure the likelihood that a result is “real” or repeatable -- is so pervasive that the American Statistical Association (ASA) felt compelled to assemble a committee of eminent statisticians to report on the problem, and an outcome was publication, by the ASA, of a first-ever position statement (Wasserstein & Lazar, 2016) on any statistical issue. Quoting from the statement itself: “P-values do not measure the probability that the studied hypothesis [null hypothesis] is true, or the probability that the results were produced by random chance alone” (p. 131) and “By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.” [p. 132, italics in original]. Even more important than those truths is the fact that a p-value provides no information about whether the result should be believed, that is, that it is a repeatable finding. As a consequence, as noted in the position statement, “The widespread use of ‘statistical significance’ (generally interpreted as “p ≤ 0.05”) as a license for making a claim of a scientific finding (or implied truth) leads to a considerable distortion of the scientific process.” (p. 131, italics added).

The basis for that last statement may seem mysterious to many, but should not be because p-values provide no, that’s right, no, information about the likelihood that an experimental result will be reproduced if a replication is carried out. This has been known for decades, has been pointed out in scores of published papers (e.g., Bakan, 1966; Berkson, 1942; Branch, 2014; Carver, 1978; Cohen, 1994; Goodman, 1999; Nickerson, 2000; Rozeboom, 1960), and therefore presumably is understood by virtually every statistics textbook author. If this comes as a surprise to the reader, please know that you are not alone. Available survey data indicate that upwards of 90% of practicing scientists mistakenly believe that p-values provide information about likely repeatability (Haller & Krauss, 2002; Oakes, 1986).

Let me recap for the Behavior Analysis community the truth about p-values. To begin, the definition of a p-value (in not quite fully formal language) is that it represents the probability of seeing a result (or a more extreme one) given that the null hypothesis is the true state of affairs. That is, it is what is called a conditional probability, in that the value depends on what the “given” is. Importantly, that means a p value is not the same as the probability that the null hypothesis is true given the results obtained. Nevertheless, the p-value is generally used to make a decision about the truth of a null hypothesis upon which it has no bearing. It is simple to show that this is the case. For any two conditions or events, the probability of one given the other is not reversible with respect to which condition is the given. For example, the probability that it is cloudy given that it is raining is not the same as the probability that it is raining given that it is cloudy, nor is the probability that a person is dead given that he or she was hanged the same as the probability that a person was hanged given that he or she is dead (examples are from Carver, 1978). In each case, the two probabilities are unrelated to each other. One tells you nothing about the other. Ironically, therefore, although p-values are computed to guess about whether the null hypothesis is true, the calculated probability is unrelated to whether the null hypothesis is in fact true. To take a salient example, modeled on one by Falk and Greenbaum (1995), consider the following so-called logic: If the next person I meet is an American (the given), it probably will not be the President (actuarial conditional probability of about .000000003). But I just met the President. Therefore, confronted with p ≤ .000000003, I reject the given as being the case, and I conclude that the President is not an American. That is precisely analogous to the logic used in null-hypothesis significance testing, an approach that is employed almost uniformly in the biological and behavioral sciences to determine whether a research finding is worthy of publication. Is it any wonder then, given that a low p-value is a common criterion for publication in the scientific literature, that published research is frequently not repeatable?

Most of us remember examples from statistics classes that did not seem as laughable as the one just told about the President. For example, you may recall something like the following. If a die is fair (the given), it should come up, in the long run, with each face 1/6th of the time. I roll the die 10 times, and it comes up six every single time. If the die is fair, the probability of that outcome is 1/6th to the 10th power (about .000000017). This may seem to be good evidence that the die is not fair – specifically, the probability that the die is unfair. But that is not the probability we calculated. Our outcome, .000000017, is simply the probability of any particular sequence of the six sides that emerges from 10 rolls, so whatever particular sequence (e.g., 1, 2, 3, 4, 5, 6, 5, 4, 3, 2) was obtained would have the same probability of occurring. So now maybe you are not so confident in declaring the die unfair. So what might be done to obtain more useful evidence? How about rolling the die 10 more times? That is a good idea, but more on that later.

A key difference between the die example and the usual practice in null-hypothesis statistical testing is that with the die we have a reasonable initial belief about the given (our null hypothesis). That is, we assume that the die is fair because for most of our lives we have found only dice that are fair, and we conduct the statistical test to see how likely our result would be if it were, in fact, fair. That is not what goes on in most scientific experiments. We do the experiments, usually based on some ideas, or even formal hypotheses, about what is going to happen. The null hypothesis is not what we expect to happen. In fact, we believe in advance that it is false and try to get additional evidence to support our assumption. But there is a serious problem with that. If the null hypothesis is not true, which we expect (or at least hope), then the p-value is meaningless. The p-value is defined as a probability given the truth of the null hypothesis. If the given is not true, then the calculated probability value has no meaning.

It is additionally the case that, for most research projects, the chosen null hypothesis predicts no effect, an assumption that is almost always empirically false. As Meehl (1978) noted, “As I believe is generally recognized by statisticians today and by thoughtful social scientists, the null hypothesis, taken literally, is always false.” (p. 822). There are many other problems inherent in null-hypothesis significance testing (cf., e.g., Branch, 2014; Cohen, 1994), but the key point here is that p-values provide no information about whether you should believe whether an experimental effect or scientific outcome should be believed. Journal reviewers and editors need to keep that fact in mind, and act accordingly. Attempting to make inferences about whether a result is likely repeatable by using p-values is like trying to measure temperature with a yardstick. A yardstick measures something, that is, length, but those measures are unrelated to temperature. A p-value measures something, but not the probability that the null hypothesis is true, which is what you would really like to know. It should now be clear that the oft-used synonym for “statistically significant, “statistically reliable,” is a non-sequitur. Statistical significance provides no information about reliability, none.

A Path to Ameliorating the Crisis?

If a p-value does not provide information about repeatability, it should not be used as a criterion for publication. What should be a “replacement” criterion then? This is where research approaches common in Behavior Analysis may have something to add in an attempt to make published science more likely to be true. In what follows, I first outline for scientists who are not familiar with Behavior Analysis research some basic characteristics of the approach, with the suggestion that researchers in other domains, like cognitive or social psychology, consider trying to incorporate them into their investigations. Then I follow with some suggestions about actions that might assist in dealing with the crisis.

A fixed, inviolable standard like p ≤ .05 is neither possible in science nor necessary. A skeptic might suggest that operating without fixed standards leaves open the door to all kinds of biases and therefore research that is not repeatable. It is hard to imagine, however, a worse status quo than the one that has arisen in Psychology with a fixed decision standard. More to the point, however, the successes of Behavior Analysis (and another domain or two that will be mentioned) show that a coherent collection of scientific facts, testable theories, and effective technologies (cf. Madden, 2013b) can be developed without reliance on a fixed statistical standard for publication. More compelling comfort may come from viewing the history of science. Statistical significance testing was invented a bit before the mid twentieth century and did not come into prominent use until the second half of that century. Foundational research that has stood the test of time in physics, chemistry, physiology, biology, and psychology was conducted and published before statistical significance was invented.

Good science before significance testing was made possible by careful experiments that were shown to be repeatable. How was that shown? By repeating the experiments, a process known technically as replication. Much Behavior Analysis research, modeling itself in part after science that preceded the invention of significance testing, is characterized by methods that are grounded in replication. Replication can be performed by researchers at other laboratories, but it can also be performed by an individual researcher as part of her/his research design. Research in Behavior Analysis has been characterized by both approaches. To focus on the latter, I shall discuss briefly how individual researchers have incorporated replication into their basic research designs.

As an example, consider the simplest kind of experimental design used by Behavior Analysis researchers, the ABA design. Replication is evident throughout. Usually multiple observations take place within Condition A, in order to establish a baseline. That sequence of observations is, of course, a series of replications of what will happen in Condition A. When Condition B is implemented, it too also subsumes multiple observations, providing another series of replications. When Condition A is re-imposed, it represents an attempt to replicate on a larger scale in that it is an attempt to replicate the previous baseline. Suppose, for example, that whatever is measured changes notably when Condition B replaces condition A and then returns to is original level when A is re-implemented. At that point, depending on a variety of factors, a scientist might decide that an interesting fact has been observed. Or, depending on the same or other factors, the scientist might say to herself, “That’s an interesting outcome. I wonder if I should believe that Condition B was the cause of the observed change in the measure? I think I’ll redo the whole process: A, then B, then A, again.” Doing it over, of course, is a replication at yet another level. Replication extends further if the experiment is repeated with additional participants. If the results are consistent across multiple levels of replication, the scientist gains confidence in the repeatability (and concomitantly the generality across people) of the results, maybe even so much so that she thinks she should make it more widely known by publishing them.

Of course, the simple design described in the preceding paragraph is appropriate only if effects of a particular experimental set of conditions are repeatable over time, in the same individual. Sometimes this is described as the effects being “reversible.” There are many, many cases, however, where that is not true. A single experience with a set of conditions may change the results of subsequent exposures. Notable examples of this are the many effects that are supposed to indicate what is called learning. Fortunately, Behavior Analysts have developed procedures to deal with circumstances like that while maintaining the focus on replication as the fundamental method of determining reliability at the level of the individual person or other animal. The interested reader can find a useful overview of such techniques in Perone and Hursh (2013) or a more comprehensive account in Johnston and Pennypacker (2009).

As intimated earlier, Behavior Analysis research does not have a monopoly on individual-case designs focused on replications. The study of sensory and perceptual processes is replete with such designs (e.g., Goldstein, 2014), and basic research in physiology has had a similar focus ever since the pioneering work of Claude Bernard (cf. Bernard, 1865/1957). There is no practical reason that current medical, behavioral, and other biological sciences cannot make greater use of the approach.

An example of how a sensory process was and can be studied without resorting to p values is provided by the familiar phenomenon of dark adaption. An experiment (cf. Aubert, 1865; Phillips, 1939; Bartlett, 1965) involves adapting a person to some level of bright light, and then switching to complete darkness. During the period of darkness, tests are periodically conducted to determine the minimum intensity of a stimulus (e.g., a small spot of light) that can be seen. There are many important details of such experiments that are being ignored in this presentation, but the basic design is presented. Figure 1 presents some hypothetical data from such an experiment. The dotted lines show data from three individuals, and the solid line the average for those three. The dotted functions show common characteristics. First, they all decline across time, showing that ever dimmer light becomes visible as adaptation progresses (The Y axis scale is arbitrary. If it were in real units of luminance it could span several log units.) Second, each individual’s curve has two discernable parts, an initial decline (that is, an increase in sensitivity) that levels out, followed by a larger decline that continues until a constant level in reached. In our fictional experiment, this two-part curve, has been replicated in the three studied participants. Actual experimentation has shown that this function is repeatable within an individual, and usually repeatable across individuals. As indicated, the duration of the first part of the curve varies from individual to individual, and additional research has shown that those differences, too, are reliable (Phillips, 1939; Pirenne, 1962; Wolf, 1960). The important discovery of the two-part function played, and plays, an important role of the duplex theory of the retina, that is, that there are two main types of receptors, cones and rods (cf. Goldstein, 2014; Bartlett, 1965). Note that the average function does not clearly indicate the two-part nature of the function for each individual, a fact that will be considered later.

Fig. 1.

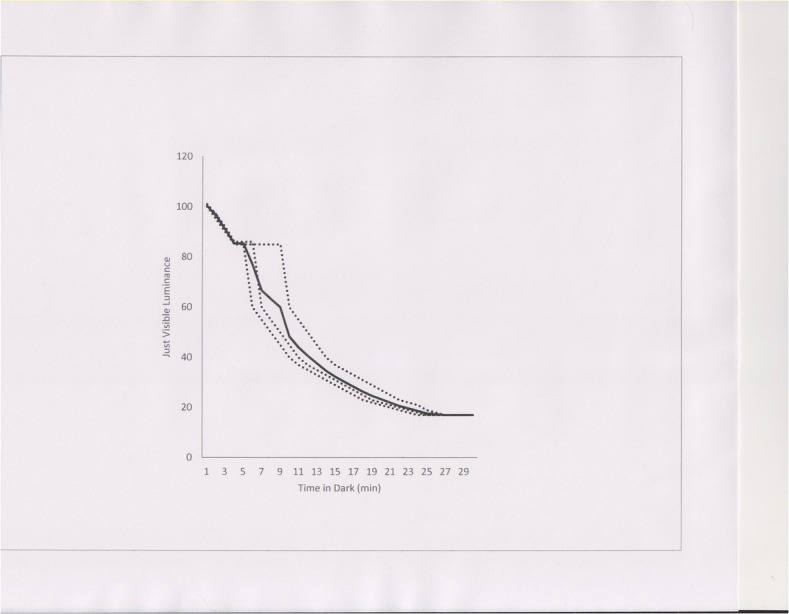
Hypothetical data from an experiment on dark adaptation. Y axis: Luminance of a just-visible spot of light (arbitrary units). X axis: time in minutes. Dotted functions display data from an individual. Solid line is the mean of the three individual-person curves

An important point to remember is that, in the no-significance-testing world of research, the first person the scientist must convince of the repeatability of the effect is herself, not journal editors or others in the scientific community. She must be convinced because her reputation as a scientist rides on it. If someone else tries and fails to replicate the effect, there is no possibility for the first scientist to claim (mistakenly, as we have seen) that, “Oh, this must have been one of the 5% of the time that a p-value indicated that an effect is not repeatable,” or “I conducted my analyses according to conventional standards, so my reputation is not at risk.” It is my view that this social safety provided by a fixed decision criterion is one of the attractions of significance testing. Granting a scientist the protection of being able to say, “I played by the conventional rules of significance testing, so I expect some percentage of the effects I claim not to be reliable.” is of little help in promoting repeatability. For a researcher whose work is found not to be replicable, the correct response is not that “It’s not my fault,” but instead, something like “Dang, what variable or variables did I overlook?” Interestingly, that is the same question frequently (at least in my research career) asked within a laboratory when experimental subjects do not show the same effect of a particular intervention.

It should be acknowledged, of course, that moving to procedures like those often used by in Behavior Analysis and the study of sensory processes is not a panacea. There is no guarantee that results from one lab will be reproducible in another, but the emphasis on replication across laboratories, and the success of such attempts, are likely to be enhanced by its emphasis within laboratories. It is difficult to believe, in any event, that an emphasis on replication can result in rate of cross-laboratory replication failure of 40–50%, which is what apparently prevails in the literatures that depend on statistical significance as a publication criterion.

A common criticism of research in Behavior Analysis is that too few participants are studied; that it relies too much on so-called N = 1 studies. What N = 1 implies to thoughtful behavior analysts is not that one participant is enough (although there are rare cases where that is true), but that each participant is studied and evaluated individually. If inter-participant generality is important, then many participants are likely needed, with each treated as an attempt at replication. One of the positive side-effects of such an approach is that it makes it simple to identify individual differences and to commence the search for variables responsible for those differences. Of historical note is that in B.F. Skinner’s Behavior of Organisms (Skinner, 1938), his description of his first experiments on operant conditioning focused on 4 rats. Over the rest of the book, however, more than 70 additional rats were successfully trained with the same method. And of course, thousands more rats (and other kinds of animals) subsequently have been effectively trained using his techniques.

Methods that do not involve tests of statistical significance share a common feature. The critical characteristic involves focusing on individuals, rather than group averages. One way to think about the approach is that each individual studied is thought of as an independent experiment. That has two valuable consequences.

First, treating individuals as experiments permits better contact with research in basic physiology where each individual, or in many cases part of an individual (for example an organ like a liver) is treated as an independent experiment. That means that when you study additional individuals or organs (like livers) you are conducting attempts at replication. Here, therefore, is a way in which replication is automatically included in the research design, simply by changing the focus of observation. No new experimental techniques are required. What is required, however, is some way of analyzing the data to emphasize that independent experiments have been conducted.

Second, and likely less appreciated, is that, at least in the behavioral and medical sciences, the focus of research methods often is on the point of most likely potential application, the individual. One of the apparently attractive features of the significance-testing-based approach is that it has encouraged the averaging of data across individuals because of the statistical relationships between group averages (and other features of aggregate data, like variance) from random samples from a population and the statistical parameters of the entire population itself. Sample statistics can be used to make estimates about population parameters. Thus the sample data can be used to say things about the entire population under study. That fact is attractive because it appears to increase generality of the research findings. What could be more general that something that applies to the entire population? That generality, however, is illusory if the goal is to understand what is happening at the level of the individual. That is because a population parameter (like mean or variance), even though it is derived from the activity of individuals, is not a measure of what individuals do. A good example of that fact appears in Fig. 1. The mean curve does not clearly reveal the two-part nature of the curves for individuals, and the two-part curve is a foundational attribute of dark adaptation and contributes directly to the analyses of the physiology associated with dark adaption.

A commonly used example of inference about population parameters is the confidence interval that can be calculated once a sample mean has been has been determined. It is an interval in which the population mean will be contained some percentage (e.g., 95%) of the time.1 The confidence interval permits inferences about the value of the population parameter, not about what any individual will do. The direction of inference is not from sample to individuals. Population parameters are actuarial data, not data that necessarily apply to individuals.

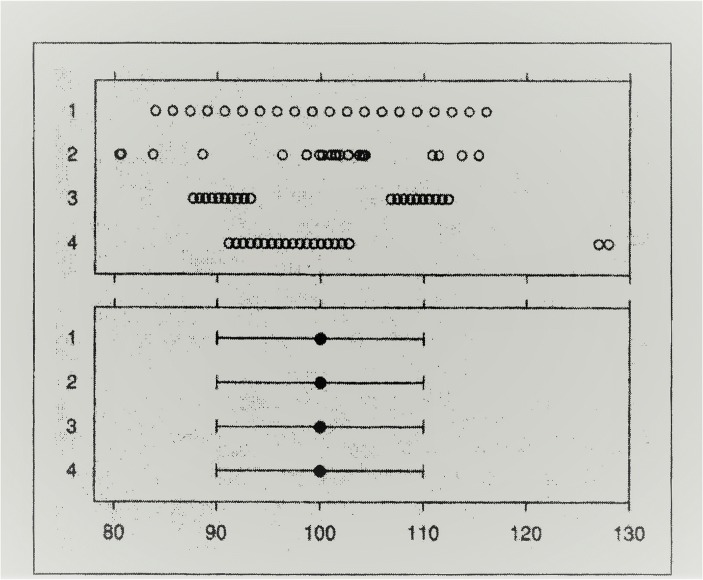
When using means in research on individuals, the representativeness of a mean is at issue. By representativeness I mean how well the mean corresponds to the scores of the individuals whose data are averaged. If the mean is representative, it permits inferences about individuals. Statements like, “the scores for individuals were all within 10% of the mean value” permit conclusions about individuals. Measures like standard deviation are less useful, partly because the exact same means and standard deviation can arise from grossly different distributions as illustrated in Fig. 2 from Cleveland (1994; see also Anscombe, 1973). The four distributions in the upper panel differ markedly, yet their standard deviations are identical.

Fig. 2.

Upper panel: Four horizontally arrayed distributions of twenty values, with each symbol representing a value along the X-axis. Lower panel: The corresponding means and standard deviations of the four distributions shown in the top panel. From Cleveland (1994, p.251, Figure 3.76.) Reprinted with permission, courtesy of AT&T Archives and History Center

The primary point being made here is that population parameters, although often highly useful for things like public health actions, do not directly deal with behavior, mind, or bodily health of individuals, nor do they automatically permit useful inferences about measures of individuals. As Sidman (1960) astutely noted long ago, “…reproducible group data describe some kind of order in the universe and, as such, may form the basis of a science. It cannot, however, be a science of individual behavior except of the crudest sort….My own feeling is that it belongs to the actuarial statistician….” (p.275).

The Issue of Generality

How do procedures grounded in replication in individuals lead to the kind of generality that seems inherent in the group averages that characterize most studies employing significance testing, which permits generalization to a population? Another way to ask this is what should a researcher who is ultimately interested in individuals do with data from independent groups that have been subjected to different procedures? There are several answers to these questions. First, to the extent that procedures developed by Behavior Analysts can be applied, their use guarantees replication attempts as part of the research design. Replication across individuals is a direct test of generality, and replication across varied conditions also provides such tests (cf. Branch & Pennypacker, 2013). Second, if the goal is to compare group averages (as is very often the case, at least in psychology), data from individuals can be emphasized, both graphically and in novel measures. Suppose, for example, two independent groups of 20 studied participants are exposed to either of two conditions, a control condition and an experimental condition. In many experiments, each participant will, in fact, be exposed individually, so his or her response will be independently obtained. We average the data across individuals and find that the mean from the control group is 100, and that of the experimental group is 110. Both sample standard deviations are 10. Consider an example from Fig. 2. Let us begin with the individual data in the second row of the top frame as data from a control group (chosen because the distribution looks like a lot of real data distributions). Then let us add 10 to each value to produce another, experimental, group. We can perform a t-test if we wish, and it will reveal a statistically significant difference (p < .004), with an effect size of 1 standard deviation, usually identified as a large effect. Recall, however, that statistical test reveals nothing about reliability of the difference and nothing about individuals unless additional analyses show the means to be representative of the individuals. If our interest is solely in group-mean effects, a good path would be to replicate the entire study to assess reliability.2

If we are interested in individuals, at least two general avenues of action present themselves. First, graphical methods can be used to illustrate what individuals in a group did. For example, dot plots, like those shown in the figure, wherein every subject’s response is shown will be completely transparent about representativeness of the average, or box-and whisker plots will summarize features of how individuals fared. Other graphical methods can be found in Tukey (1977) and Cleveland (1994). The second approach is to engage in additional data analyses that focus more on individuals. As an illustration, the data would permit simple counts of a variety of possibilities that focus on individuals. Suppose for instance, you were interested, post experiment, in whether any randomly selected pair, one from each group, would reveal a difference at least as big as the mean difference. You could compare all the possible pairs and determine the percentage of cases in which such a difference occurs. That would give you an estimate about what goes on at the individual-subject level, an estimate you could use to predict the likelihood of such differences for individuals. In the case of the current example, such a count reveals that 53% of the 400 individual comparisons would yield a difference of 10 or larger between the two individuals tested. So in this case, a large statistical effect permits effective prediction at the individual level about half the time. As a side note, adding 10 to each value in the 4th row and comparing it to our control group yields the same values for the t-test (because the means and standard deviations are the same as for the first test), but results in only 36% of the paired-individual comparisons showing a difference greater than the mean difference. Such a comparison reveals the potential importance of the distributions of values that could be missed if one were simply using only standard data analysis procedures grounded in statistical significance.

In any event, behavioral and biomedical researchers tend to be very clever people who surely could invent new methods of analyzing data, ways that promote a focus on individual changes and predictions about them. Examples of additional ways to direct the focus onto individuals and to emphasize replication can be found in Branch (2014), Loftus (1996), and Thompson (1993, 1994). I note with satisfaction that there is increasing interest in prediction for individuals in the medical sciences (e.g., Goodman, 1999; Kent & Hayward, 2007a, b; Morgan & Morgan, 2001; Penston, 2005; Williams, 2010).

There is also a “grass roots” approach to dealing with the problem of relying on statistical significance as a publication criterion. Of course, substantial influence can and should come from journal editors. Certainly, it would not be improper to implement a policy that indicates that mere statistical significance will not be considered as evidence of likely reliability. That is, evidence of other sorts, such as replications within the experimental design, or the careful utilization of standardized techniques that have already been shown to produce reproducible results, would be required. A good start is to employ techniques that bring data analyses closer to what individuals do (e.g., Thompson, 1993, 1994; Tukey, 1958). Reviewers, too, could assist by first gently pointing out that statistical significance provides no information about reliability (since many researchers apparently still believe that it does), and then offering suggestions about how data and characteristics of the research design and implementation can be presented in ways that focus on evidence of repeatability.

Conclusions

Behavioral and biomedical sciences have reached an important crossroads. Historically, scientific knowledge has held a believability advantage over everyday discourse. It did so because the scientific literature was doubly checked before it was made public. The two checks were peer review and replication. The first check was for logical consistency and verbal clarity, as well as assessment of the rigor of the measurements and designs. The second check, replication, was the acid test. The first check has been critically weakened by the advent of statistical significance testing. Reviewers have mistakenly given unwarranted emphasis to p-values, with less attention to indicators that the results will survive replication tests. That is due, in large measure, to a failure of adequate training in statistics, wherein the severe limits to what p-values actually mean have not been effectively communicated.

The replicability crisis has not gone unnoticed by the public, perhaps most damagingly by politically motivated persons, who increasingly ignore science in deciding courses of action. If science is to regain its just position, it has to correct the problem of unrepeatable research results. A first step would be to remove statistical significance as a criterion for publication.