Real-time optical properties and oxygenation imaging using custom parallel processing in the spatial frequency domain

Abstract

The development of real-time, wide-field and quantitative diffuse optical imaging methods is becoming increasingly popular for biological and medical applications. Recent developments introduced a novel approach for real-time multispectral acquisition in the spatial frequency domain using spatio-temporal modulation of light. Using this method, optical properties maps (absorption and reduced scattering) could be obtained for two wavelengths (665 nm and 860 nm). These maps, in turn, are used to deduce oxygen saturation levels in tissues. However, while the acquisition was performed in real-time, processing was performed post-acquisition and was not in real-time. In the present article, we present CPU and GPU processing implementations for this method with special emphasis on processing time. The obtained results show that the proposed custom direct method using a General Purpose Graphic Processing Unit (GPGPU) and C CUDA (Compute Unified Device Architecture) implementation enables 1.6 milliseconds processing time for a 1 Mega-pixel image with a maximum average error of 0.1% in extracting optical properties.

1. Introduction

The use of optical measurement methods has shown a strong potential for improving patient treatment planning, surgical guidance and post-operative monitoring [1–3]. Among the many methods developed, diffuse optical imaging methods have already demonstrated capabilities for the quantitative measurement of the functional and structural state of living tissues over a wide field of view [4–7]. One of these diffuse optical imaging methods termed Spatial Frequency Domain Imaging (SFDI) uses spatial modulation of light (i.e. patterns of light), and from a few images acquired (typically 6 images) allows the determination of wavelength-dependent optical properties of the entire surface of a turbid sample such as living tissue [8–10]. By repeating these acquisitions at several wavelengths, the method allows to measure functional parameters such as oxy-hemoglobin, deoxy-hemoglobin, water and lipids, as well as structural parameters of the tissue [11,12]. The need to acquire several images at multiple wavelengths has been for a long time a main limitation for the use of SFDI technology in time-sensitive environment such as surgery [13–15].

To overcome this limitation, we first introduced Single Snapshot of Optical Properties (SSOP), a specific SFDI method allowing to extract optical properties from a single acquired image in real-time at the cost of image degradation [16,17]. More recent work optimized SSOP acquisition and processing to improve imaging quality and significantly reduced the amount of artifacts from a single phase measurement [18]. However, while only a single image was necessary for extracting optical properties at a single wavelength, multispectral acquisition were performed by using a wheel filter, a tunable filter, or a multispectral camera with sequential acquisitions to distinguish each wavelength [19–21]. To overcome this limitation, temporal encoding of wavelengths combined with the spatial encoding for optical properties has allowed true real-time acquisition of multispectral sets of optical properties [22–24].

The next logical step in providing real-time tissue status assessment is to provide real-time processing capabilities. Many contributions have been made with the goal of accelerating processing methods for SFDI, especially by avoiding interpolation techniques used to extract optical properties from pre-computed lookup tables or by using machine or deep learning techniques [25–27]. While the state-of-the-art method allows to process large sets of data (572 x 672 pixels) in 18 milliseconds using linearized lookup tables in diffuse reflectance, this process is only applied to a single wavelength, and does not include temporal demodulation of wavelength information nor the extraction of functional parameters.

The objective of this study is to explore the possibilities offered by graphic processing unit (GPU) processing of SFDI data modulated in time (for wavelength encoding) and in space (for optical properties extraction) for fast quantitative multispectral diffuse optical imaging. More specifically, we propose GPU implementations to perform real-time processing of spatio-temporally modulated data sets, allowing the extraction of optical properties maps and functional parameters as fast as 1.6 milliseconds for a 1 megapixel data set. We take advantage of the parallel computation capabilities of general purpose GPU to improve processing time. In the first part, we briefly describe the method for spatio-temporal modulation of light for the extraction of optical properties at two wavelengths and computation of tissue oxygen saturation. In the second section, we describe the specific processing implementations, both in CPU using MATLAB, in GPU using MATLAB and in GPU using a custom developed CUDA (Compute Unified Device Architecture) algorithm. Finally, we test these implementations onto real SSOP data obtained from a human hand and compare their different processing times and accuracies.

2. Materials and methods

2.1 Principle of spatio-temporal modulation of light

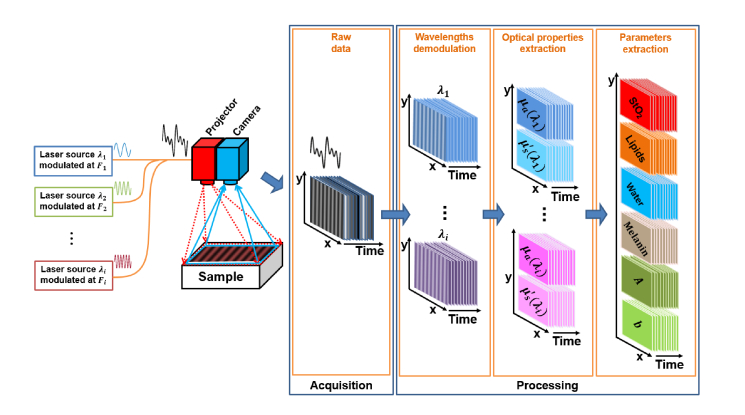
A detailed description and validation of the spatio-temporal modulation of light method used in this study is available here [24]. Briefly, to extract the optical properties of the tissue of interest, patterns of light are projected onto the tissue to obtain optical properties (as with any SFDI acquisition), but the light source is composed of discrete wavelengths that are encoded by modulating the sources in time (temporal modulation). To perform this acquisition, as shown in Fig. 1 , the typical system is composed of several modulated laser sources, a projection system and a high speed camera. From the acquired images, the spectral contribution of each modulated wavelength is extracted by means of discrete Fourier transforms carried out in time. The resulting images are then processed in the spatial frequency domain to quantify the optical properties of the measured tissue using SSOP. Finally, the optical properties measured at different wavelengths are used to determine the physiological and structural parameters of the sample of interest.

Fig. 1.

Schematics of the SSOP imaging system using spatio-temporal modulation of light associated with the processing workflow.

2.1.1 Wavelengths modulation and demodulation

The wavelengths multiplexing step consists of modulating in time i laser diode sources with different wavelengths λ_i in a sinusoidal manner at different frequencies F_i. As shown by the Eq. (1), the value of the chosen frequencies F_i (avoiding harmonics or power-line frequencies) are exact frequencies in the discrete Fourier domain (to avoid crosstalk) and depend on the camera framerate fps, the number of images used for the demodulation process N, and the frequency positions in the Fourier domain $\left(k\in \left[1,\frac{N}{2}+1\right[\right)$.

$$F_k=\frac{k\times \mathit{\text{fps}}}{N}$$ (1)

In the wavelengths demodulation step, the spectral contribution of each wavelength is isolated from the acquired stack of N images by processing in time the amplitude modulation X_k at frequency F_i for each pixel p_xy. This operation is performed continuously in time using discrete Fourier transforms (DFT) in a rolling window scan strategy [24,28]. At the end of the demodulation process, this scan strategy enables an output framerate equal to that of the acquisition stage framerate. X_k is given by:

$$X_k={\displaystyle \sum }_{n=1}^{N-1+1}{x}_n\text{cos}\left(-2\pi \frac{\left(\mathit{\text{n mod N}}\right)k}{N}\right)+j{\displaystyle \sum }_{n=1}^{N-1+1}{x}_n\text{sin}\left(-2\pi \frac{\left(\mathit{\text{n mod N}}\right)k}{N}\right)$$ (2)

where x_n is the amplitude of the pixel p_xy being processed in image n. From this equation, significant gain in processing time can be achieved by subtracting the contribution of the first image on the stack and adding the new image contribution instead of performing N multiplications. This leads to the following equations for cosine and sine components of X_k.

$$\begin{array}{l}\hfill {\displaystyle \sum _{n=1}^{N-1+1}{x}_n\text{cos}\left(-2\pi \frac{\left(n\text{mod}N\right)k}{N}\right)}={\displaystyle \sum _{n=0}^{N-1}{x}_n\text{cos}\left(-2\pi \frac{\left(n\text{mod}N\right)k}{N}\right)}\hfill \\ \hfill -x_0\text{cos}\left(-2\pi \frac{\left(0\text{mod}N\right)k}{N}\right)+x_N\text{cos}\left(-2\pi \frac{\left(N\text{mod}N\right)k}{N}\right)\hfill \end{array}$$ (3)

$$\begin{array}{l}\hfill {\displaystyle \sum _{n=1}^{N-1+1}{x}_n\text{sin}\left(-2\pi \frac{\left(n\text{mod}N\right)k}{N}\right)}={\displaystyle \sum _{n=0}^{N-1}{x}_n\text{sin}\left(-2\pi \frac{\left(n\text{mod}N\right)k}{N}\right)}\hfill \\ \hfill -x_0\text{sin}\left(-2\pi \frac{\left(0\text{mod}N\right)k}{N}\right)+x_N\text{sin}\left(-2\pi \frac{\left(N\text{mod}N\right)k}{N}\right)\hfill \end{array}$$ (4)

Finally, because each pixel p_xy is independent in time from its neighbors, the method is perfectly adapted for GPGPU computing for temporal de-multiplexing.

2.1.2 Optical properties extraction

SSOP is a particular implementaiton of SFDI that is used for fast extraction of optical properties [16,17]. From a single acquired frame per wavelength, by using forward and inverse 2D fast Fourier transform (FFT), filtering operations in the spatial Fourier domain are performed with custom-made filter masks DC (Low pass) and AC (High pass) [18], allowing to extract the amplitude modulation M_DC and M_AC at respectively the spatial frequency 0 mm⁻¹ and at the projected spatial frequency, e.g. f_x = 0.2 mm⁻¹. From these measurements, the diffuse reflectance images R_d,DC and R_d,AC are obtained respectively at the spatial frequency 0 mm⁻¹ and f_x > 0 by using a calibration measurement:

$$R_{d,\mathit{\text{AC}}}\left(p_{\mathit{\text{xy}}},f_x\right)=\frac{M_{\mathit{\text{AC}}}\left(p_{\mathit{\text{xy}}},f_x\right)}{M_{\mathit{\text{AC}},\mathit{\text{ref}}}\left(p_{\mathit{\text{xy}}},f_x\right)}\times R_{d,\mathit{\text{AC}},\mathit{\text{ref}}}\left(p_{\mathit{\text{xy}}},f_x\right)$$ (5)

$$R_{d,\mathit{\text{DC}}}\left(p_{\mathit{\text{xy}}},f_0\right)=\frac{M_{\mathit{\text{DC}}}\left(p_{\mathit{\text{xy}}},f_0\right)}{M_{\mathit{\text{DC}},\mathit{\text{ref}}}\left(p_{\mathit{\text{xy}}},f_0\right)}\times R_{d,\mathit{\text{DC}},\mathit{\text{ref}}}\left(p_{\mathit{\text{xy}}},f_0\right)$$ (6)

where M_DC,ref(p_xy,f₀) and M_AC,ref(p_xy,f_x) are measured on the calibration phantom, and R_d,DC,ref(p_xy,f₀) and R_d,AC,ref(p_xy,f_x) are modeled using the known optical properties of the phantom. The measured reflectance (for both frequencies 0 mm⁻¹ and f_x) allow the extraction of the absorption and reduced scattering coefficients (µ_a, µ_s’) by interpolation within a pre-computed high density lookup table (LUT) generated using White Monte Carlo simulations [25,29].

2.1.3 Physiological and structural parameters extraction

In order to determine the physiological parameters of the sample, it is necessary to decouple the contributions of the intrinsic biological chromophores. The optical absorption at a single wavelength ${\lambda }_i$ is given by:

$${\mu }_a\left({\lambda }_i\right)={\displaystyle \sum _{m=1}^M{\epsilon }_m}\left({\lambda }_i\right)c_m$$ (7)

Where µ_a(λ_i) is the measured optical absorption coefficient, ε_m(λ_i) the chromophore extinction coefficient at λ_i, c_m is the chromophore concentration, and M the number of chromophores [30].

Considering the Eq. (7), the measurements of the absorption coefficient at different wavelengths λ_i can be expressed as a system of i equations:

$$\{\begin{array}{c}{\mu }_a\left({\lambda }_1\right)={\displaystyle \sum _{m=1}^M{\epsilon }_m}\left({\lambda }_1\right)c_m\\ ⋮\\ ⋮\\ {\mu }_a\left({\lambda }_i\right)={\displaystyle \sum _{m=1}^M{\epsilon }_m}\left({\lambda }_i\right)c_m\end{array}$$ (8)

For example, solving a system of 4 equations (i.e. measurements at 4 wavelengths) leads to the determination of 4 chromophore concentrations such as oxy-hemoglobin (HbO₂), deoxy-hemoglobin (HHb), water, and lipid.

In our case, we used only 2 dedicated wavelengths (665 nm and 860 nm) allowing the extraction of blood oxygenation with high accuracy, assuming a 50% water-volume fraction and a 2% lipid-volume fraction [11]. Saturated oxygenation (StO₂) level can be computed using the following expression:

$${\mathit{\text{StO}}}_2\left(\%\right)=100\times \frac{{\mathit{\text{HbO}}}_2}{{\mathit{\text{HbO}}}_2+\mathit{\text{HHb}}}$$ (9)

Further optical parameters such as scattering amplitude A and scattering power b can also be determined by fitting the reduced scattering coefficient measurements over several wavelengths [30].

2.2 Imaging system

The imaging system was custom built using a digital micro-mirror device (DMD, Vialux, Germany) for the projection of custom patterns, fiber-coupled to two laser diodes at 665 nm and 860 nm (LDX Optronics, Maryville, TN). Intensity from the diodes are modulated over time at frequency 20 Hz (860 nm) and 30 Hz (665 nm) corresponding to k = 2 and k = 3, respectively, for a chosen number of images (N = 10) and a frame rate of 100 Hz. The projection system projects a sine wave pattern at 45 cm working distance. Images were acquired over a 130 x 130 mm² field of view and at a resolution of 1024 x 1024 pixels using a scientific CMOS camera (PCO Edge 5.5, Kelheim, Germany). The camera uses a high speed frame grabber (microEnable 5 marathon AF2, SiliconSoftware, Mannheim, Germany) and was synchronized with the modulation signal generators. Polarizers (PPL05C, Moxtek, Orem, UT), arranged in a crossed configuration, were used to minimize the contribution from specular reflections at the surface of the sample. A silicone-based optical phantom (210 mm × 210 mm × 20 mm) was used for calibration and built using titanium dioxide (TiO2) as a scattering agent and India ink as an absorbing agent [31] with (µ_s’ = 1.1 mm⁻¹ and µ_a = 0.01 mm⁻¹ at 665 nm), and (µ_s’ = 0.8 mm⁻¹ and µ_a = 0.02 mm⁻¹ at 860 nm). A workstation with the following characteristics was used for the processing: Intel i7-7800x 3.5GHz central processing unit, 16 GB of RAM, and an NVIDIA GeForce GTX 1080TI graphics processing unit (3584 Cores CUDA, 11 GB of RAM).

2.3 Processing

2.3.1 General processing workflow

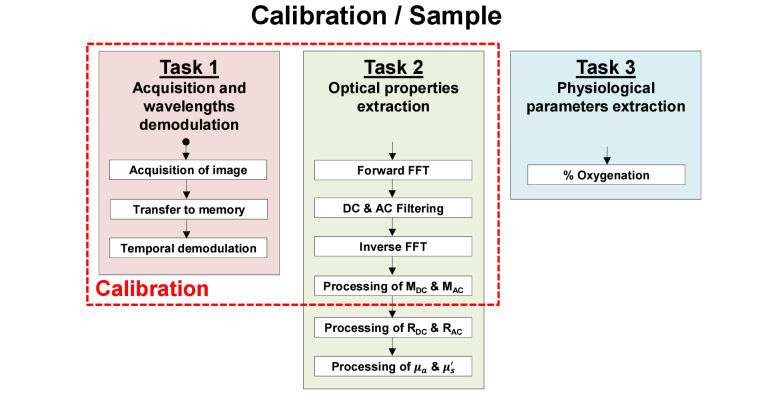
The processing diagram flow of the performed implementations is illustrated in Fig. 2 . The first task of the implementation executes the time demodulation algorithm by computing the amplitude modulation over time at each pixel with the DFT Eq. (3) and (4). For this purpose, the cosine and sine DFT coefficient at k = 2 and k = 3 are pre-computed and stored in memory. The acquired images are read in the acquisition order and stored in a ring buffer array of N + 1 images allowing to have access to the oldest image of the stack and to the new one.

Fig. 2.

General processing diagram flow

In the second task, from the demodulated wavelengths images, the M_DC and M_AC images are extracted using fast Fourier transform along with the DC and AC filter masks. M_DC is simply obtained by fast Fourier transform (FFT), filtering of the DC component and inverse FFT. M_AC is obtain by using a Hilbert transform with 4 processing steps: FFT, single-sideband high pass filter, element-wise product between the filter and the data, and inverse FFT. Filters used for demodulation have been described previously [18]. All the previous steps are done for both the calibration and the tissue measurement. Then, diffuse reflectance values R_d,DC and R_d,AC at wavelengths 665 nm and 860 nm are calculated with Eq. (5) and (6). Finally, the optical properties µ_a and µ_s’ are estimated with various processing methods. Two types of lookup tables (LUTs) were used to extract optical properties, one using linear optical properties LUT (standard method, used for reference) and the second using linear diffuse reflectance LUT, the fastest processing method described so far in the literature [25]. In order to study the compromise between computation time and accuracy, the latter LUT (linear diffuse reflectance) was further divided into a small-size low density table (with steps of 0.001 in R_d) and a large-size high density table (with steps of 0.0001 in R_d). Both LUTs have the same range.

In the third and last task, oxy-hemoglobin (HbO₂) and deoxy-hemoglobin (HHb) are extracted by solving a system of 2 equations (Eq. (8) from the measured absorption coefficients and extinction coefficients at 665 nm and 860 nm [30]). The saturated oxygenation level is then computed with Eq. (9).

2.3.2 Processing implementations

The general processing workflow described above was performed using different computation environments:

• -MATLAB CPU (Reference) processing was used with the linear optical properties LUT along with non-linear interpolation (griddata function in MATLAB) as a reference measurement since this is the most common implementation used today.
• -MATLAB CPU processing was also used with the linear diffuse reflectance LUTs along with either bilinear interpolation (interp2 function in MATLAB) on the low density LUT, or nearest value (by rounding [25]) on both low density and high density LUTs.
• -MATLAB GPU processing was used with the linear diffuse reflectance LUTs along with either bilinear interpolation (interp2 function in MATLAB) on the low density LUT, or nearest value (by rounding [25]) on both low density and high density LUTs. This particular implementation uses the MATLAB Parallel Computing Toolbox.
• -C CUDA GPU processing was used with the linear diffuse reflectance LUTs along with either bilinear interpolation on the low density LUT, or nearest value (by rounding [25]) on both low density and high density LUTs. This particular implementation uses our custom-made C CUDA GPU code.

Note that all processing uses single precision with the exception of MATLAB CPU reference since the griddata function only works with double precision. A detailed description of each processing implementation is described below.

MATLAB CPU processing

The first step is the computation of the temporal DFT using pre-computed DFT cosine and sine coefficients stored in MATLAB workspace. The extraction of M_DC and M_AC images in spatial frequency domain is then performed using the SSOP demodulation principle with the MATLAB functions fft2, ifft2 and abs. The optical properties µ_a and µ_s’ estimation for the MATLAB CPU reference implementation is performed with either griddata triangulation-based 2D interpolation MATLAB function or bilinear interpolation MATLAB function interp2 on the LUT. Note that the processing using the griddata function was carried out in double precision since this function was not designed to work in single precision. The other processing parts are custom-made code as described by their equations.

MATLAB GPU processing

The MATLAB GPU processing uses the same code as the MATLAB CPU implementation but is specifically processed on the GPU. In fact, the previously described MATLAB CPU implementation is fully compatible with the MATLAB Parallel Computing Toolbox and the MATLAB gpuArray function is used to copy all the input variables in MATLAB workspace to the GPU at the beginning of the process.

C CUDA GPU processing

Our custom processing code in C CUDA is made with Microsoft Visual Studio and NVIDIA CUDA toolkit environment with basic operations and the cuFFT library of NVIDIA.

First, it is necessary to reserve GPU memory spaces for processing and to configure the system: (1) a memory space is reserved for cosine and sine coefficients needed for the computation of the DFT, (2) a memory space is reserved for the pre-computed filtering masks DC and AC, (3) a ring buffer with a dimension of N + 1 images is setup for the camera output images, (4) a memory space is reserved for the resulting images, (5) a cufftHandle is created and uses cufftPlanMany to configure a complex to complex (C2C) 2D FFT processing plan, (6) constant memory is used for scalar coefficients, (7) texture memory is allocated to store the LUT, and finally (8) memory space is assigned to store intermediate results. After accomplishing memory allocation, the coefficients for the DFT and the filtering masks are then computed on the CPU and they are transferred to the GPU memory. Once the initialization is finished, the processing loop can begin.

In the first task, each time an image is acquired, it is stored in the ring buffer of size N + 1. The temporal demodulation kernel is then called to compute the DFT as explained above. This function directly returns an image for each demodulated wavelength. These results are stored as cufftComplex variable.

In the second task, the forward 2D FFT function cufftExecC2C is called with the created 2D plan, followed by the filtering kernel where FFT results are multiplied by the pre-computed filtering masks. Then the inverse 2D FFT is called with the same cufftExecC2C function. The M_DC and M_AC images are obtained by computing the complex magnitude of the previous results. Diffuse reflectance R_d,DC and R_d,AC are computed as explained above. Finally, the 3 different implementations to extract optical properties from linear diffuse reflectance LUT were performed with custom-made code. The bilinear interpolation on low density is computed using the following formula:

$$\begin{array}{ll}{\mu }_{R_{d,\mathit{\text{AC}},x}}^{R_{d,\mathit{\text{DC}},x}}=& \left(R_{d,\mathit{\text{DC}},1}-R_{d,\mathit{\text{DC}},x}\right)\left(R_{d,\mathit{\text{AC}},1}-R_{d,\mathit{\text{AC}},x}\right){\mu }_{R_{d,\mathit{\text{AC}},0}}^{R_{d,\mathit{\text{DC}},0}}\\ & +\left(R_{d,\mathit{\text{DC}},x}-R_{d,\mathit{\text{DC}},0}\right)\left(R_{d,\mathit{\text{AC}},1}-R_{d,\mathit{\text{AC}},x}\right){\mu }_{R_{d,\mathit{\text{AC}},0}}^{R_{d,\mathit{\text{DC}},1}}\\ & +\left(R_{d,\mathit{\text{DC}},1}-R_{d,\mathit{\text{DC}},x}\right)\left(R_{d,\mathit{\text{AC}},x}-R_{d,\mathit{\text{AC}},0}\right){\mu }_{R_{d,\mathit{\text{AC}},1}}^{R_{d,\mathit{\text{DC}},0}}\\ & +\left(R_{d,\mathit{\text{DC}},x}-R_{d,\mathit{\text{DC}},0}\right)\left(R_{d,\mathit{\text{AC}},x}-R_{d,\mathit{\text{AC}},0}\right){\mu }_{R_{d,\mathit{\text{AC}},1}}^{R_{d,\mathit{\text{DC}},1}}\end{array}$$ (10)

where R_d,DC,0 and R_d,DC,1 are the nearest neighbor value in the LUT of the measured R_d,DC,x, while R_d,AC,0 and R_d,AC,1 are the nearest neighbor value in the LUT of the measured R_d,AC,x, and µ represents either µ_a or µ_s’ extracted from the LUT. In the last task, a custom-made function is used to compute the saturated oxygenation level.

Processing times depend strongly on the GPU configuration. We create here one thread for each pixel that we group into blocks of 64 threads, giving 100% GPU occupancy, since for all the custom-made kernels the pixels p_xy are independent in time and in space.

2.4 Analysis

To evaluate the performance of the different implementations, we measured a hand as an in vivo complex sample positioned on a tissue-simulating phantom with a projected spatial frequency of 0.3 mm⁻¹ for 2 seconds with a rate of 100 Hz on the system described above [24]. Processing was performed on the acquired images in their native format (1024 x 1024) and as well as with a smaller image size (512 x 512) obtained using software 2 x 2 binning. The resulting images (absorption, scattering and oxygenation) were compared with the reference MATLAB CPU results. These comparisons were done by measuring the mean percentage error given by the following formula:

$$\mathit{\text{Error}}\left(\%\right)=\frac{1}{N\times M}{\displaystyle \sum _{n=0}^{N-1}{\displaystyle \sum _{m=0}^{M-1}\left|100\times \frac{{\mathit{\text{Result}}}_{n,m}^{\mathit{\text{TEST}}}-{\mathit{\text{Result}}}_{n,m}^{\mathit{\text{REFERENCE}}}}{{\mathit{\text{Result}}}_{n,m}^{\mathit{\text{REFERENCE}}}}\right|}}$$ (11)

where N = M are the image pixel size (1024 or 512) and Result represents either (µ_a, µ_s’ or StO2).

In MATLAB, a stopwatch timer is used to measure performance with the “tic” “toc” function. For the GPU processing, NVIDIA Nsight environment is used to trace the CUDA code timing performance. It is important to note that we report processing time only, and not transfer time. For GPU processing, the CPU – GPU transfer time is 338 µs for 1024 x 1024 images and 86 µs for 512 x 512 images.

3. Results

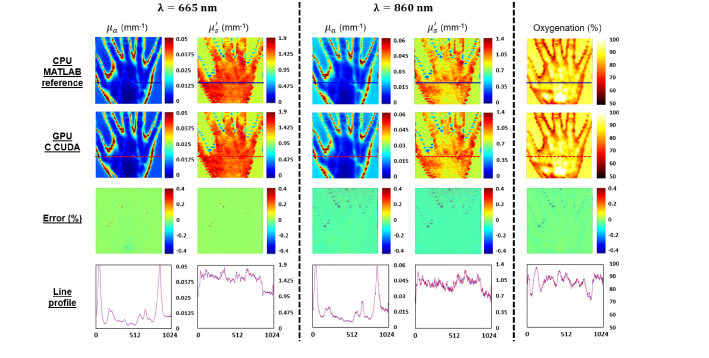
The main results obtained from the processing methods described above are the demodulated wavelength images, the absorption and reduced scattering coefficients recovered for each wavelength and the saturated oxygenation level. First, absorption, reduced scattering and oxygenation images obtained by the reference MATLAB CPU implementation and the C CUDA GPU implementation are reported in Fig. 3 . In addition, the mean percentage error images and cross-section lines profiles are shown. One can notice good agreement between the C CUDA GPU results and the MATLAB CPU reference results, with maximum mean percent errors less than 0.1%.

Fig. 3.

Results obtained with the MATLAB CPU reference code and with GPU C CUDA code. Absorption and reduced scattering map recovered at 665 nm (left columns) and 860 nm (center columns) and saturated oxygenation level (right column) obtained with reference MATLAB CPU processing (first row) and the custom-made GPU C CUDA processing (second row). Percentage errors compared with the reference processing (as described in Eq. (11) are also shown in the third row. Finally cross section line profiles are shown in the fourth row, in solid blue for the reference MATLAB CPU processing and in dash red for the C CUDA GPU processing.

Table 1 presents a detailed description of the percent error score of the extracted maps compared to the reference MATLAB CPU processing. Only the precision results obtained with 1024 x 1024 images are presented in the table as they are substantially equal to those obtained with 512 x 512 images. In summary, compared to the reference implementation (linear optical properties LUT), all implementations with linear diffuse reflectance LUTs have a precision error of less than 1%. Best results are obtained with 2D interpolation on the low density LUT with a precision error less than 0.1%, followed by the implementations using direct reading on the high density LUT with a precision error less than 0.2% and finally, those using direct reading on the low density LUT with a precision error less than 1%. In addition, we note globally a trend towards a positive percentage error with optical properties at 665 nm and a negative percentage error at 860 nm. However, the low level of the errors does not make this observation interpretable.

Table 1. Mean percentage error in absorption and reduced scattering at 665 nm and 860 nm compared to the reference MATLAB CPU implementation.

Image 1024$\mathbf{\times }$1024	Percentage of error (in %)
	LUT linear op	LUT linear rd
	MATLAB CPU (Reference)	MATLAB CPU			MATLAB GPU			C CUDA GPU
	Nonlinear interpolation (griddata *)	Linear interpolation (interp2)	Low density rounding	High density rounding	Linear interpolation (interp2)	Low density rounding	High density rounding	Linear interpolation (interp2)	Low density rounding	High density rounding
Absorption at $\mathbf{\lambda }$ = 665 nm	-	0.01 %	0.38 %	0.04 %	0.01 %	0.38 %	0.04 %	0.02 %	0.38 %	0.04 %
Absorption at $\mathbf{\lambda }$ = 860 nm	-	0.02 %	0.65 %	0.08 %	0.02 %	0.65 %	0.08 %	0.08 %	0.67 %	0.12 %
Reduced scattering at $\mathbf{\lambda }$ = 665 nm	-	0.00 %	0.49 %	0.05 %	0.00 %	0.49 %	0.05 %	0.02 %	0.48 %	0.04 %
Reduced scattering at $\mathbf{\lambda }$ = 860 nm	-	0.02 %	0.88 %	0.11 %	0.02 %	0.88 %	0.11 %	0.08 %	0.93 %	0.16 %

^*Double precision only

The analysis of processing times for the different implementations is summarized in Table 2 for an image size of 512 x 512 pixels and Table 3 for an image size of 1024 x 1024 pixels. In summary, on our workstation, with the reference implementation (linear optical properties LUT) and for an images size of 512 x 512, we can extract the absorption coefficient, the reduced scattering coefficient and determine the saturated oxygenation level in 9 seconds. It takes only a maximum of one hundred milliseconds for the CPU process when the linear diffuse reflectance LUT is used. This processing time can be divided by 5 and reach 20 milliseconds when the GPU computing power is used by MATLAB Parallel Computing Toolbox. The programming of the GPU in C CUDA that has been achieved in this work has allowed us to go even further and get these measurements in just 400 microseconds, 50 times faster than the MATLAB GPU process, 200 times faster than the MATLAB CPU process and 20,000 times faster than the standard method.

Table 2. Processing time (in milliseconds) from wavelength demodulation to saturated oxygenation level measurement for $512\times 512$ images.

Image 512$\mathbf{\times }$512	Processing time (in ms)
	LUT linear op	LUT linear rd
	MATLAB CPU (Reference)	MATLAB CPU			MATLAB GPU			C CUDA GPU
	Nonlinear interpolation (griddata *)	Linear interpolation (interp2)	Low density rounding	High density rounding	Linear interpolation (interp2)	Low density rounding	High density rounding	Linear interpolation (interp2)	Low density rounding	High density rounding
Temporal demodulation	23.76	13.27			1.94			0.05
Get MDC & MAC	72.29	40.18			15.53			0.28
Get RDC & RAC	13.53	7.63			0.45			0.04
Get ${\mathit{\mu }}_{\mathit{a}}$ & ${\mathit{\mu }}_{\mathit{s}}^{\mathit{\prime }}$	8890.20	41.91	18.23	25.72	2.51	3.45	4.11	0.05	0.03	0.39
Oxygenation	0.91	0.91			0.12			0.02
TOTAL	9000.69	103.90	80.22	87.71	20.55	21.49	22.15	0.44	0.42	0.78

^*Double precision only

Table 3. Processing time (in milliseconds) from wavelength demodulation to saturated oxygenation level measurement for $1024\times 1024$ images.

Image 1024$\mathbf{\times }$1024	Processing time (in ms)
	LUT linear op	LUT linear rd
	MATLAB CPU (Reference)	MATLAB CPU			MATLAB GPU			C CUDA GPU
	Nonlinear interpolation (griddata *)	Linear interpolation (interp2)	Low density rounding	High density rounding	Linear interpolation (interp2)	Low density rounding	High density rounding	Linear interpolation (interp2)	Low density rounding	High density rounding
Temporal demodulation	101.56	50.63			2.80			0.21
Get MDC & MAC	317.26	175.33			28.54			1.01
Get RDC & RAC	51.42	26.84			0.45			0.14
Get ${\mathit{\mu }}_{\mathit{a}}$ & ${\mathit{\mu }}_{\mathit{s}}^{\mathit{\prime }}$	14141.03	87.18	71.98	94.35	3.29	5.45	6.49	0.17	0.11	1.65
Oxygenation	6.52	4.47			0.12			0.07
TOTAL	14617.79	344.45	329.25	351.62	35.20	37.36	38.40	1.60	1.54	3.08

^*Double precision only

For 1024 x 1024 images, the processing was at best performed in only 1.6 milliseconds, 20 times faster than with the MATLAB GPU process, 200 times faster than with the MATLAB CPU process and 9,000 times faster than with the standard method. It can also be noted that for C CUDA implementations the processing time is almost linearly dependent of the image size. It should be noted that parallelized implementations on CPU are possible and would perform better than the MATLAB CPU code. In this manuscript, we chose to focus our work on GPU implementations.

Overall, with a C CUDA implementation using 2D interpolation on low density linear diffuse reflectance LUT the measurements can be obtained in 440 microseconds and 1.6 milliseconds respectively for images of sizes 512 x 512 and 1024 x 1024 with error rates below 0.1%. It should be noted that acquisition time is the same for all processing methods, consisting of N = 10 frames acquired at 100 frames per second, hence an equivalent acquisition time of 100 milliseconds. Since we use a rolling window processing method for temporal demodulation, following the first 10 frames, results are calculated every frame, i.e. every 10 milliseconds. Therefore fast processing is required to reach real-time capabilities (here processing time faster than 10 milliseconds, preferably 5 milliseconds).

4. Discussion

This work provides solutions to speed up processing times in SFDI. Particularly, it demonstrates that in the case of a multi-spectral acquisition (2 wavelengths in our case) using spatio-temporal modulation of light with a GPU, linearized diffuse reflectance LUT and single precision processing, we can extract optical properties and tissue oxygenation for a 1 Megapixel image in only 1.6 milliseconds. While the definition of real-time depends on the target application, the number of physiological parameters that will need to be processed will increase in the future. Our goal is to provide interpretable information to healthcare practitioners at a rate of at least 25 frames per second. Given that up to 6 physiological parameters could be extracted (oxy-hemoglobin, deoxy-hemoglobin, water, lipids, melanin, and yellow pigments [30]) both processing and acquisition time will need to be improved to allow to capture and process the necessary information.

However, this work is not without limitations. It would be expected that the processing time would increase linearly with the image size when using GPU processing. While this linearity is observed when using the C CUDA implementation, it is not the case when using the MATLAB Parallel Computing Toolbox. We believe this can be attributed to the difference in accuracy of the measurement tools between MATLAB and NVIDIA CUDA toolkit, especially when it comes to measuring very short processing times. It should also be noted that the MATLAB CPU/GPU implementation of the direct reading of the linear diffuse reflectance LUT we have written is more suitable for CPU processing, and quite different from the one we wrote in C CUDA. Overall, with the processing times obtained for C CUDA implementation and the observed linear evolution, it can be predicted that it would be possible to process the optical properties of 6 wavelengths in less than 4.8 milliseconds and to derive 6 physiological parameters, with the acquisition time depending on the camera frame rate and the number of wavelengths used. However, scaling up to a larger number of wavelengths remains a significant challenge with the limited dynamic range of camera systems at high frame rates and with the need to balance the contributions of each wavelengths within the available dynamic range.

In this work we have demonstrated that a low density linear diffuse reflectance LUT (steps of 0.001) enables very good measurement accuracy by using simple bilinear interpolations. Yet, this density was chosen for the ease of handling. It should be expected that depending on the margin of error that can be tolerated, a lower density linear LUT could be used, and lead to shorter processing times. It can also be noticed that the accuracy of the measurements obtained for wavelength 665 nm is better than that obtained for the wavelength 860 nm. This difference is essentially related to a lower signal-to-noise ratio of the images obtained at 860 nm due to the lower quantum efficiency of the camera in this spectral range. Despite these limitations, we have shown by the obtained precision errors that single precision SSOP processing on linear LUT does not result from any significant loss in measurement accuracy.

Finally, for quantitative optical imaging of in vivo samples, it is necessary to take into account the sample profile since errors can reach values as high as 10% per cm. It is therefore necessary to integrate the sample profile for height correction into future implementations to have a robust, real-time measurement for clinical guidance [32].

5. Conclusion

In summary, we have presented a comparison between CPU and GPU processing of data modulated in space and time in the frequency domain. We demonstrated that we are able to extract optical properties maps of absorption and reduced scattering for two wavelengths 665 nm and 860 nm, as well as saturated oxygenation level onto a 1 megapixel image in as low as 1.6 milliseconds processing time with GPU implementation directly written in C CUDA. This work shows the strong potential of such GPU implementation to enable multi-spectral, quantitative and wide-field visualization in real-time during surgical procedures.

Funding

European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (715737); France Life Imaging WP3;. the French program “Investissement d’Avenir” run by the “Agence Nationale de la Recherche” (ANR-11-INBS-006); the University of Strasbourg IdEx.

Disclosures

The authors declare that there are no conflicts of interest related to this article.