Skip to main content
PMC home page
Biomedical Optics Express logoLink to Biomedical Optics Express
. 2019 Jul 3;10(8):3789–3799. doi: 10.1364/BOE.10.003789

Dual-band refractometric terahertz biosensing with intense wave-matter-overlap microfluidic channel

Feng Lan 1,2,*, Feng Luo 1, Pinaki Mazumder 2, Ziqiang Yang 1, Lin Meng 1, Zhengqiang Bao 3, Jun Zhou 1, Yaxin Zhang 1, Shixiong Liang 4, Zongjun Shi 1, Abdur Rauf Khan 1, Ziqi Zhang 1, Luyang Wang 1, Jing Yin 1, Hongxin Zeng 1
PMCID: PMC6701553  PMID: 31452975

Abstract

We theoretically and experimentally demonstrate a label-free terahertz biosensor with ultrahigh sensitivity and distinctive discretion. By constructing a metal-air-metal (MAM) metamaterial perfect absorber (MPA) with a metallic paired-ring resonator array, a hollow microfluidic channel, and a backed reflector, a novel dual-band absorptive sensing platform is proposed in the THz range. The near field coupling by dipole-induced trapped modes and the magnetic momentum caused a vertical to transverse power flux that dramatically enhanced the electromagnetic field on top of the metasurface and in the microfluidic channel, respectively. Both the resonant modes exhibit perfect absorption and produce ultrahigh normalized sensitivities of 0.47/RIU (refractive index unit, RIU) and 0.51/RIU at 0.76 THz and 1.28 THz, respectively. Compared with conventional microfluidic sensors, the salient advantages of our design are the perfect spatial overlap for light-matter interaction and polarization insensitivity. Characterized by THz time domain spectroscopic absorption quantification measurements with different concentrations of bovine serum albumin (BSA), the proposed sensor exhibits promising applications in microfluidic biosensing.

1. Introduction

Attributed to its large molecular fingerprint recognition, low photon energy and high penetration characteristics, terahertz spectroscopy has emerged as a promising technique for studying chemical and bio-molecules [1,2]. Conventional biological detection methods, such as polymerase chain reaction (PCR), fluorescence microscopy (EFM) and flow cytometry (FC) are characterized by label needed, long process, high cost, complex procedures and limited sensitivity. With the development of terahertz time domain spectroscopy (THz-TDS) and portable terahertz spectroscopic tool, THz sensing technology has shown great potential in highly sensitive and on-site detection/identification of minute amounts of biomolecule (proteins, RNA and DNA) [3,4], protein synthesis (membrane, enzymes) [5,6], and cell division (bacterial,tumor) [7,8]. Due to the dimension mismatch between biological molecules/cells (nm~um) and THz wave length (30 um~3 mm), resulting low scattering cross-section and weak absorption, enhanced THz resonance at sub-wavelength scale needs to be utilized to achieve strong light harvesting. Compared with the traditional bio-sensors, metamaterials (MMS) based sensors exhibit stronger light-matter harvesting and miniaturized footprints, deemed as a prominent candidate for label free, on-chip scale, and ultrasensitive sensing [9–11]. Up to date, massive terahertz metamaterial biosensors have shown promising performances in detection of biomolecule attachment in strong interaction structure [12–16]. However, the sensitivity and signal to noise ratio (SNR) are still limited by the less confined EM field and smaller overlap of the sensing area. Moreover, owing to strong water absorption at THz frequencies, most of these studies have been limited to dry or partially hydrated specimens.

Ultrahigh Q factor value favors to higher sensitivity due to its sharp resonance, reflecting significant frequency shift according to the minute change of analyte permittivity. High Q valued resonance modes can be obtained by introducing the trapped modes or higher order modes, which requires the metamaterial to support the sub-radiation modes, such as Fano, Quadrupole and electromagnetically induced transparency (EIT) resonances [17–19]. Since most of the terahertz biosensors are based on transmission spectrum detection, the sensitivity can be greatly reduced in the case of lossy microfluidic analyte interacts with THz wave weakly through the one-way transmission. Compared with the transmission structure, the reflective structure can provide twice interactions between the terahertz wave and the microfluidic analyte during incidence and reflection process, which is more favorable for the spatial overlap interaction. As well known, the metamaterial perfect absorber (MPA) indicates the incident wave fully trapped in the spacer between the two metal layers by matching the radiative damping rate with resistive damping rate of the metal-insulator-metal (MIM) resonant mode. In recent years, a large overlap with greatly confined cavity resonance of the MPA, resulting ultra high sensitivity detection, has aroused widespread concerns in the research field of terahertz sensing [20]. In 2010, N. Liu reported a near infrared plasmonic sensor based on narrowband perfect absorber, the detection sensitivity was 420nm/RIU [21]. In 2015, L.Cong compared the sensitivity of terahertz MMs absorber and metasurface with the same resonator, the results show that the figure of merit (FOM) was increased by an order of magnitude because the Fabry-Perot cavity significantly enhanced the EM field concentration in the absorber [22]. In 2016, X. Hu presented a terahertz MPA integrated microfluidic sensor, a high sensitivity of 3.5 THz/RIU is predicted by the greatly enhanced light-matter interaction [20]. However, performance enhancement including in trade-off between high Q and high SNR, polarization insensitivity, and multi-resonant probing, etc., is still needed for the microfluidic sensing.

In this paper, a MPA based ultrasensitive microfluidic sensor has been demonstrated through numerically and experimentally in terahertz region. Two trapped-mode induced sharp transverse resonances were engineered for ultrahigh sensitivity by combining the fundamental ring-shaped dipole mode and the meta-mirror magnetic coupling mode. These two near unity absorption peaks occur at 0.76 THz and 1.28 THz, which give birth to the intensely confined EM field in the micofluidic channel and henceforth the distinctive SNR along with minute dielectric variation. In addition, a flexible and low-permitivity polyimide (PI) film with marginal metallization serves as a cap of the microfluidic channel, which significantly enhances the sensing response by minute perturbation in the microfluidic channel. The absorptive sensing mechanism is elucidated by the effective impedance theory and resonant field/power flux in the channel. We overcome the limitation of water absorption by confining the analyte-aqueous solution in a micron-volumetric fluidic chamber, integrated on a highly concentrated resonant cavity of metamaterial. The trapped mode resonators confine electromagnetic fields in extremely subwavelength space and hence allow for the enhanced interaction overlap between the BSA solution and terahertz waves, while minimizing the water absorption loss. Maximum frequency shift over 400 GHz around 1.2 THz under different solutions of BSA injection has been observed accordantly both in simulation and measurement. The proposed THz sensor with both high sensitivity and high SNR has great potential for chemical and biochemical detection.

2. Design and mechanism

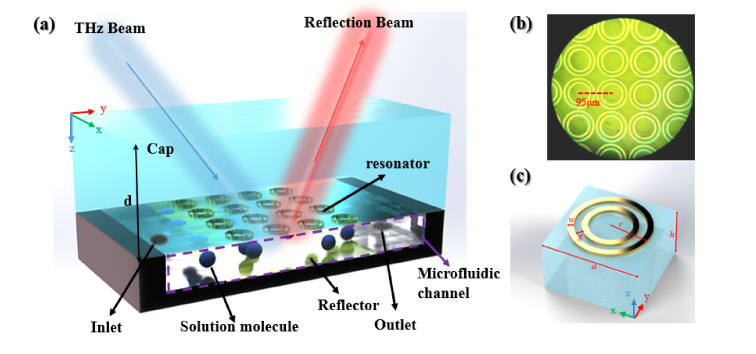
Figure 1(a) depicts the schematically perspective view of the reflective terahertz sensor based on a tri-layer MPA concept. A microfluidic channel was sandwiched between an inversely displaced polyimide cap with paired-ring meta-atoms and a metallic reflector backed with a Si holder. The microifluidic channel serves as an absorptive refractometric chamber, wherein the hydrated analyte will be circulated in an inlet-outlet loop. Figure 1(b) shows a partial microscopic image of the resonant concentric paired-ring array, followed by which is the accordant unit cell shown in Fig. 1(c). Benefited from the horizontally stacked symmetrical ring structure, incident polarization insensitivity and a dual-mode resonances have been adopted to simplify measurement setup and expand the sensing characteristic match. As labeled in Fig. 1, the geometrical model parameters in μm are: a = 95 μm, r = 46 μm, g = 8 μm, w = 6 μm, d = 50 μm, and h = 5 μm. Using Floquet model, a unit cell with periodic boundary was equivalently simulated for the whole array, including lossy 200 nm thickness aluminum with σ =3.72×107 S/m for metallic part, 50 μm thickness PI with complex permittivity ε=3.5+0.05i for the cap, and 500 μm thickness high-resistivity n-type silicon for the substrate.

Fig. 1.

Fig. 1

Open in a new tab

(a) Schematic diagram of the microfluidic sensor, (b) microscopic image of the meta-atoms, (c) resonant unit.

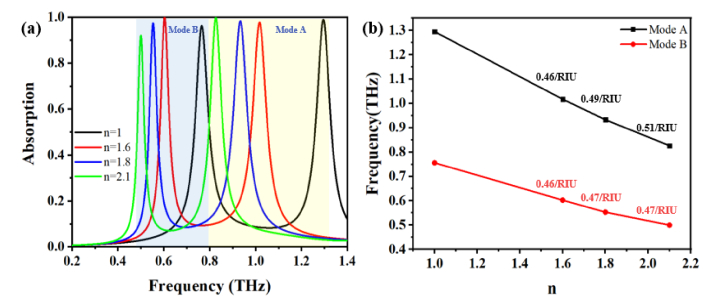
Since the absorption peaks shift accordingly with the minute change of the dielectric variations of the analyte, absorptive characterization of the sensor was calculated by A(ω) = 1- |S11(ω)|2 firstly. In which, A(ω) is the absorption coefficient, |S11(ω)|2 represents the reflection coefficient at frequency ω, and the transmission coefficient |S21(ω)|2 has been ignored as the 200 nm thickness of the bottom reflector was set far beyond the skin depth for the entire sensing spectrum from 0.2 THz to 1.4 THz. Figure 2(a) shows the calculated absorption spectra with refractive indices n of analytes varying from 1.0 to 2.1, peaking at 1.28 THz for mode A and 0.76 THz for mode B under n = 1 for vacant channel. Near unity absorption coefficients of both higher order mode A and lower order mode B under n = 1, 1.6, 1.8 and 2.1 indicate excellent SNR and distinctive resonant redshifts. Attributed to variation in the nearfield plasmon coupling in between the Al meta-atoms and the continuous Al film, the perfect absorbance in the microfluidic channel accommodates an effective energy trap for THz waves. Further discussion on the perfect absorption effect based on the effective impedance matching theory is in the latter session. Understanding of the sensing mechanism from the view of RLC resonance by T. Driscoll [23], capacitance enhancement due to the permittivity increment near the confined EM field leads to the resonant redshift, and vice versa. Typically, the sensitivity is defined by S = Δf/Δn, wherein Δf denotes the relevant resonant frequency shift and the refractive index variations in the channel, respectively. In order to get quantification of sensing capability, a normalized sensitivity can be defined as SN = Δf/fr × Δn (/RIU), where fr is the referenced resonant frequency. By linearly fitting the simulated resonance peaks for mode A and mode B under index variations, as shown in Fig. 2(b), the highest normalized sensitivities of 0.51/RIU for mode A and 0.47/RIU for mode B are marked on black curve and red curve, respectively. Different compositions of hybrid solution can exhibit disparate frequency shifts and absorption loss. By investigating the influence of different pure liquids and liquid mixtures on the resonance frequency, the relation between the resonance frequency and the refractive index of the different hybrid liquids can be set as signature parameters for sensing.

Fig. 2.

Fig. 2

Open in a new tab

(a) Absorption spectra of the MPA sensor with refractive indices for different analytes varying from 1.0 to 2.1, (b) resonance peaks of two modes under refractive index variations marked with highest sensitivities apart.

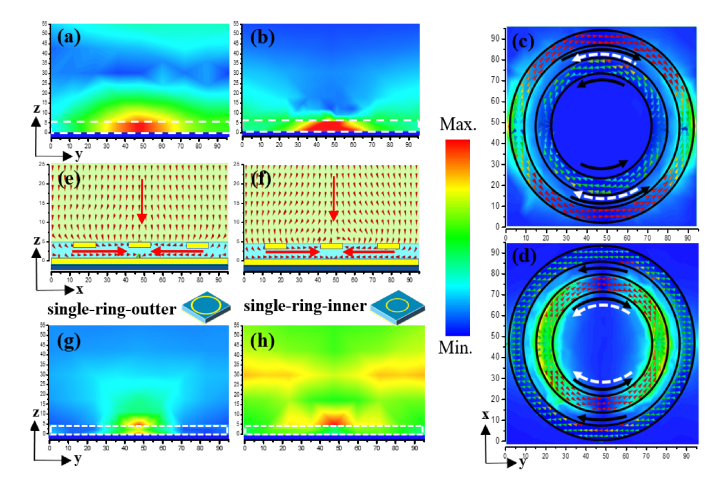
Due to the weak interaction between analytes with either the localized near field or decayed resonant mode outside the cavity, most of the THz sensors scarcely have perfect overlap for the strongest field interaction. In the proposed MPA sensor, the microfluidic channel is fully overlapped with the resonant field, thus leading to strong electromagnetic interaction with analyte. To specifically explore the absorptive sensing mechanism, investigated by normal illumination with y-polarized electric component, the resonant EM fields and surface current distributions for mode A and B are illustrated in Fig. 3(a)-(d). In Fig. 3(a) and (b), the white dash line delineates the flank profile of the microfluidic channel, noticeably, almost all the EM field energy is confined in the cavity, thus enables largest duty cycle of the interaction zone for higher sensitivity. Although the single-ring absorbance is still as high as the paired-ring, the absorption occurs mostly in the cap other than the channel, contributing barely to the sensing overlap, which can be observed from Fig. 3(g) and (h). However, as shown in Fig. 3(c) and (d), attributed to local coupling between inner and outer rings, the anti-phase dipolar currents on inner and outer rings weaken the dominant radiative single-ring dipolar mode and transfer it into sub-radiative trapped mode. Besides, the current loops forming by the on-top dipolar currents and the on-bottom image currents excite the H field along x direction. Concomitantly, the strong electrically resonant components occur in the vertical direction by relocation of the positive and negative electrons at the two ends of each dipole. As a result of the nearfield coupling, the calculated power flux in the chamber is clearly along the y direction as shown in Fig. 3(e) and (f), indicating a field transition from vertical Fabry-Perot resonance to transverse magnetic resonance. In general, the radiative damping rate of the resonant mode can be significantly reduced by the transverse resonance, which is controlled by engineering the deep-subwavelength height of the microfluidic channel, leading to near 100% absorption.

Fig. 3.

Fig. 3

Open in a new tab

(a) and (b) lateral view of the resonant magnetic field distributions for the paired-ring resonator, mode B and mode A from left to right, the white dash line identifies the microfluidic chamber; (c) and (d) resonant electric field and surface current distributions on the paired-ring resonator for mode B and mode A, black solid arrows and the white dash arrows indicate the on-top and on-bottom surface currents’ directions in the microfluidic channel, respectively; (e) and (f) lateral view of the vertical to transverse power flux for mode B and mode A, respectively; (g) and (h) magnetic field distributions in the channel for the single-ring resonator of outer (left) and inner (right) rings, respectively.

.

3. Discussion

Based on the effective medium theory, the relative impedance Z(w) and the absorption coefficient of the sensor read as follow [24], wherein the transmission coefficient is also ignored for the aforementioned reason:

Z(w)=(1+S11(w))2−S212(1−S11(w))2−S212=1+S11(w)1−S11(w) (1)
A(w)=1−|S11(w)|2=1−Z−1Z+1=2[Re(Z)+1][Re(Z)+1]2+Im(Z)2−i2Im(Z)2[Re(Z)+1]2+Im(Z)2 (2)

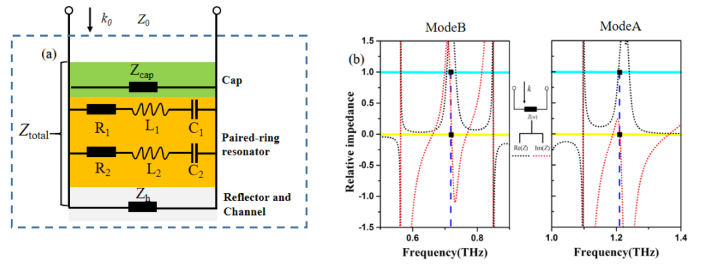
For merely suppressing the reflection to obtain the perfect absorption, the relative impedance of the sensor should match the impedance to the free space one (Z0 = 377 Ω is normalized as 1), in another word, the real part and the imaginary part of the relative impedance in (2) should approach to Re(Z) = 1 and Im(Z) = 0. As shown in Fig. 4 (a), the sensor can be equivalently modeled as a parallel circuit, consisting of a transmission line impedance as the cap, the parallel-connected two series L-C resonators as the resonant meta-array, and a short circuited impedance as a combination of the channel and reflector. Accordingly, the real part and imaginary part of the relative impedance Z are shown in Fig. 4 (b), with Re(Z) = 1 and Im(Z) = 0 closely at the two resonant frequencies, indicating the perfect impedance match for the MPA sensing.

Fig. 4.

Fig. 4

Open in a new tab

(a) Equivalent circuit of the proposed sensor, (b) calculated real and imaginary parts of the relative impedance.

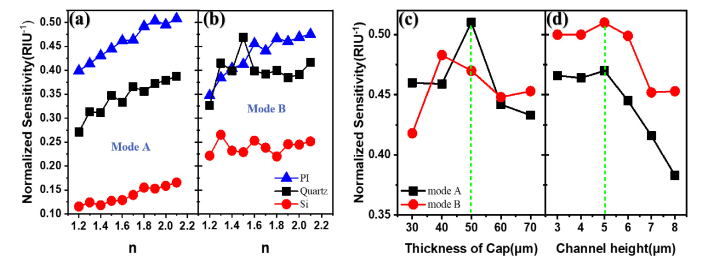
Furthermore, the normalized sensitivities of both modes under different cap materials and thicknesses of both cap and channel are shown in Fig. 5(a)-(d) for comparison. In the view of Hara [25], the total capacitance of the proposed sensor is generally a summation of C1 and C2, which represent the capacitance values in between the cap and the metallic structure and the structural one with injected analyte, respectively. Once the resonant structure of the sensor was fixed, a trade-off optimization counted on both sensitivity and SNR can be implemented on the cap material choice and its thickness and also on the channel thickness, contributing separately to C1 and C2, which dramatically impact on the LC resonance and impedance matching. Observed from Fig. 5(a) and (b), for both mode A and mode B, along with the variation of the analyte indices, the average values of the normalized sensitivity for PI (ε = 3.5 + 0.05i), quartz (ε = 4.41 + 0.004i), and Si (ε = 11.9 + 0.15i) are 0.475, 0.36, and 0.14 RIU−1 for mode A and 0.46, 0.41, and 0.26 RIU−1 for mode B, respectively. While choosing PI as the cap material, next, calculation results for the thicknesses of both cap and channel are shown in Fig. 5(c) and (d). Obviously, the largest average sensitivities occur at thicknesses of 50 um for the cap and 5 um for the channel. Disparate from the traditional sensor, the sensitivity of our sensor is much higher under deep subwavelength channel height or namely the analyte volume other than under the larger one, especially favorable for introducing the transverse resonance for perfect absorption as shown in the Fig. 3 (e) and (f).

Fig. 5.

Fig. 5

Open in a new tab

The normalized sensitivities with: (a), (b) different caps; (c) different thicknesses of cap, (d) channel heights.

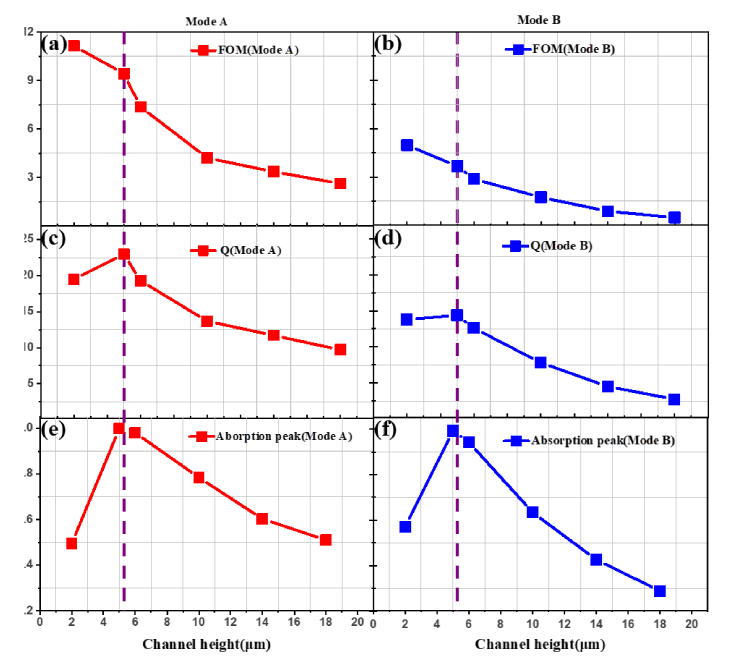
In addition, to further obtain a quantitative description for the sensing performance, we estimated the figure of merit (FOM) of our sensor corresponding to the channel height, which is widely used for evaluate the sensing capability. Here we defined FOM = S/FWHM, where S is the sensitivity and FWHM denotes the full width at half maximum of absorption, respectively. In Fig. 6(a)-(d), there is a similar trend that the values of the Q factor and FOM for both modes decrease gradually with the increment of the channel height. Moreover, the values of the Q factor and FOM of mode A are significantly larger than that of mode B, which are 23 and 9.4 for mode A, 14.4 and 3.7 for mode B at 5 μm of the channel height. Remarkably, the absorption peak reaches the maximum at 5 μm height vacuum channel as shown in Fig. 6(e) and (f), due to the solid evidence that the perfect absorption and maximized overlap happened simultaneously at this point. In general, the optimized FOM value with near perfect absorption exhibit a cogent proof for our sensor to stand out as an ideal sensing platform.

Fig. 6.

Fig. 6

Open in a new tab

(a) and (b) The figure of merit of the sensor, (c) and (d) the quality factor, (e) and (f) the absorption peaks with different channel heights at both modes.

4. Experiments

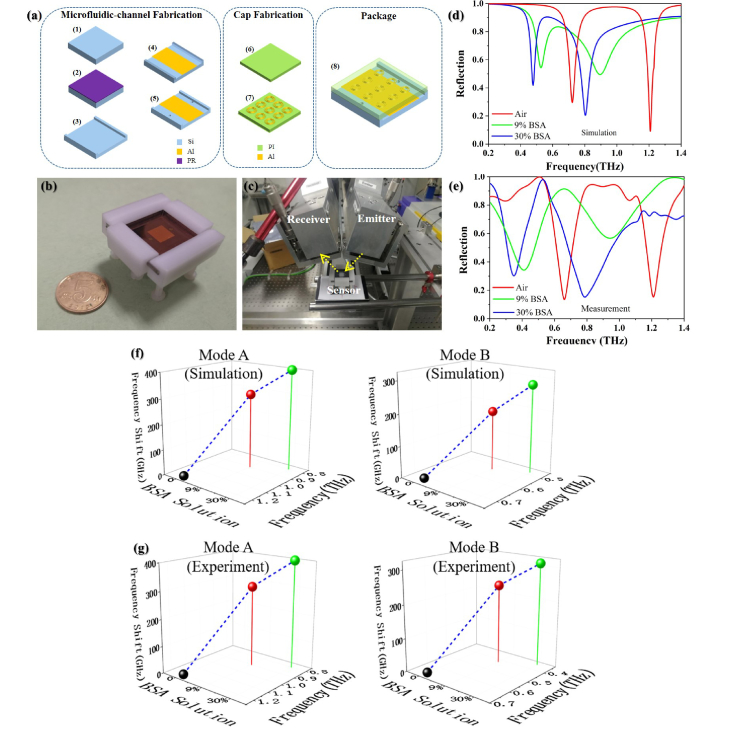
The microfluidic sensor has been streamlined by advanced micro-machining techniques, including coating and spray, photolithography, evaporation, etching, liftoff, laser drilling, bonding and other process steps. As the substrate is used as a holder and ground plane, its EM property is irrelevant to sensing performance. Si wafer becomes a candidate for easy fabrication of the microfluidic channel structure. For considerations of both low dissipation loss and transparency, we choose Polyimide (PI) as the cap material. The reactive ion etching on Si substrate can be precisely controlled to ensure the accuracy of the microfluidic channel height and sidewall verticality. For avoiding interference, the inlet and outlet are placed in Si substrate rather than the cap. Generally, the prototype processing was divided into three steps: the first one is the microfluidic channel fabrication, the second one is the cap fabrication and the third one is the assembly work for combining the cover and holder. The specific process flow is shown in the Fig. 7(a): (1)-(3) PR coating, photolithography and ICP etching processes to form the microfluidic channel, respectively; (4) electron beam evaporation and liftoff to fabricate the reflector area; (5) laser drilling for perforation of the inlet and outlet both with 1 mm diameter; (6) hardening process on PI film; (7) cap patterning by standard photolithography on PI film; (8) Si substrate and PI cap can be aligned and packaged together by a polyformaldehyde (POM) fixture. The sensor assembly is shown in Fig. 7(b), the size of the microfluidic channel is 14 mm*14 mm*5 μm. As our testing THz wave ranges from 0.2 THz to 1.4 THz (wavelength from 214 μm to 1500 μm), the diffraction limit of the smallest diameter of the waves' focal spot should be no less than half of the largest operating wavelength, which is 750 μm. A focused THz beam beyond the diffraction limit with 2.5 mm radius was impinged upon the detection region, covering 71% effective area while maintaining sufficient power density. Besides, the compactness of the sensor benefits from the light harvesting by the focus-point-like sinking interference and the subwavelength meta-atom array (scaled from 1/2 to 1/16 wavelength), thereby eliminating or reducing the diverging waves. Measured by step apparatus, the microfluidic channel height is 5.042 μm (only an error of 0.042 μm), with a near 90°sidewall and high degree of surface smoothness. The tightness of the device is very good due to the flatness of the Si holder and the PI film, and no leakage or deformation will happen if the analyte is slowly and limitedly injected by an airtight syringe.

Fig. 7.

Fig. 7

Open in a new tab

(a) Fabrication process, (b) sensor assembly, (c) measurement platform on the THz-TDS, (d) and (e) simulated and experimental reflection spectra for both modes, respectively, (f) and (g) simulated and experimental frequency shifts for both modes under different BSA solutions, respectively.

To investigate the performance of the proposed sensor, different solutions of BSA analyte was injected into the microfluidic channel from the inlet by a fine airtightness microliter syringe through a PFA pipes. In CST simulation, the BSA samples were characterized by 1st order Debye Model as [26]:

ε(ω)=ε∞+εs−ε∞1−jωτ (3)

where ε∞ represents the infinite dielectric constant, εs is the static dielectric constant and τ is the relaxation time. Air (n = 1.0), 9% solution BSA (n≈1.8) and 30% solution BSA (n≈2.1) were approximately characterized as sensing samples in the simulation. The bovine serum albumin (BSA:100 mg/ml in liquid) was dissolved in 10 mM NaCl and the pH of the solution was adjusted to a value of 7.0. We prepared the solvate analyte by dissolve the BSA powder into the liquid buffer to achieve the respective final concentrations, where the solutions in percentage were referenced by 100% as 100 mg/ml in BSA hybrid. Then the solvate BSA was injected into the microfluidic channel with thickness of 5 μm, where the water absorption loss can be ignored and a high sensitivity can be guaranteed. During the measurement, the temperature was kept at 295 K, strictly followed by the storage condition of the BSA sample. Besides, the incidence angle, beam width and polarization state remained in constant. For each sample of the BSA solution, we repeated three times to get reliable results.

As shown in the Fig. 7(c), a terahertz time-domain spectroscopy (THz-TDS) in 13° tilted reflection configuration was settled in constant temperature and humidity environment. The TDS modeled as TPS Spectra 3000 from Tera View, which supplies full access to 0.06-4 THz spectral region with 0.006 THz resolution and 80 dB dynamic range. The simulation and experimental results are shown in Fig. 7(d) and (e), respectively. A significant red shift appears in the reflection spectra of the fabricated sensor with different solutions and without BSA analyte. The simulated reflection dips are at 1.20 THz (Air), 0.80 THz (in 30% solution) and 0.90 THz (in 9% solution) of mode A, and 0.71 THz (Air), 0.48 THz (in 30% solution) and 0.53 THz (in 9% solution) of mode B. The measured ones are 1.20 THz, 0.80 THz (in 30% solution) and 0.90 THz (in 9% solution) of mode A, 0.66 THz (Air), 0.35 THz (in 30% solution) and 0.42 THz (in 9% solution) of mode B. The experimental results are in a good agreement with the simulation results for Mode A while shows a little discrepancy for mode B. The small discrepancy is ascribed to the fabrication error, BSA model inaccuracy and the measurement error.

Figure 7(f) and (g) intuitively demonstrate the frequency shift varying along the different analytes, as a result, the frequency shifts are 400 GHz for mode A and 310 GHz for mode B from 0% to 30% solution of BSA, as well as 300 GHz for mode A and 240 GHz for mode B from 0% to 9% solution of BSA, which possessing the ultrahigh sensitivity and reliability. To our best knowledge, the highest normalized sensitivities of our design are further improved compared to the previously reported results, which are 0.51/RIU for mode A at around 1.2 THz and 0.47/RIU for mode B at around 0.7 THz. With the sensor, a refractive index resolution up to 0.01 by measuring the resonance shift with a slope of 0.51 THz/RIU can be utilized for selectively biosensing in advanced functionalization.

5. Conclusion

In conclusion, we have theoretically and experimentally demonstrated an ultrahigh sensitive microfluidic sensing platform in terahertz range. Owing to the subradiated dipole resonances and vertically concurrent nearfield coupling, the highly concentrated EM field distribution leads to the sharp dual-band perfect absorption, as a salient trait being favorable for high wave-matter overlap. Furthermore, the ideal impedance matching optimized by low dielectric cap and channel heights significantly improve the sensitivity and distinguishable absorption for minute variation of analytes. In contrast to the conventional sensors which lack of a high-performance THz biosensing with aqueous solution, we overcome the limitation of water absorption by confining the analyte-aqueous solution in the micron-volumetric fluidic chamber, integrated on the highly concentrated resonant MPA cavity. The trapped mode resonators confine electromagnetic fields in extremely subwavelength space and hence allow for the maximized interaction overlap between the BSA solutions and terahertz waves, while minimizing the water absorption loss. Two dual-band frequency shifts can reflect the minute variations of the biochemical dielectric characteristics in aqueous environment, demonstrating robust reliability and functionality in a wide refractometric scope. The dual-mode normalized sensitivities of 0.47/RIU and 0.51/RIU at 0.76 THz and 1.28 THz, respectively, have been predicted and verified. The TDS spectroscopic measurement for different BSA solutions demonstrates the frequency shifts of 300 GHz for mode A and 240 GHz for mode B from 0% BSA to 9% BSA, and 400 GHz for mode A and 310 GHz for mode B from 0% BSA to 30% BSA, respectively, which are in good accordance with the simulation results. By this sensor, a refractive index resolution up to 0.01 by measuring the resonance shift with 5 GHz can be utilized for selectively biosensing in advanced functionalization. The proposed sensor with wide refractive index scope, micron-volumetric fluidic channel, ultrahigh sensitivity, rotational polarization independence, and distinctive SNR paves the way to label free and real time biosensing in microfluidic trace.

Funding

National Natural Science Foundation of China (61871419 and 11775046); China Postdoctoral Science Foundation Funded Project (2017M623000); Terahertz Science and Technology Key Laboratory of Sichuan Province Foundation under Grant (THZSC201701); Fundamental Research Funds of Central Universities of China (2672018ZYGX2018J039).

Disclosures

The authors declare that there are no conflicts of interest related to this article.

References

  • 1.Yang X., Zhao X., Yang K., Liu Y., Liu Y., Fu W., Luo Y., “Biomedical applications of terahertz spectroscopy and imaging,” Trends Biotechnol. 34(10), 810–824 (2016). 10.1016/j.tibtech.2016.04.008 [DOI] [PubMed] [Google Scholar]
  • 2.Dhillon S. S., Vitiello M. S., Linfield E. H., Davies A. G., Hoffmann M. C., Booske J., Castro-Camus E., “The 2017 terahertz science and technology roadmap,” J. Phys. D Appl. Phys. 50(4), 043001 (2017). 10.1088/1361-6463/50/4/043001 [DOI] [Google Scholar]
  • 3.Nagel M., Haring Bolivar P., Brucherseifer M., Kurz H., Bosserhoff A., Büttner R., “Integrated THz technology for label-free genetic diagnostics,” Appl. Phys. Lett. 80(1), 154–156 (2002). 10.1063/1.1428619 [DOI] [Google Scholar]
  • 4.Nagel M., Bolivar P. H., Brucherseifer M., Kurz H., Bosserhoff A., Büttner R., “Integrated planar terahertz resonators for femtomolar sensitivity label-free detection of DNA hybridization,” Appl. Opt. 41(10), 2074–2078 (2002). 10.1364/AO.41.002074 [DOI] [PubMed] [Google Scholar]
  • 5.Park S. J., Hong J. T., Choi S. J., Kim H. S., Park W. K., Han S. T., Park J. Y., Lee S., Kim D. S., Ahn Y. H., “Detection of microorganisms using terahertz metamaterials,” Sci. Rep. 4(1), 4988 (2015). 10.1038/srep04988 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Markelz A. G., Roitberg A., Heilweil E. J., “Pulsed terahertz spectroscopy of DNA, bovine serum albumin and collagen between 0.1 and 2.0 THz,” Chem. Phys. Lett. 320(1–2), 42–48 (2000). 10.1016/S0009-2614(00)00227-X [DOI] [Google Scholar]
  • 7.Berrier A., Schaafsma M. C., Nonglaton G., Bergquist J., Rivas J. G., “Selective detection of bacterial layers with terahertz plasmonic antennas,” Biomed. Opt. Express 3(11), 2937–2949 (2012). 10.1364/BOE.3.002937 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Shiraga K., Ogawa Y., Suzuki T., Kondo N., Irisawa A., Imamura M., “Characterization of dielectric responses of human cancer cells in the terahertz region,” J. Infrared Millim. Terahertz Waves 35(5), 493–502 (2014). 10.1007/s10762-014-0067-y [DOI] [Google Scholar]
  • 9.Chen T., Li S., Sun H., “Metamaterials application in sensing,” Sensors (Basel) 12(3), 2742–2765 (2012). 10.3390/s120302742 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Salim A., Lim S., “Review of recent metamaterial microfluidic sensors,” Sensors (Basel) 18(1), 232 (2018). 10.3390/s18010232 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Xu W., Xie L., Ying Y., “Mechanisms and applications of terahertz metamaterial sensing: a review,” Nanoscale 9(37), 13864–13878 (2017). 10.1039/C7NR03824K [DOI] [PubMed] [Google Scholar]
  • 12.Lee D. K., Kang J. H., Kwon K. J., Lee J. S., Lee S., Woo D. H., Seo M., “ Nano metamaterials for ultrasensitive Terahertz biosensing,” Sci,” Rep-UK 7(1), 8146 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Chen X., Fan W., “Ultrasensitive terahertz metamaterial sensor based on spoof surface Plasmon,” Sci. Rep. 7(1), 2092 (2017). 10.1038/s41598-017-01781-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Liu W., Fan F., Chang S., Hou J., Chen M., Wang X., Bai J., “Nanoparticles doped film sensing based on terahertz metamaterials,” Opt. Commun. 405, 17–21 (2017). 10.1016/j.optcom.2017.07.086 [DOI] [Google Scholar]
  • 15.Zhang Z., Ding H., Yan X., Liang L., Wei D., Yao J., “Sensitive detection of cancer cell apoptosis based on the non-bianisotropic metamaterials biosensors in terahertz frequency,” Opt. Mater. Express 8(3), 659–667 (2018). 10.1364/OME.8.000659 [DOI] [Google Scholar]
  • 16.Park S. J., Cha S. H., Shin G. A., Ahn Y. H., “Sensing viruses using terahertz nano-gap metamaterials,” Biomed. Opt. Express 8(8), 3551–3558 (2017). 10.1364/BOE.8.003551 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Singh R., Cao W., Al-Naib I., Cong L., Withayachumnankul W., Zhang W., “Ultrasensitive terahertz sensing with high-Q Fano resonances in metasurfaces,” Appl. Phys. Lett. 105(17), 171101 (2014). 10.1063/1.4895595 [DOI] [Google Scholar]
  • 18.Ding C., Jiang L., Wu L., Gao R., Xu D., Zhang G., Yao J., “Dual-band ultrasensitive THz sensing utilizing high quality Fano and quadrupole resonances in metamaterials,” Opt. Commun. 350, 103–107 (2015). 10.1016/j.optcom.2015.03.062 [DOI] [Google Scholar]
  • 19.Papasimakis N., Fu Y. H., Fedotov V. A., Prosvirnin S. L., Tsai D. P., Zheludev N. I., “Metamaterial with polarization and direction insensitive resonant transmission response mimicking electromagnetically induced transparency,” Appl. Phys. Lett. 94(21), 211902 (2009). 10.1063/1.3138868 [DOI] [Google Scholar]
  • 20.Hu X., Xu G., Wen L., Wang H., Zhao Y., Zhang Y., Chen Q., “Metamaterial absorber integrated microfluidic terahertz sensors,” Laser Photonics Rev. 10(6), 962–969 (2016). 10.1002/lpor.201600064 [DOI] [Google Scholar]
  • 21.Liu N., Mesch M., Weiss T., Hentschel M., Giessen H., “Infrared perfect absorber and its application as plasmonic sensor,” Nano Lett. 10(7), 2342–2348 (2010). 10.1021/nl9041033 [DOI] [PubMed] [Google Scholar]
  • 22.Cong L., Tan S., Yahiaoui R., Yan F., Zhang W., Singh R., “Experimental demonstration of ultrasensitive sensing with terahertz metamaterial absorbers: A comparison with the metasurfaces,” Appl. Phys. Lett. 106(3), 031107 (2015). 10.1063/1.4906109 [DOI] [Google Scholar]
  • 23.Driscoll T., Andreev G. O., Basov D. N., Palit S., Cho S. Y., Jokerst N. M., Smith D. R., “Tuned permeability in terahertz split-ring resonators for devices and sensors,” Appl. Phys. Lett. 91(6), 062511 (2007). 10.1063/1.2768300 [DOI] [Google Scholar]
  • 24.Huang H. L., Xia H., Guo Z. B., Xie D., Li H. J., “Design of broadband metamaterial absorbers for permittivity sensitivity and solar cell application,” Chin. Phys. Lett. 34(11), 117801 (2017). 10.1088/0256-307X/34/11/117801 [DOI] [Google Scholar]
  • 25.O’Hara J. F., Singh R., Brener I., Smirnova E., Han J., Taylor A. J., Zhang W., “Thin-film sensing with planar terahertz metamaterials: sensitivity and limitations,” Opt. Express 16(3), 1786–1795 (2008). 10.1364/OE.16.001786 [DOI] [PubMed] [Google Scholar]
  • 26.Fu X., Li X., Liu J., Du Y., Hong Z., “Thermal denaturation of protein studied by terahertz time-domain spectroscopy,” Millimeter-Wave, and Terahertz Technologies II 12, 856218 (2012). 10.1117/12.981864 [DOI] [Google Scholar]

Articles from Biomedical Optics Express are provided here courtesy of Optica Publishing Group

RESOURCES