Predict, Control, and Replicate to Understand: How Statistics Can Foster the Fundamental Goals of Science

Abstract

Scientists abstract hypotheses from observations of the world, which they then deploy to test their reliability. The best way to test reliability is to predict an effect before it occurs. If we can manipulate the independent variables (the efficient causes) that make it occur, then ability to predict makes it possible to control. Such control helps to isolate the relevant variables. Control also refers to a comparison condition, conducted to see what would have happened if we had not deployed the key ingredient of the hypothesis: scientific knowledge only accrues when we compare what happens in one condition against what happens in another. When the results of such comparisons are not definitive, metrics of the degree of efficacy of the manipulation are required. Many of those derive from statistical inference, and many of those poorly serve the purpose of the cumulation of knowledge. Without ability to replicate an effect, the utility of the principle used to predict or control is dubious. Traditional models of statistical inference are weak guides to replicability and utility of results. Several alternatives to null hypothesis testing are sketched: Bayesian, model comparison, and predictive inference (p_rep). Predictive inference shows, for example, that the failure to replicate most results in the Open Science Project was predictable. Replicability is but one aspect of scientific understanding: it establishes the reliability of our data and the predictive ability of our formal models. It is a necessary aspect of scientific progress, even if not by itself sufficient for understanding.

To understand why scientists seek to replicate a finding, and why we are in a “replication crisis” (Branch, 2018) —repeated failures to achieve a significant effect when attempting to replicate an important finding—it is necessary to situate replication within a larger scientific framework. For the behavioral community comprising the main readership of this article, the nominal goals of our science are prediction and control. For the larger community, the goal is to achieve understanding. Replication is an essential tool in attaining all of these goals. There are various types of prediction, control, replication, and understanding, each playing an important role in science and its technology.

When there are fundamental problems in a field, their solution requires reexamination of fundamental assumptions, as the weighty problems settle on that ground. This is undertaken in the first half of this article. It will have little that is new to sophisticated readers, and may be plodding, pedantic, or perplexing for casual or naïve readers. For those audiences I recommend paging ahead to the section “Predictive Inference” after scanning the following to know what they will be missing:

• Prediction is not the same as achieving consilience (e.g., fitting a model curve), and is seldom achieved in our field (or other scientific fields). Peirce (1955) emphasized prediction because it was a good way to test hypotheses, but that is something that behavior scientists rarely do. The one case where predict might be loosely used is when we are able to generalize the results from one person to another, or from one experimental situation to another. This is really replication and is treated in its own right.

• We control, as a means of making a process easier to understand, and to rule out other potential causes of the effects that we study. We may control either by restricting the variables affecting our subject (this is the typical approach in the Analysis of Behavior), or by adding a manipulation to one (experimental) group, and not to another (control) group; or to the same subjects sequentially in an ABA design. In scientific analysis control is a technique, a means; only in applications of the technology is it an end. A potential downside of the restriction of variables is that it may make it difficult to generalize the results to novel situations; a downside of between group experiments is that inferential techniques used to analyze such data typically assume that the subjects are random variants around a mean, but substantial differences may exist that interact with the manipulation and undermine the inferences.

• To replicate is to make an exact copy of something. We may attempt to replicate a design and hope to replicate its data, but neither is possible. The experimenters and subjects and apparatus will differ at least minimally (this is called “realization variance” or “random effects”), and data will never be exactly the same. Replication is important if we hope to achieve principles of some generality. But just how close to an “exact copy” is close enough to call it a successful replication? It will be demonstrated that neither the original nor the replication attempt need achieve a particular level of significance to be close enough. These are issues that behavior scientists have largely avoided addressing; either believing that N = 1 methodology insulates them from the threat (it does not; it exacerbates the threat), or that their data are highly replicable (they may be, in a pigeon box).

• A villain in the “replicability crises” has been the use of Null-Hypothesis Statistical Testing (NHST; Cohen [1994] resisted calling it Statistical Hypothesis Inference Testing), both in the original and replicate experiments. One source of the villainy is that the typical index of merit, the t-score, multiplies the effect size by the square-root of the number of observations, so that small effect-sizes may be compensated by large group sizes. Another is its illegitimate use to reject or accept hypotheses. Alternatives to NHST, such as Bayesian analysis and model comparison, are noted. Another alternative, predictive inference employing the statistic p_rep, is described in more detail.

If the above synopsis satisfies, this is where you jump ahead to pick up the narrative in “Predictive Inference.”

Predict

Predict means “to say ahead [of an event].” Respecting this etymology, it follows that we cannot predict an event that has already happened (Rubin, 2017). Thus, it is incorrect to fit a curve such as a matching line to data and say that it predicts the data, or predicts P% of the variance in the data. In such cases “accounts for” is a better word. We may, of course, predict an accomplished fact that we are ignorant of. Although this is a stretch of the word, we may make it reach to cover by reinterpreting predict to mean “say ahead of [knowledge of] an event.” This is a less perfect kind of prediction, because correlated events that you do know of may improve your odds, and a successful prediction in that case cannot be credited wholly to the model you were using to make the prediction.

Why Predict?

There are two kinds of reasons for making predictions: practical and scientific.

Practical Prediction

Whereas scientific predictions are a way of testing the validity of our conjectures—our hypotheses and models—practical predictions take care of business. Weather forecasting has become amazingly accurate, given the complex dynamic system with which it deals. Predictive type-ahead rips your thoughts from your fingers, rendering their spelling more accurately than you, and on occasion maintaining your arousal level with a Cupertino (Okrent, 2013). Social media bots know who you are and what you want sometimes better than you do. Smart cars drive you safer than you drive you. You can make a market with practical predictions, and there is clearly a technology about how to best make them. Yet often these predictions are made with deep-learning machines whose connections we can inspect with no more insight than we can the wiring of brains. This kind of prediction increasingly makes the world go around. It might be harnessed for science, but except for a few interesting exceptions, it has seen little use in our field.

Scientific Prediction

Prediction is relatively rare in science (Hoffmann, 2003); why then is it so valued? Francis Bacon required the collection of facts to build toward generalizations, and the testing of those generalizations by negative instances where they may fail (Urbach, 1987, p. 30). A generalization by itself is based on known instances, and so is not a prediction: it is an induction—a valuable accomplishment in its own right. Testing that generalization by application to unknown cases is prediction (sometimes called “out of the box” prediction, as it is made without tuning to the new data set). In his System of Logic, John Stuart Mill (1904) offered five rules for streamlining such predictions, and reducing the likelihood of what today we call “confounds.” Bacon’s “Instances where they may fail” may be read as one of those, the “method of residues.”

Peirce (1955) envisioned three logical processes in scientific inquiry: induction generates general statements (this is the main process—or hope of one—in our field). Abduction helps us select which general statements/laws/models may be operative in a particular context. Deduction permits us to test the selected model through prediction. Peirce developed pragmatism as a way of testing such general statements, or conjectures: if a conjecture leads to valid predictions, that increases our confidence that it may be true and relevant to that context. The cycle of inducing models, selecting from among them, and then testing them through predictions is the heart of the modern vision of the scientific process (see, e.g., Wikipedia, 2017b).

Not all predictions are created equal. Some are more informative than others, and it is the informative ones that add the most to our confidence in a conjecture. Informative ones are “instances where they may fail.” After an animal makes a certain pattern of responding on 25 trials, to predict that it will do so on the 26th adds little new information. To predict instead that it will then attempt to escape from the box, or vocalize, or turn three circles (not having seen this before), gives huge credibility to whatever conjecture you were using to make that prediction. This may be qualitatively understood in terms of Bayes’s Theorem (further clarified below): the probability of a hypothesis given the data, p(H|D), equals the probability of the data given the hypothesis, p(D|H), multiplied by the ratio of the probability of the hypothesis to the probability of the data: p(H|D) = p(D|H)•p(H)/p(D). Let us suppose that the hypothesis makes an unequivocal (rather than probabilistic) prediction, so that p(D|H) = 1. The terms in the ratio on the right are called priors. We are seldom confident in assigning a value to them, but for this illustration that does not matter. Inspecting the equation, we can see that if the prior probability of the data is large (say, p(D) ≈ 1; as the case for the sun rising tomorrow), then observation of the predicted outcome adds little new information: it leaves the posterior probability of the hypothesis, p(H|D), pretty much equal to the prior p(H). No one would be impressed with a theory that predicted sunrise. But if the prior probability of the data is small, as is the case for the sun rising green, because it is a small fraction in the denominator, its observation then gives a large increase in our confidence in the conjecture, p(H|D). This is why making surprising predictions, ones “where the conjecture may fail,” is so valuable to the scientific community (see, e.g., Nuzzo, 2014): it provides a more acute, informative test of a hypothesis. In summary, prediction is valuable because it helps us to test the reliability of hypotheses (scientific prediction) or it helps us to plan for the future (pragmatic prediction).

The Relation of Prediction to Replication

There are several types of replication. Repeating the same experiment in the same laboratory on similar subject tests repeatability, and its measure is reported with a standard deviation. Exact replication occurs when independent experimenters in different laboratories carefully follow the same procedures with similar subjects. It tells us how replicable the data are. Replication of data is a crucial first step for a field, to know what it is worthwhile for models to address.

Experimenters must interpret results, setting them within a larger framework. They might, for instance, conclude that a person learns discriminations faster when the positive stimulus has a feature added than when it has a feature deleted. Other experimenters who attempt to get the same effect with different species or different stimuli are essentially treating that inference as if it were a prediction. They are testing how replicable the qualitative outcome predicted by the model is. If it fails, the statement—the verbal model—will have to be qualified. This a crucial second step, to test the generality of the words and equations with which we represent and understand the important aspects of data.

Finally, there are the rare true predictions based on theory, such as that of gravitational lensing by general relativity theory. A prediction deriving from the theory of the static aether was tested 100 years ago by the elegant Michelson-Morley experiment; the prediction failed, leading to the subsequent abandonment of that hypothesis. The general conformity of response rates on interval schedules to Herrnstein’s “hyperbolic” model has a long history of quantitative replication: it generally fits the data well. But when its qualitative predictions were tested by McDowell and colleagues (McDowell, 1986; McDowell & Dallery, 1999; Dallery, McDowell, & Lancaster, 2000), the model failed. Such attempts at true predictions and their experimental evaluation are rare in our field. This is in part because of its historic antagonism to theoretical models, of which there are few, and that are required for any prediction that is not simply a generalization to similar organisms in similar circumstances.

Control

As a noun, control is defined as the power to influence or direct people’s (or machines’) behavior; as a verb, it means effecting that power. If control is not repeatable or replicable, it is useless for scientific purposes. Control also refers to a group or individual that is used as a standard of comparison for checking the results of a survey or experiment. Control groups constitute the baseline against which to check the efficacy of an intervention, and are essential, in one form or another, to test the replicability of an effect.

Why Control?

Controlling outcomes is a proof-of-concept: If you can control the behavior of another, you have predicted and engaged the variables of which that behavior is a function. Such control validates an intervention; it is a prediction made true. Three kinds of control noted here are scientific control of conditions, control groups, and technological control.

Scientific Control of Variables

Control your conditions and you shall see order—thus spake Pavlov. He harnessed his dogs to the study of digestive processes, ignoring most of the other things that they were struggling to do (Jenkins, Barrera, Ireland, & Woodside, 1978). By so controlling interacting variables he was able to study parts of a system in isolation. This is called analysis. It is a centrally important part of science. A Faraday cage controls the electromagnetic radiation in its environment. A Skinner cage controls sound and light and odor and temperature in its environment. Often the control exerted in these chambers is approximately “open-loop” (loose loop): the behavior of the subject has little effect on scheduling of events in the chamber. Pavlovian conditioning, interval and concurrent interval schedules of reinforcement are examples, because they maintain relatively constant rates or allocations of consequences over a wide range of response rates and kinds. The correlation between what the organism does and what happens to it can be quite small.

Behavior engendered by closed-loop arrangements such as ratio schedules and concurrent ratio schedules is harder to predict, as some of the control of the events is left in the hands/paws/beak of the subject. Small deviations in one direction or another can amplify into divergent trajectories (Pant & Starbuck, 1990). One of the reasons that Herrnstein gave for rejecting Thorndike’s law of effect was that, in a report of Ferster and Skinner, one of two pigeons transitioning from an interval to a ratio schedule increased its rate of responding, whereas the other stopped responding. Herrnstein (1970, p. 243) rejected Thorndike’s law because it could not predict a change in response rate, let alone that divergence. (Herrnstein omitted to mention that his own law of effect, the matching law, could also predict neither a change in rate [matching concerns stable performances, not dynamic ones], nor its divergence in the two subjects [that requires a stochastic version of the law with different basins of attraction.])

Learning is a process both central to our field and one in which output feeds back upon input, generating a similar exponential change away from predictability. Whereas tight scientific control permits us to generate laws for the situations so controlled, generalizing the performance to open-loop or interacting systems, as in the Ferster and Skinner experiment, is an order of magnitude harder. We cannot expect the laws of open-loop (or loose-loop) performance—the bulk of the laws in our field—to generalize to closed-loop systems. Analytic control increases data replicability while at the same time decreasing model replicability. Our field needs dynamic models that can follow behavior’s course when it is unleashed from loose-loop control; progress in that endeavor will ensure our discipline’s future.

Control Comparisons

To know whether what you manipulated caused the effect that you observed, you must know what would have happened absent that manipulation. This mantra of science invokes a counterfactual conditional—what would have happened had things been different. Counterfactual conditionals are a deep problem in logic and everyday inference alike (Nickerson, 2015). The concept of a control condition or control group was invented to address that problem by generating an alternative scenario where it is not counterfactual that the manipulation didn’t happen. The use of such groups is an instance of another of Mills’s principle of induction, the method of differences.

A crucial part of that method is that the object of study must be exactly the same except for the variable of interest. This is not so hard to achieve, or closely approximate, with physical things, as in analytic chemistry. It is an ongoing problem in the behavioral sciences. Much of the methodology of social and behavioral psychology is designed to make proper comparisons between experimental and control groups or conditions. If things other than what you expect vary, your inferences may well be flawed by such confounds.

Single Case Designs

In these, more than one organism is studied, but the interest resides in the individual subject’s data, not the group means, and those same individual subjects in an alternate condition serve as their own control. Perone and Hursh (2013) provide an invaluable review of these designs, which minimize intersubject variability. It would seem to be simple enough to watch an organism for a while, then do something (e.g., startle it), and note the effect. In this “AB” design, the initial baseline is the control condition A; B is the experimental condition. If the startle stimulus is not initiated by the observer (who might inadvertently cue it on some behavior of the organism), this gives useful information. But there are always potential confounds when a replication is attempted. One could attempt to repeat the experiment later in the day. Circadian phase affects a range of behaviors, however, from reaction times (Van Dongen & Dinges, 2000) to fear conditioning (Chaudhury & Colwell, 2002). Even when that is controlled, the subject has changed: the speed and magnitude of the startle will decrease through habituation. Indeed, one cannot with confidence even “recover the baseline” in any repeated measures design, due to generalized anxiety or arousal; or because the context has become “conditioned” (i.e., has become a CS). Harlow (1949) famously showed that primates can “learn how to learn,” so are changed in important ways with each learning experience. Research strategies are evolving for such single-case experimental designs (e.g., Barlow & Hayes, 1979; Barlow, Nock, & Hersen, 2008; Smith, 2012), but, with interesting exceptions (e.g., Tryon, 1982; Unicomb, Colyvas, Harrison, & Hewat, 2015) statistical analysis of them lags (Shadish, Rindskopf, & Hedges, 2008; Shadish, Cook, & Campbell, 2002).

Between-Groups Designs

An alternative tactic is to study an organism that has not been subject to the experimental manipulation as a control. This between-groups design is the most common means of testing the effect of a manipulation in psychology. It provides the data to feed all of the statistics we learned as undergraduates, comparing two or more groups using ANOVA or regression analyses. If the method of differences could be applied exactly, you would need only one subject per group, the experimental subject and its clone. But littermates or strangers are often used, randomly assigned to conditions. This is reasonable, but the former demands a different type of statistics (hierarchical models). The classic attempt to hold all variables constant but one is given up for the hope of averaging out differences that are inevitable. Statistics are a patch for the inevitable problems of individual differences and inadequate control. In studying the effects of a drug such as cocaine, for instance, some of the animals in both groups are likely to be dopers, and others to be abstemious, increasing within-group variance and undermining inferences about between-group differences. It leads to attempts to overwhelm the “noise” by increasing group size (Fitts, 2010, shows how to do this parsimoniously). What is needed are statistical techniques that don’t assume that all within-group differences are random deviations from a population mean. Permutation techniques (Weaver & Lloyd, 2018) and model comparison approaches offer opportunities for creative solutions, as does hierarchical Bayesian modeling. Skinner found a simpler way to minimize within-group variance in his new approach to a science of behavior.

Technological Control

Skinner foreswore control groups and statistics, opting instead for procedures that maximize effect size: “No one goes to the circus to see the average dog jump through a hoop significantly oftener than untrained dogs raised under the same circumstances” (Skinner, 1956, p. 228). Nor do people go to a laboratory to see that. People go to the circus to see animals conditioned with techniques that Skinner studied, trainers employ, and his students in the field improved. Trainers must generate behavior that is perfectly replicable. One needn’t worry about control groups or statistics if you can do that. And with some dogs in some contexts you obviously can do that. Some of the techniques resulting from this approach are finding their way back to human skill training (Levy, Pryor, & McKeon, 2016). The trainer is also being trained, of course, adjusting her goals to accommodate the natural action patterns that the animals bring to the setting (as famously noted by Breland & Breland, 1961). Perone (1999, p. 115) observed that this is one of the great virtues of “single-case” (small-N) designs: The “intensive interplay between experimenter and subject” tends to shape scientific judgment, a not inconsiderable virtue of the Skinnerian approach. A prominent cognitive psychologist agrees:

I believe that it is bad scientific practice to routinely use convenience samples and their averages as units of analysis. Rather, the default should be to analyze each individual on its own. This allows researchers to minimize the real error, to recognize systematic individual differences, and—last but not least—to know one’s data. (Gigerenzer, 2006, p. 248)

This knowledge is abetted by exploratory data analysis (see, e.g., Church, 1979), rather than inferential analyses, and is beautifully exemplified in Perone (2018).

Not all results from such intense involvement with a few subjects are so replicable, unfortunately, especially outside controlled environments. An enormous number of resources have gone into training social skills to children with ADHD, in the hope of improving their success in the classroom and in life in general.

Improvements in children’s target behaviors often occur in the treatment settings where contingencies are in place and delivered consistently. However, generalization of treatment effects across settings and over time—the overarching clinical objective of psychosocial interventions—remains an elusive goal. (Abikoff, 2009, p. 207)

Skilled trainers have trouble getting the learned behaviors to generalize out of training context—to replicate. The kind of therapeutic control the world needs is often elusive. New behavioral principles—not the kind “demonstrated by elephants” in a circus (Skinner, 1956, p. 228)—but the kind that can be replicated across settings, individuals, and time, in particular with special populations such as ASD and ADHD, are needed.

Replicate

Replicate means to “make an exact copy of; reproduce” (Oxford Living Dictionaries). As a noun, it means the copy itself. We may replicate an experimental design, and the data collected in it may replicate those found in the original study. Then those data are replicates. I use duplicate for the first sense. In scientific usage, exact is too exact a word to modify copy; close would be better. A pivotal question is how close a replicate needs to be in order to be good enough for the results to qualify as replication. Another pivotal question is whether the scientists are attempting to replicate the data (a direct, or exact replication), or to replicate the support that they gave to a hypothesis (a conceptual replication). We are said to be in a replication crisis today (Wikipedia, 2017a; Ioannidis, 2005; Yong, 2015; but see Gilbert, King, Pettigrew, & Wilson, 2016). Why that matters and what do about it occupy the next several sections.

Why Duplicate in Order to Replicate?

Inductive scientists like Skinner, who search for descriptive regularities among accumulating data, hope to extend those regularities in time and place and subject, in duplicate experiments conducted later, elsewhere, by other scientists. Successful replication confirms the description and extends the generality over those domains. If we do not succeed, the generalization is too hobbled, in space, time, and execution, to be of general interest to the scientific community. “You may well have gotten the effect, but if we, after sedulous duplication of your methods cannot, of what use is it to the world?”

Abductive scientists search for descriptive regularities among accumulating data; finding them they try to match them to a principle (If these conditions are satisfied, then those things happen). Deductive scientists then tests those principles, especially in cases where they may fail. If they do fail, the principle is either rejected, modified, or restricted as not applying to the new domain of data. In all cases, Mill’s method of differences helps eliminate the potential confound of particular experimenter, location, and subjects used in the original, to validate the generalization or principle.

Exact/Direct Versus Conceptual Replication

To know if results are durable, attempts must be made to replicate them with exactly the same methodology and with subjects as similar as possible. This is what the “registered replication attempts” (e.g., APS, 2017), now frequenting the literature, strive to achieve. The subjects and experimenters differ, but all other details (excepting number of subjects, which may be increased) are duplicated (as far as procedural descriptions allow). If the data have passed that hurdle, scientists ask more than whether the data are reliable. They ask whether the hypothesis, or principle, that motivated them and interpreted them can be sustained in the general sense of the words used to formulate it—a different kind of replicability, model replicability tested by this conceptual replication. If performance increases with motivation to a maximum, then decreases, as the Yerkes Dodson principle avers, you will try to replicate those effects with different kinds of motivators and different kinds of performances.

Damned Lies

The current replication crisis is due in part to a narrow construction of what it means to replicate a phenomenon. A heavy part of that blame falls on the round shoulders of null-hypothesis statistical tests (NHST), a principle statistical approach to evaluating replication attempts. In the behavioral and psychological literatures, exact predictions (e.g., “this manipulation will cause rats to increase their response rate by 20 rpm”) are seldom possible. The alternative is the “composite” hypothesis (e.g., the increase in response rate will be some value greater than 0). NHST permits one to evaluate how unlikely the resulting data are if the Null (here, 0 increase) were really true. The user hopes to invalidate the negation of the hypothesis/principle/conjecture that she is attempting to establish—to reject the null. Unfortunately, little of interest can be concluded if she succeeds; and even less if she fails. This all sounds, and is, complicated because it involves both counterfactual inference and inverse logic. Echoing Branch’s (2018) recent broadside, the Appendix of this article summarizes the involuted logic and impotent conclusions of NHST. In brief, NHST can estimate the probability of finding data more extreme than observed, if nothing was going on (i.e., given that the null is true). It cannot, however, tell you the probability that something is going on (that the hypothesis that motivated the research is true) given the data; or even the probability that the null is true, or that it is false. “Such a test of significance does not authorize us to make any statement about the hypothesis in question in terms of mathematical probability” (Fisher, 1959, p. 35). Fisher argued that little could be inferred from a test that returned results with a p-value just under .05 without replication. But, as Robert Matthews noted: “The plain fact is that 70 years ago Ronald Fisher gave scientists a mathematical machine for turning baloney into breakthroughs, and flukes into funding. It is time to pull the plug” (Matthews, 1998, cited in Colquhoun, 2017).

To say that one has “rejected the null” is, if not a “damned lie,” a fundamental confusion/miseducation about what such tests license one to say. The p-values derived from NHST only poorly predict replicability (Branch, 1999; Open Science Collaboration, 2015); furthermore, they confound effect size with group size, and editors place criteria for publication on that confound (Meehl, 1978, 1990). It is clear to all serious students of the situation that alternatives are needed.

What to Do

It is not clear why traditional statistical inference continues when it is so inept and its “warts” so conspicuous (Krueger, 2001; Nickerson, 2000, 2015; Wagenmakers, 2007; Trafimow, 2003; Branch, 2014). It provides a junk filter of sorts (see Nickerson, 2000, and the suffix to Krueger & Heck, 2017). Behavioral momentum, maintained by a historically dense schedule of reinforced publications?—perhaps. An esoteric and technical knowledge that practitioners are loath to give up?—maybe. Low cost computer analyses?—for sure. Authority? The lack of alternatives?—That hypothesis can certainly be rejected: there are alternatives aplenty, including Bayesian inference, model comparison, and predictive inference (Kline, 2004; Harlow, Mulaik, & Steiger, 1997).

Bayesian Inference

The basis of Bayesian inference, Bayes’s rule was written as a minor part of an essay that formulated what is now called the beta distribution. Its clarification and posthumous publication by Richard Price, a friend of Bayes, in 1763 initiated a controversy that has yet to abate. In its original context, however, Bayes’s rule is not problematic. Inspect Fig. 1, which gives the probabilities of H and of D as Euler circles (a simple version of Venn diagrams), with area proportional to those probabilities. Where they overlap is the probability of both H and D being true: p(H•D). That intersection may be calculated by the two equations in Fig. 1. Two things equal to a third are equal to each other. So, we may write: p(H|D)p(D) = p(H•D) = p(D|H)p(H), drop the middle term, and rearrange to derive Bayes rule: p(H|D) = p(D|H)p(H)/p(D).

Fig. 1.

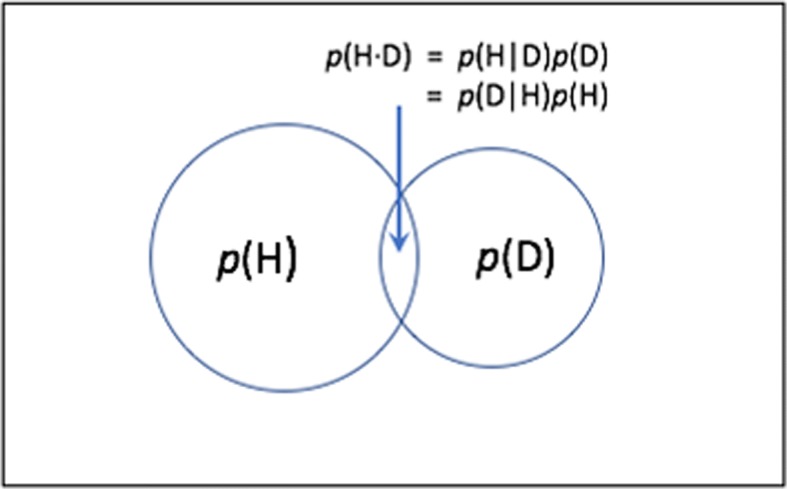
The derivation of Bayes rule

If we think of H and D as labels on beans and jars, there is no controversy. But when we interpret them as Hypotheses and Data, the camel’s ugly nose has entered the tent. If H is simply “all the beans are black” and the data are the colors of the first four beans that are drawn, then all is well. If H is “Herrnstein’s hyperbola is true,” however, then problems arise. What in fact does p(H) mean when applied to statements or models such as Herrnstein’s? Such hypotheses are not like white and black beans that you select at random from a jar and can talk of selecting one 25% as often as another. You might relate it to your betting odds that the model will turn out correct: “The odds that McDowell’s model will outperform Herrnstein’s are 3-to-1.” It is useful to have such beliefs, but does 3/(3 + 1) constitute a probability?1

The variable p(D) is another problem: How does one assign a probability to a data set? This problem is relatively easily fixed: Instead of asking for the absolute probability of the hypothesis, H₁, given the data, we can ask for the odds that it is better than the alternative, H₀. We write Bayes’ rule for both and take their ratio. Because p(D) is common to both, it cancels to give:

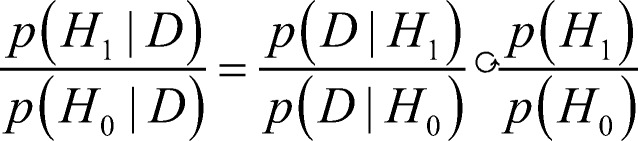
The ratio on the left is the (posterior) probability of the hypothesis given the data, relative to that of the null (or other competing) hypotheses. The first fraction on the right is the ratio of prior predictive probabilities, also called the Bayes factor. It informs us of the weight of evidence for or against H₁. The denominator of the Bayes factor is not the p value from NHST, because that gives the probability of anything more extreme. It is the exact (minuscule) probability of exactly those data (technically, their likelihood: the value of the density function above them). The second fraction on the right is the ratio of the prior probabilities of the hypotheses/models. Specification of these constitutes the most problematic aspect of the Bayesian enterprise (Killeen, 2006b). The utility of having explicit priors, and the various approaches to stipulating them, are reviewed by Wagenmakers (2007). There is a beauty and a logic to these various schemes, but they are not a panacea (Gigerenzer & Marewski, 2015), and are often difficult to implement in other than an ad hoc way (for a clear, forceful, and engaging take on the problems with both p-values and with Bayes, see Colquhoun, 2017). The Bayesian alternative to NHST does not directly address replicability, so here I abandon the reader to the helpful introduction to Bayes provided by Masson (2011), and a recent issue of the Psychonomic Bulletin and Review (see Vandekerckhove, Rouder, & Kruschke, 2018).

Model Comparison

Model comparison is the Bayesian approach outlined above, minus the problematic priors (Killeen, 2006b), plus a decision tool called the Akaike Information Criterion (AIC). The AIC permits one to compare models with different numbers of parameters. It can tell you, for instance, whether the data justify having separate means for two groups, similar to rejecting the null of no difference. Excellent introductions are available (Burnham & Anderson, 2002; Myung, 2003; Burnham & Anderson, 2004). Applications in our own field abound (Boomhower & Newland, 2016; Davison, 2016; Hunter & Davison, 1982; Lau & Glimcher, 2005; DeHart & Odum, 2015; Brackney, Cheung, Neisewander, & Sanabria, 2011). All of the kinds of inferences one wishes to make but cannot under NHST may be addressed with model comparison and its right-hand tool, the AIC. It is much simpler than a full-fledged Bayesian approach (see Wagenmakers [2007], in particular the last section of that article), although a well-informed Bayesian approach, where possible, will be more powerful. I encourage readers to take their first step away from classic NHST to permutation/randomization statistics. These are coherent, simple to understand and implement with computer programs, and are the gold standard to which traditional parametric statistics are an approximation (see, e.g., the introduction in Berry, Mielke, & Johnston, 2016; Edgington & Onghena, 2007). Finally, step up to model-comparison, which can be based on such randomization tests (but need not be). I find these to be my inferential tools of choice, and from them, prediction of replicability is a small step.

Predictive Inference

The above approaches attempt to make inferences concerning hypotheses based on data. That is fundamental to our prevalent treatment of science as testing conjectures, but it is at the same time at the heart of the difficulties with most inferential approaches: They attempt inverse inference, from data to theory (Killeen, 2005b). It would be great to be able to prove conjectures, but wishful thinking and its maven NHST cannot deliver such proofs. If we divest ourselves of this Platonic aspiration of truth-seeking, an alternative goal is within easy reach: to be able to predict the replicability of data. Making replicability, not truth, our criterion for contributions to science liberates us from NHST—while yoking us to the responsibility of generating replicable data. How is that done, and how is it measured?

Powerful Questions

Most studies in psychology as a whole, and in our field in particular, are “underpowered” (Maxwell, 2004; Button et al., 2013): They utilize an insufficient number of subjects. One may think that, with our N = 1 stance, power is irrelevant. That is incorrect; N = 1 doesn’t constitute a rationale for under-powered studies—it is a counsel to spend the same amount of effort in understanding a phenomenon in a few subjects as in larger groups, as in between-subjects comparisons (Killeen, 1978; Ashby & O’Brien, 2008; Kyonka, 2018). This makes it possible to understand the phenomenon in each individual, if we take advantage of that opportunity. I suggest how to analyze such studies below. But a study with but one subject only tells us what is possible, giving us some understanding of it for that particular subject. It gives us little information about whether it will work for another subject -- no information about its replicability. An N = 4 study, which is about the modal number for each experimental condition in some of our journals, is better, especially if there are other conceptual replications in the report. In many studies that I have reviewed over the years, one animal of four or five behaves substantially differently from the others. What does one make of that, or of its evidential value for the conclusions that are drawn from the study? If one subject goes one way and all the rest the other, at least seven must agree for the binomial probability that the odd one occurred by chance to be less than 5%. Some people recommend 12 subjects per group (Julious, 2005) or more (Simmons, Nelson, & Simonsohn, 2018). Revusky (1967), however, developed a multiple-baseline, within-subjects experimental design and nonparametric statistical analysis that can get by with as few as four or five subjects. It needs to be deployed more frequently than it has been cited. The reason for this concern is not to pay homage to traditional statistical p-values, but rather because those values can be used to generate measures of replicability, as we shall see. To do so with any confidence, however, we must have some confidence in them.

Do it Again

The best way to establish replicability is to duplicate. Run the study again, with different subjects, making predictions about the range of the dependent variables. (Give the predictions to a colleague, because a post-hoc renegotiation with oneself of what was to be predicted is too tempting). A replication study is an excellent first part of a thesis.

What if the replicate does not achieve an adequate level of “significance” when the original did? Although many would take this to be the dread “failure to replicate,” that may be because they have an arbitrarily high sense of what it means to replicate. How close does a result have to be to make it a replicate? What if the replication only adds weak positive evidence for the effect? Well, that is still positive evidence. If those data had been collected in the original study, there is a good chance that they would have increased the “significance level” of the original study by increasing the sample size, N.

How Big Does it Need to Be?

Estes (1991, pp. 19–23) showed one way to address this question of value-added. Consider a pilot experiment with an alpha level2 of α₁ = 0.10, with the researcher determined to ask a colleague in another laboratory to conduct a follow-up experiment if her results achieve that level of significance, and not otherwise. It did exceed that level, and the second experiment was conducted, with an alpha level of α₂ = 0.05. What is the probability of a False Alarm (FA; a Type 1 error)—rejecting a true null hypothesis—at the end of that sequence? It is α₁ (the probability of a FA in the pilot) times α₂: p(FA) = α₁ α₂. Notice that for any preestablished significance level of either experiment the result of this combined set of experiments is stronger than either alone. If α₁ = 0.10 and α₂ = 0.05 then p = p(FA) decreases to 0.005. Echoing Fisher, there is strength in systematic accumulation of evidence, even if on their own the respective bits of evidence are weak.

To further develop this approach, consider first Cohen’s measure of effect size (Hedges & Olkin, 1985);

$$d=\left(M_2–M_1\right)/s$$

and next the t statistic underlying the probability test for the difference between the means of two independent groups3: t = (M₂ – M₁)/(s$\sqrt{2/n}$). In both equations, the first parenthetical term is the difference in means of the experimental and control groups. The sample standard deviation, s is estimated from the pooled standard deviations of the groups, and n is the number of subjects in each group (assumed equal for now). Substitute the first equation above into the second and rearrange to write: t = d√(n/2): The t score, which determines the level of significance, may be computed from the effect size d by multiplying d by the root of n over 2. This explains how one can compensate for small effect sizes with large n to achieve significance. Some critics believe this to be the core problem in evaluating hypotheses with traditional statistics (Meehl, 1990; Jiroutek & Turner, 2017).

Assume that an experimenter achieved statistical significance in her study, and an exact duplication (a replication attempt) with the same number of subjects and similar variance failed to achieve significance. Was that “a failure to replicate?” Many consider it so (Ioannidis, 2005). But what if the experimenter herself had conducted the duplication and included it in her report, pooling the results of the two studies? In the follow-up study, t’ = d’(n/2)^½. Combine the data from the two studies: t” = (d+d’)/2 • (2n/2) ^½ by averaging the effect sizes and doubling the group size (cf. Shadish & Haddock, 1994). What effect size in the replication study (d’) is necessary to improve the significance level (p-value) of the combined studies? We can write this question as “for what d’ is (d+d’)/2 • (2n/2) ^½ > d(n/2)^½? ” We can answer it by solving for the minimal necessary replicate effect size, d’. Some algebra reduces that to the simple d’ > (√2 – 1)d ≈ 0.414 d. The replicate d’ need only be larger than 42% the size of the original d to have made it a more “significant” effect (viz. increase its t-score); if the sample size of the replicate is larger, even smaller values of effect size suffice. The precise value will vary with experimental design and statistical analysis, but you can always get by with less, and often (as long as d’ ≥ 0.42d) strengthen the evidential claim of an original study with a replication that fails to achieve significance.

Another way to think about this value of supportive but nonsignificant results is Bayesian. We may choose to analyze the first experiment with uninformative (flat) priors (Killeen, 2005a). But when duplicating an experiment, we may choose to use the results of the original experiment to inform our priors, and doing so will increase the likelihood of the set of data above that of either experiment taken on its own. Science concerns the cumulation of knowledge, and these are ways for later research to quantitatively build on the results of earlier research.

The Probability of Replicating an Effect, p_rep

Predictive inference attempts to avoid using anything other than observed data to predict future data. Consider an experiment that generated a sampling distribution for effect size looking like the tallest right curve in Fig. 2, centered over d₁. Shifted to the left, that distribution constitutes the null hypothesis. The p-value of the data under that null hypothesis (that the true effect size δ = 0) is the probability that by chance you would observe a sample with a mean anywhere4 to the right of d₁, given by the area under the left distribution to the right of d₁.

Fig. 2.

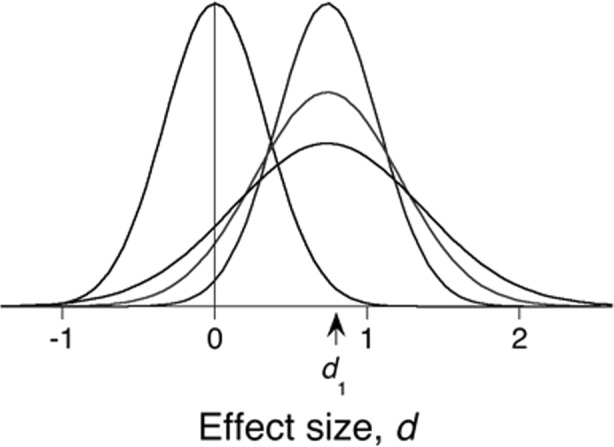
The tallest density centered on d₁ is a sampling distribution for a measured variable (z) or effect size (d). In the latter case it gives the predicted distribution of mean effect sizes in replications if the true effect size, δ, equals the recorded effect size d₁. The tail to the left of the origin gives the probability of getting a mean of d₁ if the population parameter were of opposite sign: this is another interpretation of the p-value. Because we do not know that δ precisely equals d₁—both the initial and study and the duplicate incur sampling error—the variance of the distribution is increased (doubled in the case of an equal-powered replication), to create the posterior predictive distribution (ppd), the intermediate distribution on the right. In the case of a conceptual rather than strict replication, additional realization variance is added, resulting in the lowest ppd. In all cases, the area under the ppds to the right of the origin gives the probability of supportive evidence in replication (p_rep). Shifted to the left over 0, the tallest density gives the distribution of mean effect sizes under the null hypothesis

To predict the sampling distribution in a replicate experiment based on your data, we compute the posterior predictive distribution (ppd). It is a posterior distribution because it is constructed after the fact of having your original data in hand; it is predictive because it provides our best estimate of what will happen in the replicate experiment. All the information about the effect is drawn from those data (it uses “uninformative priors”). Its mean is located at the mean of the prior distribution, but its variance is increased from σ²(1/n₁) to approximately σ²(1/n₁ + 1/n₂). If the number of observations is the same in each (n₁ = n₂), then the variance will be doubled σ²(2/n₁). This is because there is uncertainty (variance) in the original study, with some chance that the population mean is not exactly equal to the sample mean; and there is the same possibility in the replication experiment that the sample mean will deviate from the population mean. This is what the right distributions display. From such ppds we can compute any statistic that we wish, such as the probability of getting the same p-value (or greater) in the replication study as in the original. We may compute the probability of getting an effect size that is at least 42% of the original. A more conservative estimate of replicability is an effect size that is 55% of the original, as that is where the Akaike criterion allows an extra parameter (e.g., separate means for control and experimental group; Killeen, 2006a). In my original work, I called the area to the right of the origin p_rep; it is the average probability of replicating the sign of the original experiment. I did this because any such replication lent some (no matter how meager) evidence for the effect being true. I also did it because there is a symmetry in interpreting the meaning of a p-value: p is the probability that the population parameter does not have a sign opposite to what you observed in the sample (it is the area of the tallest right curve that lies to the left of the origin; Jones & Tukey, 2000). But p_rep predicts replicability, not whether observed data are likely under a null hypothesis that you hope is false. Where p gives the probability that the original study got the sign of the effect wrong, p_rep gives the probability that a replicate experiment will find the same sign as the original.

P_rep is easy to compute if you have the p-value (Lecoutre, Lecoutre, & Poitevineau, 2010). Let z(p/2) be the z-score corresponding to a particular (two-tailed) value of p (however it was derived), and N(z) the p-value. Then p_rep = N(-z(p/2)/√2)). In Microsoft Excel® this may be computed as p_rep = NORMSDIST(-NORMSINV(p/2)/SQRT(2))), where p is the 2-tailed p value returned by your inferential test. This gives the probability that an equal-powered exact replication will return evidence in your favor (no matter how weak that evidence is). If you wish to know how likely you are to get the same sign of effect in a single individual—perhaps you are contemplating using a clinical technique on a client—the variance of the posterior predictive distribution increases5 to σ²(1/n₁ + 1).

One can easily modify p_rep to predict the probability of getting any particular effect size in replication. If one wishes to set more stringent criteria for replication, d_C, compute instead p_repC = 1 - NORMDIST(d_C - NORMSINV(p/2), SQRT(2), TRUE). For d_C = 0 this reduces to the original p_rep. To compute the probability of a successful replication at the criterion α, use d_C = z(1- α/2)—in EXCEL, d_C = NORMSINV(1- α/2). In his article on the replicability crises, Branch (2018) gave an example using 20 made-up data in which p < 0.004 with an effect size of 1.0, and noted that “that statistical test reveals nothing about reliability of the difference” (p. 10). If these were real data, however, we could use the above equations to tell us that, whereas the probability of any supportive evidence is very high (p_rep ≈ 0.98), the proportion of replicates achieving significance at the α = 0.05 level would only be 0.74. Of course, all values of p_rep are estimates, as the original or replicate has some chance of being non-representative (Cumming, 2005).

Field Testiness

P_rep is firmly grounded on the Bayesian posterior predictive distribution (Winkler, 2003; Bolstad, 2004). Does this really work? Aspersions have been cast by many. Being novel, and a member of neither church, p_rep was criticized by both Frequentists and Bayesians (Iverson, Lee, & Wagenmakers, 2009; Iverson, Wagenmakers, & Lee, 2010; Wagenmakers & Grünwald, 2006; Trafimow, MacDonald, Rice, & Clason, 2010; Miller, 2009; Macdonald, 2005; Maraun & Gabriel, 2010). All criticisms were rebutted (Killeen, 2005a, 2006b, 2010; Lecoutre & Killeen, 2010). But proof of a principle is always better then rebuttal of its denial. I tested p_rep’s ability to make predictions from data collected in the field, using meta-analyses of research on the same topics. Killeen (2005c) reported one analysis of 37 studies whose median p_rep was .71; 70% of those studies showed the predicted effect. In another analysis, the median p_rep was .75; after correcting for publication bias the authors reported 75% in the correct direction. Killeen (2007) performed a similar reanalysis of a meta-analysis, with similar excellent predictions (using the random effects variance reported by the author).

The Open Science Collaboration (2015) reported the results of their attempt to systematically replicate the results of 100 important scientific reports in four top psychology journals. They were less than perfectly successful. They used many indices of replication success. A prominent one was the proportion of replication attempts that achieved significance (at the .05 two-tailed level). Overall, this was a disappointing 36%. “These results make for grim reading” (Yong, 2015); “‘The success rate is lower than I would have thought,’ says John Ioannidis. .. whose classic theoretical paper ‘Why Most Published Research Findings are False’ has been a lightning rod for the reproducibility movement” (quoted in Yong, 2015). So, what does p_rep say? The average p-value in those studies was 0.028. Place this in the above formula, with d_C = z(.975) = 1.96. This calculation predicts that 55% of the attempted replicates will achieve significance, substantially more than they found, although well below a value of 95% as some naïve observers might expect. Furthermore, the effect size in replication was half of that in the original studies. If a greater proportion of significant replications is desired, increase the t-score of the original experiment, either by increasing its n, or by increasing the effect size through cleaner experimentation.

More precise explications of p_rep are available (Killeen, 2007), as are more introductory ones with additional applications (Sanabria & Killeen, 2007; Killeen, 2015). Irwin (2009) shows how to extend p_rep to signal detection theory and, of interest to the present audience, Ashby and O’Brien (2008) give a generalization for small-N research. It is true that no one goes to a circus to watch an average dog blunder. The technology of training matters. With tools such as p_rep we can predict how high Rex the Amazing Circus Dog will jump in the typical night, how often he will make it through the hoop in the next days’ circuses; and even how safe it is to raise the height of the hoop. We can also address scientific questions, knowing what statistics are best used for.

What Statistics Are for

Royall (1997, 2004) noted that statistics can address three types of questions: How should I evaluate this evidence? What should I do? What should I believe? The basic p_rep described above addresses the first question. It is intrinsically Bayesian but assumes no prior knowledge of the effect under investigation: It is constructed with “flat priors.” It is unfair to burden a new study with the bad results of earlier studies, so p_rep starts with a blank slate. P_rep can also play an important role in action (Killeen, 2006a), the second question, but that is not addressed here. It can address the third question, what should I believe, but not with flat priors. Should I believe Daryl Bem’s (2011) demonstration of precognition because the vanilla p_rep estimates its replicability as ever so slightly greater than chance? No: belief should be based on the totality of evidence (including, surprisingly, Cardeña, 2018), and this is achieved by incorporating well-informed priors into the computation of replicability. What this does is to effectively regress the estimates of replicability toward their prior mean (Killeen, 2007).

Understand

We can replicate many things without understanding them. I can throw a switch to turn on an LED, with the probability of failure p < .005, but still not understand how the diode emits cold light. Prediction and control show that we have a procedure that worked; exact replication shows that it wasn’t a fluke, and conceptual replications show that we have a model that works in other people’s hands on other subjects. That model constitutes a formal cause (a representation or description of inputs, operations, and outcomes; the blueprint of some system). Through the model, we understand some of the efficient causes that make a phenomenon occur. But understanding requires more. If I showed you a novel device, you might ask its name. Not recognizing the name, you would next ask “what is it for?” Function, or purpose, is thus another key component in understanding phenomena. Finally, you could “look under the hood” of the device. If you gleaned some sense of the machinery, then you would have a more complete understanding. The four kinds of questions—What starts it? How do we talk about, predict, and control it? What’s it for? and How does it do that?—are all coherent parts of scientific understanding (Killeen, 2001, 2013). Replicability concerns only one, the valid mapping of models to data; but because models are the tools by which we understand the world, it is an essential one.

Appendix : The Convoluted Logic of NHST

All principles, laws, generalizations, models, and regularities (conjectures; when discussing logic and Bayes, rules; when discussing inferential statistics, hypotheses) may be stated as material implications: A implies B, or A ➔ B, or if A then B. It is easier to disprove such conditional rules than to prove them. If A is present and B absent (or “false”: ~B), then the rule fails. If A is absent and B present, no problem, as there are usually many ways to get a B (many sufficient causes of it). Indeed, if A is false or missing the implication is a “counterfactual conditional” in the presence of which both B and ~B are equally valid (“If wishes were autos then beggars would ride”). If A is present and B then occurs “in a case where this rule might fail”, it lends some support (generality) to the rule, but it cannot prove the rule, as B might still have occurred because of other sufficient causes—perhaps they were confounds in the experiment, or perhaps happenstances independent of it. This is a universal problem in the logic of science: no matter how effective at making validated predictions, we can never prove a general conjecture true (indeed, conjectures must be simplifications to be useful, so even in the best of cases they will be only sketches; something must always be left out). Newton’s laws sufficed for centuries before Einstein’s, and still do for most purposes. Falsified models, such as Newton’s, can still be productive: it was due to the failure of stars in the outer edges of the galaxy to obey Newtonian dynamics that caused dark matter to be postulated. Dark matter “saved the appearance” of Newtonian dynamics. Truth and falsity are paltry adjectives in the face of the rich implications of useful theories, even if some of their details aren’t right.

Conditional science. To understand the contorted logic of NHST requires further discussion of material implication. If the rule A ➔ B holds and A is present, then we can predict B. If B is absent (~B), then we can predict that A must also be absent: ~B ➔ ~A (if either prediction fails, the rule/model has failed and should be rejected). “If it were solid lead it would sink; it is not sinking. Therefore, it is not solid lead.” This process of inference is called modus tollens and plays a key role in scientific inference, and in particular NHST. Predict an effect not found then either the antecedent (A) is not in fact present, or the predictive model is wrong (for that context). All general conjectures/models are provisional. Some facts (which are also established using material implication; see Killeen, 2013) and conjectures that were once accepted have been undone by later research. Those with a lot going for them, such as Newton’s laws, are said to have high “verisimilitude.” They will return many more true predictions than false ones, and often that matters more than if they made one bad call.

An important but commonplace error in using conditionals such as material implication is, given A ➔ B, to assume that therefore B ➔ A. This common error has a number of names: illicit conversion, and the fallacy of affirming the consequent among them. If you are the president of the United States, then you are an American citizen. It does not follow that if you are an American citizen, then you are the president of the United States. Seems obvious, but it is a pervasive error in statistical inference. If A causes B, then A is correlated with B, for sure. But the conversion is illicit: If A is correlated with B, you may not infer that A causes B. Smoke is correlated with fire, but does not cause it.

Counterfactual conditionals play an important role in the social and behavioral sciences. Some sciences have models that make exact predictions: There are many ways to predict constants such as Avogadro’s number, or the fine-structure constant, to high accuracy. If your model gets them wrong, your model is wrong. But in other fields exact predictions are not possible; predictions are on the order of “If A, then B will be different than if ~ A.” If I follow a response with a reinforcer, the probability of the response in that context will increase. Precise magnitudes, and in many cases even directions, of difference cannot be predicted. What to do?

Absurd science. Caught in that situation, statisticians revert to a method known in mathematics and logic as a reductio ad absurdum: assume the opposite of what you are trying to prove. Say you are trying to prove A, and show that its opposite implies B, ~ A ➔ B, but if we know (or learn through experiment) that B is false, then (by modus tollens) we conclude that “not A” must also be false, and ~ ~ A ➔ A. Voila, like magic, we have proved A. Fisher introduced this approach to statistical analysis, to filter conjectures that might be worth pursuit from those that were not. Illegitimate versions of it are the heart of NHST (Gigerenzer, 1993, 2004).

Here is how it works in statistics. You have a new strain of knock-out mouse and want to see if the partial reinforcement extinction effect (PREE) holds for it. The PREE predicts that mice that receive food for every fifth response (FR5) will persist longer when food is withheld (experimental extinction) than when given for every response (FR1). You conduct a between group experiment with 10 mice in each group. What you would like to predict is A ➔ n(FR5) > n(FR1), where A is the PREE effect, and n(FR) is the number of responses in extinction. But you have two problems: Even if you found the predicted effect, you could not affirm the proposition A (illicit conversion; affirming the consequent); and you have no idea how much greater the number has to be to count as a PREE. Double the number? 5% more? So, you revert to reductio ad absurdum, and posit the opposite of what you want to prove: ~ A ➔ H₀: n(FR5) = n(FR1). That is, not knowing what effect size to predict, predict 0 effect size: On the average, a zero difference between the mean extinction scores of the two groups. This prediction of “no effect” is the null hypothesis. If your data could prove the null hypothesis false, p(H₀|D) = 0, you could legitimately reject the rejection of your proposition, and conclude that the new strain of mice showed the PREE! Statistical inference will give you the probability of the data that you analyzed (along with all bigger effects), given that the null hypothesis is true: p(D|H₀). It is the area in Fig. 2 under the null distribution to the right of d₁. What the above conditional needs in the reductio, alas, is the probability of the hypothesis given that the data are true: p(H₀|D); not p(D|H₀), which is what NHST gives! Unless you are a Bayesian (and even for them the trick is not easy; their “approximate Bayesian computations” require technical skill), you cannot convert one into the other without making the fallacy of illicit conversion. You cannot logically ever “reject the null hypothesis” even if your p < 0.001, any more than you can assume that all Americans are presidents. All you can do is say that the data would be unlikely had the null been true; you cannot say that the null is unlikely if the data are true; that is a statement about p(H₀|D). You cannot use any of the standard inferential tools to make any statement about the probability of your conjecture/ hypothesis, on pain of committing a logical fallacy (Killeen, 2005b). Fisher stated this. Neyman and Pearson stated this. Many undergraduate stats text writers do not. You can never logically either accept or reject the null. Whiskey Tango Foxtrot! And the final indignity: even if you could generate a probability of the null from your experiment, material implication does not operate on probabilities, only on definitive propositions (Cohen, 1994). Is it surprising that we are said to be in a replication crisis when the very foundation of traditional statistical inference (NHST) in our field is fundamentally illogical, and its implementations so often flawed (Wagenmakers, 2007)? Even if you could make all these logical problems disappear, it is the nature of NHST to ignore the pragmatic utility of the results (the effect size), beyond its role in computing a p value. Even if it could tell you what is true, it cannot tell you what is useful.