dynr.mi: An R Program for Multiple Imputation in Dynamic Modeling

Abstract

Assessing several individuals intensively over time yields intensive longitudinal data (ILD). Even though ILD provide rich information, they also bring other data analytic challenges. One of these is the increased occurrence of missingness with increased study length, possibly under non-ignorable missingness scenarios. Multiple imputation (MI) handles missing data by creating several imputed data sets, and pooling the estimation results across imputed data sets to yield final estimates for inferential purposes. In this article, we introduce dynr.mi(), a function in the R package, Dynamic Modeling in R (dynr). The package dynr provides a suite of fast and accessible functions for estimating and visualizing the results from fitting linear and nonlinear dynamic systems models in discrete as well as continuous time. By integrating the estimation functions in dynr and the MI procedures available from the R package, Multivariate Imputation by Chained Equations (MICE), the dynr.mi() routine is designed to handle possibly non-ignorable missingness in the dependent variables and/or covariates in a user-specified dynamic systems model via MI, with convergence diagnostic check. We utilized dynr.mi() to examine, in the context of a vector autoregressive model, the relationships among individuals’ ambulatory physiological measures, and self-report affect valence and arousal. The results from MI were compared to those from listwise deletion of entries with missingness in the covariates. When we determined the number of iterations based on the convergence diagnostics available from dynr.mi(), differences in the statistical significance of the covariate parameters were observed between the listwise deletion and MI approaches. These results underscore the importance of considering diagnostic information in the implementation of MI procedures.

I. Introduction

THE past decade has seen growing interest in collecting and analyzing intensive longitudinal data (ILD) to study everyday life human dynamics in the social and behavioral sciences [1], [2]. Under an intensive longitudinal design, researchers often record participants’ physiological data and self-report data over an extended period of time using web- or smartphone based applications, and/or unobtrusively using wearable devices, smartphones, and other mobile devices. Self-report data that serve to capture the participants’ states in the moment, and in naturalistic ecological settings are often referred to as ecological momentary assessment (EMA) data [3], [4]. These various forms of ILD bring both new opportunities and challenges. They afford opportunities for researchers to study participants’ behaviors in more naturalistic settings, as oppose to in a traditional laboratory setting. However, data collection issues, such as device failures and noncompliance of the participants, also make missing observations common in such data sets. Unfortunately, most software’s missing data handling functions, even when they are present, are not designed to capitalize on fundamental features of ILD. In this paper, we present dynr.mi(), a function in the R package, Dynamic Modeling in R (dynr) [5], that implements ILD-inspired multiple imputation (MI) procedures in parallel with the fitting of dynamic systems models.

A. Missing Data and Multiple Imputation

Missingness in ILD, similar to any other data format, can be described by three major missing data mechanisms, namely, missing completely at random (MCAR), missing at random (MAR), and not missing at random (NMAR). According to Rubin’s classification [6], MCAR refers to the cases in which the missingness mechanism — specifically, the probability of whether a variable is missing at any particular time point for a participant — does not depend on any variables. In contrast, if the data are MAR, the probability of having a missing record depends on some observed variables. When predictors of the missing observation are unobserved, then the data are said to be NMAR. In the context of ILD with both physiological and EMA data, an example of MCAR could be the random failure of the wearable devices we use to collect physiological data. Persistent missing records early in the mornings are likely a case of MAR because such missingness depends on the time of the day. Finally, in the study of emotions, participants may choose not to report their current emotions when they are feeling especially upset. This kind of missing data is NMAR because the missingness mechanism depends on information that is unobserved in the data, the participants’ current emotions.

Previous research has shown that most contemporary missing data handling techniques, including listwise deletion, interpolation, pattern mixture models, may not work for ILD [7]. MI, however, has sufficient flexibility in dealing with missingness in ILD when implemented appropriately. Handling missing data using MI methods involves three steps [8]. First, missing observations in the data set are filled in with imputed values, namely, possible data values generated based on a pre-specified missing data model, resulting in multiple imputed data sets. These imputed data sets are then used in the model fitting procedures in the second step as if they were observed data sets without missing observations. As the final step, multiple sets of parameter estimation results from the model fitting procedure are pooled to obtain a set of final consolidated parameter point estimates and standard error estimates by the pooling rules proposed by Rubin [8].

One way to perform the imputation procedure for multivariate missing data is through fully conditional specification (FCS). With this method, possible values for missing observations in each variable are imputed iteratively as conditional on observed and imputed values in a particular data set by Markov Chain Monte Carlo (MCMC) techniques [9]. This method can be carried out with an R package: Multivariate Imputation by Chained Equations (MICE) [10], which performs imputation on a variable-by-variable basis using a series of chained equations [11], with imputation of the current variable performed as conditional on the subset of variables that have been imputed prior to the current imputation. To implement this method with ILD, an important adaptation is to include the preceding or following observation of the missing values in the imputation model to inform the imputation process. In a simulation study, two variations of the MI procedure were proposed and examined, namely full MI and partial MI [7]. The full MI approach requires imputation of all missing observations in the dependent variables as well as the covariates before any model fitting procedures. With the partial MI approach, however, only missingness in covariates is imputed, whereas Full Information Maximum Likelihood method (FIML [12]) is used to handle missingness in the dependent variables by using only the available observations to compute the log-likelihood function for parameter and standard error estimation purposes. Previous simulation results showed that with vector autoregressive (VAR) models, adopting the partial MI approach in handling missingness in longitudinal data produced best estimation results for parameters that appear in the dynamic model (see (2)) under conditions with low to moderate stability at the dynamic level, regardless of missing data mechanisms (i.e. MCAR, MAR, NMAR) [7].

B. Affect Arousal and Valence

Emotional experience in daily life can be captured as variations in individuals’ “core affect” [13], a neurophysiological state that is changing over the course of the day due to internal (e.g., hormonal fluctuations) and external influences (e.g., social interactions). Core affect can be conceptualized as an integral blend of momentary levels of valence (how pleasant vs. unpleasant one feels), and arousal (how active vs. lethargic one feels). Characteristics of the core affect have been found to be indicative of a person’s health and well-being [14], [15]. Core affect is consciously accessible, therefore we can ask people to provide self-reports on their core affect states to reflect variations in their emotional states [16]. However, core affect self-reports are prone to missingness, as for example participants might not be motivated to report their current arousal levels when they are feeling lethargic. Ignoring this kind of potentially NMAR data would lead to biases in the estimation process.

C. Psychophysiological Markers of Affect

As a result of technological progress in wearable health monitors, we can collect high-quality, multi-stream biomarker data in a relatively unobtrusive way. These markers can be used to infer psychological states and include measures of the sympathetic and parasympathetic nervous system activities, such as skin conductance and heart rate. Emotional or physical stressors tend to produce sympathetic arousal responses that are measurable via electrical changes on the skin surface. This electrodermal activity (EDA) has been linked to emotional arousal [17]. Parasympathetic activation helps the body achieve a relaxed state by slowing down the heart rate. At the same time, heart rate variability has been found to be indicative of stress [18]. Thus, EDA and heart rate are used in the present study to explain individuals’ self-report valence and arousal levels.

Physical activity levels might also influence affect — being physically active is generally associated with people feeling more pleasant and active. Some studies showed positive links between physical activity and both valence and arousal [19], with participants reporting increased positive affect and energy [20]. However, other studies [21] also reported the opposite patterns. In terms of directionality of the effect, [22] and [23] showed that feeling more positive predicted more subsequent physical activity.

II. Dynamic Modeling Framework in Dynr

The utility function described in the present study resides within an R package, dynr [5], that provides fast and accessible functions for estimating and visualizing the results from fitting linear and nonlinear dynamic models with regime-switching properties. The model fitting procedures in dynr can accommodate both longitudinal panel data (i.e., data with a large number of participants and relatively few time points), and ILD (i.e. single or multiple-subject data with a large number of time points). The modeling framework includes cross-sectional continuous data as a special case [24], but this special case does not fully utilize the key strengths of dynr. The dynr.mi() function described in this article is a utility function for performing MI concurrently with estimation of a subclass of models within dynr, namely, discrete-time state-space or different equation models. All computations within dynr are performed in C, but a series of user-accessible functions are provided in R. The MI approach is performed through repeated internal calls to another R package, MICE, as described in Section I, through incorporation of specially constructed lagged and related variables that, based on our experience [7], enhance the recovery of dynamics in ILD. The utility function serves to automate the procedures for handling missingness in the dependent variables and/or covariates through MI, thereby removing some of the barriers to dynamic modeling in the presence of missing data.

A. General Modeling Framework

At a basic level, the general modeling framework is composed of a dynamic model which describes how the latent variables change over time, and a measurement model which relates the observed variables to latent variables at a specific time. Currently, dynr.mi() has been tested only with linear discrete-time models. As such, we present only the broader model that can be viewed as a special case of the more general dynr modeling framework.

For discrete-time processes, the dynamic model exists in state-space form [25] as

$${\eta }_i\left(t_{i,j+1}\right)=f\left({\eta }_i\left(t_{i,j}\right),t_{i,j},x_i\left(t_{i,j+1}\right)\right)+w_i\left(t_{i,j+1}\right),$$ (1)

where i indexes the smallest independent unit of analysis, t_i,j (j = 1, 2, T_i) indicates a series of discrete-valued time points indexed by sequential positive integers. The term f(.) is a vector of dynamic functions that describe η_i(t_i,j+1), an r × 1 vector of latent variables at time (t_i,j+1) for unit i on occasion j + 1 as they relate to η_i(t_i,j) from the previous occasion, time (t_i,j), and x_i(t_i,j+1), a vector of covariates at time (t_i,j+1). Here, w_i(t_i,j) denotes a vector of Gaussian distributed process noises with covariance matrix, Q.

A linear special case of (1) can be obtained as:

$${\eta }_{\mathit{i}}\left(t_{i,j+1}\right)=\alpha +F{\eta }_i\left(t_{i,j}\right)+B{x}_i\left(t_{i,j+1}\right)+w_i\left(t_{i,j+1}\right),$$ (2)

where α is an r×1 vector of intercepts, F is an r × r transition matrix that links η_i(t_i,j+1) to η_i(t_i,j); and B is a matrix of regression weights relating the covariates in x_i(t_i,j+1) to η_i(t_i,j+1).

Due to the dependencies of η_i(t_i,j+1) on η_i(t_i,j) in (1) and (2), the initial conditions for the dynamic processes have to be “started up” at the first unit-specific observed time point, t_i,1. Here, we specify these initial conditions for the vector of latent variables, denoted as η_i(t_i,1), to be normally distributed with means μ_η1 and covariance matrix, Σ_η1 as

$${\eta }_i\left(t_{i,1}\right)~N\left({\mu }_{{\eta }_1},{\Sigma }_{{\eta }_1}\right).$$ (3)

Complementing the dynamic model in (1) is a discrete-time measurement model in which η_i(t_i,j) at time point t_i,j is indicated by a p × 1 vector of manifest observations, y_i(t_i,j). Missing data are accommodated automatically by specifying missing entries as NA, the R default for a missing value. The vector of manifest observations is linked to the latent variables as

$$\begin{gathered} y_i\left(t_{i,j}\right)={\tau }_{S_i\left(t_{i,j}\right)}+{\Lambda }_{S_i\left(t_{i,j}\right)}{\eta }_i\left(t_{i,j}\right)+A_{S_i\left(t_{i,j}\right)}{x}_i\left(t_{i,j}\right)+{\mathit{ϵ}}_i\left(t_{i,j}\right), \\ {\mathit{ϵ}}_i\left(t_{i,j}\right)~N(0,R), \end{gathered}$$ (4)

where τ is a p × 1 vector of intercepts, $A_{S_i\left(t_{i,j}\right)}$ is a matrix of regression weights relating the covariates to the observed variables, ${\Lambda }_{S_i\left(t_{i,j}\right)}$ is a p × r factor loading matrix relating the observed variables to the latent variables, and ϵ_i(t_i,j) is a p × 1 vector of measurement errors assumed to be serially uncorrelated over time and normally distributed with zero means and covariance matrix, R.

B. Estimation Procedures

The estimation procedures underlying dynr for fitting the model shown in (1)–(4) are described in detail in [5] and [26]. Here, we provide a shortened description of the key procedures.

Broadly speaking, the estimation procedures implemented in dynr are extensions of the Kalman filter (KF)[27], and its various continuous-time, nonlinear, and regime-switching counterparts. In the case of the linear discrete-time model shown in (1)—(4), the extended KF is applied to obtain the estimates of latent variable values and other by-products for parameter optimization. Assuming that the measurement and process noise components are normally distributed and that the measurement equation is linear as in (4), the prediction errors, y_i(t_i,j)−E (y_i(t_i,j)|Y_i(t_i,j)), where Y_i(t_i,j) = {y_i(t_i,k), k = 1, … , j}, are multivariate normally distributed. Capitalizing on this normality assumption, a log-likelihood function known as the prediction error decomposition function [24], [28]–[30] can be computed based on the by-products of the KF. By optimizing the prediction error decomposition function, we obtain the maximum-likelihood estimates of all time-invariant parameters as well as information criterion (IC) measures [29], [31] (e.g., Akaike Information Criterion (AIC) [32] and Bayesian Information Criterion (BIC) [33]). By taking the square root of the diagonal elements of the inverse of the negative numerical Hessian matrix of the prediction error decomposition function at the point of convergence, we obtain the standard errors of the parameter estimates.

C. Steps for Preparing and “Cooking” a Model

The package name “dynr” is pronounced the same as “dinner”. Consonant with the name of the package, we name the core functions and methods in dynr based on various processes surrounding the preparation of dinner, such as gathering ingredients (data in our case), preparing recipes (submodels), cooking (namely, applying recipes to ingredients), and serving the finished product.

The general procedure for using the dynr package can be grouped under five steps. The MI procedure, as we will describe in this article, constitutes an optional sixth step. First, the data (ingredients) are declared with the dynr.data() function.

Second, the recipes — namely, submodels corresponding to various components of (1)–(4) — are prepared. This is declared as a series of prep.*() functions to yield an object of class dynrRecipe. These recipe functions are shown below.

1. The prep.measurement() function defines elements of the measurement model as shown in (4), except for the structure of R.

2. The dynamic model is defined using one of two possible functions: prep.matrixDynamics() is used to defined elements of (2) in the linear special case by specifying α, F and B; prep.formulaDynamics() provides more flexibility in defining any nonlinear dynamic functions that adhere to the form of (1).

3. The prep.initial() function defines the initial conditions for the dynamic processes as shown in (3), specifically, the structures of μ_η1 and Σ_η1.

4. The prep.noise() function defines the covariance structures of the measurement noise covariance matrix (i.e., R in (4); denoted as “observed” within this function), and the dynamic (denoted as “latent”) noise covariance matrix (i.e., Q).

5. (Optional) The prep.regimes() function specifies the regime switching structure of the model in cases involving multiple unobserved regimes (or phases) characterized by different dynamics or measurement structures. The models considered in the present article are single-regime models and thus do not require the specification of this function.

Following the data and recipe declaration processes, the third step combines the data and recipes together via the dynr.model() function. Fourth, the model is cooked with dynr.cook() to estimate the free parameters and standard errors. Fifth and finally, results may be served using any of the summary and presentation functions within dynr, such as: summary() — for summarizing parameter and standard error estimates from dynr.cook(); printex() — for automating the generation of modeling equations and TEX code in LATEX format; plotFormula() — for plotting the key modeling equations in the plotting window; and various plotting functions including plot(), dynr.ggplot(), and autoplot() [5].

In the next section, we describe a newly added function within the dynr package, dynr.mi(). This function constitutes an optional sixth step in the model cooking procedure, namely, to perform MI to handle missingness in the covariates, x_i(t_i,j+1), and optionally, the manifest variables in y_i(t_i,j+1).

III. Dynr.mi()

The dynr.mi() function is designed to handle ignorable and possibly non-ignorable missingness in the dependent variables and/or covariates in a user-specified dynamic systems model of the form shown in (1)–(4). dynr.mi() accomplishes this by integrating the estimation functions in dynr package and the MI functions in the MICE package. The dynr.mi() function is described in Fig. 1, with a summary of the list of arguments in Table I.

Fig. 1.

The usage of dynr.mi()

TABLE I.

List of Arguments in dynr.mi()

Parameter	Type	Meaning
dynrModel	dynrModel	Data and model setup
which.aux	character	Names of the auxiliary variables used in the imputation model
which.lag	character	Names of the variables to create lagged responses for imputation purposes
lag	integer	Number of lags of variables in the imputation model
which.lead	character	Names of the variables to create leading responses for imputation purposes
lead	integer	Number of leads of variables in the imputation model
seed	integer	Random number seed to be used in the MI procedure
m	integer	Number of multiple imputations
Iter	integer	Number of MCMC iterations in each imputation
imp.exo	logical	Flag to impute the exogenous variables
imp.obs	logical	Flag to impute the observed dependent variables
diag	logical	Flag to use convergence diagnostics
Rhat	numeric	Value of the $\widehat{R}$ statistic used as the criterion in convergence diagnostics
verbose	logical	Flag to print the intermediate output during the estimation process
conf.level	numeric	Confidence level used to generate confidence intervals

In the following subsections, we explicate the major steps underlying a call to dynr.mi(). These steps begin with (A) the extraction of modeling and additional MI information from a dynrModel object, followed by: (B) creation of variables thought to be especially helpful in MI of ILD; (C) execution of MI; (D) inspection of convergence diagnostics; (E) cooking and pooling of dynr.cook() results following evaluation of convergence diagnostics. We describe each of these steps in turn, and elaborate within each step pertinent arguments from the overall dynr.mi() function.

A. Extract Information from dynrModel Object

As described in Section II, data and recipes should be prepared and mixed together into a dynrModel object. Therefore the first step in dynr.mi() is to extract information needed in the MI and parameter estimation procedure from a dynrModel object, including data, names of the observed variables and covariates, as well as other modeling details.

In the call to dynr.mi() above, the argument which.aux allows users to specify auxiliary variables that can be included in the imputation model. Auxiliary variables are variables that do not appear in the dynamic systems models, but are related to the missing data mechanism. Thus, including these variables in the imputation model provides imputed values that conform approximately to the MAR condition, thereby improving the parameter estimates relevant to the variables of interest [7], [34]. The argument which.aux can be supplied either as a single string, or a vector of strings corresponding to a list of auxiliary variables to be included in the imputation model. The strings provided to which.aux have to be consistent with the column names in the data set. The default value is NULL, meaning no auxiliary variables are included in the imputation model.

B. Create Lagged and/or Leading Variables

Dynamic systems often show dependencies of the current value of the system at time t_i,j on its own previous (lagged; e.g., at times t_i,j−1, t_i,j−2, and so on) and future (leading; e.g., at times t_i,j+1, t_i,j+2, and so on) values. As such, these lagged and/or leading values become relevant variables that are important to be included in the imputation model [7], [35]. This step prepares the lagged and/or leading variables to be included in the imputation model. Arguments that are pertinent to the set-up of this particular step include:

• which.lag: A single string or a vector of strings indicating a list of variables whose lagged values are to be included in the imputation model. The strings have to match the column names in the data set. The default value is NULL, meaning no lagged variables are included in the imputation model.

• lag: An integer specifying the maximum number of lags of variables when creating lagged variables. The default value is 0, meaning no lagged variables are included in the imputation model.

• which.lead: A single string or a vector of strings indicating a list of variables whose leading values are to be included in the imputation model. The strings have to match the column names in the data set. The default value is NULL, meaning no leading variables are included in the imputation model.

• lead: An integer specifying the maximum number of leads when creating leading variables. The default value is 0, meaning no leading variables are included in the imputation model.

C. Implement Imputations via Automated Call to MICE

The imputations of missing data are implemented using the default imputation methods in the mice() function in MICE package. For instance, numerical variables are imputed using the predictive mean matching method, and binary variables are imputed using the logistic regression method [10]. In this step, users have to make further decisions on the specification of the imputation model. For instance, users need to specify number of imputations and number of MCMC iterations in each imputation. dynr.mi() also allows users to choose whether to use full MI or partial MI approach by specifying the value of imp.obs. After this step, m imputed data sets are generated for further use in the estimation process. Pertinent arguments concerning this step include:

• seed: An integer providing the random number seed to be used in the MI procedure. The default value is NA, meaning no explicit random number seed is specified.

• m: An integer indicating the total number of imputations in the MI procedure. The default value is 5.

• iter: An integer indicating the total number of MCMC iterations in each imputation in the MI procedure. The default value is 5.

• imp.exo: A logical value indicating whether missingness in the covariates is to be handled via MI. The default value is TRUE.

• imp.obs: A logical value indicating whether missingness in the dependent variables is to be handled via MI. The default value is FALSE, meaning that a partial MI approach is requested. If the value is TRUE, dynr.mi() will implement the full MI approach.

D. Conduct Convergence Diagnostic Check

The dynr.mi() function allows users to check the convergence of the MCMC process in the MI procedure by automating the output generated by the mice() function in MICE package, supplemented with $\widehat{R}$ plots added by us. The $\widehat{R}$ statistic assesses the convergence of computations across multiple MCMC chains by comparing the within-chain variance to the variance of the pooled draws across multiple chains [36]. Brooks and Gelman used $\widehat{R}<1.2$ as a guideline for convergence [37]. The more stringent criterion can be $\widehat{R}<1.1$, which is used as the default criterion in dynr.mi(). The $\widehat{R}$ plots allow users to check the values of $\widehat{R}$ statistic given numbers of MCMC iterations, thus facilitating the decision making on the number of MCMC iterations to specify in the MI procedure. Pertinent arguments that arise in this step include:

• diag: A logical value indicating whether convergence diagnostics are to be output to help monitor the convergence of the MCMC process in the MI procedure. The default value is TRUE. If the value is FALSE, dynr.mi() will not print the convergence diagnostic results.

• Rhat: A numeric value of the $\widehat{R}$ statistic. The default is to use 1.1 as the threshold for flagging potential convergence issues in the $\widehat{R}$ plots.

E. Cooking and Pooling of Estimation Results

The final step in dynr.mi() is to perform model estimation separately for each of the m imputed data sets, and pool m sets of parameter and standard error estimates into one set of estimates following Rubin’s procedure [8]. m sets of parameter and standard error estimates are obtained via automated internal calls to the dynr.cook() function using each of the m imputed data sets. Output from this step includes parameter and standard error estimates, values of the t statistics, confidence intervals, and p values. Pertinent arguments that arise in this step include:

• verbose: A logical value indicating whether intermediate output for the estimation process is to be printed. The default value is TRUE.

• conf.level: A cumulative proportion indicating the level of desired confidence intervals for the final parameter estimates. The default value is 0.95.

IV. Empirical Study

We use data collected in a 4-week long EMA study at The Pennsylvania State University to illustrate the analysis of data with missingness via dynr.mi(). All participant interactions were overseen by the University’s Institutional Review Board. The data consisted of 25 participants’ physiological measures and self-report emotional states and psychological well-being. The age of the participants ranged from 19 to 65, and 67% of them were female.

Physiological measures were collected via participants wearing Empatica’s E4’s wristbands [38]. The E4 is a research-grade wearable health monitor which has four types of sensors: (1) A pair of tonic EDA sensors measuring skin conductance response at a 4 Hz sampling rate; (2) a photoplethysmographic sensor monitoring blood volume pulse (BVP) at 64 Hz sampling rate; (3) a 3-axis accelerometer recording motion at 32 Hz sampling rate; and (4) an infrared thermopile recording skin temperature at 4 Hz sampling rate. In terms of physiological measures used in the data analysis, EDA was obtained from EDA sensors; heart rate was calculated based on BVP; root mean squared acceleration was calculated from the 3 data streams of the accelerometer.

Participants were asked to report six times daily on their emotional states and psychological well-being, such as their levels of valence, arousal, relaxedness, and feelings of love. Each time they received a text message on their smartphones with a link to a web survey, prompting them to click on the link and complete the survey right away. The text messages arrived on a semi-random schedule: participants’ regular awake time was divided into six equal intervals and a random prompt was scheduled to each. In terms of self-report measures used in the data analysis, core affect was obtained from self-reports on how pleasant and active the participants felt at the moment; relaxadness was measured by asking how relaxed they felt at the moment; feelings of love was measured by asking how much they felt love at the moment. Answers were provided on a digital sliding scale ranging from 0 (not at all) to 100 (extremely).

A. Data Preparation

Missingness in self-reports might have occurred on occasions where it was inconvenient for participants to respond to the survey prompts (e.g., they felt really down) or when they simply missed the survey prompts. Missingness in the physiological measures might have occurred when participants recharged the E4 and uploaded data every other night or on occasions that they did not use the devices correctly. However, it is also possible that although the participants were not wearing the wristband (e.g., they took it off for shower), it was still recording data. We filtered out such data based on skin temperature and heart rate readings. For instance, if the skin temperature and heart rate did not fall into the liberal range one would expect from human participants (between 30 and 43 Celsius degrees for skin temperature and between 30 and 200 beats per minute for heart rate), all physiological data obtained from the wearable device at that time would be regarded as invalid and set to NA. This resulted in deleting around 6.3% of the records.

To pair physiological measures and self-report measures, for all measures, we aggregated them into four blocks (i.e., 12am-6am, 6am-12pm, 12pm-6pm, 6pm-12am) per day to represent the sleeping, morning, afternoon, and night periods. Therefore in our final data set, each participant had 28 × 4 records. The proportions of missingness for each participant ranged from 8% to 42% in terms of physiological data, and 9% to 32% in terms of self-report data. For the overall missing rates, there were around 20% missingness in physiological data and 26% missingness in self-report data.

Finally, for each participant, both physiological measures and self-report measures were standardized to zero means and unit variances.

B. Data Analysis

In the analysis below we focus on the association between the two elements of core affect, valence and arousal, over time. Two physiological measures, acceleration and heart rate, were included in the model as covariates. We built a VAR model to examine the relationships among the participants’ physical activity (acceleration), heart rate, and self-report core affect while handling the missingness via the full and partial MI approaches. The VAR model can be described as:

$$\begin{gathered} \left[\begin{array}{c}va{l}_{it}\\ aro{u}_{it}\end{array}\right]=\left[\begin{array}{ll}{a}_{11}\hfill & a_{12}\hfill \\ a_{21}\hfill & a_{22}\hfill \end{array}\right]\left[\begin{array}{c}va{l}_{i,t-1}\\ aro{u}_{i,t-1}\end{array}\right]+\left[\begin{array}{cc}{c}_1& d_1\\ c_2& d_2\end{array}\right]\left[\begin{array}{c}ac{c}_{it}\\ h{r}_{it}\end{array}\right]+\left[\begin{array}{c}{u}_{1it}\\ u_{2it}\end{array}\right] \\ {\left[\begin{array}{ll}{u}_{1it}\hfill & u_{2it}\hfill \end{array}\right]}^{\text{T}}~N({\left[\begin{array}{cc}0& 0\end{array}\right]}^{\text{T}},\left[\begin{array}{cc}{\sigma }_{u_1}^2& {\sigma }_{u_1{u}_2}\\ {\sigma }_{u_1{u}_2}& {\sigma }_{u_2}^2\end{array}\right]) \end{gathered}$$ (5)

where a₁₁ and a₂₂ are auto-regression parameters — i.e., the within-construct association between valence (arousal) at time t and time t − 1; a₁₂ and a₂₁ are cross-lagged regression parameters — i.e., the across-construct association between valence (arousal) at time t and arousal (valence) at time t – 1; c₁ and c₂ are the coefficients of acceleration — i.e., the association between physical activity and core affect; d₁ and d₂ are the coefficients of heart rate — i.e., the association between heart rate and core affect. u_1it and u_2it are the measurement errors for valence and arousal at time t, which are assumed to be normally distributed and correlated.

Data analysis implemented in dynr is described below. The R codes can be found in the Appendix. First, the data set was structured to be a long format and passed to dynr.data(). In dynr.data(), we specified the names of the ID variable, TIME variable, observed variables, and covariates. Then we prepared all recipes needed in the model fitting procedure using prep.*() functions described in Section II. Finally, data and recipes were passed to dynr.model() to build a dynrModel object, which was then passed to dynr.mi(). The specification of arguments in dynr.mi() is shown in Fig. 2.

Fig. 2.

An example of using the dynr.mi() function

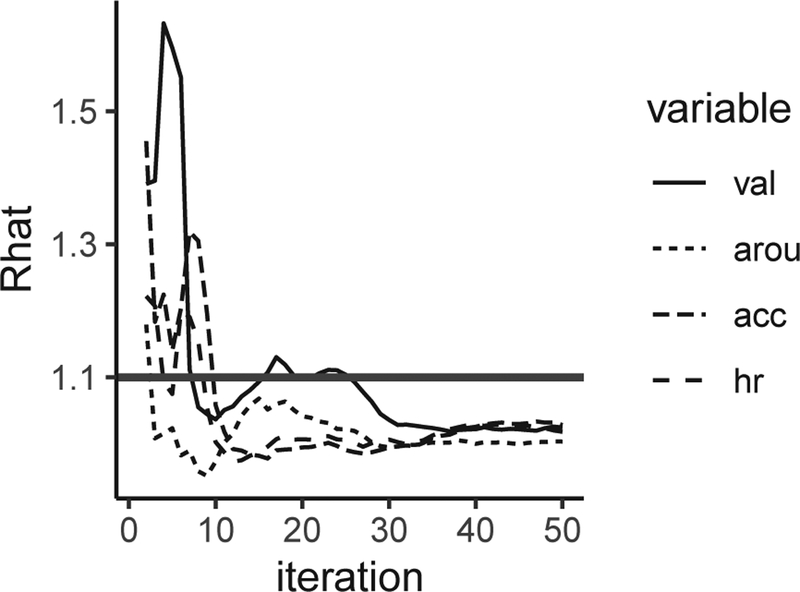
Specifically, EDA, feelings of love, and relaxedness were selected to be auxiliary variables given their possible associations with variations in the participants’ core affect, acceleration, and heart rate. In addition to auxiliary variables, we included lagged information for both valence and arousal up to the previous time point (i.e., lag of 1) in the imputation model. imp.obs was set as FALSE to request a partial MI approach. Results from the partial MI approach were then compared to those from the full MI approach and listwise deletion approach. With listwise deletion approach, only entries with missingness in covariates were deleted. We set the number of imputations as 5, which is the default number of imputations in the mice() function in MICE package. The number of MCMC iterations in each imputation was set as 30 based on the $\widehat{R}$ plot shown in Fig. 3 to obtain stable imputation results. The $\widehat{R}$ plot was obtained by setting iter as 50.

Fig. 3.

Values of $\widehat{R}$ statistics under iterations ranging from 2 to 50. The criterion of convergence was set as $\widehat{R}<1.1$

C. Results

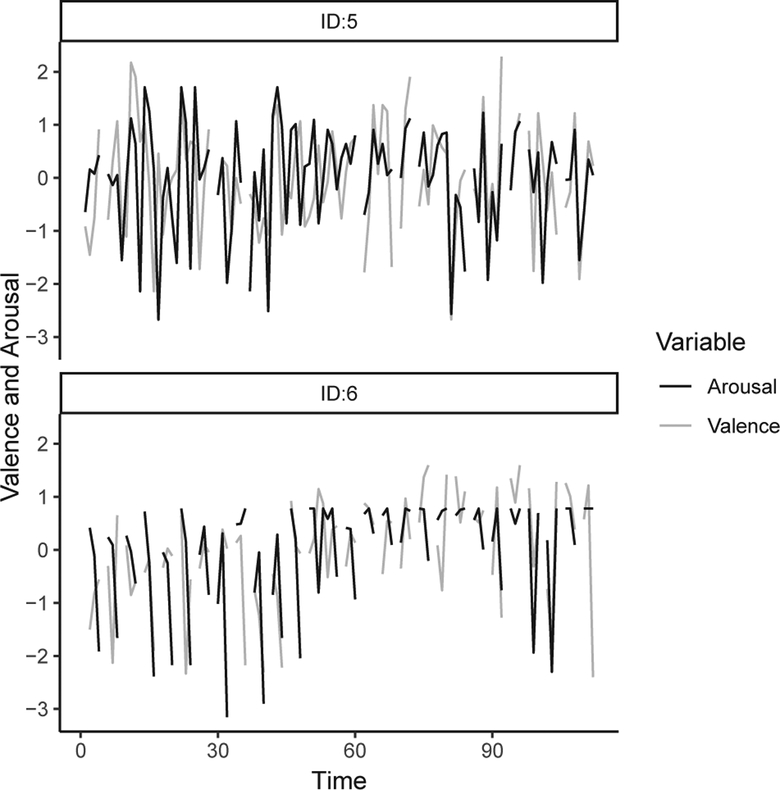
The trajectories of core affect for two participants are shown in Fig. 4. From the plot we can see that valence and arousal were associated with each other over time. Parameter estimation results from the VAR model using the three approaches considered are shown in Table II. Here, we focus on describing results from the partial MI approach in detail. As we can see from Table II, there was significant within-construct stability over time. Specifically, participants’ levels of valence were positively associated with previous levels of valence (a₁₁ = 0.23, SE = 0.03, p < 0.05), indicating moderately high continuity in participants’ valence levels. High positive values of auto-regression parameters have been described as high inertia in the affect literature [14], [39], reflecting a construct’s relative resistance to change. In a similar vein, participants’ levels of arousal were positively associated with their previous levels of arousal (a₂₂ = 0.09, SE = 0.03, p < 0.05).

Fig. 4.

Individual trajectories of core affect from two participants over 28 × 4 time points. Valence and arousal were assessed using self-reports of how pleasant and active they felt respectively, rated on a scale ranging from 0 (not at all) to 100 (extremely). The data were scaled to zero mean and unit variance

TABLE II.

Parameter Estimates for Empirical Data

	Listwise Deletion			Partial MI			Full MI
Parameter	Estimate	SE	95% CI	Estimate	SE	95% CI	Estimate	SE	95% CI
a11	0.19*	0.03	(0.13, 0.25)	0.23*	0.03	(0.17, 0.28)	0.18*	0.03	(0.12, 0.24)
a12	0.10*	0.03	(0.05, 0.16)	0.09*	0.03	(0.04, 0.15)	0.06*	0.03	(0.01, 0.12)
a21	0.09*	0.03	(0.04, 0.14)	0.12*	0.03	(0.07, 0.18)	0.10*	0.02	(0.05, 0.15)
a22	0.08*	0.03	(0.02, 0.13)	0.09*	0.03	(0.03, 0.14)	0.05*	0.03	(0.00, 0.11)
c1	0.04	0.03	(−0.02, 0.10)	0.04	0.03	(−0.02, 0.10)	0.04	0.03	(−0.02, 0.10)
c2	0.14*	0.03	(0.08, 0.20)	0.14*	0.03	(0.08, 0.20)	0.13*	0.03	(0.07, 0.19)
d1	0.06	0.03	(−0.01, 0.12)	0.07*	0.03	(0.01, 0.13)	0.08*	0.03	(0.02, 0.15)
d2	0.21*	0.03	(0.14, 0.27)	0.24*	0.04	(0.16, 0.31)	0.28*	0.04	(0.21, 0.36)

Note:

^*p < 0.05.

There was significant across-construct stability over time. That is, participants’ levels of valence were positively associated with previous levels of arousal (a₁₂ = 0.09, SE = 0.03, p < 0.05), indicating that participants who felt more active might subsequently feel more pleasant. In addition, participants’ levels of arousal were positively associated with previous levels of valence (a₂₁ = 0.12, SE = 0.03, p < 0.05), indicating that participants who were more pleasant would feel more active at the following measurement time point.

Furthermore, significant associations were found among the covariates and the dependent variables. Specifically, participants’ acceleration was found to be positively associated with levels of arousal (c₂ = 0.14, SE = 0.03, p < 0.05), indicating that participants who reported higher levels of physical activity also felt more active. However, we did not find significant association between acceleration and valence. In addition, heart rate was found to be positively associated with both valence (d₁ = 0.07, SE = 0.03, p < 0.05) and arousal (d₂ = 0.24, SE = 0.04, p < 0.05). The size of the regression coefficient was three times as large for arousal than for valence. Given that the dependent variables and covariates were both standardized, this suggested a much stronger link between arousal and heart rate than between valence and heart rate.

Results from the two MI approaches were similar to each other, but some differences were observed in comparison to results from the listwise deletion approach. Specifically, interpretations concerning the VAR dynamics of the dependent variables were similar across all approaches. However, some differences were observed with regard to the statistical significance of the covariates. Valence and heart rate were found to be significantly associated under the full MI and partial MI approaches, but this association was not statistically significant under the listwise deletion approach. Such divergence in results between the listwise deletion approach and the other MI approaches only emerged after we used 30 MCMC iterations to obtain each imputed data set based on the information from the diagnostic plot shown in Fig. 3. For instance, when we used 20 MCMC iterations in the MI procedure, the association between valence and heart rate was not statistically significant under both MI and listwise deletion approaches. This shows the importance of considering diagnostic information in determining details of the MI procedures.

V. Discussion and Conclusions

In the present study, we introduced dynr.mi(), a funtion in dynr package that implements MI with dynamic systems models, and demonstrated its use in handling missingness in both dependent variables and covariates in a VAR model.

The VAR model provided a platform for examining the relationships among individuals’ self-report core affect, acceleration, and heart rate. Auxillary variables used for imputation of missingness included EDA, relaxedness, and feelings of love. In line with previous studies, the present study showed that the psychophysiological markers were associated with the psychological states. For instance, heart rate was found to be positively associated with both valence and arousal levels, indicating that higher levels of heart rate might be associated with feeling more pleasant and active. In terms of the relationship between physical activity and self-report core affect, previous studies showed mixed results [20], [21]. Our analysis found that levels of physical activity were positively associated with arousal levels but not associated with valence levels, indicating that participants who have higher levels of physical activity might feel more active. The present study also found that participants’ current core affect could be predicted by their previous core affect.

Several features of dynr.mi() make it particularly valuable. First, currently dynr can only handle missingness in dependent variables via FIML but cannot handle missingness in covariates [5], which limits the application of dynr in fitting more complex models. By incorporating MI approaches, the dynr.mi() function extends the dynr package so that dynr can be applied to fit a wider range of dynamic systems models. Second, MI approaches have advantages over other approaches in handling missing data. Compared to listwise deletion approach which directly removes records with missingness from the data set, MI approaches preserve these records in the data set and conduct imputation based on available information. Compared to FIML which cannot handle missingness in covariates, MI approaches are more flexible in terms of accommodating various types of variables. Such flexibility enables us to include more information in the imputation procedure such as auxiliary variables, leading and/or lagged variables. Third, dynr.mi() allows for checking of convergence based on the $\widehat{R}$ statistic. The $\widehat{R}$ statistic provides information to facilitate making an informed decision on the appropriate number of MCMC iterations needed to evaluate convergence.

Although MI approaches can be relatively flexible, it is highly recommended that users exercise caution when specifying the imputation model. For instance, auxiliary variables may increase biases in the parameter estimates if they are not chosen appropriately, so sensitivity tests are highly recommended to examine the influence of auxiliary variables on the parameter estimation results [34]. The other critical step is the specification of number of imputations. In many cases, 5 imputations would be sufficient [8], but more imputations may be needed when it comes to higher missing rates, more complex models, smaller sample sizes, and longitudinal designs [40], [41]. Finally, previous studies did not sufficiently consider the number of MCMC iterations needed to obtain stable imputation results. Here, our results underscore the importance of careful consideration of diagnostic information such as that obtained through the $\widehat{R}$ statistic.

The present study only examined the performance of dynr.mi() in an empirical study. Further studies are needed to examine the effectiveness of dynr.mi() under different missing data scenarios via Monte Carlo simulation studies. Previous simulation studies have found that the two MI approaches illustrated in the present article demonstated better performance than listwise deletion approach under all missing data mechanisms (i.e., MCAR, MAR, NMAR) [7], [42]. The partial MI approach was found to have better performance than the full MI approach, especially for point estimates of auto- and cross-regression parameters [7]. However, such results were obtained only from a specific model (VAR model) with relative low auto-regression parameters (i.e., low inertia). Further simulation studies are in order to more thoroughly investigate the performance of MI approaches in fitting other dynamic systems models and VAR models with greater stability over time.

Biography

Yanling Li is a graduate student in the Department of Human Development and Family Studies at the Pennsylvania State University. Her research focuses on the development of dynamic systems models for the analysis of intensive longitudinal data and the application of statistical methods to substantive areas such as emotion and substance use. She is also interested in the implementation of statistical methods in the Bayesian framework and has been working on developing user-friendly software tools to facilitate the dissemination of Bayesian methods.

Linying Ji is a graduate student in the Department of Human Development and Family Studies at the Pennsylvania State University. Her research interest lies broadly in developing and applying statistical methods to the study of child development processes in the context of family systems. In particular, she is interested in developing and applying dynamic systems modeling techniques to study intra-individual change as well as inter-individual differences using repeated measurement data with ecological momentary assessment design and wearable devices.

Zita Oravecz is an assistant professor in the Department of Human Development and Family Studies at the Pennsylvania State University. Her research focuses on developing and applying latent variable models for repeated measurement data to characterize differences among individuals in emotional and cognitive functioning and development. She employs the ecological momentary assessment design to collect intensive longitudinal data on people’s everyday life experiences and physiological functions to uncover the underlying pathways in these psychological processes.

Timothy R. Brick is an assistant professor in the Department of Human Development and Family Studies at the Pennsylvania State University where he heads the Real Time Science Laboratory. His research focuses on methods and paradigms to measure, model, and manipulate human behavior as it occurs. He focuses specifically on modeling and intervention approaches related to affect and well-being, especially in cases where affect shows intricate dynamics, such as dyadic and multiadic social interaction, and addiction recovery.

Michael D. Hunter is an assistant professor in the School of Psychology at the Georgia Institute of Technology in Atlanta where he heads the Modeling Dynamics of Humans lab. Dr. Hunter develops the statistical R packages dynr and OpenMx. He also continues to work on multiple research studies at the University of Oklahoma Health Sciences Center, including multi-site and state-wide longitudinal trials. These projects span a range of topics from youth with problematic sexual behaviors, to children with autism, to young people involved in Child Welfare Services. His research interests include methods for intensive longitudinal data analysis, latent variable models, and lifespan development.

Sy-Miin Chow is Professor of Human Development and Family Studies at the Pennsylvania State University. The focus of her work has been on developing and testing longitudinal and dynamic models, including differential equation models, time series models and state-space models; and practical alternatives for addressing common data analytic problems that arise in fitting and evaluating these models. She is a winner of the Cattell Award from the Society of Multivariate Experimental Psychology (SMEP) as well as the Early Career Award from the Psychometric Society.

Appendix

An Example of Using dynr

## The data are declared with the dynr.data() function

rawdata <- dynr.data(data, id=“PID”, time=“Time”,
                            observed=c(“val”,“arou”),
                            covariates=c(“acc”,“hr”))

## Define elements of the measurement model

meas <- prep.measurement(
  values.load=matrix(c(1,0,
                       0,1),ncol=2,byrow=T),
  params.load=matrix(rep(“fixed”,4),ncol=2),
  state.names=c(“val”,“arou”),
  obs.names=c(“val”,“arou”)
)

## Define elements of the dynamic model

formula =list(
  list(val ~ a_11*val + a_12*arou + c1*acc + d1*hr,
       arou ~ a_21*val + a_22*arou + c2*acc + d2*hr
  ))

dynm <- prep.formulaDynamics(formula=formula,
                                    startval=c(a_11 = .5, a_12 = .4,
                                               a_21 = .4, a_22= .5,
                                               c1 = .3, c2 =.3,
                                               d1 = .5, d2 = .5
                                    ), isContinuousTime=FALSE)

## Define the initial conditions of the model

initial <- prep.initial(
  values.inistate=c(0.6,0.6),
  params.inistate=c(’mu_val’, ’mu_arou’),
  values.inicov=matrix(c(3,0,
                         0,2),byrow=T,ncol=2),
  params.inicov=matrix(c(“v_11”,“c_12”,
                         “c_12”,“v_22”),byrow=T,ncol=2))

## Define the covariance structures of the measurement noise
covariance matrix and the dynamic noise covariance matrix

mdcov <- prep.noise(
  values.latent=matrix(c(0.5,0.05,
                         0.05,0.5),byrow=T,ncol=2),
  params.latent=matrix(c(“v11”,“c12”,
                         “c12”,“v22”),byrow=T,ncol=2),
  values.observed=diag(rep(0,2)),
  params.observed=diag(c(’fixed’,’fixed’),2))

## Pass data and recipes into dynrModel object

model <- dynr.model(dynamics=dynm, measurement=meas,
                           noise=mdcov, initial=initial,
                           data=rawdata,
                           outfile=paste(“trial.c”,sep=“”))

## Implement MI and model fitting with dynr.mi() function

dynr.mi (model,
         which.aux = c(“eda”,“love”,“relax”),
         which.lag = c(“val”,“arou”),
         lag = 1,
         which.lead = NULL, lead = 0,
         m = 5, iter = 30,
         imp.obs = FALSE, imp.exo = TRUE,
         diag = TRUE, Rhat = 1.1,
         conf.level = 0.95,
         verbose = TRUE, seed = 12345)