Abstract
The neurobiological mechanisms of nonsymbolic number processing in humans are still unclear. Computational modeling proposed three successive stages: first, the spatial location of objects is stored in an object location map; second, this information is transformed into a numerical summation code; third, this summation code is transformed to a number-selective code. Here, we used fMRI-adaptation to identify these three stages and their relative anatomical location. By presenting the same number of dots on the same locations in the visual field, we adapted neurons of human volunteers. Occasionally, deviants with the same number of dots at different locations or different numbers of dots at the same location were shown. By orthogonal number and location factors in the deviants, we were able to calculate three independent contrasts, each sensitive to one of the stages. We found an occipitoparietal gradient for nonsymbolic number processing: the activation of the object location map was found in the inferior occipital gyrus. The summation coding map exhibited a nonlinear pattern of activation, with first increasing and then decreasing activation, and most activity in the middle occipital gyrus. Finally, the number-selective code became more pronounced in the superior parietal lobe. In summary, we disentangled the three stages of nonsymbolic number processing predicted by computational modeling and demonstrated that they constitute a pathway along the occipitoparietal processing stream.
Introduction
Extracting the number of elements from a visual display, usually referred to as nonsymbolic number or numerosity, requires a great deal of computation. In recent years, the neurobiological mechanisms of nonsymbolic number processing have started to become unraveled. As with other quantitative dimensions (Salinas, 2006; Verguts, 2007), it was found that there are two ways in which neurons can code numerosity. In the first, number-selective coding, different neurons have their own preferred numerosity and respond as a function of the distance between their preferred numerosity and the displayed numerosity. Such neurons have been identified in monkey frontal and parietal cortex (Nieder and Miller, 2004). In humans, there is both fMRI (Piazza et al., 2004) and behavioral (Reynvoet et al., 2002) evidence for number-selective coding. The second, summation coding, is achieved by neurons exhibiting a monotonic rate code for number (e.g., stronger response for larger number). Such neurons have been observed in monkey parietal cortex (Roitman et al., 2007), and there is behavioral (Roggeman et al., 2007) and fMRI (Santens et al., 2010) evidence for summation coding in humans.
A critical but unresolved issue concerns the relationship between these two coding schemes and the preceding visual preprocessing stages. Computational models (Dehaene and Changeux, 1993; Verguts and Fias, 2004) have proposed three different stages for numerosity processing. In the first stage, the spatial locations of the to-be-enumerated elements are stored in an object location map (Goldberg et al., 2002). Rather than being specifically devoted to number processing, this map has a more general function, for instance, supporting spatial working memory (Roggeman et al., 2010). This information is then transformed into a summation code in the second stage, which is subsequently transformed into a number-selective code in the third stage.
This functional organization remains to be empirically determined. Previous studies have taken partial steps toward this issue. Roggeman et al. (2010) obtained evidence for an object location map in regions traditionally implied in visuospatial working memory (Todd and Marois, 2004). Santens et al. (2010) observed a larger blood oxygenation level-dependent (BOLD) signal for larger numerosities in the posterior superior parietal cortex. However, these studies did not allow distinguishing between different stages. Here, we go beyond this earlier work by using fMRI adaptation to identify the three postulated stages of numerosity processing and their anatomical location relative to one another.
In each fMRI run, we repeatedly presented the same nonsymbolic numerosity (collection of dots) with dots at the same locations in the visual field to adapt neurons involved in the processing of this numerosity (comprising object location, summation, and number-selective neurons). Occasionally, a deviant stimulus with a deviant number of dots and/or dots at deviant locations was presented. A factorial design was created over the deviant stimuli, which allowed us to calculate three independent contrasts, each sensitive to one of the three stages.
Materials and Methods
Participants.
Twenty-three healthy right-handed male volunteers (25.8 ± 4.5 years) participated after giving written informed consent. The study was approved by the ethical committee of the Medical Department of Ghent University.
Stimuli and procedure.
Stimuli were patterns of one to five white dots (size between 0.2 and 0.63 visual degrees), spanning maximally 10° on a black background. The majority of stimuli were adaptation stimuli, which always contained the same number of dots (2, 3, or 4) at the same locations. The locations of the dots were chosen randomly at the start of each run and were then fixed for the remainder of that run. To avoid the stimuli being perceived as flickering and to allow for numerically larger deviants at the same location, we used twice the number of locations as the adaptation numerosity (4, 6, and 8 locations for numerosities 2, 3, and 4, respectively). Hence, each possible location was occupied by a dot in half of the adaptation stimuli. We reasoned that neurons in the object location map would adapt, even if they were only targeted in half of the adaptation stimuli.
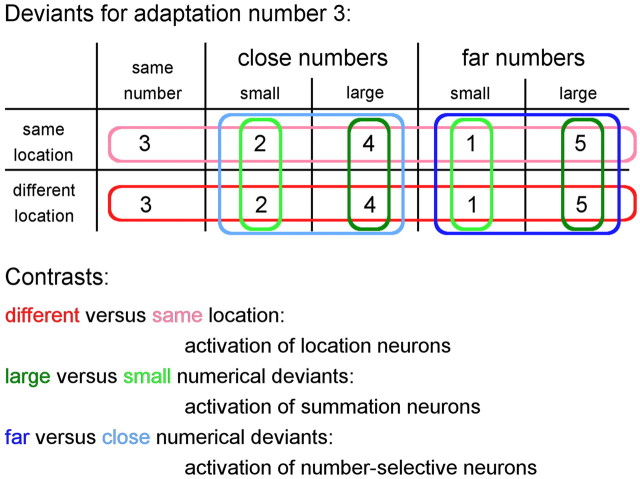
Occasionally, a deviant stimulus with a different number of dots and/or with dots at different locations was shown. Numerically, deviants could differ from −2 to +2 from the adapted numerosity, but were constrained to the range of 1–5 (Fig. 1). Deviants could have dots at different locations (i.e., different locations in the visual field; location deviants) or at the same locations as the adaptation stimuli. All deviant stimuli together therefore defined orthogonal number and location factors (numerical distances −2, −1, 0, +1, and +2, crossed with same vs different locations). The contrast (Fig. 1) between different location deviants versus same location deviants (hereafter called “different versus same location”) allowed localizing object location coding regions. Contrasting numerically larger deviants (+1 and +2) versus numerically smaller deviants (−1 and −2; both same and different locations, hereafter called “large versus small”) allowed localizing summation coding regions. Finally, contrasting numerically far deviants (+2 and −2) versus numerically close deviants (+1 and −1; both same and different locations, hereafter called “far versus close”) allowed localizing number-selective coding regions.
Figure 1.
Design: deviants for adaptation number 3. For each type of deviant, two separate predictors, for each type of control, were created. Contrasts (for information how they were created over both types of control, see Stimuli and procedure) are indicated by colors. For adaptation number 2, the numbers would be 2, 1, 3/4 and for adaptation number 4, the numbers would be 4, 3, 5, 2.
For the contrasts far versus close and large versus small, non-numerical parameters were controlled to exclude potential confounds. These confounding parameters fall in two sets of mutually dependent parameters: individual item size and total luminance, and total area spanned and individual distance between the dots. To control for these, we used the method developed by Piazza et al. (2004). Total luminance of the display was equated across the deviant stimuli, meaning that larger numerical deviants had smaller individual item size (Fig. 2). In contrast, individual item size was decorrelated from numerosity in the adaptation stimuli by sampling individual item sizes randomly from a distribution that spanned the range of values used for the deviant stimuli. In this way, individual item size was uncorrelated with number in the adaptation stimuli, total luminance was uncorrelated with number in the deviants, and an interaction between adaptation and deviant numerosity (i.e., far versus close contrast) could only be due to number. For the contrast large versus small deviants, item size would vary incongruently with numerosity (larger numerical deviants had smaller individual item size) and would therefore be a confound. To solve this problem, we also included the reverse control in other runs, where item size was equated across the deviant stimuli and total luminance was decorrelated from numerosity in the habituation stimuli. Effects were then calculated as a conjunction from both runs (Price et al., 1997). Total area spanned and individual distances between dots were always equated for the adaptation stimuli, since dots were always shown at the same locations in these stimuli. For the location deviants, in half of the stimuli we used the same total area spanned as in the adaptation stimuli, and in the other half of the stimuli we used the same individual distances between dots. Both controls were combined in the same run. Dot displays were generated randomly by an adapted version of a Matlab program (Matlab 7.0.4; MathWorks) described by Piazza et al. (2004) and by S. Dehaene, V. Izard, and M. Piazza, unpublished work (www.unicog.org).
Figure 2.
Examples of stimuli for adaptation number 3. The first two adaptation stimuli together indicate the six fixed locations in this run. The next four stimuli are random variations of these same six locations. In these stimuli, individual item size in the adaptation stimuli was decorrelated from numerosity, and luminance of the display was equated across the deviant stimuli. In another run (stimuli not shown), the control of non-numerical parameters was reversed.
Stimuli were presented for 150 ms, followed by a blank of 1050 ms. Subjects were instructed to fixate on a permanently visible yellow fixation cross throughout the experiment. Participants were asked to attentively watch the stimuli, but number was not mentioned. A run began with an adaptation period of 23–26 adaptation stimuli (26.4 to 30 s) (Grill-Spector et al., 1999; Piazza et al., 2007). After this period, deviant stimuli were shown occasionally, with the restriction that deviants were separated by at least three and at most 11 adaptation stimuli. Each type of deviant was shown six times in each run. Together with the initial adaptation period, this yielded 48 deviant stimuli and 368 adaptation stimuli in runs with adaptation numerosity 2 or 4, and 60 deviants and 452 adaptation stimuli in runs with adaptation numerosity 3. The complete experiment consisted of six runs: two runs of each numerosity adaptation, each with a different control (see above). The order of runs was counterbalanced between participants. The experimental procedure was controlled using Presentation (version 13.0; Neurobehavioral Systems). Stimuli were back-projected on a screen at the head of the scanner bore, which participants viewed through a mirror.
Images were collected with a 3T Magnetom Trio MRI scanner (Siemens Medical Systems). First, 176 high-resolution anatomical images were acquired using a T1-weighted three-dimenional sequence [repetition time (TR), 1550 ms; echo time (TE), 2.89 ms; image matrix, 256 × 256; field of view (FOV), 220 mm; flip angle, 9°; slice thickness, 0.9 mm; voxel size, 0.9 × 0.871 × 0.871 mm3 (resized to 1 × 1 × 1 mm3), 176 sagittal slices). Whole-brain functional images were collected using a T2*-weighted EPI sequence (TR, 2400 ms; TE, 40 ms; image matrix, 64 × 64; FOV, 224 mm; flip angle, 90°; slice thickness, 3.0 mm; distance, 17%; voxel size, 3.5 × 3.5 × 3 mm3; 33 axial slices). Runs with adaptation numerosity 2 and 4 consisted of 219 images, runs with adaptation numerosity 3 consisted of 267 images.
Data analysis.
Data analysis was performed using SPM5 (http://www.fil.ion.ucl.ac.uk/spm/). Functional volumes were realigned to the first image of each run and coregistered with the anatomical image. Next, functional and anatomical images were normalized to the Montreal Neurological Institute (MNI) template. Functional images were high-pass (140 s) filtered and smoothed with a Gaussian kernel of 6 mm full width at half maximum before statistical analysis. Activations were modeled using a general linear model with 20 predictors. Ten predictors correspond to the cells in Figure 1, and we created separate predictors for each type of control for non-numerical parameters (two types of runs; see above). The predictors were built by convolving the onset times of the deviants with the hemodynamic response function. Habituation stimuli were not modeled. Time and dispersion derivatives and motion parameters were included. Finally, six run-specific predictors were added to model differences between mean activation of the runs. With this model, eight contrast images were made for each subject (see above) (Fig. 1): different versus same location, large versus small, far versus close, and numbers versus baseline (which contrasted all deviants against baseline). These four contrast images were made for each type of control (run) separately, yielding eight contrasts in total. All these contrasts are mutually orthogonal. It is important to understand that all contrasts, except the numbers versus baseline contrast, were based on comparisons of deviants only. Even the cell “same number, same location” in Figure 1 are deviants: although they have the same number of dots and the same dot locations as the habituation stimuli, they were made with the non-numerical parameters of deviants. The contrast images of all participants were then subjected to a random-effects analysis. To exclude the influence of non-numerical parameters, we calculated the effect added across both control conditions, exclusively masked with the interaction of control (Price et al., 1997). By calculating the contrast across controls, we ensured identifying voxels that were active for both control conditions. By masking exclusively with the interaction of both controls, we excluded voxels where the activation was different for the two control conditions. Hence, reported activations could not be due to activation in only one of the control conditions, and thus could only be explained by number. Data are reported with p < 0.01 (uncorrected) at the voxel-level, and p < 0.05 (corrected for multiple comparisons) at the cluster-level. Thus, only clusters which survive the correction for multiple comparisons at the cluster level are reported. Mask p value (interaction of control) was set at 0.01. Contrasts were corrected for a small volume consisting of an anatomically defined occipitoparietal mask (WFU Pickatlas toolbox, version 2.4) (Maldjian et al., 2003). The contrast numbers versus baseline was calculated in the same way (i.e., voxel-level p < 0.01, cluster-level p < 0.05) for the purpose of subsequent region-of-interest (ROI) analyses. ROI analyses were performed using the Marsbar toolbox (Brett et al., 2002).
Results
Whole brain analysis
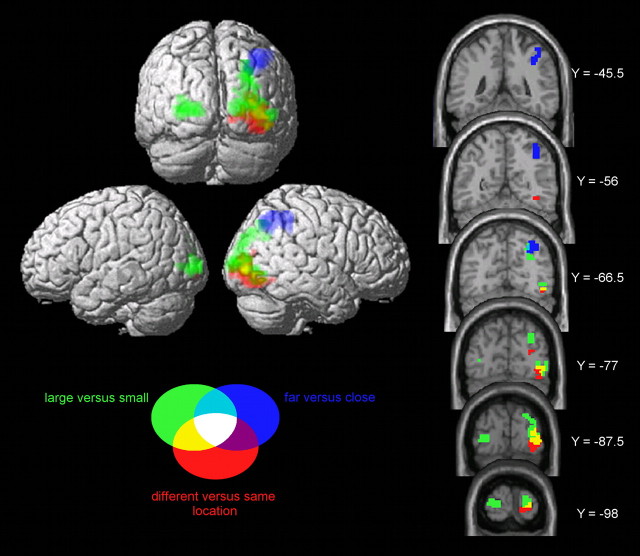
The contrast different versus same location (Fig. 3) yielded a large cluster in the right inferior occipital gyrus (MNI coordinates: 35, −84, −12; 140 voxels, cluster-level p = 0.003). In the contrast large versus small, two clusters were detected bilaterally in the middle occipital gyrus (25, −98, 9; 244 voxels, cluster-level p < 0.001 and −25, −91, 3; 79 voxels, cluster-level p = 0.036). Finally, the contrast far versus close revealed a large cluster in the right superior parietal lobe (39, −63, 45; 117 voxels, cluster-level p = 0.011). A small cluster in the left superior parietal lobe (−42, −56, 48) did not reach a significant cluster level.
Figure 3.
Whole-brain analysis for the three contrasts of interest (for details, see Results). Activations of the different contrasts are shown in different colors. Only clusters with a cluster-level p < 0.05 (corrected) are shown.
ROI analysis
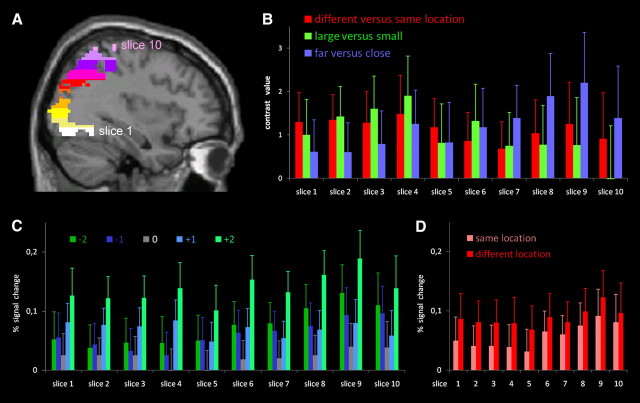
The results of the whole brain analysis indicated a gradient for processing numerosity over the occipitoparietal pathway for the three successive stages. To formally test this gradient, we defined 10 non-overlapping ROI slices sampling the right occipitoparietal pathway. First, we defined an ROI based on the contrast numbers versus baseline, restricted to the right hemisphere and anatomically masked with an occipitoparietal mask. Note that this choice is orthogonal and therefore unbiased toward the three contrasts of interest (Kriegeskorte et al., 2009). This ROI was then divided into 10 equidistant slices along the z-axis (Fig. 4A). The ROI ran from Z = −17 to Z = 68, resulting in slices 8.5 mm thick. For each of these ROI slices, the average contrast value for each contrast was extracted for each subject separately. These values were entered in an ANOVA with ROI slice, contrast, and control as within-subject factors. To correct for nonsphericity in the data, we report the Greenhouse–Geisser corrected p values.
Figure 4.
A, ROI based on the contrast numbers versus baseline, restricted to the occipitoparietal cortex in the right hemisphere. This ROI was then divided in 10 equidistant slices along the z-axis, shown in different colors. B, Average contrast value for all voxels within each slice, for each contrast, averaged over subjects. Since neither main effect nor interactions with control were significant, values were averaged over both control conditions. C, Percentage signal change for each condition (numerical distance from habituation number: −2 to +2) in each of the ROI slices, averaged across location and control conditions. D, Percentage signal change for the same and different location conditions in each of the ROI slices, averaged across distance and control conditions.
The main effects of ROI slice (F(3.4,74.1) = 1.89, p = 0.13), contrast (F(1.9,41.7) = 0.047, p = 0.95), and control (F(1.0,22.0) = 0.019, p = 0.89) were not significant. Importantly, the ROI slice × contrast interaction (F(4.3,93.5) = 2.47, p = 0.047) was significant. This supports the notion of a gradient over the different contrasts in the occipitoparietal pathway. Other interactions were not significant.
To further specify the nature of the ROI slice × contrast interaction, we tested all contrasts for linear and quadratic trends. For the different versus same location contrast, neither the linear (F(1,22) = 0.40, p = 0.54) nor the quadratic (F(1,22) = 0.08, p = 0.78) trend was significant. For the large versus small contrast, both the linear (F(1,22) = 6.9, p = 0.015) and the quadratic (F(1,22) = 4.7, p = 0.041) trends were significant. For the far versus close contrast, the linear trend was again significant (F(1,22) = 5.03, p = 0.035), but the quadratic trend was not (F(1,22) = 0.08, p = 0.78).
Consistent with this (Fig. 4B), the far versus close contrast value increased across ROI slices. In Figure 4C, we plotted the percentage signal change at each of the five distances (−2 to +2) in each of the 10 ROI slices, averaging across same and different locations. Across ROIs, one observes a gradual shift from a summation coding signature (increasing activation for larger deviants, except for distance 0), which gradually transforms into a V-shaped activation curve, the classical signature of number-sensitive coding (Piazza et al., 2004). This is consistent with the linear increase of the far versus close contrast. Finally, in Figure 4D, we plotted the percentage signal change of same versus different locations across the 10 ROI slices, averaging across the distance (−2 to +2) conditions. This latter contrast remains approximately constant across ROIs (no linear or quadratic effects; see above).
Discussion
We attempted to empirically distinguish the three stages of number processing postulated in earlier computational models (Dehaene and Changeux, 1993; Verguts and Fias, 2004). The main result was that different stages, tested by three different contrasts, were indeed differently represented in different brain areas along the lines postulated by these models. The activation of the object location map was present from the earliest stage of the occipitoparietal processing. The summation coding map exhibited a primarily nonlinear pattern of activation, with first increasing and then decreasing activation. The number-selective coding map became more pronounced further along the occipitoparietal processing stream.
The location of the number-selective coding map corresponds to the results of previous research (Piazza et al., 2004, 2007; Santens et al., 2010). However, our object location and summation coding regions are overall located more posteriorly and inferiorly than the number-sensitive (i.e., either object location or summation coding) areas reported in Santens et al. (2010). This should not be surprising, as the occipitoparietal stream contains multiple visuospatial maps from V1 to the intraparietal sulcus (Schluppeck et al., 2006; Silver and Kastner, 2009), which can be differentially recruited depending on the nature of the task. In Roggeman et al. (2010), it was shown that activation in the superior parietal area was task-dependent. When the task required subjects to attend to numerosity, activation increased with numerosity up to some point and then decreased, but when no attention was required, the activation showed a reverse pattern. Occipital areas, however, showed increasing activation with increasing numerosity independent of task (Roggeman et al., 2010; C. Roggeman, W. Fias, T. Verguts, unpublished data). Together, this shows that activation of parietal visuospatial maps is primarily determined by the nature of the task, whereas occipital visuospatial maps are more stimulus-driven. We propose that in the current design, which featured no task, a low-level object location map was involved, thus giving rise to an object location map earlier in the occipitoparietal stream. Future work should investigate whether it is possible to find summation coding and number-selective maps more anterior and superior from the areas found in this study, using a design where numerosity is task-relevant. Evidence reported by Dehaene et al. (2003) is in line with this idea, as more anterior number-related activity is reported in high-level tasks. However, in none of the reviewed studies was it possible (or attempted) to distinguish between the three processing stages. It remains to be investigated whether a gradient similar to the one obtained here can be found in more anterior parts of the occipitoparietal processing stream with more high-level mathematical tasks.
The fact that there are multiple object location maps along the occipitoparietal stream also helps to illuminate one finding that was not in line with the model's prediction. In particular, in the final processing stage (slices 8, 9, 10) (Fig. 4B), the object location map contrast (different versus same location) was also active. Given the widespread occurrence of visuospatial maps (Schluppeck et al., 2006; Silver and Kastner, 2009), it is not surprising that activation of an object location map is also found in the parietal cortex. However, whether this particular spatial map is also a part of the numerical pathway remains to be investigated.
The activation in our study, using nonsymbolic numbers, was observed predominantly in the right hemisphere. We argue that the right hemisphere dominance for spatial processing is responsible for the right lateralized activation in this study. A related left/right asymmetry in number processing holds that the left hemisphere is relatively more specialized for exact and format invariant number processing, whereas the right hemisphere is relatively more specialized for approximate number processing (Cohen Kadosh et al., 2007; Piazza et al., 2007). We tentatively suggest that the right hemisphere dominance for spatial processing, which is necessary for processing nonsymbolic number formats, leads to dominance in nonsymbolic number processing. Given that nonsymbolic number is developmentally the first number format for approximate number processing (Piazza, 2010), this right-sided dominance could lead to a preference for approximate number processing in the right hemisphere.
The processing gradient across occipitoparietal cortex is similar to gradients that have been observed in occipitotemporal cortex for letter and word processing (Vinckier et al., 2007) and to gradients for object processing more generally (Grill-Spector et al., 1999). These earlier studies observed gradients in the ventral visual stream that exhibited greater invariance for different stimulus properties (e.g., stimulus location) in a posterior-to-anterior direction. In the current study, a similar principle was described for the dorsal visual stream. In particular, to extract number, one must abstract across various irrelevant dimensions, such as object size and position. Dehaene and Changeux (1993) demonstrated how the object location map can be constructed such that it abstracts over object size. Further, the goal of the summation code is to abstract over object positions. Finally, a number-selective code is mathematically equivalent to a summation code, but number-selective coding is computationally more efficient for some tasks (Salinas, 2006; Verguts, 2007). Together with these earlier studies (Grill-Spector et al., 1999; Vinckier et al., 2007), this study illustrates that a stimulus-dependent to stimulus-invariant gradient is a common organizational principle in the human brain, not only for object or word recognition in the ventral stream, but also for other stimulus properties in the dorsal processing stream.
Footnotes
This work was supported by the Belgian Science Policy, Interuniversity Attraction Poles program (P6/29, to C.R.), Ghent University Research Council BOF Grant 01J01406 and a postdoctoral fellowship by the Research Foundation–Flanders (to S.S.), and Ghent University BOF/GOA Grant BOF08/GOA/011 and the Ghent University Multidisciplinary Research Partnership “The integrative neuroscience of behavioral control” (to T.V. and W.F.).
References
- Brett M, Anton JL, Valabregue R, Poline JB. Region of interest analysis using an SPM toolbox. Presented at the 8th Human Brain Mapping Conference; Sendai, Japan, June. 2002. [Google Scholar]
- Dehaene S, Changeux JP. Development of elementary numerical abilities: a neuronal model. J Cogn Neurosci. 1993;5:390–407. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, Cohen L. Three parietal circuits for number processing. Cogn Neuropsychol. 2003;20:487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Goldberg ME, Bisley J, Powell KD, Gottlieb J, Kusunoki M. The role of the lateral intraparietal area of the monkey in the generation of saccades and visuospatial attention. Ann N Y Acad Sci. 2002;956:205–215. doi: 10.1111/j.1749-6632.2002.tb02820.x. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Kushnir T, Edelman S, Avidan G, Itzchak Y, Malach R. Differential Processing of objects under various viewing conditions in the human lateral occipital complex. Neuron. 1999;24:187–203. doi: 10.1016/s0896-6273(00)80832-6. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R, Cohen Kadosh C, Kaas A, Henik A, Goebel R. Notation-dependent and -independent representations of numbers in the parietal lobes. Neuron. 2007;53:307–314. doi: 10.1016/j.neuron.2006.12.025. [DOI] [PubMed] [Google Scholar]
- Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI. Circular analysis in systems neuroscience: the dangers of double dipping. Nat Neurosci. 2009;12:535–540. doi: 10.1038/nn.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maldjian JA, Laurienti PJ, Kraft RA, Burdette JH. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. Neuroimage. 2003;19:1233–1239. doi: 10.1016/s1053-8119(03)00169-1. [DOI] [PubMed] [Google Scholar]
- Nieder A, Miller EK. A parieto-frontal network for visual information in the monkey. Proc Natl Acad Sci U S A. 2004;101:7457–7462. doi: 10.1073/pnas.0402239101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piazza M. Neurocognitive start-up tools for symbolic number representations. Trends Cogn Sci. 2010;14:542–551. doi: 10.1016/j.tics.2010.09.008. [DOI] [PubMed] [Google Scholar]
- Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron. 2004;44:547–555. doi: 10.1016/j.neuron.2004.10.014. [DOI] [PubMed] [Google Scholar]
- Piazza M, Pinel P, Le Bihan D, Dehaene S. A magnitude code common to numerosities and number symbols in human parietal cortex. Neuron. 2007;53:293–305. doi: 10.1016/j.neuron.2006.11.022. [DOI] [PubMed] [Google Scholar]
- Price CJ, Moore CJ, Friston KJ. Subtractions, conjunctions, and interactions in experimental design of activation studies. Hum Brain Mapp. 1997;5:264–272. doi: 10.1002/(SICI)1097-0193(1997)5:4<264::AID-HBM11>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Reynvoet B, Brysbaert M, Fias W. Semantic priming in number naming. Q J Exp Psychol A. 2002;55:1127–1139. doi: 10.1080/02724980244000116. [DOI] [PubMed] [Google Scholar]
- Roggeman C, Vergutsa T, Fias W. Priming reveals differential coding of symbolic and nonsymbolic quantities. Cognition. 2007;105:380–394. doi: 10.1016/j.cognition.2006.10.004. [DOI] [PubMed] [Google Scholar]
- Roggeman C, Fias W, Verguts T. Salience maps in parietal cortex: imaging and computational modeling. Neuroimage. 2010;52:1005–1014. doi: 10.1016/j.neuroimage.2010.01.060. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Brannon EM, Platt ML. Monotonic coding of numerosity in macaque lateral intraparietal area. PLoS Biol. 2007;5:e208. doi: 10.1371/journal.pbio.0050208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salinas E. How behavioral constraints may determine optimal sensory representations. PLoS Biol. 2006;4:e387. doi: 10.1371/journal.pbio.0040387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santens S, Roggeman C, Fias W, Verguts T. Number processing pathways in human parietal cortex. Cereb Cortex. 2010;20:77–88. doi: 10.1093/cercor/bhp080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schluppeck D, Curtis CE, Glimcher PW, Heeger DJ. Sustained activity in topographic areas of human posterior parietal cortex during memory-guided saccades. J Neurosci. 2006;26:5098–5108. doi: 10.1523/JNEUROSCI.5330-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver MA, Kastner S. Topographic maps in human frontal and parietal cortex. Trends Cogn Sci. 2009;13:488–495. doi: 10.1016/j.tics.2009.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd JJ, Marois R. Capacity limit of visual short-term memory in human posterior parietal cortex. Nature. 2004;428:751–754. doi: 10.1038/nature02466. [DOI] [PubMed] [Google Scholar]
- Verguts T. How to compare two quantities? A computational model of flutter discrimination. J Cogn Neurosci. 2007;19:409–419. doi: 10.1162/jocn.2007.19.3.409. [DOI] [PubMed] [Google Scholar]
- Verguts T, Fias W. Representation of number in animals and humans: a neural model. J Cogn Neurosci. 2004;16:1493–1504. doi: 10.1162/0898929042568497. [DOI] [PubMed] [Google Scholar]
- Vinckier F, Dehaene S, Jobert A, Dubus JP, Sigman M, Cohen L. Hierarchical coding of letter strings in the ventral stream: dissecting the inner organization of the visual word-form system. Neuron. 2007;55:143–156. doi: 10.1016/j.neuron.2007.05.031. [DOI] [PubMed] [Google Scholar]