The Number of Components of Enhancement Contributing to Short-Term Synaptic Plasticity at the Neuromuscular Synapse during Patterned Nerve Stimulation Progressively Decreases As Basal Release Probability Is Increased from Low to Normal Levels by Changing Extracellular Ca²⁺

Abstract

Presynaptic short-term plasticity (STP) dynamically modulates synaptic strength in a reversible manner on a timescale of milliseconds to minutes. For low basal vesicular release probability (prob₀), four components of enhancement, F1 and F2 facilitation, augmentation (A), and potentiation (P), increase synaptic strength during repetitive nerve activity. For release rates that exceed the rate of replenishment of the readily releasable pool (RRP) of synaptic vesicles, depression of synaptic strength, observed as a rundown of postsynaptic potential amplitudes, can also develop. To understand the relationship between enhancement and depression at the frog (Rana pipiens) neuromuscular synapse, data obtained over a wide range of prob₀ using patterned stimulation are analyzed with a hybrid model to reveal the components of STP. We find that F1, F2, A, P, and depletion of the RRP all contribute to STP during repetitive nerve activity at low prob₀. As prob₀ is increased by raising Ca_o²⁺ (extracellular Ca²⁺), specific components of enhancement no longer contribute, with first P, then A, and then F2 becoming undetectable, even though F1 continues to enhance release. For levels of prob₀ that lead to appreciable depression, only F1 and depletion of the RRP contribute to STP during rundown, and for low stimulation rates, F2 can also contribute. These observations place prob₀-dependent limitations on which components of enhancement contribute to STP and suggest some fundamental mechanistic differences among the components. The presented model can serve as a tool to readily characterize the components of STP over wide ranges of prob₀.

Introduction

Chemical synapses are major sites of information transfer between neurons and from neurons to effectors, such as muscle cells. A characteristic property of such synapses is that the amount of transmitter released from nerve terminals by each action potential can change dramatically during a train of impulses (Cowan et al., 2001; Atwood and Karunanithi, 2002; Zucker and Regehr, 2002; Neher and Sakaba, 2008). These changes, referred to as short-term synaptic plasticity (STP), have dramatic reversible effects on synaptic strength (Liley and North, 1953; Zengel et al., 1980; Magleby and Zengel, 1982; Dittman et al., 2000; Wesseling and Lo, 2002; Abbott and Regehr, 2004; Pan and Zucker, 2009; Kandaswamy et al., 2010; Müller et al., 2010).

Components of STP that increase transmitter release (enhancement) include first (F1) and second (F2) components of facilitation with time constants of 50 and 300 ms (Mallart and Martin, 1967; Magleby, 1973a; Zengel and Magleby, 1982; Goda and Stevens, 1994; Bennett et al., 2007), augmentation (A) with a time constant of 4–7 s (Magleby and Zengel, 1976a; Zengel and Magleby, 1982; Stevens and Wesseling, 1999), and potentiation (P) with a time constant of tens of seconds to minutes (Liley and North, 1953; Magleby, 1973b). For low basal vesicular release probability, prob₀, all four enhancement processes, F1, F2, A, and P, make major contributions to STP during repetitive nerve activity (Magleby and Zengel, 1982). In contrast, at normal prob₀, depression, typically indicated by a rundown of postsynaptic potential amplitudes during a train of impulses, can develop depending on the specific synapse and the stimulation rate (Liley and North, 1953; Mallart and Martin, 1968; Magleby, 1973b; Wu and Betz, 1998; Dittman et al., 2000; Wesseling and Lo, 2002; Stevens and Williams, 2007). The contributions of F1, F2, A, and P to STP during depression are less clear, as previous studies suggest that some of the components of enhancement may no longer contribute for normal prob₀ (Dittman et al., 2000; Kandaswamy et al., 2010; Müller et al., 2010).

To explore this question, we examine the interaction of the components of enhancement with depression over a wide range of prob₀ to change the level of depression. Experiments are performed on the neuromuscular synapse where the components of enhancement and depression were initially characterized (Liley and North, 1953; Takeuchi, 1958; Mallart and Martin, 1967; Magleby and Zengel, 1976a, 1982) and where depletion and recovery of synaptic vesicles is well described (Richards et al., 2003; Rizzoli and Betz, 2005). To reveal the components of STP during repetitive stimulation, a quantitative model that accounts for transmitter release at low quantal content (Magleby and Zengel, 1982) is expanded to incorporate depletion and replenishment of synaptic vesicles, and patterned stimulation is used to facilitate identification of the various components. We find that the specific components of enhancement contributing to STP during repetitive stimulation depend on prob₀, with first P, then A, and then F2 no longer contributing as prob₀ is increased from low to normal by increasing extracellular Ca²⁺ (Ca_o²⁺), whereas F1 always contributes.

Materials and Methods

Animals, solutions, and surface recording of end plate potentials

End plate potential (EPP) amplitude is used to track STP, as under the conditions of our experiments EPP amplitude is proportional to the number of synaptic vesicles releasing their transmitter after each nerve impulse (Zengel and Sosa, 1994; Zengel and Magleby, 1981). EPP amplitudes were recorded from the sartorius nerve–muscle preparation of northern grass frogs (Rana pipiens) of either sex with a surface electrode, as described previously (Magleby, 1973a). Animal protocols were approved by the Institutional Animal Care and Use Committee at the University of Miami Miller School of Medicine and are in accordance with National Research Council Guidelines for the Care and Use of Laboratory Animals. The preparation was bathed in modified Ringer's solution containing the following (in mm): 115 NaCl, 2 KCl, 2 CaCl₂, 1 MgCl₂, 5 HEPES, 5 glucose, and 0.03 choline chloride. pH was adjusted to 7.3. Experiments were performed within the physiological temperature range for frogs (18–21°C), as temperature alters STP (Zengel et al., 1980; Klyachko and Stevens, 2006). The extracellular concentration of Ca²⁺ was reduced or raised, as indicated, to decrease or increase prob₀, respectively. Tubocurare was added at concentrations of ∼2–5 μm to reduce EPP amplitudes well below threshold for the generation of action potentials in the muscle fibers.

A surface electrode was used to record the summed response of EPPs from a large number of end plates, each with thousands of active zones, thereby greatly reducing the measured stochastic variation in response. To further reduce variation, EPP amplitudes from three to five trains obtained from the same end plate region of a single muscle were averaged. Such surface recording gives a good measure of average intracellular response (Magleby, 1973a). Under the conditions of our experiments, where EPP amplitudes are typically a few millivolts or less because of low quantal content or the presence of curare, nonlinear summation of EPP amplitudes (McLachlan and Martin, 1981) is minimal and quantal size (miniature EPP amplitude) and postsynaptic sensitivity remain constant during a stimulation train (Magleby and Pallotta, 1981; Zengel and Sosa, 1994). Hence, observed changes in EPP amplitudes (synaptic strength) and STP in our experiments are presynaptic in origin, arising from a change in the number of vesicles whose contents are released by each nerve impulse. Examples of surface recorded EPPs have been presented previously (Magleby, 1973a; Magleby and Zengel, 1976a). The basal (control) EPP amplitude was obtained from the average of five EPPs delivered one every 5 or 10 s before the train. Rest periods between trains of impulses were typically 6 min.

Estimating the contributions of F1, F2, A, P, and depression to STP

A hybrid model was used to quantify the contributions of F1, F2, A, and P during repetitive stimulation. The model is an extension of the quantal hypothesis proposed by del Castillo and Katz (1954) that often serves as a starting point for more extensive models of transmitter release (Varela et al., 1997; Wu and Borst, 1999; Dittman et al., 2000; Zucker and Regehr, 2002; Trommershäuser et al., 2003; Kalkstein and Magleby, 2004; Pan and Zucker, 2009; Kandaswamy et al., 2010) as follows:

where EPP_t is the number of quanta (vesicles) released by a nerve impulse to generate an EPP at time t during a train, RRP_t is the number of vesicles in the readily releasable pool (RRP) available for release at time t, and prob_t is the vesicular release probability given by the fraction of vesicles in the RRP that are released by a nerve impulse at time t. EPP₀, prob₀, and RRP₀ indicate the values of these parameters in the fully rested state at time 0 before the start of the train. At the frog neuromuscular synapse, RRP₀ is ∼10,000 vesicles (Rizzoli and Betz, 2005), and a single action potential in the rested state for conditions of normal quantal content (2 mm Ca²⁺) releases ∼200 vesicles from the RRP (Heuser et al., 1979; Van der Kloot and Molgó, 1994), giving a prob₀ of ∼0.02. Vesicles released from the RRP are assumed to be replenished from a recycling pool (RP) with a content of ∼75,000 vesicles (Rizzoli and Betz, 2005). There is an additional relatively fixed reserve pool of ∼400,000 vesicles, which is not included in the considered models. With ∼300 active zones and ∼40 vesicles per active zone, ∼12,000 vesicles appear docked at each frog neuromuscular synapse, similar to the size of the RRP (Rizzoli and Betz, 2005).

Enhancement.

The model of Magleby and Zengel (1982) is based on the accumulation and decay of release enhancing factors for F1, F2, A, and P, and accounts for STP at low quantal content in the absence of apparent depression. Their model is expanded to include depletion of the RRP, as follows:

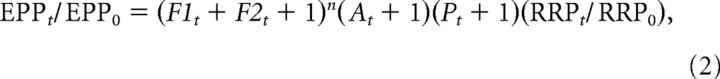where EPP_t/EPP₀ is the ratio of the number of vesicles released by a nerve impulse at time t during the train divided by the number of vesicles released by a nerve impulse in the basal condition. Under the recording conditions of our experiments EPP amplitude is proportional to the number of quanta released (see above). EPP_t/EPP₀ thus gives a normalized measure of the changes in transmitter release during the train. F1_t, F2_t, A_t, and P_t are the magnitudes of the first and second components of facilitation, augmentation, and potentiation, respectively, at time t immediately before each nerve impulse. For Equation 2, enhancement arises from increases in F1, F2, A, and P, and depression from the loss of vesicles from the RRP, although depression may be more complex than simple depletion of synaptic vesicles (Zucker and Regehr, 2002; Sippy et al., 2003; Xu et al., 2007; Young and Neher, 2009; Neher, 2010).

The magnitude of each enhancement component is given by the fractional increase in transmitter release when all the other components are zero and there is no depression, D. For example, when only F1 is present, then its magnitude is given by the following:

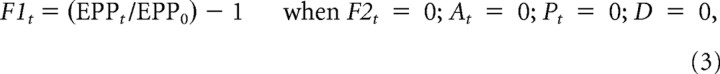with similar definitions for F2, A, and P.

The equations describing the buildup and decay of F1, F2, A, and P during and after repetitive stimulation under conditions of low quantal content have been presented previously (Magleby and Zengel, 1982; Zengel and Magleby, 1982). Briefly, F1, F2, A, and P arise from the underlying factors, F1*, F2*, A*, and P*. Each nerve impulse adds an increment of these factors, f₁*, f₂*, a*, and p*, during repetitive stimulation. The growth in the magnitude of A can increasingly accelerate during a train of impulses (Magleby and Zengel, 1976a) and has been modeled as an increase in the effective increments of a* added by each impulse during the train as follows:

where a*₀ is the increment of A* added by the first impulse in the train (in the rested state), a* is the increment added for impulse number N during the train, and Z is a parameter with a value ≥1 that determines the rate of increase in a* with each successive impulse (Zengel and Magleby, 1982). If Z = 1, there is no increase in a*.

F1*, F2*, and A* decay exponentially between nerve impulses with characteristic time constants, τ_F1*, τ_F2*, and τ_A*. For example, the decay of F1* is given by the following:

where F1*_t is the magnitude of F1* at time t during the train, and F1*_t+Δt is the magnitude of F1* Δt after time t. The change in F1* during the train is given by the following:

where f₁* is the increment of F1* added by each nerve impulse, k_F1* is the rate constant (given by 1/τ_F1*) for removal (or deactivation) of F1* from its site of action, and J(t) is an impulse function with a value of 1 at the time of each nerve impulse and 0 at all other times. Equations 5 and 6 with appropriate substitutions for the different components also apply for F2*, A*, and P*, with the exception that the decay of P depends on the magnitude of P (Magleby and Zengel, 1975, 1982) as follows:

where τ_P0 is the time constant for the decay of P after the first impulse in the train, P(t) is the magnitude of P at time t during the train, and B is the parameter that sets the increase in τ_P as P increases during the train. Mechanisms that could increase the time constant of decay of potentiation have been considered previously (Magleby and Zengel, 1976c; Tank and Zucker, 1997; García-Chacón et al., 2006). Mean estimates of B in this paper were ∼23, which could lead to a 15% increase in τ_P by the end of the trains, depending on the magnitude of P.

The observed potentiation P is not directly proportional to the underlying factor P*, but appears to saturate, as follows:

where G sets the level of saturation (Magleby and Zengel, 1982).

Depression.

In addition to enhancement of transmitter release, reflected as an increase in the probability of release caused by increases in one or more of the components F1, F2, A, and P, repetitive stimulation can also lead to a depression of transmitter release. In the model we use to study STP, depression arises from a depletion of vesicles from the RRP during stimulation. The RRP is then replenished from a recycling pool (RP). The formulation used for depletion is similar to previous studies (Schikorski and Stevens, 1997, 2001; Wu and Betz, 1998; Richards et al., 2003; Kalkstein and Magleby, 2004; Rizzoli and Betz, 2005; Neher and Sakaba, 2008; Pan and Zucker, 2009; Kandaswamy et al., 2010). Depletion occurs because vesicles are released from the RRP faster than they are replaced as follows:

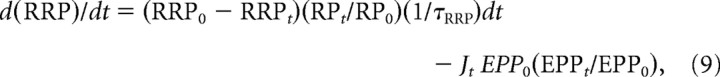where d(RRP_t)/dt is the rate of change in the number of vesicles in the RRP, J_tEPP₀(EPP_t/EPP₀) is the number of vesicles released by a nerve impulse at time t, where J_t equals 1 at the time of each nerve impulse and zero at all other times, EPP₀ is the quantal content of the first EPP in the train, EPP_t/EPP₀ is given by Equation 2, RRP₀ − RRP_t is the number of vesicles in the RRP that are depleted, RP_t/RP₀ is the fractional fullness of the RP, and 1/τ_RRP is the rate constant for replenishment of the RRP from the RP. Movement of vesicles from the RRP to the RP is not included, as this process is slow (Murthy and Stevens, 1999) compared with the durations of the stimulation trains.

In a similar manner, the change in the number of vesicles in the RP with time, d(RP)/dt, is given by the following:

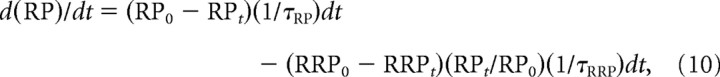where 1/τ_RP is the rate constant for refilling the RP.

The predicted EPP amplitudes during a train are calculated from the numerical solution of Equations 2–8 for enhancement together with Equations 9 and 10 for synaptic vesicle turnover and depression. Estimates of the parameters in this study are those that give the least-squares error [i.e., the least sum of ((predicted − observed)/predicted)²) for each EPP amplitude during the train, determined using an iterative approach to search for the parameter values that minimized the error using a program written in the laboratory (EPP37S54)]. If the search routine reduced the magnitude of a component of enhancement or depression to negligible values, then the component no longer contributed to STP, becoming undetected. RRP₀ was fixed at 10,000 synaptic vesicles (Rizzoli and Betz, 2005). For data obtained at low prob₀, depletion of the RP was small so that the RP₀ and τ_RP were poorly defined, with their values having little effect on the goodness of fit as long as RP₀ > 20,000 and τ_RP > 10 s.

The key to revealing the faster components of STP during repetitive stimulation and the interaction between these components and depression was to apply step changes in stimulation rate throughout the train (Magleby, 1973a; Magleby and Zengel, 1982; Wesseling and Lo, 2002; Müller et al., 2010). Whereas application of natural stimulation patterns serves the same purpose while allowing the critical decoding of natural synaptic input (Dittman et al., 2000; Hermann et al., 2009; Kandaswamy et al., 2010), such irregular stimulation does not readily allow direct visual observation of the components and their time course, as is the case when step changes in stimulation rate are applied systematically.

Testing additional mechanisms.

The data and analysis presented in this paper are for replenishment of the RP from unspecified sources, as described by Equation 10. We also examined a model in which the number of vesicles available to refill the RP depends on the number of vesicles incorporated into the presynaptic membrane that have not yet been retrieved and are available for recycling, such that Equation 10 is replaced by the following:

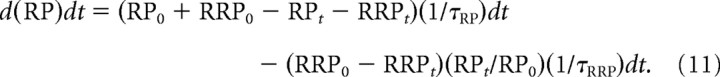We found that the ability to describe the data was essentially the same assuming either replenishment versus strict recycling for the examined stimulation patterns. As an additional test, the data were fitted with various models with three compartments for vesicle recycling instead of two. If a component of enhancement was found to be negligible with the two-compartment model, its contribution with the three-compartment models was also negligible (data not shown).

In addition to Equation 2, we also examined the ability of Equation 12 to describe STP. This equation is consistent with the idea that the mechanisms of the components of enhancement are fully independent of the other components:

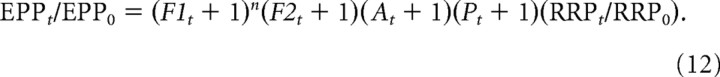We found that Equation 12 gave descriptions of STP almost identical with those of Equation 2.

We left n a free parameter in Equations 2 and 12 to maximize the possibility of finding the facilitation components, as there is typically a power relationship for facilitation (Zengel and Magleby, 1982; Zucker and Regehr, 2002). As will be shown in the results, estimates of n were ∼1.5 for low and intermediate prob₀, and ∼0.8 for normal to elevated prob₀, indicating possible cooperativity for lower prob₀ and possible saturation for higher prob₀. Nevertheless, STP could be described about equally well using a linear relationship by setting n = 1.0, consistent with previous observations of difficulty in distinguishing the power for facilitation models (Zengel and Magleby, 1982; Dittman et al., 2000; Kandaswamy et al., 2010).

Kandaswamy et al. (2010) described F1 and F2 and A with a saturation formulation such that for F1 (in our terminology) is given as follows:

where F1 is the observed facilitation, F1* is an exponentially decaying factor that gives rise to F1, and η is a saturation factor that relates F1* to F1. The same form of saturation applied to F2 and A in their study. Kandaswamy et al. (2010) set θ = 1.0, as higher values led to no significant improvement, and found η = 1.2 for F1* and F2* and 0.59 for A. To test whether their formulation for saturating facilitation could be applied to the neuromuscular synapse, we substituted Equation 13 for F1 and F2 with θ = 1.0 into Equation 12, and set n = 1.0 in Equation 12, and fit the data. Estimated values of η in Equation 13 ranged from 0.02 to 0.13, consistent with limited saturation at the neuromuscular synapse (see above). The description of STP with the Kandaswamy et al. (2010) formulation for saturation of facilitation was little changed from the description with our formulation of facilitation. We did not examine a saturating A because in our formulation of STP the increment of A* added by each impulse was found to increase during the trains (Eq. 4), consistent with previous studies (Zengel and Magleby, 1982). P in our formulation was saturating (Eq. 8), also consistent with previous studies (Magleby and Zengel, 1982).

Results

STP is highly dependent on prob₀

To examine the relationship between the components of enhancement and depression, STP was studied over a wide range of prob₀, obtained by changing external Ca²⁺. Prob₀ is the probability that a synaptic vesicle in the RRP releases its contents into the synaptic cleft after a nerve impulse is delivered under basal (resting) conditions when the components of STP are at their baseline values (i.e., the probability of vesicular release for the first impulse in a train of impulses). The nerve leading to the presynaptic nerve endings was stimulated at 33/s, with a dropped or added impulse every 20 stimuli to test for facilitation. Figures 1B, 2B, and 3B, which plot normalized EPP amplitudes during the trains, show that STP is profoundly different for low prob₀ (Fig. 1, 0.2 mm Ca²⁺), intermediate prob₀ (Fig. 2, 1.0 mm Ca²⁺), and normal prob₀ (Fig. 3, 2.0 mm Ca²⁺).

Figure 1.

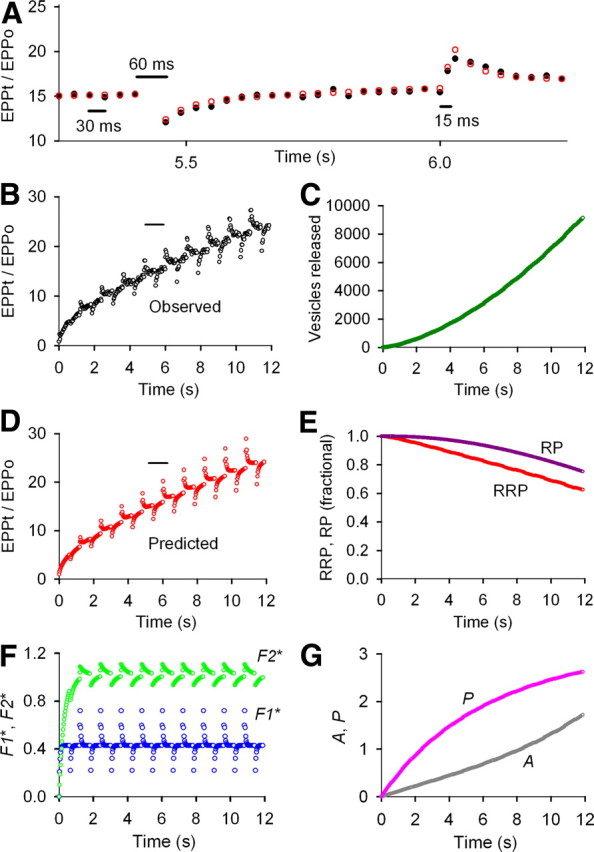
F1, F2, A, P, and partial depletion of the RRP determine STP during repetitive stimulation under conditions of low prob₀ obtained with low (0.2 mm) Ca_o²⁺. A, Testing for facilitation during repetitive stimulation by dropping and adding nerve stimuli. Normalized EPP amplitudes for observed (black circles) and predicted (red circles) data are plotted against the indicated time during a train of nerve stimuli delivered at 33/s with a dropped or added impulse every 20 impulses. EPP_t/EPP₀ indicates EPP amplitude at time t divided by the control EPP amplitude in the absence of repetitive stimulation. B, D, Normalized EPP amplitudes plotted against time for observed (B) and predicted (D) data during a 400 impulse train with dropped and added impulses as described in A. The short horizontal lines above the trains in B and D indicate the part of the trains plotted on expanded timescale in A. C, Plot of the cumulative number of vesicles released during the 400 impulse train. E, Plots of the fractional size of the RRP and RP during the train compared with the values before the first impulse. F, Plots of the magnitudes of the underlying F1* and F2* facilitation factors during the train. G, Plots of the magnitudes of augmentation A and potentiation P during the train. The plotted magnitudes of the various pools and components are those immediately before each nerve impulse. (The values of the pools and components between impulses are not shown.) The fixed (when indicated) and fitted parameters are as follows: EPP₀ = 1.50 vesicles, prob₀ = 0.00015, f₁* = 0.408, τ_F1* = 44.8 ms, f₂* = 0.107, τ_F2* = 299 ms, n = 1.54, a₀* = 0.00349, Z = 1.00409, τ_A* = 5.13 s, p* = 0.0182, G = 7.71, B = 20.2, τ_P0 = 20.0 s (fixed), RRP₀ = 10,000 vesicles (fixed) (Rizzoli and Betz, 2005), τ_RRP = 3.41 s, RP₀ = 21,496 vesicles, τ_RP = 499 s. Fixing RP₀ to 50,000 vesicles had little effect on the parameters except to slow τ_RRP somewhat. The results from three experiments of this type are in Table 1. At low prob₀, four robust components of enhancement with limited depletion make this a highly facilitating synapse.

Figure 2.

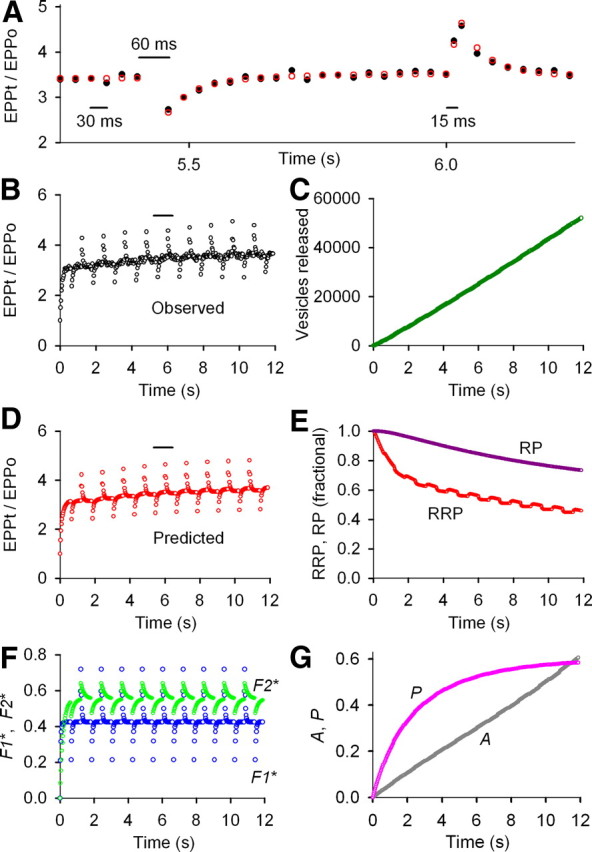
F1, F2, reduced A, reduced P, and appreciable depletion of the RRP determine STP during repetitive stimulation under conditions of intermediate prob₀ obtained with 1.0 mm Ca_o²⁺. A–G, Same stimulation pattern and types of plots as in Figure 1. The reduced amplitudes of A and P and the greater depletion of the RRP when compared with Figure 1 give a mean 3.6-fold increase in EPP amplitude during the train rather than the mean 24-fold increase in Figure 1 and produce a weakly facilitating synapse. EPP₀ = 38.4 vesicles, prob₀ = 0.00384, f₁* = 0.415, τ_F1* = 44.0 ms, f₂* = 0.0976, τ_F2* = 185 ms, n = 1.70, a₀* = 0.00173, τ_A* = 6.01 s, Z = 1.00261, p* = 0.0185, G = 1.88, B = 9.93, τ_P0 = 20.0 s (fixed), RRP₀ = 10,000 vesicles (fixed), τ_RRP = 0.904 s, RP₀ = 100,000 vesicles (limited ≤100,000), τ_RP = 8.54 s. Results for six experiments of this type are in Table 1. For preparations in the upper range of intermediate prob₀, P did not contribute to STP (Fig. 8).

Figure 3.

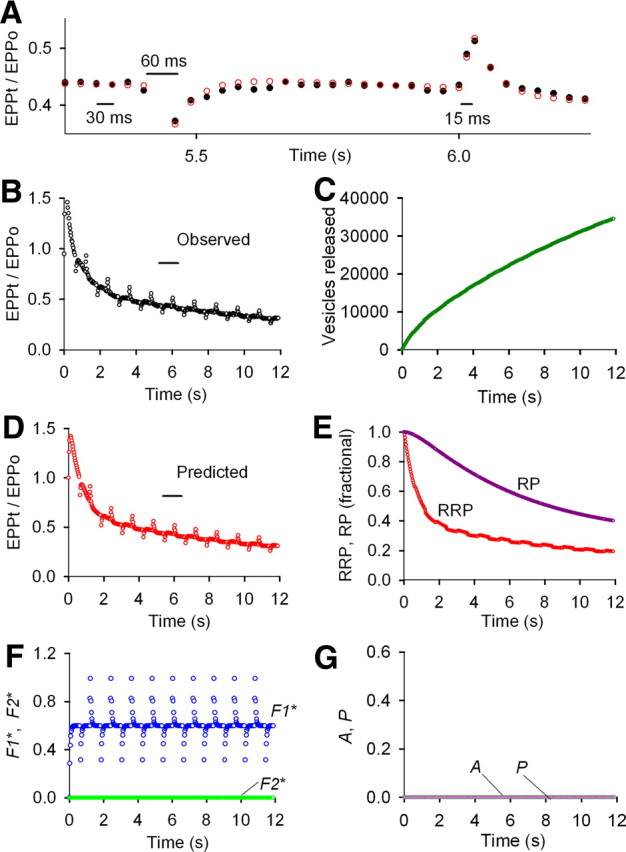
F1 and marked depletion of the RRP determine STP during repetitive stimulation under conditions of normal prob₀ obtained with 2.0 mm Ca_o²⁺. A–G, Same stimulation pattern and types of plots as in Figures 1 and 2. Only the F1 component of enhancement contributes to STP during the rundown, as estimates of F2, A, and P are zero. The absence of the buildup of F2, A, and P during the train together with marked depletion of the RRP leads to pronounced rundown and obvious depression during repetitive stimulation. EPP₀ = 176 vesicles, prob₀ = 0.0176, f₁* = 0.541, τ_F1* = 46.6 ms, f₂* = 0.0, n = 1.0 (fixed), a₀* = 0.0, p* = 0.0, RRP₀ = 10,000 vesicles (fixed), τ_RRP = 1.90 s, RP₀ = 31,302 vesicles, τ_RP = 16.9 s. When n was a free parameter, n = 0.801 and f₁* = 0.764 with little effect on the other parameters or the least-squares error. Results for eight experiments of this type are in Table 1.

During the 12 s train of patterned stimulation at low prob₀, EPP mean amplitudes increased 24-fold above the first (control) EPP in the train (Fig. 1B), reflecting the buildup of F1, F2, A, and P during the train (Magleby and Zengel, 1982). At the low prob₀ used for this experiment, the stepwise increase in EPP amplitudes after each added impulse and rapid decay back to the mean response (Fig. 1A) mainly reflects F1 and F2 facilitation added by the extra impulse (Magleby, 1973a; Magleby and Zengel, 1982; Zengel and Magleby, 1982). Similarly, the step decrease in EPP amplitudes after each dropped impulse and return to the mean response mainly reflects the absence of the increments of F1 and F2 that would have been added by the dropped impulse. It is the faster time constants of decay of F1 (∼50 ms) and F2 (∼300 ms) compared with the slower time constants of decay of A (∼6 s) and P (tens of seconds to minutes) and the larger increments of F1 (∼0.8) and F2 (∼0.15) added by each impulse when compared with the smaller increments of A (∼0.005) and P (∼0.01) that enables the detection of F1 and F2 with dropped and added impulses when these components are superimposed on A and P during repetitive stimulation at low prob₀ (Magleby, 1973a; Magleby and Zengel, 1982).

In contrast to the 24-fold increase in mean EPP amplitude at low prob₀ (Fig. 1B), at intermediate release probability mean EPP amplitudes increase 3.6-fold during the train (Fig. 2B), and at normal release probability EPP amplitudes increase 1.5-fold during the first few impulses and then run down to 30% of the control level by the end of the 12 s train (Fig. 3B). Despite the marked differences in the mean responses during the trains, two consistent features are present at all release probabilities: EPP amplitudes increase rapidly at the very start of the trains and there are step changes in EPP amplitudes with rapid return after the dropped and added impulses (Figs. 1A,B, 2A,B, 3A,B). At low prob₀, these rapid changes in STP arise predominantly from F1 and F2, as discussed above. The presence of similar features at intermediate and normal prob₀ suggests that F1 and possibly also F2 also contribute to STP at intermediate and normal prob₀. In the following sections, the contributions of F1, F2, A, and P, and the depletion of the RRP to STP during repetitive stimulation are determined by fitting the data with the model presented in Materials and Methods. Dissecting out the components of STP during repetitive stimulation requires a model because of the complex relationship between the various components and transmitter release (see Materials and Methods).

F1, F2, A, P, and partial depletion of the RRP all contribute to STP at low prob₀

Estimates of F1, F2, A, P, RRP, and RP during the train at low prob₀ are shown in Figure 1E–G. F1 and F2 rapidly increase at the start of the train to near steady-state levels after the first 5 and 30 impulses, respectively, and then undergo step decreases and increases (with rapid return) from these levels after each dropped and added impulse during the train (Fig. 1F). The components of A and P increase throughout the train (Fig. 1G), and the RRP and RP decrease during the train, becoming depleted by 37 and 23%, respectively, because of depletion of vesicles from each pool (Fig. 1E). The product of RRP_t and prob_t (Eq. 1) predicts the observed STP during the train (Fig. 1A,B,D). Hence, F1, F2, A, P, and partial depletion of the RRP all contribute to STP at low quantal content. The partial depletion of the RRP did not give rise to observable depression during the train because the increases in F1 and F2 at the start of the train and the continuing increase in A and P during the train more than compensated for the decreasing RRP during the train. Thus, even though obvious depression is not observed during repetitive stimulation at low prob₀, partial depletion of the RRP contributes to STP by making the transmitter release less than what would be expected from enhancement processes alone. Mean parameters for three experiments like that in Figure 1 are presented in Table 1.

Table 1.

Synaptic parameters that determine STP for low, intermediate, and normal to elevated prob₀

Parameters and datab	Prob0a
	Low (0.0002–0.0009)	Intermediate (0.0011–0.0095)	Normal to elevated (0.017–0.043)
EEP0	5.5 ± 2.1	41 ± 15	270 ± 31
f1 *	0.74 ± 0.34	0.79 ± 0.11	1.15 ± 0.25
τF1* (ms)	39 ± 5	40 ± 3	47 ± 4
f2*	0.13 ± 0.04	0.11 ± 0.03	0.0
τF2* (ms)	275 ± 36	190 ± 57	NAc
n	1.5 ± 0.1	1.4 ± 0.1	0.81 ± 0.08
a*0	0.0037 ± 0.0017	0.0021 ± 0.0008	0.0
τA* (s)	6.0 ± 1.2	4.9 ± 1.4	NA
Z	1.0045 ± 0.0048	1.0024 ± 0.0010	NA
A(400)b	2.27 ± 1.21	0.67 ± 0.30	0.0
p*	0.012 ± 0.003	0.004 ± 0.002	0.0
τP0 (s)	20 ± 1	38 ± 14	NA
B	24.6 ± 13.6	21.5 ± 9.3	NA
G	4.8 ± 1.7	1.76 ± 0.45	NA
P(400)b	1.46 ± 0.63	0.35 ± 0.14	0.0
RRP0d	10,000	10,000	10,000
τRRP (s)	3.2 ± 1.2	2.8 ± 1.8	1.1 ± 0.1
RP0	92,800 ± 53,900	36,800 ± 8,000	34,800 ± 2,100
τRP (s)	236 ± 142	28 ± 15	17 ± 2

^aRange of prob₀ grouped into low, intermediate, and normal to elevated classes obtained with 0.14–0.3, 0.2–1.0, and 2.0–4.0 mm Ca²⁺_o, respectively, for three, six, and eight different nerve–muscle preparations. Prob₀, EPP₀, and other parameters were obtained by fitting with Equations 2–10 for data obtained with the stimulation pattern used for Figures 1–3. Parameters are defined in Materials and Methods where the equations are presented. Values are mean ± SEM.

^bA(400) and P(400) are the magnitudes of the observed augmentation and potentiation at 400 impulses of stimulation.

^cNA indicates not applicable as the component was not detected.

^dRRP₀ was fixed at 10,000 vesicles (Rizzoli and Betz, 2005). One atypical experiment at elevated prob₀ was excluded from the table because it had a P(400) = 0.31 compared with 0.0 for the other seven experiments of the same type. This excluded experiment is included in Figure 8.

Figure 1C shows why a partial depletion of the RRP develops during repetitive stimulation at low prob₀ even though prob₀ in this experiment is <1% of prob₀ at normal release probability. Although the first EPP in the train at low prob₀ releases only 1.5 vesicles on average, after 400 impulses the release per impulse has increased to >36 vesicles, so that the cumulative release during the train sums to ∼9000 vesicles, which is sufficient to partially deplete the RRP even though vesicles are being mobilized from the RP to the RRP.

The model used to describe STP in the present study is the same as the one used by Magleby and Zengel (1982) to describe STP at low release probability, but with the added feature that depletion of the RRP can occur. Magleby and Zengel (1982) did not include depletion in their studies, assuming that there would be little depletion at the low quantal contents used in their study. We fit the two sets of data in the study by Magleby and Zengel (1982), their Figure 6, with the expanded model to allow possible depletion and found a small (8%) depletion of the RRP at the end of their 200 impulse trains and also a small increase in enhancement to compensate for the depletion (results not shown), consistent with both the assumption in Magleby and Zengel (1982) of limited depletion and the findings in Figure 1 that a small partial depletion of the RRP contributes to STP at low prob₀.

Figure 6.

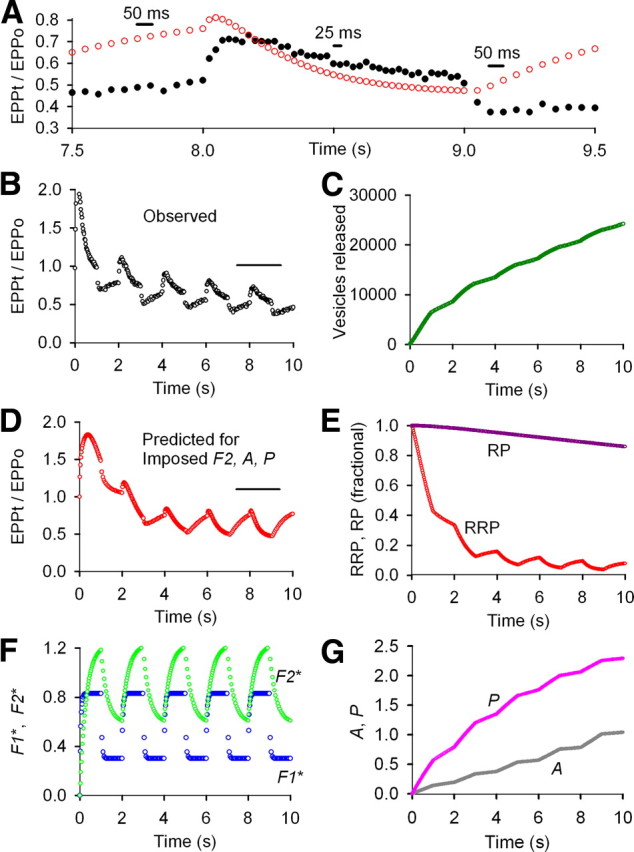
Imposing F2, A, and P during repetitive stimulation at normal prob₀ for an amplifying stimulation pattern no longer describes STP. A–G, Same experimental data, types of plots, and analysis as in Figure 5 except that increments of F2, A, and P added by each impulse were imposed by fixing the parameters for these components to those listed in Figure 1 and then refitting the data. Imposing F2, A, and P gave results inconsistent with the experimentally observed STP, suggesting that these components were not present. A, B, Experimentally observed EPP amplitudes from Figure 5 are plotted as black circles. A, D, Predicted EPP amplitudes after imposing increments of F2, A, and P added by each impulse and refitting (red circles). E, The fitted RRP with imposed F2, A, and P depletes more during the train (compare with Fig. 5E) to keep the observed mean rundown of EPP amplitudes the same as in the absence of the imposed components (compare Fig. 6B,D, Fig. 5B,D). The smaller RRP results in larger fractional increases and decreases in the size of the RRP during the slower and faster stimulation rates, respectively, giving predicted STP inconsistent with the experimental data (A, B, D). Imposed parameters were as follows: f₂* = 0.107, τ_F2* = 299 ms, a₀* = 0.00349, Z = 1.00409, τ_A* = 5.13 s, p* = 0.0182, τ_P = 20 s, B = 20.2, G = 7.71 (from Fig. 1). Fitted (unless indicated) parameters were as follows: EPP₀ = 93.9 vesicles, prob₀ = 0.00939, RRP₀ = 10,000 vesicles (fixed), f₁* = 0.632, τ_F1* = 44.1 ms, n = 0.60 (limited ≥0.6), RP₀ = 105,212 vesicles, τ_RP = 499 s. Imposing smaller increments of f₂*, a₀*, and or p* progressively improved the description of STP, with the best description obtained when F2, A, and P were all zero.

Components of STP during repetitive stimulation at intermediate prob₀

For the experiment shown in Figure 2 at intermediate prob₀, F1, F2, A, P, and depletion of the RRP contribute to STP (Fig. 2E–G), and the product of the RRP_t and prob_t predicts the observed STP during the train (Fig. 2A,B,D). The 53% depletion of the RRP and 25% depletion of the RP during the train at intermediate prob₀ (Fig. 2E) is greater than at low release prob₀ (Fig. 1E), and the buildup of A and P during the train is considerably less at intermediate prob₀ (Fig. 2G, note change in scale) than at low prob₀ (Fig. 1G). It is the increased depletion of the RRP and the decreased buildup of A and P that limits the mean increase in EPP amplitudes during the train to 3.6-fold at intermediate prob₀ (Fig. 2B) compared with 24-fold (Fig. 1B) at low prob₀ (Fig. 1). No obvious depression is observed at intermediate prob₀ (Fig. 2B) because the increases in F1 and F2 (Fig. 2F) and the smaller but continuing increase in A and P during the train (Fig. 2G) are still sufficient to compensate for the larger depletion of the RRP. Mean parameters for six experiments like that in Figure 2 are summarized in Table 1.

In experiments of this type, differences in prob₀ among different frogs for the same 1.0 mm Ca_o²⁺ could lead to differences in the contribution of P during the train. As will be shown in a later section, when EPP₀ for the first EPP in the train was <40 vesicles, as was the case for Figure 2, P was present during the train, and when it was >40 vesicles, P was typically absent. Hence, at intermediate prob₀, F1, F2, A, and partial depletion of the RRP contribute to STP, and in some experiments at the lower range of intermediate prob₀, P also contributes.

As indicated by the changes in EPP amplitudes in Figure 2, A and B, there is a period of time after a dropped impulse when fewer vesicles are released. This is the case because the dropped impulse itself does not release vesicles and the decreased facilitation after the dropped impulse leads to fewer vesicles released for the next seven to eight impulses. Inversely, more vesicles are released for a period of time when an impulse is added because the added impulse itself releases additional vesicles and because facilitation from the added impulse leads to more vesicles released for the next seven to eight impulses. These decreases and increases in vesicles released during the train lead to increases and decreases in the size of the RRP during the train (Fig. 2E), which then lead to small increases and decreases in mean EPP amplitudes during the train after facilitation approaches steady-state levels (marginally visible in Fig. 2A,B,D, but will be more apparent in later figures with different stimulation patterns). Such changes in EPP amplitudes after changes in stimulation rate have been exploited to estimate the fullness of the RRP (Wesseling and Lo, 2002).

F1 and marked depletion of the RRP can account for STP during rundown at normal prob₀

At normal prob₀ with associated rundown of EPP amplitudes during the train (Fig. 3B), only F1 and marked depletion of the RRP contribute to STP (Fig. 3E,F). F2, A, and P were not detected (Fig. 3F,G), so that the product of RRP_t and prob_t, where prob_t included only F1, was sufficient to predict the observed STP during the train (Fig. 3A,B,D). The 85% depletion of the RRP and 60% depletion of the RP during the rundown at normal prob₀ (Fig. 3E) can be compared with the 53 and 25% depletion at intermediate prob₀ (Fig. 2E) and the 37 and 23% depletion at low prob₀ (Fig. 1E). After the 1.5-fold increase in EPP amplitudes at the start of the train in Figure 3B, the rundown of the EPP amplitudes tracked the depletion of the RRP (Fig. 3E) because there was no buildup of F2, A, and P during the train to counter the decrease in the RRP. That F1 still contributes during the train can be seen by the response to the dropped and added impulses. Mean parameters for eight experiments like that in Figure 3 with marked depression are presented in Table 1 (listed under normal to elevated prob₀). Consistent with the absence of F2 at normal prob₀, Mallart and Martin (1968) did not observe F2 after five impulses of high frequency stimulation.

Imposing F2, A, and P at normal prob₀ gives a response inconsistent with the data, indicating that these processes do not contribute to STP during rundown

The question arises as to whether F2, A, and P were not detected during rundown because they were missing or because the fitting program could not find them. If F2, A, and P were contributing to STP but not detected, then it should be possible to describe the data by imposing F2, A, and P and refitting. When this was done, the mean response during the rundown was approximated (Fig. 4B,D), but the predicted responses after dropped and added impulses were incorrect, being opposite to what was observed (Fig. 4A,B,D). Imposing F2, A, and P in various combinations and with various magnitudes also did not describe the data (data not shown), and when F2, A, and P were given initial values and then allowed to freely change during fitting, their values went to zero (Fig. 3F,G). Hence, F1 and depletion of the RRP were sufficient to account for STP during the rundown in Figure 3, with no evidence that F2, A, and P contribute.

Figure 4.

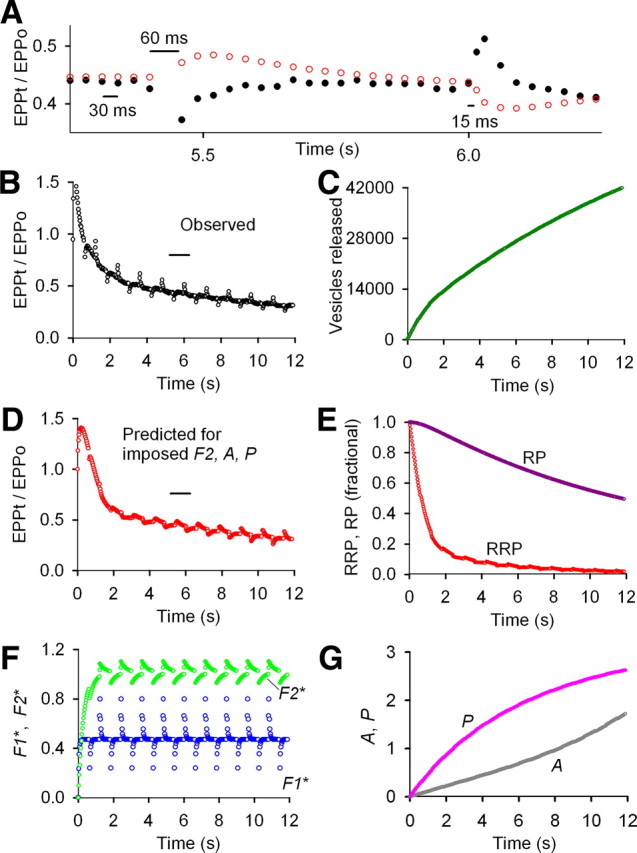
Imposing F2, A, and P during repetitive stimulation at normal vesicular release probability for the data in Figure 3 no longer describes STP. A–G, Same experimental data, types of plots, and analysis as in Figure 3 except that the parameters defining F2, A, and P added by each impulse were imposed by fixing the values to those in Figure 1 and then refitting the observed EPP amplitudes during the train. Imposing F2, A, and P gave results inconsistent with the experimentally observed STP, increasing the least-squares error 12-fold. Hence, it is unlikely that these components are present but undetected because imposing the components and refitting made the fits considerably worse. A, B, Experimentally observed EPP amplitudes from Figure 3 are plotted as black circles. A, D, Predicted EPP amplitudes after imposing increments of F2, A, and P added by each impulse and fitting are plotted as red circles. E, With imposed F2, A, and P, the fitted RRP depletes considerably more during the train than when the these components are zero (compare with Fig. 3). This greater rundown keeps the observed mean rundown of EEPs the same as in the absence of the imposed components. The greatly reduced RRP then gives larger fractional increases and decreases in the size of the RRP after the dropped and added impulses. These larger fractional changes in the RRP lead to changes in the EPP amplitudes inconsistent with the experimental data (A, B, D). The poor fit (shown centered on 5.75 s in A) becomes worse as the duration of the train increases as seen by comparing B to D at longer times. The imposed parameters were as follows: f₂* = 0.107, τ_F2* = 299 ms, a₀* = 0.00349, Z = 1.00409, τ_A* = 5.13 s, p* = 0.0182, τ_P = 20 s, B = 20.2, G = 7.71 (from Fig. 1). Fitted (unless indicated) parameters: EPP₀ = 207 vesicles, prob₀ = 0.0207, f₁* = 0.459, τ_F1* = 44.1 ms, n = 0.60 (limited to ≥ 0.6), RRP₀ = 10,000 vesicles (fixed), τ_RRP = 2.33 s, RP₀ = 56,789 vesicles, τ_RP = 56.4 s. Imposing smaller increments of f₂*, a₀*, and or p* improved the description of STP with the best description obtained when F2, A, and P were 0.0.

As additional support for why F2, A, and P do not contribute to STP during the rundown, it is worthwhile to consider why imposing these components and refitting gave such a poor description of the response after dropped and added impulses. Imposing F2, A, and P led to large progressive increases in prob_t during the train. Therefore, to describe the rundown with this large imposed increase in prob_t, the program optimized the parameters to severely deplete the RRP (Fig. 4E) so that the product of prob_t × RRP_t during the rundown would remain the same as in the absence of imposed F2, A, and P. The responses after dropped and added impulses were not predicted when the RRP was severely depleted in the presence of imposed F2, A, and P for the following reason. During the slow phase of the rundown, most of the vesicles released by each nerve impulse are replaced from the RP during the interval before the next impulse. When an impulse is dropped, the transmitter that would have been released by the dropped impulse is not released so that the RRP is increased by that amount of transmitter, compared with if the impulse were not dropped. For example, when F2, A, and P were imposed, the RRP was 94% depleted at 5.4 s so that the dropped impulse led to a large ∼16% fractional increase in the RRP (Fig. 4E, determined from numerical data). The consequence of such a large fractional increase in the RRP is that the predicted EPP amplitudes increase after the dropped impulse (Fig. 4A, red circles, ∼5.4 s) in contrast to the experimentally observed decrease (Fig. 4A, black circles), even though facilitation decreases because of the dropped impulse.

Conversely, with imposed F2, A, and P, the fractional decrease in the size of the RRP for an added impulse was much greater (∼18%) than without imposed F2, A, and P (∼3%), so that the predicted EPP amplitudes decreased (Fig. 4A, red circles, ∼6 s) in contrast to the experimentally observed increase (Fig. 4A, black circles), even though facilitation increased because of the added impulse. Hence, F2, A, and P do not contribute to STP during rundown at normal prob₀, because if they did, the response to patterned stimulation would be opposite to what was observed.

Absence of F2, A, and P during rundown at normal prob₀ using a stimulation pattern that amplifies the contributions of these components

As an additional test for F2, A, and P during rundown at normal prob₀, we applied stimulation that amplifies the contributions of the components of enhancement by applying 40 impulses at 40/s alternating with 20 impulses at 20/s (Fig. 5). With such a pattern, the changes in F2, A, and P should be approximately twice as great at the higher than the lower stimulation rate. With this amplifying stimulation pattern, F1 and depletion of the RRP were still sufficient to account for STP during the train, as F2, A, and P were not detected (Fig. 5). As was the case for Figure 4, imposing F2, A, and P gave far worse descriptions of the data (Fig. 6).

Figure 5.

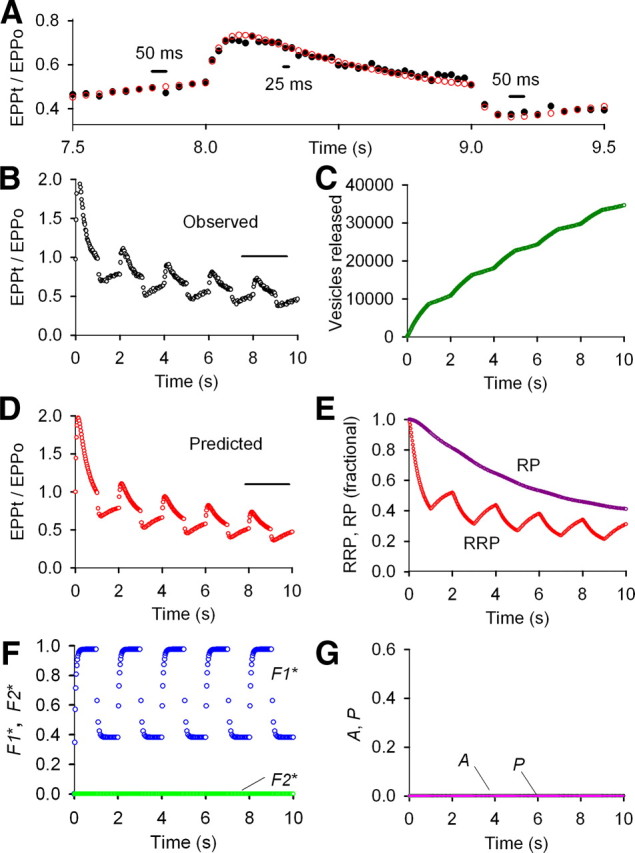
F1 and marked depletion of the RRP are sufficient to account for STP during repetitive stimulation under conditions of normal prob₀ (2.0 mm Ca_o²⁺) for a stimulation pattern that would amplify contributions from the components of enhancement. A–G, Same type of analysis and plots as in Figures 1–3, except that the stimulation pattern alternated between 40 s for 1 s and 20/s for 1 s for an average stimulation rate of 30/s. With this pattern, increments of the components of enhancement are added two times faster at the higher stimulation rate than at the lower stimulation rate, so there would be large differences in the magnitudes of the various components of enhancement, if present, during the successive alternating stimulation rates. Despite the amplifying pattern of stimulation, only the F1 component of enhancement contributed to STP during repetitive stimulation, as estimates of F2, A, and P were zero. EPP₀ = 149 vesicles, prob₀ = 0.0149, f₁* = 0.538, τ_F1* = 56.9 ms, f₂* = 0.0, n = 1.28, a₀* = 0.0, p* = 0.0, RRP₀ = 10,000 (fixed), τ_RRP = 1.39 s, RP₀ = 28,760 vesicles, τ_RP = 10 s (limited ≥10 s).

For low stimulation rates at normal prob₀, F2, in addition to F1 and depletion of the RRP, can also contribute to STP

Because of the large fractional release of transmitter at normal prob₀, it is possible that the limited time for refilling release sites between nerve impulses might contribute in some way to the loss of F2, A, and P at normal prob₀ for the high average stimulation rates (≥30/s) used in Figures 3 and 5. To explore this possibility, we applied stimulation patterns with a low average stimulation rate of 5/s to increase the average time between nerve impulses (Fig. 7A,B, black open circles). For these slow stimulation rates at normal prob₀, F1 (blue) and now also F2 (green) contributed to enhancement during the rundown (Fig. 7F), compared with no contribution from F2 at higher stimulation rates (Figs. 3F, 5F). As was the case at higher stimulation rates for normal prob₀, there was no contribution from A and P at the slower stimulation rates at normal prob₀ (data not shown). Hence, for low stimulation rates at normal prob₀, F1, F2, and depletion of the RRP are sufficient to account for STP (Fig. 7A,B,D,F).

Figure 7.

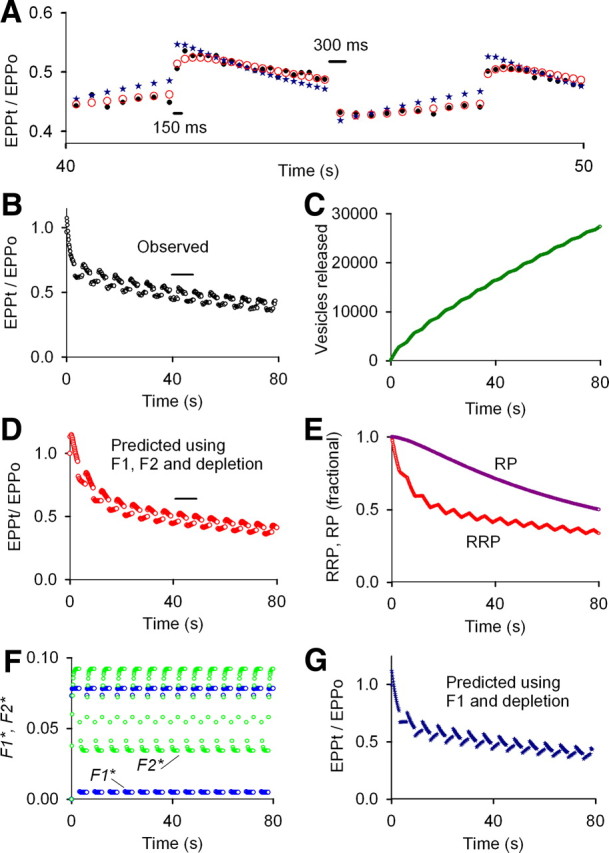
Both F1 and F2 and marked depletion of the RRP contribute to STP during the slow phase of rundown for low stimulation rates at normal prob₀ (2.0 mm Ca_o²⁺). To examine STP at slower stimulation rates at normal prob₀, the stimulation pattern was alternated between 6.67/s for 3 s and 3.33/s for 3 s for a total of 80 s of stimulation at an average stimulation rate of 5/s. Both F1 and F2 as well as depletion of the RRP were required to describe STP during the slow phase of rundown for slow stimulation at normal prob₀, in contrast to F1 and depletion (Figs. 3–6) for higher stimulation rates at normal prob₀. A, B, Experimentally observed EPP amplitudes are plotted as black circles for the train in B and for 40–50 s during the train in A. To look for STP during the slow phase of rundown, the least-squares error for fitting the data in B was calculated for EPPs 95–405 of the 405 impulse train, with the calculations proceeding from the start of the train. F1 and F2 (F, blue and green circles, respectively) and depletion of the RRP and RP (E) were found. The fitted parameters described STP after step changes in stimulation rate during the slow phase of rundown (A, D, red circles), but the predicted fast phase of rundown was slower than the observed (compare D, B). In contrast, fitting EPPs 1–395 revealed only F1 and depletion, and predicted the fast phase of rundown during the first 3 s of the train (G), but not the response to step changes in stimulation rate during the slow phase of rundown (compare observed data as black circles in A and B, with predicted response as blue stars in A and G). Estimates of A and P were zero for fitting either the full train or the partial train (data not shown). Parameters for fitting EPPs 95–405, which gave the predicted responses in A (red circles) and C–F are as follows: EPP₀ = 124 vesicles, prob₀ = 0.0124, f₁* = 1.10, τ_F1* = 55.2 ms, f₂* = 0.0635, τ_F2* = 285 ms (fixed), n = 1.29, a₀* = 0.0, p* = 0.0, RRP₀ = 10,000 vesicles (fixed), τ_RRP = 14.5 s, RP₀ = 33,243, τ_RP = 173 s. These same parameters could predict the STP to the full length of the train of 800 EPPs (data not shown). Parameters for fitting EPPs from 1 to 395 giving the predicted response plotted as blue stars in A and G: EPP₀ = 231 vesicles, prob₀ = 0.0231, f₁* = 2.00 (limited to ≤2.0), τ_F1* = 57.2 ms, f₂* = 0.0, n = 1.0 (fixed), a₀* = 0.0, p* = 0.0, RRP₀ = 10,000 (fixed), τ_RRP = 6.17 s, RP₀ = 93,830 vesicles, τ_RP = 93.8 s.

As an additional test of the contribution of F2 to STP at the low stimulation rates during rundown, F2 was fixed to zero and the data refitted. The responses to the step changes in stimulation rate were no longer predicted (Fig. 7A, blue stars; compare G with B, D), consistent with F2 contributing to STP during rundown for slower stimulation rates at normal prob₀. Transmitter output for low-frequency simulation is maintained by recycling rather than mobilization from the reserve pool (Richards et al., 2003), which might contribute to differences in F2 at different stimulation rates. This variable contribution of F2 to STP at normal prob₀, depending on the stimulation rate, adds another complexity to STP.

Solving for EPP₀ and RRP₀

When solving for the components of STP, fixing the size of RPP₀ to values in the literature gave a calculated value for EPP₀ in Equation 1. For example, setting RRP₀ to 10,000 vesicles (Rizzoli and Betz, 2005) for the experiments in Figures 1–3 for low, intermediate, and normal prob₀ gave calculated values for EPP₀ of 1.5, 38, and 176 vesicles, respectively (and see Table 1), consistent with expected experimental values for the levels of extracellular Ca²⁺ used in these experiments (Dodge and Rahamimoff, 1967; Magleby and Pallotta, 1981; Rizzoli and Betz, 2005). Prob₀ for these same experiments would then be 0.00015, 0.0038, and 0.018, given by EPP₀/RRP₀. Alternatively, fixing the value of EPP₀ in normal Ca²⁺ to the previously calculated value of 176 vesicles (found in Fig. 3), setting new starting parameters, and refitting with RRP₀ as a free parameter gave estimates of RRP₀ within 0.5% of 10,000 synaptic vesicles. Hence, given either EPP₀ or RRP₀, the unspecified parameter can be determined together with EPP amplitudes during a train expressed as the number of released vesicles. In the absence of a specified value for either EPP₀ or RRP₀, RRP₀ can be set to 1.0 and the equations then give normalized EPP amplitude (normalized synaptic strength) with the fitted value of EPP₀ giving prob₀. In terms of the equations, it is the ratio of EPP₀/RRP₀ that determines STP by setting prob₀. Prob₀ then determines the depletion rate of the RRP and the components of enhancement that contribute during the train, as shown in the next section.

The components of enhancement contributing to STP during repetitive stimulation depend on prob₀

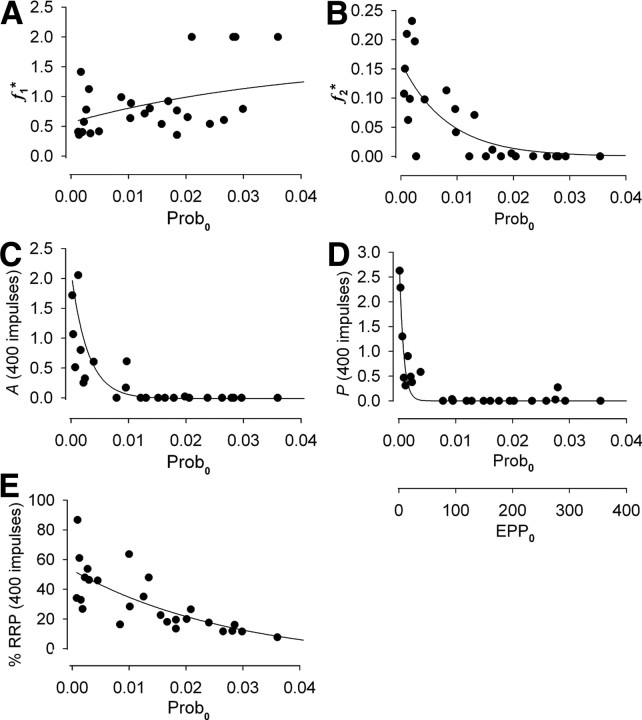
Twenty-three additional experiments for a variety of stimulation patterns over a wide range of prob₀, including three experiments with 4 mm Ca_o²⁺, were performed to estimate the components of STP during repetitive stimulation. The observations in these additional experiments are consistent with those presented in previous sections. RRP₀ was fixed at 10,000 vesicles (Rizzoli and Betz, 2005) and EPP₀ was determined by fitting the trains. Prob₀ was then calculated from EPP₀/RRP₀. Figure 8 summarizes the results. The increments of F1 and F2 added by each impulse, f₁* and f₂*, are plotted against prob₀ in Figures 8, A and B. The magnitudes of A and P and the percentage of the RRP remaining just before impulse 400 in the train are also plotted against prob₀ in Figure 8C–E, respectively. EPP₀ is also plotted in Figure 8D and applies to all parts of the figure.

Figure 8.

The contributions of the components of enhancement to STP during repetitive stimulation depend on prob₀. Parameters and predicted responses obtained by fitting EPP amplitudes during repetitive stimulation with Equations 2–10 are plotted against prob₀. Prob₀ is given by EPP₀/RRP₀, with RRP₀ fixed at 10,000 vesicles (Rizzoli and Betz, 2005). EPP₀ is shown in D and applies to all plots in the figure. Data are for a variety of applied stimulation patterns with an average stimulation rate of ≥30/s. The lines through the data are empirical. A, Each nerve impulse adds an increment of F1 facilitation, f₁*, over the examined range of prob₀. B, The increment of F2 facilitation, f₂*, added by each impulse is greatest for low prob₀, decreasing to zero as prob₀ increases. C, D, The magnitudes of A and P at 400 impulses of stimulation, A(400) and P(400) are greatest for low prob₀, decreasing to zero as prob₀ increases. Off scale in C is a point at prob₀ = 0.00088 and A = 4.6. E, The fraction of the RRP remaining at 400 impulses decreases as prob₀ increases. In the fitting, n was a free parameter. Fixing n = 1 gave the same general findings.

Figure 8 shows that F1 is a major contributor to STP for all examined levels of prob₀. In contrast, the contributions of F2, A, and, P decrease as prob₀ increases, with the contributions of P, A, and F2 becoming negligible when prob₀ is greater than ∼0.005, 0.01, and 0.015, respectively, or when EPP₀ is greater than ∼50, 100, and 150 vesicles, respectively. Hence, as prob₀ is increased, the three slower components of enhancement disappear in order of longer to shorter time constants of decay. (The information in Fig. 8 and Table 1 could be used to set parameters to estimate STP for a given prob₀ using Eqs. 2–10.)

Whereas changes in Ca_o²⁺ were used to change synapses from highly facilitating to highly depressing in the experiments reported in this paper, the data have been presented in terms of prob₀ for the following reasons: (1) consistent with the findings in Figures 1–8, synaptic strength (which is related to prob₀) has been associated with determining whether synapses are facilitating or depressing (Mallart and Martin, 1968; Magleby, 1973b; Atwood and Karunanithi, 2002; Zucker and Regehr, 2002); (2) the STP response is not always strictly tied to Ca_o²⁺, as the STP responses for neuromuscular synapses from different frogs can differ somewhat for the same Ca_o²⁺; and (3) neuromuscular synapses can become more facilitating during extended durations of experimentation, even though Ca_o²⁺ is kept constant (Magleby and Zengel, 1976b). Variability in STP properties at the same Ca_o²⁺ for calyx synapses from different rats has previously been observed (Weis et al., 1999; Hennig et al., 2008).

Presenting the data in terms of prob₀ rather than Ca_o²⁺ removed much of the synaptic variability and has the advantage that, in terms of the examined models, prob₀ is a major determinant of the initial rate of depletion of the RRP, giving immediate insight into the expected type of response. Nevertheless, it was Ca_o²⁺ that was altered to change the type of synaptic response. Thus, the results in Figures 1–3 are the same for low (0.2 mm), intermediate (1.0 mm), and normal (2.0 mm) Ca²⁺ as for low (0.00015), intermediate (0.00384), and normal (0.0176) prob₀. When the data from multiple experiments were grouped in terms of low (0.14–0.2 mm), intermediate (1.0 mm), and normal to high (2–4 mm) Ca_o²⁺, the parameter values and trends were very similar to those in Table 1 for low, intermediate, and normal to elevated prob₀, but with more variability in some of the parameters (data not shown). Thus, our findings in terms of the components contributing to enhancement are essentially the same for changes in either Ca_o²⁺ or prob₀. This is not surprising, as changing Ca_o²⁺ would change both Ca²⁺ entry and residual Ca²⁺, which has been associated with the components of enhancement (see Discussion).

Whereas Figure 8 describes the relationships between prob₀ and the various enhancement components of STP, such a relationship is unlikely to apply to all synapses or for all experimental conditions, because prob₀ can be uncoupled from STP. For example, Young and Neher (2009) have shown that overexpressing mutated synaptotagmin leaves intrinsic Ca²⁺ sensitivity intact while loosening the tight coupling between Ca²⁺ influx, release, and STP, most likely by interfering with the positioning of vesicles with respect to Ca²⁺ channels. Additional support for possible uncoupling comes from the observations of Sippy et al. (2003), who found that a depressing synapse can be converted into a facilitating synapse without changing basal synaptic strength by increasing the level of neuronal calcium sensor-1, effectively uncoupling prob₀ from STP. Changes in Ca²⁺ currents or changes in increments in intracellular Ca²⁺ with each nerve impulse during trains (Borst and Sakmann, 1998; Narita et al., 2000; von Gersdorff and Borst, 2002; Xu et al., 2007) might also be expected to partially uncouple prob₀ from STP.

Discussion

Summary of findings

Presynaptic STP encompasses a broad range of responses, from highly facilitating synapses to deeply depressing synapses (Cowan et al., 2001; Zucker and Regehr, 2002). Whereas all four components of enhancement, F1, F2, A, and P, contribute to STP at a highly facilitating neuromuscular synapse induced by low Ca_o²⁺ (Magleby and Zengel, 1982), the contributions of these components to STP is less clear for moderately facilitating to strongly depressing synapses. To address this question, we explored which components contribute to STP at the neuromuscular synapse as it was progressively transformed from a highly facilitating synapse to a deeply depressing synapse by changing prob₀ over a 280-fold range, from very low (0.00015) to above normal (0.043), by changing Ca_o²⁺ in the range of 0.14–4.0 mm.

We found that F1, F2, A, P, and partial depletion of the RRP all contribute to STP during repetitive nerve activity at low prob₀ (Figs. 1, 8). Interestingly, significant depletion of the RRP can occur at low prob₀ because the robust buildup of enhancement during the trains greatly increases release (Fig. 1). As prob₀ was increased by raising Ca_o²⁺, the contributions of the slower components of enhancement to STP progressively decreased to negligible levels, with first P, then A, and then F2 no longer contributing (Figs. 2–6, 8). For levels of prob₀ that led to appreciable rundown during repetitive stimulation, only F1 and depletion of the RRP were needed to account for STP (Figs. 3–6, 8), with F2 also contributing during rundown for low stimulation rates ≤5/s (Fig. 7). Despite the essentially unconstrained parameters during the fitting, the properties of the detected components were consistent with those in the literature obtained by other methods, lending support to the approach and analysis.

Our expectation when starting this study was that the kinetic model combined with step changes in stimulation rate would reveal all four components of enhancement for the explored levels of depression, provided that the RRP contained excess synaptic vesicles. The presence of F1 throughout the rundowns indicates that excess vesicles were immediately available for release. Indirect support for excess vesicles also comes from the observation that the calculated RRP contained vesicles in large excess over the number released by any individual nerve impulse during the rundown. Thus, the absence of F2, A, and P during rundown at normal prob₀ did not arise from a lack of vesicles available for release.

Imposing slower enhancement components for those experiments where the slower components were undetected and then refitting gave predictions of STP that were inconsistent with the experimental data (Figs. 4, 6). Hence, slow components that were not detected were not contributing to STP, because if they were, it would not have been possible to describe STP (Figs. 4, 6).

Limitations of analysis

The models described by Equations 1–12 were suitable to test for the components of STP during repetitive stimulation under the conditions of our experiments, and provided excellent descriptions of the dynamics of STP over wide ranges of prob₀. Nevertheless, the equations are not meant as a comprehensive description of transmitter release, because the long-term recovery processes of some of the component parameters are not known and, consequently, not included. Related to this limitation, the models would not be able to predict the delayed onset of P after extensive stimulation at normal prob₀ (Magleby, 1973b) that gives rise to posttetanic potentiation, because a recovery process for undetected P is not incorporated. Furthermore, the recycling of synaptic vesicles is more complicated than included in the model (Stevens and Wesseling, 1998; Wang and Kaczmarek, 1998; Wesseling and Lo, 2002; Richards et al., 2003; Sudhöf, 2004; Schweizer and Ryan, 2006; Denker and Rizzoli, 2010), and additional factors that can contribute to STP are not included (Zucker and Regehr, 2002; Neher and Sakaba, 2008; Todd et al., 2010).

The mechanism of the Ca²⁺-dependent release process is not part of the model, but replaced by an impulse function that places few restrictions on fundamental release mechanisms. Such mechanisms have been considered by others (Bennett et al., 2004; Neher and Sakaba, 2008; Pan and Zucker, 2009; Parnas and Parnas, 2010). To fully understand STP, it will be necessary to extend physical models based on underlying cellular physiology and structure, such as those by Bennett et al. (2007) and Pan and Zucker (2009) to account for all observed STP phenomena. Descriptive models such as Equations 2–13 are useful in that they provide dynamic descriptions of STP and provide a tool to study underlying physical processes.

Comparison with previous work

Our observations that F1, F2, A, and P components of enhancement all contribute to STP for a low prob₀ highly facilitating amphibian synapse are consistent with highly facilitating invertebrate synapses (Kamiya and Zucker, 1994) and mammalian ganglion synapses (Zengel et al., 1980). In addition, our studies suggest that some depletion of the RRP is also likely to contribute to STP even at highly facilitating synapses (Fig. 1).

For intermediate prob₀ leading to moderately facilitating synapses, release increases severalfold at the start of a train and then changes by only limited amounts during the train (Fig. 2). Our observations that F1, F2, and A (and also P for the lower range of intermediate prob₀) together with a sequential two pool depletion and replacement of vesicles can account for STP at such moderately facilitating synapses (Fig. 2) are consistent with previous descriptions of STP at moderately facilitating excitatory hippocampal synapses (Kandaswamy et al., 2010) and also at moderately facilitating cutaneous pectorus neuromuscular synapses (Kalkstein and Magleby, 2004).

Our observations that F1 and depression, but not F2, A, and P, contribute to STP for highly depressing synapses with marked rundown because of normal or elevated prob₀ (Figs. 3–6) are consistent with previous observations from depressing calyx synapses (Müller et al., 2010) and visual cortex layer 2/3 synapses (Varela et al., 1997), where STP arises mainly from a fast component of facilitation and one or two components of depression. Calyx synapses can also exhibit fast and slow phases of rundown (Hennig et al., 2008), as is the case for the neuromuscular synapse (Fig. 3). Hence, the model we present for STP has major features in common with STP at calyx and visual cortex layer 2/3 synapses. Nevertheless, depending on the stimulation pattern, STP at calyx may be simpler (Hermann et al., 2009) or more complicated (Hennig et al., 2008) than a fast component of facilitation and one or two components of depression.

Dittman et al. (2000) accounted for STP at three different CNS synapses ranging from highly facilitating to depressing with a general model that included depression and a fast component of facilitation, with Ca²⁺-dependent refilling of empty release sites. Whereas our findings are consistent with theirs for depressing synapses, their model had fewer components of enhancement for highly facilitating and moderately facilitating synapses than either our model or the model of Kandaswamy et al. (2010). This difference may reflect that their trains were generally brief so that the slower components of enhancement, if present, would have made only small contributions.

That F1, F2, A, and P components of miniature EPP frequency (Zengel and Magleby, 1981) are still observed in the presence of depression (Zengel and Sosa, 1994) suggests that the presumed Ca²⁺-dependent driving processes for the enhancement components (Kamiya and Zucker, 1994; Tank and Zucker, 1997; Suzuki et al., 2000; Zucker and Regehr, 2002; Kalkstein and Magleby, 2004; García-Chacón et al., 2006) are still present during marked rundown, but uncoupled from evoked release so that F2, A, and P of evoked release are not detected. The reason for this uncoupling during marked depression is not known but may be related to the fact that spontaneous and evoked release may have differences in location and/or molecular components (Washbourne et al., 2002; Zucker and Regehr, 2002; Maximov and Südhof, 2005; Wadel et al., 2007; Young and Neher, 2009; Yoshihara et al., 2010). Our observations that F1 contributes to STP under conditions where F2, A, and P are undetected (Figs. 3–8) supports previous studies suggesting that the mechanism for F1 has some differences from F2, A, and P (Delaney and Tank, 1994; Kamiya and Zucker, 1994; Neher and Sakaba, 2008).

Significance

Facilitating synapses typically have lower prob₀ than depressing synapses (Zucker and Regehr, 2002) and Figures 1–8. Our systematic study characterizes yet another mechanistic difference. At low prob₀, the four enhancement processes F1, F2, A, and P are robust, overcoming the partial depletion of the RRP, leading to a facilitating synapse. In contrast, as prob₀ increases, the contributions of the three slower enhancement components F2, A, and P progressively decrease so there is little enhancement (except from F1) to compensate for the increased depletion of the RRP, leading to rundown. Thus, prob₀-dependent enhancement adds additional complexity to STP that will need to be taken into account. On this basis, experimental procedures that alter prob₀ might also be expected to alter F2, A, and P, even if they do not directly act on these components.