Abstract
Saccades are imprecise, due to sensory and motor noise. To avoid an accumulation of errors during sequences of saccades, a prediction derived from the efference copy can be combined with the reafferent visual feedback to adjust the following eye movement. By varying the information quantity of the visual feedback, we investigated how the reliability of the visual information affects the postsaccadic update in humans. Two elements of the visual scene were manipulated, the saccade target or the background, presented either together or in isolation. We determined the weight of the postsaccadic visual information by measuring the effect of intrasaccadic visual shifts on the following saccade. We confirmed that the weight of visual information evolves with information quantity as predicted for a statistically optimal system. In particular, we found that the visual background alone can guide the postsaccadic update, and that information from target and background are optimally combined. Moreover, these visual weights are adjusted dynamically and on a trial-to-trial basis to the level of visual noise determined by target eccentricity and reaction time. In contrast, we uncovered a dissociation between the visual signals used to update the next planned saccade (main saccade) and those used to generate an involuntary corrective saccade. The latter was exclusively based on visual information about the target, and discarded all information about the background: a suboptimal use of visual evidence.
Introduction
Long sensory delays compared with the duration of a saccade make it impossible to control eye movements with a simple sensory feedback. In consequence, the CNS uses a corollary discharge of the motor commands (efference copy) to monitor the state of the oculomotor plant (Helmholtz, 1867; Holst and Mittelstaedt, 1950; Sperry, 1950; Robinson, 1975). This corollary discharge allows a fast and accurate prediction of the position of the eye in the orbit during a sequence of saccades: for example, if the target of a saccade jumps to a new location immediately before the eye movement, a second saccade to the new position of the target can be executed with little or no delay after the first saccade (Becker and Jürgens, 1974). A similar behavior is observed when the first saccade is forced by an electrical microstimulation (Mays and Sparks, 1980).
When available, visual information is a complementary source of information. Presaccadic and postsaccadic information can be optimally combined to determine target position (Vaziri et al., 2006); their comparison can also be used in combination with the efference copy to update the internal estimate of the state of the oculomotor system (Munuera et al., 2009). This latter study showed that the weight of visual target information is consistent with an optimal integration of sensory information with respect to its noise (visual noise) compared with the noise in the efference copy (motor noise). In other words, the sensory information in the oculomotor system seems to be processed as in a Kalman filter, each signal being weighted according to its relative reliability (Kalman and Bucy, 1961). Similar optimal estimation processes have been reported in the control of arm movement or body posture (Wolpert et al., 1995; van Beers et al., 1999; Saunders and Knill, 2004; Kuo, 2005; Guigon, 2010).
However, the 2009 study (Munuera et al., 2009) was subject to some methodological limitations. In particular, stereotyped visual stimuli could have biased the subjects toward cognitive strategies. Furthermore, the determination of optimality relied on experimental estimates of motor noise, which are notoriously difficult. In the present study, we assess this issue from a more straightforward perspective. We reasoned that if visual information is used in a statistically optimal way, the reliability of the visual information should affect the postsaccadic update of the eye state. This idea was tested by varying the amount of available information: here, visual information could consist in the target of the saccade only, in a wide textured background, or in both target and background. Additionally, the natural fluctuations in the latencies of saccades involved in the task introduced variations in the reliability of visual information, which allowed testing of dynamical adjustments of the weight of visual information.
The results demonstrate that visual cues are differentially used to generate a corrective saccade or to modify the initially planned next saccade. Only the latter demonstrates an optimal uptake of visual information.
This suggests the existence of two distinct mechanisms for saccadic visuo-motor integration: an optimal controller taking into account sensory and motor reliabilities and planning the next voluntary saccade; and a fast but suboptimal correction based solely on the postsaccadic visual target.
Materials and Methods
Subjects.
Fourteen healthy human subjects (6 males, 8 females, ages 18–37 years) participated in this study. Two of the authors participated in the experiment; all other participants were naive to the purpose of the study. No subject (even authors) detected the intrasaccadic manipulations. All subjects had normal or corrected-to-normal vision. Correction exclusively used soft contact lenses.
Setup.
Stimuli were presented in a dark room on a large back-projection screen with a fast video projector (DepthQ, LightSpeed Design; resolution 800 × 600 pixels, 120 Hz refresh rate, one frame delay). The projected surface was 112 cm wide by 85 cm high, and subjects were seated so that their eyes were 50 cm away from the screen. This resulted in an apparent field of view of 96 × 80°. All experiments were performed in monocular vision, the left eye covered with a black patch. The projection was slightly decentered with respect to the right eye so as to maximize the monocular field of view. Both vertical and horizontal eye orientations were recorded at 250 Hz using a head-mounted infrared eye tracking system (Eyelink I, SR Research). Movements of the subject's head were prevented by the use of a chin rest and a bite bar. The precise synchronization of the video display to the eye-tracker events was checked with a photodiode connected to a real-time acquisition system (ADwin, Keithley).
Task.
The task was adapted from classic double-step experiments (Westheimer, 1954; Becker and Jürgens, 1979). A trial started with the presentation of an open green square in front of the subject's right eye; that was the initial fixation point (FP) for the subject. When ready, the subject pressed a key that triggered the eye tracker offset correction. Then, while the subject was still maintaining fixation, a target, formed of a green + (target 2: T2), was briefly presented. After T2 extinction, a more eccentric target, consisting of a filled green square, was presented (target 1: T1). When the fixation point was turned off, the subject was required to perform a sequence of two saccades, first toward the location of T1 (saccade S1), and second toward the location of T2 (saccade S2). The presentation of the targets in reverse order was chosen to preclude the memorization of the T1-T2 vector. All targets were 3 pixels wide and high, which corresponded to 0.6°. The possible locations of the targets are presented in Figure 1A (choice of the nasal hemifield for T1 was dictated by monocular view and the average position of the blind spot). To vary the amount of visual information available to the subject during the task, we used different visual backgrounds. In some conditions, targets were presented over a uniform gray background fading to black on the borders of the screen; in the other conditions, an identically fading textured background was rendered under the targets (Fig. 1E). The global luminance of these backgrounds was matched. This textured background was generated by adding grayscale Gabor patches to a black background. These patches were sized to span a wide range of spatial frequencies. They were presented at random orientations and were arranged on a virtual sphere centered on the right eye of the subject. A new background was generated for each trial.
Figure 1.
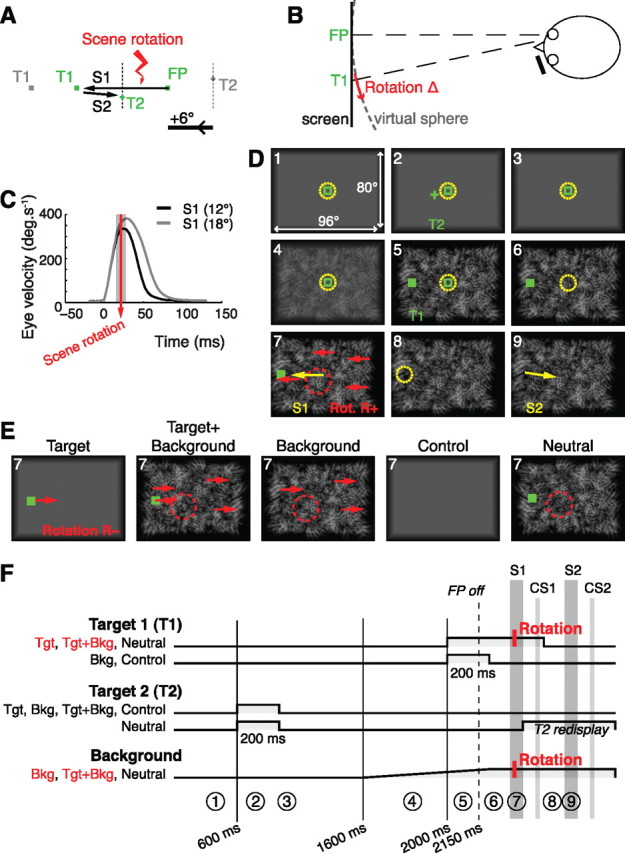
Experimental protocol. A, Spatial configuration of the targets with an example of eye trajectory. Gray, Alternative positions for T1 and T2; dotted segments, range of T2 locations. The visual perturbation (rotation of the visual scene) took place during S1. To ease understanding, the positive x-axis was oriented to the left, in the direction of the first saccade. B, Top view of the experimental setup. The scene was rendered on a virtual sphere centered on the viewing eye. Perturbations were rotations of angle ±Δ of the virtual sphere. C, Precise timing of the visual perturbation relative to mean eye velocity profiles. Grayed area, 95% confidence interval on perturbation timing. D, Representative trial, in the condition Target+Background, for a positive intrasaccadic rotation. Numbers indicate the order of events. Targets are shown in green, eye position as a dashed yellow circle, saccades as yellow arrows, and intrasaccadic perturbation as red arrows. The dashed red circle denotes the scrambling of the background around the T2 location. For clarity, the distance between targets and the amplitude of rotation were exaggerated. E, For each of the five experimental conditions are depicted the events occurring during the saccade S1. Conditions with perturbation are here represented with a negative intrasaccadic rotation. F, Timing of stimulus presentation in the different conditions. Only conditions in red include trials with visual perturbations. Circled numbers refer to the trial steps of D. T2 was displayed before T1; T2 was always flashed, whereas T1 was sometimes maintained until 100 ms after the S1 saccade. In the condition neutral, T2 was redisplayed after S1 to guide the execution of S2. When a textured background was present, it was gradually introduced before T1.
We monitored several parameters to check that the subject was performing the task appropriately. In particular, the program enforced no blinking, no anticipation (reaction time >100 ms), and accuracy (tolerances: 1.5° for fixation, 40% of saccadic amplitude for S1, 50% of saccadic amplitude for S2). In case of error, the trial was interrupted and presented again later in the experiment.
Visual perturbations.
To evaluate the weight of the visual information in the postsaccadic eye position estimate, the visual scene was sometimes displaced during the execution of the S1 saccade. This displacement was a brisk horizontal rotation of the whole visual scene around the vertical axis passing through the viewing eye. The visual feedback caused by such a virtual rotation is identical to the feedback received after a saccadic error (Fig. 1B), which would not be the case for a simple translation of the visual scene. The amplitude of the rotation (noted Δ) was 20% of the FP-T1 distance (i.e., 2.4° or 3.6°), either in the same direction as S1 (R+) or in the opposite direction (R−). The displacement was completed before the eye velocity peak (Fig. 1C). We measured how the subsequent saccade S2 to the memorized location of T2 compensated for this intrasaccadic perturbation; the extent of this compensation allowed us to derive the weight of postsaccadic visual information (see Model, below). A typical perturbed trial is presented in Figure 1D. Three experimental conditions included perturbed trials (Fig. 1E,F), varying the level of visual information available for the presaccadic/postsaccadic comparison.
In the Target condition, T1 was to be the only source of visual information common to the presaccadic and postsaccadic visual scenes. Therefore, we presented targets against a uniform gray background, and the intrasaccadic rotation of the visual scene boiled down to a translation of T1 only. T1 was turned off 100 ms after S1 ended. In the Background condition, the visual background was to be the only source of visual information common to the presaccadic and postsaccadic visual scenes. Accordingly, a textured background gradually replaced the gray background between the extinction of T2 and the presentation of T1. Then, T1 was extinguished before S1 onset (50 ms after the go signal), so that on perturbed trials, only the background was rotated. As in the Target condition, the only differences between the presaccadic and postsaccadic visual scene were those caused by the potential intrasaccadic displacements. The Target+Background condition was a combination of Background and Target conditions so that maximal visual information was available. The textured background and T1 were both present during S1. In perturbed trials, they were both coherently displaced.
To prevent a trivial visual anchoring of T2 on salient features of the background, the latter was designed to provide no strong positional cues, and was presented well after the offset of T2. Furthermore, a 6° wide circular portion of the background was systematically scrambled around the location of T2 during the saccade to T1 (random displacement and rotation of the Gabor patches in this region).
In each of these conditions, the perturbation was either absent (one third of trials; hereafter, R0), in the direction of the saccade to T1 (one third of trials, R+), or in the direction inverse to S1 (one third of trials, R−). As four spatial configurations were possible (resulting in 12 or 18° S1 amplitudes, and 6, 12, 18, or 24° S2 amplitude; Fig. 1A), each combination of condition and perturbation was repeated 32 times for a subject (4 configurations by 8 repetitions).
Two additional conditions were imposed. The neutral condition was designed to prevent potential saccadic adaptation; neutral trials were inserted after each perturbed trial and reused the same T1 location (192 trials). This condition was similar to the Target+Background condition with no perturbation, except that T2 was redisplayed after S1. In a control condition, no visual information was given while the subjects performed the sequence of saccades: the background was uniform and postsaccadic information about T1 or T2 was not available (32 repetitions).
Trials were pseudo-randomly ordered so as to prevent the repetition of identical conditions and perturbation directions. In total, each subject performed 512 trials, separated into four sessions conducted over 2 days. Sessions were all identical up to trial order.
Eye-tracker calibration.
For accuracy and usability reasons, a custom calibration procedure was developed. It was performed at the beginning of each session and each time the drift correction exceeded 2°. Eleven targets spanning the eccentricity range were used. A luminance change detection task ensured the proper accuracy of the fixations. The raw eye-tracker output was then least-squares fitted to horizontal and vertical eye orientations using two biquadratic equations (Bonnetblanc and Baraduc, 2007; van Beers, 2007).
Model.
We hypothesized that the visual perturbations affected S2 endpoints by biasing the estimate of the eye displacement brought out by S1. Computation of this internal estimate was modeled as a Kalman filtering, combining the efference copy of S1 with presaccadic and postsaccadic visual information.
In mathematical terms, a saccade to T2 was hence based on its memorized location, T̂2, corrected by the estimate êS1 of the eye displacement brought out by the first saccade, S1. Noting eS1, the actual eye position after S1, and T̂1, the initial estimate of T1 location,
then the endpoint of S2 (Munuera et al., 2009) is:
In these equations, the terms ε and ε′ correspond to the motor (execution) noise.
The estimated eye displacement êS1 can be obtained from the efference copy and from the comparison of the expected and actual postsaccadic visual information. If postsaccadic visual information is optimally used to update the state of the oculomotor system, then the difference V − V̂ between expected and actual postsaccadic visual information should be weighted according to its reliability, relative to the reliability of the efference copy. Here we write κ for this optimal weight of postsaccadic visual information. Assuming that T̂1 is the eye position estimate derived from the efference copy, we have:
where V and V̂ are, respectively, the actual and efference copy-predicted postsaccadic visual feedback.
The postsaccadic visual error is:
where Δ is the absolute amplitude of the perturbation and where η = −1, 0, or 1 for R−, R0, and R+, respectively. Assuming that T̂2, V̂, and eS1 are independent of the occurrence of an intrasaccadic rotation, such a perturbation shifts the mean S2 endpoint by κηΔ. If this filter is statistically optimal, that is, minimizes the variance of eS2, we have:
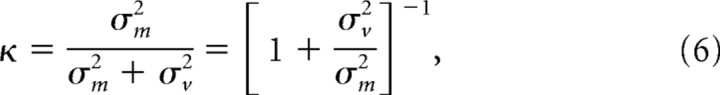 |
where σm2 is the variance of the motor execution noise, and σv2 is the variance of the localization of the visual scene before S1 (Munuera et al., 2009). If there is no motor noise, κ = 0. If motor noise is 40% of total noise (condition Target; van Beers, 2007), κ = 0.4.
Taking into account extraocular proprioception slightly modifies the model. If both vision and proprioception were used in postsaccadic updating, and assuming a linear filter, the following eye position estimate after S1 would be:
with P being the postsaccadic proprioceptive signal of variance σp2, and P̂ the prediction of the proprioceptive feedback from the efference copy. It is straightforward to show that for an optimal linear filter,
The use of proprioceptive inflow in postsaccadic updating would imply a reduction in the weight of vision.
Data analysis.
Eye positions were analyzed on the horizontal axis, which was oriented along the direction of S1. The eye position trace was digitally differentiated, then segmented into individual saccades using fixed start and stop velocity thresholds (7.5°/s). A saccade was considered directed to T1 or T2 on the basis of both its order in the sequence and which was the closest target at saccade onset and end. A valid trial contained one main saccade S1 (saccade from FP to T1) possibly followed by one corrective saccade CS1 (around T1), then followed by a main saccade, S2 (saccade from T1 to T2). When present, corrective saccades CS2 (around T2) were also segmented.
Potential outliers were detected and removed as follows. Trials were first grouped by target configuration and by perturbation (no perturbation, perturbation R+, or perturbation R−). Then, trials with S1 endpoints >3 SDs away from the median S1 endpoint for the group were removed, as well as trials with S2 endpoints >4 SD away from the median S2 endpoint. SDs were computed using the median absolute deviation, a robust estimator. Overall, the rejection of invalid or outlying trials removed 5.2% of the data. Statistics were computed in Matlab (MathWorks) and R.
The compensation of the perturbation by S2 was assessed using an N-way ANOVA on raw S2 endpoint errors (S2 endpoint location relative to T2) normalized by perturbation amplitude, with factors: perturbation (R−, R0, or R+), condition (Target, Target+Background, or Background), subject (random factor), and target configuration. Post hoc tests were honestly significant difference multiple-comparisons tests.
The influence of parameters such as perturbation direction, target position, or condition was analyzed using a synthetic measure of the compensation of the visual perturbation. In light of the above section, it is easy to see that the weight of postsaccadic vision on a given trial should be equal to the deviation of the S2 endpoint from the baseline, normalized by the amplitude of the perturbation:
 |
In the above formula, eS2 is the endpoint location of S2 for the trial; 〈sj, cf, cd〉, used as baseline, is the expectation over the R0 trials with the same subject, spatial configuration, and experimental condition; Δcf is the amplitude of the possible intrasaccadic visual displacement for the target configuration. According to the model, the intrasaccadic rotations shift the mean S2 endpoint by κηΔcf, so the observed normalized compensation C in perturbed trials should be an unbiased measure of κ, up to its sign. Note that C can also be defined in unperturbed trials; it then only indicates the relative endpoint error (the normalization by Δcf allowing comparisons and pooling).
To analyze the effect of latency on perturbation compensation, linear mixed models were used. The dependent variable was the unsigned perturbation compensation, and the factors were the latency and the direction of perturbation; subjects were modeled as random intercepts. For each subject and condition (visual stimulus and presence/absence of CS), the slope of the compensation as a function of the latency in trials without perturbations was subtracted from the unsigned compensation. The temporal stability of several parameters across the experiment (signed perturbation compensation, S1 latency, S1–S2 latency) was assessed using linear mixed models with perturbation direction and session number as independent factors.
To compare the correction introduced by CS1 to the perturbation compensation by S2 for similar latencies in the Background condition while eliminating any difference attributable to sample size or latency distribution, we randomly resampled from both distributions in the 150–350 ms latency range (the overlap of latency distributions). Fifty trials in each category (CS1 or S2, R+, or R− perturbations) were selected with replacement, so as to follow the same normal distribution of CS1 or S2 latencies (mean, 250 ms; SD, 45 ms; random values were generated from this distribution, and trials with latencies closest to these values were selected). Then, the perturbation compensations (by CS1 and S2, respectively) were computed over these 50 trials, as well as their significance. These operations were repeated 10,000 times.
Results
The outline of this section is the following. We first describe how the intrasaccadic perturbation was compensated. This leads to several assessments of our hypothesis of optimal cue combination, for different targets, subjects, and saccade latencies. Then, we focus on corrective saccades and show that they optimally integrate target information while discarding information from the background.
As a reminder, we use the following abbreviations for targets (FP, initial fixation point; T1, initial target 1; T2, target 2) and saccades (S1, S2, saccade to T1 or T2; CS1, CS2, corrective saccade to T1 or T2). The notation T1post specifies the postsaccadic T1, which was different from T1 on perturbation trials.
Compensation of the visual perturbation
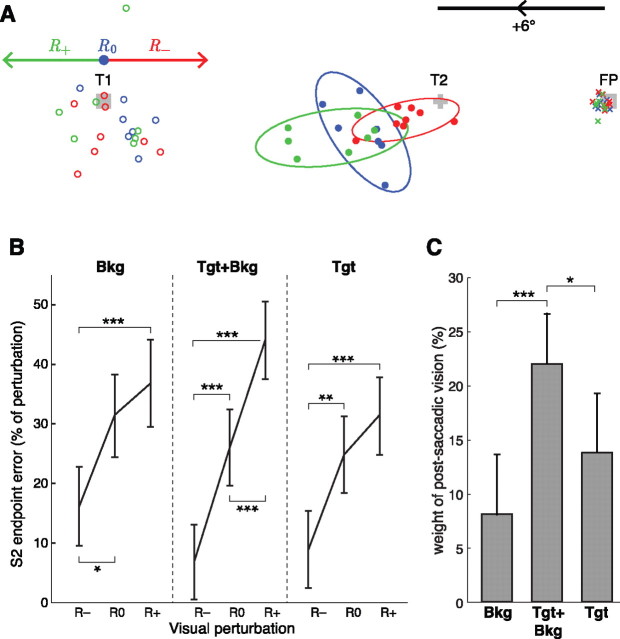
When a rotation of the visual scene was applied during S1, the endpoints of S2 were significantly shifted in the direction of the visual perturbation that occurred during S1. The shift in S2 endpoint was consistent with a partial use of the visual information available at the end of S1 to correct the internal estimate of eye position: the apparent S1 undershoot caused by an R+ perturbation was partially compensated by a shorter S2, and conversely for R−. Figure 2A illustrates this effect for one subject in one target configuration; note that baseline S2 saccades (R0) were markedly hypometric.
Figure 2.
A, Raw endpoint data for one subject and one target configuration in the condition Target+Background. Crosses, Initial fixation; open circles, S1 endpoints; filled circles, S2 endpoints. The 95% tolerance ellipses are figured for the S2 endpoints. Red, Perturbation R−; blue, no perturbation R0; green, perturbation R+; gray, visual targets FP, T1, and T2 (drawn to scale). Arrows show the direction and amplitude of the scene rotation in the respective conditions. To synthesize data as presented below (B), raw S2 endpoint errors were pooled for the four target configurations by considering endpoint errors as a percentage of the potential perturbation amplitude. Note that the baseline used to compute the weight of postsaccadic vision (C) corresponds to the mean R0 error. B, Mean effect of the visual perturbation on the eye position at the end of S2. Error bars are 95% confidence intervals, ANOVA on S2 endpoint errors with factors perturbation, condition, target configuration, and subject. Endpoints are shown as errors relative to actual T2 location, expressed as a percentage of the potential (R0) or actual (R+, R−) visual perturbation amplitude Δ. Endpoints were adjusted for the aforementioned covariates. *p < 0.05, **p < 0.01, ***p < 0.001. C, Mean weight of the postsaccadic visual information for the different visual scenes.
To assess the global influence of the perturbation on S2 endpoints across all subjects and configurations, we normalized the S2 endpoint errors (relative to T2) to the potential perturbation amplitude Δ. The difference between R− and R+ was significant for all the experimental conditions (Fig. 2B). The compensation of the perturbation was slightly asymmetrical, as S2 endpoints for perturbations R− were, in general, further away from R0 than endpoints for perturbations R+. This was apparent in the Target and Background conditions.
As S2 latency modulates the perturbation compensation significantly, only trials with S2 latency >250 ms were kept for further analyses (for a detailed justification, see below, Optimal integration of target and background information, Temporal dynamics of the visual information processing, The effect of the delay between S1 and S2). The overall compensation was modest. When expressed as percentage of the visual perturbation, the mean compensation corresponds to the weight of the postsaccadic visual information. The weights of the postsaccadic visual information were the following: 14% in Target condition, 8% in Background condition, and 22% in Target+Background condition (Fig. 2C). In this latter condition, the weight of postsaccadic vision was significantly larger than in Background or Target conditions alone (p < 0.05, ANOVA on perturbation compensation with factors perturbation, condition, target configuration, and subject).
These compensations cannot be attributed to conscious strategies since no subject detected any visual perturbation (as assessed by the experimental debriefings). Moreover, the existence of a perturbation compensation in the Background condition demonstrates that this effect cannot be simply ascribed to a relative coding of T2 with respect to T1. An anchoring of T2 on the background is also unlikely. Indeed, S1 saccades in Background trials were affected by latency in the same way as in control trials: saccades with long latencies were more variable and had a higher gain than saccades with low latencies, which is characteristic of memory-guided saccades (White et al., 1994).
Last, compensations were not due to a correction of the first saccade, since the visual perturbation induced no significant online modification of S1 (p = 0.8, ANOVA on S1 endpoints with factors perturbation, condition, target configuration, and subject). This was expected, since vision-based online corrections were only reported for much longer saccades (>120 ms in the study by Gaveau et al., 2003; here, mean S1 duration was 56 ms).
Optimal integration of target and background information
Optimal cue combination for different cue reliabilities
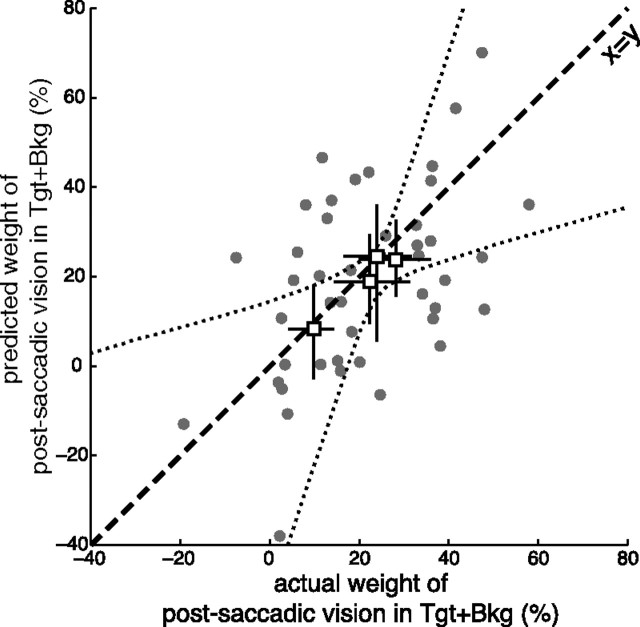
If visual information is used in a statistically optimal manner, its weight should increase with the reliability of the visual input. Accordingly, the weight of the postsaccadic visual information was higher in the Target+Background condition than in the separate Background and Target conditions. Optimal fusion predicts that the variance of the Target+Background combination is determined by the variances of the individual visual signals (Eq. 10b). The weight κTB of postsaccadic vision in the Target+Background condition can thus be predicted from the weights of the postsaccadic visual information in Background and Target conditions (respectively, κB and κT) as follows:
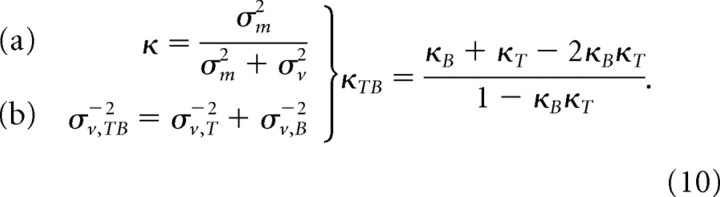 |
This prediction was first tested on the average visual weights obtained for each target configuration. This prediction proved to be correct (Fig. 3, white squares). The slope of the bidimensional regression through these points was significantly different from zero (p = 0.015; bootstrap with 10,000 runs).
Figure 3.
Integration of postsaccadic visual information in the subsequent saccade S2 is statistically optimal. Predicted weight of postsaccadic vision in the Target+Background condition (from weights in Background and Target conditions; see Eq. 10) versus actual weight of postsaccadic vision in Target+Background condition. White squares, Group averages for the four target configurations, with confidence intervals (averages were computed by weighting the data of each subject according to their variance using an expectation-maximization algorithm; confidence intervals were obtained by bootstrap). The dotted lines mark the confidence zone for the bidimensional regression over the target configurations. Gray points, Data for each subject and target configuration; dashed line, main diagonal. “Express” responses, which did not show use of postsaccadic information (S1–S2 delay <250 ms; Fig. 5), were not considered.
As visual noise increases with target eccentricity (Wertheim, 1891; Low, 1947; Klein and Levi, 1987), the location of the targets could affect the weight of postsaccadic vision. Actually, the contribution of visual noise to saccade endpoint variance increases with target eccentricity (van Beers, 2007; Morel and Baraduc, 2010). We would hence expect a decrease of visual weight with T1 eccentricity. Indeed, in all conditions, the weight of postsaccadic vision was significantly higher for small amplitudes of S1 (p = 0.006, N-way ANOVA on mean perturbation compensation as percentage of perturbation with factors condition, S1 amplitude, and S2 amplitude nested in S1). Thus, as expected, different target configurations lead to different visual weights. Since visual acuity differs among subjects, the optimal weight should also be subject dependent. We then went a step further and assessed the statistical optimality of the cue combination considering the weights measured for each subject and each target configuration (Fig. 3, gray points). Although the data averaged on these small subsets were noisy, the adequacy between the prediction and the data was good. Bootstrapping across subjects showed that the optimal fusion model was a better fit to the data than a simple additive model, κTB = κB + κΤ, in 75% of cases; it was also better than a maximum model, κTB = max(κB, κT) in 91% of cases (10,000 runs).
Temporal dynamics of the visual information processing
The combination of postsaccadic visual evidence was close to optimal. However, saccadic reaction time modulates the amount of visual information available, both before and after the saccade. To further test the hypothesis of optimality, we examined how reaction time influenced the weight of visual information.
Time course of the initial information uptake.
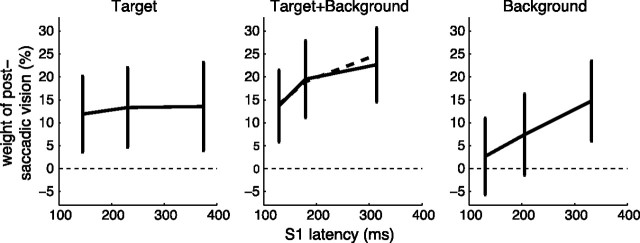
The reaction time before S1 should affect the reliability of the encoding of the presaccadic scene, especially in conditions with the presence of the background, which was only fully visible during the latency period of S1 (whereas T1 was presented 200 ms before the go signal). In accordance with this prediction, trials with a longer S1 latency showed a significantly larger weight of postsaccadic vision than trials with a short S1 latency in Background and Target+Background conditions (p = 0.007, ANOVA on unsigned perturbation compensation with S1 latency bin as a factor). In the Background condition, trials with a low S1 latency showed no significant use of postsaccadic visual information (Fig. 4). This evolution of the weight of the postsaccadic visual information reveals that >100 ms are needed to encode the visual information contained in the background.
Figure 4.
Time course of the initial uptake of visual information. Weight of postsaccadic vision as a function of initial saccade (S1) latency for the three perturbation conditions. Data were binned by tertiles on S1 latency. Error bars indicate 95% confidence intervals computed from honestly significant difference multiple-comparisons tests after ANOVA. Dashed line, Prediction of the weight in Target+Background from values in the single Target and Background conditions (Eq. 10). The initial part of the dashed curve overlays the data.
If the cue combination is statistically optimal, we should be able derive the relationship between S1 latency and postsaccadic visual weight in the condition Target+Background from the corresponding relationships in the single conditions Target and Background, using Equation 10. Satisfyingly, the prediction of the optimal estimation theory (Fig. 4, middle, dashed line) was in close correspondence to the actual data. This suggests that the postsaccadic visual information is optimally combined with the efference copy, whatever the level of visual noise.
The effect of the delay between S1 and S2.
In a manner similar to S1, the reaction time of S2 should affect the accumulation of visual evidence and thus the weight of the postsaccadic vision. Indeed, the S1-S2 delay significantly modulated the weight of the postsaccadic visual information. This modulation revealed the temporal dynamics of the updating process.
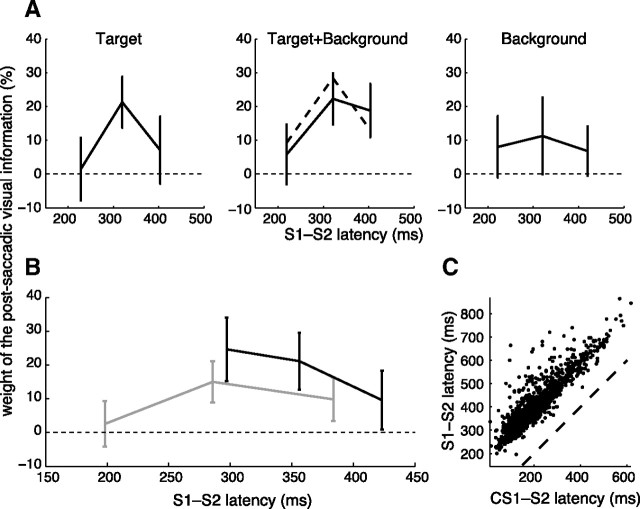
In contrast to S1, the situation for S2 is complicated by the occurrence of corrective saccades, and by competition effects between these corrective saccades and the next planned saccade in the sequence. Extracting the temporal dynamics thus required some caution. As a consequence, to measure the pure perturbation compensation, we computed the half-difference between R+ and R− trials, binned in latency tertiles. The overall effect of S1-S2 latency is presented in Figure 5A for the three perturbation conditions.
Figure 5.
Time course of the postsaccadic integration process. A, Weight of the postsaccadic visual information for different latencies between the end of S1 and the onset of S2 (S1–S2 latency). The different conditions of perturbation are represented separately, but with identical binning. Dashed line, Prediction of the Target+Background weight from weights in the single Target and Background conditions (Eq. 10). Error bars represent 95% confidence intervals. B, Weight of the postsaccadic visual information, separating trials with and without CS1. Gray, Trials without corrective saccade CS1 (conditions Target, Target+Background, and Background pooled). Black, Trials with CS1 (conditions Target and Target+Background pooled). C, Total S1–S2 latency as a function of CS1–S2 latency, for trials with CS1.
One readily observes that the weight of the postsaccadic visual information was significant only for large S1-S2 latency (Fig. 5A). An absence of postsaccadic visual information uptake for trials with short S1-S2 latencies was visible in Target and Target+Background trials; such an effect was not apparent in Background, likely because S1-S2 latency was longer for Background trials (p < 0.001). A late decrease of the weight of postsaccadic vision was also visible in the target condition: trials with a latency >400 ms probably failed to take Target information into account. In these trials, target information was only available during 100 ms after S1 ended, while the background stayed on in Background and Target+Background trials.
Then we checked whether the optimal use of visual information would predict such curves. As described previously, we computed the theoretical latency–weight relationship for the Target+Background condition from the Target and Background curves using Equation 10. Again, we found a good agreement between the prediction of the optimal estimation theory (Fig. 5A, dashed line) and the experimental data.
Latency and corrective saccades.
To get a better understanding of the apparent absence of visual information uptake for short S1-S2 latencies, and whether corrective saccades modulate the effect at longer latencies, we collated all the perturbation conditions and simply separated the trials on the basis of the occurrence of a CS1 (Fig. 5B). This analysis indicated that 250 ms is the minimal reaction time for the visuomotor system to take into account the postsaccadic visual information. The statistics confirmed this observation: in trials without corrective saccades, we found a significant positive influence of the latency on the weight of the postsaccadic visual information (p = 0.0038, linear mixed models; Data analysis).
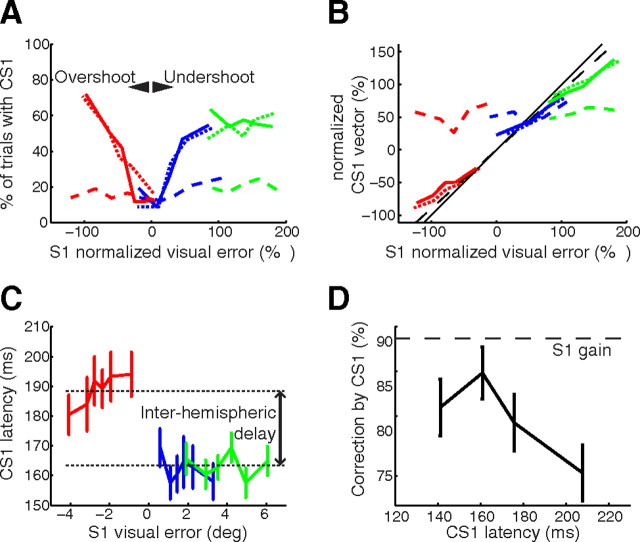
Note that trials with corrective saccades and a short S1-S2 latency (corresponding to a short CS1-S2 latency, Fig. 5C) presented a higher weight of postsaccadic vision than trials without corrective saccades of similar latency (p < 0.001, ANOVA on perturbation compensation with occurrence of a corrective saccade and subjects as factors, for S2 latencies between 250 and 350 ms). This difference became insignificant for trials with longer latencies, due to Target trials. In light of the results presented in the following section, we propose an explanation of this observation in the Discussion.
Corrective saccades as markers of visual information uptake
As in all experiments with intrasaccadic target displacements (equivalent to the Target condition), the additional visual error is usually largely reduced by corrective saccades. Therefore, these saccades shed a complementary light on the use of postsaccadic visual information by the oculomotor system. Of particular interest is the consistency between the corrective saccade and the further compensation during S2.
Corrective saccades are triggered by the postsacccadic T1
In trials with T1 still displayed after S1, the probability of making a corrective saccade was dependent on the visual error: trials with low visual errors presented a low probability of corrective saccade occurrence (<20%), while trials with larger visual errors showed a higher rate of corrective saccades (up to a plateau of 60%). However, in Background trials, while informative visual information was available (and used to correct S2, as seen above), the visual error had no influence on the probability of performing a corrective saccade (Fig. 6A).
Figure 6.
Reflexive corrective saccades after S1 only provide a suboptimal correction. A, Frequency of corrective saccades as a function of the signed visual error at the end of S1. The visual error is expressed as a percentage of the potential intrasaccadic perturbation amplitude (dotted lines, Target; solid lines, Target+Background; dashed lines, Background; red, perturbation R−; blue, no perturbation R0; green, perturbation R+). Note that the generation of a corrective saccade was unrelated to the actual motor error in the Background condition. B, Undercorrection of corrective saccades. Signed amplitude of CS1 as a function of the signed visual error at the end of S1 for different conditions and perturbations (same legend as A). Visual error and CS1 vector are expressed as percentage of the potential intrasaccadic perturbation amplitude. Note that visual target information is necessary (no correlation between visual or motor error and CS1 vector in Background). Black solid line, Full correction of the visual error; black dashed line, partial correction of the visual error with mean gain of S1 (0.91). C, Latencies of corrective saccades as a function of the signed visual error for different perturbations in Target and Target+Background conditions (same conventions as in A). D, Correction of the visual error introduced by CS1 as a function of CS1 latency in Target and Target+Background conditions.
Moreover, in Target and Target+Background, the corrective saccades brought the eye closer to the actual position of the target T1post (Fig. 6B). On the contrary, in the Background condition, in the rare trials in which a corrective saccade was made, the corrective saccades did not compensate for the actual visual error, but for what appeared to be a stereotypical hypometria of the saccade. This non-use of background information for corrective saccades cannot be ascribed to their shorter delay. Indeed, when comparing Background trials having a CS1 latency in the 150–350 ms range, with Background trials having an S2 latency in the exact same range, the former showed no statistically significant influence of background displacement on CS1 endpoints (p = 0.99), while there was a significant influence of the displacement on S2 endpoints (p = 0.002). To ascertain that these significance differences were not attributable to differences in latency distribution or number of trials, we used a trial resampling method (see Materials and Methods, Data analysis) so as to make sample size and distribution of CS1 and S2 latencies similar (inside the 150–350 ms range). We observed that the perturbation affected S2 endpoints more than CS1 endpoints in 98% of the resamples. Moreover, the effect of the perturbation on S2 was significant in 70% of the resamples, while being significant on CS1 for only 0.02% of the resamples. This demonstrates that latency differences cannot account for differences in visual weight.
In short, in Background trials, corrective saccades were unrelated to the actual visual error. This is reminiscent of corrective saccades observed in a featureless Ganzfeld (Becker and Fuchs, 1969; Prablanc and Jeannerod, 1975; Shebilske, 1976) and shows that fast corrective saccades were driven by a visual error signal generated from target information only. Without such information, corrective saccades were also delayed: their latency in the condition Background was larger than in Target and Target+Background conditions, comparing corrective saccades of same amplitude and direction (multiple comparisons after ANOVA on CS1 latency with factor condition for trials with centrifugal corrective saccades between 0.8° and 1.2°, p < 0.001).
Link between corrective saccades and perturbation compensation
It is usually assumed that corrective saccades are performed to re-foveate the target. In laboratory conditions, the gain of corrective saccades is <1, akin to the gain of the main saccades (Straube et al., 1997). However, Figure 6B shows that even by using the average S1 gain (noted as γ in the following equations) of 0.91, corrective saccades CS1 undercorrect the visual error at the end of S1.
We hypothesize that a part of this incomplete correction is a marker of the use of a Bayesian estimate of T1 location. At the end of S1, the sensorimotor system can evaluate the position of T1 on the basis of the perceived visual error V, but also on the basis of the prediction of this visual error V̂ (the use of this internal prediction is apparent in the corrective saccades observed in the control condition, where no visual error is available). The optimal corrective saccade should then be given by the following equations:
 |
The difference V − V̂ in the above equation (Eq. 11) can also be found in the equation describing the compensation of the perturbation by S2 (Eq. 4). If CS1 and S2 are based on the same optimal estimate of the postsaccadic visual error, correction by CS1 and compensation by S2 should be related. From Equation 11 we can isolate this V − V̂ difference by computing the residual visual error after CS1:
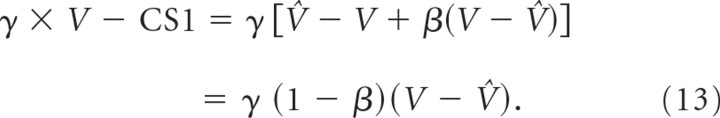 |
As the compensation of the perturbation is also linearly related to V − V̂ with factor κ (Eq. 4), there should be a linear relationship of slope κ/[γ(1 − β)] between the residual visual error after CS1 and the later compensation of the perturbation. In contrast, if CS1 and S2 are not based on the same estimate of the postsaccadic visual error but are independent from each other, it is straightforward to verify that one would expect both a noisier correlation and a slope κ/γ differing from the expected slope by a factor 1/(1 − β) ≃ 4. This alternative is not supported by our experimental results.
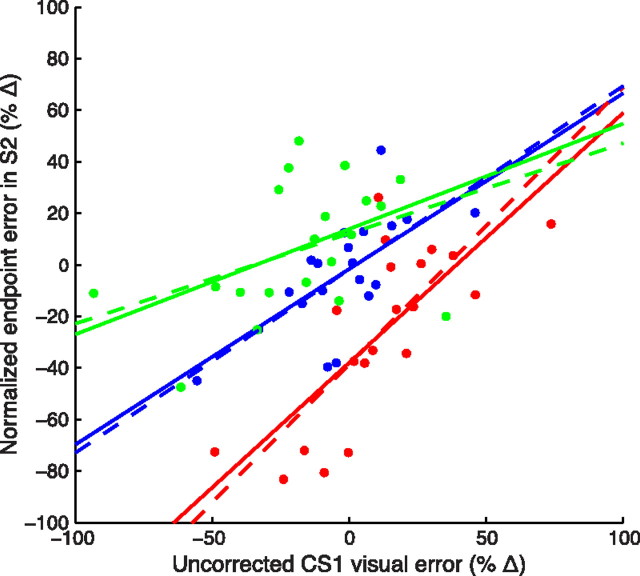
Indeed, in Target trials with corrective saccades CS1, the remaining error after CS1 execution was strongly correlated with the compensation of the perturbation (Fig. 7) in all conditions (p-values 10−6, 0.003, and 0.006 for R−, R0, and R+ perturbations, respectively). Trials with a lower remaining error (i.e., trials with a higher correction by CS1) showed a larger compensation of the perturbation. The slopes of these correlations are close to the predicted slopes (Fig. 7, dashed lines), which indicates that both corrective saccades and eye position estimates were based on a common target-based estimate of visual error.
Figure 7.
The relationship between the error compensation by corrective saccades CS1 and by subsequent S2 in Target trials is predicted by a Bayesian model. Bin-averaged uncorrected CS1 visual error is plotted against S2 endpoint error. Trials were binned on the basis of the uncorrected CS1 visual error (Eq. 13; 20 bins); then, for each bin, the mean uncorrected CS1 visual error and the mean normalized S2 endpoint error (C; Eq. 9) defined a dot. Solid lines, Robust regression; dashed lines, slopes κ/[γ(1 − β)] predicted from the model. The γ and β values were computed separately for each subject, γ being the mean gain of S1 and β being computed from the mean amount of correction introduced by CS1. Mean κ values were computed using the estimator C for each perturbation direction (for R0, the average visual weight was considered). Red, R−; blue, R0; green, R+.
In Target+Background trials, the background acted as an additional source for the estimate of the visual error. However, corrective saccades were only based on target-related visual error. Indeed, β × γ in Target and Target+Background were not significantly different (p = 0.27; see also Fig. 6), while the perturbation compensation was significantly higher in Target+Background. As a consequence, the relationship between corrective saccades and compensation of the perturbation was less marked (only significant for R− perturbations, p = 0.005).
If the preparation of CS1 and S2 shared the same estimate of visual error in the Target condition, the use of this visual error appeared suboptimal for CS1. Indeed, Equations 11 and 12 predict an increase of the percentage correction induced by corrective saccades with the eccentricity of T1, as σV̂2 increases with S1 amplitude. In contrast, the relative correction of CS1 (γ × β) decreased with S1 amplitude. This is likely due to a competition between the execution of a corrective saccade and the execution of S2. Such a competition affected the very occurrence of corrective saccades (only 60% of trials with CS1 for large visual errors) as well as the compensation introduced by CS1. Indeed, the percentage corrections computed for corrective saccades CS2, not followed by main saccades, were significantly higher (mean 0.82, neutral condition) than corrections computed for CS1 (mean 0.66, p = 0.005, paired t test). Moreover, the amount of correction introduced by a corrective saccade depended on its latency (Fig. 6D), in a manner reminiscent of what is seen for S2 in Target trials (Fig. 5A). Overall, the correction brought by CS1 was lower than the statistically optimal correction.
Predictability of postsaccadic T1 and latency of corrective saccades
The latency of the corrective saccades was inversely related to their amplitude, as reported by Henson (1978). Here, interestingly, for corrective saccades of the same amplitude, the latency depended on the direction of the corrective saccade: when CS1 was in the same direction as S1 (correction of hypometria, in R0 or R+ trials), the latency was on average 26 ms lower than when CS1 was directed opposite to S1 (R− trials) (Fig. 6C). When reported before, such latency differences were confounded with amplitude differences (Henson, 1978; Vergilino-Perez and Findlay, 2003). In contrast, Kapoula and Robinson (1986) found that CS of the same amplitude had similar latencies, whether caused by under- or overshoots; thus, latency differences cannot be ascribed to motor delays. However, the distribution of postsaccadic visual errors in their study reflected an internal bias (“range effect”), whereas our scene rotations were unpredictable. This suggests that the predictability of T1 (in other words, the computation of V̂ in Eq. 11) could be the main component of the CS1 latency difference: the corrective saccades took longer to initiate when T1 reappeared in the hemifield where it could not be predicted.
Discussion
During a sequence of saccades, subjects integrate visual information at the end of a saccade to correct the next one. Analyzing the compensation of an intrasaccadic visual perturbation for various levels of visual noise, we provide here several lines of evidence that this integration of postsaccadic visual information approximates a statistically optimal process. When two sources of visual information were available, their combination was weighted optimally. This was repeatedly verified, whatever the reliability of the visual information. As expected, target eccentricity or saccade latency modulated the visual weight. In all conditions, the weight of several cues combined agreed with the theoretical value.
The small corrective saccades that are often present at the end of the main saccades are based on postsaccadic signals; thus, these saccades could be guided by a similar optimal integration. When solely visual target information was available after the saccade, the corrective saccade and the adjustment of the next main saccade were based on the same estimate. However, in contrast to the main saccades, corrective saccades were not influenced by the visual information provided by the background.
We will now discuss these main findings in more detail.
Optimal use of postsaccadic visual information
We show here that when multiple postsaccadic visual cues are available, the oculomotor system combines them optimally. Evidence of such an intramodality fusion has been provided for quite a long time in perception (Hillis et al., 2002). It is thus possible that a common mechanism of cue combinations underlies both perceptual and sensorimotor functions.
The value of the maximum weight (obtained in Target+Background) is consistent with the conclusions of van Beers (2007) and Munuera et al. (2009): even in a structured visual environment, visual noise dominates motor execution noise. However, this weight was smaller than expected (14% in condition Target vs predicted ∼40%) from the noise estimates of van Beers (2007), if vision is the only sensory modality contributing to the postsaccadic update. In contrast to Munuera et al. (2009), estimates of motor noise by covariance between saccades were found to be unreliable. An analysis of the longitudinal structure of the noise in other data from the same subjects was undertaken and led to lower estimates of motor execution noise (Morel and Baraduc, 2010); from these values we would predict an average weight of 33% in Target. Overall, the weight values observed here are below what is predicted from current noise estimations. It could be argued that the perturbations introduced visual noise, and this would have led to a decrease in the weight of postsaccadic visual evidence throughout the experiment. However, such an adaptation of the weights was not observed. We think it is more likely that proprioception may have reduced the effect of the visual perturbation (see Model). Indeed, extraocular proprioception is fed back to the oculomotor system, at least at the cortical level, with a latency compatible with its use in the postsaccadic update (Wang et al., 2007).
Interestingly, the modulation of the weight by the latency of S1 and S2 indicates a correlation between latency and information representation; this suggests that the instantaneous (trial-specific) signal uncertainty may be represented in the CNS (rather than the average variance), and the information weighted accordingly. This could explain the larger weight for R− trials, postsaccadic visual variance being lower.
Overall, in all the configurations/subjects tested, we found a good agreement between the theoretical visual weight predicted by an optimal cue combination and the experimental weight values. This validates the idea that the various elements of the postsaccadic visual scene are optimally used to guide the subsequent saccade.
Temporal dynamics of the sensorimotor integration
The visual perturbation was only taken in account if the delay between the first and the second saccade exceeded 250 ms. This may seem long but is consistent with the latency of neural responses related to visual error signals. Remapping neurons in the frontal eye fields (FEFs) or lateral intraparietal area (LIP) tonically fire for ∼200 ms after the saccade onset and concurrent stimulus extinction (Goldberg and Bruce, 1990; Duhamel et al., 1992; Heiser and Colby, 2006). A similar if rarer behavior can be seen in the superior colliculus (Walker et al., 1995). In the cerebellum, Soetedjo et al. (2008) showed that complex spikes in the vermis encode the direction of the visual error between 100 and 150 ms after saccade end.
The rise of the compensation between 250 and 300 ms in condition Target and Target+Background can be viewed in two radically different ways. First, it may truly reflect the temporal evolution of the postsaccadic information update process, interrupted at random by the generation of S2. According to this hypothesis, the update process would progressively unfold in ∼50 ms, the updated information then being (or not, cf. Target) maintained in memory. Alternatively, this rise may mask a sharp transition between trials in which visual postsaccadic information was ignored and trials in which the integration of postsaccadic information was maximal, the apparent smooth increase being an effect of intersubject and intertrial variability. Two observations corroborate this latter hypothesis: (1) the slightly late Background trials do not show this gradual effect; (2) overall, R− trials showed larger use of postsaccadic visual information than R+, and S2 saccades were on average earlier in R−.
In any case, the weight of visual information generally increased with saccadic latency; this was always consistent with the delays in the visual system and with the notion that visual information accumulates (and noise decreases) during the reaction time (Carpenter and Williams, 1995; Hanes and Schall, 1996). Thus, sampling different levels of uncertainty linked to S1 or S2 latency gave additional support to the hypothesis of optimal cue combination.
Suboptimal corrective saccades
Corrective saccades were only truly corrective when the target of the main saccade was part of the postsaccadic visual scene (Target and Target+Background conditions). Background visual information alone was not able to drive corrective CS1, even though it was taken into account to plan the following saccade. We may hypothesize that the presaccadic/postsaccadic comparison takes longer for a complex visual scene, and that corrective saccades were released before the update process was completed. Contradicting this idea, however, the fastest S2 saccades in Background condition had the same latency as the slowest corrective saccades CS1 and compensated the intrasaccadic perturbation like longer-latency S2 saccades. Rather, this dissociation between information used to direct CS1 and to plan S2, congruent with the voluntary/involuntary difference, suggests different neural processes and different neural structures (see below).
Since they discarded background visual information, corrective saccades were suboptimal in most cases. However, the CS1 correction in condition Target was correlated to the compensation of the perturbation by S2. Thus, when the only landmark was the target T1, CS1 was also based on the optimal estimate of the postsaccadic visual error (and not on the raw visual error).
The compensation of the intrasaccadic perturbation was larger in trials with a corrective saccade. The existence of a common error signal for the generation of CS1 and S2 now suggests that a selection bias explains this observation, as corrective saccades are performed only when the estimate of the visual error is sufficiently large (Fig. 6A).
Neural bases of the postsaccadic update process
The central idea of Kalman filtering is to compare a prediction of the sensory feedback to the actual reafference, and to correct the internal state of the system accordingly. In an oculocentric system, this would entail a modification of the representation of the next movement goal. There is now a large body of evidence for neural correlates of this process. Neurons predicting the postsaccadic visual feedback have been found in many places in the primate oculomotor control network: remapping cells exist in LIP (Duhamel et al., 1992), FEF (Umeno and Goldberg, 1997), and the superior colliculus (Walker et al., 1995). In FEF, this remapping is driven by a corollary discharge of the saccadic motor signals fed back from the superior colliculus (Sommer and Wurtz, 2002, 2006). The representation of the visual scene conveyed by populations of such neurons could be compared with the actual postsaccadic visual signals to derive the appropriate motor correction for the next saccade. Recently, Crapse and Sommer (2008) have described cells in FEF tuned to intrasaccadic shifts of the visual field. These cells would be ideally suited to compute the postsaccadic correction, as they would directly encode the visual prediction error. In accordance with this view, Murthy et al. (2007) found with a double-step task a link between FEF activity and the latency of “corrective saccades”—actually large (>10°) saccades that resemble our S2 saccades. Overall, it is likely that FEF plays a major role in the postsaccadic updating.
What drives the involuntary corrective saccades (CS1) that are executed in the middle of the sequence remains an open question. As shown here, these corrections are blind to non-target visual information. This was observed regardless of CS1 latency, ruling out that FEF simply receives or processes background later than target information. We speculate that these involuntary corrective saccades may be generated by structures lower in the control hierarchy, possibly by the superior colliculus. In any case, our results suggest that only target information is shared among the structures controlling involuntary and planned saccades.
Footnotes
This work was supported by the Agence Nationale de la Recherche Grant ANR05JCJC0132. We thank Michel Desmurget and Philippe Vindras for many stimulating discussions and their critical reading of the manuscript. We also acknowledge the constructive input from our three reviewers.
The authors declare no conflict of interest.
References
- Becker W, Fuchs AF. Further properties of the human saccadic system: eye movements and correction saccades with and without visual fixation points. Vision Res. 1969;9:1247–1258. doi: 10.1016/0042-6989(69)90112-6. [DOI] [PubMed] [Google Scholar]
- Becker W, Jürgens R. Saccadic reactions to double-step stimuli: evidence for model feedback and continuous information uptake. In: Lennerstrand G, Bach-y Rita P, editors. Basic mechanisms of ocular motility. Oxford: Pergamon; 1974. pp. 519–524. [Google Scholar]
- Becker W, Jürgens R. An analysis of the saccadic system by means of double step stimuli. Vision Res. 1979;19:967–983. doi: 10.1016/0042-6989(79)90222-0. [DOI] [PubMed] [Google Scholar]
- Bonnetblanc F, Baraduc P. Saccadic adaptation without retinal postsaccadic error. Neuroreport. 2007;18:1399–1402. doi: 10.1097/WNR.0b013e3282c48cc1. [DOI] [PubMed] [Google Scholar]
- Carpenter RH, Williams ML. Neural computation of log likelihood in control of saccadic eye movements. Nature. 1995;377:59–62. doi: 10.1038/377059a0. [DOI] [PubMed] [Google Scholar]
- Crapse TB, Sommer MA. Frontal eye field neurons report intrasaccadic translations of visual stimuli. Soc Neurosci Abstr. 2008;34:165–11. [Google Scholar]
- Duhamel JR, Colby CL, Goldberg ME. The updating of the representation of visual space in parietal cortex by intended eye movements. Science. 1992;255:90–92. doi: 10.1126/science.1553535. [DOI] [PubMed] [Google Scholar]
- Gaveau V, Martin O, Prablanc C, Pélisson D, Urquizar C, Desmurget M. On-line modification of saccadic eye movements by retinal signals. Neuroreport. 2003;14:875–878. doi: 10.1097/00001756-200305060-00020. [DOI] [PubMed] [Google Scholar]
- Goldberg ME, Bruce CJ. Primate frontal eye fields. iii. maintenance of a spatially accurate saccade signal. J Neurophysiol. 1990;64:489–508. doi: 10.1152/jn.1990.64.2.489. [DOI] [PubMed] [Google Scholar]
- Guigon E. Active control of bias for the control of posture and movement. J Neurophysiol. 2010;104:1090–1102. doi: 10.1152/jn.00162.2010. [DOI] [PubMed] [Google Scholar]
- Hanes DP, Schall JD. Neural control of voluntary movement initiation. Science. 1996;274:427–430. doi: 10.1126/science.274.5286.427. [DOI] [PubMed] [Google Scholar]
- Heiser LM, Colby CL. Spatial updating in area lip is independent of saccade direction. J Neurophysiol. 2006;95:2751–2767. doi: 10.1152/jn.00054.2005. [DOI] [PubMed] [Google Scholar]
- Helmholtz Hv. Handbuch der physiologischen Optik. Leipzig: Voss; 1867. [Google Scholar]
- Henson DB. Corrective saccades: effects of altering visual feedback. Vision Res. 1978;18:63–67. doi: 10.1016/0042-6989(78)90078-0. [DOI] [PubMed] [Google Scholar]
- Hillis JM, Ernst MO, Banks MS, Landy MS. Combining sensory information: mandatory fusion within, but not between, senses. Science. 2002;298:1627–1630. doi: 10.1126/science.1075396. [DOI] [PubMed] [Google Scholar]
- Holst E, Mittelstaedt H. Das reafferenzprinzip. Naturwissenschaften. 1950;37:464–476. [Google Scholar]
- Kalman RE, Bucy RS. New results in linear filtering and prediction theory. Trans ASME Ser D J Basic Eng. 1961;83:95–108. [Google Scholar]
- Kapoula Z, Robinson DA. Saccadic undershoot is not inevitable: saccades can be accurate. Vision Res. 1986;26:735–743. doi: 10.1016/0042-6989(86)90087-8. [DOI] [PubMed] [Google Scholar]
- Klein SA, Levi DM. Position sense of the peripheral retina. J Opt Soc Am A. 1987;4:1543–1553. doi: 10.1364/josaa.4.001543. [DOI] [PubMed] [Google Scholar]
- Kuo AD. An optimal state estimation model of sensory integration in human postural balance. J Neural Eng. 2005;2:S235–S249. doi: 10.1088/1741-2560/2/3/S07. [DOI] [PubMed] [Google Scholar]
- Low FN. Peripheral visual acuity of 55 subjects under conditions of flash presentation. Am J Physiol. 1947;151:319–324. doi: 10.1152/ajplegacy.1947.151.2.319. [DOI] [PubMed] [Google Scholar]
- Mays LE, Sparks DL. Saccades are spatially, not retinocentrically, coded. Science. 1980;208:1163–1165. doi: 10.1126/science.6769161. [DOI] [PubMed] [Google Scholar]
- Morel P, Baraduc P. Dissociating the impact of sensory and motor noise in human saccades. Proceedings of the Fifth French Conference on Computational Neuroscience; Lyon. 2010. pp. 153–158. [Google Scholar]
- Munuera J, Morel P, Duhamel JR, Deneve S. Optimal sensorimotor control in eye movement sequences. J Neurosci. 2009;29:3026–3035. doi: 10.1523/JNEUROSCI.1169-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy A, Ray S, Shorter SM, Priddy EG, Schall JD, Thompson KG. Frontal eye field contributions to rapid corrective saccades. J Neurophysiol. 2007;97:1457–1469. doi: 10.1152/jn.00433.2006. [DOI] [PubMed] [Google Scholar]
- Prablanc C, Jeannerod M. Corrective saccades: dependence on retinal reafferent signals. Vision Res. 1975;15:465–469. doi: 10.1016/0042-6989(75)90022-x. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Oculomotor control signals. In: Lennerstrand G, Bach-y Rita P, editors. Basic mechanisms of ocular motility and their clinical implications. Oxford: Pergamon; 1975. pp. 337–374. [Google Scholar]
- Saunders JA, Knill DC. Visual feedback control of hand movements. J Neurosci. 2004;24:3223–3234. doi: 10.1523/JNEUROSCI.4319-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shebilske WL. Extraretinal information in corrective saccades and inflow vs outflow theories of visual direction constancy. Vision Res. 1976;16:621–628. doi: 10.1016/0042-6989(76)90009-2. [DOI] [PubMed] [Google Scholar]
- Soetedjo R, Kojima Y, Fuchs AF. Complex spike activity in the oculomotor vermis of the cerebellum: a vectorial error signal for saccade motor learning? J Neurophysiol. 2008;100:1949–1966. doi: 10.1152/jn.90526.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH. A pathway in primate brain for internal monitoring of movements. Science. 2002;296:1480–1482. doi: 10.1126/science.1069590. [DOI] [PubMed] [Google Scholar]
- Sommer MA, Wurtz RH. Influence of the thalamus on spatial visual processing in frontal cortex. Nature. 2006;444:374–377. doi: 10.1038/nature05279. [DOI] [PubMed] [Google Scholar]
- Sperry RW. Neural basis of the spontaneous optokinetic response produced by visual inversion. J Comp Physiol Psychol. 1950;43:482–489. doi: 10.1037/h0055479. [DOI] [PubMed] [Google Scholar]
- Straube A, Fuchs AF, Usher S, Robinson FR. Characteristics of saccadic gain adaptation in rhesus macaques. J Neurophysiol. 1997;77:874–895. doi: 10.1152/jn.1997.77.2.874. [DOI] [PubMed] [Google Scholar]
- Umeno MM, Goldberg ME. Spatial processing in the monkey frontal eye field. I. predictive visual responses. J Neurophysiol. 1997;78:1373–1383. doi: 10.1152/jn.1997.78.3.1373. [DOI] [PubMed] [Google Scholar]
- van Beers RJ. The sources of variability in saccadic eye movements. J Neurosci. 2007;27:8757–8770. doi: 10.1523/JNEUROSCI.2311-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Beers RJ, Sittig AC, Gon JJ. Integration of proprioceptive and visual position-information: an experimentally supported model. J Neurophysiol. 1999;81:1355–1364. doi: 10.1152/jn.1999.81.3.1355. [DOI] [PubMed] [Google Scholar]
- Vaziri S, Diedrichsen J, Shadmehr R. Why does the brain predict sensory consequences of oculomotor commands? Optimal integration of the predicted and the actual sensory feedback. J Neurosci. 2006;26:4188–4197. doi: 10.1523/JNEUROSCI.4747-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vergilino-Perez D, Findlay JM. Foveal stimulation and saccadic latencies. Exp Brain Res. 2003;150:255–258. doi: 10.1007/s00221-003-1418-4. [DOI] [PubMed] [Google Scholar]
- Walker MF, Fitzgibbon EJ, Goldberg ME. Neurons in the monkey superior colliculus predict the visual result of impending saccadic eye movements. J Neurophysiol. 1995;73:1988–2003. doi: 10.1152/jn.1995.73.5.1988. [DOI] [PubMed] [Google Scholar]
- Wang X, Zhang M, Cohen IS, Goldberg ME. The proprioceptive representation of eye position in monkey primary somatosensory cortex. Nat Neurosci. 2007;10:640–646. doi: 10.1038/nn1878. [DOI] [PubMed] [Google Scholar]
- Wertheim T. Peripheral visual acuity. Z Psychol Physiol Sinnesorgane. 1891;7:172–187. Reprinted in: Am J Optom Physiol Opt 57:915–924 (Dunsky IL, translator). 1980. [Google Scholar]
- Westheimer G. Eye movement responses to a horizontally moving visual stimulus. AMA Arch Ophthalmol. 1954;52:932–941. doi: 10.1001/archopht.1954.00920050938013. [DOI] [PubMed] [Google Scholar]
- White JM, Sparks DL, Stanford TR. Saccades to remembered target locations: an analysis of systematic and variable errors. Vision Res. 1994;34:79–92. doi: 10.1016/0042-6989(94)90259-3. [DOI] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science. 1995;269:1880–1882. doi: 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]