Visual Feedback Processing of the Limb Involves Two Distinct Phases

Abstract

Muscle responses to mechanical disturbances exhibit two distinct phases: a response starting at ~20 ms that is fairly stereotyped, and a response starting at ~60 ms modulated by many behavioral contexts including goal-redundancy and environmental obstacles. Muscle responses to disturbances of visual feedback of the hand arise within ~90 ms. However, little is known whether these muscle responses are sensitive to behavioral contexts. We had 49 human participants (27 male) execute goal-directed reaches with visual feedback of their hand presented as a cursor. On random trials, the cursor jumped laterally to the reach direction, and thus, required a correction to attain the goal. The first experiment demonstrated that the response amplitude starting at 90 ms scaled with jump magnitude, but only for jumps <2 cm. For larger jumps, the duration of the muscle response scaled with the jump size starting after 120 ms. The second experiment demonstrated that the early response was sensitive to goal redundancy as wider targets evoked a smaller corrective response. The third experiment demonstrated that the early response did not consider the presence of obstacles, as this response routinely drove participants directly to the goal even though this path was blocked by an obstacle. Instead, the appropriate muscle response to navigate around the obstacle started after 120 ms. Our findings highlight that visual feedback of the limb involves two distinct phases: a response starting at 90 ms with limited sensitivity to jump magnitude and sensitive to goal-redundancy, and a response starting at 120 ms with increased sensitivity to jump magnitude and environmental factors.

SIGNIFICANCE STATEMENT The motor system can integrate proprioceptive feedback to guide an ongoing action in ~60 ms and is flexible to a broad range of behavioral contexts. In contrast, the present study identified that the motor response to a visual disturbance exhibits two distinct phases: an early response starting at 90 ms with limited scaling with disturbance size and sensitivity to goal-redundancy, and a slower response starting after 120 ms with increased sensitivity to disturbance size and sensitive to environmental obstacles. These data suggest visual feedback of the hand is processed through two distinct feedback processes.

Introduction

An impressive feature of our motor system is the ability to move and interact in a complex world such as the act of reaching for a cup. If our arm is unexpectedly bumped, the motor system uses visual and proprioceptive feedback to generate corrective movements to reach and even reorient the hand to grasp the cup handle. However, how we correct must consider many factors related to the cup (behavioral goal) and the presence of other objects such as a vase near the cup (environment).

Recent studies have explored how quickly participants can incorporate behavioral contexts (e.g., goal or environment) when correcting for mechanical loads (Franklin and Wolpert, 2011; Shemmell, 2015; Scott, 2016). The earliest muscle response arises 20 ms after applying an unexpected load, and is modulated by the size of the displacement (Gottlieb and Agarwal, 1980; Jaeger et al., 1982; Crevecoeur et al., 2012). However, it is inflexible to many task constraints (but see Weiler et al., 2019) and the speed of this response would indicate that it could only be generated by the spinal cord (Scott, 2016). In contrast, the long-latency response starting at ~60 ms is modulated by many contexts (Marsden et al., 1981; Shemmell et al., 2009; Scott, 2016). For example, participants correct less to a load when reaching for a wide goal than a narrow goal (Nashed et al., 2012; Lowrey et al., 2017). Muscle activity reflecting this difference begins in the long-latency epoch. Similarly, to avoid obstacles participants can increase or decrease muscle responses starting in the long-latency epoch (Nashed et al., 2012, 2014). Frontoparietal circuits are likely involved in generating the long-latency response as they respond to proprioceptive feedback in a context-dependent manner (Evarts and Tanji, 1976; Wolpaw, 1980; Chapman et al., 1984; Omrani et al., 2016).

Far less is known about how behavioral context influences processing of visual feedback of the hand, often represented by a cursor. A jump of the cursor can generate muscle responses ~90 ms after the jump (Brenner and Smeets, 2003; Saunders and Knill, 2004; Franklin and Wolpert, 2008). Kinematic responses scale with the jump size (Veyrat-Masson et al., 2010; Franklin et al., 2016), however, scaling of the muscle response amplitude has only been observed when cursor errors occur frequently and are task relevant (Franklin et al., 2014). Furthermore, few studies have examined whether this muscle response is sensitive to behavioral contexts.

Several groups assume the earliest muscle response to a cursor jump is generated by frontoparietal circuits (Knill et al., 2011; Dimitriou et al., 2013; Franklin, 2016; Scott, 2016) that are also involved in generating long-latency responses. This is supported by studies showing slowed corrective responses to a visual disturbance when parietal cortex is lesioned (Desmurget et al., 1999; Pisella et al., 2000; Reichenbach et al., 2011). Thus, the 90 ms response for cursor jumps should parallel the complexity of the 60 ms long-latency response for a mechanical load.

Alternatively, studies investigating visual jumps of the goal have suggested a two-phase corrective response, with an early response insensitive to an instruction that required a change in spatial goal (Day and Lyon, 2000). Instead, participants required ~40 ms to incorporate this instruction. This delay resembles a time penalty for changing goals when a mechanical load is applied, with muscle responses starting at 75 ms, not 60 ms (Nashed et al., 2014). Furthermore, studies suggest that visual feedback of the hand and goal are represented separately (Brenner and Smeets, 2003; Reichenbach et al., 2014; Franklin et al., 2016), limiting the inference one can make between responses for cursor and goal jumps.

We performed three experiments to explore the earliest muscle response to: the magnitude of a cursor jump, goal-redundancy, and environmental obstacles. Our data revealed two phases in the muscle response to visual feedback: one that started at 90 ms sensitive to goal redundancy but limited modulation for jump magnitude, and a response that started after 120 ms that reflects environmental obstacles and stronger modulation for jump magnitude.

Materials and Methods

Participants.

A total of 49 individuals (18–30 years old: 27 males) participated in one of three experiments. All participants were right-handed, had no neurological impairments and gave written consent according to a protocol approved by the Queen's University Research Ethics Board. One participant completed both Experiment 2 and Experiment 3B, a second participant completed Experiment 1B and Experiment 3A, and a third participant completed Experiment 1B and 3C.

Apparatus.

All experiments involved participants making goal-directed reaches while seated with their arm supported in a robotic exoskeleton (KINARM, BKIN Technologies) that maintained the arm in the horizontal plane and could apply mechanical loads to the elbow and shoulder joints (Scott, 1999; Singh and Scott, 2003). The device included a virtual reality system that presented spatial goals and visual feedback of the limb (white cursor at index finger, radius 0.5 cm) in the horizontal workspace.

Experiment 1: influence of cursor jump magnitude on muscle response.

This experiment tested whether the muscle response scales with the size of the cursor jump. At the start of the trial, participants stabilized their hand inside a start target (radius 0.8 cm). After a random hold period (1–1.5 s), a goal (radius 1 cm) would appear 15 cm directly in front of the participant (Fig. 1A). Participants had 400–800 ms to reach the goal once it appeared and the goal would change color at the end of the reach to blue or red if the participant was too slow or fast, respectively. On random trials, the cursor was jumped laterally to the reach direction after participants moved 3 cm from the start target. However, because of delays in the projection system, the cursor jump occurred ~5 cm into the reach. The exact timing of the jump was identified using the VSYNC output of the video card that allowed us to determine when the video monitor would refresh its screen. We also calculated the constant delay between when the video card sent a frame and when the display actually displayed it by mapping the latency of the display updates using photodiodes. We could predict display update within ±2 ms (95% CI). In Experiment 1A, cursor jumps were ±2, ±5, and ±8 cm. In Experiment 1B, cursor jumps were ±0.5, ±1, ±2, and ±8 cm. Ten individuals participated in Experiment 1A and a separate 10 individuals participated in Experiment 1B.

Figure 1.

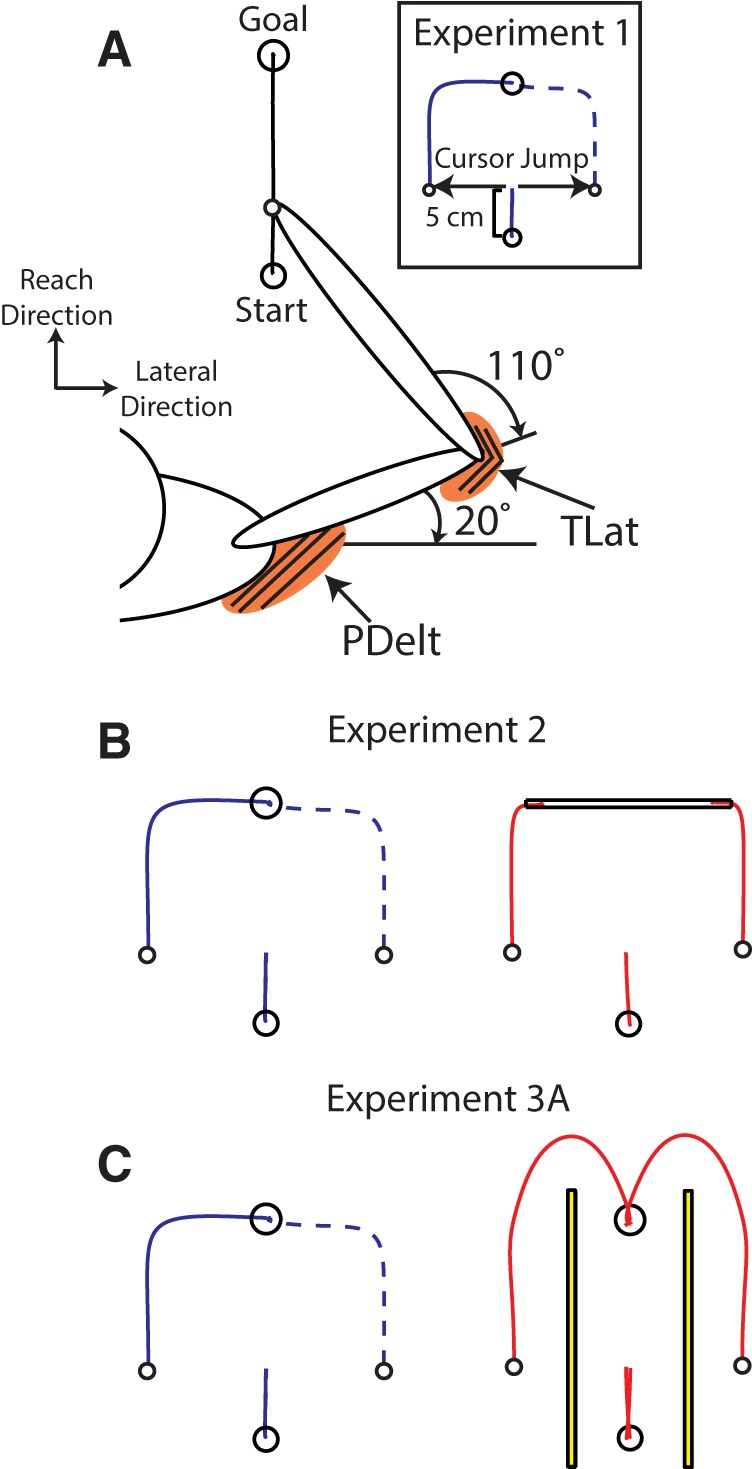
Experimental setup. A, All experiments had participants make 15 cm goal-directed reaches. Visual feedback of the hand was presented as a white cursor (radius = 0.5 cm). On 33–50% of trials, when the participant was 5 cm from the start target, the cursor would jump laterally (inset). B, Setup for Experiment 2 for reaches to the narrow (blue radius = 1 cm) and wide goal (red width = 1 cm, length = 14 cm). C, Setup for Experiment 3A for reaches without and with obstacles requiring whole-limb extension movement to avoid the obstacles. Obstacles were placed 4 cm on either side of the straight path from the start and goal.

We relaxed timing constraints for trials with cursor jumps, giving individuals an additional 300 ms to complete their reach. Cursor jumps were presented on 50% of trials and participants completed 30 successful reaches for each perturbation for a total of 360 and 480 successful trials for Experiments 1A and 1B, respectively.

A constant flexion load of 0.5 and 1.0 Nm was applied to pre-excited elbow and shoulder extensor muscles, respectively, and was present for the entire session (Fig. 2F). Participants completed 60–100 practice trials to familiarize themselves with the task, its constraints and adapt to the background loads.

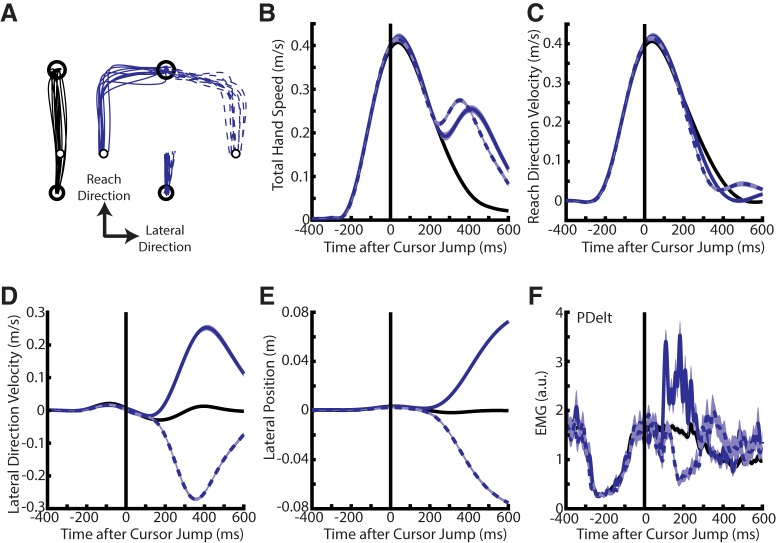
Figure 2.

Exemplary participant during Experiment 1A. A, Exemplary participant's hand paths for no cursor jump trials (black) and ±8 cm cursor jumps (blue). B, The same participant's total hand speed after aligning onto the time of the cursor jump. C–E, Same format as B except for reach velocity, lateral velocity, and lateral position, respectively. F, Activity of the PDelt for no cursor jump and cursor jump trials. Data are plotted as mean and SE.

Experiment 2: influence of goal redundancy on muscle response.

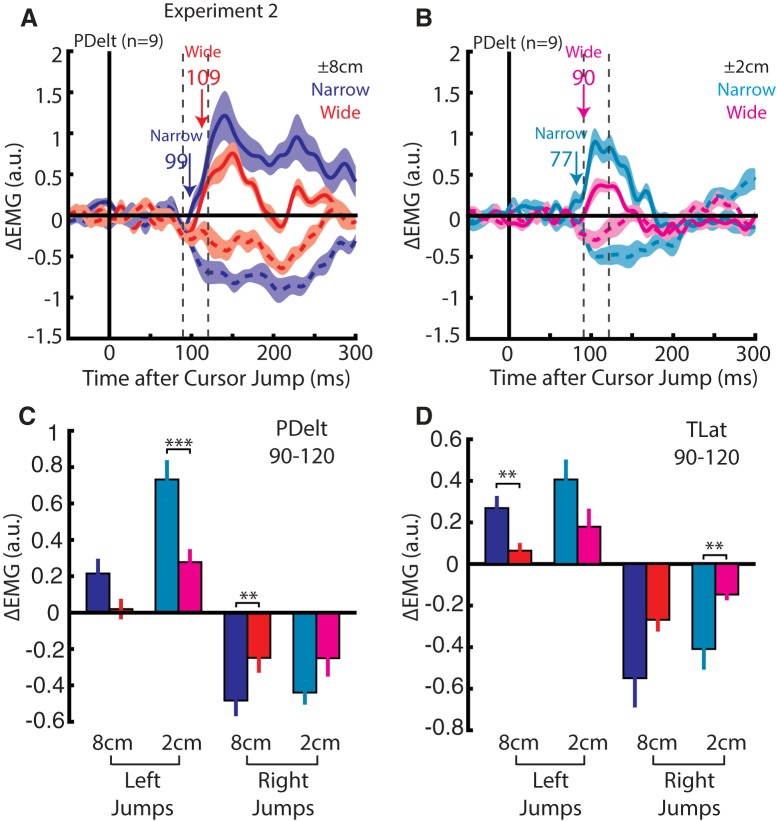
These experiments examined how goal redundancy modulates the muscle response, as in our studies with mechanical loads (Nashed et al., 2012; Lowrey et al., 2017). The experiment was identical to Experiment 1 except participants reached for either a narrow, circular dot with a radius of 1 cm or a wide, rectangular bar with a width of 14 cm and height of 1 cm (Fig. 1B). Narrow and wide goals were interleaved randomly within a block. Cursor jumps of ±2 or ±8 cm occurred on 50% of trials and randomly interleaved. Participants completed 30 successful trials for each perturbation size for a total of 480 successful trials. Nine participants participated in Experiment 2.

Experiment 3: influence of obstacles on muscle response.

These experiments examined how environmental obstacles in the workspace modulate the muscle response to cursor jumps. The experiment was identical to Experiment 1 except rectangular obstacles were positioned ±4 cm (except in Experiment 3C) lateral to a straight line between the start and goal (Fig. 1C). On random trials, the cursor was jumped (±8 cm), and thus, the obstacle now blocked a direct path to the goal. In Experiment 3A, the position of the obstacle required the participant to reach past the goal to avoid hitting the obstacle (whole-limb extension; Fig. 1C), whereas in Experiment 3B and C the position of the obstacle required the participant to return the hand back toward the start target to avoid the obstacle and reach the goal (whole-limb flexion). In Experiment 3C the obstacles were arranged in a narrow and wide configuration where the right obstacle was placed 2 and 5 cm away from a direct line between the start and goal locations. Trials were immediately stopped if the cursor collided with the obstacles and required participants to repeat the trial at the end of the block. No-obstacle and obstacle trials were interleaved randomly within a block. Cursor jumps were presented on 30% of trials and participants completed 360 successful reaches for Experiments 3A and 3B. To reduce fatigue, participants only completed 25 blocks for Experiment 3C resulting in 450 successful reaches. Experiment 3A and 3B had eight participants each and Experiment 3C had seven.

Muscle recordings.

Electromyography (EMG) from the posterior deltoid (PDelt), and the lateral head of the triceps (TLat) were recorded using bipolar surface electrodes (Nashed et al., 2012; Cluff and Scott, 2013; Delsys). Alcohol swabs were used to lightly abrade the skin over the muscle belly before electrode placement and a ground electrode was placed on the elbow. EMG signals were amplified (gain 10⁴; Delsys, Bagnoli 8 Channel System) and digitized at 1 kHz.

Data analysis

Kinematic analysis.

Angular position and velocity were digitized at 1 KHz and low-pass filtered with a third order, zero-phase lag, 20 Hz Butterworth filter. Differences of each participant's mean lateral velocity for left and right cursor jumps of the same magnitude (i.e., +8 and −8 cm) was averaged in two epochs: 180–230 and 230–280 ms, which coincide with earlier studies (Franklin and Wolpert, 2008; Dimitriou et al., 2013; Franklin et al., 2017; de Brouwer et al., 2017). Reach endpoints were determined on a trial-by-trial basis by finding the first time point the hand speed fell <5% of its maximum.

Muscle analysis.

On cursor-jump trials, we aligned the trials to when the jump occurred and filtered with a third order, zero-phase lag, Butterworth filter with a pass band of 20–450 Hz, and then full-wave rectified. We further low-pass filtered muscle signals with a sixth order, zero-phase lag, 50 Hz Butterworth filter to reduce variance (Corneil et al., 2004; Saijo et al., 2005; Lowrey et al., 2017). For no-jump trials, we aligned the trials to the time when a jump would have occurred and followed an identical filtering procedure. The no-jump and cursor-jump trials were trial averaged separately. Then, the no-jump time-series was subtracted from the cursor-jump time-series yielding the change in EMG for each participant (ΔEMG). We then normalized each participant's muscle activity by the mean activity in an initial set of trials where the participant maintained their hand inside a target while resisting a ±1 Nm elbow or shoulder mechanical load and then averaged across trials. For each participant we then binned the ΔEMG into an early epoch 90–120 ms and a late epoch 120–180 ms coinciding with previous reports (Dimitriou et al., 2013; Franklin et al., 2014; Gu et al., 2016).

Statistical analysis

ROC analysis.

We used receiver-operator characteristic (ROC) analysis (Corneil et al., 2004; Pruszynski et al., 2008) to identify when kinematic and muscle responses to the cursor jump started to diverge across conditions (e.g., narrow vs wide goal) for each participant. At each time point, a ROC curve was generated from the two signals-of-interest and we calculated the area under the ROC curve. The area under the ROC curve represents how discriminable the two signals are with 0 and 1 representing perfect discrimination and 0.5 representing chance discrimination. For our kinematic analysis, we used a procedure identical to Pruszynski et al. (2008), where a significant separation between signals occurred if the area under the ROC curve exceeded a threshold of >0.75 or <0.25 and was maintained for five consecutive time points. A linear regression was then used based on 15 time points centered around the threshold crossing that was regressed back to find the ROC knee at 0.5.

As muscle responses tended to be noisier than kinematic signals, we lowered the significance threshold to >0.7 or <0.3 which had to be maintained for at least 8 of the next 10 time points (1 ms each; Corneil et al., 2004; Gu et al., 2016; Pruszynski et al., 2016). The ROC knee was defined by looking backward in time starting from the threshold to the first point <0.55 or >0.45 (Pruszynski et al., 2016). To ensure that reducing the threshold for muscle activity did not significantly impact our results, we estimated a chance level for a false-positive rate with a bootstrap procedure. First, we randomly sampled with replacement from the no-jump trials of the PDelt for eight participants (Experiment 3A) to generate two shuffled samples. The trials were aligned on when a jump would have occurred. We then calculated the area under the curve at each time point for these two shuffled samples and tested whether the ROC curve exceeds the thresholds of <0.55 or >0.45. We repeated this procedure 10,000 times to estimate the chance level for a false-positive. As time increases, the chance of a false-positive also increases, thus we focused on the first 200 ms after a jump would have occurred. We found that the false-positive rate within this time frame was <7%. By comparison, we repeated this analysis using a significance threshold of >0.75 or <0.25 that was maintained for 8 of 10 consecutive time points and found the false-positive rate was ~0.5%.

For kinematic and muscle responses, the earliest response was detected by estimating the time when there was a difference between jump sizes of equal magnitude and opposite direction (e.g., +8 cm with −8 cm). In Experiment 1, size-dependent timing was detected by estimating for each direction when each cursor jump size differentiated from the 8 cm cursor jump. In Experiment 2, goal-dependent timing was detected by estimating for each direction when narrow and wide goal responses differentiated. As in Experiment 3, obstacle-dependent timing was detected by estimating when no-obstacle and obstacle responses differentiated for each direction.

Difference Functions.

Some timing onsets for kinematic and muscle activity could not be detected at the individual level (e.g., Experiment 1A when 5 cm jumps differentiated from 8 cm jumps) requiring a group level analysis. However, we found that ROC analysis on group level data tended to estimate onsets that were unphysiological (<60 ms for the earliest muscle response to a cursor jump), likely reflecting the small group sample (e.g., n = 7 for Experiment 2) used to construct the ROC curve. Instead, we opted to estimate onsets at the group-level using Difference Functions, which we found were consistent with onsets estimated using ROC analysis at the individual level when it was available. For each participant, we calculated the difference in mean muscle activity between different conditions and group averaged the resulting time series (Omrani et al., 2016). We defined a threshold of ±3 SD from mean baseline activity (100 ms before perturbation) and found the first time point to exceed this threshold for 20 consecutive milliseconds following the disturbance. We estimated the variability in this metric using a bootstrap procedure, in which we generated a new group-level Difference Function from randomly sampling participants with replacement. The new onset was calculated from the Difference Function and this procedure was repeated 1000 times. We only included samples that had an onset between 50 and 300 ms and times are only reported in Table 1 if >50% of bootstrapped onsets were between this time interval.

Table 1.

Onset timing across experiments

Experiment	Onset type	Kinematics	Posterior deltoid		Triceps lateral head
		ROC, mean ± SE	ROC, mean ± SE	Diff Function, median (25th, 75th)	ROC, mean ± SE	Diff Function, median (25th, 75th)
1A	Earl onset	134 ± 4 (8 cm)	84 ± 5	88 (87,89)	90 ± 6	90 (88,92)
		142 ± 6 (5 cm)	88 ± 3	88 (86,90)	88 ± 4	90 (88,91)
		124 ± 5 (2 cm)	77 ± 5	78 (76,81)	85 ± 5	84 (81,86)
	2 cm from 8 cm (L/R)	216 ± 25/202 ± 7	168 ± 10/164 ± 15	149 (135,153)/132(128,191)	218 ± 34/173 ± 16	151 (148,153)/152 (142,191)
	5 cm from 8 cm (L/R)	279 ± 8/238 ± 15	NF	175 (173,180)/225 (221,234)	NF	NF
1B	Earl onset	145 ± 4 (8 cm)	93 ± 4	94 (89,99)	93 ± 4	90 (87,96)
		126 ± 7 (2 cm)	85 ± 4	87 (85,90)	NF	89 (85,92)
		130 ± 8 (1 cm)	88 ± 8	89 (87,91)	NF	90 (89,93)
		125 ± 4 (0.5 cm)	116 ± 24	81 (79,83)	NF	NF
	0.5 cm from 8 cm	191 ± 8/169 ± 4	130 ± 7/	112 (108,140)/122(115,127)	NF	129 (118,141)/128 (124,190)
	(L/R)		131 ± 9
	1 cm from 8 cm (L/R)	204 ± 7/178 ± 8	147 ± 11/141 ± 9	147 (145,149)/125(118,131)	NF	128 (125,135)/184 (145,193)
	2 cm from 8 cm (L/R)	234 ± 8/213 ± 7	145 ± 10/159 ± 9	148 (145,150)/191(164,204)	NF	149 (143,161)/192 (189,196)
2	Earl onset narrow 8 cm	145 ± 6	98 ± 6	99 (98,101)	94 ± 2	95 (93,96)
	Earl onset wide 8 cm	157 ± 6	115 ± 7	109 (105,112)	102 ± 3	101 (97,108)
	Earl onset narrow 2 cm	124 ± 7	NF	77 (75,87)	NF	86 (82,92)
	Earl onset wide 2 cm	126 ± 16	NF	90 (85,94)	NF	99 (96,102)
	Narrow from wide 8 cm (L/R)	165 ± 11/161 ± 9	181 ± 16/125 ± 13	122 (117,180)/108 (105,146)	NF	138 (132,224)/NF
	Narrow from wide 2 cm (L/R)	NF	NF	88 (78,94)/111(102,121)	NF	109 (106,111)/125 (94,132)
3A	Earl onset no Obs	150 ± 5	96 ± 7	92 (88,103)	96 ± 3	91 (89,95)
	Earl onset Obs	140 ± 4	NF	92 (90,95)	NF	91 (88,96)
	No Obs from Obs (L/R)	298 ± 70/194 ± 7	163 ± 10/179 ± 15	150 (149,153)/NF	240 ± 27/154 ± 9	NF/160 (156,169)
3B	Earl onset no Obs	140 ± 4 ms;	92 ± 4	92 (90,94)	88 ± 3	89 (87,92)
	Earl onset Obs	121 ± 6 ms	NF	92 (90,95)	NF	91 (90,108)
	No Obs from Obs (L/R)	203 ± 11/174 ± 14	NF/126 ± 8	NF/135 (132,137)	173 ± 25/165 ± 26	151 (150,155)/NF
3C	Earl onset no Obs	140 ± 4	86 ± 4	88 (82,93)	NF	NF
	Earl onset	124 ± 4	NF	97 (96,100)	NF	NF
	Obs wide config
	(L/R)
	Earl onset	114 ± 9	NF	94 (92,97)	NF	NF
	Obs narrow config
	No Obs from Obs wide config	NF/186 ± 9	NF/136 ± 8	NF/119 (117,135)	NF	NF
	(L/R)
	No Obs from Obs narrow config (L/R)	NF/190 ± 9	NF/121 ± 10	NF/122 (120,124)	NF	NF

For each experiment, the table shows the kinematic onsets as calculated from ROC and the EMG onsets as calculated from ROC analyses and Difference Functions. ROC analysis was calculated for each individual. The interquartile range reported for the Difference Functions was calculated from a bootstrap procedure. Earl, Earliest; Obs, Obstacle; L/R, left cursor jumps /right cursor jumps; NF, not found.

Onset analysis.

All ANOVAs and t tests were calculated using SPSS v24 (IBM). All size-dependent and context-dependent onset times were averaged across the left and right direction to limit bias related to the load (see Results). In Experiment 1, a two-way repeated-measures (RM) ANOVA was applied with jump size and onset type (earliest and size-dependent as levels) as factors. Interaction effects were decomposed using separate one-way RM ANOVAs on each onset type with jump size as a factor. If a main effect was significant, paired t tests were used to compare between shift sizes. For Experiments 2 and 3, we used a one-way RM ANOVA with three levels [i.e., earliest muscle response for 2 different conditions (narrow and wide or obstacle and no obstacle) and goal-dependent onset]. If a significant main effect was found, we applied paired t tests with Bonferroni Corrections.

Epoch analysis on kinematics.

For Experiment 1, we applied a one-way RM ANOVA on the binned lateral velocity for each time epoch with jump size as a factor. If a significant main effect was found, we applied paired t tests with Bonferroni Corrections. In Experiments 2 and 3, we applied paired t tests to the binned lateral velocity in each time epoch between conditions.

Epoch analysis on muscle activity.

In Experiment 1, we applied a two-way RM ANOVA that included jump size and direction as factors for each time epoch. If a significant interaction effect was found, we then applied a one-way RM ANOVA for each direction with jump size as a factor with a Bonferroni correction factor. In Experiment 2, we applied a three-way RM ANOVA with jump size, direction, and goal shape as factors. If a significant interaction effect was found between goal shape and direction, we then applied a two-way RM ANOVA for each direction with jump size and goal shape as factors. If a significant main effect was found for goal shape, we applied paired t tests comparing narrow versus wide goal responses with a Bonferroni correction. In Experiment 3, we applied a two-way RM ANOVA with jump direction and obstacles (present or absent) as factors. If a significant interaction effect was found, we then applied paired t tests comparing no obstacle and obstacle responses with a Bonferroni Correction.

Results

Experiment 1: A jump sizes ±2, ±5, or ±8 cm; B ±0.5, ±1, ±2 or ±8 cm

Figure 2A (black lines) highlights a typical participant's 15 cm reach to a spatial goal (radius 1 cm) against a static mechanical load that pre-excited shoulder and elbow extensors. On random trials, the cursor (white dot radius 0.5 cm) would jump in the direction that was lateral to the direct path from the start to the end goal (Fig. 2A, blue lines). Figure 2B shows the participant's total hand speed and illustrates the rapid corrective movement following the cursor jump. Note the apparent delay between correcting for right (dashed) and left (solid) cursor jumps that is likely related to the static load that resists corrections for left jumps and assists corrections for right jumps. Although small changes in the reach direction velocity could be detected following the cursor jump (Fig. 2C), the corrective movement was mainly in the lateral direction (Fig. 2D,E). Figure 2F shows the participant's PDelt activity for no-jump and cursor-jump trials. Note, the small drop in activity <100 ms after the cursor jumped, although this drop was not consistently observed across participants.

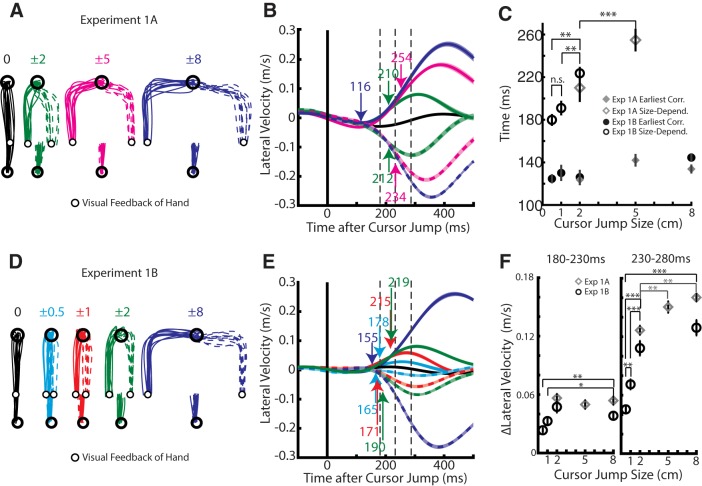
Figure 3A highlights the same participant's hand trajectories in Experiment 1A for all three different-sized cursor jumps with Figure 3B displaying the corresponding lateral hand velocities. The onset for the 8 cm kinematic correction was detected at 116 ms (blue arrow) with similar onsets for the 2 and 5 cm jumps. However, estimates of when the 2 cm jump differentiated from the 8 cm jump (size-dependent onset) occurred later than the earliest-corrective onset at 212 and 210 ms for jumps to the right and left, respectively. Correspondingly, differentiation between the 5 and 8 cm jumps was detected at 234 and 254 ms for jumps to the right and left, respectively. Similar results were observed across the population (Fig. 3C, diamonds). A two-way RM ANOVA, with onset type (“earliest” and “size-dependent” as levels) and jump size (levels: 2 and 5 cm) as factors, revealed a significant main effect for onset type (F_(1,9) = 76, p < 0.001) and an interaction effect (F_(1,9) = 20, p = 0.002). Note, the 8 cm cursor jump was omitted from the ANOVA as size-dependent onsets were defined relative to the 8 cm jump. A separate one-way RM ANOVA, with jump size (levels: 2, 5, and 8 cm) as a factor was applied to the earliest onsets and revealed a main effect (F_(2,9) = 4.4, p = 0.049), but no post hoc test yielded significance. However, a paired t test confirmed the size-dependent onset of the 2 cm cursor jump was significantly earlier than the size-dependent onset for the 5 cm cursor jump (t₍₉₎ = 3.9, p = 0.004).

Figure 3.

Kinematics from Experiments 1A and 1B. A, Hand paths from an exemplary participant in Experiment 1A during no cursor jump (black) and cursor jump reaches. Numbers overhead indicate the size of the cursor jump. B, Lateral hand velocity from the same exemplary participant. Blue arrow indicates the earliest-corrective (corr) movement to a cursor jump (8 cm left vs right jump ROC analysis). Green and magenta arrows indicate when 2 and 5 cm cursor jumps differentiated from the 8 cm cursor jump, respectively (ROC analysis). Dashed lines mark the 180–230 and 230–280 ms epochs. C, Group average onset times for each jump size differentiating from the 8 cm jump (size-dependent; open) as well as the earliest-corrective onset (earliest; filled) in both Experiments 1A (diamond) and 1B (circle). Note error bars on the earliest-corrective onset are shaded gray for clarity. D, E, Same format as A and B except for Experiment 1B. F, The group average difference between the lateral hand velocity for the same magnitude cursor jump but opposite directions (i.e., 2 cm minus −2 cm) within the 180–230 ms epoch. Data are plotted as mean and SE. *p < 0.05, **p < 0.01, ***p < 0.001.

Detecting timing onsets can be biased based on the magnitude and variability of the response (Oostwoud Wijdenes et al., 2014). As a result, we binned the average difference between the lateral velocities for left and right cursor jumps of the same magnitude (i.e., +8 vs −8 cm) into the 180–230 and 230–280 ms epochs (Fig. 3F, left and right, respectively). For the 180–230 ms epoch, we found that the lateral hand velocity showed no significant scaling with jump size as determined by a one-way RM ANOVA with jump size as a factor (F_(2,18) = 1.2, p = 0.3). In contrast, the lateral velocity within the 230–280 ms epoch had a significant main effect (F_(2,18) = 15.1, p < 0.001). Post hoc analysis (Fig. 3F, right) indicated an increase in lateral velocity with shift size in the 230–280 ms epoch. These results are consistent with our onset analysis and suggest that the lateral velocity differentiates >200 ms after the cursor jump for this range of jump sizes.

Motivated by the fact that cursor jumps generated similar-sized corrective movements in the 180–230 ms epoch over the range of tested jump sizes, we conducted a second experiment using jumps sizes of ±0.5, ±1, ±2, and ±8 cm. Figure 3, D and E, shows the hand paths and lateral hand velocity of a representative participant for each cursor jump size. For this participant, the earliest corrective onset was detected at 155 ms (blue arrow), while size-dependent timing began over a range from 170 to 240 ms. Across the population, we found that the earliest corrective onsets were detected on average in <150 ms for all jump sizes, whereas the average size-dependent timing ranged from 180 to 230 ms (Fig. 3C, circles; Table 1). A two-way RM ANOVA, with onset type and jump size (levels: 0.5, 1, and 2 cm) as factors, revealed a significant main effect for onset type (F_(1,8) = 105, p < 0.001) and an interaction effect (F_(2,16) = 10, p = 0.002). A separate one-way RM ANOVA, with jump size (levels: 0.5, 1, 2, and 8 cm) as a factor, was applied to the earliest onset and did not reveal a significant main effect (F_(3,24) = 1.9, p = 0.16). A one-way RM ANOVA, with jump size (levels 0.5, 1, and 2 cm) as a factor was applied to the size-dependent onset timing and revealed a significant main effect for jump size (F_(2,18) = 26.2, p < 0.001). Post hoc analysis (Fig. 3C) indicated that larger jumps resulted in later size-dependent onsets.

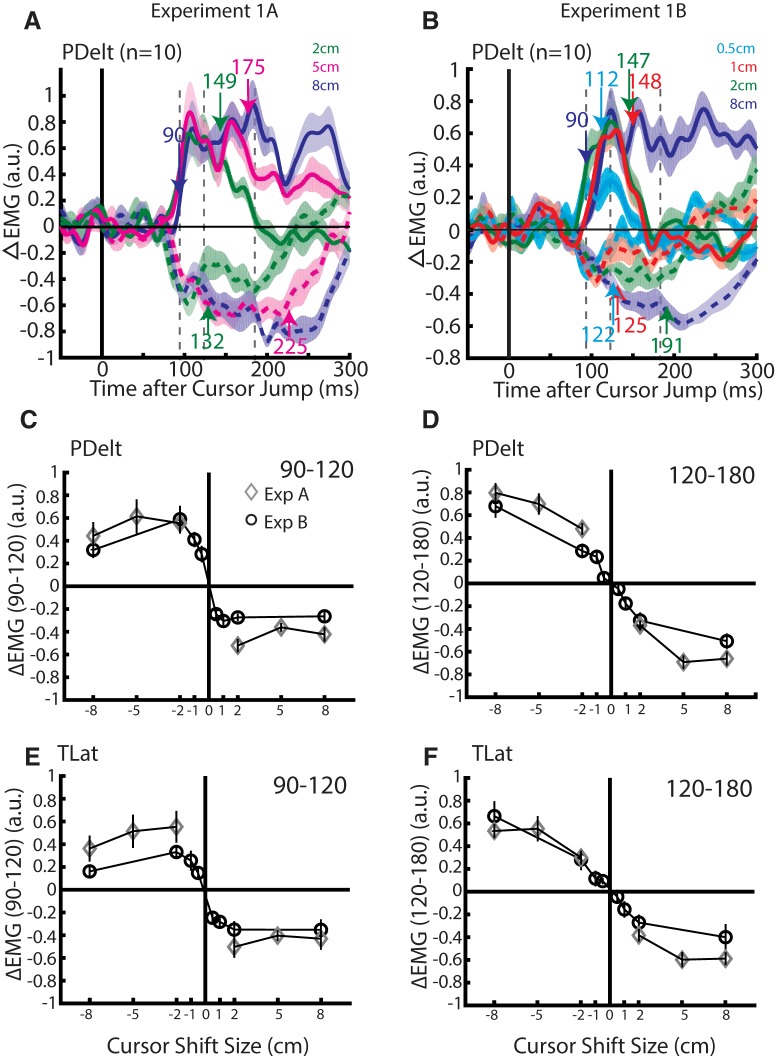
Figure 4A shows the group average change in PDelt activity in Experiment 1A. Changes in PDelt activity to the cursor jumps were calculated by subtracting each participant's PDelt activity on no-jump trials. For the 8 cm cursor jump, changes in PDelt activity were detected at 90 ms (blue arrow). Similar results were found for the other jump sizes as well as for TLat and for Experiment 1B (Table 1).

Figure 4.

Muscle activity from Experiments 1A and 1B. A, Group average change in muscle response (ΔEMG) of the PDelt in Experiment 1A to each condition. Blue arrow indicates time onset of the earliest muscle response (+8 cm minus −8 cm response Difference Functions). Green and magenta arrows indicate when 2 and 5 cm jumps differentiated from the 8 cm jump, respectively (Difference Functions). Dashed vertical lines mark the 90–120 and 120–180 ms epochs. B, Same format as A except for Experiment 1B. Cyan, red, and green arrows indicate when the 0.5, 1, and 2 cm jumps differentiated from the 8 cm jump, respectively. C, The group average muscle response in the PDelt inside the 90–120 ms epoch for each jump size in Experiments 1A (diamond) and 1B (circle). D, Same format as C for TLat. E, Same format as C for 120–180 ms epoch. F, Same format as E for TLat.

For Experiment 1A the initial muscle responses did not change with the magnitude of the cursor jump. The muscle response for the left (right) 8 cm cursor jumps displayed a rapid rise (fall) in activity within the first 20 ms to a fairly constant plateau. The 2 and 5 cm jumps followed a similar abrupt onset and plateau. The change in muscle activity for 2 cm cursor jumps decreased in absolute magnitude as compared with the 8 cm cursor jump at 149 ms for left jumps (excitation) and 132 ms for right jumps (inhibition). Correspondingly, the muscle response for the 5 cm cursor jump decreased in absolute magnitude at 175 ms for left jumps and 225 ms for right jumps. Similar patterns were observed in TLat (Table 1).

For Experiment 1B we found that all jump sizes, except for the 0.5 cm jump, evoked a similar rise or decay in PDelt activity that quickly plateaued (Fig. 4B). PDelt activity reduced in absolute magnitude from the 8 cm jump for the 1 and 2 cm jump at 148 and 147 ms for left jumps (excitation) and 125 and 191 ms for right jumps (inhibition). For the 0.5 cm cursor jumps, we found that muscle activity increased/decreased at the same rate as the other cursor jumps; however, it peaked at a smaller plateau. This resulted in the earliest size-dependent onset we observed at 112 ms for left jumps (excitation) and 122 ms for right jumps (inhibition). Similar trends were observed in TLat (Table 1).

We binned EMG responses into an epoch from 120 to 180 ms identical to previous work studying visual feedback of the limb (Franklin and Wolpert, 2008; Dimitriou et al., 2013; Franklin et al., 2014). We also binned activity in the 90–120 ms epoch to capture the earliest muscle response to a cursor jump which has previously been estimated to start at 90 ms (Franklin and Wolpert, 2008; Dimitriou et al., 2013; Scott, 2016).

Figure 4, C and E, shows the PDelt and TLat responses in Experiment 1A (diamond) for the 90–120 ms epoch plotted against jump size. Muscle responses for each jump direction showed little modulation for jump size. A two-way RM ANOVA, with jump size and jump direction as factors, found no significant main effect for jump size for either muscle and an interaction effect only for the TLat muscle (PDelt: F_(2,18) = 1.2, p = 0.3; TLat: F_(2,18) = 4.7, p = 0.02). For TLat, separate one-way RM ANOVAs were applied for each jump direction and revealed only a significant main effect for left cursor jumps (left: F_(2,18) = 4.7, p = 0.04; right: F_(2,18) = 0.7, p = 1). However, the trend for TLat muscle responses for leftward cursor jumps was a decrease with jump size, inconsistent with the hypothesis of scaling muscle responses with jump size.

For Experiment 1B, in the 90–120 ms epoch we now observed a sharp, sigmoid-like trend and modulation for jump sizes <2 cm for both muscle groups (Fig. 4C,E, circles). A two-way RM ANOVA revealed a significant interaction for direction and cursor jump size for both muscles (PDelt: F_(3,27) = 3.9, p = 0.02 TLat: F_(3,27) = 3.3, p = 0.04). Separate one-way RM ANOVAs were applied for each jump direction and revealed a significant main effect for jump size for left cursor jumps in both muscles (PDelt: F_(3,27) = 4.7, p = 0.02; TLat: F_(3,27) = 3.9, p = 0.04). For right cursor jumps we did not observe a significant main effect for jump size (PDelt: F_(3,27) = 0.6, p = 1 TLat: F_(3,27) = 1.5, p = 0.4) that may reflect the limited range a muscle can inhibit even when loaded.

Figure 4, D and F, highlights the muscle responses for the 120–180 ms epoch, which shows a more linear trend with jump size than the 90–120 ms epoch for both experiments. A two-way RM ANOVA revealed a significant interaction effect between jump size and direction for Experiment 1A (PDelt: F_(2,18) = 18.8, p < 0.001; TLat: F_(2,18) = 16.0, p < 0.001) and Experiment 1B (PDelt: F_(3,27) = 43.2, p < 0.001; TLat: F_(3,27) = 30.9, p < 0.001). Separate one-way RM ANOVAs were applied for each jump direction and revealed a significant main effect for left (Experiment 1A, PDelt: F_(2,18) = 10.2, p = 0.002; TLat: F_(2,18) = 11.2, p = 0.002; Experiment 1B, PDelt: F_(3,27) = 20.3, p < 0.001; TLat: F_(3,27) = 17.8, p < 0.001) and right (Experiment 1A PDelt: F_(2,18) = 17.8, p < 0.001; TLat: F_(2,18) = 15.5, p < 0.001; Experiment 1B, PDelt: F_(3,27) = 33.2, p < 0.001; TLat: F_(3,27) = 10.5, p < 0.001) cursor jumps in both experiments. These results indicate the 120–180 ms epoch exhibited stronger modulation for cursor jump size than the 90–120 ms epoch.

A possibility for the response to the 0.5 cm jump in the 90–120 ms epoch is that it reflects an average of trials when a muscle response was triggered by the jump and trials when it was absent. If this were the case, the variance of our actual 0.5 cm response would equal a random sampling of no-jump and jump trials. For each participant, we combined 12 (40%) random trials from no-jump trials with 18 (60%) trials from 1 cm cursor-jump trials. Percentages from each trial were selected to match the approximate size of the 0.5 cm response in the EMG relative to the 1 cm response size (~60%). We calculated the SD of the random sample (SD_random) and repeated this procedure 10,000 times for each participant, muscle and direction. We then averaged over all repeats yielding 20 values for SD_random (10 participants × 2 directions) for each muscle. For TLat we found that the SD_random was larger than the SD of the actual 0.5 cm jump (SD_actual) for all but one of the 20 values. A two-way RM ANOVA, with jump direction and SD type (levels: SD_actual and SD_random) as factors, yielded a main effect for SD type (F_(1,9) = 19.4, p = 0.002). For PDelt we found that the SD_random was larger than SD_actual for all but six values. However, a two-way RM ANOVA did not find a significant main effect for SD type (F_(1,9) = 1.3, p = 0.28). These data suggest the modulation of the 0.5 cm response was not the result of combining trials where a muscle response was either triggered or absent.

Experiment 2: goal redundancy

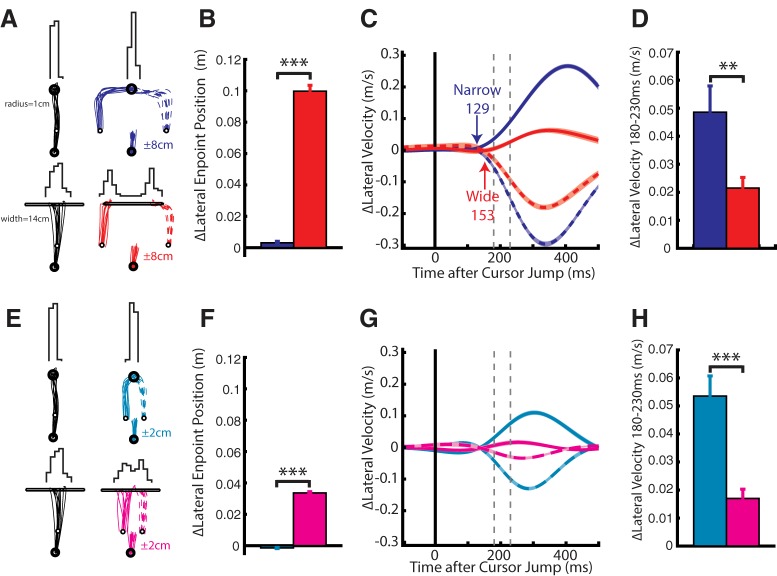
In our second experiment, we examined whether the early muscle response exhibits modulation by properties of the behavioral goal. Figure 5A shows an exemplary participant's hand trajectories to a narrow (top; radius = 1 cm) and wide goal (bottom; width = 14 cm) as well as their endpoint distributions (histograms) for 8 cm cursor jumps. For the narrow goal, the participant made reaches to the center of the goal on no-jump (black) and jump trials (blue) as observed by the tight endpoint distribution. Correspondingly, for the wide goal, an increase in endpoint dispersion can be observed for no-jump trials, and on jump trials the participant only corrected enough to reach either edge of the goal illustrated by the bimodal endpoint distribution (Fig. 5A). Across the population, we found that the lateral endpoint dispersion was significantly larger for the wide goal on jump trials (Fig. 5B; paired t test, t₍₈₎ = 27, p < 0.001). Figure 5E shows the exemplary participant's hand trajectories and endpoints for 2 cm cursor jumps. Again, we observed significantly larger endpoint dispersion for the wide goal across the population (Fig. 5F; t₍₈₎ = 37, p < 0.001).

Figure 5.

Kinematics from Experiment 2. A, Hand paths of an exemplary participant for reaches to the narrow (top radius = 1 cm) and wide (bottom width = 14 cm) goal for unperturbed and ±8 cm perturbations. Top, Histogram showing the participant's endpoint dispersion for each goal. B, Group difference of the endpoint positions (n = 9) between +8 and −8 cm cursor jumps for both goal shapes. C, Change in lateral hand velocity from the same exemplary participant by subtracting the no cursor jump hand velocity for narrow and wide reaches (Δlateral velocity). Blue and red arrows indicate the earliest corrective movement to a cursor jump for narrow and wide goal, respectively (ROC analysis). D, The group average difference between the lateral hand velocity for the +8 and −8 cm cursor jump inside the 180–230 ms epoch. E–H, Same format as A–D for 2 cm cursor jump. Data are plotted as mean and SE. **p < 0.01, ***p < 0.001.

As similarly reported (Keyser et al., 2017; Lowrey et al., 2017), several participants would reach with a small systematic bias toward one of the corners of the wide goal. As a result, comparisons of their lateral hand velocity between narrow and wide goals also showed this systematic bias. We mitigated this bias by subtracting the lateral velocity of the no-jump trials from each jump trial (Δlateral velocity). An exemplary participant's Δlateral velocity is shown in Figure 5C for 8 cm cursor jumps. Kinematic corrections to a cursor jump for the narrow goal was detected at 129 ms (blue arrow) and for the wide goals at 153 ms (red arrow). Across the population, the earliest corrective onset for the narrow and wide goal was detected at 145 ± 6 and 157 ± 6 ms, respectively, whereas the separation between narrow and wide goals (goal-dependent onset) was detected at 163 ± 9 ms (Table 1). A one-way RM ANOVA, with the earliest corrective onsets for the narrow and wide goal and goal-dependent onset timing as levels, did not find a significant main effect (F_(2,16) = 3.4, p = 0.06).

Figure 5G shows the participant's lateral velocity for the 2 cm cursor jumps for both goal shapes (Table 1). Across the population, participants reduced their lateral velocity in the 180–230 ms epoch by >50% for both jump sizes when reaching for the wide goal (Fig. 5D,H). A two-way RM ANOVA, with jump size and goal shape as factors, revealed a significant main effect for goal shape (F_(1,8) = 37.3, p < 0.001) with post hoc analysis plotted in Figure 5, D and H. Similar results were found in the 230–280 ms epoch (data not shown).

Figure 6A shows the group average change in PDelt activity for 8 cm cursor jumps. Changes in activity could be detected for the narrow goal at 99 ms (blue arrow) and at 109 ms for the wide goal. Figure 6B shows the group average change in PDelt for 2 cm cursor jumps with onsets starting at 77 and 90 ms for the narrow and wide goal, respectively. Participants reduced their PDelt and TLat activity in the 90–120 ms epoch by >50% when reaching for the wide goal (Fig. 6C,D). A three-way RM ANOVA, with cursor jump size, direction and goal shape as factors, revealed a significant interaction of the goal shape and direction for both muscles (PDelt: F_(1,8) = 14.7, p = 0.005; TLat: F_(1,8) = 16.4, p = 0.004). Separate two-way RM ANOVAs were applied for each direction and yielded a significant main effect of the goal shape for left (PDelt: F_(1,8) = 17, p = 0.006; TLat: F_(1,8) = 15.5, p = 0.008) and right (PDelt: F_(1,8) = 8.6, p = 0.04; TLat: F_(1,8) = 7.9, p = 0.04) cursor jumps. Post hoc analysis (Fig. 6C,D) confirmed a reduction in muscle responses for the wide goal. Similar results were observed for the 120–180 ms epoch (data not shown). These results highlight that the 90–120 ms response is sensitive to goal-redundancy.

Figure 6.

Muscle activity from Experiment 2. A, Group average change in PDelt activity for 8 cm cursor jumps for narrow (red) and wide (blue) goals. Blue and red arrows indicate the onset timing of the earliest muscle response for a cursor jump for narrow and wide goal reaches, respectively (Difference Functions). Dashed vertical lines mark the 90–120 ms epoch. B, Same format as A for the 2 cm jump. C, The group average PDelt activity inside the 90–120 ms epoch for each jump size and goal shape. D, Same format as C for TLat. Data are plotted as mean and SE. **p < 0.01, ***p < 0.001.

Experiment 3A: obstacle avoidance requiring whole-limb extension

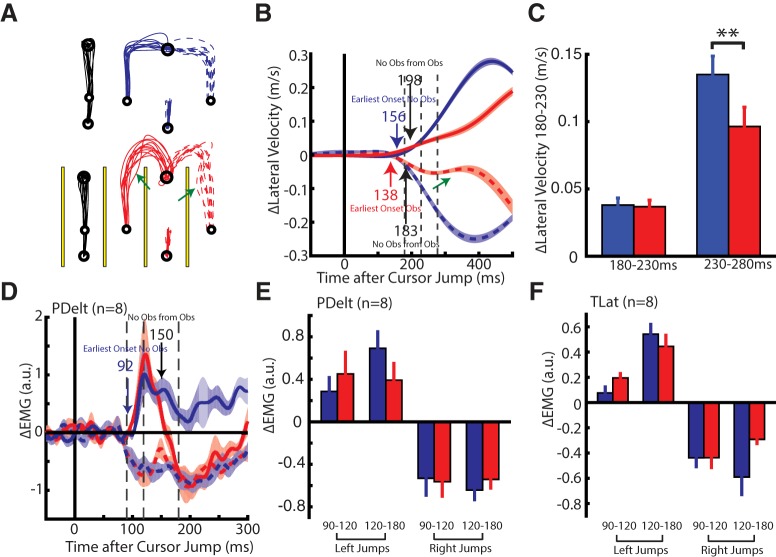
In our third experiment, we examined whether the early muscle response is modulated by environmental obstacles. Figure 7A shows the hand trajectories of an exemplary participant for no-obstacle (top) and obstacle reaches (bottom). The obstacles were designed to block participants correcting directly to the goal, as they would do when the obstacles were absent. Instead, participants needed to make whole-arm extension movements to navigate around the obstacles (red hand paths). Occasionally, when the cursor jumped the participant would initiate a kinematic correction toward (green arrow) and even collide with the obstacles (average number of collisions per participant 9.9 ± 3, number of successful trials needed 60). This initial movement toward the obstacles was reflected in the participant's lateral velocity as a reduction starting at ~300 ms (Fig. 7B, green).

Figure 7.

Kinematic and muscle activity from Experiment 3A. A, Hand paths of an exemplary participant for reaches when the obstacles (yellow) were absent (top) and present (bottom) in Experiment 3A. Obstacles were placed 4 cm on either side of the straight path from the start target and the goal. Green arrows indicate trials where the participant appeared to initially correct into the obstacles. B, Change in lateral hand velocity from the same exemplary participant. Blue and red arrows indicate the earliest-corrective movement to a perturbation for when the obstacles were absent and present, respectively. Black arrows indicate when corrective movements differentiated based on whether the obstacles were absent or present (ROC analysis). Green arrow indicates a reduction in hand speed. Dashed vertical lines mark the 180–230 and 230–280 ms epochs. C, The group average difference between the change in the lateral hand velocity inside the 180–230 and 230–280 ms epochs. D, Group average change in PDelt activity for when obstacles are absent and present. Blue arrow indicates onset of the earliest muscle response when the obstacles were absent. Black arrow indicates when muscle responses differentiated based on whether the obstacles were absent or present. Dashed vertical lines mark the 90–120 and 120–180 ms epochs. E, The group average muscle response in the PDelt inside the 90–120 and 120–180 ms epoch. F, Same format as E for TLat. Data are plotted as mean and SE. **p < 0.01.

Figure 7B also shows that the earliest-corrective onsets could be detected in the lateral velocity for no-obstacle trials at 156 ms (blue arrow) and obstacles at 138 ms (red arrow). Differences in corrective movements for no-obstacles and obstacle trials (obstacle-dependent) were detected at 198 ms for left jumps and 183 ms for right jumps (black arrows). Across the population, the earliest corrective onset was detected at 140 ± 4 and 150 ± 5 ms for obstacle and no-obstacle trials, respectively, whereas the average obstacle-dependent onset timing started at 239 ± 30 ms (Table 1). A one-way RM ANOVA, with earliest corrective onset for no-obstacle and obstacle trials, and obstacle-dependent onset timing as levels, revealed a significant main effect (F_(2,14) = 8.5, p = 0.004). Post hoc paired t tests revealed that the difference between the earliest corrective onsets (no-obstacle and obstacle) and obstacle-dependent onsets were trending toward significance (comparison with: no-obstacle t₍₇₎ = 2.7, p = 0.05; obstacle t₍₇₎ = 3.2, p = 0.05).

Figure 7C (left) shows the average change in the lateral velocity for the 180–230 ms epoch. We applied a paired t test and found no significant differences between no-obstacle and obstacle trials (t₍₇₎ = 0.5, p = 0.631). In contrast a significant reduction in the 230–280 ms epoch was found when the obstacles were present (Fig. 7C, right; t₍₇₎ = 4.7, p = 0.002).

Figure 7D shows the group average change in PDelt activity for obstacle and no-obstacle trials. The earliest changes in muscle activity could be detected 92 (blue arrow) and 93 ms (data not shown) after the cursor jump for no-obstacle and obstacle trials, respectively. Surprisingly, for no-obstacle and obstacle trials a leftward cursor jump elicited a rapid excitation in PDelt that remained similar between the two conditions (blue and red dashed lines). The excitation was unexpected because the obstacles required participants to make whole-limb extension movements to navigate around, thus requiring shoulder flexion and an inhibition of PDelt. The excitation response we observed is appropriate for correcting unobstructed to the goal. We detected that the inhibition of PDelt began at 150 ms when the obstacles were present (black arrow). For rightward cursor jumps, we found PDelt showed similar rapid inhibition whether the obstacles were present or absent for >200 ms after the cursor jump. For TLat, we observed a similar pattern, however, differentiation based on the obstacles was detected for right cursor jump at 147 and at 164 ms for left cursor jumps (Table 1).

Figure 7, E and F, shows the muscle responses of PDelt and TLat in the 90–120 ms epoch and 120–180 ms epochs. For the 90–120 ms epoch, a two-way RM ANOVA, with direction and obstacles (if they were present or absent) as factors, found a significant interaction effect for TLat only (PDelt: F_(1,7) = 3.85, p = 0.09; TLat: F_(1,7) = 7.6, p = 0.03). However, post hoc paired t tests did not reveal any significant differences between TLat responses when obstacles were present or absent (left jumps: t₍₇₎ = 2.0, p = 0.18; right jumps: t₍₇₎ = 0.06, p = 1.0). In contrast, analyzing muscle responses in the 120–180 ms epoch using the same ANOVA structure exhibited significant interaction effects for both muscles (PDelt: F_(1,7) = 9.7, p = 0.02; TLat: F_(1,7) = 15.9, p = 0.005). Post hoc analysis for PDelt responses revealed a trend for reduced excitation when the obstacles were absent (t₍₇₎ = 2.6, p = 0.07, Bonferroni correction). Similarly, for TLat, there was a trend for reduced inhibition for right jumps when obstacles were present (t₍₇₎ = 2.3, p = 0.11).

Experiment 3B: obstacle avoidance requiring whole-limb flexion

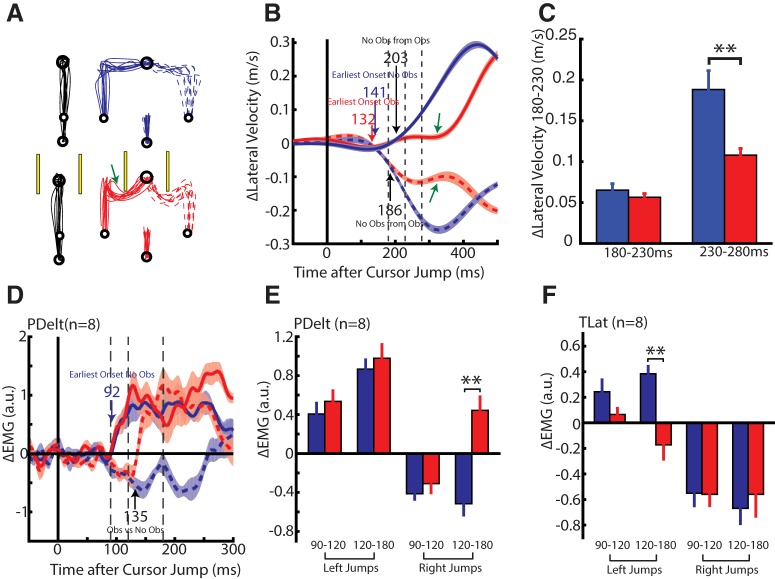
In this experiment we increased the urgency of participants' corrective movements to improve the separation of the corrective response for obstacle and no-obstacle trials. This was done by placing the obstacles so that participants had to make whole-limb flexion movements to navigate around the obstacle (Fig. 8A). This posed a greater challenge than Experiment 3A as participants could no longer use the momentum from the original reach to navigate around the obstacles when the cursor jumped, but instead, had to reverse direction. As in Experiment 3A, for obstacle trials the participant would initiate a kinematic correction to a cursor jump toward (green arrow) and even collide with the obstacles (average collisions per participant 4.6 ± 2 of 60 trials). For obstacle trials we again observed a reduction in the lateral velocity starting at ~300 ms (Fig. 8B, green arrows).

Figure 8.

Kinematic and muscle activity from Experiment 3B. A, Hand paths of an exemplary participant for reaches when the obstacles were absent (top) and present (bottom) in Experiment 3B. Green arrows indicate trials where the participant appeared to initially correct into the obstacles. B, Change in lateral hand velocity from the same exemplary participant. Blue and red arrows indicate the earliest corrective movement to a perturbation for when the obstacles were absent and present, respectively. Black arrows indicate when corrective movements differentiated based on whether the obstacles were absent or present. Green arrow indicates a reduction in hand speed. Dashed vertical lines mark the 180–230 and 230–280 ms epochs. C, The group average difference between the change in the lateral hand velocity inside the 180–230 and 230–280 ms epochs. D, Group average change in PDelt activity for when obstacles are absent and present. Blue arrow indicates onset of the earliest muscle response when the obstacles were absent. Black arrow indicates when muscle responses differentiated based on whether the obstacles were absent or present. Dashed vertical lines mark the 90–120 and 120–180 ms epochs. E, The group average muscle response in the PDelt inside the 90–120 and 120–180 ms epoch. F, Same format as E for TLat Data are plotted as mean and SE. **p < 0.01.

The participant's earliest kinematic correction for no-obstacle trials was detected at 141 ms (blue arrow) and for obstacle trials at 132 ms (red arrow). Obstacle-dependent timing was detected at 203 ms for left jumps and 186 ms for right jumps (black arrows). Across the population the earliest corrective onset was detected at 121 ± 6 and 140 ± 4 ms for obstacle and no-obstacle trials, respectively, whereas the obstacle-dependent onset was detected at 194 ± 13 ms. A one-way RM ANOVA, with the earliest corrective onset for no-obstacle and obstacle trials, and obstacle-dependent onset as levels, revealed a significant main effect (F_(2,14) = 24, p < 0.001). Post hoc paired t tests revealed that obstacle-dependent onsets were significantly later than the earliest corrective onsets for no-obstacle (t₍₇₎ = 5.1, p = 0.002) and obstacle (t₍₇₎ = 5.2, p = 0.002) trials. The change in the lateral velocity in the 180–230 ms epoch was not significantly different for no-obstacle and obstacle trials (Fig. 8C; paired t test, t₍₇₎ = 1.4, p = 0.214). In contrast, participants significantly reduced their lateral velocity in the 230–280 ms epoch when obstacles were present (t₍₇₎ = 3.82, p = 0.007).

Figure 8D shows the group average change in PDelt activity for no obstacle and obstacle trials. The earliest changes in muscle activity could be detected at 92 ms (blue arrow) for both no-obstacle and obstacle trials (Table 1). Right cursor jumps elicited a rapid inhibition in the PDelt for no-obstacle and obstacle trials. However, PDelt inhibition was inappropriate when obstacles were present as participants had to perform a whole-limb flexion movement to navigate the obstacles, thus requiring PDelt excitation. We observed a rapid excitation in PDelt starting at 135 ms for right cursor jumps when the obstacles were present. In TLat we observed a similar pattern, with the earliest changes in muscle activity detected at 89 and 91 ms for no-obstacle and obstacle trials, and differentiation occurring for the left cursor jumps at 151 ms.

Figure 8, E and F, shows the muscle responses of PDelt and TLat in the 90–120 and 120–180 ms epochs. For the 90–120 ms epoch, a two-way RM ANOVA, with direction and obstacles as factors, found no significant interaction effects for either muscle (PDelt: F_(1,7) = 0.04, p = 0.9; TLat: F_(1,7) = 2.3, p = 0.17). In contrast, analyzing muscle responses in the 120–180 ms epoch using the same ANOVA structure exhibited significant interaction effects for both muscles (PDelt: F_(1,7) = 13.7, p = 0.008; TLat: F_(1,7) = 19.0, p = 0.003). Post hoc analyses are plotted in Figure 8, E and F, and display a significant excitation in the PDelt for right jumps and significant inhibition of TLat for left jumps, consistent with our onset analysis.

Experiment 3C: obstacle avoidance with obstacles at different peripheral distances

One explanation for why the initial muscle response at 90 ms did not accurately account for the presence of obstacles is because of a Kalman-like process that integrates visual feedback with the present prediction of the hand position (Izawa and Shadmehr, 2008). Following a cursor jump, the predicted cursor position is between the obstacles while visual feedback signals that the cursor is either left or right of the obstacle. As a result, weighting of the predicted cursor position with the visual error would result in an estimate still between the obstacles but biased toward the visual error. Only after integrating the visual error over time does the estimate of the cursor position transition from between the obstacles to either left or right of both obstacles, thus requiring a correction similar to what we observed at ~130 ms. The prediction is that muscle responses to avoid an obstacle will occur earlier if the obstacles are positioned nearer the unperturbed hand trajectory.

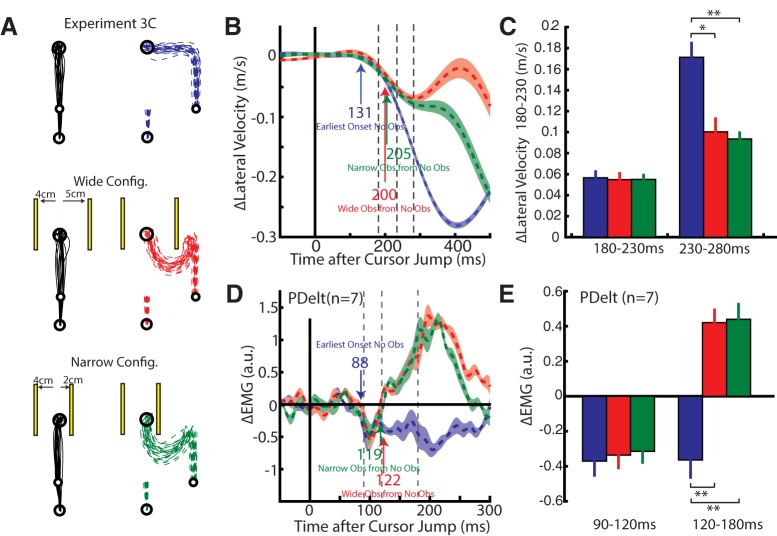
We had participants make reaches when obstacles were absent and present (Fig. 9A). As in Experiment 3B, we placed obstacles that required whole-limb flexion movements to avoid the obstacles. In this experiment, we placed the right obstacle either 2 cm (narrow configuration) or 5 cm (wide configuration) away from the direct path between the start and end goal. We manipulated the position of the right obstacle as right cursor jumps evoked the clearest obstacle-dependent onset in PDelt (Fig. 8D).

Figure 9.

Kinematic and muscle activity from Experiment 3C. A, Hand paths from an exemplary participant for unperturbed (left column) and right cursor jump trials (right column). The left obstacle (second and third row) was placed 4 cm laterally while the right obstacle was placed 5 (middle row) and 2 cm (bottom row) laterally. B, Change in lateral hand velocity from the same exemplary participant. Blue arrow indicates the earliest-corrective movement to a perturbation for when the obstacles were absent (ROC analysis). Red and green arrows indicate when corrective movements differentiated based on whether the obstacles were absent or present for the wide and narrow configuration, respectively (ROC analysis). Dashed vertical lines mark the 180–230 and 230–280 ms epochs. C, The group average difference for the lateral hand velocity inside the 180–230 and 230–280 ms epochs. D, Group average ΔEMG for PDelt. Blue arrow indicates onset of the earliest muscle response (Difference Functions). Red and green arrows indicate muscle responses differentiated based on whether the obstacles were absent or present for wide and narrow configuration, respectively (Difference Functions). Dashed vertical lines mark the 90–120 and the 120–180 ms epochs. E, The group average muscle response in the PDelt inside the 90–120 and 120–180 ms epoch. *p < 0.05, **p < 0.01.

Figure 9A shows the hand trajectories for an exemplary participant. From the lateral velocity (Fig. 9B) the earliest corrective onset for no-obstacle trials was detected at 131 ms (blue arrow). For rightward cursor jumps, obstacle-dependent timing was detected at 200 ms for the wide configuration and 205 ms for the narrow configuration. Across the population, obstacle-dependent onsets were detected at 190 ± 9 and 186 ± 9 ms for the narrow and wide configuration, respectively, and were not significantly different (paired t test, t₍₆₎ = 0.9, p = 0.4). Furthermore, a one-way RM ANOVA, with no obstacle and obstacles as levels, was applied to the change in the lateral velocity in the 180–230 ms epoch and did not reveal a significant main effect (Fig. 9C; F_(2,7) = 0.04, p > 0.9). Instead, we found a significant main effect in the 230–280 ms epoch (F_(2,7) = 17.8, p < 0.001). Post hoc analysis are plotted in Figure 9C and revealed that participants reduced their lateral velocity when obstacles were present, whereas no differences were observed between obstacle configurations.

Figure 9D shows the group average change in PDelt activity for no obstacle and obstacle trials. Changes in muscle activity were detected 89, 97, and 94 ms after the cursor jump for no-obstacle, wide- and narrow-configuration trials, respectively. As in Experiment 3B, rightward cursor jumps elicited rapid inhibition in PDelt that was incorrect when obstacles were present. Differentiation of PDelt activity based on whether the obstacles were present or absent could be detected at 119 and 122 ms (Table 1) for the narrow and wide configuration and were not significantly different (ROC values, paired t test, t₍₆₎ = 1.6, p = 0.16). Furthermore, a one-way RM ANOVA was applied to the PDelt activity in the 90–120 ms epoch and revealed no main effect (F_(2,10) = 0.14, p = 0.871). Instead a significant main effect was found in the 120–180 ms epoch (F_(2,10) = 31.5, p < 0.001) and post hoc analyses are plotted in Figure 9E. A significant reversal in PDelt activity was present for both obstacle configurations; however, there was no significant difference in the 120–180 ms epoch between either obstacle configuration. These data suggest that the difference between the earliest and the obstacle-dependent onset timing in the muscle responses was not due to Kalman-like integration of visual feedback.

Discussion

We explored how participants use visual feedback of their hand, presented as a cursor, to execute goal-directed reaches. We show that the muscle response starting at 90 ms only scaled for cursor jumps <2 cm and could incorporate goal redundancy. However, this response did not accurately account for obstacles. These results highlight how task-related factors can influence rapid visual feedback processing during voluntary actions.

We found a nonlinearity between the size of a cursor jump and the corresponding muscle response amplitude. Beginning at 90 ms, muscle responses scaled with the jump size up to 2 cm but appeared to plateau for larger jumps. After 120 ms, muscle responses for jumps >2 cm decreased from this plateau at different times depending on the jump size. Kinematic corrections also showed linear scaling with jump magnitudes of <2 cm (Veyrat-Masson et al., 2010) and nonlinear scaling for jumps >2 cm beginning at ~170 ms (Franklin et al., 2016). However, by using EMG we showed that the nonlinearity reflects two distinct phases: an early phase that scales amplitude with jump size and a later phase that scales the duration of muscle activity with jump size.

The nonlinear muscle response to cursor jumps >2 cm may reflect the artificial nature of the visual disturbance. A jump of 2 cm in a single video frame (16.7 ms) reflects a 120 cm/s transient disturbance. By comparison, our studies of mechanical disturbances never generated limb motion >1 cm over the first 50 ms, a rate of 20 cm/s (Cluff and Scott, 2015; Lowrey et al., 2017). These mechanical disturbances evoke responses 2× larger than observed for visual disturbances, even though the displacement was 6× smaller. This indicates the plateau we observed did not reflect a saturation of the motor output.

Whether the motor system viewed the error generated by a cursor jump as self or externally generated may also influence muscle responses. Wei and Körding (2009) examined trial-to-trial adaptation to errors in cursor feedback of hand position and found participants adapted at a linear rate when small errors were introduced to the cursor position and at a constant rate for larger errors. A model where participants adapted based on whether the visual error was probably (linear rate) or improbably (constant rate) generated by the motor system could explain the observed behavior. This may explain why muscle responses scaled for jumps <2 cm and nonlinearly for jumps >2 cm as the former could reasonably be generated by the motor system during a reach.

Last, the scaling between jump size and corrective response may reflect a strategy to cope with signal-dependent noise. A model comparing saccade amplitudes of increasing size exhibited little modulation of the initial eye velocity with amplitude size when signal-dependent noise was included (Harris and Wolpert, 1998). Why jump size exhibits nonlinear scaling with corrective response requires further investigation.

Surprisingly, muscle responses plateaued for cursor jumps >2 cm, but can be altered based on goal shape, similar to previous findings (Knill et al., 2011; de Brouwer et al., 2017). In particular, the magnitude of the muscle response was reduced for the wide goal, suggesting the earliest muscle response is sensitive to some contexts that require simple gain responses.

However, we found that the earliest muscle response was not sensitive to the presence of obstacles. Muscle responses beginning at 90 ms were similar whether the obstacles were present or absent. Absence of a context-dependent change at 90 ms was not obscured by saturation, as observed with the stretch response for digit muscles (Rothwell et al., 1980). Specifically, in Experiments 3B and 3C the PDelt response that started at 90 ms was inhibition for left jumps, appropriate when making a correction directly toward the goal. In contrast, after 120 ms there was an abrupt excitation required to pull the hand back to avoid the obstacle. Similarly, Carroll et al. (2019) showed that the initial correction for a cursor jump was not modulated by the reward outcome, instead additional time was required to generate the task-dependent response. Overall, these data suggest visual feedback of the limb involves two phases: a response that starts at 90 ms and a more complex response that starts at 120 ms.

Recent studies demonstrate that visual feedback of the hand and target are processed independently for online corrections (Reichenbach et al., 2014; Franklin et al., 2016). However, our results highlight some similarities in how they are processed. Target jumps evoke a muscle response in ~90 ms (Soechting and Lacquaniti, 1983; Fautrelle et al., 2010; Pruszynski et al., 2016). This response always drives participants toward the jumped target even if instructed to move in the opposite direction of the target jump. Instead, participants require an additional ~40 ms to incorporate the instruction to move in the opposite direction (Day and Lyon, 2000; Gritsenko and Kalaska, 2010). A two-phase response also arises during reaching when background motion is applied (Saijo et al., 2005). These early responses show limited sensitivity to the magnitude of the target jump or speed of the background motion (Saijo et al., 2005; Franklin et al., 2016; Pruszynski et al., 2016; Zhang et al., 2018). This suggests a two-phase response is a common feature for visual feedback processing. We predict that target jumps and background motion will show similar timing for obstacles as we observed for cursor jumps.

Most motor control models assume feedback from different sensory modalities are integrated together to form a state estimate of the limb (Sober and Sabes, 2003; Wei and Körding, 2009; Oostwoud Wijdenes and Medendorp, 2017). This estimate is used by a control policy to generate the appropriate motor commands (Todorov and Jordan, 2002; Scott, 2004). However, the presence of two phases for visual feedback of the hand suggest a more complex organization. The long-latency muscle response for mechanical disturbances incorporates a broad range of behavioral factors, including: magnitude (Crevecoeur et al., 2012), goal redundancy (Nashed et al., 2012; Lowrey et al., 2017), and obstacles (Nashed et al., 2014). In contrast, the 90–120 ms visual response does not incorporate all of these factors indicating that it is distinct from the flexible long-latency response. This suggests that the response at 90 ms reflects a purely visual feedback process (Oostwoud Wijdenes and Medendorp, 2017).

The similarities in the task-dependent feedback processing of the 60 ms proprioceptive response and the 120 ms visual response may reflect the output from a limb estimate that integrates visual and proprioceptive feedback. However, the large difference in their respective delays could impact how each modality is weighted. Traditional Bayesian models of multisensory integration predict vision should dominate over proprioception as the former is more reliable (Welch and Warren, 1980; Ernst and Banks, 2002; Knill and Pouget, 2004; Fetsch et al., 2013). However, our group has recently put forth a dynamic Bayesian model where sensory signals are weighted based on their reliability and delay (Crevecoeur et al., 2016). Including sensory delays accounts for the accumulation of motor noise over the delay period that reduces the value of the sensory signals (Crevecoeur and Körding, 2017). Our finding that the delay for vision to update the common state estimate may be longer (120 ms) than we previously estimated (90 ms) further supports the prediction that proprioceptive feedback initially dominates visual feedback for online control (Crevecoeur et al., 2016).

However, note that the 120 ms visual and 60 ms proprioceptive response may only be partially integrated as participants correctly identified the cursor was outside of the obstacles. Similarly, participants always ended their reach with the cursor on the target, not the hand or a combined estimate of the hand and cursor. This may reflect separate estimates of cursor and hand position used by the controller. However, other state variables may be integrated from visual and proprioceptive feedback, such as hand velocity (Saunders and Knill, 2004).

Many assume the muscle response starting at 90 ms reflects a transcortical feedback process through motor cortex (Knill et al., 2011; Dimitriou et al., 2013; Gaveau et al., 2014; Franklin, 2016; Scott, 2016). However, motor cortex is involved in generating context-dependent muscle responses for proprioceptive feedback within 60 ms (Evarts and Tanji, 1976; Shemmell et al., 2009; Pruszynski et al., 2011; Omrani et al., 2016). If motor cortex is involved in generating the control policy for voluntary control, it seems surprising that it incorporates factors such as obstacles for proprioceptive feedback and not visual feedback. Thus, transcortical feedback is likely involved in the visual responses that started after 120 ms, but not the response that started at 90 ms.

The superior colliculus may be involved in the muscle response starting at 90 ms (Pruszynski et al., 2010; Fautrelle and Bonnetblanc, 2012; Corneil and Munoz, 2014; Day, 2014; Cluff et al., 2015; Wood et al., 2015; Gu et al., 2016). Behaviorally, the superior colliculus has been implicated in rapid motor responses following a target jump (Day and Brown, 2001). Neural activity in the superior colliculus correlates with upper limb reaching (Werner, 1993; Kutz et al., 1997; Stuphorn et al., 1999) and stimulation can evoke reaching-like movements (Courjon et al., 2004; Philipp and Hoffmann, 2014). Projections from motor cortex to superior colliculus (Fries, 1984, 1985) could provide a gain to modulate visual feedback processing depending on the behavioral context (Gu et al., 2018).