New trend in old-age mortality: Gompertzialization of mortality trajectory

Abstract

There is a great interest among gerontologists, demographers and actuaries to the question about the limits to human longevity. Attempts to get answers to this important question stimulated many studies on late-life mortality trajectories, often with opposite conclusions. One group of researchers believes that mortality stops growing with age at extreme old ages, hence there is no fixed limit to lifespan. Other studies found that mortality continues to grow with age up to extreme old ages. This study suggests a possible solution to this controversy. We found that mortality deceleration is best observed when older, less accurate lifespan data are analyzed, while in the case of more recent and reliable data there is a persistent mortality growth with age. We compared performance (goodness-of-fit) of two competing mortality models - the Gompertz model and the “mortality deceleration” Kannisto model at ages 80–105 years using data for 1880–1899 single-year birth cohorts of U.S. men and women. The mortality modeling approach suggests a transition from mortality deceleration to the Gompertzian mortality pattern over time for both men and women. These results are consistent with the hypothesis about disappearing mortality deceleration over time due to improvement in the accuracy of age reporting. In the case of more recent data mortality continues to grow with age even at very old ages. This observation may lead to more conservative estimates for the future human longevity records.

1. INTRODUCTION

There is a great interest among gerontologists, demographers and actuaries to the question what are the limits to human longevity, and whether the fixed limits exist at all. Attempts to get answers to these important questions stimulated many studies on late-life mortality trajectories, often with opposite conclusions. One group of researchers claims that mortality stops growing with age at extreme old ages, hence there is no fixed limit to lifespan [1]. Other studies found that mortality continues to grow with age even at late life [2]. Recent debates in “Gerontology” journal about the limit to human lifespan highlighted the need to know better the shape of mortality trajectories at extreme old ages [3, 4]. It was long believed that the exponential growth of the force of mortality with age (the Gompertz law) is followed by the period of deceleration when mortality growths slower than predicted by the Gompertz law [5–8]. Thatcher and colleagues tested several models of mortality using data on thirteen countries with presumably good quality of mortality statistics and found downward deviation of mortality from the Gompertz law after age 80 years [7, 8]. Horiuchi and Wilmoth analyzed age trajectories of life table aging rate in Sweden and Japan and found that the life table aging rate has a tendency to decline after 75–80 years of age suggesting mortality deceleration [6]. This mortality deceleration eventually produces “late-life mortality leveling-off” and “late-life mortality plateaus” at extreme old ages [5, 9, 10]. Actuaries (including Gompertz himself) first noted this phenomenon and they proposed a logistic formula for mortality growth with age in order to account for mortality deceleration at advanced ages. The same phenomenon of ‘almost non-aging’ survival dynamics at extreme old ages was observed in other biological species. In some species (medflies and house flies) mortality plateau can occupy a sizable part of their life [11]. The existence of mortality plateaus is now well documented for a number of lower organisms (see review in [11]). However, later studies reported no mortality deceleration at older ages for primates [12, 13], rodents and humans [2, 14]. In another study, Gompertz-like mortality was found for Australia, Canada and the United States and mortality deceleration for a number of European countries [15].

The estimation of the force of mortality at very old ages faces difficulties, because of very small number of survivors to these ages and because of age misreporting by older persons. The age misreporting may be a problem affecting estimates of mortality at older ages [16–19]. Even a small percentage of inaccurate data can greatly distort mortality trajectories at advanced ages [20, 21]. In most cases, age misreporting at older ages leads to mortality underestimation [22] and even rare errors in age reporting can accumulate at extreme old ages leading to spurious mortality deceleration [21]. Taking into account that the accuracy of age reporting is positively correlated with education [23], we can hypothesize that improvement of education over time would lead to more accurate age reporting and hence less prevalent mortality deceleration. Also, it is known that birth registration in the United States was introduced gradually with only six states having official birth registration between 1841 and 1890 [24]. Introduction of birth registration improves the quality of age reporting among subsequent birth cohorts. Preliminary data suggest that mortality at advanced ages in earlier U.S. birth cohorts shows stronger deceleration compared to mortality in later birth cohorts [14].

Here we analyze historical evolution of mortality trajectories at advanced ages using age-specific death rates for 20 cohorts born in 1880–1899 in the United States. We study two competing models describing mortality trajectories (the Gompertz model and the Kannisto model) with Akaike goodness-of-fit criterion. We hypothesize that mortality deceleration should fade away in more recent birth cohorts due to improvement in age reporting over time.

2. DATA AND METHODS

The Human Mortality Database (HMD) provides mortality and population data [25]. Age-specific death rates are used as empirical estimates for the force of mortality [26]. Datasets of age-specific cohort death rates (central mortality rates) of men and women are available in HMD for ages up to 110 years or older. We selected data available in one-year age and time increments denoted as M_x, where x indicates single year of age. Yearly central death rate for cohort c at age x is defined as number of deaths to the cohort c between ages x and x+1 divided by number of person-years lived by the cohort c between ages x and x+1 [27]. We study 1880–1899 single-year birth cohorts of the United States and analyze data for men and women separately.

Study of data quality at older ages found that U.S. data quality is conditionally acceptable [28]. U.S. data pass the tests of age heaping and Whipple’s index for centenarians, but consistently shows moderate data quality problems [28]. Age-specific women to men ratios confirm that the U.S. data are of sufficiently good quality up to ages 106–107 years [14]. However, age misreporting rapidly increases after age 105 years [18, 29]. For this reason, mortality was fit in the age interval 80–105 years.

We fit mortality with two competing models used earlier in the study by Thatcher and coauthors [8]: the Gompertz model and the logistic model (a simplified two-parameter logistic model, also called the Kannisto model):

$$\text{Gompertz:}\text{μ}(x)=a{e}^{bx}$$ (1)

$$\text{Kannisto:}\text{μ}(x)=\frac{a{e}^{bx}}{1+a{e}^{bx}}$$ (2)

where μ(x) is the force of mortality, x is age, a and b are parameters.

Parameters a and b are called the intercept and the slope parameters respectively.

Parameter a determines the initial level of mortality while parameter b determines the rate of mortality increase with age.

According to the Gompertz law (suggested by the British actuary, Benjamin Gompertz, in 1825), the logarithm of the force of mortality (hazard rate) increases linearly with age. This is often used in order to illustrate graphically the validity of the Gompertz law – the data are plotted in the semi-log scale (known as the Gompertz plot) to check whether the logarithm of the hazard rate is indeed increasing with age in a linear fashion.

The Kannisto model was suggested by Vaino Kannisto in 1994 in order to take into account the observed mortality deceleration at advanced ages [30]. With the logistic Kannisto model, there is an asymptote of mortality at the oldest ages equal to one, and hence the Kannisto model fits mortality better in the case of mortality deceleration.

We test these two models for their performance of fitting the empirical data. We run a weighted nonlinear regression model in the age interval 80–105 years (using Stata command nlin). Age-specific exposure values are used as weights in nonlinear regression analyses [31].

Akaike Information Criterion (AIC) is used to evaluate goodness of fit for the Gompertz and the Kannisto models:

$$AIC=2k-2\ln (L)$$ (3)

where ln(L) is the maximized log-likelihood of the model and k is the number of parameters estimated. AIC was computed using Stata post-estimation command estat. Both the nlin and estat commands are described in the Stata manual [32].

The best model has the minimal value of the Akaike Information Criterion [33]. It is not the absolute size of the AIC value, it is the difference of values for compared models (Δ_i), that is important in model selection. AIC difference higher than 10 suggests strong support of better model by data [33]:

$${\mathit{\Delta }}_i=AI{C}_i-AI{C}_{min}$$ (4)

where Δ_i is the AIC difference for the ith model, AIC_i is the Akaike Information Criterion value for the ith model and AIC_min is the value of criterion for the best model with minimal AIC.

Analyses were conducted using Stata statistical software, release 14.

3. RESULTS

Figure 1 presents the results of model fitting (AIC values) for the U.S. 1880–1899 birth cohorts. It demonstrates clear transition from lower values of AIC (better fit) for the Kannisto model in the case of earlier birth cohorts to lower values (better fit) of AIC for the Gompertz model in the case of later birth cohorts. This phenomenon means that mortality deceleration, which is observed for both men and women in earlier birth cohorts, disappears in more recent birth cohorts. This historical change in the pattern of mortality trajectories from mortality deceleration to the Gompertz law occurs for persons born around 1886–1887 (Figure 1).

Figure 1.

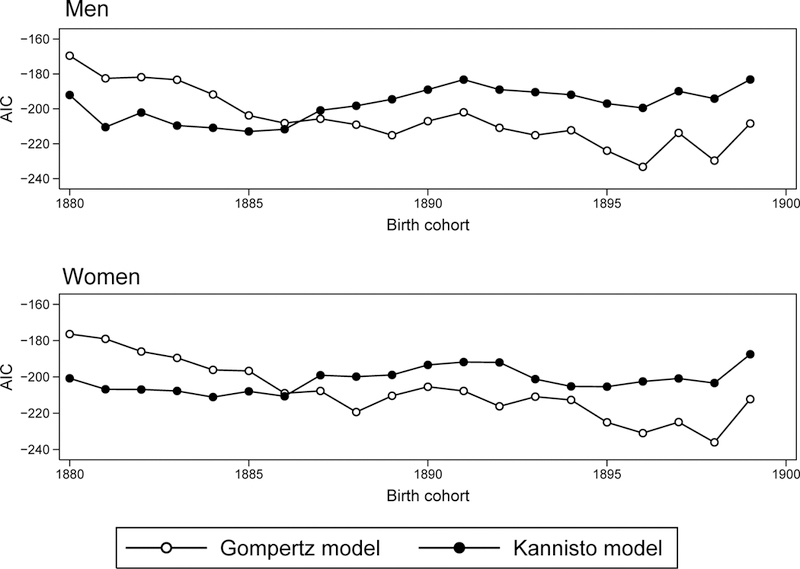
Changes of Akaike Information Criterion (AIC) across birth cohorts for the Gompertz and the Kannisto models fitting the U.S. mortality. Lower AIC values correspond to a better model fit.

Table 1 presents changes in AIC and AIC difference for subsequent birth cohorts. Note that in most cases AIC difference is higher than 10 suggesting strong support by data for either the Kannisto (in the case of earlier cohorts) or the Gompertz (in the case of later cohorts) models. Thus, we may conclude that mortality in the past indeed demonstrated deceleration while later it changed to the Gompertz pattern.

Table 1.

Testing two competing models: Akaike Information Criterion (AIC) and AIC differences for Gompertz and Kannisto models. Smaller values of AIC for the Gompertz model and negative values of AIC difference correspond to better fit by the Gompertz model.

Birth cohort	Men			Women
	Gompertz model (1)	Kannisto model (2)	AIC difference, Δi(1)-(2)*	Gompertz model (1)	Kannisto model (2)	AIC difference, Δi(1)-(2)*
1880	−169.55	−192.07	22.52	−176.34	−200.78	24.44
1881	−182.52	−210.46	27.94	−179.01	−206.80	27.79
1882	−181.83	−202.12	20.29	−185.98	−206.89	20.91
1883	−183.31	−209.56	26.25	−189.48	−207.74	18.26
1884	−191.75	−210.89	19.14	−196.12	−211.12	15.00
1885	−203.78	−212.98	9.20	−196.67	−207.93	11.26
1886	−208.18	−211.71	3.53	−208.96	−210.66	1.70
1887	−205.67	−200.85	−4.83	−207.71	−199.09	−8.62
1888	−209.03	−198.26	−10.77	−219.34	−199.84	−19.50
1889	−215.13	−194.48	−20.65	−210.41	−198.90	−11.51
1890	−207.04	−188.96	−18.07	−205.40	−193.38	−12.02
1891	−201.96	−183.22	−18.74	−207.72	−191.80	−15.92
1892	−210.89	−188.96	−21.92	−216.20	−192.00	−24.20
1893	−215.09	−190.38	−24.71	−210.89	−201.20	−9.70
1894	−212.31	−191.89	−20.42	−212.68	−205.22	−7.46
1895	−223.97	−196.96	−27.02	−225.02	−205.37	−19.65
1896	−233.26	−199.47	−33.80	−230.94	−202.51	−28.43
1897	−213.76	−189.90	−23.86	−224.90	−200.85	−24.05
1898	−229.67	−194.13	−35.54	−236.07	−203.37	−32.70
1899	−208.38	−183.20	−25.18	−212.28	−187.50	−24.77

Figure 2 illustrates historical changes of mortality trajectories presenting age-specific mortality in semi-log scale for earlier (1881) and later (1898) birth cohorts of women in the United States. Mortality pattern of earlier birth cohort demonstrates an obvious deceleration of mortality growth with age while mortality of later birth cohort is presented by a persistent growth (straight line). Figure 3 demonstrates similar mortality patterns for earlier and later birth cohorts of U.S. men.

Figure 2.

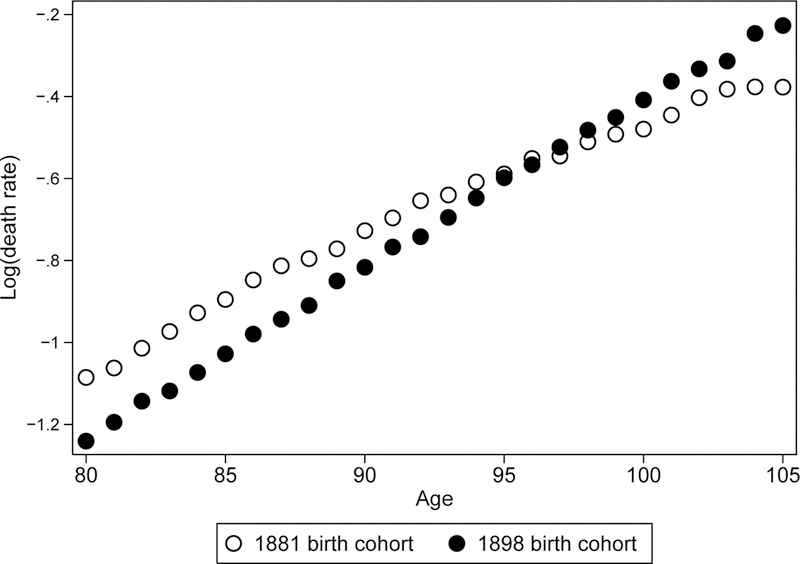
Mortality (death rate) as a function of age for earlier (1881) and later (1898) birth cohorts of U.S. women.

Figure 3.

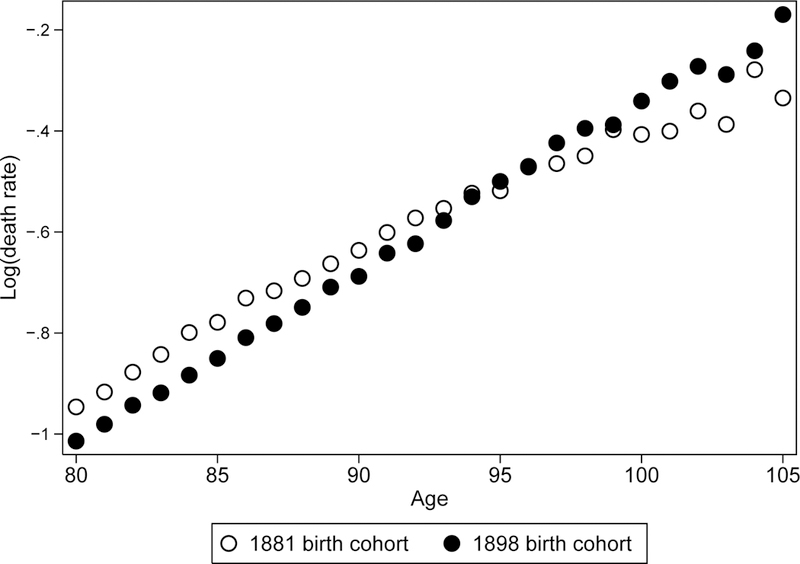
Mortality (death rate) as a function of age for earlier (1881) and later (1898) birth cohorts of U.S. men.

Note that after age 95 years mortality estimates for earlier birth cohort are even lower than mortality estimates for later birth cohort. This paradoxical observation is most likely related to a better quality of age reporting in a more recent birth cohort.

4. DISCUSSION

This study of 1880–1899 single-year birth cohorts found that mortality deceleration is more prevalent in historically earlier birth cohorts while more recent birth cohorts tend to demonstrate the Gompertzian pattern of mortality. These results support the hypothesis that mortality deceleration disappears over time apparently due to improvement in age reporting. These results agree with previous reports of Gompertzian mortality in the U.S. cohorts born after 1889 [2, 14].

Our results may help to understand why earlier studies found mortality deceleration and mortality leveling-off [6–8, 30], while more recent studies did not confirm these initial findings [2, 14]. More frequent age misreporting in the past by older individuals is one of the most likely reasons for this phenomenon [14, 21, 34]. Studies conducted more than 20 years ago used data for earlier birth cohorts when age reporting was not particularly accurate [28]. Later study found that old-age mortality in Australia, Canada and the United States is compatible with the Gompertzian model confirming our findings [15].

Age misreporting in the United States could be particularly prevalent, because this country did not have an established uniform system of birth registration up to 1933 [24]. For example, Kestenbaum and Ferguson were able to find only 52 birth certificates of long-lived persons out of 325, whereas age of 256 persons was validated through the early U.S. censuses [35]. According to our experience, age misreporting indeed is able to produce false mortality deceleration [11]. We conducted a direct age validation procedure for records of persons born in 1900 and aged 106 years and over by linking data available in the U.S. Social Security Administration Death Master File to early historical resources, including early censuses. We found that data cleaning (removing records with unconfirmed age) resulted in higher mortality estimates at advanced ages and more Gompertz-like mortality trajectories [11]. The proportion of records with unconfirmed age increases with age from 12% at age 100 years to 17% at age 105 years and 35% at ages 109 years and over [18]. The advantage of studying U.S. mortality is its large population size with significant number of survivors to advanced ages, which allows researchers to obtain more reliable estimates for the force of mortality (hazard rate).

In addition to age misreporting, some other causes of transition from the late-life mortality deceleration to the Gompertzian mortality may be involved. It was recently observed that mortality of centenarians in the United States did not decrease noticeably in the past decades, despite a significant decline in mortality of younger age groups [3]. In some countries (Japan, France, Switzerland and Sweden) historical decline of mortality among centenarians has stopped about 10–20 years ago [36]. Historical stagnation of mortality at ages 100 years and older may lead to steeper mortality curves for cohorts at extreme old ages while historical mortality decline after age 100 years may produce apparent decelerating pattern of mortality with age. Feehan studied cohort mortality after age 80 years in different countries [37]. He found that in some countries Gompertz model performed poorly while in other countries this model performed reasonably well. He suggests that period effects may have altered the shape of cohort mortality producing the strongest evidence of non-Gompertz death rates for cohorts that experienced continuous historical improvements in mortality at advanced ages [37]. Our results do not completely exclude possibility that the age at onset of mortality deceleration in the United States has moved beyond 105 years of age. Indeed, it was found that mortality in European countries does show deceleration, but the age at onset of mortality deceleration is shifting over time to older ages [15]. Thus, the same process could happen in the United States too.

It is possible that both the improvement of age reporting and stagnation of mortality among centenarians contribute to the observed historical transition from mortality deceleration to the Gompertzian pattern. Overall, it appears that the onset of mortality deceleration occurs now at much older ages than was reported earlier [6–8, 38].

Also there are theoretical models [39, 40] and simulation studies [41] suggesting that mortality deceleration at advanced ages may be a consequence of population heterogeneity. Heterogeneity hypothesis predicts that the age of onset for mortality deceleration should increase over time as frailer individuals reach more advanced ages due to lower mortality at younger ages [6, 42]. Studies of the U.S. period mortality [42] and cohort mortality in other countries [6, 15] provide some empirical support for this prediction. A study of the U.S. period mortality revealed an expansion of life span inequalities over time among survivors to older ages suggesting that more heterogeneous populations are reaching older age now [43].

5. CONCLUSION

Our results demonstrate that there is no single universal answer to the question about mortality pattern at extreme old ages, because this answer depends on the historical period of mortality analysis. In old historical data the late-life mortality deceleration is observed. In more recent data mortality continues to grow exponentially with age even at very old ages. This observation may lead to more conservative estimates for the future human longevity records.