Validation of mean upper cervical cord area (MUCCA) measurement techniques in multiple sclerosis (MS): High reproducibility and robustness to lesions, but large software and scanner effects

Abstract

Introduction

Atrophy of the spinal cord is known to occur in multiple sclerosis (MS). The mean upper cervical cord area (MUCCA) can be used to measure this atrophy. Currently, several (semi-)automated methods for MUCCA measurement exist, but validation in clinical magnetic resonance (MR) images is lacking.

Methods

Five methods to measure MUCCA (SCT-PropSeg, SCT-DeepSeg, NeuroQLab, Xinapse JIM and ITK-SNAP) were investigated in a predefined upper cervical cord region. First, within-scanner reproducibility and between-scanner robustness were assessed using intra-class correlation coefficient (ICC) and Dice's similarity index (SI) in scan-rescan 3DT1-weighted images (brain, including cervical spine using a head coil) performed on three 3 T MR machines (GE MR750, Philips Ingenuity, Toshiba Vantage Titan) in 21 subjects with MS and 6 healthy controls (dataset A). Second, sensitivity of MUCCA measurement to lesions in the upper cervical cord was assessed with cervical 3D T1-weighted images (3 T GE HDxT using a head-neck-spine coil) in 7 subjects with MS without and 14 subjects with MS with cervical lesions (dataset B), using ICC and SI with manual reference segmentations.

Results

In dataset A, MUCCA differed between MR machines (p < 0.001) and methods (p < 0.001) used, but not between scan sessions. With respect to MUCCA values, Xinapse JIM showed the highest within-scanner reproducibility (ICC absolute agreement = 0.995) while Xinapse JIM and SCT-PropSeg showed the highest between-scanner robustness (ICC consistency = 0.981 and 0.976, respectively). Reproducibility of segmentations between scan sessions was highest in Xinapse JIM and SCT-PropSeg segmentations (median SI ≥ 0.921), with a significant main effect of method (p < 0.001), but not of MR machine or subject group. In dataset B, SI with manual outlines did not differ between patients with or without cervical lesions for any of the segmentation methods (p > 0.176). However, there was an effect of method for both volumetric and voxel wise agreement of the segmentations (both p < 0.001). Highest volumetric and voxel wise agreement was obtained with Xinapse JIM (ICC absolute agreement = 0.940 and median SI = 0.962).

Conclusion

Although MUCCA is highly reproducible within a scanner for each individual measurement method, MUCCA differs between scanners and between methods. Cervical cord lesions do not affect MUCCA measurement performance.

Highlights

• •Mean upper cervical cord area (MUCCA) was obtained with five different methods.
• •MUCCA was determined in a unique scan-rescan multi-vendor MR study.
• •Reproducibility: MUCCA did not differ between scan-rescan images for any method.
• •Robustness: MUCCA differed between methods and between scanners.
• •Performance of MUCCA methods was not affected by the presence of lesions.

1. Introduction

Multiple sclerosis (MS) is a demyelinating and neurodegenerative disease of the central nervous system (CNS). Abnormalities in the spinal cord such as lesions and atrophy often manifest early in the disease course and have been shown to be important predictors of disease progression and prognosis (Casserly et al., 2018; Kearney et al., 2015). Relevance of mean upper cervical cord area (MUCCA) from magnetic resonance imaging (MRI) has been shown in early as well as late stages of MS (Biberacher et al., 2015; Hagstrom et al., 2017; Lukas et al., 2013; Rashid et al., 2006).

Since manual MUCCA measurements are labor-intensive and can suffer from large intra- and inter-rater variability (Cadotte et al., 2015; De Leener et al., 2014; El Mendili et al., 2015; Kearney et al., 2014), several (semi-)automated methods have been developed, such as SCT-PropSeg (De Leener et al., 2014), SCT-DeepSeg (Gros et al., 2019), NeuroQLab (Lukas et al., 2008), Xinapse JIM (Horsfield et al., 2010) and ITK-SNAP (Yushkevich et al., 2006). However, these methods are generally developed for dedicated cord imaging instead of head imaging, and although previous research has shown that it is possible to obtain accurate MUCCA measures not only from cord imaging, but from brain imaging as well (Liu et al., 2016; Liu et al., 2015), research regarding their reproducibility and robustness in whole brain images is not yet available. This knowledge is needed to incorporate MUCCA measurement from head images in standardized clinical care, and to facilitate research on cervical cord atrophy in MS, specifically to analyze MUCCA retrospectively in data in which 3D T1-weighted cervical cord images are not available as well as prospectively without the need for separate spinal cord imaging.

Moreover, subjects with MS often exhibit lesions in the upper cervical cord (Eden et al., 2019). Since lesions in the brain are known to severely affect brain atrophy measurements (Amiri et al., 2018; Battaglini et al., 2012; Chard et al., 2010; Gonzalez-Villa et al., 2017; Popescu et al., 2014; Sdika and Pelletier, 2009), it is important to investigate the effect of lesions in spinal cord on MUCCA measurements as well. Although a study using SCT PropSeg did not observe an obvious effect of lesion on the spinal cord segmentation through visual inspection (Yiannakas et al., 2016), a quantitative assessment of the effect of lesions on the quality of cervical spinal cord segmentation and MUCCA measurement is lacking.

Therefore, the aim of this study was twofold: (a) to assess the reproducibility and robustness of these (semi-)automatic spinal cord segmentation methods in whole-brain 3D T1-weighted images by measuring MUCCA in scan and rescan images (reproducibility) acquired on three different MR machines (robustness); and (b) to quantitatively investigate whether the presence of lesions in the cervical spinal cord affects the performance of these segmentation methods.

2. Methods

2.1. Subjects

The institutional review board approved the study protocols and written informed consent was obtained from all individuals, according to the Declaration of Helsinki.

For this study, two different existing datasets were used, which are hereafter referred to as dataset A for reproducibility and robustness and dataset B for the effect of lesions. For both datasets, subjects with MS according to McDonald 2010 criteria (Polman et al., 2011) were included and were allowed to use disease modifying treatment. All subjects were enrolled at the same institution.

Dataset A consisted of 6 healthy controls and 21 subjects with MS (relapsing remitting MS n = 16; secondary progressive MS n = 1; and primary progressive MS n = 4). All subjects underwent two sessions of MRI examinations (hereafter defined as ‘scan’ and ‘rescan’) on three 3 T MR machines from different vendors (General Electric [GE], Philips and Toshiba) in the same center. The scan and rescan sessions within one MR machine were always performed on the same day and the different MR machine examinations were all performed preferably over the course of a single day, or within a maximum of eight days from each other.

Dataset B consisted of 21 subjects with RRMS selected from a larger cohort of 196 patients with relatively long disease duration (Daams et al., 2014; Steenwijk et al., 2014) who were scanned on a 3 T GE scanner. Selection of these subjects was based on the amount of cervical cord MS lesions as previously reported(Daams et al., 2014), and subjects were divided into two groups: with (at least 11 counted) lesions in the cervical cord (n = 14) and without lesions (n = 7). The two groups were balanced for gender, mean EDSS as well as for mean MUCCA values as obtained previously in the C1-C2 area using an older version of NeuroQLab (Daams et al., 2014) (see Inline Supplementary Table S1).

Table S1.

Demographics of subjects from dataset B, selected from a previous study (Daams et al., 2014).

	Without lesions (n = 7)	With lesions (n = 14)
Age (years, mean ± SD)	53.32 ± 11.76	49.74 ± 8.86
Sex (m/f, %f)	2/5 (40%)	4/10 (40%)
EDSS score (median, Q1-Q3)	4.0 (3.5–4.5)	4.0 (3.0–7.0)
MUCCAa (mm2, mean ± SD)	74.43 ± 10.23	72.64 ± 10.18

^aMUCCA as measured by NeuroQLab in the study from Daams et al., 2014.

2.2. MRI examination

The subjects in dataset A underwent MRI examinations on three different 3 T whole body MRI scanners with a head coil, all including a sagittal 3D T1-weighted sequence: (1) GE Discovery MR750 (GE Healthcare, USA) with a fast spoiled gradient echo sequence (FSPGR with TR/TE/TI = 8.2/3.2/450 ms and resolution 1.0 × 1.0 × 1.0 mm); (2) Philips Ingenuity with a turbo field echo sequence (TFE with TR/TE/TI = 7.9/4.5/900 ms and resolution 1.0 × 1.0 × 1.0 mm); and (3) Toshiba Vantage Titan with a fast field echo sequence (FFE with TR/TE/TI = 5.7/2.4/1050 ms and resolution 1.0 × 1.0 × 1.2 mm).

Subjects from dataset B underwent MRI examination as described earlier (Daams et al., 2014). In summary, subjects were scanned using a 3 T HDxt GE scanner (GE Healthcare, USA) with a head-neck-spine coil with a sagittal 3D T1-weighted FSPGR sequence (TR/TE/TI = 7.3/3.0/450 ms with acquired resolution 1.09 × 1.09 × 1.0 mm, reconstructed to 0.55 × 0.55 × 1.0 mm). The aforementioned lesion count was performed in a previous study (Daams et al., 2014) based on a separate cervical 2D PD/T2-weighted image (TR/TE = 6200/21–84 ms, resolution 0.57 × 0.57 × 4.0 mm) covering the entire cervical cord.

2.3. MR image analysis

2.3.1. Preprocessing

To correct for gradient nonlinearity effects on the MUCCA measurement (Papinutto et al., 2018), all images from dataset A were corrected with 3D distortion correction available on each scanner, and images from dataset B were corrected off-line using the grad_unwarp software(Jovicich et al., 2006).

All T1-weighted images were bias field corrected using the default options from the segmentation tool FAST from the FSL Toolbox (Zhang et al., 2001).

2.3.1.1. Region selection

In order to perform an objective, unbiased comparison, all methods were evaluated within the same region, which was pre-defined in each subject by selecting a fixed set of contiguous axial slices starting from the most superior point of C1 and ending at a position 30 mm more inferior, where the 30 mm length was measured perpendicular to the axial plane. For Xinapse JIM, this entailed definition of manually selected input points, as described below under “Xinapse JIM”. For all methods, it entailed creating a subselection of the segmentations produced by accepting only the portion of the segmentations that fell within these pre-defined sets of contiguous slices, as described below under “Post-processing”.

2.3.2. Spinal cord segmentation

For the segmentation of the spinal cord, five (semi-)automated methods were used: SCT-PropSeg, SCT-DeepSeg, NeuroQLab, Xinapse JIM, and ITK-SNAP. In addition, a manual segmentation was created for dataset B to obtain a ground truth segmentation. The segmentation methods are summarized below.

2.3.2.1. SCT-PropSeg

SCT-PropSeg (De Leener et al., 2014) is a fully automated spinal cord segmentation method incorporated in the Spinal Cord Toolbox (SCT version 3.0.8) (De Leener et al., 2017). It has a two-step working mechanism. First, spinal cord detection is done by maximizing mutual information of the left and right part of an axial slice and finding the central line. The image is cropped in an area of 5 cm around this medial line, and a Hough transform is applied assuming an approximate guess of the spinal cord radius of 4 mm (default). These steps are then performed on multiple axial slices, after which the results are validated based on the contrast between cerebrospinal fluid and the spinal cord. After spinal cord detection, propagation of the spinal cord segmentation is started and conducted using a mesh deformation model based on maximizing the local contrast gradient (De Leener et al., 2014).

2.3.2.2. SCT-DeepSeg

SCT-DeepSeg is another fully automated spinal cord segmentation method incorporated in the Spinal Cord Toolbox (SCT version 3.1.1) (De Leener et al., 2017) (Gros et al., 2019). It is based on a deep learning convolutional neural network (CNN) module trained to effectively segment the spinal cord from MRI images. The version of the method used in this paper operates in a 2D fashion, treating each slice separately.

2.3.2.3. NeuroQLab

NeuroQLab (MeVisLab, Fraunhofer Mevis, Bremen, Germany) also provides a semi-automated method for cervical cord segmentation (Lukas et al., 2009). For this, the user selects a cuboid ROI manually, after which interactive watershed transformation (IWT) is applied to the image, removing non-CNS matter. IWT results in over-inclusive spinal cord segmentation, therefore fully automated regional histogram analysis is performed to accurately quantify the spinal cord tissue volume. NeuroQLab only provides MUCCA values but does not give voxel wise labeled segmentation files as output, and therefore no overlap measures could be computed for this method (see Section 2.5.3 and 2.6).

2.3.2.4. Xinapse JIM

Xinapse JIM (Xinapse JIM 8.0, 2018) contains (semi-)automated software for spinal cord segmentation based on the 2D active surface contour method (Horsfield et al., 2010). For this, the Cord Finder tool was used with fixed parameters for all datasets (number of shape coefficients: 24; order of longitudinal variation: 10; nominal cord diameter: 8 mm). In this tool, the centerline of the spinal cord is defined semi-automatically, followed by automatic determination of the cord contour on each axial slice. As indicated above (“Region selection”), the cervical cord was segmented in a section of 30 slices (1 mm slice thickness) starting at the top of the C1 vertebra. The mean cervical spinal cord area (CSA) was obtained by dividing the generated cervical cord volume by the section length (30 mm). For further comparison with the other evaluation methods, binary mask images were generated from the segmented cord sections of each individual. For this purpose the segmented cord outlines of each slice were saved as region-of-interest files and converted into binary masks using the Masker-tool provided in the JIM software package.

2.3.2.5. ITK-SNAP

ITK-SNAP is a semi-automated method based on active contour models which can be applied to segment any image, and is not specialized for the spinal cord (ITK-SNAP version 3.6.0) (Yushkevich et al., 2006). For this study, segmentation was based on region competition, which requires user input to provide the intensity window on which this competition should be based. Then, a 3D snake is propagated with a velocity based on the manually selected intensity window. The snake propagation is both initiated and terminated by the user.

2.3.2.6. Manual segmentation

For dataset B, manual outlining was needed to establish a ground truth segmentation, since no scan-rescan images were available. Manual segmentation was performed on the 3D FSPGR images in ITK-SNAP (version 3.6.0) (Yushkevich et al., 2006) by a single rater by in-painting the axial slices on a slice-by-slice basis, resulting in a binary segmentation image. Five scans were segmented twice on two separate occasions to assess intra-rater variability and Dice's similarity index (SI). Manual segmentation was performed from the most superior slice of C1 and continued for 56 slices (30 mm).

2.3.3. Post-processing

All methods resulted in a binary spinal cord segmentation, except for NeuroQLab, which only gives MUCCA measurements as output. The output image of each of the other methods were post-processed as follows: for each segmentation, a mask was manually created to select a subset of the axial slicesstarting from the most superior point of C1 and ending at a position 30 mm more inferior For dataset A 31 axial (reformatted) slices with a 1.0 mm slice thickness were selected and for dataset B 56 axial (reformatted) slices with a 0.55 mm slice thickness, thereby covering the cervical cord from section C1 up to section C2, depending on the subject's orientation in the coil (Panjabi et al., 1991). This mask was applied to the full binary segmentations in order to obtain a segmentation image of the relevant area in the upper cervical cord and to ensure a direct comparison between the different segmentation methods All subsequent data-analysis was performed on these post-processed segmentation images.

2.4. MUCCA

The “SCT Process Segmentation” routine included in the SCT Toolbox (De Leener et al., 2017) was used to obtain actual values for MUCCA for all segmentations. The post-processed segmentation images from all methods (except NeuroQLab) were used as input, from which SCT Process Segmentation calculates the total spinal cord area perpendicular to the centerline for each slice, and then averages this over the length of the section to obtain MUCCA. In this way, the orientation of the cord with respect to the slices is taken into account when calculating MUCCA, thereby diminishing the effects of both slice orientation and cord curvature on MUCCA values.

2.5. Dataset A: reproducibility and robustness

2.5.1. Reproducibility: within-scanner intra-class correlation coefficient (ICC)

To evaluate the reproducibility of the various spinal cord segmentation methods, we calculated the within-scanner ICCs for absolute agreement (ICC_abs) with their 95% confidence intervals between the scan and rescan images. Furthermore, we calculated the coefficient of variation (COV) as the ratio of the standard deviation of within-scanner differences to the mean MUCCA (scan and rescan) as a measure of dispersion.

2.5.2. Robustness: between-scanner intra-class correlation coefficient (ICC)

To evaluate the robustness of the various spinal cord segmentation methods, we calculated the between-scanner ICCs for absolute agreement and consistency (ICC_con) with their 95% confidence interval. For the between-scanner ICCs, only the images of the first scan session were used.

2.5.3. Voxel wise agreement: Dice's similarity index (SI)

Rescan images were linearly registered to the scan images using default FSL FLIRT with an affine transformation (12 parameters), correlation ratio cost function, and tri-linear interpolation followed by a threshold of 0.5 (Jenkinson et al., 2002; Jenkinson and Smith, 2001), after which fslmaths and fslstats were used to calculate Dice's similarity index (SI) between scan and rescan segmentations.

2.6. Dataset B: effect of lesions

Intra-rater variability of the manual segmentations was assessed by calculating SI and COV. Next, MUCCA was measured as described above and ICCs for absolute agreement and consistency were calculated between MUCCA values from manual segmentations and each of the (semi-)automated methods. Furthermore, SI was calculated between the manual and automated segmentations using the same pipeline described above.

2.7. Statistical analyses

Statistical analysis was performed in IBM SPSS Statistics for Windows, version 22.0 (IBM Corp., Armonk, N.Y., USA). All parameters were tested for normality with a Shapiro-Wilk test.

In dataset A, repeated measures ANOVA (parametric data) and Friedman Test (non-parametric data) were used for MUCCA per scan session, segmentation method, MR machine and subject group (HC vs MS); and for SI per segmentation method, MR machine and subject group.

In dataset B, repeated measures ANOVA (parametric data) and Friedman Test (non-parametric data) were used for MUCCA per segmentation method and subject group (with or without lesions); and for SI per segmentation method, MR machine and subject group.

For the repeated measures ANOVA, Mauchly's test of sphericity was performed to assess equal variances of the differences between all within-subject factors. When the assumption of sphericity was violated, degrees of freedom were corrected using Huyn-Feldt estimates of sphericity.

When appropriate, post-hoc analyses were conducted using Mann-Whitney U tests (unpaired) or Wilcoxon Signed Ranks tests (paired) for single effects, and Bonferroni correction for interaction effects. Inter quartile range was determined by the 25th and 75th percentile. Results were considered statistically significant upon p-value < 0.05.

3. Results

3.1. Dataset A: reproducibility and robustness

3.1.1. MUCCA across scan sessions, MR machines, and methods

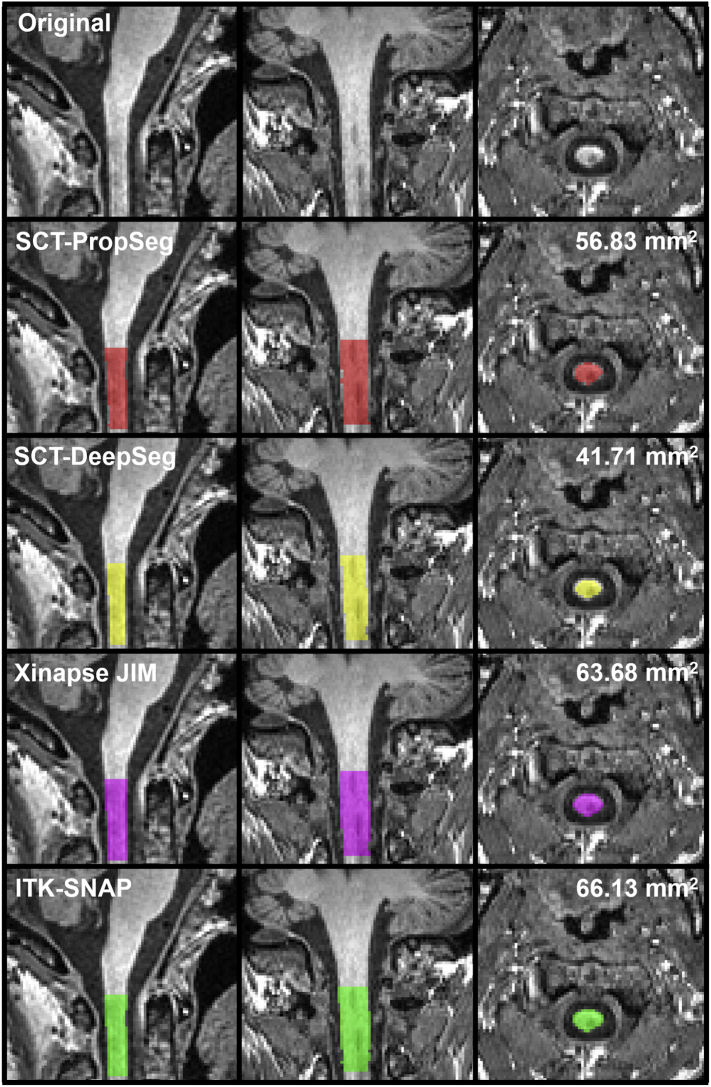
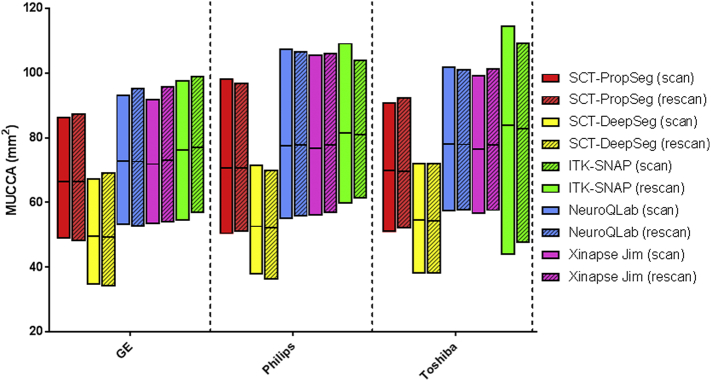
An example of the various spinal cord segmentation methods is shown in Fig. 1. The segmented MUCCA is depicted in mm², showing great differences between the methods in this particular example subject (NB. images from a patient at the first scan session on the GE MR machine). Fig. 2 and Supplementary Table 1 show the mean MUCCA values obtained in all subjects, separated by scan session, MR machine and upper cervical cord segmentation method. Here, mean MUCCA also clearly varied between methods and between MR machine (e.g. mean MUCCA in GE varied depending on the method from 49.50 to 73.31 mm²; and mean MUCCA in SCT-PropSeg varied depending on the MR machine from 66.49 to 70.55 mm²), as shown by the repeated measures ANOVA for MUCCA that found a significant interaction between MR machine and method (F(8,200) = 3.804, p = 0.025). As expected, no effect of scan session was found (F(1,25) = 0.972, p = 0.334), indicating that scan and rescan MUCCA values did not differ systematically. There was no significant effect of subject group (F(1,25) = 2.756, p = 0.109).

Fig. 1.

Example of the spinal cord segmentation methods; scans obtained from a 52 year old female with RRMS in the first scan session on the GE machine. In this particular case, MUCCA differs between the methods from 41.71 mm² obtained from SCT-DeepSeg (yellow) to 66.13 mm² obtained from ITK-SNAP (green). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 2.

Interleaved low-high floating bar plot (line at mean) of MUCCA (mm²) from all subjects (i.e. HC and MS grouped) per MR machine (GE [left], Philips [middle], Toshiba [right]), per segmentation method (SCT-PropSeg [red], SCT-DeepSeg [yellow], NeuroQLab [blue], Xinapse JIM [pink] and ITK-SNAP [green]) and per scan session (scan [clear], rescan [striped]). Pairwise differences can be seen between segmentation methods and between MR machines, but not between scan sessions. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Because of the interaction effect of MR machine and method, a post-hoc analysis was performed separately for the effect of MR machine per method and the effect of method per MR machine. For all methods, MUCCA differed between GE and Philips (all p ≤ 0.001) and between GE and Toshiba (all p ≤ 0.001). However, between Philips and Toshiba images, only SCT-DeepSeg MUCCA were different (p < 0.001), but not MUCCA obtained from the other methods.

All pairwise MUCCA differences between methods were significant for all MR machines (all p ≤ 0.014), except for the comparison between NeuroQLab and Xinapse JIM MUCCA for Philips and for Toshiba.

3.1.2. Reproducibility and robustness: ICC and COV

The within-scanner agreement (i.e. reproducibility) assessed by means of the ICC_abs and COV, and the between-scanner agreement (i.e. robustness) assessed by means of the ICC_con, are shown per segmentation method and per MR machine in Table 1. In general, within-scanner agreement was high (ICC_abs ≥ 0.904 and COV ≤ 5.03%) with the most reproducible results obtained in Toshiba images with NeuroQLab segmentations (ICC_abs = 0.996 and COV = 0.97%) and Xinapse JIM segmentations (ICC_abs = 0.996 and COV = 0.88%).

Table 1.

Reproducibility (i.e. within-scanner agreement) and robustness (i.e. between-scanner agreement) of the different MR machines and different methods.

		SCT-PropSeg	SCT-DeepSeg	NeuroQLab	Xinapse JIM	ITK-SNAP
a. Within-scanner agreement
GE	ICCabs (95% CI)	0.994 (0.986–0.997)	0.994 (0.987–0.997)	0.995 (0.989–0.998)	0.995 (0.989–0.998)	0.954 (0.903–0.979)
	COV	1.20	1.38	1.06	1.00	3.28
Philips	ICCabs (95% CI)	0.995 (0.989–0.998)	0.988 (0.973–0.994)	0.983 (0.963–0.992)	0.995 (0.988–0.998)	0.919 (0.831–0.962)
	COV	1.10	1.86	2.03	1.11	4.35
Toshiba	ICCabs (95% CI)	0.994 (0.988–0.997)	0.990 (0.978–0.995)	0.996 (0.991–0.998)	0.996 (0.992–0.998)	0.904 (0.803–0.955)
	COV	1.15	1.64	0.97	0.88	5.03
b. Between-scanner agreement
GE vs Philips	ICCcon (95% CI)	0.970 (0.934–0.986)	0.985 (0.967–0.993)	0.971 (0.938–0.987)	0.978 (0.951–0.990)	0.905 (0.804–0.956)
GE vs Toshiba	ICCcon (95% CI)	0.983 (0.964–0.992)	0.977 (0.950–0.989)	0.980 (0.956–0.991)	0.982 (0.962–0.992)	0.882 (0.758–0.944)
Philips vs Toshiba	ICCcon (95% CI)	0.982 (0.961–0.992)	0.976 (0.948–0.989)	0.984 (0.966–0.993)	0.982 (0.961–0.992)	0.827 (0.657–0.917)

Abbreviations: ICC_abs = intraclass correlation coefficient, within-scanner absolute agreement; COV = coefficient of variance; ICC_con = intraclass correlation coefficient, between-scanner consistency; CI = confidence interval.

Between-scanner agreement was highest between Philips and Toshiba images (ICC_con range from 0.827 and 0.984). The most robust segmentation method was Xinapse JIM (ICC_con range from 0.978 to 0.982). However, the most robust results were obtained in SCT-PropSeg segmentations between GE and Philips images (ICC_con = 0.985).

3.1.3. Anatomical reproducibility: Dice's similarity index

The anatomical reproducibility of the segmentation methods, assessed as Dice's similarity index (SI) between segmentations from scan and rescan images, is shown in Table 2. Since NeuroQLab does not provide segmentation images but solely gives MUCCA values as output, no overlap between scan and rescan could be calculated for this method. SI was generally high, with median SI in all cases above 0.910, but varied significantly between methods (Friedman Test: χ²(3) = 87.504, p < 0.001). SI did not vary systematically with MR machine (χ²(2) = 1.352, p = 0.509) or subject group (Mann Whitney U test p ≥ 0.405). Post-hoc analysis showed differences between all combinations of methods (all p ≤ 0.001), except between SCT-PropSeg and Xinapse JIM.

Table 2.

Dice's similarity index between scan and rescan images for the three MR machines and four segmentation methods.

Dice's similarity index	SCT-PropSeg	SCT-DeepSeg	Xinapse JIM	ITK-SNAP
GE	0.927 (0.909–0.946)	0.910 (0.894–0.928)	0.928 (0.906–0.941)	0.925 (0.898–0.937)
Philips	0.923 (0.900–0.944)	0.911 (0.891–0.939)	0.921 (0.898–0.943)	0.916 (0.891–0.939)
Toshiba	0.922 (0.901–0.939)	0.922 (0.894–0.923)	0.929 (0.905–0.939)	0.920 (0.897–0.931)

SI listed as median with interquartile range (Q1-Q3); because NeuroQLab does not provide segmentation images, no SI could be calculated for NeuroQLab.

3.2. Dataset B: effect of lesions

3.2.1. Lesions found in C1-C2 region

In dataset B, we compared subjects with and without lesions in the spinal cord, based on the study from Daams et al. (2014). Since we measure MUCCA only at C1-C2 level, we checked the subjects that were selected in the lesions group for the actual presence of lesions at the C1-C2 level, i.e. in our spinal cord mask. Per subject, at least 3 lesions were found in our region of interest with a median of 5 lesions per subject (Q1-Q3: 3.75–5.50 lesions).

3.2.2. Manual segmentations

Quality of the manual segmentations was assessed through intra-rater reproducibility in five cases that were performed twice in dataset B, which showed high intra-rater agreement with a mean SI of 0.966 ± 0.005 (range 0.957–0.971) and an overall COV of 3.65%.

3.2.3. MUCCA across lesion groups and methods

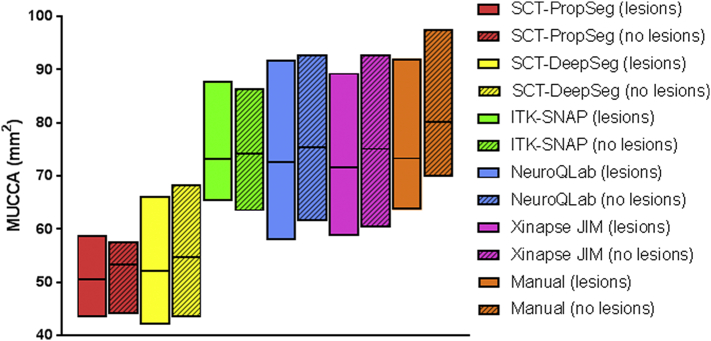
Mean MUCCA values by lesion group and by method are provided in Fig. 3 and Supplementary Table 2. No effect of lesion group on MUCCA was found (F(1,19) = 0.925, p = 0.348), which is consistent with the matching of groups on previously determined MUCCA values as per the study design.

Fig. 3.

Interleaved low-high floating bar plot (line at mean) showing MUCCA (mm²) in subjects with with lesions (clear) and without lesions (striped) per segmentation method (SCT-PropSeg [red], SCT-DeepSeg [yellow], NeuroQLab [blue], Xinapse JIM [pink], ITK-SNAP [green] and Manual [orange]). Differences can be seen between segmentation methods. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Mean MUCCA varied between methods in both lesion groups, e.g. ranging from 53.36 ± 4.51 mm² in SCT-PropSeg to 80.23 ± 9.39 mm² in manual segmentations in the no lesions group. The effect of method on MUCCA was significant (repeated measures ANOVA F(5,95) = 260.036, p < 0.001). Post-hoc analysis showed that these differences between methods were present for almost all pairwise comparisons (p ≤ 0.022). Methods that did not show significant different MUCCA values from one another were: (a) SCT-PropSeg versus SCT-DeepSeg; (b) NeuroQLab versus manual or Xinapse JIM; (c) ITK-SNAP versus manual or NeuroQLab or Xinapse JIM.

3.2.4. Volumetric agreement: ICC

Table 3 shows the volumetric agreement assessed by ICC with manual MUCCA per segmentation method and per lesion group. The differences between manual and some automated MUCCA measurements reported above (Fig. 3) are reflected by low values for ICC_abs, e.g. 0.075 (SCT-PropSeg, group without lesions) or 0.184 (SCT-DeepSeg, group with lesions). Compared to manual, the best volumetric agreement was obtained by NeuroQLab in the group with lesions (ICC_abs = 0.846), and by Xinapse JIM in the group without lesions (ICC_abs = 0.940). ICC_con values for the automated methods versus manual MUCCA were generally higher and all >0.57.

Table 3.

Volumetric agreement of the different methods with manual MUCCA per lesion group.

Within-scanner agreement		SCT-PropSeg	SCT-DeepSeg	NeuroQLab	Xinapse JIM	ITK-SNAP
Without lesions	ICCabs (95% CI)	0.106 (−0.023–0.427)	0.181 (−0.013–0.582)	0.931 (0.804–0.977)	0.940 (0.774–0.982)	0.883 (0.674–961)
	ICCcon (95% CI)	0.707 (0.304–0.896)	0.894 (0.703–0.965)	0.930 (0.797–0.977)	0.954 (0.863–0.985)	0.876 (0.658–0.958)
With lesions	ICCabs (95% CI)	0.075 (−0.028–0.438)	0.184 (−0.006–0.665)	0.846 (−0.032–0.976)	0.837 (0.031–0.973)	0.577 (−0.089–0.907)
	ICCcon (95% CI)	0.572 (−0.226–0.911)	0.946 (0.720–0.990)	0.947 (0.725–0.991)	0.924 (0.628–0.987)	0.685 (−0.042–0.938)

3.2.5. Voxel wise agreement: SI

The voxel wise agreement compared to manual in the two lesion groups is shown for the different methods in Table 4, showing that mean SI varies between methods and between lesion groups (range: 0.791 to 0.962). SI was generally high, with all SI above 0.79, but varied significantly between methods (Friedman Test: χ²(3) = 51.229, p < 0.001). Post-hoc analysis showed differences between all combinations of methods (all p ≤ 0.033), except between ITK-SNAP and Xinapse JIM. Wilcoxon Signed Ranks test found no effect of lesion group in any of the methods (p ≥ 0.176).

Table 4.

Dice's similarity index between manual and automated segmentation methods in the lesion groups.

Dice's similarity index	SCT-PropSeg	SCT-DeepSeg	Xinapse JIM	ITK-SNAP
Without lesions	0.782 (0.756–0.823)	0.824 (0.789–0.829)	0.956 (0.941–0.968)	0.955 (0.904–0.971)
With lesions	0.818 (0.793–0.833)	0.835 (0.811–0.849)	0.962 (0.959–0.968)	0.959 (0.953–0.964)

SI listed as median with interquartile range (Q1-Q3).

4. Discussion

In this study, we investigated the performance of five (semi-)automated spinal cord segmentation methods to measure MUCCA in brain images by quantifying within-scanner reproducibility, between-scanner robustness, and performance in the presence of cervical cord lesions. Within-scanner volumetric and anatomical reproducibility of MUCCA were high, but MUCCA varied between scanners and segmentation methods. Interestingly, the volumetric and voxel wise agreement of the MUCCA measurements did not differ between subjects with or without upper cervical cord lesions.

Despite our small sample size in dataset A, we found significant differences between MUCCA from the acquisition protocols of GE, Philips and Toshiba. In general, MUCCA measured in GE images was lower than images obtained in Philips and Toshiba images. It is unlikely that spatial resolution had a major influence, since this was slightly different only on Toshiba. We can only speculate that small variability in contrast between spinal cord and surrounding CSF, arising from acquisition differences, especially in timing parameters, could lead to differences in partial volume effects at the border of the spinal cord. Previous research in which acquisition was homogenized between centers still showed low between-scanner agreement (Lukas et al., 2018; Papinutto et al., 2018), supporting our finding that cross-sectional MUCCA cannot be easily compared in multi-center, multi-vendor research. This emphasizes the importance of relative instead of absolute MUCCA comparisons in multi-vendor studies, i.e. with normalized UCCA percent change over time as a measure for upper cervical cord atrophy (Lukas et al., 2015; Valsasina et al., 2015).

Next to differences in MUCCA between MR machines, we also found significant differences in MUCCA between methods. In both dataset A and B, SCT-PropSeg and SCT-DeepSeg segmentations resulted in lower MUCCA than for other methods, which was also shown in an earlier study (Yiannakas et al., 2016). This under estimation may be due to the use of the head and head-neck coil instead of a spine coil, for which the Spinal Cord Toolbox is optimized (De Leener et al., 2014; De Leener et al., 2017). Differences in spinal cord to CSF contrast-to-noise ratio may affect these methods. Previous research did show that MUCCA values obtained with either head or head-neck images are comparable for both NeuroQLab and XinapseJIM (Y. Liu et al., 2016; Z. Liu et al., 2015), but the effect of the coil (head, head-neck, spine) used should be further investigated for the other spinal cord segmentation methods. In addition to these volumetric differences, the amount of manual labor needed differed between methods as well. Dependent on the study type and the amount of data, it is important to take these differences in robustness into account in order to assure equal comparisons between subjects; for example, ITK-SNAP is less suited for larger studies due to the manual labor required, and NeuroQLab may be less suited when segmentation images are preferred in addition to MUCCA values only. In the present study we did not systematically optimize parameters for the automated methods; it is possible that performance of the automated methods could be improved by adjusting parameters for each dataset, which should be investigated further.

With our unique scan-rescan research design, we were able to show high volumetric and voxel wise agreement between scan sessions for all method-scanner combinations, with the exception of NeuroQLab, since it only provides MUCCA output and no segmentation images. This high anatomical reproducibility shows that all methods are robust to changes in cervical cord orientation that occur in a scan/rescan setting, which has not been reported previously. This suggests that MUCCA measurement from head images is suitable for single-patient monitoring in the clinic, as long as subjects are examined on the same MR scanner and MUCCA measurement is performed with the same method, which may lead to more accurate predictions of disability and possible disease course (Biberacher et al., 2015; Hagstrom et al., 2017; Lukas et al., 2013; Rashid et al., 2006).

It would be interesting to study if differences between processing methods project to meaningful sample-size differences in clinical studies. While within-scanner reproducibility was high for each of the cross-sectional methods investigated here, there were some differences in COV (Table 1). It remains to be investigated how this translates to sensitivity of longitudinal MUCCA evaluations. A comparable scan-rescan investigation of both inherently longitudinal and repeated cross-sectional methods in a cohort with long enough follow-up to expect sufficient MUCCA decrease, will allow quantification of the reproducibility of the methods, their sensitivity to MUCCA change, and the required sample sizes in a clinical trial setting with MUCCA change as outcome.

Another point of attention for longitudinal MUCCA measurement is the ROI selection. In this study, since we were interested in the differences between segmentation methods, we pre-selected the upper cervical cord area as a mask, starting from the top of C1 and continuing for 30 mm. Although this fixed length may lead to minor differences between subjects concerning the portion of the cervical cord selected, in the present study this allowed unbiased comparison of segmentation methods. However, to achieve clinical implementation of MUCCA measurement, automated selection of this region is needed in order to ensure MUCCA measurement in equal segments of the cord over time. Future work should therefore further validate methods such as SCT_process_segmentation for the automated selection of the desired cord section, especially in head images, to allow high-throughput (clinical) processing in a more automated fashion.

In subjects with MS, an important question is whether the presence of lesions in the upper cervical cord influences MUCCA measurement performance, since previous studies have found that the brain's grey matter volume may be underestimated in the presence of lesions (Gonzalez-Villa et al., 2017). Extending on previous research, which found that SCT-PropSeg segmentations were not influenced by lesions upon visual inspection (Yiannakas et al., 2016), we observed that the presence of lesions in the upper cervical cord did not affect MUCCA measurement performance, neither on a volumetric (ICC) nor on a voxelwise (SI) level for any of the investigated MUCCA measurement methods. This is an important finding, especially in view of the potential clinical application of MUCCA measurement in MS, as it implies that no additional measures are required and existing software can be applied as is if overall MUCCA is the desired outcome, in contrast to brain MRI. Since no specific analyses of lesion volume, lesion location or T1-weighted lesion intensity was performed here, all of which are known to severely influence brain MRI segmentations, future research for their effect on MUCCA in the different software packages should be performed for more anatomical detailed analysis of cervical cord atrophy in MS.

An important topic of research is how lesions and atrophy of the spinal cord develop in MS and how they are related to each other. Valsasina and colleagues, using Xinapse JIM, did not find a relation between upper cervical cord lesions and MUCCA (Valsasina et al., 2018), but did not investigate whether the presence of cervical cord lesions affected their MUCCA measurement. Our current results show that accurate MUCCA measurement is possible in the presence of cervical cord lesions, for Xinapse JIM as well as for the other methods, thereby reinforcing the finding reported by Valsasina et al. on the independence of the two disease phenomena. In the current study, we could not investigate such disease-related questions directly, because we matched subjects for their previously obtained MUCCA values (Daams et al., 2014). By design, we were therefore unable to answer any disease-related questions about MUCCA or its relation to cervical lesions. Nevertheless this is an interesting topic that warrants further investigation in future research, for which the current study lays the foundation by demonstrating that measurement of MUCCA can be performed without an effect of cervical cord lesions for any of the investigated methods.

In conclusion, the choice of automated spinal cord segmentation method has a large effect on MUCCA measurement, as well as the type of MR machine used. However, all methods show high within-scanner agreement between scan and rescan session, both for volumetric and voxel wise MUCCA measures. Most importantly, performance of the MUCCA software tested was not affected by the presence of upper cervical cord lesions.

Funding

This study is supported by the Dutch MS Research Foundation (grant 14-876 MS); Amsterdam Neuroscience (grant PoC-2014-BIT-3); Novartis Pharma (grant SP037.15/432282); and the German Federal Ministry for Education and Research, BMBF, German Competence Network Multiple Sclerosis KKNMS (grant 01GI1601I and 01GI0914). FB is supported by the NIHR Biomedical Research Centre at UCLH.

Declaration of Competing Interest

None.

Appendix A. Supplementary data

Supplementary material