A mathematical insight into cell labelling experiments for clonal analysis

Abstract

Studying the progression of the proliferative and differentiative patterns of neural stem cells at the individual cell level is crucial to the understanding of cortex development and how the disruption of such patterns can lead to malformations and neurodevelopmental diseases. However, our understanding of the precise lineage progression programme at single‐cell resolution is still incomplete due to the technical variations in lineage‐tracing approaches. One of the key challenges involves developing a robust theoretical framework in which we can integrate experimental observations and introduce correction factors to obtain a reliable and representative description of the temporal modulation of proliferation and differentiation. In order to obtain more conclusive insights, we carry out virtual clonal analysis using mathematical modelling and compare our results against experimental data. Using a dataset obtained with Mosaic Analysis with Double Markers, we illustrate how the theoretical description can be exploited to interpret and reconcile the disparity between virtual and experimental results.

Introduction

The mammalian cerebral cortex is the outer layer of neural tissue in the telencephalon. It is composed of a large variety of cell types (Lodato & Arlotta, 2015; Markram et al. 2015; Mancinelli & Lodato, 2018; Tasic et al. 2018) and shows considerable areal variation depending on the circuit elements required to perform specific computational functions (Goulas et al. 2018). The location and quantity of cortical neurons are determined during embryonic development and are crucial to the emergence of cognitive functions in the adult brain. Understanding cortical development is key to shedding light on both the fundamental mechanisms that give rise to correct brain formation and evolution, and the abnormalities that cause malformations (Clowry et al. 2010; Geschwind & Rakic, 2013; Silbereis et al. 2016; Lein et al. 2017). The successful development of the cortex requires a controlled sequence of cell division events which, starting from an initial pool of neuroepithelial stem cells, results in a diverse pool of specialised neurons (Pfeiffer et al. 2016; Nowakowski et al. 2017). The developmental programme leading to the formation of the cerebral cortex is the result of a complex regulation of cellular processes in space and time, involving a variety of progenitor cell types (Fig. 1).

Figure 1.

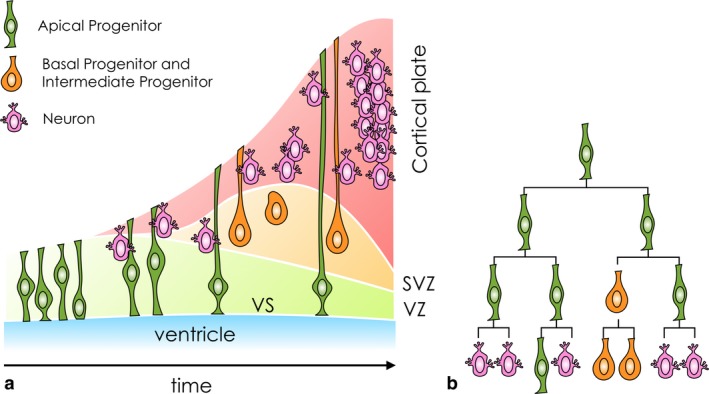
General pattern of development of the cerebral cortex in mammals. (a) The temporal expansion of progenitors populating the proliferative zones (VZ, ventricular zone; SVZ, subventricular zone), and the production and positioning of neurons in the cortical plate. The horizontal axis is a proxy for time. A simplistic categorisation of progenitor cells is based on their position in the proliferative zones. (b) Clonal lineages determine the neuronal and non‐neuronal composition of the cell population, crucial for the correct quantitative and temporal production of cortical neurons.

Observing the unfolding of the developmental programme at the level of an individual progenitor cell gives us a fundamental understanding of the processes involved in progenitor cell division strategies. The recent development of new cell‐labelling techniques allows us to characterise clonal lineages, addressing the need to obtain temporally resolved data. But the clonal analysis techniques currently available have limited ability to extensively track clonal lineages (Garcia‐Moreno et al. 2014), often resulting in contradictory conclusions (Guo et al. 2013; Gil‐Sanz et al. 2015). A variety of labelling techniques have been developed, such as retroviral vectors (Mayer et al. 2015) and Mosaic Analysis with Double Markers (MADM; Ma et al. 2018), but neither of them alone can capture the full spectrum of division types and lineages. There are limitations in the resolution of the data, and difficulties in their interpretation, preventing reliable and testable predictions. The main caveat is that the majority of the currently available lineage‐tracing methods rely on retrospective interpretation. In other words, a stem cell and its lineage is marked at a given developmental time and analysed at the end time point (i.e. after development is complete). Thus, the temporal information is restricted to the start and end points of analysis, and the processes in between are not evident. Moreover, the magnitude of naturally occurring progenitor and neuronal cell death, and its role in the developmental programme, are still the subject of debate (McConnell et al. 2009). The only methodology that allows the creation of entire lineage trees is live imaging in situ during neural progenitor proliferation. However, accessibility to the developing brain is limited to a relatively short period of observation, and even with live imaging over extended periods the lineage trees obtained are not complete (Noctor et al. 2004; Wang et al. 2011; Betizeau et al. 2013). To trust our understanding of the cell‐based division strategies during neurogenesis, we need a theoretical framework that can reliably model, test and interpret the results of clonal analysis studies.

In the following we will present a theoretical framework, based on a stochastic birth–death process, which can be calibrated with data obtained from clonal analysis experiments, and consequently used to interpret the dynamics of cell division and cell cycle exit events in the developing cortex.

The exact rate and proportions of naturally occurring progenitor and post‐mitotic neuronal death are not known. Some studies suggest low, others, large‐scale cell death during cortical neurogenesis (McConnell et al. 2009). Here we model cell death without a priori assumptions on its magnitude. The only restriction we include involving the birth and death rates is that they cannot be the same. Indeed, we find that the greater the difference between these values, the easier it becomes to predict their values. Although this restriction is simply for mathematical convenience, it does not cause a loss of generality from the biological point of view, as (as discussed in the following) the parameter region in which these rates are close to each other is not biologically realistic. One of the key results of the model, parameterised on our dataset, is that a small rate of ongoing cell death is expected throughout the neurogenic process.

We will use a dataset obtained through MADM (Hippenmeyer et al. 2010). MADM is a technique specifically developed for mouse models, allowing incorporation of two distinct labels (red and green) in the two subclones resulting from the first round of division of the injected progenitor cell. To broaden the scope of this framework, we aim to reconstruct any individual clonal lineage, considering each MADM subclone of this dataset individually. In doing so, we will develop a method that can be applied to datasets obtained with any equivalent labelling technique. Hence, unless we are specifically referring to the MADM dataset (consisting of pairs of subclones), in the following we will refer generically to any group of labelled cells as a clone.

Virtual clonal analysis assays will replicate the tracking methods of the MADM technique over realisations of the stochastic birth–death process. From many repetitions of the in silico clonal analysis (with known parameters, chosen arbitrarily), we can test that the theoretical model accurately captures clonal distributions. The theoretical description can then be used to gain an insight into the clonal distributions experimentally obtained, guiding the biological study towards a conclusive characterisation of the processes occurring during cortical neurogenesis.

Materials and methods

The MADM dataset

MADM is a unique lineage‐tracing tool. In a MADM event two fluorescent markers are reconstituted in a dividing stem cell and transmitted to the two daughter cells. The markers are stable and are transmitted along the entire subclone (Hippenmeyer et al. 2010; Ma et al. 2018). Because the MADM labelling can be induced at any given time, this experimental paradigm provides exact information on birth dates of clones and their division patterns. For this study we focused on interval sampling and compiled a set of MADM clones across different time points during cortical development. Hence, the dataset consists of the sizes of the green and red subclones, quantified at analysis time, t _A, following the initial injection at t ₀ (Data S1; Fig. S1). The dataset includes a sparse combination of 16 experimental setups, defined by different injection and analysis times, over the neurogenic window E10–E17 (Fig. 2).

Figure 2.

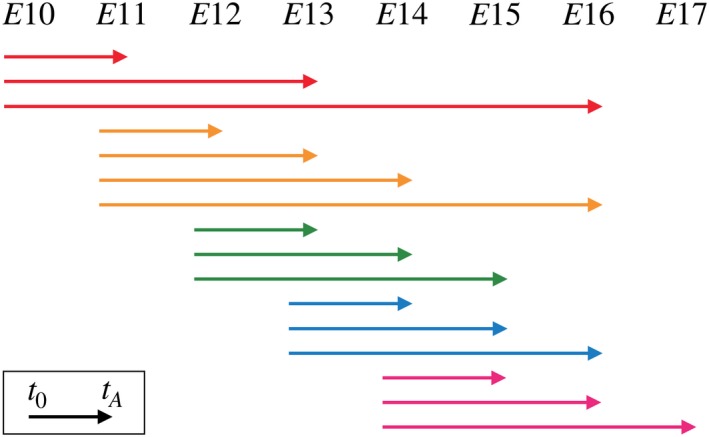
Experimental setups of the Mosaic Analysis with Double Markers (MADM) dataset include intervals defined by injection and analysis time, t ₀ and t _A, respectively, over the mouse neurogenic window E10–E17. The MADM labelling is induced at t ₀ and the sizes of subclones are quantified at t _A. For a representation of the entire dataset, see Fig. S1.

For each experimental setup, a varied number of replicates is produced. The approach used is the same as described in previous publications by the experimental group (Gao et al. 2014; Beattie et al. 2017), and an illustrative outcome is pictured in Fig. 3.

Figure 3.

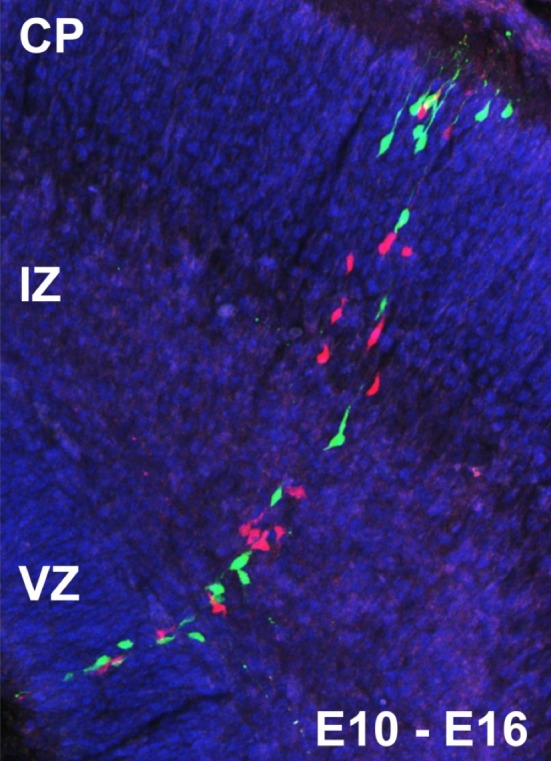
A single Mosaic Analysis with Double Markers (MADM) clone in vivo in the developing cortex with tamoxifen‐mediated induction at E10 and analysis at E16. A G2‐X event (see Hippenmeyer et al. 2010 for an illustration of the MADM principle) results in two columns of green and red labelled cells. Neurons migrate along the processes of radial glia progenitor cells from the ventricular zone (VZ), through the intermediate zone (IZ), toward their final position in the developing cortical plate (CP). Figure reused from Hippenmeyer et al. (2010) with permission.

We aim to reconstruct each individual subclone, i.e. given a subclone of size N, for injection time t ₀ and analysis time t _A, we aim to describe the cell division and cell death events that lead to the outcome N. We adopt a binary tree representation, where the N labelled cells correspond to the tree leaves, and the first cell to incorporate the (green or red) label corresponds to the tree root.

Note that because of the nature of the assay with short sampling windows, we cannot infer birth time of an individual cell. Hence, without information about its location and cell cycle progression, a fluorescent cell present at time t _A could be a progenitor captured during ongoing cell cycling, or a post‐mitotic neuron produced at t < t _A, having permanently exited the cell cycle. Therefore, we are going to consider a one‐species branching process, without a distinction between cell types.

By using the experimental paradigm above, we cannot deterministically reconstruct a lineage tree. Even assuming that generations are equally spaced in time, and disregarding cell death, the combinatorial range of binary trees that match a clonal size of N is intractable, especially for larger subclones in the dataset (e.g. N = 180). It can be shown that this range includes all trees of depth l, with $\lceil 1+{\text{log}}_{2}N\rceil \le l\le N$. Note that the issue is exacerbated in the case of experiments of longer duration (affecting the values that l can realistically take). Figure S2 illustrates the combinatorial explosion, showing examples of possible binary trees for small l, and corresponding outcomes N.

Not only are the assumptions that consecutive generations appear at fixed frequency and that no cells die along the way highly unrealistic but, also, by attempting to deterministically reconstruct lineage trees, we are disregarding the evolving and stochastic nature of the developmental programme followed by individual progenitor cells at different stages of the neurogenic window (Noctor et al. 2004; Taverna et al. 2014). In fact, previous MADM‐based lineage‐tracing experiments indicate that while the overall dynamics of the total population unfolds in a predictable manner, the behaviour of the individual progenitors appears to be stochastic (Gao et al. 2014). In the following we are going to present a stochastic mathematical description of clonal lineages, which does not rely on the assumption of fixed cell cycling time, and allows for cell death.

The continuous time birth–death branching process

Using the tree representation of clones allows us to repurpose work used in phylogeny (Nee et al. 1994) to reconstruct lineage trees as the outcome of random branching processes (cell division, or species differentiation) and trimming processes (cell death, or species extinction). We define a time coordinate t starting at the root of the tree (injection time, t₀) and ending at the present time (analysis time, t_A); hence, t ₀ ≤ t ≤ t _A. The tree is characterised by a birth rate, λ, and a death rate, μ. For a set t ₀, we define N as a random variable, representing the number of branches extant at time t _A. Its probability density function is:

$$\mathbb{P}(N=n)=\left\{\begin{array}{cc}1-P_{(t_0,t_A)},\hfill & n=0\hfill \\ P_{(t_0,t_{\mathrm{A}})}\left(1-u_{(t_0,t_{\mathrm{A}})}\right)u_{(t_0,t_{\mathrm{A}})}^{n-1},\hfill & n>0\hfill \end{array}\right.,$$ (1)

where $P_{(t_0,t_{\mathrm{A}})}$ is the probability that a tree starting at time t ₀ has not gone extinct at time t _A, and $u_{(t_0,t_{\mathrm{A}})}$ is the probability of speciation. These two quantities are defined in terms of the birth and death rates of the branching process:

$$P_{(t_0,t_{\mathrm{a}})}=\frac{\mathrm{\lambda }-\mathrm{\mu }}{\mathrm{\lambda }-\mathrm{\mu }{e}^{-(\mathrm{\lambda }-\mathrm{\mu })(t_{\mathrm{A}}-t_0)}};u_{(t_0,t_{\mathrm{A}})}=\frac{1-e^{-(\mathrm{\lambda }-\mathrm{\mu })(t_{\mathrm{A}}-t_0)}}{1-\frac{\mathrm{\mu }}{\mathrm{\lambda }}{e}^{-(\mathrm{\lambda }-\mathrm{\mu })(t_{\mathrm{A}}-t_0)}}.$$ (2)

Hence, for non‐extinct clones, N follows a geometric distribution. For more details on the derivation of Eqs (1) and (2), see Nee et al. (1994). Note that in the case of our MADM dataset, t ₀ is some time later than the injection time, and corresponds to the time of appearance of the first cell inheriting one of the two labels (red or green). This adjustment will be discussed later.

Results

Simulated clonal lineages and virtual clonal analysis

In order to assess the validity of the theoretical representation introduced, we will create an in silico dataset based on known values of λ and μ, and test its distribution against the theory (Eq. (1)). We will then simulate the results of a clonal analysis technique on a portion of the dataset, aiming to recover the known values of λ and μ.

We implement a Gillespie algorithm (Gillespie, 1977, 2007) for two reaction events:

$$A\stackrel{\mathrm{\lambda }}{⟶}A+A;A\stackrel{\mathrm{\mu }}{⟶}\mathrm{\varnothing }$$ (P1)

where A represents a cell (tree branch) that can undergo a mitotic event or die. Figure S3 shows a few realisations of the stochastic process with λ = 1 day⁻¹ and μ = 0.1 day⁻¹ over a 6‐day window of time. It can be appreciated that the further we move from the injection time, the wider the range of values across realisations. Figure 4 shows the clonal sizes attained over 2000 realisations of the stochastic process. Quantifications are obtained for five analysis times, and mimic the clonal analysis carried out experimentally. The distribution of clonal sizes at different analysis times matches the theoretical distribution derived in Eq. (1).

Figure 4.

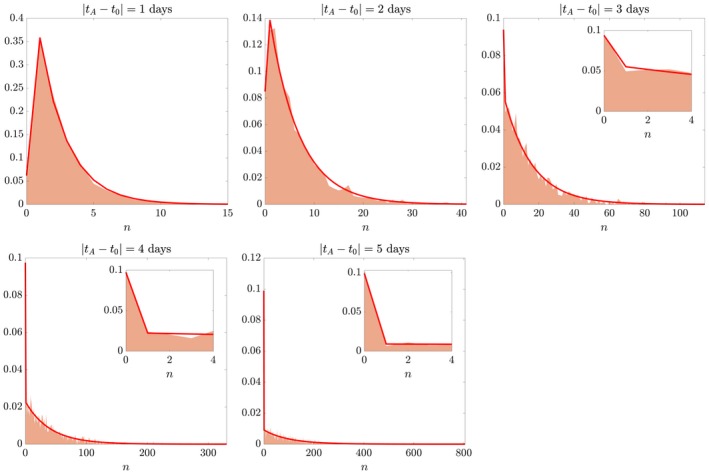
Virtual clonal analysis. Checking theory (solid line) against simulated data (coloured patches) with known parameters λ = 1 day⁻¹ and μ = 0.1 day⁻¹. For ease of visualisation, the distributions of simulated data are plotted as midpoints of bins centred around each clonal size n. Insets show a magnification on the smaller range of clonal sizes n, including the case n = 0 of extinct clones. Vertical axis is probability density.

Having confirmed the validity of the theoretical formulation, we use it to recover the known parameter values λ and μ from a virtual dataset of 10 experiments extracted from the set of 2000 realisations. We implement a least squares search looking for a single point in the (λ, μ) $\mathrm{ϵ}$ [0, 1] × [0, 1] space that minimises the distance between Eq. (1) and the data collected across analysis times. Doing so, we correctly recover the parameter values λ and μ for a virtual clonal analysis of sample size as low as 10 replicates (Fig. 5). In order to exclude the possibility that the correct guess is a result of a lucky choice of parameter values, we studied the accuracy of the least squares search algorithm in the entire parameter space (Fig. S4). We found that the least squares search only leads to incorrect predictions in the region of the (λ, μ) space corresponding to biologically unrealistic values. Indeed, it is sensible, both mathematically and biologically, to expect cell birth rates to be larger than cell death rates. A stochastic birth–death process with λ < μ would result in clones that, on average, tend to extinction according to the solution N(t) &propto; e ^{(−μ + λ)t}. Furthermore, it is worthwhile noting that for λ = μ the geometrical distribution (Eq. (1)) is not meaningful. From a purely biological point of view, although some amount of ongoing cell death is known to trim the population throughout neurogenesis, it would be highly inefficient to sustain proliferation, with cell death killing most of the cells that are born. Current estimates of developmental cell death range between 4 and 10% depending on the experimental setup and the model system (McConnell et al. 2009; Gao et al. 2014). In order to test the validity of the estimation method, we studied convergence of the least squares search for increasingly larger sample size S. Figure S5 shows that the estimation error of the distribution function (Eq. (1)) goes to zero across the parameter space as sample size increases. Figure S6 shows an example of the estimation results for S = 100. Note that for large values of μ it is more likely that the virtual clonal analysis finds only extinct clones. In this case, the clonal distributions are single‐valued, centred around 0 (see histograms in Fig. S6), and the problem is underspecified as two parameters must be recovered from one data point. This further supports the choice to restrict the search to the λ > μ region when applying the estimation routine to real datasets, where extinct‐clones‐only results are extremely rare.

Figure 5.

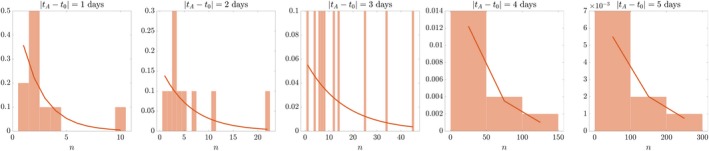
Recovering known values of λ and μ from 10 experiments of virtual clonal analysis with analysis times 1 day apart. The parameter values estimated are: ($\overline{\mathrm{\lambda }}$, $\overline{\mathrm{\mu }}$) = (1, 0.1) day⁻¹, coinciding with the values used to create the in silico clones. The solid line is the theoretical distribution parameterised on the estimated values. Vertical axis is probability density.

Application to the MADM dataset

Having tested the validity of the theoretical representation and its use in the parameterisation of the stochastic process for a virtual clonal analysis dataset, we now apply the framework to the MADM dataset previously described. The application of the developed framework to any experimental dataset requires a careful preprocessing of the data, based on considerations from the use of the in silico data. Hence, in the dataset used here we will:

• exclude experimental setups with too small a sample size: [E11–E12] (six replicates), [E14–E15] (eight replicates), [E14–E17] (four replicates);

• consider each subclone individually, avoiding assumptions on the interdependence of pairs of subclones, and with the added benefit of doubling the sample size;

• group experimental setups by injection times, so that they can be interpreted as observations over different lengths of time of the same stochastic process starting with one cell. Hence, we will obtain an estimate for parameters λ and μ for each injection time;

• restrict the search to (λ, μ) ∈ [0.5, 1] × [0, 0.5] to avoid the possibility that the search algorithm identifies values in a biologically non‐realistic region of the parameter space. This is particularly necessary for noisy or sparse datasets (compare, for example, the E13–E15 experiments, resembling the target distribution, with the E11–E16 experiments, where the fitting algorithm is more likely to fail). A discretisation step of 0.01 is used for both dimensions of the parameter space;

• adjust t ₀ with an estimate of the time taken for the first mitosis to occur. Indeed, the reported injection time in the MADM dataset does not correspond with the appearance of the first cell of the clonal lineage. Therefore, the root of the tree representing the subclone is one of the daughter cells of the injected progenitor. The estimated time to first mitosis is taken from the literature (Takahashi et al. 1996).

The results of the parameterisation are shown in Fig. 6. A temporal evolution of the birth and death rates over different ages is shown in Fig. 6f. The corresponding cell cycle length, T _C, is obtained from the birth rate, and is to be interpreted as the average intermitotic time over the entire process. Note that the predicted values for early ages (E10–E12) fall into the expected range, below 18 h, in agreement with the existing literature (Takahashi et al. 1996). Predictions for later ages overestimate the values in the literature. However, given difficulties in obtaining consistent measures experimentally, at this stage it is not possible to draw conclusions on the validity of such predictions. As discussed later, the discrepancy could be attributed either to the quality and quantity of the data or to the model being inappropriate in capturing regimes at later ages of the neurogenic process.

Figure 6.

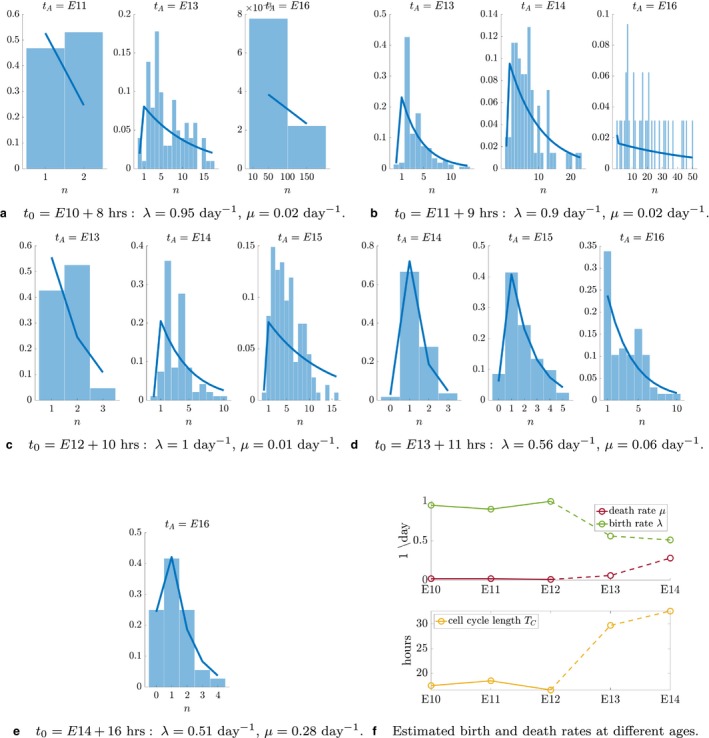
Parameterisation of the stochastic birth–death process using the Mosaic Analysis with Double Markers (MADM) dataset. Values of λ and μ are guessed for each injection time. (a–e) The solid line is the theoretical distribution parameterised on these values. Histograms show the distribution of the experimental data. The error is quantified as the Euclidean distance between the two, i.e. $\Vert {\mathbf{y}}_{(\mathrm{\lambda },\mathrm{\mu })}-{\mathbf{y}}_{\mathrm{data}}{\Vert }_2$, where y is the probability density function described by Eq. (1). (f) Temporal evolution of model parameters and predicted average cell cycle length [calculated as: T _C = log(2)/λ]. The dashed portion of lines indicates predictions that do not match the existing literature and need validation via experimental quantification.

In order to test the predicted parameterised model, we run the stochastic birth–death process with the predicted values of λ and μ, and compare the distribution obtained over 1000 simulations against the MADM dataset. A representative pool of experimental setups is shown in Fig. 7 (full set in Fig. S7). In the E10–E13 window (Fig. 7a), the stochastic process fails to capture the distribution exhibited by the MADM experiments. Specifically, a large portion of the tail of the theoretical distribution cannot be observed in the experimental counterpart. A corresponding overestimation of the density for smaller clonal sizes (0 ≤ n ≤ 20) follows. In the E13–E15 window (Fig. 7b), the discrepancy is more evenly distributed in the density of small clonal sizes (0 ≤ n ≤ 5). However, similarly to the previous case, a considerable portion of the tail of the distribution is missing in the MADM data. Finally, in the E14–E16 window (Fig. 7c), the correspondence between data and theory is considerably more satisfactory.

Figure 7.

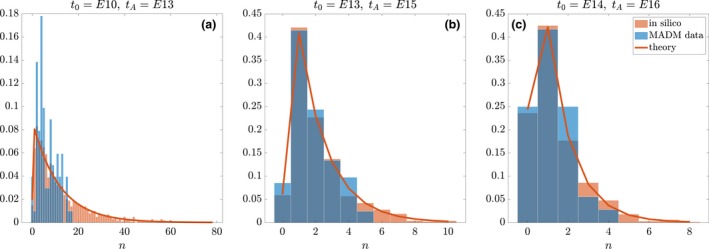
Comparing parameterised stochastic birth–death process (orange histograms) with the Mosaic Analysis with Double Markers (MADM) dataset (blue histograms). The in silico data consist of 1000 realisations. The solid line is the theoretical distribution parameterised on the guessed values (λ, μ) for each injection time. Representative examples of (a) E10–E13, (b) E13–E15 and (c) E14–E16. Vertical axis is probability density.

Understanding the discrepancy between virtual and real clonal analysis outcome

Across all experimental setups the match between the theoretical and experimental distributions varies in a range from misrepresentation of a consistent portion of the larger clonal sizes, to an almost perfect match (see full set of results in Fig. S7). In order to obtain predictive insight into the experimental data, it is crucial that we interpret correctly the discrepancy found. The understanding of such a discrepancy can only be found in either the quality and quantity of the experimental data or the failure of the theoretical model to represent the processes occurring during the production of such lineages. In the first perspective the solution is straightforward: more experimental data must be collected. A larger sample size will likely reveal more rare occurrences of very large clones, ‘filling’ the tail of the theoretical distribution. However, the acquisition of a large dataset is costly and time consuming, and current ethical guidelines discourage the unjustified increase in the number of replicates in any one experimental setup.

We therefore focus on the second perspective, i.e. to theoretically understand the reason for the mismatch, so as to offer possible correction criteria for the interpretation of the experimental data. This interpretation is based on the assumption that the dataset is representative of the stochastic variability of the neurogenic process. In other words, we assume that the acquisition of more data would not change the support (that is, the range of bin sizes) of the experimental distribution, but only smooth its profile. Under this assumption the tail of the distribution can only be attributed to the overestimation of the proliferative potential of the initial progenitor cell. As previously mentioned, the model does not distinguish between states of differentiation of cells. Indeed, a one‐species stochastic process was chosen as the best descriptor of an experimental setup unable to discriminate between progenitors and neurons. An intrinsic problem of this theoretical representation is that it cannot capture the correct proportion of cells exiting the cell cycle in the neurogenic window. As a result, the model parameterisation overestimates the number of cells that re‐enter the cell cycle, hence allowing for larger clones to be produced in the in silico lineages. This can be tested by introducing a simple extension to the stochastic process, which considers two types of cells: B, a cycling cell; and C, a post‐mitotic cell that has exited the cell cycle. Three reaction events and corresponding rates are then defined as follows:

$$B\stackrel{{\mathrm{\lambda }}_1}{⟶}B+B;B\stackrel{{\mathrm{\lambda }}_2}{⟶}B+C;B\stackrel{\mathrm{\mu }}{⟶}\mathrm{\varnothing }.$$ (P2)

The first reaction corresponds to symmetric self‐renewal, the second to asymmetric division, the third to cell death. We maintain that the experimental setup is unable to discriminate between cell types; hence, virtual clonal analysis can only quantify the clonal size (B + C). In the particular case λ ₁ = λ, λ ₂ = 0, this process is identical to Eq. P1 (Fig. S8). For λ ₁ + λ ₂ = λ, this process is equivalent (hence comparable) to the previous one, as the frequencies of birth and death are the same. Figure 8 shows that the distribution obtained by Eq. P2 displays a mismatch around the tail of the distribution qualitatively consistent with the one observed in the MADM data (Fig. 7).

Figure 8.

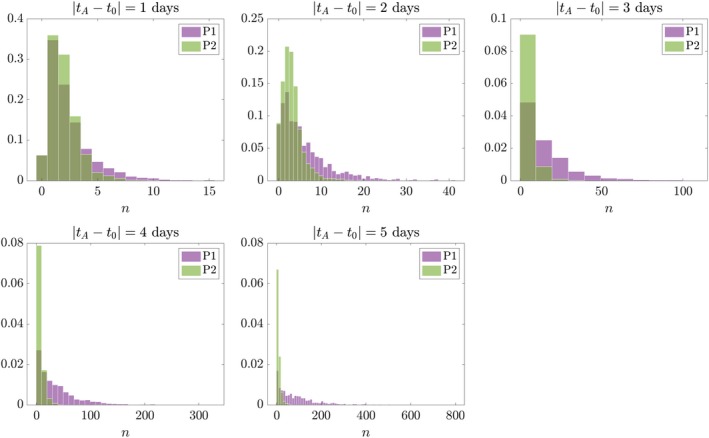
Example of two processes with a mismatch in the outcome found between virtual and real clonal analysis outputs. One‐species process (P1) with λ = 1 day⁻¹, μ = 0.1 day⁻¹; and two‐species process (P2) with λ ₁ = 0.3 day⁻¹, λ ₂ = 0.7 day⁻¹, μ = 0.1 day⁻¹. Histograms show distributions of A cells and B + C cells, respectively. Vertical axis is probability density.

An interesting extension of this work will be to identify and quantify the tails. This metric would serve as an indication of the discrepancy between two distributions, eventually allowing the experimentalist to relate a given mismatch between in silico and experimental data to the prevalence of different division modes. This extension is out of the scope of this paper and will be discussed in future publications.

Discussion

We chose a one‐species stochastic birth–death process in an attempt to mathematically model the neurogenic processes of cell differentiation in the cerebral cortex.

In terms of modelling scale, we developed the theory around the experimental design, focussing on single‐cell‐level dynamics. Population‐level models are well suited to capture large‐scale variations between cortices in different species (Picco et al. 2018), or to quantify differences between mutant and wild‐type cortices (Hsu et al. 2015). These models allow us to capture the variety of cell cycle exit dynamics, but are inappropriate to describe clonal lineage experiments focussed on individual cell dynamics that are stochastic by nature.

Additionally, because the clonal analysis techniques currently available have limited ability to infer the composition of a subclone in terms of progenitor and neuronal cell types, a more refined model would include too many free parameters that cannot be resolved with the resolution of the data currently available. A drawback of considering a one‐species branching process is that we cannot accurately identify modes of cell division resulting in a given clonal size. However, we circumvented this by aggregating data obtained from varied experimental setups. Specifically, if the experimental window is too short we cannot capture the amplification potential of progenitors (e.g. given more time the tagged cell could be a progenitor that would have gone on to self‐amplify further). Too long an experimental window, however, increases the uncertainty of a given outcome to be associated with a pair of λ, μ values. In fact, there are a range of events that could have led to the same outcome (see argument on combinatorial explosion as the tree length increases). By fitting the model at once to all data obtained from experiments with the same injection time and varied analysis times, we integrated the temporal information gathered by experimental setups that observe overlapping time windows. The parameterisation will therefore implicitly pick up on the post‐mitotic composition at a given age, which justifies clonal distributions at later ages.

The resolution of the data currently available is a crucial limiting factor, and the field is now increasing its efforts in this direction, in order to address key questions related to the heterogeneity of the cerebral cortical progenitor population. This heterogeneity can be only appreciated if a large population is followed, or specifically selected for, using genetic tools (Llorca et al. 2018) or following transcriptomic differences of progenitor populations (Pollen et al. 2014). Some radial glial progenitors that can be selected with Fezf2 and Sox9 generate most groups of excitatory neurons in an inside‐out temporal sequence (Guo et al. 2013; Kaplan et al. 2017). Selecting progenitors with Cux2 or Emx2 promoters revealed lineage‐restricted progenitors that mostly contribute to upper cortical layers with callosal projections (Franco et al. 2012; Garcia‐Moreno & Molnar, 2015; Gil‐Sanz et al. 2015). These progenitors lack neurogenic potential during early neocortical development. After self‐renewing and transit‐amplifying mitoses, these radial glial progenitors exclusively give rise to callosal upper‐layer neurons and glia.

In the future the method we propose could be used with datasets equivalent to the one used here, or expanded to newly available and better resolved ones. Some careful considerations along the line of the ones discussed for the MADM technique are, however, necessary. This framework should not be applied to data where there is an indication that the dynamics could fall around the region of λ ≈ μ. Indeed, if frequencies of birth and death are comparable, then the theory would not be able to attribute a specific regime to the dynamics observed. Additionally, it is crucial that each new dataset is carefully curated before it is fed to the fitting algorithm. If a clonal distribution does not qualitatively resemble the target geometric distribution, then one should ask the question why and understand what can cause the shift of the dataset to a given distribution shape. We showed an example of such an approach by considering the modified process (Eq. P2), which resembles the same mismatch with respect to Eq. P1 found in some experimental setups of the MADM dataset.

Finally, predicted rates of birth and death at late ages (Fig. 6) need further experimental investigation. Both cortical progenitors (McConnell et al. 2009) and post‐mitotic neurons are removed during early cortical development through cell death, but the exact proportions are still subject to debate. The lack of quantification of cell cycle length is also a crucial setback in the field of cortical neurogenesis. As we pointed out in a previous study (Picco & Woolley, 2018), this leaves many open questions due to the impossibility of validating theoretical predictions.

Conclusion

We proposed a theoretical representation of the cell division and cell death processes operating during the neurogenic window in cerebral cortex development. While the overall neurogenesis process is a coordinated one with a clear temporal instructive component, there are a number of stochastic elements that need to be considered. These elements may act differentially at distinct stages, i.e. during symmetric expansive divisions vs. asymmetric neurogenic vs. intermediate progenitor‐mediated division, but in their entity lead to sequential neurogenesis. We found that key limitations to our understanding of the developmental programme are the lack of characterisation of cell cycle dynamics, and the lack of identification of cell types in lineages. Characterising the temporal and stochastic modulation of cell cycle dynamics is crucial to the understanding of correct and abnormal development, and recently led to the refinement of experimental techniques for clonal analysis. Studying the mismatch between theoretical and experimental distributions, we have touched upon a crucial question in the field and showed how the integration of mathematical and experimental models can address such open questions. Radial glia progenitors might be very heterogeneous. Some can have considerable lineage restrictions, while others contribute to most cortical layers. The idea that some progenitors only contribute to upper layers at later stages of neurogenesis is still highly debated, although there is some evidence for this notion (Franco et al. 2012; Garcia‐Moreno & Molnar, 2015; Gil‐Sanz et al. 2015; Llorca et al. 2018). At the moment, the theory is limited by the resolution and type of experimental data available. The high degree of stochasticity found in cortical progenitor behaviour at E12 (Llorca et al. 2018) results in a wide range of lineages, and reveals the importance of characterising the temporal evolution of dynamics in the entire neurogenic window. The model proposed here, parameterised on a dataset obtained on several experimental windows, integrates the temporal information to justify clonal distributions at different ages. With this study we introduced a theoretical model that can produce experimentally testable predictions and suggest a key biological direction. We propose that future investigations be theoretically guided, to avoid potentially unnecessary increase of sample sizes in the experimental design, while using the modelling insight to interpret the results of clonal analysis studies.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

Fig. S1 Subclonal distributions for all experimental windows in the MADM dataset.

Fig. S2 Full set of binary trees of depths l = 2, 3, 4 and corresponding clonal size N.

Fig. S3 100 realisations of the Gillespie algorithm for the stochastic one‐species birth–death process (P1) with λ = 1 day⁻¹ and μ = 0.1 day⁻¹.

Fig. S4 Testing the ‘recovery ability’ of the least squares search algorithm.

Fig. S5 Testing the convergence of the estimate method for increased sample size S.

Fig. S6 Recovering known values of λ and μ from S = 100 experiments of virtual clonal analysis with analysis times 1 day apart (t _A = {1, 2, …, 6} days).

Fig. S7 Comparing parameterised stochastic birth–death process (orange histograms) with the MADM dataset (blue histograms).

Fig. S8 Equivalence of stochastic processes P1 and P2. One‐species process (P1) and two‐species process (P2) are identical when λ ₁ = λ and λ ₂ = 0.

Data S1 Dataset obtained through Mosaic Analysis with Double Markers, reporting sizes of subclones for 16 experimental windows (Fig. 2). Full details of the experimental setup in Hippenmeyer et al. 2010.