A Common Optimization Principle for Motor Execution in Healthy Subjects and Parkinsonian Patients

Abstract

Recent research on Parkinson's disease (PD) has emphasized that parkinsonian movement, although bradykinetic, shares many attributes with healthy behavior. This observation led to the suggestion that bradykinesia in PD could be due to a reduction in motor motivation. This hypothesis can be tested in the framework of optimal control theory, which accounts for many characteristics of healthy human movement while providing a link between the motor behavior and a cost/benefit trade-off. This approach offers the opportunity to interpret movement deficits of PD patients in the light of a computational theory of normal motor control. We studied 14 PD patients with bilateral subthalamic nucleus (STN) stimulation and 16 age-matched healthy controls, and tested whether reaching movements were governed by similar rules in these two groups. A single optimal control model accounted for the reaching movements of healthy subjects and PD patients, whatever the condition of STN stimulation (on or off). The choice of movement speed was explained in all subjects by the existence of a preset dynamic range for the motor signals. This range was idiosyncratic and applied to all movements regardless of their amplitude. In PD patients this dynamic range was abnormally narrow and correlated with bradykinesia. STN stimulation reduced bradykinesia and widened this range in all patients, but did not restore it to a normal value. These results, consistent with the motor motivation hypothesis, suggest that constrained optimization of motor effort is the main determinant of movement planning (choice of speed) and movement production, in both healthy and PD subjects.

Introduction

Among the different deficits caused by Parkinson's disease (PD), bradykinesia is one of the most disabling. This feature, which consists of an abnormal slowness of movement, affects most movements, including reaching (Flowers, 1976) and locomotion (Azulay et al., 1999). Though long recognized and extensively studied, its exact origin remains unclear.

Recently, several studies in PD patients (Desmurget et al., 2003, 2004; Mazzoni et al., 2007) and monkeys with pharmacological inactivations of the basal ganglia motor output nuclei (Desmurget and Turner, 2008, 2010; Turner and Desmurget, 2010) have emphasized that leaving their abnormal speed aside, the movements performed by PD patients and the lesioned animals have normal kinematic characteristics. This led some authors to suggest that basal ganglia dysfunction does not affect motor planning and control per se, but rather the implicit specification of movement speed (Majsak et al., 1998, Ballanger et al., 2006, Mazzoni et al., 2007, Shadmehr et al., 2010, Turner and Desmurget, 2010). In particular, a recent article of Mazzoni et al. (2007) provides convincing evidence in support of this idea by showing that PD patients have a preserved motor control with a reduced motor drive.

During the last two decades, the framework of optimal control has been a compelling tool for linking movement characteristics with a cost/benefit optimization process. Several authors have proposed that movement speed emerges from the optimization of an internal cost, either set by external factors (Harris and Wolpert, 1998), equated to final accuracy (van Beers, 2008) or a mix of accuracy and effort (Todorov and Jordan, 2002), viewed as an internal choice of effort (Guigon et al., 2007a) or explicitly linked to the movement-related reward (Shadmehr et al., 2010).

Although optimal control has not yet been used to investigate movement characteristics in PD patients, this framework represents a powerful approach to determine whether slowness of movement really reflects a downward shift of the internal cost (or effort) that PD patients allocate to the movement (Ballanger et al., 2006, Mazzoni et al., 2007, Turner and Desmurget, 2010). If so, a single model should be able to capture the motor performance of PD subjects and healthy individuals. Furthermore, in the patients, this model should also be able to account for the restoring effect of deep brain stimulation (DBS), which is known to improve bradykinesia and increases the isotonic force of PD patients (for review, see Romito and Albanese, 2010). If subthalamic nucleus (STN)-DBS acts by increasing the patient's effort level, movements performed by PD patients with or without STN-DBS should share common kinematic properties, with only a global change in speed.

The results of this study support these hypotheses. In all subjects, choice of movement speed is explained by the use of a predetermined dynamic range of motor commands: in other words, PD and control subjects make the fastest and most efficient movement possible while their motor signals remain inside preset bounds. In PD patients this range is abnormally narrow, which leads to bradykinesia. STN-DBS widens the motor range, but does not restore it to normal.

Materials and Methods

Subjects.

Eighteen akinetic-rigid right-handed PD patients with efficient chronic STN-DBS for at least 3 months and no sign or symptom of peripheral nerve disorders were recruited for the study. Two patients quit because they could not tolerate long periods without stimulation and two were excluded because of a mild tremor that prevented them from completing the task. Finally, 14 PD patients (10 males, 4 females; age 59.7 ± 6.3 years; range, 48–69 years) and 16 age-matched control subjects with no known neurological or motor disease (6 males, 10 females; age 57.1 ± 7.0 years; range, 45–71 years) took part in the study. The experiment was approved by the local ethics committee and all subjects gave informed consent before participation as defined in the Declaration of Helsinki.

Clinical features of the patients studied are summarized in Table 1.

Table 1.

Clinical data for the participating PD patients

Patient	Age	Sex	Disease duration (year)	STN-DBS duration (month)	UPDRS III Off-DBS	UPDRS III On-DBS	UPDRS improvement (%)	levodopa eq. dosage (mg/d)	Stimulation parameters
1	57	F	13	14	28	8	71	300	L1: 2.9 V, 60 μs,130 Hz
									R6: 3.5 V, 60 μs,130 Hz
2	60	M	14	17	23	5	78	400	L2: 2.5 V, 60 μs,130 Hz
									R6: 3.2 V, 90 μs,130 Hz
3	61	M	9	25	39	8	79	300	L3: 3.5 V, 60 μs,130 Hz
									R6: 3.2 V, 90 μs,130 Hz
4	52	M	15	39	28	10	64	300	L2: 3.0 V, 60 μs,130 Hz
									R6: 3.1 V, 60 μs,130 Hz
5	59	M	8	3	27	13	52	700	L2: 3.5 V, 60 μs,70 Hz
									R5: 3.7 V, 60 μs,70 Hz
6	48	F	17	60	49	22	55	150	L3: 2.6 V, 90 μs,160 Hz
									R6: 3.1 V, 60 μs,160 Hz
7	61	M	18	6	31	11	65	550	L2: 2.6 V, 60 μs,130 Hz
									R6: 3.0 V, 6.0 μs,130 Hz
8	61	M	14	48	31	15	52	175	L3: 2.5 V, 60 μs,130 Hz
									R7: 3.0 V, 60 μs,130 Hz
9	65	M	13	36	25	6	76	500	L1: 2.9 V, 90 μs,160 Hz
									R5: 2.7 V, 90 μs,160 Hz
10	58	F	14	38	17	8	53	900	L2: 5.0 V, 60 μs,70Hz
									R5: 5.0 V, 60 μs,70 Hz
11	51	M	10	3	29	8	72	350	L2: 2.3 V, 60 μs,130 Hz
									R6: 2,7 V, 60 μs,130 Hz
12	69	F	13	6	22	12	45	400	L2: 3.2 V, 60 μs,130 Hz
									R6: 3.1 V, 60 μs,130 Hz
13	68	M	28	35	13	3	77	0	L2: 3.0 V, 60 μs,130 Hz
									R6: 2.8 V, 60 μs,130 Hz
14	66	M	17	41	30	17	43	300	L2: 3.0 V, 60 μs,130 Hz
									R6: 3.5 V, 90 μs,130 Hz
μ ± σ	59.7 ± 6.3		14.5 ± 4.9	26.5 ± 18.5	28 ± 8.8	10.4 ± 5.1	63 ± 12	380 ± 230

STN stimulation parameters: pulse height, width, and frequency. Contact points of the stimulation tetrodes are numbered from L0 to L3 (left side, L) and R4 to R7 (right side, R) from ventralmost to dorsalmost. These contacts are spaced by 2 mm. Average and SD of the numerical data across the group are provided at the bottom of each column, when relevant. Levodopa equivalent calculation: 100 mg levodopa = 10 mg bromocriptine = 6 mg ropinirole = 1 mg pergolide = 60 mg piribedil = 0.7 mg pramipexole (Thobois, 2006).

Apparatus and task.

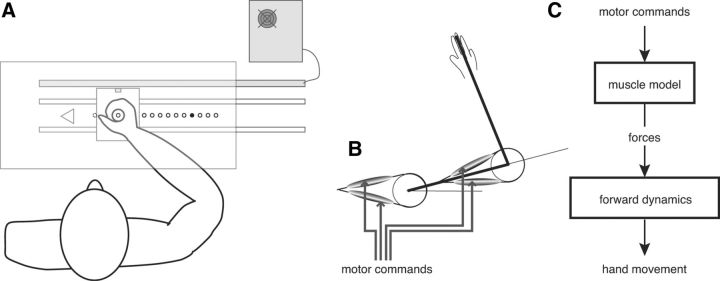
Subjects were seated in a dimly lit room. They viewed in a semisilvered mirror the virtual image of 11 light-emitting diodes (LEDs) arranged along the frontal axis (Fig. 1A). An LED placed directly in front of the subject served as starting point. The 10 remaining LEDs were targets, equally spaced from 12 to 30 cm to the right of the start LED. A cardboard mask placed under the half-mirror limited the view of the hand in a 2 cm disk around the starting point. The subjects were asked to grasp a handle that was sliding on ball bearings along the line from start to targets. At the beginning of each trial, the start LED was lit, and the subjects were required to move the handle fully to the left against a stopping plate. In that position, the tip of the handle was visible and appeared on the start LED, and this was pointed out to the subjects at the beginning of the experiment. This procedure ensured a precise initial positioning of the hand and intended to prevent any proprioceptive drift during the course of the study (Wann and Ibrahim, 1992). After a variable delay (800–1300 ms), the start LED was extinguished and the target LED was switched on. The subjects were instructed to place the tip of the handle on the target as quickly and precisely as possible. Six seconds after trial initiation, the target was extinguished and a new trial began. No visual feedback of final hand position was given.

Figure 1.

A, Experimental setup. Subjects held the handle and made linear movements toward the targets. Targets were 5 mm diameter LED, seen reflected on a semisilvered mirror. The tip of the handle contained an LED that was extinguished during the movements. This LED appeared 5 mm below the virtual plane of the targets. Handle position was measured by a magnetostrictive device connected to a real-time computer controlling the LEDs. B, Biomechanical model used: a two-link planar arm with four muscles. C, Model structure: transformation from muscle commands to kinematics. In the model, the muscle command minimizes the total neuromuscular cost.

Handle position was captured with a linear magnetostrictive transducer (WayCon; resolution 0.2 mm) and recorded at 1 kHz. LED control and data collection processes were run on a real-time computer (ADWin Pro; Jäger/Keithley). Data were logged between trials on a standard PC with MATLAB (The MathWorks).

Task conditions.

To analyze the sole effects of STN-DBS, all patients were tested after at least 12 h of withdrawal from antiparkinsonian medication. Two conditions were contrasted in two successive sessions: under chronic STN stimulation (On-DBS; see Table 1 for stimulation parameters) and without stimulation (Off-DBS). We left at least 30 min between the sessions, which is a sufficient time for the main parkinsonian signs to disappear and reappear (Lopiano et al., 2003; Temperli et al., 2003; Keresztenyi et al., 2007). A session comprised 10 blocks; in each block, each target was presented once in a different pseudorandom order. Control subjects participated in only one session. STN-DBS condition order was randomized and balanced across patients. In each STN-DBS condition we performed a clinical examination and determined the Unified Parkinson's Disease Rating Scale motor score (UPDRS; Fahn et al., 1987) before the patients engaged in the task. This scale is the most widely used to characterize the severity of motor signs in Parkinson's disease.

Data analysis.

Positional data were filtered and numerically differentiated with a two-point difference algorithm (cutoff 10 Hz) to compute in turn hand velocity and acceleration. We applied a Hilbert–Huang transform (Mellone et al., 2011) to all PD acceleration traces to remove potential action tremor (note that this procedure has no effect in the patients with no action tremor; i.e., in the patients for whom no higher frequency oscillations superimpose on the acceleration trace). The onset of the movement was defined as the moment when the hand velocity exceeded both 2% of the peak velocity of the movement and 5 mm/s. Movement was considered finished when the hand velocity reached its first local minimum <30 mm/s and did not cross this threshold again in the following 100 ms. Endpoint variance was determined using a robust estimate: the Median Absolute Deviation from the median (MAD; variance = (1.48 × MAD)²; Hampel, 1974).

Statistical analysis was done with MATLAB (Statistics Toolbox and custom permutation tests). Analysis focused on means across repetitions and subjects; however the median across subjects was chosen to express endpoint variability to increase statistical robustness (mean endpoint variance is much more sensitive to outliers than median). When not specified otherwise (e.g., permutation test), intergroup comparisons of means were done with ANOVAs (when applicable, repeated-measures ANOVAs) and post hoc tests corrected for multiple comparisons; for group medians, a nonparametric permutation test was used (Good, 1999). All linear regressions and associated statistics were computed with MATLAB's robustfit function (robust regression). To derive the fit of Fitts' law (expressed as MD = a + b.log(A/W_e) and MD = c + d.A), we first computed within-subject values for amplitude A, movement duration MD (mean across repetitions) as well as endpoint SD W_e (from the MAD), then fit the six regressions on the median values across subjects of MD, A/W_e, and A.

Model.

To examine the conjecture that the motor organization of movements in PD patients was similar to that of healthy controls, we tested whether the same model could reproduce the movements of both groups. Optimization of neuromuscular cost was previously shown to finely reproduce the kinematic and dynamic characteristics of arm movements as observed in healthy subjects [e.g., movement velocity profile, trajectory curvature, influence of loading, electromyography (EMG); Guigon et al., 2007a, 2007b]. We thus expanded on this approach. We started with a two-link planar model of the arm, with two pairs of antagonist muscles (Fig. 1B). Arm parameter values were derived from biomechanical studies (Winter, 1979) and took into account the inertia of the setup handle (Table 2). The transformation from muscle command to arm kinematics was governed by a cascade of differential equations (Fig. 1C).

Table 2.

Model parameter values

Parameter	Symbol	Value
Body mass	m	70
Handle (moving) mass	mh	0.5
Mass of first segment	m1	0.028 m
Mass of second segment	m2	0.022 m
Length of first segment	l1	0.3
Length of second segment	l2	0.35
Center of gravity coefficient, first segment	c1	0.43
Center of gravity coefficient, second segment	c2	(0.41 m2 + mh)/(m2 + mh)
Mass distribution coefficient, first segment	k1	0.10
Mass distribution coefficient, second segment	k2	0.22
Muscle time constant	τ	0.04
Muscle torque scaling factor	γ	30
Soft rectification parameter	σ	10

For the full description of the model, see Materials and Methods. Values in S.I. units: length in m, mass in kg, time in s.

In more detail, the dynamics of the two-link planar arm with four muscles obeyed the equation:

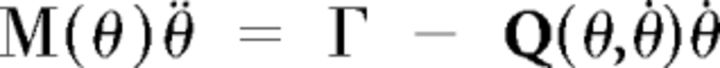where θ is the vector of arm angles, M is the arm inertia matrix, Γ are the active torques, and Q is the matrix used to derive Coriolis and inertial torques.

These matrices can be expressed as:

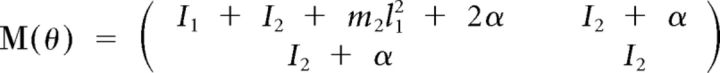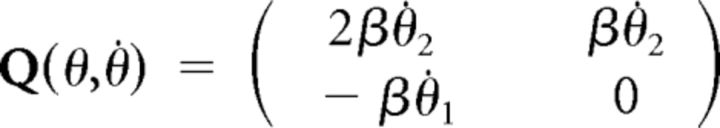with the following definitions:

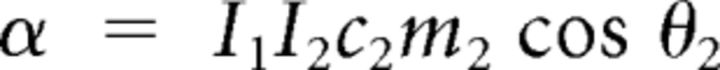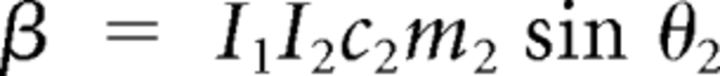and

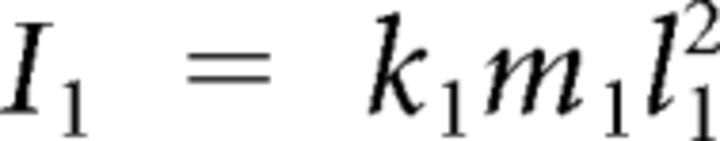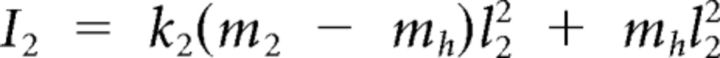Here subscripts 1 and 2 correspond to shoulder and elbow, respectively, and subscript h to the apparatus handle. In the preceding equations, I_i denotes the moment of inertia of link i around its center of rotation. Mechanical moment arms were assumed constant, so active torques were defined as follows:

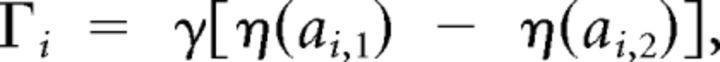with a_i,j denoting the activation of muscle j at joint i (j = 1, 2 for flexor and extensor, respectively), and η being a C^∞ (infinitely differentiable) approximation of the rectification function as follows:

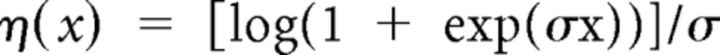Muscle activation and excitation were modeled as a cascade of two first-order differential equations from the muscle motor command u_i,j (Winters and Stark, 1985) with a soft positivity constraint implemented through η′, a C^∞ approximation of the Heaviside function:

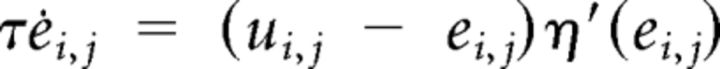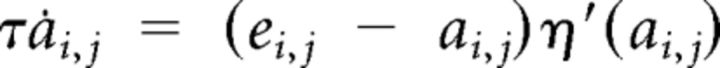Note that the scale of the motor commands was arbitrary (choice of γ). This is unimportant since the motor commands were always normalized with respect to another motor command. With these definitions, total neuromuscular cost was ∫₀^T Σ_iΣ_j u_i,j²(t)dt.

We then fixed movement duration T as experimentally measured, and used numerical methods to look for trajectories that minimized the neuromuscular cost while satisfying the constraint of reaching the measured endpoint (Guigon et al., 2007a). We could thus compare four key kinematic parameters of the model trajectories (timing and value of peak velocity and peak acceleration) with the same parameters in actual data, for each subject and condition. This also gave us the peak motor command predicted by the model. Simulations were run separately for each recorded trial of each participant, healthy or PD (On-DBS or Off-DBS). Cost optimization was done using the Newton–Raphson method (Bryson, 1999).

As the motor command peak was found to be constant in each subject (see Results), in a second step we reversed the logic and looked for the movement duration of minimum-cost movements that respected the experimentally observed dynamic range of motor commands. This was done to calculate the predicted movement times for a wider set of movement extents than recorded experimentally (in particular, for small movements). Derivation of movement duration from motor range was done with an iterative method. For each subject, we computed the motor range in each trial, and we took the median across repetitions of these motor ranges for each target. The median of these target-related values across all targets was taken as the subject's characteristic motor range. We then simulated the trajectories, first for the actual amplitudes of the movements, and then for a wider set of 12 movement amplitudes between 10 and 400 mm, to describe the predictions of the model for short movements. The initial movement duration we set for the simulated trajectories was the mean movement duration of the subject. The neuromuscular cost was then minimized for the chosen movement amplitude and duration, and the peak command of the model trajectory was computed. The movement duration was then increased or decreased by a 2.5% step to move the peak command closer to the upper value of the motor range. Iterations stopped when this border was crossed. The final movement duration was obtained by linear interpolation of the last two values so that the motor commands would exactly fit inside the observed motor range.

We checked the agreement between model and data by computing the residual relative error (model-data)/data for each variable considered. For each individual, we then ran a permutation test (on targets, 10⁵ permutations) to get individual significance. We finally combined individual results to get a group value using the partial conjunction method (Heller et al., 2007; Benjamini and Heller, 2008), which assesses the probability of the tested hypothesis being false for at least u subjects. As suggested in Heller et al. (2007), we took u = half of the subjects (u = 7/14 for the PD group, u = 8/16 for the controls).

Results

Reaction and movement times

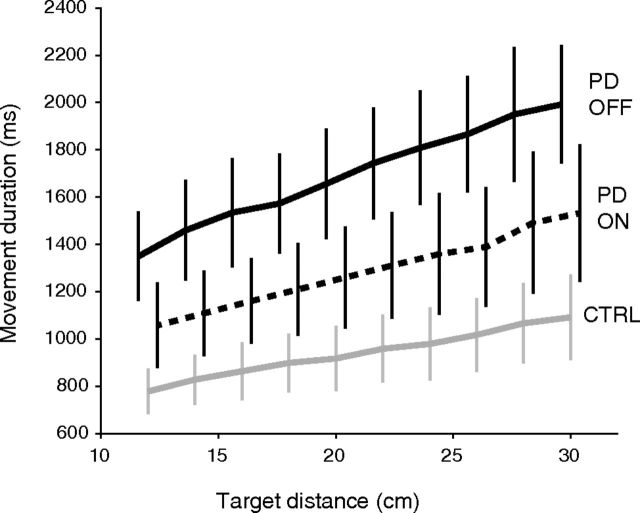
As expected, PD patients without STN-DBS were slower to initiate and complete the movements than the control subjects. Mean reaction time was 91 ms longer for Off-DBS patients (352 ms) than for control subjects (261 ms, p = 0.017 for PD effect). As expected, movement duration was larger for PD than for controls (1693 ms vs 940 ms, p < 10⁻⁴ for PD effect). It was modulated by movement extent in all groups and conditions (p < 10⁻⁴), following a quasilinear relationship, as shown on Figure 2.

Figure 2.

Mean movement time as a function of movement amplitude for the two groups. Error bars indicate 95% confidence intervals. Solid black: PD patients Off-DBS. Dotted: PD patients On-DBS. Gray: control subjects. For clarity, bars were slightly offset horizontally.

STN-DBS stimulation markedly improved patients' performances. With respect to Off-DBS values, mean reaction time and movement duration were, respectively, 14% (304 ms, p < 10⁻⁴) and 24% shorter (1288 ms, p < 10⁻⁴) when stimulation was turned on. Reductions in reaction time and movement time induced by STN-DBS were not correlated across subjects (computed on subjects' overall means, p = 0.27), in agreement with the observation that basal ganglia lesions affect these two variables differently (Turner and Desmurget, 2010).

Accuracy and precision

Without stimulation, patients like control subjects were slightly hypometric (mean across subjects of average error: −14.0 mm for PD, −6.6 mm for controls; nonsignificant difference between groups: p = 0.61). STN-DBS significantly reduced the modest hypometria of the patients, who became normometric (mean error 0.0 mm; significant effect of DBS: p = 0.018) and still not significantly different from the controls. There was no correlation between hypometria and bradykinesia (increased movement duration) in the patient group (p = 0.48 Off-DBS, p = 0.30 On-DBS). Endpoint variability was increased for patients Off-DBS (median endpoint variance = 265 mm²) compared with the control subjects (126 mm²), and this difference was statistically significant (permutation test, p = 0.001). DBS slightly increased the variability of the endpoints (median variance with stimulation was 370 mm²) as could be expected due to the increased movement velocity. However, this change was not significant (p = 0.18).

The speed-accuracy trade-off of PD patients and controls is illustrated in Figure 3 for each target. The link between precision and movement time is correctly described by Fitts' law in both the control and PD group, On- or Off-DBS (solid lines). However, it may be worth noting that this was only true if actual endpoint dispersion rather than target size was considered. Indeed, although target size was identical for all movement extents, endpoint variability increased with movement amplitude in all groups (Fig. 3). This does not agree with the suggestion that subjects choose their movement duration as the minimum time that allows to meet the final endpoint variance required by the task (Harris and Wolpert, 1998). According to this model the endpoint variance, like target size, would have been constant, independent of movement extent. In contrast, close targets were systematically associated with reduced movement time and reduced variability. An alternative explanation for the choice of movement time is offered below (see Materials and Methods, Model).

Figure 3.

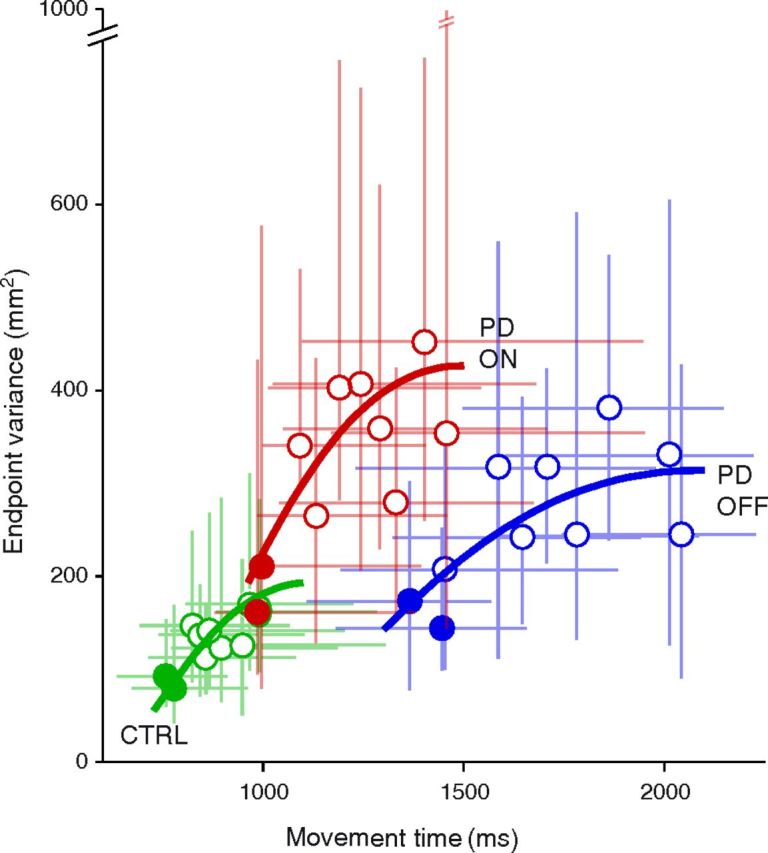
Median endpoint variance as a function of median movement duration. Filled symbols denote the two smallest amplitudes. Blue: PD patients, Off-DBS. Red: PD patients, On-DBS. Green: control subjects. For each group, a fit corresponding to Fitts' law is figured in bold lines of corresponding color (using a system of two equations, MD = a + b.log(A/W_e) and MD = c + d.A where MD is movement duration, A is movement amplitude, and W_e the SD of endpoints; see Materials and Methods). Error bars indicate the interval between the first and last quartile.

Kinematics

Unsurprisingly, patients showed marked differences in movement speed with respect to control subjects. Without stimulation, the mean peak velocity for patients was far lower (239 mm/s) than for controls (472 mm/s, p = 2.10⁻⁴; Fig. 4A). The mean time to reach this peak velocity was also longer (756 ms vs 446 ms, p < 10⁻⁴). Accordingly, the mean peak acceleration was markedly lower (712 mm/s²) in patients than in controls (2 264 mm/s², p < 10⁻⁴, Fig. 4B), and the mean time to reach this peak acceleration was longer (327 ms vs 207 ms, p < 10⁻⁴).

Figure 4.

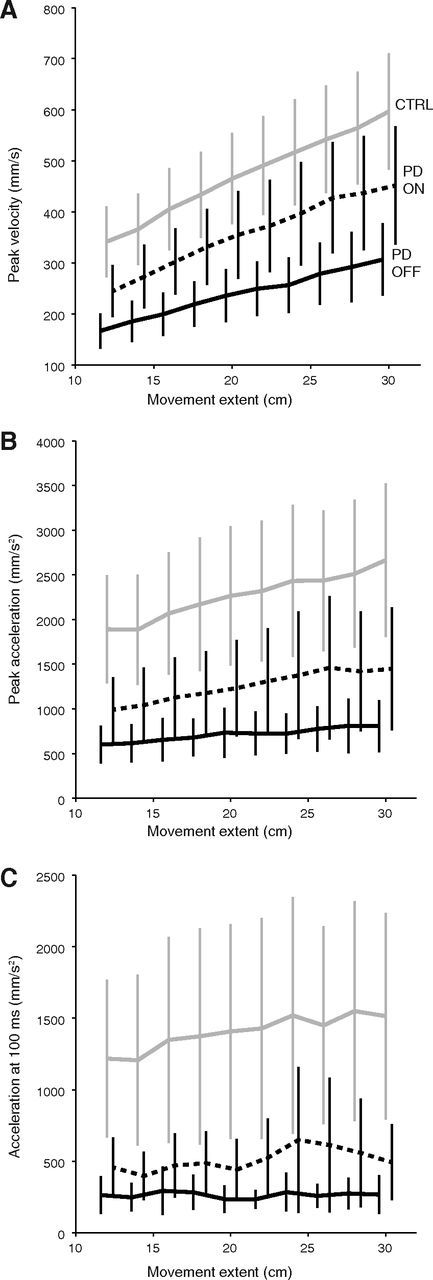
Kinematic parameters of the movement. Mean peak velocity (A), peak acceleration (B), and initial acceleration 100 ms after movement onset (C), as a function of movement amplitude. Conventions as in Figure 2.

These slower kinematics were partly remediated by STN-DBS. Under stimulation, the mean peak velocity increased by 120 mm/s (p < 10⁻⁴, Fig. 4A) and the average time to reach this peak was shortened by 119 ms (p < 10⁻⁴). Peak acceleration was higher (an increase of 546 mm/s², p < 10⁻⁴, Fig. 4B) and occurred 32 ms earlier (p < 10⁻⁴). Overall, the reduction of movement time produced by the stimulation was reflected in the faster initial kinematics, as depicted in Figure 4. Nevertheless, DBS did not restore peak velocity and acceleration to normal levels: peak velocity was still on average 24% lower (p = 0.041) and peak acceleration was 44% lower (p = 0.024) than in controls. Movement extent significantly modulated these variables in all groups and conditions (p < 3.10⁻⁴).

Initial acceleration

Patient kinematic deficits were clearly apparent in the hand acceleration, which is consistent with the observation that the early phase of movement initiation is impaired in these patients (Hallett and Khoshbin, 1980; Godaux et al., 1992; Pfann et al., 2001). We decided to characterize movement initiation using initial acceleration at 100 ms, a parameter that has been shown to be free of feedback modulations (Prablanc and Martin, 1992; Desmurget et al., 2005). Strikingly, the initial acceleration of PD patients Off-DBS plateaued at a mean 263 mm/s², independently of the target to be reached (p = 0.92). In contrast, the initial acceleration of On-DBS patients was moderately but significantly modulated by movement extent (p = 0.026). The strongest modulation was seen for control subjects (observe the slopes in Fig. 4C; p < 10⁻⁴). Because a faster rate of rise of muscle force allows reaching a higher level of acceleration after the initial 100 ms, these data make it tempting to speculate that the patients were slower because they were constrained by a lower upper bound in motor commands. Indeed, a narrow motor dynamic range would result in both a smaller initial acceleration and a lower modulation of initial acceleration with amplitude (to the point where the modulation of initial acceleration by amplitude be too modest to be detected statistically, when Off-DBS). This hypothesis of a narrow motor range (possibly related to a deficit in neuronal activity or recruitment, see Discussion) is evaluated below using an optimal control model.

The minimum-effort model

The optimization of the movement neuromuscular cost is a principle that explains many of the characteristics of human arm trajectories (Todorov and Jordan, 2002; Tanaka et al., 2006; Guigon et al., 2007a). We computed the trajectories predicted by this principle. It may be worth emphasizing that this model has no adjustable parameter. As a consequence, nothing was fit to the data. The values of the biomechanical parameters were taken from the literature for an average subject (Winter, 1979).

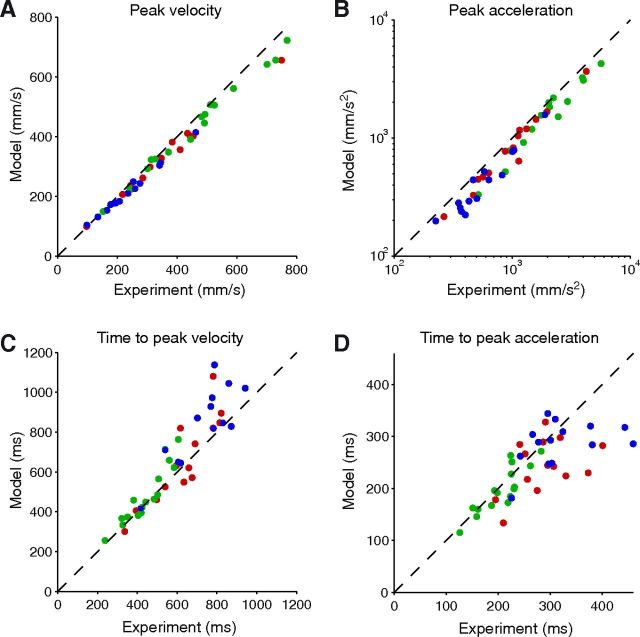
We first constrained the model to respect the movement extent and duration of each trial, and usual kinematic markers were extracted from the predicted trajectories. These values were determined by taking medians across repetitions to the same target. For each PD or Control subject, the median value across targets of the predicted peak velocity, peak acceleration, and time to peak velocity are shown on Figure 5, compared with their actually observed counterparts. The model correctly described the data, with a slight underestimation of peak velocity and acceleration, and even if the exact timing of the acceleration peak is more difficult to reliably estimate in the slowest PD patients. Overall, the continuum between the data of each group is striking and consistent with the claim that the minimum-effort model similarly applies to healthy subjects and patients whether On-DBS or Off-DBS.

Figure 5.

Results of a minimum-effort model constrained to respect the actual movement durations. The predicted peak velocity (A), peak acceleration (B), time to peak velocity (C), and time to peak acceleration (D) are plotted as a function of the actual data for each PD patient (blue: Off-DBS, red: On-DBS) and control subject (green). Each point corresponds to the median across targets of the median across repetitions to this target. Note the continuum between the results of each group. Dashed line: main diagonal. For clarity, a logarithmic scale was used for B.

To test the agreement between model and data, we used permutation tests on the residual relative error for each of the four variables considered on Figure 5. This was done for each subject. We then combined these individual p values in a synthetic group value according to the method of Benjamini and Heller (2008) (see Materials and Methods). Table 3 lists this value for each group and variable, as well as the number of subjects for which the individual test was significant at p = 0.05. This analysis confirmed that the model explains to a high degree the experimental variables in all groups.

Table 3.

Statistical significance of the model for each variable considered (rows) and subject group (columns)

	PD OFF	PD ON	Controls
Peak velocity (5A)	< 10−4 (13/14)	< 10−4 (14/14)	< 10−4 (16/16)
Peak acceleration (5B)	< 10−4 (14/14)	< 10−4 (14/14)	< 10−4 (16/16)
Time to peak velocity (5C)	< 10−4 (13/14)	< 10−4 (13/14)	< 10−4 (16/16)
Time to peak acceleration (5D)	0.018 (11/14)	0.011 (10/14)	0.013 (10/16)

Permutation tests were used for each subject on the relative error of the model, defined as (model-data)/data. These tests defined a p value for each individual and variable considered. The group p value listed in the table is the probability of the test outcome being due to chance in at least half of the individuals (for conjunction group analysis, see Materials and Methods). Values in parentheses are the number of subjects in which the individual test was significant at the 0.05 level.

Motor commands use a preset dynamic range

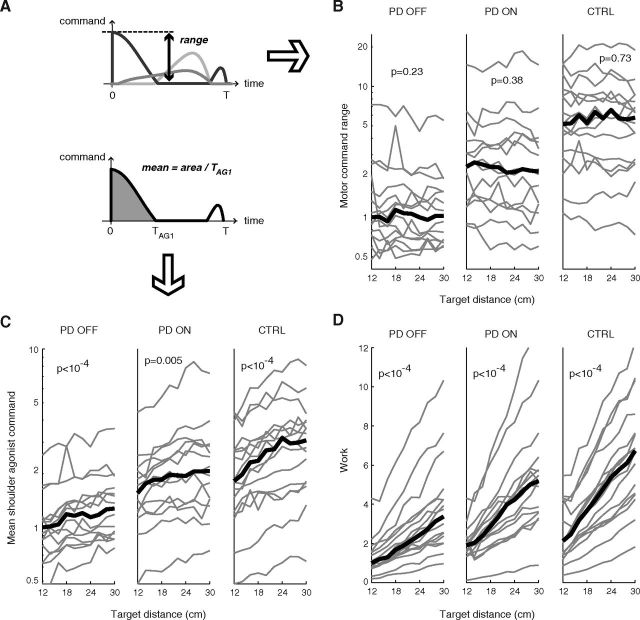
As shown above, optimization of neuromuscular effort accurately describes the reaching movements of both healthy participants and PD patients. Why then is the absolute level of motor effort different in both groups, as indicated by obvious differences in movement speed? Motor effort is difficult to measure experimentally, but can easily be gained from our theoretical approach. In our model, each motor command expresses the global motoneuronal drive on a given muscle. The dynamic range of the motor command thus corresponds to the range from baseline to the maximum population activity in the motoneurons. For the particular task studied in this paper, the wider motor command range was always reached in the shoulder agonist (extensor) muscle, which was the prime mover (Fig. 6A). In all subjects, we observed that this dynamic range showed little evolution with movement amplitude (Fig. 6B), in contrast to the mean shoulder agonist command (Fig. 6C) or the total work (Fig. 6D), which both increase with amplitude since they depend on movement duration (so does also the mean elbow command; data not shown). In other words, in each subject the CNS used a given dynamic range for the motor commands, this motor range being held constant, independent of the amplitude of the movement.

Figure 6.

Influence of movement extent on different measures of effort. A, Definition of the motor command range and mean agonist command shown in B and C. Gray lines illustrate motor command signals. B, Motor command range, as derived from the experimental data. Left: PD patients, Off-DBS; middle: PD, On-DBS; right: control subjects. For each experimental trial, the model was constrained to respect actual movement extent and duration. The range is shown averaged across repetitions to the same target and normalized to the median across Off-DBS patients of the mean range for the nearest target (12 cm). Slopes of robust linear fits to the curves were computed for each individual; we indicate the group significance of these slopes. The median across subjects is shown in bold line. C, Average first shoulder agonist command, as in B. D, Total movement work, as in B. For the sake of clarity, the ordinate scale in B and C is logarithmic.

The fact that work steadily increased with amplitude shows that energy expenditure is not a limiting factor. This observation is consistent with the studies of Nishikawa et al. (1999) and Kistemaker et al. (2010) who showed that human arm trajectories were poorly predicted by an optimization of mechanical energy. Like work, the mean agonist command was significantly modulated by movement extent (Fig. 6C), as already observed experimentally in control subjects and PD patients (Berardelli et al., 1986; Pfann et al., 2001; Robichaud et al., 2002). This increase, mostly due to a lengthening of the agonist command for the longest movements, highlights the difference between global (mean) and peak motor activation.

The determination of movement kinematics

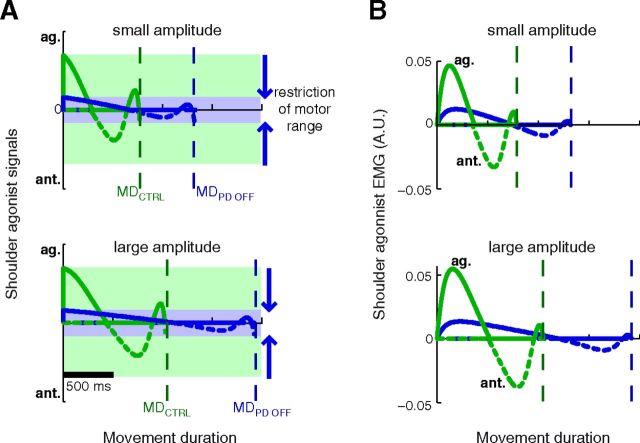
This and the preceding analysis suggest that the kinematics of PD patients as well as control subjects are mostly determined by the existence of a preset motor envelope for motor commands. In other words, the CNS seems to make the most efficient movement that fully uses the available motor range (set independently of movement extent). As a consequence of this concept, the preset motor range determines movement kinematics. Indeed, making the most efficient movement to a target while keeping the motor command inside a given motor range amounts to choosing a movement duration. A narrower motor range leads to a lengthening of movement duration (Fig. 7A); so does a longer movement amplitude (Fig. 7A, compare top and bottom). The scaling of peak muscle activity with movement amplitude follows as a consequence of the scaling of movement duration (Fig. 7B, compare top and bottom).

Figure 7.

Illustration of the consequences of a restricted motor range on motor signals (A) and muscle activity (B) for the muscles of the shoulder joint during two movements, one of small amplitude (top row) and one of large amplitude (bottom row). The agonist (solid lines) and antagonist (dashed) signals are represented for an average healthy subject (green) or Off-DBS PD patient (blue). The antagonist trace is inverted for clarity. A, As the neuromuscular effort to reach the target is always minimized, the restriction of motor range translates into longer movement times, for movements of small (top) or large amplitude (bottom). The constraint of the motor range also results in a scaling of movement duration (MD) with movement extent (compare MD for a small and a large amplitude, in both an average healthy and PD subject). B, The restricted motor range leads to lower muscle activities. Nevertheless, peak muscle activity scales with movement amplitude (compare the amplitude of the first agonist burst for a small (top) or large (bottom) movement). This can be observed in both healthy and PD subjects, although it is only clearly visible for the former on these graphs.

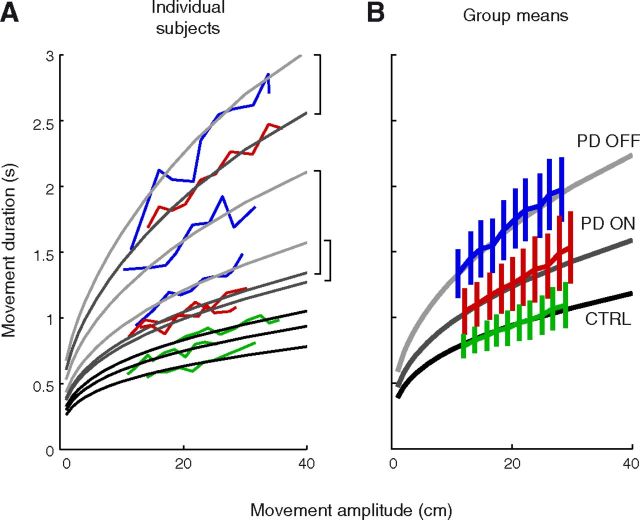
To further illustrate this important point, we ran the model leaving now movement duration as a free variable but with the constraint of respecting for each subject both his/her available motor range, as determined from an across-amplitude average of the data on Figure 6B (see Materials and Methods). We ran the model for a range of movement amplitudes between 10 and 400 mm. The model predicted that we should observe bradykinesia in PD patients for any movement extent, in accordance with existing observation (Flowers, 1976); this prediction is illustrated for three PD patients and three healthy controls (Fig. 8A). This figure highlights how a restricted motor range is not equivalent to a clipping of motor commands above a threshold (which would happen if the required force exceeded the available maximum force); the latter ceiling effect would imply that PD patients have normal kinematics for small movements. According to our model this is not the case because each movement, however small, utilizes all the available motor range. This is further illustrated in the group analysis. Since the motor plant is not linear and subjects were diversely hypometric or hypermetric (Vindras et al., 2005), we did not expect the average subject to perfectly model the average behavior. Nevertheless, using the average motor range of each group, the model predicted to a satisfying degree the mean movement time of On-DBS and Off-DBS PD patients as well as control subjects (Fig. 8B). Such a presentation allows a quick comparison between groups and nicely summarizes how between-group differences in motor range entail differences in movement kinematics, for similar movement extents.

Figure 8.

Prediction of the movement duration from the measured motor range, over a wide span of movement amplitudes. The minimum effort model was constrained to respect the motor range of each subject. A, Movement duration as a function of amplitude for six representative subjects, three PD patients On-DBS and Off-DBS, and three control subjects (colored lines, same conventions as in Fig. 6), compared with the prediction derived from their average motor range across targets (gray lines). Brackets indicate the correspondence between the Off-DBS and On-DBS state for each patient. B, Same plot as A, for the group average of movement duration and the prediction derived from the average motor range of each group. Note that due to nonlinearities in the biomechanics, this virtual “mean subject” is not expected to be a perfect fit to the mean behavior. The average upper limit of the motor range was defined as the across-subject geometric mean of limits. Shades of gray identify the group modeled. Light gray, PD Off-DBS; medium gray, PD On-DBS; dark gray, controls. Error bars indicate 95% confidence intervals.

Interindividual variations in motor range

The motor range was variable across subjects, although there was a clear effect of the group factor (Kruskal–Wallis test on individual means, p < 10⁻⁴). The median motor upper limit of this range across the healthy subjects was 5.7 times higher than for Off-DBS patients and 2.5 times higher than for On-DBS patients. As expected, there was a very clear correlation between motor range and average movement velocity across subjects within in each group (all within-group correlation coefficients r > 0.95; all p < 10⁻⁴; correlations computed on log-transformed upper limit of the range for linearization, compare Fig. 6B), and across all subjects (r = 0.96, p < 10⁻⁴). We found no significant correlation between the breadth of the motor range and the UPDRS III score (p = 0.52 for On-DBS and p = 0.60 for Off-DBS conditions) or between the motor range and the duration of the disease (p = 0.91 and p = 0.75, for the respective conditions). There was no correlation either between motor range and hypometria (p = 0.57 for On-DBS and p = 0.83 Off-DBS). It is worth mentioning that the actual absolute value of the motor range should be taken with caution. Since the model computes the optimal muscle activations that minimize the neuromuscular effort, cocontraction is reduced to a minimum. A nonzero level of tonic cocontraction during a subject's movements would lead to an underestimation of the motor range. Nevertheless, such an underestimation cannot account for the difference between the On-DBS or Off-DBS patients and healthy controls, or between the STN-DBS conditions in the same patient. Indeed, if the missing range had been taken up by cocontraction, the broadening of motor range caused by DBS would imply a decrease in cocontraction; nevertheless this DBS-induced broadening of motor range was not at all correlated with a reduction in rigidity (limb stiffness; see below).

The STN-DBS boost

For each patient, there was a clear correlation between the breadth of the motor range in the Off-DBS and On-DBS conditions (p = 6.10⁻⁴; Fig. 9A). Thus for each patient, the effect of STN-DBS on upper limb motility could be quantified by the ratio of the motor range breadth with and without stimulation: this ratio can be seen as a measure of the “STN-DBS boost.” This boost was variable across subjects, ranging from 1.1 to 7.6; the median boost was 2.0. It was positively correlated to the observed reduction in UPDRS motor score (p = 0.012, correlation computed on log-transformed boost). This correlation was even tighter with the UPDRS right-hand score (p = 4.10⁻⁴, Fig. 9B). In contrast, there was no significant correlation of the log STN-DBS boost with age (p = 0.65), disease duration (p = 0.81), months spent with DBS (p = 0.59) or equivalent-levodopa level (p = 0.76). Likewise, there was no correlation between this boost and the reduction of rigidity as clinically assessed in the UPDRS (p = 0.83), which suggests, in accordance with most experimental studies, that cocontraction did not significantly contribute to the change of the motor range. Last, there was no correlation between the DBS boost and the reduction in reaction time generally brought about by the stimulation (p = 0.39), suggesting that different mechanisms are at play in the improvement of reaction versus movement times (Evarts et al., 1981; Berardelli et al., 2001; Desmurget and Turner, 2008).

Figure 9.

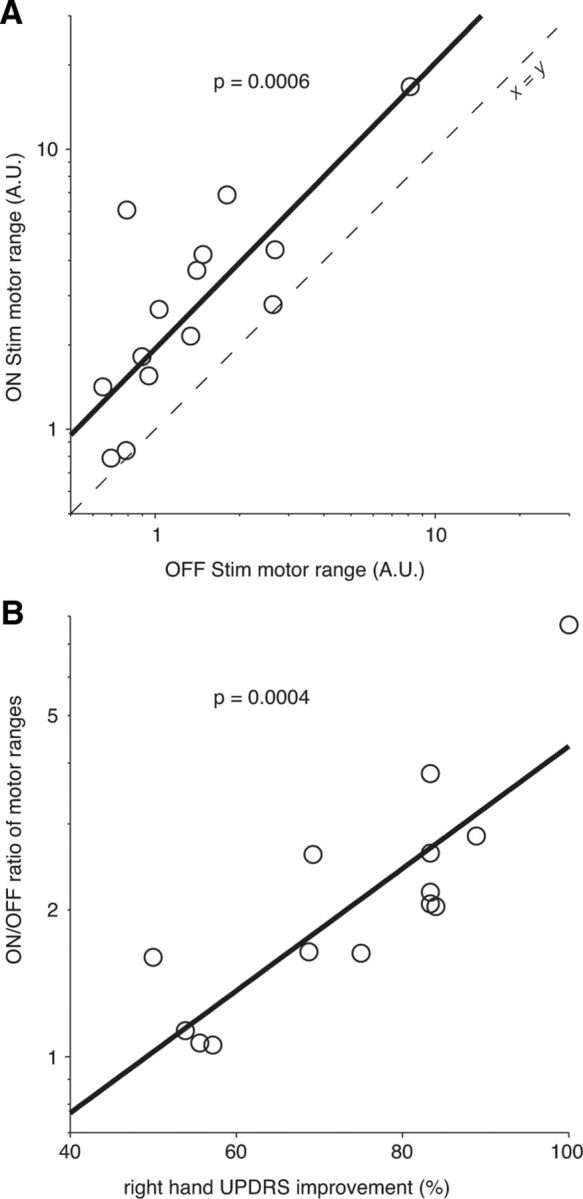
Effect of STN-DBS on the motor range (A) and relationship between DBS-induced widening of motor range and improvement of the UPDRS restricted to right-hand items (B). A, The motor range when On-DBS was systematically wider than its Off-DBS counterpart, for each patient (circles). Both motor spans were strongly correlated over the population. Bold line, linear regression; dashed line: first diagonal. Note the logarithmic scale on both axes. B, The On/Off ratio of motor ranges was correlated to the reduction of the UPDRS score restricted to right-hand items. Bold line: linear regression. Note the logarithmic scale for ordinates.

Discussion

We have shown here that a single cost-optimization model captures movement characteristics in healthy subjects and PD patients (with or without STN-DBS). PD and controls make the fastest and most efficient movement possible while their motor signals remain inside preset bounds (“motor range”). The free choice of movement duration seems thus related to a single parameter, the amplitude of this motor range, a subject-specific value likely modulated by urgency, motivation, or arousal. The distinctive feature of the patients lay only in an abnormally narrow motor range. This deficit was partially restored by STN-DBS. This strengthens the recent view that PD does not lead to any fundamental difference in movement organization but simply slows motor performance (Mazzoni et al., 2007; Desmurget and Turner, 2008, Shadmehr and Krakauer, 2008; Shadmehr et al., 2010, Turner and Desmurget, 2010). The possible functional meaning and neural bases of the motor range are discussed below.

The narrow motor range of PD patients

Charcot (1886) and Wernicke (1906), both cited in De Ajuriaguerra (1975), suggested long ago that the role of the basal ganglia was to facilitate motor effort or supply motor energy. Modern authors tend to refer to the term “vigor” to convey a similar idea (Mazzoni et al., 2007; Turner and Desmurget, 2010). Several observations are consistent with this concept. Inactivation of the internal globus pallidus (GPi; the main motor output of the basal ganglia) causes a slowing of movement (Horak and Anderson, 1984; Inase et al., 1996; Desmurget and Turner, 2008, 2010), sometimes accompanied with a global reduction in EMG activity (Horak and Anderson, 1984; Desmurget and Turner, 2008). Imbalance between the direct and indirect pathways in the basal ganglia has been suggested to be the main cause of these effects (DeLong, 1990; Leblois et al., 2006; Mallet et al., 2006). PD patients seem indeed to be subject to a difficulty in generating a strong initial agonist activity and can compensate by producing multiple contractions (Hallett and Khoshbin, 1980; Berardelli et al., 1986; Flament et al., 2003). Interestingly, these multiple burst are also observed in healthy subjects making purposely slow movements, matched in amplitude and duration with those of PD patients (Farley et al., 2004).

Typically, patients' weaker agonist bursts are improved by medication (Baroni et al., 1984; Berardelli et al., 1986) or by STN-DBS (Brown et al., 1999; Vaillancourt et al., 2004). In contrast to this amplitude reduction, the temporal organization of the agonist bursts and their scaling with extent and external dynamics seem normal in these patients (Berardelli et al., 1986) and in monkeys with pharmacological inactivation of the basal ganglia motor output nuclei (Desmurget and Turner, 2008). Godaux et al. (1992) showed that agonist weakness was related to a depression in the rate of rise of muscle activity. This body of observations led Berardelli et al. (1986) to suggest that bradykinesia in PD patients is mostly due to an underestimation of the size of the necessary impulsive force, or to a limitation in the mechanism that produces the motor commands. Our results are consistent with this second view and suggest that motor signals are constrained into a preset dynamic range in both patients and controls, but that this range is pathologically narrow in PD (with in some patients the superposition of some tremor oscillations on the motor commands; Lance et al., 1963, Brown et al., 1997, Wenzelburger et al., 2000). Nevertheless, this limitation is not absolute, as demonstrated by the existence of paradoxical kinesia (Souques, 1921, Majsak et al., 1998, Ballanger et al., 2006, 2009).

Theoretically, a narrowing of the range of motor commands predicts, among other things, a correct scaling of EMG with movement amplitude but with a lower rate of rise of muscle activity. Note, however, that peak motor command does not generally correspond to a maximum effort; it was the case here since movements were of self-determined speed. Rather, the motor range can be seen as a flexible envelope, possibly related to the level and/or dynamics of recruitment among neuronal populations, and modulated by the context of the action (see below). For any movement, our model posits that subjects take advantage of all this available motor range: this explains why PD patients are always bradykinetic compared with controls, even for short movements. In controls, this model nicely captures previous observations showing a similar rise in the agonist EMG for arm movements of different distances (Wadman et al., 1979; Gottlieb et al., 1989; Buneo et al., 1994; Pfann et al., 2001).

Effect of DBS on the motor range

The STN-DBS did not change the motor organization of the patients, but improved their kinematics, as reported previously (Brown et al., 1999; Levy et al., 2002; Lopiano et al., 2003; Taylor Tavares et al., 2005; Tabbal et al., 2008; Timmermann et al., 2008). Our model shows that the effect of DBS reflected an increase in the level of motor outflow reached during the movement. How DBS changes this level remains unclear. In monkeys, STN-DBS increases the activity in the external globus pallidus and inhibits the GPi (Kita et al., 2005). Such a reduction in the inhibition exerted by the GPi would indeed have effects similar to raising a limit. This reduction of GPi activity may also underlie the global decrease of activity in the basal ganglia found with positron emission tomography in humans (Grafton et al., 2006). Nevertheless, the mechanisms of STN-DBS action are more complex and seem to involve changes in neuronal firing patterns, among other things (Hashimoto et al., 2003; Shi et al., 2006). This supports the suggestion that the basal ganglia facilitate the synchronization of cortical activity (Brown and Marsden, 1998). In this case, the upper limit of the motor range of PD patients may appear lower than normal due to a deficit in synergistic action among populations of neurons. Whatever its exact mechanisms, the widening of motor range due to DBS compactly captures the effectiveness of the stimulation on upper arm motor function.

What reduces the motor range in PD?

Different mechanisms can lead to a limitation of the motor commands. In the motor control domain, the basal ganglia have been claimed to be important for selecting the appropriate muscle groups for action (Hallett, 1979; Mink, 1996). Within this context, a narrower range of efferent motor commands could then be due to an incomplete disinhibition of agonist activity, or to a deficit in selecting agonist from antagonist muscle groups (Berardelli et al., 1986, Mink, 1996). In agreement with this view, abnormal supraspinal regulation of spinal networks has been reported to induce a reduction in long-latency reflexes (Berardelli et al., 1983; Rothwell et al., 1983) and reciprocal inhibition (Hayashi et al., 1988; Meunier et al., 2000) as well as a downregulation of autogenic inhibition (Delwaide et al., 1991). This could lead to agonist–antagonist coactivation during movement. Nevertheless, direct evaluations have suggested that excessive antagonist activity does not substantially slow down arm movements (Pfann et al., 2001; Robichaud et al., 2002). Actually, while STN-DBS or pedunculo-pontin nucleus-DBS help restore normal spinal reflexes in PD patients (Pötter et al., 2004; Pierantozzi et al., 2008; Marchand-Pauvert et al., 2011), these changes are mostly correlated with improvements of axial functions, such as gait and posture (Pötter et al., 2004; Stefani et al., 2007). Thus, according to current research, it seems unlikely that the narrower upper limb motor range of PD patients could be attributable to peripheral motor limitations (Berardelli et al., 2001).

The basal ganglia have been attributed a second role in the sensorimotor domain: translating incentives into action, that is, allocating effort as a function of reward (for review, see Turner and Desmurget, 2010). In the framework of this hypothesis, PD patients would face an internal limit on neuronal effort, like a lack of central motor activation. Several observations are consistent with this hypothesis. For instance, when placed in situations of urgency, PD patients can reach velocities comparable to those of controls in standard nonurgent conditions (the so-called “paradoxical kinesia”; Majsak et al., 1998; Ballanger et al., 2006, 2008). Likewise, when asked to reach preset kinematic criteria, PD patients can produce normal (nonbradykinetic) movements, although after more attempts than controls. This led Mazzoni et al. (2007) to suggest that a motivational deficit rather than a motor weakness could underlie the bradykinesia observed in PD. This hypothesis is consistent with the recent finding that disorders of the basal ganglia affect the translation of monetary incentives into isometric force (Schmidt et al., 2008). Within this context, the DBS-induced widening of the available motor range could be interpreted as a change in the level of motor motivation. This higher motivation would echo the higher impulsivity in patients treated with dopaminergic agonists (Weintraub et al., 2010) or STN-DBS (Frank et al., 2007; Ballanger et al., 2009; Hälbig et al., 2009).

The issue of whether our data support a deficit of the will (motor motivation hypothesis) or a restriction in the span of choices (impossibility to generate greater effort) remains open to debate. Whatever the interpretation, it appears that patients (like controls) make the fastest possible movements that minimize total effort while recruiting all the motor range that is available for a given motivation, context, and emotional state. By summarizing in a single parameter (motor range) the movement speed of a single individual, for a wide range of movement extents, this model provides a theoretical framework in which the influence of urgency, motivation, or therapies can be analyzed in further studies, both in brain-damaged patients and healthy subjects.