Imprint of Assortative Mating on the Human Genome

Abstract

Preference for mates with similar phenotypes, assortative mating (AM), is widely observed in humans^1–5 and has evolutionary consequences^6–8. Under Fisher’s classical theory⁶, AM is predicted to induce a signature in the genome at trait-associated loci that can be detected and quantified. Here, we develop and apply a method to quantify AM on a specific trait by estimating the correlation (θ) between genetic predictors of the trait from SNPs on odd- versus even-numbered chromosomes. We show by theory and simulation that the effect of AM can be quantified in the presence of population stratification. We applied this approach to 32 complex traits and diseases using SNP data from ~400,000 unrelated individuals of European ancestry. We found significant evidence of AM for height (θ=3.2%) and educational attainment (θ=2.7%), both consistent with theoretical predictions. Overall, our results imply that AM involves multiple traits, affects the genomic architecture of loci that are associated with these traits and that the consequence of mate choice can be detected from a random sample of genomes.

Non-random mating in natural populations has short and long-term evolutionary consequences. In many species, including humans, mate choice is often associated with phenotypic similarities between mates^9,10. Such phenotypic similarities have multiple sources, for example social homogamy, the preference for a mate from the same environment, or because of primary assortment on certain traits observable at the time of mate choice. In humans, AM involves multiple complex traits^1–5 and can sometimes lead to similar susceptibility to diseases^11–14. The genetic effects of AM were first studied in the seminal articles of Fisher (1918)⁶ and Wright (1921)⁷. Those two founding contributions, further complemented by Crow & Kimura (1970)⁸ and others^15–17 have set the basis of the theory of AM on complex traits. AM theory predicts three main genetic consequences of a positive correlation between the phenotypes of mates in a population: (i) an increase of the genetic variance in the population, (ii) an increase in the correlation between relatives and (iii) an increase of homozygosity (deviation from Hardy-Weinberg Equilibrium; HWE), in particular at causal loci. These seemingly distinct consequences are nonetheless explained by the same cause: directional correlation between trait-increasing alleles (TIA), also referred to as gametic phase disequilibrium (GPD), induced both within and between loci (Fig. 1). AM-induced GPD implies correlations between physically distant loci (between chromosomes for example) and is thus distinct from local linkage disequilibrium. AM therefore leads to a genomic signature of trait-associated loci that can be quantified by estimating GPD.

Figure 1.

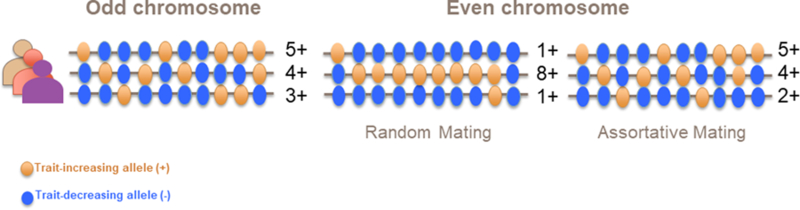
Schematic illustration of the effect of assortative mating (AM) on the correlation between trait-associated alleles. Each line represents a chromosome of an individual in the population and each coloured bead represents an allele (orange: trait-increasing alleles (TIA); blue: trait-decreasing alleles) at a particular locus on that chromosome. Under random mating, the distribution of alleles between odd and even chromosomes are uncorrelated (no-consistent pattern between chromosomes). Under AM, the distributions of alleles are correlated between chromosomes, such that the number of TIAs on odd chromosomes predicts the number of TIAs on even chromosomes.

Previous studies^18–20 have been successful at detecting GPD by direct quantification of increased homozygosity at ancestry-associated loci. Beyond ancestry, such endeavour is particularly challenging for polygenic traits as theory⁸ predicts an increase of homozygosity due to AM inversely proportional to the number M of causal variants^8,21. For a highly polygenic trait like height with an estimated M~100,000 for common variants²², the expected increase in homozygosity would be of the order of $~1/2M=5\times {10}^{-6}$, i.e. negligible (Supplementary Notes). Extremely large studies would therefore be required to quantify systematic deviation from HWE at height-associated single-nucleotide polymorphism (SNP) as shown in a recent study¹⁸ that failed to detect such an effect. Another study²³ in ~6,800 participants of European ancestry, reported evidence of deviation from HWE at height associated loci. This study however did not account for within-sample population stratification and therefore their reported estimates are likely inflated for this reason. Overall, study designs using deviation from HWE for quantifying GPD can be successful for detecting ancestry-based AM (ancestral endogamy) because the number of loci distinguishing ancestries is relatively small²⁴, and ancestral endogamy is strong¹⁸, but are less powerful to detect trait-specific AM. In contrast to HWE-based estimation strategies, quantifying GPD on the basis of pairwise correlations between TIAs is much more tractable as the number of pairs of loci involved, of the order of ~M², compensates for the magnitude of the expected covariance for each pair, $~1/2M$. The number of pairwise covariance terms is much larger than the number of causal loci, and thus the vast majority of the increases in genetic variance in a population from AM is due to between-locus covariance (GPD) rather than within-locus covariance (increased homozygosity) ^8,21.

GPD due to AM causes individuals that carry TIAs at one locus to be more likely to carry TIAs at other loci than expected under gametic phase equilibrium. Consequently, individuals with many TIAs on even chromosomes are likely to have more than average TIAs on odd chromosomes. We quantify this effect by calculating genetic predictors for a trait from the SNPs on odd chromosomes and from the SNPs on even chromosomes and then calculating the correlation (θ) between these two predictors. We chose to group SNPs according to the parity of their chromosomes number because it divides the genome in two approximately equally sized fractions. To calculate these predictors we use estimates of the effect of each SNP on a trait from publicly available summary statistics from genome-wide association studies (GWAS) of large sample size. We apply these estimated SNP effects to individuals in a separate sample who have SNP genotypes available. We can calculate the trait predictor based on odd and even chromosomes separately and estimate the correlation between them (i.e. θ). Our method measures the effect on the genome due to AM in previous generations and thus does not require observed phenotypes or the use of mate pairs. Under the null hypothesis of random mating, the correlation between alleles on different chromosomes is expected to be 0 as a consequence of the independent segregation of chromosomes. However, population stratification can induce spurious correlations between alleles, even at distant loci. Intuitively, if θ is estimated from a mixture of two sub-populations with distinct allele frequencies, then having TIAs more frequent in one of the sub-populations (even by chance) would result in an apparent correlation between TIAs even when such correlation is absent in each sub-population (Supplementary Notes). We show through simulations how the effect of population stratification can be corrected with our method. We then applied our method to estimate AM-induced GPD for 32 traits and diseases in samples of unrelated genomes from three independent cohorts: ~350,000 participants of the UK Biobank (UKB), ~54,000 participants of the Genetic Epidemiology Research on Adult Health and Aging (GERA) cohort and ~8,500 participants of the US Health and Retirement Study (HRS). We find evidence of AM for a number of complex traits, including height and educational attainment.

We derived (Supplementary Notes) the expected value of the correlation across individuals between the trait predictors from SNPs on odd (S_o) and even (S_e) chromosomes as a function of the phenotypic correlation between mates ($r$), the equilibrium heritability of the trait ($h_{eq}^2$), the fraction of that heritability captured by SNPs $\left(f_{eq}\right)$, the sample size ($N$) of the reference GWAS in which effect sizes are estimated using classical linear regression, one SNP at a time; and the number of causal loci $\left(M\right)$ contributing to the trait (which differs from the number of statistically associated loci). The main result is that for a large number of trait loci,

$$\theta =\frac{\rho f_0}{2-\rho \left(2-f_0\right)}{\left[1+\frac{M\left(1-\rho \right)}{N{h}_{eq}^2}{\left(1+\frac{\rho f_0}{2\left(1-\rho \right)}\right)}^{-3}\right]}^{-1}$$ (1)

with $\rho =r{h}_{eq}^2$ being the correlation between additive genetic values of mates expected under AM¹⁷ and $f_0\approx f_{eq}/\left(1-\rho \right)$, the fraction of heritability captured by SNPs in the base population (Supplementary Notes). These parameters do not need to be known or estimated, but can be used to provide a priori expectation of θ or a posteriori rationalisation. Hence, quantification of GPD can be directly obtained from estimates of θ using empirical data. For the sake of simplicity, we hereafter refer to estimates of θ as estimates of GPD. Equation (1) implies that the expected correlation θ between S_o and S_e increases with $N$, i.e. with better estimation of SNP effects from the reference GWAS, and with $f_{eq}$, i.e. with better tagging of causal variants underlying the full narrow sense heritability.

We derived (Supplementary Notes) that estimates of θ from the regression of S_o on S_e can be inflated by population stratification, especially when TIAs are highly differentiated between sub-populations. We performed a number of simulations (Supplementary Notes) to validate the impact of population stratification on our estimator of GPD and show how to adjust for it using genotypic principal components (PCs) derived separately for odd and even chromosomes (Supplementary Figures 1 and 2, Supplementary Notes). More specifically, Supplementary Figures 1 and 2 show that in the presence of population stratification akin to that observable within Europe, GPD estimates can be seriously upwardly biased and that adjusting for at least 10 PCs as covariates is effective at correcting this bias. Our simulations also revealed that correcting GPD estimates using PCs calculated from SNPs from both odd- and even-numbered chromosomes induces downward biases in GPD estimates (Supplementary Figures 1 and 2). We demonstrated in Supplementary Notes (Equation. 2.5) that the latter result is expected and we therefore recommend, when estimating θ from the regression of S_o onto S_e (or S_e onto S_o), to adjust GPD estimates for PCs calculated from SNPs on even- (or odd-) numbered chromosomes only (Methods). We used this approach to quantify GPD in real data, and conservatively adjusted all GPD estimates for 20 PCs to correct within sample population stratification (Methods). We observed that estimates obtained from the regression of S_e onto S_o are very similar to those obtained from regression of S_o and S_e (Supplementary Figure 3). Therefore, using one or the other approach has little impact on the outcome of our analyses. Also, given that most GPD estimates are small, all GPD estimates (correlations) reported below are expressed as percentages (e.g. 3% instead of 0.03).

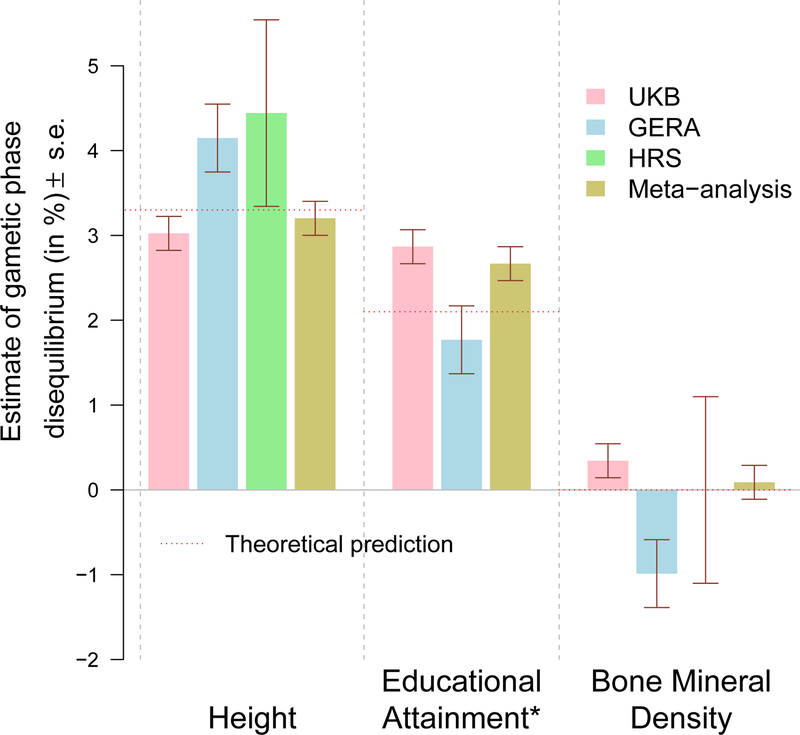
We first analysed height and educational attainment (EA), two reference traits with long-standing evidence of a positive correlation between mates. For height, we used estimated effect sizes, from summary statistics of the latest GWAS meta-analysis of the GIANT consortium (Wood et al. 2014)²⁵, of 9,447 near independent HapMap3 (HM3) SNPs selected using the LD clumping algorithm implemented in the software PLINK²⁶ (linkage disequilibrium (LD) r²<0.1 for SNPs < 1 Mb apart and association p-value < 0.005). We thus selected these SNPs to be enriched for true association with height. We estimated in UKB participants the correlation between height increasing alleles on odd versus even chromosomes to be θ_height=3.0% (s.e. 0.2%; Fig. 2) and replicated this finding in GERA (θ_height=4.1%, s.e. 0.4%; Fig. 2) and HRS (θ_height=4.4%, s.e. 1.1%; Fig. 2). A meta-analysis of these three estimates yields a combined GPD among height-increasing alleles of 3.2% (s.e. 0.2%, p=6.5×10⁻⁸⁹). To dismiss possible biases due to cryptic sample overlap or residual population stratification in summary statistics from the Wood et al. study, we re-estimated θ_height using summary statistics of a family-based GWAS that provide stringent control for population stratification²⁷. We therefore meta-analysed summary statistics from the Robinson et al. (2015) study²⁷ in 17,500 quasi-independent sib pairs with that from a similar analysis performed in 21,783 quasi-independent sib-pairs identified in the UKB (Methods). Using effect sizes of the 9,447 selected SNPs, re-estimated in the combined family-based GWAS, we found consistent GPD estimates between UKB not including sib-pairs (θ_height=2.1%, s.e. 0.2%; p=8.4×10⁻³⁶), GERA (θ_height=2.1%, s.e. 0.4%; p=1.4×10⁻⁶) and HRS (θ_height=2.5%, s.e. 1.1%; p=0.02). The meta-analysis of these three estimates yields θ_height=2.1% (s.e. 0.2%; p=4.7×10⁻⁴²). Note that lower estimates (2.1% vs 3.2%) are expected here because of the smaller sample size (N=39,283) of this family-based GWAS, as predicted by equation (1).

Figure 2.

Estimate of assortative mating (AM) induced gametic phase disequilibrium (GPD) among trait increasing alleles in three independent cohorts: UKB (N=348,502), GERA (N=53,991) and HRS (N=8,552). GPD is estimated as the correlation between trait-specific genetic predictors from SNPs on odd chromosomes versus even chromosomes. Bone mineral density was selected as a trait on which AM does not occur (negative control). Estimates are adjusted for 20 genotypic principal components from SNPs on either odd or even chromosomes to correct the effect of population stratification. *The HRS cohort was not included in the meta-analysis of GPD estimates among educational attainment increasing alleles, as HRS was included in the Okbay et al. study. Theoretical predictions are obtained from equation (1) assuming the number of causal variants for each trait to be of the order of ~100,000.

For EA, we used estimated effect sizes, from the summary statistics of a large GWAS meta-analysis of the number of years of education (Okbay et al. 2016)²⁸, of 4,618 near independent HM3 SNPs selected using the same LD clumping procedure described above. Using genotypes of 238,193 UKB participants not included in the Okbay et al. study (Methods), we found that θ_EA=2.9% (s.e. 0.2%; Fig. 2) and replicated this finding in GERA (θ_EA=1.8%, s.e. 0.4%; Fig. 2). We also attempted replication in HRS but the estimate we found (θ_EA=8.9%, s.e. 1.1%; Fig. 2) was likely inflated given that HRS was part of the Okbay et al. meta-analysis (Supplementary notes). We therefore only meta-analysed GPD estimates from UKB and GERA and found the average correlation between EA increasing alleles on odd versus even chromosomes to be θ_EA=2.7% (s.e. 0.3%, p=6×10⁻⁴⁶; Fig. 2). We also re-estimated the effect sizes of the 4,618 selected SNPs on EA, using the same within-family procedure described above. We found GPD estimates of ~0.4% (s.e. 0.4%) in GERA and ~0.3% (s.e. 0.1%) in UKB participants unrelated with any of the 21,783 sib-pairs used to estimate effect sizes. The meta-analysis of the latter two estimates is θ_EA=0.31% (s.e. 0.16%; p=0.05). As shown below, this lower estimate is expected as the consequence of the smaller sample size used to estimate SNPs effects.

We performed a series of sensitivity analyses (Supplementary Notes; Supplementary Figures 4) to assess the robustness to population stratification of our estimates of GPD in height- and EA-increasing alleles. In particular, we re-estimated θ_height and θ_EA adjusting for different numbers of PCs (from 1 to 30) and also adjusting for both within-sample and projected PCs (i.e. based on SNPs loading from an external dataset; see Methods). We also assessed the robustness of our estimates to alternative choices to split the genome in two equally sized fractions. We furthermore assess the impact of using a different imputation accuracy threshold to select SNPs for analysis by re-estimating GPD using SNPs with an imputation quality score >0.95. We finally re-estimated standard errors using a block-jackknife approach (Supplementary Figures 5). Altogether, these sensitivity analyses confirm that our GPD estimates are robust to population stratification and that our regression-based standard errors are appropriate to quantify the statistical significance of our estimates.

We next compared GPD estimates with theoretical predictions of θ from equation (1). Equation (1) predicts θ from the sample size of the reference GWAS (N=253,288 for height and 293,723 for EA), the correlation between mates, the equilibrium heritability (here assumed to be 80% and 40% for height and EA respectively²⁹), the number of causal variants SNPs (here assumed to be between M~10,000 and M~100,000 for both traits) and the heritability captured by SNPs used to estimate θ. Using ~1,000 unrelated trios (two parents and one offspring) from UKB³⁰ we estimated the correlation between mates for height and EA to be 0.24 (s.e. 0.03) and 0.35 (s.e. 0.03), respectively. We estimated the SNP heritability captured by each set of SNPs used to estimate θ in HRS using the software GCTA³¹, resulting in estimates of $h_{\text{height}}^2=27.3\%$ (s.e. 1.7%) and $h_{\text{EA}}^2=15.1\%$ (s.e. 1.3%). With these five input parameters, equation (1) predicts θ to be between ~3.2% and ~4.2% versus 3.2% observed for height and between ~1.9% and ~3.0% versus 2.7% observed for EA. We recall here that predictions from equation (1) depend on the sample size of the GWAS from which SNP effects are estimated. In a smaller GWAS, estimated SNPs effects are less precise (i.e. prone to errors) and therefore, equation (1) would predict a smaller value of θ. Using estimated effective sample sizes of within-family GWAS (N_eff = 39,283 for height and 15,559 for EA; see Methods), equation (1) predicts θ to be between ~1.3% and ~3.6% versus 2.1% observed for height and between ~0.2% and ~1.4% versus 0.3% observed for EA. Overall, our estimates of GPD among trait-associated (θ_height=3.2%, s.e. 0.2; θ_EA=2.7%, s.e. 0.3%) are therefore consistent with these predictions. Everything held constant, equation (1) also predicts that with a much larger sample size of the discovery GWAS, for instance >1,000,000 participants, θ_height would be between ~4.0% and ~4.3% and θ_EA between ~2.7% and ~2.9%.

We extended our primary analysis of height and EA to detect GPD in 30 additional complex traits and diseases (Supplementary Table 1) using the same strategy. Among these traits, we analysed bone mineral density (BMD)³² as a null trait given that non-significant mate correlation was previously reported³³. As expected, we did not find significant GPD associated with BMD (meta-analysis of UKB, GERA and HRS: θ_BMD=0.09%, s.e. 0.2%; p=0.64). After Bonferroni correction applied to the meta-analysis of UKB, GERA and HRS (p<0.05/32≈1.56×10⁻³), we did not detect significant GPD for any of these other traits. We believe that this observation is likely explained by lack of statistical power, in particular resulting from the smaller sizes of GWAS used for these traits (on average ~73,000 participants compared to ~273,000 on average for height and EA) or from smaller variance explained by SNPs (using GCTA) selected to calculate genetic predictors of these traits. As an example, although the GWAS of body mass index (BMI) used in this study is similar in size with that of height (Supplementary Table 2), our estimation in HRS participants of the phenotypic variance explained by the 2,362 BMI-associated SNPs selected (Supplementary Table 1) is only ~6.2% (s.e. 0.9%) versus ~27.3% (s.e. 1.7%) for height. A much larger GWAS would therefore be required to detect any GPD among BMI-associated alleles using our method.

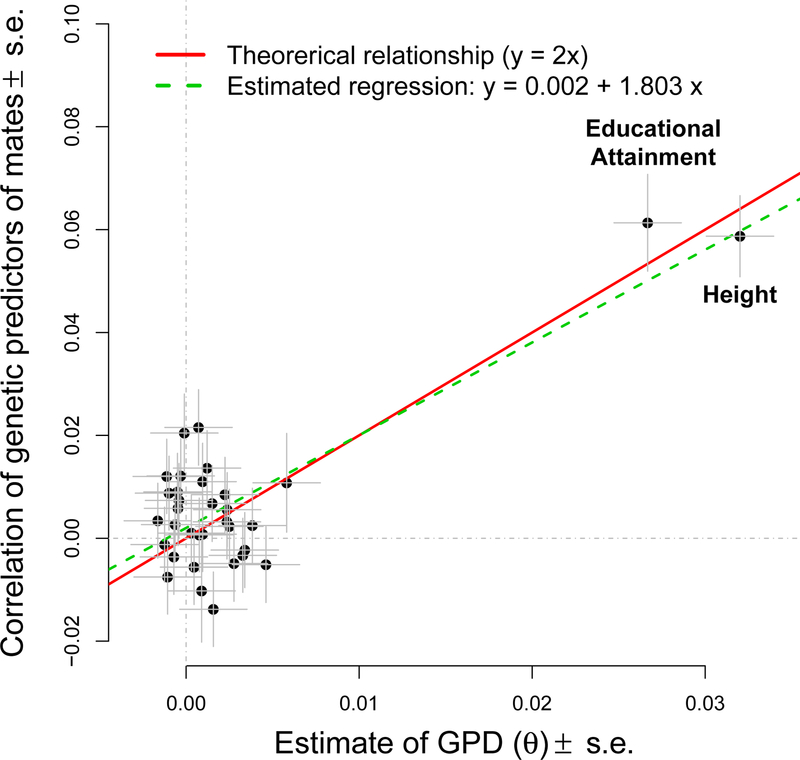
Another independent approach to quantify the genetic effect of AM on a particular trait consists of estimating the correlation of genetic predictors of this trait between mates^33–35. Compared to θ which measures AM in the parental generation, the correlation (r_m) of genetic predictors between mates quantifies AM in the current population. We derived (Supplementary notes) that if the population has reached an equilibrium after multiple generations of AM, then r_m ≈ 2θ (Supplementary notes, equation 4.20). We quantified r_m for all 32 traits (Supplementary Table 3) using 18,984 unrelated couples identified in the UKB (Methods). We found significant correlations between mates for genetic predictors of height (r_m=5.9%, s.e. 0.8%, p=9.2×10⁻¹⁴) and EA (r_m=6.1%, s.e. 0.9%, p=7.3×10⁻¹¹). Across all traits, we estimated the regression slope of r_m estimates onto θ estimates to be 1.8 (s.e. 0.2) (Fig. 3), which is consistent with our derivation predicting the expected mate correlation of genetic predictors to be approximately twice the expected value of θ.

Figure 3.

Correlation of genetic predictors in 18,984 mates pairs (y-axis; values from Supplementary Table 3) as a function of within-individual estimates of gametic phase disequilibrium (GPD: x-axis) for 32 complex traits and diseases (meta-analysis from Supplementary Table 1 in N=411,045 participants). Theory derived in Supplementary Notes predicts a regression slope equal to 2. Estimated linear regression intercept and slope are 0.002 (standard error, s.e. 0.002) and 1.8 (s.e. 0.23) respectively.

In summary, we have shown in this study that the genomic signature of AM can be detected and quantified using SNP data in a random sample of genomes from the population, even in the absence of data on mate pairs. This is an important aspect of our method since large datasets on mate pairs are rare and may be absent in natural populations. We confirm the genetic basis for AM for height and EA, consistent with the assumption of primary assortment on these traits. We showed that our estimates of GPD from real data are consistent with theoretical predictions made under simplifying assumptions such as equal SNP effect sizes, population being at equilibrium and that the number of common causal variants of the order of ~100,000 (Supplementary Notes). We did not however detect significant GPD for the other traits and diseases analysed in this study. Beyond true negatives such as bone mineral density, we believe that the relatively smaller size of GWAS used in our inference has reduced the power to detect the genetic signature of AM in more traits and diseases. We cannot therefore draw firm conclusion from our observations on the importance of primary assortment (as opposed to environmental correlation) to the resemblance between mates for some of these traits such as smoking habits³⁶, alcohol consumption³⁶ or susceptibility to psychiatric disorders¹⁴. Overall, our methodology is straightforward and can be applied to a wider variety of traits and in other species, provided that summaries of trait-variant associations are available. AM is multi-dimensional in essence as mate choice depends on multiple physical and behavioural traits which may or may not share a common genetic basis^2,37. Studying networks of traits and genes driving AM is one of the challenges to meet for improving our understanding of the genetic consequences of AM in a population. As a step in this direction, our method can be for example applied to quantify consequences of AM on gene expression or at any other molecular level, through the use of SNP predictors of these endogenous traits.

Our study has a number of limitations. The first one is that certain aspects of our approach are very conservative. We have attempted to quantify GPD induced by AM while applying stringent correction for population stratification. Although such strategy is expected in theory to yield unbiased estimates, it still faces the difficulty of distinguishing ancestry-based AM from AM based on traits that are genetically correlated with ancestry. Height is a typical example. AM on height occurs but, in addition, people tend to marry within geographical sub-populations (countries for example) which differ in mean height²⁷. Correcting for population stratification using PCs would consequently remove part of the signal that we want to detect. We have nevertheless been able to detect GPD among height increasing alleles as a consequence of the large sample size of the discovery GWAS, the strength of assortment of mates, and the high heritability of this trait. Finally, we note that correction for population stratification using PCs may reveal additional challenges in admixed populations, although this is beyond the focus of our study, which was conducted in relatively homogeneous populations.

The second limitation relates to our strategy for SNP selection. We have included in our analyses SNPs using a low and arbitrary threshold (p<0.005) on the significance of association with the trait. Although this strategy is not expected to bias the covariance between S_e and S_o, it may increase both their variances and thus potentially induces downward biases in GPD estimates. We chose nonetheless this strategy to maximize the fraction of heritability captured by SNPs, which influences the expected correlation between S_e and S_o as derived in equation (1). As an example, if GPD is inferred using genome-wide significant SNPs from Okbay et al. (2016), which explain ~3% of the variance of EA, the expected correlation between S_e and S_o would only be ~0.45% under assumptions made above. Such small correlation is nearly undetectable in cohorts with less than 300,000 participants (Methods). Another SNP selection strategy could have been used to reach a better trade-off between bias and power but this would generally require observed phenotypes to optimize genetic predictors^33,34 (find the best p-value threshold or shrinkage parameter).

In conclusion, our study provides empirical quantification of GPD induced among trait-associated alleles, a phenomenon predicted by theory exactly a century ago by Fisher (1918)⁶. The human genome has a pattern of trait-associated loci that is shaped by human behaviour (mate choice), as well as natural selection^33,38–40. The imprint of assortative mating on the contemporary human genome reflects mate choice in the 1930–1970s and in generations prior to that. Although there is much more mobility within and between human populations in the 21^st century, preference for similarly statured and similarly educated mates remains stable^13,35, and we may expect to continue to see its effect in the genome. Our findings have multiple implications for genetic studies. One is that they predict, for traits affected by AM, that estimates of SNP effects from within-family experimental designs tend to be smaller than those from a population sample, even in the absence of population stratification (Lee et al.; 2018).⁴¹ A second implication is that a genetic predictor generated from a population sample will explain less variation than expected when applied to a population not undergoing AM. A third implication is that previously published heritability estimates using, e.g., twin designs might be biased to the degree that AM occurs on the trait in question.⁴² A final health-related implication is that AM for liability to disease is expected to increase the prevalence and the relative risk to relatives in the population relative to a population under random mating. Altogether, our study shows that AM leaves a signature on the genome and that accounting for this effect may improve power of genome-wide association studies and accuracy of genetic predictions.

Methods

Estimation of GPD from SNP data

Our inference of GPD in a given sample of genomes is based on the correlation θ between polygenic scores S_e and S_o calculated from SNPs on even- and odd-numbered chromosomes respectively. For each individual from the study population, these scores are obtained as linear combinations of SNPs allele counts weighted by their estimated effect sizes from publicly available GWAS of complex traits and diseases (Supplementary Notes). We used publicly available summary statistics (regression coefficients for each tested SNP and p-values) from large GWAS on 32 traits (Supplementary Table 2). Also URLs to download these summary statistics are given in Supplementary Notes. These include GWAS on cognitive traits (educational attainment, intelligence quotient), anthropometric traits (height, body mass index, waist-to-hip ratio), psychiatric disorders (attention deficit hyperactivity disorder, autism spectrum disorder, bipolar disorder, anxiety, major depressive disorder, post-traumatic stress disorder and schizophrenia), other common diseases (coronary artery disease, type 2 diabetes, Crohn’s disease and rheumatoid arthritis), blood pressure, reproductive traits, personality traits, alcohol and smoking, and bone mineral density as a null trait. It is important that the sample of people whose genotypes were used was independent of the sample of people used to estimate SNP effects on each trait. Otherwise large biases can be expected as shown in Supplementary Notes. We applied LD score regression (LDSC) for quality control and only kept summary statistics with a corresponding ratio statistic (ratio = (LDSC intercept – 1) /(mean chi-square statistic over all SNPs - 1)) non-significant from 0 (i.e. estimate / standard error < 2) or < 0.2 (Supplementary Table 2). Significance of the GPD estimates was assessed using p-values from Wald-tests, with the null hypothesis “H₀: θ = 0” versus the alternative “H₁: θ ≠ 0”.

Correction of population structure

We used genotypic principal components to correct for population stratification. We calculated 20 principal components from 70,531 near independent HM3 SNPs (35,301 on odd chromosomes and 35,230 on even chromosomes) selected using the LD pruning algorithm implemented in PLINK (r²<0.1 for SNPs < 1Mb apart). We denote these principal components as PCO for SNPs on odd chromosomes and PCE for SNPs on even chromosomes. When θ is estimated from the regression of S_e onto S_o, the effect of population stratification is corrected by adjusting the regression for PCOs (and vice versa). This can be summarised using the following regression equations: $S_e=\theta S_o+{\text{PCO}}_1+\dots +{\text{PCO}}_{20}$ or $S_o=\theta S_e+{\text{PCE}}_1+\dots +{\text{PCE}}_{20}$. Since S_e and S_o may not have exactly the same variance as a result of SNPs sampling, we chose to estimate θ from the regression onto the genetic predictor with the larger variance. We observed nonetheless that estimates obtained from the regression of S_e onto S_o are very similar to those obtained from regression of S_o and S_e (Supplementary Figure 3). In the simulation studies (Supplementary Notes) we also considered the case where principal components are calculated from all SNPs available (odd and even chromosomes) and showed that downward biases are expected in this case. In our simulations, principal components were calculated using R version 3.1.2, while in real data principal components were calculated using the fast PCA approach⁴³ implemented in PLINK version 2.0.

Statistical power

Theory underlying statistical power to detect correlation is well established⁴⁴. We used equation (2) derived from Ref.⁴⁴ to determine the smallest correlation detectable with at least $1-\beta =80\%$ of statistical power at a significance level of $\alpha =5\%$:

$$\text{log}\left(\frac{1+\theta }{1-\theta }\right)=\frac{2|z_{\alpha /2}+z_{\beta }|}{\sqrt{n-3}}$$ (2)

In equation (2), n represents the size of the sample used to estimate $\theta$, and $z_{\alpha /2}$ and $z_{\beta }$ are the $\alpha /2$- and $\beta$-upper quantiles of the standard normal distribution (mean 0 and variance 1). With $\alpha =5\%$ and $\beta =20\%$, $z_{\alpha /2}\approx 1.96$ and $z_{\beta }\approx 0.84$. We can therefore detect GPD as small as 1.2% and 0.5% in GERA and UKB respectively, and 0.4% for the meta-analysis of UKB and GERA. For the analysis of mate-pairs we can detect correlation as small as 1.5%.

SNP Genotyping

UK Biobank data

We used genotyped and imputed allele counts at 16,652,994 SNPs imputed to the Haplotype Reference Consortium⁴⁵ imputation reference panel, in 487,409 participants of the UKBiobank^30,46 (UKB). We restricted our analysis to 1,312,100 HM3 SNPs, as HM3 SNPs were optimized to capture common genetic variation⁴⁷. Extensive description of data can be found here²⁷. We restricted the analysis to participants of European ancestry and SNPs with imputation quality ≥0.3, minor allele frequency (MAF) ≥1% and Hardy-Weinberg equilibrium test p-value > 10⁻⁶. Ancestry assignment was performed as follows. We calculated the first two principal components from 2,504 participants of the 1,000 Genomes Project⁴⁸ with known ancestries. We then projected UKB participants onto those principal components using SNP loadings of each principal component. We assigned each individual to one of five super-populations in the 1,000 Genomes data: European, African, East Asian, South Asian and Admixed. Our algorithm calculated, for each participant, the probability of membership to the European super-population conditional on their principal components coordinates. The 456,426 out of the original 487,409 participants who had a probability of membership > 0.9 for the European cluster were assigned to the European super-population. Next, to obtain a sample of conventionally unrelated individuals, we estimated the genetic relationship matrix (GRM) for individuals in the subsample of Europeans using GCTA³¹ version 1.9. We iteratively dropped one member from each pair of individuals whose estimated relationship coefficient exceeded 0.05, until no pairs of individuals with a relationship coefficient above 0.05 remained in the sample. This restriction resulted in a sample of 348,502 conventionally unrelated Europeans. In total, we included 348,502 participants in this analysis and 1,124,803 SNPs. The North West Multi-centre Research Ethics Committee (MREC) approved the study and all participants in the UKB study analyzed here provided written informed consent.

Genetic Epidemiology Research on Adult Health and Aging (GERA) cohort data

We analyzed 60,586 participants of the GERA cohort using genotype data only. Ancestry was assigned using a procedure similar to that described for UKB. Genotype quality control involved standard filters (exclusion of SNPs with missing rate ≥ 0.02, Hardy-Weinberg equilibrium test p-value > 10⁻⁶ or minor allele count < 1, and removing individuals with missing rate ≥ 0.02). We imputed genotypes data to the 1,000 Genomes reference panel using IMPUTE2 software. We used GCTA to estimate the GRM of all participants using HM3 SNPs (MAF ≥ 0.01 and imputation INFO score ≥ 0.3). We finally include in the analysis 53,991 unrelated (GRM < 0.05) European participants with genotypes at 1,163,290 HM3 SNPs.

Health and Retirement Study (HRS) data

We analysed 8,552 unrelated (GRM < 0.05) participants of the HRS cohort. GRM was calculated from 1,118,526 SNPs HM3 imputed to the 1,000 Genomes reference panel using IMPUTE2 software. SNP and samples quality control was similar to what described above for GERA.

SNP selection

We used the LD clumping algorithm implemented in PLINK to identify for each trait near independent SNPs (LD threshold r²<0.1 for SNPs < 1 Mb apart and association p-value < 0.005). LD clumping was performed using genotypes from HRS participants. We restricted the analysis to 1,060,523 HM3 SNPs that passed all quality controls in UKB, GERA and HRS datasets.

Sample overlap

The Okbay et al. (2016) GWAS of educational attainment, the Sniekers et al. (2017) GWAS of intelligence quotient al. (2017) and the Kemp et al. (2017) GWAS of bone mineral density, included ~150,000 participants of the UKB (first release of genotypes). To avoid bias due to sample overlap, analyses performed in UKB for these traits were restricted to 238,193 unrelated participants (UKB release 2 only), who also were not related to any of the participants included in those studies (UKB release 1). Participants of the HRS cohort were included in the Okbay et al. (2016) study as well as in the Day et al. (2015) GWAS of the onset of menopause. For the other GWAS considered in this study, no sample overlap with UKB, GERA or HRS was reported.

Sib pairs analyses

Selection

We used 21,783 sib pairs of European ancestry previously identified in the UKB³⁰ using identity-by-descent sharing estimated from SNP data. We applied the within-family QFAM procedure of PLINK, as in Robinson et al. (2015)²⁷, to assess the association between HM3 SNPs and height and EA. When applied to sib pairs, this procedure is equivalent to regressing the difference of height or EA between sibs onto the difference of allele counts. These estimates are therefore robust to population stratification. For height, we moreover performed a sample size weighted meta-analysis of estimates from the Robinson et al. (2015) study in 17,500 quasi-independent sib pairs, with those obtained in the UKB and used these newly estimated effect sizes to re-estimate GPD in UKB (not including any of the sib-pairs), GERA and HRS. In total we used 21,783 sib-pairs for EA and 39,283 sib-pairs for height.

Effective sample size

We defined the effective sample size (N_eff) of within-family GWAS using $N_{pairs}$ independent sib pairs as the sample size of a standard GWAS (where SNP effect are estimated from simple linear regression) such that the estimated SNP effects from the within-family GWAS have the same expected sampling variance as the estimated SNP effects from standard GWAS. This leads to the following equation (derived in Supplementary Notes)

$${\text{N}}_{eff}=N_{pairs}/[2(1-r_{pairs}]$$ (3)

In equation (3), $r_{pairs}$ represents the phenotypic correlation between sibs. We observed between sibs identified in UKB a correlation ~0.5 for height and ~0.3 for educational attainment. Therefore, the corresponding effective sample sizes for the within-family GWAS of height and EA are 39,283/(2×(1–0.5)) = 39,283 and 21,283/(2×(1–0.3)) = 15,559.

Mate pairs analyses

We first used 999 unique mate pairs from 1,065 trios composed of both parents and one child, identified among UKB participants using identity-by-descent sharing estimated from SNP data. Details about software and algorithms used to identify those trios are given in Ref.³⁰ To increase power, we also used household sharing information to identify putative spouse pairs among UKB participants with European ancestry. We therefore selected 18,984 (including 117 from the trios) sex-discordant pairs of participants, recruited from the same centre, who reported living with their spouse or partner in the same type of accommodation, at the same location (east and north coordinates rounded to 1 kilometre), for the same amount of time, with the same number of people in the household, with the same household income, with the same number of smoker in the household, with the same Townsend deprivation index and with a genetic relationship < 0.05.

Data availability

We used genotypic data from the Resource for Genetic Epidemiology Research on Adult Health and Aging (GERA: dbGaP phs000674.v2.p2), genotypic and phenotypic from the Health and Retirement Study (HRS: dbGaP phs000428.v1.p1), as well as genotypic and phenotypic data from the UK Biobank under project 12505.