Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2013 Sep 11;33(37):14921–14926. doi: 10.1523/JNEUROSCI.1313-13.2013

Informational Basis of Sensory Adaptation: Entropy and Single-Spike Efficiency in Rat Barrel Cortex

Mehdi Adibi 1,3, Colin W G Clifford 2, Ehsan Arabzadeh 1,3,✉
PMCID: PMC6705159  PMID: 24027291

Abstract

We showed recently that exposure to whisker vibrations enhances coding efficiency in rat barrel cortex despite increasing correlations in variability (Adibi et al., 2013). Here, to understand how adaptation achieves this improvement in sensory representation, we decomposed the stimulus information carried in neuronal population activity into its fundamental components in the framework of information theory. In the context of sensory coding, these components are the entropy of the responses across the entire stimulus set (response entropy) and the entropy of the responses conditional on the stimulus (conditional response entropy). We found that adaptation decreased response entropy and conditional response entropy at both the level of single neurons and the pooled activity of neuronal populations. However, the net effect of adaptation was to increase the mutual information because the drop in the conditional entropy outweighed the drop in the response entropy. The information transmitted by a single spike also increased under adaptation. As population size increased, the information content of individual spikes declined but the relative improvement attributable to adaptation was maintained.

Introduction

Here, we apply information theory (Shannon, 1948) to explore how sensory information is carried in the response of neuronal populations and how sensory adaptation affects the efficiency of coding. In the whisker sensory cortex (the “barrel” cortex), adaptation has been shown to scale the neuronal input–output function to the stimulus distribution (Maravall et al., 2007). Adaptation has also been shown to reduce detectability and enhance discriminability of whisker motions in barrel cortex neurons (Wang et al., 2010). Recently, we quantified the functional effect of adaptation on the population response of cortical neurons in the rat whisker-barrel system (Adibi et al., 2013). At the population level, adaptation increased correlations in the trial-to-trial response variability across neurons (noise correlation). Nonetheless, the net effect of adaptation was to increase the information conveyed by the neuronal population about the total stimulus set. Here, we first apply Fisher information to quantify the precision of coding for each stimulus. We then use information theory (Shannon, 1948) to establish the contribution of the fundamental elements of the mutual information (MI) between neuronal responses and the stimulus set: the response entropy and conditional response entropy. We further quantify the efficiency of information transmission at the level of single spikes as a function of adaptation state.

To gain a quantitative understanding of sensory encoding at the population level and the effect of adaptation, we address the following questions. How does adaptation modulate the response distribution of cortical neurons (quantified in terms of neuronal response entropy)? How does adaptation affect the response of neurons to a specific sensory stimulus (neuronal response entropy conditional on the presented stimulus)? Does the trial-to-trial covariability across neurons affect the distribution of their pooled activity and, if so, how does this in turn influence their coding efficiency? An information theoretic approach (Shannon, 1948; Cover and Thomas, 1991) allows us to parse out the mechanisms that underlie adaptation-induced changes in information transmission.

Materials and Methods

Neuronal data acquisition.

For the present study, we reanalyzed the neuronal data recorded by Adibi et al. (2013). Briefly, under urethane anesthesia (1.5 g/kg), neuronal activity was acquired from the barrel cortex using a 32-channel four-shank multielectrode probe (NeuroNexus Technologies). Each trial contained 20 cycles of adaptor (250 ms, 80 Hz sinusoidal vibration of 0, 6, and 12 μm amplitude) followed by a half-cycle (6.25 ms) pause and a single cycle of test stimulation (12.5 ms) at one of the 12 different amplitudes (0–33 μm with increment steps of 3 μm). Each test stimulus was repeated 100 times per adaptation condition. In six male rats, a total of 73 single units and 86 multiunit clusters were recorded across a total of 16 sessions. Each session contained a distinct set of simultaneously recorded neurons that were isolated using an online amplitude threshold and an offline template-matching procedure.

Fisher information analyses.

To quantify the precision with which neuronal responses encode sensory stimuli, we calculated the Fisher information function 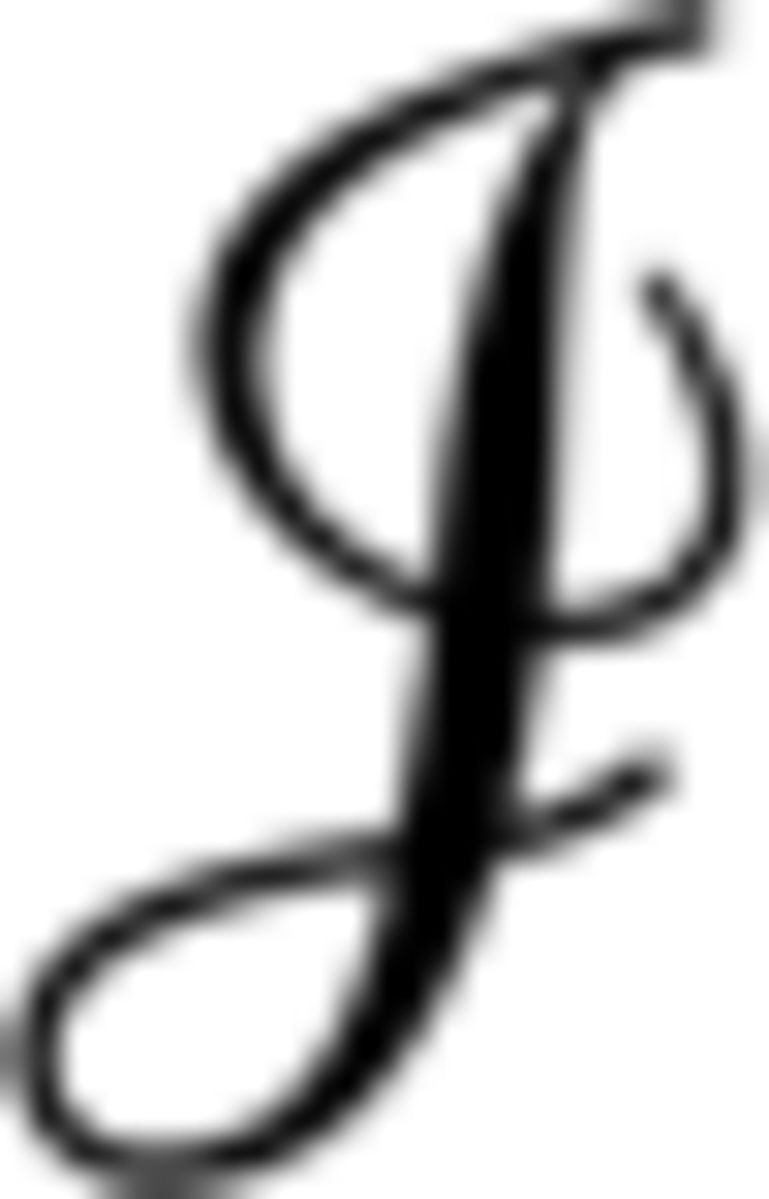Inline graphic(s) for individual neurons using the following equation:

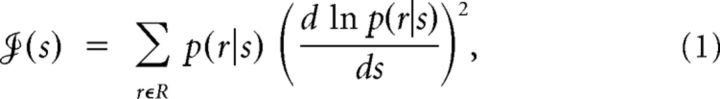graphic file with name zns03713-4480-m01.jpg

where p(r|s) is the conditional probability of observing response r given the presentation of stimulus s and R denotes the set of neuronal responses across all trials. The derivative was estimated using a five-point stencil approximation on the piecewise cubic interpolation of p(r|s).

Information theoretic analyses.

The response entropy H(R), conditional response entropy H(R|S), and MI between test stimuli and neuronal responses were calculated using the following formulae (Cover and Thomas, 1991):

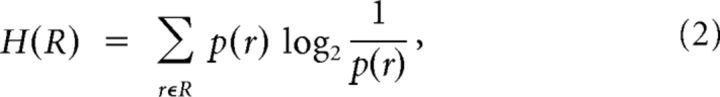graphic file with name zns03713-4480-m02.jpg
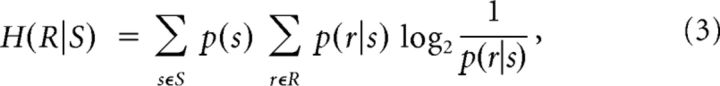graphic file with name zns03713-4480-m03.jpg
graphic file with name zns03713-4480-m04.jpg
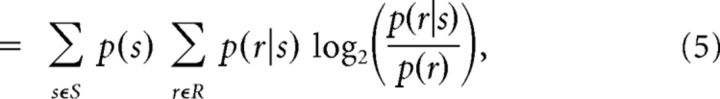graphic file with name zns03713-4480-m05.jpg

where S and R denote the set of stimuli (n = 12) and neuronal responses across trials, and p(s), p(r), and p(r|s) represent the probability of presenting test stimulus s, the probability of observing response r evoked across all stimuli, and the conditional probability of observing response r given the presentation of stimulus s. For population analysis, r represents the summed activity across neurons in the population. The probabilities in Equation 2 are estimated from a limited number of stimulus repetitions (100 trials per stimulus), potentially leading to an upward bias in information and entropy measures (Panzeri and Treves, 1996; Panzeri et al., 2007). To calculate the bias, we used the Panzeri-Treves method (Panzeri and Treves, 1996; Panzeri et al., 2007; Magri et al., 2009). Given the high number of trials relative to the number of combinations of responses, this method provides a reliable estimation of the bias. For analysis that involved pooled activity of a high number of neurons (Fig. 1), we further verified the accuracy of the bias estimation by reducing the dimensionality of the pooled response space R by grouping spike counts into a smaller number of classes. The MI was independent of the number of response classes (from 12 to the maximum number possible). For all reported results, this bias was subtracted from the estimated information measures.

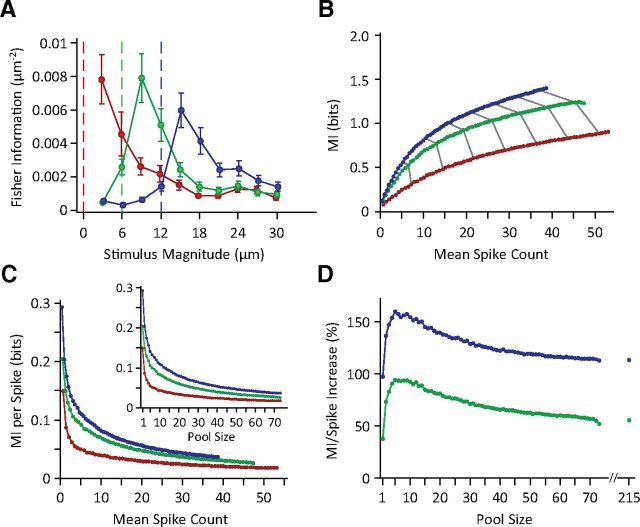
Figure 1.

Figure 1.

Open in a new tab

Information content of neuronal populations and individual spikes. A, Single-neuron Fisher information as a function of stimulus magnitude. Average Fisher information is illustrated for the non-adapted state (red), 6 μm adaptation (green), and 12 μm adaptation (blue). Error bars indicate the SEM across neurons. B, MI between the population activity and the whole stimulus set as a function of mean population spike count for the three adaptation states. Color conventions are as in A throughout. Each data point corresponds to a population size from 1 to 73 single units. The gray lines indicate increments of 10 in population size. To generate the mean population spike count, the summed spike counts of neurons in every population size were averaged across all trials and stimuli. For each population size, 1000 random selections of that size were averaged. This was done with the exception of the population sizes of 1, 72, and 73 neurons, in which the numbers of possible selections were limited to 73, 73, and 1, respectively. Trials from simultaneously recorded neurons were shuffled to remove noise correlation. C, The average information of individual spikes in the three adaptation states. The inset replots the same data but as a function of population size. D, Percentage increase in the single-spike information in the adapted states relative to the non-adapted state. The data points after the break in the abscissa include multiunit clusters with the single-unit data to provide the full population response across all recordings. From the firing rates, we estimate that the total population consisted of ∼215 single units.

For neuronal populations, such as those in the present study, maintaining spike labels would exponentially expand the number of response conditions, rendering the information analysis impossible with the number of trials available. Previously, we demonstrated that, when a pair of neurons were recorded from within the same barrel, pooling was nearly as effective as a “labeled-line” code in which spikes are labeled according to the source neurons (Arabzadeh et al., 2004). Therefore, we use the sum of spikes as a computationally tractable population code, which allows biologically plausible decoding.

The average single-spike information was calculated by dividing the MI values by the average number of spikes across all stimuli.

Results

We recorded a total of 73 single neurons (up to 11 simultaneously) and 86 multiunit neuronal clusters. To characterize the neuronal response to each test stimulus, we used the neuronal spike count in a 50 ms window poststimulus onset. Previous recordings revealed that most of the vibration information is transmitted within this time window (Arabzadeh et al., 2004; Adibi and Arabzadeh, 2011). We first quantified the effect of sensory adaptation on the neuronal coding precision at each stimulus. Figure 1A illustrates the average Fisher information across single neurons (n = 73) as a function of stimulus amplitude. The coding accuracy peaks at amplitudes higher than that of the adapting stimulus. Sensory adaptation produced systematic shifts in the stimulus region with elevated coding efficiency consistent with previous findings in barrel cortex (Adibi et al., 2013), as well as in other sensory modalities (Dean et al., 2005; Durant et al., 2007).

To characterize the information content of neuronal populations about the whole stimulus set, we apply information theoretic analysis. Figure 1B plots MI as a function of mean population spike count: each data point corresponds to a population size from 1 to 73 single units (the mean population spike count increases linearly with population size). MI values increase monotonically with the population size. MI values are systematically higher for the 12 μm adaptation state (blue) compared with the non-adapted state (red), with intermediate values for the 6 μm adaptation state (green).

Adaptation decreases mean population spike counts: under adaptation, a specific spike count is reached at a systematically higher number of neurons (the gray lines indicate increments of 10 in population size). This indicates that individual spikes are more informative under adaptation. This is directly captured in Figure 1C, which plots information values per spike. As population size grows, individual spikes become less and less informative. Nevertheless, each spike on average carries more information under adaptation. Figure 1D quantifies the improvement in the single-spike information, which exhibits a characteristic profile as a function of pool size. Peak improvement is observed at five neurons, in which individual spikes are 94 and 160%, respectively, more informative under 6 and 12 μm adaptation states compared with the non-adapted state. On average, under 6 and 12 μm adaptation states, the single spikes were asymptotically >55 and 113% more informative as in the non-adapted state. Adaptation thus improved single-spike information and population response information across both populations with the same size and populations with the same average firing rate.

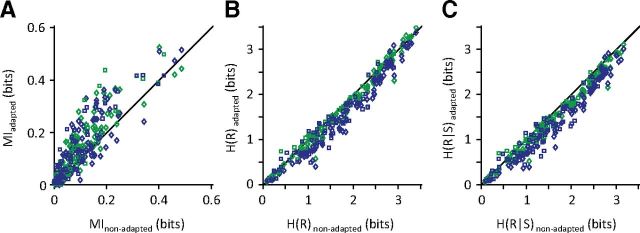
Figure 2A compares the MI carried by individual neurons in the adapted and non-adapted states. Under the 6 μm adaptation state, 74% of single units and 78% of multiunits showed enhanced MI compared with the non-adapted condition. Likewise, the 12 μm adaptation increased the information content of >75% of single units and 63% of multiunits compared with the non-adapted state. A Wilcoxon's signed-rank test revealed that adaptation significantly increased the overall MI values in both adaptation states (p values <0.0001). For single units, the average information value increased by 45 and 47% for the 6 and 12 μm adaptation states, respectively. For multiunits, the average information value increased by 37 and 29% for the 6 and 12 μm adaptation states, respectively. Thus, adaptation significantly improved neural coding efficiency at the level of individual neurons and small clusters of neurons.

Figure 2.

Figure 2.

Open in a new tab

Information content and entropy of neuronal responses. A, MI between the whole stimulus set and the neuronal responses in 6 μm adaptation (green) and 12 μm adaptation states (blue), denoted by MIadapted, versus the non-adapted state, denoted by MInon-adapted. Each data point corresponds to a single neuron (n = 73; square markers) or a cluster of multiunits (n = 86; diamonds). B, As in A but plotting the response entropy of individual neuronal recordings. C, As in A and B but plotting the response entropy conditional on the stimulus.

We further extended the results to information efficiency by normalizing the MI by the response entropy (Reinagel and Reid, 2000; Vinje and Gallant, 2002; Arabzadeh et al., 2006; Gaudry and Reinagel, 2007). Under the 6 μm adaptation state, 81% of single units and 85% of multiunits showed enhanced information efficiency compared with the non-adapted condition. Likewise, the 12 μm adaptation increased the information efficiency of >86% of single units and 80% of multiunits compared with the non-adapted state. Across single units, the average information efficiency improved by 42 and 72% in the 6 and 12 μm adaptation states compared with the non-adapted state (p values <0.0001, Wilcoxon's signed-rank test). For multiunit clusters, the average information efficiency improved by 38 and 40% in the 6 and 12 μm adaptation states compared with the non-adapted state (p values <0.0001, Wilcoxon's signed-rank test).

The MI between stimulus and neuronal responses is the reduction in the uncertainty about the stimulus given observation of the response. In mathematical terms, MI is defined as the difference between the response entropy across the entire stimulus set and the response entropy conditional on the stimulus (Cover and Thomas, 1991). Hence, the observed adaptation-induced improvement in MI could potentially be attributable to (1) a pure increase in the neuronal response entropy (source coding), (2) a pure reduction in the conditional entropy, or (3) a combined change in both variables that produces a net increase in their difference. Figure 2 decomposes the MI value (Fig. 2A) into its two components: (1) the response entropy (Fig. 2B) and (2) the conditional response entropy (Fig. 2C).

The response entropy showed a statistically significant decrease under adaptation (p values <0.0001, Wilcoxon's signed-rank test). This is consistent with the adaptation-induced drop in population response counts observed in Figure 1A. Compared with the non-adapted state, the response entropy of >75% of single units and 83% of multiunit clusters decreased after 6 μm adaptation. For the 12 μm adaptation, the percentages were 81 and 94%, respectively. The entropy of single units decreased by 2.6 and 12.4% in the 6 and 12 μm adaptation states compared with the non-adapted state. The entropy of multiunit clusters decreased by 7.5 and 16.8% in the 6 and 12 μm adaptation states, respectively. Moreover, we observed a significant difference between the two adaptation states; the average decrease in the entropy of single units and multiunit clusters in the 6 μm adaptation state (2.6 and 7.5%, respectively) was smaller than the average decrease in the 12 μm adaptation state (12.4 and 16.8%; for the two comparisons, p values <0.0001, Wilcoxon's signed-rank test).

This was surprising, because the reduction in response entropy would by itself predict a reduction in the MI under adaptation. The increase in the MI despite a reduction in the response entropy indicates that the drop in the conditional response entropy outweighs the drop in the response entropy. More than 82% of single units and 92% of multiunits exhibited reduced conditional entropy after 6 μm adaptation. Similarly, in the 12 μm adaptation state, the conditional entropy of 88% of single units and 98% of multiunits decreased compared with the non-adapted state. On average, the conditional entropy of single units decreased by 4.9 and 15.9% in the 6 and 12 μm adaptation states compared with the non-adapted state (p values <10−5, Wilcoxon's signed-rank test). The conditional entropy of multiunit clusters decreased by 10.3 and 19.5% in the 6 and 12 μm adaptation states, respectively (p values <10−5, Wilcoxon's signed-rank test). In addition, a significant difference was observed between the two adaptation states (for the both comparisons of single units and multiunits, p values <10−9, Wilcoxon's signed-rank test). The average decrease in the conditional entropy in the 12 μm adaptation state was 258% (for single units) and 190% (for multiunits) greater than the average decrease in the 6 μm adaptation state.

We then ran a simulation to quantify the extent to which a pure lateral shift in the neuronal response statistics could predict the above findings. To simulate neuronal response in the adapted condition, we shifted the non-adapted response function by an amount equal to the amplitude of the adaptor. This was achieved by remapping the response to every stimulus s in the non-adapted state to a new stimulus, s + adaptor, in the adapted state. The non-adapted spontaneous responses were allocated to the stimuli with amplitudes lower than or equal to the adaptor. The simulated shift in the response function resulted in an increase in the MI: the 6 μm shift increased the average MI values by 28.5% (single units) and 26.1% (multiunits), and the 12 μm shift increased the average MI values by 29.1% (single units) and 24.0% (multiunits). The simulation also reproduced the drop in response entropies: the 6 μm shift decreased the average response entropy by 5.6% (single units) and 5.7% (multiunits), and the 12 μm shift decreased the average respose entropy values by 12.7% (single units) and 12.6% (multiunits). Overall, the difference between the average simulated and true entropies were small, ranging from 0.1 to 2.1%.

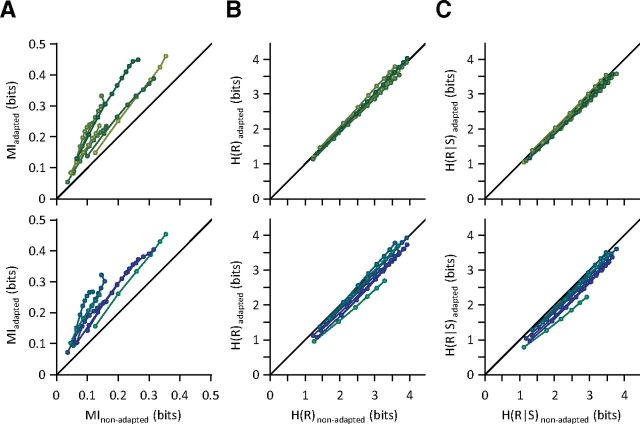
We further quantified the MI, response entropy, and conditional response entropy of populations of simultaneously recorded neurons. For every recording session, we calculated the information content of all possible populations of simultaneously recorded neurons with any size (up to the maximum number of single neurons simultaneously recorded in that session). For each session, increasing the population size resulted in an increase in the information content of the neuronal population. Across all population sizes, adaptation improved MI, and this effect was greater for larger populations (Fig. 3A). For each session, increasing the population size resulted in an increase in entropies (Fig. 3B,C). Similar to the pattern observed for individual neurons, the entropy of the pooled neuronal responses decreased with adaptation (Fig. 3B). Likewise, the conditional entropy of the pooled neuronal responses exhibited a decrease. The reduction in conditional entropy (Fig. 3C) outweighed the reduction in entropy of the pooled response, increasing the information content of the population through sensory adaptation, as shown in Figure 3A. As was the case for individual neurons, information efficiency, defined as the ratio of MI to the response entropy, was improved through sensory adaptation: the information efficiency increased by 70.6 ± 31.1% (mean ± SD across sessions) and 87.0 ± 28.6% in the 6 and 12 μm adaptation states compared with the non-adapted state.

Figure 3.

Figure 3.

Open in a new tab

Population information content and entropy. A, MI between pooled neuronal responses and the whole stimulus set for the 6 μm adaptation state (top) and 12 μm adaptation state (bottom) versus the non-adapted state. B, As in A but plotting the entropy of the pooled neuronal response. C, As in A but plotting the conditional entropy of the pooled neuronal response. Each point corresponds to a population size. For each population size, the values for all possible selections of that size were averaged within each session. Each line connects different population sizes within a session of simultaneously recorded single neurons. Within each session, MI and entropies increase with population size. For better visibility, multiple levels of brightness are used for different sessions.

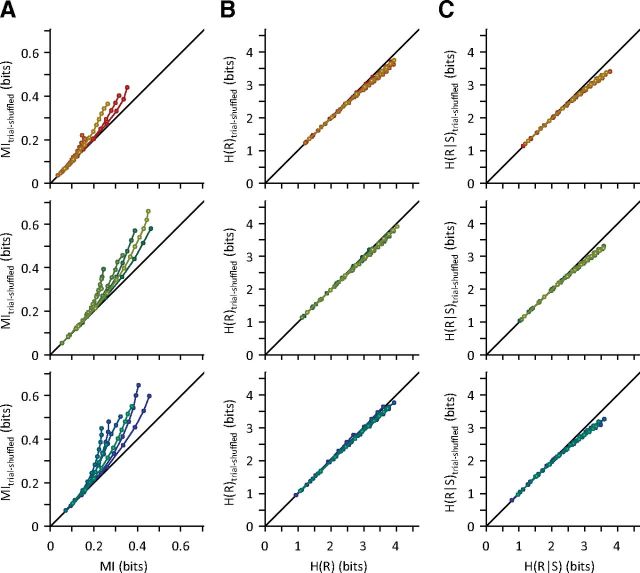
Cortical neurons in the primary somatosensory cortex, similar to other brain areas (Cohen and Kohn, 2011), exhibit a significant positive trial-to-trial covariability (Khatri et al., 2009; Adibi et al., 2013). How does the trial-to-trial covariability (noise correlation) across neurons affect the distribution of their pooled activity? To address this question, we further compared the information content (Fig. 4A), response entropy (Fig. 4B), and conditional entropy (Fig. 4C) of neuronal populations in the presence and absence of noise correlation. To decorrelate neuronal responses, we shuffled the order of trials for every neuron in the population. Shuffling trial sequences across neurons eliminates the trial-to-trial correlations without affecting the marginal distributions for individual neurons. Figure 4B compares the entropy of the pooled neuronal responses with and without artificial decorrelation. Across all adaptation states, trial shuffling reduced the entropy of the pooled neuronal responses. This is because correlation in neuronal activity increases the spread of the pooled responses. Removing noise correlations by trial shuffling decreased the conditional entropy (Fig. 4C). The reduction in conditional entropy (Fig. 4C) outweighed the reduction in entropy of the pooled response (Fig. 4B), as indicated by a net increase in MI values (Fig. 4A). This increase in the MI grew with population size. The increase in information with trial shuffling was greater under adaptation compared with the non-adapted state and greater in the 12 μm adaptation state compared with the 6 μm adaptation state (all p values <10−6, Wilcoxon's signed-rank test across population sizes and sessions).

Figure 4.

Figure 4.

Open in a new tab

The effect of noise correlations on the population information and entropy. A, MI for simultaneously recorded single neurons compared with the MI for the shuffled responses for each session in the non-adapted state (top), the 6 μm adaptation state (middle), and the 12 μm adaptation state (bottom). The shuffling procedure was repeated 50 times, and the average MI value is plotted as MItrial-shuffled. All conventions are the same as in Figure 3. B, as in A but plotting the entropy of pooled responses. C, As in A but plotting the pooled-response entropy conditional on stimulus.

Discussion

Adaptation has been shown to increase the efficiency of information transmission by matching neuronal response functions to the statistics of the environment (Barlow, 1961b; Smirnakis et al., 1997; Kvale and Schreiner, 2004; Dean et al., 2005; Hosoya et al., 2005; Durant et al., 2007; Maravall et al., 2007; Kobayashi et al., 2010; Adibi et al., 2013), accompanied by corresponding changes in perception (Clifford and Langley, 1996; Clifford and Wenderoth, 1999; Clifford et al., 2001; Noudoost et al., 2005; Krekelberg et al., 2006; Pestilli et al., 2007; Price and Born, 2013). How is this enhanced efficiency best understood? Does the sensory cortex act as an “adaptive source encoder” that maximizes the entropy of its codes (spike rate) (Attneave, 1954; Barlow, 1961a; Srinivasan et al., 1982; Atick, 1992) similar to an optimum source coder in the realm of communications (Shannon, 1948)? Or does it adaptively reduce the uncertainty of its code words (spike rate) for sensory stimuli to improve or maintain the information transmission?

Here, we focused on vibration coding in the rat whisker-barrel system, which provides efficient cortical processing and a high correlation between neuronal and behavioral performance (Adibi et al., 2012; Diamond and Arabzadeh, 2013). To identify the source of adaptation-induced enhancement in coding efficiency, we decomposed the information content of population responses into the entropy of the pooled neuronal responses and the conditional response entropy given stimulus. We demonstrated that, despite increasing the net information content of neuronal populations, adaptation slightly decreased the response entropy of the neurons. The enhancement in information content is attributable to the fact that adaptation reduced the conditional response entropy given the stimulus more than it did the response entropy across the entire stimulus set. Thus, barrel cortex neurons adaptively reduce the overall uncertainty of their responses to vibrotactile stimuli instead of increasing the entropy of neuronal responses (entropy maximization).

The reduction in entropy accompanied by a larger reduction in conditional entropy was also observed consistently at the level of single neurons. The reduction in response entropy through adaptation can be understood in terms of the lateral shift in the amplitude response function of individual neurons. The lateral shift increases the range of stimuli to which neurons respond at their spontaneous level. This results in a less uniform response distribution and consequently a reduction in the response entropy. This was accompanied by a greater reduction in stimulus-conditioned response entropy attributable to a reduction in the trial-to-trial response variance. Single-neuron response variance increases with firing rate. The lateral shift in the response function increases the range of stimuli to which neurons respond in a low response regimen, thus decreasing the overall response variance. At the level of single neurons, the reductions in entropy and conditional entropy can thus both be understood as a consequence of a lateral shift in the amplitude response function. The greater reduction in conditional entropy results in an increase in MI at the level of single neurons through adaptation. Because the lateral shift in response function lowers overall responsiveness (spike counts averaged across the whole stimulus set), this enhanced coding comes at a lower metabolic cost.

The effect of adaptation on the population response entropies reflects the effects of adaptation on single-neuron responses and, in addition, any effects of adaptation on the covariability between neurons in the population. Population response covariability is expected to widen the spread of summed responses compared with when they were decorrelated. We showed previously that cortical neurons exhibited positive correlations in their trial-to-trial variability, and adaptation increased these correlations (Adibi et al., 2013). These increased correlations in variability widen the spread of the pooled population responses and hence tend to increase pooled response entropy (Fig. 4B). However, covariability between neurons increases conditional response entropy by a greater amount (Fig. 4C), tending to reduce MI (Fig. 4A). Thus, the effect of adaptation on covariability between neurons is to reduce MI, diminishing the enhancement inherited from the responses of individual neurons.

Footnotes

This work was supported by the Australian Research Council Discovery Projects DP0987133 and DP130101364 and Australian National Health and Medical Research Council Project Grant 1028670. E.A. and C.W.G.C. are supported by Future Fellowships from the Australian Research Council.

References

  1. Adibi M, Arabzadeh E. A comparison of neuronal and behavioral detection and discrimination performances in rat whisker system. J Neurophysiol. 2011;105:356–365. doi: 10.1152/jn.00794.2010. [DOI] [PubMed] [Google Scholar]
  2. Adibi M, Diamond ME, Arabzadeh E. Behavioral study of whisker-mediated vibration sensation in rats. Proc Natl Acad Sci U S A. 2012;109:971–976. doi: 10.1073/pnas.1116726109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Adibi M, McDonald JS, Clifford CWG, Arabzadeh E. Adaptation improves neural coding efficiency despite increasing correlations in variability. J Neurosci. 2013;33:2108–2120. doi: 10.1523/JNEUROSCI.3449-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Arabzadeh E, Panzeri S, Diamond ME. Whisker vibration information carried by rat barrel cortex neurons. J Neurosci. 2004;24:6011–6020. doi: 10.1523/JNEUROSCI.1389-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Arabzadeh E, Panzeri S, Diamond ME. Deciphering the spike train of a sensory neuron: counts and temporal patterns in the rat whisker pathway. J Neurosci. 2006;26:9216–9226. doi: 10.1523/JNEUROSCI.1491-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Atick JJ. Could information theory provide an ecological theory of sensory processing? Network. 1992;3:213–251. doi: 10.1088/0954-898X/3/2/009. [DOI] [PubMed] [Google Scholar]
  7. Attneave F. Some informational aspects of visual perception. Psychol Rev. 1954;61:183–193. doi: 10.1037/h0054663. [DOI] [PubMed] [Google Scholar]
  8. Barlow HB. The coding of sensory messages. In: Thorpe WH, Zangwill OL, editors. Current problems in animal behaviour. New York: Cambridge UP; 1961a. pp. 331–360. [Google Scholar]
  9. Barlow HB. Possible principles underlying the transformation of sensory messages. Sens Commun. 1961b:217–234. [Google Scholar]
  10. Clifford CWG, Langley K. Psychophysics of motion adaptation parallels insect electrophysiology. Curr Biol. 1996;6:1340–1342. doi: 10.1016/S0960-9822(02)70721-5. [DOI] [PubMed] [Google Scholar]
  11. Clifford CWG, Wenderoth P. Adaptation to temporal modulation can enhance differential speed sensitivity. Vision Res. 1999;39:4324–4332. doi: 10.1016/S0042-6989(99)00151-0. [DOI] [PubMed] [Google Scholar]
  12. Clifford CWG, Wyatt AM, Arnold DH, Smith ST, Wenderoth P. Orthogonal adaptation improves orientation discrimination. Vision Res. 2001;41:151–159. doi: 10.1016/S0042-6989(00)00248-0. [DOI] [PubMed] [Google Scholar]
  13. Cohen MR, Kohn A. Measuring and interpreting neuronal correlations. Nat Neurosci. 2011;14:811–819. doi: 10.1038/nn.2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Cover TM, Thomas JA. Elements of information theory. New York: Wiley; 1991. [Google Scholar]
  15. Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci. 2005;8:1684–1689. doi: 10.1038/nn1541. [DOI] [PubMed] [Google Scholar]
  16. Diamond ME, Arabzadeh E. Whisker sensory system—from receptor to decision. Prog Neurobiol. 2013;103:28–40. doi: 10.1016/j.pneurobio.2012.05.013. [DOI] [PubMed] [Google Scholar]
  17. Durant S, Clifford CWG, Crowder NA, Price NSC, Ibbotson MR. Characterizing contrast adaptation in a population of cat primary visual cortical neurons using Fisher information. J Opt Soc Am A Opt Image Sci Vis. 2007;24:1529–1537. doi: 10.1364/JOSAA.24.001529. [DOI] [PubMed] [Google Scholar]
  18. Gaudry KS, Reinagel P. Benefits of contrast normalization demonstrated in neurons and model cells. J Neurosci. 2007;27:8071–8079. doi: 10.1523/JNEUROSCI.1093-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hosoya T, Baccus SA, Meister M. Dynamic predictive coding by the retina. Nature. 2005;436:71–77. doi: 10.1038/nature03689. [DOI] [PubMed] [Google Scholar]
  20. Khatri V, Bruno RM, Simons DJ. Stimulus-specific and stimulus-nonspecific firing synchrony and its modulation by sensory adaptation in the whisker-to-barrel pathway. J Neurophysiol. 2009;101:2328–2338. doi: 10.1152/jn.91151.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kobayashi S, Pinto de Carvalho O, Schultz W. Adaptation of reward sensitivity in orbitofrontal neurons. J Neurosci. 2010;30:534–544. doi: 10.1523/JNEUROSCI.4009-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Krekelberg B, van Wezel RJA, Albright TD. Adaptation in macaque MT reduces perceived speed and improves speed discrimination. J Neurophysiol. 2006;95:255–270. doi: 10.1152/jn.00750.2005. [DOI] [PubMed] [Google Scholar]
  23. Kvale MN, Schreiner CE. Short-term adaptation of auditory receptive fields to dynamic stimuli. J Neurophysiol. 2004;91:604–612. doi: 10.1152/jn.00484.2003. [DOI] [PubMed] [Google Scholar]
  24. Magri C, Whittingstall K, Singh V, Logothetis NK, Panzeri S. A toolbox for the fast information analysis of multiple-site LFP, EEG and spike train recordings. BMC Neurosci. 2009;10:81. doi: 10.1186/1471-2202-10-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Maravall M, Petersen RS, Fairhall AL, Arabzadeh E, Diamond ME. Shifts in coding properties and maintenance of information transmission during adaptation in barrel cortex. PLoS Biol. 2007;5:e19. doi: 10.1371/journal.pbio.0050019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Noudoost B, Adibi M, Moeeny A, Esteky H. Configural and analytical processing of familiar and unfamiliar objects. Brain Res Cogn Brain Res. 2005;24:436–441. doi: 10.1016/j.cogbrainres.2005.02.012. [DOI] [PubMed] [Google Scholar]
  27. Panzeri S, Treves A. Analytical estimates of limited sampling biases in different information measures. Network. 1996;7:87–107. doi: 10.1088/0954-898X/7/1/006. [DOI] [PubMed] [Google Scholar]
  28. Panzeri S, Senatore R, Montemurro MA, Petersen RS. Correcting for the sampling bias problem in spike train information measures. J Neurophysiol. 2007;98:1064–1072. doi: 10.1152/jn.00559.2007. [DOI] [PubMed] [Google Scholar]
  29. Pestilli F, Viera G, Carrasco M. How do attention and adaptation affect contrast sensitivity? J Vis. 2007;7(7):9, 1–12. doi: 10.1167/7.7.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Price NS, Born RT. Adaptation to speed in macaque middle temporal and medial superior temporal areas. J Neurosci. 2013;33:4359–4368. doi: 10.1523/JNEUROSCI.3165-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Reinagel P, Reid RC. Temporal coding of visual information in the thalamus. J Neurosci. 2000;20:5392–5400. doi: 10.1523/JNEUROSCI.20-14-05392.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. 1948;27:379–423. 623–656. [Google Scholar]
  33. Smirnakis SM, Berry MJ, Warland DK, Bialek W, Meister M. Adaptation of retinal processing to image contrast and spatial scale. Nature. 1997;386:69–73. doi: 10.1038/386069a0. [DOI] [PubMed] [Google Scholar]
  34. Srinivasan MV, Laughlin SB, Dubs A. Predictive coding: a fresh view of inhibition in the retina. Proc R Soc Lond B Biol Sci. 1982;216:427–459. doi: 10.1098/rspb.1982.0085. [DOI] [PubMed] [Google Scholar]
  35. Vinje WE, Gallant JL. Natural stimulation of the nonclassical receptive field increases information transmission efficiency in V1. J Neurosci. 2002;22:2904–2915. doi: 10.1523/JNEUROSCI.22-07-02904.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wang Q, Webber RM, Stanley GB. Thalamic synchrony and the adaptive gating of information flow to cortex. Nat Neurosci. 2010;13:1534–1541. doi: 10.1038/nn.2670. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES