Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Aug 2;4(8):13209–13217. doi: 10.1021/acsomega.9b01359

Improving the Quantum Capacitance of Graphene-Based Supercapacitors by the Doping and Co-Doping: First-Principles Calculations

Qiang Xu †,‡, Guangmin Yang §,*, Xiaofeng Fan †,*, Weitao Zheng †
PMCID: PMC6705244  PMID: 31460448

Abstract

graphic file with name ao9b01359_0008.jpg

We explore the stability, electronic properties, and quantum capacitance of doped/co-doped graphene with B, N, P, and S atoms based on first-principles methods. B, N, P, and S atoms are strongly bonded with graphene, and all of the relaxed systems exhibit metallic behavior. While graphene with high surface area can enhance the double-layer capacitance, its low quantum capacitance limits its application in supercapacitors. This is a direct result of the limited density of states near the Dirac point in pristine graphene. We find that the triple N and S doping with single vacancy exhibits a relatively stable structure and high quantum capacitance. It is proposed that they could be used as ideal electrode materials for symmetry supercapacitors. The advantages of some co-doped graphene systems have been demonstrated by calculating quantum capacitance. We find that the N/S and N/P co-doped graphene with single vacancy is suitable for asymmetric supercapacitors. The enhanced quantum capacitance contributes to the formation of localized states near the Dirac point and/or Fermi-level shifts by introducing the dopant and vacancy complex.

1. Introduction

Supercapacitors with a simple charging circuit have high power delivery and long lifetime and are thus widely used in a wide temperature range.1−8 They are also called electric double-layer capacitors (EDLCs), and their capacitance is much higher than that of traditional dielectric capacitors. In conventional capacitors, metals are used as electrodes and the limited surface area hinders the enhancement of capacitance. In supercapacitors, different kinds of carbon materials are generally used and the electrode–electrolyte interface with large area makes the improvement of capacitance possible since the charges can be stored electrostatically with reversible adsorption of ions at the interface. Graphene is a single-atom-layer material and has been promising in EDLCs in recent years.9−11 However, in the experiments, such as those of Biener et al.,12,13 graphene-based electrodes were used and the results are contrary to what is expected. For an ideal metal, perfect screening can result in the confinement of excess charge on its surface. Therefore, its capacitance can be ignored when it is used as part of the electrode.14 However, graphene-based materials do not undergo good screening due to the low density of free electrons. It has been noted that the quantum capacitance of these materials plays an important role15 when they are used as electrode materials. From the theoretical work of Paek and co-workers,14 quantum capacitance of graphene is the key limiting factor affecting the total capacitance when it is used as part of electrode. In addition, pristine graphene has also been limited by poor accessibility to the electrolyte in practical implementation.10,16−19

With low-dimensional materials as electrodes, for example, carbon nanotubes and graphene, total capacitance CT is a reflection of the overall effect of electrode capacitance (also named quantum capacitance CQ) and double-layer capacitance CD, with the theoretical relationship20−23 1/CT = 1/CQ + 1/CD. Although the CQ value of pristine graphene is limited, in graphene-like two-dimensional systems, CQ is comparable to CD. Some theoretical works have demonstrated that the quantum capacitance of graphene could be modulated by different ways, including nonmetal and metal doping, metal adsorption, and vacancy defects.24−30 Experimental works have shown that the doping with defects or functionalization of graphene can improve the capacitance considerably.31 To date, experimental works have been focused on co-doped graphene supercapacitor materials such as the co-doping of N/S and N/P.31−38 It has been noted that the theoretical research on the quantum capacitance of co-doped graphene is insufficient, especially for N/S(P) co-doping. The concentration effect of co-doping, interaction between heteroatoms, and structure stability issues introduced via the doping have been almost ignored.

In this paper, critical issues of graphene-based materials as the electrodes of supercapacitor have been investigated using first-principles methods. We examined the effects of doping/co-doping with dopants, including B, N, P, and S atoms; concentration of dopants; and the ratio of dopants in co-doping on the stability, electronic structure, and quantum capacitance of graphene. The electronic properties of N/S, N/P, and P/S co-doped graphene, the interaction between doped atoms, and the influence on the CQ–V curves have been investigated in detail. The quantum capacitance has been found to be enhanced based on proper doping with defects. We discussed the ways these doping experiments were used to improve the overall performance of graphene-based electrode materials.

2. Computational Methods

All of the calculations were performed by the projector-augmented wave potentials method on the basis of density functional theory (DFT) as implemented in the VASP code.39,40 The generalized gradient approximation41 with the parameterization of Perdew–Burke–Ernzerhof was used to express the exchange–correlation energy of interacting electrons. The high-density k-space integral with plane-wave basis set was chosen to ensure that the total energy was converged at 1 meV/atom level. For the plane-wave expansion, the kinetic energy cutoff of 450 eV was determined to be sufficient. The Monkhorst–Pack method was used to sample the k-points in the Brillouin zone. We chose the lattice constant of graphene with 2.465 Å, which was consistent with the experimental results. On the basis of primitive cell, four hexagonal structures as the ideal models in Figure 1 have been used to simulate the doping effect, including the dopants B, N, P, and S, considering the spin polarization effect. The vacuum space of 18 Å along the Z direction is selected in the supercell method. The Brillouin zones of 6 × 6, 5 × 5, 4 × 4, and 3 × 3 supercells were sampled with the Γ-centered k-point grids of 8 × 8 × 1, 10 × 10 × 1, 12 × 12 × 1, and 16 × 16 × 1, respectively.

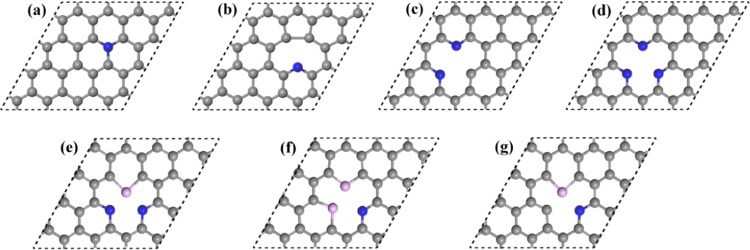
Figure 1.

Figure 1

Open in a new tab

Atomic structures of proposed doping models of graphene, including (a) quaternary N(B, P, S)-doped graphene (model-a); (b–d) single-vacancy graphene with the single pyridine-N (B, P, S) doping (mode-b), double-N (B, P, S) doping (model-c), and triple-N (B, P, S) doping (model-d); and (e–g) single-vacancy graphene with the NNS(P) co-doping (model-e), NSS(P) co-doping (model-f), and NS(P) co-doping (model-g).

The electrochemical potential μ can be altered rigidly by the local potential Φ with the formula μ = eΦ, where e is the elementary charge. Therefore, on the electrode, the excess charge density can be obtained by modulating the local potential with the formula42

2. 1

where D(E) is the calculated density of states (DOS), f(E) is the Fermi–Dirac distribution function, and E is the energy of Fermi level EF. The quantum capacitance is expressed as CQ = dQ/dΦ, where dQ and dΦ represent the differentials of local charge density and local potential, respectively. Using the analytical expression (eq 1) of ΔQ, the quantum capacitance CQ can be written as14

2. 2

where the thermal broadening function FT(E) is represented as

2.

In the calculation, the temperature is set to 300 K, kB is the Boltzmann constant, and high-accuracy D(E) is calculated from DFT using a linear interpolation method for the integral calculation.

3. Results and Discussion

3.1. Geometric and Electronic Properties of Doped Graphene

We have selected B, N, P, and S as the dopants for graphene, to investigate the effect of different dopants on the electronic properties. The structural models including the doping and co-doping are shown in Figure 1a–g. The calculation results show a C–C bond length of 1.403 Å for pristine graphene, which is consistent with the previous calculation.43 Structural parameters, containing C–X bond lengths, X–X bond lengths, C–X–C bond angles, formation energy ΔEf, and Bader charge ρB from the graphene plane are listed in Table S1. In the relaxed structure of the P-doping (S-doping) with the quaternary doping model (model-a) in Figure 1a, the atom of P(S) is projected out of the graphene plane with P(S)–C bond length of 1.61(1.62) Å and C–P(S)–C bond angle of 120.01°. Along with P(S)-atom protrusion, three nearest-neighboring carbon atoms protrude from the graphene plane, and the length of the neighboring C–C bond is changed from 1.402 to 1.394 Å (1.382 Å). Among the four doping models in Figure 1a–d, the N (or B)-doped graphene with model-a has notable lower value for the calculated formation energies, as shown in Table S1. The formation energies in doping systems with model-a are in the order of S > P > B > N. In general, compared to carbon atoms, the size and electronegativity of atomic dopants have significant effects on the stability of doped graphene structure. The larger atomic size and the lower electronegativity25,44 of the dopants result in the decrease of structure stability. The N atom has a higher electronegativity and relatively smaller atomic size comparable to carbon atom. Thus, in the case of model-a system, the N doping graphene is the most stable.

From Table S1, we can find that the stability is enhanced with increasing doping concentration for the B-, N-, and S-doping with single vacancy based on model-b, model-c, and model-d of the same dopant (Figure 1b–d), while the P-doping shows an opposite behavior. The formation energies with model-d are in the order of P > B > N > S, and the P-doped graphene structure shows the largest formation energy among the investigated structures, which suggests that the structure is very unstable. In the structures of triple-B, -N, and -S doping with model-d, the presence of single vacancy assists the structures to be more stable with lower formation energies. For the triple-P doping, it may be due to the largest size of dopant, which induces the higher formation energy. According to Bader analysis, the charge transfer occurs from B, P, and S atoms to graphene because of the lower electronegativity of B, P, and S than C, and only N atom shows an opposite behavior.

For the co-doping, such as N/S, N/P, and P/S in Table S1, the dopants occupy the sites around vacancies in the models. Such configurations are more stable than other configurations with dopants on other sites away from vacancies. It is found that the formation energies of N/S and N/P co-doping are smaller than that of P/S. In Table S1, it is also indicated that the N/S and N/P co-doping is even more stable than the single-element doping models with vacancies in Figure 1b–d. In experiments, graphene oxides are generally used as the precursor and the defects of vacancies are popular in the synthesized graphene. In these co-doped graphene, the configurations with the complex of dopants around vacancies are popular, as reported in experiments about N/S and N/P co-doping.31−38

Figure S1 in the Supporting Information shows the DOSs of pristine graphene, the B-, N-, P-, and S-doping with model-a in Figure 1a. For the doped graphene, all of these dopants result in the shift of Fermi level with a small band gap at the Dirac point. The dopant B results in p-type doping, and others result in n-type doping. From the DOS of pyridine B-, N-, P-, and S-doping with model-b, the B-doping introduces obvious localized states near Fermi level in Figure S2 in the Supporting Information. For double-B-, N-, P-, and S-doping with model-c in Figure 1c, only the P-doping has no localized states near the Fermi level (Figure S3 in the Supporting Information). For the triple B-, N-, P-, and S-doping with model-d in Figure 1d, all of them have higher localized states near Fermi level (Figures S4 and S5). To evaluate the effect of N/S, N/P, and P/S co-doped graphene on the supercapacitor performance, the DOS and LDOS of these co-doped systems are considered in Figures S6–S8 in the Supporting Information. The change of electronic properties will be discussed in detail in the next section.

Figure 2 shows the band-decomposed charge density isosurfaces above and below Fermi level from −0.5 to 0.5 eV for the triple B-, N-, P-, and S-doping with model-d. In all of the cases, the charges near Fermi level are distributed mainly around the vacancy. Compared to the charges of triple B- and S-doping, the charge distributions of triple N- and P-doping are more localized. In the case of triple-B(N, P)-doped graphene, the Fermi level has the trend of moving down to the valence band of the pristine graphene due to electron deficiency, while the triple-S-doped Fermi level moves up to the conduction band, in Figure S5 in the Supporting Information. This can be understood by the basic chemical valance states about the configurations with three dopant atoms around single vacancy. For example, three P (N) atoms around vacancy have 15 valance electrons and 4 C atoms in pristine graphene have 16 valence electrons. Thus, compared to Fermi level at the Dirac point of pristine graphene, the Fermi level of triple-B (N, P) doping around vacancy will be shifted down. In Figure S5(b) in the Supporting Information, with the case of triple-N doping as example, the bands near Fermi level indicate that there are two degenerate states (quasi-localized) and one nonlocal state at Γ point. In addition, the bands near Fermi level are spin-polarized for the cases of N and P doping. For these electronic structures, we can expect that when excess holes are injected, the states associated with the N lone pairs will be emptied first.

Figure 2.

Figure 2

Open in a new tab

(a–d) Band-decomposed charge density isosurfaces (5.3 × 10–3 e/Å3) above and below Fermi level from −0.5 to 0.5 eV for the triple-B(N, P, S)-doped graphene with model-d in Figure 1d.

3.2. Quantum Capacitance of Doped Graphene

Figure 3 shows the calculated quantum capacitances for doping graphene with the models in Figure 1a–d, based on eq 2. The CQ resembles their respective DOS profiles under thermal broadening. In a previous report, CQ of pristine graphene has a minimum value around 0.58 μF/cm2 at zero applied potential, where the Dirac point is located (note that the value of CQ under zero potential is zero without thermal effect).45 In experiment,46 the measured minimum CQ of pristine graphene was reported to be 2.5 μF/cm2. The significant disparity of graphene’s quantum capacitance between the experimental and theoretical values results from the fact that there is no perfect structure of graphene in the experiment. It is clearly seen that the doping alters the DOS of graphene, thus CQ is modified. All of these doping systems about graphene are liable to have highly irregular CQ profiles, with sharp local enhancement near the neutral point.

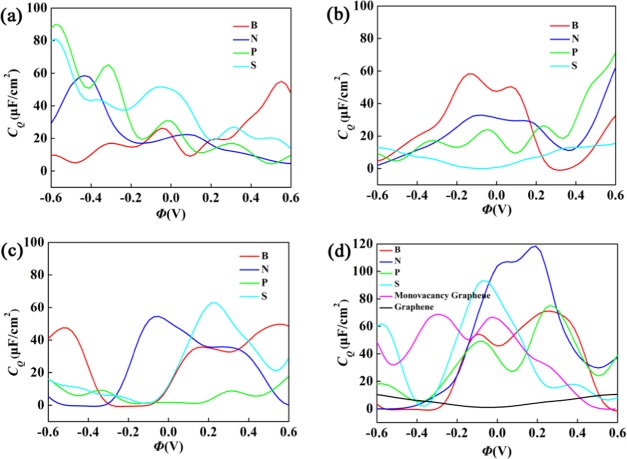
Figure 3.

Figure 3

Open in a new tab

Calculated quantum capacitance (CQ) as a function of local electrode potential (Φ) for the B(N,P,S)-doped graphene with (a) model-a, (b) model-b, (c) model-c, and (d) model-d. The results are obtained with the supercell 4 × 4.

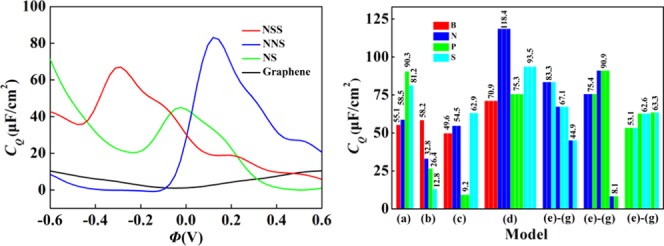
For the quaternary-B, -N, -P, and -S doping based on model-a in Figure 1a, the local maxima of CQ near 0 V are 55.1, 58.5, 90.3, and 81.2 μF/cm2, respectively. By checking whether the CQ values under positive and negative bias voltages are similar, we can define the symmetric and asymmetric behaviors. We can observe that the CQ values of the single-B (model-b) and triple-S (model-d) doping do not have obvious difference under positive and negative bias voltages and thus exhibit symmetric behavior, whereas the double-B, -N, and -S doping (mode-c) have obvious asymmetric behavior. At larger negative bias, quaternary-P, -S-doped graphene with model-a shows a huge quantum capacitance, while triple N, S doping with model-d shows a higher quantum capacitance under smaller bias, negative or positive. It is because of the higher density of states near the Fermi level compared to other doped systems. Based on the doping models in Figure 1b–d, the quantum capacitance enhances, with increasing N and S concentrations from single-atom doping to triple-atom doping. For the B-doping, as the concentration increases, it decreases first and then increases. For the P-doping, the enhancement of quantum capacitance is not very high. For the triple B-, N-, P-, and S-doping, the local maxima of CQ near zero bias are 70.9, 118.4, 75.3, and 93.5 μF/cm2, respectively. This indicates that the triple-atom doping with single vacancy can obviously increase the CQ value of pristine graphene. Especially, the triple N- and S-doping show a markedly improved CQ. They also exhibit a lower formation energy suggesting a more stable structure. Based on these results, the triple-N, S doping (Figure 3d) is strongly recommended for use as an electrode in symmetric supercapacitors. On the other hand, the double-N, S doping graphene (Figure 3c) has broad application prospects as the electrode material of asymmetric supercapacitors.

The surface charge density at some potential drop Φ is obtained by the formula

3.2. 3

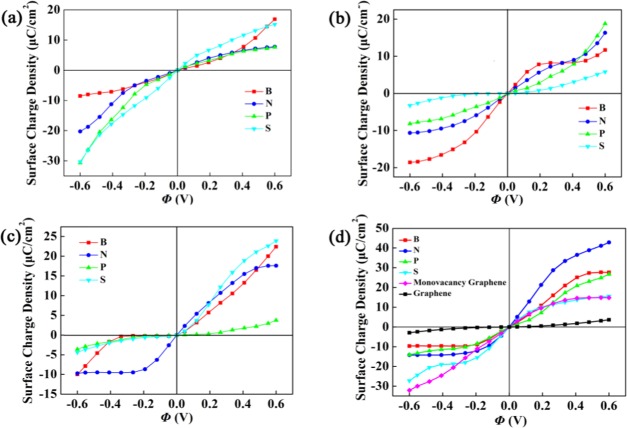
where CQ(V) is quantum capacitance at local electrode potential V. Figure 4 shows the surface charge density vs potential drop Φ at a given electrode potential for different dopants. The doped graphene electrodes can generally store more charge than pristine graphene with the change of potential drop from −0.6 to 0.6 V. The increase in charge capacity is attributed to the direct result of additional availability of states near Fermi level. The results show that charge accumulation under negative bias is more advantageous for the quaternary-S(P) doping with model-a, and positive bias for the triple-N doping with model-d. Scilicet, getting the same electrode charge density, a lower positive Φ is sufficient for the triple-N doping. However, it is also clear that these electrodes no longer store charges symmetrically. As a consequence, the different doping types may be suited for different terminals. Among these models in Figure 1, the triple-atom doping with single vacancy (model-d) exhibits the best performance. The triple-N doping is the best at positive Φ, and the triple-S doping is the best at negative Φ.

Figure 4.

Figure 4

Open in a new tab

Surface charge vs potential drop Φ between −0.6 and 0.6 eV for the B(N,P,S)-doped graphene with (a) model-a, (b) model-b, (c) model-c, and (d) model-d. The results are obtained with the supercell 4 × 4.

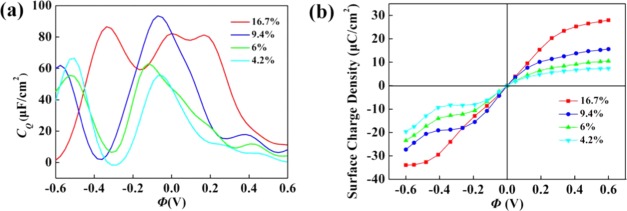
The concentration effect of the triple-S doping with model-d is also investigated. The S concentration is changed by modulating the ratio of 3S+ vacancy complex and C atoms with supercell methods. Due to the contribution of the 3S+ vacancy complex, the DOS of graphene near Fermi level has been changed significantly (Figure S9 in the Supporting Information). With the increase of S concentration, the curve of CQ and the surface charge vs potential drop Φ at a given electrode potential for different S concentrations is shown in Figure 5. With S doping, the location of the local minimum under negative bias voltage shifts to about 0.2–0.4 V, as S concentration increases from 4.2 to 16.7%. The maximum value of CQ increases from 55.2 to 93.5 μF/cm2 at approximately zero bias. Clearly, following the increase of the concentration of 3S+ vacancy complex, CQ and surface charge are increased for small potential drop. In addition, the energy region of potential drop with high CQ value becomes broad. These can be attributed to the increase of localized states near Fermi level. In addition, with the increase of defect concentration, the interaction between defects becomes obvious and results in the broadening of energy region of localized states near Fermi level.

Figure 5.

Figure 5

Open in a new tab

(a) Calculated quantum capacitance (CQ) as a function of local electrode potential (Φ) and (b) surface charge vs potential drop Φ between −0.6 and 0.6 eV for the triple-S-doped graphene with model-d and with different S concentrations, including 4.2, 6, 9.4, and 16.7%. The results are obtained with the supercells including 6 × 6, 5 × 5, 4 × 4, and 3 × 3.

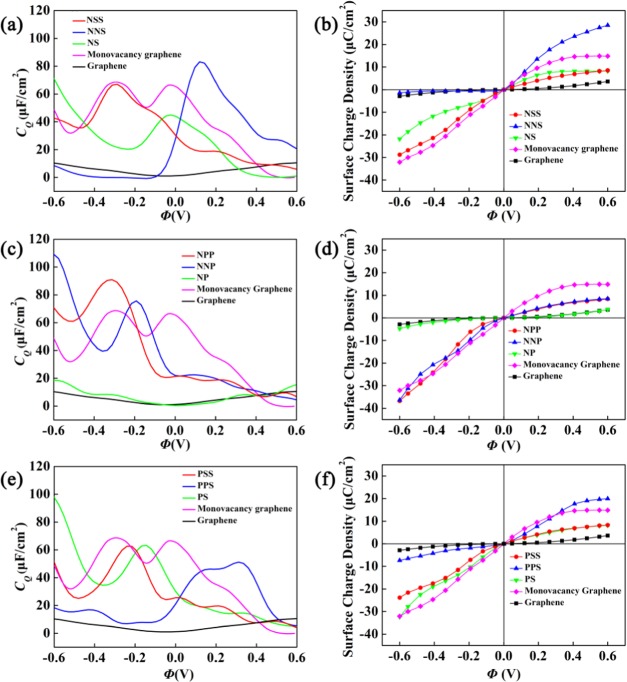
For the N/S, N/P, and P/S co-doping, the CQ and surface charge density vs the potential drop in the range of −0.6 to +0.6 V are shown in Figure 6. For the N/S co-doping system, it is obvious that the CQ value is higher than that of graphene doped with N alone because the introduced S heteroatom forms new hybrid states near Fermi level. Following the change of N/S ratio based on the NS-doping, the maximum of CQ increases from 44.9 μF/cm2 at −0.024 V to 83.3 μF/cm2 at 0.13 V for the NNS-doping and 67.1 μF/cm2 at −0.29 V for the NSS-doping. From the observation of LDOS and band structure (Figures S6 and S10 in the Supporting Information), this can be attributed to the quasi-localized states near Fermi level induced by the doped N and S. For the NS-doping, the surface charge density is obviously larger than that of pristine graphene in Figure 6b. For the NSS-doping, the surface charge density under negative bias is increased, compared to that of NS-doping, while the surface charge density of NNS-doping is increased under positive bias. In the band structures of the N/S co-doped systems, N atom doping shifts the Fermi level to the valence band, whereas S atom co-doping shifts the Fermi level to the conduction band and forms a new electrode state near the Fermi level. By analyzing the geometrical structures of the NSS-doping and NNS-doping (Table S1), the C–S–C angle is larger than that of the NS-doping, but less than 120°. The C–N bond length is shorter than the C–S bond length. This indicates that the connection between N and C atoms is more firm.

Figure 6.

Figure 6

Open in a new tab

(a, c, e) Calculated quantum capacitance (CQ) as a function of local electrode potential (Φ) and (b, d, f) surface charge vs potential drop and Φ between −0.6 and 0.6 eV for the N/S co-doping, N/P co-doping, and P/S co-doping with model-e, model-f, and model-g. The quantum capacitance and surface charge vs potential drop of pristine graphene are shown as a reference. The results are obtained with the supercells of 4 × 4.

For the N/P co-doping, the results are shown in Figure 6c,d. For the NP-doping, no quasi-localized states are found near the Dirac point. The U-shaped CQ–V curve is formed, and the CQ value is much small around 0 V. Its CQ–V curve is mostly coincident with pristine graphene around zero bias voltage, and the CQ value enhances along with the located electrode potential in the ranges of 0 −–0.6 V and 0–+0.6 V. When another N or P atom is embedded into the NP co-doped graphene, from the observation of LDOS (Figure S7 in the Supporting Information), quasi-localized states near Fermi level are induced by the doped N and P atoms. The CQ value of NNP- and NPP-doped graphene in Figure 6c shows maximum values of 75.3 and 93.5 μF/cm2 at −0.19 and −0.32 V, respectively. For both NPP-doping and NNP-doping, the surface charge density is found to obviously increase under negative bias.

For the P/S co-doping with different ratios, including 1:1 (PS-doping), 1:2 (PSS-doping), and 2:1 (SSP doping), CQ and surface charge density vs the potential drop in the range of −0.6–+0.6 V are shown in Figure 6e,f. For the P/S co-doping system, it is obvious that the CQ value is higher than that of graphene. Following the increase of P or S based on the PS-doping, the maximum of CQ decreases from 63.3 μF/cm2 at −0.14 V to 51.1 μF/cm2 at 0.31 V for the PPS-doping and to 62.6 μF/cm2 at −0.24 V for the PSS-doping. The curve of surface charge density of PSS-doping is similar to that of PS-doping. For the PPS-doping, the surface charge density increases under positive bias and decreases under negative bias compared to PS-doping. This is attributed to the fact that both the PS-doping and PSS-doping result in the n-type doping and the PPS-doping induces the shift-down of Fermi level, besides the local density of states near Fermi level (Figure S8 in the Supporting Information).

The triple-N-doped graphene obtains the maximum CQ value (118.4 μF/cm2) at 0.21 V, which is greatly increased compared to that of the N/S, N/P, P/S co-doped graphene and other investigated systems, as shown in Figure 7. It can be attributed to the localized/nonlocalized states near Fermi level due to the introduction of 3N+ vacancy complex. It is indicated that at low/high doping concentration, such as 2/31 and 3/31 (double-N, triple-N-doped graphene with single vacancy) where the number of heteroatoms is divided by the total number of atoms, substituting one N atom with S could change the electronic states and reduce the quantum capacitance slightly. The maximum CQ of the triple-N-doped graphene is larger than that of the NPP and NNP-doping. Especially, at low N doping concentration, such as 2/31, replacing one nitrogen atom with P could vary the electronic states and reduce the quantum capacitance seriously. The NP-doping has a detrimental effect on quantum capacitance. This behavior is attributed to the suppression of states near Fermi level by co-doping N into single P-doped graphene with single vacancy. At a higher doping concentration, such as 3/31, replacing one N atom with P reduces the quantum capacitance slightly. Based on these results, NNP- and NPP-doped graphene is recommended as cathode material for asymmetric supercapacitors. On the contrary, for the triple-N, S doping, it could be a promising candidate as an electrode material for symmetric supercapacitors.

Figure 7.

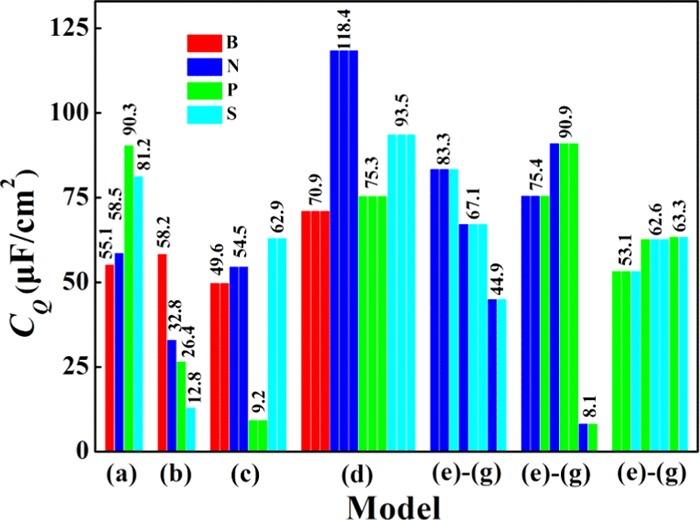
Figure 7

Open in a new tab

Change trend chart of the maximum value of CQ for the B(N, P, S)-doped graphene with different doping models (model-a, model-b, model-c, and model-d) and the N/S, N/P-co-doped graphene with different models (model-e, model-f, and model-g). The results are obtained with the supercell 4 × 4.

In current experiments on the use of doped graphene as the electrodes of supercapacitors, the graphene-based materials have much vacancies because graphene oxides are generally used as the precursor.43 Vacancies play a major role in the doping/co-doping processes since vacancies can reduce the formation energies of doping defects.47 For the doping, the dopants would like to occupy the sites around vacancies to form the dopant + vacancy complex. Therefore, we focus on the effect of the dopant + vacancy complex (the models in Figure 1) on the CQ of graphene. Due to the synergistic effect, the N/S and N/S co-doping is found to be easier than the doping with single elements (Table S1). It is interesting that a large number of experiments have been focused on the N/S and N/P co-doping.31−38

The CQ of pristine graphene is small due to the limited density of states around the Dirac point. From the above analysis, we can find that all of the three ways, including doping, co-doping, and vacancies, can enhance the CQ of pristine graphene to some extent. The enhancement of CQ is ascribed to the increase of DOSs near Fermi level. The single vacancy can induce the localized states near Fermi level with the breaking of the Dirac point24 and thus enhance the CQ. The single-atom doping (model-a in Figure 1a) can shift Fermi level to the energy region with high density of states and thus enhance the CQ. The doping and co-doping with the models in Figure 1b–g can introduce the dopant + vacancy complex to induce the localized states near Fermi level or/and shift Fermi level and thus increase the DOSs near Fermi level to enhance the CQ. The experimental results can just give the total capacitance and does not separate the CQ from the total capacitance.34−38 All of the experimental results indicate the total capacitance is enhanced by the doping or/and co-doping. From the previous research,14 the small CQ of graphene limits mainly the enhancement of total capacitance of graphene-based materials. It can be deduced that the enhancement of quantum capacitance has a major contribution to the increase of total capacitance. Therefore, the formation of dopant + vacancy complex is an important factor for the high total capacitance observed in experiments due to the co-doping, such as N/P and N/S.

Here, we also analyze theoretically the total capacitances (CT) of N-doped graphene (model-d) and pristine graphene as the electrodes. The total interfacial capacitances can be represented as a series of CQ and CD. CD is obtained from classical molecular dynamics simulation for the 1 M NaCl aqueous electrolyte.23 With the CQ and CD values calculated above, we estimate CT as a function of applied potential ϕ, as shown in Figure S11. The CT curve of pristine graphene is U-shaped. From the CT curve of nitrogen-doped graphene, the CT is obviously improved. Under small potential drop, the CT from pristine graphene is about 40 F/g and that of nitrogen-doped graphene is about 140 F/g. These are consistent with the previous experimental results about N-doped graphene.11

4. Conclusions

The effects of doping (B, N, P, S) and co-doping (N/S, N/P, P/S) on the structural parameters, electronic properties, and quantum capacitance of graphene have been investigated systematically with first-principles methods. Based on the calculated results, it is clearly shown that the quantum capacitance of graphene can be increased prominently by the doping. These modulations significantly change the band structure by introducing localized states near Dirac point and/or Fermi-level shifts. The localized states formed near Fermi level are found to enhance the quantum capacitance of pristine graphene. Among these doping models, the triple N- and S-doping with single vacancy is the best candidate among the investigated structures for the EDLCs’ electrode. With the increase of doping concentrations, such as triple-S doping with single vacancy, the quantum capacitance increases monotonically. The investigation also provides a deeper understanding of N/S, N/P, and P/S co-doped graphene, and a potential and effective method to enhance quantum capacitance is proposed by controlling configuration and the ratio of N/S, N/P, and P/S, which can serve as asymmetric supercapacitor electrodes. For N/S co-doping, N and S atoms have opposite effects on the electronic structure; when N or S is embedded, Fermi levels move to valence band or conduction band, respectively. The new electronic density of states near the Fermi level were introduced when S was embedded into pyridinic-N-doped graphene, which causes the increase of maximum quantum capacitance of co-doped graphene to nearly 50%. Among all of these doping types, including the co-doping, the triple N doping with single vacancy is found to afford the largest quantum capacitance.

Acknowledgments

X.F. acknowledges the financial support from the National Key R&D Development Program of China (Grant no. 2016YFA0200400). G.Y. acknowledges the support by the thirteenth Five-year Planning Project of Jilin Provincial Education Department Foundation (Grant no. JJKH20170651KJ), Natural Science Foundation of Jilin Province (Grant no. 20170101099JC), and Natural Science Foundation (No. 001010) of Changchun Normal University. Q.X. acknowledges the support by the Natural Science Foundation of Changchun Institute of Technology.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b01359.

  • DOS and band structures of graphene with different types of defects (Figures S1−S10); total DOS and LDOS are the sum of spin-up and spin-down bands; spin-up and spin-down band structures of B, N, P and S doping graphene models; The total interfacial capacitance of nitrogen-doped and pristine graphene (Figure S11) ; Calculated parameters for B, N, P and S doping graphene (Table S1) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b01359_si_001.pdf (1.5MB, pdf)

References

  1. Zhang L. L.; Zhou R.; Zhao X. S. Graphene-based materials as supercapacitor electrodes. J. Mater. Chem. 2010, 20, 5983–5992. 10.1039/C000417K. [DOI] [Google Scholar]
  2. Chen Y.; Zhang X.; Zhang D.; Yu P.; Ma Y. High performance supercapacitors based on reduced graphene oxide in aqueous and ionic liquid electrolytes. Carbon 2011, 49, 573–580. 10.1016/j.carbon.2010.09.060. [DOI] [Google Scholar]
  3. Stoller M. D.; Park S.; Zhu Y.; An J.; Ruoff R. S. Graphene-based ultracapacitors. Nano Lett. 2008, 8, 3498–3502. 10.1021/nl802558y. [DOI] [PubMed] [Google Scholar]
  4. Vivekchand S.; Rout C. S.; Subrahmanyam K.; Govindaraj A.; Rao C. Graphene-based electrochemical supercapacitors. J. Chem. Sci. 2008, 120, 9–13. 10.1007/s12039-008-0002-7. [DOI] [Google Scholar]
  5. Chang P. A novel kind of activated carbon foam electrode for electric double layer capacitors. Int. J. Electrochem. Sci. 2017, 1846–1862. 10.20964/2017.03.29. [DOI] [Google Scholar]
  6. Parida K.; Bhavanasi V.; Kumar V.; Wang J.; Lee P. S. Fast charging self-powered electric double layer capacitor. J. Power Sources 2017, 342, 70–78. 10.1016/j.jpowsour.2016.11.083. [DOI] [Google Scholar]
  7. Xu Y.; Chang L.; Hu Y. H. KOH-assisted microwave post-treatment of activated carbon for efficient symmetrical double-layer capacitors. Int. J. Energy Res. 2017, 41, 728–735. 10.1002/er.3676. [DOI] [Google Scholar]
  8. Simon P.; Gogotsi Y. Materials for electrochemical capacitors. Nat. Mater. 2008, 7, 845–854. 10.1038/nmat2297. [DOI] [PubMed] [Google Scholar]
  9. Xia J.; Chen F.; Li J.; Tao N. Measurement of the quantum capacitance of graphene. Nat. Nanotechnol. 2009, 4, 505–509. 10.1038/nnano.2009.177. [DOI] [PubMed] [Google Scholar]
  10. Liu C. G.; Yu Z. N.; Neff D.; Zhamu A.; Jang B. Z. Graphene-based supercapacitor with an ultrahigh energy density. Nano Lett. 2010, 10, 4863–4868. 10.1021/nl102661q. [DOI] [PubMed] [Google Scholar]
  11. Jeong H. M.; Lee J. W.; Shin W. H.; Choi Y. J.; Shin H. J.; Kang J. K.; Choi J. W. Nitrogen-doped graphene for high-performance ultracapacitors and the importance of nitrogen-doped sites at basal planes. Nano Lett. 2011, 11, 2472–2477. 10.1021/nl2009058. [DOI] [PubMed] [Google Scholar]
  12. Biener J.; Stadermann M.; Suss M.; Worsley M. A.; Biener M. M.; Rose K. A.; Baumann T. F. Advanced carbon aerogels for energy applications. Energy Environ. Sci. 2011, 4, 656–667. 10.1039/c0ee00627k. [DOI] [Google Scholar]
  13. Biener J.; Dasgupta S.; Shao L.; Wang D.; Worsley M. A.; Wittstock A.; Lee J. R.; Biener M. M.; Orme C. A.; Kucheyev S. O.; Wood B. C.; Willey T. M.; Hamza A. V.; Weissmuller J.; Hahn H.; Baumann T. F. Macroscopic 3D nanographene with dynamically tunable bulk properties. Adv. Mater. 2012, 24, 5083–5087. 10.1002/adma.201202289. [DOI] [PubMed] [Google Scholar]
  14. Paek E.; Pak A. J.; Hwang G. S. A computational study of the interfacial structure and capacitance of graphene in [BMIM][PF6] ionic liquid. J. Electrochem. Soc. 2013, 160, A1–A10. 10.1149/2.019301jes. [DOI] [Google Scholar]
  15. Paek E.; Pak A. J.; Kweon K. E.; Hwang G. S. On the origin of the enhanced supercapacitor performance of nitrogen-doped graphene. J. Phys. Chem. C 2013, 117, 5610–5616. 10.1021/jp312490q. [DOI] [Google Scholar]
  16. Liu C.; Yu Z.; Neff D.; Zhamu A.; Jang B. Z. Graphene-based supercapacitor with an ultrahigh energy density. Nano Lett. 2010, 10, 4863–4868. 10.1021/nl102661q. [DOI] [PubMed] [Google Scholar]
  17. Yang X.; Cheng C.; Wang Y.; Qiu L.; Li D. Liquid-mediated dense integration of graphene materials for compact capacitive energy storage. Science 2013, 341, 534–537. 10.1126/science.1239089. [DOI] [PubMed] [Google Scholar]
  18. Yoo J. J.; Balakrishnan K.; Huang J.; Meunier V.; Sumpter B. G.; Srivastava A.; Conway M.; Reddy A. L.; Yu J.; Vajtai R.; Ajayan P. M. Ultrathin planar graphene supercapacitors. Nano Lett. 2011, 11, 1423–1427. 10.1021/nl200225j. [DOI] [PubMed] [Google Scholar]
  19. Choi B. G.; Hong J.; Hong W. H.; Hammond P. T.; Park H. Facilitated ion transport in all-solid-state flexible supercapacitors. ACS Nano 2011, 5, 7205–7213. 10.1021/nn202020w. [DOI] [PubMed] [Google Scholar]
  20. Paek E.; Pak A. J.; Hwang G. S. Curvature effects on the interfacial capacitance of carbon nanotubes in an ionic liquid. J. Phys. Chem. C 2013, 117, 23539–23546. 10.1021/jp408085w. [DOI] [PubMed] [Google Scholar]
  21. Pak A. J.; Paek E.; Hwang G. S. Relative contributions of quantum and double layer capacitance to the supercapacitor performance of carbon nanotubes in an ionic liquid. Phys. Chem. Chem. Phys. 2013, 15, 19741–19747. 10.1039/C3CP52590B. [DOI] [PubMed] [Google Scholar]
  22. Pak A. J.; Paek E.; Hwang G. S. Tailoring the performance of graphene-based supercapacitors using topological defects: A theoretical assessment. Carbon 2014, 68, 734–741. 10.1016/j.carbon.2013.11.057. [DOI] [Google Scholar]
  23. Zhan C.; Zhang Y.; Cummings P. T.; Jiang D.-e. Enhancing graphene capacitance by nitrogen: effects of doping configuration and concentration. Phys. Chem. Chem. Phys. 2016, 18, 4668–4674. 10.1039/C5CP06952A. [DOI] [PubMed] [Google Scholar]
  24. Yang G. M.; Zhang H. Z.; Fan X. F.; Zheng W. T. Density functional theory calculations for the quantum capacitance performance of graphene-based electrode material. J. Phys. Chem. C 2015, 119, 6464–6470. 10.1021/jp512176r. [DOI] [Google Scholar]
  25. Hirunsit P.; Liangruksa M.; Khanchaitit P. Electronic structures and quantum capacitance of monolayer and multilayer graphenes influenced by Al, B, N and P doping, and monovacancy: Theoretical study. Carbon 2016, 108, 7–20. 10.1016/j.carbon.2016.07.005. [DOI] [Google Scholar]
  26. Zhan C.; Neal J.; Wu J.; Jiang D. Quantum effects on the capacitance of graphene-based electrodes. J. Phys. Chem. C 2015, 119, 22297–22303. 10.1021/acs.jpcc.5b05930. [DOI] [Google Scholar]
  27. Mousavi-Khoshdel S. M.; Jahanbakhsh-bonab P.; Targholi E. Structural, electronic properties, and quantum capacitance of B, N and P-doped armchair carbon nanotubes. Phys. Lett. A 2016, 380, 3378–3383. 10.1016/j.physleta.2016.07.067. [DOI] [Google Scholar]
  28. Mousavi-Khoshdel S. M.; Targholi E. Exploring the effect of functionalization of graphene on the quantum capacitance by first principle study. Carbon 2015, 89, 148–160. 10.1016/j.carbon.2015.03.013. [DOI] [Google Scholar]
  29. Chen L.; Li X.; Ma C.; Wang M.; Zhou J. Interaction and quantum capacitance of nitrogen/sulfur co-doped graphene: a theoretical calculation. J. Phys. Chem. C 2017, 121, 18344–18350. 10.1021/acs.jpcc.7b04551. [DOI] [Google Scholar]
  30. Mousavi-Khoshdel M.; Targholi E.; Momeni M. J. First-principles calculation of quantum capacitance of codoped graphenes as supercapacitor electrodes. J. Phys. Chem. C 2015, 119, 26290–26295. 10.1021/acs.jpcc.5b07943. [DOI] [Google Scholar]
  31. Tran N. Q.; Kang B. K.; Woo M. H.; Yoon D. H. Enrichment of pyrrolic nitrogen by hole defects in nitrogen and sulfur co-doped graphene hydrogel for flexible supercapacitors. ChemSusChem 2016, 9, 2261–2268. 10.1002/cssc.201600668. [DOI] [PubMed] [Google Scholar]
  32. Gopalsamy K.; Balamurugan J.; Thanh T. D.; Kim N. H.; Lee J. H. Fabrication of nitrogen and sulfur co-doped graphene nanoribbons with porous architecture for high-performance supercapacitors. Chem. Eng. J. 2017, 312, 180–190. 10.1016/j.cej.2016.11.130. [DOI] [Google Scholar]
  33. Wang T.; Wang L.-X.; Wu D.-L.; Xia W.; Jia D.-Z. Interaction between nitrogen and sulfur in co-doped graphene and synergetic effect in supercapacitor. Sci. Rep. 2015, 5, 9591 10.1038/srep09591. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhang D.; Zheng L.; Ma Y.; Lei L.; Li Q.; Li Y.; Luo H.; Feng H.; Hao Y. Synthesis of nitrogen- and sulfur-codoped 3D cubic-ordered mesoporous carbon with superior performance in supercapacitors. ACS Appl. Mater. Interfaces 2014, 6, 2657–2665. 10.1021/am405128j. [DOI] [PubMed] [Google Scholar]
  35. Wang C.; Zhou Y.; Sun L.; Zhao Q.; Zhang X.; Wan P.; Qiu J. N/P-codoped thermally reduced graphene for high-performance supercapacitor applications. J. Phys. Chem. C 2013, 117, 14912–14919. 10.1021/jp4015959. [DOI] [Google Scholar]
  36. Liang J.; Jiao Y.; Jaroniec M.; Qiao S. Z. Sulfur and nitrogen dual-doped mesoporous graphene electrocatalyst for oxygen reduction with synergistically enhanced performance. Angew. Chem., Int. Ed. 2012, 51, 11496–11500. 10.1002/anie.201206720. [DOI] [PubMed] [Google Scholar]
  37. Kannan A. G.; Samuthirapandian A.; Kim D.-W. Electric double layer capacitors employing nitrogen and sulfur co-doped, hierarchically porous graphene electrodes with synergistically enhanced performance. J. Power Sources 2017, 337, 65–72. 10.1016/j.jpowsour.2016.10.109. [DOI] [Google Scholar]
  38. Su Y.; Zhang Y.; Zhuang X.; Li S.; Wu D.; Zhang F.; Feng X. Low-temperature synthesis of nitrogen/sulfur co-doped three-dimensional graphene frameworks as efficient metal-free electrocatalyst for oxygen reduction reaction. Carbon 2013, 62, 296–301. 10.1016/j.carbon.2013.05.067. [DOI] [Google Scholar]
  39. Hohenberg P.; Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  40. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  41. Perdew J. P.; Chevary J. A.; Vosko S. H.; Jackson K. A.; Pederson M. R.; Singh D. J.; Fiolhais C. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671 10.1103/PhysRevB.46.6671. [DOI] [PubMed] [Google Scholar]
  42. John D. L.; Castro L. C.; Pulfrey D. L. Quantum capacitance in nanoscale device modeling. J. Appl. Phys. 2004, 96, 5180–5184. 10.1063/1.1803614. [DOI] [Google Scholar]
  43. Fan X.; Zheng W. T.; Kuo J.-L. Adsorption and diffusion of Li on pristine and defective graphene. ACS Appl. Mater. Interfaces 2012, 4, 2432–2438. 10.1021/am3000962. [DOI] [PubMed] [Google Scholar]
  44. Sivek J.; Sahin H.; Partoens B.; Peeters F. M. Adsorption and absorption of boron, nitrogen, aluminum, and phosphorus on silicene: Stability and electronic and phonon properties. Phys. Rev. B 2013, 87, 085444 10.1103/PhysRevB.87.085444. [DOI] [Google Scholar]
  45. Yang G. M.; Xu Q.; Fan X.; Zheng W. T. Quantum capacitance of silicene-based electrodes from first-principles calculations. J. Phys. Chem. C 2018, 122, 1903–1912. 10.1021/acs.jpcc.7b08955. [DOI] [Google Scholar]
  46. Zhang L. L.; Zhao X.; Ji H.; Stoller M. D.; Lai L.; Murali S.; Mcdonnell S.; Cleveger B.; Wallace R. M.; Ruoff R. S. Nitrogen doping of graphene and its effect on quantum capacitance, and a new insight on the enhanced capacitance of N-doped carbon. Energy Environ. Sci. 2012, 5, 9618–9625. 10.1039/c2ee23442d. [DOI] [Google Scholar]
  47. Wang H. H.; Yang G.; Chen Z.; Liu J. L.; Fan X. F.; Liang P.; Huang Y. Z.; Lin J. Y.; Shen Z. X. Nitrogen configuration dependent holey active sites toward enhanced K+ storage in graphite foam. J. Power Sources 2019, 419, 82–90. 10.1016/j.jpowsour.2019.02.029. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b01359_si_001.pdf (1.5MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES