Model-Implied Instrumental Variable - Generalized Method of Moments (MIIV-GMM) Estimators for Latent Variable Models

Abstract

The common Maximum Likelihood (ML) estimator for structural equation models (SEMs) has optimal asymptotic properties under ideal conditions (e.g., correct structure, no excess kurtosis, etc.) that are rarely met in practice. This paper proposes Model Implied Instrumental Variable - Generalized Method of Moments (MIIV-GMM) estimators for latent variable SEMs that are more robust than ML to violations of both the model structure and distributional assumptions. Under less demanding assumptions the MIIV-GMM estimators are consistent, asymptotically unbiased, asymptotically normal, and have an asymptotic covariance matrix. They are “distribution-free”, robust to heteroscedasticity, and have overidentification goodness of fit J tests with asymptotic chi square distributions. In addition, MIIV-GMM estimators are “scalable” in that they can estimate and test the full model or any subset of equations and hence allow better pinpointing of those parts of the model that fit and do not fit the data. An empirical example illustrates MIIV-GMM estimators. A simulation study explores their finite sample properties and finds that they perform well across a range of sample sizes.

1. INTRODUCTION

The Maximum Likelihood (ML) estimator is a mainstay in the use of structural equation models (SEMs) across the social and behavioral sciences. In an ideal world our model structure would be exactly correct, our observed variables would be from multinormal distributions, our disturbances would be homoscedastic, our samples would be large, and our iterative estimators would always converge. Under these conditions the ML estimator for SEMs would be hard to surpass as a consistent, asymptotically efficient, asymptocally normal estimator with correct asymptotic standard errors and a chi square (likelihood ratio) test of model fit (Lawley, 1947; Jöreskog, 1969; 1973; 1977).

But the real world of modeling departs from this utopia. Nearly all models are to some degree structurally misspecified (e.g., Browne & Cudeck, 1993); observed variables from nonnormal distributions are more likely than from normal distributions (Micceri, 1989); heteroscedastic disturbances are not rare (Davidson & MacKinnon, 1993 pg. 60); our samples are often not large (Nevitt & Hancock, 2004); and nonconvergence is not unusual (Boomsma & Hoogland, 2001). As a result most of the ideal world properties of the ML estimator need not hold in the real world. For instance, structural misspecifications can undermine the consistency of the ML estimator (Cragg, 1968; Bollen, Kirby, Curran, Paxton, & Chen, 2007) and the accuracy of standard errors and chi square tests (Yuan & Hayashi, 2006). The problem is made worse in that the ML estimator is a full information estimator so that a specification error in one equation can spread asymptotic bias across several equations even if these latter equations are perfectly specified (Kolenikov, 2011). Small samples coupled with misspecifications can make nonconvergence more common and cast doubt on the accuracy of the significance tests of the model (Bentler & Yuan, 1999). Furthermore, researchers often want tests of parts of a model rather than the whole model to better localize where the model fails (Bollen and Pearl, 2013).

These facts demand the exploration of other estimators that are better suited to real world conditions. Most efforts have concentrated on nonnormality. Researchers have found conditions where the ML significance tests are distributionally robust (e.g., Satorra 1990), have developed asymptotic standard errors and chi square tests that account for nonnormality (e.g., Bollen & Stine, 1990, 1993; Satorra & Benter, 1995), and have developed Weighted Least Squares (WLS) estimators that permit excess multivariate kurtosis (e.g., Browne, 1984). Though impressive these efforts are not without problems. For example, it is difficult to verify whether robustness conditions hold (Satorra, 1990) and the sample size requirements for the WLS estimator to reach its asymptotic properties are often excessive (Hu, Bentler & Kano, 1992). But more fundamental than these problems is that the corrections for nonnormality do not address the inconsistency and asymptotic bias that likely results from structural misspecifications. That is, the corrections assume that the structural specification is perfectly valid (Kolenikov & Bollen, 2012). In addition, the chi square test remains a global test of fit which if significant does not pinpoint the parts of the model that are the source of the problem. Furthermore, these distributional corrections do nothing to prevent nonconvergence of these iterative estimators which often is made worse when sample size is not large (Gerbing & Anderson, 1984; Boomsma & Hoogland, 2001).

Instrumental variable (IV) methods address some of these problems. Madansky (1964), Hägglund (1982), Jöreskog (1983), Ihara & Kano (1986), Bentler (1982), and others have suggested IV estimators for factor analysis. However, many of these are limited to exploratory factor analysis, assume uncorrelated errors, or do not provide significance tests and overidentification tests.

Bollen’s (1996a, 2001) Model Implied Instrumental Variable - Two Stage Least Squares (MIIV-2SLS) estimator for latent variable SEMs differs from these other IV estimators and addresses these issues. It is a limited information rather than full information estimator in that MIIV-2SLS estimates the structural equation model equation-by-equation rather than dealing with all equations at the same time like the usual ML estimator. The limited information nature better isolates structural misspecifications from spreading across many equations (Bollen, et al., 2007); overidentification tests are available for each overidentified equation to better localize problems (e.g., Kirby & Bollen, 2009); it is asymptotically “distribution free” (Bollen, 1996a); heteroscedastic-consistent standard errors are available (Bollen, 1996b); and as a noniterative estimator, the MIIV-2SLS eliminates problems with convergence. Though MIIV-2SLS has several advantages over the ML estimator, it also has limitations. For example, a researcher can estimate only the equations that are part of the latent variable model and not estimate the measurement model, but this would be done for each equation of the latent variable model rather than simultaneously estimating all equations of just the latent variable model. This leads to certain efficiency losses, although Bollen et. al. (2007) found these losses to be minor. A related problem is that the chi square test for overidentification is for one equation at a time and it is not a joint test for a group of equations. Furthermore, the applicability of the chi square test is uncertain when the disturbances are heteroscedastic.

The purpose of this paper is to propose and develop Generalized Method of Moments (GMM) estimators using MIIVs. These MIIV-GMM estimators have several desirable properties. MIIV-GMM is a distribution free estimator like the MIIV-2SLS, but unlike MIIV-2SLS the MIIV-GMM is a scalable estimator. Researchers can estimate a single equation or any subset including all equations in the model. Furthermore, it provides an overidentification test for the set of equations that are estimated. A chi square test statistic that tests all overidentified equations that are estimated permits the testing of pieces of the model as a way of finding the good and bad fitting parts. In addition, the chi square test and asymptotic standard errors are robust to heteroscedasticity, and may achieve asymptotic efficiency under an arbitrary form of heteroscedasticity. The flexibility of the MIIV-GMM is even greater in that it encompasses a family of estimators that can be altered by the selection of a weight matrix. Indeed, a researcher can set the weight matrix for MIIV-GMM to lead to the MIIV-2SLS estimator as a special case, though, as we explain below, other choices potentially will increase its asymptotic efficiency.

Another benefit of the MIIV-GMM estimator is that there is a rich literature on GMM estimators in econometrics devoted to single and simultaneous equations of observed (not latent) variables (Hansen, 1982; Hall, 2005; Matyas, 1999; Newey & McFadden, 1986). In this paper we show how we can convert latent variable SEMs into observed variable models and with this transformation how we can apply many of the results from the econometric literature to the MIIV-GMM estimator in this paper. The resulting MIIV-GMM estimator for latent variable SEMs has assumptions and features that are more applicable to real world conditions than the alternative full information estimators (e.g., ML) that now dominate the field. MIIV-GMM also has greater flexibility than the MIIV-2SLS estimator which is a special case of it. We view the MIIV-GMM estimator as an alternative to, rather than a replacement of, ML estimators for SEMs.

In the next section, we present the latent variable SEM including the special case of CFA. This is followed by a section on transforming these latent variable equations into equations with observed variables only. After this we explain the concept of MIIVs and how it applies to latent variable SEM. These latter two sections summarize material presented in various papers by Bollen and colleagues, but that are applied for this new approach. Following this are sections developing the family of MIIV-GMM estimators and the use of the J test, a chi square test, with it. The capability of estimating and testing subsets of equations is covered next, which we believe to be the most intriguing feature of the new estimator. An empirical example and simulation study illustrate the results. Conclusions and implications are in the final section.

2. MODEL AND ASSUMPTIONS

We use a modified version of Jöreskog’s (1977) LISREL notation that includes intercept terms. The latent variable model is:

$${\eta }_i={\alpha }_{\eta }+\mathbf{B}{\eta }_i+\Gamma {\xi }_i+{\zeta }_i$$ (1)

where i indexes the observations. The η_i vector contains the latent endogenous variables. The vector of α_η contains the intercept terms. The coefficient matrix B gives the effect of the ηs on each other, and has zeroes on the main diagonal for identification purposes. The latent exogenous variables are in the vector ξ_i. The coefficient matrix Γ contains the coefficients for ξ’s impact on the ηs. A vector ζ_i contains the disturbances for each latent endogenous variable. We assume that E(ζ_i) = 0, COV(ξ_i, ζ_i) = 0, and for now we assume that the disturbance for each equation is uncorrelated across cases although heteroscedasticity is permitted. The variances of ζs from different equations can differ and these ζs can correlate across equations. The covariance matrix of ζ_i is Σ_ζζi, and the covariance matrix of ξ is Σ_ξξ.

The measurement model is:

$${\mathbf{y}}_i={\alpha }_{\mathbf{y}}+{\Lambda }_{\mathbf{y}}{\eta }_i+{ϵ}_i$$ (2)

$${\mathbf{x}}_i={\alpha }_{\mathbf{x}}+{\Lambda }_{\mathbf{x}}{\xi }_i+{\delta }_i$$ (3)

The vector y_i contains the indicators of the ηs. The coefficient matrix Λ_y(the “factor loadings”) gives the impact of the ηs on the ys. The unique factors (“errors”) are in the vector ϵ_i. We assume that E(ϵ_i) = 0) and COV(η_i, ϵ_i) = 0. The covariance matrix for the ϵ_i is Σ_ϵϵi. There are analogous definitions and assumptions for measurement equation (3) for the vector x_i. We assume that ζ_i, ϵ_i, and δ_i are uncorrelated with ξ_i and in most models these vectors of disturbances and errors (ζ_i, ϵ_i, and δ_i) are assumed to be uncorrelated with each other, though the latter assumption is not essential. We also assume that the errors are uncorrelated across cases, though heteroscedasticity might be present. The MIIV-GMM estimator we use is robust to heteroscedasticity. Finally, we assume that the error terms in all regressions, i.e., ζ_i, ϵ_i, δ_i, have finite second order moments, and that the cross-moments $\mathrm{E}{\xi }_i^2{\zeta }_i^2$, $\mathrm{E}{\xi }_i^2{ϵ}_i^2$, $\mathrm{E}{\xi }_i^2{\delta }_i^2$, $\mathrm{E}{\zeta }_i^2{ϵ}_i^2$, $\mathrm{E}{\zeta }_i^2{\delta }_i^2$, $\mathrm{E}{ϵ}_i^2{\delta }_i^2$ are finite.

3. FROM LATENT TO OBSERVED VARIABLES

GMM estimation sets up “estimating equations”, as they are commonly referred to in statistics, or “moment conditions” as they are commonly referred to in econometrics, that utilize normal regression equations associated with relations (1)–(3). The coefficients are chosen to satisfy these moment conditions as near as possible. If the equation is exactly identified, parameter estimates can exactly satisfy these conditions. But with overidentified equations, the moment conditions will not be exactly satisfied. With the preceding latent variable SEM, GMM estimation does not seem possible. For instance, from the perspective of GMM the assumption E[ξ_iζ_i] = 0 gives rise to a sample counterpart relationship of

$$N^{-1}\sum _i^N{\xi }_i({\eta }_i-{\widehat{\alpha }}_{\eta }+\widehat{\mathbf{B}}{\eta }_i+\widehat{\Gamma }{\xi }_i{)}^{\prime }=0$$ (4)

where the disturbance ζ_i is replaced by $({\eta }_i-{\widehat{\alpha }}_{\eta }-{\widehat{\mathbf{B}}}_{{\eta }_i}-\widehat{\Gamma }{\xi }_i)$, the “^” signifies the sample estimator of the parameter and ${\widehat{\alpha }}_{\eta }$, $\widehat{\mathbf{B}}$, and $\widehat{\Gamma }$ are chosen to minimize the discrepancy from zero of the equation (4), in a sense that we shall make specific in Section 5, and i indexes the cases in the sample from 1, 2,…,N. If ξ_i and η_i were observed variables, we could proceed with the GMM approach common in econometric applications. But ξ_i and η_i are not observed so we cannot form this sum for estimation. We suggest that this is one of the major reasons that no one before us has applied GMM to factor analysis and latent variable models that are based on the individual values of variables.

To implement a GMM estimator for a latent variable SEM, we need to transform the model into one of observed variables. This section follows Bollen (1996a, 2001) in arriving at such transformation. First, we scale each latent variable by choosing one of its indicators (we recommend that the indicator thought to be most reliable and most free from measurement error correlations be chosen) and setting its intercept to zero and its factor loading to one. We assume that the scaling indicator has a moderate to strong relation to the latent variable. Of course, a scaling indicator unrelated to its latent variable will cause serious problems with the MIIV-GMM estimator as it would for other estimators such as ML. Fortunately, one can test the quality of the scaling indicator using the tests for weak instruments (see Section 4).

Consider the equation for y_1i that we assume loads only on η_1i so that we have y_1i = α_y1 + λ_y11η_1i + ϵ_1i. If y_1i is the scaling indicator, then we set α_y1 = 0 and λ_y11 = 1 leading to y_1i = η_1i + ϵ_1i. This scales the latent variable in the sense that (1) a one unit difference in the latent variable corresponds to a difference of one in the conditional expected values of the scaling indicator given the values of η_1i and (2) when the latent variable is zero, the expected value of the scaling indicator is zero. Similarly assume that we set scaling indicators for the remaining ηs. Partitioning the vector y_i into the scaling indicators, y_Si, and the remaining nonscaling indicators, y_Ti we have

$${\mathbf{y}}_i=\left[\begin{array}{c}\hfill {\mathbf{y}}_{Si}\hfill \\ \hfill {\mathbf{y}}_{Ti}\hfill \end{array}\right]$$ (5)

We rewrite the measurement model for y_i of equation 2 as

$$\left[\begin{array}{c}\hfill {\mathbf{y}}_{Si}\hfill \\ \hfill {\mathbf{y}}_{Ti}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill {\alpha }_{{\mathbf{y}}_T}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill \mathbf{I}\hfill \\ \hfill {\Lambda }_{{\mathbf{y}}_T}\hfill \end{array}\right]{\eta }_i+\left[\begin{array}{c}\hfill {ϵ}_{Si}\hfill \\ \hfill {ϵ}_{Ti}\hfill \end{array}\right]$$ (6)

and this implies

$${\mathbf{y}}_{Si}={\eta }_i+{ϵ}_{Si}$$ (7)

which we can solve for η_i,

$${\eta }_i={\mathbf{y}}_{Si}-{ϵ}_{Si}$$ (8)

By a similar series of steps we can partition the x_i vector, write the measurement equation for x_i in partitioned form to get

$${\mathbf{x}}_{Si}={\xi }_i+{\delta }_{Si}$$ (9)

and

$${\xi }_i={\mathbf{x}}_{Si}-{\delta }_{Si}$$ (10)

Following Bollen (1996), we substitute equation (8) for η_i and equation (10) for ξ_i into equations (1) to (3) and consolidate these three equations into a partitioned single equation

$$\begin{gathered} \left[\begin{array}{c}\hfill {\mathbf{y}}_{Si}\hfill \\ \hfill {\mathbf{y}}_{Ti}\hfill \\ \hfill {\mathbf{x}}_{Ti}\hfill \end{array}\right]= \\ \left[\begin{array}{c}\hfill {\alpha }_{\eta }\hfill \\ \hfill {\alpha }_{{\mathbf{y}}_T}\hfill \\ \hfill {\alpha }_{{\mathbf{x}}_T}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill \mathbf{B}\hfill & \hfill \Gamma \hfill \\ \hfill {\Lambda }_{{\mathbf{y}}_T}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\Lambda }_{{\mathbf{x}}_T}\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\mathbf{y}}_{Si}\hfill \\ \hfill {\mathbf{x}}_{Si}\hfill \end{array}\right]+\left[\begin{array}{ccccc}\hfill (I-B)\hfill & \hfill 0\hfill & \hfill -\Gamma \hfill & \hfill 0\hfill & \hfill \mathbf{I}\hfill \\ \hfill -{\Lambda }_{{\mathbf{y}}_T}\hfill & \hfill \mathbf{I}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -{\Lambda }_{{\mathbf{x}}_T}\hfill & \hfill \mathbf{I}\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill {ϵ}_{Si}\hfill \\ \hfill {ϵ}_{Ti}\hfill \\ \hfill {\delta }_{Si}\hfill \\ \hfill {\delta }_{Ti}\hfill \\ \hfill {\zeta }_i\hfill \end{array}\right] \end{gathered}$$ (11)

Here we have substituted out the latent variables for observed variables and have created composite disturbances that generally correlate with the right hand side variables of the equation in which each appears. This correlation renders Ordinary Least Squares (OLS) an inconsistent and asymptotically biased estimator for these equations (Wooldridge, 2010). Although the latent variables are eliminated from these equations, the coefficients are the same as the original equations. So if we derive consistent estimators of the coefficients in the transformed equation, they are consistent estimators of the coefficients from the original equations with latent variables.

Let us further simplify the model in equation (11) by using new symbols:

$${\mathbf{y}}^{\ast }=\mathbf{ZA}+\mathbf{u}$$ (12)

where y* is a N(p + q − n) × 1 vector (N =# of cases, p =# of ys, q =# of xs, n =# of ξs) that contains the N values of y_Si, y_Ti, and x_Ti stacked in a vector in order of equations. Let Z be a block diagonal matrix,

$$\mathbf{Z}=\left[\begin{array}{cccc}\hfill {\mathbf{Z}}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{Z}}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{Z}}_{p+q-n}\hfill \end{array}\right]$$ (13)

where Z₁ is an N row matrix that has a column of ones with the other columns being the N values of only those variables in y_S and x_S that correspond to the variables that have a direct effect in the first equation. And the other matrixes are defined analogously. Also in (12), A is the matrix of regression coefficients being estimated, and u is the composite error. An example to illustrate this notation is in Appendix 1.

4. MODEL IMPLIED INSTRUMENTAL VARIABLES (MIIVs)

Although equation (12), y*= ZA + u, has eliminated the difficulty of dealing with latent variables, we cannot consistently estimate its coefficients with OLS since u is correlated with Z. We use an Instrumental Variables (IVs) method to overcome this problem. IVs must have several properties. Define V_j to be an N row matrix with the first columns consisting of ones and the remaining columns being the values of all the IVs that correspond to the j-th equation. IVs are observed variables that meet four conditions: (1) V_j must correlate with Z_j (COV(Z_j, V_j) ≠ 0), (2) there must be at least as many variables in V_j as there are in Z_j, (3) the covariance matrix of V_j is nonsingular, and (4) V_j must not correlate with u_j (COV(u_j, V_j) = 0). We can check condition (1) by regressing the variables in Z_j on those in V_j and checking for nonzero R²s that are sufficiently high for the asymptotic properties of IV estimators to be reliable. Low R²s can lead to problems even in samples of several thousand cases. Tests for “weak instruments”, as well as quantitative rules of thumb as to what constitutes sufficiently strong instruments, also are available (Staiger & Stock, 1997; Stock, Wright, & Yogo, 2002; Stock &Yogo, 2005), though space constraints prevent us from discussing these. Condition (2) is just a matter of counting up the number of IVs relative to the observed endogenous variables to make sure that there are enough to permit identification. Condition (3) requires that the covariance matrix has an inverse which is straightforward to determine. Condition (4) is key to the consistency of the estimator. It requires that the IVs be uncorrelated with the disturbance. In equations where we have more than the minimum number of IVs [see condition (2)], we can test whether all IVs are uncorrelated with the disturbance. We discuss this in more detail later when we present the J-test.

Unlike in mainstream economics, where an inventive choice of the instrumental variables is often the most interesting part of an empirical paper (Angrist and Pischke, 2009), structural equation models that we study produce an abundance of model-implied instrumental variables. This method was proposed in Bollen (1996a) and automated in Bollen and Bauer (2004). Appendix 2 describes the MIIVs process of selecting observed variables from the model. In nearly all cases if a latent variable SEM is identified, then there will be sufficient MIIVs for each equation of the model. Though we have not come across identified models that do not have sufficient MIIVs, we suspect that it is possible such as in a model that involves linear or nonlinear constraints among the parameters. Searching for variables external to the model is not needed. Instead, a subset of the observed variables that are already part of the model will serve as MIIVs. Once the researcher has built an identified model based on substantive expertise, the MIIVs flow from the structure of the model.

The MIIVs will typically differ from one equation to the next, rather than being the same set for all equations as is typical in simultaneous equations in econometrics. Hence the use of the subscript j is necessary to distinguish the IVs for the jth equation from those of the others. We assemble the V_j for all equations into a block diagonal matrix V,

$$\mathbf{V}=\left[\begin{array}{cccc}\hfill {\mathbf{V}}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathbf{V}}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathbf{V}}_{p+q-n}\hfill \end{array}\right]$$ (14)

where V_j is the N row matrix of IVs with a vector of ones in the first column for the jth equation. Given u from equation (12), assumption (4) for the instrumental variables given above, and equation (14), we have

$$\mathrm{E}[\mathbf{uV}]=0$$ (15)

With these definitions and properties, we can now present the MIIV-GMM estimator.

5. MIIV-GMM ON TRANSFORMED EQUATIONS

The prior sections used Bollen’s (1996a) approach to transform the latent to observed variables and to select the MIIVs for the latent variable SEM. We now depart from Bollen (1996a) and develop a GMM approach that is more general than his MIIV-2SLS estimator.

5.1. The general GMM estimator

We combine the estimating equations (15) from above with research on GMM (e.g., Hall, 2005; Hansen, 1982; Matyas, 1999; Newey & McFadden, 1986) summarized in Appendix 3 to develop a MIIV-GMM family of estimators for latent variable models that has not been previously developed. We use the population (vector of) estimating equations

$$\mathrm{E}[{{\mathbf{V}}^{\prime }}_i({\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\mathbf{A})]=0$$ (16)

where ${\mathbf{V}}_i^{\prime }$, ${\mathbf{y}}_i^{\ast }$, and Z_i are V′, y*, and Z respectively for the ith case, we assume that $E[{\mathbf{V}}_i^{\prime }{\mathbf{Z}}_i]$ has a full column rank equal to the row dimension of A. In general, the parameters in (16) are overidentified (i.e., there are more equations than parameters), so we cannot solve (16) exactly. Instead, we can attempt to jointly make the components of (16) small. A relatively easy way to achieve this is to minimize a quadratic form in the empirical analogue of (16) with a weight W_N that may depend on the data. Following Newey and McFadden (1994), we assume that W_N is (a sequence of) symmetric positive semidefinite matrices and that plim[W_N] = W, with W also being positive semidefinite.

The MIIV-GMM estimator chooses the value $\widehat{\mathbf{A}}$ which minimizes

$${\left[\sum _{i=1}^N{{\mathbf{V}}^{\prime }}_i({\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\widehat{\mathbf{A}})\right]}^{\prime }{\mathbf{W}}_N\left[\sum _{i=1}^N{{\mathbf{V}}^{\prime }}_i({\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\widehat{\mathbf{A}})\right]$$ (17)

Upon solving (17) for the optimal $\widehat{\mathbf{A}}$ in a manner similar to the derivations in weighted least squares regression, one obtains

$$\widehat{\mathbf{A}}=({\mathbf{Z}}^{\prime }{\mathbf{VW}}_N{\mathbf{V}}^{\prime }\mathbf{Z}{)}^{-1}({\mathbf{Z}}^{\prime }{\mathbf{VW}}_N{\mathbf{V}}^{\prime }{\mathbf{y}}^{\ast })$$ (18)

where Z′VW_N V′Z is nonsingular (see condition 13 in Appendix 3). Under a relatively general set of assumptions the estimator $\widehat{\mathbf{A}}$ is consistent, asymptotically unbiased, and asymptotically normally distributed with an asymptotic covariance matrix of

$$\begin{gathered} \text{AVAR}\left[\sqrt{N}(\widehat{\mathbf{A}}-\mathbf{A})\right] \\ =[(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }\mathbf{W}(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]){]}^{-1}\times \\ (\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }\mathbf{W}\Omega \mathbf{W}(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}])[(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }\mathbf{W}(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]){]}^{-1} \end{gathered}$$ (19)

where Ω is the variance of V′u (Hansen, 1982; Newey & MacFadden, 1986; Matyas, 1999; Hall, 2005). The sample estimate form of equation (19) is

$$\begin{gathered} \widehat{v}(\widehat{A})=[(N^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}{)}^{\prime }{\mathbf{W}}_N(N^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}){]}^{-1}\times \\ (N^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}{)}^{\prime }{\mathbf{W}}_N\widehat{\Omega }{\mathbf{W}}_N(N^{-1}{\mathbf{V}}^{\prime }\mathbf{Z})[(N^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}{)}^{\prime }{\mathbf{W}}_N(N^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}){]}^{-1} \end{gathered}$$ (20)

where $\widehat{\Omega }$ is a consistent estimator of Ω. In the following subsections we describe methods to estimate $\widehat{\Omega }$. The variance estimator (20) and the asymptotic normality of $\widehat{\mathbf{A}}$ provide us a means by which we can test hypotheses about the coefficients in these models. A valuable aspect of the asymptotic variance is that it holds for any symmetric positive semidefinite matrix W provided that [(N⁻¹V′Z)′W_N (N⁻¹V′Z)] is invertible and that it converges to a positive definite matrix as N → ∞ and when the observed variables have finite fourth order cross-moments, as stated in the section on the model and assumptions. The invertibility means that the rank of W_N and W must be greater than or equal to the column dimension of Z, i.e., the number of parameters being estimated. As long as no assumptions about the distribution of the observed variables, beyond the existence of certain moments, are being made, the formula is robust to nonnormal distributions of the observed variables. In this sense, the MIIV-GMM is a distribution-free estimator for a broad class of weight matrices. The MIIV-GMM estimator is actually a family of estimators where each specific member is determined by (i) equations from the model that are being estimated, and (ii) the choice of weight matrix (W_N). Even though these properties were originally derived for observed variable models, our conversion of the latent variable SEM into a model of observed variables makes them applicable in this new context. In the next subsections we introduce examples of weight matrices that researchers can use for the family of MIIV-GMM estimators.

5.2. Identity Weight Matrix (W_N = I)

Setting the weight matrix to the identity matrix (W_N = I) is the simplest choice in that it chooses $\widehat{\mathbf{A}}$ to minimize the sum of the IVs (${\mathbf{V}}_i^{\prime }$) times the residual (${\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\widehat{\mathbf{A}}$) times itself or

$${\left[\sum _{i=1}^N{{\mathbf{V}}^{\prime }}_i({\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\widehat{\mathbf{A}})\right]}^{\prime }\left[\sum _{i=1}^N{{\mathbf{V}}^{\prime }}_i({\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\widehat{\mathbf{A}})\right].$$ (21)

In this case,

$$\begin{gathered} {\widehat{\mathbf{A}}}_{\mathbf{I}}=({\mathbf{Z}}^{\prime }{\mathbf{VIV}}^{\prime }\mathbf{Z}{)}^{-1}({\mathbf{Z}}^{\prime }{\mathbf{VIV}}^{\prime }{\mathbf{y}}^{\ast }) \\ =({\mathbf{Z}}^{\prime }{\mathbf{VV}}^{\prime }\mathbf{Z}{)}^{-1}({\mathbf{Z}}^{\prime }{\mathbf{VV}}^{\prime }{\mathbf{y}}^{\ast }) \end{gathered}$$ (22)

where ${\widehat{\mathbf{A}}}_{\mathbf{I}}$ is the MIIV-GMM $\widehat{\mathbf{A}}$ with (W_N = I). Using equation (20), ${\widehat{\mathbf{A}}}_{\mathbf{I}}$ has an asymptotic covariance matrix of

$$\begin{gathered} \text{AVAR}\left[\sqrt{N}({\widehat{\mathbf{A}}}_{\mathbf{I}}-\mathbf{A})\right] \\ =[(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]){]}^{-1}(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }\Omega (\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}])[(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]){]}^{-1} \end{gathered}$$ (23)

The sample estimate of this asymptotic variance is equation (20) where W_N = I and $\widehat{\Omega }$ is a consistent estimator of Ω, e.g., (30) or (33) below. As we will explain shortly, ${\widehat{\mathbf{A}}}_{\mathbf{I}}$ is not the most asymptotically efficient estimator of A.

5.3. Latent Variable 2SLS Weight Matrix (W_N = N(V′V)⁻¹)

Bollen (2001) shows that by stacking all the dependent variables and their instrumental variables, one can obtain a system-wide estimator

$${\widehat{\mathbf{A}}}_{2\mathit{SLS}}=({\widehat{\mathbf{Z}}}^{\prime }\widehat{\mathbf{Z}}{)}^{-1}{\widehat{\mathbf{Z}}}^{\prime }{\mathbf{y}}^{\ast }$$ (24)

with

$$\widehat{\mathbf{Z}}=\mathbf{V}({\mathbf{V}}^{\prime }\mathbf{V}{)}^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}$$ (25)

Substituting the right-hand side of $\widehat{\mathbf{Z}}$ into the right-hand side of ${\widehat{\mathbf{A}}}_{2\mathit{SLS}}$ leads to

$$\begin{gathered} {\widehat{\mathbf{A}}}_{2\mathit{SLS}}=\{[\mathbf{V}({\mathbf{V}}^{\prime }\mathbf{V}{)}^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}{]}^{\prime }\mathbf{V}({\mathbf{V}}^{\prime }\mathbf{V}{)}^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}[\mathbf{V}({\mathbf{V}}^{\prime }\mathbf{V}{)}^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}]\}{\mathbf{y}}^{\ast } \\ =[{\mathbf{Z}}^{\prime }\mathbf{V}({\mathbf{V}}^{\prime }\mathbf{V}{)}^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}{]}^{-1}{\mathbf{Z}}^{\prime }\mathbf{V}({\mathbf{V}}^{\prime }\mathbf{V}{)}^{-1}{\mathbf{V}}^{\prime }{\mathbf{y}}^{\ast } \end{gathered}$$ (26)

Comparing ${\widehat{\mathbf{A}}}_{2\mathit{SLS}}$ of equation (26) to the general MIIV-GMM of equation (18), we can see that substituting W_N = N(V′V)⁻¹ into (18) and simplifying leads to ${\widehat{\mathbf{A}}}_{2\mathit{SLS}}$. Thus we can view the latent variable MIIV-2SLS estimator from Bollen (1996a; 2001) as a special case of the MIIV-GMM estimator for a single regression equation. This MIIV-2SLS estimator is a limited information estimator, as it does not use variances and cross-correlations between equations to develop estimates. As such, it trades off asymptotic efficiency for greater robustness to structural specification errors: its asymptotic efficiency will be no better than and likely less than the latent variable MIIV-GMM estimator with a different weight matrix that we describe in the next section (Hall, 2005, sec. 3.6). An advantage of the latent variable MIIV-2SLS estimator is its greater robustness to structural misspecifications than that of full information estimators such as the MIIV-GMM, WLS, or ML (Bollen et al., 2007) simultaneously applied to all equations. Later in the paper we explain how the MIIV-GMM estimator is scalable so that we can estimate a single equation or any subset of equations and thus make the MIIV-GMM estimator more robust to structural misspecifications than the full information ML estimator. In essence, with the right weight matrix we can specialize the MIIV-GMM estimator to be equivalent to the MIIV-2SLS estimator or we can estimate multiple equations but not all equations at once so as to treat a larger “chunk” of the model than MIIV-2SLS does and with the potential of greater asymptotic efficiency. We say more about this later.

5.4. Optimal Weight Matrix (${\mathbf{W}}_N={\widehat{\Omega }}^{-1}$)

Using an identity weight matrix (W_N = I) or the 2SLS weight matrix (W_N = N(V′V)⁻¹), the weight matrices are positive definite and have inverses. The asymptotically efficient weight matrix is the estimator of the inverse of Ω, the covariance matrix of V′u (sec. 5.2 and theorem 5.2 of Newey & McFadden 1986; sec. 3.6 and theorem 3.4 of Hall 2005). The MIIV approach generates the IVs for each equation in a multiequation system. When the MIIVs for each equation are combined, there are some models for which the moment conditions for GMM are redundant leading to a singular Ω which has an incomplete rank, and is positive semidefinite rather than positive definite. This is much less likely in the typical applications of GMM. Fortunately, the desirable properties of the MIIV-GMM estimator remain the same, but we must use the generalized inverse of Ω rather than the usual inverse as the weight matrix (Newey & McFadden 1986). In the subsection on the Two Step Estimator, we first present the results for models where Ω is nonsingular and then describe the necessary modifications to accommodate a singular Ω.

5.4.1. Two Step Estimator

Positive definite Ω The optimal weight matrix that minimizes the asymptotic variance of the estimator is to set ${\mathbf{W}}_N={\widehat{\Omega }}^{-1}$ where Ω is the variance of V′u (Hansen, 1982; Hall, 2005, theorem 3.4, p. 88) and $\widehat{\Omega }$ is a consistent estimator of a positive definite Ω. This leads to

$${\widehat{\mathbf{A}}}_{{\widehat{\Omega }}^{-1}}=({\mathbf{Z}}^{\prime }\mathbf{V}{\widehat{\Omega }}^{-1}{\mathbf{V}}^{\prime }\mathbf{Z}{)}^{-1}({\mathbf{Z}}^{\prime }\mathbf{V}{\widehat{\Omega }}^{-1}{\mathbf{V}}^{\prime }{\mathbf{y}}^{\ast })$$ (27)

with an asymptotic variance of

$$[(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }{\Omega }^{-1}(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]){]}^{-1}$$ (28)

To practically construct the ${\widehat{\mathbf{A}}}_{{\widehat{\Omega }}^{-1}}$ estimators, we need to estimate the population matrix Ω. We need an estimate of Ω for ${\widehat{\mathbf{A}}}_{{\Omega }^{-1}}$, but we also need Ω to estimate the asymptotic variances of ${\widehat{\mathbf{A}}}_{\mathbf{I}}$, ${\widehat{\mathbf{A}}}_{2\mathit{SLS}}$, or any other MIIV-GMM estimators resulting from different weight matrices since Ω is part of the formula for determining the asymptotic variance of all MIIV-GMM estimators.

The first step in estimating Ω is to get a consistent estimator of A which we refer to as $\tilde{\mathbf{A}}$. ${\widehat{\mathbf{A}}}_{\mathbf{I}}$ and ${\widehat{\mathbf{A}}}_{2\mathit{SLS}}$ are consistent estimators of A so a researcher could use either. We use $\tilde{\mathbf{A}}$ to compute the residuals as

$${\tilde{\mathbf{u}}}_i={\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i\tilde{\mathbf{A}}$$ (29)

which we use to estimate $\tilde{\Omega }$ as

$$\tilde{\Omega }=N^{-1}\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\tilde{\mathbf{u}}}_i{\tilde{\mathbf{u}}}_i^{\prime }{\mathbf{V}}_i$$ (30)

We can use $\tilde{\Omega }$ to estimate the asymptotic variances of the ${\widehat{\mathbf{A}}}_{\mathbf{I}}$ and ${\widehat{\mathbf{A}}}_{2\mathit{SLS}}$ (Newey & McFadden, 1986, sec. 4.1–4.3; Hall, 2005, sec. 3.5, p. 74). It should be noted that both Newey & McFadden (1986) and Hall (2005) make a point that the estimators of Ω, and hence the variance estimators $\widehat{v}(\widehat{\mathbf{A}})$ that rely on them, are only consistent when the model structure is correctly specified, at least in the equations used for estimation.

Following Hansen (1982), we use $\tilde{\Omega }$ to obtain the ${\widehat{\mathbf{A}}}_{{\Omega }^{-1}}$ estimator by substituting ${\tilde{\Omega }}^{-1}$ for Ω⁻¹ in (27) and run the GMM estimation procedure again to obtain the second step estimates. We estimate the asymptotic variance of ${\widehat{\mathbf{A}}}_{{\Omega }^{-1}}$ using either the first step residuals covariance matrix ${\tilde{\Omega }}^{-1}$

$$\tilde{v}(\widehat{\mathbf{A}})={\left[({\mathbf{V}}^{\prime }\mathbf{Z}{)}^{\prime }{\tilde{\Omega }}^{-1}({\mathbf{V}}^{\prime }\mathbf{Z})\right]}^{-1}$$ (31)

or the second step residuals covariance matrix

$$\widehat{v}(\widehat{\mathbf{A}})={\left[({\mathbf{V}}^{\prime }\mathbf{Z}{)}^{\prime }{\widehat{\Omega }}^{-1}({\mathbf{V}}^{\prime }\mathbf{Z})\right]}^{-1}$$ (32)

where

$$\widehat{\Omega }=N^{-1}\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_i{\widehat{\mathbf{u}}}_i^{\prime }{\mathbf{V}}_i$$ (33)

and the second step residuals are

$${\widehat{\mathbf{u}}}_i={\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i{\widehat{\mathbf{A}}}_{{\Omega }^{-1}}$$ (34)

Asymptotically it should not matter whether we use equation (31) or (32) to estimate the variance of ${\widehat{\mathbf{A}}}_{{\Omega }^{-1}}$.

Positive Semidefinite Ω The previous section assumes that $\widehat{\Omega }$, $\tilde{\Omega }$, and Ω are positive definite as is typical in GMM treatments. A positive semidefinite matrix $\widehat{\Omega }$, $\tilde{\Omega }$, or Ω might be singular so that the usual inverses of $\widehat{\Omega }$, $\tilde{\Omega }$, or Ω do not exist. If these matrices are singular, we can use the generalized inverses which we can represent as ${\widehat{\Omega }}^{+}$, ${\tilde{\Omega }}^{+}$, or ${\Omega }^{+}$. There are a variety of generalized inverses. Probably the best known is the Moore-Penrose generalized inverse for Ω (e.g., Searle, 1982, page 212). Fortunately, the results from the prior subsection apply when the Moore-Penrose generalized inverse replaces the usual inverse. For instance, the ${\widehat{\mathbf{A}}}_{{\widehat{\Omega }}^{+}}$ is

$${\widehat{\mathbf{A}}}_{{\widehat{\Omega }}^{+}}=({\mathbf{Z}}^{\prime }\mathbf{V}{\widehat{\Omega }}^{+}{\mathbf{V}}^{\prime }\mathbf{Z}{)}^{-1}({\mathbf{Z}}^{\prime }\mathbf{V}{\widehat{\Omega }}^{+}{\mathbf{V}}^{\prime }{\mathbf{y}}^{\ast })$$ (35)

with an asymptotic variance of

$$[(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]{)}^{\prime }{\Omega }^{+}(\mathrm{E}[{\mathbf{V}}^{\prime }\mathbf{Z}]){]}^{-1}$$ (36)

assuming that (${\mathbf{Z}}^{\prime }\mathbf{V}{\widehat{\Omega }}^{+}{\mathbf{V}}^{\prime }\mathbf{Z}$) and (E[V′Z])′Ω⁺(E[V′Z]) are nonsingular.

The consistency, asymptotic normality, and asymptotic variance for the GMM estimator is not changed when the weight matrix uses the generalized inverse for the weight matrix. Newey & McFadden (1986, pages 2132, 2148, 2160), for instance, establish these properties for GMM estimators in general and only require that the weight matrix to be positive semidefinite. Their results apply to our MIIV-GMM estimators.

6. TESTS OF MODEL

The usual full information ML estimator for latent variable SEM have tests for individual coefficients, groups of coefficients, and likelihood ratio tests to assess the overall fit of models. Drawing on the literature for GMM estimators we have analogous capabilities for the latent variable MIIV-GMM estimator.

6.1. Coefficient significance tests

The preceding subsections provided the asymptotic covariance matrices of the latent variable MIIV-GMM estimators. The square roots of the main diagonal elements of these matrices are estimates of the asymptotic standard errors that a researcher can use to test the statistical significance of any coefficient estimate. Or a Wald test permits testing several parameters at once using the estimated asymptotic covariance matrix of the coefficient estimates (sec. 9, Newey & McFadden, 1986; sec. 5.3, Hall 2005).

6.2. Overidentification J Test

The ML estimator for latent variable SEMs has a likelihood ratio chi square test to compare the fit of hypothesized model to that of the saturated model (Jöreskog, 1969; Jöreskog, 1973). This also is a test of all the overidentifying restrictions in the model (Bollen, 1989). Again drawing on the work of Hansen (1982) and others (e.g., Sargan, 1958) we have an overidentification J test for the MIIV-GMM estimator when researchers use

$$J=\left({\left[N^{-\frac{1}{2}}\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_i\right]}^{\prime }{\widehat{\Omega }}^{-1}\left[N^{-\frac{1}{2}}\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_i\right]\right)$$ (37)

where J has an asymptotic chi square distribution with df equal to the number of columns of V_i minus the number of unrestricted coefficients in the model in A, $\widehat{\Omega }$ is a consistent estimator of a positive-definite Ω, and ${\widehat{\Omega }}^{-1}$ is the inverse of $\widehat{\Omega }$. The number of columns of V_i gives the number of moment conditions that are hypothesized to be zero in the population. For positive df we have overidentifying restrictions in the model and we can test whether these restrictions are valid. The null hypothesis is that all IVs for each equation are uncorrelated with the disturbance of the same equation and this is true for each equation in the system. Rejection of the null hypothesis means that at least one IV in at least one equation is invalid.

As we discussed above, sometimes the Ω is positive semidefinite rather than positive definite due to redundant moment conditions. We propose a more general form of the J test statistic as

$$J=\left({\left[N^{-\frac{1}{2}}\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_i\right]}^{\prime }{\widehat{\Omega }}^{+}\left[N^{-\frac{1}{2}}\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_i\right]\right)$$ (38)

where ${\widehat{\Omega }}^{+}$ is the generalized inverse of $\tilde{\Omega }$. The ${\widehat{\Omega }}^{+}$ is equivalent to the usual inverse ${\widehat{\Omega }}^{-1}$ when $\widehat{\Omega }$ is nonsingular.

By virtue of a suitable central limit theorem, in large samples, $\left[N^{-\frac{1}{2}}{\sum }_{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_i\right]$ follows a normal distribution with mean of zero and finite variance of Ω (van der Vaart, 1998). The J test statistic asymptotically follows a chi-square distribution with df equal to the rank(Ω⁺Ω) provided that (Ω⁺Ω) is idempotent [e.g., Searle, 1982, page 356] minus the number of unrestricted coefficients in the model. Idempotency of (Ω⁺Ω) follows given (Ω⁺Ω)(Ω⁺Ω) = (Ω⁺ΩΩ⁺)Ω = Ω⁺Ω, which follows from the properties of Moore-Penrose generalized inverses. The df defined as the difference of the rank(Ω⁺Ω) minus the number of coefficients gives us the “excess” number independent moments that permit tests of the IVs uncorrelatedness with the disturbances.

The test of the IVs is important from the perspective of model specification. As discussed in the section on MlIVs and in Appendix 2, we described the MIIV method from Bollen (1996a; 2001). It is the model specification that determines which observed variables meet the conditions of IVs for each equation. If the test rejects the null hypothesis, then the literal interpretation is that one or more of the instruments are correlated with the (composite) error terms, which in turn means there are unaccounted correlations or regression links in the SEM, which raises doubts about the structural specification. Thus the overidentification test of IVs is a test of the model specification.

One final comment regarding the J test concerns its asymptotic distributional robustness. As mentioned in the beginning of Section 2, the minimal assumption GMM needs is that of finite second order moments (assumption 10 in Appendix 3). It does not need additional knowledge about the distribution of the data, such as normality or an elliptically contoured shape. Under this main assumption of finite second order moments and some fourth order cross-moments (or alternatively the assumption of independence of the error terms, rather than just their uncorrelatedness), it achieves the asymptotic chi-square distribution regardless of the distribution that underlie the variables. It can be conjectured that a high degree of nonnormality and small sample sizes may lead to deviations from that asymptotic distribution. However at this point no further SEM-specific results are available.

6.3. Nested Tests

In this subsection we assume that a researcher uses a consistent estimator of the optimal weight matrix (e.g., ${\mathbf{W}}_N={\widehat{\Omega }}^{+}$). Let ${\widehat{\mathbf{A}}}_f$ be the “free” estimate of coefficients without linear, Cθ = b or nonlinear C(θ) = b restrictions where b is a vector of constants. Assume that C or the derivative matrix ∂C/∂θ is of full rank. Define ${\widehat{\mathbf{A}}}_r$ to be the estimates with the restrictions imposed. Assume that we use the same weight matrix W_N for both ${\widehat{\mathbf{A}}}_f$ and ${\widehat{\mathbf{A}}}_r$. We define the residuals for each model as

$${\widehat{\mathbf{u}}}_{fi}={\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i{\widehat{\mathbf{A}}}_f$$ (39)

$${\widehat{\mathbf{u}}}_{ri}={\mathbf{y}}_i^{\ast }-{\mathbf{Z}}_i{\widehat{\mathbf{A}}}_r$$ (40)

Hansen (1982) shows that the test statistic

$$T_1=N^{-1}\left({\left[\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_{ri}\right]}^{\prime }{\mathbf{W}}_N\left[\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_{ri}\right]-{\left[\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_{fi}\right]}^{\prime }{\mathbf{W}}_N\left[\sum _{i=1}^N{\mathbf{V}}_i^{\prime }{\widehat{\mathbf{u}}}_{fi}\right]\right)$$ (41)

follows an asymptotic chi square distribution with degrees of freedom (df) equal to the number of linear restrictions, or in general, the rank of the derivative matrix ∂C/∂θ, imposed when estimating ${\widehat{\mathbf{A}}}_r$. This test statistic permits a simultaneous test of linear or nonlinear restrictions when comparing two nested model. Comparing equations (41) to (37) we see that the nested test is the difference in the J test for two nested models (Hall, 2005, page 162) provided that the same matrix is used for both estimators.

7. SUBSETS OF EQUATIONS

So far our presentation of the latent variable MIIV-GMM estimator has largely assumed that we are estimating and testing all equations simultaneously. In this way the MIIV-GMM estimator is similar to the ML, WLS, and other system-wide estimators that dominate the latent variable SEMs field. However, there are some important differences. We already have shown that Bollen’s (1996a; 1996b; 2001) latent variable MIIV-2SLS estimator is a special case of the latent variable MIIV-GMM and hence the latter can have the same properties as the former. But there is another feature of MIIV-GMM not possessed by MIIV-2SLS or ML. This is the simultaneous estimation and testing of a subset of equations from a model.

What are the advantages of estimating subsets of equations of the model? Consider the common situation where a researcher is most interested in the coefficients of the latent variable model. With MIIV-GMM a researcher can estimate and have a chi square J test for just the latent variable model. This would not be possible using ML because it cannot estimate only the latent variable equations. With MIIV-2SLS we would be restricted to estimating and testing one equation at a time rather than the full subset. Alternatively, analysts might want to find misspecified parts of a large model and only estimate and test those suspected parts. For example, if three indicators of one latent variable and two of another were suspected to have problems, an analyst could estimate and test just those five equations. We will illustrate some of these capabilities with empirical and simulated data.

8. EMPIRICAL EXAMPLE

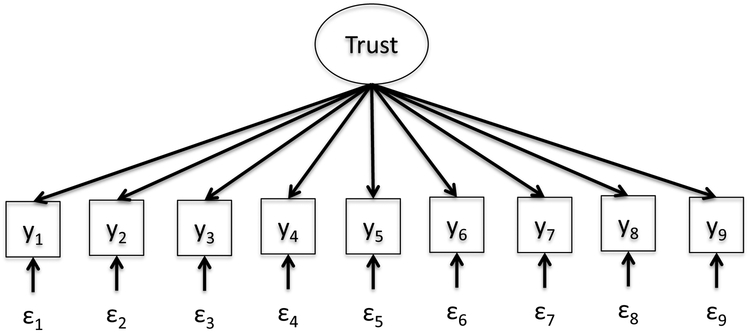
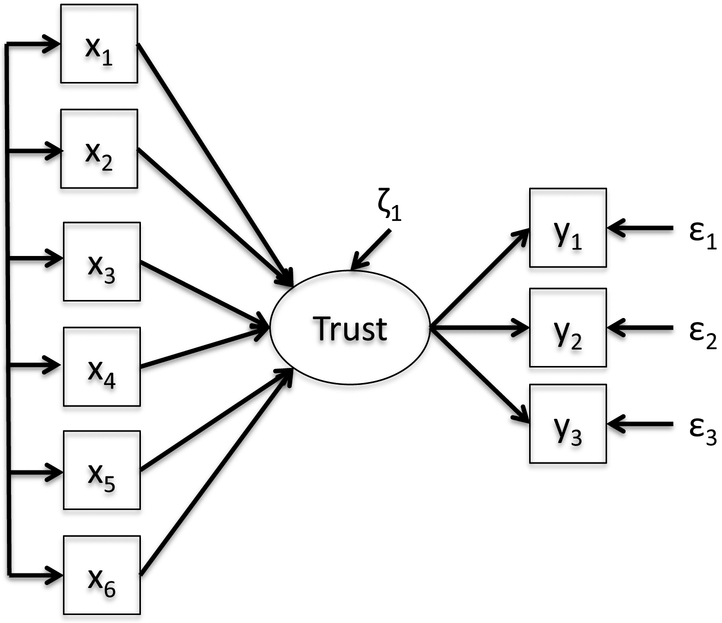
In this section we provide an empirical example that uses the MIIV-GMM estimator. Glanville and Paxton (2007) develop two models of trust (see Figures 1 and 2). The first model is a confirmatory factor analysis model with a single latent dimension for propensity to trust and eight indicators. The equations for this model are given by

$$y_{ji}={\alpha }_j+{\lambda }_j{\eta }_{1i}+{ϵ}_{ji},$$ (42)

where j = 1, …, 8, an index for the eight effect (or reflective) indicators. If we treat the first indicator as the scaling indicator, then we have η_1i = y_1i – ϵ_1i. We can then substitute the scaling indicator minus its error in for the latent variable in the remaining eight equations, which results in

$$y_{ki}={\alpha }_k+{\lambda }_k{y}_{1i}-{\lambda }_k{ϵ}_{1i}+{ϵ}_{ki},$$ (43)

where k = 2, …, 8, an index for the remaining 7 effect indicators. This transforms the CFA model into an observed variable model.

Figure 1:

CFA Model for Trust.

Figure 2:

MIMIC Model for Trust.

Glanville and Paxton (2007) note, however, that six of the indicators capture trust in specific local domains (x₁ = trust in family members, x₂ = trust in neighbors, x₃ = trust in coworkers, x₄ = trust in members of church, x₅ = trust in members of clubs, and x₆ = trust in store workers) while two of the indicators capture more general feelings of trust (y₁ = people can be trusted and y₂ = people are helpful). Based on this distinction, they propose an alternative MIMIC model with the six indicators based on local domains having an effect on a latent generalized trust which is measured by the two general indicators of trust. If we relabel the six indicators y₂ – y₈ as x₁ – x₆, then the equations for this model are given by

$${\eta }_{1i}={\alpha }_{\eta }+{\gamma }_{11}{x}_{1i}+\cdots +{\gamma }_{16}{x}_{6i}+{\zeta }_i$$ (44)

$$y_{ji}={\alpha }_j+{\lambda }_j{\eta }_{ji}+{ϵ}_{ji},$$ (45)

where j = 1, 2, an index for the two effect indicators. As with the first model, if we treat the first effect indicator as the scaling indicator, then we have η_1i = y_1i – ϵ_1i. When we substitute the scaling indicator minus its error into (44) and (45), we obtain

$$y_{1i}={\alpha }_{\eta }+{\gamma }_{11}{x}_{1i}+\cdots +{\gamma }_{16}{x}_{6i}+{ϵ}_{1i}+{\zeta }_i$$ (46)

$$y_{2i}={\alpha }_2+{\lambda }_2{y}_{1i}-{\lambda }_2{ϵ}_{1i}+{ϵ}_{2i},$$ (47)

This transforms the MIMIC model into an observed variable model.

The next step is to determine the MIIVs for each model. We note again that there is no search for ad hoc IVs that are located outside of the model. Both models are overidentified so we expect that each equation will have the needed MIIVs to estimate the equation. In the CFA model, (43), y₁ is correlated with the composite disturbance −λ_kϵ_1i + ϵ_ki for all k equations, so we need IVs for every equation. Since there are no correlations among any of the disturbances, the MIIVs for every equation consist of all of the effect indicators other than y₁ and the respective dependent variable (see Table 1).

Table 1.

MIIVs for the Two Models of Trust.

Equation	CFA MIIVs	MIMIC MIIVs
y2	y3 – y8	x1 – x6
y3	y2, y4 – y8	-
y4	y2, y3, y5 – y8	-
y5	y2 – y4, y6 – y8	-
y6	y2 – y5, y7 – y8	-
y7	y2 – y6, y8, y8	-
y8	y2 – y7	-

Note: y₂ – y₈ in the CFA model correspond to x₁ – x₆ in the MIMIC model.

For the MIMIC model, we see that in equation (46) all of the right hand side variables are uncorrelated with the composite disturbance ϵ₁ + ζ₁. Therefore we can obtain estimates for the γs by simply regressing y₁ on x₁, …, x₆. In equation (47), however, y₁ is correlated with the composite disturbance −λ₂ϵ_1i + ϵ_2i for the remaining equation, so we need IVs for this equation. The exogenous xs are valid IVs for the y₂ equation (see Table 1).

The information in Table 1 provides the essential ingredients for applying any of the MIIV-GMM estimators that we proposed for latent variable models. We can estimate any subset of or all of the equations in the model. The estimates permit heteroscedastic disturbances for each equation. And we can vary the weight matrix.

To illustrate the MIIV-GMM estimators, we focus on the factor loadings (λs) for the effect indicators in the two models. The data come from the Social Trust Survey (STS) fielded by Pew to respondents in Philadelphia in 1998 (Pew Research Center 1998).We use the second form of the survey that contains six measures of local trust and two measures of generalized trust (“fairness” and “helpfulness”). See Glanville and Paxton (2007) for a more detailed discussion of the data. We use the GMM procedure from Stata 12 (StataCorp, 2011, version 12) for all GMM estimates and Mplus version 6 (Muthén and Muthén, 2010) for all ML estimates. The “gmm” package can be used to estimate these models in R (Chausse, 2012). We compare the MIIV-GMM estimator to the dominant ML estimator.

For both the ML and MIIV-GMM estimators we use versions that are robust to heteroscedastic errors (MLR estimator in Mplus) and estimate all of the equations for the measurement models simultaneously. We use the MIIV-GMM two-step estimator with the identity matrix as the weight in the first step. When estimating all equations with the MIIV-GMM estimator, we use the generalized inverse matrix of ${\mathbf{W}}_N={\widehat{\Omega }}^{+}$ which is equivalent to ${\mathbf{W}}_N={\widehat{\Omega }}^{-}$ when Ω is nonsingular. The degrees of freedom (df) are the number of columns in V minus the number of unrestricted coefficients in A. If a model has redundant moment conditions, the df equals the rank(Ω⁺Ω) which we estimate as rank(${\widehat{\Omega }}^{+}\widehat{\Omega }$) minus the number of unrestricted coefficients in A. At the bottom of Table 2 are the J tests of overidentification, df, and p-values.

Table 2:

ML and MIIV-GMM Estimates for Trust Models.

	CFA Model		MIMIC Model
	ML	MIIV-GMM	ML	MIIV-GMM
λ2	0.61 (0.08)	0.74 (0.08)	0.61 (0.08)	0.61 (0.08)	λ2
λ3	0.33 (0.06)	0.20 (0.04)	0.04 (0.08)	0.06 (0.09)	γ11
λ4	0.99 (0.08)	0.89 (0.08)	0.34 (0.05)	0.32 (0.06)	γ12
λ5	0.76 (0.09)	0.59 (0.07)	0.02 (0.06)	0.02 (0.06)	γ13
λ6	0.65 (0.07)	0.49 (0.06)	0.05 (0.07)	0.09 (0.07)	γ14
λ7	0.80 (0.08)	0.68 (0.07)	0.24 (0.06)	0.23 (0.07)	γ15
λ8	0.83 (0.08)	0.71 (0.08)	0.19 (0.05)	0.19 (0.05)	γ16
χ2 / J	36.19	50.25	3.15	3.24
df	20	20	5	5
p-value	0.014	0.000	0.677	0.660

Notes: N = 584. The df = $\text{rank}({\widehat{\Omega }}^{+}\widehat{\Omega })$ minus the # unrestricted coefficients. Estimates for the γs in the MIIV-GMM column were obtained from an OLS regression and are not reflected in the J-test.

In the CFA model for trust, we find all of the λs are statistically significant in the expected direction, but both the J test and Satorra-Bentler scaled test indicate that the model does not fit the data well (see Table 2). In addition, some of the estimates of the same λ differ more than expected when comparing the ML and MIIV-GMM estimator with the latter tending to be smaller than the former.

We can estimate subsets of equations with the MIIV-GMM estimator, which allows us to obtain more information about potential sources of misspecification. Table 3 reports the J tests from estimating two different subsets of equations for the CFA model. The first subset includes the generalized measures of trust and the second subset includes the measures of trust in specific domains. Based on the J tests, we see that the model treating the generalized measures of trust as effect indicators is consistent with the data, but the model treating the measures of trust in specific domains is not consistent with the data. This pattern of results is consistent with the MIMIC model specification.

Table 3:

MIIV-GMM J-Tests for Subsets of Equations of CFA Model.

	J statistic	df	p-value
λ2	3.24	5	0.663
λ3 – λ8	49.49	20	0.000

It is also interesting to note the contrast in results if we use covariance or correlation residuals from the ML estimates versus the J test. The J test points to problems with the variables that are treated as causal indicators in the MIMIC version of the model. The correlation residuals are all less than 0.05 (in absolute value) for these variables. The highest correlation residual (0.13) is between trust and helpful which could lead a researcher to introduce correlated errors between these variables while missing the other possibility of the MIMIC model. The situation is similar to high leverage points in regression analysis: while the residuals of the high leverage points are generally low, if these points are in fact outliers, this leads to misspecification of the model as a whole.

Turning to the MIMIC model, we find that the estimates for λ₂, γ₂₁, γ₁₅, and γ₁₆ are statistically significant in the expected direction (see Table 2). We do not find statistically significant effects for all of the local measures of trust. We see that the J test and Satorra-Bentler scaled test indicate that the MIMIC model fits the data reasonably well. We also note that the ML and MIIV-GMM estimates are generally closer for this model than they are for the CFA model. These results are similar to what Glanville and Paxton (2007) found and suggest that MIMIC model is preferred over the CFA model for trust.

9. SIMULATION STUDIES

9.1. Simulation Study 1

This section presents a simulation study that examines the performance of the MIIV-GMM estimator for a general SEM. The simulation study is designed to explore two things: (1) the small-sample properties of the MIIV-GMM estimator as compared with an ML estimator and (2) the advantage of the ability for the MIIV-GMM estimator to be used for a subset of equations that would not be possible for an ML estimator. The study considers a broad range of sample sizes, N = 50, 100, 250, 500, and 1000. The estimators are assessed with respect to bias, efficiency, the Type I error for the J tests, and the conformity of the J statistics to a χ² distribution with the corrected degrees of freedom (df = rank(${\widehat{\Omega }}^{+}\widehat{\Omega }$) minus the # unrestricted coefficients).

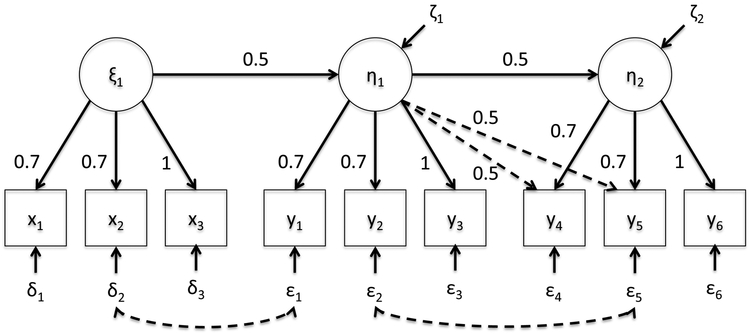
9.1.1. Population Model

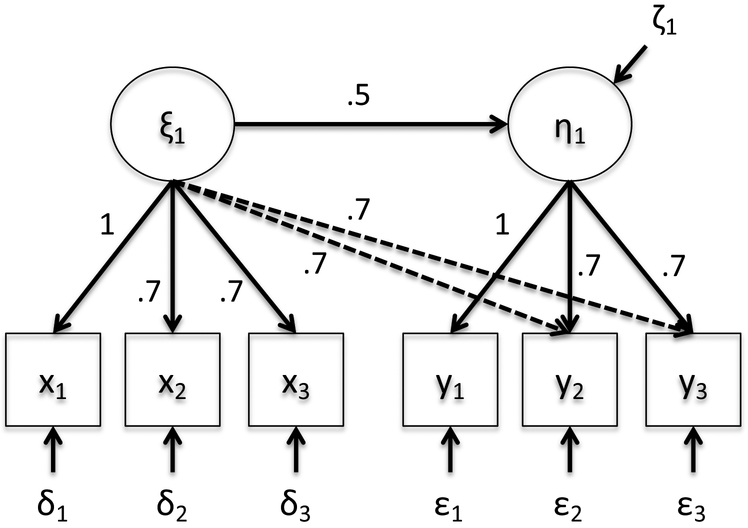
The population model is a general SEM that involves three latent variables with three indicators each (see Figure 3). The three latent variables are related to each other in a causal chain with the population values given in Figure 3. The disturbances, ζ_1i and ζ_2i, are independent standard normal random variables. The population model includes two cross-loadings among the indicators and two correlations among the disturbances of the indicators represented by dashed lines in Figure 3. The dashed lines signify that these relationships are present in the population, but are not included in the models estimated in the simulation study and therefore a source of misspecification. The variances of the disturbances for six of the indicators were allowed to depend on the latent variables to illustrate the performance of the MIIV-GMM with heteroskedastic errors. The following equations were used to generate heteroskedasticity

$${\delta }_{1i}=\text{exp}[-0.5{\xi }_{1i}-0.25]z_{1i}$$ (48)

$${\delta }_{2i}=\text{exp}[{\xi }_{1i}-1]z_{2i}$$ (49)

$${ϵ}_{1i}=\text{exp}[-0.5{\eta }_{1i}-0.25]z_{3i}$$ (50)

$${ϵ}_{2i}=\text{exp}[{\eta }_{1i}-1]z_{4i}$$ (51)

$${ϵ}_{4i}=\text{exp}[-0.5{\eta }_{2i}-0.25]z_{5i}$$ (52)

$${ϵ}_{5i}=\text{exp}[{\eta }_{2i}-1]z_{6i},$$ (53)

where z_ji are six independent standard normal random variables. These functions were chosen to ensure the unconditional variance for each disturbance equaled 1.

Figure 3:

Population Model.

Stata 12 was used to draw 1000 samples based on the population model for each of the five sample sizes. To ensure that the generated data had the desired distributional characteristics, we performed Mardia’s multivariate skewness and kurtosis tests on each data set (Mardia, 1970). At sample sizes greater than 50, Mardia’s test for multivariate skewness rejects the null in every sample, and at N = 50 Mardia’s test for multivariate skewness rejects the null in 99.5 percent of the samples. Similarly, at sample sizes greater than 100, Mardia’s test for multivariate kurtosis rejects the null in every sample, and at N = 50 and N = 100 Mardia’s test for multivariate kurtosis rejects the null in 80.9 and 99.7 percent of the samples respectively. We can thus conclude that the data exhibit very strong lack of multivariate normality that may affect the ML results.

9.1.2. Model Implied Instrumental Variables (MIIVs)

MIIVs for the simulation study models (i.e., the population model with the dashed lines omitted) were obtained using the procedures outlined in Appendix 2. The following table provides the MIIVs for all of the equations. For example, the y₃ equation has the composite disturbance γ₁₁δ_3i+ϵ_3i+ζ_1i. All of the indicators of η_1i and η_2i are indirectly affected by ζ_1i and are therefore eliminated from consideration. This leaves x_1i and x_2i as the MIIVs for this equation. We emphasize that these are the MIIVs for the misspecified model that fails to incorporate the relationships indicated by the dashed lines in Figure 3. For some equations, the MIIVs would be different had we used the correct model. For other equations, the MIIVs are the same under the true or misspecified equations and hence are robust to these errors. See Bollen (2001) for discussion on robustness of MIIVs to structural misspecifications. In Table 4 the first column lists the given equation, the second column indicates the MIIVs used in the estimation of the misspecified model, the third column indicates the MIIVs that are valid based on the population model, and the final column indicates the differences between the two sets of MIIVs for each equation.

Table 4:

MIIVs for the Simulation Models.

Equation	IVs implied by fitted model (solid paths only)	IVs implied by true model (solid and dashed paths)	Incorrect IVs in fitted model
y3	x1, x2	x1, x2	-
y6	x1 – x3, y1, y2	x1 – x3, y1, y2	-
x1	x2, y1 – y6	x2, y1 – y6	-
x2	x1, y1 – y6	x1, y2 – y6	y1
y1	x1 – x3, y2, y4 – y6	x1, x3, y2, y4 – y6	x2
y2	x1 – x3, y1, y4 – y6	x1 – x3, y1, y4, y6	y5
y4	x1 – x3, y1 – y3, y5	x1 – x3, y1, y2, y5	y3
y5	x1 – x3, y1 – y4	x1 – x3, y1, y4	y2, y3

9.1.3. MIIV-GMM Estimator

The simulation study relies on the two-step GMM estimator with an identity matrix as the weight matrix in the first step and an allowance for heteroskedastic errors. For each sample two GMM models and one ML model were estimated: (1) a GMM model for only the latent model (i.e., just equations y₃ and y₆), (2) a GMM model for the full misspecified SEM, and (3) a ML model for the full misspecified SEM. It is not possible to only estimate the latent variable model with the ML estimator, though it is with the MIIV-GMM estimator. This is one of the advantages of the MIIV-GMM estimator. For this model, the MIIVs for the latent variable model are the same in the misspecified and the correct model. This means that the MIIV-GMM estimator for the latent variable model is robust to the structural misspecifications in the full model (Bollen, 2001). With this example we illustrate the flexibility of the MIIV-GMM estimator to apply to just a part of the model and to limit the consequences of structural misspecification.

9.1.4. Simulation Results

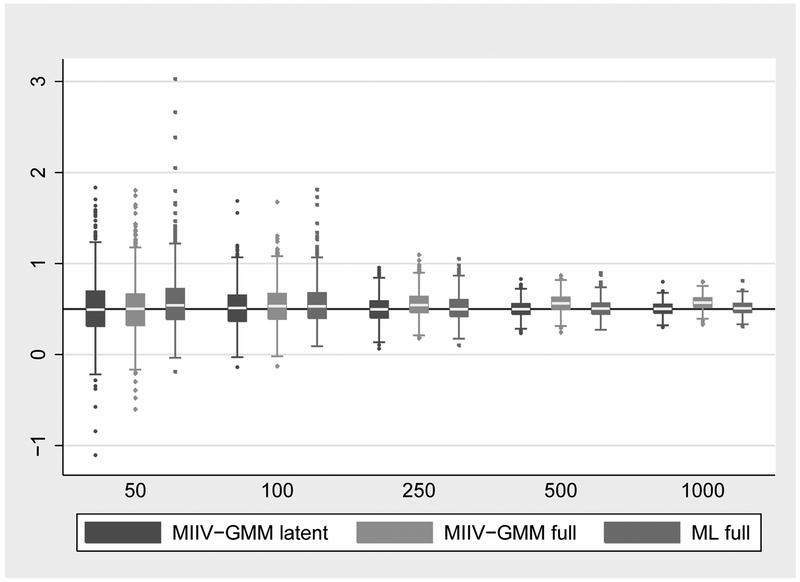
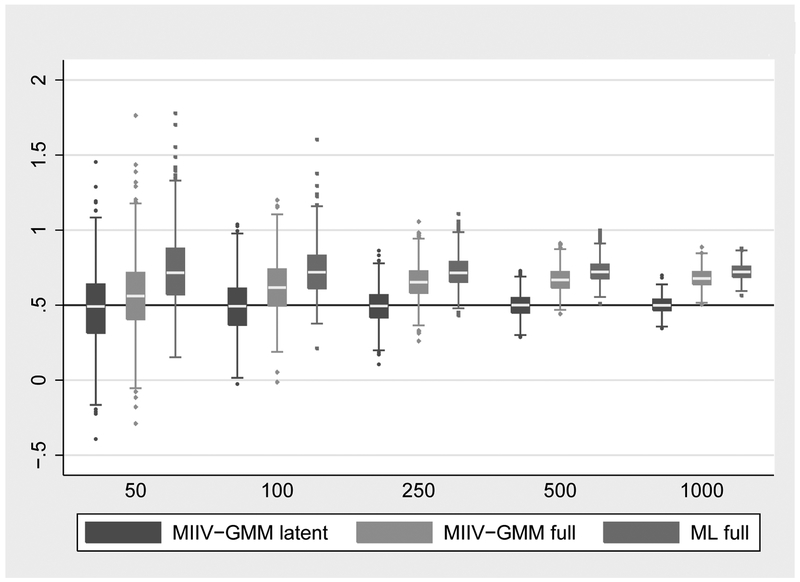
Figures 4 and 5 provide box plots of the coefficient estimates of the latent variable model using MIIV-GMM latent model only, MIIV-GMM full model, and ML full model. Figure 4 gives the distribution of ${\widehat{\gamma }}_{11}$, the effect of ξ₁ on η₁ across the five sample sizes (one outlier estimate from the MIIV-GMM full model at N = 50 has been removed to improve the readability of the graph). In the population γ₁₁ = 0.5 which is marked by the horizontal line in the graph. Overall the three estimators perform similarly across the sample sizes: they have small biases and have similar variances. At the smallest sample sizes (N = 50, 100), the ML estimator has more extreme outliers and a skew to the right, though these differences go away at higher sample sizes.

Figure 4:

Estimates for γ₁₁ by Sample Size.

Figure 5:

Estimates for β₂₁ by Sample Size.

A different story emerges for β₂₁, the effect of η₁ on η₂, as shown in Figure 5. The population value of β₂₁ is 0.5 as represented with the horizontal line. The most striking feature of this graph is the better performance of the MIIV-GMM latent variable estimator compared to the MIIV-GMM full model and ML full model estimators. The median MIIV-GMM is essentially .5 across all sample sizes. The ML full is the most biased estimator followed by the MIIV-GMM full model with a little less bias. The variability of the estimators are similar for each sample size, though the ML estimator tends to have more right skew at the smaller samples. These results illustrate the scalability advantage of the MIIV-GMM estimator, in that applying this estimator to the latent part of the model allows one to better isolate specification error than the full system estimators, either MIIV-GMM full or ML full.

Table 5 reports the proportion of samples with a significant J test across each sample size for the MIIV-GMM latent model estimator. Given that the latent model is correctly specified, one would expect that the fraction of the samples where the J test statistics exceeds the χ² critical value to be close to the nominal 5%, at least in large samples. The third column of Table 5 reports the p-value from a two-tailed binomial probability test for whether the observed proportion of samples with significant J tests differs from the expected 0.05. Since we are conducting five significance tests we apply a Bonferroni correction and the significance level becomes 0.01. The results indicate that the J tests reject the null too often only at a sample size of N = 50.

Table 5:

Proportion of Samples with p ≤ 0.05.

N	Proportion	Binomial test of Ho : p = 0.05
50	0.022	< 0.001*
100	0.035	0.029
250	0.047	0.717
500	0.033	0.011
1000	0.041	0.217

^*Statistically significant at 0.05 after Bonferroni correction

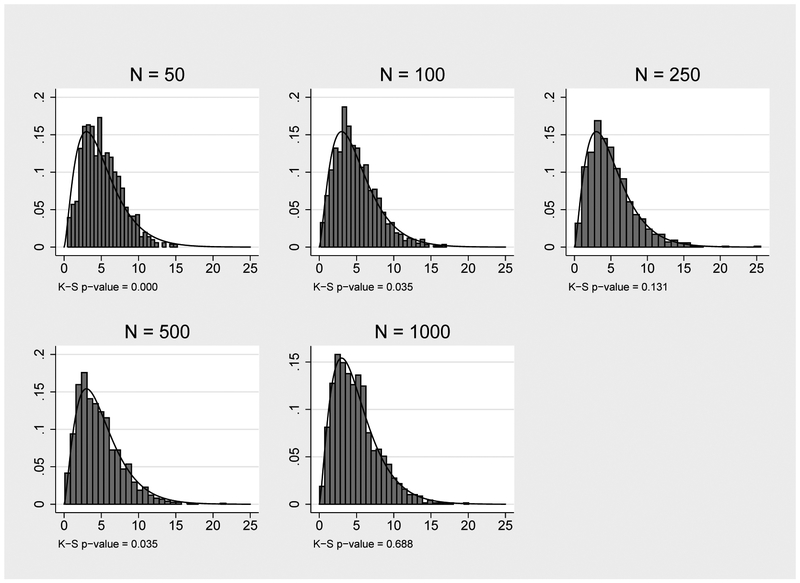
We also applied Kolmogorov-Smirnov tests of whether the J statistic follows the expected χ² distribution. Applying the Bonferroni correction, the tests indicate that the distribution of the J statistic significantly differs from the expected χ² distribution only at N = 50. Figure 6 provides histograms of the J statistics for the MIIV-GMM latent models across each of the sample sizes. The solid line in the histograms shows the χ² distribution with the corrected degrees of freedom.

Figure 6:

Distribution of J–statistics in Latent Model.

9.1.5. Simulation 1 Summary

We designed this simulation to examine the finite sample performance of the MIIV-GMM estimator and the scalability advantage of the MIIV-GMM estimator that can apply to any subset of equations. Our results illustrate the robustness to a structurally misspecified model where we used MIIV-GMM just to estimate the latent variable model. The MIIV-GMM estimator for just the latent variable model was more robust than either ML or the MIIV-GMM applied to the full model. The popular ML estimator for SEM could not be applied just to the latent variable model. All the estimators had similar variability. We also illustrated the scalability feature of the MIIV-GMM estimator to test the latent variable model in isolation from the rest of the model structure. The J-test performed well for all but the smallest sample size (N = 50).

9.2. Simulation Study 2

We simulated a simpler model for just one sample size to further illustrate the behavior of MIIV-GMM when estimating and testing a subset of equations. Figure 7 is the path diagram of the model where the solid and dashed lines represent the true model and the dashed lines are mistakenly omitted paths. A researcher confident in the latent variable model could use MIIV-GMM to only estimate and test the latent variable equation and when this is done in a sample size of 500 with 1000 replications the mean coefficient value is 0.51, within sampling fluctuation of the population value of 0.5. In addition, the proportion of samples with a p-value for the J-test less than 0.05 is 0.05. In contrast, with ML we estimate the whole system of equations and find a coefficient of 0.66 for the latent variable equation, a bias of roughly +32%. The proportion of samples with a p-value from the chi square test less than 0.05 is 0.82 which reveals a potential problem, but the mean values of the fit indices are within acceptable ranges (mean CFI = 0.98, TLI = 0.96, RMSEA = 0.06). Conventional practice would lead many researchers to accept this misspecified model along with its bias estimator of the coefficient from the latent variable model.

Figure 7.

Notes: The dashed lines for the cross-loadings indicate that these effects are present in the true model but are not included in the estimated model. Var(δ_j) = Var(ε_j) = Var(ζ₁) = Var(ξ₁) = 1 for j = 1, 2, 3.

Suppose that we suspect that the measurement model of the second latent variable is invalid. If we isolated just these three indicators and estimated a factor analysis model with ML, then the model would be exactly identified and no overidentification test is available. In contrast, with MIIV-GMM we can estimate just the three indicators for the second latent variable and test the fit of the model. When this is done the proportion of samples with a p-value of the J-test less than 0.05 is 0.81 and we have clear evidence that this part of the model is problematic.

10. CONCLUSION

Two problems have hindered the diffusion of GMM estimators into latent variable modeling. These are that typically GMM estimators are formulated for observed not latent variables and the instrumental variable versions of GMM require methods for finding IVs.

This paper uses Bollen’s (1996a; 2001) MIIV approach to transform latent into observed variable models and to use the structure of the original model to determine the MIIVs for a model. In addition, we develop the estimator permitting a positive semidefinite weight matrix rather than the usual GMM estimator that assumes a positive definite weight matrix. These tools combined enable us to create a family of MIIV-GMM estimators that apply to latent variable modeling, a result not available elsewhere.

Applying our MIIV-GMM comes down to three steps: (1) convert the latent variable model to an observed variable model, (2) find the MIIVs for each equation, and (3) use MIIV-GMM estimator with the J tests. The conversion from latent to observed variables is reproduced from Bollen (1996a) and is given in an early section of the paper. To find MIIVs a researcher can refer to Appendix 2 or the empirical examples of this paper. Essentially, the procedure of searching the MIIVs consists of a special way of examining the total effects of the composite disturbances on the observed variables for each equation. An automated procedure to find the MIIVs can be found in Bollen & Bauer (2004). Finally, Stata and R both have GMM procedures for observed variable models that are easily adapted to the MIIV-GMM estimator for latent variable models that we described in this paper. The Psychometrika website has an online appendix that has the Stata code for our empirical example.

The proposed framework offers additional SEM diagnostic tools to those willing work outside the traditional SEM approach.

First of all, similar to the earlier work on instrumental variables by Bollen and colleagues, the MIIV-GMM is a framework that operates on equations, rather than on (observed vs. implied) covariances. Researchers using latent variable models conceptualize and present them at the level of latent variables and the relations between them, as is usually seen in path diagrams presented in substantive papers. The latent variable model is often of greater interest than the measurement model, with the latter being seen as but a stepping stone towards estimating the relations between the latent variables. Bollen (1989, 1996) proposed a single equation solution for estimating the latent variable model and this paper demonstrates how an asymptotically efficient estimator for the latent variable model can be built.

Second, the proposed framework allows testing goodness of fit in otherwise complicated situations. In simulation study 2, the standard approach to verifying the measurement models would be to consider the CFA model for each latent variable separately. However, in the standard covariance-matrix based SEM framework, these models are saturated, and thus do not allow goodness of fit testing. The MIIV-GMM approach, however, brings in additional instruments from other parts of the model, and allows a more flexible and more general testing of these measurement models.

Third, the MIIV-GMM approach is potentially promising in allowing a somewhat easier treatment of models nonlinear in latent variable models, such as quadratic and interaction terms. While adding nonlinear terms to the standard covariance-based SEMs often leads to considerable difficulties in specifying the indicators of the nonlinear terms, adding these nonlinear terms into GMM-MIIV may be as simple as adding nonlinear terms into regular regression. Research into this topic is in progress.

By way of summary, Table 6 contrasts the MIIV-GMM with the MIIV-2SLS and ML and other full information estimators to highlight the similarities and differences between these estimators. The MIIV-GMM estimator allows analysts to work with as few as one equation at a time to as many as all of the equations, whereas ML estimators require all equations and MIIV-2SLS estimators only work with one equation at a time. This flexibility can be used to isolate specific parameters of interest and help guard against bias due to misspecification in other parts of the model. In addition, the MIIV-GMM estimator is robust to heteroscedasticity, while ML estimators are only robust under certain conditions and corrections must be applied for the MIIV-2SLS estimator to be robust to heteroscedasticity. When applied to a subset of equations, the MIIV-GMM estimator can be robust to local structural misspecification, a property not shared with full-information ML estimators. Furthermore, MIIV-GMM has a chi square test statistic J that applies to single or nested models, something not possible with ML or MIIV-2SLS. Finally, similar to the MIIV-2SLS, the MIIV-GMM estimator does not make strong distributional assumptions and does not need to be an iterative estimator, all in contrast to the ML estimator. As such, the MIIV-GMM estimator has several potential advantages over both the ML estimator and the MIIV-2SLS estimator.

Table 6:

Contrast of Classic Maximum Likelihood (ML), Model-Implied Instrumental Variable Two Stage Least Squares (MIIV-2SLS), and Model-Implied Instrumental Variable Generalized Method of Moments (MIIV-GMM) Estimators.

Property	Classic ML	MIIV-2SLS1	MIIV-GMM
Scalable estimation2	no	no	yes
Scalable test statistics	no	no	yes
Heteroscedastic robustness	no3	no4	yes
Distributional robustness	no3	yes	yes
Local structural misspecification robustness	no	yes	yes5
Noniterative estimator	no	yes	yes

Notes:

¹Bollen, 1996a; 1996b.

²One equation to all equations.

³Under special conditions some standard errors and test statistics are robust.

⁴Correction for heteroscedastic consistent standard errors described in Bollen (1996b).

⁵Assumes a subset (not all) of equations are estimated.

Under minimal assumptions the MIIV-GMM estimators are consistent, asymptotically unbiased, and asymptotically normal. A consistent estimator of their covariance matrix of the coefficient estimators is readily available. While MIIV-GMM estimator is asymptotically efficient, this efficiency result relates only to the estimators that use the same estimating equations. When the set of estimating equations is extended, greater efficiency can be achieved (Hall 2005, theorem 6.1).

The properties of the MIIV-GMM are asymptotic, so we included a simulation study to explore its finite sample properties for small (N = 50) to large (N = 1000) sample sizes. The bias of coefficient estimates is negligible even at the smallest sample size for the MIIV-GMM estimator for the latent variable model, despite the data being heavily non-normal. We also found that the J overidentification test for the MIIV-GMM estimator for all equations and for subsets of equations generally had good Type I error rates for all sample sizes and follows a chi-square distribution with the corrected degrees of freedom for all but the smallest sample size. Though we clearly need more simulation studies under different conditions, these preliminary results are promising.

Some additional extensions of the proposed estimators may be worth mentioning. One computational option that we considered in simulations was an iterative GMM estimator in which the process of estimating Ω is repeated iteratively where the new ${\widehat{\Omega }}^{-1}$ replaces Ω⁻¹ in (27) and the steps are repeated until there is little change in $\widehat{\Omega }$ from one step to the next (Hall, 2005, sec. 3.6). Our preliminary experience with the iterative MIIV-GMM estimator is that convergence problems were too frequent and the efficiency advantages were minor at best. These convergence issues for the iterative GMM are consistent with other researchers’ experiences in a different GMM context than ours (e.g., see Hall, 2005, p.90).

Another property of the MIIV-GMM is that it really refers to a family of estimators that depend on the weight matrix, the subset of equations, and the MIIVs in the analysis. In a correctly specified model, the estimators are consistent regardless of the weight matrix or MIIVs. This means in large samples we expect the estimates to be close regardless of the MIIVs or weight matrix. Indeed, if estimates differ significantly across either different sets of MIIVs, different weight matrices, or different subsets of equations, then this is evidence of structural misspecification in the model.

The treatment of missing data is not well explored in the traditional GMM literature and we see this as a future area of research. We see no reason that would prevent researchers applying multiple imputation methods with the MIIV-GMM estimator. The authors conducted a simple simulation study and found that multiple imputation led to a consistent MIIV-GMM estimator in a MAR condition for two different types of SEMs, a three indicator CFA and a general SEM model. However, a much more systematic examination is needed.

Another area requiring further research is MIIV-GMM in multiple group analysis. One possibility is to use dummy variables to code groups and to detect differences in intercepts. Products of the dummy variables with other continuous observed variables would permit tests of whether slopes differ across groups. But research is needed to assess this approach.

While we have only explored the linear latent variable models with continuous variables, the generalized methods of moments framework is extremely flexible, and allows more complicated features of latent variable models to be incorporated into the GMM approach. For instance, nonlinearity in the response process can be treated in a way this is done with generalized linear models. That is, a likelihood score equation for a binary or a Poisson response can be formed, and further multiplied by an instrumental variable to form a moment condition (e.g., see Foster (1997) for an illustration of using IVs in logistic regression).

Perhaps most encouraging about the MIIV-GMM estimator is that by making the links to latent variable modeling, this paper opens the door to the vast research from econometrics on GMM. Many of these results are now potentially applicable to latent variable models.