Computation of Object Size in Visual Cortical Area V4 as a Neural Basis for Size Constancy

Abstract

Even when we view an object from different distances, so that the size of its projection onto the retina varies, we perceive its size to be relatively unchanged. In this perceptual phenomenon known as size constancy, the brain uses both distance and retinal image size to estimate the size of an object. Given that binocular disparity, the small positional difference between the retinal images in the two eyes, is a powerful visual cue for distance, we examined how it affects neuronal tuning to retinal image size in visual cortical area V4 of macaque monkeys. Depending on the imposed binocular disparity of a circular patch embedded in random dot stereograms, most neurons adjusted their preferred size in a manner consistent with size constancy. They preferred larger retinal image sizes when stimuli were stereoscopically presented nearer and preferred smaller retinal image sizes when stimuli were presented farther away. This disparity-dependent shift of preferred image size was not affected by the vergence angle, a cue for the fixation distance, suggesting that different V4 neurons compute object size for different fixation distances rather than that individual neurons adjust the shift based on vergence. This interpretation was supported by a simple circuit model, which could simulate the shift of preferred image size without any information about the fixation distance. We suggest that a population of V4 neurons encodes the actual size of objects, rather than simply the size of their retinal images, and that these neurons thereby contribute to size constancy.

SIGNIFICANCE STATEMENT We perceive the size of an object to be relatively stable despite changes in the size of its retinal image that accompany changes in viewing distance. This phenomenon, called size constancy, is accomplished by combining retinal image size and distance information in our brain. We demonstrate that a large population of V4 neurons changes their size tuning depending on the perceived distance of a visual stimulus derived from binocular disparity. They prefer larger or smaller retinal image sizes when stimuli are stereoscopically presented nearer or farther away, respectively. This property makes V4 neurons suitable for encoding the actual size of objects, not simply the retinal image sizes, and providing a possible mechanism for perceptual size constancy.

Introduction

We perceive the size of an object to be relatively stable despite changes in the size of its projected retinal image that accompany changes in viewing distance (Fig. 1A). In this perceptual phenomenon, called size constancy, the visual system estimates an object's size by combining image size and distance information (Gregory, 1997). Although the importance of distance information in size perception has been known for 2000 years since it was suggested by Claudius Ptolemaeus (Ross and Plug, 1998), how the neural computation for size constancy is performed remains poorly understood.

Figure 1.

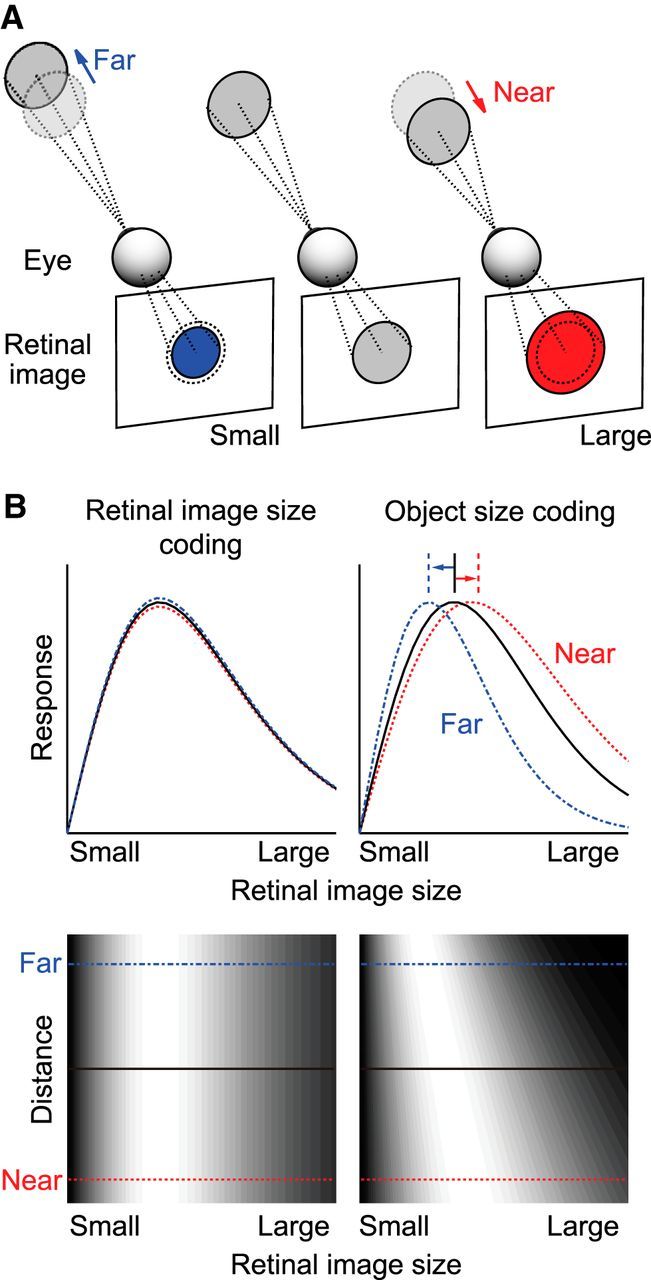
Rationale of this study. A, Schematic view of the size of the retinal image projected from an object located at various distances. B, Response properties of hypothetical neurons that encode retinal image size (left) and object size (right). Top plots, Retinal image size tuning curves. Bottom plots, Discharge rates are indicated in grayscale in 2D space, where the abscissa represents retinal image size and the ordinate represents distance. Neurons that encode retinal image size should not change their tuning curves dependent on distance. Object size-coding neurons should have a preference for larger retinal images when objects are located at nearer positions, and smaller retinal images when objects are located at more distant positions.

Neurons in various visual cortical areas respond preferentially to a particular range of sizes of visual objects (Desimone and Schein, 1987; DeAngelis et al., 1994; Gegenfurtner et al., 1996, 1997; DeAngelis and Uka, 2003). The responses are thought to be tuned to the retinal image size of an object, rather than to the size of the object itself, although no study has tried to tease apart the two possibilities. By definition, neurons tuned to retinal image size should prefer the same retinal image size even when the distance to the object is varied (Fig. 1B, left). Instead, if neurons encode the size of an object, their preference for retinal image size should systematically vary with the observer-to-object distance. They should prefer a larger image when an object is located at a nearer position and a smaller image when it is located at a more distant position (Fig. 1B, right). If object size-coding neurons exist, they could potentially provide neural signals for size constancy.

Here, we searched for object size-coding neurons in cortical area V4 of the macaque monkey, a mid-tier area in the ventral visual pathway (Roe et al., 2012). Lesion studies have shown that V4 is involved in the discrimination of stimulus size (Schiller and Lee, 1991; Cohen et al., 1994; Schiller, 1995; Frassinetti et al., 1999) and the prestriate cortex, including V4, plays a role in size constancy (Ungerleider et al., 1977). V4 neurons are sensitive to the size of solid figures (Desimone and Schein, 1987; Umeda et al., 2007) and to binocular disparity, a robust and quantitative cue for depth (Hinkle and Connor, 2001, 2005; Watanabe et al., 2002; Tanabe et al., 2004, 2005). We examined whether tuning of V4 neurons to the size of visual stimuli embedded in random dot stereograms (RDSs) is modulated by altering their stereoscopic distance without any changes in monocular visual features.

We first show that human observers systematically changed the perceived size of an object in RDSs with changes in its perceived distance. We then demonstrate that a majority of neurons recorded from macaque V4 scaled their size tuning depending on the sign and the magnitude of binocular disparity. The shifts of the perceived size in human observers and of the preferred size of V4 neurons were consistent with those expected to support size constancy. We suggest that a population of V4 neurons encodes object size by scaling their tuning to retinal image sizes according to the perceived distance to objects.

Materials and Methods

Psychophysical experiments.

Three subjects, two naive subjects (K.K., S.Y.) and an author (S.T.), participated in psychophysical experiments. They had normal or corrected-to-normal vision. The experimental protocol was approved by the research ethics committee of Osaka University. Informed consent was obtained from all subjects.

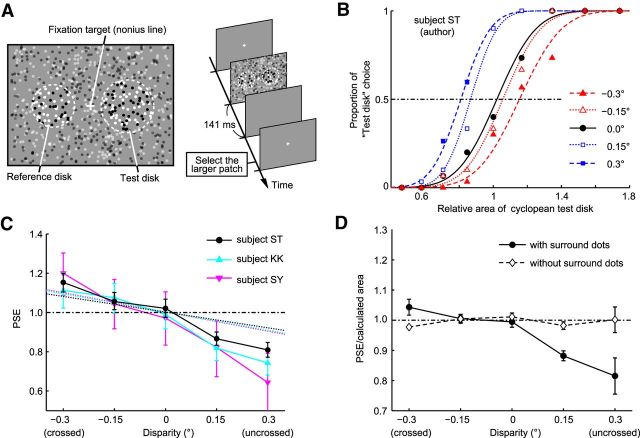
Subjects were seated in front of a cathode ray tube (CRT) monitor (21-inch; Multiscan E230, Sony). They held their head on a chin rest in a dark room, with the monitor placed 57 cm away from the base of the chin rest. In each trial, they viewed two cyclopean disks positioned to the left and right of a fixation target through stereo-shutter glasses (RE7-CANE, Elsa). After the subjects fixated on the target (nonius line) at the beginning of each trial, they clicked a mouse button. The two disks were then presented for 141 ms (see Fig. 3A). This short stimulus duration avoids a break in fixation, a change in vergence angle, and a resultant change in binocular disparities of cyclopean disks during the stimulus presentation period. The subjects were asked to judge which of the two disks looked larger, and then select the larger disk by clicking the left or right mouse button. After clicking the mouse button, the fixation target was presented again to start the next trial.

Figure 3.

Effects of perceived depth on size perception in human subjects. A, The stimulus and the time course of events in the psychophysical experiments. B, Example psychometric curves from one subject (author S.T.). The proportion of test-disk choice is plotted as a function of the area of the test disk relative to the reference disk. The cumulative Gaussian functions were fitted to the data points. The points where the curves crossed the 50% choice line are referred to as PSEs. C, Systematic change of PSEs with binocular disparity (data from an author and two naive subjects). Dashed lines indicate the geometrically calculated relationship between relative image size and binocular disparity for each subject. Error bars indicate 95% confidence intervals. D, The ratio of PSE to the geometrically calculated image area. When the stimuli did not have surrounding uncorrelated dots (i.e., the contour of the disk was visible with one eye), the calculated ratio was ∼1 for all disparities tested. When the stimulus had surrounding dots, the ratio was <1 for the uncrossed disparity condition. Error bars indicate SEM.

A custom-made program using OpenGL was used for visual stimulus presentation and task control. Each RDS was composed of the same number of bright dots (1.90 cd/m²) and dark dots (0.01 cd/m²) on a mid-luminance background (0.95 cd/m²). The luminance was measured through the shutter glasses. The size of a single dot was 0.14°. Random dots covered the entire area of the display, with a dot density of 15%. Dot patterns were refreshed every 4 frames (21 Hz). Positional differences between related dot patterns projected to each eye, or binocular disparities, evoked depth perception. When subjects viewed the RDSs monocularly, no figure was visible because of the lack of depth cues. Within each RDS, the center disk region consisted of binocularly correlated dots (i.e., the location of the black/white dots was related but displaced horizontally by a set distance between the images shown to each eye). The region surrounding this disk consisted of uncorrelated dots (i.e., there was no relationship between the location of dots between eyes).

Specifically, to generate RDSs with uncorrelated surround dots, we first determined the position and the size of the correlated center disk and randomly allocated dots within this region. The positions of these dots were consistent but were shifted horizontally to a given amount between left and right eye images to create binocular disparity. To manipulate disparity magnitude, we changed the amount of the displacement between the dot patterns for left and right eyes. We randomly distributed dots around the center disk to fill the remaining area of the entire display. Because the surrounding random dots were allocated for the left and right images separately, they were uncorrelated between left-eye and right-eye images. In the image for one eye, the dots that had a partner in the other eye's image seamlessly joined to a region where the dots did not. In viewing this image monocularly, one does not see any figure and cannot detect any change of the image when the position, size, and binocular disparity of the center disk were manipulated (see Fig. 2).

Figure 2.

Examples of RDSs with uncorrelated and correlated surround dots. When one views the right and center dot patterns with the left and right eyes, respectively, five disks hovering among the background uncorrelated noise dots are perceived. When one views the center and left dot patterns with the left and right eyes, respectively, disks hovering on the background plane and holes in the background plane are perceived. Values on the right side of the RDS indicate the binocular disparity (arbitrary unit) when the stereogram is viewed cross-eyed.

When a subject binocularly fuses the images, a disk (“cyclopean disk”) hovering among the background uncorrelated noise dots is perceived (see Fig. 2, right pair). Although the border of the cyclopean disk surrounded by the uncorrelated dots (see Fig. 2, right pair) is blurred and less vivid than that of the cyclopean disk surrounded by correlated dots (see Fig. 2, left pair), we used uncorrelated rather than correlated dots in the background for the following reason. If correlated dots were used for the entire RDS, subjects perceive a hole in the surrounding plane and a plane through the hole instead of a disk with an uncrossed disparity (see Fig. 2, left pair). The edge of the perceived hole belongs to the surrounding plane, and the depth of the edge is fixed to the surrounding plane and independent of the binocular disparity inside the hole. Furthermore, if we use correlated dots for background, we cannot define the figure by binocular disparity of the dots, which are same as that of surrounding dots (i.e., zero disparity for both figure and surround; see Fig. 2, left pair). These prevent us from examining the relationship between the perceived size of the disk and its binocular disparity. In contrast, the RDSs used in this study (i.e., a disk region consisting of correlated dots surrounded by uncorrelated dots) enables subjects to perceive a cyclopean disk even when the disk region is given an uncrossed or zero disparity. We finally note that for some observers the background of binocularly uncorrelated dots may appear to be higher in dot density than the center of correlated dots.

The distance between cyclopean disks and the fixation target was 5°. One of the disks was the reference disk, 6° in diameter and 0° binocular disparity. The other disk was a test disk that varied in diameter and binocular disparity across trials. The range of the diameter of the test disk was determined depending on the size discrimination acuity of each subject determined in pretest trials. Binocular disparity of a test disk varied from −0.3° to 0.3° with a step of 0.15°. The left-right position of a test disk was determined randomly in each trial. Each stimulus condition was repeated 30 times.

In the psychophysical experiments, we calculated the proportion of choices where the subjects perceived the test disk as larger for each stimulus condition. We then plotted it against the area of the test disk relative to the reference disk to obtain psychometric functions for the five binocular disparity conditions. Cumulative-Gaussian functions were fitted independently to the data for the five disparities. For this procedure, we applied a bootstrap method using the “fminsearch” function in MATLAB (The MathWorks). The mean of this function provides an estimate of the point of subjective equality (PSE), which is defined as the relative area of test disk for which the subjects chose the test disk with 50% probability (i.e., they perceived the two disks as identical in size).

Physiological experiments.

We used one female Japanese monkey (Macaca fuscata; body weight 6.4 kg; Monkey H) and one male rhesus monkey (Macaca mulatta; body weight 6.2 kg; Monkey I). Details of the surgical procedure have been described previously (Uka et al., 2000; Tanaka et al., 2001). In brief, we implanted a head post on the top of the monkey's skull so that it could later be fastened to a chair through holding the post. A recording chamber was implanted at the stereotaxic coordinates at 5 mm posterior, 25 mm dorsal to the external canal for mounting of an electrode micromanipulator (Watanabe et al., 2002; Tanabe et al., 2005; Umeda et al., 2007). Scleral search coils were implanted under the conjunctiva of both eyes to monitor the monkey's eye movements. After a recovery period, the monkeys were trained to perform a fixation task. After completing the training, we drilled a hole through the skull inside the recording chamber for electrode insertion. All animal care protocols were approved by the Animal Experiment Committee of Osaka University and conform to the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Electrophysiological experiments were performed in a dark room. The monkeys were seated in a chair in front of a 21-inch CRT monitor (Flexscan T965, Nanao) with their implanted head post fixed to the chair. They viewed the visual stimuli on the display through stereo shutter glasses (Displaytech). The distance between their eyes and the display was 57 cm. The edge of the display was masked by a black screen with a square hole at the center placed in front of the monkey. When a fixation point (0.2° × 0.2°) was presented at the center of the display, the monkey was required to keep its gaze on it for 1.25 s. If the monkey moved its gaze beyond a fixation window of 1.2° × 1.2° or a vergence window of ±0.4°, the task was aborted. During the fixation, visual stimuli were presented for 500 ms after a 500 ms prestimulus period. In additional experiments with varying vergence angles, we made a positional difference between fixation points for left and right eyes on the CRT monitor (−0.5° or 0.5°). After each successful trial, the monkey was rewarded with a drop of water. The tasks were controlled using a commercially available software package (TEMPO, Reflective Computing).

Visual stimuli were presented by using a custom-made program with the same parameters used in the psychophysical experiments. We placed a cyclopean disk over the classical receptive field (RF) of a neuron under study. The cyclopean disks consisted of correlated dots, with the surrounding region consisting of uncorrelated dots. The binocular disparity of the correlated dots was changed from −0.75° (or −0.6° or −0.9°) to 0.75° (or 0.6° or 0.9°) with a step of 0.25° (or 0.2° or 0.3°). The binocular disparity applied to the correlated dots changed the perceived position in depth without any changes in the physical position in depth or in the physical size of the correlated-dot region. The diameter of the correlated-dot region was varied from 25% to 200% of the classical RF diameter with a step of 25%.

A custom-made glass-coated tungsten microelectrode (0.3–1.5 MΩ at 1 kHz) was inserted into the prelunate gyrus using a micromanipulator mounted onto the recording chamber. Voltage signals were amplified (×10,000) and bandpass filtered (0.2–2.0 kHz) (amplifier: BAK Electronics; filter: NF Corporation). Action potentials from a single neuron were isolated with a template-matching spike isolation system (Multi-Spike Detector, Alpha-Omega Engineering). The spike timing was recorded at a sampling rate of 1 kHz. When extracellular activity was isolated from a single neuron, we determined its classical RF by moving a small patch of RDS and mapping the minimum RF. Because the RF was mapped only once for each neuron, we cannot provide any statistics for the reliability of the RF size and the relative preferred size (see Fig. 6E,F). In the recording sessions, area V4 was identified based on the relationship between the RF eccentricity and the diameter of classical RFs of recorded neurons (Desimone and Schein, 1987; Gattass et al., 1988; Watanabe et al., 2002), the visuotopic map (Gattass et al., 1988), and the position of the surrounding sulci. After all recording sessions were completed, the monkeys were subjected to histological analysis. The recording sites were confirmed to reside in area V4. When an isolated neuron responded well to cyclopean stimuli, we recorded its responses to combinations of various binocular disparities and sizes of cyclopean disks. All stimulus conditions were randomly ordered within a block, and 3–10 (median 10) blocks were repeated.

Figure 6.

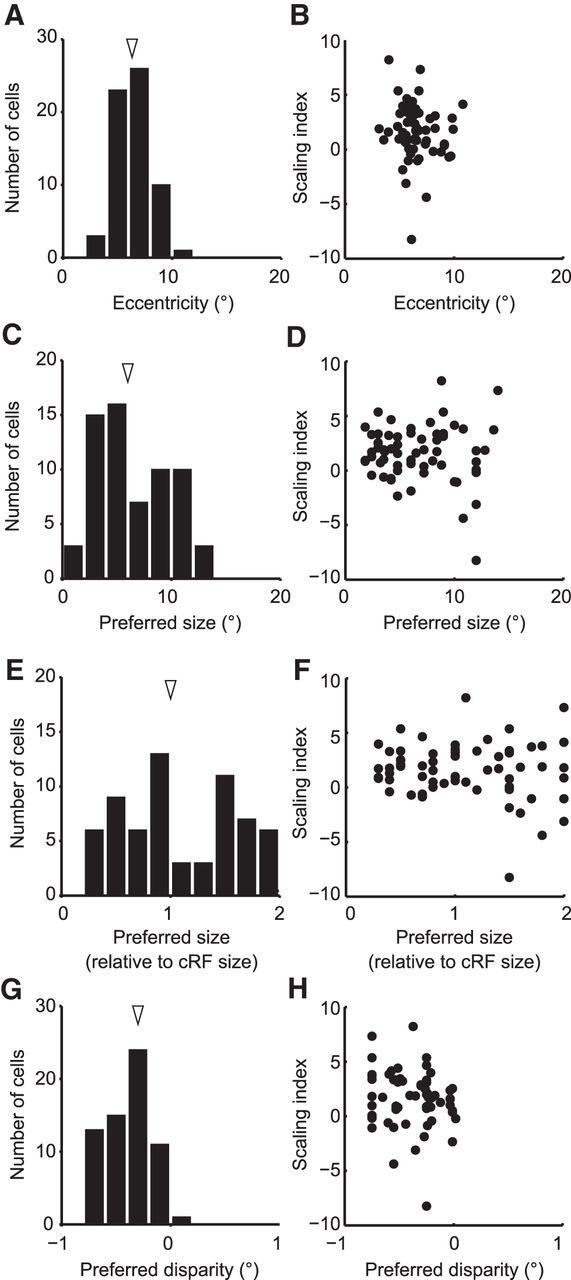
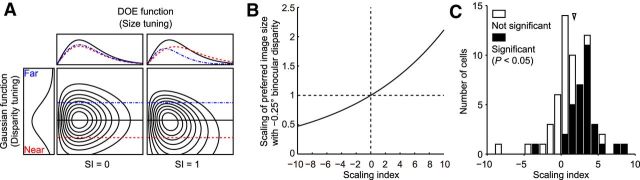
Relationship between SI and other parameters of recorded neurons. A, The distribution of the RF eccentricities of recorded neurons. The median RF eccentricities were 6.3°. B, The RF eccentricities and the SIs did not show any correlation (Spearman's rank correlation, r = −0.19, p = 0.13). C, The distribution of the preferred diameter. Arrowhead indicates the median (6.7°). D, There was no correlation between SI and preferred diameter (Spearman's rank correlation, r = −0.046, p = 0.72). E, The distribution of the preferred image size relative to the diameter of the RF. Arrowhead indicates the median (1.08). F, There was no correlation between relative preferred image sizes and SIs (Spearman's rank correlation, r = −0.075, p = 0.56). G, The distribution of the preferred disparities calculated from a Gauss·DoE function fitted to the data. The distribution of preferred disparities was significantly biased toward the crossed disparities with a median of −0.30° (signed-rank test, p < 10⁻¹²). H, There was no correlation between SIs and preferred disparities (Spearman's rank correlation, r = −0.19, p = 0.14).

Data analysis.

For each combination of stimulus size and binocular disparity, we computed the mean firing rate for a duration of 500 ms, starting from 80 ms after the onset of stimulus presentation. The 80 ms shift of the time window was to compensate for the response latency of V4 neurons. The spontaneous firing rate was calculated as the mean firing rate during the 250 ms before stimulus onset, a period when the monkey had already fixated.

To quantify the scaling of size tuning according to binocular disparity, neural responses were fitted using the Gauss-DoE function, which is the outer product of the Gaussian function and the difference of error (DoE) function as follows:

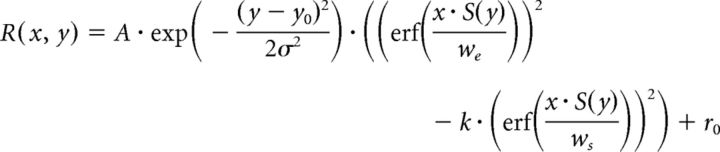where R(x, y) denotes the response to a cyclopean disk with radius x and binocular disparity y, A the amplitude of response modulation, y₀ the center of the Gaussian function, σ the width of Gaussian function, w_e and w_s the widths of the positive and negative error functions, k the amplitude ratio for the negative error function, and r₀ the response baseline. The error function erf(x) is the integral of a Gaussian function over the range of zero to x and given by the following:

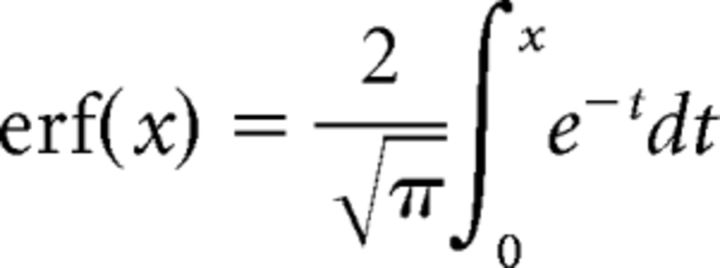S(y) means the extent of scaling dependent on binocular disparity y; therefore, x · S(y) denotes the relative size of the object that gives retinal image size x at each position in depth represented by binocular disparity y. S(y) was defined as follows:

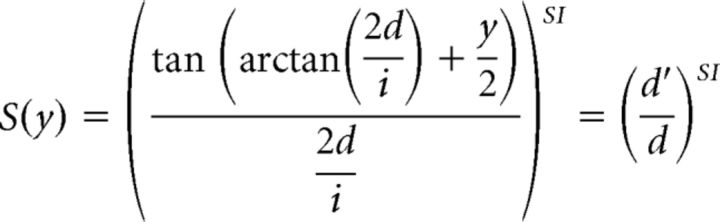where i is the interpupillary distance (33 mm for Monkey H, 31 mm for Monkey I), d the distance between the fixation point and the middle point of the two pupils, and d′ the geometrically calculated distance between the cyclopean disk and the middle of the two pupils. SI is defined as a scaling index, which is a metric to evaluate the effect of binocular disparity on size tuning curves. An SI of 0 indicates that the size tuning curve is not scaled depending on binocular disparity and that there is no shift in the peak position (see Fig. 5A, left). Therefore, the neuron is tuned to retinal image size, not object size. When the SI is >0, the preferred size shifts depending on binocular disparity in the direction expected for size constancy. The preferred size becomes larger for the crossed disparity (see Fig. 5A, right; black line to red line, near) and smaller for the uncrossed disparity (see Fig. 5A, right; black line to blue line, far). An SI of 1 indicates that the neuron perfectly represents the object size with a viewing distance of 57 cm.

Figure 5.

SI as a metric applied to quantify the scaling of image size tuning. A, The schematic view of the Gauss·DoE function used to explain the response. In this function, the SI was used to denote whether the neuron represents object size or not. With an SI of 0, the cell responds best to a particular retinal image size regardless of the binocular disparity. With an SI of 1, the cell perfectly represents object size by changing its preferred retinal image size depending on the binocular disparity, and shows a tilted response field in the 2D plane of disparity tuning versus size tuning. B, The relationship between the SI and the scaling of the preferred image size with −0.25° binocular disparity when fixating on 57 cm distant plane. C, The distribution of the SIs for 63 V4 neurons. Arrowhead indicates the median SI (1.73). Filled columns represent significant scaling (sequential F test, p < 0.05).

The fit was performed to determine the combination of parameters (A, r₀, k, w_c, w_s, σ, y₀, SI, d) that minimized the sum-squared error between the response of the neuron and the value of the function (R(x, y)). When calculating the SI, we fixed the distance parameter (d) at 57 cm. When calculating an optimal fixation distance at which the neuron represents the object size accurately, we fixed the SI at 1 and treated the distance (d) as a free parameter. However, fitting the function to all size-disparity responses with a free distance parameter did not yield optimum results. This is because uncrossed disparities have a physical limit. In an extreme case where we view infinite distance, it is geometrically impossible to achieve an uncrossed disparity. Even if the fixation distance parameter was not infinite, the physical limit of uncrossed disparity became smaller than the largest uncrossed disparity used in the experiment when the fixation distance parameter in our fitting approached the maximum (0 < d < 1000 cm). Because the calculated value of the function (R(x, y)) becomes negative infinity as the uncrossed disparity exceeds the physical limit, the parameters obtained from the fitting of the function to all size-disparity responses cannot be properly interpreted. Therefore, we excluded the data recorded with an uncrossed disparity from the analysis calculating the optimum fixation distance (see Fig. 9C,D).

Figure 9.

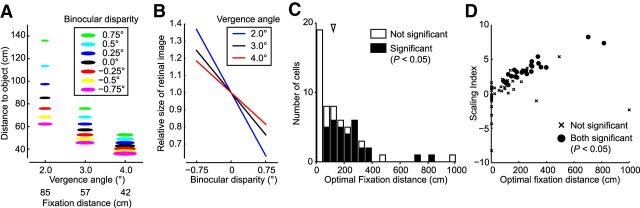
Distribution of the optimal fixation distances for V4 neurons. A, The relationship between distance, binocular disparity, and retinal image size. Colors of the symbols represent the values of binocular disparity. Sizes of the symbols represent the relative size of the retinal image. When fixating on a point farther away, the degree of depth represented by binocular disparity becomes larger (e.g., compare the 85 cm case with the 57 cm case). B, The extent of change in retinal image size that occurred with the change in binocular disparity becomes larger for more distant fixations (i.e., smaller vergence angles). C, The distribution of the optimal fixation distances for each neuron. The arrowhead indicates the median of the distance parameter (118 cm). Filled columns represent significant scaling (sequential F test, p < 0.05). D, The relationship between the optimal fixation distance and the SI. The optimal fixation distance was positively correlated with the SI (Spearman's rank correlation, r = 0.74, p < 0.01).

The “fmincon” function in MATLAB (The MathWorks) was used to perform the fittings with the following constraints (Tanabe et al., 2004, 2005; Umeda et al., 2007). The amplitude of the function (A) was constrained to values between one-fifth and 5 times the difference between the maximum and minimum responses of all the trials. The baseline (r₀) was constrained to values between half the mean response to zero radius stimuli and twice the mean response to zero radius stimuli. The amplitude weight for the negative error function (k) was constrained to values between 0.2 and 1.2. The widths of the error function (w_c, w_s) were constrained to values within the radius range being tested. The width of the Gaussian function (σ) was constrained to values between 0.01 and the total range of tested disparities. The disparity offset (y₀) was constrained to values within the disparity range being tested. When calculating the SI, SI was constrained to be within −10 and 10. When calculating the optimal distance (see above), the distance parameter (d) was constrained to values between zero and 1000 cm.

We calculated size discrimination index (SDI) to the cyclopean figure size at each disparity as follows:

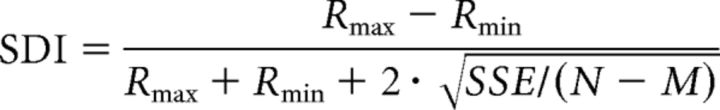where R_max and R_min are the maximum and minimum mean responses, SSE the sum of the squared error of the response, N the number of trials, and M the number of the stimulus diameters tested.

Statistical tests.

The quality of fit was evaluated using a goodness-of-fit R² measure. To test statistically whether the size tuning curves were scaled with changes in the binocular disparity of the cyclopean disk, the sequential F test was performed (Draper and Smith, 1998).

Model simulation.

To explain the response properties of recorded neurons, we developed a simple model based on the difference of Gaussian (DoG) model (DeAngelis et al., 1994) and the disparity energy model (Ohzawa et al., 1997). The model consists of two binocular complex cells, an excitatory unit and a suppressive unit, with the RF of the excitatory unit being larger than that of the suppressive unit. Each complex cell consists of four simple-cell subunits S1, S2, S3, and S4. The output responses of the four subunits to a stimulus are given by the following:

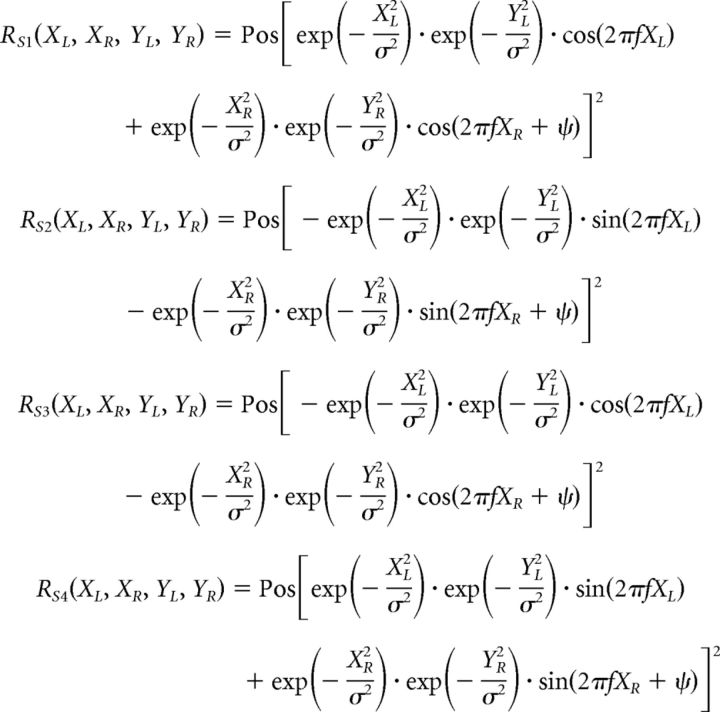where R(X_L, X_R, Y_L, Y_R) denotes the response to the stimulus positioned at (X_L, Y_L) on the left retina and (X_R, Y_R) on the right retina. σ determines the area of the subunit RFs, and f is the spatial frequency of the sinusoidal factor. The parameter ψ is the phase difference between the left and right RFs. Pos[v] is a half-rectifying function given by the following:

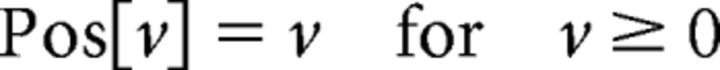The response of complex cell C is the summation of the responses of simple-cell subunits as follows:

The stimuli used as an input to calculate the output response in Figure 12 were RDSs similar to those used in our psychophysical and physiological experiments. A total of 2000 points are randomly generated in an area of a 40.0 × 40.0 (arbitrary unit) x-y plane. Half of the points were bright, with a contrast value of 1. The other half of the points were dark, with a contrast value of −1. The diameter of the circular center region was varied from 0 to 30 with a step of 1. The points in the center region of the stimulus were binocularly correlated. The binocular disparity of the points varied from −3.5 to 3.5 with a step of 0.5. The points in the surrounding region were binocularly uncorrelated. The center position of the center disk was identical to the center position of an excitatory unit and a suppressive unit. The parameters, σ, f, and ψ, for the RF of the excitatory unit were 4.5, 0.03, and 0.25π, respectively. The parameters for the RF of the suppressive unit were 9.0, 0.035, and 0.11π, respectively. To generate the response of the size-coding unit, the response of the suppressive unit was subtracted from the response of the excitatory unit after half-wave rectification. The responses to 300 patterns of RDSs were averaged.

Figure 12.

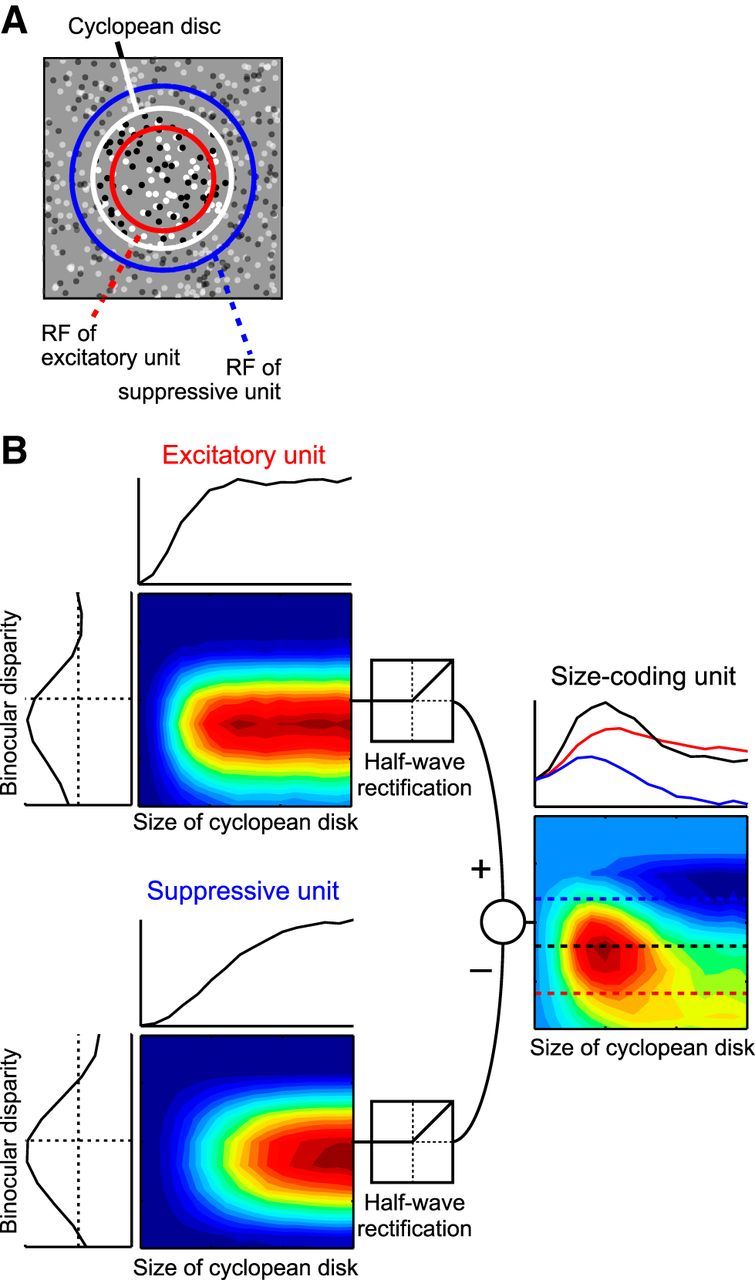
Simple model to explain the V4 response to the size of a cyclopean figure. A, Two binocular complex cells (excitatory unit and suppressive unit) based on the disparity energy model share their center with the cyclopean disk. The suppressive unit possesses a larger RF than that of the excitatory unit. B, The two units show disparity-tuning curves with slightly different phases and frequencies. These units change their responses according to the size of cyclopean disks but do not show size suppression. The subtraction of the two units generates a size-coding unit that shows size tuning curves with size suppression and a tilted response field similar to those of our recorded V4 neurons.

Results

Effects of binocular disparity on perceived size of cyclopean figures

We first examined whether human observers changed their perceived size depending on the sign and amplitude of binocular disparity using dynamic RDSs as visual stimuli. McKee and Welch (1992) examined the effects of binocular disparity on size perception using solid figures (bars) as stimuli. They showed that a bar is judged to be shorter (longer) when it is stereoscopically presented nearer (further). This result suggests that the brain exploits distance derived from binocular disparity to scale the perceived size and achieve size constancy. However, changing binocular disparity in solid figures inevitably causes a positional change in their monocular images on the two retinas. Here we extended this finding by examining whether binocular disparity embedded in dynamic RDSs has a similar scaling effect. Dynamic RDSs can create depth without any changes in the monocular visual features (Julesz, 1971) and permit a strict test as to whether and how the perceived depth affects size perception (Fig. 2).

While fixating a center fixation point, subjects were presented with an RDS in which two circular regions were placed side by side (Fig. 3A). The circular region of each RDS consisted of binocularly correlated dots, and the rest was filled with uncorrelated dots (Fig. 2, right pair). The resulting perceived disks were “cyclopean” in nature (i.e., they were visible only when the left-eye and right-eye images of the RDSs were binocularly fused). The RDSs used in this study enabled subjects to perceive a cyclopean disk, not a hole in the background, even if uncrossed disparity was applied to the correlated-dots region (Fig. 2; see Materials and Methods).

They were required to discriminate in a two-alternative forced choice manner which of the two disks (test vs reference disks) was larger. The reference disk was always 6° in size and presented at 0° binocular disparity. The test disk varied its diameter and binocular disparity across trials (9 diameters at 5 disparities). Each combination of size and disparity was tested 30 times. We plotted the proportion of test-disk choices against the size of the test disk relative to the reference disk to obtain psychometric curves, one each for the five binocular disparities.

Data from a subject (author S.T.) are shown in Figure 3B. When binocular disparity of a test disk was uncrossed (open and closed squares; far perception), the psychometric curves were shifted to the left relative to the curve obtained from trials with test disks at zero disparity. When the binocular disparity of the test disk was crossed (open and closed triangles; near perception), the curves were shifted to the right. The shift was larger for larger disparity amplitudes. To quantify the shifts, we determined the PSE, or relative size of the test disk at which the psychometric curve crossed the 50% choice line. For the test disk with 0 binocular disparity (closed circles), the PSE was 0.99, indicating no perceptual bias in size judgment. When the test disk had uncrossed disparities, the PSEs were <1.0 (0.87 and 0.80 for 0.15° and 0.3°, respectively). When the test disk had crossed disparities, the PSE became >1.0 (1.06 and 1.15 for −0.15° and −0.3°, respectively). In all 3 subjects, the PSE became gradually smaller as the perceived position of the test disk became farther away (Fig. 3C). Human observers thus perceive a larger test disk with crossed disparity (near) or a smaller test disk with uncrossed disparity (far) as the same size as the reference disk on the fixation plane. The relationship between the PSE and binocular disparity is consistent with the relationship between the size of the retinal image projected from an object and the distance to it (Fig. 1A). This result indicates that human observers use distance information derived from binocular disparity to estimate the size of cyclopean figures in the same way that they estimate the size of solid figures.

In all subjects, the changes in perceived size with crossed disparities followed the prediction based on geometrically calculated image sizes, whereas the PSEs for the uncrossed disparity conditions markedly deviated from the prediction (Fig. 3C,D). The ratio of the PSE to the geometrically calculated image size was ∼1 for zero and crossed disparities but was 0.88 at 0.15° and 0.81 at 0.3° for uncrossed disparities (Fig. 3D, closed circles). This means that, for the uncrossed disparity condition, the subjects estimated the size of the test disk as larger than the image size that was geometrically calculated with the binocular disparity. This overestimation of the size at uncrossed disparities did not occur when we used RDSs without surrounding uncorrelated dots (Fig. 3D, open diamonds). This overestimation may be caused by an overestimation of the image size of cyclopean disks because the surrounding monocular dots could be perceived as part of the cyclopean disk in the uncrossed disparity condition (Shimojo and Nakayama, 1990) (see Discussion).

These results indicate that human observers changed their perceived size of the cyclopean disk dependent on the sign and amplitude of binocular disparity.

Systematic shifts of preferred image size by stereoscopic depth

Having confirmed that the visual system exploits disparity information in RDSs to scale the perceived size, we examined responses of V4 neurons to RDSs similar to those used in the psychological experiments. We recorded 152 neurons from two monkeys (47 neurons from Monkey H and 105 neurons from Monkey I) while they performed a fixation task and passively viewed the RDSs (Fig. 4A, right). A cyclopean disk was positioned to cover the RF of each neuron under study (Fig. 4A, left). We changed the size and binocular disparity of the disk to probe the size tuning functions at different stereoscopic depths. A total of 112 neurons (40 neurons from Monkey H and 72 neurons from Monkey I) responded to at least one of the stimulus conditions (t test with Bonferroni correction for multiple comparisons, p < 0.05) and were significantly selective both for binocular disparity and stimulus size (two-way ANOVA, p < 0.05). These neurons were subjected to the following analyses.

Figure 4.

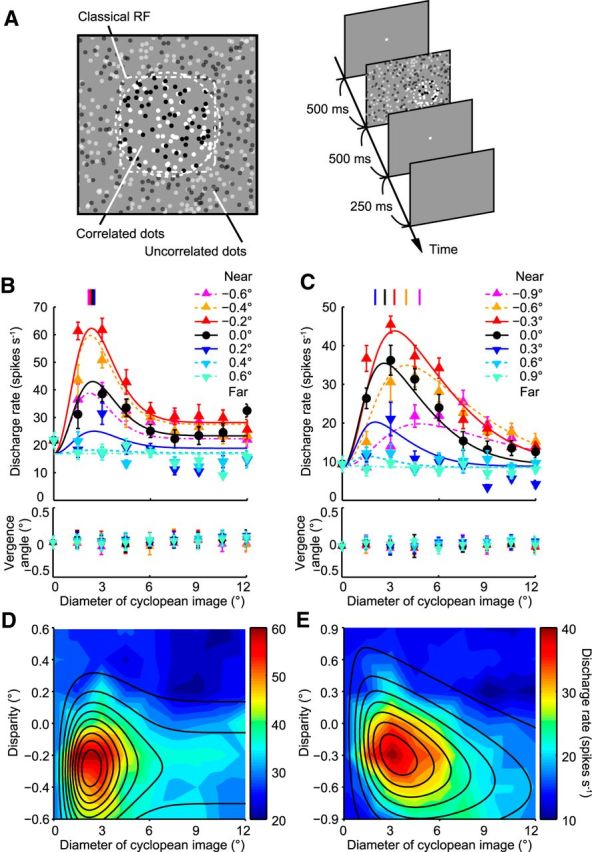
Effects of binocular disparity on size tuning curves of V4 neurons. A, Schematic drawing of stimulus used in physiological experiment and time course of events. B, Size tuning curves of a sample V4 neuron that did not change its size preference for the cyclopean figure depending on binocular disparity. B, C, Vertical lines at top indicate the peak size preference derived from fitting curves in each binocular disparity condition. Bottom graphs represent the time-averaged vergence angle of the stimulus duration with respect to the prestimulus period as a function of binocular disparity of the stimulus. DoE functions were fitted to the data points obtained at different disparities. Error bars indicate SEM. C, Size tuning curves of a sample V4 neuron that varied its size preference for the cyclopean figure with changing binocular disparity. D, E, Examples of response fields on the plane of stimulus size and binocular disparity. Discharge rate is represented with the color scale shown on the right of each panel. Solid lines indicate the contour plots of the Gauss·DoE function fitted to the data points. The calculated SIs were −0.41 (D) and 2.50 (E), respectively.

V4 neurons in this study exhibited tuning to the size of the cyclopean disk (Fig. 4B,C) in a manner similar to that of V4 neurons tested with solid figures in previous reports (Desimone and Schein, 1987; Umeda et al., 2007). As the size of the correlated region became larger, the responses gradually increased toward a maximum before declining and stabilizing along an asymptote. It should be noted that a disk cannot be seen monocularly in our RDSs and that monocular images do not vary with the change in size of the binocularly correlated region. The V4 neurons are thus tuned to the size of cyclopean (i.e., perceived) disks. The mean decrease of responses from the peak to the asymptote examined in the 0 disparity condition was 111%, which was similar to the value obtained with solid figures for a subset of neurons (95%; Wilcoxon's signed-rank test, p = 0.09, n = 23). An important next question was whether this size tuning was based on retinal image size or object size.

The neuron shown in Figure 4B represents an example of a V4 neuron that was tuned to retinal image size. The preferred size of this neuron was constant across different binocular disparities. The peak position of the size tuning curves remained the same at 1.5°–3.0° of visual angle for stimuli with different binocular disparities. The magnitude of responses changed across different binocular disparities, indicating that this neuron was disparity-selective. The neuron shown in Figure 4C represents an example of a V4 neuron that changed its preferred size depending on the binocular disparity of the disk, as did the majority of V4 neurons. The preferred size (marked by vertical lines at the top) shifted from small to large with the change in the stimulus position in depth from far to near. This relationship between preferred size and depth was consistent with the geometric relationship between retinal image size and distance; as objects move to nearer positions, the retinal image size becomes larger (Fig. 1A).

During the stimulus presentation, the monkeys kept their fixation on the fixation point; therefore, the vergence angle should be stable within a predetermined window (±0.4°; see Materials and Methods). However, if the monkeys systematically changed their vergence angle within this range with binocular disparity or stimulus size, it was possible that the selectivity to the binocular disparity or stimulus size of the recorded neuron may not have genuinely depended on the stimulus disparity or size but on the vergence angle. While recording the neuron in the first example, the time-averaged vergence angle was dependent on the binocular disparity and stimulus size (Fig. 4B, bottom panel; two-way ANOVA, p = 0.0023 and p = 0.0034, respectively). For the neuron in the second example, the time-averaged vergence angle did not show any systematic change during the recording period (Fig. 4C, bottom panel; two-way ANOVA, p = 0.89 for binocular disparity, p = 0.24 for stimulus size). The time-averaged vergence angle depended on the binocular disparity in only 23 of the 112 cells (21%), and on the stimulus size in only 9 of the 112 cells (8%; two-way ANOVA, p < 0.05). Therefore, vergence eye movements are unlikely to account for the sensitivity to size, binocular disparity, and their interaction.

To better visualize the interaction between size tuning and binocular disparity tuning, we plotted neural responses on a 2D graph where the x-axis represents retinal image size and the y-axis represents binocular disparity (Fig. 1B, bottom). The response field was elongated vertically for the first example neuron (Fig. 4D), whereas it was tilted toward the left for the second neuron (Fig. 4E). For the 2D plots of responses, we fitted disparity tuning with a Gaussian function and size tuning with a DoE function (Fig. 5A, left). We then calculated a metric, SI, to assess how binocular disparity affected size tuning curves (see Materials and Methods). When the SI was near 0, the response field was elongated parallel to the Cartesian axes, indicating that size tuning and binocular disparity tuning are independent (i.e., the combined tuning to size and disparity can be obtained by the product of tuning to size and tuning to disparity). When the SI was >0, the response field was tilted toward the left, indicating that the neuron changes its size tuning depending on binocular disparity in such a way that it prefers larger sizes for nearer stimuli. The relationship between SIs and the degrees of scaling for an example case of −0.25° binocular disparity is shown in Figure 5B. As an SI becomes larger, the degree of scaling becomes larger, indicating that the response field is tilted more. An SI of 10 in this case indicates that the preferred image size becomes 2.1 times larger. The neuron shown in Figure 4B, D has SI = −0.41 (not different from 0; sequential F test, p = 0.52), and the neuron shown in Figure 4C, E has SI = 2.50 (different from 0; p < 0.01).

Across 63 neurons for which the Gauss·DoE function fitted well to the response field (R² > 0.65), SIs were widely distributed with a median of 1.73 (Fig. 5C). The overall distribution of SIs deviated from zero toward positive values (signed-rank test, p < 10⁻⁶). At the single-neuron level, 32 of the 63 neurons had an SI significantly different from 0, and all but one of them had positive values (Fig. 5C, filled columns). Manipulation of binocular disparity of the stimulus caused a shift of the preferred image size in the direction consistent with size constancy.

The 63 neurons with well-fit tuning functions had RF centers at eccentricities of 3.1°–10.8° (Fig. 6A). Their preferred image size determined from the Gauss·DoE function ranged from 1.8° to 14° (Fig. 6C) or 0.3–2 times that of the RF size (Fig. 6E). The SI values were not correlated to any of these RF characteristics (Fig. 6B,D,F). As has been repeatedly reported previously (Hinkle and Connor, 2001; Watanabe et al., 2002; Tanabe et al., 2005), our V4 neurons also exhibited a striking bias for near-disparity preferences (Fig. 6G). The SI values were not correlated to the preferred disparity (Fig. 6H).

To examine the relationship between the size discriminability and the biased disparity preference (Fig. 6G) of V4 neurons, we calculated the SDI (see Materials and Methods) for crossed and uncrossed disparities. The SDIs for crossed and uncrossed disparity conditions were significantly different (Fig. 7; mean = 0.48 in crossed disparity conditions, mean = 0.39 in uncrossed disparity conditions; Wilcoxon's signed-rank test, p < 0.01, n = 112), suggesting that size discrimination ability of our V4 neurons is higher for stimuli with crossed disparities than for those with uncrossed disparities.

Figure 7.

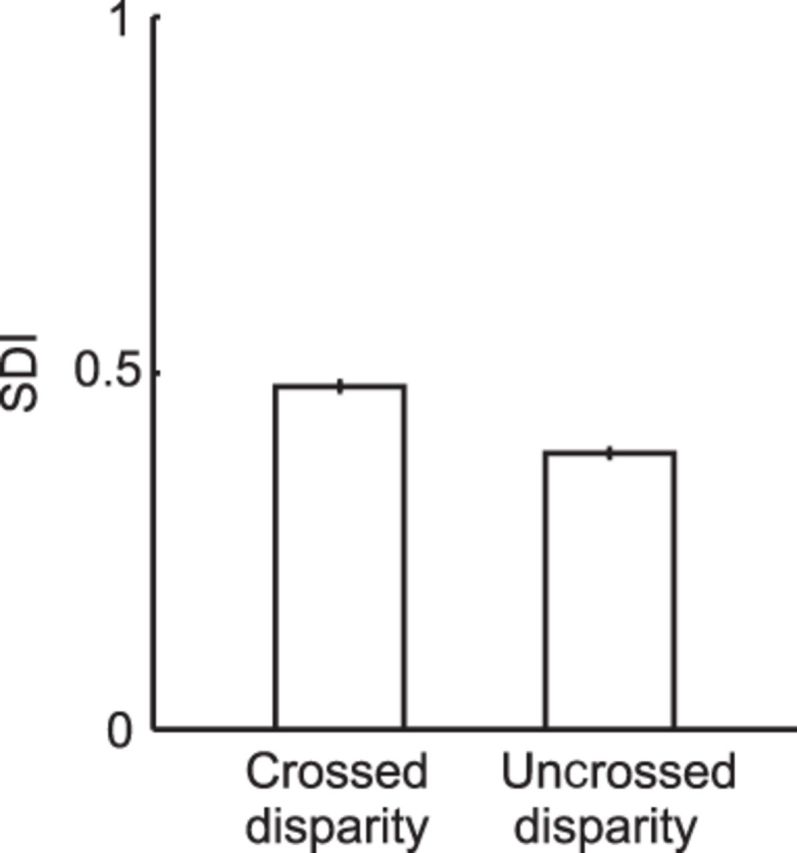
Relationship between size discrimination index (SDI) and binocular disparity. The SDIs calculated for crossed and uncrossed disparity conditions were significantly different (Wilcoxon's signed-rank test, p < 0.01, n = 112). Error bars indicate SEM.

We also examined the selectivity for relative disparity and calculated the shift ratio with the same methods described in previous studies (Thomas et al., 2002; Umeda et al., 2007). In this experiment, we manipulated binocular disparities of the center circle and surrounding annulus independently and analyzed how the disparity tuning to the center was affected by relative disparity between the center and the surround. After the size-disparity selectivity test, we examined the relative disparity selectivity when we could maintain isolation of the recorded neuronal activity. We recorded from 54 neurons. Twenty-seven cells were selective to binocular disparity (Kruskal–Wallis test, p < 0.05) and shift ratios could be calculated from well-fitted Gabor functions (R² > 0.65). The distribution of the shift ratio was significantly >0 (signed-rank test, p < 0.001) with a median of 0.14 (Fig. 8A). Shift ratios significantly different from 0 were indicated as black bars (sequential F test, p < 0.01). The median shift ratio of 0.14 was substantially smaller than that previously reported (0.41 in Umeda et al., 2007). This discrepancy may have resulted from the difference in the stimuli for searching single units. The RDSs we used to survey neurons in this study had only one binocularly correlated plane and produced only absolute disparity. Therefore, our sample was likely to be biased for absolute-disparity coding neurons and resulted in the smaller shift ratio. Fourteen neurons were also selective to the size of cyclopean disks and well fitted using a Gauss·DoE function. The shift ratios calculated from this population were also >0 (signed-rank test, p = 0.0076) with a median of 0.14. There was no correlation between the SI and shift ratio (Spearman's rank correlation, r = −0.021, p = 0.91). The distribution of SI calculated in this analysis was not different from that of all neurons (Fig. 8B; Wilcoxon's rank-sum test, p = 0.75).

Figure 8.

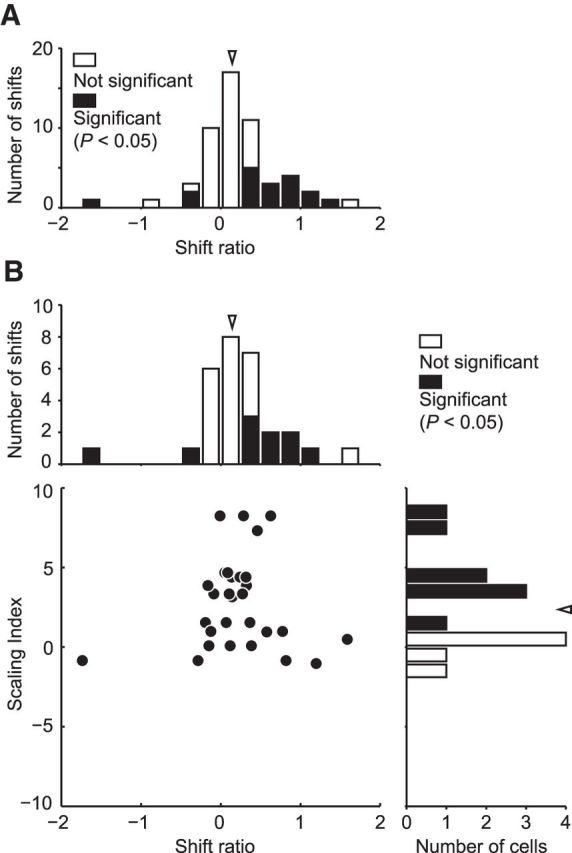
Relationship between SI and relative disparity selectivity. A, The distribution of the shift ratio calculated from 54 neurons. Arrowhead indicates the median of the shift ration (0.14). Filled columns represent significant shift (sequential F test, p < 0.05). B, There was no correlation between the SI and shift ratio calculated from 14 neurons that were also selective to the size of cyclopean disks and well fitted using a Gauss·DoE function (Spearman's rank correlation, r = −0.021, p = 0.91). Top, Arrowhead indicates the median of the shift ration (0.14). Right, Arrowhead indicates the median of the SI (2.36).

Fixation distance versus SI

The SIs of many neurons exceeded 1 (Fig. 5C). When we calculated SIs for individual neurons, we fixed the distance parameter (d) at 57 cm (see Materials and Methods). Therefore, an SI of 1 indicates perfect encoding of the size of an object only when the monkey is fixating 57 cm away. To encode the size of objects at different fixation distances, neurons with an SI of 1 determined for d = 57 are not optimal. This is because fixation distance affects how a given amount of change in binocular disparity corresponds to a change in the retinal image size of a visual stimulus. The farther the fixation distance, the larger the distance from the fixation plane to the object needs to be to generate a particular binocular disparity (Fig. 9A). Concurrently, the magnitude of change of retinal image size that occurs with that particular binocular disparity also becomes larger for farther fixation distances or for smaller vergence angles (Fig. 9B). We consider two possible ways for neurons to cope with this effect of fixation distance on the coding of object size. The first is that different pools of neurons may encode object size for different fixation distances. The second is that individual neurons change their SI systematically with changes in fixation distance.

If different V4 neurons are tailored for different fixation distances, neurons with an SI >1 or <1 may represent the relationship between image size and binocular disparity at a point of fixation farther away or closer than the tested 57 cm. The calculation of SIs with d = 57 would not give a proper estimate of their object size-coding ability. We therefore subsequently fixed the SI value at 1 and calculated the distance parameter (d) as a free parameter to estimate the range of “optimum” fixation distances of our neurons. Our calculations resulted in a broad distribution with a median of 118 cm (n = 61; Fig. 9C). The distance parameter was highly correlated with the SI (Fig. 9D; Spearman's rank correlation, r = 0.74, n = 61, p < 0.01). Neurons with an SI >1 or <1 may be used when the monkey fixates on a point more distant or closer than 57 cm.

Given the above assumption that our V4 neurons are ideal object-coding neurons with SI = 1 and that their optimum distance can be calculated, we were able to determine the preferred object size of each neuron [Preferred object size = 2·distance·tan(preferred image size/2)]. The preferred object sizes thus determined were broadly distributed over a range of 4.4–50.5 cm (median 13.6 cm; Fig. 10A; n = 32) for the neurons with significant scaling effects (i.e., neurons shown in Fig. 9C, filled columns). The preferred object size did not change with the eccentricity of the neuron's RF (Fig. 10B; Spearman's rank correlation, r = 0.17, p = 0.34), and varied across cells at every RF eccentricity. In contrast, the preferred image size was positively correlated with the RF eccentricity (Fig. 10C; Spearman's rank correlation, r = 0.51, p = 0.0027) in agreement with the RF size-eccentricity relationship (Desimone and Schein, 1987; Watanabe et al., 2002). To generate such a uniform distribution of preferred object sizes at every visual field location, the optimal fixation distances of individual neurons should be negatively correlated with their RF eccentricity. However, the correlation between the optimal fixation distance and RF eccentricity was slightly short of statistical significance (Fig. 10D; Spearman's rank correlation, r = −0.31, p = 0.086). Overall, the results suggest that V4 neurons encode a range of object sizes at every eccentric location in the visual field.

Figure 10.

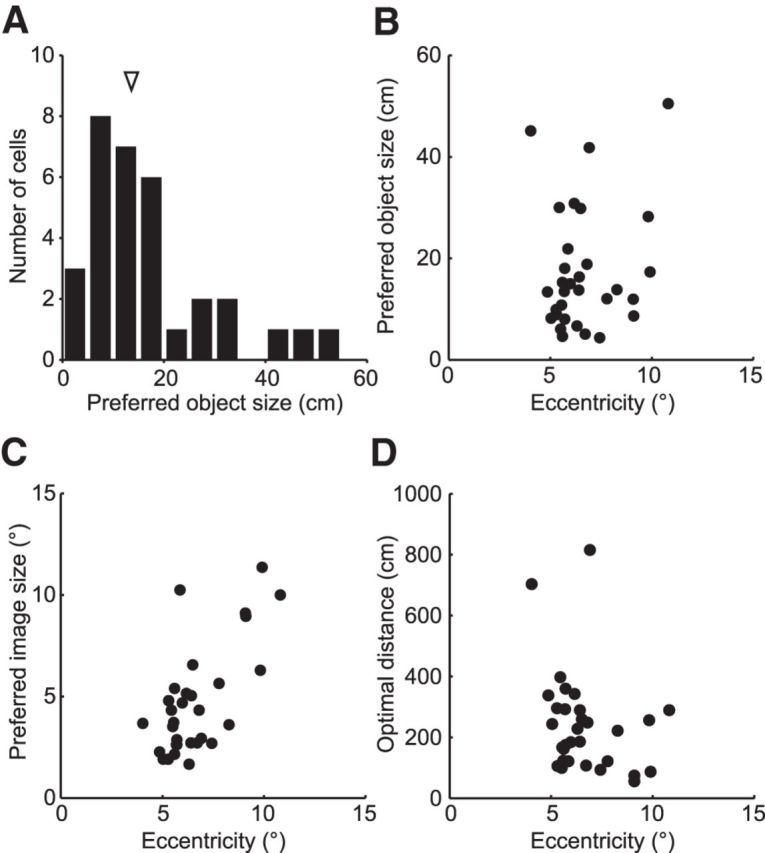
Distribution of preferred object sizes. A, The distribution of preferred object sizes for 32 presumed object size-coding neurons. The arrowhead indicates the median of the preferred object size (13.6 cm). The preferred object sizes were calculated from the object size-coding neurons that showed significant scaling when calculating optimal fixation distance (Fig. 9C, filled columns). B, The relationship between the preferred object size and the RF eccentricity. There was no correlation between the preferred object size and the RF eccentricity (Spearman's rank correlation, r = 0.17, p = 0.34). C, The relationship between the preferred image size and the RF eccentricity. The preferred image size was positively correlated with the RF eccentricity (Spearman's rank correlation, r = 0.51, p = 0.0027). D, The relationship between the optimal fixation distance and the RF eccentricity. There was no correlation between the optimal fixation distance and the RF eccentricity (Spearman's rank correlation, r = −0.31, p = 0.086).

Effects of vergence angle on SI

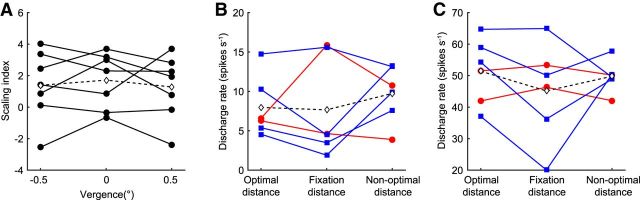
An alternative way for neurons to cope with the effects of fixation distance would be for individual neurons to change their SI systematically according to fixation distance. To test this, we manipulated vergence angle. The vergence angle provides a cue for distance estimation (Mon-Williams and Tresilian, 1999; Viguier et al., 2001), which can then be used for size constancy (Oyama and Iwawaki, 1972). To test whether SIs depend on vergence angle, we examined the responses of a small subset of neurons with two additional vergence angles (vergence angle on the initial fixation point −0.5 and 0.5°). The SIs did not change systematically with vergence angle (Fig. 11A; two-way ANOVA, p = 0.73, n = 7), indicating that the scaling of size tuning curves by binocular disparity was not affected by vergence angle or therefore by fixation distance.

Figure 11.

Effect of vergence angle on V4 neuron responses. A, SIs of 7 neurons (filled circles) and the mean SIs across them (open diamonds) at three different vergence angles. The calculated SIs did not vary with vergence angle (n = 7; two-way ANOVA, p = 0.73). B, Average firing rates calculated across all size-disparity stimulus conditions of far-optimal (SI > 1) neurons (red circles) and of near-optimal (SI < 1) neurons (blue squares). Open diamonds represent the mean of the average firing rates at each vergence angle. The calculated average firing rates did not vary with vergence angle (n = 6; two-way ANOVA, p = 0.54). C, The maximum firing rates calculated from all size-disparity stimulus conditions of far-optimal neurons (SI > 1, red circles) and of near-optimal neurons (SI < 1, blue squares). Open diamonds represent the mean of the maximum firing rates at each vergence angle. The calculated maximum firing rates did not vary with vergence angle (n = 6; two-way ANOVA, p = 0.45).

Because the SI was highly correlated with the optimal fixation distance (Fig. 9D) and an SI of 1 indicates perfect encoding of the size of an object when fixating 57 cm away, the optimal fixation distance of V4 neurons with SI > 1 (or SI < 1) would be further (or nearer) than the actual fixation distance (57 cm). If vergence angle is used to select the optimal size-coding neurons, the average firing rates or the peak response of the recorded V4 neurons should be modulated by vergence angle. The average firing rate or the peak response should become larger when the vergence angle correspond to the optimal fixation distance of the V4 neurons and become smaller in the unbalanced case. However, we could not find any systematic modulation by the vergence angle of the average firing rate (Fig. 11B; two-way ANOVA, p = 0.54, n = 6) and the peak response (Fig. 11C; two-way ANOVA, p = 0.45, n = 6).

We assume that accommodation has little effect, if any, on the distance estimation in our experiments. We controlled the monkey's vergence angle by applying a positional difference between fixation points for left and right eyes. Therefore, even when we controlled the vergence angle, accommodation of our animals should have been adjusted to the constant focal distance (57 cm) because it can be adjusted by blurred retinal images (Fincham and Walton, 1957; Cumming and Judge, 1986). Furthermore, because the experiments were performed in a dark room and the animals could not see anything, except for the stimulus display, they could not use any pictorial cues, such as shadows, perspective, and texture gradient, for distance estimation. The viewing distance was 57 cm, which was too close for atmospheric perspective to be used. The motion parallax was not available because the stimuli did not contain any motion component. Therefore, the factors for estimating the viewing distance were restricted, if not totally unavailable, in our experimental conditions.

A computational model

Finally, we developed a simple model, which can explain the shift of preferred image size with binocular disparity. This model consists of units with known physiological properties of the early visual cortex. The initial stage of the model consists of two binocular complex cells: an excitatory unit and a suppressive unit. These units were constructed by the disparity energy model (see Materials and Methods) (Ohzawa et al., 1997). An important assumption here is that the RF of the excitatory unit is smaller than that of the suppressive unit in a similar way to DoG and rate of Gaussian models (Cavanaugh et al., 2002). A disk of binocularly correlated dots was centered on their RFs (Fig. 12A). A second assumption is that the two units have a slight difference in their preferred binocular disparities. The simulated responses of either unit were not tuned to a particular stimulus size; they did not exhibit size suppression (Fig. 12B, left). Outputs from these units were then rectified, followed by subtraction between them, and fed into a unit at the next processing stage. This latter unit showed size suppression, having a peaked size tuning curve (right of Fig. 12B). Importantly, this unit had a tilted response field similar to that observed for a majority of V4 neurons (Fig. 4E); peak position shifted with binocular disparity (compare red, black, and blue tuning curves in Fig. 12B). This model thus produces a tilted response field without any information about fixation distance.

Manipulation of RFs of the two units at the first stage can generate various response fields of the second-stage unit in the size-disparity plane. Binocular disparity selectivities of the two units are especially important for determining the tilt of the response field of the second-stage unit. If preferred disparities and the widths of the disparity-tuning curves of the two units are the same, then subtraction of the two responses leads to a nontilted response field like the one shown in Figure 4D.

The computation performed by this model is similar to that performed by the disparity energy model and a model of creating relative disparity selectivity of V2 neurons (Ohzawa et al., 1997; Thomas et al., 2002). These models have a key common component that integrates two input units and produces output with a rectification process.

Discussion

Our brain takes the distance of an object into account when we perceive its size. We explored this neural process by examining the interaction between size and binocular disparity information in area V4. Many V4 neurons preferred larger (or smaller) stimulus sizes as the stereoscopic depth of stimuli became nearer (or farther away). This property makes V4 neurons suitable for encoding the size of objects and enabling perceptual size constancy (Fig. 1).

Binocular disparity as a distance cue for estimating the sizes of cyclopean figures

The brain exploits binocular disparity as a distance cue to estimate the size of solid figures (McKee and Welch, 1992). By using RDSs consisting of a correlated disk surrounded by uncorrelated dots, we extended this finding to show that binocular disparity was used to calibrate the perceived size of cyclopean images (Fig. 3). Observers perceived a larger figure at a nearer position and a smaller figure farther away as the same size as a reference disk at the fixation distance.

However, the subjects overestimated the size of cyclopean figures embedded in uncorrelated RDSs for uncrossed disparities (Fig. 3C,D). When a disk-shape patch of dots was presented without surrounding dots, the subjects estimated the image size correctly for all binocular disparities tested. The cues for fixation distance did not differ between the two conditions, and the subjects should have estimated the distance to the fixation point with equal accuracy. The overestimation of the size for uncrossed disparities was likely to be caused by an estimation error of the size or binocular disparity of the center disk in the presence of surround dots.

An estimation error of the disk size may be caused by surrounding monocular dots. When a foreground plane occludes a background plane, a small monocular region is present in the background plane. In this situation, we perceive the monocular region as part of the background plane (Shimojo and Nakayama, 1990). For RDSs with surrounding monocular dots, the monocular dots may be perceived as part of the cyclopean disk in the uncrossed disparity condition. Subjects then estimate the size of the cyclopean disk as larger than the area of the binocularly correlated dots.

V4 neurons have strikingly biased preference for crossed disparity (Hinkle and Connor, 2001; Watanabe et al., 2002; Tanabe et al., 2005), and we confirmed this for our dataset (Fig. 6G). Moreover, the size discriminability of V4 neurons at uncrossed disparities was poorer than that at crossed disparities (Fig. 7). Although these neuronal properties may account for the inaccuracy of estimation of the binocular disparity at uncrossed disparities, they cannot explain why the stimulus size was overestimated.

Scaling of size tuning by stimulus distance

The use of binocular disparity embedded in RDSs has critical advantages for the present experiments. In RDSs, the shape and depth of an object are defined only by binocular disparity. No monocular cues for size (e.g., luminance contour) and distance (e.g., occlusion, perspective, and texture gradients) are present. Therefore, any effects on the size tuning curve by changing binocular disparity can be taken as evidence for effects of (perceived) distance on size tuning. Because pictorial cues, such as perspective or texture gradients, provide a powerful depth cue for size constancy, we could have examined the effects of such cues on V4 neurons by placing the pictorial cues outside the RFs. However, the effects of these cues would be difficult to interpret because manipulation of pictorial cues inevitably causes a change in various visual parameters that could potentially modify neuronal responses independently of distance. The complex effects of stimuli placed outside the RFs of V4 neurons are poorly understood. Another important advantage of the RDSs is that the relationship between binocular disparity, stereoscopic depth, and size can be determined geometrically. This allows us to quantitatively evaluate the reference frame for the size-coding of V4 neurons by calculating the SI.

We demonstrated that a majority of V4 neurons were sensitive to the size of cyclopean figures and scaled the tuning curve with changes in the stereoscopic distance (Fig. 4). We suggest that the size tuning of V4 neurons is an important element for the neural representation of size. Lesions in V4 impair the ability of monkeys to detect a target from distractors based on stimulus size (Schiller and Lee, 1991; Schiller, 1995). Because size discrimination requires the computation of size, these studies support the importance of area V4 for this neuronal process.

The relationship between binocular disparity and retinal image size projected from an object changes with the fixation distance (Fig. 9). Computation of the object size from the retinal size and binocular disparity requires information about the fixation distance. We considered two possible mechanisms for this process. One is that different populations of neurons are tailored to different fixation distances. The other is that each neuron changes its response properties depending on fixation distance. In the latter case, information about fixation distance must be integrated with information about retinal image size. V4 neurons did not change their response properties according to fixation distance cued by vergence angle (Fig. 11), supporting the first hypothesis. Our model also supports this possibility because the model does not need any distance information to modulate the size tuning curves by stereoscopic depth (Fig. 12).

Downstream areas may use cues for fixation distance, such as vergence angle, to preferentially receive the outputs of V4 neurons that are appropriate for a particular fixation distance. V4 receives information about fixation distance, and physical viewing distance modulates the amplitude of tuning curves for stimulus size (Dobbins et al., 1998). The fixation distance may either enhance the responses of optimal object size-coding neurons or suppress the inappropriate neurons. Because the vergence angle had no effect on the responses of V4 neurons (Fig. 11B,C), other distance cues may be used to select the appropriate neurons. The distance signals could also change the gain of output from V4 neurons by modulating the synaptic efficacy without changing the response magnitude (Briggs et al., 2013). V4 neurons as a population preferred wide-ranging object sizes at every visual field location (Fig. 10). Object size may be encoded by a selected population of V4 neurons, each representing a particular object size at a distance, with a population coding strategy (Pouget et al., 2000).

An error in estimation of the viewing distance may possibly explain the wide distribution of SIs >1. To generate the biased distribution of SIs, the monkeys should overestimate the viewing distance and the response field of recorded neurons should increase the tilt angle. To realize this scenario, the responses of the recorded neurons have to be modulated by the estimated viewing distance. However, vergence angle had no systematic effect on the SIs of V4 neurons (Fig. 11A). Other cues for fixation distance were controlled to be constant or not available for distance estimation in this experiment (see Results). Therefore, an estimation error of the fixation distance is unlikely to explain the biased distribution of SIs.

Receptive field structure and size perception

Perceived distance modulates the spatial extent of hemodynamic activation by an object in human V1 in a manner consistent with changes in perceived size; the topographic representation of a stimulus in V1 becomes larger when its physical or perceived location in depth becomes farther away (Murray et al., 2006, Sperandio et al., 2012). A recent study showed that monkey V1 neurons shift their RFs by perceived distance in a manner consistent with the changes in the perceived size (Ni et al., 2014). A study in Monkey MT also showed that attention to a visual stimulus causes a shrinkage and positional shift of RFs toward the attended side (Womelsdorf et al., 2006). The shrinkage and positional shift of RFs modify the retinotopic representation of a visual stimulus and may underlie an increase in perceived size of a stimulus via attention (Anton-Erxleben et al., 2007). Our study, together with these previous observations, suggests that the transformation of RF profiles leads to changes in perceived size.

The transformation of RFs in V1 and MT by distance or attention may result from top-down signals from higher cortical areas. Top-down attention modulates the spatial response properties of V4 neurons (Connor et al., 1997) and V4 receives extraretinal signals about distance information (Dobbins et al., 1998). However, our findings suggest that bottom-up computation may be critical in changing the size tuning curve with stereoscopic distance. First, the vergence angle did not change the SIs of V4 neurons. Second, the modulation of size tuning curves by stereoscopic depth can be accounted for by a combination of V1 neuron-like units without invoking a top-down mechanism of distance information.

In conclusion, a great majority of V4 neurons prefer a larger image size when a stimulus is shown farther away, and a smaller size when it is shown nearer. This property makes them suitable for encoding the size of an object per se, not the size of its retinal image. These object-size coding neurons can provide a possible mechanism for size constancy.