Counting Vesicular Release Events Reveals Binomial Release Statistics at Single Glutamatergic Synapses

Abstract

Many central glutamatergic synapses contain a single presynaptic active zone and a single postsynaptic density. However, the basic functional properties of such “simple synapses” remain unclear. One important step toward understanding simple synapse function is to analyze the number of synaptic vesicles released in such structures per action potential, but this goal has remained elusive until now. Here, we describe procedures that allow reliable vesicular release counting at simple synapses between parallel fibers and molecular layer interneurons of rat cerebellar slices. Our analysis involves local extracellular stimulation of single parallel fibers and deconvolution of resulting EPSCs using quantal signals as template. We observed a reduction of quantal amplitudes (amplitude occlusion) in pairs of consecutive EPSCs due to receptor saturation. This effect is larger (62%) than previously reported and primarily reflects receptor activation rather than desensitization. In addition to activation-driven amplitude occlusion, each EPSC reduces amplitudes of subsequent events by an estimated 3% due to cumulative desensitization. Vesicular release counts at simple synapses follow binomial statistics with a maximum that varies from 2 to 10 among experiments. This maximum presumably reflects the number of docking sites at a given synapse. These results show striking similarities, as well as significant quantitative differences, with respect to previous results at simple GABAergic synapses.

SIGNIFICANCE STATEMENT It is generally accepted that the output signal of individual central synapses saturates at high release probability, but it remains unclear whether the source of saturation is presynaptic, postsynaptic, or both presynaptic and postsynaptic. To clarify this and other issues concerning the function of synapses, we have developed new recording and analysis methods at single central glutamatergic synapses. We find that individual release events engage a high proportion of postsynaptic receptors (62%), revealing a larger component of postsynaptic saturation than anticipated. Conversely, we also find that the number of released synaptic vesicles is limited at each active zone. Altogether, our results argue for both presynaptic and postsynaptic contributions to signal saturation at single glutamatergic synapses.

Introduction

Central mammalian synapses are very diverse. Recent studies of synaptic mechanisms have often been conducted on large synapses such as the calyx of Held because such synapses lend themselves more easily to measurements of presynaptic parameters. These synapses are composite structures containing a large number of synaptic units, each of which contains a single presynaptic active zone and a single postsynaptic receptor density. In contrast, many central mammalian synapses, called “simple synapses” (Kondo and Marty, 1998), contain a single synaptic unit. Certain aspects of signaling in simple synapses, including possible intersynaptic variations and mechanisms underlying quantal fluctuations, are difficult to derive from the study of giant synapses. Accordingly, recording from isolated simple synapses has long been recognized as an important goal, but effective methods to achieve this in mammalian brain tissue are still lacking (Auger and Marty, 2000; Nauen, 2011). In recent years, we have explored new approaches to studying simple GABAergic synapses among molecular layer interneurons (MLIs) in the cerebellum, providing new insight into the nature of the readily releasable pool and its relation to presynaptic docking sites (Trigo et al., 2012; Pulido et al., 2015). However, it remains unclear whether a similar approach can be applied to simple glutamatergic synapses.

MLIs receive glutamatergic input from parallel fibers (PFs). PF boutons make synaptic contacts onto either Purkinje cells or MLIs that usually contain a single active zone (Masugi-Tokita et al., 2007; Indriati et al., 2013). At PF–MLI synapses, associated quantal signals are particularly large, yielding excellent signal-to-noise conditions (Llano and Gerschenfeld, 1993; Carter and Regehr, 2002). In cerebellar slices, extracellular stimulation can be adjusted to stimulate a single PF, giving rise to multivesicular release (MVR) in MLIs (Soler-Llavina and Sabatini, 2006; Crowley et al., 2007; Bender et al., 2009). These studies point to the PF–MLI connection as a potential simple synapse model that could be representative of other small, central glutamatergic synapses. However, a quantitative description of vesicular release statistics at simple PF–MLI synapses or at other simple glutamatergic synapses is still lacking.

At giant synapses such as the skeletal muscle neuromuscular junction or at the calyx of Held, efficient methods have been developed to extract vesicular release rates using a template reflecting miniature currents (the deconvolution approach; Neher and Sakaba, 2003; Ruiz et al., 2011). These methods must deal with complicating factors linked with variability of quantal shape among synaptic sites, with receptor saturation and desensitization, with cross talk among neighboring release sites, and with slow diffusion of the neurotransmitter out of the synaptic cleft. Several of these complicating factors should be more easily addressed in simple synapses, making deconvolution a particularly attractive option in such cases. Furthermore, deconvolution can reveal the timing of individual release events rather than release rates, thus opening new avenues to study stochastic properties of release. Deconvolution has been used to improve the temporal resolution in the detection of spontaneous synaptic activity (Pernía-Andrade et al., 2012), but, to our knowledge, deconvolution or other matched filtering methods have not yet been applied to simple synapses for the study of evoked release.

Here, we show that applying such an approach to simple PF–MLI synapses allows the determination of the number and timing of vesicular release events with a high degree of accuracy. We further show that the extent of receptor saturation is higher than previously suspected. We finally use the vesicle counting method to study release statistics. The results reveal common underlying mechanisms, as well as substantial quantitative differences, in glutamatergic versus GABAergic inputs onto MLIs.

Materials and Methods

Preparation.

Slices (200 μm thick) were prepared from the cerebellar vermis of Sprague Dawley rats of either sex at postnatal days 13–16 following the animal care guidelines of our host institution (approval number A-750607). Slices were cut parallel to the sagittal plane. In these conditions, MLI dendrites were contained in a plane parallel to the cutting plane, whereas PFs were orthogonal to that plane. Recorded MLIs were ∼10–50 μm below the surface (see Fig. 2A,B). Approximately 2/3 of the recordings were from basket cells, defined as MLIs located in the proximal 1/3 of the molecular layer, and the remaining 1/3 were stellate cells.

Figure 2.

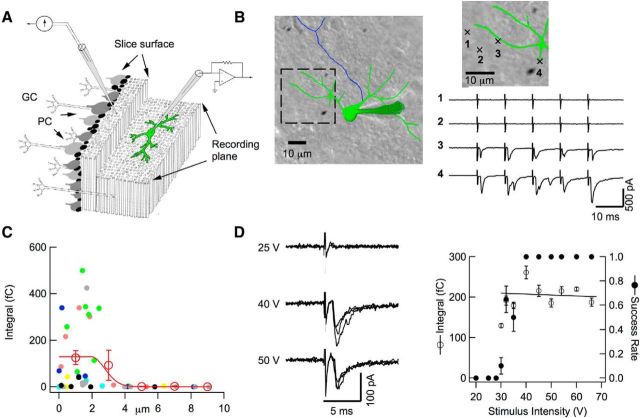
Local stimulation of PF–MLI connections. A, Schematics of recording conditions. In a parasagittal slice, the dendritic arborization of a recorded MLI is parallel to the slice surface (left, granule cell layer; right, molecular layer), whereas PFs are orthogonal to the MLI plane. GC, Granule cell; PC, Purkinje cells. A θ-glass pipette is positioned on top of the MLI arborization on the slice surface to stimulate presynaptic PFs. B, Representative experiment comparing the responsiveness of 4 presynaptic pipette positions located at the slice surface (green: somatodendritic domain and recording pipette; blue: axon; stimulation positions shown in enlarged image), with 2 responsive positions directly above the dendritic arborization and 2 other positions outside of the arborization (5 stimuli, 100 Hz; same stimulus conditions for all positions: 0.1 ms duration, 31 V amplitude). C, Group results from seven experiments as in B, where results from individual cells are color coded, showing a sharp drop of responsiveness (calculated as the mean EPSC integral for the first response) as a function of distance to the nearest dendrite. In each experiment, the stimulation intensity was adjusted such that at least one dendritic site would respond, and was then kept constant for all positions of the stimulation pipette. Open circles and associated error bars show binned averages ± SEM. The results are fitted with a constant (over a distance of 1.9 μm) followed with a half-Gaussian decay with an SD of 0.8 μm, so that responsive spots were located within a distance to the nearest dendrite of 1.9 + 0.8 = 2.7 μm. D, Intensity-response curve of a potential simple synapse. Left, Representative traces obtained with 3 stimulation intensities (stimulation duration: 0.1 ms; 3 superimposed traces at each intensity). Right, By careful selection of the presynaptic pipette position, it is possible to obtain a step-like intensity-response curve (dots: mean success probability for first stimulation; circles: mean current integral for successful first stimulations; error bars indicate ± SEM; n = 10–20 trials for each intensity) with a narrow transition region (here, at 30–35 V). A regression line through the first stimulation integral data points fails to reveal any significant relation to stimulation intensity. Such results are consistent with single PF stimulation. For simple synapse recording, stimulation intensity is set just above threshold (near 40–45 V in this example).

Recording procedures.

Procedures to record from MLIs were as described previously (Llano and Gerschenfeld, 1993). The composition of the standard extracellular solution was as follows (in mm): 130 NaCl, 2.5 KCl, 26 NaHCO₃, 1.3 NaH₂PO₄, 10 glucose, 2 CaCl₂, and 1 MgCl₂, osmolarity 300 mosm/L. This solution was equilibrated with 95% O₂ and 5% CO₂, pH 7.4. The standard internal recording solution contained the following (in mm): 144 K-glutamate, 6 KCl, 4.6 MgCl₂, 1 EGTA, 0.1 CaCl₂, 10 HEPES-K, 4 ATP-Na₂, and 0.4 GTP-Na, pH 7.3, osmolarity 300 mosm/L. Alexa Fluor 488 was included in this solution to visualize the dendritic tree (see Fig. 2B). Recordings were made at 30–34°C. Uncompensated access resistance values were 10–20 MΩ during recording. A 50–60% resistance compensation was applied. For extracellular stimulation, a θ-glass double-barreled pipette was filled with a HEPES-buffered extracellular solution. This pipette was positioned at the slice surface directly above the dendritic tree and short voltage pulses (0.1 ms duration, amplitude 10–50 V) were applied. Trains of up to 8 pulses were applied at either 100 or 200 Hz, with a waiting time of 10 or 15 s between trains. For simple synapse recording, the position of the stimulation pipette and the amplitude of the stimulation voltage were finely adjusted, as explained in the Results section. As soon as a potential simple synapse was identified, the extracellular solution was switched to a new solution containing 3 mm external calcium (Ca_o) to enhance release probability. NMDA receptors and GABA_A receptors were blocked by perfusion of APV (50 μm) and gabazine (15 μm) in the recording solution.

Decomposition of EPSCs.

Several methods have been developed to decompose a trace of postsynaptic current into the contributions by individual quanta, based on the assumption that each synaptic event is a scaled version of a fixed template having the shape of miniature EPSCs (mEPSCs: Clements and Bekkers, 1997; Pernía-Andrade et al., 2012; Andor-Ardó et al., 2012). These approaches, either by template matching or by various methods of deconvolution, convert individual mEPSCs into narrow spikes. It is the resulting sequence of spikes, rather than the originally recorded current, that is used for further analysis. In its simplest form, an event is counted whenever the resulting trace (e.g., center trace in Fig. 3D) crosses a predefined threshold. We used a deconvolution algorithm developed earlier (Neher and Sakaba, 2003) for this purpose. Deconvolution essentially extracts from a complex trace the rate of occurrence of an underlying template function (in the present case, a representation of the average mEPSC). When applied to the template, it returns in principle a delta function. When applied to a waveform that differs slightly from the template, the delta function is widened into a somewhat broader spike, which is further widened by noise optimization steps in the calculation. However, this spike is still narrower than the original waveform. This is of advantage for the separation of closely spaced quantal events. In this study, we made further efforts to optimize the separation of events and thereby to improve their “counting” by fitting superimpositions of idealized spikes to the deconvolved EPSC traces, as described below.

Figure 3.

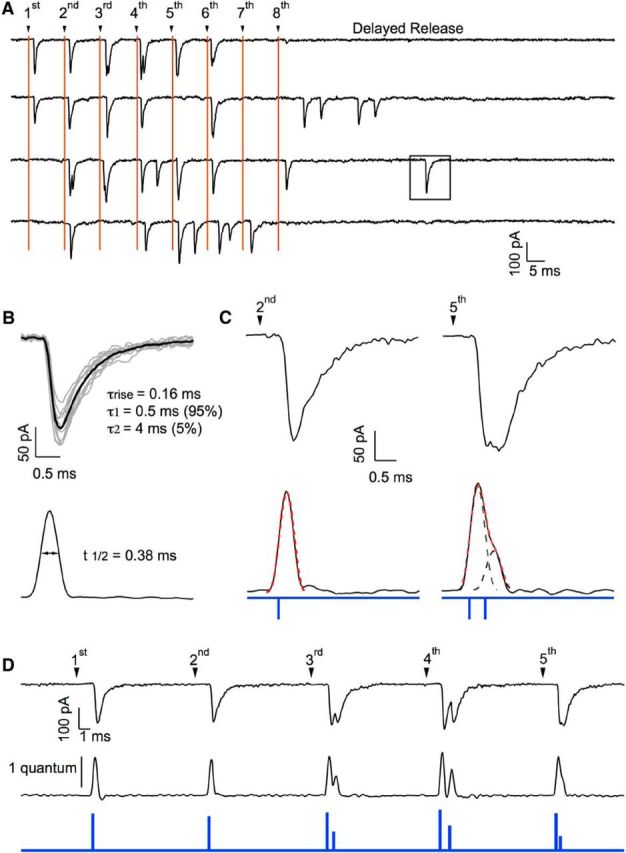
Event detection at a simple synapse. A, Responses to trains of APs (8 APs at 100 Hz; 10 s between trains) in a presumed simple synapse recording. Stimulation artifacts have been blanked, but stimulation times are marked with vertical lines. Responses appear as a mixture of failures, single EPSCs, and multiple EPSCs. After the end of the train, a period of delayed release was observed (∼50 ms in duration), during which quantal EPSCs could be isolated (square). B, Quantal EPSCs from the same experiment were aligned and averaged. The resulting average mEPSC was fitted with a sum of three exponentials, as indicated. A matched-filter was calculated from the 3-exponential fit, yielding the filtered version of the mEPSC shown below (“spike”: half peak amplitude width 0.38 ms). C, Applying the same matched filter to two individual EPSCs (first trial in A; responses to second and fifth stimulations) produces in one case, a single spike (left; dotted red line: spike-shaped curve with appropriate time positioning and vertical scaling; spike onset indicated by blue tick below) and, in the other case, a broader signal that can be decomposed into two components (dotted black curves; corresponding spike onsets indicated by blue ticks below; dotted red curve is the sum of the two components). D, Same analysis performed on a series of EPSCs (first trace in A), with the filtered trace below (calibration bar: spike amplitude for one quantum) and the resulting timing and amplitude of individual release events (blue trace).

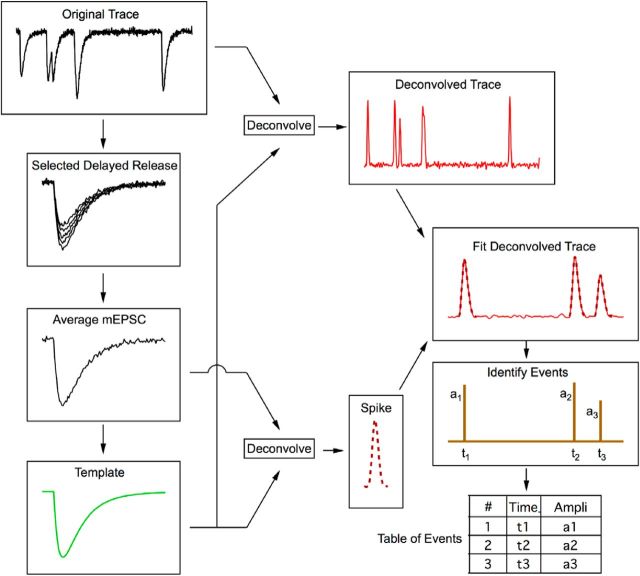
Specifically, approximately five to 10 stand-alone mEPSCs of a given synapse were selected as a first step in forming a deconvolution template. Suitable EPSCs can typically be found during the delayed-release response observed after the end of a stimulation train. These mEPSCs were averaged, with their peaks aligned (Fig. 1). The resulting average mEPSC was fit by a triple-exponential function, with five free parameters (rise time, amplitude, fast decay time constant, slow decay time constant, and amplitude fraction of slow decay). These parameters were adjusted such that the deconvolved mEPSC trace after mild low-pass filtering resulted in a narrow spike (Fig. 1). Parameters of mEPSCs typically vary between synapses in the range of 50–300 μs (rise time), 0.2–1 ms (fast decay time constant), 0.5–5 ms (slow decay time constant), and 5–15% (amplitude fraction of slow decay). An example of an average mEPSC, together with the resulting spike, is shown in Figure 3. Individual data traces were deconvolved after blanking of stimulus artifacts using the parameters derived from the fit of the average mEPSC. This resulted in sequences of spikes, some of them single, some of them superimposed onto one another (Fig. 1; see Fig. 3C for examples). At this stage, a first criterion regarding the homogeneity of quanta could be applied: if spike waveforms had variable kinetics, then the experiment was discarded because this was taken as an indication of multiple synapses. For experiments passing this selection, the improvement in time resolution was substantial. Although the half-widths of mEPSCs had a mean value of 0.88 ± 0.10 ms, those of corresponding deconvolved signals were 0.37 ± 0.02 ms. The next task was to fit a given deconvolved trace by a sum of spikes. We found a substantial variation in the peak amplitudes of individual quantal events (Fig. 1), whereas the corresponding kinetics were quite reproducible. In addition, due to receptor saturation and receptor desensitization, the peak EPSC amplitudes varied during a train (see Figs. 6, 7, 8). To take these variations into account, we left the amplitude of each spike as a free parameter. To perform the analysis, we first subdivided a given trace into segments containing events (in which most data points were above a certain threshold); these typically contained one to four spikes. Each such segment was fitted repetitively and automatically by an increasing number of spikes. The routine stopped when an adequate fit along the whole segment was found. The criterion for adequacy was a mean square deviation below an empirically determined threshold. Successful fits and failures of automatic fitting were presented to the experimenter for acceptance or rejection. Typically, 98% of fits were accepted upon first pass. In the remaining cases, the experimenter was asked to guide further fitting by entering guesses for locations of peaks. The routine then took these values as starting parameters for further optimization. Using this interactive procedure, the final rejection rate could be reduced to <0.5%.

Figure 1.

Decomposition of EPSCs. A flowchart shows the various steps involved in the decomposition of EPSCs. Starting from a response trace to a train of stimuli, individual EPSCs are selected during delayed release. After alignment, these EPSCs are averaged together, building the mEPSC average, and they are then fitted with a multiexponential curve, the template. Using the template, deconvolution is applied both to the original trace and to the mEPSC average, producing a deconvolved trace containing a series of spikes in the first case and a single spike in the second case. After fitting the deconvolved trace with appropriately scaled spikes, a series of events are identified. Finally, a table is produced listing each event together with its occurrence time and amplitude.

Figure 6.

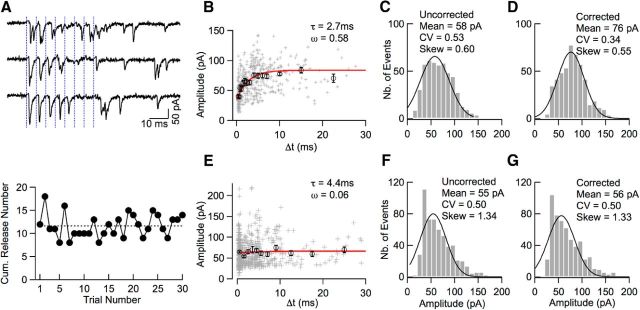
Time-dependent amplitude occlusion in simple synapse recordings. A, Top, Representative traces from a presumed simple synapse recording (8 stimuli at 200 Hz, blue). In several cases (e.g., first, second, and third stimulations in first trace), double and triple responses are observed with smaller EPSC amplitudes for the second or third event compared with the first. Bottom, Stability of the summed number of released synaptic vesicles across trials (dotted line: average; traces in above panel correspond to trial numbers 25–27). B, Plot of EPSC amplitude as a function of Δt, the time interval since the previous event, reveals an amplitude drop for small Δt values (crosses: individual events; circles: averages of binned data). Extrapolation of the model exponential curve (red) to Δt = 0 suggests a maximum amplitude occlusion ω = 0.58 (see text). C, Uncorrected EPSC amplitude distribution from the experiment shown in A and B. Continuous curve: Gaussian fit (mean: 58 pA; CV: 0.53). D, Corrected amplitude distribution from the same experiment using the exponential curve shown in B for correction. The corrected amplitude distribution displays a higher mean, lower CV, and smaller skew than the uncorrected distribution. E–G, As in B–D, in another recording classified as originating from a multiple synapse. Here, the amplitude dependence on Δt is absent and the correction procedure does not affect significantly the amplitude distribution.

Figure 7.

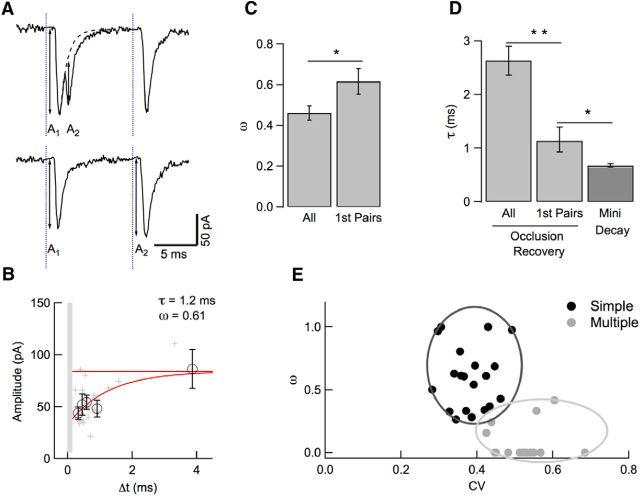
Amplitude occlusion in first EPSC pairs. A, In this analysis, amplitude occlusion is examined only for the first two EPSCs in a train stimulation, with amplitudes A₁ and A₂. B, The plot of A₂ (as illustrated in A) as a function of Δt reveals a faster time constant and higher occupancy than that obtained with the preceding analysis on all events (1.2 vs 2.7 ms and 0.61 vs 0.58). Circles and associated error bars indicate binned data ± SEM. The asymptote (red) was constrained to fit the mean amplitude of isolated quantal events. Light gray area delimits the Δt range where event detection is ambiguous (Fig. 4). C, D, Group data analysis of amplitude occlusion, indicating higher amplitude occlusion (p < 0.05) and smaller recovery time constant (p < 0.01) for first-pairs analysis than for all-events analysis. In addition, the recovery time constant obtained with first-pairs analysis is slightly larger than the time constant of decay of miniature synaptic currents (p < 0.05). E, Two-component analysis distinguishes simple synapses (black) from multiple synapses (gray) based on peak amplitude CV (abscissa; calculated over the entire train period) and first-pairs amplitude occlusion (ordinate). Simple and multiple synapse outlines are drawn empirically around corresponding clusters.

Figure 8.

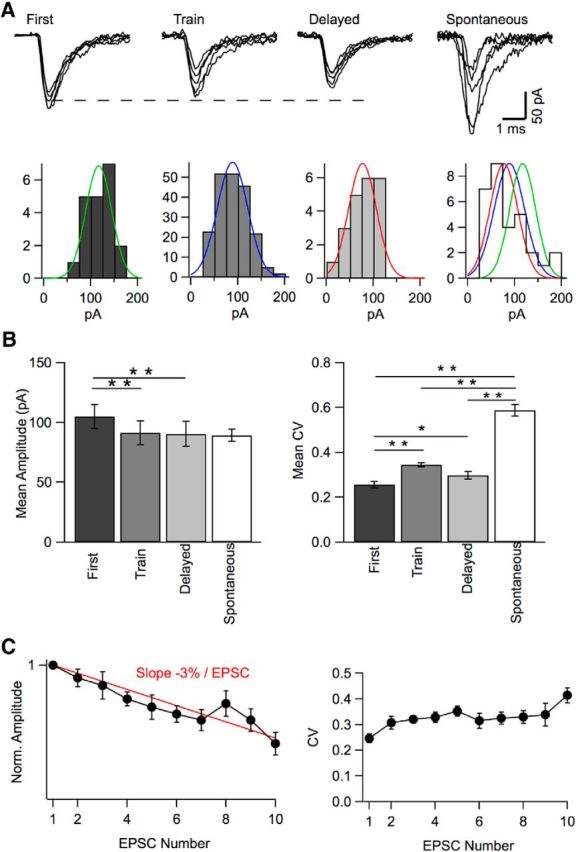
Mean and CV of peak amplitudes in simple synapse experiments. A, Representative superimposed EPSCs from a simple synapse experiment illustrating first events, showing large and homogeneous amplitudes; train events, showing more heterogeneous, somewhat smaller amplitudes (reflecting receptor activation and desensitization from previous events); delayed-release events, also with smaller amplitudes (reflecting cumulative desensitization). Right, Spontaneous events (from another recording), with very heterogeneous amplitudes (reflecting mixed contributions from several synapses; mean: 86 pA, CV: 0.50). Amplitude histograms with Gaussian fits are shown below each set of traces (right: with superimposed normalized Gaussian fits of first, train, and delayed traces). Respective mean and CV values: 117 pA, 0.23 (green); 89 pA, 0.36 (blue); 77 pA, 0.40 (red). B, Group data from 24 simple synapse experiments showing mean and CV of peak amplitudes for first events (after exclusion of presumed double events, following the criterion of Fig. 5), train events (after correction for amplitude occlusion from previous events), and delayed events. Data for spontaneous events are also shown for comparison (n = 13). First events display larger mean amplitude than train events or delayed events (p < 0.001 in each case). They also display a lower CV than train events (p < 0.001) and delayed events (p < 0.05). Spontaneous events have a mean that is not different from that of first events, train events, or delayed events. However, they have a CV that is larger than that of first, train, or delayed events (p < 0.001 in each case). C, Plot of EPSC amplitudes (left) and CV (right) as a function of their order of appearance in each trace. Results were corrected as in Figure 6. They were normalized in each experiment with respect to the amplitude of the first EPSC and were averaged across 11 experiments performed at 200 Hz stimulation. The amplitude plot shows a continuous decline and can be fitted with a line having a slope of 3% per EPSC (red). The CV increases from the first to the second EPSC and stabilizes thereafter.

The result of the fitting procedure is a table of events (Fig. 1) in which each event is associated with the corresponding trace number, together with its time of occurrence within the trace and its peak amplitude (the scaling factor of the fit multiplied by the amplitude of the mini-template). In addition, the table contains times of beginning and end of individual event-containing segments. Data from this table were subsequently used for further analysis, such as forming various amplitude histograms, frequencies of quanta within certain time bins, and so on.

A critical feature of the analysis is the separation of closely spaced quanta. Because the average half-width of the spike is 0.37 ms, the automatic fitting routine fails to separate two events if the separation is less than ∼0.15 to 0.2 ms, depending on the goodness of fit criterion used. A test illustrated in Figure 4 is consistent with this prediction (see Results section). A second test for the quality of separation of closely spaced events was derived from the time course of release, based on the expectation that the separation should be particularly difficult shortly after a stimulus, when the rate of quantal release is high. To test this expectation, we compared the deconvolution of the average postsynaptic current trace (usually 30 sweeps) with the average trace of frequency of events, as obtained from deconvolution and fitting of individual traces. If there were no separation problem, then the two curves should match after appropriate scaling. We observed (see Fig. 5) that, for a scaling factor that brought the majority of the two traces into register, the data points of highest activity were lower by up to 50% in the trace of decomposed event frequencies compared with the deconvolution of the original trace. To compensate for this deficit, we chose the largest amplitude events and split them into two consecutive events until the appropriate number of events was reached. Using this correction procedure, the proportion of duplicated events was 8.5% in the experiment shown in Figure 5. The mean event frequency before correction in the most strongly affected time bin was 0.5 event per bin (of 0.2 ms) per trial. The events resulting from the splitting procedure were included in the analysis of event numbers but, because it was impossible to decide on the amplitude of each split event, these events were not considered in amplitude analysis (e.g., they were excluded from the analysis shown in Fig. 8B).

Figure 4.

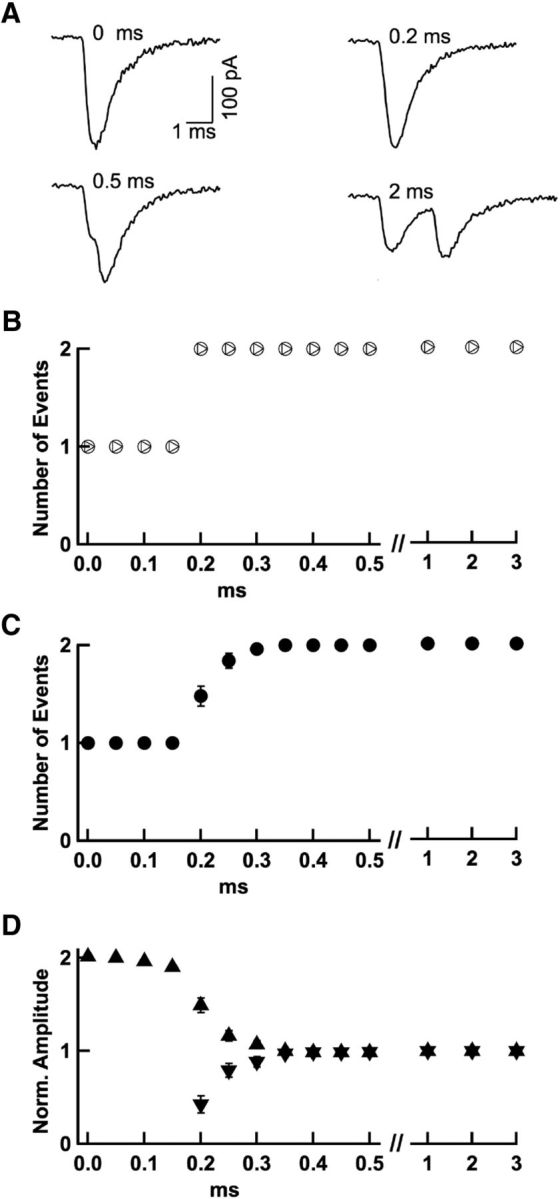
Time resolution of event detection. A, Two experimentally recorded quantal EPSCs from the same experiment were artificially added together with various intervening time intervals ranging from 0 to 5 ms. The event detection procedure was run on these traces to determine the minimum interval required for event disambiguation. B, The procedure correctly discerned the 2 events down to a separation of 0.2 ms in the example shown in A (circles); for shorter intervals, a single event with double amplitude was reported. In another simulation, the second EPSC was scaled following an exponential function of the separation between the two EPSCs, to mimic amplitude occlusion (as detailed in Fig. 6–7). This gave the same time resolution (triangles). C, Group results from 25 experiments as in A indicate detection threshold with separations of 0.2 to 0.3 ms (closed symbols; associated error bars, when visible, indicate ± SEM). D, Associated amplitude measurements from the same experiments (upward triangles: amplitudes of first detected EPSCs; downward triangles, amplitudes of second detected EPSCs, when applicable; note double amplitude of single events for separations of 0–0.15 ms and intermediate amplitudes in 0.2–0.3 ms separation range).

Figure 5.

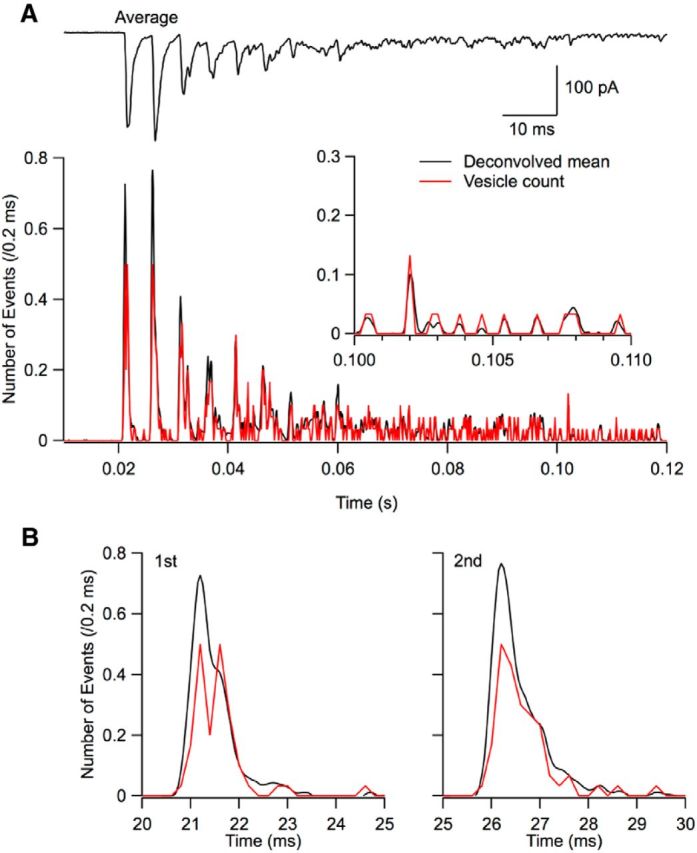
Correction for missed events. A, Top trace, Average response to an 8 AP train (30 trials, 200 Hz; 3 mm Ca_o). Bottom, Comparison between the histogram of the timings of detected events (red, with associated left scale; binwidth, 0.2 ms) and the trace obtained by deconvolution of the average current response across trials (black). The black trace has been scaled such that the two curves are superimposed at late times (inset). B, Blow-up of the first two peak responses (respective stimulation times, 20 and 25 ms) showing a deficit of the red curve compared with the black one. This deficit represents undetected double events. To estimate it, areas are calculated under individual peak responses for the black and red curves. To compensate for the deficit, EPSCs are ranked in decreasing amplitude order and an appropriate number of the largest EPSCs are split into two immediately consecutive events.

With respect to the timing of events and the variance analysis, we considered an additional problem: due to intrinsic quantal size variation, the amplitude distributions of single events and of unresolved double events are not clearly separated. For this reason, our event-splitting correction sometimes splits events even though they are actually single and, likewise, occasionally omits to split events that are actually double. The number of split events is such that the total number of events in the ensemble of traces is correct (see above). However, due to the overlap, a fraction of the splits happen in the wrong trace. We estimated this fraction, based on the percentage of split events (maximum 50%, see Fig. 5B), on the CV of the amplitude distribution of first events (0.253; see Fig. 8B) and on the value of ω (0.62; see Fig. 7C), to amount to 12% for the time bin with the highest event frequency. To estimate the consequences of this error, we performed Monte Carlo simulations assuming a binomial model with four docking sites operating independently. We reshuffled in this model 12% of the entries in response to the first and second stimulations and performed a parabolic fit to the variance/mean data before and after reshuffling, finding N values of 4.0 and 4.8, respectively. This indicates that, due to misplacement of some of the split events, our analysis somewhat overestimates N values. However, due to the relatively small size of this residual error, no additional correction was applied.

Vesicular release statistics.

We call s_i the random variable representing the number of synaptic vesicles released after stimulation number i. s_i statistics can be modeled by assuming several docking sites operating in parallel. Each docking site is assumed to accommodate at most one vesicle. Calling N the number of docking sites and P_i the probability that one docking site releases one vesicle for stimulus number i, the mean and variance of s_i follow the relations:

such that:

Therefore, the plot of var (s_i) as a function of < s_i > should be a parabola with an initial slope of 1, as exemplified in Figure 9B below. The equations hold also in the case that both the occupancy of sites (vesicle replacement) and release are random processes. However, the release probability P_i then is actually the product of the probability of occupancy of a site and the probability that the corresponding vesicle is being released at the time of stimulus i (Vere-Jones, 1966; Quastel, 1997; Scheuss and Neher, 2001). In our experimental conditions, < s_i > and the accompanying P_i varied markedly during a train, reflecting at least in part a gradual decrease of mean docking site occupancy. This allowed us to test the above prediction of a parabolic var (s_i) plot at various < s_i > values. After determining N by extrapolation of the parabola (see Fig. 9B), P_i can readily be calculated as follows:

An alternative method to obtain N and P_i is to fit the distribution of s_i values with the expectations of a binomial distribution, as illustrated in Figure 9C. The binomial model predicts that the probability that s_i takes the value k is as follows:

Note that the sum of p[s_i = k] for all possible values of k is 1.

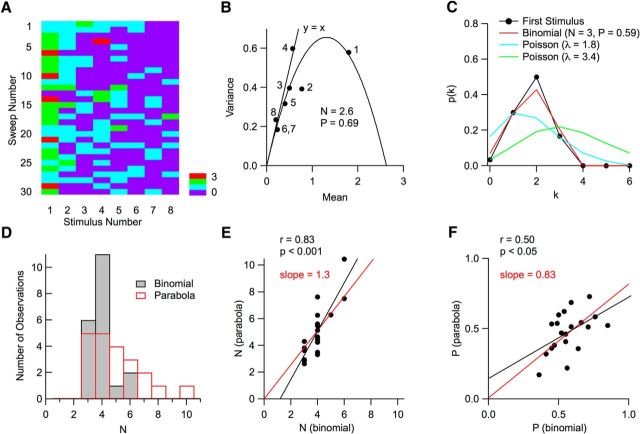
Figure 9.

Counts of vesicular release events per AP follow binomial statistics. A, Matrix of vesicular release counts (color coded) as a function of stimulus number (columns; 100 Hz stimulation) and trial number (rows). B, For each stimulus number, the mean and variance of the number of released vesicles was determined in a 5 ms period after individual stimulations (dots). Stimulation numbers are indicated; note that the vesicle counts for the sixth and seventh stimuli are identical, so that the corresponding dots are superimposed. The resulting curve can be fitted with a parabola indicating a number N = 2.6 of releasing units and a maximum release probability (for the first stimulus) P = 0.69. For late stimuli, experimental points are close to the y = x line that would be predicted for a Poisson model. C, Here, the probability distribution p(k) to observe k vesicular release events is displayed for the first stimulus in A. As can be seen in the first column in A, k varies between 0 and 3, with 5 observations of k = 3, and 0 observation of k > 3. The experimental data (dots) are compared with two Poisson models, one with the same mean release number as the data (λ = 1.8; blue) and the other with the same failure number as the data (λ = 3.4; green). In both cases, poor fits are obtained. In contrast, the binomial model approximates the data closely (red; N = 3; mean probability P = 0.59; see Materials and Methods). D, Distributions of N values obtained with the variance–mean parabola (red) and with a binomial fit (black). E, Plot of the N value obtained by extrapolation of the parabolic fit to variance data, as in B, as a function of binomial N, obtained from the stimulus with maximum release probability by the method illustrated in C. Depending on the experiment, this maximum occurred for the first stimulation (as in the case shown in A), or for the second stimulation. The 2 N estimates are significantly correlated (black regression line; p < 0.001) and the regression line passing through the origin (red) has a slope of 1.3. F, Corresponding plot of the maximum release probability with the two methods. Again, the two estimates are significantly correlated (black regression line; p < 0.05) and the regression line passing through the origin (red) has a slope of 0.83.

This method gives valuable N and P_i estimates provided that P_i is high. Therefore, the binomial distribution analysis was performed for the stimulus number that gave the maximum < s_i > value, usually obtained with i = 1 or i = 2. For this value of i, we note P_i = P. N and P were adjusted to minimize summed squared deviations between the binomial prediction and data. This way, a reasonable fit was obtained (cf. red trace, black data points in Fig. 9C).

In contrast to the binomial model, the Poisson model predicts the following:

as depicted by the y = x line in Figure 9B.

In addition, the Poisson model predicts a distribution of s_i values given by the following:

where λ = < s_i >. Such distributions (with different λ values) are illustrated by the blue and green curves in Figure 9C.

Statistical evaluation of group results.

Results of group data analysis are presented as mean ± SEM or as regression lines; n values represent the number of independent experiments. When analyzing means, p-values are based on Wilcoxon's rank test (either paired or unpaired). When analyzing correlations illustrated with regression lines, r represents Pearson's correlation coefficient and p assesses the probability of correlation given the value of r and the number of degrees of freedom of the data.

Results

Local stimulation of PF–MLI synapses

MLIs are contained in parasagittal planes and PFs are orthogonal to these planes. Therefore, in sagittal slices, many MLIs are intact but PFs are cut, with a small fraction of the fibers still connected to the granule cell soma through the ascending axon (Fig. 2A). Even though PFs are severed, extracellular stimulation in the molecular layer still results in successful PF-EPSCs in MLIs, showing that at least a fraction of the PFs are excitable and capable of inducing transmitter release (Atluri and Regehr, 1998; Glitsch and Marty, 1999; Clark and Cull-Candy, 2002). Previous studies indicate that, when small stimulation intensities are used, EPSCs exhibit very marked quantal fluctuations (Atluri and Regehr, 1998; Rancillac and Crépel, 2004; Rancillac and Barbara, 2005), as well as MVR (Crowley et al., 2007; Bender et al., 2009; Satake et al., 2012). Furthermore, by selecting optimal conditions, single PF stimulation can be achieved (Soler-Llavina and Sabatini, 2006; Crowley et al., 2007). In the case of single PF stimulation, partial occupancy of postsynaptic AMPA receptors elicits occlusion of EPSC amplitude by immediately preceding events, whereas no such occlusion occurs with multiple PF stimulation (Crowley et al., 2007). These experiments suggest that, at single PF–MLI synapses, successive MVR events share the same set of receptors located in one postsynaptic density.

In the present work, we performed single PF stimulation experiments in sagittal slices of rats at postnatal days 13–16. This age group was selected because MLI dendrites are then short and thick, minimizing distortion of PF-EPSCs through dendritic filtering (Pouzat and Marty, 1999; Abrahamsson et al., 2012). The postsynaptic pipette was filled with an Alexa Fluor dye so that the dendritic tree could be visualized (Fig. 2B; note that the parasagittal organization of MLIs facilitates imaging). Whereas previous studies used monopolar stimulation, we used a θ-glass double-barreled pipette to restrict the stimulated area and positioned this pipette at the surface of the slice directly above the dendritic tree of the recorded MLI (Fig. 2A). As shown in Figure 2B, responses were obtained if the stimulation pipette was located above the dendritic tree, but were abolished if the pipette was moved away from the dendrite outline. Group results from 7 such experiments show that the sensitivity decreased very abruptly with distance from the dendritic tree, with an average cutoff distance of 2.7 μm (Fig. 2C). These results indicate that successful stimulations are very local. Within the area outlined by the dendritic tree, individual locations of the stimulation pipette resulted in very heterogeneous response amplitudes, indicating a mixture of hot spots and unresponsive or poorly responsive sites (Fig. 2C).

Within the responsive area, pipette position was finely adjusted so as to obtain a stepwise intensity-response curve (Fig. 2D). Choosing a stimulation intensity just above threshold, candidate simple synapse recordings were then collected.

Vesicle counting using deconvolution

Having established a local PF–MLI connection, we applied trains of stimuli (e.g., 8 stimuli at 100 Hz repeated every 10 s). We used in the present work an elevated external calcium concentration (Ca_o = 3 mm) to increase the probability of transmitter release. Under these conditions, MVR was readily apparent and trains of action potentials (APs) evoked a succession of apparently single responses, multiple responses, and failures (Fig. 3A). The success rate for the first stimulus was high (range: 0.4–1). A stable, high success rate for the first stimulus (Fig. 2D, dots), together with a stable EPSC integral (Fig. 2D, circles), indicated reliable AP firing for each stimulus in the presynaptic PF. The analysis procedure leading to vesicle counting is explained in full in Materials and Methods and is illustrated here for the experiment shown in Figure 3A. The first goal of the analysis was to obtain an estimate of the averaged quantal EPSC (averaged mEPSC) appropriate for that synapse. This was necessary because amplitude and time course of quantal events vary significantly among single synapses (Auger and Marty, 1997; Crowley et al., 2007). For this purpose, isolated events were cut out from the late part of the responses (“delayed release”; boxed event in Fig. 3A), where multiple events were infrequent. The mean frequency of delayed release (time window: 10–60 ms after end of train) was 33 Hz compared with 0.19 Hz for spontaneous release before the train, showing that the contamination by spontaneous events is negligible. Having aligned several delayed-release events with respect to their peaks, their average was calculated and this averaged mEPSC was fit using a combination of exponentials (Fig. 3B, top). This model curve was used as a template to perform deconvolution. When applied to the averaged mEPSC, deconvolution resulted in a narrow bell-shaped curve (“spike”; half-width duration: 0.38 ms in the example shown; Fig. 3B, bottom). The same deconvolution method was likewise applied to the entire initial record, resulting in a sequence of spike-shaped events, some of them appearing isolated, others superimposed onto one another. Ideally, if all mEPSCs had exactly the shape of the template, then the result would be a series of delta functions, each of which would reveal a quantal event together with its time of occurrence. In practice, deconvolved traces had to be fitted as a sum of amplitude-scaled spikes, leaving the occurrence time and the scaling factor of each event as free parameters (Fig. 3C,D). In the example of Figure 3C, left, the original trace has a time course similar to that of mEPSCs and the deconvolved trace could be fitted with a single spike. In contrast, in Figure 3C, right, a single EPSC with an atypically broad peak is apparent in the original trace. Therefore, deconvolution resulted in a waveform broader than the reference spike, which was split in the fitting procedure into 2 successive events with a separation of 0.3 ms. On the longer trace sample shown in Figure 3D, responses to the first and second stimulations appear to be made up of well separated spikes representing individual release events, whereas the responses to the third to fifth stimulations give rise to broader or double spikes that are resolved into doublets of release events. The timing and amplitude of events is indicated in the blue trace below, where it may be noted that, for closely consecutive events, the second event amplitude is smaller than that of the preceding event.

Clearly, this procedure of separating events will fail if mEPSCs follow each other too closely. To estimate the time resolution of this procedure and to correct for its limitations, we performed two types of analysis. First, for a test of time resolution, 2 experimentally recorded mEPSCs were artificially time shifted by intervals ranging from 0 to 5 ms and superimposed (Fig. 4A). The detection procedure was applied to the paired mEPSCs. In the experiment shown, a single event was found with double amplitude up to a separation of 0.15 ms and, from 0.2 ms on, 2 events with approximately correct amplitudes were found (Fig. 4B). Examples from 25 different experiments were analyzed in this way, indicating an effective time resolution of event detection of 0.226 ± 0.008 ms (Fig. 4C,D). The consequences of this limitation are explored in the next section.

Correction for missed events

Due to the time resolution of our event detection method, the analysis occasionally returns a single, large-amplitude EPSC when there were in fact two almost synchronous EPSCs. In our recording conditions (3 mm Ca_o), EPSCs were depressing and maximum release rates occurred in response to the first or second stimulation (Fig. 5A) so that the proportion of missed events was likely highest for these two stimulations. To estimate the number of such errors, we performed a deconvolution on the trace obtained by averaging together all trials (usually 30) from a series. This procedure, which is the standard use of deconvolution analysis (as described by Neher and Sakaba, 2003), results in a trace proportional to release rate. We compared this deconvolved average with the ensemble sum of detected events, which should also be proportional to release rate. When scaling the two curves such that they overlapped at low release rate (black and red traces, respectively, in Fig. 5A), a clear deficit was apparent for the sum of detected events at the peak of the responses to the first stimulations (Fig. 5B). This deficit corresponds to events that were erroneously taken as single, when in fact two EPSCs occurred in the original trace. To estimate the deficit, the areas of individual responses to a given stimulation number were compared for the two curves and the number of entries in the list of detected EPSCs was increased by splitting single events into two. Because double EPSCs have larger amplitudes than single ones, we ranked EPSCs according to their amplitudes and split the EPSCs of the largest amplitudes into two immediately consecutive events until the appropriate number of new EPSCs had been entered (see details in Materials and Methods). In our recording conditions (3 mm Ca_o), this splitting procedure concerned, on average, 4% of events. However, in some experiments displaying high release rates, such as that illustrated in Figure 5, the proportion of split events rose to as much as 55% during peak release rates. Due to synaptic depression, the average correction was maximal on the response to the first stimulation, where it amounted to 38% (range: 19–55%).

Three tests for selecting suitable simple synapse recordings

Once a local EPSC was obtained as shown in Figure 2, the position of the stimulation pipette was optimized to select potential simple synapses. We looked for an abrupt stimulation-intensity onset (as in Fig. 2D) and for homogeneous EPSC sizes, particularly during delayed release. If they passed this initial screening, results were kept and analyzed offline to decide whether they represented a suitable simple synapse recording. Three complementary criteria were used for this purpose. The first criterion concerned stability. Because the effectiveness of extracellular stimulation was exquisitely sensitive to the exact position of the stimulation pipette, stability was indeed a major concern. Having counted the number of vesicular release events, as in Figure 3, the sum of events obtained during a train was plotted as a function of train number. If this plot showed a significant (usually downward) trend, then the recording was discarded. In contrast, the example of Figure 6A illustrates a successful case in which the sum of release counts did not vary significantly with train number. Two additional criteria were developed specifically to identify simple synapses. They concerned amplitude CV and receptor occupancy and are described next (Figs. 6B–G, 7, bottom). The use of these two criteria is based on previous work on both GABAergic and glutamatergic synapses indicating that PSCs generated at simple synapses have little amplitude variability and display amplitude decrement at short intervals (Auger and Marty, 2000; Crowley et al., 2007).

Amplitude occlusion during train stimulations

As may be seen in the example of Figure 6A, in which three successive trials are illustrated (200 Hz stimulation), responses to individual stimuli often displayed short bursts of two to three events, in which the second and third event had smaller amplitudes than the first. Having detected a series of individual events, we set aside those occurring first in each trial and plotted the amplitude of remaining events as a function of the time interval since the preceding event. In simple synapse recordings, the resulting plot showed a clear reduction for short time intervals, which could be approximated by an exponential function (Fig. 6B). We refer to this phenomenon as “amplitude occlusion” in the following. Amplitude occlusion occurs at simple synapses as receptors participating in a first EPSC become unavailable, reducing the amplitude of an immediately subsequent EPSC (Auger and Marty, 2000; Crowley et al., 2007). Calling A₀ and A_ss, respectively, the extrapolated amplitude for time interval 0 and the asymptotic amplitude, the degree of amplitude occlusion at the peak of the EPSC can be calculated as follows (Auger and Marty, 1997; Crowley et al., 2007):

giving a value of 0.58 in the example shown.

Multisite amplitude distributions tend to be broad and to exhibit a rightward (positive) skew, whereas single site distributions tend to be narrower and more symmetrical (Auger and Marty, 2000). However, the consequence of amplitude occlusion is to broaden the amplitude distribution histogram because smaller secondary events are mixed with larger first events or stand-alone events (Fig. 6C). To correct for these time-dependent effects, we used the exponential relation shown in Figure 6B to scale up amplitudes throughout a train stimulation depending on the time interval Δt. The corrected amplitude histogram (Fig. 6D) displays a higher mean, lower skew, and lower CV compared with uncorrected amplitude distribution (Fig. 6C). In contrast, Figure 6, E and F, illustrates the results of an experiment in which amplitudes measured as a function of Δt fail to exhibit a clear decrease at short Δt values, presumably because the recording involved a multiple synapse (Crowley et al., 2007). In this case, the correction is minimal and does not modify the shape of the amplitude histogram significantly (cf. Fig. 6F,G). In addition, the corrected histogram (Fig. 6G) displays a larger skew and a larger CV than the corresponding histogram of the presumed simple synapse experiment (Fig. 6D).

Amplitude occlusion primarily reflects receptor activation

Binding of glutamate to AMPA receptors leads to a number of states, including occupied closed states, activated states (with durations of ∼1 ms), and desensitized states (with durations of ∼10–100 ms; Robert and Howe, 2003). So far, EPSC-induced desensitization has been documented mainly in large synapses displaying a calyx shape (Otis et al., 1996). In contrast to calyceal synapses, PF–MLI synapses are approximately planar and exhibit a very small postsynaptic density (Masugi-Tokita et al., 2007; Abrahamsson et al., 2012). Furthermore, there is no glial covering, so diffusion escape of glutamate should be very quick. Because the extent of desensitization is small for very short agonist transients (Robert and Howe, 2003), desensitization is an unlikely explanation for EPSC amplitude occlusion after a single release event. Nevertheless, during train stimulation, as the number of release events increases, the possibility exists that cumulative desensitization would become significant.

The analysis of Figure 6 was performed on events occurring throughout a stimulation train. Under these conditions, the EPSC amplitude is not only determined by the time of the previous event, but is also a complex function of all preceding events because receptor saturation from the immediately preceding event is combined with cumulative receptor desensitization from further preceding events. To isolate the effects of a single EPSC, we repeated the analysis focusing on the first two events of a train response (Fig. 7A). For these two events, cumulative desensitization should be minimal, so occlusion should primarily reflect the extent and time course of receptor activation. As illustrated in Figure 7B for the experiment of Figure 6, A–D, the results indicate a faster recovery time constant (1.2 ms instead of 2.7 ms) and a slightly higher amplitude occlusion (0.61 instead of 0.58) compared with the previous analysis of all events in the same experiment. Group results indicate that amplitude occlusion is higher in first-pairs analysis (0.62 ± 0.06, n = 17; Fig. 7C) than previously estimated based on all-events analysis (0.37 in Crowley et al., 2007, 0.46 in our study; Fig. 7C). The first-pairs estimate is similar to that obtained previously for GABAergic synapses in MLIs (Auger and Marty, 1997). The mean time constant of recovery of amplitude occlusion for first pairs is 1.1 ms, smaller than estimates based on all-events analysis (5.1 ms in Crowley et al., 2007, 2.6 ms in our analysis; Fig. 7D). Conversely, this time constant is slightly larger than the time constant of decay of mEPSCs (0.67 ± 0.04 ms; n = 29; p < 0.05; Fig. 7D). The small difference could reflect lingering glutamate at occupied closed states. Nevertheless, the modest size of the difference suggests that, after receptor activation at the peak of the first EPSC, receptor availability is not significantly compromised by desensitization, but rather follows a direct recovery path via occupied closed states toward the resting state. This conclusion is also consistent with the absolute value of the recovery time constant (1.1 ms), which is much too small to correspond to recovery from desensitization (Robert and Howe, 2003) or to a possible diffusion of desensitized receptors away from the postsynaptic density (Constals et al., 2015). Therefore, amplitude occlusion primarily represents the percentage of receptor occupancy associated with peak receptor activation.

Simple synapse selection criteria

Multiple synapses collect EPSCs from several postsynaptic densities with different receptor numbers and this heterogeneity generates variability in EPSC amplitudes. In contrast, in simple synapses, the variability is smaller because the number of receptors is fixed (Auger and Marty, 2000). Therefore, we considered EPSC amplitude CV together with amplitude occlusion to distinguish between simple and multiple synapses (Fig. 7E). We formed a plot in which each experiment was represented by a point having the corrected amplitude CV as abscissa and the occlusion parameter ω calculated from first pairs as ordinate (Fig. 7E; when the plot of amplitude as a function of time interval failed to converge, we entered an ω value of 0). The ω versus CV plot was separated in 2 clusters: a first cluster with ω > 0.2 and CV < 0.5, corresponding to simple synapses (black), and a second cluster with ω < 0.4 and CV > 0.4, corresponding to multiple synapses (gray). The proportion of experiments yielding points located in the overlap area is small, indicating that, in most cases, the double (ω, CV) criterion is able to distinguish simple synapses from multiple synapses.

Evolution of mean and CV of peak amplitudes during trains

Having established simple synapse selection criteria, we next examined group results of peak amplitude analysis in simple synapses. Although first-pair comparisons mainly reveal amplitude occlusion due to receptor activation, it seemed likely that, during train stimulations and delayed release, mixed effects combining amplitude occlusion and cumulative desensitization could be observed.

As illustrated in the simple synapse experiment of Figure 8A, the first EPSCs elicited by a train stimulation exhibited homogeneous peak amplitudes. During the train, EPSC amplitudes were corrected as shown in Figure 6, C and D, to minimize effects of amplitude occlusion. In addition, large-amplitude EPSCs, often occurring at the beginning of the train, were eliminated from the analysis when they were suspected to represent double events according to the criterion of Figure 5. Despite these two sets of corrections, EPSCs displayed smaller amplitudes and were more heterogeneous during the train compared with first events (Fig. 8B). During delayed release, EPSCs were again homogeneous in size but remained slightly reduced compared with first events, as seen from the deviation of their peak amplitude from the dotted line in Figure 8A. Amplitude differences between train events and first events likely reflect in part cumulative desensitization. In addition, they may be due to imperfect correction for amplitude occlusion. This correction only considers the last preceding event, whereas train events typically follow >1 preceding EPSC, so that their amplitude is affected in a complex manner by receptor saturation and receptor desensitization resulting from preceding events. In accordance with these interpretations, group results show significantly larger mean amplitudes, and lower CV, for first events compared with either train events or delayed events (first events: A = 105 ± 10 pA, CV = 0.256 ± 0.014; train events: A = 92 ± 10 pA, CV = 0.344 ± 0.009; delayed events: A = 91 ± 10 pA, CV = 0.299 ± 0.016; n = 24; p < 0.001 for each paired comparison except for the first vs delayed CV comparison where p < 0.05; Fig. 7B). The ratio between average amplitudes of delayed events and first events is 0.87, indicating that an 8-stimulus train reduces EPSC amplitudes by 13%. Because, on average, these stimulations elicited 8.6 synchronized EPSCs, the results indicate an amount of cumulative desensitization of 13/8.6 = 1.5% per EPSC, neglecting recovery from desensitization. To test this idea further, we ranked EPSCs in each trace according to their occurrence order. In each experiment, we normalized EPSC amplitudes with respect to that of first EPSC and built a plot of normalized amplitudes as a function of order of appearance. This analysis was restricted to 200 Hz stimulation experiments to minimize recovery from desensitization. The results indicate a continuous amplitude decrement with a slope of 3% per EPSC (Fig. 8C). The twofold difference with the previous estimate indicates partial recovery from desensitization in delayed-release amplitude measurements, which were taken 10–110 ms after the end of the train. Overall, the results suggest a gradual decrease of mean amplitude during the train due to cumulative desensitization. In contrast to the gradual amplitude decrement, CV values remain approximately constant during the train for EPSC numbers ranking between 2 and 9 (Fig. 8C, right).

We next compared peak amplitude statistics for evoked EPSCs with those obtained during spontaneous release (Fig. 8A, right). In cerebellar slices, granule cells are silent, so spontaneous EPSCs recorded in MLIs are mostly monoquantal. Accordingly, we found no difference between spontaneous EPSC frequencies or amplitudes recorded with and without tetrodotoxin (respective frequencies: 0.16 ± 0.02 Hz, n = 4 and 0.19 ± 0.04 Hz, n = 18; respective amplitudes: 95.8 ± 13.0 pA, n = 4 and 86.6 ± 6.2 pA, n = 18; p > 0.05 for each comparison), so results in both conditions were pooled together. The mean amplitudes of these spontaneous events were not significantly different from those of first, train, or delayed events (Fig. 8B, left). However, spontaneous EPSCs displayed more diverse amplitudes and kinetics than simple synapse EPSCs (Fig. 8A). Accordingly, group results reveal a much larger amplitude CV than for simple synapses (Fig. 8B, right). This suggests that several synapses with different mean EPSC amplitudes contribute to the spontaneous EPSCs recorded in any given cell, whereas simple synapse EPSCs have more homogeneous amplitudes.

Variance analysis at simple synapses

Variance analysis of EPSC amplitudes performed in various preparations, including PF–MLI synapses, indicates a saturation of the variance at high release probability (Clements and Silver, 2000; Ishiyama et al., 2014). This suggests the existence of an upper limit to the signal that a synapse can deliver. However, the origin of this saturation may be presynaptic, postsynaptic, or both presynaptic and postsynaptic. Previous studies have focused on the presynaptic side, proposing a limitation in the maximum number of synaptic vesicles that can be released per AP for one active zone. However, on the postsynaptic side, receptor saturation may occur as several vesicles are released in the same simple synapse, leading to a sublinear relation between release probability and EPSC peak amplitude (Tang et al., 1994). The above results indicating a value of 0.62 for ω at PF–MLI synapses suggest that this component of saturation is larger than previously anticipated. It is therefore legitimate to ask whether the previously privileged presynaptic component of synaptic saturation is genuine. Fortunately, the methods presented in Figures 3, 4, 5, 6, and 7 have the potential to disambiguate presynaptic and postsynaptic sources of saturation because they provide an evaluation of the number of vesicular release events occurring at one active zone. If this number has an upper limit, vesicular release will likely follow binomial statistics rather than Poisson statistics. Furthermore, in this case, the maximum number of vesicles released in a simple synapse presumably represents the number of docking sites in one active zone (Trigo et al., 2012; Pulido et al., 2015).

To address the nature of vesicular release statistics, it is important to optimize recording conditions. A high release probability is required to constrain the variance/mean plot (Clements and Silver, 2000). However, if this probability is too high, then a significant proportion of multiple release events occurs within the time resolution of event detection, as determined in Figures 3 and 5, preventing the separation of presynaptic and postsynaptic saturation effects. We found that recording in 3 mm Ca_o provided a good compromise, so we performed our variance analysis under these conditions.

Having detected individual release events in a simple synapse recording, we built a matrix representing the number of released vesicles as a function of stimulus number (rows) and of trial number (columns) (Fig. 9A). For each stimulus number, the mean and variance of vesicle counts were calculated across trials. As may be seen from Figure 9B, the plot may be approximated by the y = x line at low mean vesicular release numbers. These points represent late stimulus numbers, when the synapse reached a low release rate due to synaptic depression. The y = x line represents the prediction of a Poisson process. At low release probability, the prediction of this model coincides with that of a binomial, so the results in this part of the graph are consistent both with a Poisson process and with a binomial model operating at low release probability.

In contrast, the results for the first and second stimulations clearly deviate from the y = x line. Whereas PF–MLI responses are typically facilitating under normal external calcium conditions (Atluri and Regehr, 1998; Satake et al., 2012), we found that, in 3 mm Ca_o, maximal responses were obtained either for the first or for the second stimulation. In the case of Figure 9B, the results for these two stimulations may be approximated with a parabola having an initial slope of 1 (Fig. 9B), as predicted from a binomial model (see Materials and Methods). The maximum N value can be obtained from the intersection of the parabola with the x-axis, giving N = 2.6 in the present case. N (or the closest integral value, here 3) is interpreted as the number of docking sites. By dividing the mean number of release events for the first stimulus by N, we obtain for this experiment a maximum release probability per docking site P = 0.69 (taking N = 2.6) or P = 0.60 (taking N = 3).

Fit of vesicular release number distributions with a binomial model

The value of N resulting from the extrapolation of the parabola in Figure 9B relies heavily on the point corresponding to the highest release probability P, obtained in this experiment for the first stimulation. Although any error on the abscissa and/or ordinate of this point would have significant effects on the estimate of N, it is important to note that this point reflects only part of the information contained in the first column in Figure 9A. To exploit this information better, we next compared the distribution of vesicle counts for this stimulation with the predictions of binomial and Poisson models (Fig. 9C). Experimental results (dots) were well approximated with a binomial model (red curve; optimal values, N = 3, p = 0.59). In contrast, Poisson models were unsatisfactory regardless of whether they were constrained to exhibit the same mean as the data (blue curve) or the same number of failures as the data (green curve). Figure 9, D–F, presents group results in which the N, P values obtained with the parabolic fit of variance/mean data are compared with the values obtained by binomial fits of count distributions. Mean N values were 5.1 ± 2.0 with the parabola method and 4.0 ± 0.9 (m. ± sd, resp. n = 21 and n = 20) with the binomial fit method (Fig. 9D). The two sets of parameters are closely correlated, indicating that the two methods yield consistent N, P estimates (Fig. 9E,F). Mean P values were 0.47 ± 0.14 with the parabola method and 0.57 ± 0.12 (mean ± SD; n = 21 and n = 20, respectively) with the binomial fit method. These values, obtained at 3 mm Ca_o, compare well with the previously obtained value P = 0.38 at 2 mm Ca_o at PF–MLI synapses (Ishiyama et al., 2014) and with the value P = 0.31 estimated at 2.5 mm Ca_o at PF–Purkinje cell synapses (Valera et al., 2012).

Together, the results shown in Figure 9 demonstrate that, at 3 mm Ca_o, vesicular release follows a binomial model rather than a Poisson model. This confirms that the saturation of variance–mean curves previously reported when analyzing EPSC amplitudes reflects at least in part a limitation in the number of vesicles that can be delivered by one active zone. We further find that the maximum binomial parameter, N, is larger than 1 for each active zone (range: 2–6 with binomial fit and 2–10 with parabolic fit). As previously suggested at GABAergic synapses (Trigo et al., 2012; Pulido et al., 2015), N presumably represents a fixed number of release competent sites in each active zone.

Although these results have important implications concerning the mechanisms of vesicular release, it is worth stressing that they were obtained under conditions of enhanced release probability. At normal Ca_o values, this probability is much lower, so that the predictions of binomial and Poisson distributions become similar (Ishiyama et al., 2014).

Discussion

Simple synapses can be used to count synaptic vesicular release

This work demonstrates the feasibility of counting vesicular release at simple synapses. It was shown previously that, at some glutamatergic synapses, the time course of EPSCs is so brief that the jitter of vesicular release results in an effective separation of successive release events (Isaacson and Walmsley, 1995). However, at multiple synapses, this separation is only possible for very low release probabilities (Del Castillo and Katz, 1954; Isaacson and Walmsley, 1995). In contrast, at simple synapses, where the total number of released vesicles is low, individual vesicular release events can be distinguished at normal or even at elevated release probabilities. We show that this can be achieved by applying deconvolution methods that had previously been developed in multiple synapses. We further show that simple synapses can be distinguished by abiding to simple rules during recording and by applying a strict post hoc selection criterion. Consistent with previous work (Auger and Marty, 1997; Crowley et al., 2007), we adopted a two-parameter criterion considering the CV of EPSC amplitudes and also amplitude occlusion (Fig. 7E).

Percentage of receptor occupancy at the peak of EPSCs

The EPSC amplitude occlusion method, as introduced by Tang et al. (1994), consists of evaluating the reduction in EPSC amplitude linked to preceding EPSCs occurring at the same synapse. By back extrapolation of the relation between the second EPSC amplitude and the time interval from the preceding EPSC, one can estimate the percentage of amplitude occlusion reached at the peak of EPSCs. This method gives valuable information on synaptic signaling, but it is demanding, first, because it requires a simple synapse measurement and, second, because, in the case of glutamatergic synapses, EPSC kinetics are very rapid, putting high demands on time resolution. Accordingly, we have introduced two changes in the present work to ameliorate these challenges. First, using deconvolution, we have been able to improve time resolution down to 0.2 ms. Second, to eliminate confounding effects linked to repetitive receptor activation, cumulative receptor desensitization, or incomplete vesicle recycling, we have restricted the analysis to the first two events after a resting period. Our best estimate of amplitude occlusion (ω) obtained with these two improvements is 0.62, substantially higher than the previous estimate obtained in the same preparation (0.37; Crowley et al., 2007). Together with a higher ω value, our analysis indicates a shorter time constant for the recovery time course of amplitude occlusion than that obtained earlier, suggesting that amplitude occlusion is primarily driven by receptor activation rather than by desensitization.

ω, the percentage of amplitude occlusion at the peak EPSC, is related to receptor occupancy because the receptors that become unavailable for activation by subsequent vesicular release are mostly transmitter bound. However, the activation pathway of AMPA receptors involves several bound states, including various numbers of bound glutamate molecules, and corresponding either to open or to closed channels (Robert and Howe, 2003). It remains possible that, during occlusion, some of the glutamate-bound receptors would be inactive but would nevertheless be susceptible to subsequent activation after the binding of additional glutamate molecules. In this case, receptor occupancy would be larger than ω and, in general, receptor occupancy can be equal to ω or larger than ω. In either case, our results indicate a higher percentage of receptor occupancy than previously anticipated. It remains to be seen whether the conclusion of a high degree of receptor activation can be extended to other central glutamatergic synapses. Previous studies using competition with low-affinity glutamate antagonists indicate a significant degree of receptor activation (Taschenberger et al., 2005), but they are not accurate enough to yield quantitative estimates. Quantitative but still indirect estimates using intracellular or extracellular glutamate uncaging gave values consistent with our estimate of 0.62. At the calyx of Held, quantal amplitudes increase by a factor of 1.46 by maximally increasing the cytosolic glutamate concentration, yielding an estimated ω value of 0.68 (Ishikawa et al., 2002). At the mossy fiber–granule cell synapse, a study using local extracellular glutamate uncaging gave an ω value of 0.49 (DiGregorio et al., 2007). However, receptor activation is likely to vary according to a variety of synapse specific parameters, such as the diameter of the active zone, the subtypes of AMPA receptors, or the presence and nature of the auxiliary proteins TARPs (Howe, 2015). Therefore, it is necessary to await ω evaluation in other preparations to decide on the generality of the present conclusions.

Advantages and limitations of counting synaptic vesicular release

Counting synaptic vesicular release offers several advantages over traditional measurements of EPSC amplitudes. A standard practice in synaptic physiology has been to evaluate the number of released vesicles by dividing the peak EPSC amplitude by the quantal size. However, at central glutamatergic synapses, the duration of quantal EPSCs is often comparable to, or shorter than, the range of synaptic latencies (Isaacson and Walmsley, 1995). This leads to broadening of composite EPSCs at the expense of amplitude summation and to a severe underestimate of released vesicle numbers derived from peak amplitudes. In addition, even if two quantal EPSCs have identical latencies, they do not necessarily add up linearly in view of possible saturation of postsynaptic receptors (Tang et al., 1994). Our present results indicating a value of 0.62 for ω at PF–MLI synapses show that this second effect can be substantial. Together, synaptic jitter and receptor saturation can lead to a several-fold underestimate of vesicle number when using EPSC amplitudes.

In contrast to previous EPSC-amplitude-based approaches, our present analysis takes into consideration both synaptic jitter and receptor saturation. Whereas synaptic jitter is a source of error when analyzing EPSC amplitudes, it favors vesicle counting by helping event separation during deconvolution. Nonlinear effects linked to receptor saturation are largely avoided by analyzing vesicular release statistics based on vesicular counts rather than on EPSC amplitudes. Vesicular counting covers an impressive range: it can report release rates up to 4 kHz (0.8 events per 0.2 ms bin; Fig. 5), which is 20,000-fold higher than the mean spontaneous release rate. Nevertheless the limit of 4 kHz cannot easily be overcome. At this rate, the fraction of detected events that are actually double events, as evaluated in Figure 4, is ∼50%. A procedure was developed to correct for these missed events (Fig. 5), but this procedure leaves a residual error behind, as explained in the Materials and Methods, and would become unreliable for release rates beyond 4 kHz.

Statistical analysis of vesicular release counts

Standard variance–mean methods are performed on PSC peak amplitudes and have two free parameters, the quantal size q and binomial N (Clements and Silver, 2000). In contrast, the variance–mean plot of Figure 9B is performed on vesicular release counts and has a single free parameter N. Apart from the previously discussed issues concerning the origin of the saturation of the variance–mean plots with the two methods, the fact that a single parameter is optimized significantly improves the reliability of N determination with the vesicular counting method.

Vesicular counting carries with it another substantial advantage: generating a full histogram of vesicle numbers. Fitting this histogram with the contrasting predictions of Poisson versus binomial models provides a powerful method to examine vesicular release statistics (Fig. 9C–F).

Simple synapses may be modeled assuming several independent vesicular docking sites

Our results confirm MVR at simple PF–MLI synapses. The finding of binomial release statistics is consistent with release models involving several discrete release competent sites (docking sites) in each active zone, rather than a distributed release probability over a homogeneous surface area. Two sets of observations suggest that docking sites function independently of each other. First, near the end of a train, when synaptic depression has reduced the probability of release, vesicular counts exhibit a variance to mean ratio close to 1, indicating a lack of cooperativity between neighboring docking sites. Second, at the peak of the response, the close fit of vesicular counts to a binomial distribution indicates independence between docking sites.

Comparison between simple glutamatergic synapses and simple GABAergic synapses

The present results offer striking similarities to those previously obtained at simple MLI–MLI synapses. In both cases, a few docking sites appear to function in parallel and PSCs are combined together in a sublinear manner due to partial receptor saturation. Nevertheless, differences emerge. The range covered by docking site numbers is lower for simple MLI–MLI synapses (from 1 to 6: Pulido et al., 2015) than for PF–MLI synapses (from 2 to 10 as obtained with variance–mean fits and from 3 to 6 as obtained from binomial fits). In particular, whereas a significant proportion (27%) of MLI–MLI synapses have a single docking site (“elementary synapses”; Pulido et al., 2015), no such case was found for PF–MLI synapses (Fig. 9D; but see discrepant results by Nahir and Jahr, 2013). Another difference arises from the contrast between decay time constants of glutamatergic and GABAergic PSCs (Llano and Gerschenfeld, 1993). Whereas the degree of receptor saturation reached at the peak of PSCs is broadly similar for the two types of PSCs (76% at MLI–MLI synapses, Auger and Marty (1997), vs 62% at PF–MLI synapses), the much quicker PSC decay observed at glutamatergic synapses translates into a much lower degree of PSC overlap between consecutive events. This, together with the much quicker kinetics of receptor activation, affords a better separation of individual PSCs in simple glutamatergic synapses, allowing us to count individual release events in the present work.