Synaptic Correlates of Low-Level Perception in V1

Abstract

The computational role of primary visual cortex (V1) in low-level perception remains largely debated. A dominant view assumes the prevalence of higher cortical areas and top-down processes in binding information across the visual field. Here, we investigated the role of long-distance intracortical connections in form and motion processing by measuring, with intracellular recordings, their synaptic impact on neurons in area 17 (V1) of the anesthetized cat. By systematically mapping synaptic responses to stimuli presented in the nonspiking surround of V1 receptive fields, we provide the first quantitative characterization of the lateral functional connectivity kernel of V1 neurons. Our results revealed at the population level two structural-functional biases in the synaptic integration and dynamic association properties of V1 neurons. First, subthreshold responses to oriented stimuli flashed in isolation in the nonspiking surround exhibited a geometric organization around the preferred orientation axis mirroring the psychophysical “association field” for collinear contour perception. Second, apparent motion stimuli, for which horizontal and feedforward synaptic inputs summed in-phase, evoked dominantly facilitatory nonlinear interactions, specifically during centripetal collinear activation along the preferred orientation axis, at saccadic-like speeds. This spatiotemporal integration property, which could constitute the neural correlate of a human perceptual bias in speed detection, suggests that local (orientation) and global (motion) information is already linked within V1. We propose the existence of a “dynamic association field” in V1 neurons, whose spatial extent and anisotropy are transiently updated and reshaped as a function of changes in the retinal flow statistics imposed during natural oculomotor exploration.

SIGNIFICANCE STATEMENT The computational role of primary visual cortex in low-level perception remains debated. The expression of this “pop-out” perception is often assumed to require attention-related processes, such as top-down feedback from higher cortical areas. Using intracellular techniques in the anesthetized cat and novel analysis methods, we reveal unexpected structural-functional biases in the synaptic integration and dynamic association properties of V1 neurons. These structural-functional biases provide a substrate, within V1, for contour detection and, more unexpectedly, global motion flow sensitivity at saccadic speed, even in the absence of attentional processes. We argue for the concept of a “dynamic association field” in V1 neurons, whose spatial extent and anisotropy changes with retinal flow statistics, and more generally for a renewed focus on intracortical computation.

Introduction

Low-level visual perception is often defined by holistic psychological laws formulated in the framework of the Gestalt theory (Wertheimer, 1912; Koffka, 1935). These rules describe generic principles used by the early visual system to link instantly stimulus attributes detected at distant points on our retina. Although these rules depend on top-down control signals in the attentive behaving nonhuman primate (Li et al., 2006; Gilbert and Li, 2013), they still require the existence of a bottom-up process driven by the stimulus configuration, which operates even in the absence of attentional processes (Polat et al., 1998; Mizobe et al., 2001; Kasamatsu et al., 2010). They account for emergent properties, such as feature grouping by form similarity and spatial proximity in the spatial domain, and common fate and motion linking in the temporal domain (Neri et al., 1998). The feature grouping in the spatial domain gives rise to perceptual facilitation for collinear visual elements (Kovács and Julesz, 1993; Polat and Sagi, 1993, 1994; Kapadia et al., 1995; Polat and Tyler, 1999), thereby forming a perceptual “association field” (Field et al., 1993; Hess and Field, 1999). Binding in space and binding across time are traditionally thought to be implemented in separate cortical loci, respectively, in V1 versus MT (Heeger et al., 1996). Despite this well-accepted hierarchy in cortical specialization (Felleman and Van Essen, 1991; Serre et al., 2007), a still unsolved issue is to determine to which degree the “horizontal” connections intrinsic to V1 already provide a built-in sensitivity to multiple scales of spatial and temporal integration, instrumental to the neural implementation of Gestalt laws.

Despite many seminal studies of the synaptic organization of the classical discharge field (Hirsch et al., 1998; Ferster and Miller, 2000; Douglas and Martin, 2004; Priebe and Ferster, 2012), few studies (Haider et al., 2010) apart from prior work from our group (Frégnac and Bringuier, 1996; Bringuier et al., 1999; Chavane et al., 2000; Baudot et al., 2013), have attempted to directly measure the synaptic nature of contextual influence originating from the far periphery (the “silent surround”) of the classical discharge field. Contrary to the classical view, the pioneer study of Bringuier et al. (1999) showed that subthreshold (“synaptic”) responses could be evoked from eccentricities several degrees beyond the classical discharge field. The strength of these synaptic responses exponentially decreased, and their latency linearly increased, with relative eccentricity from the receptive field (RF) center.

These data allowed us to propose the existence of propagating waves of visual activity relayed by the horizontal connectivity, and traveling within the plane of the V1 layers at an apparent speed in the range 0.1–0.3 m/s (for review, see Frégnac, 2012; Sato et al., 2012). This propagation speed is 10 times slower than that of X-thalamic axons and feedback from higher cortical areas and 100 times slower than the fast Y-pathway (Hoffman and Stone, 1971; Nowak and Bullier, 1997). These horizontally traveling waves of visual activity are therefore most likely explainable by slow propagation along unmyelinated horizontal axons, and our intracellular measures agree with those done in vitro (Hirsch and Gilbert, 1991) and in vivo in other primary areas (Moore and Nelson, 1998).

Modulatory effects of the surround, both suppressive and facilitatory, have already been described in the past (Polat et al., 1998; Chen et al., 2001; Kasamatsu et al., 2001; for review, see Seriès et al., 2003) as well as more recently (Kim et al., 2012). However, here we conjecture that the conduction properties and the anatomical specificity of intracortical horizontal connectivity allow to infer precise spatiotemporal constraints, where a boost of sensory responsiveness should be observed depending on the relative timing (imposed by the visual input pattern) of feedforward and horizontal inputs to the same V1 neuron.

We have tested this working hypothesis by exploring systematically the visual responses in the “silent” (nonspiking) surround of V1 RFs to static stimuli, as well as to two-stroke apparent motion (2S-AM) stimuli whose speed in visual space matched horizontal propagation in cortical space. We report here a diversity of subthreshold processes that all could play a role in the genesis of figure-ground segregation, colinearity detection, and, more unexpectedly, global motion flow sensitivity at saccadic speed.

Materials and Methods

Animal preparation and electrophysiological recordings.

All experiments were performed in anesthetized (althesin, 3 mg/kg/h) and paralyzed (pancuronium bromide, 0.2 mg/kg/h) adult cats of either sex, according to the American Physiological Society's Guiding Principles for the Care and Use of Animals. The animals used in the experiments were bred in the Central CNRS Animal Care (French Agriculture Ministry Authorization: B91-272-105) under required veterinary and National Ethical Committee supervision. Intracellular recordings were performed in area 17 (V1) with sharp electrodes pulled from 1.5-mm-thick borosilicate capillaries. Electrode pipettes were filled with a 2 m potassium methyl sulfate and 4 mm KCl solution. The electrodes used had resistance between 60 and 90 mΩ. Recordings were performed using an Axoclamp 2A amplifier.

Visual stimulation.

The visual stimulation was generated by the ELPHY software (G. Sadoc, UNIC, CNRS) and presented on a gamma-corrected CRT monitor with a refresh rate of 150 Hz. The RF position of each recorded cell was first localized with moving light bars. This preliminary localization of the RF position also allowed to assess ocularity (i.e., the strength of the cell's visual responses to stimuli presented to each eye in isolation). In all subsequent stimulation protocols, only the eye providing the strongest responses was left seeing the screen. The mapping of the ON and OFF zones of the subthreshold RF (minimal synaptic RF [MSF]) was then performed by forward correlation of the responses to a “sparse noise” stimulation protocol. In this protocol, the visual region of interest was divided in a 10 × 10 regular matrix, in which a random sequence of nonoverlapping white (23 cd · m⁻²) or dark (1 cd · m⁻²) squares was presented one at a time on a 12 cd · m⁻² background. The size of the subthreshold RF thus characterized; we next determined the orientation, phase, and spatial frequency tuning properties of the subthreshold RF with a randomized “Gabor noise” stimulation protocol (Fournier et al., 2011). The templates of the Gabor patches were drawn from a discrete uniform distribution consisting of six orientations (in steps of 30°), four phase values (0°, 90°, 180°, and 270°), and five spatial frequencies (0.20, 0.26, 0.34, 0.53, and 1.1 cycles per degree). The orientation, phase, and spatial frequency of the Gabor patch used for the subsequent protocols were each chosen from the tuning curve for the parameter under study, after collapsing across the other two parameters.

Once the Gabor template covering the recorded cell's subthreshold RF defined, the visual field was paved using a hexagonal lattice (for optimal coverage) of possible stimulation nodes/tiles centered on the RF and aligned to its preferred orientation. The size of each tile (i.e., the distance between neighboring nodes) was chosen to be the diameter of the Gabor template, so that stimuli could not overlap and peripheral stimuli could not encroach on the RF center. The stimulus set was composed of 114 (6 orientations × 19 nodes) one-stroke (1S) stimuli, and 288 (6 directions × 24 trajectories × 2 configurations) two-stroke (2S) stimuli. In each block of trials, each stimulus was presented only once. In addition, 36 trials during which no stimulus was presented (henceforth “blank trials”) were also included in each block. The resulting set of 438 trials (each lasting 93 ms) was presented in random order in each block. Recordings lasted for 13–50 blocks (median 38). In almost all recordings, and in particular for the example cells presented in Figures 2 and 5, the contrast of Gabor patches was low (0.25–0.5) in the central node and high in the rest of the nodes (0.75–1.0), to better reveal peripheral influences (for review, see Seriès et al., 2003).

Figure 2.

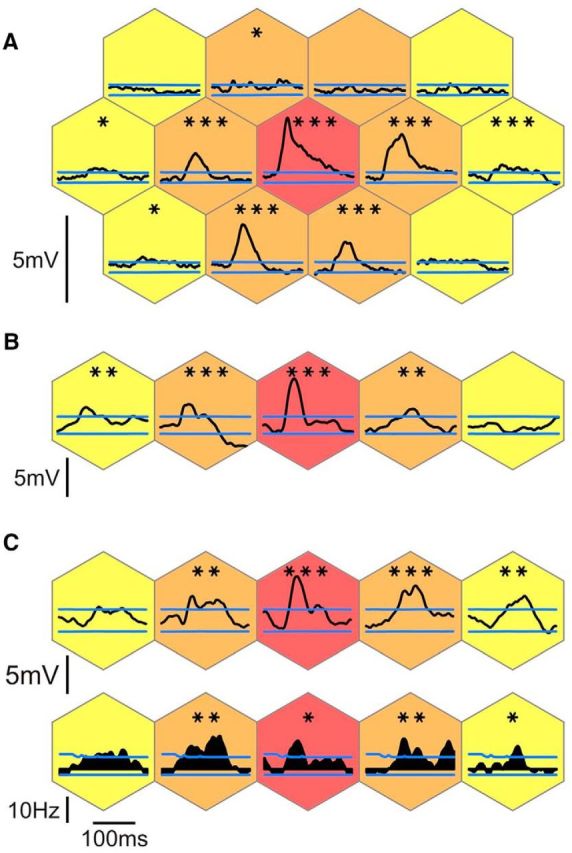
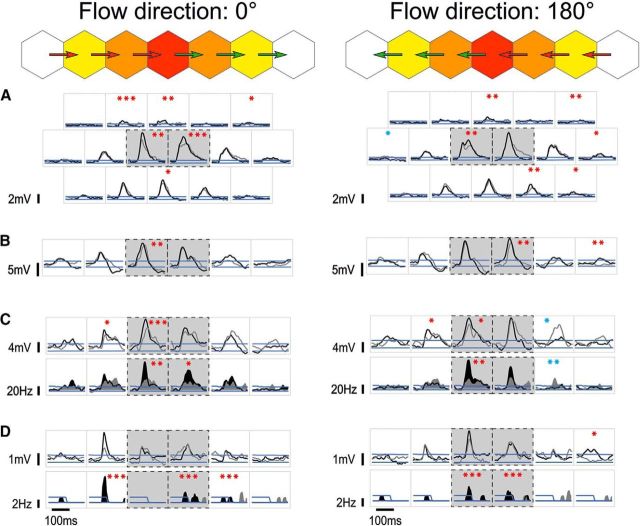
Spatial extent of responses to static (1-stroke) flashed Gabor patches. A–C, Synaptic responses of three example cells to flashed Gabor patches of the same orientation as the cell's preferred orientation. The relative eccentricity from the RF center is color-coded, as in Figure 1. C, Spiking responses are shown in the row below the synaptic responses. Blue lines indicate the levels above or below which responses were significantly (p < 0.05, one-tailed) above or below the activity during blank trials (see Materials and Methods). Statistical significance level of the maximum of the visual responses against the null distribution of maxima during blank trials: *p < 0.05 (one-tailed); **p < 0.01 (one-tailed); ***p < 0.001 (one-tailed). The internode spacing (i.e., the size of the hexagonal tiles) was 6° (A), 4° (B), and 4.5° (C), respectively, and the number of trials was n = 50, n = 50, and n = 36 trials, respectively.

Figure 5.

Diversity of summation effects by synchronizing feedforward and horizontal activations. Single-cell examples of responses to 2S-AM trajectories (directions 0°, left, and 180°, right) along the preferred orientation axis. Top diagrams use the same conventions as in Figure 1C and represent the link between the hexagonal tiles and the trajectories (arrows) for the trajectories along the main axis. In each square inset, the black trace represents the response to the corresponding trajectory, overlaid on its respective linear prediction (LP), shown in gray. Black dashed boxes indicate the two trajectories where one of the two flashed Gabor patches stimulates directly the RF (henceforth, “central trajectories”). As in Figure 2, the one-tailed response significance thresholds at p < 0.05 are shown in blue. Asterisks indicate the statistical significance level of the nonlinear summation (all one-tailed, paired permutation test), measured in the 20 ms preceding the peak of significant responses (see Materials and Methods). Red asterisks indicate when the nonlinearity is facilitatory. Blue asterisks indicate when the nonlinearity is suppressive. We found that suppressive nonlinearity is the exception, not the rule (see also Fig. 6). A–C, Same three example cells as shown in Figure 2. A, Facilitatory interaction can be found for various trajectories across the visual field, and not only on the main axis. B, Occasionally, de novo responses could be revealed in the far periphery, as is the case for the 180° centripetal distal trajectory (rightmost trajectory in the figure). C, D, Spiking responses are shown in the row below the synaptic responses. C, Even relatively small facilitation at the subthreshold level can translate into much larger facilitation at the spiking level. D, Example of highly localized nonlinearity (second left). Note also another de novo distal synaptic response (rightmost trajectory in the figure). For this cell, n = 38 trials.

Response quantification and statistical significance.

Spikes were threshold-detected and replaced by α functions in the membrane potential trace (α(t) = a × t × e^−t/τ, where a is the slope at the start of the spike-taken as the point of maximal second derivative-, and τ is the half-width of the spike), as done in previous studies (Monier et al., 2003; Fournier et al., 2011). The resulting traces were bandpass filtered (0.1–300 Hz) and averaged across trials in a peristimulus triggered waveform (PSTW), whereas spikes were accumulated in a peristimulus time histogram (PSTH, bin width 20 ms). Average traces (PSTWs) and PSTHs were smoothed with a Gaussian filter (SD = 3 ms), except for analyses in Figures 4 and 7.

Figure 4.

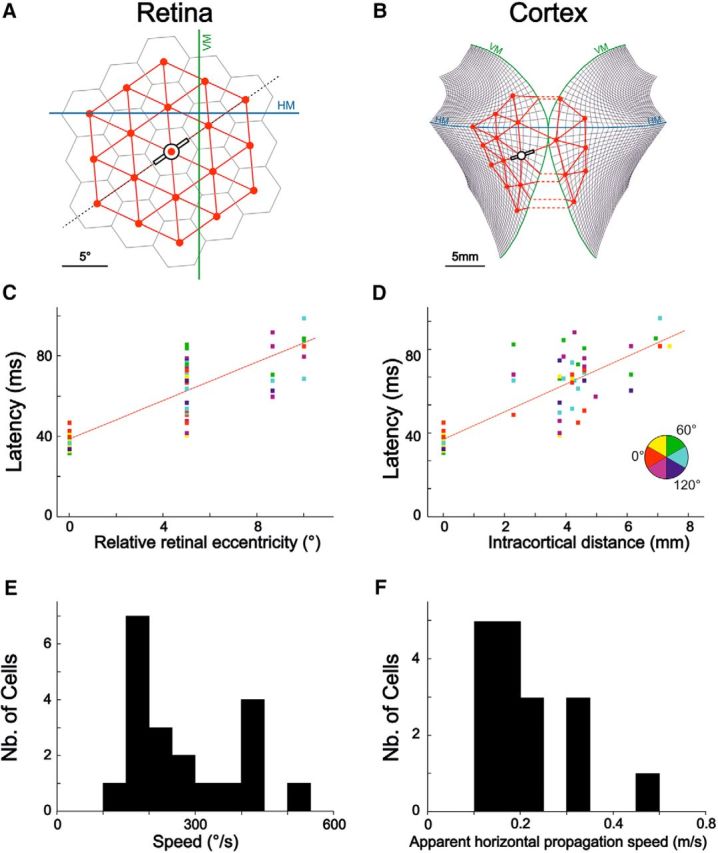
Inference of slow intracortical horizontal propagation from synaptic response latency measurements. Left, Results in retinal coordinates. Right, Results in visual cortical retinotopic coordinates. VM and HM denote the vertical and horizontal meridians of the visual field, respectively. A, The hexagonal paving and the corresponding node lattice are plotted in visual (retinal) coordinates for an example cell. B, The corresponding retinocortical projection of the node lattice on a flattened map of cat V1, using the stereotaxic atlas published by Tusa et al. (1978) (thin black lines). The two hemispheric projections are shown tangential to each other for illustration purposes. C, Linear latency increase (R² = 0.74; p < 2 × 10⁻¹⁶) as a function of relative retinal eccentricity for the same example cell. D, Same data as in C, but expressed here as a function of relative intracortical distance (i.e., the shortest distance within cortex from the considered node to the RF center) computed from the projection illustrated in B. The relationship was also linear (R² = 0.72; p < 2 × 10⁻¹⁶). E, F, Population analysis. E, Histogram of estimated horizontal propagation speed in the visual space (n = 20). F, Same as E, but using cortical distance, thus yielding an estimate of intracortical horizontal propagation speed, in m/s (n = 17, a precise measure of the area centralis coordinates being unavailable for 3 of the cells in E).

Figure 7.

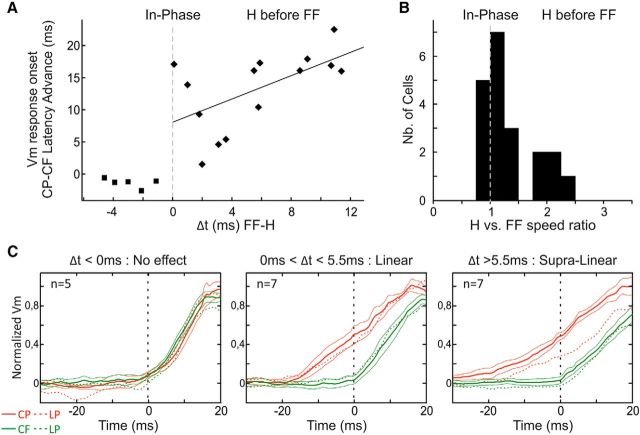
Synaptic response latency advance induced by synchronizing in-phase the feedforward drive and the horizontal input. A, Scatterplot of the latency difference at half-height between synaptic responses to centripetal and centrifugal central trajectories in the ISO configuration along the main axis, as a function of the temporal lag (Δt) between feedforward drive and horizontal inputs inferred from results in Figure 4E. B, Population histogram of the ratio between the inferred horizontal propagation speed in visual space and the physical speed of the 2S-AM sequence. C, Population analysis of responses to the central trajectories along the main axis. Neurons were grouped by Δt, and their normalized responses pooled within groups using the centrifugal response as a reference. Responses are shown as mean ± SEM across cells, and their LP is illustrated as a dotted line of the same color.

All statistical significance tests fell into two categories: quantifying the significance of a response to a stimulus or comparing a data statistic between two conditions. To do the former, we relied on the activity during blank trials, which provides the null distribution for visual responses (i.e., the activity that would occur should the cell not respond to the stimulus, which is the null hypothesis). To do the latter, we performed permutation tests (with 100,000 repetitions), paired or unpaired depending on the data to be compared.

We describe here in more details how statistical significance of visual responses was tested. Let N_blocks designate, in all the following, the number of blocks for which the recording lasted. Each response was therefore the average of single-trial responses to N_blocks trials. At each time point, we built the null distribution for this average from the activity during blank trials. More specifically, for each full recording protocol, a set of 100,000 null PSTWs (resp. PSTHs) was constructed by randomly picking, in each block, one blank trial among the 36, and averaging the membrane potential traces (resp. binned spiking activity) across these N_blocks blank trials. Note that 36^Nblocks ≫100,000, so that the sampling of the set of possible null PSTWs (resp. PSTHs) remains actually very sparse. Sorting at each time point the values of the 100,000 null PSTWs (resp. PSTHs) allowed us to compute at each time point the thresholds above or below which a visually evoked PSTW (resp. PSTH) is above or below blank (null) values, at a given confidence level. Those thresholds are depicted by the blue waveforms in Figures 2 and 5 for the 95% confidence level (one-tailed). At each time point, the median value of the distribution of null PSTWs (resp. PSTHs) was computed and then subtracted from all responses and thresholds, to remove any average background fluctuation along the course of a trial. In addition, we extracted from this set of null PSTWs (resp. PSTHs) the null distribution of the maximum of visually evoked PSTWs (resp. PSTHs) by gathering the maximum of each of the null PSTW (resp. PSTH) in the relevant time window. The median of this null distribution of maxima is depicted in Figure 3A by the dotted circles and asterisks in Figure 2 indicate the significance level against this null distribution. The relevant time window for all analyses relying on a response strength computation (whether that is the maximum, or the integral of the significant response) was chosen to be 30–120 ms. Indeed, no response maximum occurred before 30 ms across our cell population and stimulus conditions, and any maximum occurring after 30 + 93 ms (93 ms being the total duration of a trial) could be the result of a contamination by a response to one of the following stimuli not dampened enough by the average across blocks.

Figure 3.

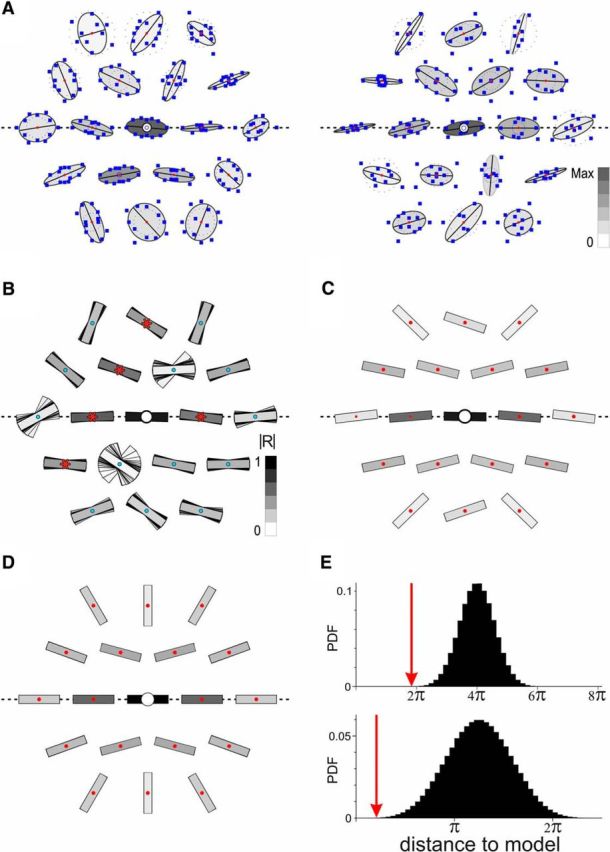
Synaptic correlate of the perceptual association field in V1. A, Static synaptic association field (S-AF) for two example cells (same as shown in Fig. 2A, B). For each node, the preferred orientation of the synaptic responses is computed from the circular average of the individual responses to each orientation (blue squares). For illustrative purposes, ellipses are fit to the polar plot of responses, with one of the ellipse's axes (in black) fixed at the preferred orientation at the node. The darkness of the ellipse's filling represents the normalized strength of the mean response at the node. Dotted circles represent the median noise level. For visualization purposes, the coordinates of each polar plot were scaled independently at each node. B, The mean S-AF is obtained by performing a circular average over the cell population of the preferred orientations, at each node (n = 25). The |R| value resulting from this average (see Materials and Methods) measures the reliability of the result and is represented by the level of gray of each oriented bar. Red asterisks indicate node positions where the |R| value is significantly higher than expected by chance (p < 0.05, one-tailed; see Materials and Methods). To illustrate the reliability of the result, the same computation is performed on all possible sets of 24 cells sampled among the 25 cells in our population. Accordingly, the 25 preferred orientation sample estimates are represented in an overlaid fashion at each node, beneath the estimate for the full population. C, Symmetrized version of the mean S-AF (B). Note the similarity in the pattern with the perceptual association field of Hess and Field (Field et al., 1993). D, A simple ad hoc model of the S-AF (see Materials and Methods; Discussion). E, Model validation. The distance to the model (red arrows) was quantified as the sum across the relevant nodes of the absolute value of the angular difference between data (B, top; or C, bottom) and the model. Each histogram represents the probability density function of the null distribution for the distance to the model (computed under the null hypothesis of random preferred orientations in the surround).

Static association field (S-AF).

To compute circular averages (i.e., averages of orientations), we used the following formula:

where each r_k is a weight and each θ_k is an angle.

The argument of this complex number (arg(R)), once divided by 2, is the end result of the circular average, whereas the modulus (|R|) is an index of the “robustness” of the circular average (from 0 for a total absence of orientation selectivity to 1 when all the averaged orientations are equal). If the θ_k are equally distributed from 0 to π, and the r_k are the responses, then |R| is simply the orientation selectivity index (OSI).

The full description of the S-AF is given in Results. To average across cells, we realigned all RFs on a common orientation preference axis. Because this realignment can be done clockwise or counterclockwise, we also computed a symmetric mean S-AF by performing a circular average of the preferred orientations for nodes symmetric around the two cardinal symmetry axes of the RF. Statistical significance was computed by building null distributions under the null hypothesis that, for each cell, preferred orientations at noncentral nodes are actually random, while keeping the nodes' OSIs fixed. This is how the |R| null distributions were computed at each node (Fig. 3B) (this method was also used for the dynamic association field (D-AF) (Fig. 9A,B). For computations of the distance to the model, we also excluded the two nodes on the axis orthogonal to the main axis because the perceptual “association field” hypothesis is agnostic about which orientation to expect in these two positions.

Figure 9.

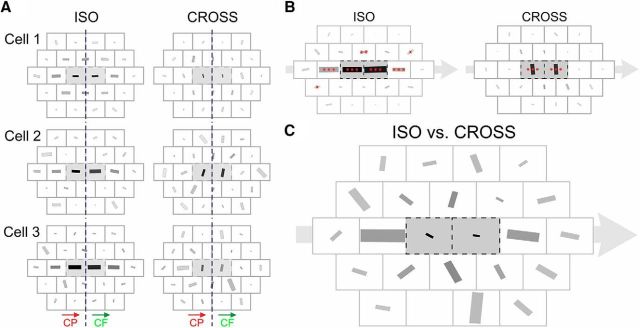
The D-AF of V1 neurons. A, Examples of single-cell D-AF. The D-AFs of the three example cells of Figure 2 are represented. Left column, Preferred RF orientation for ISO trajectories. Right column, CROSS configuration. For the ISO configuration, the RF orientation giving maximal 2S responses is robustly coaligned with the radial motion flow axis for trajectories along the main axis. For the CROSS configuration, the preferred stimulus orientation differs with eccentricity from the RF center. Indeed, for trajectories toward and from the center (where one of the two Gabor patches stimulates directly the RF), the maximal response is observed when the RF orientation is orthogonal to the motion flow axis. In this case, the preferred RF orientation is that of the local Gabor inducer used for the stimulation, a result predictable from the orientation tuning in the RF center. In contrast, for more distal CROSS trajectories, such as the Cp1 on-axis trajectory, the preferred RF orientation is more variable and sometimes aligned with the motion flow axis (i.e., flipped by 90° compared with what is expected from the local feature selectivity of the RF), as in cells 2 and 3. B, Population average of individual D-AFs (n = 25). Asterisks represent the significance of the magnitude of the |R| value of the population average (i.e., where the population average of preferred RF orientations is more robust than expected by chance) (all one-tailed; see Materials and Methods). The sizes of the bars are normalized to the maximal |R| value (0.316 in this case, for the centrifugal ISO central trajectory). C, The preferred RF orientations for the ISO and the CROSS configurations are averaged vectorially for each trajectory and for each cell. These values are then averaged across the population of cells, and the net result is represented by the orientation and size of the bars. The size of each bar thus denotes whether the responses for this trajectory are more influenced by the global motion flow (size = 1) or by the local feature selectivity (here, the tuning to orientation) (size = 0). For illustration purposes, the size of the bars was normalized. The on-axis Cp1 trajectory was the most influenced by the global motion flow (|R| = 0.326).

The conceptual model of the S-AF shown in Fig. 3D was built by mixing two constraints, namely, radial and iso-orientation preference biases. First, the radial bias reflects the underlying bias in preferred orientation across V1 (see Discussion). Its strength was assumed as constant across the surrounding visual field, with an exact value of the same order of magnitude as the mean “noise” bias, the |R| value resulting from averaging random orientations, in this case, 0.20. Second, the iso-orientation bias was assumed to decrease (linearly) with relative eccentricity and disappear for the most distal positions (second ring). The two biases were set to sum to 1.0 in the center. Thus, the proposed model has no free parameter. Specifically: R_model(r,θ) = 0.2 × e^iθ + (0.8 − 0.4 × r) where r is the relative eccentricity from the RF center (expressed in number of tiles: 0, 1, or 2) and θ is the polar angle in the RF reference frame (with the convention θ = 0 in the center).

Response latency and horizontal speed estimates.

Because our working hypothesis depends on the relative timing of synaptic inputs to the cell, the latency of a response was defined as the estimated time of the visually evoked post-synaptic potential onset and not that at which the subthreshold response instantaneous amplitude first becomes significant. However, this latter computation (with a p value of 0.05) was used to guide a semiautomated estimation of response latencies. Indeed, computations relied on small-amplitude synaptic events, and their analysis required a dual-step measurement process.

To estimate the horizontal propagation speed, we then performed, for each cell, a linear regression on the distribution of response latency as a function of stimulus eccentricity from the RF center. The resulting estimate was accepted if an R² > 0.2 criterion was fulfilled by this linear regression.

In the semiautomated latency estimation procedure, responses were reviewed one by one. Some visually obvious false positives were discarded, and similarly obvious false negatives included (e.g., when a lower-than-average baseline prevented responses from reaching the significance threshold). The visual criterion used for this sorting of responses and latency adjustment was the change of the PSTW curve derivative, compared with the baseline activity found early in the trial. The results in Figures 4 and 7 were confirmed by using as the latency estimate the (automatically detected) first crossing of the p < 0.01 significance threshold. However, results were noisier and fewer cells fulfilled the R² > 0.2 criterion for inclusion in the analyses, hence our presentation of the results using the semiautomated latency estimates.

All responses were used for the analyses in Figures 4 and 7, regardless of the stimulus type. Indeed, separating 1S and 2S responses, or separating by 1S Gabor orientation or 2S trajectory direction, and even including the center responses or excluding them yielded very consistent estimates of horizontal propagation speeds across the population: distributions had a mean between 200°/s and 350°/s and an SD in the order of 150°/s typically. However, reducing the number of data points increased variability and fewer cells reached the R² > 0.2 criterion.

Measures of nonlinear summation.

Linear predictors (LPs) were built by adding the two responses to the respective 1S stimuli used in the considered 2S sequence, with the appropriate AM interstimulus time delay (20 ms) applied to the second one. The contributions from the third ring of relative eccentricity (typically 12° away from the RF center) were ignored (1S stimuli were not presented in the third ring), as most 1S responses in the second ring were already close to noise level.

The statistical significance of nonlinear summation was characterized using a permutation test for paired data (the single-trial response and its LP in each block), with 100,000 repetitions. Specifically, the set of N_blocks single-trial responses to one 2S stimulus was compared with the set of N_blocks single-trial linear predictors of responses to this 2S stimulus. These single-trial linear predictors were built using the two single-trial responses (within the same block) to the two relevant 1S stimuli.

We considered synaptic summation as nonlinear when the following two requirements were met. First, the response or its LP reaches statistical significance. For this purpose, the significance of the LP was computed from a null distribution for linear predictors, built by linearly adding two null PSTWs with the appropriate 20 ms time lag. Second, the difference between the response and its LP reaches statistical significance (determined using the permutation test described above) at some point within the 20 ms preceding either the peak of the response or the peak of its LP, whichever was most statistically significant.

The rationale for choosing as a reference the most statistically significant peak between that of the response and that of the response's LP was that, except for the most distal trajectories, the LP is the sum of two responses (to 1S stimuli), and its baseline variance is thus bigger than the baseline variance of single responses. To avoid biases, we therefore had to normalize each peak to a common standard before comparing the peak of the response to that of its LP. To do this, we divided each peak by its respective (positive) significance level. This normalization was done only to choose which of the two peaks was to be used as the temporal reference for the investigation of significant differences between the response and its LP, and not for the actual comparison using the permutation test. All analyses in Figures 5 and 6 rely on this comparison between the peak of the response and that of its LP (except for the most peripheral trajectories, where the two peaks were directly compared).

Figure 6.

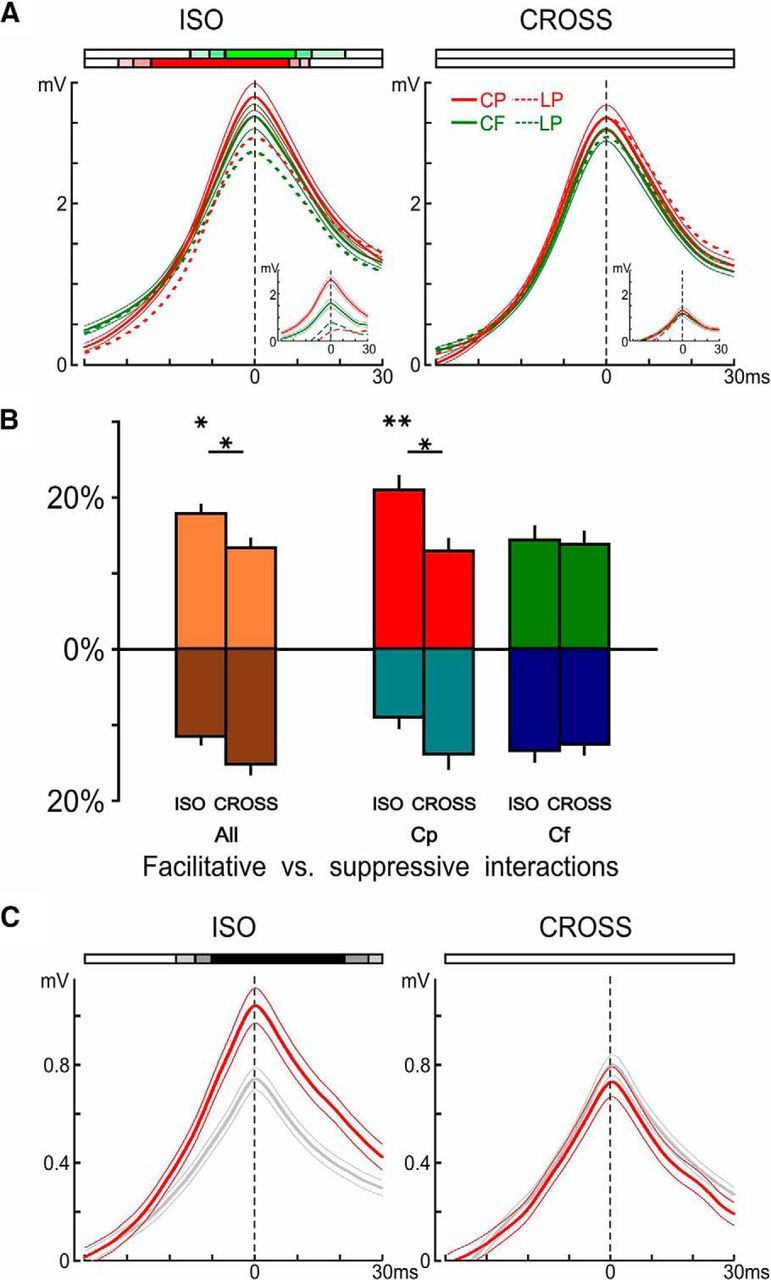
Nonlinearities in the dynamic association field (D-AF). A, Peripeak response waveforms, averaged across all cells and significant responses (see Materials and Methods), grouped by configuration (ISO, left; and CROSS, right) and trajectory type (centripetal, red; and centrifugal, green). Average response to centripetal and centrifugal is shown as mean ± SEM (n = 462 for centripetal ISO, n = 463 for centrifugal ISO, n = 388 for centripetal CROSS, and n = 412 for centrifugal CROSS). Ribbons at the top represent when the average response was significantly higher than its LP at a given significance level (color coding for three levels p < 0.05, p < 0.01, and p < 0.001 depicted by the fully saturated color, one-tailed paired permutation test). Insets, Same analysis but restricting the averages to the pairs of nodes where the response to the centripetal ISO trajectory was significantly bigger than its LP (n = 140). Even when the centripetal ISO trajectory elicits supralinear summation, the corresponding centripetal CROSS trajectory did not, on average. B, Proportion of statistically significant evoked nonlinear interactions (in %). For each cell, the proportions of significant (p < 0.05, one-tailed, paired permutation test) evoked facilitative, and suppressive, nonlinear interactions were computed for trajectories where the 2S-AM response or its LP is significantly above the activity during blank trials (p < 0.01, one-tailed), as in A. These proportions were then averaged across the population of cells (n = 25) and represented as mean ± SEM, along the positive y-axis for facilitatory interactions and along the negative y-axis for suppressive interactions. Top asterisks indicate, for each trajectory type, significant differences in average proportions of facilitatory versus suppressive interactions. We also tested for significant differences between the ISO and CROSS configurations (bottom asterisks). Both used two-tailed, paired permutation tests. C, Peripeak response waveforms, averaged across all cells and all peripheral centripetal trajectories, but separated by motion axis: red represents average response to trajectories along the main axis (i.e., direction 0° and 180°, n = 400 = 2 directions × 8 noncentral centripetal trajectories × 25 cells); gray represents average response to those along the two other axes (n = 800).

The comparison of peripeak response waveforms with their LP (see Fig. 6A) relied on a permutation test for paired data with 100,000 repetitions, over the population of responses and their respective LP. For instance, the set of responses to centripetal ISO trajectories (see Fig. 1) was compared with the set of LPs of the responses to these same trajectories. The comparisons between average proportions of nonlinear interactions (see Fig. 6B) also relied on a permutation test for paired data (each cell provides a set of proportions, one proportion for each condition) with 100,000 repetitions.

Figure 1.

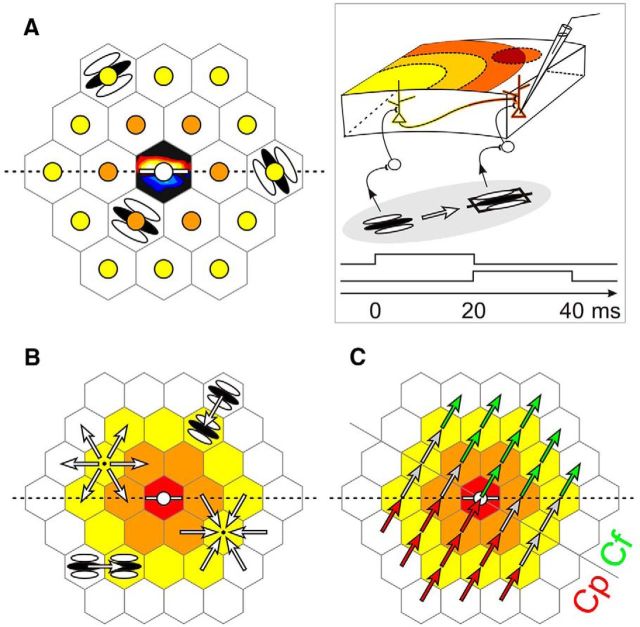
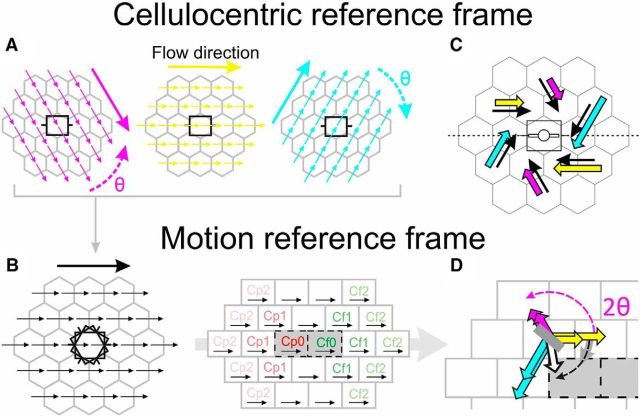
Probing the synaptic integration field. A–C, The visual field was paved with a hexagonal lattice centered on the subthreshold RF. A, The RF is schematized by ON (red) and OFF (blue) subfields overlaid over the central tile (black). The size of the stimuli was chosen to be that of the RF. For each recorded cell, the lattice was positioned with a symmetry axis (dotted line) aligned along the cell's preferred orientation (white bar), represented by convention as the horizontal axis. The size of the hexagonal tiles was also chosen to be that of the RF, so that stimuli flashed in neighboring tiles could not overlap, and peripheral stimuli could not encroach on the RF. These conventions define a cellulocentric reference frame whose polar coordinates (relative eccentricity from the RF center, measured in number of tiles; and orientation from the preferred horizontal axis) are independent of the RF size or the absolute orientation preference of each cell. The “rings” of same relative eccentricity from the RF center are depicted by the colors of nodes or tiles. A, B, Sparse static (1S) and dynamic (2S) AM Gabor noises were applied in a randomly interleaved fashion to measure the static profile of the synaptic association field (S-AF) and its dynamic associative properties (D-AF), respectively. Gabor patches were each flashed for 20 ms. The 20 ms interval between stroke onsets was chosen based on previous reports of apparent horizontal propagation speed in cat V1 (Bringuier et al., 1999), to maintain the horizontal input and the feedforward drive on average in phase (see Box). A, Stimuli of six possible orientations were flashed at each node in the static protocol. Stimuli were presented in isolation, so that the center was not stimulated while peripheral nodes were explored. B, Each possible 2S-AM sequence converging onto or originating from each node was presented in the dynamic protocol, and defined a “trajectory” (white arrows). The 2S stimuli could either be in the ISO configuration (illustrated bottom left) or in the CROSS configuration (illustrated top right). C, A different parametric reading of the dynamic protocol. Acquisition records are grouped by motion flow direction and relative eccentricity of the AM trajectory. Trajectories along which relative eccentricity decreases are centripetal (Cp, in red), whereas those along which relative eccentricity increases are centrifugal (Cf, in green). Box inset, The working hypothesis is that the facilitatory effect of intra-V1 horizontal connectivity is maximal when the feedforward and horizontally mediated synaptic inputs reach in phase the intracellularly recorded cell.

Results

To characterize quantitatively the spatiotemporal properties of the synaptic integration field of visual cortical neurons, we performed long duration (>1 h) intracellular recordings in V1 of the anesthetized and paralyzed cat. Indeed, in vivo intracellular electrophysiology during sensory processing offers the unique possibility of listening to the “synaptic rumor” of the V1 network effectively at work (for review, see Frégnac, 2012), and is thus essential to dissect out the differential influence of the various circuits afferent to V1 cells. The anesthetized cat preparation has therefore crucial advantages as an experimental model. First, performing long duration intracellular recordings is more tractable in the cat than in primates. Furthermore, the spatial extent of horizontal connections intrinsic to V1 has been reported to be much wider in the cat, spanning up to 8–10 mm of cortex and 8–10° of visual angle (Gilbert and Wiesel, 1989; Callaway and Katz, 1990; Kisvárday et al., 1997; but see Martin et al., 2014) than in the nonhuman primate (4 mm and 1°-2° of visual angle) (Angelucci and Bressloff, 2006), making the cat an ideal model for the study of horizontal connectivity.

RFs were typically centered within 5° of the area centralis, and recordings sampled all layers. Reconstructed morphologies from biocytin-labeled neurons were dominantly pyramidal. The present study used a total of 25 cells for which a complete set of parametric conditions could be compared. Because no relationship was found between the results we report hereafter and either the simpleness index of the subthreshold RF or the laminar location, we present the results obtained from the whole population of recorded cells.

Parametric mapping of the synaptic integration field of V1 neurons

We first characterized the minimal subthreshold integration field (MSF): the region of retinal space where the presentation of positive (“ON”) or negative (“OFF) contrast impulses elicits a detectable subthreshold or “synaptic” response (Frégnac and Bringuier, 1996). This synaptic responsive region represents the core of the RF and encompasses the classical minimal discharge field (Barlow et al., 1967; for review, see Bishop and Henry, 1972). Since a recent imaging and intracellular study has shown that the functional bias for iso-preference binding requires a minimal level of input cooperativity to become functionally expressed (Chavane et al., 2011), the stimuli we chose for subsequent protocols were Gabor patches whose diameter covered the whole extent of the MSF (Fig. 1A). Indeed, the spatial period, phase, and orientation of these oriented profiles of luminance fit with the ON- and OFF-subfield arrangement of simple cell RFs (Daugman, 1985), thereby recruiting cortical orientation columns efficiently, which, we reasoned, should facilitate the detection of long-distance synaptic influence. Finally, the preferred orientation of the cell was estimated using the subthreshold tuning curve to the orientation of randomly presented Gabor patches of the chosen diameter (range 2.0°–6.5°, median 4°), and of various orientation, phase, and spatial frequency (Ringach et al., 1997), collapsed across spatial frequencies and phases. Throughout the rest of this paper, we refer to the MSF simply as the cell's RF.

We then paved the surrounding visual field with a hexagonal lattice of possible stimulation nodes (the optimal 2D paving with nonoverlapping discs) and designed two paradigms to explore both “static” and “dynamic” properties of the synaptic integration field of the recorded neurons:

1. In the static paradigm (Fig. 1A), we stimulated a single node at a time (1S stimulus). In this systematic exploration, the node location and the Gabor patch orientation were randomized across trials.

2. The dynamic paradigm (Fig. 1B,C) was designed to test specific predictions from our working hypothesis (see Introduction; Fig. 1, Box). To combine the impact of feedforward and horizontal activation, the “silent” surround was explored using a sparse 2S-AM sequence. Each 2S-AM stimulus consisted of the asynchronous stimulation of two neighboring nodes, defining a vector in visual space, which we will refer to in the text as a “trajectory.” To disambiguate between local feature (orientation) and global feature (motion) processing, two stimulus configurations were studied: the orientations of the two local Gabor elements used to form the AM sequence were either coaligned with the motion path (“ISO” configuration) or orthogonal to it (“CROSS” configuration) (Fig. 1B).

To compare the synaptic responses elicited by the 2S-AM stimulation with their linear prediction computed from the responses to each of the 1S stimuli, the two paradigms (static and dynamic) were interleaved in the same protocol. To avoid temporal interaction between successive stimuli, this protocol was temporally sparse (Nelson, 1991), as each node was stimulated less than once per second on average.

The static association field (S-AF): probing the synaptic response properties in the “silent” surround of V1 RFs

We found that stimulation of the “silent” surround with Gabor patches of the full MSF size could evoke significant synaptic responses even in the far periphery of the RF, up to 10°–12° away from the RF center (Fig. 2). Those peripheral responses were more prominent along the cells' axis of preferred orientation (henceforth “main axis”). Strong responses could also be evoked at nodes outside the main axis (Fig. 2A) and for various Gabor patch orientations, mostly at the closest neighbors to the RF center (first ring [R1] of relative eccentricity). Moreover, because of spatial summation, spiking responses in some cells could also be elicited as far away as 9° from the minimal discharge field center, along the main axis (Fig. 2C). However, responses from the far surround remained subthreshold in most cells.

To reveal the putative structure of functional horizontal interactions, we estimated the preferred stimulus orientation at each node, across our cell population (n = 25). To do this, we performed circular averages (i.e., averages of orientations; see Materials and Methods). We first performed a cell-by-cell analysis where we estimated the preferred stimulus orientation at each node individually for each recorded cell (Fig. 3A). We next sought to average these estimates across the cell population. To lessen the impact from cells which responded approximately equally to all orientations (i.e., with small OSI) at a given node, we weighted each individual orientation preference estimate (θ_k) by its corresponding OSI value (i.e., we chose the OSI value as the r_k for cell k at the node). This population average revealed functional biases in the form of a coherent spatial structure of preferred orientations in the “silent” surround (Fig. 3B). To further illustrate these biases, we collapsed the data across the four quadrants delimited by the main and orthogonal axis to obtain a symmetric version of the structure of preferred orientations in the periphery. Indeed, there is no reason to observe systematic biases between these quadrants because the realignment of the RF axis between cells could have been done clockwise or counterclockwise. The result of this symmetrization (Fig. 3C) revealed a pattern highly similar to the human psychophysical biases in contour perception described by Field et al. (1993).

To quantify how significant this spatial structure is, we modeled it as the sum of a uniform bias for radial orientation and an iso-orientation preference that decreases with relative eccentricity (Fig. 3D). There was no free parameter in this model (see Materials and Methods). Next, we quantified the distance to the model as the sum across relevant nodes of the absolute angular difference between the data and the model. Finally, taking as the null hypothesis that the cells' preferred orientations at relevant nodes are actually random, we built null distributions for the distance to the model. Strikingly, we found that the data in Figure 3, B and C, were both significantly (respectively p = 4 × 10⁻⁵ and p = 10⁻⁴, one-tailed) closer to the model than expected by chance (Fig. 3E), indicating that the systematic functional biases we revealed were robust across our population of V1 cells. The similarity of the model predictions (Fig. 3D) with the experimental data (Figs. 3B,C) was obtained in the absence of a data-driven fitting process, thus validating post hoc the simplicity of the assumptions made to build the model (see Materials and Methods).

We next confirmed this result by performing alternative analyses. Indeed, the analysis proposed above can be decomposed in three steps: Step a, extracting a response strength value from the synaptic response; Step b, computing a preferred orientation at each node; and Step c, averaging across the population. Even though Step a should always precede Step b (we need single response strength values to compute circular averages), Step c can be done at any stage, resulting in two more possible analyses. The results for step sequences (c-a-b) and (a-c-b) were both very similar to those showed here (data not shown). Finally, the response strength (Step a) can be defined either as the peak of the voltage trace, or as the integral of the voltage trace remaining significantly above noise during the response time window. The results using the latter measure (data not shown) were also strikingly similar to those using the former measure (presented above), again pointing at the robustness of the spatial structure of orientation preference in the “silent” surround.

Our systematic exploration of the “silent” surround of V1 cells thus revealed that the subthreshold functional connectivity structure in V1 averaged across the recorded cell population matches in its mean anisotropies the psychophysical biases measured in humans (Kovács and Julesz, 1993; Polat and Sagi, 1993, 1994; Kapadia et al., 1995; Polat and Tyler, 1999) and defined as the perceptual “Association Field” (Field et al., 1993). This represents the first quantification at the synaptic level of the “horizontally” mediated functional connectivity kernel of V1 neurons. It can be seen as the direct neural substrate of the collinear facilitation process predicted by human psychophysics, and thereby validates earlier proposals from our laboratory (Frégnac and Bringuier, 1996; Chavane et al., 2000) It further demonstrates that this built-in bias is present in the anesthetized preparation, independently of attention-related top-down signals (see Discussion).

Evidence for slow intracortical horizontal propagation

Horizontal connections are not the only type of cortical connectivity susceptible to transmit information between distant parts of the visual field. Another plausible substrate, especially in the nonhuman primate, could be feedback projections from higher-order cortical areas onto V1 (Felleman and Van Essen, 1991; Nowak and Bullier, 1997) because of their large degree of spatial spread (Angelucci et al., 2002; their Fig. 9). However, a crucial difference can distinguish feedback projections from horizontal connectivity intrinsic to V1. Indeed, feedforward, feedback, and interhemispheric callosal connections are mediated by fast conducting myelinated axons, whereas horizontal axons tend to become unmyelinated along their gray matter course (Sanides and Hoffmann, 1969). Thus, the intra-V1 horizontal propagation operates at a much slower speed (one to two orders of magnitude) than feedforward or feedback activation (Nurminen and Angelucci, 2014). Consequently, the latency of horizontal inputs should increase with the relative eccentricity of their point of origin, whereas that of feedback inputs should be independent of relative eccentricity.

We thus estimated at each node the latency of responses and studied whether response latency depended on the relative eccentricity of the stimulus from the RF center. Synaptic response latencies were always shortest at the RF center and systematically increased with relative eccentricity of the stimulus from the RF center, measured in degrees of visual angle, often in a linear fashion (Fig. 4C). A linear regression then yielded an estimate of the slope of this linear relationship. The inverse of this slope provided an estimate of the apparent speed of information propagation in retinal space. The estimated propagation speeds ranged typically from 100°/s to 500°/s across our cell population (Fig. 4E), in agreement with previous measurements in our laboratory (Bringuier et al., 1999; their Fig. 4D). Given that the magnification factor decreases with distance from the area centralis (Tusa et al., 1978) (although less strongly in cat than in monkey), and that we observed responses extending over large regions in the visual field, we projected the hexagonal lattice (Fig. 4A) on a flattened map of cat V1 (Fig. 4B) to convert node positions in the visual field into feedforward impact points in cortex. The similarly linear increase of latency with cortical distance (Fig. 4D) yielded putative horizontal propagation speeds in the range of 0.1–0.5 m/s (Fig. 4F). The fact that the same level of variability in propagation estimates was observed using cortical transforms or retinal node coordinates suggests that factors beyond eccentricity and magnification factor (e.g., horizontal axons' possibly nonstraight paths) impact upon effective intracortical propagation speed.

One way to visualize both the dependency of response latency on relative eccentricity and the spatial structure of the S-AF is to use the responses to the 2S-AM stimuli and represent the spatiotemporal gradient of synaptic responses as a tensor (Movie 1). At each node, radial vectors represent the individual 2S-AM responses across time. The read-out map of the vectorial sums of these vectors at each node gives a combined illustration of the gradient of the “spatial hill of sensitivity” (when the modulus of the vectorial sum reaches its maximum) and the “latency basin” of synaptic latencies (see legend for details).

Movie 1.

Download video file ^{(821.7KB, mp4)}

DOI: 10.1523/JNEUROSCI.4492-15.2016.video.1

“Spatial hill of sensitivity” and “latency basin.” This video shows the time course of the subthreshold responses of one example cell to 2S-AM stimuli in the ISO configuration. At any point in time, the magnitude of the blue vectors represents the instantaneous strength of the subthreshold response to the trajectory originating at the node of origin of the blue vector and directed in the direction of the blue vector. Each red vector is the vectorial average of the six blue vectors having their origin at the considered node. The map of red vectors gives a tensorial representation of the cell's response to apparent motion stimuli. From this representation, two results can be visualized simultaneously. First, the “spatial hill of sensitivity” of the synaptic association field: The movie still shows, beneath the numbers, the spatial map of the tensor vectors (played in the movie), frozen in each node at the time where the magnitude of the vectorial sum (in red) reaches its maximal value. All the red vectors point to the core of the RF (yellow star). These red vectors give at each node the magnitude and the direction of the gradient of the “spatial hill of sensitivity” centered on the RF. Second, the “latency basin” of the synaptic association field: The movie still also shows at each node the latency for which the tensor reaches its maximum magnitude. The shortest latency is observed in the RF center. Note the increase of latency with relative eccentricity. VM, Vertical meridian.

In summary, the linear increase of response latency with intracortical distance (or relative eccentricity in the visual field) and the corresponding inferred propagation speeds both confirm our previous proposal that slow horizontal propagation along horizontal projections is the likely neural substrate of the S-AF.

Nonlinear interactions between feedforward and horizontal input

For each cell, the horizontal propagation speed estimated by the linear regression provided an estimate of the temporal delay with which horizontal inputs reached a neighboring node. Across the population, this delay τ was in the range of 5–25 ms (median 16.4 ms) and matched the 20 ms interstimulus asynchrony we chose for 2S-AM stimuli (see also Fig. 7).

Strikingly, the comparison between the actual 2S responses and their linear predictors revealed that for AM sequences at these high speeds (a few 100s of °/s, in the range of saccadic flow), suppression was the exception, and not the rule (for single-cell examples, see Fig. 5). Suppression (i.e., sublinear summation) was mostly limited to the late phase of the response, resulting eventually in more transient responses. When suppression did occur in the early or peak phases of the response, it could often be interpreted as the result of trespassing the spiking threshold (which makes an upper bound that linear predictors can cross but not the actual biological responses). Most responses were additive (linear), and most of the remaining responses showed a significant supralinear summation (i.e., a facilitatory nonlinear interaction) (for the population analysis, see Fig. 6), even at the spiking level (Fig. 5C,D).

Surprisingly, we found that even supralinear subthreshold interactions of apparently modest relative magnitude could translate into a doubling or even tripling of the spiking response strength, as is the case for the cell presented in Figure 5C. Overall, these supralinear interactions could occur across wide parts of the visual field (Fig. 5A) but could also be restricted to only one peripheral position. The most striking such example is presented in Figure 5D: in this cell, a doubling of the peak synaptic response and a spiking response in an otherwise silent cell were elicited for a single trajectory. Interestingly, this centripetal ISO trajectory physically corresponded to fast motion flow along the horizontal meridian and toward the fovea.

To first gain a broad understanding of the dependence of nonlinear interactions on trajectory type (centripetal, centrifugal) and configuration (ISO, CROSS), we computed the peripeak response waveforms averaged across all cells and significant responses (Fig. 6A). We found that the average response was significantly supralinear for both centripetal and centrifugal ISO trajectories around the peak, but that toward the early part of the responses the supralinearity remained strongly significant for centripetal trajectories, whereas it disappeared for centrifugal trajectories. The average responses to CROSS trajectories did not show any significant nonlinearity at any point.

We next investigated the proportion of significant responses where significant nonlinearities occurred (Fig. 6B). We found that the average proportion of supralinear interactions was significantly larger than that of sublinear interactions in the ISO configuration and that this was not the case for the CROSS configuration. There were also more supralinear interactions in the ISO than CROSS configuration. This differential ISO versus CROSS effect was specific to centripetal trajectories, as it was absent for centrifugal trajectories.

Finally, we compared the 2S responses to noncentral trajectories directed along the main axis versus along the two nonmain axes (Fig. 6C) and found that our population of V1 cells integrated peripheral 2S stimuli significantly better along their main axis than along other axes, and that this was specific to the ISO configuration.

In summary, our results suggest that 2S-AM stimulation extends and enhances the response properties seen for a static (1S) stimulation. Responses were most prominent along the main axis and were enhanced through supralinear interactions specifically for centripetal trajectories in the ISO configuration. These two properties suggest that motion at the speed of saccade-induced retinal flow could boost responsiveness by allowing effective temporal interaction between feedforward and horizontally relayed visual activation.

Latency advance induced by pairing in-phase feedforward and horizontal activation

In the early visual system, how early the composite postsynaptic response to AM starts to grow in V1 cells and how fast it reaches spike initiation may have a crucial importance in the way a downstream collector area, such as MT, decodes motion flow (Seriès et al., 2002). We therefore investigated more closely the initial phase of responses to 2S trajectories stimulating the RF center with its preferred orientation and compared the responses to centripetal versus centrifugal trajectories. Indeed, according to our working hypothesis, no interaction should be found between horizontal and feedforward inputs in the early phase of responses to centrifugal central trajectories (those originating from the RF center), whereas for centripetal central trajectories an effect on the early phase of the response is expected if, and only if, the horizontal inputs reach the cell before the feedforward drive does.

We estimated the time needed for horizontal inputs to travel the distance between two nodes by dividing this distance (in °) by the horizontal propagation speed in °/s (Fig. 4E). Subtracting this time τ from 20 ms (the actual time between the two strokes) defined the time lag (Δt) between feedforward drive and horizontal inputs imposed by the two stroke protocol. The ratio between the apparent horizontal propagation speeds and the physical speed of the 2S-AM sequence was also computed for each cell (Fig. 7B). We found that the five cells with a speed ratio <1 (i.e., a negative Δt) indeed did not show any latency difference between centripetal and centrifugal central responses (Fig. 7A, filled squares), providing an important internal control for our working hypothesis. In addition, cells where horizontal inputs preceded or were in phase with the feedforward drive (Δt ≥ 0) showed shorter response latencies to centripetal than to centrifugal central trajectories. The magnitude of this response latency advance increased with the time lag (R² = 0.34, p = 0.028), confirming the link between the properties of the initial phase of responses and the interaction (or lack thereof) between horizontal input and feedforward drive.

To dissect out this effect further, we divided our cell population into three groups. First, we grouped the cells with a negative time lag. Next, because there was no obvious cutoff value across the rest of the cells, we simply divided them into two halves according to the magnitude of their time lags. We then pooled the neuronal responses within each group, using the centrifugal responses as the “feedforward” reference (i.e., normalizing their peak to 1 and realigning their onset latency to 0) (Fig. 7C). This analysis confirmed that cells with negative time lags showed the same initial response to centripetal and centrifugal central trajectories (Fig. 7C, left). Interestingly, we also found that the interaction between horizontal and feedforward inputs was supralinear only for the group of cells having the larger time lags (>5.5 ms) (Fig. 7C, middle and right). This finding supports the interpretation that a minimal integration time is needed to recruit nonlinear voltage-dependent mechanisms recruited by horizontal connectivity, such as the persistent sodium current or NMDA receptor activation (Hirsch and Gilbert, 1991; Frégnac et al., 1996).

Computing the dynamic synaptic association field (D-AF) of V1 neurons

One of the aims of the AM protocol was to explore systematically all possible motion flow directions (Fig. 1C). Because we wanted to dissect out the effect of the motion flow itself, we reorganized the data visualization so that the 2S-AM stimuli all flow along the same motion axis. In other words, for each motion direction, we moved from the retinotopic cellulocentric reference frame defined by the RF (Figs. 1A, 8A) to a new representational framework still centered on the RF center, but realigned with the motion axis, independently of the geometric relation with the orientation preference of the cell (Fig. 8B). Thus, each set of six trajectories invariant by rotation around the RF center (Fig. 8C) will be represented at the same coordinates in the motion-flow reference frame. The properties of each trajectory (centripetal or centrifugal, relative eccentricity) become readily identifiable by their coordinates in this new reference frame (Fig. 8B, right). The reference to absolute retinotopic coordinates is lost when comparing, for the same cell, various motion directions. What becomes the focus of the analysis is the link between motion sensitivity and the trajectory properties, irrespectively of the orientation preference of the cell.

Figure 8.

Computing the D-AF. A, B, Change of reference coordinates, from a cellulocentric (A) to a motion-axis aligned (B) framework. Each of the three (among six) maps illustrated in A can be combined by realigning them (by rotation, θ) such as to share a common motion axis (0°, horizontal arrow) as shown in B (left). B, Horizontal axis indicates the motion axis, and not the cell's preferred orientation. Thus, the new framework combines responses from different parts of the visual field but corresponding to similar trajectories (B, right), defined by rotation invariance around the RF center (C, black arrows). In other words, once in the motion reference frame, the term “trajectory” designates a particular set of coordinates in this new reference frame, which in turn corresponds to the set of trajectories invariant by rotation around the RF center in the cellulocentric reference frame. C, D, Schematic explanation of the D-AF computation. The strength of the responses to a set of six trajectories invariant by rotation around the cell RF (black arrows) is schematically illustrated by the size of the colored arrows (C). The circular average of those responses is then computed in the motion reference frame (D). It consists of the vectorial average (over [−π,π]) of the colored arrows in C given the angle 2 × θ (with θ being the angle depicted in A), and results in the white arrow. The modulus of this sum vector (i.e., |R|) gives the selectivity index of the directional response for this trajectory (illustrated by the size of the gray bar). The angle with the motion flow axis of this sum vector, once divided by 2, gives the preferred RF orientation for the trajectory (orientation of the gray bar, within [−π/2, π/2]): that is, the RF orientation for which the response to the trajectory (in the motion-reference-frame's generic sense) would be maximal. The gray level intensity of the bar denotes the strength of the mean response for the trajectory (normalized to the maximum across trajectories).

In this new reference frame, we set out to investigate the general structure of the recorded cells' responses to 2S-AM. To do this, we performed for each set of six trajectories invariant by rotation in the RF reference frame a circular average of the responses to these six trajectories (Fig. 8C,D). We computed the angle (arg(R)/2, as shown in Fig. 8D) that corresponds to the estimate of the “optimal” RF orientation maximizing the response to this given trajectory, as well as the robustness (|R|) of the circular average (i.e., the tuning tightness for that orientation estimate). This computation represents the converse of that used for the S-AF: we looked at the preferred stimulus orientation at a given node in the RF reference frame, whereas for the D-AF we are looking at the preferred RF orientation for a given AM trajectory in the motion reference frame. The result quantifies how the visual flow is globally integrated by V1 cells.

This seemingly artificial computation has an obvious computational interest: it allows to establish a linear prediction of how V1 would respond to a full field motion flow. Let us assume that all the recorded cells cover uniformly the parafoveal and central visual field and that the global population orientation preference distribution of recorded cells is uniform. Under such assumptions, the computation shown in Figure 8 would be equivalent to the convolution of the retinal flow with an idealized average ensemble of hypercolumns (integrating distributed flow information over orientation and retinotopic space). This measure can be seen as the linear prediction of the V1 network response to a directional (energy) impulse applied to the whole retina, and hence characterizes its global axial flow sensitivity. This linear prediction can be eventually matched with psychophysical measurements (see Discussion).

Figure 9A represents the result for the three example cells shown in Figures 2 and 5, while Figure 9B shows the average of the single-cell D-AF across the population. The preferred RF orientation was robustly aligned along the central motion flow axis in the ISO configuration, and orthogonal to it in the CROSS configuration for the two trajectories stimulating the RF center, mirroring in both cases the local orientation attribute of the Gabor patch used to produce the AM trajectory. Weaker responses in the periphery translated in weaker robustness of the circular average with relative eccentricity, but, for the ISO configuration, with an anisotropy maintained along the central motion flow axis (e.g., compare the size of the bars between the Cp1 trajectory on the motion axis and the two Cp1 trajectories off the motion axis), as may have been expected from Figure 6C (left). These observations were robust and held when using response integrals instead of peak responses, or performing alternative analyses methods (data not shown).

Peculiarly, the almost trivial dominance of local feature selectivity, which was obvious for the two trajectories stimulating the RF, broke down when looking at the preferred RF orientation for the centripetal radial trajectory from the second to the first relative eccentricity rings (Cp1, on-axis) in the CROSS configuration. Indeed, depending on the cell, the preferred RF orientation for this CROSS trajectory could sometimes be collinear to the motion axis (i.e., orthogonal to what would be expected if the response was dictated by the sole dependency on orientation, a local feature), as in cells 2 and 3 in Figure 9A, and (weakly) across the population (Fig. 9B). Especially for this trajectory, motion seemed to sizably compete with orientation selectivity to define the response properties.

This prompted us to look more closely at the balance between fast motion-flow sensitivity (a “dynamic” global feature requiring combined integration of form and axial motion) and orientation selectivity (a “static” local feature depending only on the stimulus attribute) in defining the response properties to each AM trajectory. To do this, we first averaged the preferred RF orientation for the ISO configuration with that for the CROSS configuration, for each trajectory and on a cell-by-cell basis. In other words, we first summed for each cell the maps for the ISO and CROSS configurations (Fig. 9A). Then, we performed a grand (circular) average, across the population, of the resulting orientation, whose result is shown in Figure 9C. Indeed, if the preferred RF orientation for the ISO configuration is orthogonal to that for the CROSS configuration (i.e., if it mirrors the relationship between Gabor patch orientation in the ISO vs CROSS configurations, Δθ = π/2), then the circular average of the two will be equal to 0 (e^2iθ + e^2i(θ+π/2) = 0). Meanwhile, when these two orientations are identical (i.e., when the motion-flow dominates the response properties to the trajectory), the modulus of the circular average (|R|) will be equal to 1. With this analysis, we found that only the two central trajectories have properties strongly dominated by the local orientation preference (for both: p < 10⁻⁵, one-tailed, under the null hypothesis that there is no systematic relationship between ISO and CROSS preferred RF orientations). On the other hand, the on-axis Cp1 trajectory is the most influenced by the global motion flow (|R| = 0.326). Interestingly, the gray bar is horizontal, indicating that this influence was especially exerted along the main axis for this trajectory (i.e., when fast axial motion points toward the RF center while remaining confined in the “silent” surround).

These latter findings have an important functional implication because they show that global motion sensitivity for fast stimuli is present in V1 cells and enhanced by collinearity in local feature processing. In summary, our results show that V1 neurons integrate saccadic speed motion in the ISO configuration better than in the CROSS configuration along almost any trajectory but that they do so most efficiently and robustly along their main axis.

Discussion

The horizontal propagation of activity, or “traveling waves,” on which our working hypothesis rests, is a well-documented hallmark of intrinsic cortical computation: ongoing and evoked traveling waves have been reported in both anesthetized and awake animals, in a wide variety of species, and even across several sensory modalities (for review, see Sato et al., 2012; Frégnac, 2012; Frégnac and Bathellier, 2015). These traveling waves are thought to be carried by horizontal connectivity intrinsic to V1, as the response latency gradient with relative eccentricity (Fig. 4) (Bringuier et al., 1999), and their systematic presence, even under (sometimes deep) anesthesia, do not accommodate well with feedback projections from higher cortical areas, the only other possible substrate of traveling waves. Moreover, the range of horizontal propagation speeds (0.1–0.5 m/s) we report in this study matches precisely that found by other experimenters in local field potentials and VSD studies of horizontal propagation in vivo. Direct in vitro measurements of activity propagation along horizontal connections in cat V1 (Hirsch and Gilbert, 1991) also reported a speed of ∼0.3 m/s, in contrast to the feedback from V2 or MT whose conduction speed is as fast as that of feedforward connections (2 m/s in Nowak and Bullier, 1997).

Horizontal projections intrinsic to V1 have long been proposed to be the neural substrate of low-level “pop-out” perception. However, this hypothesis relies almost exclusively on anatomical correlates in cats and ferrets, electrophysiological studies of center-surround interactions in cats and monkeys, and indirect inferences from human psychophysics. A complete characterization of the direct influence from the “silent” surround and its synaptic nature was still missing, and the present study thus provides the first (to our knowledge) systematic investigation of subthreshold (synaptic) response properties to elementary stimuli presented in sparse mode one at a time and at random locations in the “silent” surround of V1 RFs.

Our results reveal at the population level a functional structure in the synaptic inputs to V1 cells from the “silent” surround, whereby neurons receive predominantly iso-oriented inputs from neighboring V1 hypercolumns, and gradually weaker and more radially biased inputs the further away from the RF center (Fig. 3C). This structure mirrors exactly that of the perceptual “association field” for collinear contours described in human psychophysics (Field et al., 1993; Polat and Sagi, 1993). But what could be the specific neural substrates of such functional bias? The fact that horizontal connections specifically link distant cortical columns sharing the same preferred orientation is well documented by anatomicofunctional studies in ferrets (Bosking et al., 1997) and cats (Gilbert and Wiesel, 1989; Callaway and Katz, 1990; Kisvárday et al., 1997; Schmidt et al., 1997; but see Martin et al., 2014), providing a straightforward putative substrate for the iso-orientation preference bias. The radial bias in the model, on the other hand, has not been reported in the anatomical pattern of horizontal connectivity. However, a radial bias in the distribution of preferred orientations in V1 has been documented in cats (e.g., Leventhal, 1983) and more recently in humans with fMRI (e.g., Sasaki et al., 2006). Together with the recent finding with VSD imaging of nonspecific radial propagation over long distances (several hypercolumns) in cat V1 (Chavane et al., 2011), and the fact that most receptive fields were recorded in the parafoveal region of the visual field, this could provide a substrate for the weak radial orientation bias component we found for synaptic responses in the far “silent” surround.

To dissect out the impact of traveling waves on the associative properties of synaptic integration, we used double-stroke stimuli flashed in rapid succession in neighboring hypercolumns, where the feedforward drive evoked by the second Gabor patch reached the retinotopically corresponding V1 cells at the same time as the intra-V1 traveling wave that was elicited by the first stroke. We found that, when, and only when, the horizontal wave (H) arrived slightly ahead of time (>5 ms) of the second feedforward volley (FF), indirect (H) and direct (FF) synaptic inputs summed supralinearly in the recorded cell, resulting in both an earlier onset of the composite response and an amplitude boost relative to the linear prediction (computed by simple summation of single stroke synaptic responses). This nonlinear effect was specific to ISO (collinear) centripetal sequences of Gabor patches, and thus constitutes a possible neural correlate as early as V1 of a human psychophysical bias in motion flow detection: collinear sequences (ISO) are perceived as moving “faster” than cross-oriented (CROSS) configuration sequences (Georges et al., 2002). Most remarkably, the boosting mechanism revealed intracellularly confirmed the computational prediction of an earlier model (Seriès et al., 2002).

Importantly, our data were collected in the anesthetized cortex, using stimuli of low contrast when stimulating the RF center, stimuli whose size covered the whole extent of the aggregate RF of a V1 hypercolumn. These conditions are those ideal to measure horizontal propagation of activity and its functional properties (Kitano et al., 1994; Chavane et al., 2011; Nauhaus et al., 2012), and allowed us to reveal functional facilitatory properties that have up to now eluded many investigators (but see Sillito et al., 1995; Polat et al., 1998). Our findings do not argue against a role of top-down attentional gain control from higher cortical areas during attentive wakefulness (Li et al., 2006, 2008): this gain control could be required to express and/or amplify during attentive wakefulness the intrinsic functional properties we have documented at the subthreshold level in this study. However, we reveal here a preexisting structural bias that could constitute the synaptic footprint of the neural architecture needed to implement Gestalt laws, and which is detectable in the anesthetized brain by averaging synaptic visual responses across cells once their RF location and orientation axis have been realigned. This last point is of importance because this “mean field” effect is seen only occasionally at the single-cell level (e.g., as in Fig. 3A) due to the intrinsic diversity of V1 cells functional repertoires and the mV scale of individual synaptic responses. In summary, using intracellular recordings in the anesthetized cat, we provide, for the first time, definitive evidence for two synaptic correlates of low-level perception, closely dependent on the spatiotemporal features of the synaptic integration field of V1 neurons, and likely carried by horizontal connectivity intrinsic to V1.

Remarkably, the range of visual flow speed corresponding to horizontal propagation within cortex (∼100s of °/s) matches exactly that of visual flow generated during saccadic eye movements. In contrast, these speeds are hardly ever experienced with motion of natural objects and are also much faster than those for which the “motion streak” effect has been described (<10°/s in Geisler, 1999). We can therefore conjecture that the architecture we have described in V1 plays a role during saccadic vision. What could this role be, and what are the implications for motion flow detection in V1?

Humans are estimated to spend several hours a day performing saccades or microsaccades (Melcher and Colby, 2008), yet the perception of static brief stimuli flashed during saccades is known to be greatly disturbed (Zuber and Stark, 1966; Ross et al., 1997; Hafed, 2013). Neural processing in V1, however, remains largely preserved during saccades (Nakamura and Colby, 2002). Therefore, using conscious reports of stimuli briefly presented during saccades might not be the right experimental paradigm to uncover the function, if any, performed by V1 during saccades. Instead, we suggest the intriguing, though quite provocative, possibility that V1 cells can operate in two modes of motion integration: the classical integration across the RF width during slow motion or fixation (Hubel and Wiesel, 1962; Orban, 1984), and the collinear-motion integration along the main axis for saccadic speeds (Judge et al., 1980; the present results). The latter mode operates well beyond the upper range of the motion-streak framework of Geisler (1999).

This possibility is supported by the finding that most saccades occur along the cardinal axes (Foulsham et al., 2008; Foulsham and Kingstone, 2010), reflecting both the statistics in natural (including indoors) images (Coppola et al., 1998), and the known (static) cardinal bias, or “oblique effect,” found in both human psychophysics and fMRI (Mansfield, 1974; Orban et al., 1984; Furmanski and Engel, 2000). Interestingly, Foulsham et al. (2008) showed that the cardinal bias in saccade directions is fixed in the image reference frame, as it changes instantly when rotating natural images, so that saccades remain most common along the horizontal and vertical axes of the rotated images. This suggests that saccades tend to follow the edges in images (Yarbus, 1967), which would result in collinear motion integration during saccades along these edges, and in turn elicit strong responses in V1 cells. The spatial anisotropy in flow integration along the main RF axis could furthermore account for the absence of saccadic suppression in the lower range of spatial frequencies reported by psychophysical measurements in humans (Castet and Masson, 2000). One obvious functional prediction from our results is that increasing speed motion to the saccadic range should flip the axial motion sensitivity of V1 RFs by 90°. Such a functional switch has been reported at the mesoscopic level by a recent imaging study: orientation preference map patterns evoked by motion-only stimuli had a 90° orientation difference when this motion was below versus >15°/s in nonhuman primate V1 (An et al., 2014).

These two different modes of operation could be reflected in separate prior expectations for visual speed: a prior for slow speeds during fixations versus one for saccadic speeds during saccades. This would reconcile seemingly conflicting reports of a low-contrast perceptual bias for slow speeds at slow speeds and for high speeds at higher speeds (e.g., Thompson et al., 2006; Stocker and Simoncelli, 2006). These different prior expectations could be implemented at the neural level by separate mechanisms: recurrent connectivity for slow speeds and horizontal connectivity for saccadic speeds. Consistent with this idea, we found in the cases where we could run our protocol for different stimulus contrasts that increasing the contrast tended to decrease the latency difference between centripetal and centrifugal responses, as well as the amount of facilitatory nonlinear interactions (data not shown). These observations agree with optimal Bayesian inference, whereby increasing contrast (i.e., the reliability of the evidence) decreases the relative influence of the prior expectation on the final posterior probability distribution.

In this way, the horizontal propagation of activity could embody an elementary form of collective predictive belief broadcast to distant parts of the network, reminiscent of the psychophysical Gestalt principles of, for example, common fate and axial collinearity (for review, see Wagemans et al., 2012). When this predictive belief matches the evidence, strong responses would occur, which could provide landmarks for visual stability across saccades and/or facilitate anticipatory responses (described at the spiking level in higher visual cortical areas in Duhamel et al., 1992) when acquiring a new target along a saccadic trajectory collinear to the orientation preference of the recorded cell (Judge et al., 1980; their Fig. 1). As a whole, our study thus supports the new concept of a Dynamic synaptic Association Field in V1 neurons, whose spatial extent and anisotropy passively adapt to the retinal flow changes during natural visuomotor exploration.