Engagement of the Rat Hindlimb Motor Cortex across Natural Locomotor Behaviors

Abstract

Contrary to cats and primates, cortical contribution to hindlimb locomotor movements is not critical in rats. However, the importance of the motor cortex to regain locomotion after neurological disorders in rats suggests that cortical engagement in hindlimb motor control may depend on the behavioral context. To investigate this possibility, we recorded whole-body kinematics, muscle synergies, and hindlimb motor cortex modulation in freely moving rats performing a range of natural locomotor procedures. We found that the activation of hindlimb motor cortex preceded gait initiation. During overground locomotion, the motor cortex exhibited consistent neuronal population responses that were synchronized with the spatiotemporal activation of hindlimb motoneurons. Behaviors requiring enhanced muscle activity or skilled paw placement correlated with substantial adjustment in neuronal population responses. In contrast, all rats exhibited a reduction of cortical activity during more automated behavior, such as stepping on a treadmill. Despite the facultative role of the motor cortex in the production of locomotion in rats, these results show that the encoding of hindlimb features in motor cortex dynamics is comparable in rats and cats. However, the extent of motor cortex modulations appears linked to the degree of volitional engagement and complexity of the task, reemphasizing the importance of goal-directed behaviors for motor control studies, rehabilitation, and neuroprosthetics.

SIGNIFICANCE STATEMENT We mapped the neuronal population responses in the hindlimb motor cortex to hindlimb kinematics and hindlimb muscle synergies across a spectrum of natural locomotion behaviors. Robust task-specific neuronal population responses revealed that the rat motor cortex displays similar modulation as other mammals during locomotion. However, the reduced motor cortex activity during more automated behaviors suggests a relationship between the degree of engagement and task complexity. This relationship emphasizes the importance of the behavioral procedure to engage the motor cortex during motor control studies, gait rehabilitation, and locomotor neuroprosthetic developments in rats.

Introduction

Motor cortex dynamics underlying forelimb movements have been extensively studied in rodents, cats, and primates. These studies revealed that motor cortex dynamics encode abstract features of movements, such as force, direction, position, and velocity (Hatsopoulos and Donoghue, 2009; Nicolelis and Lebedev, 2009; Shenoy and Carmena, 2014). Cortical dynamics underlying locomotion have also been studied from recordings of the forelimb motor cortex, primarily in cats (Table 1 highlights prior experiments on quadrupedal locomotion). These studies showed that the motor cortex exhibits reproducible neuronal responses over the gait cycle. This modulation typically peaked during swing and sharply increased during precision walking (Drew et al., 2002, 2008; Beloozerova et al., 2010; Drew and Marigold, 2015).

Table 1.

Prior experiments that studied cortical activity during quadrupedal locomotion^a

Authors	Year	Species	Cortical area	Limb studied	Freely-moving	Paradigm(s)
Armstrong and Drew (a,b)	1984	Cat	86% forelimb; 14% hindlimb	Forelimb	Yes	Treadmill
Drew	1988	Cat	Forelimb	Forelimb	Yes	Obstacles on treadmill
Beloozerova et al.	1993, 2010	Cat	Forelimb	Forelimb	Yes	Overground versus ladders
Widajewicz et al.	1994	Cat	Hindlimb	Hindlimb	Yes	Obstacles on treadmill
Beloozerova et al.	2005	Cat	61% forelimb; 39% hindlimb	Posture	Yes	Standing on platform
Karayannidou et al.	2009	Cat	52% forelimb; 48% hindlimb	Forelimb and hindlimb	Yesb	Posture, walking on tilting versus nontilting treadmill
Song et al.	2009, 2011	Rat	Hindlimb/trunk	Hindlimb	No	Treadmill
Foster et al.	2014	Rhesus	PMd	Forelimb	Yes	Treadmill
Yin et al.	2014	Rhesus	Hindlimb	hindlimb	Yes	Overground; treadmill
Current article	2016	Rat	Hindlimb	Hindlimb	Yes	Overground versus treadmill; overground versus stairs; overground versus ladder

^aStudies have been grouped by experimental procedures. Fitzsimmons et al. (2009) and Rigosa et al. (2015) were both excluded because recordings were obtained during bipedal locomotion.

^bStudy authors noted that the cats stabilized their head position relative to feeder.

Compared with the forelimb, our knowledge of hindlimb motor cortex properties during locomotion is more restricted (Table 1). Indeed, this knowledge is conspicuously limited in rats, although rodents are the most commonly used animal models for neuroscience and therapeutic developments. Previous work suggested that cortical contribution to the production of hindlimb movements is unnecessary in rodents, especially during locomotion because this behavior can be largely controlled subcortically in this species (Orlovsky et al., 1999; Stuart and Hultborn, 2008). Yet, this facultative role of the motor cortex does not preclude the encoding of hindlimb features in motor cortex dynamics. In rats, hindlimb motor cortex has been studied during a button-pressing task (Manohar et al., 2012), during stepping on a treadmill while attached to a robotic loading and brain-machine interface system (Song and Giszter, 2011; Song et al., 2015), and during robot-assisted bipedal walking (Rigosa et al., 2015). These studies decoded ballistic events, interaction forces with the robot, gait timing, and kinematics from cortical activity. These studies showed that the hindlimb motor cortex displays modulation in rats under specific, well-controlled conditions.

In ecological settings, rodents exhibit bouts of locomotion to reach targets, often climb over obstacles, walk along uneven terrains, and display varying velocities. These ecological locomotor activities differ from the behavioral procedures predominantly used to study locomotion and develop therapeutic treatments in rats, which are generally limited to treadmill-restricted stepping behaviors. These paradigms lack essential components underlying natural locomotion, including visual flow, self-selected pace, and volitional movement. These features impact motor cortex activity in cats (Beloozerova and Sirota, 1993; Drew et al., 2002), but the impact of these task-specific behavioral cues on hindlimb motor cortex dynamics have not been studied in rats.

Here, we investigated the impact of behavioral context on hindlimb motor cortex activity during locomotion in rats. To address this question, we established a recording platform that allowed recording of spiking activity from neuronal ensembles in conjunction with hindlimb muscle synergies and whole-body kinematics in freely moving rats performing a broad range of natural locomotor behaviors. We found that the hindlimb motor cortex of rats anticipates gait initiation and exhibits robust neuronal population responses that closely parallel the modulation of hindlimb kinematics and muscle activity during locomotion. Moreover, motor cortex activity reorganized during tasks requiring enhanced muscle activity or precise paw placement, as previously documented in cats. In contrast, the motor cortex was less engaged during more automated behaviors, such as stepping on a treadmill. These results stress the importance of establishing behavioral procedures requiring volitional components to study hindlimb motor control, to develop gait rehabilitation interventions, and to design locomotor neuroprostheses.

Materials and Methods

Animal training and behavioral procedures.

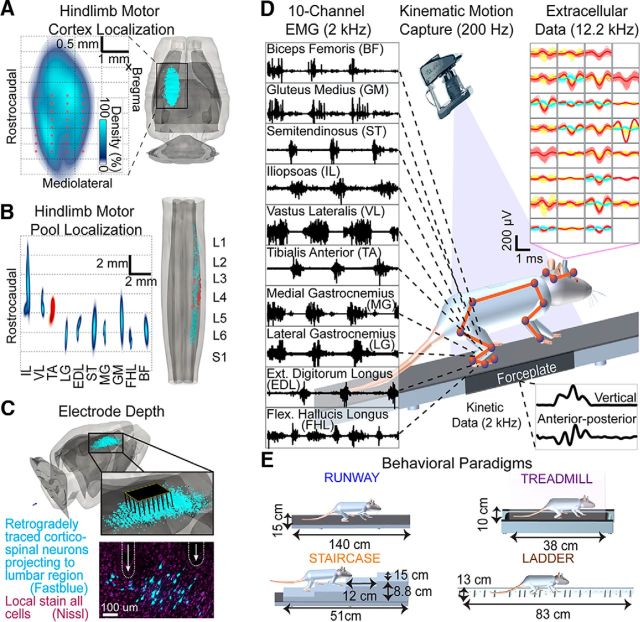
The Veterinarian Office of the canton of Vaud, Switzerland, approved all experimental and surgical procedures. Two cohorts of 8 adult female Lewis rats each (∼225 g) participated in this study. Rats were trained 5 d per week for 2 months to perform the tested behavioral procedures. The first cohort was trained to walk across a straight runway to reach a reward. Chocolate yogurt was delivered on a variable-interval schedule, typically every 2–4 trials. They were also trained to produce continuous stepping on a treadmill. Chocolate yogurt was given after each trial, which lasted ∼60 s. Finally, rats were tested walking over a ladder with irregularly spaced rungs (without prior training). In this first cohort, no rats were excluded for hardware, behavior, or health issues on the day of treadmill recording; thus, the overground-treadmill cohort size was composed of 8 rats. Only 6 of the 8 rats performed a sufficient number of continuous steps on the ladder (2 rats were excluded for inconsistent behavior). The second cohort was trained to traverse the runway and climb a staircase. The yogurt reward schedule on the ladder and stairs was the same as the straight runway. Rats in this cohort were also tested during voluntary, self-initiation of gait along the straight runway, without any cue. Rats initiated locomotion from a quadrupedal standing posture. We only analyzed trials during which gait was initiated with the right hindlimb. In this cohort, 3 rats had to be excluded due to hardware deficiencies (muscle or brain implants) or health (infection) issues; thus, the overground-stairs and initiation cohort size was composed of 5 rats. For all rats, all data from a single day were processed together, which allowed for a direct comparison between tasks. The dimensions of each paradigm are reported in Figure 1.

Figure 1.

Anatomical experiments and recording conditions. A, The 3D anatomical reconstruction of corticospinal and motor neuron locations. Density and location of retrogradely traced corticospinal neurons following FastBlue injections into lumbar segments. Red dots represent average electrode locations. B, Density and location of retrogradely traced motor neurons following Fluorogold injections into hindlimb muscles. The tibialis anterior served as an anatomical landmark to align tracing from multiple rats. C, The 3D representation of the 32 electrode array inserted into layer V of cortical territories projecting to lumbar segments. The photograph represents the location of two electrode tips in the vicinity of corticospinal neurons projecting to lumbar segments from a single rat. D, EMG activity recorded from right hindlimb muscles during locomotion. Twelve high-resolution cameras monitored the 3D displacements of reflective markers to measure bilateral limb and head kinematics. Single-unit and multiunit activity was extracted from extracellular recordings in the left cortex. Each panel represents an electrode. A distinct color represents each sorted unit. Ground reaction forces were monitored during overground gait initiation. E, Characteristics of the locomotor paradigms; rung spacing on the ladder was irregular.

Surgical procedures.

Surgical procedures have been described previously (van den Brand et al., 2012) and were performed under full general anesthesia with isoflurane in oxygen-enriched air (1%–2%). Briefly, a 32 channel microwire array (Tucker-Davis Technologies, RRID:SCR_006495) was inserted stereotaxically (array center at −1.75, 2.25 mm; Fig. 1A) into the layer V (average depth 1.54 mm; see Fig. 1C) of the left cortical region containing neurons directly projecting to lumbar segments. The microwire array is 8 × 4 with 0.25 mm and 0.375 mm row and column spacing, respectively; each microwire diameter is 0.05 mm. Only the wire tips, which are cut at 30 degrees, are noninsulated. These electrodes have a manufacturer-specified average impedance of 20 kOhm in saline at the time of manufacturing. During the same surgery, bipolar electrodes were implanted into 10 flexor and extensor muscles spanning each joint of the right hindlimb to record EMG activity. The following muscles were implanted: gluteus medius (GM), iliopsoas (IL), vastus lateralis (VL), semitendinosus (ST), biceps femoris (BF), gastrocnemius medialis (MG), gastrocnemius lateralis (LG), tibialis anterior (TA), extensor digitorum longus (EDL), and flexor hallucis longus (FHL). Four rats of the first cohort had only two muscles implanted per hindlimb: gastrocnemius medialis and tibialis anterior. Electrode locations were verified postmortem.

Anatomical localization of motoneurons and corticospinal tract neurons.

A separate cohort of Lewis rats (n = 20) received injections of Fluorogold (2% in sterile saline, 30–80 μl per muscle) into the tibialis anterior and into one of the recorded muscles. The location of labeled motoneurons was reconstructed using Neurolucida (MBF Bioscience, RRID:SCR_001775). To merge reconstruction from several rats into a unified digital library, the tibialis anterior motor column was used as a landmark in each rat (Fig. 1B). To label corticospinal neurons projecting to lumbar segments, the retrograde tracer Fastblue (2% in 0.1 m phosphate buffer and 2% DMSO) was infused unilaterally into each segment spanning L1-L6. A total of 1.6 μl was pressure-injected over four sites for each segment (depth 1.5 mm). The stereotaxic location of retrogradely labeled pyramidal cells was reconstructed using Neurolucida.

Multimodal recording platform.

Whole-body kinematics were recorded using a high-speed motion capture system (Vicon Motion Systems), combining 12 infrared cameras (200 Hz). A total of 23 reflective markers were attached bilaterally overlying anatomical landmarks of the hindlimbs, forelimbs, and head. The 3D position of the markers was reconstructed offline using Vicon Nexus software. The body was modeled as an interconnected chain of rigid segments and joint angles were generated accordingly. The main limb axis termed “hindlimb” in the figures was defined as the virtual line connecting the greater trochanter to the lateral malleolus (Ivanenko et al., 2008). The EMG signals (2 kHz) were amplified, filtered (10–1000 Hz bandpass), stored, and analyzed off-line. Ground reaction forces (2 kHz) in the vertical, anterior–posterior, and mediolateral directions were monitored during overground gait initiation using a force plate (HE6X6, AMTI) located below the rat. An electrophysiology workstation (Tucker-Davis Technologies, RZ2, RRID:SCR_006495) captured raw neural data at 12.2 kHz. The platform is shown in Figure 1D with representative signals in Movie 1. We aimed to study neuronal ensemble activity and thus placed the microwire array centrally within the hindlimb sensorimotor cortex. Therefore, we did not differentiate between (nor identify) pyramidal, corticostriatal, interneurons, or other cell types located in the same area. We implemented a computational pipeline to derive global and detailed features from kinematics, kinetics, muscle activity, and cortical neuronal modulation across the behavioral procedures.

Movie 1.

Download video file ^{(3.4MB, mp4)}

DOI: 10.1523/JNEUROSCI.4343-15.2016.video.1

Multimodal recording platform for freely walking rats. Representative kinematic, muscular, and cortical raw signals and extracted features.

Raw data processing.

The analyzed gait cycles were selected based on inclusion criteria. Each trial was manually curated to exclude any step comprising recording artifacts or during which rats did not step continuously (11.1% of all steps). To satisfy this criterion, all initial or final steps of overground locomotion were also automatically excluded. Any steps after a pause or stopping during stepping on a treadmill were excluded for the same reason (13.2% of analyzed steps were excluded). The number of gait cycles analyzed per rat was 26 ± 7 steps on the runway and 65 ± 24 steps on the treadmill (mean ± SD). These steps were selected from an average of 11.1 ± 1.1 trials and 3.9 ± 0.8 trials on the runway and treadmill, respectively. To allow for direct comparison between the runway and treadmill, we normalized the duration of each phase of gait. The ends of the stance and swing phases were fixed at 70% and 100% of the gait cycle duration, respectively, by scaling each stance and swing phase independently. The number of gait cycles analyzed per rat was 36 ± 7 steps on the runway and 44 ± 12 steps on the ladder (mean ± SD). These steps were selected from an average of 10.7 ± 2.3 trials and 17.7 ± 4.2 trials on the runway and ladder, respectively. The time normalization was the same as the runway-treadmill comparison. We recorded 8 ± 1 gait initiation attempts per rat, which resulted in a total of 31 (75.6% of all initiations) gait initiations during which the hindlimb contralateral to cortical recordings was the first hindlimb to move. In all included gait initiation sequences, the rats supported their entire body weight on all four limbs while standing on the force plate before initiation. In the second cohort, the number of gait cycles analyzed per rat was 25 ± 7 steps on the runway and 26 ± 3 steps on the stairs (mean ± SD). These steps were selected from an average of 10.6 ± 1.3 trials and 11.2 ± 1.8 trials on the runway and stairs, respectively.

For all rats and behaviors, we recorded the maximal number of trials per day (balanced across both tasks) such that the rats continued to perform the tasks. This corresponded to ∼40 min of testing per rat, including a 5 min stoppage when switching tasks.

Neural signal processing.

Neural signals passed through a wavelet bank filter to reduce background noise (Citi et al., 2008); a wavelet representation detected spike events (Nenadic and Burdick, 2005). We implemented an automated algorithm based on superparamagnetic clustering to classify these spikes (Fig. 2) into single units and multiunits (Quiroga et al., 2004). The waveform shape and interspike interval histograms of the sorted units were visually verified. The minimum acceptable interspike interval time was 2 ms; <6% of spikes had interspike interval between 2 and 5 ms. The signal-to-noise ratio of all identified units was 3.51 ± 0.48. The signal was calculated using the peak-to-peak amplitude of the identified units. The noise was calculated by estimating the peak-to-peak value of the first and final two samples of all spike events on each electrode.

Figure 2.

Neural processing framework. A, Color-coded decomposition of hindlimb movement during two successive gait cycles along the runway. B, Statistical test to define neuronal activation. The distribution shown is resting firing rates for a particular neuron. Activation is defined based on whether the sampled firing rate during locomotion is inside (nonmodulated, gray) or outside (active, blue) the 95% confidence intervals of the resting firing rate distribution for that neuron. C, Distributions of changes in firing rates (the resting firing rate for each neuron has been subtracted) for active neurons (blue) versus nonmodulated neurons (in light gray) during locomotion (left histogram). Distributions of modulation depths (maximum − minimum fitted firing rate) over the gait cycle during locomotion (right). Pie chart represents the percentage of active neurons during locomotion (n = 13 rats). D, Raw extracellular data from the contralateral cortex for the same gait cycles, including two sorted units (±SD) from this electrode. Raster plots from all electrodes are shown below. E, Color-coded change in firing rate with respect to quiet standing (±95% confidence intervals) for three representative units that were statistically classified as active (upregulated or downregulated) or nonmodulated during gait. Numbers refer to the raster plot in D. F, Ensemble firing rate obtained by averaging firing rates of all active neurons over the gait cycle for a single rat. G, Firing rates of active neurons are normalized and sorted by peak firing time. H, Distribution of peak firing time showing the number of neurons peaking at a given time of the gait cycle.

All units from a single day were processed together, which allowed for a direct comparison between tasks. Firing rates were estimated using the following procedure for each sorted unit: (1) action potentials within a gait cycle are converted to a time-base of percentage of gait cycle; (2) all gait cycles are compiled together; (3) firing rate is estimated in nonoverlapping, ΔC% (ΔC is equivalent to 25 ms in gait cycle percentage based on the average gait cycle duration) bins; and (4) this firing rate is fitted with a Bayesian Adaptive Regression Splines (BARS) (Dimatteo et al., 2001) (Fig. 2E). The Ensemble Firing Rate was calculated as the average of fits for all neurons that were active in either behavioral procedure (see Time normalization during fitting). The cohort ensemble firing rate is the average of fits across all rats (Fig. 2F). To combine active neurons within unified cohort modulation maps (Fig. 2G), each neuron was first normalized to its absolute maximum firing rate across both behavioral procedures recorded on the same day (i.e., overground vs treadmill, overground vs ladder, or overground vs stairs). Fits were organized within each behavioral procedure to position neurons with earlier peak firing at the bottom of the map. The empirical distribution of firing rate peaks was calculated for 10% bins of the gait cycle (Fig. 2H).

Time normalization during fitting.

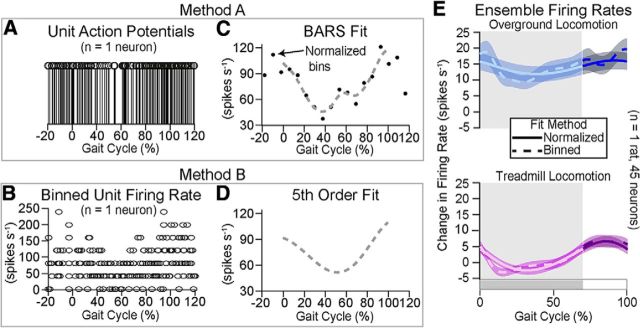
We evaluated two methods to convert neural firing into percentage of the gait cycle.

Method B (estimating firing rate once per gait cycle and then apply fitting): (1) firing rates within each gait cycle (±100 ms) were estimated using 25 ms, nonoverlapping bins, i.e., (no. of action potentials)/0.025 s; (2) firing estimates from each gait cycle were converted from time (e.g., 0, 25, 50 ms) to percentage of gait cycle, and then all gait cycles were compiled together (Fig. 3B); and (3) a fifth-order polynomial fit was calculated for over these compiled firing rates, as shown in the fitted firing rate for the sorted unit (Fig. 3D).

Figure 3.

Comparing methods for fitting neuronal modulations. We compared two approaches for resolving time normalization between gait cycles (A) All action potentials were converted to a percentage of the gait cycle they occurred in. Here, they are concatenated over all gait cycles (n = 13) for one neuron (Method A). B, Alternatively, firing rates were estimated within each gait cycle using nonoverlapping 25 ms bins of action potentials (Method B). C, Normalized firing rates (black dots) were estimated from (A) using nonoverlapping ΔC percentage bins of action potentials. A BARS fit (gray dashed line) was calculated over these firing rate estimates. D, Alternatively, a fifth order polynomial fit (gray dashed line) was applied over the binned firing rates in (B). E, The ensemble firing rate was calculated by averaging all fits for a representative rat during stepping on a treadmill (purple) and overground (blue).

Method A (time normalization time before estimating the firing rate once over all gait cycles and then apply fitting): (1) action potentials within each gait cycle (±100 ms) were converted to percentage (Fig. 3A) of gait cycle: by gait cycle (0–100%) for the runway versus stairs; or by stance (0%–70%) and swing (70–100%) for runway versus treadmill and runway versus ladder comparisons; (2) based on the average gait cycle length, the change in percentage (ΔC) corresponding to 25 ms time bins was calculated; (3) firing rates were estimated (Fig. 3C, black dots) within the 25 ms, nonoverlapping bins on all the action potentials compiled from all gait cycles; and (4) a BARS fit was applied over this firing rate, as shown in the fitted firing rate for the sorted unit (Fig. 3D, dashed line).

When normalization was performed in time before estimating the firing rate once over all gait cycles (Method A), the variance in firing rates was reduced for all the tasks compared with Method B. This normalization does distort time. Specifically, firing rates of action potential from gait cycles with shorter durations than the average gait cycle duration were underestimated. This underestimation was due to the bin length (ΔC, calculated based on average gait cycle length), which represented <25 ms in shorter duration gait cycles. For example, if the average gait cycle was 250 ms, then ΔC is 10%. Action potentials within the first ΔC of a 200 ms gait cycle only spanned 20 ms instead of 25 ms. Conversely, action potential from gait cycles with longer durations than the average gait cycle duration were overestimated because the bin length (ΔC) then represented >25 ms. In balance, it should have been a reasonable estimate of mean firing rate.

To validate this procedure, we compared both methods in single rats and cohorts of rats that performed overground locomotion and stepping on a treadmill. We found negligible differences between both methods (e.g.; Fig. 3C vs Fig. 3D). However, the higher variance and less accurate fitting in Method B often added noise that partially “washed out” the modulation of the neuron. Yet, the relationships between mean firing rates in the two tasks remain preserved (Fig. 3E).

Defining neuron activation.

We established a statistical procedure to define whether a neuron was active for some portion of the performed behavior (Fig. 2B), rather than use an empirical threshold of 10 Hz used by Armstrong and Drew (1984a). The distribution mean (x) and SD (μ) of baseline firing rates was calculated for each neuron during quiet standing. The 95% confidence interval (c) was calculated using those values and the length of the sample to compare (n) in Equation 1. The neuron was labeled as active when the mean value (X) of bootstrap sampling of 15% (this gives the number of observations, n) of the 201 samples (without replacement) of the fitted modulation during locomotion fell outside the 95% confidence interval of baseline firing in >100 of 2000 (5%) sampling repetitions (Equation 2 defines activation of a neuron for all gait cycles, each sample is i). Activation was also calculated during gait initiation based on the number of concurrently active neurons over time. Specifically, the mean firing rate was calculated over a 250 ms sliding window. If this instantaneous firing rate was outside the baseline firing rate confidence intervals, then that neuron was defined as active at the time corresponding to the middle of the sliding window (this is detailed in Equation 3, where b are 25 ms binned [nonoverlapping] estimates of firing rate, t is time, and the sample average is calculated over ± 125 ms). The activation threshold was defined as when the percentage of active neurons reached −3 dB (29.2%) of the rise between the baseline and the maximum as follows:

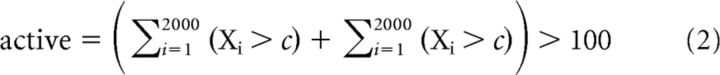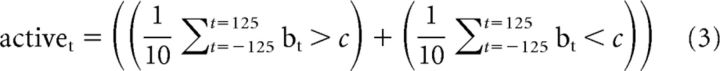Kinematics analysis.

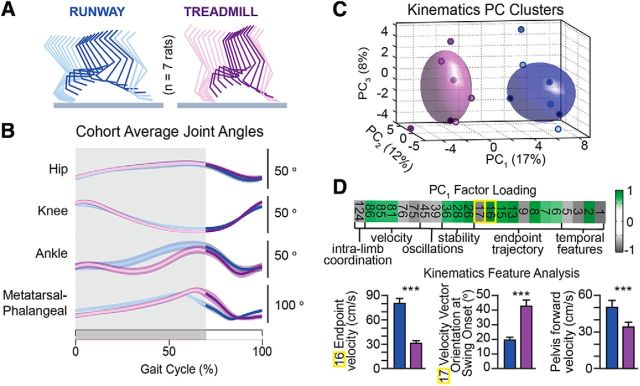
Kinematic data were converted into 126 parameters providing a comprehensive quantification of locomotor features. Established methods were used to generate the parameters, which are reported by Dominici et al. (2012). We comprehensively compared the kinematic patterns of the same rats during locomotion along a runway and treadmill-restricted stepping. Instead of scrutinizing parameters and selecting them subjectively, we applied principal component (PC) analysis (Dominici et al., 2012), to extract the parameters that captured the largest amount of variance across rats and between behaviors. A PC analysis was applied on all computed parameters from all gait cycles of all rats. Gait cycles were visualized in the new PC space created by PC_1–3, which accounted for ∼37% of the total data variance. Next, we extracted scores on each PC to identify the type of information captured on each axis. This analysis showed that PC1 differentiated locomotor behaviors, whereas PC₂ and PC₃ captured rat-specific gait patterns. The parameters that highly correlated with PC₁ (weight ≥ 0.6 on PC1) were then extracted and regrouped into functional clusters corresponding to basic gait features explaining differences between both locomotor procedures. We named the functional clusters for clarity and also represented a few raw parameters with high correlations with PC₁ in Figure 5.

Figure 5.

Kinematic modulation during locomotion along a runway versus treadmill-restricted stepping. A, Decomposition of hindlimb movements underlying both behavioral procedures at matched speeds. B, Average changes in hindlimb joint angles over the entire cohort of rats (n = 8 rats). C, PC analysis applied on all computed kinematic parameters distinguished gait patterns underlying locomotion along a runway versus stepping on a treadmill. Small purple or blue circles filled with different shades of gray represent average gait for each rat. D, Factor loading on PC₁, which explained most of the variance between behaviors. Numbers correspond to raw kinematic parameters (see Materials and Methods). Plots reporting mean ± SEM values of the raw kinematic parameters that showed the highest correlation (factor loading) with PC_1. Additionally, pelvis forward velocity over the entire gait cycle is shown. Two-sample t tests: #16: t₍₃₉₁₎ = 39, p < 1 × 10⁻¹⁰; #17: t₍₃₉₁₎ = −22.4, p < 1 × 10⁻¹⁰; pelvis: t₍₇₁₉₎ = 15, p < 1 × 10⁻¹⁰. ***Two-sample t test: p < 1 × 10⁻⁵ (Bonferroni correction for p < 0.05 with 126 comparisons is p < 7.9 × 10⁻⁵).

Analysis of muscle activity.

EMG signals were high-pass filtered (50 Hz), full-wave rectified, low-pass filtered (20 Hz), time interpolated over individual gait cycles to fit a normalized time base with 201 points, and averaged across all gait cycles performed by the individual rat. To visualize spatiotemporal map of motor neuron activity, we first estimated the rostrocaudal location of the motoneuron columns in the spinal cord. EMG signals were then mapped onto that location (Cappellini et al., 2010). This approach provides an interpretation of the motor pool activation at a segmental level rather than at the individual muscle level. Here, the maps were constructed by adding up the contributions of each muscle to the total activity at each spinal segment. The motor output pattern of each spinal segment S_i was estimated by the following equation:

where ni is the number of EMGjs corresponding to the ith segment, EMGj represents the normalized muscle activity, MNij is the number of motor neurons related to muscle j for the segment i, MNj is the total number of motor neurons for the muscle j, and Ni is the number of muscles innervated by the i^th spinal segment. These maps can be directly compared between tasks because the MN terms in the equation are not task specific.

Muscle synergies.

We applied a non-negative matrix factorization algorithm to compute muscle synergies using previously described methods (Dominici et al., 2011). To facilitate the comparison between rats and among different tasks, the EMG from each muscle was normalized to its peak value from overground locomotion. Briefly, we applied the algorithm on the averaged EMG activity to derive the weighting components and temporal activation profiles of each synergy. To compute synergies on a step-by-step basis, we applied the algorithm on the [m × t] matrix of EMG signals, where m indicates the number of muscles and t is the time base. NMF was applied to a single averaged gait cycle (normalized to runway) for each behavior. Albeit more variable, the temporal activation profiles were similar when applying the NMF to full cycle time series or the concatenated single averaged gait cycles for both tasks (data not shown). For all the studied behaviors, four muscle synergies were sufficient to account for >90% of total EMG variance.

Neuronal decoding.

Individual unit firing rates were estimated using nonoverlapping, 50 ms bins. This vector of firing rates was time-embedded to preserve 150 ms of prior (motor) or future (sensory) information. For each rat, 70% of all available data for a single task was used as a training set and the remaining 30% as a testing set. The division point between these sets was randomly chosen. This sampling was repeated 50 times. All data were normalized to zero-mean and unit-variance. A least-squares regression was calculated between the time-embedded firing rates and the hindlimb angle in the training set. Performance is reported only within the test sets, which evaluate the generalization of the decoding performance as opposed to overfitting. The average correlation was calculated over the 50 test sets for each rat. Statistical tests were evaluated on the rats' average correlation values (n = 8 values per condition).

Statistics.

All the values are reported as mean ± SEM values, unless otherwise specified. One-way ANOVAs, Student's paired t tests, and two-sample t tests were used to evaluate differences between normally distributed data (Kolmogorov–Smirnov test). A Bonferroni correction was applied in the case of multiple comparisons, specifically pairwise comparisons of the 126 parameters computed from kinematic recordings.

Results

Identification of motoneurons and cortical neurons underlying hindlimb movement

We injected retrograde tracers into antagonist muscles spanning the hindlimb joints to visualize the location of motoneurons in Lewis rats. Motoneurons innervating hindlimb muscles spanned the entire extent of lumbar segments (Fig. 1B), consistent with data in Long–Evans rats (Mohan et al., 2015). We then identified the location of pyramidal neurons projecting to spinal segments containing the motoneurons innervating hindlimb muscles using retrograde tracer injections (Fig. 1A). Corticospinal neurons with direct axonal projections to lumbar segments spanned a 7 mm² surface (Fig. 1A) that intersected the previously identified location of hindlimb motor cortex in other strains of rats (Hall and Lindholm, 1973; Donoghue and Wise, 1982).

High-resolution recordings and analysis of hindlimb motor control

Rats were implanted with bipolar electrodes into each of the 10 traced hindlimb muscles to record EMG activity and a 32-microwire array into the identified cortical region to record single-unit and multiunit activity (Fig. 1C). We used the integrated Vicon recording platform to acquire cortical ensemble modulation, muscle activity, and whole-body kinematics during locomotion (Movie 1).

Motor cortex dynamics underlying natural locomotion

We first characterized the basic properties of neuronal population responses during natural locomotion. We recorded the rats during self-paced, unconstrained locomotion toward a food reward. In all tested rats, neuronal population responses displayed regular patterns of modulation that were phase-locked to the cyclic changes in hindlimb movements (Fig. 2).

We studied the basic electrophysiological properties of hindlimb motor cortex neurons. Raw neural data were decomposed into single-unit and multiunit firing using wavelet filtering and superparamagnetic clustering (Quiroga et al., 2004). These methods identified a total of 796 neurons, with 48.5 ± 2.1 neurons per rat for each day of recording (n = 13 rats). A majority of neurons displayed phasic modulation of firing rates that was locked to the gait phases. To determine whether a given neuron exhibited a significant change in firing rate during locomotion compared with standing, we established a multistep statistical procedure that labeled active versus nonmodulated neurons (Fig. 2B; for details, see Materials and Methods). This criterion revealed that 68.4 ± 3.6% of all recorded neurons were active during at least one phase of locomotion (Fig. 2C). The mean frequency modulation depth of activated neurons during locomotion was 14.2 ± 4.2 spikes/s, with a mean firing rate of 36.8 ± 8.6 spikes/s (Fig. 2C).

We calculated the averaged firing rate of each active neuron and ordered them based on the timing of their peak-firing rate over the entire gait cycle (Fig. 2G). Distributions of neuronal responses over the entire population of recorded cells revealed that hindlimb motor cortex neurons most frequently exhibited peak firing rates during the transitions between gait phases (Fig. 2H), and displayed an enhanced probability of peaks throughout the entire swing phase compared with the stance phase. To derive a compact representation of neuronal population responses, which included individual neurons with low and high baseline firing rates, we normalized changes in firing rate for each active neuron relative to standing and computed the average change in firing rate across the population. Without this normalization, units with higher firing rates washed out any modulations in units with lower firing rates. This average neuronal population response confirmed that maximum firing rates of hindlimb motor cortex neurons occurred during phase transitions, both for single rat (Fig. 2F) and the entire cohort (Fig. 4).

Figure 4.

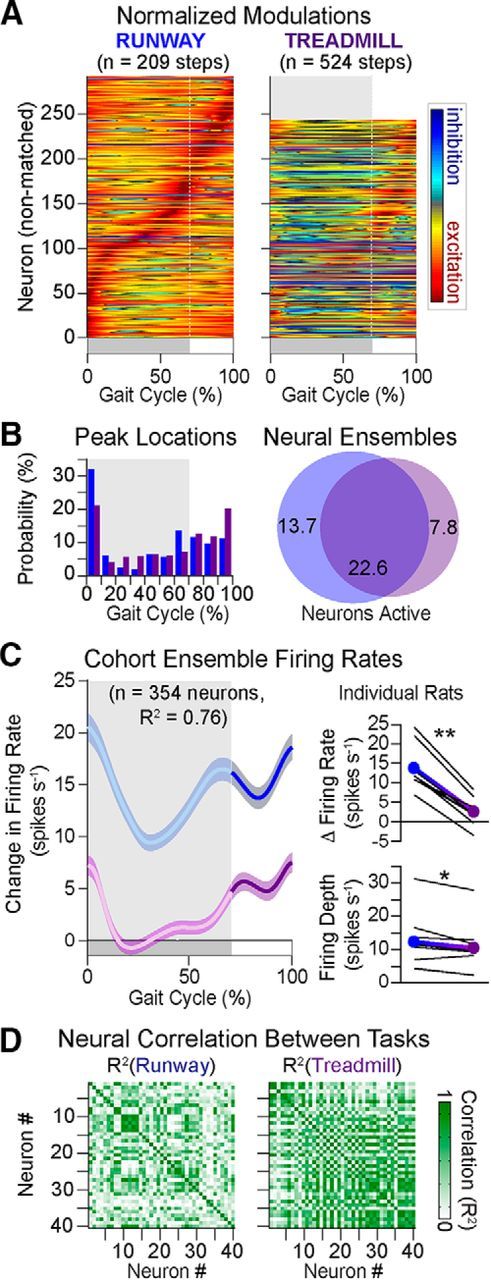
Neuronal population responses during locomotion along a runway versus treadmill-restricted stepping. A, Average modulation of active neuron over the duration of the gait cycle. Each firing rate is normalized to the absolute maximum value measured for each neuron across both behaviors (n = 8 rats). B, Distribution of peak firing rates within the neuronal ensemble for both behaviors. Venn diagrams reporting subensembles of active neurons for each behavior. Blue represents runway. Purple represents treadmill. The size of the circle is proportional to the number of neurons. These diagrams reveal both task-independent (overlapping segment) and task-specific (nonoverlapping slices) activation of neurons across the tested locomotor behaviors. C, Ensemble change in firing rate (mean ± SEM) computed from all active neurons in both behavioral procedures. The zero or negative changes in firing rate during stance for treadmill means that the ensemble is not firing differently or is slightly inhibited relative to resting firing rates. To allow for direct comparison between behaviors, the duration of stance and swing phases has been normalized. Right, Mean firing rate and depth for the cohort (filled circles) and individual rats (black lines). D, Cross-correlation between firing rates of active neurons for a representative rat. Average cross-correlation was significantly higher (n = 7690 pairs; p < 1 × 10⁻⁵) on the treadmill (R² = 0.35) than the runway (R² = 0.27). *p < 0.05 (two-sample t test). **p < 1 × 10⁻⁴ (two-sample t test).

Motor cortex activity is attenuated during treadmill-restricted stepping

We then compared neuronal population responses in the same rats recorded on the same day during overground locomotion along a runway versus treadmill-restricted stepping (n = 8 rats). Rats performed overground locomotion at self-selected speed. The measured speed was then used to set the velocity of the treadmill for each rat. We isolated all the consistent steps across all the recorded trials in the 8 rats, which resulted in a total of 209 and 524 analyzed steps for executions overground and on the treadmill, respectively.

Neuronal population responses remarkably differed during treadmill-restricted stepping compared with natural locomotion. First, the total number of active neurons significantly decreased during treadmill-restricted stepping (16.3 ± 6.4% decrease, Student's t test, t₍₇₎ = 2.67, p = 0.03; Fig. 4A). More importantly, in each and every rat, the active neurons displayed a fivefold reduction in average firing rate (Student's t test, t₍₇₎ = 10.31, p = 1.7 × 10⁻⁵; Fig. 4C). Although the overall profile of the modulation was preserved, the change in firing rates compared with baseline activity was nearly absent during the stance phase of gait on the treadmill. This zero change in firing rate indicates that the neuronal ensemble displayed the same firing rate during stance as during standing (rest). The average change in firing rates were 13.9 ± 1.2 spikes/s for overground versus 2.6 ± 0.7 spikes/s for treadmill. Modulation depth was also significantly reduced during stepping on a treadmill (Student's t test, t₍₇₎ = 2.93, p = 0.02; Fig. 4C). While the change in ensemble firing rate was higher during swing compared with stance for both tasks, we detected a shift in the temporal structure of neuronal responses. Peak firing occurred before the end of stance during overground locomotion, whereas this peak shifted to the beginning of the swing phase during treadmill-restricted stepping. The relative number of neurons exhibiting peak firing times just before the stance to swing transition reached 13.2% during overground locomotion versus 6.2% on the treadmill (Fig. 4B).

We then studied the temporal relationships within the neuronal population. For this, we computed cross-correlation (R²) between the firing rates of all possible pairs of active neurons for each behavior and represented these analyses in a correlation matrix (Fig. 4D, shown for a representative rat). We found a significant increase in the degree of similarity between individual neuronal responses during treadmill-restricted stepping compared with overground locomotion (one-way ANOVA, F_(2,23067) = 191, p < 1 × 10⁻¹⁰; post hoc testing with Bonferroni correction p < 1 × 10⁻¹⁰, cohort averages: R² = 0.41 vs R² = 0.27).

Changes in hindlimb kinematics during treadmill-restricted stepping

We next evaluated whether rats displayed similar hindlimb kinematics during treadmill-restricted stepping versus overground locomotion (Fig. 5). While these two tasks have been considered equivalent biomechanically (Pereira et al., 2006), we detected modest yet consistent differences in hindlimb kinematics between both behavioral procedures.

In each rat, hindlimb kinematics were reproducible across gait cycles within each task, as evidenced by the relatively small SE in Figure 5B. The cohort average profiles of proximal joint angles overlapped during treadmill-restricted stepping and overground locomotion. In contrast, we identified a systematic discrepancy in amplitude and coordination between angular changes of distal joints (Fig. 5B). Such modifications of distal joint angles would directly affect paw placement and positioning.

We then implemented PC analysis to expose task-specific gait cycle clusters and identify the parameters that contributed most to this specificity (Dominici et al., 2012). We computed a large array of gait parameters (n = 126) to provide a comprehensive quantification of locomotion and applied a PC analysis on all recorded gait cycles from all rats in both behavioral procedures. We visualized gait patterns in the new space created by PC_1–3 (Fig. 5C), where PC₁ differentiated treadmill-restricted stepping versus overground locomotion (5.9 ± 1.1 vs −2.6 ± 0.8, PC scores for runway vs treadmill), whereas PC₂ and PC₃ captured inter-rat variability. This analysis suggested that all rats produced task-specific adjustments of gait patterns. To identify these features, parameters that highly correlated (|factor loadings| > 0.6) with PC₁ were organized into functional clusters corresponding to basic movement features (Fig. 5D). This analysis revealed that, compared with overground locomotion, treadmill-restricted stepping led to a decrease in the mean and peak velocity of changes in joint angles and endpoint trajectory. Additionally, trunk movements and balance-related features displayed increased variability during overground locomotion compared with treadmill-restricted stepping. In turn, extraction of parameters loading on PC₂ (data not shown) indicated that inter-rat variability emerged from differences in intralimb coordination and ranges of joint angle amplitude, revealing the idiosyncratic gait patterns of each rat.

Changes in hindlimb muscle activation patterns during treadmill-restricted stepping

We then studied whether changes in muscle activity paralleled the detected adjustments in hindlimb kinematics (Fig. 6). Analyses of single muscles showed that task-specific difference primarily occurred in the extensors during stance (VL and GM), knee flexor (ST), ankle flexor (TA), and foot muscles (FHL and EDL) around the stance-swing transition (Fig. 6B). To visualize all the recorded hindlimb muscles in a compact representation, we constructed the spatiotemporal map of motoneurons activation. For this, we projected the EMG activity from all recorded muscles onto the identified rostrocaudal locations of motoneuron pools. We found that motoneuron activation underlying natural locomotion is decomposed into two bursts of activity spanning L4-L6 segments during stance and mostly centered around L2-L4 segments during swing (Fig. 6C). While spatiotemporal maps of motoneuron activation were similar between both behaviors, there was an overall reduction of motoneuron activation during treadmill-restricted stepping. This decrease was more pronounced during the stance phase, which amounted to a 15% reduction of activation during treadmill-restricted stepping (Fig. 6C). To further visualize these differences, we applied a non-negative matrix factorization algorithm onto pooled EMG signals across steps to calculate muscle synergies. Four activation profiles spanning the entire duration of the gait cycle were sufficient to reconstruct >90% of the variance in the EMG signals for each rat. We focused on muscle synergies because their spatial and temporal activation profiles reflect the neural command distributed across motoneurons (Dominici et al., 2011; Walter et al., 2014). The amplitude of the C2 muscle synergy significantly decreased during treadmill-restricted stepping (Student's t test t₍₃₎ = 4.76, p = 0.02; Fig. 6D). This synergy, which peaks during mid-stance, reflects the activation of the ankle extensor muscles MG and LG (weights; Fig. 6D). We also detected a significant difference in the onset of the C3 muscle synergies (Fig. 6D). These synergies are related to the activation of flexor muscles, including ST and TA, which was delayed during treadmill-restricted stepping compared with natural locomotion, paralleling the observed lag in distal joint coordination (Fig. 6D). To measure differences in muscle activation profiles for each muscle independently, we calculated correlations between muscle activity profiles underlying each behavior (Fig. 6E). While correlations between tasks were high, all rats showed the lowest intertask correlation for the BF, GM, ST, and FHL muscles; these muscles weighted on the muscle synergy C2 and C3 during both behaviors. Similarly, correlation analysis applied to muscle synergies confirmed that intertask correlation was lower (0.715) for C2 and C3 compared with C1 and C4 (0.785); this suggested that task-specific differences were more evident in muscle synergies C2 and C3 (Fig. 6E).

Figure 6.

Modulation of muscle activity during locomotion along a runway versus treadmill-restricted stepping. A, Scheme explaining the methods used to analyze the EMG activity of the 10 recorded muscles. B, Group-average EMG activity. C, Group-average spatiotemporal maps of motoneuron activity underlying each behavioral procedure (n = 4 rats). D, Mean (±SEM) temporal profiles of muscle synergies with corresponding weights for each muscle shown below (±SEM). E, Cross-correlation between muscle activity envelopes and between muscle synergy activation profiles during locomotion along a runway and stepping on a treadmill. The color-coded matrix reports correlation value for each muscle and each muscle synergy activation profiles across the four tested rats. (VL electrodes were broken in Rat 1; this muscle was not included in the analysis).

Influence of locomotor velocity on motor cortex dynamics

While we set treadmill belt velocities for each rat based on the mean values observed during natural locomotion, post hoc analysis of all steps showed slower velocity on the treadmill for each rat. We therefore verified that difference in velocities of locomotor movements was not responsible for the observed changes in cortical activity. The velocity of locomotor movements, computed from the displacement of the pelvis, was highly reproducible over steps during treadmill-restricted stepping. The velocity was more variable during overground locomotion, both within and across rats. To account for this variability, we measured the distribution of locomotor velocity across all the steps performed along the runway by all the rats, and used the mean of this distribution to divide gait cycles into steps labeled as normal (39.0 ± 3.8 cm/s) versus fast (61.1 ± 5.4 cm/s) (Fig. 7A). The locomotor velocity of normal steps and treadmill-restricted steps (34.3 ± 3.8 cm/s) overlapped for the cohort (Fig. 7B). PC analysis showed that the previously described task-specific differences in gait patterns were preserved between treadmill-restricted steps and both normal and fast steps (Fig. 7C). Likewise, the locomotor velocity had minimal influence on neuronal population responses. Despite a 56% increase in velocity, fast steps only exhibited a slight increase in mean change in firing rate compared with normal steps (mean difference, 2.4 ± 5.6 spikes/s). This similarity contrasted with the sharp decrease in cortical activity during treadmill-restricted stepping (mean difference, 10.4 ± 7.7 spikes/s). These results confirmed that the fivefold attenuation in change in firing rates reported in Figure 4C was maintained regardless of the rats' velocity (Fig. 7D).

Figure 7.

Influence of speed on neural and kinematic modulation. A, Distributions of mean velocities for all recorded gait cycles along the runway and on a treadmill for a representative rat. Gait cycles are subdivided into normal and fast steps based on the distribution of velocities. B, Histogram of fast and normal steps performed along the runway and on the treadmill for the entire cohort (n = 8 rats). Velocities of normal steps along the runway and steps on a treadmill overlapped completely. C, Gait clusters computed by applying a PC analysis on all computed kinematic parameters. Whereas normal and fast steps occupied separate locations in the PC space, gait clusters underlying locomotion along runway (blue and black) versus stepping on a treadmill (purple) emerged on the opposite side of the PC1 axis, indicating that these gait executions involved distinct motor control behaviors. Each dot represents a gait cycle from a given rat, which are each differentiated by a distinct grayscale color. D, Ensemble firing rates for both fast and normal steps along the runway and steps on the treadmill.

Motor and sensory encoding in motor cortex dynamics

The hindlimb motor cortex of rats exhibits a large overlap between sensory and motor representations (Hall and Lindholm, 1973). Therefore, we asked whether the neuronal responses recorded from the hindlimb motor cortex of rats were more related to past or future changes in hindlimb kinematics. To address this question, we built linear decoders (Fig. 8A,B) that received neural firing rates estimated before or after the occurrence of changes in hindlimb kinematics, thus creating motor- and sensory-related decoders. We decoded the changes in the hindlimb angle (i.e., the angle between the hip and the foot), which captures the combined oscillations among lower limb segments (Ivanenko et al., 2008). We selected a temporal embedding that was short enough (150 ms) to avoid influences from prior or future gait cycles (cycle duration, 406 ± 35 ms). For all 8 rats, the decoders displayed significantly higher improved performance when the motor-related information was used to train the decoder, both on the runway and treadmill (Student's t tests, runway: t₍₇₎ = 7.08, p = 1.9 × 10⁻⁴; treadmill: t₍₇₎ = 5.45), p = 9.4 × 10⁻⁴; Figure 8C).

Figure 8.

Decoding motor cortex modulation. A, Changes in hindlimb angle and tibialis anterior envelope during locomotion along the runway and their alignment with prior and future firing rate estimates. B, Least-squared regression using prior (motor) or future (sensory) neuronal information. C, Mean values of correlations for each decoder based on a total of 50 randomized test sets per rat. Left, Runway data. Right, Treadmill data. Individual lines indicate each rat (n = 8 rats). Filled colored circles connected by a thicker line represent group-average performances. Overground and treadmill-restricted motor decoding accuracy were not significantly different (p = 0.21). **p < 1 × 10⁻² (Student's t test). ***p < 1 × 10⁻³ (Student's t test).

Motor cortex activation precedes initiation of locomotion

The results presented in the previous sections showed that the hindlimb motor cortex exhibited more robust modulation during overground locomotion than during treadmill-restricted stepping. The phase and amplitudes of kinematic and muscle activity also suggested that hindlimb movements were more automated during treadmill-restricted stepping. These findings suggest that the motor cortex is more engaged in tasks involving volitional components. To provide additional insight into this question, we studied the spontaneous initiation of voluntary locomotion. This procedure provides the opportunity to evaluate whether volitional gait initiation is reflected in the anticipated motor cortex activation. Five rats were tested during initiation of locomotion. The rats stood quietly with full weight support for at least 3 s with the four limbs on the force plate before spontaneously initiating locomotion from the hindlimb contralateral to motor cortex recordings (Fig. 9). Transition from standing to continuous locomotion comprised slow inactivation of a postural muscle synergy, followed by the coordinated activation of locomotor related synergies to initiate gait (Fig. 9C). The recruitment of these muscle synergies produced stereotypical spatiotemporal maps (Fig. 9B) of motoneuron activation that were highly reproducible across initiations and rats. To identify neurons that became active during initiation, we determined when the firing rate diverged from the distribution of firing rates during standing (Fig. 9E). This analysis revealed that changes in firing rates anticipated any detected changes in motoneuron activation maps, single muscle activation, muscle synergies, or vertical ground reaction forces by at least 76 ± 40 ms (Fig. 9D).

Figure 9.

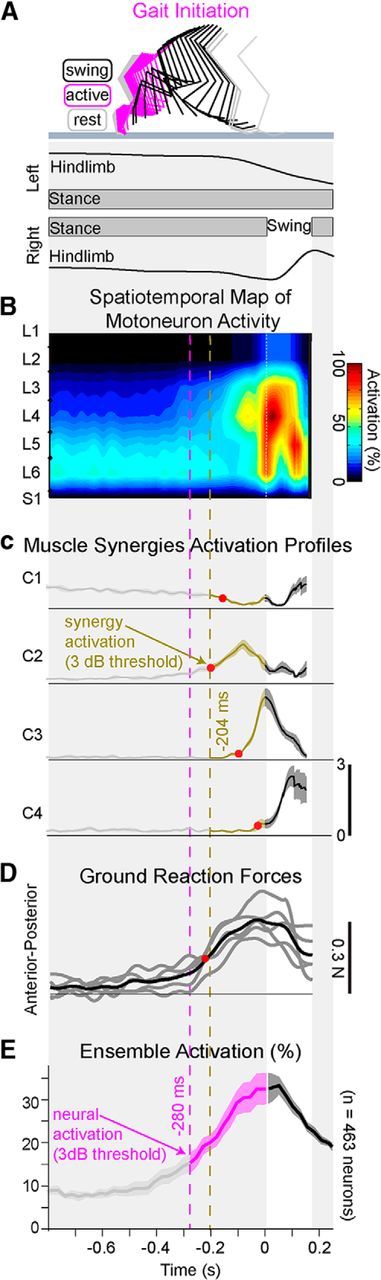
Neuronal population responses during gait initiation along the runway. A, Color-coded decomposition of right hindlimb movements and elevation angle of the hindlimb axis during gait initiation. Gait was initiated with the right hindlimb. B, Group-average spatiotemporal map of motoneuron activity during gait initiation (n = 5 rats). C, Mean (±SEM) temporal activation profiles of muscle synergies C1–C4 during gait initiation. The progressive inactivation of C1 (ankle extensor muscles) and activation of C2 (knee extensor muscles) trigger anticipatory postural adjustments. Red dots represent the 3 dB activation thresholds for all the activation profiles C1-C4. D, Changes in anterior–posterior ground reaction forces for all the rats (black) and individual rats (gray). Red dots represent the 3 dB threshold. The anticipatory postural adjustment phase correlates with the activation time of the synergy C2. E, Percentage (±SEM) of cortical neurons becoming active during gait initiation. The group average (n = 5 rats) activation threshold occurred 76 ms before the activation of muscle synergies. The same analysis applied for individual steps (n = 26 steps) produced similar delays (Student's t test, t₍₅₀₎ = −2.8, p = 0.007).

Tasks requiring volitional gait adjustments correlate with enhanced cortical activation

We finally tested whether natural tasks requiring volitional adjustments of hindlimb kinematics and muscle activity would lead to task-specific modulation of motor cortex activation compared with basic overground locomotion. For this purpose, the same rats were recorded during locomotion along the irregularly spaced rungs of a horizontal ladder. We also evaluated a new cohort of 5 rats during locomotion along a flat runway and when climbing a staircase.

To progress along the staircase, the rats increased foot elevation to place the paw onto the elevated stair (Fig. 10A). These adjustments of hindlimb kinematics resulted from substantial augmentation of motoneuron activation, which corresponded to a 25% overall increase of activity across the entire gait cycle duration when climbing stairs compared with locomotion along a runway (Fig. 10B). During stair climbing, rats showed a significant increase in EMG activity of proximal extensor muscles during stance (Student's t test, t₍₂₄₎ = −4.35, p = 2.19 × 10⁻⁴) and proximal flexor muscles during swing (Student's t test, t₍₁₄₎ = 3.6, p = 0.003), which was reflected in task-specific amplifications of muscle synergies (Fig. 10C). These changes in kinematic and muscular activity were prominent during the period spanning mid-stance to early swing.

Figure 10.

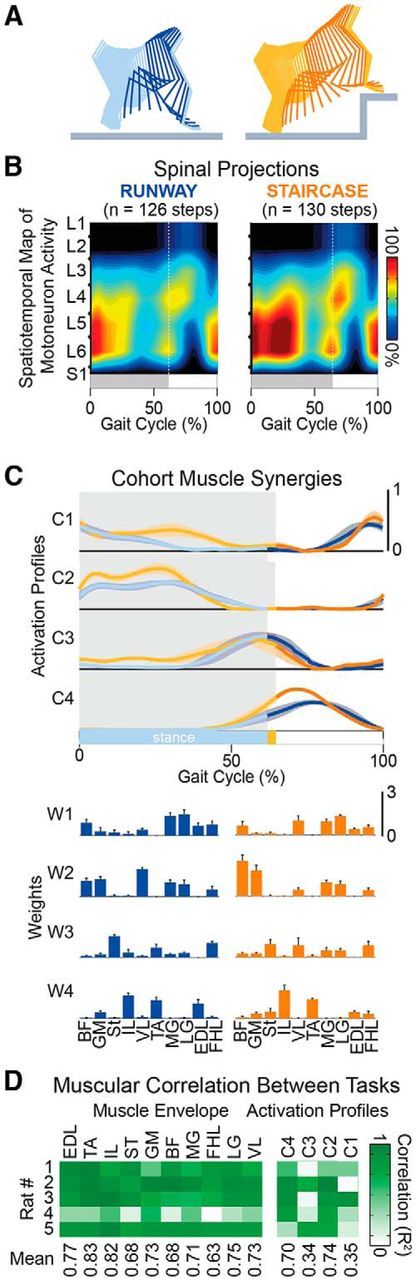
Modulation of hindlimb kinematic and muscle activity during locomotion along a runway and onto a staircase. A, Color-coded decomposition of right hindlimb movements during a step on a runway and onto a staircase. B, Group-average spatiotemporal maps of motoneuron activity during both behavioral procedures (n = 5 rats). Conventions are the same as in Figure 6. C, Mean (±SEM) temporal profiles of muscle synergies with corresponding weights for each muscle shown below (±SEM). D, Cross-correlation between muscle activity envelopes and between muscle synergy activation profiles during locomotion along a runway and climbing on a staircase for the 5 rats.

Task-specific increase in hindlimb muscle activity coincided with a commensurate augmentation of neuronal population responses when the rats climbed the staircase. During this task, we found a 10 ± 2.8% increase in the number of active neurons (Student's t test, t₍₄₎ = −3.9, p = 0.02; Fig. 11A,B). Compared with overground locomotion, these neurons exhibited an average 81 ± 26% increase in firing rate (Student's t test, t₍₄₎ = −3.7, p = 0.02; Fig. 11C). However, the temporal structure of neuronal population responses remained globally unchanged between both tasks (R² = 0.88; Fig. 11C,D). The increased change in firing rate was not restricted to the period during which muscle activity was adapted to climb the staircase but instead spanned the entire gait cycle.

Figure 11.

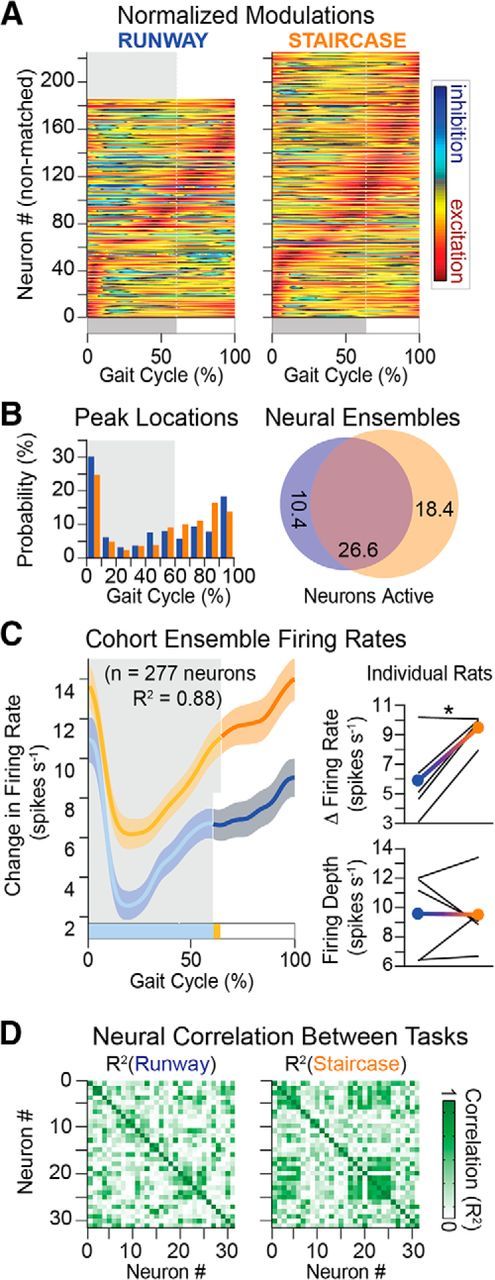
Neuronal population responses during locomotion along a runway and onto a staircase. A, Average modulation of active neuron over the duration of the gait cycle (n = 5 rats). Conventions are the same as in Figure 4. B, Distribution of peak firing rates and Venn diagrams, as shown in Figure 4. C, Ensemble firing rate (mean ± SEM) computed from all active neurons in both behaviors. Right, Mean firing rate and depth of modulation for the cohort (filled circles) and individual rats (black lines). D, Cross-correlation between neurons is shown for a representative rat. Cross-correlation between firing rates of active neurons for a rat. Average cross-correlation was significantly higher (n = 4767 pairs; p < 1 × 10⁻⁵) on the stairs (R² = 0.29) than the runway (R² = 0.23). One-way ANOVA, F_(2,14298) = 61, p < 1 × 10⁻¹⁰, post hoc testing with Bonferroni correction p < 1 × 10⁻¹⁰ (runway vs stairs). *p < 0.05 (Student's t test).

Crossing the ladder required the rats to position their paws onto the rungs with precision. The execution of this behavior led to pronounced adaptations in muscle synergies and hindlimb kinematics (Fig. 12). Instead of activating all extensor muscles simultaneously at the beginning of stance, rats reorganized the activity of multiple extensor muscles throughout the stance and swing phases of gait (Fig. 12C,D), which was reflected in the substantial rearrangement of spatiotemporal map of motoneuron activation (Fig. 12B).

Figure 12.

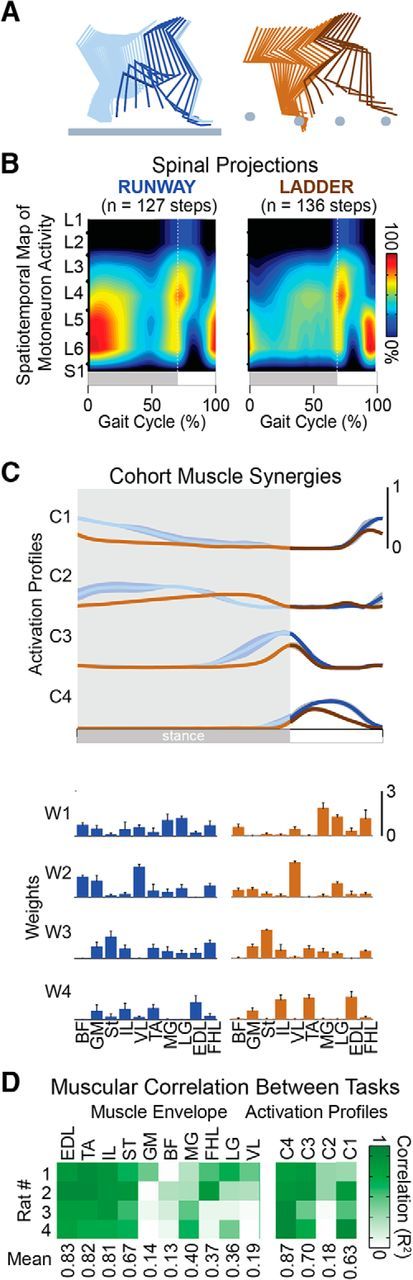
Modulation of hindlimb kinematic and muscle activity during locomotion along a runway and over a ladder. A, Color-coded decomposition of right hindlimb movements during a step on a runway and over a ladder. B, Group-average spatiotemporal maps of motoneuron activity during both behavioral procedures (n = 4 rats). Conventions are the same as in Figure 6. C, Mean (±SEM) temporal profiles of muscle synergies with corresponding weights for each muscle shown below (±SEM). D, Cross-correlation between muscle activity envelopes and between muscle synergy activation profiles during locomotion along a runway and over a ladder for the 4 rats with 10 EMG.

These task-specific adaptations were associated with a restructuring of cortical modulation. First, the number of active neurons increased slightly but not significantly during locomotion along the ladder compared with overground locomotion. Second, the modulation depth of neurons increased from 11 ± 0.7 to 14.6 ± 1.2 spikes/s (Student's t test, t₍₅₎ = −3.09, p = 0.027; Fig. 13C). Yet, the mean firing rate did not change significantly (Fig. 13C). Third, a large number of neurons shifted the occurrence of their peak firing to the swing phase of gait (Fig. 13).

Figure 13.

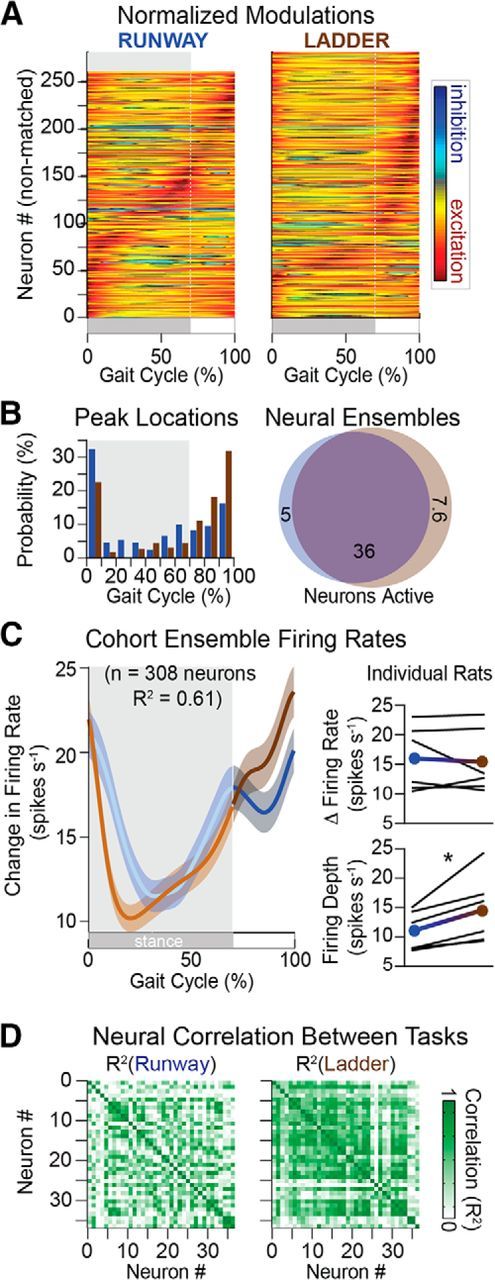
Neuronal population responses during locomotion along a runway and over a ladder. A, Average modulation of active neuron over the duration of the gait cycle (n = 6 rats). Conventions are the same as in Figure 4. B, Distribution of peak firing rates and Venn diagrams, as shown in Figure 4. C, Ensemble firing rate (mean ± SEM) computed from all active neurons in both behaviors. Right, Mean firing rate and depth of modulation for the cohort (filled circles) and individual rats (black lines). D, Cross-correlation between firing rates of active neurons for a rat. Average cross-correlation was significantly higher (n = 7189 pairs; p < 1 × 10⁻⁵) on the ladder (R² = 0.36) than the runway (R² = 0.31). One-way ANOVA, F_(2,21564) = 101, p < 1 × 10⁻¹⁰; post hoc testing with Bonferroni correction p < 1 × 10⁻¹⁰ (runway vs ladder). *p < 0.05 (Student's t test).

Discussion

Motor cortex activity underlying locomotion has been extensively studied in cats. Despite the preponderant role of rodent models in neuroscience research, our knowledge of cortical dynamics during walking is disproportionally lower in that species, especially during natural locomotion. Here, we show that the hindlimb motor cortex of rats exhibits neuronal population responses that are comparable with cats. Moreover, we found a marked reduction of cortical activity when rats performed more automated stepping movements. These relationships have not been explicitly investigated in other species. We discuss the activation patterns of muscles and motor cortex neurons in rats in the framework of the extensive literature in cats, and the implications of reduced motor cortex activity during automated stepping for motor control principles, neuroprosthetics, and rehabilitation.

Spatiotemporal maps of motoneuron activation during locomotion

We identified the location of cortical neurons that project to lumbar segments containing the motoneurons innervating hindlimb muscles. We used this anatomical quantification to reconstruct the spatiotemporal maps of motoneuron activation across all the tested locomotor behaviors. These results were consistent with previous observations in cats and humans (Yakovenko et al., 2002; Cappellini et al., 2010; Mohan et al., 2015). Specifically, motoneuron activation patterns during locomotion involved a succession of hotspots that propagated rostrocaudally along lumbar segments during the gait cycle. Task-specific changes in hindlimb kinematics were captured in the adjustment of temporal structure and intensity of these hotspots. These results provide a useful framework to design task-specific control policies for locomotor neuroprostheses (Wenger et al., 2016).

Motor cortex dynamics underlying natural locomotion

The first analyses of motor cortex modulation underlying forelimb (Armstrong and Drew, 1984a, b) and hindlimb (Widajewicz et al., 1994) locomotor movements in cats using single electrode penetrations reported that more than half of the recorded neurons significantly changed their firing rates compared with rest. We found a comparable modulation of hindlimb motor cortex neurons in rats. Two-thirds of the recorded neurons significantly modulated their firing rate during locomotion.

Cortical neuronal responses in rats were synchronized with task-specific spatiotemporal patterns of motoneuron activation and cyclic changes in hindlimb kinematics. These population neuronal responses were remarkably similar across rats. The changes in firing rates of the modulated cells peaked during gait phase transitions and were larger during the swing phase. Likewise, motor cortex neurons of cats and primates display active periods of elevated firing rates that frequently occur toward the end of stance and persist throughout the swing phase. Thus, the temporal activation profile of neurons located in the rat motor cortex matched the general properties of cells recorded in rats, cats, and nonhuman primates (Drew, 1988; Beloozerova and Sirota, 1993; Song et al., 2009; Beloozerova et al., 2010; Foster et al., 2014; Yin et al., 2014).

Behaviors requiring skilled movements robustly engage motor cortex neurons in cats. For example, adjustments in limb trajectories to pass an obstacle (Drew, 1988) or place the paw onto the rungs of an horizontal ladder (Beloozerova et al., 2010) involve a pronounced tuning of motor cortex activity. This tuning, which includes an increased depth of modulation and a shift in the timing of peak firing rates, coincides with adjustments of limb kinematics and muscle activity (Drew, 1988, 1993; Beloozerova and Sirota, 1993; Widajewicz et al., 1994; Beloozerova et al., 2010).

We found a remarkably similar tuning of motor cortex neurons when rats traversed a ladder or climb a staircase. Moreover, adaptation of cortical activity was coherent with the concurrent modulation of muscle activation patterns. For example, muscle synergy analysis revealed that precision walking involved a reorganization of the temporal structure of muscle synergies. This temporal tuning was reflected in the shift in peak firing rate of population neuronal responses, with otherwise unchanged mean firing rates. In contrast, stair climbing required an overall increase in the amplitude of muscle synergies associated with antigravity muscles to climb up the staircase, and hindlimb flexion to position the paw onto the staircase. A global enhancement of neuron firing rates paralleled the increased amplitude of muscle synergy activation. However, the temporal structure of population neuronal responses remained unaffected.

Decoding algorithms additionally suggested that, despite the overlap between sensory and motor hindlimb representations in rats, hindlimb cortex modulations were more closely related to future than past hindlimb kinematics. Previous studies also decoded a plethora of kinematic features from motor cortex activity in rats attached to robotic systems (Song et al., 2009; Song and Giszter, 2011; Rigosa et al., 2015). Here, we replicated these results in unrestrained rats walking on a treadmill. Useful signals for brain-computer interfaces were also extracted from motor cortex activity in healthy (Song and Giszter, 2011; Rigosa et al., 2015; Song et al., 2015) and spinal cord injured rats (Alam et al., 2014).

These combined results reveal that the hindlimb motor cortex of rats display comparable neuronal population responses as cats across a wide spectrum of locomotor behaviors. Despite the more facultative role of the rodent motor cortex (Starkey et al., 2011; Dominici et al., 2012), the neuronal responses occurring during locomotion mirrored task-specific modulation of hindlimb kinematics and muscle synergies, as previously reported in higher mammals that more heavily rely on motor cortex integrity to produce locomotion.

We propose that this cortical activity reflects the supervision of downstream circuits in the brainstem and spinal cord that are directly involved in hindlimb movement production (Orlovsky et al., 1999; Stuart and Hultborn, 2008). The anticipated activation of the motor cortex before gait initiation reinforced this hypothesis, suggesting that motor cortex signals may instruct downstream locomotor circuits in the brainstem to trigger the motor program for walking. However, causal experiments are required to unveil the precise function of cortical dynamics for the initiation, production, and supervision of hindlimb locomotor movements.

Motor cortex activity is reduced during treadmill-restricted stepping

All tested rats exhibited up to a sixfold decrease in firing rates during treadmill-restricted stepping compared with overground locomotion. The reduction of motor cortex activity was not due to differences in speed because this variable exerted a minimal impact on cortical dynamics, as previously documented in cats (Armstrong and Drew, 1984a, b). Moreover, the timing of neuronal responses shifted during treadmill-restricted stepping. Although neuronal population responses peaked before foot clearance during overground locomotion, this peak was delayed to early swing during treadmill-restricted stepping.

These adaptations were consistent with alterations in kinematics and muscle activity. Activation of extensor muscles was reduced during stance, whereas the recruitment of flexor muscles was delayed during treadmill-restricted stepping compared with overground locomotion. These alterations delayed the onset of foot dorsiflexion during swing and led to an overall reduction in the velocity of hindlimb movements. These changes fit the interpretation that locomotor movements were more automated during treadmill-restricted stepping. Specifically, the swing phase appeared automatically triggered in response to the backward pull of the hindlimb on the belt (Pearson, 2008), as opposed to a supraspinal drive to progress forward. We attributed these differences in kinematics and muscle synergies to less volition during treadmill-restricted stepping and hypothesized that the attenuated cortical activity reflects this lack of volition.

We propose that the degree of volitional engagement in the execution of the locomotor task exerts a non-negligible impact on hindlimb motor cortex modulations in rats. This observation presents parallels with the optimal feedback control theory. Behavioral and model-based experiments on reaching movements led to the proposition that the brain assists motor execution when necessary (Todorov, 2009). Thus, optimal feedback controller theory predicts that motor cortex engagement should augment with increasing demands in task accuracy (Todorov, 2004). We observed similar relationships between task complexity and motor cortex activity in rats.

Implications for motor control paradigms, rehabilitation, and neuroprosthetics

Treadmill-restricted paradigms enable collection of large datasets within short time windows in well-controlled conditions. Consequently, these paradigms are the most commonly used procedures to study locomotion. However, the marked differences in kinematics, muscle synergies, and cortical activity on the treadmill compared with natural locomotion must be taken into consideration when studying locomotor control, or when developing neuroprosthetic systems (Song and Giszter, 2011; Jarc et al., 2013; Alam et al., 2014; Wenger et al., 2014). Our results suggest that overground locomotor behaviors may be more appropriate to extract cortical patterns resembling natural locomotion.

Reduced cortical modulation during treadmill-restricted stepping also resonates with previous findings on task-specific rehabilitation in rats. Step training coupled with volitional components in neuroprosthetic environments induced cortical plasticity in injured rats, even on a treadmill (Song and Giszter, 2011; Oza and Giszter, 2015; Song et al., 2015). However, treadmill-restricted rehabilitation paradigms that did not require cortically driven neuroprosthetic control failed to promote neuroplasticity of descending pathways after severe injuries. Overground rehabilitation designed to encourage volitional participation led to a robust remodeling of motor cortex axonal projections that contributed to motor recovery (van den Brand et al., 2012). Studies in humans similarly showed that robotic systems encouraging active participation led to improved recovery compared with less-engaging treadmill-restricted stepping paradigms (Hornby et al., 2005).

These combined results reemphasize the importance of volitional participation and task-specific challenges to maximize the engagement of the brain in motor control during rehabilitation.