Interaction of Instrumental and Goal-Directed Learning Modulates Prediction Error Representations in the Ventral Striatum

Abstract

Goal-directed and instrumental learning are both important controllers of human behavior. Learning about which stimulus event occurs in the environment and the reward associated with them allows humans to seek out the most valuable stimulus and move through the environment in a goal-directed manner. Stimulus–response associations are characteristic of instrumental learning, whereas response–outcome associations are the hallmark of goal-directed learning. Here we provide behavioral, computational, and neuroimaging results from a novel task in which stimulus–response and response–outcome associations are learned simultaneously but dominate behavior at different stages of the experiment. We found that prediction error representations in the ventral striatum depend on which type of learning dominates. Furthermore, the amygdala tracks the time-dependent weighting of stimulus–response versus response–outcome learning. Our findings suggest that the goal-directed and instrumental controllers dynamically engage the ventral striatum in representing prediction errors whenever one of them is dominating choice behavior.

SIGNIFICANCE STATEMENT Converging evidence in human neuroimaging studies has shown that the reward prediction errors are correlated with activity in the ventral striatum. Our results demonstrate that this region is simultaneously correlated with a stimulus prediction error. Furthermore, the learning system that is currently dominating behavioral choice dynamically engages the ventral striatum for computing its prediction errors. This demonstrates that the prediction error representations are highly dynamic and influenced by various experimental context. This finding points to a general role of the ventral striatum in detecting expectancy violations and encoding error signals regardless of the specific nature of the reinforcer itself.

Introduction

Since the early days of psychology, theorists and experimentalists have struggled with the question of which associative structures control human actions (Pavlov, 1927; Thorndike, 1933; Tolman, 1948). Evidence collected over decades of behavioral and neuroscientific research indicates that decision-making behavior is under the dynamic control of at least three different systems (Dolan and Dayan, 2013): (1) a passive Pavlovian system that associates predictive cues with rewarding or punishing outcomes (stimulus-outcome learning [S-O]) and that elicits basic approach or avoidance behavior; (2) an instrumental system that involves the formation of stimulus–response associations (stimulus–response learning [S-R]) that is initially strengthened by outcomes, but eventually leads to outcome-insensitive habits; and (3) a flexible goal-directed system that encodes the relationship between an action and the delivery of its outcome (response–outcome learning [R-O]) and that is capable of adapting to changes therein. Although many behavioral phenomena arising within these systems have been characterized and the underlying, and partially overlapping, neural circuits have been mapped out in recent years (Philiastides et al., 2010; Hunt et al., 2012; Daw and O'Doherty, 2014), there is relatively little knowledge of how these systems cooperate and compete with each other for the control over decision-making. Understanding their interaction may provide insights into pathological disorders of human decision-making (Everitt and Robbins, 2005; Montague et al., 2012; Belin-Rauscent et al., 2016).

Recent human neuroimaging studies have revealed the common and unique neural correlates of S-R and R-O associations by contrasting habitual with goal-directed control of instrumental responses (Valentin et al., 2007; Gläscher et al., 2010) and by studying the transition from goal-directed behavior to habits through extensive training (Tricomi et al., 2009; Liljeholm et al., 2015). In a variety of S-R learning tasks, studies have convincingly revealed activities in both ventral and dorsal striatum which are consistent with prediction error (PE) signals (Pessiglione et al., 2008). The R-O learning system also involves the encoding of PE signals in the striatum as well as value representations in the orbital and medial prefrontal cortices (Hare et al., 2008; Gläscher et al., 2009). Together, these findings suggest that S-R and R-O learning systems converge in the striatum and might lead to decisions concurrently. Yet little is known about how these two learning systems interact, especially during the formation of their respective associations, and it remains unclear how the ventral striatum would be recruited during learning in cases where the S-R and R-O controllers promote competing actions in parallel. The present study aims to fill this gap in the field.

To this end, we developed a two-armed bandit task, in which subjects had to choose a location (left/right) where a stimulus would appear on a computer screen with a specific probability that was unknown to the subjects. If the subject made a correct choice and the stimulus appeared in the chosen location, then and only then, the subject would receive a reward with another specific probability. The paradigm thus involves two learning objectives: (1) to learn where the stimulus is most likely to appear (i.e., S-R learning); and (2) to learn where the reward is most likely to be delivered (i.e., R-O learning). We designed two sets of experimental conditions. In the unbiased condition, the stimulus appeared with equal probability in either location and was therefore uninformative for R-O learning. In the biased condition, the stimulus appeared in one location with higher probability. Critically, the smaller reward probability was assigned to the location with the larger stimulus probability. This created a conflict between the two objectives that permitted us to disentangle the interaction of both learning systems.

Materials and Methods

Participants

A total of 29 participants were recruited from the student population at the University of Hamburg. Each participant was paid a base rate of €10 for participating in the experiment plus a bonus depending on the amount of money won during the experiment (mean ± SEM, €8.9 ± 0.26). The final analysis included 27 subjects (mean age, 26 years; age range, 20–36 years; 14 male and 13 female). Two subjects were excluded: one because of excessive head motion and the other because of failure to perform more than half responses during the task. This study was approved by the Ethics Committee of the Medical Association of Hamburg (PV3661).

Experimental design and task

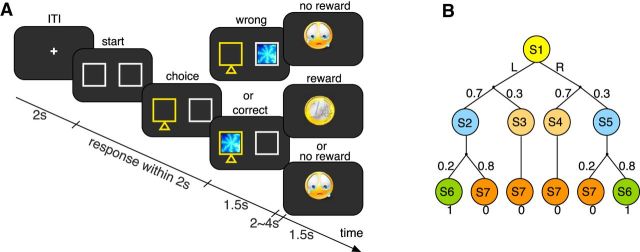
At the beginning of each trial, two lottery boxes were displayed on the left and right sides of the screen (see Fig. 1A). Subjects were instructed to predict the location of the lottery ticket by pressing a button with the right index or middle finger. If the lottery ticket appeared in the chosen location, they had a chance to win €1. If the lottery ticket appeared in the other location, they received no reward. Subjects were informed that the lottery ticket would occur on each side with a specific stimulus probability and the reward would be delivered with a specific reward probability after the lottery ticket appeared in the chosen location. As a consequence, they might or might not receive a reward, even though the ticket location had been correctly predicted. Each trial started with a 2 s interval, during which a fixation cross was presented at the center of the screen. The two lottery boxes were then displayed and subjects had to make a choice. If no choice was made within 2 s, a message “Too slow!” was displayed for 4 s and that particular trial was abandoned. The chosen box was highlighted, after which the lottery ticket in the form of a fractal image was shown for 1.5 s. After a jittered interval of 2–4 s (uniform distribution), the outcome, either a coin (indicating a reward of €1) or a crying face (indicating no reward), was presented for 1.5 s. Every participant completed 8 blocks of 40 trials. We assigned one fractal imager per block (8 in total) and instructed the subjects that every block required a different strategy. The assignment of the fractal images and the ordering of the blocks were fully counterbalanced across subjects. Every block was scanned as one run in the scanner. We conducted two runs for each of the 4 experimental conditions (for the stimulus and outcome contingencies, see Table 1), to make sure that each run was <10 min and the subjects stayed alert during learning. Behavioral results are presented in Figure 2 with within-subjects SEM (Loftus and Masson, 1994; Morey, 2008).

Figure 1.

Experimental design. A, Illustration of the lottery prediction task. Subjects had to make a choice between the two white boxes, which appeared on the left and right sides of the central fixation cross. In this example, the left box was chosen (highlighted in yellow), after which a lottery ticket (fractal image) appeared in one of the two boxes. If the lottery ticket appeared in the chosen box (here: left side), subjects could receive a coin indicating a reward of 1€ or a crying face indicating no reward. If the lottery ticket appeared in the nonchosen box, subjects always received the crying face. B, Markov decision process underlying the lottery prediction task. In the first step, the choice action a_t ∈ {L, R} leads from the initial state, s₁, to one of the four “latent states,” s₂ := (a_t = L & stim_t = L), s₃ := (a_t = L & stim_t = R), s₄ := (a_t = R & stim_t = L), s₅ := (a_t = R & stim_t = R), according to the associated probabilities for the stimulus presentation. In the second step, a transition takes place to one of the two outcome states “reward,” S₆ := (r_t = 1), and “no reward,” S₇ := (r_t = 0). Stimulus and reward probabilities shown correspond to the biased condition. Subjects can select an action only at the initial state s₁.

Table 1.

Description of experimental conditions^a

	Experimental condition	Stimulus likelihood (left, right)	Conditional reward (left, right)	Relative outcome (left, right)
Biased	1	0.3, 0.7	0.8, 0.2	0.63, 0.37
	2	0.7, 0.3	0.2, 0.8	0.37, 0.63
Unbiased	3	0.5, 0.5	0.8, 0.2	0.8, 0.2
	4	0.5, 0.5	0.2, 0.8	0.2, 0.8

^aLikelihoods for stimulus and reward presentations for the four different experimental conditions. Pairs of numbers indicate probabilities for the left (first value) and right (last value) locations. “Relative outcome” indicates the normalized product of stimulus likelihood and conditional reward.

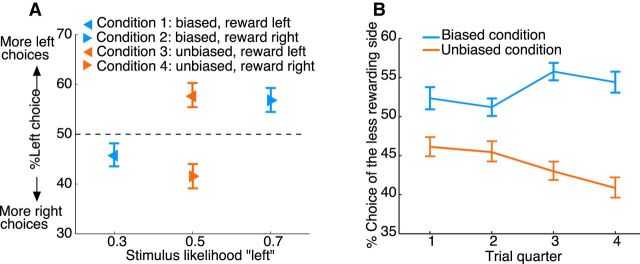
Figure 2.

Choice behavior. A, Percentage of subjects' left choices in each condition as a function of the likelihood that the lottery ticket (stimulus) appeared in the left box. Results are shown separately for the four different conditions (Table 1). The pointing direction of the triangles indicates the side of larger expected reward. Blue represents biased condition. Red represents unbiased condition. B, Percentage of choices of the side associated with lower expected reward as a function of time. Choice data were binned into four 10-trial bins (trial quarters). Blue represents data for the biased conditions. Red represents data for the unbiased conditions. Error bars indicate SEM.

Computational modeling

To explain the subjects' choice behavior, we considered 6 variants of RL models. Let a_t ∈ {L, R} denote the subject's choice of location in trial t (L, left; R, right). Let λ_t ∈ {1, 0} denote whether the subject correctly indicated the location of the stimulus (λ_t = 1) or not (λ_t = 0). The reward is denoted by r_t ∈ {1, 0}.

Reward model.

The first model is the standard Rescorla–Wagner model (Rescorla and Wagner, 1972). The expected reward EV of the chosen location is modified at each trial by a reward prediction error δ_RPE, which is given by the difference between the received and the expected rewards as follows:

α₁ is the expected reward learning rate.

Stimulus model.

The second model applies Rescorla–Wagner type of learning to estimate the expected stimulus likelihood ES, using a stimulus prediction error δ_SPE as follows:

α₂ is the stimulus likelihood learning rate.

Hybrid model.

Both EV and ES are estimated independently and then linearly combined using an interaction parameter η whose value changes with time as follows:

Because of the salience of the visual stimulus, we assume that subjects start off with stimulus learning and over time they shift to reward learning. Therefore, we applied a nonlinear weighting function (i.e., η is an exponential function of trial t) that would reflect such transitions. Both the initial value I and the slope K are fitted as free parameters; thus, this exponential function is quite flexible in capturing different functional forms of the transition (e.g., near linear decrease or exponential increase). While we assume that subjects shift from stimulus to reward learning, the empirically informed parameter estimates could also accommodate a transition from reward to stimulus learning or no transition at all. In addition, the reward and stimulus models are nested: i.e., the hybrid model reduces to the reward model when I = 0 and to the stimulus model when I = 1 and K = 0. We analyzed two variants of the hybrid model using the same (α₁ = α₂) as well as different (α₁ ≠ α₂) learning rates for the stimulus and reward updates (hybrid vs hybrid2LR model in Table 2).

Table 2.

Best-fitting model parameters and DIC values^a

Model	ΔDIC	Learning rate α		Noise parameter β	Offset I	Decay constant K
Reward	397	0.56, 0.47		0.38, 0.70	—	—
Stimulus	412	0.16, 0.11		1.13, 1.76	—	—
Hybridb	672	0.32, 0.50		2.07, 0.82	0.97, 0.92	0.09, 0.30
Hybrid2LR	667	α1	α2	1.81, 1.14	0.99, 0.86	0.02, 0.03
		0.15, 0.13	0.14, 0.42
Forward	529	0.04, 0.02		6.68, 13.35	—	—
TD FPE	608	α1	α2	1.57, 1.09	—	—
		0.14, 0.23	0.92, 0.92

^aThe differences (ΔDIC) between the DIC scores of the RL learning models and a “random choice” reference model, as well as the maximum a posteriori of the group parameters' posterior distribution. Pairs of numbers indicate parameter values derived for the biased (first value) and unbiased (last value) conditions. α₁ and α₂ indicate the respective stimulus and reward learning rates for the models, for which these values can be different.

^bBest model according to the DIC criterion.

Forward model.

“Model-based” RL requires the agents to learn a model of the environment. In the case of our lottery prediction task, the environment (i.e., each trial) is characterized by a two-step Markov decision process (see Fig. 1B). Let stim_t ∈ {L, R} denote the stimulus location at trial t (L, left; R, right). In the first step, the choice action leads the agent from the initial state, s₁, to one of the four “latent states,” s₂ := (a_t = L & stim_t = L), s₃ := (a_t = L & stim_t = R), s₄ := (a_{t =} R & stim_t = L), s₅ := (a_t = R & stim_t = R), with the associated probabilities for the stimulus presentation. In the second step, a transition takes place to one of the two outcome states, “reward” s₆ := (r_t = 1) and “no reward” s₇ := (r_t = 0). The transition functions T (s₁, a_t, s), which is the probability distribution by which the choice action a_t at state s₁ leads to the next state s ∈ {s₂,s₃, …, s₅}, and T(s, s′), which is the reward probability out of s′ ∈ {s₆,s₇}, have to be learned from experience. Let V(s) and V(s′) be the expected rewards in states s and s′. After a trial transition through s, we update:

σ_s,s′, σ_{s1, s} ∈ {0, 1} are binary indicators that equal 1 for the observed transitions and 0 for the unobserved transitions. The expected reward out of state s₁ is then given by the following:

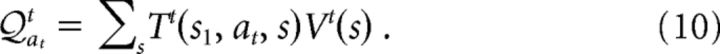Temporal-difference fictive PE (TD FPE) model.

Subjects may use information from the fact that the location of the stimulus is always revealed independently of the subjects' actions by computing FPEs to estimate the expected stimulus likelihood ES. Therefore, ESs are reestimated for both locations when the stimulus is revealed as follows:

The estimate of the expected reward EV is changed by Equations 1 and 2 when the outcome is revealed, but only for the chosen location.

Action selection.

The probability of taking a choice action for all models is given by the following:

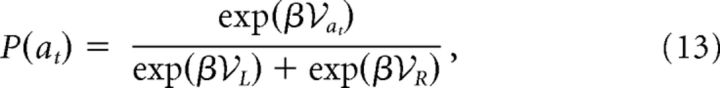with 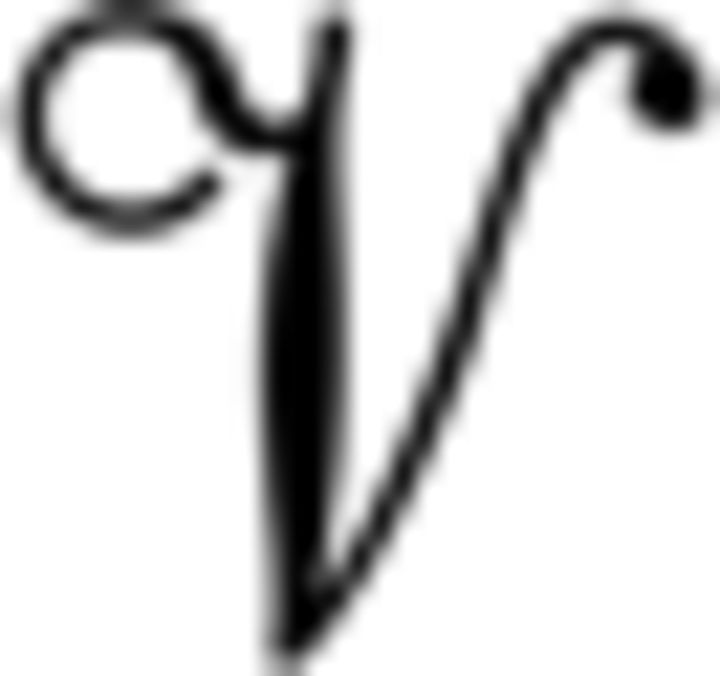∈ {ES, EV, 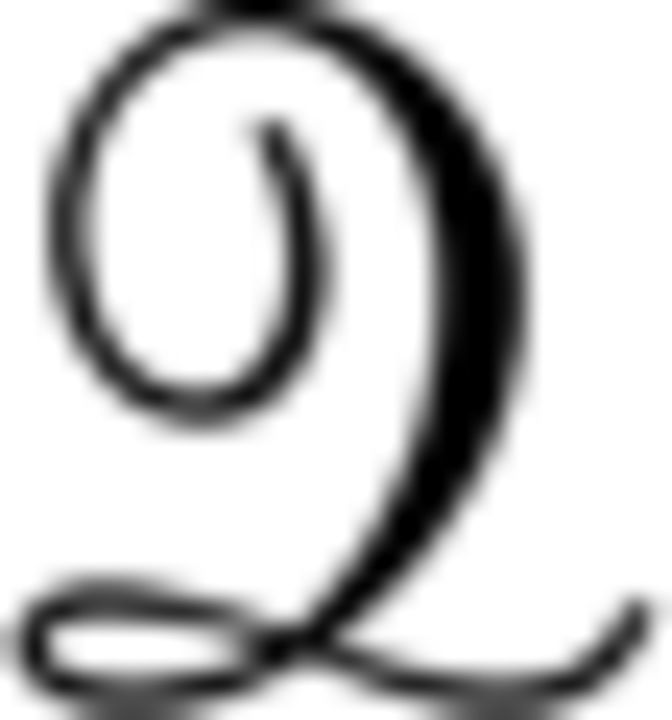} for the different RL models, respectively. β is the noise parameter, which captures the trade-off between exploration and exploitation.

Model fitting and parameter estimation

Model fitting and parameter estimation were conducted using a hierarchical Bayesian analysis (HBA) (Shiffrin et al., 2008). The model parameters that were estimated included the learning rate(s), the noise parameter, and the offset and decay constant of the interaction parameter. In the Bayesian hierarchical model, individual parameters for each participant were drawn from group-wise beta distributions initialized with uniform priors. HBA proceeded to estimate the actual posterior distribution over the free parameters through Bayes rule by incorporating the experimental data. The posterior was computed through Markov chain Monte Carlo (MCMC) methods using the JAGS software (Plummer, 2003). Three MCMC chains were run for 150,000 effective samples after 150,000 burn-in samples, which resulted in 90,000 posterior samples after a thinning of 5. Each estimated parameter was checked for convergence both visually (from the trace plot) and through the Gelman-Rubin test (Gelman et al., 2013). The maximum a posteriori of the group parameters' posterior distribution was used as the best-fitting parameter.

To quantitatively compare the model fit, we computed the Deviance Information Criterion (DIC) (Spiegelhalter et al., 2002), which is a hierarchical modeling generalization of the Bayesian information criteria. The DIC is calculated as DIC = D(θ̄) + 2p_D, where θ̄ is the average of the model parameters, D(θ̄) is proportional to a log likelihood function of the data, and p_D is the effective number of parameters, all calculated from the MCMC simulation. D(θ̄) measures how well the model fits the data, whereas p_D is a penalty on the model complexity. We reported the relative DIC scores, ΔDIC : = DIC_random − DIC_RL, where DIC_random is the DIC score of a random agent (−2 log(0.5) for two choice options), and DIC_RL is the DIC score of each candidate model. The ΔDIC scores indicate how much better computational models perform compared with the null model of random choices. The larger the ΔDIC is, the better a model fits the data. The group parameters were used to generate trial-by-trial time series for the model-based fMRI analysis because unregularized parameter estimates from individuals tend to be too noisy to obtain reliable neural results (Daw, 2011).

fMRI data acquisition

fMRI data were collected on a Siemens Trio 3T scanner with a 32-channel head coil. Each brain volume consisted of 40 axial slices acquired in descending order, with the following T2*-weighted EPI protocol: repetition time, 2260 ms; echo time, 26 ms; flip angle, 80°; field of view, 220 mm; slice thickness, 2 mm; interslice gap, 1 mm. Slice orientation was upward tilted in an oblique orientation of 30° to the anterior-posterior commissure line to optimize signal quality in the orbitofrontal cortex (Deichmann et al., 2003). Data for each subject were collected in 8 runs. The first 4 volumes were discarded to obtain a steady-state magnetization. Between runs, subjects were encouraged to take a self-paced break while keeping their heads still. In addition, a gradient echo field map (short TE, 5 ms; long TE, 7.46 ms; number of echos, 48; echo spacing, 0.73) was acquired before the EPI scanning to measure the magnetic field inhomogeneity, and a high-resolution (1 mm³ voxels) T1-weighted structural image was acquired after the experiment with an MP-RAGE pulse sequence.

fMRI data preprocessing

fMRI data analysis was performed using SPM8 (Wellcome Trust Centre for Neuroimaging, London, UK; http://www.fil.ion.ucl.ac.uk/spm/software/spm8/). All images were slice-time corrected to the middle slice. A voxel displacement map was calculated from the field map to account for the spatial distortion due to the inhomogeneity of magnetic field. Incorporating the voxel displacement map, the EPI images were corrected for motion and spatial distortions through realignment and unwarping (Andersson et al., 2001). Each subject's anatomical image was manually reoriented by setting the origin to the anterior commissure. The EPI images were then coregistered to the origin-corrected anatomical image. The anatomical image was segmented using the New Segment tool. The gray and white matter images were used with the DARTEL toolbox to create individual flow fields (Ashburner, 2007). Finally, the EPI images were normalized to the MNI space using the respective flow fields and smoothed with a Gaussian kernel of 8 mm FWHM through DARTEL's normalization tool.

Model-based fMRI analysis

We conducted model-based statistical analyses of the fMRI data (Gläscher and O'Doherty, 2010) by estimating each subject's time courses of the δ_SPE, the δ_RPE, and the interaction parameter η, using the maximum a posteriori of the model parameters' group posterior distribution. The design matrix for the first-level analysis for each of the 8 runs consisted of the following: (1) two onset regressors for stimulus and outcome presentations; (2) three parametric regressors calculated from Equations 2, 4, and 6 of the hybrid model, where the stimulus event was modulated by η and δ_SPE, and the outcome event was modulated by δ_RPE; and (3) 6 motion parameters and a constant term as nuisance regressors. All the regressors were convolved with the canonical hemodynamic response function and entered into a GLM without orthogonalization. We avoided the default orthogonalization procedure in SPM to ensure that each regressor only captures the unique signal variance (Mumford et al., 2015). Correlation of the δ_SPE and δ_RPE regressors was low (mean correlation coefficient = 0.1041, SEM = 0.0047), so was the correlation between the regressors of η and δ_SPE (mean correlation coefficient = −0.0072, SEM = 0.0035). Therefore, we were confident to identify dissociable neural correlates for each regressor, if they existed.

We calculated first-level single-subject contrasts for each regressor of the parametric modulator. We entered the contrasts of PEs to a 2 × 2 repeated-measures ANOVA analysis with factors PE (SPE, RPE) and condition (biased, unbiased) to test for a significant effect across the entire group. The contrasts of η served in the second-level group analysis as a random effect, using one-sample t tests. We chose a whole-brain-corrected threshold of p < 0.05 as our statistical threshold. In case of simple effects (e.g., the presence of a specific PE signal tested against an implicit baseline), we chose a voxel-level whole-brain FWE threshold, whereas for the more specific differential contrasts (i.e., the interaction ANOVA contrast and the η contrast), we chose a cluster-level whole-brain FWE threshold. For display purposes, we showed the statistical maps at their respective thresholds accordingly. The whole-brain-corrected cluster thresholds (Forman et al., 1995) were calculated using the 3dClustSim program in AFNI (version AFNI_16.2.09) (Cox, 1996) with the following parameters: voxelwise p value 0.001, cluster threshold 0.05, 10,000 simulations, 146,519 voxels in the whole-brain mask, and the inherent smoothness estimated from the data. The simulation determined that cluster sizes of 92–143 voxels, depending on the specific contrast analysis, corresponded to the corrected threshold.

To further show how well the parametric modulators fit the data, we plotted the regression coefficient of PE regressors with BOLD activity for the interaction effect (see Fig. 5F) and percentage signal change (PSC) for the η modulator (see Fig. 6B) using the rfxplot toolbox (Gläscher, 2009). For the interaction contrast, the search volume is defined as the region identified by the group analysis (i.e., see Fig. 5E). For the η contrast, we used an independent anatomical amygdala mask (Amunts et al., 2005) as the search volume. For each subject, the average parameters or PSCs were extracted from an 8 mm sphere centered on the peak voxel within the search volume. In Figure 6B, trials were split into 4 bins according the quartile values of η (i.e., 25th, 50th, 75th, and 100th percentiles), and the parameters were estimated for the onset regressors of each bin. These PSCs for each bin indicate the average magnitude of the BOLD response.

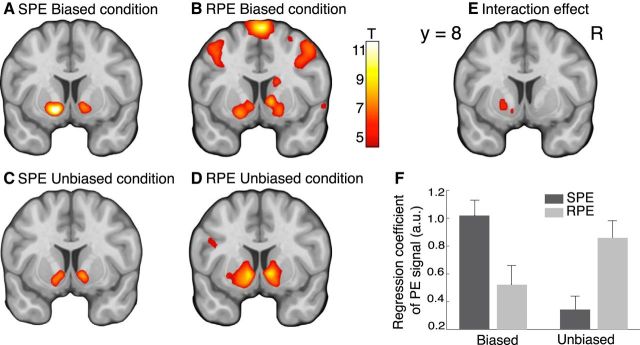
Figure 5.

Neural representations of SPEs and RPEs. A–D, Maps of the T-statistics for the correlations with the SPE and RPE from both conditions. E, Map of the T-statistics for the interaction effect with factors PE (SPE, RPE) and condition (biased, unbiased). F, Correlation of the BOLD activity with the SPE (dark gray) or RPE (light gray) regressor for each condition, regression coefficient extracted from an 8 mm sphere centered on the peak voxel within the region identified in E. Error bars indicate SEM. Results are shown at y = 8 (MNI coordinates), p < 0.05, whole-brain FEW-corrected.

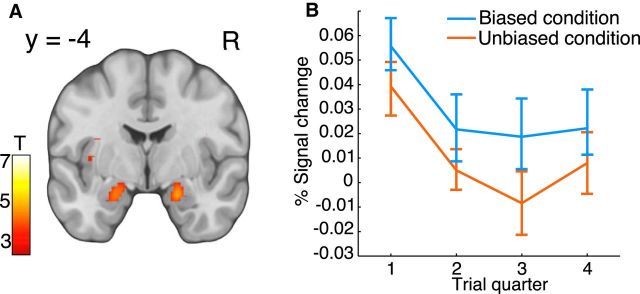
Figure 6.

Neural correlations to the weighting of S-R and R-O learning. A, Map of the T-statistics for the neural modulation by the time-dependent interaction parameter η, p < 0.05, whole-brain FWE corrected. B, Mean percentage signal change for the parametric modulator encoding η, extracted from an 8 mm sphere centered on the peak voxel within an independent anatomical amygdala mask. Trials were split into four 10-trial bins (trial quarter) according to the quartile values of the parametric regressor. Blue represents data for the biased conditions. Red represents data for the unbiased conditions. Error bars indicate SEM.

Results

Behavioral results

We recorded neural activity using fMRI while participants performed a decision-making task designed to dissociate the neural basis of S-R and R-O learning. Subjects were told a cover story which described a lottery prediction task (Fig. 1A) and were informed that they would receive the money they won by the end of the experiment. Subjects were informed about neither the stimulus nor the outcome contingencies but had to learn both from repeated trials. In the unbiased conditions, the two locations had equal stimulus probabilities (i.e., probabilities of the presentation of the lottery ticket) of 0.5. In the biased conditions, one location was associated with a higher stimulus probability of 0.7 and the other location was associated with a lower stimulus probability of 0.3. The probability of reward conditioned on the stimulus was 0.2 (0.8) at the location of higher (lower) stimulus probability (Table 1). The rationale behind this design was to provide distinct experimental contexts for the stimulus-induced S-R learning and the reward-based R-O learning. In the biased condition, subjects earned €6.9 ± 0.21 (mean ± SEM, average across subjects), which was significantly less than what would have been expected under chance performance (€7.6, average across trials, t₍₂₆₎ = 3.4, p = 0.002, one-sample t test). This suggests a rather strong influence of the “misleading” (in terms of maximizing reward) stimulus likelihood. In the unbiased condition on the other hand, subjects earned €10.9 ± 0.46 (mean ± SEM, average across subjects), which significantly exceeded the chance performance (€10, average across trials, t₍₂₆₎ = 2, p = 0.03, one-sample t test) and the performance in the biased condition (t₍₂₆₎ = 7.9, p = 2.2e-08, paired t test). This suggests that the reward probabilities had a stronger influence on subjects' decisions when the stimulus likelihood was uninformative.

Figure 2A shows the percentage of subjects' left choices in each condition plotted as a function of the probability that the stimulus appeared on the left side (stimulus likelihood “left,” Table 1). Under the assumption of a matching response, an optimal reward-learning model predicts that the proportion of left (right) choices matches the expected reward observed on the left (right) side (relative outcome, Table 1). An optimal stimulus-learning model predicts that the proportion of choices matches the stimulus likelihood. Our data, however, suggest that subjects showed sensitivity to both sources of information. In the biased condition, subjects preferred the side of higher stimulus probability but lower expected reward (Conditions 1 and 2, Fig. 2A; Table 1), deviating from the objective of maximizing reward. For instance, despite a reward bias to the left in Condition 1 (Fig. 2A, blue left-pointing triangle), subjects more often chose the right side. In the unbiased condition, subjects preferred the side of the higher expected reward (Conditions 3 and 4, Fig. 2A; Table 1). This was also revealed by a significant interaction effect in a 2 × 2 repeated-measures ANOVA with the factors of condition (biased, unbiased) and side of higher expected reward (left, right) (F_(1,26) = 18.93, p = 1.86e-04). The main effects were not significant (F_(1,26) < 1.3, p > 0.3). Furthermore, choice behavior was consistently symmetric across location-counterbalanced blocks of trials (Fig. 2A): subjects showed almost the same proportion of right choices in Condition 1: 54% (Condition 4: 59%) as the proportion of left choices in Condition 2: 56% (Condition 3: 57%) (t₍₂₆₎ < 0.79, p > 0.43, paired t test). These results suggest that choice decisions were modulated by both stimulus likelihood and expected reward.

To further explore the subjects' learning process, we collapsed data from location-counterbalanced conditions and examined the change of behavior across trials (Fig. 2B). Subjects chose the side associated with lower expected reward, but higher stimulus likelihood, more frequently in the biased condition. The mean percentage of choices of the side with lower expected reward decreased in the unbiased condition, from 46% in the first to 41% in the last quarter of the trial sequence (t₍₂₆₎ = 2.38, p = 0.01, paired t test). No such decrease was observed in the biased condition. A 2 × 4 (condition × time) repeated-measures ANOVA revealed a significant main effect of condition (F_(1,26) = 14.29, p = 8.29e-04) and a significant interaction effect (F_(3,78) = 3.1, p = 0.04). The main effect of time was not significant (F_(3,78) = 0.4, p = 0.67). These results suggest that subjects' choices were initially dominated by S-R learning because the task instructions emphasized that a reward could only be obtained if the stimulus appeared at the chosen location. However, with experience and gradually more knowledge about the probabilistic structure of the task, subjects shifted to R-O learning and chose the location with the higher reward probability to maximize their payoff, even if that meant choosing the location with the smaller stimulus likelihood in the biased condition.

Model-based analyses

We developed 6 computational models using the framework of reinforcement learning (RL) (Sutton and Barto, 1998). We fitted the RL models to subjects' trial-by-trial choices using a HBA and evaluated the relative goodness of fit by the Bayesian model comparison index DIC, which takes into account both accuracy of the fit and model complexity (for details, see Materials and Methods). Model parameters and DIC values are summarized in Table 2. A difference of DIC scores greater than 10 are considered substantial (Spiegelhalter et al., 2002).

We extended the trial-based RL schemes to simultaneously estimate both expected rewards (R-O learning) and stimulus probabilities (S-R learning) using RPEs and SPEs. Estimates were additively combined, weighted by an interaction parameter η, which decayed exponentially with time to capture a potential shift from stimulus-based to reward-based decisions (hybrid model). The hybrid model nested two simpler models: (1) a model where decisions were based on estimates of the stimulus likelihood, ignoring the fact that subjects were instructed to acquire reward (stimulus model); and (2) a model where decisions were based on estimates of reward, consistently overcoming any confounds induced by the stimulus (reward model). The DIC scores showed that the hybrid model fitted the behavioral data best, reflecting the finding that subjects' decisions were influenced by both stimulus and reward. We also evaluated a model with different learning rates for the stimulus and reward estimates (hybrid2LR model), but the model fits, quantified by the DIC, did not improve.

We then tested the hypothesis that subjects might learn stimulus–reward associations (i.e., the conditional probability of a reward given the stimulus) associated with a location. The corresponding computational model assumed that subjects built a state space of the task structure (model-based RL) (Gläscher et al., 2010) and treated the stimuli as different latent states (forward model). Although the DIC scores suggested that this model reflected the data better than the stimulus model and the reward model, it did not outperform the hybrid model. Finally, we asked whether subjects used information from the fact that the location of the stimulus was always revealed independent of subjects' actions by computing fictive PEs (counterfactual learning) (Tobia et al., 2014) for estimating the stimulus likelihood (TD FPE model), but again, the DIC scores did not prefer this hypothesis to the hybrid model.

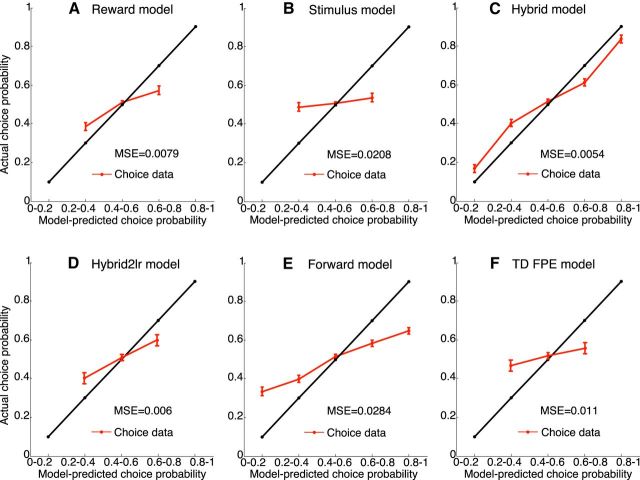
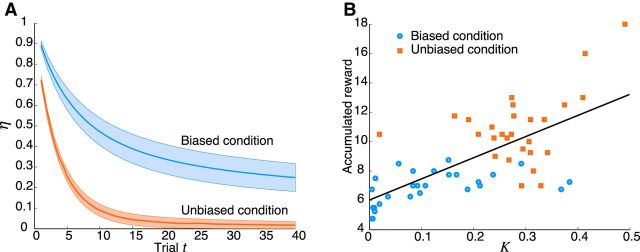
In summary, the DIC scores provided strongest evidence for the hybrid model, demonstrating that the hybrid model was performing best in predicting subjects' choices. Figure 3 compares subjects' choice behavior with the choice probabilities predicted by the RL models, showing that the hybrid model outperforms all the others. The interaction parameter η decayed more quickly in the unbiased condition, suggesting a faster transition to purely reward-based choices (Fig. 4A; Table 2). The decay constant K of η was significantly larger for the unbiased than that for the biased condition (t₍₂₆₎ = 8.4, p = 6.8e-09, paired t test). The corresponding offset values I of η were not significantly different (t₍₂₆₎ < 1.9, p > 0.06, paired t test), indicating an initial dominance of stimulus-based decisions for both conditions. Subjects' performance in terms of accumulated reward was strongly and positively correlated with the best-fitting values of the decay constant K of η (correlation coefficient = 0.68, p = 1.2e-08; Fig. 4B).

Figure 3.

Subjects' choice behavior in comparison with the choice probabilities predicted by the RL models. The figures show the fraction of subjects' choices for “left” as a function of the choice probabilities for “left” predicted by the RL models. The model-predicted action probability was split into five equal-sized bins. The black line indicates an ideal model fit, in which model-predicted choice probability (x-axis) and actual choice probability (y-axis) match perfectly. Actual choice probabilities are computed as the fraction of subjects' choices, for the trials whose model-predicted action probabilities fell into the respective bins. Red lines indicate the mean actual choice probability across subjects with respect to the model-predicted choice probability. Error bars indicate SEM. Smaller deviations between the red and the black line indicate a better model fit to the data. Comparison of the different model fits shows that the hybrid model outperforms all others.

Figure 4.

Model-based behavioral analysis. A, Interaction parameter η as a function of trial number for the biased (blue) and unbiased (red) experimental conditions. Shading represents the SEM for each subject's trace of the best-fitting η. B, Scatter plot of subjects' accumulated rewards plotted against the best-fitting decay constant K. Data indicate subjects' mean accumulated rewards, averaged across blocks of the same condition. Accumulated reward increased with larger values of the decay constant. Black line indicates the result of a linear regression (y = 14.4x + 6, r² = 0.47). Blue represents data for the biased conditions. Red represents data for the unbiased conditions.

fMRI results

Our model-based behavioral results suggest that subjects were simultaneously estimating stimulus and reward contingencies based on separate PEs and dynamically adjusted their decision strategy toward reward-based choices. Thus, we used the hybrid model for the model-based fMRI analysis. We first tested for brain regions showing changes in activity related to the SPE and the RPE because such representations would be indicative of regions supporting the S-R or R-O learning. We found a coexistence of both PEs in the ventral striatum, suggesting that this region responded to surprising stimulus events as well as to unexpected reward delivery or omission. The activation patterns of the respective PEs were different under different conditions. The SPE was stronger in the biased condition whereas the RPE was stronger in the unbiased condition (Fig. 5A–D; Table 3), which presumably reflect the fact that subjects' choices were primarily based on the stimulus likelihood in the biased condition but were more influenced by the expected reward in the unbiased condition. The interaction contrast in Figure 5E confirmed our hypothesis about specific, differential involvement of the ventral striatum in representing different PE signals in various experimental context. The interaction effect is further visualized in Figure 5F, and additional repeated-measures ANOVA (conditions × PEs) test on the regression coefficients confirmed the interaction effect (F_(1,26) = 16.69, p = 0.0004) as well. These results indicate that the shift of context from primarily S-R learning in the biased condition to primarily R-O learning in the unbiased condition modulated the PE representations in the ventral striatum.

Table 3.

Statistical results for the contrasts of the parametric regressors^a

Contrast	Region	Hemisphere	x	y	z	Peak T
SPE	Putamen	L	−14	8	−9	10.68
	Caudate	R	12	10	−6	9.79
	Inferior occipital gyrus	L	−26	−92	−6	14.03
		R	30	−92	−3	14.54
RPE	Putamen	L	−10	10	−6	9.24
	Caudate	R	12	12	−3	11.20
	Insula	L	−30	22	−6	11.56
		R	34	22	−3	12.29
	Anterior cingulate cortex	R	10	42	12	9.83
	Middle frontal gyrus	R	44	50	6	8.05
	Superior frontal gyrus	R	6	26	45	7.13
Interaction of PEs and conditions (ANOVA)	Putamen	L	−12	8	−9	4.92
Interaction parameter η	Amygdala	L	−20	−4	−18	4.91
		R	22	0	−21	6.08
	Fusiform gyrus	L	−34	−48	−15	10.46
		R	34	−36	−21	9.88
	Inferior occipital gyrus	L	−38	−76	−12	8.74
		R	38	−74	−12	10.39
	IPS/superior parietal lobe	L	−30	−60	45	6.33
	IPS/angular gyrus	R	34	−56	48	6.81

^aCoordinates for the peak voxel and its maximum T value. All peaks are corrected for a whole-brain comparison threshold of p < 0.05. L, Left; R, right; IPS, intraparietal sulcus.

We next tested for areas showing changes in activity related to the parametric modulation of the interaction parameter η. We found significant correlations in the amygdala and a decay of the PSC with time (Fig. 6; Table 3). These findings suggest that the amygdala was initially activated, when decisions were stimulus-based, but that its activation faded away as the decisions became strongly based on the expected reward. The faster decay across trials of the amygdala activation in the unbiased condition matched the faster decay of the interaction parameter η in the unbiased condition (Fig. 6B vs Fig. 4A). We also examined other regions (i.e., intraparietal sulcus, occipital and anterior visual area, Table 3) that were correlated with the interaction parameter η. After fitting an exponential function to the time courses of the PSC from each region, only the decay constants from the amygdala showed significant differences between experimental conditions (mean ± SEM, 0.18 ± 0.04 in the unbiased condition and 0.08 ± 0.04 in the biased condition, t₍₂₆₎ = 2.8, p = 0.0048, paired t test). Thus, although other regions correlated with the interaction parameter η, only the amygdala exhibited different decay constants similar to the differences in the decay constants derived from the behavioral data.

Discussion

Our fMRI analyses revealed that the activations in the ventral striatum were elicited differentially by two distinct PE signals, corresponding to stimulus and reward learning. Choice behavior was mostly consistent with the predictions of an RL model based on a time-dependent interaction of S-R and R-O associations, supporting the hypothesis that decisions are dynamically shifted from mainly stimulus-based to more reward-oriented.

Hierarchical structure of stimulus-based and reward-based learning

On each trial, our task has two levels of hierarchy (stimulus and outcome), and the subjects must update their knowledge about both events. The stimulus has no direct bearing on the subjects' actual benefit in terms of earning a greater amount of reward but initially dominates the subjects' choices. One plausible explanation is that expected values for both stimuli and rewards are represented via a common currency and reinforce actions by the same RL mechanism. Our results are most directly comparable with those of Diuk et al. (2013), which demonstrated two simultaneous, but separable, RPEs in the ventral striatum in humans performing a hierarchical gambling task. Their task also has two levels of hierarchy (casinos and slot machines), and the subjects are asked to estimate expected rewards at both levels. Their results provide neural evidence for the idea that PEs arise from events at each level of a hierarchical RL (Botvinick, 2012) but leaves open the question of whether the ventral striatum also represents PEs in response to task subroutines that are not themselves directly associated with rewards. Our results address this question by showing that the learning of a nonrewarding subroutine is driven by an SPE signal in the ventral striatum.

Implications for the ventral striatum

In addition to the original RPE hypothesis (Tobler et al., 2006), our hybrid model computes the SPEs exactly in the same way as computing the RPEs, but renders orthogonal teaching signals. This suggests that the ventral striatum may encode PE signals regardless of the specific nature of the reinforcer itself. Consistent with this idea, recent fMRI studies have revealed a much broader function of the PE computations in the ventral striatum, including state PE in model-based RL learning (Daw et al., 2011), fictive PE in counterfactual learning (Lohrenz et al., 2007), and PEs for social decision-making (Ruff and Fehr, 2014). These findings, when taken together with our results, point to a universal role of the ventral striatum in multiple forms of learning.

The BOLD activity in the ventral striatum of humans is presumably associated with the dopaminergic projections from the midbrain (Haber and Knutson, 2010), and recent physiological recordings in primates have suggested that the midbrain dopamine neurons (i.e., the RPE-coding neurons) (Bayer and Glimcher, 2005) generate PE signals in a similar manner for unrewarded sensory cues in rewarded contexts (Bromberg-martin and Hikosaka, 2009; Kobayashi and Schultz, 2014). The biological reward-learning system may thus take the reward-predicting cues as a proxy for the primary reward, which may explain why subjects make nonoptimal choices under certain circumstances. The selective representation of different PE signals in the ventral striatum, however, raises questions about the timing at the neuronal level. Does the entire population of neurons encode both prediction errors in a serial manner, but at a finer temporal scale? Or do subgroups of neurons exist, which encode the different prediction errors in parallel? Such questions invite further single-unit electrophysiological recordings in animals performing similar hierarchical tasks that require the computation of multiple, simultaneous prediction errors.

Amygdala's involvement in the stimulus and reward learning

Our results suggest that the BOLD activity in the amygdala reflects the weighting of S-R and R-O controllers, matching the one that dominates decisions. This finding is consistent with a contribution of the amygdala in representing motivational control of instrumental responses (Baxter and Murray, 2002; Balleine and Killcross, 2006). Previous studies mainly demonstrated amygdala's involvement in mediating between S-O and R-O associations by using the Pavlovian-to-Instrumental Transfer paradigm (Huys et al., 2011; Prévost et al., 2012; Hebart and Gläscher, 2015), where the two associations are learned separately and their interaction is examined afterward during extinction. However, our subjects had no prior training for associating the stimulus to primary reward. Our results therefore demonstrate that amygdala's involvement in motivational influences is not restricted to Pavlovian-to-Instrumental Transfer.

What then is the amygdala's exact role in the behavioral control of S-R and R-O associations? One possibility is that the amygdala is sensitive to environmental uncertainty. The gradual decrease of the amygdala activation in the course of our experiment is consistent with early studies (Büchel et al., 1998; Davis and Whalen, 2001) interpreting such a pattern as uncertainty or novelty coding. However, there are two sources of uncertainty in our task: one associated with the stimulus likelihood and the other associated with the reward probabilities. Both human and animal studies have demonstrated the amygdala's engagement in learning environmental contingencies (Hsu et al., 2005; Herry et al., 2007; Madarasz et al., 2016), showing greater activation of the amygdala in response to stimuli associated with greater degrees of uncertainty or unpredictability. Thus, the greater amygdala response in the biased condition of our task may reflect a greater amount of reward uncertainty due to the conflict between stimulus and reward likelihood. Computational analysis (Li et al., 2011) has also suggested that the amygdala might gate the strength of RL learning according to the estimated uncertainty (associability). A question for future research is how the amygdala might balance between different types of uncertainty that could arise between parallel learning processes.

Another possibility is that the amygdala negotiates between the S-R and R-O controllers through attention-guided value coding. Previous studies have shown that the amygdala integrates information about both the spatial configuration of visual stimuli and the reward values (Peck et al., 2013; Ousdal et al., 2014) such that the processing resources are allocated to selective information in a given situation. This explains why subjects went for the stimulus location but gradually shifted their focus to the reward location. At the neural level, the stimulus may have engaged more cognitive attention at the initial stage of learning, especially in the biased condition. The amygdala is likely to assemble different sources of information and negotiate multiple valuation systems by virtue of its anatomical and functional interconnection with the ventral visual stream (Pessoa and Adolphs, 2010), prefrontal cortex (Hampton et al., 2007), and ventral striatum (Seymour and Dolan, 2008; Popescu et al., 2009).

Stimulus-based learning and model-based RL

Our results paint a different picture of the negotiations between multiple learning systems compared with recent works contrasting model-free and model-based RL algorithms (Gläscher et al., 2010; Daw et al., 2011; Lee et al., 2014). These studies used multistep Markov tasks with uniquely identifiable state and action cues, whereas in our task the state structure is not directly identifiable. Although it is possible to formally conceptualize our task as a two-step Markov decision process (forward model in Table 2), the intermediate states have to be inferred from the presence (forward model, states 2 and 5 in Fig. 1B) or absence (forward model, states 3 and 4 in Fig. 1B) of the stimulus. Learning transitions from such nonunique intermediate states would require a high cognitive effort. Furthermore, the fact that the forward model did not provide a superior model fit to the data supports the rejection of our task as a multistep Markov decision problem.

Whereas an early study (Gläscher et al., 2010) reported evidence for a time-dependent transition from R-O to S-R learning, our computational analysis, however, showed a transition in the opposite direction. This suggests that the negotiation between the two systems might flexibly depend on the motivational context and on which system is triggered first. The initial absence of rewards in the study of Gläscher et al. (2010) triggered model-based learning of state transitions first. Our emphasis on the stimulus as an inevitable, but sometimes misleading cue on the “path to reward,” put the initial focus on S-R learning, which gradually gave way to R-O learning.

In conclusion, we found a contextual modulation of PE representations in the ventral striatum during instrumental and goal-directed learning. A parsimonious explanation for the present results is that multiple valuation systems may be integrated into a single coherent decision-making framework through the functions of ventral striatum and amygdala.