A Model of the Superior Colliculus Predicts Fixation Locations during Scene Viewing and Visual Search

Abstract

Modern computational models of attention predict fixations using saliency maps and target maps, which prioritize locations for fixation based on feature contrast and target goals, respectively. But whereas many such models are biologically plausible, none have looked to the oculomotor system for design constraints or parameter specification. Conversely, although most models of saccade programming are tightly coupled to underlying neurophysiology, none have been tested using real-world stimuli and tasks. We combined the strengths of these two approaches in MASC, a model of attention in the superior colliculus (SC) that captures known neurophysiological constraints on saccade programming. We show that MASC predicted the fixation locations of humans freely viewing naturalistic scenes and performing exemplar and categorical search tasks, a breadth achieved by no other existing model. Moreover, it did this as well or better than its more specialized state-of-the-art competitors. MASC's predictive success stems from its inclusion of high-level but core principles of SC organization: an over-representation of foveal information, size-invariant population codes, cascaded population averaging over distorted visual and motor maps, and competition between motor point images for saccade programming, all of which cause further modulation of priority (attention) after projection of saliency and target maps to the SC. Only by incorporating these organizing brain principles into our models can we fully understand the transformation of complex visual information into the saccade programs underlying movements of overt attention. With MASC, a theoretical footing now exists to generate and test computationally explicit predictions of behavioral and neural responses in visually complex real-world contexts.

SIGNIFICANCE STATEMENT The superior colliculus (SC) performs a visual-to-motor transformation vital to overt attention, but existing SC models cannot predict saccades to visually complex real-world stimuli. We introduce a brain-inspired SC model that outperforms state-of-the-art image-based competitors in predicting the sequences of fixations made by humans performing a range of everyday tasks (scene viewing and exemplar and categorical search), making clear the value of looking to the brain for model design. This work is significant in that it will drive new research by making computationally explicit predictions of SC neural population activity in response to naturalistic stimuli and tasks. It will also serve as a blueprint for the construction of other brain-inspired models, helping to usher in the next generation of truly intelligent autonomous systems.

Introduction

Saccades and fixations are essential for efficient perception and action, making these behaviors key to understanding selective attention in the brain. Modern computational models of attention predict fixations using saliency maps (Itti and Koch, 2001) and target maps (Zelinsky, 2008), which prioritize locations for fixation based on bottom-up feature contrast and top-down target goals, respectively. These models are powerful in that they are image based, meaning that they can be applied to any pattern that can be depicted in the pixels of an image, and this versatility has led to their widespread adoption and use by researchers studying the allocation of visual attention in realistic contexts. But whereas many models in this class are biologically plausible, none have looked to the oculomotor system for design constraints or parameter specification. Consequently, these models, although broadly inspiring research into the brain mechanisms coding priority, have not generated predictions of presaccadic neural activity in specific brain structures.

Conversely, models of saccade programming are tightly coupled to underlying neurophysiology. Indeed, these are primarily models of a particular brain area, the superior colliculus (SC; for review, see Girard and Berthoz, 2005). The SC is a multilayered midbrain structure implicated in saccade programming and visual attention (Krauzlis et al., 2013). SC cells have visual, visuomotor, and motor responses and are topographically organized into what can be described as visual and motor maps, each distorted by foveal magnification. Central to SC architecture is the coding of responses as point images, which are roughly circularly symmetric and size-invariant neural populations that activate in response to a visual point stimulus or before a saccade, depending on whether cells in the point image have visual or motor responses (McIlwain, 1975, 1986; Ottes et al., 1986; Munoz and Wurtz, 1995; Anderson et al., 1998; Moschovakis et al., 2001; Goossens and Van Opstal, 2006). Saccades are programmed by integrating over movement vectors in the motor point image (Lee et al., 1988). Saccade programming models capture these core neurophysiological constraints and have been hugely influential in stimulating research into the mechanism of overt attention, but they are limited in that they can accept as input only isolated coordinates in space (Ottes et al., 1986) or hypothetical distributions of neural activity (Trappenberg et al., 2001), leaving open the question of how the brain programs saccades to visually complex targets.

Saccade programming models and image-based models of attention therefore have complementary strengths and weaknesses; the former predict the neural processing leading up to a saccade but are not applicable to real-world stimuli and tasks, and the latter predict fixations in a variety of real-world contexts but are not specified at a level useful to understanding saccade programming in the brain and its interplay with attention.

Here we introduce MASC, a model of attention in the superior colliculus. MASC bridges the cognitively oriented literature focused on understanding attention allocation in complex environments with the lower-level literature focused on understanding the mechanism of overt attention in the brain, combining the strengths (and offsetting the weaknesses) of both. It does this by using image-based computational methods to create an intelligent “front end” for a primarily neural-level model of the SC, making possible the prediction of SC population activity preceding saccades to visually complex common objects and scenes. MASC generates sequences of saccades to categorically diverse real-world stimuli in the context of free-viewing and search tasks, and we test these predictions against the behavior of human participants viewing the identical stimuli and performing the same tasks. We show that MASC outperforms existing state-of-the-art models of scene viewing and visual search in its prediction of overt attention movements, a performance boost that can be attributed directly to MASC's inclusion of constraints and operations known to exist in the SC. We conclude that, although the cortical prioritization of visual information is obviously important for predicting shifts of overt attention, additional prioritization occurs in the SC, making an understanding of this structure essential to a complete understanding of overt attention.

Materials and Methods

Model methods.

MASC is a high-level model of the SC, meaning that our intent was to capture well accepted organizational principles and operations known to exist in the SC but not the fine-grained collicular circuitry. This was done so as to keep MASC simple with relatively few parameters, essential for the model to have widespread appeal among visual attention researchers. MASC is therefore a proof of concept showing that a brain-inspired model reflecting core aspects of SC organization, such as the foveal magnification of space and the use of population averaging, can predict the allocation of overt attention as well or better than state-of-the-art competitors. With respect to behavior, MASC is fixation based. Underlying each of its fixations is a repeating sequence of processing stages, starting with an image input and ending with the generation of a saccade. Figure 1 illustrates the general model pipeline. All models, like all biological systems, need parameters to work, and this is especially true for models applied to real-world tasks and stimuli. Finding good parameters is a daunting challenge for modelers, but MASC points to a simple solution. In it we assume that the brain has already found highly optimized parameters for directing overt attention and that it is in the brain that we should focus our search for design inspiration and parameter specification. Here we provide details about these parameters, each grounded in estimates from neurophysiology, for MASC's key processing stages.

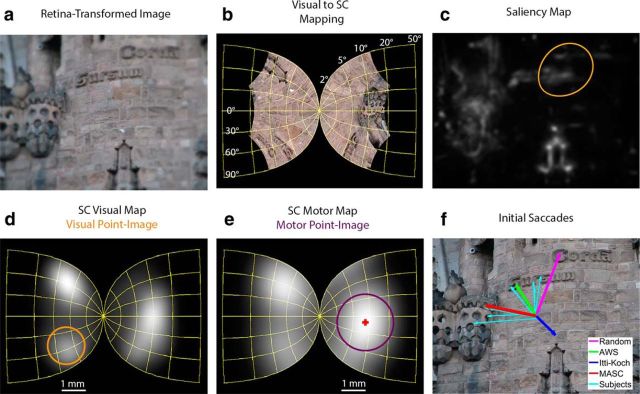
Figure 1.

Anatomy of MASC. a, Input is an image, blurred to reflect retinal acuity limitations. b, This image shown projected onto the SC. c, A priority map (here a saliency map) generated from the blurred image. d, The priority map projected into SC space, where it is averaged over visual point images computed throughout the visual map. The ring indicates the size of one visual point image; the visual receptive field for the neuron at the center of this point image is shown in c. e, Activity from d after a second stage of averaging over the larger motor point images. Shown is the maximally active point image, with the vector average of this population (indicated by the cross) determining the end point of MASC's initial saccade in visual space. f, Initial saccades from the four models tested and 8 (randomly selected from the 15) subjects.

To better equate the visual information used by MASC to human observers, at the start of each new fixation, the method from Geisler and Perry (2002) was used to blur the input image to reflect the visual acuity limitations that would exist if that image was viewed from a given fixation location (Fig. 1a). This method uses a multiresolution pyramid (Burt and Adelson, 1983) to create a resolution map indicating the degree of low-pass filtering applied to each image point relative to its distance from current fixation. The current implementation used fixed parameters that provide a reasonable estimate of human contrast sensitivity as a function of viewing eccentricity for a range of spatial frequencies (Geisler and Perry, 2002). The resulting retina-transformed version of the input image approximates the progressive blur that occurs in human vision with increasing distance from the high-resolution fovea. Both the scenes in Experiment 1 and the object arrays in Experiment 2 were dynamically retina transformed after each change in fixation, and this was done for MASC and the other image-based models to which it was compared. Note, however, that the images of targets used as cues in the exemplar search task were not retina transformed, as these objects were viewed foveally by participants.

These retina-transformed images were then used to create a priority map, a construct for capturing the biasing or prioritization of each location of visual space for the purpose of directing visual attention (Bisley and Goldberg, 2010; Zelinsky and Bisley, 2015). This prioritization can be based on many factors, two of which are considered here. One is a low-level and task-independent biasing of basic hue, orientation, and luminance feature maps at different spatial scales to obtain a single map reflecting the overall bottom-up feature contrast in an image. This prioritization of visual space is commonly referred to as a saliency map (Itti et al., 1998; Itti and Koch, 2001). There are many methods of constructing saliency maps (Borji et al., 2013), but in this study we adopted the Itti–Koch implementation from Harel et al. (2006) because it consistently outperforms other versions and because it is part of the widely accessible GBVS (Graph-Based Visual Saliency) Matlab package. This saliency map (Fig. 1c) was used in Experiment 1 by both MASC and the Itti–Koch model to prioritize the selection of saccades during the free viewing of naturalistic scenes. Experiment 2 used a search task, and in search the prioritization of visual information is captured by a target map (Zelinsky, 2008; Zelinsky and Bisley, 2015). A target map is a top-down and task-dependent (i.e., cortical) biasing of information to reflect visual similarity to a target goal. Two types of target maps were used in Experiment 2, exemplar target maps and categorical target maps.

An exemplar target map reflects a visual similarity estimate (Zelinsky, 2008) between an image of a cued target and every location in an image of a search display (Fig. 2a), obtained in the current implementation by a top-down weighting (Navalpakkam and Itti, 2007) of orientation (Bay et al., 2006) and color (Swain and Ballard, 1991) features. These features were first extracted from 450 Hemera objects (Hemera Technologies), none of which were used as targets or distractors in the search displays, to learn a Bag of Words (BoW) dictionary consisting of 200 orientation and 200 color visual words. The BoW method uses feature clustering and dimensionality reduction to obtain histogram-based descriptors for complex visual patterns (for additional details, see Csurka et al., 2004). At the start of each new fixation on every trial, we obtained the dot product between the BoW histogram representation of the cued target and the BoW histogram for each object in the retina-transformed search display and created from these values a target map (Fig. 2e). Pixel intensity on this map codes target–distractor visual similarity; thus, as illustrated in Figure 2e, the brightest points are at the location of the cued leaf exemplar target in the search display. Differences in intensity also exist between the distractors, but these more subtle differences in target–distractor similarity are less visible in this figure.

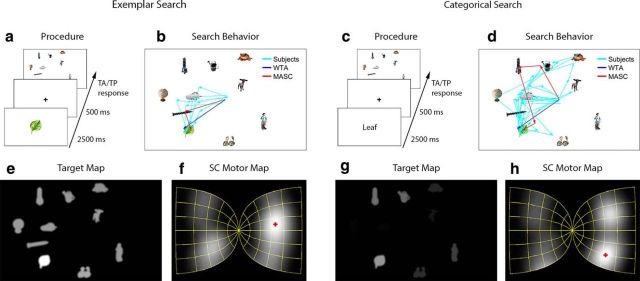
Figure 2.

Search experiments. a, Procedure for exemplar search. b, Representative exemplar search scanpaths from subjects and the models. c, Procedure for categorical search. d, Categorical search scanpaths. e, Target map for a specific leaf exemplar (shown enlarged in a). f, Motor map activity resulting from the target map in e projected onto the SC. The red cross indicates the center of the most active motor point image. Not shown is the preceding averaging over the visual map. g, Target map for the “leaf” category. h, Categorical target map projected onto the SC motor map.

A categorical target map prioritizes locations in a search display based on their visual similarity to a cued target category and is used to predict the preferential fixation of categorically defined targets during search (Schmidt and Zelinsky, 2009; Alexander and Zelinsky, 2011). A categorical target map differs from an exemplar target map in that its target–distractor similarity estimates cannot be derived directly from the target cue, now a category name (Fig. 2c, “leaf”), as the features of the text cue bear no resemblance to the features of the target object in the search display. Using the above-described BoW method and the same orientation and color features used for exemplar search, we trained 25 target/nontarget linear Support Vector Machine (SVM) classifiers (Chang and Lin, 2011) for each of 25 target categories (Fig. 3). Positive training samples were 12 target exemplars from each category, none of which appeared as targets in the search displays. Negative samples were 450 Hemera objects (same objects used to train the exemplar BoW dictionary), also a disjoint set from the testing objects. For each trial, the classifier corresponding to the cued target category was selected and distances were computed between its classification boundary and each object appearing in the search display (see also Zelinsky et al., 2013a,b,c). These distances were converted into probabilities (Platt, 1999) and plotted as a categorical target map (Fig. 2 g). Similar to an exemplar target map (Fig. 2e), intensity on this map indicates the probability of an object being the cued target, now a category of object. Note that the leaf target is less bright in Figure 2g compared with Figure 2e, resulting in a less efficient guidance of MASC's search behavior to the categorical target on this trial, similar to what was observed in the participants' behavior (Fig. 2, compare b, d).

Figure 3.

The 125 objects appearing as targets in the search displays from Experiment 2. Note that in the exemplar search task these identical objects were used as picture cues to indicate the specific target before each search display, whereas in the categorical search task the target was cued by presenting one of the 25 category names. Each of the five search set size conditions used a different target from the five target exemplars per category.

Preceding each of MASC's saccades, a saliency map or a target map is projected onto the flipped and foveally magnified map of SC space. Figure 1b illustrates these distortions, although note that the priority map, and not the raw image, is actually projected onto the SC. The projection from visual to collicular space was made using the anisotropic logarithmic mapping function from Ottes et al. (1986), which takes a pixel location in the image of radius/eccentricity R and angle/direction φ and maps it to a millimeter coordinate u (distance from the rostral pole representation of the fovea) and v (distance from the midline representation of the horizontal meridian) in collicular space:

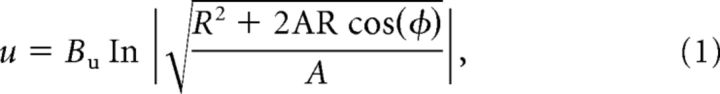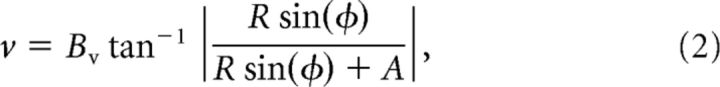where B_u = 1.4 mm, B_v = 1.8 mm, and A = 3°. The collicular map was modeled as a two-dimensional array of neurons (640 × 480 pixels), where 1 mm² of the SC mapped to 76 × 76 square pixels of the collicular map.

Once in the SC, the prioritized visual information is segregated into abstracted maps of SC visual and motor activity. The motor map in MASC reflects the responses of neurons in intermediate SC (SCi) and deeper layers showing premotor selectivity (Sparks and Hartwich-Young, 1989). Visually responsive neurons can be found in both superficial SC (SCs) and SCi (Sparks and Hartwich-Young, 1989), and the visual map reflects these responses from neurons in both layers. Treating these combined visual responses as a single map is, in part, a modeling convenience; visual biases are used identically in the programming of saccades regardless of whether they arise from salience or top-down target goals. However, this simplifying assumption also reflects the fact that several cortical areas project what appear to be saliency signals to both SCs and SCi (Schall and Cohen, 2011), making it premature, in our opinion, to be more specific in our segregation of saliency signals to particular SC layers. Although it may be the case that salience and top-down priority are represented in SCs and SCi, respectively (White and Munoz, 2011), should evidence become definitive on this point it will be trivial to implement more specialized visual maps in a future generation of MASC.

The core version of MASC assumes two cascading stages of population averaging over its visual and motor maps. Averaging first occurs over the visual point images in the SC visual map (Fig. 1d), believed to reflect short-range excitatory connections (McIlwain, 1982). Visual point images were computed by convolving the SC visual map with a Gaussian window, which we estimated from data by Marino et al. (2008) to have a diameter of 1.6 mm and a σ of 0.4 mm based on a total average area of 2 mm². Note that a visual point image is computed for each point in the projected priority map (not just the one point at the center of the ring in Fig. 1d), with this first stage of averaging being functionally equivalent to mapping out the receptive field (RF) of each neuron in the SC visual map (as shown for the RF in Fig. 1c, corresponding to a neuron at the center of the point image in Fig. 1d) and averaging activity within these RFs. The second stage averages SC activity over motor point images computed throughout the SC motor map, again the convolution of a Gaussian with the map activation (Fig. 1e). MASC's motor point image size, 2.4 mm in diameter with a σ of 0.6 mm, was also estimated from data by Marino et al. (2008) based on a total area of 4.5 mm².

To generate a saccade, MASC assumes competition between the saccade vectors coded by the motor point images. MASC is agnostic to the detailed collicular circuitry specifying where and how this competition for saccade vectors takes place, whether it is exclusively mediated by inhibitory interactions in the SCs or SCi (or both; Munoz and Istvan, 1998; Phongphanphanee et al., 2014), or perhaps even through interactions between SC layers (Vokoun et al., 2014; Bayguinov et al., 2015). We model this competition as a winner-take-all (WTA) computation performed across the landscape of motor map activity, the purpose of which is to isolate the maximally active motor point image. Averaging the movement vectors (Lee et al., 1988) over this winning ensemble of neurons in the SC motor map determines the subsequent saccade vector. For example, the red cross in Figure 1e (and Fig. 2f,h) is the coordinate in collicular space corresponding to the center of the maximally active motor point image. The corresponding coordinate in visual space, the landing position of the subsequent saccade, is indicated by the red arrow in Figure 1f and is obtained by taking the inverse of the transformation used to convert visual space to collicular space (Ottes et al., 1986). To code vertical or nearly vertical saccades MASC assumes that a motor point image, and the averaging occurring within the point image, extends across the two colliculi, consistent with the suggestions of Van Gisbergen et al. (1987) and Van Opstal et al. (1990).

Finally, after each fixation inhibition is injected into the priority map at the fixated location before its projection to the SC, implementing a form of inhibition of return (IOR; Posner and Cohen, 1984) known as inhibitory tagging (Klein, 1988; Mirpour et al., 2009; Wang and Klein, 2010). Inhibitory tagging is widely used in models of scene viewing (Itti and Koch, 2001; Garcia-Diaz et al., 2012) and visual search (Wolfe, 1994; Zelinsky, 2008) as a mechanism for breaking current fixation and generating sequences of saccades. MASC implemented inhibitory tagging by adding Gaussian-distributed activity, with a diameter of 6° and a σ of 1.5°, to the location of each fixation on a separate inhibition map of visual space, which accumulates and maintains this activity [perhaps coded by lateral intraparietal cortex (LIP); Mirpour et al., 2009]. With each new fixation, MASC then subtracts activity on the current inhibition map from activity on the new priority map before its projection onto the SC, thereby biasing the competition for the next winning motor point image against previously fixated locations. MASC's parameters were identical in Experiments 1 and 2, and the same fixation-based blurring and IOR was used in all models to which MASC was compared.

Behavioral data collection.

Two sets of behavioral data were used in this study, corresponding to Experiments 1 and 2. However, the new behavioral data collection was limited to Experiment 2, as the data from Judd et al. (2009) were used for Experiment 1. Experiment 1 stimuli were 1003 images of random-category real-world scenes, each having a horizontal visual angle of ∼30° during testing. The 15 Experiment 1 participants freely viewed each of these scenes for 3000 ms (starting from central fixation), during which their eye movements were recorded using an ISCAN ETL 400 eye-tracker (Judd et al., 2009). The original source should be consulted for additional details. Data from Experiment 2 are divided into exemplar search and categorical search tasks, which used different participants but the identical search displays. The only difference between the two was the cue used to designate the target (as shown in Fig. 2a,c). Therefore, only general methods will be provided, with task-specific methods included as they pertain to the target cue manipulation.

Experiment 2 used images of common objects (Hemera Technologies). Targets were from a dataset provided by Konkle et al. (2010), where subsets of Hemera objects were organized into categories consisting of 17 exemplars. From these, we selected five high-typicality exemplars to be used as targets from each of 25 target categories. Figure 3 shows the target categories and the specific exemplars presented to participants. Distractors were 3770 objects selected at random and without replacement from the Hemera collection, and no distractor was an exemplar of any of the 25 target categories. Objects averaged 3.5 × 3.5° in size and were arranged into 5, 10, 15, 20, or 25 object displays. Objects were placed randomly in a display with the constraints that they could not overlap or appear within 2° of the display center, a location corresponding to starting fixation. In total, 260 unique search arrays were generated (250 experimental and 10 practice), each subtending 47° horizontal and 28° vertical based on a viewing distance of 57 cm (fixed using a chinrest and headrest). Neither targets nor distractors repeated across these search displays. Stimuli were presented in color against a white background on a flat-screen CRT monitor set at a 1680 × 1049 pixel resolution and operating at a refresh rate of 100 Hz. Eye movements were recorded using an EyeLink 1000 (SR Research; tower-mount configuration) eye-tracker, which sampled the right-eye position every millisecond with an estimated accuracy of 0.25–0.50° of visual angle. Saccades and fixations were defined using the eye-tracker's default settings. Nine-point calibrations were not accepted until average and maximum tracking errors were <0.46 and 0.98°, respectively. Manual responses were made using a gamepad controller.

Participants in Experiment 2 were 30 Stony Brook University undergraduates (of either sex), 15 in the exemplar search task and 15 in the categorical search task. The number of participants in each Experiment 2 task was chosen so as to match the number of participants in Experiment 1. All had normal or corrected-to-normal vision, by self-report, and informed consent was obtained before participation in accordance with Stony Brook University's institutional review board responsible for overseeing research conducted using human subjects. Each trial began with the presentation of a target cue for 2500 ms at the center of the display, followed by a central fixation cross for 500 ms and finally by presentation of a search array. In the exemplar search task, the cue was an image of the target that was identical in size and appearance to the target in the target-present search display (Fig. 2a). In the categorical search task, the cue was the name of the target category (Fig. 2c). Participants indicated their target-present or target-absent judgment by pressing the right or left triggers of the game pad, respectively. Accuracy feedback was not provided. The 250 experimental trials, randomized for each participant and separated into two blocks (with a short break between the two), were evenly divided into five set sizes (distributed over the five exemplars per category) and target-present and target-absent trials, all randomly interleaved, leaving 25 trials per cell of the design.

Results

Free viewing

Experiment 1 tested MASC against the scene-viewing dataset from Judd et al. (2009). For clarity in making model comparisons, we will hereafter refer to this version of MASC as MASC-S, reflecting the use of only saliency information in its priority map. The 1003 scenes shown to participants were input to MASC-S in their original sizes. For each scene, MASC-S made a series of “free viewing” saccades based on the corresponding visual-saliency map projected onto the SC (see Materials and Methods, Model methods), thereby generating the data for the following analyses. Figure 4 shows representative scanpaths, each truncated to the first six saccades, from MASC-S and 6 (of 15) participants, superimposed over the scenes that were viewed. Note that only a subset of the behavioral data is visualized for each scene so as to reduce clutter and make individual scanpaths more discernable; participants were selected randomly for visualization, not to maximize agreement with the model. In all cases, MASC-S's behavior seems well within the scanpath variability of the participants. From these qualitative visualizations, it is also clear that MASC-S is not generating odd or patently artificial viewing behavior (behavior that can sometimes be hidden in more quantitative analyses).

Figure 4.

Representative scenes and scanpaths from MASC-S (red) and six participants (cyan), randomly selected from 15, showing the first six saccades made during the Experiment 1 free-viewing task.

Movie 1 provides a more detailed, but still qualitative, look at MASC-S's behavior. It shows the first 10 saccades from the model for the scene illustrated in Figure 1, along with visualizations of key processing stages underlying each of these movements of overt attention. In the top left panel, a cross indicating MASC-S's current fixation location is superimposed over a dynamically changing retina-transformed image of the scene. Note that scene locations near the cross are not blurred, whereas locations farther from the cross are. In the top right panel, a priority map (in this case a saliency map) is generated at the start of each new fixation based on the retina-transformed image from the current fixation. Note also that after each change in fixation, inhibition is injected into this map at the previously fixated location, causing the appearance of darker regions of dampened activity. The buildup of this inhibition over fixations creates a form of inhibitory tagging (Klein, 1988; Mirpour et al., 2009; Wang and Klein, 2010) that motivates the model to fixate new regions of the scene. The bottom right panel shows the predicted neural activity on the SC visual map after projection of the priority map into SC space and averaging activity over the visual point images. Note how the distribution of activity on this map changes with each saccade, reflecting fixation at a new location in visual space and the buildup of inhibition. Similarly, the bottom left panel shows predicted SC motor map activity after averaging visual map activity over the motor point images. The cross indicates the center of the most active point image, which corresponds to the landing position of the subsequent saccade (the new fixation appearing in the top left panel).

Movie 1.

Download video file ^{(826.4KB, mp4)}

DOI: 10.1523/JNEUROSCI.0825-16.2016.video.1

MASC performing a representative free-viewing task. Top left, A cross indicating current fixation location superimposed over a dynamically changing retina-transformed image of the scene. Note that scene locations near the cross are not blurred whereas locations far from the cross are blurred. Top right, The priority map (in this case a saliency map) generated from the retina-transformed image based on the current fixation location. After each change in fixation, inhibition is injected into this map at the previously fixated location, needed to motivate the model to fixate different parts of the scene. Note the buildup of this inhibition creating darker regions of dampened activity. Bottom right, The SC visual map is generated by projecting the priority map into SC space and averaging activity over the visual point images. Note how the distribution of activity on this map changes with each saccade, reflecting fixation at a new location in visual space and the buildup of inhibition. Bottom left, The SC motor map is generated by averaging visual map activity over the motor point images. The cross indicates the center of the most active point image, which determines the landing position of the subsequent saccade (top left).

To evaluate MASC-S more quantitatively, we compared its behavior with the behavior generated from two saliency models applied to the dataset of Judd et al. (2009). One of these was an Itti–Koch model (Itti and Koch, 2001), implemented by Harel et al. (2006). The other was the Adaptive Whitening Saliency (AWS) model (Garcia-Diaz et al., 2012), a top performer in a saliency model evaluation by Borji et al. (2013). These models used WTA to select points from their saliency maps for fixation, with each fixated region then tagged with inhibition to generate scanpaths. There was also a Subject model, formed by having the mean behavior of n − 1 subjects predict the behavior of the subject left out, and a Random model, which randomly selected points in an image to fixate.

Each of the first six saccades were evaluated using two measures of prediction error: saccade landing position, the Euclidean distance between the predicted and behavioral saccade landing positions from each subject, averaged over scenes and then over subjects, and a similar measure computed for saccade amplitude. Both measures are commonly used in the scanpath comparison literature (Cristino et al., 2010; Dewhurst et al., 2012). The Subject and Random models provide lower and upper limits, respectively, on these prediction-error measures. In particular, because the Subject model captures the fixation agreement among participants that could potentially be predicted by a model, the success of a model's predictions would not be expected to exceed the predictive success of the Subject model.

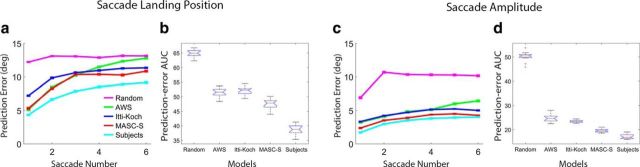
Figure 5 shows plots of prediction error for each model as a function of saccade number for the saccade landing position (Fig. 5a) and saccade amplitude (Fig. 5c) measures. Smaller errors mean better model predictions of fixation behavior. Of first note is the general tendency for predictions to become worse with an increasing number of saccades. Agreement in participants' fixation behavior lessened with each saccade, and all of the models, except Random, captured this trend in both saccade landing positions and saccade amplitudes. To evaluate MASC-S's predictive success, and to compare its predictions with the other models, for each model we obtained the area under its prediction-error curve (prediction-error AUC), an estimate of prediction error that collapses over saccades. Doing this for all 15 participants produced 15 prediction-error AUC estimates for each model. The box and whisker plots in Figure 5b show prediction-error AUC for the saccade landing position measure. Figure 5d shows the same plots for saccade amplitude. MASC-S's prediction errors were smaller than Itti–Koch, AWS, and Random for both saccade landing position (p values <0.001) and amplitude (p values <0.001), although larger than the Subject model for both measures (p values <0.05). Notably, MASC-S outperformed the Itti–Koch model despite sharing the identical saliency information (a point that we return to in the Discussion).

Figure 5.

Evaluation of MASC-S in the Experiment 1 free-viewing task. a, Mean error in predicting the landing positions of the first six saccades, plotted for MASC-S (red), an Itti–Koch model (blue), the AWS model (green), a Random model (pink), and a Subject model (cyan). Error bars indicate 1 SEM. Note that the small error bars reflect stability obtained in the data after averaging over 1003 images for each subject. b, Model comparison showing for each a box and whisker plot of the area under its prediction-error curve (AUC from the curves in a) for saccade landing position. c, Similar plot of prediction errors for saccade amplitude. d, Similar model comparison for saccade amplitude.

Exemplar and categorical search

Experiment 2 tested MASC against behavioral data from exemplar (Fig. 2a,b) and categorical (Fig. 2c,d) search tasks. Extending MASC to a search task involved simply replacing the Itti–Koch saliency map used in Experiment 1 with either an exemplar or categorical target map. We will refer to this version of the model as MASC-T, reflecting its sole use of a target map to estimate priority. Except for the type of target map that it computed and used, MASC-T's underlying operations were identical in the exemplar and categorical search tasks, as were the search displays used as input (Fig. 2, compare b, d).

Movies 2 and 3 show MASC-T's behavior and key operations for exemplar and categorical search, respectively. In the two illustrated trials the model is searching for a leaf target embedded in the same array of nine random-category distractors (top left). The cross indicates the current fixation location, which was always at the display's center at the start of a trial. Note the blurring of objects from this central viewing location and that this blurring changes with each fixation. A target map (top right) is generated from the retina-transformed image of the search display based on the current viewing location. To compute the target map in the exemplar search task, the image of the target exemplar shown to participants at cue is compared with the objects in the search display. This was done by taking the dot product between BoW histograms derived from orientation and color features extracted from the cue and search display images. Note from Movie 2 and Figure 2e that the location of the leaf target in the search display appears bright on this target map, indicating a strong target-guidance signal. Note also that fixation on the screw object resulted in inhibition that largely removed its associated activity from the target map and the SC maps. The creation of a categorical target map differs from exemplar search in that MASC-T no longer inputs an image of the target shown at cue: knowledge of the target is provided instead in the form of a trained SVM classifier. Orientation and color features are again extracted from each object in a search display, only now they are compared with the target category's SVM classification boundary to derive the categorical target map. Priority estimates on the categorical target maps were generally lower than those on the exemplar target maps. Comparing Movies 2 and 3, this difference in priority resulted in the fixation of two distractors before the target in the categorical search task, one more than the number of distractors fixated for this same image shown in the exemplar search task. The exemplar or categorical target map is then projected onto the SC visual map (bottom right), exactly as described for the free-viewing task, where activity is averaged over the visual point images. Note that the relatively small visual point images enable individual objects to be largely resolved on the visual map (most evident at starting fixation). Finally, the SC motor map is generated by averaging visual map activity over the larger motor point images (bottom left). This second stage of averaging causes the previously individuated objects to become merged into larger populations of neural activity. The cross indicates the center of the most active motor point image, which determines the landing position of the subsequent saccade (top left). Note from Movies 1–3 that the only thing differing among the scene-viewing, exemplar search, and categorical search tasks is the prioritization of visual information projected onto the SC; operations occurring within the SC, cascaded population averaging across the distorted visual and motor maps and the selection of the maximally active motor point image, were identical.

Movie 2.

Download video file ^{(369.7KB, mp4)}

DOI: 10.1523/JNEUROSCI.0825-16.2016.video.2

MASC performing an exemplar search task for a specific leaf target. Top left, Dynamically changing retina-transformed search display. The cross indicates the current fixation location, which was always initially at the center. Top right, The priority map (in this case an exemplar target map) generated from the retina-transformed image based on the current fixation location. Note that fixation on the screw object resulted in inhibition that largely removed its associated activity from the target and SC maps. Bottom right, The SC visual map is generated by projecting the priority map into SC space and averaging activity over the visual point images. Note that the relatively small visual point images enable individual objects to be largely resolved on the visual map (most evident at starting fixation). Bottom left, The SC motor map is generated by averaging visual map activity over the larger motor point images. Note that this second stage of averaging causes individual objects to become merged into larger populations of neural activity. The cross indicates the center of the most active point image, which determines the landing position of the subsequent saccade (top left).

Movie 3.

Download video file ^{(624.4KB, mp4)}

DOI: 10.1523/JNEUROSCI.0825-16.2016.video.3

MASC performing a categorical search task for the target category of “leaf.” Top left, Dynamically changing retina-transformed search display, with the cross indicating current fixation location. Top right, The priority map (in this case a categorical target map) generated from the retina-transformed image based on the current fixation location. Note that two distractors were fixated before the target, one more than the number of distractor fixations occurring for this same image presented in the exemplar search task. Bottom right, The SC visual map is generated by projecting the priority map into SC space and averaging activity over the visual point images. Bottom left, The SC motor map is generated by averaging visual map activity over the larger motor point images; the cross indicates the center of the most active point image and the landing position of the subsequent saccade (top left). Note that the only thing differing among the scene-viewing, exemplar search, and categorical search tasks is the prioritization of visual information projected onto the SC; operations occurring within the SC, cascaded population averaging across the visual and motor maps and the selection of the maximally active motor point image, were identical.

Behavioral eye movement data from both the exemplar and categorical search tasks were analyzed using two measures of search guidance: distance traveled, computed by summing saccade amplitudes until gaze reached the target, and target-first-fixated, the proportion of trials in which the target was the first fixated object during search. The distance-traveled measure captures weak guidance effects that accumulate over multiple search saccades, while the target-first-fixated measure captures strong and immediate guidance to a target. Note that these are not the same measures used in Experiment 1, and the reason for this is because the tasks themselves differ. Fundamental to a search task is the concept of a target, requiring that dependent measures of performance be relative to the target goal. Our focus on measures of search guidance is therefore appropriate; changes in guidance reflect different representations of the cued target and the match between this target representation and the target's actual appearance in a search display. Targets are undefined in a free-viewing task, making measures of target-related guidance impossible.

Although goal-directed biases, to the extent that they exist in free viewing, are unknown, in the case of search top-down prioritization and bottom-up salience might both affect movements of overt attention. We therefore consider another version of MASC that combines bottom-up and top-down biases into a single priority map that is then projected onto the SC, rather than just a target map or just a saliency map. We refer to this combined model as MASC-T.S, with the T.S designation indicating a dot product (Peters and Itti, 2007) between the target map (either exemplar or categorical) and the bottom-up saliency map (Harel et al., 2006). Except for its use of both salience and top-down target goals to determine priority, MASC-T.S and MASC-T are identical, thereby enabling a meaningful analysis of how saliency biases affect target guidance in the context of search.

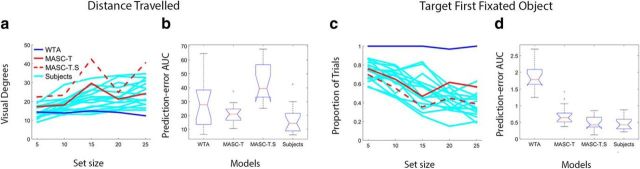
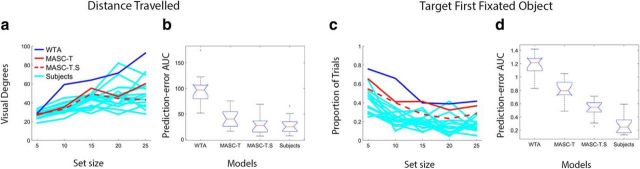
Turning first to the exemplar search data, of the 1875 target-present behavioral trials (125 × 15 subjects), 4% were excluded because of participants making a target-absent response (scored as a “miss”). Trials were also excluded if initial fixation was not at the display's center or if a participant failed to fixate the target before making a judgment, leaving 1427 trials for analysis. Mean saccade distance traveled and the proportion of target-first-fixated trials were calculated for MASC-T and MASC-T.S just as they were for the behavioral data. Figure 6a shows saccade distance traveled for both versions of MASC and all 15 participants as a function of set size. Although there is high variability in the behavioral responses, clear evidence exists for a positive set size effect in this measure; gaze moved a greater distance as objects were added to the search display (p < 0.001). To test whether MASC-T and MASC-T.S exhibited a comparable set size effect, we correlated their predicted distance traveled at each set size with the behavior of individual participants. Combining these using a Fisher z-transformation, we obtained significant correlations of 0.67 (p < 0.01) for MASC-T and 0.51 (p < 0.05) for MASC-T.S, indicating that MASC captured the same positive trend. Figure 6c plots the proportion of trials in which the target was the first fixated object, again as a function of set size. Replicating a previously reported pattern (Zelinsky et al., 2013a), here we found a negative set size effect; immediate guidance to the target decreased with increasing set size. Moreover, this trend existed in the behavioral data (p < 0.001), for MASC-T (r = 0.64; p < 0.01), and for MASC-T.S (r = 0.78; p < 0.01), based again on an averaged correlation after Fisher z-transformation. Comparing the two versions of MASC, MASC-T better captured the behavioral trend in saccade distance traveled. Both models successfully predicted target-first-fixated, although MASC-T.S predicted a slightly lower proportion of immediate target fixations. These differences can be explained by bottom-up salience interfering with the efficient top-down guidance of attention to a search target, supporting previous work showing that humans largely discount salience in their prioritization of attention movements when knowledge exists about an exemplar-specific target goal (Chen and Zelinsky, 2006; Zelinsky et al., 2006).

Figure 6.

Evaluation of MASC in the Experiment 2 exemplar search task. a, Plots showing mean distance traveled to the target for all subjects (cyan), MASC-T (solid red), MASC-T.S (dashed red), and WTA (blue), as a function of set size. b, Box and whisker plots comparing prediction-error AUC computed from MASC-T, MASC-T.S, WTA, and a Subject model for distance traveled to the target. Note that AUC was calculated from prediction-error curves (not shown) derived from the data in a. c, Plots showing the proportion of trials in which the target was the first fixated object for participants and the models. d, Box and whisker plots comparing MASC-T, MASC-T.S, WTA, and Subject model prediction-error AUC for the conservative target-first-fixated measure of search guidance.

We also evaluated MASC by comparing its performance with a WTA model that made its saccades to maximally active points on the same target map used by MASC-T. The inputs to WTA were also the same retina-transformed search images input to MASC, and the model used the identical inhibitory tagging process to generate scanpaths. The behavior of WTA is shown by the blue functions in Figure 6, a and c, where it can be seen that this model captured neither the positive set size effect observed in saccade distance traveled to the target (Fig. 6a) nor the negative set size effect observed in the proportion of target-first-fixations (Fig. 6c). Moreover, WTA predicted an unrealistically strong level of target guidance. This was expressed as an underestimation of saccade distance traveled and an overestimation of the proportion of cases in which the target was fixated first, where WTA predicted that this should happen on nearly every target-present trial. In contrast to WTA's unrealistic behavior, MASC produced more human-like levels of target guidance for both measures. The reason why MASC did not similarly outperform participants in this regard, despite the model having perfect knowledge of the target's appearance, stems from its use of Gaussian convolution over foveally magnified SC visual and motor maps. This Gaussian averaging, combined with the retina-transformed visual inputs, resulted in a blurring of the priority signals and, in turn, the frequent fixation of distractors that appeared at less eccentric visual locations than the target. As was the case for its conceptual predecessor (Zelinsky, 2008), the assumption of a foveated retina, now in combination with constraints introduced by the SC, was essential to MASC's generation of realistic search behavior.

As in Experiment 1, we also conducted a more quantitative analysis comparing MASC-T and MASC-T.S with both WTA and the Subject model. To make this comparison, we obtained prediction-error curves for our two measures by subtracting the behavior of each model from each of the 15 subjects and taking the absolute value of the error. For the Subject model, each subject's behavior was subtracted from the average behavior of the remaining subjects. We then computed prediction-error AUC for each model, which we show as bar and whisker plots in Figure 6b for distance traveled and in Figure 6d for target-first-fixated. For both of these measures, MASC-T's behavior did not differ reliably from the Subject model (p values ≥0.3). MASC-T.S differed from the Subject model for distance traveled (p < 0.01) but not for target-first-fixated (p = 0.5). This better performance by MASC-T suggests that a target map is a better predictor of fixations than a combined target–saliency map in the context of exemplar search. Salience may play less of a role in the direction of the later saccades in a sequence, resulting in a greater prediction error for MASC-T.S in distance traveled. In contrast, WTA was significantly less predictive of target-first-fixated than MASC-T, MASC-T.S, or the Subject model (p values <0.01), suggesting that either version of MASC is preferable to a model that simply makes saccades to the peaks on a target map.

Figure 7 shows parallel analyses conducted on data from the categorical search task. Behavioral data were trimmed as before to exclude misses (8%) and cases in which fixation did not start at the display's center or end on the target, leaving 1508 of the original 1875 target-present trials for analysis. Participants again varied greatly in saccade distance traveled (Fig. 7a), but the same positive trend of distance increasing with set size was observed (p < 0.001). In fact, this trend was more pronounced than in the exemplar search task (note the different y-axis scale), reflecting the greater difficulty of categorical search. Both versions of MASC captured this set size effect, indicated again by significant correlations with individual participants (average r after Fisher z-transformation was 0.87 for MASC-T, p < 0.01, and 0.87 for MASC-T.S, p < 0.01). In contrast, the WTA model now underestimated search efficiency by predicting too steep of a set size effect. For the more conservative target-first-fixated measure (Fig. 7c), all of the models captured the observed decrease in guidance with increasing set size (averaged r = 0.88 for MASC-T, p < 0.01; 0.83 for MASC-T.S, p < 0.01; and 0.75 for WTA, p < 0.01). However, the models all overestimated the proportion of target-first-fixated trials, with the relatively low immediate target fixation rate for MASC-T.S making it best aligned with the behavioral data in this more challenging search task.

Figure 7.

Evaluation of MASC in the Experiment 2 categorical search task. a, Plots showing mean distance traveled to the target for all subjects (cyan), MASC-T (solid red), MASC-T.S (dashed red), and WTA (blue), as a function of set size. b, Box and whisker plots comparing MASC-T, MASC-T.S, WTA, and Subject model prediction-error AUC for distance traveled to the target. c, Plots showing the proportion of trials in which the target was the first fixated object for subjects and the models. d, Similar model comparison for the conservative target-first-fixated measure of search guidance.

Prediction-error curves were again computed for MASC-T, MASC-T.S, WTA, and a Subject model, as described for exemplar search, and the area under these curves is plotted for saccade distance traveled (Fig. 7b) and target-first-fixated (Fig. 7d). MASC-T and MASC-T.S outperformed WTA for both measures (p values <0.001; comparing AUC against behavior) and did not differ reliably from the Subject model in predicting distance traveled to the target (p > 0.5). As in the case of exemplar search, MASC-T was more predictive than WTA despite both models using the same target maps. MASC-T.S outperformed MASC-T for target-first-fixated (p < 0.01), although it was still significantly less predictive of behavior than the Subject model (p < 0.01).

In summary, whereas MASC-T and MASC-T.S performed similarly and both better than WTA, MASC-T.S's predictions were as good or better than MASC-T, except in the case of the distance-traveled measure for the exemplar search task. The fact that MASC-T.S performed best in the context of categorical search dovetails nicely with the relatively weaker level of guidance observed in this task; as top-down guidance from the target goal became weaker, bottom-up guidance likely played a larger role. Finally, although this general preference for MASC-T.S is not intended to suggest that bottom-up and top-down priority signals are combined before their projection to the SC (as opposed to being combined within the SC itself), the observed improvement in prediction does suggest that both sources of bias are ultimately integrated and used by the SC to guide overt attention.

Predicting weakly guided searches

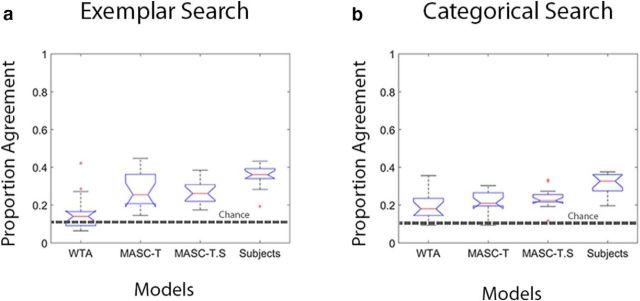
The analyses so far showed that MASC successfully predicted the proportion of trials in which participants first fixated the target during their search. However, these were the trials in which the target generated a strong guidance signal, the easy trials with respect to search difficulty. Here we evaluate model predictions on the more difficult search trials, ones where the target was not the first fixated object. These difficult trials provide a more stringent test of the models, requiring them to predict the directions of the initial saccades when participants failed to look immediately to the target. For each subject, we isolated the trials in which the target was not the first fixated object and determined the proportion of those trials where the models' initial saccade was in the same direction (+/−22.5°) of the participant's initial saccade axis, a measure we refer to as proportion of agreement. We also calculated the level of fixation agreement among subjects to establish an upper limit on prediction success. This Subject model was calculated on a subject-by-subject and trial-by-trial basis; for a given trial in which subject x made his or her initial saccade in direction y, where y is a direction away from the target, what proportion of the other subjects also looked initially in direction y?

The results are shown in Figure 8 for both exemplar and categorical search tasks. To the extent that direction predictions are above chance, based on a random selection of 45° segments over 360°, this would be evidence for a model capturing agreement in where participants looked initially when not looking toward the target. Moreover, to the extent that predictions do not differ from the Subject model, this would be evidence that these predictions are as good as could be expected given the variability in the participants' looking behavior. The MASC models were above chance in predicting the direction of participants' initial saccades. This was true for exemplar (p values <0.01) and categorical (p values <0.01) search, although this agreement was slightly but significantly less than the agreement among participants (p values < 0.05, except in the case of exemplar search where MASC-T did not differ from the Subject model, p > 0.1). Compared with either version of MASC, WTA was significantly worse at predicting participants' initial saccade direction during exemplar search (p < 0.01), largely because of its over-prediction of immediate target fixations on these difficult search trials. No reliable differences were found between WTA and MASC for categorical search. To summarize, the MASC models passed a very difficult test; they predicted where participants initially shifted their attention on trials in which the target was not immediately fixated, and they did this nearly as well as could be expected given the agreement in search behavior.

Figure 8.

Model evaluation of predicted initial saccade direction for exemplar and categorical search trials in which saccades were not directed initially to the target. a, Box and whisker plots comparing WTA, MASC-T, MASC-T.S, and a Subject model in their ability to predict initial saccade direction on difficult exemplar search trials. The proportion of agreement in initial saccade direction is calculated between participants and each model and averaged over trials in which the target was not the first fixated object. The dashed line indicates the chance level of agreement based on 45° angular segments and a random direction of initial saccades. b, A similar model evaluation performed for categorical search.

Dissecting MASC: one versus two stages of averaging

We know that MASC generally outperformed its competitors and that this better performance stemmed from its inclusion of core principles of SC organization in its design. But which of its collicular constraints is responsible for this improvement? Here we explore one of these, the role played by a second stage of population averaging. MASC's architecture includes two cascading stages of population averaging, first over visual point images and then a second over motor point images. This design choice was motivated by neurophysiological studies, spanning monkey, cat, and rodent, showing different-sized visual and motor point images in the same SC layer (SCi; Marino et al., 2008) and across different layers (McIlwain, 1975; see also Phongphanphanee et al., 2014). However, recent work by Vokoun et al. (2014) has called this assumption into question. Recording from slices of rodent SC, they observed integration of neural responses in SCs after stimulation of neurons in SCi. This provocative finding suggests that there may be only one stage of population averaging in the SC, not two.

To speak to this possibility, we dissected MASC to determine the effect of one versus two stages of population averaging on its prediction of fixations. We did this by comparing the two-stage version of MASC described in Materials and Methods, Model methods, with versions of MASC that used only a single stage of Gaussian averaging. To settle on a single averaging window for comparison with MASC, we varied window size to best predict the critical separation between two stimuli leading to the breakdown of saccade averaging reported by Vokoun et al. (2014) using a saccade-targeting task. We define this breakdown in averaging by at least 50% of the initial saccades landing on one or the other of the dual targets rather than at an intermediate location between the two. Given that the emergence of bimodality in the landing position distribution was gradual, a range of averaging window sizes predicted their psychophysical data equally well. Coincidentally, we found that the motor point image estimated from Marino et al. (2008) and already used by MASC fell within this range, so we adopted this window size for our single stage of averaging. We refer to these single-averaging models, otherwise identical to MASC-S and MASC-T, as MASC-Sm and MASC-Tm, with the “m” designation indicating that there is only one stage of averaging over a window corresponding to the motor point image (2.4 mm in diameter with a σ of 0.6 mm). For completeness, we also included single-averaging versions of MASC having a smaller averaging window (1.6 mm in diameter with a σ of 0.4 mm) corresponding to the estimated visual point image. We refer to these versions as MASC-Sv and MASC-Tv.

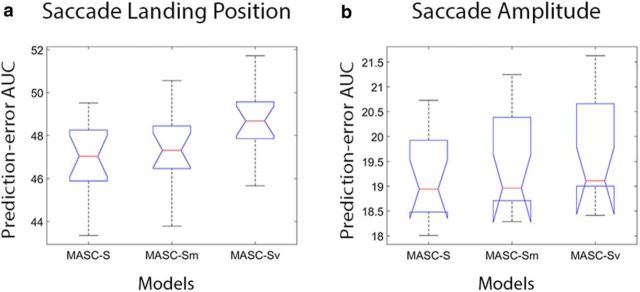
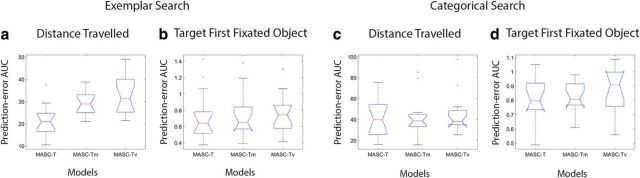
Figure 9 shows an evaluation of these models for the Experiment 1 free-viewing data. MASC-S numerically outperformed MASC-Sm and MASC-Sv, but the only difference in prediction-error AUC attaining statistical significance was between MASC-S and MASC-Sv for the saccade landing position measure (p < 0.05). Results for the two search tasks from Experiment 2 are shown in Figure 10. Here again, MASC-T generally outperformed MASC-Tm and MASC-Tv, although only the comparisons of distance traveled for exemplar search were statistically significant (MASC-Tm, p < 0.05; MASC-Tv, p < 0.01). Collectively, these data suggest a predictive advantage for two stages of population averaging in the SC rather than just one. Specifically, a version of MASC implementing the architecture suggested by Vokoun et al. (2014), one using a single averaging window that best predicted the saccade averaging observed in a behavioral dataset, cannot be preferred over dual-averaging versions of MASC. However, the small differences observed make the results from this computational experiment inconclusive; additional experimental work is needed to gain clarity on how rodents and primates differ with respect to integration and competition operations occurring within the SC circuit.

Figure 9.

Evaluation of how the number of SC averaging operations (1 vs 2) and the profiles of the averaging windows (corresponding to motor and visual point image estimates) affect model predictions in the Experiment 1 free-viewing task. a, Box and whisker plots of prediction-error AUC for saccade landing position comparing dual-averaging (MASC-S) and single-averaging (MASC-Sm and MASC-Sv) versions of the model. b, Similar model comparison for saccade amplitude.

Figure 10.

Evaluation of how the number of averaging windows and their profiles affect model predictions in the Experiment 2 search tasks. a, Box and whisker plots comparing MASC-T, MASC-Tm, and MASC-Tv prediction-error AUC for saccade distance traveled to the target during exemplar search. b–d, Similar model comparisons for target-first-fixated in exemplar search (b), distance traveled in categorical search (c), and target-first-fixated in categorical search (d).

Discussion

MASC is an image-based computational model of attention in the superior colliculus. We tested its predictions against fixation behavior observed in free-viewing, exemplar search, and categorical search tasks, and for all three tasks found that these predictions were as good or better than those from more specialized, state-of-the-art models. Such generalization across tasks is uncommon and speaks to MASC's robustness. But what most distinguishes MASC from other image-based models of attention is that it was inspired by the brain. MASC outperformed comparable competitors despite using the identical, cortically derived attentional priority signals (the same priority maps), a finding that highlights the role played by processing internal to the SC in predicting fixations. Part of MASC's predictive success stems from its adoption of organizing principles central to the SC, a structure that programs the behaviors being predicted (saccades). MASC's parameters and their values were also firmly grounded in SC neurophysiology, and herein lies another core reason for its success. Whereas other models adopt the less principled approach of searching large spaces to find parameters that best fit data, in MASC we assume that this search is unnecessary—that the brain already found the best parameters.

MASC follows other brain-inspired models of attention in that it is grounded in a biased-competition framework (Desimone and Duncan, 1995; Desimone, 1998). Making a saccade to a location in visual space requires selecting one motor vector from the many thousands of others that would have brought attention to different scene locations (Zelinsky, 2012). This selection is not random, but rather is biased by priority maps (Bisley and Goldberg, 2003, 2010; Zelinsky and Bisley, 2015) toward patterns matching a high-level goal (Zelinsky, 2008) or having pronounced low-level feature contrast (Itti and Koch, 2001). Although MASC assumes the existence and use of cortically derived priority maps for directing visual attention, it also incorporates into its design core principles of the SC that are fundamental to its organization and function: an over-representation of foveal information, size-invariant population codes, population averaging over visual and motor maps, and competition between motor point images for saccade vectors. Under MASC, these factors further modulate priority internal to the SC, a position that dovetails with evidence suggesting that the SC plays a causal role in selective attention (Carello and Krauzlis, 2004; McPeek and Keller, 2004). In particular, the population-averaging operations performed over the distorted visual and motor SC maps reprioritize the cortically derived priority signals and ultimately change the programming of saccades. MASC's mechanism for selection is also brain inspired. Rather than having a saccade's landing position be determined by the location of peak activity on a priority map, under MASC the selection of a saccade vector is determined by a competition between neural populations in the SC motor map. The competition for where attention should be shifted in space is therefore biased both by priority signals originating in the cortex (Fecteau and Munoz, 2006) and by processing occurring subsequent to the projection of these biases to the SC.

MASC differs from other biased-competition models of attention in that it is a proof of concept for how neural population averaging in the SC, a principle at the core of saccade programming (Lee et al., 1988), can be realized in the form of an image-based model. It shows that the averaging of priority signals before the competition for selection results in different, and better, predictions of saccade landing positions, a demonstration arguing against the continued neglect of population averaging in the image-based modeling of attention. MASC also provides a theoretical framework for studying the relationship between population averaging and the attentional modulation of neural activity in the context of realistic stimuli and tasks. For example, the current implementation of MASC assumed that averaging occurred over fixed-size point image populations, but what if this assumption was wrong? The literature is relatively settled on the translation-invariant property of SC point images (McIlwain, 1986; Munoz and Wurtz, 1995; Goossens and Van Opstal, 2006), but the profile of this translation-invariant averaging window has not been systematically explored outside the context of simple saccade-targeting tasks using highly impoverished stimuli. Indeed, given the ample evidence that attention can modulate the sizes of RFs in V4 and LIP (Connor et al., 1997; Ben Hamed et al., 2002; Anton-Erxleben and Carrasco, 2013), the opposite assumption is more likely: that point image profiles in the SC can similarly be modulated by attention and task demands. Following Ottes et al. (1986), MASC also assumed that SC point images are circularly symmetric. However, more recent studies have challenged this notion, suggesting that population-activity profiles might be biased toward the fovea (Munoz and Wurtz, 1995; Meredith and Ramoa, 1998; see also Anderson et al., 1998) or away from it (Phongphanphanee et al., 2014; Bayguinov et al., 2015), as a result of rostrocaudal asymmetries in lateral inhibitory connections. MASC can drive research into these questions by generating testable predictions for how differently sized attention-modulated point images should be expressed in neural and behavioral responses and by testing different population-activity profiles to determine which best accounts for saccadic behavior.

Finally, MASC differs from other models of saccade programming in that it is computational, meaning that its predictions can be derived from the same images shown to participants (Tsotsos and Rothenstein, 2011). This is a significant contribution. MASC's versatile image-based “front end” allows for computationally explicit predictions of behavioral and neural responses to visually complex objects and scenes, something that was not previously possible. Specifically, it predicts sequences of behavioral responses (saccade scanpaths) and the neural landscapes of activity across the SC's visual and motor maps preceding each eye movement. Although testing MASC's behavioral predictions was the focus of the present study, its predictions linking neural activity to attentional priority can also be tested by recording from the SC and directly observing neural responses, potentially revealing dissociations between saliency and goal-directed activity at different anatomical layers. The fact that these and other predictions would be possible using common objects and scenes as stimuli means that it will no longer be necessary to sacrifice visual complexity for prediction specificity; MASC allows for both.

But the current implementation of MASC is not without limitations. For one, MASC makes the simplifying assumption that there exist saliency maps and target maps of visual space without addressing the various cortical origins of these maps (Fecteau and Munoz, 2006). MASC also fails to consider the potentially different organizations of different priority maps, and how each might project to the SC. For example, MASC assumed that priority maps respect the same logarithmic transformation from visual to SC space described by Ottes et al. (1986). This assumption is partially justified by work showing consistencies in the gross cortical representation of visual space (Schwartz, 1980; Van Essen et al., 1984; Bruce and Goldberg, 1985; Sommer and Wurtz, 2000), but it may nevertheless prove to be false. MASC would need to be modified should new neurophysiological studies of these cortical areas show different visual mappings and/or afferent connectivities to the SC. Relatedly, MASC's predictions of fixation behavior were based on a visuomotor transformation identified in monkeys (Ottes et al., 1986), not humans. However, the fact that MASC performed as well as it did despite potential species differences in the structure and dimension of the SC means that its predictions might improve once this transformation is specified in humans and incorporated into MASC. It would be interesting to compare the saccadic behavior of humans and monkeys performing the same scene-viewing and search tasks to see which is best described by the model. Another limitation of MASC is that it neglects the time course of activation buildup in the SC, making MASC currently unable to predict saccade latencies or other time-dependent processes affecting the orienting of overt attention. This omission was intentional, as our goal in developing MASC was to provide a proof of concept before introducing temporal dynamics that might obscure the model's simplicity. A related limitation is that MASC is only a high-level model of the SC, one capturing its core organizing principles but not its detailed circuitry. This, too, was intentional so as to maintain simplicity and encourage widespread use. It would be an interesting direction for future work to systematically add in these details and determine how each contributes to even better predictions of saccade target selection in the context of visually complex stimuli and tasks. Finally, the SC is only one structure in a much larger attention network. We focused on the SC so as to highlight the unique role this structure plays in integrating cortically derived priority signals into a saccade program, but future work will need to adopt a more systems-level perspective that better situates MASC alongside the other brain structures implicated in overt attention. These limitations and simplifying assumptions will be addressed in future work, where the next generation of MASC will attempt to predict not just where activity should, and should not, be highest across the SC, but also the time course of this neural activity and from where top-down biases originate in the larger network of brain areas serving selective attention.