Social Status–Dependent Shift in Neural Circuit Activation Affects Decision Making

Abstract

In a social group, animals make behavioral decisions that fit their social ranks. These behavioral choices are dependent on the various social cues experienced during social interactions. In vertebrates, little is known of how social status affects the underlying neural mechanisms regulating decision-making circuits that drive competing behaviors. Here, we demonstrate that social status in zebrafish (Danio rerio) influences behavioral decisions by shifting the balance in neural circuit activation between two competing networks (escape and swim). We show that socially dominant animals enhance activation of the swim circuit. Conversely, social subordinates display a decreased activation of the swim circuit, but an enhanced activation of the escape circuit. In an effort to understand how social status mediates these effects, we constructed a neurocomputational model of the escape and swim circuits. The model replicates our findings and suggests that social status–related shift in circuit dynamics could be mediated by changes in the relative excitability of the escape and swim networks. Together, our results reveal that changes in the excitabilities of the Mauthner command neuron for escape and the inhibitory interneurons that regulate swimming provide a cellular mechanism for the nervous system to adapt to changes in social conditions by permitting the animal to select a socially appropriate behavioral response.

SIGNIFICANCE STATEMENT Understanding how social factors influence nervous system function is of great importance. Using zebrafish as a model system, we demonstrate how social experience affects decision making to enable animals to produce socially appropriate behavior. Based on experimental evidence and computational modeling, we show that behavioral decisions reflect the interplay between competing neural circuits whose activation thresholds shift in accordance with social status. We demonstrate this through analysis of the behavior and neural circuit responses that drive escape and swim behaviors in fish. We show that socially subordinate animals favor escape over swimming, while socially dominants favor swimming over escape. We propose that these differences are mediated by shifts in relative circuit excitability.

Introduction

In many social species, dominance hierarchy formation facilitates group organization, and social ranks are easily discerned through differences in behavior patterns (Wilson, 1975). Group members are faced with behavioral choices that promote the execution of critical motor outputs over less urgent ones. Often, these decisions are dictated by context-dependent integration of social cues. The neural bases underlying these behavioral decisions and the dynamics of neural circuits that permit animals to adapt to changes in social environment have been investigated in invertebrates and vertebrates (Yeh et al., 1996; Neumeister et al., 2010; Whitaker et al., 2011; Pearson et al., 2014; Chang et al., 2015; Platt et al., 2016).

Zebrafish (Danio rerio) has emerged as a model system in behavioral neuroscience and is used to study social stress (Giacomini et al., 2016), major depressive disorders (Manuel et al., 2014; Fonseka et al., 2016), and aggression (Paull et al., 2010; Oliveira et al., 2011), and their social behaviors have been well described (Dahlbom et al., 2012). When paired, zebrafish interact aggressively with ritualized displays that increase in intensity until a social dominance emerges. A stable social dominance consists of dominant and subordinate individuals (Larson et al., 2006; Oliveira et al., 2011; Pavlidis et al., 2011). Although aggressive displays subside, they persist at low levels. This presents an opportunity to study the long-term effects of chronic social aggression on activation dynamics of identified neural circuits underlying specific behaviors. Here, we focus on two well-studied behaviors: swimming and the Mauthner-mediated startle escape. The functional and anatomical organization of the underlying neural circuits mediating swim and escape have been studied in larval and adult zebrafish and goldfish (Zottoli, 1977; Zottoli et al., 1987; O'Malley et al., 1996; Ali et al., 2000; Eaton et al., 2001; Severi et al., 2014; Thiele et al., 2014; Wang and McLean, 2014).

The neural basis of Mauthner escape behavior has been investigated extensively in teleost fishes (Eaton et al., 2001; Korn and Faber, 2005). An abrupt auditory pulse to the ear elicits a highly stereotypical startle escape response (c-start) that is controlled by a distinct reticulospinal neural network in the hindbrain centered around the Mauthner neurons (M-cells; Fig. 1A). The M-cells are a pair of identified neurons that receive ipsilateral synaptic sensory input and project axons to innervate contralateral spinal cord motor neurons (MNs; Fig. 1A,B). A unilateral stimulus elicits a reflexively fast flexion of the body away from the threat (Eaton et al., 1977; Zottoli, 1977; Zottoli et al., 1987; Eaton and Emberley, 1991; Canfield, 2003; Preuss et al., 2006; Szabo et al., 2006; Weiss et al., 2006, 2009).

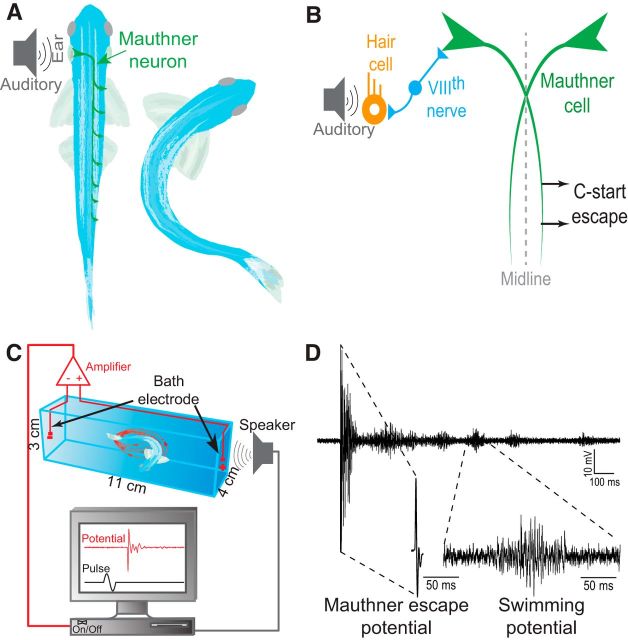
Figure 1.

Schematic illustrations of the M-cell escape circuit, experimental setup, and recording. A, Zebrafish startle response is activated by auditory stimuli. C-start behavior is mediated by the well-characterized Mauthner neural circuit. Activation of the M-cell is necessary for C-start escape. The M-cell innervates spinal cord motor neurons. B, Schematic illustration of the M-cell escape circuit. The M-cell escape response is initiated via activation of the VIIIth sensory nerve. C, A pair of bath electrodes is placed on either side of the testing chamber. Bath electrodes detect neuromuscular field potentials generated as the M-cell escape response is activated. M-cell escape is activated by an auditory pulse. Field potentials and stimuli are time locked and digitally recorded. D, An illustrative example of a phasic field potential recording recorded during activation of the C-start escape response mediated by the M-cell. This phasic response was followed by repeated swim bursts that were significantly lower in amplitude.

The neural circuit underlying swimming behavior is more distributed, but still displays a clear hierarchical organization (Severi et al., 2014; Thiele et al., 2014; Wang and McLean, 2014). Stimulation of the mesencephalic locomotor region (MLR) evokes swimming (Kashin et al., 1974; Cabelguen et al., 2003). Descending outputs from the MLR are transmitted to reticulospinal neurons located in the mid- and hindbrain. Their axonal projections excite spinal central pattern generators (CPGs) that drive coordinated rhythmic swimming activity (Deliagina et al., 2002). Interestingly, both the escape and swim circuits receive visual and postural sensory information (Sato et al., 2007; Kohashi and Oda, 2008; Mu et al., 2012) and are regulated by neuromodulatory inputs (Pereda et al., 1992; McLean and Fetcho, 2004). This suggests that the circuits and the behaviors they produce may be susceptible to plastic changes influenced by social experience.

Here, we investigated how social regulation affects the activation patterns of escape and swim behaviors by using a noninvasive technique to monitor the patterns in freely behaving animals (Issa et al., 2011). We show that these neural circuits shift their activation with changes in the animal's social status. To link the behavioral observation with cellular changes, we present a computational model to illustrate how a change in the relative excitability of these circuits can facilitate the transition between the dominant and subordinate behavioral phenotypes.

Materials and Methods

Animal maintenance.

All experimental procedures were approved by the Institutional Animal Care and Use Committee at East Carolina University (Animal Use Protocol #D320). Adult male (7–12 months old) wild-type zebrafish AB strain (Danio rerio, RRID:ZIRC_ZL1) were housed at the Zebrafish Core Facility at 28°C under a 14/10 h light/dark cycle and fed three times daily to satiation with a commercial food (Otohime B2, Reed Mariculture) containing a high protein content and supplemented with newly hatched artemia (Brine Shrimp Direct). Food was placed on the top right corner of the tank. Animals of mixed sex were group housed at a density of ∼20 fish per 10 gallon tank before social isolation and pairing. In all experiments, the lighting system was placed on the top of the tank so that it was uniformly illuminated (Movie 1).

Movie 1.

Download video file ^{(607KB, mp4)}

DOI: 10.1523/JNEUROSCI.1548-16.2017.video.1

A brief video illustration of social interactions, spatial distribution, and swimming activity of a pair of adult male zebrafish within an experimental arena.

Social isolation, pairing, and behavioral observations.

Male fish were initially isolated for a period of 1 week in individual tanks (23 × 13 × 6 cm) to prevent any physical and visual interactions with conspecifics and to minimize residual social effects from previous social interactions animals acquired during group housing. After isolation, animals were paired continuously for 2 weeks by transferring two fish into a novel tank of equal size to the isolation tank. Social interactions between fish were observed for 5 min periods daily for 2 weeks between 10:00 A.M. and 12:00 P.M. Two behavioral displays were recorded to assess the social rank: aggressive behaviors (attacks, bites and chases) and submissive behavior (retreats). Dominance for each observation session was based on the total number of aggressive and submissive behaviors displayed. Animals with a high index of aggressive behavior/submissive behavior were considered dominants. In rare instances when the dominance relationship was unstable or reversed, the pairs were excluded from the study (n = 2 out of 39 pairs).

In addition to observing aggressive behaviors, pairs were filmed daily (early afternoons) for 1 min to monitor changes in their swimming activity using a Canon Camcorder (camera model: digital video ZR500). Videos were digitized, and movement (distance traveled over 1 min periods) of each fish was analyzed using NIH ImageJ software (RRID:SCR_003070; Manual Tracking plug-in). Instances when animals were interacting with one another resulted in the exclusion of those video frames from analysis. Total tracked distance was normalized by the number of remaining video frames.

Experimental setup.

At the end of the pairing period, both animals were placed into two separate but identical testing chambers (dimensions, 11 × 4 × 3 cm) containing double distilled water with a resistance of ∼15 MΩ-cm and temperature of 25°C. The chambers were equidistant from the speaker (4 cm; Fig. 1C). The animals were acclimatized for 30 min before testing. The use of highly resistive water improves the signal-to-noise ratio of the electrical field generated during swimming and escape behavior by preventing dissipation of the electrical signals. Previous reports have shown that highly resistive water, such as that used in this study, did not have any obvious impact on the behavior or stress level of the animals (larvae and adults), even after an extended and continuous exposure of 3 d (Issa et al., 2011; Monesson-Olson et al., 2014).

Electric field potentials were recorded using a pair of conductive electrodes (1 mm bare thickness, 3–5 mm metal exposure) placed on either end of each testing chamber (Fig. 1C). Electric signals were amplified 1000-fold using an AC differential amplifier (AM-Systems, model 1700). Electrical signals were low-pass filtered at 300 Hz and high-pass filtered at 1 kHz. Signals were digitized using a Digidata-1322A digitizer then stored using Axoscope software (Molecular Devices).

Short-latency M-cell-mediated escape occurs between 5 and 15 ms after stimulus and is associated with a characteristically large and phasic electric field potential (Fig. 1D). Conversely, long-latency escapes and swimming occur between 15 and 40 ms after stimulus and are associated with variable and low-amplitude electric field potentials. The electric signals of the short- and long-latency escape responses and swimming are qualitatively and quantitatively distinct (Prugh et al., 1982; Issa et al., 2011; Monesson-Olson et al., 2014). The field potential of the M-cell is at least tenfold larger in amplitude compared to the field potentials of the swims (average M-cell field potential, 3.381 ± 0.217 mV; average swim potential, 0.325 ± 0.044 mV). The duration of the M-cell field potential is also significantly different (2 ± 0.031 ms) compared to swim burst potentials (50 ± 7.753 ms). These two distinguishing features facilitated the unambiguous characterization of the field potentials generated by these two behaviors (Issa et al., 2011).

Response sensitivity tests.

Auditory pulses were generated digitally via computer using the Audacity open source audio editor and recorder software (audacityteam.org). The amplitudes of auditory pulses were calibrated before the experiments using a decibel meter (Sinometer MS6700). Auditory stimulus consisted of a phasic 1 ms pulse (sine wave). The animals' auditory sensitivity and threshold of the escape response was measured by delivering pulses at a randomized dB at midrange levels (repeated three times at each level) with a minimum of 2 min intervals between trials. Pulses ranged from 70–105 dB re 20 μPa with 5 dB increments. Randomization of stimulus intensity was necessary to avoid order effects, possible response sensitization or habituation. Repeated trials at each decibel level were averaged, and then the data were curved-fitted using a nonlinear regression analysis using the Boltzmann sigmoidal equation Y = bottom + (top − bottom)/(1 + exp[(V50 − X)/slope]) (see Fig. 4B).

Figure 4.

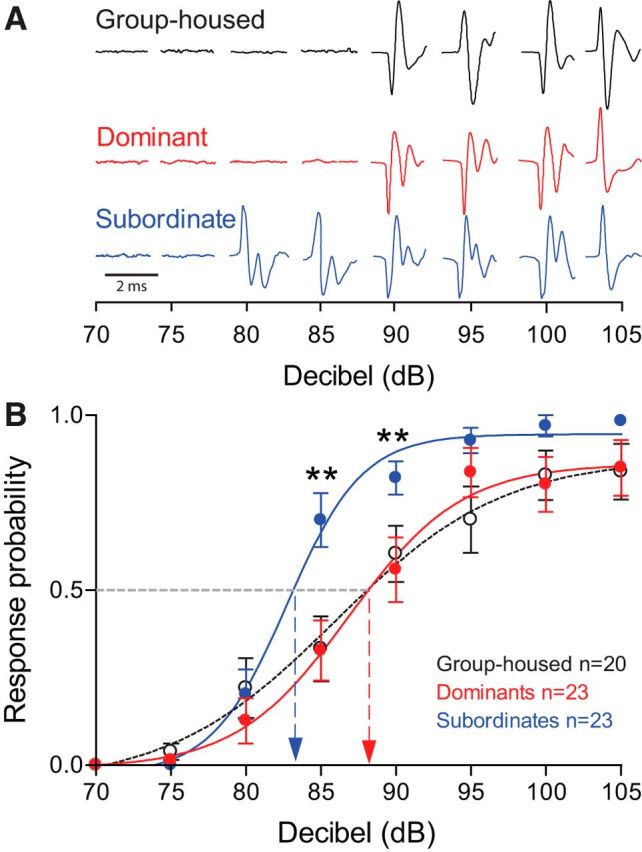
Startle escape response is significantly more sensitive in subordinate animals compared to dominant and group-housed animals. A, Individual examples of C-start field potential from three different animals at increasing decibel intensities. B, Probability of initiating an escape response is significantly higher in subordinates compared to dominants and group-housed animals at 85–90 dB. Means ± SEM are plotted (*p < 0.05; **p < 0.005).

Measurement of bursting activity.

Animals were placed in the testing chamber and allowed to acclimate for 30 min. Subsequently, field potentials of burst swimming activity were recorded continuously for 1 min. Data acquisition, amplification, digitization and storage were the same as stated above.

Swim bursts were detected and sorted using the “threshold” search tool of the Clampfit software (Molecular Devices). Detected bursts were processed and verified according to the following criteria: a burst was included if it was larger than 12 mV in total amplitude and 50–200 ms in duration. Markers were assigned to each burst at the half-width of the burst (usually at the peak burst amplitude) for all bursts during the 60 s recording period.

Data analysis.

The latency of the escape response was measured using the field potential signals recorded by measuring the time between stimulus onset and the beginning of the field potential response. The zebrafish escape response is categorized into two main types of escapes. Activation of the M-cell generates a short-latency escape response with a time onset ranging between 5 and 15 ms. Zebrafish also produce long-latency non-Mauthner-mediated escapes with a time onset ranging between 15 and 40 ms (Eaton et al., 2001). Each type of escape generates a distinct electric field potential signal that permits the reliable identification of the type of escape based on the field potential signature and its latency from stimulus onset (Issa et al., 2011). The latency of the electrical signal was defined as the time difference between the onset of the auditory stimulus and the beginning of the large phasic field potential generated during the short-latency M-cell-mediated escape response. Data were tabulated in Microsoft Excel, and all values are provided as mean ± SEM unless stated otherwise.

All statistical analyses were performed in R (www.r-project.org; RRID:SCR_001905), IBM-SPSS (RRID:SCR_002865), and Prism (GraphPad; RRID:SCR_002798). Unless specified otherwise, all comparisons were first subjected to one-way ANOVA or mixed-design (a mixture of one between-group and repeated-measures variables) ANOVA followed by the least significant difference (LSD) post hoc test for all multiple comparisons. Before using mixed-design ANOVA, sphericity was tested by using Mauchly's test. When the assumption of sphericity was violated, the degree of freedom in Greenhouse–Geisser correction was used.

The movement of animals was tracked using the Manual Tracking plug-in for ImageJ to extract X–Y coordinates within the housing tank (Fig. 2). Videos were downsampled to three frames per second, and coordinates for dominant and subordinate animals were loaded into R software using a custom script. X–Y coordinates encompassing periods of social interactions were removed from analysis. Filled contour plots combining data of all dominant or subordinate animals were produced using 2D kernel density estimations generated by the kde2d function of the MASS package [CRAN (Comprehensive R Archive Network) Repository; Venables and Ripley, 2002]. The algorithm used disperses the mass of the empirical distribution function over a regular grid of 512 points and uses the fast Fourier transform to convolve this approximation with a discretized version of the kernel followed by linear approximation to evaluate the density at the specified points. To facilitate illustration of the large data set for both social phenotypes, density data were converted into a heat-map probability plot as illustrated in Figure 2 B₁.

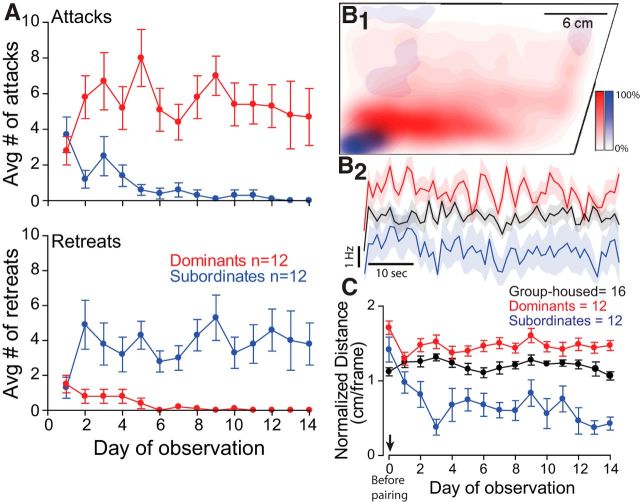
Figure 2.

Adult male zebrafish form stable social relationships, and behavior patterns diverge significantly as social relationships solidify. A, Social interactions are characterized by aggressive behaviors (attacks, top) performed predominantly by dominants and submissive behaviors (retreats, bottom) displayed mainly by subordinates. B₁, Social status affects swimming activity. Kernel heat-map estimation plot of swimming activity over a 1 min period of filming for dominants (red) and subordinates (blue) on day 14 after pairing (n = 12 dominants and 12 subordinates). B₂, Average swimming frequency of all animals plotted in B₁ over a 1 min period of observation on day 14 after pairing for paired animals and day 14 for group housed animals. The shaded area illustrates the variance in swimming frequency (SEM). C, Quantification of filmed swimming activity [distance traveled (in centimeters) per frame] for all animals tested during a 1 min period each day for a 14 d pairing period (n = 16 group housed, n = 12 for dominants and 12 subordinates). Video frames during which the animals were interacting were excluded from analysis. Total tracked distance was normalized by the number of remaining video frames. Day 0 marks observations of animals before they were paired (before pairing; arrow). A, B₂, and C plot the mean ± SEM.

Neuronal model.

A simplified single-compartment conductance-based biophysical model of the escape and swim circuits of zebrafish was developed based on experimental data (see Fig. 5A; Eaton et al., 2001; for review, see Korn and Faber, 2005; Liao and Fetcho, 2008; Song et al., 2015). In the model, we assume that the M-cells are the main command neurons in the escape behavior and the stimulus is directly delivered to the M-cells. Other Mauthner homologs including MiD2 and MiD3 cells may also play an important role (O'Malley et al., 1996). But, if an external stimulus excites one of two M-cells, its contralateral homolog is inhibited by inhibitory commissural neurons (for review, see Zottoli and Faber, 2000; Korn and Faber, 2005). Hence, this reciprocal inhibition is not essential in the simulation as long as M-cell cannot be active without an external input (for a model network, see Fig. 5A).

Figure 5.

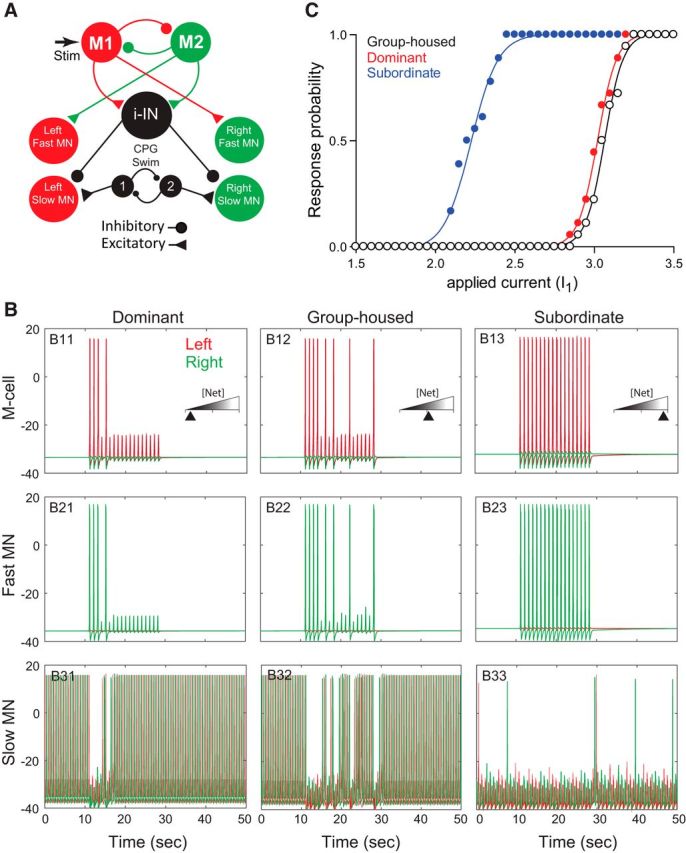
Neurocomputational model of the escape and swim circuits. A, A schematic illustration of the model neural network that reproduces the responses observed in group-housed, dominant, and subordinate animals. The M-cell (M1 or M2) excites the fast MNs and i-IN. Each M-cell mutually inhibits its homolog. The swim CPG excites the slow MNs, while the i-IN inhibits the slow MNs. The model is based on Eaton et al. (2001) (for review, see Korn and Faber, 2005; Liao and Fetcho, 2008; Song et al., 2015). B, Activities of model M-cells (top), fast MNs (middle), and slow MNs (bottom) for the three animal groups to repeated depolarizing current stimulation injected into the left M-cell (repeated 18 times; 1 s interstimulus interval) with100 ms duration. B11, B21, and B31 show dominant animals with ag_max = 4.5 and w_i-IN = 1. B12, B22, and B32 show group-housed animals with ag_max = 4.7 and w_i-IN = 1. B13, B23, and B33 show subordinate animals with ag_max = 9.5 and w_i-IN = 2.25. In the top panels, the red spikes represent the active (left) M-cell, while the green trace represents the silent (right) M-cell. “[Net]” in the insets represents the total amount of excitability of the M-cells, i-IN, and fast MNs: low (dominant), intermediate (group housed), and high (subordinate). In the middle panels (B21–B23), the green trace represents the active right fast MN, while the red trace represents the silent left fast MN. In the bottom panels (B31–B33), the green trace represents the right slow MN, while the red trace represents the left slow MN. C, A change in the amplitude of the applied current I₁(τ) and the response rate of M-cells to the 18 stimuli for three animal groups.

The model incorporates two different motor neuron populations, fast and slow, which are not functionally overlapped (Ampatzis et al., 2013, 2014; Song et al., 2015). Fast motor neurons that drive the escape behavior are excited by the M-cells. On the other hand, the slow motor neurons receive excitatory inputs from the CPGs for swimming behavior and an inhibitory input from the inhibitory interneuron (i-IN). In turn, the i-IN receives excitatory inputs from the M-cells. Inhibition plays multiple roles in the generation of the activity patterns in the model. For example, the reciprocal inhibition between CPGs is essential to generate alternate swimming patterns of slow MNs, which is crucial in the normal swimming patterns of the zebrafish. The inhibition from the i-IN to the slow MNs is also crucial to pause the swimming activity during the escape behavior and to resume it with the termination of the escape (for an alternate model, see Discussion).

We use conductance-based modified Morris–Lecar neuronal models (Morris and Lecar, 1981; Izhikevich, 2007; Ermentrout and Terman, 2010) with additional calcium-dependent potassium current. The membrane potential of each cell obeys the following current balance equation:

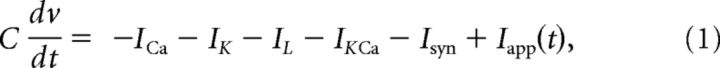where I_K = g_Kn(v − v_K), I_Ca = g_Cam_∞(v)(v − v_Ca), I_Kca = g_Kca{[Ca]/([Ca] + k₁)}(v − v_K), and I_L = g_L(v − v_L) represent the potassium, calcium, calcium-dependent potassium, and leak currents, respectively. m_∞ is the instantaneous voltage-dependent gating variable for the calcium current, where

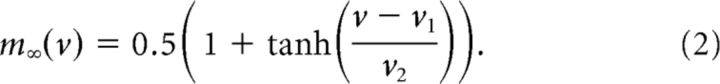The concentration of intracellular Ca²⁺ is governed by the following calcium balance equation:

n is a gating variable for the potassium current obeying the following:

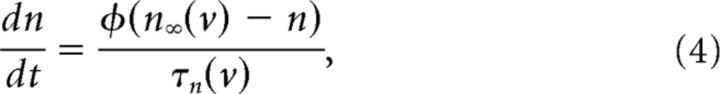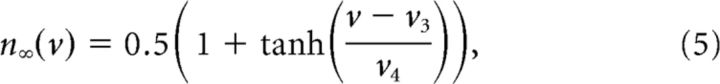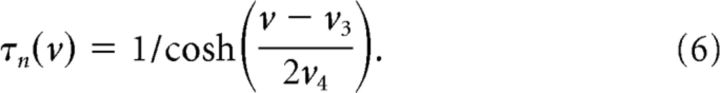The synaptic variable, s, is modeled by an equation for the fraction of activated channels:

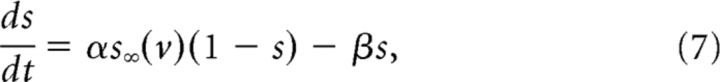where

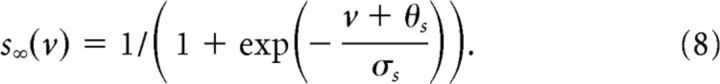The term I_syn in Equation 1 represents the synaptic input from other cells and is given by the following:

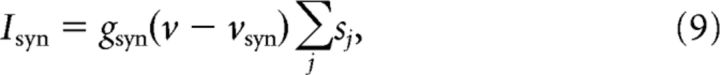where the summation is over all neurons projecting to a given neuron. The synaptic current for M-cells is as follows:

where i ≠ j and i, j ∈ {1, 2}. The synaptic current for fast MNs is as follows:

where s_M,i is the synaptic variable of the corresponding M-cell. Note that the right fast MN receives synaptic input from M-cell 1, while the left fast MN receives synaptic input from M-cell 2. The synaptic current for slow MNs is as follows:

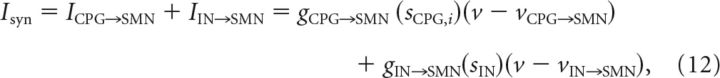where s_CPG,i is for the corresponding CPG and s_IN is for the i-IN. Note that the left slow MN receives synaptic input from CPG 1, while the right slow MN receives synaptic input from CPG 2. All slow MNs also get an inhibitory input from the i-IN. The synaptic current for the i-IN is as follows:

where s_M,i is for M-cell i. The synaptic current for CPGs is as follows:

where i ≠ j and i, j ∈ {1, 2}. While the applied current I_app(t) is a fixed constant in CPGs and slow MNs, these are time and activity dependent in M-cells, fast MNs, and the i-IN. The applied current I_app(t) in the M-cell for i = 1, 2 is modeled as follows:

where I₀ is a fixed constant, I_i(τ) is the stimulus at time τ, w_M is a fixed constant for the weight, and Net(t) is the activity-dependent spike adaption. Net(t) obeys the following equation:

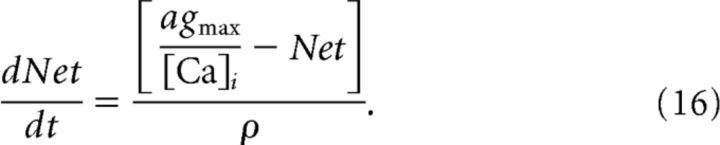Here, ag_max and ρ are fixed constants, and [Ca]_i is the [Ca] for M-cell i.

The applied current in fast MNs is modeled as follows:

where I₀ and w_FMN are fixed constants, and Net(t) is as in the above equation, where [Ca] is for each corresponding fast MN. Note that Net(t) in fast MNs is not essential as long as the fast MNs are activated by the M-cells.

Similarly, the applied current in the i-IN is modeled as follows:

where I₀ and w_i-IN are fixed constants, and Net(t) is as in the above equation, where [Ca] is for the i-IN.

For all neurons, the basic set of parameter values are given by the following unless specified in the neuron. We let g_Ca = 4, g_KCa = 0.25, g_K = 8, g_L = 2, ε = 0.005, ν_Ca = 120, ν_K = −84, ν_L = −60, k₁ = 10, θ_s = 0, ν₁ = −1.2, ν₂ = 18, ν₃ = 12, ν₄ = 17.4, k_Ca = 1, μ = 0.2, c_M = 20, and φ = 0.23. For M-cells, we let α = 10, β = 0.08, g_M→M = 0.5, ν_M→M = −50, ν₄ = 17, δ_s = 4, I₀ = 40.5, w_M = 1, I₁(τ) = 3, I₂(τ) = 0, and ρ_M = 10,000. For fast MNs, we let g_M→FMN = 0.4, ν_M→FMN = 30, I₀ = 38, w_FMN = 0.5, φ = 0.225, ρ_FMN = 10,000. For slow MNs, we let g_CPG→SMN = 0.37, ν_CPG→SMN = 30, g_IN→SMN = 0.7, ν_IN→SMN = −50, and I₀ = 40.4. For i-IN, we let α = 10, β = 0.0014, φ = 0.225, g_M→IN = 0.2, ν_M→IN = 30, I₀ = 40.4, δ_s = 1, w_i-IN = 1, ρ_i-IN = 4000. For CPGs, we let g_CPG→CPG = 0.5, ν_CPG→CPG = −50, I₀ = 45, δ_s = 0.2, α = 10, and β = 0.2. Some parameters were modified to reflect different firing properties of each cell based on experiments (Eaton et al., 2001; for review, see Korn and Faber, 2005; Liao and Fetcho, 2008; Song et al., 2015). We note that M-cells, fast MNs, slow MNs, and the i-IN are excitable cells, so they do not fire action potentials unless they receive enough excitatory inputs from other active cells or external stimulus. On the other hand, CPGs are self-oscillatory cells, so they fire action potentials at the fixed frequency and they do not receive other inputs except inhibitory input from another active CPG (see Fig. 5A). The main parameter that we controlled to implement these firing properties is the baseline level of applied current I₀. With an increase of I₀, the activity patterns of the model neuron change from silence to tonic spiking (Izhikevich, 2007; Ermentrout and Terman, 2010). For example, CPGs have higher I₀ value for their self-oscillatory activity patterns.

In our study, we also changed two main parameters (ag_max, w_i-IN) to explore possible cellular mechanisms for the observed social status dependent differences in the escape and swim circuits. These two main parameters were based on the previous finding about the endocannabinoid 2-arachidonoylglycerol (2-AG) in mediating the cellular and behavioral switch between escape and swim (Song et al., 2015; for details, see Results and Discussion). One may consider an alternate model where the i-IN inhibits CPGs (for details, see Discussion).

To simulate the effect of an external stimulus on the M-cell, a depolarizing current pulse was applied to the M-cell model neuron. A single model neuron represents the same set of neurons on each side. Simulations were performed on a personal computer using the software XPP (Ermentrout, 2002). The numerical method used was an adaptive-step fourth-order Runge–Kutta method with a step size 0.1 ms.

Results

Formation and stability of social dominance

Paired zebrafish quickly form stable dominance relationships. We observed the social agonistic interactions of paired adult male zebrafish and counted aggressive (attacks) and submissive (retreats) behaviors performed by each fish. Dominance relationships were established by the third day of interactions and remained stable for the remainder of the 2 weeks of observation. To investigate attacking and retreating behaviors between paired animals, mixed design ANOVA (within-subject factor days, between-subject factor group) was performed. There was significant main effect of group (attacks, F_{(1, 22)} = 5.40e+1, p = 2.24e-7, Fig. 2A, top; retreats, F_{(1, 22)} = 3.19e+1, p = 1.10e-5, Fig. 2A, bottom), but no effect of days (attacks, F_{(6.23, 137.10)} = 1.09, p > 0.05, Fig. 2A, top; retreats, F_{(4.78, 105.18)} = 7.88e-1, p > 0.05, Fig. 2A, bottom). There was some effect of interaction between group and days for attacks (F_{(6.23, 137.10)} = 2.19, p = 4.58e-2), but no effect of interaction between group and days for retreats (F_{(4.78, 105.18)} = 1.72, p > 0.05). In particular, post hoc test showed that the average number of attacks of dominants against subordinates was significantly higher (LSD, p = 2.24e-7, Figure 2A, top), while the average number of retreats of subordinates from dominants was significant higher (LSD, p = 1.10e-5, Fig. 2A, bottom); that is, during this period, the dominant animal of each pair performed most of the aggressive biting behavior, while the subordinates mainly retreated from interactions (Fig. 2A).

Changes in the pattern of aggressive behavior were accompanied by a significant decrease in swimming activity in subordinates compared to dominants. Two weeks of social interactions led subordinates to limit their swimming only to the bottom corner of the tank while dominants swam freely (Fig. 2B₁, Movie 1). The heat-map plot illustrates the kernel probability distribution of all animals observed over 1 min of filming sampled at 3 frames/s. Status-dependent differences in spatial distribution were reflected in swimming frequency over the same observational period (Fig. 2B₂). To quantify this observation we measured the average swim distances for each day of pairing for a 1 min interval for 14 consecutive days. We performed mixed-design ANOVA (within-subject factor days, between-subject factor group) to compare the average swim distances among three animal groups. There were significant main effects of group (F_{(2, 37)} = 4.49e+1, p = 1.26e-10) and days (F_{(5.56, 205.81)} = 6.12, p = 1.20e-5; Fig. 2C). There was also effect of interaction between group and days (F_{(11.13, 205.81)} = 4.21, p = 1.10e-5; Fig. 2C). In particular, a post hoc test showed that the normalized swim distance of dominants was significantly longer than those of group-housed (LSD, p = 2.66e-2) and subordinate animals (LSD, p = 7.40e-11; Fig. 2C), and the normalized swim distance of group-housed animals was also significantly longer than that of subordinates (LSD, p = 1.08e-8; Fig. 2C); that is, subordinates significantly decreased their swimming activity as dominance was formed. This decline of swimming persisted for the remainder of pairing. Conversely, dominant animals increased their swimming activity in comparison to group-housed animals (Fig. 2B₁–C; n = 12 for dominants and subordinates each, and n = 16 for group-housed animals). Place preference for the lower back of the tank and decline of swimming activity of subordinates is likely to avoid repeated attacks by the dominants who roamed the majority of the arena and had first access to food, given daily from the top right corner (Fig. 2B₁).

We also measured the animals' swim burst activity. Animals were tested individually by placing them in the testing chamber and recorded spontaneous swimming burst field potentials for 1 min after a 30 min period of acclimatization on day 12 of pairing (Fig. 3A). We found that the bursting activity of dominant and subordinate fish diverged in opposite directions compared to group-housed controls (Fig. 3B,C; n = 14 for dominants and subordinates each, and n = 15 for group-housed animals). We performed mixed-design ANOVA (within-subject factor time bin, between-subject factor group) to compare the average number of bursting swim activities among three animal groups. There was significant main effect of group (F_{(2, 40)} = 1.49e+1, p = 1.50e-5), but no effect of time bin (F_{(6.58, 263.23)} = 1.28, p > 0.05; Fig. 3C). There was also no effect of interaction between group and time bin (F_{(13.16, 263.23)} = 4.08e-1, p > 0.05; Fig. 3C). A post hoc test showed that the average number of bursting swims of dominants was significantly higher compared to group-housed fish (LSD, p = 1.75e-3) and subordinates (LSD, p = 3.00e-6; Fig. 3C). The average number of bursting swims of group-housed fish was also significantly higher compared to subordinates (LSD, p = 3.80e-2; Fig. 3C). We also compared the total number of swim bursts with a one-way ANOVA (factor, group). We found a significant main effect of group (F_{(2, 40)} = 1.49e+1, p = 1.48e-5; Fig. 3D). A post hoc test showed that dominants had significantly higher number of swim bursts compared to group-housed (LSD, p = 1.75e-3) and subordinate animals (LSD, p = 3.00e-6; Fig. 3D). Group-housed fish also showed significantly higher number of swim bursts compared to subordinates (LSD, p = 3.80e-2; Fig. 3D). While dominants substantially increased their bursting swim activities compared to both group-housed and subordinate fish, subordinates significantly decreased their bursting swims from those of group-housed fish and dominants (Fig. 3C,D). These results suggest that social interactions impacted the swim circuits of both dominant and subordinate animals, but in opposite ways. Social dominance caused an increase in swimming, while social submission led to a decrease in the activity of the swim circuit.

Figure 3.

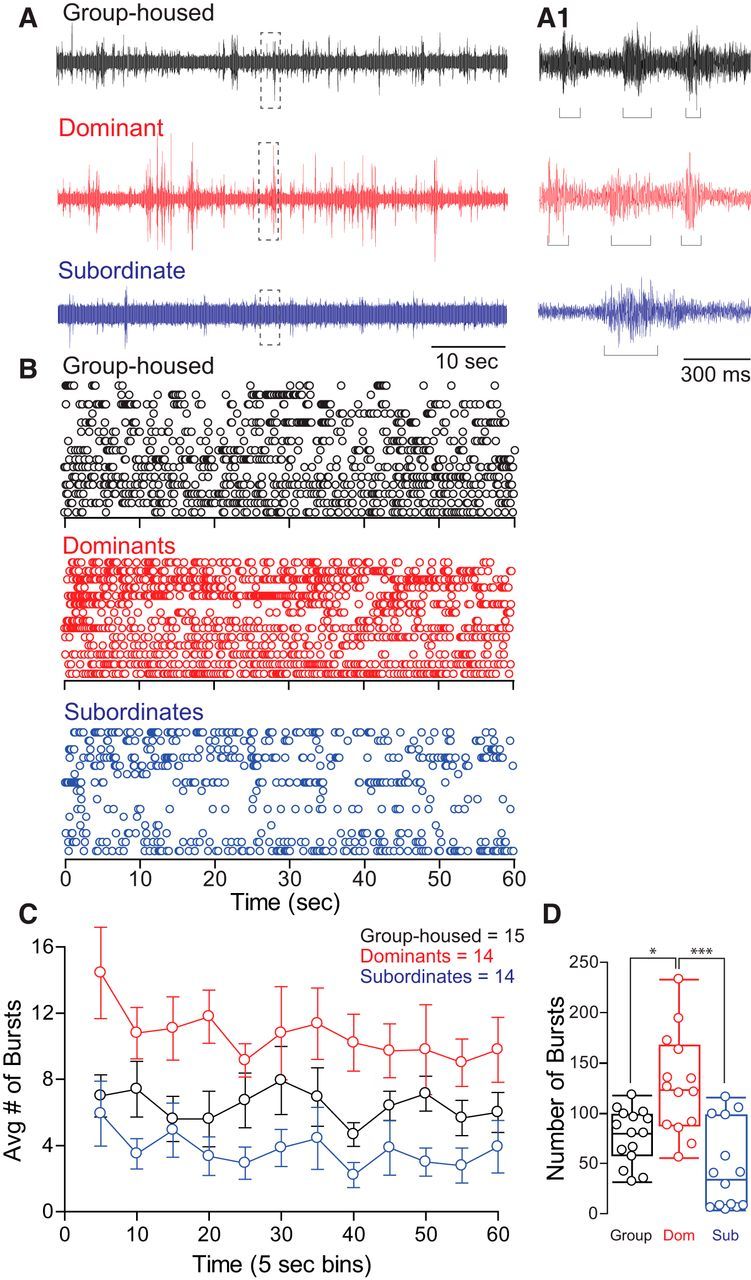
Social status affects swimming burst frequency. A, One minute individual trace recordings of field potentials from group-housed, dominant, and subordinate animals. Swim bursts are easily identifiable and individually sorted (A1, brackets) (dashed boxes denote areas that are enlarged in A1). B, Raster plots of each social animal group tested. Each row represents the burst swim responses of one animal, and each circle represents one swim burst (for burst analysis and quantification, see Materials and Methods). C, Averaged binned data of swim burst activity of data illustrated in A and B (burst activity was binned over 5 s). Means ± SEM are plotted. D, Box plot summary illustrating differences in the number of bursts produced over 1 min of recording. Each dot represents sum of spontaneous swim bursts for each animal during 60 s of recording. The horizontal line within each box plot denotes the data median; the box represents 90% of data. Error bars represent the max/min values (n = 15 group housed, 14 dominants, 14 subordinates).

Social status–dependent sensitivity of the Mauthner escape response

To determine whether social experience affects the activation threshold of the M-cell escape, we tested the animals' sensitivity to auditory pulses of randomized decibel intensities. At low decibels, both social phenotypes displayed similarly low response probabilities (Fig. 4A). To compare the difference of response probabilities to auditory pulses among three animal groups, we performed a mixed-design ANOVA (within-subject factor decibel, between-subject factor group). There were significant main effects of group (F_{(2, 63)} = 3.86, p = 2.63e-2; Fig. 4B) and decibel (F_{(4.39, 276.46)} = 1.55e+2, p < 1.0e-16; Fig. 4B). There was also a significant effect of interaction between group and decibel (F_{(8.78, 276.46)} = 2.49, p = 1.03e-2; Fig. 4B). We then further performed the post hoc test to determine which animal groups had higher response probability. We observed that the response probability to auditory pulses for subordinates was significantly higher compared to group-housed (LSD, p = 1.75e-2) and dominant animals (LSD, p = 2.26e-2; Fig. 4B). But there was no difference of response probabilities between group-housed and dominant animals (LSD, p > 0.05; Fig. 4B); that is, as sound intensity increased, subordinates were significantly more sensitive and were more likely to respond to auditory pulses compared to dominants and group-housed animals (Fig. 4B). Data were curved fitted with a nonlinear regression with Boltzmann sigmoidal curve fit (goodness of fit R² for 20 group-housed fish = 0.9868, 23 dominants = 0.9924, 23 subordinates = 0.9926). Response probability of subordinate animals reached the 50% mark at 82.73 dB compared to dominants' 86.86 dB and group-housed animals' 85.30 dB. At suprathreshold stimuli (95 dB and higher), the response probability of animals plateaued to similar levels. Comparison of the sensitivity curves of dominant and subordinate animals to group-housed animals shows that pairwise interactions had a significantly bigger impact on the response sensitivity of socially subordinate animals compared to dominants.

In particular, we observed that the response sensitivities among three animal groups at 85 and 90 dB were significantly different (Fig. 4B). Thus, we performed a one-way ANOVA (factor, group) to find the difference of the response sensitivities among three animal groups at 85 and 90 dB, respectively. Note that the stimuli were randomized at each decibel and the response sensitivities at each decibel per each animal were averaged so that there was only one probability for each animal at each decibel (see Materials and Methods). At 85 dB, there was a significant main effect of group (F_{(2, 63)} = 5.58, p = 5.86e-3; Fig. 4B). A post hoc test showed that the response sensitivity of subordinates at 85 dB was significantly higher compared to group-housed (LSD, p = 4.78e-3) and dominant animals (LSD, p = 6.33e-3; Fig. 4B). There was no difference of the response sensitivities between dominants and group-housed animals at 85 dB (LSD, p > 0.05; Fig. 4B). Similarly, at 90 dB, there was a significant main effect of group (F_{(2, 63)} = 3.56, p = 3.44e-2; Fig. 4B). Post hoc test showed that the response sensitivity of subordinates at 90 dB was significantly higher compared to group-housed animals (LSD, p = 4.96e-2) and dominants (LSD, p = 1.47e-2; Fig. 4B). There was no difference in the response sensitivities at 90 dB between dominants and group-housed animals (LSD, p > 0.05; Fig. 4B). Our results suggest that the activation threshold of the M-cell in subordinates decreased significantly compared to both dominant and group-housed animals.

Social status–dependent latency of Mauthner-mediated escape response

To measure the latency of response of M-cell-mediated escapes to supra–threshold auditory pulses at 95 dB, we performed a one-way ANOVA (factor, group). There was a significant main effect of group (F_{(2, 73)} = 9.51, p = 2.14e-4; group housed, n = 20; dominants, n = 28; subordinates, n = 28). Average latencies of response onsets were 3.61 ± 0.15 ms (mean ± SEM) for subordinates, 4.31 ± 0.29 ms for dominants, and 5.12 ± 0.24 ms for group-housed animals. A post hoc test indicated that the latency of response of M-cells for subordinates was significantly shorter compared to group-housed animals (LSD, p = 4.30e-5) and dominants (LSD, p = 2.99e-2). The latency of response of M-cells for dominants was also significantly shorter compared to group-housed animals (LSD, p = 2.24e-2).

The asymptotic frequency of escape response at high stimulus intensity did not differ among the groups. All three groups responded nearly 92% of the time (group housed, 93 ± 3.6%; dominants, 92 ± 4.3%; subordinates, 91 ± 2.5%). This suggests that repeated testing and possible differences in habituation rates at the applied frequency (once every 2 min) were not factors in the observed differences in both sensitivity and response latency.

Neurocomputational model of escape and swim circuits

To investigate the mechanisms underlying the status-dependent differences in startle sensitivity and shift in network activation between escape and swim, we built a simplified mathematical neural model of both escape and swim circuits (Fig. 5A). We found that a simple circuit model composed of conductance-based modified Morris–Lecar model neurons can account for the observed social status differences in circuits' dynamics. The model incorporates the main neural elements that comprise the M-cell escape circuit, a swimming CPG circuit, an i-IN, and fast and slow MNs that are connected to the M-cell escape and CPG swim circuits, respectively (for details, see Materials and Methods).

It is well established that the excitability of the escape and swim circuits is subject to descending neuromodulation (Oda et al., 1998; Preuss and Faber, 2003). The neuromodulators serotonin and dopamine directly enhance the excitability of the M-cell and indirectly by modulating presynaptic inputs (Cachope et al., 2007; Medan and Preuss, 2011; Whitaker et al. 2011). However, it is little understood how a change in M-cell excitability alters circuit activation and promotes a switch between escape and swim depending on social status. Here, we hypothesized that modulation of network properties may account for the observed differences in circuit activation between dominants and subordinates. To test our hypothesis we controlled two intrinsic synaptic parameters (ag_max and w_i-IN) which are modulated by presynaptic neurotransmitters. Here, ag_max is the maximal net excitabilities in the M-cell, Fast MN, and i-IN while w_i-IN is the weight of the maximal net excitability in i-IN.

We repeatedly applied depolarizing current pulses to the model M-cell (1 s interstimulus interval) for 100 ms duration on the left M-cell to explore the behavior of the escape and swimming activities for each animal group (Fig. 5B). We changed ag_max in Net(t) (Eqs. 15, 17, 18) and the weight w_i-IN for the i-IN in I_app(t) (Eq. 18). We assumed that low values of ag_max and w_i-IN correspond to the dominant and group-housed fish, while the high values of ag_max and w_i-IN correspond to the subordinates. These two assumptions were based on a previous finding that implicated the endocannabinoid 2-AG in mediating the cellular and behavioral switch between escape and swim (Song et al., 2015). 2-AG was shown to prolong swimming suppression in slow MNs and promote the activation of the startle escape response by lowering the threshold for the initiation of escape. Furthermore, blocking 2-AG synthesis decreased the duration of swimming inhibition in slow MNs. Finally, slowing 2-AG degradation prolonged the inhibition of slow MNs and swimming behavior. These results strongly suggest that differences in the availability and concentration of 2-AG may account for the status-dependent activation of the escape and swim circuits observed in our experiments. Therefore, we assumed that dominants and subordinates have different levels of excitability: dominants have low excitability, while subordinates have high excitability (see Discussion). In the model, this difference was represented by different levels of ag_max and w_i-IN depending on social status. Note that these two parameters (ag_max and w_i-IN) were chosen carefully to reproduce the experimental results while keeping all other biophysically driven parameters constant. Moreover, the parameter ag_max was chosen to reflect the availability of 2-AG (Song et al., 2015). The change of w_i-IN was the only way to reflect the changes of the swimming frequency for subordinates (for an alternate model where the i-IN inhibits CPGs, see Discussion).

Switch between escape and swimming activities

Figure 5B shows the activities of neurons (M-cells, fast MNs, and slow MNs) for all three animal groups. A depolarizing current pulse that activates the M-cell (Fig. 5, B11–B13) leads to the activation of the contralateral fast MNs (Fig. 5, B21–B23, right fast MN) and initiation of the escape response. Concurrently, activation of the M-cell excites the i-IN, which directly inhibits all slow MNs. As a result, there is a pause of swimming activity during escape, but swimming resumes once the escape response ends (Fig. 5, B31–B33).

Effect of social status on the swimming activity in the model

To determine how social experience may account for the observed changes in swim circuit activation, we tested the activities of slow MNs before, during, and after repeated stimulation of the M-cell. The bottom panels in Figure 5B shows the response of slow MNs of models that simulated responses of dominants (Fig. 5, B31), group-housed fish (Fig. 5, B32), and subordinates (Fig. 5, B33) without any stimulus input (before 10 s and after 30 s). Then, we increased parameter values ag_max and w_i-IN to determine the effect on swimming behavior. As described earlier, low ag_max and w_i-IN values simulate conditions that represent group-housed and dominants, while high values represent subordinates. We found that swimming frequency before and after the stimuli did not change for each animal group. We also observed that slow MNs for group-housed and dominants were active most of the time except during activation of the escape circuit. On the other hand, higher ag_max and w_i-IN increased the excitability of i-IN and even made the i-IN fire at low frequency without any excitatory input from the M-cell. Since the active i-IN inhibits all slow MNs, increasing ag_max and w_i-IN led to a dramatic decrease in swim circuit activation prior, during, and after escape circuit activation for subordinates (Fig. 5, B33). This result mimics our empirical results that show an inhibition of swimming activity in subordinate animals (Figs. 2, 3).

Social status–dependent sensitivity of M-cell escape response in the model

To probe possible cellular mechanisms that account for the observed social status–dependent changes in the sensitivity of the M-cell, we changed the amplitude of the applied current in the M-cell and measured the response probability over the repeated stimuli. As in the previous simulation, the left M-cell receives 18 stimuli. Amplitude of the applied current I₁(τ) was gradually increased, and response probability of the M-cell was recorded. For example, the response probabilities of M-cells in Figure 5 (top) are 4/18 for dominants, 8/18 for group-housed animals, and 18/18 for subordinates. We used the same parameters as in the above simulation for each animal group. We found that decreasing ag_max and w_i-IN, which mimics low 2-AG concentration, increases the activation threshold of the model M-cell as observed in dominant and group-housed animals. But when ag_max and w_i-IN values were increased, which mimics an increase in 2-AG concentration, the activation threshold of the model M-cell decreased significantly as we observed experimentally in subordinate animals (Fig. 5C). Together, these results suggest that social status–dependent changes in the M-cell may be mediated, in part, by intrinsic changes in M-cell excitability and are sufficient to enhance the escape response and to switch circuit activation from swim to escape as was observed experimentally (Fig. 3C, 4B).

Discussion

As social relationships solidify between competing zebrafish, behavior patterns begin to shift to reflect social standing. These behavioral patterns (swim and escape) are part of the decision-making process in which animals must choose adaptive behavioral strategies. In this study, subordinate animals shifted their behavioral pattern from swimming to escape and reduced their swimming frequency to avoid repeated aggression by dominants. Conversely, dominants increased their swimming frequency to maximize their access to potential resources. These behavioral changes are based on persistent changes in the underlying neural circuits that mediate swim and escape behavior, and that social experience facilitates the shift in the balance of network dynamics (Fig. 6).

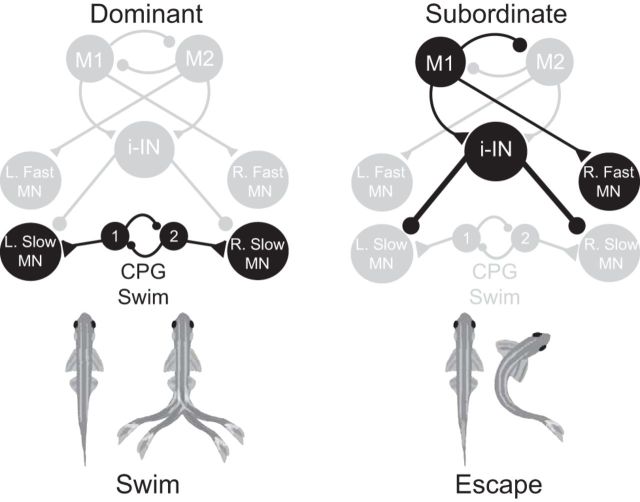
Figure 6.

A schematic illustrating the shift in network activation between escape and swimming in socially dominant and subordinate animals. In dominant animals, a low level or absence of inhibition from inhibitory interneurons with the continuous excitatory input from swim CPG potentiates swimming activity. However, in subordinate animals, an increase in excitability of the inhibitory neurons suppresses the slow MNs and swimming behavior. Simultaneously, an increase in Mauthner sensitivity promotes the excitation of the escape circuit and inhibition of the swim circuit. In the illustrated example, stimulation of the left M-cell activates the right fast MN and bilateral suppression of the slow MNs. Suppressed pathways are dimmed, while strengthened synaptic pathways are emphasized in black (for details, see Materials and Methods and Results).

To determine possible cellular mechanisms that account for the observed status-dependent differences, we built a neural circuit model of the escape and swim circuits based on a simplified representation of the properties of the relevant neurons. Although our simplified model circuit does not include all the detailed neural elements that may act in vivo, it enabled the reproduction of several important network activity patterns observed experimentally. First, we showed that a depolarizing current that mimics an external stimulus activates the M-cell, which in turn excites the fast MN for the escape and excites the inhibitory interneuron to inhibit slow MN resulting in a pause of swimming activity during the escape response. Second, the swimming activities resume at the termination of the escape behavior without a change of the swimming frequency. Third, we showed that the sensitivity of the startle escape response to an increase in stimulus intensity, simulated by an increasing depolarizing current, depends on social status. Submissives showed elevated response rate of the startle escape to stimuli and low swimming frequency, while group-housed and dominant animals showed relatively low startle response rate and very high swimming frequency. A change in intrinsic synaptic and network parameters was sufficient to obtain the transition between dominants and subordinates activity patterns while maintaining the network architecture.

The escape circuit is prone to behavioral and cellular plasticity mediated by modulatory inputs (Oda et al., 1998; Preuss and Faber, 2003). Modulation of network properties may be responsible for the observed changes in startle sensitivity between dominants and subordinates. Neumeister et al. (2010) demonstrated that the lowered threshold for initiation of escape is due to a change in the presynaptic inhibitory drive to the M-cells. Serotonin is one prime candidate for mediating the socially controlled plasticity in M-cells (Whitaker et al. 2011; Medan and Preuss, 2014). Previous experiments have also shown that startle plasticity in M-cells could be modulated by the action of 2-AG (Song et al., 2015). Moreover, activity-dependent production and release of 2-AG at the M-cell lateral dendrite triggers presynaptic release of dopamine that enhances M-cell activation (Cachope et al., 2007). In our model, to obtain the social status–induced differences in M-cell activation, we controlled one intrinsic synaptic parameter, the maximal net excitation in the M-cell, which is modulated by presynaptic neurotransmitters. Since calcium modulates inhibitory presynaptic neurotransmitter release via retrograde signaling and endocannabinoids act as retrograde messengers (Diana and Bregestovski, 2005), we assumed that intracellular calcium level governs the maximal net excitation of the M-cell. In fact, both presynaptic release of dopamine and postsynaptic activation of the M-cell are calcium dependent (Cachope et al., 2007). Our computational results show that the dynamical changes in the excitability of the M-cell may mediate the social status–dependent difference in the sensitivity of the startle response.

To reproduce reduced swimming activity in subordinates, the hallmark of social status–induced behavioral difference observed in subordinate animals, we varied the excitability in the local inhibitory interneuron, which represents a neurotransmitter modulated local network property. In an invertebrate model, it was shown that social status affects the configuration of local neural circuits (motor neurons and interneurons) to produce different, status-dependent behavioral responses (Issa et al., 2012). It was shown that differences between animals of different social status are due to changes in thresholds of excitatory and inhibitory interneurons. However, in zebrafish, longer swimming suppression in the slow motor neurons is mediated by potentiation of the inhibitory inputs via 2-AG (Song et al., 2015), which might reflect an increased excitatory synaptic transmission to the inhibitory interneurons. Thus, the excitability in the local inhibitory interneuron modulates the amount of excitatory synaptic transmission to the cell by dynamically changing the excitability threshold in interneurons (Fig. 6). This permits the inhibitory interneuron to be active even without the excitatory input from the M-cell at low frequency, resulting in prolonged swimming suppression. Our model suggests that social status–dependent differences could be mediated, in part, by differences in neuromodulator availability; however, our proposition remains to be determined experimentally.

One may consider another model in which inhibitory interneurons inhibit CPGs instead of slow motor neurons. Under this scenario, during an escape response, swim CPGs will receive inhibitory inputs, preventing them from activating and failing to provide sufficient excitation to drive the slow motor neurons. Thus, there will be a pause of the swimming activity during the escape. Therefore, the swimming patterns may be similar to our model before and during the stimulus. However, when there is a strong (or prolonged) inhibition from inhibitory interneurons to CPGs due to the strong or repeated stimuli, CPGs will be silent and their membrane potentials will be very close to each other. As inhibition subsides, the CPG's half-center oscillators will rebound and burst almost simultaneously because of postinhibitory rebound. This will lead to the simultaneous activation of all slow MNs, which would not produce normal swimming behavior. This suggests that the inhibitory connection from interneurons to CPGs may not be an essential substrate for the escape and swimming activities. In the absence of definitive anatomical information, our model can be of benefit by comparing the expected activity patterns emerging from various likely connectivity architectures and by characterizing the conditions under which the network may exhibit the desired decision-making output.

The surprising decrease in response latency of the M-cell reveals an interesting possibility that the escape circuit may be primed for activation. However, the cellular mechanism underlying this phenomenon remains unknown. Either intrinsic or extrinsic neuromodulatory factors may potentiate the activation of the escape circuit by acting on the sensory inputs or the M-cell directly. Cachope et al. (2007) demonstrated that the M-cell can potentiate its own activation through the synthesis and presynaptic release of 2-AG that acts on innervating dopaminergic inputs to regulate dopamine release. Thus, 2-AG-mediated potentiation of the mixed electrical and chemical synapses between the sensory neurons and the M-cell could potentially increase synaptic transmission and speed up activation of the escape response. Interestingly, we found that the response latency in dominants is also shorter compared to group-housed animals. This suggests that although pairwise social interactions exert greater effects on subordinate animals, dominants are also affected but to a lesser extent.

Differences in behavior patterns of dominant and subordinate animals of many species suggests that social regulation of neural circuits is a widespread phenomenon. As with zebrafish, the M-cells in cichlid (Astatotilapia burtoni) and goldfish (Carassius auratus) display behavioral and cellular plasticity (Medan and Preuss, 2014). The M-cell receives direct serotonergic and dopaminergic inputs (Pereda et al., 1992; McLean and Fetcho, 2004; Neumeister et al., 2010; Medan and Preuss, 2011; Whitaker et al., 2011; Mu et al., 2012), its sensitivity is socially regulated, and depends on serotonergic modulation (Medan and Preuss, 2011; Whitaker et al., 2011). Unlike zebrafish, the response of the M-cell in dominant cichlid is enhanced compared to subordinates (Neumeister et al., 2010), suggesting species-dependent adaption to different ecological constraints. Body coloration in cichlids is socially regulated such that dominants are conspicuously brighter in coloration compared to subordinates (Korzan et al., 2008). Consequently, higher selective pressure in the form of increased predation of dominants is likely to occur, which translates into an enhanced sensitivity of the startle response. Although zebrafish do not undergo obvious changes in body coloration, visual cues enhance the excitability of the M-cell and reticulospinal neurons via descending dopaminergic input. This suggests that visual social cues other than coloration might regulate the activation of escape and swim circuits (Mu et al., 2012). The effects of social regulation on serotonergic and dopaminergic function in controlling the activation dynamics of escape and swim circuits in zebrafish, however, remains unknown.

Other mechanisms similar to those observed in our experiment are likely to contribute to a shift in activation dynamics of competing circuits, including changes in the availability of 2-AG, and hormonal regulation (O'Connell and Hofmann, 2011; Issa et al., 2012; Maruska, 2014; Oldfield et al., 2015). Additional cellular mechanisms that may underlie status-related differences have been reported in other species, including changes in transmitter or neuromodulator concentration (Gutzler et al., 2010) and receptor populations (Burmeister et al., 2007). Along with our proposed model, the synergistic action of one or few of these mechanisms may enable animals to adapt to changes in their social environment by selecting the most appropriate behavior while suppressing competing ones.