The Role of Human Primary Motor Cortex in the Production of Skilled Finger Sequences

Abstract

Human primary motor cortex (M1) is essential for producing dexterous hand movements. Although distinct subpopulations of neurons are activated during single-finger movements, it remains unknown whether M1 also represents sequences of multiple finger movements. Using novel multivariate functional magnetic resonance imaging (fMRI) analysis techniques and combining evidence from both 3T and 7T fMRI data, we found that after 5 d of intense practice, premotor and parietal areas encoded the different movement sequences. There was little or no evidence for a sequence representation in M1. Instead, activity patterns in M1 could be fully explained by a linear combination of patterns for the constituent individual finger movements, with the strongest weight on the first finger of the sequence. Using passive replay of sequences, we show that this first-finger effect is due to neuronal processes involved in the active execution, rather than to a hemodynamic nonlinearity. These results suggest that M1 receives increased input from areas with sequence representations at the initiation of a sequence, but that M1 activity itself relates to the execution of component finger presses only. These results improve our understanding of the representation of finger sequences in the human neocortex after short-term training and provide important methodological advances for the study of long-term skill development.

SIGNIFICANCE STATEMENT There is clear evidence that human primary motor cortex (M1) is essential for producing individuated finger movements, such as pressing a button. Over and above its involvement in movement execution, it is less clear whether M1 also plays a role in learning and controlling sequences of multiple finger movements, such as when playing the piano. Using cutting-edge multivariate fMRI analysis and carefully controlled experiments, we demonstrate here that, while premotor areas clearly show a sequence representation, activity patterns in M1 can be fully explained from the patterns for individual finger movements. The results provide important new insights into the interplay of M1 and premotor cortex for learning of sequential movements.

Introduction

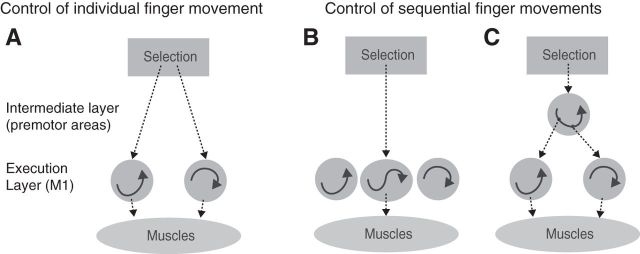
Primary motor cortex (M1), with its direct projection to spinal motoneurons, plays a critical role in fine hand control (Lawrence and Kuypers, 1968; Muir and Lemon, 1983). Populations of neurons in M1 involved in individuated finger movements show considerable overlap (Schieber and Hibbard, 1993). Yet, they form large enough clusters to be detected with functional magnetic resonance imaging (fMRI), as unique activation patterns are associated with each individual finger (Indovina and Sanes, 2001; Ejaz et al., 2015). Each of these populations can be conceptualized as a dynamical system (Churchland et al., 2012; Fig. 1A, arrows inside the two circles), that produces the continuous sequence of muscle activities necessary for the movement of a single finger. Whether such subpopulations in M1 can also learn to represent longer sequences that span movements of multiple different fingers is, however, still debated (Picard et al., 2013; Kawai et al., 2015).

Figure 1.

Two ways of representing sequential movements. A, Before training sequences are produced through a sequential selection of single-finger movements. The execution layer (M1 and spinal cord) contains populations of neurons that, once activated, generate the muscle activity patterns necessary for a single-finger movement through their intrinsic population dynamics. The selection layer acts directly on these representations. B, After learning, the repeated sequential activation of two execution primitives leads to the formation of a new population of neurons that produces the two presses as a single unit. C, Alternatively, a newly formed neural population in an intermediate layer could activate the execution primitives for the two fingers in the correct order.

One idea is that M1 develops dedicated populations of neurons that encode the sequences of two or more finger movements (Fig. 1B). Such representations could function in a similar way as artificial recurrent neural networks, capable of learning and storing multiple dynamic patterns (Laje and Buonomano, 2013). In this scenario, the neural activity for pressing the second digit would be different depending on whether it was executed in the sequence 1-2 or 3-2. This representation would allow M1 to autonomously generate the spatiotemporal activity pattern necessary for sequence production. Indeed, it has been suggested that M1 acquires such representations of finger sequences after a few days of training (Karni et al., 1995).

Alternatively, M1 could lack a true sequence representation, and the neural activity here may solely reflect the ongoing elementary movements independent of the sequential context (Mushiake et al., 1991; Ashe et al., 1993). In this scenario, the learned sequence would be represented in secondary motor areas, such as dorsal premotor cortex (PMd) or supplementary motor area (SMA; Mushiake et al., 1991; Shima and Tanji, 1998; Hikosaka et al., 2002; Diedrichsen and Kornysheva, 2015), which then activate the corresponding execution-related populations in M1 (Fig. 1C).

Here we sought to distinguish between these two possibilities by analyzing fine-grained activity patterns in M1 using fMRI during the performance of well learned finger sequences. Because of the low temporal resolution of fMRI, we cannot resolve the activity related to each individual press, but can only measure the activity averaged over the whole sequence. This makes the detection of true sequence representations challenging. Nonetheless, if activity in M1 represents movement sequences (Fig. 1B), then even sequences that consist of the same elementary movements in a different order should elicit distinguishable patterns of activity.

However, the finding of differentiable activity patterns for different sequences in M1 (as we have indeed found in previous studies: Wiestler and Diedrichsen, 2013; Kornysheva and Diedrichsen, 2014; Wiestler et al., 2014) does not provide conclusive evidence for a true sequence representation. Differences between activity patterns could also arise if different individual movements were unequally weighted depending on their sequential position, i.e., when in a sequence they occurred. By comparing activity patterns elicited by single-finger presses with those elicited by sequences, we show here that pattern differences in M1 can be fully explained by the fact that the first finger has a stronger influence on the overall pattern than subsequent fingers. In contrast, activation patterns in premotor and parietal cortices could not be explained by a combination of the activity patterns for the elementary movements, thereby providing evidence for a true representation of the sequential context. Through control experiments with passive finger movements, we further establish that the first-finger effect is linked to the active execution of the sequence, and is not an artifact of nonlinearities in the fMRI signal. This suggests that premotor areas comprise representations of movement sequences, which then activate the representations of the individual component movements in M1 (Fig. 1C).

Materials and Methods

Participants

After providing written informed consent, nine healthy, right-handed volunteers (3 females, 6 males, age: 23 ± 4) participated in Experiment 1, and 14 healthy, right-handed volunteers (8 females, 6 males, age: 23 ± 3) participated in Experiment 2. There was no overlap in the participants in the two experiments. The experimental procedures were approved by local ethics committees at the University of Western Ontario (London, Canada) and University College London (London, UK). None of the participants had any known neurological history. We excluded participants that were professional musicians. On average, participants reported 5.3 ± 5.3 years (Experiment 1) and 4.8 ± 4.1 years (Experiment 2) of practice with instruments that demand rapid and complex finger sequences (e.g., piano, violin, guitar).

Apparatus

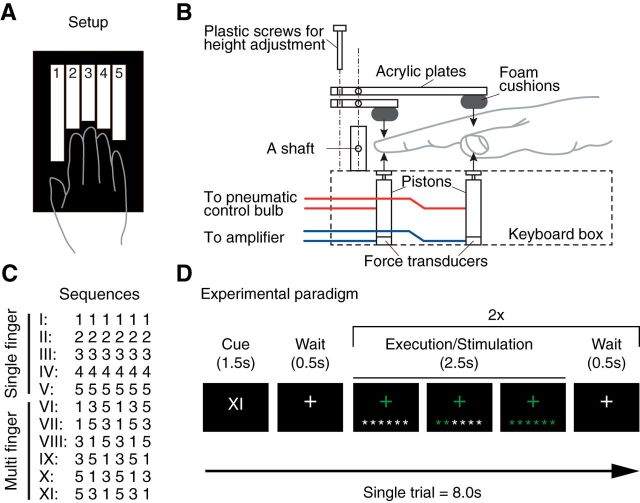
We used a custom-built five-finger keyboard (Fig. 2A) with a force transducer (Honeywell FS series) mounted underneath each key. The keyboard was built for the right hand. The keys were immobile and measured isometric finger force production. The dynamic range of the force transducers was 0–16 N and the resolution <0.02 (N). A finger press/release was detected when the force crossed a threshold of ∼3 N. The threshold was slightly adjusted for each finger to ensure that each key could be pressed easily. The forces measured from the keyboard were low-pass filtered, amplified, and sent to PC for online task control and data recording. The forces were recorded at 200 Hz. Passive stimulation of the fingers was achieved using a pneumatic air piston mounted underneath each key (Fig. 2B). The pistons were driven by compressed air (100 psi) from outside the MRI scanning room through polyvinyl tubes. The force exerted by each piston was controlled by pressure-regulating valves. During the passive stimulations, finger movement was prevented by a frame mounted above the fingers. Therefore, the main function of the pistons was to apply pressure to the fingertips, comparable to the active condition.

Figure 2.

Methods for Experiment 1. A, Participants generated isometric finger presses on a custom-built keyboard with force transducers and pneumatic pistons embedded within each key. B, Schematic diagram of the passive pneumatic device used in Experiment 1. C, Participants were trained on five single-finger and six multi-finger sequences. D, Schematic illustration for a trial during scanning. A Roman numeral indicated the sequence to be executed. Participants then executed the sequence twice, receiving online visual feedback for each correct press. fMRI activity measurements were averaged across the two executions of the sequence, thereby removing temporal information from the activity profiles.

Sequence training for Experiment 1

During the training sessions, participants were seated in front of an LCD monitor and placed their fingers on the keyboard. They learned to produce five single-finger sequences and six multi-finger sequences. For the single-finger sequences, one of five fingers had to be pressed six times (e.g., 3 3 3 3 3 3); for the multi-finger sequences, one of the six possible permutations of fingers 1, 3, and 5 was pressed twice (e.g., 5 3 1 5 3 1; Fig. 2C). All fingers remained on the keyboard at all times, such that the overt movement of the fingers was minimized.

At the start of each trial, a visual cue was presented (for 1.5 s) to indicate which of the sequences was to be performed (Fig. 2D). Each of the 11 sequences was associated with a different Roman numeral (I, II, …, XI). At the beginning of training, we provided both the sequence cue (Roman numeral) and the six to-be-pressed digits on the screen. Over the course of the training, we replaced the digits with asterisks (*), to encourage the participants to memorize the sequences (Fig. 2D). The participants practiced the sequences for 3 d so they were able to produce the sequences in the scanner within 2.5 s from memory given only the visual cue.

Training consisted of a total of 1716 sequence executions (156 executions per sequence type). The order of the 11 sequences was pseudorandomized within each session. During a trial, the color of each asterisk turned to green immediately after a press of the correct finger was registered, and it turned to red if the press was incorrect. To ensure equal execution speed across single- and multi-finger sequences, we provided a visual pacing signal that blinked at a reference frequency. This reference frequency gradually increased during the training sessions with a constant rate until it reached to 4 Hz. On the last day of training, participants practiced the imaging protocol (involving also passive stimulation trials, see below), while lying on a mock MRI scanner bed.

Sequence training for Experiment 2

The sequence task was similar to the first experiment. In Experiment 2, participants (N = 14) learned to produce eight different sequences with 11 presses from the memory. The first half of the participants were trained for 5 d; for the second half, we added a sixth day to ensure that all participants could correctly produce the sequences within 4 s. On average, the training took a total of 10–12 h. As in Experiment 1, the sequences were cued with Roman numerals I–VIII. All the sequences were matched with the number of finger presses used; two presses with the thumb, middle, ring, and little fingers, and three presses with the index finger, respectively. Four of the sequences started with the thumb, two sequences started with the middle finger, and the rest of two sequences started with the little finger. There was no passive condition in Experiment 2. The detailed training protocol and the behavioral results of training and transfer test (conducted after the imaging) will be reported in a separate paper.

Imaging procedures for Experiment 1

During the imaging session, the participants lay supine on the scanner bed with knees slightly bent and supported by a wedge-shaped cushion. The pneumatic keyboard was comfortably placed on their lap, and visual stimuli were presented on a back-projection screen which was viewed through a mirror attached to the head coil.

In Experiment 1, participants conducted both active and passive conditions. Each trial started with the presentation of the sequence cue for 1.5 s (Roman numeral I–XI). Participants were then instructed to execute the cued sequence twice, with a time limit of 2.5 s for each execution (Fig. 2D). Each execution was triggered by a fixation cross turning green. To ensure similar pressing speeds for the single-finger and multi-finger sequences, we provided a visual pacing signal that blinked at 4 Hz. The order of the 11 sequences was pseudorandomized and included one rest trial of 8 s, during which the participants only passively viewed the fixation cross. Each sequence was repeated three times within each imaging run, resulting in a total of 66 sequence executions per run. Participants completed seven runs in the active condition. For these runs, there was no significant difference in the pressing frequency (Hz) between single and multi-finger sequences (4.58 ± 0.36, 4.59 ± 0.39, t₈ = −0.176, p = 0.865). The percentage of correct sequence executions was slightly higher for single-finger than for multi-finger sequences (99.5 ± 0.17 vs 95.7 ± 0.66; t₍₈₎ = 6.182, p = 0.00026).

Alternating with the active runs, participants also completed seven imaging runs in the passive condition, to examine to what degree the observed movement representations could be explained by passive sensory inflow. During the active run, we recorded force data, and replayed these forces through the pistons in the subsequent passive run. The participants were told not to produce any active finger movement, but to relax the hand and passively receive stimulations to their fingers. The sequence cue, pacing signal, and trial timing were exactly the same as in the active runs, ensuring that participants were well aware of which sequence they were going to receive. Due to the nonlinear response property of pneumatic pistons, the resultant passive forces were slightly lower than the forces in the active condition. We confirmed, however, that passive stimulation elicited robust single-finger representations that were comparable to the active condition (see Results).

Imaging procedures for Experiment 2

The imaging procedures for Experiment 2 were similar; however, we only measured eight active multi-finger sequences (see above) and did not include passive or single-finger conditions. In the beginning of each trial, the sequence cue (I–VIII) was presented for 2.5 s. This was followed by two execution phases of 4 s each, with 0.5 s ITI. During the execution phase, only the fixation cross and asterisks were presented. The order of sequences was pseudorandomized, and each of the eight sequences was repeated three times during each run. The performance was not paced; however, the average pressing frequency for Experiment 2 (4.47 ± 1.05 Hz) was not significantly different from that in Experiment 1 (t₍₁₉₎ = 0.298, p = 0.769). Four resting trials of 10.5 s were randomly interspersed. We conducted nine runs, each of which lasted ∼7 min. On average across participants, 81.0 ± 9.4% of the sequence executions were correct.

Imaging data acquisition

Experiment 1 was conducted in a Siemens Magnetom Syngo 7T MRI scanner system with a 32-channel head coil at the Centre for Functional and Metabolic Mapping, Robarts Research Institute (London, Ontario, Canada). Inhomogeneity of the magnetic field was adjusted by B0 and B1 shimming at the beginning of the whole session. Functional images were acquired for 14 imaging runs (7 active and 7 passive runs) of 300 volumes per each using multiband 2-D echoplanar imaging sequence (TR = 1.00 s, multiband acceleration factor = 2, in-plane acceleration factor = 3, resolution = 2.0 mm isotropic with 0.2 mm gap between slices, and 44 slices interleaved). The first four volumes of each run were discarded to ensure stable magnetization. The slices were acquired close to axial to cover the dorsal aspects of the brain, including most of the frontal, parietal, occipital lobes, and basal ganglia. The ventral aspects of the frontal and temporal lobes, brainstem, and the cerebellum were not covered. Each functional imaging run of Experiment 1 lasted for 5 min. A T1-weighted anatomical image was obtained in a separate session using a MP2RAGE sequence (TR = 6.0 s, resolution: 0.75 mm isotropic).

Experiment 2 was conducted on a Siemens Trio 3T scanner system with a 32-channel head coil at the Welcome Trust Centre for Neuroimaging (London, United Kingdom). B0 field maps were acquired at the beginning of the session to correct for inhomogeneities of the magnetic field (Hutton et al., 2002). Functional images were acquired for nine runs of 135 volumes each, using a 2-D echoplanar imaging sequence (TR = 2.72 s, in-plane acceleration factor = 2, resolution = 2.3 mm isotropic with 0.3 mm gap between each slice, and 32 slices interleaved). The first five volumes of each run were discarded to ensure stable magnetization. The coverage was similar to Experiment 1. A T1-weighted anatomical image was obtained using MPRAGE sequence (1 mm isotropic resolution).

Behavioral data analysis

Recorded force data were analyzed offline. The data for both the training and scanning sessions was first smoothed with a second-order Butterworth filter with a cutoff frequency of 10 Hz to remove remaining RF noise. Press and release timings were defined as the time point where the pressing force first crossed the threshold (3 N) and the time when the pressing force fell below the threshold. Movement time (MT) was measured as the elapsed time from the start of the first press to the release of the last press. Sequence executions containing one or more incorrect presses were marked as error trials.

Imaging data analysis

Preprocessing and first-level model

Experiment 1.

Functional imaging data were preprocessed using SPM12 (http://www.fil.ion.ucl.ac.uk/spm/). Functional images were first motion corrected, and then coregistered to the individual anatomical image. As we had a relatively fast TR (1.0 s), we did not apply slice timing correction. The data were then submitted to a first-level GLM to estimate the size of the evoked activity for each sequence type in each run. We modeled the temporal autocorrelation using the “FAST” option in SPM12, which provides a flexible basis function to model dependencies on longer time scales. High-pass filtering was achieved by temporally pre-whitening the matrix using this temporal autocorrelation estimate.

Experiment 2.

Preprocessing and GLM were conducted as in Experiment 1, with the exception that we applied slice timing correction (given the slower TR). We also corrected for B0 inhomogeneity by using field-map images. Given the slower TR, we used the standard high-pass filtering with a cutoff frequency of 128 s before GLM estimation. For the GLM, we applied robust-weighted least square estimation (Diedrichsen and Shadmehr, 2005). The data from two participants in Experiment 2 were excluded from further analyses due to poor behavioral performance during scanning (58% correct vs 81% correct for all other subjects). These individuals also failed to achieve any correct execution of one or more sequence types in some of the imaging runs. Hence, only the data from the remaining 12 participants were submitted to subsequent analyses.

Searchlight and ROI definition

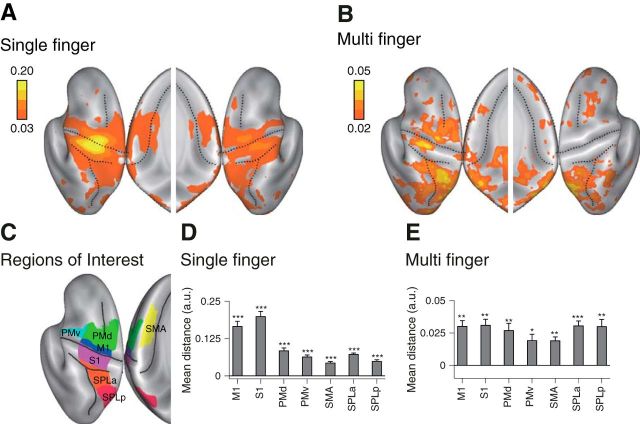
Individual cortical surfaces (i.e., the pial and white/gray matter surfaces) were reconstructed from the anatomical image using the FreeSurfer software (Fischl et al., 1999). We defined a continuous surface-based searchlight (Oosterhof et al., 2011) as small circular cortical patches (∼11 mm radius) centered on each node defined on the reconstructed cortical surface, each of which contained 160 voxels. Anatomical regions of interest (ROIs) were defined on this reconstructed surface (Fig. 3C) exactly as reported in previous studies (Wiestler and Diedrichsen, 2013; Kornysheva and Diedrichsen, 2014; Wiestler et al., 2014).

Figure 3.

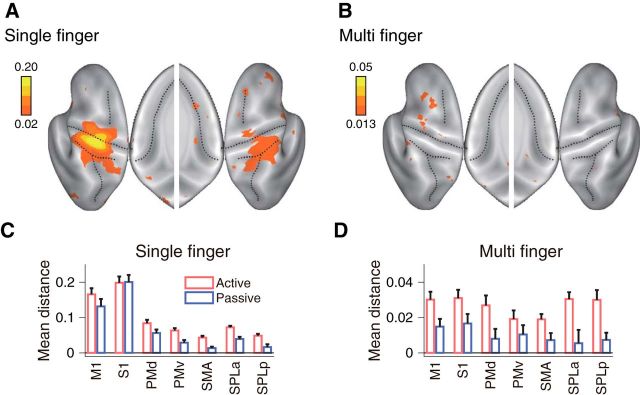
Searchlight map for movement representation. A, Averaged distance for single-finger sequences. B, Averaged distance for multi-finger sequences. Results are shown on an inflated view of the left and right cortical hemisphere, with the inset showing distance on the medial wall. C, Seven ROIs were defined on each hemisphere of the reconstructed cortical surface. D, E, Mean distances calculated for single-finger sequences (D), and multi-finger sequences (E). Asterisks indicate a significant difference from zero based on the group t test. *p < 0.05, **p < 0.01, ***p < 0.001. M1: primary motor cortex, S1: primary sensory cortex, PMd: dorsal premotor cortex, PMv: ventral premotor cortex, SMA: supplementary motor cortex, SPLa: anterior superior parietal lobule, and SPLp: posterior superior parietal lobule (posterior parietal cortex).

Multivariate fMRI analysis

Within each of these groups of voxels (surface-based searchlight or anatomically-defined ROIs), we extracted the β-weights for each sequence type and imaging run. To optimally integrate evidence across voxels, we spatially pre-whitened the activity estimates in each area using multivariate noise-normalization, using a regularized estimate of the overall noise-covariance matrix (Walther et al., 2016). This procedure renders the remaining noise in each voxel approximately uncorrelated with noise in other voxels (Diedrichsen et al., 2016; Diedrichsen and Kriegeskorte, 2017).

Using the representational model framework (Diedrichsen and Kriegeskorte, 2017), we then asked how different sequences were represented in these local multivariate activity patterns. The central statistical quantity in this framework is the second moment matrix of the activity patterns. If U represents the true activity patterns for the K experimental conditions (sequences) of P voxels, then the K-by-K second moment matrix between the activity patterns is defined as follows:

Large numbers in the matrix indicate pairs of activity patterns have good correspondence across voxels, and zeros indicate that they are uncorrelated. Conceptually, the second moment matrix can be interpreted similarly to a covariance matrix, only in that the mean across voxels is not removed (Diedrichsen and Kriegeskorte, 2017).

We then analyzed the representational structure defined by the second moment matrix using two complementary approaches: representational similarity analysis (RSA) to establish basic features of the representation and for visualization purposes, and pattern component modeling (PCM) to compare more complex representational models.

Representational similarity analysis

In RSA, we quantify the representational structure by measuring how distinct pairs of activity patterns are from each other. The squared Euclidean distance (scaled by the number of voxels) between the activity pattern u₁ and u₂ is as follows:

and can therefore be directly calculated from the second moment matrix G. Calculated on spatially pre-whitened data, this distance is equal to the squared Mahalanobis distance. One problem is that estimates of this distance based on noisy data are positively biased; i.e., the average distance estimate will be larger than zero, even if the true distance is zero. This is because pattern estimates will always differ slightly based on random noise. To remedy the situation, we used the “crossnobis estimator” (Diedrichsen et al., 2016; Walther et al., 2016; Diedrichsen and Kriegeskorte, 2017), a distance calculated from a cross-validated estimate of the second moment matrix G:

where M is the total number of partitions (e.g., imaging runs), Û_m is estimated pre-whitened activity patterns for partition m, and Û_m̃ is the estimate of the patterns based on all other partitions. The crossnobis estimator is unbiased, meaning its average will be zero if the two patterns only differ by noise. The estimator can therefore be directly used to test if two patterns are statistically different: finding a consistently positive distance estimate implies that the two condition activity patterns differ from each other more than expected by chance.

To visualize the representational structure, we used classical multidimensional scaling. We projected the activity patterns into a lower dimensional subspace by finding the Eigenvectors of the group-averaged Ĝ matrix, weighted by the square root of the corresponding Eigenvalues. The projection displayed in Figure 4B was then rotated to maximize the differences between the single-finger movements.

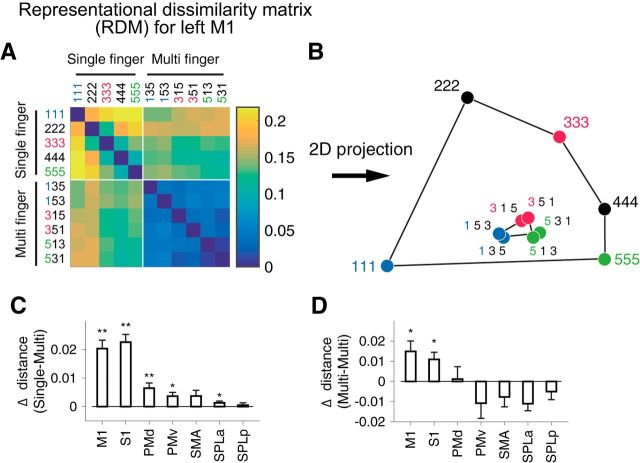
Figure 4.

Representational structure in the left M1. A, RDM calculated from the activation pattern within left M1 (contralateral to the performing hand). B, Low-dimensional projection of the RDM by multidimensional scaling (MDS). Each dot represents a movement condition (1–5: single-finger, 135–531: multi-finger). C, D, Test for the first-finger effect (see Materials and Methods). C, Mean distance between the single-finger presses (1, 3, or 5) and the multi-finger sequences that start with the same finger minus the distance between the same single-finger presses and multi-finger sequences that start with a different finger. A positive difference indicates that the pattern for each multi-finger sequence is weighted toward the pattern of the first finger. D, Mean distance between two multi-finger sequences that start with different fingers minus the mean distance between sequences that start with the same finger. A positive difference indicates that the difference between sequences can partly be explained by the difference between the first finger. Asterisks indicate statistical significance assessed by one-sided paired t test. *p < 0.05, **p < 0.01.

Pattern component modeling

To compare different representational models, we used PCM (Diedrichsen et al., 2011, 2017; Diedrichsen and Kriegeskorte, 2017). Like RSA or encoding models, PCM can test how well the data can be described by a specific representational structure or a specific set of features. Going beyond the other two approaches, however, it provides a principled and analytical way for testing arbitrary combinations of feature sets or representational structures. PCM directly evaluates the likelihood of the data under the linear model

Here, Y is an N-by-P matrix representing noise-normalized activity pattern after the first-level GLM (Walther et al., 2016), where N is the number of estimates (number of conditions × number of runs) and P is the number of voxels. Z (N-by-K matrix) is the design matrix that associates the true activity profiles U and Y. B represents the patterns of no interest, in our case the mean activity pattern in each run. Finally, E represents trial-by-trial measurement errors.

Importantly, PCM considers the true activity profile of each voxel u_p (columns of matrix U) to be a random variable from a multivariate normal distribution, u_p ∼ N(0, G). G is the second moment matrix of activity profiles, which determines the similarity structure across movement conditions. In evaluating models, PCM integrates over the actual activity profiles, i.e., it evaluates the marginal likelihood of the data (simply termed likelihood in this paper);

where θ represents model parameters that determine the shape of G (for example as the mixture proportions of different representations), the signal strength, and noise variances (Diedrichsen et al., 2017). In other words, the explicit estimation of the patterns U is not necessary, because the second moment (G) is a sufficient statistic to obtain the marginal likelihood of the data. Using this approach, we fitted a number of models to explain the representational structure of the patterns associated with the multi-finger sequences.

Null model.

As a baseline, we used a model in which all the sequences elicit the same common pattern; i.e., there were no differences between the activity patterns and hence no representation of the sequence.

First-finger model.

In this model, we assumed that the activity patterns for the multi-finger sequences were a weighted linear combination of the patterns for the constituent single-finger presses. If all fingers were weighted equivalently, the overall patterns would be identical, as each sequence contains exactly the same fingers. Instead, the first-finger model assumes that the first finger press is more strongly weighted than subsequent presses. This predicts that pairs of sequences that start with the same finger share high covariance, and sequences that start with different fingers have low covariance (Fig. 5A).

Figure 5.

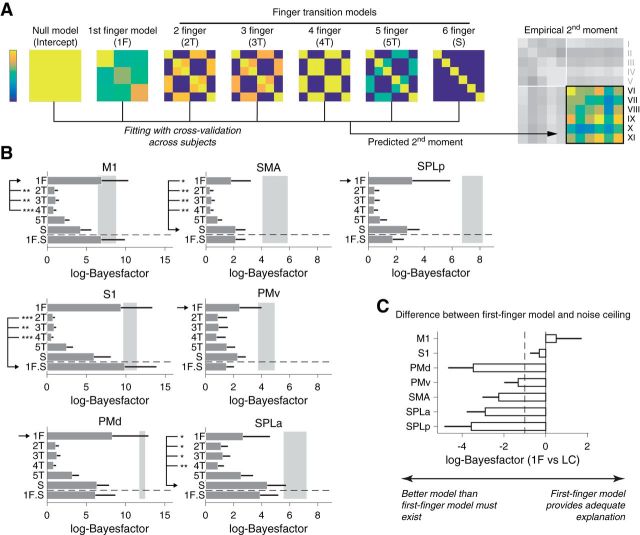
Evaluating representational models of multi-finger sequences. A, The empirical second moment of the activity patterns for the multi-finger sequences (a 6 × 6 matrix: on the right) is modeled using a combination of the predicted second moment matrices for each of the models. As in a covariance matrix, high values (yellow) indicate tight correspondence between the two activity patterns, whereas low values (blue) indicate uncorrelated activity patterns. B, The difference in log-likelihood compared with the null-model (log-Bayes-factor) for each component model. The gray area denotes the upper and lower noise ceiling. The combination of the first-finger model and the six-finger transition model (1F.S) is shown below the horizontal dashed line. The winning model is marked by the arrow. Significant differences (assessed by Wilcoxon's rank sum test on individual log-Bayes-factors) between the winning and the other models are marked by asterisks (*p < 0.05, **p < 0.01, ***p < 0.001). Error bars represent SE across subjects. C, Log-Bayes-factor of the first-finger model compared with the lower noise ceiling for each ROI. The dashed line shows the typical threshold value for model selection (Kass and Raftery, 1995).

More formally, the activity patterns for multi-finger sequences are modeled as a weighted sum of the activity patterns for the single-finger sequences,

where U_sq is the patterns for multi-finger sequences (6 × P matrix), U_sf is the activation patterns for the single-finger presses of the thumb, middle, and little fingers (3 × P matrix), and M_1f is the weighting matrix. Because each finger is present in each sequence equally often, we can simply model the difference in weight between the first and the subsequent fingers, such that M_1f is set to 1 for the first finger, and 0 otherwise (6 × 3 matrix). Therefore, the predicted similarity structure across multi-finger sequences (i.e., the second moment of the pattern G_1f) is fully determined from the similarity across the single-finger presses (i.e., G_sf):

To make the predictions for the first finger model (Fig. 5A), we used Ĝ_sf estimated from the patterns of single-finger sequences. Note that second moment matrix for single fingers simply scales by a constant factor when the presses are repeated (Diedrichsen et al., 2017).

N-finger transition model.

This model family predicts the similarity structure based on neural circuits that encode the transitions between finger presses. Unique transitions can be defined based on two or more subsequent presses. For instance, each sequence has five specific two-finger transitions, four three-finger transitions, etc. The activity patterns of the multi-finger sequences are can be modeled as follows:

In this case, the weighting matrix M_trans indicates, for each sequence, how many of the possible two-digit transitions (9 total), three-digit transitions (27 total), etc. the sequences contained, and U_trans represents specific activation patterns for each possible transition. Under these assumptions, the predicted second moment matrix is as follows:

Because we did not measure patterns for individual transitions, we assumed that (1) the patterns are independent with each other, and (2) the strength with which each pattern is represented is proportional to the frequency of occurrence of that particular transition during the training period. The second assumption is consistent with the observation that performance improvement (e.g., RT reduction) for a particular transition is proportional to its probability (Stadler, 1992).

In Experiment 1, any of the six possible transitions between the three fingers occurs equally often. Therefore, U_transU_trans^T = θ_transI, where θ is a constant that indicates the overall strength of the transition encoding and I is an identity matrix. Note that this approach is equivalent to fitting an encoding model with a separate regressor for each transition and using ridge regression to estimate the parameter weights (Diedrichsen and Kriegeskorte, 2017).

Combining these assumptions, the predicted second moment matrix is as follows:

The resultant predicted second moment matrix for each N-finger transition model can be seen in (Fig. 5A). Note that the six-finger transition model predicts that all sequences are equally distinct from each other, as each sequence has only one unique six-finger transition (the entire sequence). In Experiment 2, the occurrence frequency of the transitions was slightly different. Therefore, we modeled the second moment matrix as follows:

where α₁, α₂, … α_N are constants proportional to the frequency of occurrence for N transitions of interest.

Model comparison.

We first fitted the six individual models (see the previous section) separately. To account for individual differences in the signal-to-noise ratio, we maximized the likelihood in respect to a noise and signal strength parameter (Diedrichsen et al., 2017); thus each model had the same two free parameters, allowing us to compare their likelihoods directly. We also fitted combinations of pairs of models, where the overall representation was a mixture of the hypothesized representations (i.e., the second moment matrix was the weighted sum of those models). In this case, each component weight added an additional free parameter (θ). Therefore, each single model had two free parameters (i.e., signal and noise parameters), and each mixture of two models had three free parameters (i.e., signal, noise, and the mixing ratio of one model over the other).

To compare models with different number of parameters, we used group cross-validation: we fitted the parameters using the data from n − 1 subjects, and then used the estimated G to fit the data from the left-out subject (Diedrichsen et al., 2017). Note that the signal and noise parameters were always fitted individually to each subject. Through this process, we obtained a cross-validated likelihood for each candidate model for each subject, which served as an estimate of the model evidence.

We then compared models by calculating the log-Bayes factor, which tells us to what degree one model provides a better description of the observed data than another model (Kass and Raftery, 1995):

logBF values were computed separately for each subject. We then used standard criteria for the average logBF proposed by Kass and Raftery (1995) to judge if a model is meaningfully “better” than the other. Instead of using the group log-Bayes factor (Stephan et al., 2009), i.e., the sum of the individual log-Bayes factors, we report here the average logBF, which is invariant to the number of participants. This provides a much more stringent criterion for model selection.

Noise ceiling.

We also estimated the data-likelihood under a model that captures all systematic variation in the data, here called a noise ceiling. The noise ceiling is an important measure to assess whether the selected model is a sufficient model, or whether the model misses a substantial aspect of the representational structure that is consistently observed across individuals. For this, we used a free (fully flexible) model, which had as many parameters as the number of the elements in the second-moment matrix. For an estimate of the free model, we simply used the mean of the cross-validated second moment matrix Ĝ across subjects, which yields nearly identical results as using the maximum-likelihood estimate (Diedrichsen et al., 2017).

We first estimated the free parameters of the model, using the data from all subjects combined. This resulted in the best achievable likelihood for a group model and therefore constitutes an upper bound for the likelihood. Because this estimate is over-fit, we also determined the cross-validated likelihood of the free model, which constitutes a lower bound estimate of the noise ceiling. If a model performs better than the lower noise ceiling, it remains possible that a better model exists. However, based on the absolute performance, we can conclude that the model already captures all consistent effects in the data.

Experimental design and statistical analysis

All experiments and analyses were conducted using a within-subject design. We used one-sided, one-sample t test for the evaluation of positive mean distance across subjects. To assess the first-finger effect, we performed two separate paired t tests: (1) if distances between two multi-finger sequences sharing the same first finger were smaller than distances between any other pair of multi-finger sequences not sharing the same first finger, and (2) if distances between a single-finger sequence and a multi-finger sequence sharing the same first finger were smaller than distances between that finger and any other multi-finger sequence. Significant differences for the above comparisons (1 and 2) were deemed as the evidence of the first-finger effect. The ratio between active and passive distances (i.e., the reduction of passive distance) was estimated using linear regression without an intercept. Estimated slopes between single- and multi-finger sequences were then compared using a simple t contrast.

For the model comparison using PCM, we used the standard interpretation of the size of the BF (Kass and Raftery, 1995). Additionally, we also report a Wilcoxon's rank sum test on the log-Bayes factors between the winning and other models. The significance level was set to p = 0.05. All the statistical analyses were performed in MATLAB (MathWorks). The MATLAB code used for the multivariate fMRI analysis (Pattern Component Modelling Toolbox; RRID:SCR_015891) are available online (https://github.com/jdiedrichsen/pcm_toolbox).

Results

M1 “encodes” both single-finger movements and sequences

We tested whether sequences are represented in M1 by comparing the fine-grained fMRI brain activation pattern associated with fast finger sequences (6 finger presses within 2.5 s) with those associated with single-finger movements. Participants practiced six sequences that comprised all orders of pressing the thumb, middle, and little finger with their right hand (Fig. 2A–C). For the single-finger movements, they produced six repetitions with the same finger. Participants were trained for 3 d, ∼6 h in total, until they could perform all sequences from memory without error and at the same speed. We localized areas that showed reliable differences between either single-finger or multi-finger sequences by using a surface-based search-light approach (Oosterhof et al., 2011). Based on previous results (Wiestler and Diedrichsen, 2013), we expected that different single-finger movements and different movement sequences would elicit differentiable activity patterns in M1.

To characterize the representation, we calculated the cross-validated Mahalanobis distance (Walther et al., 2016) between the activity patterns for different conditions. If this measure is systematically larger than zero, we can conclude that the true underlying patterns are different (see Materials and Methods). As expected, we found evidence for a representation of single fingers in the hand area of M1 and somatosensory cortex (S1; Fig. 3A,D). Consistent with previous studies (Wiestler et al., 2011; Diedrichsen et al., 2013; Ejaz et al., 2015), weaker differences between patterns for single-finger movements were found in secondary motor areas such as PMd and ventral premotor cortex (PMv), and the SMA in the anterior superior parietal lobule (SPLa; Fig. 3D) and the ipsilateral hemisphere (Diedrichsen et al., 2013).

Multi-finger sequences elicited differentiable activity patterns in premotor and parietal areas (Wiestler and Diedrichsen, 2013; Kornysheva and Diedrichsen, 2014; Wiestler et al., 2014; Fig. 3B). Importantly, we also found significantly different activity patterns for different sequences in M1 and S1, as indicated by the systematically positive crossnobis estimates (Fig. 3E). The pattern distances for multi-finger sequences were only 19 ± 9% of those for single-finger presses, but they were reliable enough to decode which of the six sequences was performed with a cross-validated accuracy of 25 ± 5% (chance level, 16.67%).

One may argue that if M1 only represented the individual finger presses, the activity patterns for the different multi-finger sequences should have been indistinguishable. However, this argument relies on the assumption that all component actions elicit the same amount of activation regardless of the order in which they were made. Before concluding that M1 exhibits a genuine sequence representation (i.e., is in a different neuronal state for each sequence), we therefore need to consider the possibility that the input from premotor areas (Fig. 1C) varied depending on whether the finger press was at the beginning or middle of the sequence. As different multi-finger sequences start with different fingers, this effect could lead to distinguishable BOLD activity patterns even if M1 only represented individual finger movements.

Differences in sequences depend on the first finger

To test for this possibility, we compared the activation patterns for the multi-finger sequences to those of the single-finger presses. We calculated the cross-validated distances between all pairs of conditions in an anatomically defined ROI (Fig. 3C) for contralateral M1. The resultant matrix of pairwise distances (55 pairs in total), the representational dissimilarity matrix (RDM), effectively summarizes the representational structure of the whole ROI (Fig. 4A).

To obtain insight into the representational structure, we applied a dimensionality reduction to the RDM by projecting it into a 2-D space (Fig. 4B; for details, see Materials and Methods). For single-finger presses (111, 333, etc.) we replicated the characteristic representational structure with the thumb showing the most unique pattern and the other fingers arranged in a semicircle (Ejaz et al., 2015).

The multi-finger sequences were arranged such that two sequences starting with the same finger were clustered together (shown in the same color in Fig. 4B). Furthermore, among all multi-finger sequence patterns, each pattern was also the most similar to the pattern associated with the first finger in the sequence. It should be noted, however, that low-dimensional projections (here designed to maximize the distances between single-finger movements; see Materials and Methods) generally only capture a very selective aspect of the representational structure. Therefore, to fairly quantify these two key observations, we compared the cross-validated distances between activity patterns of single- and multi-finger sequences in the (un-projected) high-dimensional space.

If the activity pattern of each sequence is mostly influenced by the starting finger, then the pattern for each individual finger should be closer (i.e., smaller distance) to sequences starting with that finger compared with other sequences. For instance, the pattern for the thumb (Fig. 4B, 111) should be closer to sequence 135 and 153 than to other sequences (e.g., 351 or 315). This was indeed the case in contralateral M1 (t₍₈₎ = 6.18, p = 1.3×10⁻⁴) and S1 (t₍₈₎ = 4.09, p = 0.0018; Fig. 4C).

Furthermore, two sequences starting with the same finger should be more similar to each other than other pairs (e.g., the distance 135 vs 153 should be smaller than 135 vs 315). Again, this effect was significant in M1 (Fig. 4D; t₍₈₎ = 2.87, p = 0.0104) and S1 (t₍₈₎ = 3.08, p = 0.0075). In contrast, no other tested ROI showed significance on both tests simultaneously (Fig. 4D).

One possible scenario which can explain both observations is that the activity patterns for sequences in M1 are a weighted sum of patterns elicited by the constituent single-finger presses, with the first finger having the highest weight. This would imply that there is no true sequence representation in M1. To evaluate whether this simple idea could fully explain the pattern differences between the multi-finger sequences in M1, we tested different candidate models for the activity patterns of multi-finger sequences using the PCM framework (Diedrichsen et al., 2011, 2017; Diedrichsen and Kriegeskorte, 2017). PCM allows us to compare different representational models by directly evaluating the likelihood of the observed patterns under the models. The method focuses on the second moment matrix; i.e., the covariance matrix of the patterns without subtraction of the mean activity across voxels. The second moment matrix has a close relationship to the RDM (see Materials and Methods). Importantly, we can compare the model likelihood to a noise ceiling, to assess whether the model can fully account for the data given the level of measurement noise and intersubject variability (see Materials and Method).

As a starting point, we tested the “first-finger” model, in which the patterns for multi-finger sequences are weighted sums of single-finger presses, with the first finger having the highest weight and all the subsequent fingers having a lower, but equal, weight (see Materials and Method). This model predicts that sequences that start with the same finger share high covariance, and sequences that start with different fingers have low covariance (Fig. 5A). We found that this model could almost fully account for the representational structure found in M1: the log-likelihood relative to the null-model (log-Bayes factor; see Materials and Methods) fell between the upper and lower bound of the noise ceiling (Fig. 5B; 6.95 vs 6.45).

We then tested whether M1 might represent movement transitions between two or more fingers (Fig. 5A). These models assume that each transition across n successive fingers is associated with a specific and independent activation pattern (i.e., representations of partial sequences). The second moment matrix (and the similarity structure) across the patterns of multi-finger sequences is fully determined by which transitions each sequence contained (see Materials and Methods). Note that a representation of a six-finger transition would mean that each sequence would have a unique activity pattern. The log-Bayes factor for these models was clearly lower than that for the first-finger model (Fig. 5B), indicating a poorer fit of these models.

We then explored linear combinations of models. Because the relative weight of each component was an additional free parameter, we evaluated the model likelihood using cross-validation across participants (see Materials and Methods). When we combined the first-finger model with the sequence model, we achieved a slightly lower likelihood than the first-finger model alone for M1 (the average log-Bayes factor reduced by 0.05). For S1, however, the addition of the sequence model achieved a slightly higher likelihood (9.37 for first-finger model alone vs 9.87 for the combined model; Fig. 5B). However, on a common scale of Bayes factors (Kass and Raftery, 1995), such a small difference would be considered “not worth more than a bare mention”.

In premotor areas, on the other hand, the representational structure was not well explained by the first-finger model. For example, in SMA and SPLa, the fit of the sequence model was systematically better than the first-finger model (Fig. 5B), indicating that the activity patterns in these regions represented sequential information. Whereas in premotor (PMd and PMv) and posterior parietal cortex, the first-finger model provided the best explanation among the fitted models, the likelihood of the first-finger model was systematically below the lower bound of the noise ceiling (Fig. 5C). The mean difference in log BF to the lower noise ceiling was substantially >1, indicating strong evidence (Kass and Raftery, 1995) that a better model must exist for these regions.

In summary, on the group level, our results provided very limited evidence for a true, unique sequence representation, or the representation of transitions between fingers in M1. Instead, the representational structure for sequences in this area could almost fully be explained by the first-finger model; i.e., assuming that the patterns for multi-finger sequences are a linear combination of the patterns associated with the individual finger presses, with the first finger weighted more strongly than the others. The same observation held true for S1. In contrast, in premotor regions, the first-finger model could not fully account for the differences between sequences, suggesting genuine encoding of sequential information in these regions.

First-finger effect in M1 is related to neural planning and execution processes

We hypothesized that the prominent activity for the first finger press in M1 is related to active planning and execution processes. Given that the BOLD signal more closely reflects synaptic input than spiking activity of output neurons (Logothetis et al., 2001), one possible explanation is that M1 receives strong input from premotor regions at the beginning of the sequence to push the neural state from the resting to the active state at movement initiation. Although M1 would still rely on premotor input to produce the subsequent finger presses, the amount of this input would be smaller as M1 is already in an active state.

Alternatively, the prominence of the first finger pattern could be due to the passive properties of M1. Specifically, the effect could have hemodynamic rather than neuronal causes. That is, the neural activity for each finger in the sequence could be exactly the same, but because of the nonlinear integration of the BOLD signal for interstimulus intervals of <6 s (Dale and Buckner, 1997), it may be that the first finger press achieved the majority of the vasodilatory response and hence dominates the overall activity pattern.

To rule out this possibility, we exploited the fact that the single-finger patterns in M1 and S1 can also be elicited by passive stimulation (Wiestler et al., 2011). In the scanner, we therefore “replayed” the recorded force traces during the active trials through pneumatic pistons mounted under each finger (Fig. 2B). If we can elicit comparable single-finger activity patterns in M1 through both active and passive movements, and if the timing of the presses is identical across conditions, then any hemodynamic, or passive neural effect, should apply equally in both situations. Thus, if the first-finger effect is due to the nonlinear translation from neural to BOLD signals, we should find a similar representational structure for active and passive multi-finger movements.

As can be seen from Figure 6A, the spatial distribution of single-finger representations was comparable to that obtained in the active condition (Fig. 3A). For a direct comparison, we calculated the average distances in each of the cortical ROIs (Fig. 6C). The distance in M1 was 82 ± 11% of what was elicited in the active condition, and 101 ± 10% in S1. Additionally, the elicited patterns matched the active patterns on a finger-by-finger basis. The average correlation between active and passive patterns (after subtracting out the mean activity pattern) of the same finger were r = 0.76 ± 0.37, p = 8.86×10⁻⁵ and r = 0.89 ± 0.05, p = 6.8×10⁻¹¹, respectively for M1 and S1. Therefore, we confirmed that the passive single-finger stimulation and active single-finger presses elicited approximately comparable activity patterns in M1 and S1.

Figure 6.

Passive stimulation elicited comparable single-finger representation, but reduced multi-finger sequence representation. A, The averaged distance for single-finger sequences, and (B) multi-finger sequences shown on an inflated view of the left and right cortical hemisphere, with the inset showing the medial wall. C, Average distance in the cortical ROIs (Fig. 3C) for single-finger sequences for active (red) and passive (blue) conditions. D, Average distance across all pairs for multi-finger sequences. Error bars represent SE across subjects.

In contrast to single-finger representations, encoding of multi-finger sequences reduced dramatically over the whole cortical surface in the passive stimulation condition (Fig. 6B). The distances between multi-finger sequences reduced to 47 ± 29% in M1 and 42 ± 42% in S1 compared with the active condition (Fig. 6D). Critically, the reduction was larger than what would be expected from the reduction in the single-finger representations (Fig. 6B; M1: t₍₁₆₎ = 1.7601, p = 0.049, and S1: t₍₁₆₎ = 2.587, p = 0.001). If the first-finger effect had been solely due to a hemodynamic nonlinearity, or to a passive adaptation of neural activity, then these effects should have equally applied to both active and passive conditions. Instead, the differences between active and passive conditions indicate that the high weighting of the first-finger press in M1 is caused by active preparation or initiation of the sequence.

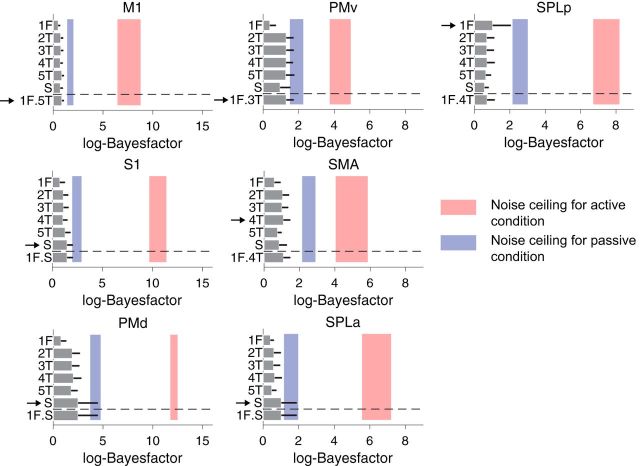
The results also show that the sequence representations found in premotor regions are due to the active planning and execution of a sequence, and not to the processing of the sensory inflow. The distances for multi-finger sequences were substantially lower (24% on average) in premotor regions (Fig. 6B) and not significantly different from 0 in four of the five premotor ROIs. Furthermore, the remaining representational structure was relatively inconsistent between subjects, as can be seen in the low noise ceiling of the model fits (Fig. 7). These findings clearly indicate that the sequence representation we observed in premotor regions for the active condition was driven by the planning/execution of a sequence.

Figure 7.

Model-fitting of multi-finger sequences for passive stimulation evaluated at each ROI. We applied the same model-fitting procedure as shown in Figure 5 to the data of the passive stimulation condition. In contrast to the active condition, all models performed nearly equally poor for all ROIs tested. Furthermore, group-wise consistency of the representational structure (blue shaded areas, lower and upper noise-ceilings) was much lower compared with active sequences (red shaded areas).

A sequence representation with longer training?

So far, we have found clear evidence of a first-finger effect, but little or no evidence for a real sequence representation in M1. We considered two reasons for this failure. First, it may be that the training period was too short. Second, the simple structure of our sequences (i.e., permutations of digit 1, 3, and 5) may have reduced the chances of forming representations of finger transitions.

We therefore conducted a second experiment, this time with 5–6 d of training of 2 h each. In the second experiment, participants learned eight arbitrary sequences, each 11 presses long and consisting of all five fingers. The trained sequences were executed at preferred speed (average 4.3 presses/s) in the scanner (see Material and Methods).

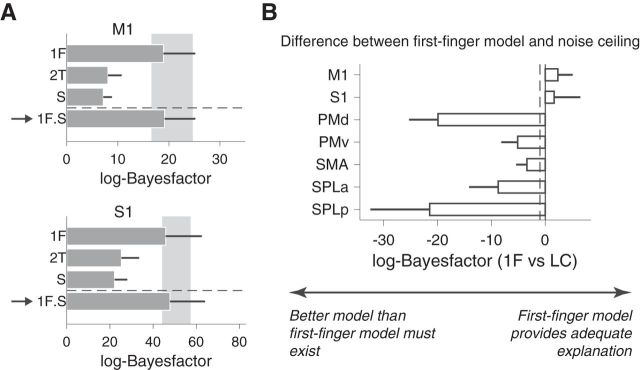
First, due to the fact that Experiment 2 had more data, the evidence for movement representation was substantially stronger. The scale of log-Bayes factor was ∼3–∼4 times larger in Figure 8 compared with Figure 5. However, despite the increased signal and ample opportunity to form representations of at least two or three finger transitions (given the longer training time), the representational structure in M1 was again fully explained by the first-finger model. The log-Bayes factor of the first-finger model was above the noise ceiling. Addition of the sequence model or a two-finger transition model did not substantially improve the fit (Fig. 8A; 18.95 vs 19.16 for first-finger model and combined model, respectively). Similar results were obtained for S1. However, combining the first-finger and sequence models in S1 slightly improved the likelihood of the model (Fig. 8A; 45.84 vs 47.84 for first-finger model and combined model, respectively). In contrast, the representational structure in premotor and parietal regions could not be explained by the first-finger model, suggesting the presence of a more complex and higher-level sequence representation (Fig. 8B). The content of these representations, and their dependence on cognitive mechanisms of movement chunking (Wymbs et al., 2012; Lungu et al., 2014), will be reported in a subsequent paper. For M1, however, these results confirm that even after week-long training, the fine-grained activity patterns reflect processes related to the individual finger presses, but not to their sequential context.

Figure 8.

More intensive training with complex sequences (Experiment 2) revealed highly similar results. Participants in the second experiment practiced eight different sequences of 11 presses for 5–6 d (2 h per d) before the imaging session. A, log-Bayes-factor (Fig. 5) for the data of M1 and S1 for the first-finger model (1F), the two-finger transition model (2T), sequence model (S) and the combination between the first-finger and sequence model (1F+S). The arrow again indicates the winning model. Error bars represent SE across subjects. B, Log-Bayes factor between first-finger and noise ceiling model. As in Experiment 1, the first-finger model provided an adequate explanation for M1 and S1, but not for secondary motor areas. The dashed line shows the typical threshold value for model selection (Kass and Raftery, 1995).

Discussion

We demonstrated that even after 5–6 d of intensive practice, there was very little evidence for a genuine sequence representation in M1. We also did not find evidence for a representation of partial sequences, such as the transition between two or more finger presses. These results contrast with previous claims of sequence representation in M1 (Karni et al., 1995; 1998; Matsuzaka et al., 2007). Instead, we found that the activity patterns for sequences could be explained by a linear combination of the activity patterns for single-finger presses, in which the weight of the first finger was higher than for the subsequent presses. This resulted in an above-chance classification accuracy for sequences beginning with different fingers. We also provided evidence that this first-finger effect was much larger during active compared with passive sequence production, arguing that it is related to active movement preparation and initiation. These results indicate that the first-finger effect had a neural origin, rather than being based on a hemodynamic nonlinearity. In contrast to M1, we observed robust sequence “encoding” in secondary motor areas (PMd, SMA, and the SPLa), and they were not explainable by the first-finger model. These areas have been shown to represent sequences such that the neural activity pattern reflects the sequential order of movement elements (Mushiake et al., 1991; Tanji and Shima, 1994; Wiestler and Diedrichsen, 2013; Wiestler et al., 2014).

Advances from the earlier studies

Although there have been numerous imaging studies on sequence production and acquisition (Karni et al., 1995, 1998; Honda et al., 1998; Doyon et al., 2002), our approach makes several advances over these earlier studies. First, we designed our experiment specifically for multivoxel pattern analysis, which allowed us to test directly for sequence representations in M1. This is not possible when looking only at the average BOLD activity within a region. Indeed, the increases and decreases reported in previous studies (Grafton et al., 1995; Karni et al., 1995, 1998; Honda et al., 1998; Kawashima et al., 1998; Sakai et al., 1998) may not necessarily reflect plastic changes in M1. Rather, they could equally well reflect changes in the input to M1, caused by sequences being learned and represented in secondary motor regions. Multivoxel pattern analysis is also sensitive to inputs from other regions but reveals the local organization of how these inputs arrive in M1. Specifically, our results suggest that the activity pattern for the first finger press is especially high, but that pattern itself only reflects the individual finger movement.

Second, we not only measured the activation pattern for the sequences but also compared them to the patterns of their constituent single-finger movements. This allowed us to determine whether the activity patterns for multi-finger sequences could be explained by a combination of single-finger movements, or whether there was evidence for a new representation that encoded the sequential context (Fig. 1B). Our results clearly argue for the former, implying that the significant differences between sequence patterns in M1 in our earlier work (Wiestler and Diedrichsen, 2013; Kornysheva and Diedrichsen, 2014; Wiestler et al., 2014) did not reflect an encoding of the order of finger presses (i.e., a genuine sequence representation), but of the sequential position of finger presses. In these studies, each sequence started with a different finger, such that we could not distinguish a real sequence representation from one caused by the first-finger effect. Importantly, our current result confirmed that the pattern differences reported in secondary motor areas likely reflect genuine sequence encoding.

Finally, we demonstrated that passive sensory stimulation could not elicit robust sequence representations in secondary motor areas. This suggests that the sequence representations observed in these areas actually reflects active movement planning/execution process, rather than sensory re-afferent signals. Of course, we cannot be certain that sensory feedback during the passive stimulation condition was exactly the same as during active sequence production. However, the nearly identical activity patterns in the single-finger conditions elicited in M1 and S1 by the passive stimuli demonstrated that the sensory feedback closely mimicked that during active presses.

The origin of the first-finger effect

The results from the passive stimulation also argue that the first-finger effect is related to the active preparation and initiation of the sequence, rather than just to the sensory inflow. More generally, the results show that the effect has a neural origin, and is not purely caused by a nonlinear integration of neural events in the production of the hemodynamic response (Dale and Buckner, 1997). Recent electrophysiological findings seem to support this conclusion (Hermes et al., 2012; Siero et al., 2013). These studies recorded the electrophysiological potentials using intracranial ECoG electrodes above M1 while human participants performed rhythmic open and close movements of hand at ∼2 Hz. Power in the high-gamma frequency band was more pronounced for the first movement of a sequence compared with subsequent movements (Hermes et al., 2012). Siero et al. (2013) also showed that the high gamma activity related nearly linearly to the observed BOLD activity recorded when subjects performed the same task in the scanner. Although the “sequence” in these experiments consisted of the repetition of the same movement elements, our results lead to the prediction that a similar effect should occur for more complex, multi-finger sequences.

What is the neural origin of this first-finger effect? First, note that both BOLD and high-frequency gamma power relate mainly to synaptic input to a region. Thus, it is not unlikely that this effect arises only on the input side and that the firing of output neurons would be matched for the different finger presses (Picard et al., 2013). The most likely explanation therefore is that the neural circuits in M1 require a large input drive to initiate a series of movements. Recent results have shown that the largest change in neural activity occurs when transitioning between a “resting” subspace to the active subspace (Elsayed et al., 2016). In our case, the driving input for this movement would arrive in form of the intention to move the first finger. Subsequent finger presses would still require input from higher-order areas, as M1 would not be able to generate the sequence autonomously, but the input drive would be much smaller as the state of the neurons would already be in the vicinity of the active subspace. This idea also predicts that if the sequence is executed slowly enough, the state in M1 should relax back to the resting subspace and the first-finger effect should disappear.

Limitations

Our data provide very little or no evidence for a sequence representation in M1 after 1 week of intensive training (1.5∼2 h per day). However, this does not exclude the possibility that longer period of training might result in the unique neural circuits for sequences acquired within M1. After 2 years of training, a single-cell recording study in the monkeys revealed some evidence for sequential representations in M1 (Matsuzaka et al., 2007). Note, however, that in this study, sequence representations were assessed as the difference between neuronal responses to trained and untrained sequences, not, as in our study, between different trained sequences. On a much shorter time scale, Karni et al. (1995) reported an expansion of the activated area in M1 over 4 weeks of daily practice. The total amount of practice was similar to the experiments reported here (∼3.5∼7 h vs 6∼10 h in our study). Again, the results only indicated that trained sequences elicited more activity than untrained sequences (a result that we have not replicated; Wiestler and Diedrichsen, 2013), but does not show the presence of neural processes that would relate to the sequential order of movement elements. Another important limitation of our study is that we could not assess representations in striatal and cerebellar circuits that closely communicate with M1 (Doyon et al., 2003; Lehericy et al., 2005; Wymbs et al., 2012). In these regions, the measurements of multivoxel patterns were not reliable enough to permit the comparison of different representational models.

Conclusion

Using representational fMRI analysis, we demonstrated that up to ∼1 week of intensive practice, activity in M1 relates to individual finger presses, but not to transitions between multiple fingers or even full sequences. At the same time, we found robust sequence representation in other higher motor areas, such as PMd, SMA, or SPLa, which is consistent with previous studies (Mushiake et al., 1991; Shima and Tanji, 1998). We will discuss the exact contents of these sequence representations in a separate paper. There was some indication that there was a weak component of the activity pattern in M1 which may reflect the sequence itself. Whether this component constitutes the beginning of true sequence representations that will increase in strength with extended training remains to be tested. The results and methodological advances presented in this paper will be crucial for evaluating this hypothesis.