Variations in Ca²⁺ Influx Can Alter Chelator-Based Estimates of Ca²⁺ Channel–Synaptic Vesicle Coupling Distance

Abstract

The timing and probability of synaptic vesicle fusion from presynaptic terminals is governed by the distance between voltage-gated Ca²⁺ channels (VGCCs) and Ca²⁺ sensors for exocytosis. This VGCC-sensor coupling distance can be determined from the fractional block of vesicular release by exogenous Ca²⁺ chelators, which depends on biophysical factors that have not been thoroughly explored. Using numerical simulations of Ca²⁺ reaction and diffusion, as well as vesicular release, we examined the contributions of conductance, density, and open duration of VGCCs, and the influence of endogenous Ca²⁺ buffers on the inhibition of exocytosis by EGTA. We found that estimates of coupling distance are critically influenced by the duration and amplitude of Ca²⁺ influx at active zones, but relatively insensitive to variations of mobile endogenous buffer. High concentrations of EGTA strongly inhibit vesicular release in close proximity (20-30 nm) to VGCCs if the flux duration is brief, but have little influence for longer flux durations that saturate the Ca²⁺ sensor. Therefore, the diversity in presynaptic action potential duration is sufficient to alter EGTA inhibition, resulting in errors potentially as large as 300% if Ca²⁺ entry durations are not considered when estimating VGCC–sensor coupling distances.

SIGNIFICANT STATEMENT The coupling distance between voltage-gated Ca²⁺ channels and Ca²⁺ sensors for exocytosis critically determines the timing and probability of neurotransmitter release. Perfusion of presynaptic terminals with the exogenous Ca²⁺ chelator EGTA has been widely used for both qualitative and quantitative estimates of this distance. However, other presynaptic terminal parameters such as the amplitude and duration of Ca²⁺ entry can also influence EGTA inhibition of exocytosis, thus confounding conclusions based on EGTA alone. Here, we performed reaction–diffusion simulations of Ca²⁺-driven synaptic vesicle fusion, which delineate the critical parameters influencing an accurate prediction of coupling distance. Our study provides guidelines for characterizing and understanding how variability in coupling distance across chemical synapses could be estimated accurately.

Introduction

Fast and synchronous neurotransmitter release from presynaptic terminals requires the coordination of molecular processes on the nanometer scale (Südhof, 2013). The coupling between voltage-gated Ca²⁺ channels (VGCCs) and the Ca²⁺ sensor for exocytosis is of particular interest because their topographical arrangement within the active zone critically determines the probability and time course of vesicular release of neurotransmitter (Eggermann et al., 2011). Moreover, it has been proposed that the diversity of synaptic strength and short term plasticity across synapses is in part determined by the nanoscale distances between VGCCs and Ca²⁺ sensors on synaptic vesicles (VGCC–sensor distance; Nusser, 2018). This VGCC–sensor distance can be altered during postnatal development (Fedchyshyn and Wang, 2005; Wong et al., 2014; Baur et al., 2015), vary within a single cell type (Johnson et al., 2017), and differ according to specific presynaptic protein expression (Yang et al., 2010; Böhme et al., 2016). Therefore, to understand how neurotransmitter release is controlled by the nanoscale topography of synaptic proteins, VGCCs, and synaptic vesicles, quantitative estimates of coupling distance are essential.

The VGCC–sensor distance is thought to span tens to hundreds of nanometers, resulting in a variation of release probability of >100-fold for a single action potential (AP) (Nakamura et al., 2015). Historically, VGCC–sensor distances have been categorized as either “tight” or “loose” and are thought to be driven by spatially restricted “nanodomains” (<100 nm) or more extended “microdomains” (>100 nm) of [Ca²⁺] changes, respectively (Neher, 1998a; Eggermann et al., 2011; Wang and Augustine, 2014). Synapses are also classified according to the number of overlapping [Ca²⁺] domains driving vesicular fusion, with one to two VGCCs mediating nanodomain-driven release and several VGCCs mediating microdomain-driven release (Matveev et al., 2011; Eggermann et al., 2011; Wang and Augustine, 2014; Stanley, 2016). Here we will refer to precise coupling distances because they are less ambiguous, and may implicate specific molecular organization necessary to set different distances (Böhme et al., 2016).

In the absence of direct measurements (e.g., imaging) of the nanoscale topography between VGCCs and releasable vesicles, exogenous Ca²⁺ chelators have been used to infer VGCC–sensor distances. According to simple diffusion theory, the distance calcium ions travel increases with time, so Ca²⁺ chelators with different binding rates will intercept calcium ions within a particular range of distances from a source as follows: space constant: λ = √(D_Ca/([B] · k_on)) (Stern, 1992). If Ca²⁺ sensors are located beyond a chelators' characteristic length, then release is inhibited. EGTA and BAPTA are two typical chelators used for such experiments because they have similar affinities, but differ in their forward binding rate constants (Adler et al., 1991). Synapses that are blocked by intracellular application of BAPTA and not by EGTA are considered tightly coupled, whereas synapses that are blocked by both BAPTA and EGTA are considered loosely coupled (Eggermann et al., 2011). Although useful for intuition, this interpretation is oversimplified because chelator inhibition of AP-evoked release is graded as a function of distance and concentration (Rozov et al., 2001). Therefore, qualitative conclusions can be misleading, particularly in cases in which the cytosolic EGTA concentration has not been estimated.

Theoretical calculations and simulations provide a quantitative approach to infer coupling distances from chelator competition experiments. The linearized buffer approximation is an analytical solution to the reaction–diffusion problem that has provided important insights into how [Ca²⁺] gradients are modified by chelators (Naraghi and Neher, 1997) and enables a quantitative estimate of coupling distance (Wang et al., 2009). However, this approach may not be effective in cases in which steady-state assumptions do not apply, such as predicting the spatiotemporal profile of [Ca²⁺] dynamics after rapid APs. Numerical simulations, although less elegant and intuitive, can accurately predict complex dynamics of [Ca²⁺] provided that numerous parameters are constrained. Numerical simulations have been used to extract coupling distances and predict the time course and probability of vesicular release at various synapses (Meinrenken et al., 2002; Bucurenciu et al., 2008; Scimemi and Diamond, 2012; Vyleta and Jonas, 2014; Pangršič et al., 2015). One surprising result of such studies was that EGTA was unexpectedly effective at blocking tightly coupled vesicles released by APs (Nakamura et al., 2015) and yet, for the same preparation, ineffective at inhibiting release driven by longer Ca²⁺ entry (Chen et al., 2015). This example suggests that quantification of coupling distance requires more than just knowledge of the chelator properties.

Here, we performed reaction–diffusion simulations to determine which biophysical parameters influence EGTA inhibition of vesicular release. We simulated different Ca²⁺ entry durations and amplitudes, VGCC densities, and endogenous buffer conditions. Our results indicate that the amplitude and duration of Ca²⁺ current and density of open VGCCs can alter quantitative estimates of the VGCC–sensor coupling distances derived from chelator competition experiments.

Materials and Methods

Reaction–diffusion simulations of Ca²⁺.

The spatial and temporal profile of the free Ca²⁺ concentration ([Ca²⁺]) after a voltage step activation of a VGCC was simulated using a Java-based simulation environment, D3D (Nakamura et al., 2015), running on Windows 7. To run multiple simulations in parallel, we used PCs equipped with multicore CPUs (typically Intel Xeon CPU E5-2640). Ca²⁺ entry, diffusion, and binding with buffers were calculated by numerically integrating partial differential equations applying an explicit finite-element (Euler) method. The elemental simulation volume (voxel) used for finite difference calculations was 5 × 5 × 5 nm (see Figs. 1B–H and 8) or 10 × 10 × 10 nm (see Figs. 1I; 2; 3; 4; 5; 6; 7, and 9). The total simulation volume was set to 0.5 (x) × 0.5 (y) × 1.0 (z) μm unless otherwise stated and contained a single Ca²⁺ entry site composed of either a single or cluster of VGCCs. The four x/y surfaces were set to reflect all diffusing species, thus being mathematically equivalent to an infinitely extended plane of AZs separated by 0.5 μm. The Ca²⁺ entry site was placed in the center of a single surface (z = 0) bounding this volume. Model parameters were set to match previous recordings performed in the dialyzed calyx of Held presynaptic terminal at room temperature (22–24°C) when possible (Nakamura et al., 2015), unless otherwise stated. This recording configuration is convenient because the ATP concentration is known and endogenous EF-hand mobile buffers have been dialyzed (Müller et al., 2007). The resting free [Ca²⁺] was set to 50 nm, the Ca²⁺ diffusion coefficient (D_Ca) to 220 μm²/s (Allbritton et al., 1992), the endogenous fixed buffer (EFB) binding ratio to 40 (Helmchen et al., 1997), the EFB concentration to 4 mm, the EFB K_D to 100 μm, and an EFB forward binding rate constant (k_on) to 1 × 10⁸ M⁻¹sec⁻¹ (Nakamura et al., 2015). We included 200 μm free ATP in the simulation, assuming the presence of 2 mm ATP (total concentration) and 3 mm Mg²⁺ (calculation using Maxchelator RRID:SCR_000459). The values for Ca²⁺ binding to ATP were set as follows: K_D = 200 μm, k_on = 5 × 10⁸ M⁻¹sec⁻¹ (Baylor and Hollingworth, 1998), D_ATP = 220 μm²/s. The k_on for EGTA was set to 1.05 × 10⁷ M⁻¹sec⁻¹ and the K_D to 70 nm (Nägerl et al., 2000), except where we tested other values: k_on = 2.5 × 10⁶ M⁻¹sec⁻¹, K_D = 180 nm (Naraghi and Neher, 1997) and k_on = 4.38 × 10⁶ M⁻¹sec⁻¹, K_D = 543 nm (Lin et al., 2017). The parameters for BAPTA were as follows: k_on, = 4.0 × 10⁸ M⁻¹sec⁻¹, K_D = 220 nm (Naraghi and Neher, 1997). The diffusion coefficient of EGTA and BAPTA was 220 μm²/s throughout (Naraghi and Neher, 1997). The parameters for parvalbumin were as follows: k_on = 1.85 × 10⁶ M⁻¹sec⁻¹, K_D = 51.4 nm (Lee et al., 2000). The parameters for calretinin were as follows: T site k_on = 1.8 × 10⁶ M⁻¹sec⁻¹, T site K_D = 28 μm, R site k_on = 3.1 × 10⁸ M⁻¹sec⁻¹, R site K_D = 68 nm (Faas et al., 2007). The diffusion coefficient of parvalbumin and calretinin was set to 20 μm²/s (Schmidt et al., 2003; Faas et al., 2007). The time step of simulation was calculated according to a stability criterion, h = (3 × D × dt)/∂x², where D is the diffusion coefficient of the fastest species and ∂x is the length of vertices of simulation voxels.

Figure 1.

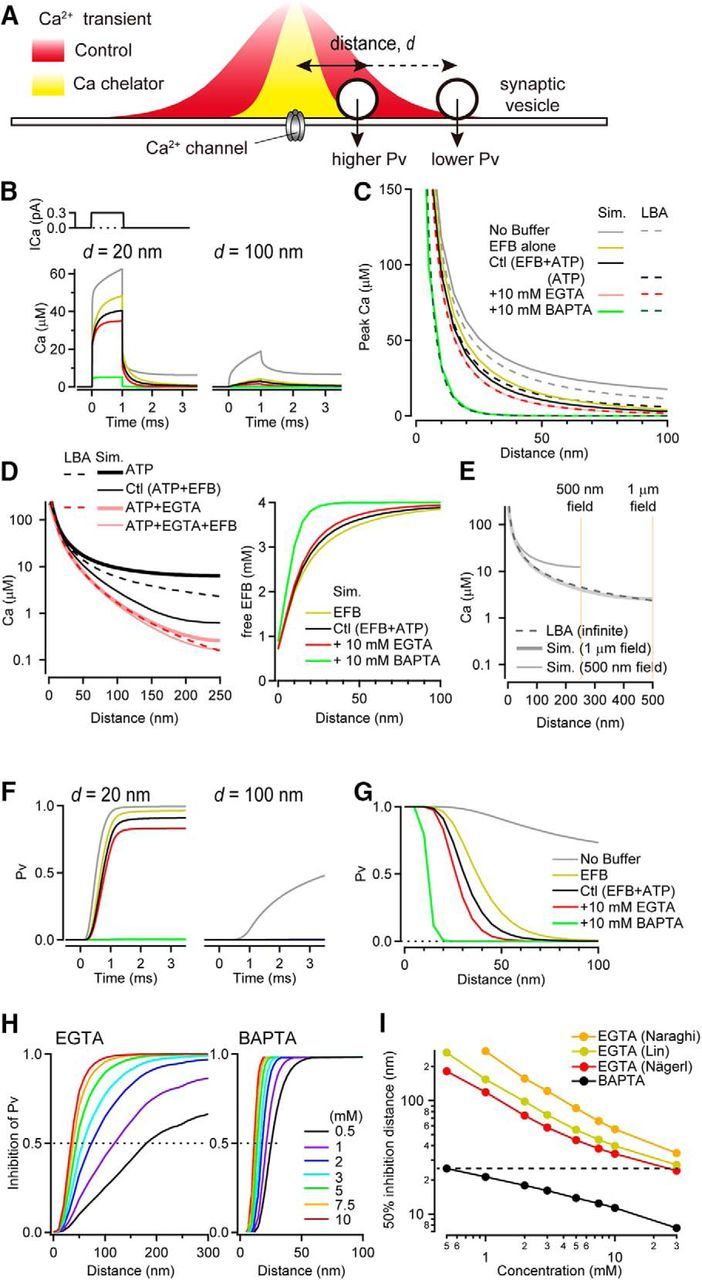
Inhibition of vesicular release probability by exogenous Ca²⁺ chelators near a single VGCC. A, Schematic diagram describing how chelators can alter the spatial profile of [Ca²⁺], which would differentially alter the probability of vesicle fusion according to a distance (d) from the VGCC. B, Ca²⁺ current through a VGCC (top; 0.3 pA amplitude, 1 ms duration), the resulting intracellular [Ca²⁺] transient (bottom) for a 20 nm (left) and 100 nm (right) distance in the presence of various Ca²⁺ buffers (see legend in C). C, [Ca²⁺] spatial profile estimated using reaction–diffusion simulations (sim; solid line) or LBA (dashed line). Ca²⁺ current amplitude was 0.3 pA for LBA calculations. Basal [Ca²⁺] was 50 nm for both estimates. D, Left, [Ca²⁺] spatial profile in the presence of ATP (black) and ATP plus 10 mm EGTA (red), with EFB (reaction-diffusion simulation: thick) or without EFB (reaction-diffusion simulation: thin solid, and LBA: dashed). Right, Free EFB concentration against distance. E, [Ca²⁺] gradients in the absence of any buffer species in various simulation volumes. F, P_v for a 20 nm (left) and 100 nm (right) coupling distance in the presence of various Ca²⁺ buffers computed from traces in B. G, P_v as a function of coupling distance. H, Inhibition of P_v as a function of coupling distance for various concentrations of EGTA (left) and BAPTA (right). Dashed lines indicate 50% inhibition. Kinetic parameters for EGTA were from Nägerl et al. (2000). I, Coupling distance exhibiting 50% inhibition of P_v (dashed lines in H) versus EGTA and BAPTA concentrations. For EGTA, results are shown for three different sets of published rate constants (Naraghi and Neher, 1997; Lin et al., 2017).

Figure 8.

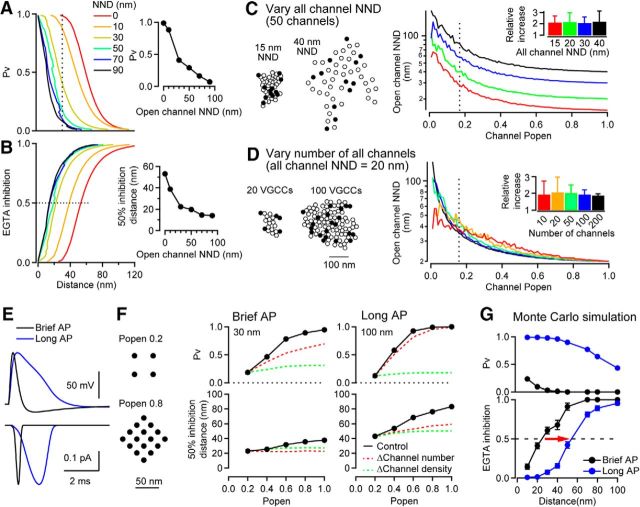
Effect of VGCC open probability on the estimate of coupling distance. A, Effect of open channel density (i.e., NND) on the spatial profile of P_v as a function of the perimeter coupling distance (d₂) for a cluster composed of 12 VGCCs (see Fig. 7A). The VGCC current amplitude and duration were 0.3 pA and 0.2 ms. Inset, P_v versus the open channel NND for a d₂ = 30 nm (dotted line). B, EGTA inhibition of P_v versus d₂. Inset, Coupling distance exhibiting 50% EGTA inhibition versus the open channel NND. C, Left, Representative simulated clusters composed of 50 VGCCs with an all channel NND of 15 and 40 nm NND. Filled and open circles represent open (n = 12) and closed (n = 38) VGCCs (P_open = 0.2). Right, Open channel NND versus P_open for a VGCC cluster composed of 50 VGCCs. The all channel NND was 15, 20, 30, or 40 nm (red, green, blue, and black, respectively). Inset, Relative increase in the open channel NND for P_open = 0.16 (dotted line) from all channel NND. The bar graph represents the mean and SEM of 100 trials. D, Left, Representative simulated clusters composed of 20 and 100 VGCCs with an all channel NND of 20 nm and P_open = 0.2. Right, Open channel NND versus P_open for a VGCC cluster with open channel NND of 20 nm. The cluster was composed of 10, 20, 50, 100, or 200 VGCCs (red, yellow, green, blue, and black, respectively). Inset, Relative increase in the open channel NND for P_open = 0.16. E, Top, Presynaptic APs recorded from the calyx of Held of an immature rat (P7). The AP half-duration was 0.42 ms in control conditions (black, brief AP) and 1.80 ms during bath application of the K channel blocker TEA (10 mm, red, long AP). Bottom, Ca²⁺ currents deduced from the recorded APs using a HH model. Peaks were scaled to 0.3 pA. F, P_v (middle top) and coupling distance exhibiting 50% EGTA inhibition (middle bottom) versus P_open for a cluster composed of 20 VGCCs with different channel P_open. Different P_open values were approximated by reducing the number of simulated channels and increasing NND (see example patterns, left). For the brief AP (left), P_v at d₂ = 30 nm was plotted. For the long AP (right), P_v was at d₂ = 100 nm. For changing channel number only, open channel NND was kept constant at 20 nm. For changing open channel density only, open channel number maintained at four throughout, whereas open channel NND was reduced from 40.3 to 20 nm. G, P_v (top) and EGTA inhibition (bottom) for brief (black) and long (blue) AP estimate using Monte Carlo simulations in MCell. For this simulation, we used a regular array of 20 channels with a mean all channel NND of 20 nm. The 50% inhibition distance was ∼25 nm for the brief AP and ∼55 nm for the long AP. Red arrow indicates an increase of 50% EGTA inhibition distance due to the increase in AP duration and channel P_open. Error bars indicate ± SEM (the number of simulation trials was 4000 for brief APs and 1000 for long APs).

Figure 2.

Inhibition of release probability by EGTA depends on the current amplitude of a VGCC. A, [Ca²⁺] transient (middle) and resulting P_v (bottom) at 20 nm from the VGCC for control (left) and 10 mm EGTA (right). The single VGCC current amplitude (top) varied from 0.075 to 0.6 pA (1 ms duration, 0 ms onset). B, Peak [Ca²⁺] (top) and P_v (bottom) at 20 nm as a function of the single VGCC current amplitude. C, D, Same as A and B but at 100 nm from the VGCC. E, Peak [Ca²⁺] and P_v in control conditions and inhibition of exocytosis as a function of coupling distance. Dashed red line is the spatial [Ca²⁺] profile for a VGCC current amplitude of 0.075 pA scaled to that of 0.6 pA for comparison. Note log x-axis. F, Summary plot showing different distances exhibiting 50% EGTA inhibition of exocytosis by EGTA depending on the single VGCC current.

Figure 3.

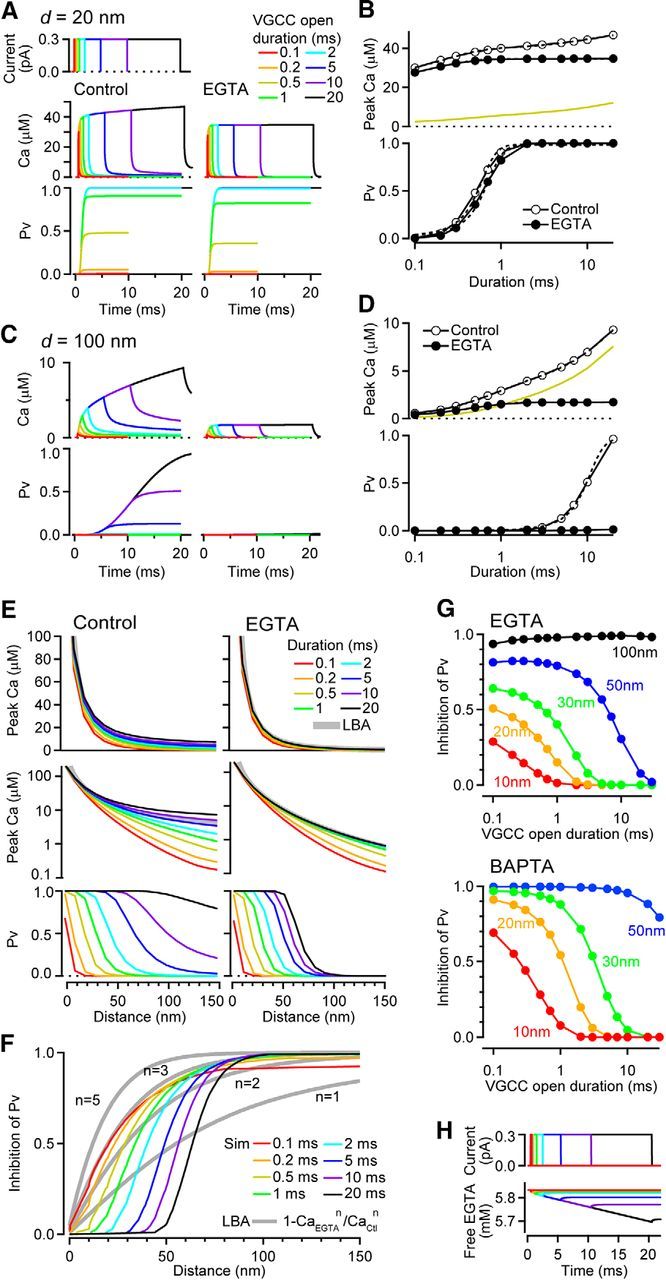
Inhibition of release probability by EGTA depends on the open duration of a VGCC. A, [Ca²⁺] transient and resulting P_v at 20 nm from the VGCC for control (left) and 10 mm EGTA (right). The VGCC open duration was varied from 0.1 to 20 ms (top; 0.3 pA amplitude). B, Peak [Ca²⁺] (top) and P_v (bottom) at 20 nm as a function of VGCC open duration. Dashed lines are a double (control) and single (EGTA) exponential fit of [Ca²⁺], and sigmoidal fits of P_v. Yellow line is the difference in [Ca²⁺]. C, D, Same as A and B but at 100 nm from the VGCC. E, Peak [Ca²⁺] (top: linear scale and middle: log scale) and P_v (bottom) for control (left) and EGTA (right) as a function of coupling distance. Gray thick line (top) indicates [Ca²⁺] profile estimated using a LBA with the same single VGCC current amplitude (0.3 pA). F, Inhibition of P_v by EGTA, calculated from P_v in E and from LBA according to Equation 22 in Neher (1998b). G, Inhibition of P_v by 10 mm EGTA (top) and 1 mm BAPTA (bottom) as a function of VGCC open duration and for different VGCC–sensor distances. H, Free EGTA concentration during various durations of channel opening for a total EGTA concentration of 10 mm.

Figure 4.

Differential dependence of EGTA inhibition of release probability on single channel current amplitude and open duration. A, Distance exhibiting 50% inhibition of P_v by EGTA (10 mm, left) and by BAPTA (1 mm, right) as a function of the VGCC open duration and for different VGCC current amplitudes. B, [Ca²⁺] transient (middle) and resultant P_v at 30 nm from a VGCC for control (left) and 10 mm EGTA (right). The current amplitude and duration of the VGCC were adjusted such that the total charge influx remained constant at 0.3 pA · ms (top). C, Peak [Ca²⁺] and P_v for control conditions and EGTA inhibition as a function of coupling distance. The shaded region denotes the range of coupling distances producing 50% inhibition. D, The 50% EGTA inhibition distances versus total Ca²⁺ charge for different open durations between 0.1 and 30 ms and VGCC current amplitudes (color code).

Figure 5.

Effect of channel flickering on release probability and EGTA inhibition. The top panel represents how frequency and amplitude of single channel current were varied. The total charge influx was held constant. Ca²⁺ current amplitude was 0.15 pA with channel flickering or 0.075 pA for continuous channel opening.

Figure 6.

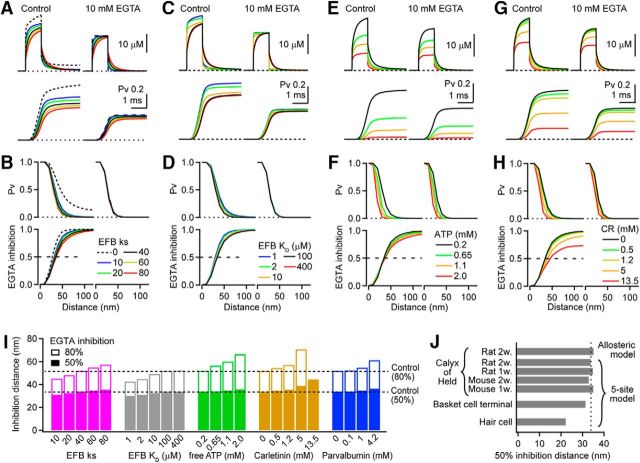
EGTA inhibition of release probability for various Ca²⁺ buffer and sensor conditions. A, Ca²⁺ transient (top) and P_v (bottom) at 30 nm from a VGCC with various EFB capacities in control (left) and 10 mm EGTA (right). The single VGCC current was 0.3 pA in amplitude with 1 ms duration. Buffer capacity (κ_s) was varied by changing the EFB concentration from 0 to 8 mm while the K_D of the EFB remained constant at 100 μm. B, Spatial profile of P_v (top) in control (left) and 10 mm EGTA (right) and the inhibitory effect of EGTA on P_v (bottom) for various EFB κ_s. C, D, Same as A and B but for various EFB affinities (by adjusting only k_off). κ_s was kept constant at 40 by adjusting the EFB concentration. E, F, Same as A and B but for various ATP concentrations. G, H, Same as A and B but for various calretinin concentrations. For A–H, black traces are identical (control). I, Summary bar graph showing coupling distances exhibiting 50% (filled) and 80% (open) inhibition of P_v by 10 mm EGTA for various buffer conditions (B, D, F, H and parvalbumin). J, Coupling distance exhibiting 50% inhibition of exocytosis by 10 mm EGTA for various release models.

Figure 7.

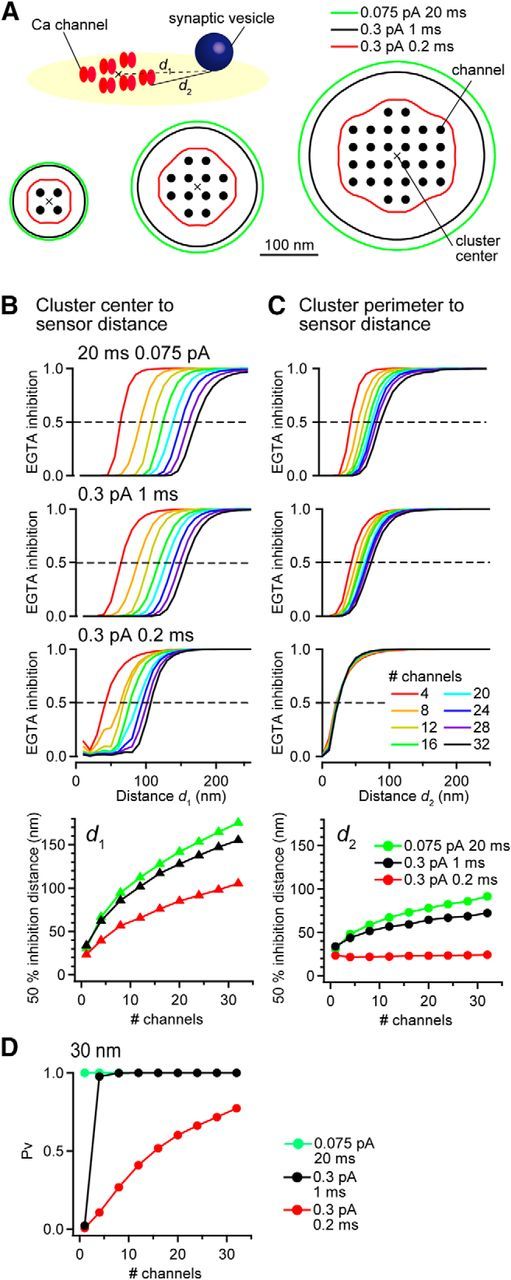
EGTA inhibition of release probability near a VGCC cluster. A, Contour spatial maps of 50% EGTA inhibition of P_v for clusters of 4, 12, and 28 open VGCCs. d₁ and d₂ are distances from the location where 50% inhibition of P_v was observed to the center of gravity of the VGCC cluster or to the closest perimeter VGCC, respectively. The NND of the VGCCs was 30 nm. Vesicular release was evoked by VGCC opening of 0.3 pA for 0.2 ms (red; similar to Ca²⁺ influx by APs), 0.3 pA for 1 ms (black; same as Fig. 1 and 6), or 0.075 pA for 20 ms (green). Diagram depicts the spatial arrangement of the VGCC cluster and Ca²⁺ sensor associated with a synaptic vesicle. Cross indicates the center of gravity of the VGCC cluster. B, Inhibitory effect of EGTA on P_v as a function of distance from the Ca²⁺ sensor to the center of the VGCC cluster (d₁). Bottom, d₁ exhibiting 50% EGTA inhibition of P_v as a function of number of VGCCs in the cluster. C, Same as B but for the distance between the Ca²⁺ sensor to the nearest VGCC (cluster perimeter to sensor distance, d₂). D, P_v at d₂ = 30 nm as a function of number of VGCCs in the cluster.

Figure 9.

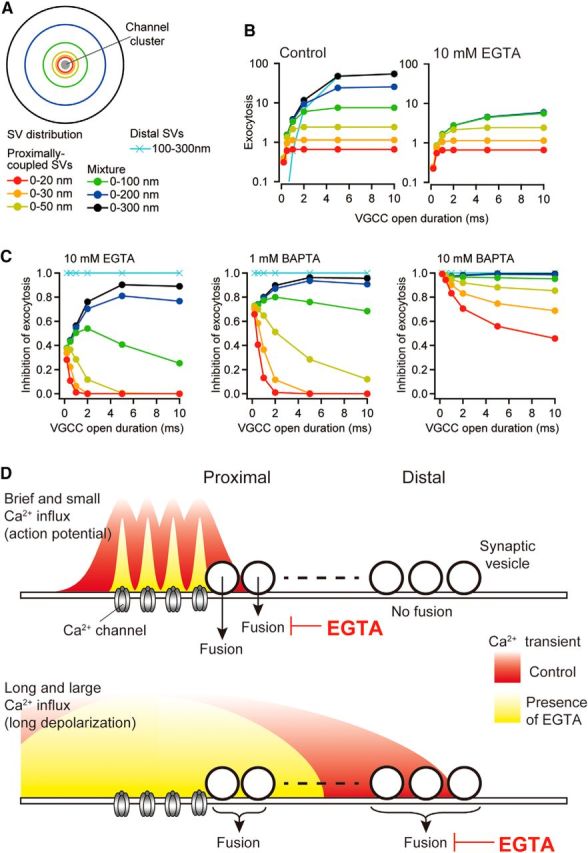
EGTA inhibition of exocytosis of multiple vesicle populations at various distances from VGCC cluster perimeter. A, Diagram depicting a hypothetical pattern of a RRP vesicle distribution around a VGCC cluster. The cluster was composed of four VGCCs with a 30 nm NND. B, Number of exocytosed vesicles evoked by various VGCC open durations for control (left) 10 mm EGTA (right) at various distances (see legend in A). The amplitude of the single VGCC current was 0.3 pA. C, Predicted inhibition of exocytosis by 10 mm EGTA (left), 1 mm BAPTA (center), and 10 mm BAPTA (right) versus open duration. D, Schematic diagrams depicting [Ca²⁺] domains formed by the different amplitude and duration of VGCC openings. Top, Brief channel openings (with small current amplitude) form [Ca²⁺] domains restricted to the vicinity of each VGCC. EGTA (10 mm) reduced the spatial extension of the [Ca²⁺] domains, thereby inhibiting exocytosis. Such brief channel openings do not evoke release of distal vesicles. Bottom, Long channel openings form [Ca²⁺] domains reaching distal vesicles. EGTA inhibits the release of distal vesicles, but not the proximal vesicles. The sensors of the proximal vesicles are saturated by the large local [Ca²⁺].

Release simulation and the estimation of vesicular release inhibition by EGTA.

To simulate vesicular transmitter release, we used a five-site model of Ca²⁺-dependent vesicle fusion in the calyx of Held derived from experiments in mature rats (Kochubey et al., 2009) unless otherwise stated (see Fig. 6J). The model was integrated using a forward Euler numerical integration routine (IgorPro 6.3, WaveMetrics RRID:SCR_000325), using the [Ca²⁺](t) generated from the reaction–diffusion simulations above. The probability over time of arriving in the fused state then considered as the probability that a single vesicle will be released as a function of time (single vesicular release rate). The cumulative release rate, which is equivalent to vesicular release probability (P_v), was estimated from the integral of the single vesicular release rate over a window from the onset of VGCC opening to 10 ms after the VGCC closing. P_v was computed at indicated distance on the release face (z = 0) of the simulation volume. The inhibitory strength of EGTA (EGTA inhibition) or BAPTA (BAPTA inhibition) was calculated by taking the ratio of the P_v in control and in the presence of the chelator. For channel clusters, stated distances refer to the average of P_v and EGTA/BAPTA inhibition values along a contour line at a fixed distance from the closest VGCC. Contour lines were calculated using built-in macros in IgorPro.

Calculation of [Ca²⁺] using a linearized buffer approximation.

The steady-state [Ca²⁺] gradient around a VGCC was computed via a linearized buffer approximation (LBA) (Naraghi and Neher, 1997; Neher, 1998b) using mathematical formulas from Bauer (2001). All parameters were the same as those in the reaction–diffusion simulations, except the EFB which is inherently excluded from LBA (Naraghi and Neher, 1997). EGTA parameters were taken from Nägerl et al. (2000) and the single channel current amplitude was set to 0.3 pA. These calculations were performed using Microsoft Excel.

Simulations of open channel density.

To estimate the influence of open channel density on EGTA inhibition, we generated VGCC clusters using a fixed nearest neighbor distance (NND) based on immunogold labeling of Ca_V2.1 (Indriati et al., 2013; Nakamura et al., 2015; Miki et al., 2017). This was achieved by sequentially placing channels in a cluster in which each new channel was placed randomly along a circumference with a radius equal to the chosen NND. However, if the randomly generated location of a channel was less than the NND from any other previously placed channels, then a channel was not placed and another location was generated. This ensured a fixed NND. An open channel pattern was then generated from each channel cluster by randomly selecting which channels would be open according to a binomial function with the mean equal to the selected channel open probability (P_open). We generated 100 open channel patterns for each condition (NND and P_open). The NND for open channels was then calculated (note: if P_open = 1, then the open cluster NND was a single value equaling the defined total channel NND). These simulations were performed in the IgorPro environment.

Stochastic simulations of Ca²⁺ dynamics and vesicular release.

We use particle-based stochastic simulator MCell (http://mcell.org, RRID:SCR_007307; Kerr et al., 2008) to perform Monte Carlo simulations of Ca²⁺ dynamics and vesicular release. The single vesicular release probability and EGTA inhibition were simulated for both the brief and long AP (see Fig. 8E). The parameters of the model simulation volume, kinetic properties, and concentration of buffers and the sensor model were set identical to those for deterministic simulations. The simulation time step was 5 ns, with a spatial resolution set by assigning 20,000 positions/μm². To model stochastic gating of VGCC, we adapted a Hodgkin–Huxley (HH) Ca²⁺ channel model (Borst and Sakmann, 1998). The rates for a 3-state HH model were adjusted to reproduce the single channel current half duration (0.26 ms) and peak amplitude (0.3 pA; see Fig. 8E) used in deterministic simulations, as well as a single channel open probability of ∼0.2 (Sheng et al., 2012). The voltage-dependent rates between the states were computed with the following parameters:

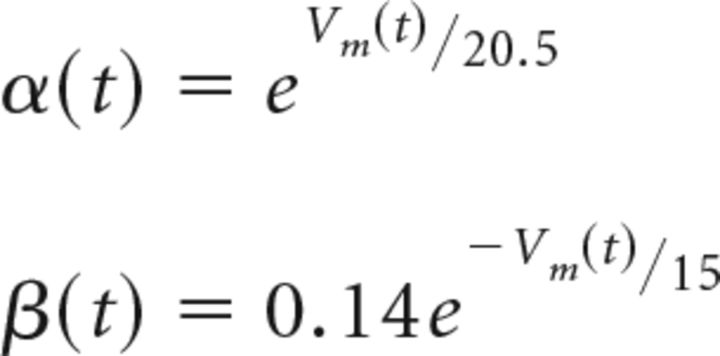where V_m(t) corresponds to the AP waveform. The number of ions passes through the open channel with the following rate:

where g is the single channel conductance (3 pS, Weber et al., 2010), e is the elementary charge and E_rev is the reversal potential (45 mV; Sheng et al., 2012). The simulations resulted in a total influx of 1180 Ca²⁺ on average (for the brief AP). The kinetic rate constants were preserved for the long AP simulation, which resulted in single channel current half duration of 1.24 ms and a peak amplitude of 0.3 pA. The average release rate for each simulation condition was computed from 1000 (for long AP) and 4000 (for brief AP) independent trials. All MCell simulations were performed on the TARS cluster of Institut Pasteur (Paris, France).

We also estimated P_v in the presence of a single synaptic vesicle modeled as a spherical boundary (radius of 20 nm, Wong et al., 2014) that was placed 5 nm above the sensor (membrane). Using the brief AP waveform, we did not observe a significant difference in the estimated P_v at the distances tested between 10 and 100 nm (1000 trials per condition, p = 0.29–1.00, χ² square population proportion comparison). We estimate that we could detect a change in P_v > 10%.

Experimental design and statistical analyses.

Differences in population distributions in the stochastic simulation were evaluated using a χ² square test and significance set at p < 0.05. Error bars in the figures are presented as SEM, with N taken to be the number of trials per condition.

Results

Estimating VGCC–sensor coupling distance using exogenous Ca²⁺ chelators

Analytical solutions to the reaction–diffusion problem can provide intuitive insights into the complex spatiotemporal dynamics of intracellular free [Ca²⁺]. A particularly useful approach is the LBA, which provides a solution for multiple buffer species (Naraghi and Neher, 1997), and can be used to estimate VGCC–sensor coupling distances in the presence of endogenous buffers (Wang et al., 2009). However, because LBA assumes linearity of buffers, an infinite volume, and steady-state conditions, it is not clear to what extent AP-evoked release can be predicted using this approach.

We examined the validity of LBA for brief AP-driven Ca²⁺ influx by comparing it with numerical simulations of reaction–diffusion. For simplicity, we first simulated the spatiotemporal profile of the [Ca²⁺] generated from the opening of a single VGCC that was placed at the center of a plane corresponding to the release surface (x–y: 0.5 × 0.5 μm; Fig. 1A). The simulation volume was confined in the z-dimension to 1 μm. In the absence of Ca²⁺ buffers, a 0.3 pA VGCC current of 1 ms duration elicited a [Ca²⁺] transient with 485 μm peak at the mouth of the open channel, 62 μm peak at 20 nm, and 18 μm peak at a 100 nm distance from the VGCC (d) (Fig. 1B,C, gray solid trace). Next, we considered the addition of endogenous Ca²⁺ buffers to the simulations to match experimental conditions at the calyx of Held (Nakamura et al., 2015). Addition of a low-affinity endogenous fixed buffer (EFB, K_D = 100 μm, 4 mm) slowed the rise of the [Ca²⁺] at 20 nm, reduced the peak amplitude, and accelerated the decay (Fig. 1B, yellow). Addition of free ATP (0.2 mm), a rapid-binding low-affinity mobile buffer, further reduced the peak [Ca²⁺] by 16% (Fig. 1B, black solid). Both EFB and ATP had a stronger reduction in the peak [Ca²⁺] at longer distances (d > 100 nm, >77%). In subsequent simulations, the condition with the two endogenous Ca²⁺ buffers (EFB and ATP) is denoted as “control.” The presence of a fixed buffer altered the gradient of [Ca²⁺], violating one of the conditions necessary to apply LBA that fixed buffers do not alter the spatial gradient of [Ca²⁺] (Pape et al., 1995; Naraghi and Neher, 1997). When we included 10 mm EGTA, simulations predicted a 14% reduction (i.e., inhibition) of the [Ca²⁺] transient at d = 20 nm, but a more potent inhibition at longer distances (Fig. 1B–D, pink solid). In contrast to the low-buffered conditions, the [Ca²⁺] nearly reached steady-state by the end of the 1 ms flux duration. This compares favorably to the rough estimate of the time to reach chemical equilibrium: τ_eq = κ_EFB/(k_on*[EGTA]) = 0.68 ms (Bauer, 2001). A 10 mm BAPTA concentration, which has a faster forward binding rate constant, produced a larger inhibition of the [Ca²⁺] transient and reached steady-state within 100 μs (calculated τ_eq = 13 μs).

To compare directly the predictions of LBA and numerical simulations, we examined the spatial profile of the [Ca²⁺] gradient of the two methods using identical parameters. [Ca²⁺] gradients in high EGTA and BAPTA cases were similar (Fig. 1C). However, LBA predicted a steeper gradient for unbuffered diffusion (Fig. 1C, gray dashed line) and a shallower gradient for control conditions (Fig. 1C, black dashed line). The “control” conditions for LBA included ATP only because EFB does not influence the calculation. We reasoned that the difference between LBA and simulations may be due to high EFB occupancy. Indeed, when the EFB was removed from the numerical simulations, the [Ca²⁺] gradient decayed less steeply than LBA (Fig. 1D, left, thick black line), similar to the buffer-free condition (Fig. 1C, gray lines). Examination of the EFB occupancy showed that free EFB was reduced significantly for d < 50 nm (Fig. 1D, right), contradicting the LBA requirement that all buffers must be in their linear regime; that is, low occupancy.

But why does the numerical simulation show a shallower [Ca²⁺] gradient for unbuffered diffusion? Increasing the numerical simulation volume to 1 μm (x–y surface) was sufficient to match the spatial profiles from LBA (Fig. 1E). Therefore, numerical simulations differ from LBA in two important and physiologically relevant ways: they account for (1) the presence of EFB and (2) the finite volume of most small presynaptic terminals. Nevertheless, for high exogenous buffer conditions, the LBA predicts [Ca²⁺] gradients accurately.

A five-site model of Ca²⁺ binding and vesicle fusion (Kochubey et al., 2009) was then used to estimate P_v from reaction–diffusion simulations of [Ca²⁺]. The [Ca²⁺] transients in Figure 1B, in the absence of Ca²⁺ buffers, elicited vesicle fusion with P_v > 0.5 even at distal locations (d > 100 nm). The addition of EFB altered the spatial dependence of P_v (Fig. 1F,G). At d = 20 nm, P_v was reduced by 3%, whereas, more distally, the EFB had a large influence on release, presumably because of the gradient in EFB occupancy (Fig. 1D, right). The EFB produced a nominal effect on the time course of release (<10% change of half-width, data not shown), suggesting that a low-affinity EFB (K_D = 100 μm) does not slow release despite the endogenous binding ratio: κ = [CaB]/[Ca]_free of 40 (cf. Delvendahl et al., 2015). The addition of 10 mm EGTA further reduced P_v at locations as close as 20 nm (by 15%), whereas 10 mm BAPTA had a strong inhibition at d = 15–20 nm (>80%; Fig. 1F, left, H). Even a small reduction in free [Ca²⁺] could result in a robust reduction of P_v because multiple Ca²⁺ are needed to trigger fusion (Fig. 1C vs G).

The concentration and kinetic rate constants of chelators are critical parameters defining the spatial extent of Ca²⁺ chelation and thus inhibition of P_v. Because 10 mm EGTA inhibits vesicular release by ∼50% in rupture experiments at the calyx of Held from postnatal day 8 (P8) to P10 rats (Borst and Sakmann, 1996) and pipette perfusion experiments using the mature calyx (P13–P15) (Nakamura et al., 2015), we examined the coupling distances corresponding to 50% EGTA inhibition (see horizontal dashed lines in Fig. 1H). The 50% EGTA inhibition distances were shorter for higher concentrations of exogenous Ca²⁺ chelators (Fig. 1I). For EGTA concentrations >5 mm, 50% inhibition occurred for d < 50 nm (Fig. 1H,I). For 10 mm EGTA, 50% inhibition occurred at 34 nm, which is shorter than its space constant (λ = 61 nm, for 50 nm resting [Ca²⁺]), in part because λ is the distance where [Ca²⁺] is reduced to 1/e (36.8%) rather than 50%, but mostly because of the nonlinearity of the Ca²⁺ sensor. BAPTA probed much smaller coupling distances than EGTA: between 10 and 30 nm for 1–10 mm concentrations. These simulations show that both BAPTA and EGTA can be used to probe coupling distances >10 nm, but precise coupling distances can be derived only from experiments in which the chelator concentration in the presynaptic terminal is known.

Coupling distance predictions from numerical simulations were then examined for the three different Ca²⁺ binding rate constants reported previously for EGTA in intracellular solutions (Fig. 1I). Among them, the rate constants estimated by Nägerl et al. (2000) were the most potent in inhibiting vesicular release, but not too different than recent reported values (Lin et al., 2017). The 0.5 mm BAPTA concentration exhibited a similar inhibition of exocytosis to 30 mm EGTA (Fig. 1I, dashed line), suggesting a 60-fold difference in potency. These results are compatible with LBA, which predicted a 50-fold difference in the concentration necessary to match BAPTA and EGTA potencies (Naraghi and Neher, 1997). Therefore, the LBA can still provide a basic intuition for the relative strength of synaptic transmission inhibition across different chelators. Moreover, it should provide reasonable estimates from the relative effects of two high-affinity exogenous chelators provided they are present in concentrations of >1 mm. LBA may fail, however, for experiments in which one condition does not include exogenous chelators (see Discussion). We will therefore examine the biophysical parameters influencing EGTA inhibition using primarily numerical simulations of reaction–diffusion.

Variation in the amplitude and duration of the VGCC current alters the inhibitory strength of EGTA

VGCCs at the nerve terminal are activated upon arrival of an AP, the time course of which can vary across cell types, within single axons (Rowan et al., 2014), and can undergo changes during high-frequency firing (Geiger and Jonas, 2000) and postnatal development (Taschenberger and von Gersdorff, 2000). The AP time course determines the duration of Ca²⁺ influx through VGCCs (Yang and Wang, 2006), which can influence the local [Ca²⁺] and thus P_v. The peak of the Ca²⁺ current appears near the completion of the repolarization phase of the AP (Borst and Sakmann, 1998; Bischofberger et al., 2002; Yang and Wang, 2006), where the membrane voltage is close to rest (∼−70 mV, Forsythe, 1994; Bischofberger et al., 2002) and the net driving force for Ca²⁺ can exceed 100 mV. Assuming that the single channel conductance of Ca_V2 is ∼3 pS (Weber et al., 2010), the single channel current amplitude during the AP is ∼0.3 pA. Because of the nonlinear transformation between [Ca²⁺] and release, we used numerical simulations to determine whether alterations in single VGCC current might alter coupling distance estimates.

To assess the effect of different amplitudes of Ca²⁺ influx on the inhibitory strength of EGTA (EGTA inhibition), we then varied the amplitude of the single VGCC current from 0.075 pA (∼0.08 pA, Lin et al., 2011) to 0.6 pA (Wong et al., 2014). At d = 20 nm, increasing the VGCC current amplitude caused a linear increase of the peak [Ca²⁺] and a supralinear increase of P_v for control conditions (Fig. 2A,B). Adding 10 mm EGTA reduced the peak [Ca²⁺] by 16% regardless of the current amplitude tested, but its inhibitory effect on P_v was larger for smaller currents because larger currents saturated the Ca²⁺ sensor. At a more distal location (d = 100 nm), the peak [Ca²⁺] also increased linearly for increasing VGCC current amplitudes for control conditions (Fig. 2C,D). However, because the peak [Ca²⁺] at 100 nm was far smaller than at 20 nm, a single VGCC opening led to a very small P_v (0.015 for 0.6 pA current amplitude). Under these conditions, adding 10 mm EGTA almost completely inhibited P_v regardless of the current amplitude. Figure 2E summarizes the effect of the VGCC current amplitude on the peak [Ca²⁺] and P_v in control conditions and EGTA inhibition of P_v at various distances. When normalized for amplitude, the spatial profile of the peak [Ca²⁺] for a VGCC current of 0.075 pA (red dashed line) closely overlapped that for a VGCC current of 0.6 pA (solid blue line), indicating that the amplitude of the [Ca²⁺] transient in the presence of multiple Ca²⁺ buffers (i.e., EFB and ATP) was linearly proportional to the current amplitude at all coupling distances. Nevertheless, the coupling distance exhibiting 50% EGTA inhibition was lengthened for increasing VGCC current amplitudes (Fig. 2F) due to the multi-site Ca²⁺ binding scheme of the Ca²⁺ sensor. Therefore, the amplitude of the single VGCC current can affect the inhibitory strength of EGTA and thus the interpretation of the coupling distance (see also Weber et al., 2010).

We next investigated the influence of Ca²⁺ influx duration on EGTA inhibition, by testing durations ranging from that of brief APs in fast nerve terminals (hundreds of microseconds, Borst and Sakmann, 1998; Geiger and Jonas, 2000; Ritzau-Jost et al., 2014), to longer durations evoked by burst opening of L-type channels in the cochlear hair cell (tens of milliseconds, Rodríguez-Contreras and Yamoah, 2003; Zampini et al., 2013). At d = 20 nm, the peak of the [Ca²⁺] transient increased for longer channel open durations (Fig. 3A) with a fast and slow component (Fig. 3B; τ_fast = 0.23 ms and τ_slow = 10.9 ms, the slow component contributed 47%). Adding 10 mm EGTA eliminated the slow component and therefore reduced the peak [Ca²⁺]. P_v also increased for longer VGCC open durations, but saturated for durations longer than 5 ms. The relationship between P_v and the VGCC open duration for control conditions was fit with a sigmoid curve with 0.54 ms half-activation duration. In the presence of 10 mm EGTA, the relationship shifted rightward, with a half-activation duration of 0.64 ms. At d = 100 nm, the [Ca²⁺] transients and P_v were smaller than at 20 nm for control conditions (Fig. 3C). The time constants of the fast and slow components of the peak [Ca²⁺] were larger 0.72 and 19.9 ms (the slow component contributed 78%; Fig. 3D). This prolonged slow component suggests that the [Ca²⁺] gradient does not reach steady-state for at least 20 ms, particularly at long distances from the VGCC. P_v at d = 100 nm exceeded 0.01 for VGCC open durations longer than 3 ms and had a 9.8 ms half-activation duration. In the presence of 10 mm EGTA, the slow component of the [Ca²⁺] transient rise was eliminated and P_v was <0.005. These simulations show that in control conditions the [Ca²⁺] gradients do not achieve steady state, whereas in high EGTA conditions, the [Ca²⁺] gradients do achieve steady state. The different time course of the [Ca²⁺] as a function of flux duration results in a duration dependence of inhibition of the peak [Ca²⁺] by EGTA.

Figure 3E summarizes how the VGCC open duration influences the peak [Ca²⁺] and P_v at various distances from the VGCC. Under control conditions, increasing VGCC open duration produced increasing peak [Ca²⁺] at all distances examined. VGCC open durations of 5–10 ms produced [Ca²⁺] gradients most similar to that predicted by the LBA (Fig. 3E, gray traces). However, when the VGCC open duration became shorter, the spatial profile of the [Ca²⁺] gradient became steeper and the discrepancy from LBA became larger, consistent with a [Ca²⁺] response that did not reach steady state. In the presence of EGTA, the discrepancy from LBA was only for durations <1 ms. Although the heavily buffered conditions minimized boundary effects of the small volume (Fig. 1D), the presence of EFB likely slowed the time to reach steady-state to 1 ms (consistent with simple calculation above). Therefore, for short AP durations (<1 ms), LBA does not apply even for 10 mm EGTA.

For simulations of P_v driven by Ca²⁺ entry of different durations, there was a clear shift in the location of 50% EGTA inhibition (Fig. 3F). Although EGTA almost completely blocked exocytosis at d >100 nm regardless of the VGCC open duration (Fig. 3G), for sensor locations close to the VGCC, EGTA more efficiently attenuated vesicular release when Ca²⁺ entry durations were brief (Fig. 3F; 0.1 ms duration produced a 51% inhibition at d = 20 nm). Close inspection of P_v versus distance curves (Fig. 3E, bottom) suggested that high Ca²⁺ occupancy of the sensor resulted in an insensitivity of P_v to 10 mm EGTA for d < 30 nm and durations longer than 5 ms. The smaller EGTA effect for longer VGCC currents was not due to saturation of EGTA because free EGTA concentration at the mouth of VGCC was 5.7 mm even after 20 ms channel opening (Fig. 3H). Therefore, the primary mechanisms for the duration dependence of EGTA inhibition of P_v are the duration dependence of EGTA inhibition of the peak [Ca²⁺], due to an inability to reach steady state in control conditions (Fig. 3A–D), and the nonlinearity of the Ca²⁺ sensor. Moreover, these mechanisms are likely to account for the differences in EGTA sensitivity found experimentally between AP-evoked and long step depolarization-evoked release (>10 ms; Chen et al., 2015). Similar effects would also be observed for BAPTA (Fig. 3G). In summary, reaction–diffusion simulations show that larger and longer single VGCC currents increase P_v and reduce the inhibitory strength of EGTA.

The Ca²⁺ domain of a single VGCC becomes expanded with larger VGCC current amplitudes (Weber et al., 2010; Fig. 2) and with longer VGCC open durations (Fig. 3), raising the possibility that the integrated ion flux through the VGCC is a more precise determinant of EGTA inhibition. However, the 50% inhibition distance was more sensitive to distance for large VGCC currents (Fig. 4A). We next varied the amplitude and duration of the single VGCC current simultaneously such that the total charge remained constant (0.3 pA · ms; Fig. 4B). Larger VGCC current amplitudes of short duration produced larger P_vs than smaller current amplitudes of longer duration (Fig. 4B,D). This is because the larger current amplitudes produced larger peak [Ca²⁺] that more efficiently drove vesicular release at longer distances (Fig. 4C). Therefore, whereas both the amplitude and duration of Ca²⁺ influx influence the inhibitory strength of EGTA, they do not have an equivalent influence because of the nonlinear Ca²⁺ sensor and the low potency of the small single channel currents to drive vesicular release.

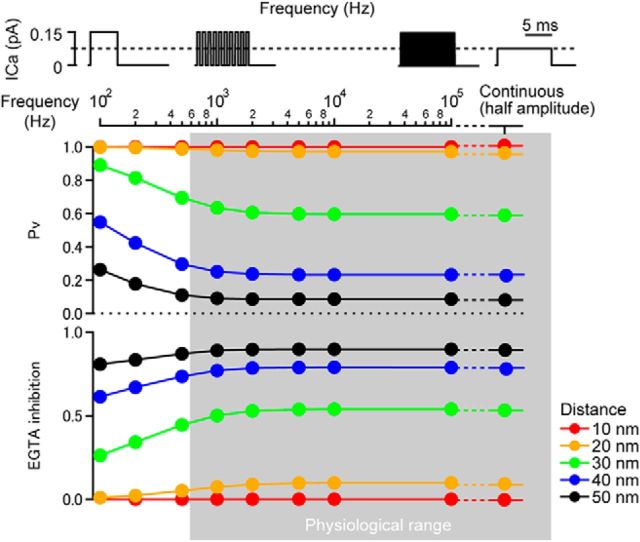
EGTA inhibition in the presence of VGCC flickering

In response to membrane depolarization VGCCs will transition between open and closed states within a few milliseconds (Fox et al., 1987). To estimate how this channel flickering influences on P_v and EGTA inhibition, we introduced channel flickering of various frequencies. Because single channel P_open at 0 mV was 0.5 in the calyx of Held (Sheng et al., 2012), we defined 100 Hz flickering as a 5 ms consecutive channel opening followed by 5 ms closing. At this frequency, a single channel current of 0.15 pA (Sheng et al., 2012) elicited maximal P_v at all locations (Fig. 5). When the flickering frequency was increased, P_v decreased and the EGTA inhibition increased, especially at distal locations. However, at frequencies in the physiological range (>1 kHz, Fox et al., 1987), both P_v and the EGTA inhibition were constant. We modeled an infinite flickering frequency as 10 ms constant current with half amplitude of 0.075 pA, which produced similar P_v and the EGTA inhibition to those at 1 kHz. Therefore, for EGTA inhibition experiments, channel flickering during longer depolarizations can be neglected. Moreover, one can approximate Ca²⁺ influx through single VGCC as a product of mean single channel current and mean P_open, as shown for the secretion model in chromaffin cells (Klingauf and Neher, 1997).

Effects of endogenous Ca²⁺ buffer species on the inhibitory strength of EGTA

Because presynaptic terminals contain a variety of endogenous Ca²⁺ buffers (Burnashev and Rosov, 2005), we next examined the influence of various buffer binding kinetics and concentrations on EGTA inhibition and the estimate of coupling distance. The buffering capacity (Ca²⁺-binding ratio; κ_s) of the EFB was varied over a range of reported values (Helmchen et al., 1997; Neher and Taschenberger, 2013; Delvendahl et al., 2015; Lin et al., 2017) by adjusting the concentration. For a 100 μm K_D and a fast k_on (Nakamura et al., 2015), changing κ_s from 10 to 80 decreased the peak [Ca²⁺] and P_v (Fig. 6A,B). EGTA inhibition for d > 20 nm became slightly smaller with higher κ_s due to competition between EGTA and EFB. However, the overall spatial profile of the EGTA inhibition was similar for the different values of κ_s because the EFB produced a parallel decrease in P_v in both control and 10 mm EGTA.

We next examined the effect of the EFB Ca²⁺ affinity (K_D), which is reportedly low in the calyx of Held (100–400 μm; Nakamura et al., 2015; Lin et al., 2017), whereas other computational studies have used a higher affinity (2 μm; Meinrenken et al., 2002). Here, we covaried the EFB concentration and k_off such that κ_s remained constant at 40. Increasing affinity increased the peak [Ca²⁺] and P_v (Fig. 6C) due to slower chelation times. However, there was little alteration in the inhibitory strength of EGTA for d < 50 nm for the different affinities (Fig. 6D), whereas for d > 50 nm, the effect was more prominent. Therefore, these simulations indicate the kinetic properties of EFB do affect P_v, but have only a modest effect on the spatial dependence of EGTA inhibition of P_v (up to 20% difference between a κ_s of 10 and 80; Fig. 6I).

The large energy demand of synapses requires high concentrations of free ATP ([ATP]; Harris et al., 2012), which can also act as a low-affinity Ca²⁺ buffer (K_D = 200 μm). Although the [ATP] in unperturbed terminals is estimated to be 1.4 mm (Rangaraju et al., 2014), direct presynaptic patch-clamp recordings often use patch solutions containing 0.2–1 mm (not Mg²⁺ bound). To examine the effect of changing the [ATP], we increased the [ATP] in our simulations from 0.2 to 2 mm and found that the peak [Ca²⁺] and P_v were both reduced (Fig. 6E). In the proximity of a VGCC (<50 nm), however, the spatial profile of EGTA inhibition of P_v was not changed (Fig. 6F). At more distal locations, the inhibitory effect of EGTA was reduced for larger [ATP]s (up to 27% change for 2 mm; Fig. 6I).

Calyces of Held (Felmy and Schneggenburger, 2004; Müller et al., 2007), as well as other mammalian synapses (Burnashev and Rozov, 2005), express fast and slow EF-hand mobile buffers. We therefore examined the potential impact of calretinin and parvalbumin. For concentrations <1 mm, which is the case for most nonribbon synapses in the CNS, there was a block of P_v (<10% at 30 nm; Fig. 6G) and no alteration of the 50% and 80% inhibition distances (<5% change; Fig. 6H). However, for higher concentrations (>1 mm) as found in hair cells, 1.2 mm calretinin (Edmonds et al., 2000) blocked P_v by 18% at d = 30 nm, and increased the 80% inhibition distance by 10%. 4.2 mm parvalbumin (Pangršič et al., 2015) reduced P_v and altered the spatial profile of EGTA inhibition (18% increase in 80% inhibition distance; Fig. 6I). A 13.5 mm calretinin concentration (Pangršič et al., 2015) not only reduced P_v, but also increased the 50% inhibition distance by 32% (Fig. 6H,I). In the presence of 13.5 mm calretinin, we could not define an 80% inhibition distance in our simulation volume. In summary, these simulations indicate that the low-affinity fixed (immobile) and submillimolar mobile Ca²⁺ buffers have little effect on the EGTA inhibition of P_v for short coupling distances (d < 50 nm), but can have a larger impact at more distal locations. High concentrations of EF-hand type buffers (>1 mm for calretinin and >4 mm for parvalbumin) do alter P_v and EGTA inhibition (Fig. 6I). Therefore, for most nonribbon synapses EGTA perturbation experiments are not influenced by reported concentrations of mobile buffers.

Thus far, we calculated P_v using a 5-site model of Ca²⁺ sensor model estimated for the calyx of Held of mature rats (Kochubey et al., 2009). However, differences in the Ca²⁺ sensitivity of the sensor could predict different P_v and thereby alter EGTA inhibition. We repeated our simulations using different vesicular release models: a five-site release model of immature rats (Kochubey et al., 2009), a five-site model of mature and immature mice (Wang et al., 2008), a five-site model from an inhibitory synapse (Sakaba, 2008), a five-site model from mice inner hair cells (Beutner et al., 2001), and an allosteric model (Lou et al., 2005). In response to a single channel current of 0.3 pA for 1 ms, all of the release models from central synapses resulted in a similar spatial profile of the EGTA inhibition (Fig. 6J), with only a 10% decrease in the estimated coupling distance using the inhibitory release model. The hair cell model, however, predicted a much shorter coupling distance compared with the other models, possibly due to a slower fusion rate. Therefore, the inhibitory strength of EGTA is insensitive to many subtle changes in currently available release models, but an accurate release model is likely needed to predict other functional aspects of neurotransmitter release.

EGTA inhibition of release probability driven by VGCC clusters

The numerical simulations described here and theoretical estimates from other studies indicate that a single VGCC can evoke vesicular release (Weber et al., 2010; Pangršič et al., 2015; Stanley, 2015). However, accumulating evidence from superresolution microscopy studies (Kittel et al., 2006; Wong et al., 2014) and SDS-digested freeze-fracture replica electron microscopy studies (Holderith et al., 2012; Indriati et al., 2013; Althof et al., 2015; Nakamura et al., 2015; Miki et al., 2017) have shown that VGCCs form clusters at active zones, indicating that vesicular release could be triggered by the cooperative action of multiple VGCCs. Moreover, seminal studies have provided reasonable constraints on the single channel current (0.3–0.6 pA, Weber et al., 2010; Sheng et al., 2012; Zampini et al., 2013), thereby allowing us to explore the impact of the number of VGCCs in a cluster on the strength of EGTA inhibition. To do this, we quantified P_v and EGTA inhibition of P_v from clusters composed of 4–32 VGCCs (compatible with experimental findings; Nakamura et al., 2015; Miki et al., 2017) placed at the center of release face in a grid-like manner (Fig. 7A). The NND of the VGCCs was set to 30 nm, similar to that of Ca_v2.1-labeled gold particles in SDS-digested freeze-fracture replica labeling (Nakamura et al., 2015). We assumed that all VGCCs opened simultaneously and the amplitude and open duration of each VGCC current were identical. We used contour lines to indicate the location surrounding the VGCC clusters where EGTA inhibition of P_v was reduced by a given percentage (e.g., 50%) and computed two measures of coupling distance: the distance from the contour line (i.e., Ca²⁺ sensor) to the center of gravity of the cluster (d₁) or to the nearest VGCC in the cluster (d₂).

Similar to our simulations with a single VGCC, the VGCC cluster simulations showed a spatial profile of EGTA inhibition of P_v that depended on the single VGCC current amplitude and open duration (Fig. 7A). For VGCC currents of 0.3 pA amplitude and 0.2 ms duration, equivalent to AP-induced Ca²⁺ influx in the calyx of Held, d₁ (50% EGTA inhibition) was 39 nm for 4 VGCCs and 105 nm for 32 VGCCs. For VGCC currents of 0.075 pA amplitude and 20 ms duration, mimicking long depolarization-induced Ca²⁺ influx in presynaptic voltage-clamp experiments, d₁ was 66 nm for 4 VGCCs and 175 nm for 32 VGCCs (Fig. 7B). In contrast, d₂ was less sensitive to number of channels: 44 nm for 4 VGCCs and 72 nm for 32 VGCCs (for 1 ms entry; Fig. 7C). When the open channel duration was 0.2 ms, the 50% inhibition distance to the nearest VGCC was nearly constant (22–24 nm) regardless of the number of VGCCs. Moreover, the estimated coupling distance increased by 2- to 3-fold when increasing the flux duration from 0.2 to 1 ms. For estimating the coupling distance, therefore, the perimeter distance (d₂) is a more reliable index than the distance to cluster center (d₁) and is used all subsequent analysis. In a previous study, the average distance from a Ca²⁺ sensor to each VGCC in a cluster was weighted by their relative contribution to [Ca²⁺] at the site of the sensor (Pangršič et al., 2015). We elected not to use this measure because the contribution of individual VGCCs to release cannot be estimated from superposition, due to nonlinearities imparted by the Ca²⁺ sensor (Fig. 1). Finally, the perimeter distance, d₂, could also provide insights into candidate linker proteins. For a 20 ms flux duration from a single channel the release probability was maximal (P_v = 1) for a 30 nm VGCC–sensor coupling distance. However, shorter flux durations, for example, 0.2 and 1 ms, generated a P_v of only 0.006 and 0.02, respectively (Fig. 7D). Therefore, the cooperative action of multiple VGCCs is necessary to trigger reliable vesicular release if Ca²⁺ influx duration is brief (<1 ms).

Impact of channel open probability on P_v and the strength of EGTA inhibition

The time course of an AP influences the P_open of VGCCs (Yang and Wang, 2006), thereby affecting not only the number of open channels, but also the open channel density of VGCCs in a cluster. Freeze-fracture replica labeling studies have reported the mean NND of VGCCs within clusters to be 20–40 nm (Indriati et al., 2013; Nakamura et al., 2015; Miki et al., 2017), a range that can critically influence estimates of the coupling distance (Nakamura et al., 2015). However, a more direct estimate of the NND of open VGCCs remains elusive because the P_open of the VGCCs is not known in most presynaptic terminals. To address this, we performed simulations of clusters composed of 12 open VGCCs while varying their NND. When the simulated VGCC NND was increased from 0 to 90 nm (thus, lowering the open channel density), P_v was reduced for a given coupling distance (Fig. 8A, d₂) due to the reduced overlap of the [Ca²⁺] domains, particularly those close to the sensor. For example, at a coupling distance of 30 nm, P_v was reduced from 0.88 to 0.28 when the NND was increased from 10 to 50 nm. The 50% inhibition distance also decreased as the NND increased (Fig. 8B). Therefore, the local open VGCC density within a cluster is another determinant of the strength of EGTA inhibition and thus estimates of VGCC–vesicle coupling distance.

Because the VGCC NND influences the strength of EGTA inhibition, we next considered how channel P_open influences the mean open channel NND. To do this, we generated different patterns of open VGCCs for a cluster of 50 VGCCs and computed the open channel NND (Fig. 8C). For P_open = 1, the mean open channel NND equals the mean NND of all VGCCs in the cluster, referred to as the all channel NND. As expected, the open channel NND increased as P_open decreased (Fig. 8C). For P_open = 0.16, the lowest experimental estimate of presynaptic VGCC P_open during APs (Sheng et al., 2012), the open channel NND was approximately twice as long as the all channel NND (Fig. 8C, inset). These simulations suggest that changes in the open channel NND due to altered P_open in a physiological range (1–0.16) can maximally affect the open channel NND by twofold. When the number of VGCCs was varied while maintaining a constant VGCC density, larger VGCC clusters produced longer open channel NNDs for small P_open (Fig. 8D). This effect is due to larger cluster areas associated with a larger number of VGCCs, which for some open channel patterns result in the nearest open channel occurring at longer distances. If the all channel NND is on the order of 20 nm (Nakamura et al., 2015; Miki et al., 2017), then physiological variation in P_open could result in a >2-fold difference in estimated coupling distance (Fig. 8B). However, if the all channel NND is >30 nm, then EGTA inhibition of P_v is relatively insensitive to P_open.

Thus far, we have shown that the strength of EGTA inhibition and the resulting estimates of the coupling distance are influenced by the VGCC number, density, and open duration. To predict how these factors combine under physiological conditions, we performed simulations using long and brief AP-evoked Ca²⁺ currents rather than step pulses and varied the VGCC P_open. Ca²⁺ current waveforms derived from experimentally recorded presynaptic APs from the calyx of Held (see Fig. 8 legend) using a modified HH model (Borst and Sakmann, 1998; see Materials and Methods). Open VGCCs were arranged in a regular array, a number corresponding to the product of P_open multiplied by 20 total channels, and an NND set according to that predicted for given P_open (Fig. 8D). The half-duration of the Ca²⁺ current waveforms was 0.26 and 1.24 ms for the brief and long AP, respectively (Fig. 8E). We found that higher P_open increased P_v and prolonged the 50% inhibition distance both for brief and long APs (Fig. 8F). We also performed simulations in which we increased the number of open VGCCs alone or increased the channel density alone (because P_open affects both). The increase in open VGCC number had a stronger influence on P_v than the open channel density. For long APs, the increase in open VGCC number also prolonged the 50% inhibition distance. However, for brief APs, we found that changes in either open VGCC number or density alone had little effect on the 50% inhibition distance. The number and density of open channels synergistically contribute to P_v and the EGTA inhibition, thereby influencing the estimate of VGCC–sensor coupling distances. These simulations therefore predict coupling distances ranging from 23 nm (P_open = 0.2 for brief AP) to 76 nm (P_open = 0.8 for long AP) if variations in P_open and AP duration were considered together.

Although deterministic numerical simulations are better suited for the examination of a large parameter space, they are also less accurate for predicting absolute release probability due to stochastic channel opening and the nonlinearity of the Ca²⁺ sensor (Modchang et al., 2010; Nakamura et al., 2015). To confirm that Ca²⁺ flux duration dependence of EGTA inhibition was robust across simulation methods, we performed Monte Carlo simulations to implement stochastic channel gating and particle-based reaction–diffusion using the MCell simulation environment. For this simulation, a regular array of 20 VGCCs (all channel NND of 20 nm) was placed on the release surface. We found a >2-fold increase in the 50% inhibition distance (Fig. 8G) between the brief AP (peak P_open = 0.2) and long AP (peak P_open = 0.8), which was slightly less than the 3-fold increase observed with equivalent deterministic simulations (data not shown). Nevertheless, both stochastic and deterministic simulations suggest that knowledge of the AP duration and P_open is critical for extracting accurate estimates of coupling distances at fast synapses.

EGTA inhibition of synaptic vesicle populations with multiple coupling distances

Thus far, we have examined P_v and the EGTA inhibition for a single Ca²⁺ sensor at a single distance from VGCCs. However at presynaptic terminals, the readily releasable pool (RRP) is thought to be composed of multiple vesicles, some of which might be located at different coupling distances (Wadel et al., 2007; Chen et al., 2015). How can an EGTA inhibition experiment be used to examine a simultaneous release from different locations? Our simulations above, and those shown previously (Chen et al., 2015), indicate that vesicular release from distal locations is only possible for tens of millisecond long depolarizations, where [Ca²⁺] increases are sufficiently large to drive vesicular release. Moreover, release from distal locations is always accompanied by release from proximal locations because there are no known manipulations that selectively trigger release of distal vesicles.

We simulated exocytosis from various flux durations at a synapse containing multiple vesicle populations placed around a cluster of four VGCCs (Fig. 9A). Because the spatial distribution of vesicles in the RRP is not well known, we assumed that vesicles were uniformly distributed with a density of 168 vesicles/μm² (Rosahl et al., 1995) over a 300 nm radius from the cluster perimeter. We did not implement vesicle replenishment in the model. In response to each VGCC opening for 0.5 ms, 86% of the vesicles within a 50 nm perimeter of the cluster were released. As the channel open duration increased, vesicles at more distal locations were recruited, resulting in an increase in the total amount of exocytosis (number of released vesicles; Fig. 9B). In the presence of 10 mm EGTA and short VGCC openings (0.5 ms), we observed a 28% reduction in the number of released vesicles located within a 20 nm perimeter. For longer VGCC openings, the total amount of exocytosis of proximal vesicles (d₂ = 0–50 nm) was similar to that in control conditions (i.e., no EGTA inhibition; Fig. 9B,C). However, EGTA greatly reduced exocytosis if the RRP included distally coupled vesicles (d₂ = 100–300 nm). In this uniform RRP vesicle distribution, exocytosis was more potently inhibited by 1 mm BAPTA. These simulations therefore make two different predictions: (1) if only proximally coupled vesicles are present, then increasing the step-pulse duration would result in a decrease of EGTA inhibition, but (2) if distal release competent vesicles (d₂ > 100 nm) were also present (Fig. 9C), then EGTA inhibition would increase with increasing step-pulse durations. The latter prediction has been demonstrated at the hair cell ribbon synapse (Johnson et al., 2017). In summary, brief VGCC open durations result in EGTA inhibition of exocytosis by several tens of a percent, solely mediated by proximally coupled vesicles. Longer open channel durations drive proximally coupled vesicles so efficiently that EGTA becomes ineffective, but distal vesicles remain remarkably sensitive to EGTA (Fig. 9D).

Discussion

To better understand the requisite experimental conditions to estimate accurately the VGCC–vesicle coupling distance from EGTA competition experiments, we performed numerical simulations of Ca²⁺ diffusion and vesicular release around single and clusters of VGCCs while varying Ca²⁺ influx, buffering, and VGCC distributions. We found that the most important parameters influencing estimates of VGCC–sensor coupling distance are as follows: the duration and amplitude of single VGCC current, the open channel density, and, to a lesser extent, the number of open VGCCs. In contrast, VGCC–sensor coupling distance estimates were rather insensitive to the properties of EFBs and the precise Ca²⁺ sensor model for vesicular release. Because the VGCC open probability and AP duration vary across presynaptic terminals (Rowan et al., 2014), and are sensitive to neuromodulation (Hoppa et al., 2014; Rowan et al., 2016), we propose that these parameters must be determined in order to infer either relative or absolute VGCC-vesicle coupling distances from experiments in which exocytosis is inhibited by exogenous Ca²⁺ chelators.

Deriving coupling distances from model simulations of synaptic transmission inhibition by a single exogenous Ca²⁺ chelator

Many Ca²⁺ chelator inhibition studies have compared the fractional block of neurotransmitter release by both BAPTA and EGTA to establish whether release is driven by tightly or loosely coupled vesicles (Eggermann et al., 2011). Simple classification of synapses as tight or loose coupling according to the presence or absence of EGTA block only works in rare cases, if at all. More often, the fractional block by both EGTA and BAPTA will vary in a continuous manner according to concentration, making it difficult to extract precise distances from experimental results alone. Moreover, we show that the Ca²⁺ flux also influences the fractional block. We suggest that numerical simulations of buffered diffusion are necessary for quantitative estimates of VGCC–vesicle distances, whether for both chelators (Meinrenken et al., 2002; Bucurenciu et al., 2008; Arai and Jonas, 2014; Vyleta and Jonas, 2014; Pangršič et al., 2015) or for a single chelator (Chen et al., 2015; Nakamura et al., 2015). In all cases, the concentration of chelator must be known (Fig. 1I). For example, the numerical simulations here show that high [EGTA] can compete with tightly coupled synaptic vesicles (∼20 nm) if the presynaptic AP is brief (Fig. 3E,F). However, BAPTA competition is more appropriate for coupling distances shorter than 20 nm (Figs. 1, 9).

Although the pioneering work by Naraghi and Neher (1997) derived LBA to interpret VGCC–vesicle coupling distances based on EGTA competition experiments, we found that numerical simulations are better suited for the rapid and localized [Ca²⁺] dynamics resulting from AP-evoked Ca²⁺ entry. LBA predicts well the [Ca²⁺] gradients in heavily buffered conditions (i.e., millimolar concentrations of EGTA and BAPTA). However, the presence of nonlinear EFBs and the finite volume of presynaptic terminals invalidate critical assumptions of LBA, particularly for low κ_s conditions (EFB and ATP only) and small terminals commonly seen in the CNS (Fig. 1C–E). In the low κ_s control conditions, the high EFB occupancy (Fig. 1D) prolongs the time to reach steady-state at early times, while at later times during influx (>1 ms) the finite volume of the terminal produces a gradual increase in terminal [Ca²⁺] that precludes steady-state gradients. Thus the peak [Ca²⁺] is different for short versus long flux durations in control conditions, but much less so when in the presence of high concentrations of exogenous chelator. In high EGTA conditions, the influence of the finite terminal volume is inconsequential and the [Ca²⁺] gradients reach steady state at ∼0.5 ms (∼50 μs for BAPTA). Therefore, provided that Ca²⁺ influx is not too brief, LBA predicts well the [Ca²⁺] gradients for high chelator concentrations, suggesting that the ratio of exocytosis in high EGTA and high BAPTA conditions, rather than that between a high chelator condition and control, would be less sensitive to variations in Ca²⁺ entry.

Another property that LBA does not predict well is the saturation of Ca²⁺ sensor. For long Ca²⁺ entry durations (>1 ms), the Ca²⁺ sensors are highly occupied both in control and in the presence of chelator, giving the apparent insensitivity of release to EGTA (Fig. 3F). Analytical predictions of EGTA inhibition of release using equations from Neher (1998b, Equation 22) and a value of three for the exponent of the sensor (n) match numerical simulations for 0.1 ms duration (Fig. 3F). Nevertheless, the LBA is not capable of predicting the duration dependence of chelator inhibition of release.

Factors affecting the estimate of coupling distance from EGTA competition experiments

At most fast synapses in the CNS, presynaptic VGCCs are activated by an AP, the waveform of which determines the duration of the single VGCC current (Augustine, 1990; Sabatini and Regehr, 1998). The duration of AP-evoked VGCC current has been measured in several large presynaptic terminals using an AP waveform voltage command. The half-duration of the presynaptic Ca²⁺ current was 0.36 ms at the calyx of Held in immature rats (Borst and Sakmann, 1998), 0.58 ms at hippocampal mossy fiber boutons (Bischofberger et al., 2002), and 0.11 ms at cerebellar mossy fiber terminals (Ritzau-Jost et al., 2014). In the small parallel fiber boutons, a first derivative of fluorescent Ca²⁺ transient was used to estimate Ca²⁺ entry duration of 0.3 ms (Sabatini and Regher, 1998). In cultured hippocampal neurons, fluorescence voltage sensor measurements suggested AP duration >2 ms (Hoppa et al., 2014). Therefore, the AP duration for most fast CNS terminals falls in a range in which EGTA is capable of inhibiting vesicular release within a few tens of nanometers. Moreover, simulations investigating EGTA inhibition for this range of Ca²⁺ current durations predict that coupling distances that could vary by a factor of 2 if the VGCC open probability is identical (Fig. 8E,F). AP duration can be modulated in an activity-dependent manner (Geiger and Jonas, 2000) and can vary across boutons within a single neuron (Rowan et al., 2016). Therefore, knowledge of the presynaptic AP duration is a prerequisite for an accurate estimation of the coupling distance.

Another factor influencing EGTA inhibition is the number and density of open VGCCs. Recent SDS-digested freeze-fracture replica labeling has shown that VGCCs can form clusters at AZs with NNDs of 20–40 nm (Nakamura et al., 2015; Miki et al., 2017). However, the observed number and density of VGCC particles are not necessarily equivalent to that for open VGCCs for two reasons: first, labeling efficiency varies between 30% and 80% (Indriati et al., 2013; Nakamura et al., 2015) and, second, only a fraction of the total VGCCs open during an AP. Single channel recordings have reported a P_open of ∼0.2 during an AP at the calyx of Held (Sheng et al., 2012), suggesting that the open channel density will be much lower than the total channel density (by nearly a factor of 2; Fig. 8D). Because NNDs <30 nm will critically influence the estimate of the coupling distance (Fig. 8B), knowledge of P_open is also important. Altering P_open from 0.2 to 1 can produce a 50% increase in the estimated coupling distance for short APs and nearly a doubling of coupling distance for long APs. Together with AP duration, the estimated coupling distance for the same level of EGTA inhibition (e.g., 50%) can vary three-fold from 20 nm for low P_open and short APs up to 80 nm for long APs and high P_open (Fig. 8F).

The presynaptic terminal contains various endogenous mobile Ca²⁺ buffers, which regulate P_v, paired-pulse facilitation, and synaptic plasticity (Burnashev and Rozov, 2005). Simulations with endogenous buffers kinetics and concentrations over a physiological range for nonribbon synapses (Blatow et al., 2003; Gall et al., 2003; Collin et al., 2005; Müller et al., 2007) had only a marginal effect on EGTA inhibition (Fig. 6). The effect of endogenous buffers on EGTA inhibition was small due in part to the higher concentration of EGTA that dominates the buffering of the terminal (Neher, 1998a). In contrast, the presence of higher concentrations of endogenous buffers, as has been described for hair cells (Edmonds et al., 2000; Pangršič et al., 2015), can indeed influence EGTA inhibition and thus should be characterized before estimating coupling distance from chelator competition experiments.

Although EGTA binding properties and its concentration are critical for estimating coupling distance (Naraghi and Neher, 1997; Lin et al., 2017; Fig. 1), many studies of VGCC–vesicle coupling have derived their conclusions from experiments using an ester derivative of EGTA (EGTA-AM). Because the intraterminal concentration of EGTA is not known in such experiments and this parameter critically influences the estimate of the coupling distance (Fig. 1F), conclusions from such experiments must be interpreted with caution. By extension, the concentration of EGTA at small and distant terminals after somatic whole-cell patch loading of chelator should also be verified (Bucurenciu et al., 2008).

Strategies for estimating VGCC–vesicle topographies

Insight into the number of channels driving vesicular release can be provided by the progressive block of vesicular release by VGCC antagonists (for review, see Matveev et al., 2011; Eggerman et al., 2011; Stanley, 2015). Low values of cooperativity (∼1–2) implicate tight coupling (Augustine, 1990; Bucurenciu et al., 2010; Scimemi and Diamond, 2012; Wong et al., 2014; Luo et al., 2015), whereas large cooperativity values (>2) implicate many channels contributing to vesicular release (Mintz et al., 1995; Fedchyshyn and Wang, 2005; Johnson et al., 2005). These qualitative insights into VGCC–vesicle coupling can also constrain numerical simulations that predict coupling distances (Wong et al., 2014; Luo et al., 2015). However, the combination of EGTA competition and knowledge of the nanoscale distribution of VGCCs can be used to predict not only VGCC–vesicle distances, but also specific topographical arrangements of VGCCs and synaptic vesicles (Nakamura et al., 2015).

The principal advantage of full reaction–diffusion simulations is that they can be used to interpret EGTA inhibition across different experimental conditions, in particular when vesicular release is evoked by long step depolarizations. Paradoxically, if the depolarization is shorter than 0.5 ms, then EGTA can more efficiently inhibit vesicular release at 10–50 nm. Conversely, 1–5 ms depolarizations can render proximal vesicular release from locations up to 100 nm much less sensitive to EGTA (Fig. 3). This alteration in EGTA sensitivity by variations in the Ca²⁺ entry duration results from a high [Ca²⁺] sufficient to drive release at long distances, especially when a large VGCC cluster evokes release. Our simulations also predict that, for synapses with heterogeneous coupling distances, the use of increasing depolarization step durations will result in a progressive increase in EGTA inhibition due to recruitment of distal vesicles. The presence of only proximal vesicles would produce a decrease in EGTA inhibition for increasing step durations due to saturation of the release sensor (Fig. 9B). In physiological conditions, proximal vesicles are those evoked by single APs, whereas distal vesicles, which require long Ca²⁺ influx durations (>5 ms; Fig. 3C), are only released after high-frequency trains of APs or long voltage step depolarizations and would contribute to a slow component of neurotransmitter release (Chen et al., 2015).

In cerebellar mossy fiber terminals, prolonged voltage steps elicit fast and slow release components, only the latter of which is preferentially blocked by 5–10 mm EGTA (Ritzau-Jost et al., 2014). Based on our simulations, the results in mossy fibers are consistent with a pool of proximally and distally coupled vesicles (Fig. 8D). Similar experimental results were observed in the calyx of Held (Chen et al., 2015), except that EGTA sensitivity occurred with higher concentrations of EGTA (20 mm), suggesting a distal pool that is slightly closer than in mossy fibers or that the Ca²⁺ flux was larger.

In conclusion, chelator competition experiments and numerical simulations together make a powerful diagnostic tool for estimating VGCC–vesicle coupling distances and topographies provided that single channel current amplitude, duration, and open channel density are known.