Short-Term Plasticity Combines with Excitation–Inhibition Balance to Expand Cerebellar Purkinje Cell Dynamic Range

Abstract

The balance between excitation (E) and inhibition (I) in neuronal networks controls the firing rate of principal cells through simple network organization, such as feedforward inhibitory circuits. Here, we demonstrate in male mice, that at the granule cell (GrC)-molecular layer interneuron (MLI)-Purkinje cell (PC) pathway of the cerebellar cortex, E/I balance is dynamically controlled by short-term dynamics during bursts of stimuli, shaping cerebellar output. Using a combination of electrophysiological recordings, optogenetic stimulation, and modeling, we describe the wide range of bidirectional changes in PC discharge triggered by GrC bursts, from robust excitation to complete inhibition. At high frequency (200 Hz), increasing the number of pulses in a burst (from 3 to 7) can switch a net inhibition of PC to a net excitation. Measurements of EPSCs and IPSCs during bursts and modeling showed that this feature can be explained by the interplay between short-term dynamics of the GrC-MLI-PC pathway and E/I balance impinging on PC. Our findings demonstrate that PC firing rate is highly sensitive to the duration of GrC bursts, which may define a temporal-to-rate code transformation in the cerebellar cortex.

SIGNIFICANCE STATEMENT Sensorimotor information processing in the cerebellar cortex leads to the occurrence of a sequence of synaptic excitation and inhibition in Purkinje cells. Granule cells convey direct excitatory inputs and indirect inhibitory inputs to the Purkinje cells, through molecular layer interneurons, forming a feedforward inhibitory pathway. Using electrophysiological recordings, optogenetic stimulation, and mathematical modeling, we found that presynaptic short-term dynamics affect the balance between synaptic excitation and inhibition on Purkinje cells during high-frequency bursts and can reverse the sign of granule cell influence on Purkinje cell discharge when burst duration increases. We conclude that short-term dynamics may play an important role in transforming the duration of sensory inputs arriving on cerebellar granule cells into cerebellar cortical output firing rate.

Introduction

The feedforward inhibition (FFI) circuit is an ubiquitous motif in the brain. In FFI pathways, an external excitatory input impinges on both a principal cell and local inhibitory interneurons that also target the principal cell. That is, an external input elicits an excitation (E) which is quickly followed by an inhibition (I) in the principal cell. FFI circuit properties have been extensively studied (for review, see Isaacson and Scanziani, 2011). In vivo, in vitro, and computational modeling studies of FFI circuits have shown that the balance and relative timing of E and I inputs are crucial in shaping the temporal window for spike discharge and the selective gating of stimulus-related activity (Wehr and Zador, 2003; Gabernet et al., 2005; Mittmann et al., 2005; Kremkow et al., 2010; Katzner et al., 2011; Bartley and Dobrunz, 2015). Moreover, correlated E and I inputs can prevent saturation of the postsynaptic spiking activity as well as extend the dynamic range for stimulus rate coding (Eccles et al., 1967; Buzsáki, 1984; Shepherd and Grillner, 2010; Isaacson and Scanziani, 2011). Another ubiquitous property of the brain is that almost all synapses show presynaptic short-term dynamics (STD) (Atluri and Regehr, 1996; Valera et al., 2012; Jackman and Regehr, 2017). Indeed, the size of the postsynaptic potential (PSP) can increase or decrease depending on the incoming spike history and presynaptic plasticity (Stevens and Wang, 1995; Markram and Tsodyks, 1996; Zucker and Regehr, 2002). Thus, the STD of synapses may strongly affect the E/I ratio and signal integration at the principal cell as the input firing rate increases.

The cerebellum computes a wide range of sensorimotor information, including very high-frequency bursts of action potentials (>100 Hz) through the mossy fiber (MF)-granule cell (GrC)-molecular layer interneurons (MLI)-Purkinje cell (PC) network, which constitutes a typical FFI pathway (Eccles et al., 1967; van Kan et al., 1993; Brunel et al., 2004; Chadderton et al., 2004; Mittmann et al., 2005; Jörntell and Ekerot, 2006; Saviane and Silver, 2006; Rancz et al., 2007; Arenz et al., 2008; van Beugen et al., 2013; Jelitai et al., 2016). PCs encode whisker position (Chen et al., 2016) or different features of locomotion (Sauerbrei et al., 2015) through a bidirectional modulation of their spontaneous firing rate (Häusser and Clark, 1997). Therefore, STD should have a strong effect on PC output and information transfer via the cerebellar FFI. However, how the interplay between E/I balance and STD at the GrC-MLI-PC synapses affect the PC discharge has not been well characterized and understood.

Here, we combine in vitro electrophysiological recordings with numerical simulation of the GrC-MLI-PC pathway to understand how E/I balance and synaptic STD influence the encoding of spike burst inputs in the PC output spike patterns. We show that the diversity of the PC output firing rate is governed not only by the E/I balance but also by the STD of the synapses. Notably, we demonstrate that because of synaptic STD, even the stimulus duration can determine the sign of the spike gain of the PC firing rate. This property of the cerebellar FFI may underlie the structured variability observed during locomotion (Sauerbrei et al., 2015) and help us understand the bidirectional modulation of the PC firing rates observed in behaving animals.

Materials and Methods

All procedures were in accordance with national and European community guidelines (2010/63/EU). Animal experimentations were approved in advance by the local French Ethics Committee of Strasbourg (CREMEAS; CEEA35; agreement number/reference protocol: A67-2018-38). Mice were bred and housed in a 12 h light/dark cycle with free access to food and water. The 3- to 8-week-old male heterozygous Thy1-ChR2-eYFP mice (B6.Cg-Tg(Thy1-COP4/EYFP)18Gfng/J from The Jackson Laboratory, IMSR catalog #JAX:007612, RRID:IMSR_JAX:007612) were used (Arenkiel et al., 2007).

Electrophysiology

Slice preparation.

Mice were decapitated under isoflurane anesthesia. The cerebellum was dissected out and quickly placed in a 4°C ACSF bubbled with carbogen (95% O₂, 5% CO₂). ACSF was composed of the following (in mm): 120 NaCl, 3 KCl, 26 NaHCO₃, 1.25 NaH₂PO₄, 2 CaCl₂, 1 MgCl₂, 20 glucose, 0.00005 minocycline. Transverse slices of 300 μm thickness were then prepared (Vibratome Microm HM 650V) in an ice-cold potassium-based medium containing the following (in mm): K-gluconate 130, KCl 14.6, EGTA 2, HEPES 20, glucose 25, minocycline 0.00005, and 1 kynurenic acid. To allow metabolic reactivation of the cells, slices were soaked in a sucrose-based medium at 34°C, containing the following (in mm): sucrose 230, KCl 2.5, NaHCO₃ 26, NaH₂PO₄ 1.25, glucose 25, CaCl₂ 0.8, MgCl₂ 8, minocycline 0.00005, and d-APV 0.05 before being transferred and maintained in ACSF medium at least 1 h before electrophysiological recordings. Slices were transferred to a submerged recording chamber under the microscope (BX61 Olympus) and perfused with oxygenated ACSF.

Recordings.

All recordings were located in the anterior part of the vermis (lobules III-VI) and performed at near physiological temperature (32 ± 0.5°C). Recorded PCs were visually identified under infrared illumination. PC discharge was initially monitored using extracellular recordings with pipettes filled with 0.5 m NaCl (resistance = 15–30 mΩ). PCs were located 50–75 μm beneath the slice surface to ensure the preservation of the FFI. PCs were then whole-cell voltage-clamped (Axopatch 200A or Multiclamp 700B, Molecular Devices) using 3–4 mΩ pipettes. All the data were acquired using WinWCP 4.5.4 freeware (John Dempster, University of Strathclyde, Glasgow, UK; RRID:SCR_014713). Recordings were sampled at 50 kHz and filtered at 2 kHz. Currents were recorded using the following pipette internal solution (in mm): 135 KMeSO₄, 6 NaCl, 10 HEPES, 4 MgATP, 0.4 Na₂GTP, 1 MgCl₂ with pH adjusted to 7.3 with KOH (osmolarity to 300 mOsm). For E/I ratios measurements, PCs were successively voltage-clamped at −60 mV and then 0 mV to measure EPSCs and IPSCs, respectively. Series resistance was monitored and compensated (80% typically) in all experiments. Voltages were not corrected for the liquid junction potential, which was calculated to be 9 mV. We accepted recordings for which the leak current at −60 mV did not exceed 1 nA. When possible, STD were estimated after extracellular recordings and E/I ratio measurements. Bursts of GrC stimuli (1, 3, and 7 stimuli) were then elicited (see below). STD were also measured in a dedicated set of experiments. PCs were whole-cell recorded, and stimulation intensity was calibrated to evoke an initial EPSC of ∼100 pA. A 7-step protocol was performed in which sequences of 1–7 stimuli were applied (see Data analysis). In these experiments, the internal solution contained the following (in mm): 135 CsMeSO₄, 6 NaCl, 10 HEPES, 4 MgATP, 1 EGTA, 0.4 Na₂GTP, 1 MgCl₂.6H₂O, and 5 QX-314. pH was adjusted to 7.3 with CsOH and osmolarity was set to 290 mOsm. All chemicals were supplied by Sigma-Aldrich and Tocris Bioscience.

GrC stimulation.

GrC firing patterns were reproduced in acute cerebellar slices using extracellular electrical stimulation of groups of GrC somas with a glass pipette filled with HEPES-buffered saline connected to an electrical stimulator (ISO-STIM 01D, NPI Electronic). HEPES-buffered saline contained the following (in mm): NaCl 120, KCl 3, HEPES 10, NaH₂PO₄ 1.25, CaCl₂ 2, MgCl₂ 1, glucose 10. Stimulated GrCs were located at a lateral distance of 100–300 μm from the recorded PC. Stimulation intensity (70 μA to 1 mA, 20 μs) was adjusted to alter PC discharge after a single stimulus and bursts of 1, 3, and 7 stimuli at 200 Hz were performed every 30 s.

Optical stimulation

Thy1-ChR2-eYFP strain of mice expresses Channelrhodopsin2 in MFs. MFs were photo-stimulated in acute slices using 470 nm LED-based illumination (collimated LED M470L2-C1 powered by a T-cube LEDD1B driver, Thorlabs) through the objective (40×). LED pulses were driven by a digital waveform generated using Igor Pro version 6.32A (Wavemetrics; RRID:SCR_000325). Illumination was composed of pulses (5 ms) of blue light triggered at random instantaneous frequencies during each trial. Illumination intensities (1–5 mW/mm²) were set in each experiment to increase the irregularity of Purkinje cell discharge as monitored by the CV2 value (see below).

Pharmacology

To limit plasticity induction during our protocols, we blocked NMDA, adenosine, CB₁, GABA_B, and mGluR₁ receptors by adding the following antagonists, respectively (in mm): 0.05 d-AP5, 0.0005 DPCPX (8-cyclopentyl-1,3-dipropylxanthine), 0.001 AM251 (N-(piperidin-1-yl)-5-(4-iodophenyl)-1-(2,4-dichlorophenyl)-4-methyl-1H-pyrazole-3-carboxamide),0.001 CGP52432 (3-[[(3,4-dichlorophenyl)-methyl]amino]propyl (diethoxymethyl) phosphinic acid), and 0.002 JNJ16259685(3,4-dihydro-2H-pyrano[2,3]β-quinolin-7-yl)(cis-4-methoxycyclohexyl) methanone). In a subset of experiments, inhibitory transmission was blocked using picrotoxin (100 μm), a GABA_A receptor antagonist. Except for picrotoxin (Sigma-Aldrich), all drugs were supplied by Tocris Bioscience.

Data analysis

Extracellular recordings.

In extracellular recordings, action potentials were detected using OpenElectrophy, an open source software (http://neuralensemble.org/OpenElectrophy/; RRID:SCR_000819) (Garcia and Fourcaud-Trocmé, 2009). Data were stored in SQL databases (Oracle). Spike trains were analyzed using Python software written in-house (SynaptiQs developed by Antoine Valera) and custom-based routines. PC discharge irregularity was assessed by two parameters: (1) the coefficient of variation for adjacent interspike intervals (ISIs) (CV2) calculated as follows:

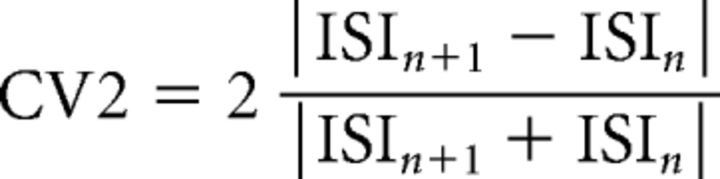where ISI_n is the ISI containing the stimulation. (2) Because PCs are spontaneously active and display a wide range of firing frequencies, we also determined the frequency-independent local variation of ISIs with a refractory period R (LvR) (Kumbhare and Baron, 2015) as follows:

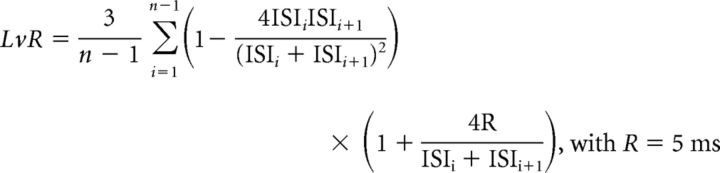Subthreshold GrC stimulation was assessed using the peristimulus time histogram (PSTH) of PCs responses to a single stimulation. The 1 ms bin width PSTHs were built by aligning at least 30 consecutive trials on the stimulus onset and by calculating the spike probability in each bin. GrC stimulations inducing an initial increase in spike probability exceeding 0.8 in a time bin of 5 ms after the stimulation were excluded as they correspond to suprathreshold inputs likely to be beyond the physiological range determined in vivo (Bower and Woolston, 1983; Jaeger and Bower, 1994; Mittmann and Häusser, 2007; Wilms and Häusser, 2015).

Spike gain.

The spike gain of PC discharges was determined as follows (see Fig. 1E) (Mittmann and Häusser, 2007): (1) the mean PSTH was computed from all the trials of each type of GrC stimulation (1, 3, and 7 stimuli); (2) the baseline level was subtracted from the mean PSTH; and (3) the spike gain is given by the cumulative sum (with a bin size of 5 ms) of the number of spikes exceeding or below the baseline. Therefore, the spike gain corresponds to the overall effect of the GrC stimulation and is not limited to the time window of the stimulation (10 ms for 3 stimuli and 30 ms for 7 stimuli).

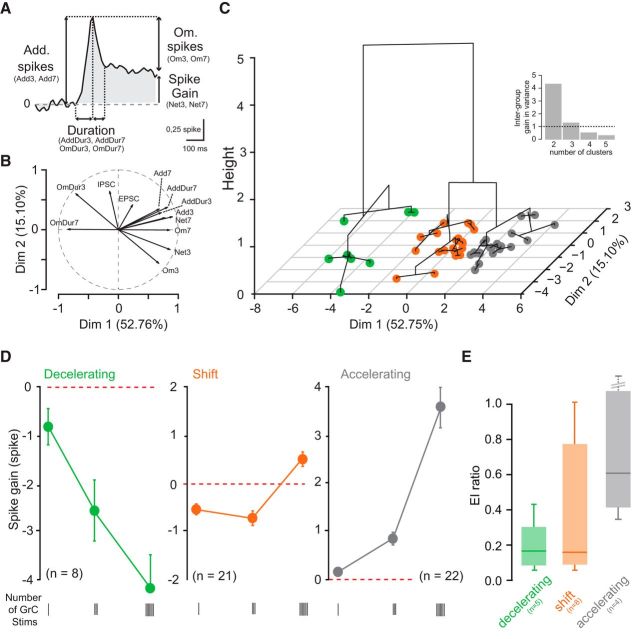
Figure 1.

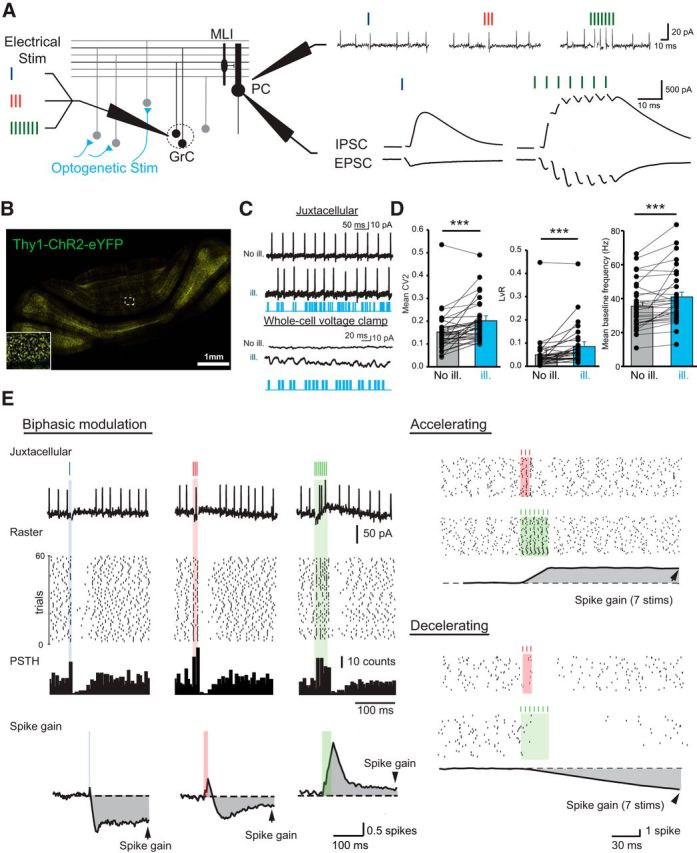
Bidirectional influence of PC discharges by short GrC burst stimuli. A, Left, Diagram of the feedforward inhibitory circuit in the cerebellar cortex. GrCs were stimulated 1, 3, and 7 times during irregular activation of many ChR2-expressing MFs by blue light illumination (optogenetic stim). PCs were first recorded in juxtacellular mode to monitor discharge (top right), then whole-cell patch-clamped to measure synaptic weights and E/I balance (bottom right). Excitation was recorded at V_m = −60 mV, inhibition at V_m = 0 mV. B, Confocal image of a transverse cerebellar section of a Thy1-ChR2-eYFP adult mouse showing strong eYFP fluorescence in MF rosettes. C, Top, PCs were recorded in juxtacellular, then whole-cell patch-clamped (bottom traces) before and during MF photostimulation (No ill and ill, respectively). Irregular firing and an increase in excitatory and inhibitory synaptic noise were observed. D, Quantitative analyses of PC discharge irregularities. The CV2, the frequency-independent LvR parameter, and the mean baseline frequency significantly increased during MF photostimulation (see Materials and Methods) ***p < 0.001, see text. Error bars indicate SEM. E, Left, Example of a biphasic modulation of PC discharge by GrC stimulation and determination of the spike gain. From the raster plots, a mean PSTH was determined and the baseline was subtracted. The spike gain was estimated by integrating this subtracted mean PSTH. Right, Two opposite examples of modulation of PC discharge by GrC stimulations.

E/I ratio and STD measurements.

EPSCs and IPSCs were recorded in whole-cell (see above), and measurements were made after averaging at least 20 traces. E/I was calculated as the ratio of EPSCs and IPSCs amplitude in response to a single GrC stimulation. EPSC-IPSC delay was determined by subtracting the EPSC and IPSC latencies measured between the stimulation artifact and 10% of EPSC/IPSC amplitude. For STD measurements, after extracellular recordings, amplitudes were measured between the peak and the extrapolation of the residual current from EPSC_n-1 or IPSC_n-1 after fitting with a monoexponential function. Amplitudes of evoked postsynaptic currents (PSCs) resulting from the n^th stimulus were defined as EPSC_n and IPSC_n. STD was calculated as follows:

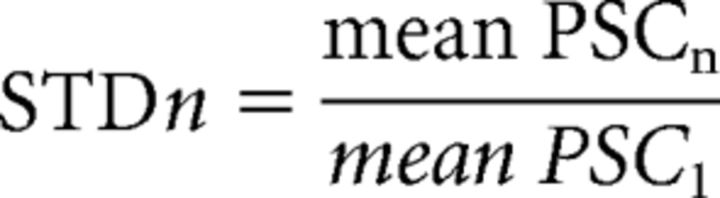In a dedicated set of experiments (see recordings) for STD measurements, GrC stimulations were delivered in a sequence of 1, 2, 3… 7 pulses, and the amplitude of the n^th PSC was estimated by subtraction of the recordings with n^th − 1 stimulations.

Principal component analysis (PCA) and hierarchical cluster analysis.

PCA and hierarchical cluster analysis were performed using FactoMineR plug-in in Ri386 3.2.2 software developed by François Husson (Lê et al., 2008; Husson et al., 2016) (RRID:SCR_014602). The 12 following variables were used for the PCA: the number of additional spikes or omitted spikes in response to 3 and 7 stimuli (Add3, Add7, Om3, Om7), the duration of these phases (AddDur3, AddDur7, OmDur3, OmDur7), the net spike output (spike gain) after 3 and 7 stimuli (Net3, Net7), and the EPSC and IPSC amplitude (see Fig. 3A). Variables were centered and reduced. The first two principal components with the higher variance (dimension 1, 52.76%; dimension 2, 15.1%) were considered and used for the hierarchical clustering algorithm (Ward's method, http://factominer.free.fr/factomethods/hierarchical-clustering-on-principal-components.html). The number of clusters in the hierarchical tree was set at 3, a value above which the gain in intergroup variance was minimal (see Fig. 3C, inset).

Figure 3.

GrC stimulation leads to three identifiable patterns of PC output. A–C, PCA and hierarchical clustering on principal components on the 51 PCs recorded. A, Description of the variables used for PCA: Add spikes, Additional spikes (variables: Add3 and Add7, additional spikes for 3 and 7 stimuli); Om. spikes, omitted spikes (variables: Om3 and Om7, omitted spikes for 3 and 7 stimuli); Duration, duration of the acceleration and deceleration phases (variables: AddDur3 and AddDur7, duration of the acceleration phase for 3 and 7 stimuli); OmDur3 and OmDur7, duration of the deceleration phase for 3 and 7 stimuli; spike gain (variables: Net3 and Net7, spike gain for 3 and 7 stimuli). B, Polar plot showing the respective contributions of the variables to the PC discharge. Projections on x and y axes give the coefficient of correlation between the variable and the two first dimensions of the PCA. C, Projection on the two first principal component dimensions (Dim 1, Dim 2) of the dendrogram distance tree obtained from the hierarchical cluster analysis. Height axis corresponds to the increase in between-group variance. Three groups have been identified (n = 51 cells). Inset, Interclass variance as a function of the number of clusters. Straight line indicates the variance below which an additional cluster does not bring a significant variance. Three clusters explain most of the variability. D, Averaged spike gain at 1, 3, and 7 GrC stimuli for each identified group: decelerating (green), shift (orange), and accelerating (gray). Error bars indicate SEM. E, Box plot (min, 25%, median, 75%, max) of the E/I ratio per group (n = 17 cells). There is scattering in the shift group.

Simulation

PC neuron.

Membrane current is calculated using the following equation:

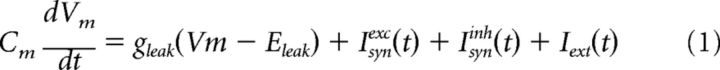where Cm is the membrane capacitance, g_leak is the leak conductance, and E_leak is the resting potential of the neuron. I_syn^exc(t) represents the total excitatory inputs arriving from the GrCs, and I_syn^inh(t) represents the total inhibitory inputs arriving from the inhibitory interneurons. In the absence of any specific stimulus PC spike at ≈30 Hz in a quasi-periodic manner (CV_isi ≈ 0.2). To mimic this ongoing activity in our simple point neuron model of the PC, we injected noisy excitatory current, I_ext(t), corresponding to a spike train drawn from a sinusoidally modulated Γ-process (frequency = 37 Hz; order = 4). The magnitude of the sinusoidal modulation was 10% of the average input rate, which was set to 2000 spikes/s to obtain 30 spikes/s as the output firing rate in the model neuron. For each trial, we used a different realization of the sinusoidally modulated Γ-process to generate the background activity in the PC. This model clearly is an oversimplification of the dynamics of PCs. Still, this simple model allows us to study the effect of synaptic dynamics on the integration of external input by a feedforward inhibitory circuit motif. Complex nonlinear dynamics of PCs could have obscured these synaptic effects.

Synapse model.

Synapses were modeled as a conductance transient as follows:

where S_a(t) (a ∈ {exc., inh.}) is the synaptic transient, V_m is the membrane potential, and E_a^rev is the reversal potential of the synapse (for the parameters, see Table 2). Each presynaptic spike induced an α function-shaped conductance transient in the postsynaptic PC as follows:

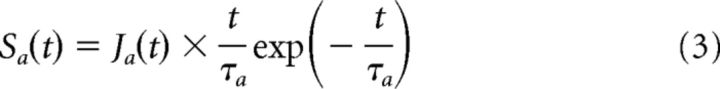where τ_a is the synaptic time constant and J_a(t) is the amplitude of the synapse. When synapses are static, J_a(t) is constant; and when synapses change according to the history of the previous presynaptic spikes, the temporal evolution of J_a(t) is given by Equation 8. To model the STD of the PSP amplitude, we used a deterministic model proposed by Tsodyks and Markram (1997).

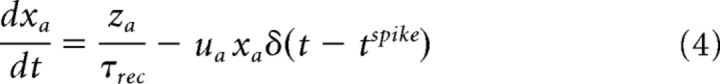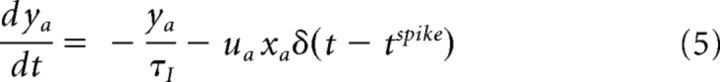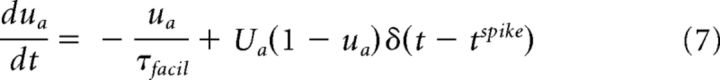where x_a, y_a, and z_a (a ∈ {exc., inh.}) are the three state variables that describe the state-dependent use of the synaptic resources in the recovered (x_a), active (y_a), and inactive (z_a) states, respectively. t^spike is the timing of the previous spike. τ_I is the decay time constant of the postsynaptic current, τ_rec is the time it takes the synaptic resources to recover from their inactive state. The variable u_a(t) keeps track of the use of the synaptic resources at a synapse. To model synaptic facilitation, the variable u_a is instantaneously increased by a small amount of U_a at the time of spike and then returns to the baseline value with a time constant τ_facil (Eq. 7).

Table 2.

Model parameters

Parameter	Value
Neuron parameters
Membrane capacitance (Cm)	250 pF
Membrane time constant (τm)	20 ms
Resting membrane potential (Vrest)	−70 mV
Refractory period (τref)	2 ms
Spike threshold (Vth)	−55 mV
Excitatory synapse properties
Excitatory reversal potential	0 mV
Excitatory time constant	1 ms
Static unitary EPSP	0.5–4 mV @ −70 mV
Synaptic delay	1 ms
Short-term dynamics of excitatory synapses
Synaptic decay time constant (τpscexc)	1.5 ms
Recovery time constant (τrecexc)	30 ms
Facilitation time constant (τfacexc)	500 ms
Fraction of opened calcium channels (Uexc)	0.02–0.5
Synaptic amplitude scaling (Aexc)	1.5–337.5 (EPSP range: 0.5–4 mV)
Inhibitory synapse properties
Inhibitory reversal potential	−80 mV
Inhibitory time constant	5 ms
Static unitary IPSP	−0.3 to −1.4 mV @ −70 mV
Synaptic delay	2.5 ms
Short-term dynamics of inhibitory synapses
Synaptic decay time constant (τpscinh)	1.5 ms
Recovery time constant (τpscinh)	100 ms
Facilitation time constant (τpscinh)	800 ms
Fraction of opened calcium channels (τpscinh)	0.03–06
Synaptic amplitude scaling (τpscinh)	−1.667 to −150 (IPSP range: −0.3 to −1.4 mV)

The effective synaptic weight was given by the following:

To systematically change the nature of the synapses from facilitating to depressing, we changed the variable U_a while keeping all other variables unchanged. Because we kept all the time constants unchanged in the model, going from facilitation to depression did not affect the frequency dependence of the synapses. The parameter A_a was changed to increase the amplitude of the postsynaptic potential independent of the STD. The values of these various parameters are provided in Table 2, and corresponding facilitation and depression of synaptic strength are shown in Figure 4.

Figure 4.

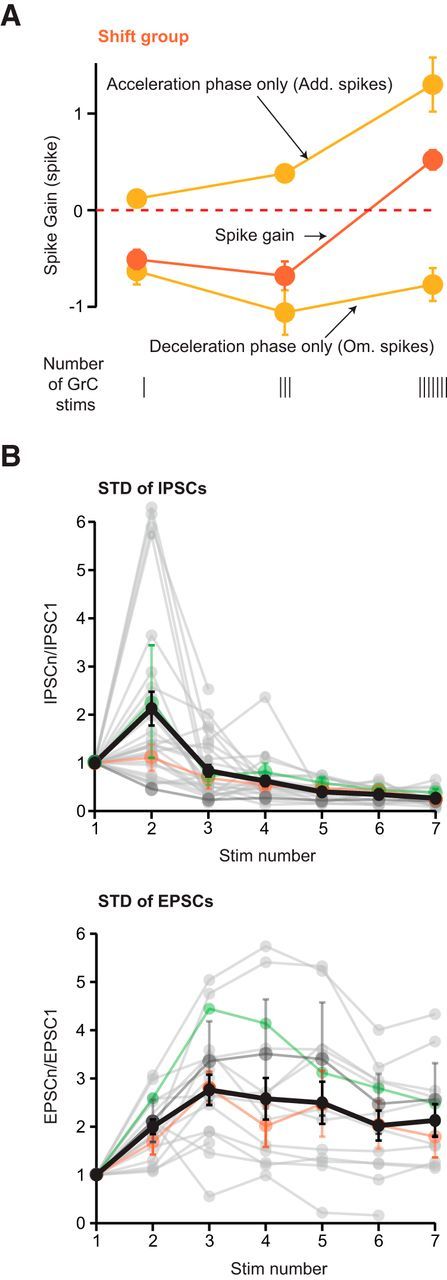
E/I ratio is strongly affected by STD. A, Evolution of the net spike number in the shift group for 1, 3, and 7 GrC stimuli. Top, Acceleration phase (Add spikes phase only). Middle, Spike gain. Bottom, Deceleration phase (Om spikes phase only). Error bars indicate SEM. B, STD of excitation and inhibition at each stimulus number in a train (1–7 stimuli) of GrC stimuli at 200 Hz. STD are determined by the ratio PSC_n/PSC₁. Gray traces represent all individual cells. Colored traces represent averaged data per group: mean ± SEM (when n > 1) for shift (orange), decelerating (green), and accelerating groups (dark gray) for cells recorded both in juxtacellular and in whole-cell mode. Black represents overall mean ± SEM.

Patterned stimulation.

The activity of the GrCs was modeled as a train of 3 or 7 spikes (ISI = 5 ms) mimicking GrC stimulation in acute slices. The feedforward inhibition created by the inhibitory interneurons was also modeled as a train of 3 or 7 spikes (ISI = 5 ms). Both spike trains were identical in each trial. The inhibitory spikes arrived at the PC 1.5 ms after the arrival of the excitatory spikes. The excitatory and inhibitory synapses exhibited STD.

All simulations were performed using the NEural Simulation Tool (RRID:SCR_002963) environment (http://www.nest-simulator.org/).

Statistical tests

Statistical analysis was performed using Sigmaplot software (version 12.0, Systat Software; RRID:SCR_003210) and Igor version 6.12A (Wavemetrics; RRID:SCR_000325). All data are presented as mean ± SD in the text and SEM on graphs. Statistical tests were specified in the text.

Results

GrC stimulations induce a wide range of PC responses

We studied how E/I balance and STD of excitatory and inhibitory synapses interact to affect PC discharge, in acute cerebellar slices. GrC groups were stimulated with 1, 3, or 7 stimulation pulses at 200 Hz as observed in vivo (Chadderton et al., 2004; Jörntell and Ekerot, 2006; Arenz et al., 2008). PC discharges were monitored using juxtacellular recordings (Figs. 1A; n = 51 cells, N = 37 mice; see Materials and Methods). Some PCs were also recorded in the whole-cell mode (n = 17 of 51, N = 15 of 37; Fig. 1A; see Materials and Methods) to measure EPSCs/IPSCs elicited by GrC stimulations.

In an in vitro preparation, the background synaptic noise is artificially low (Häusser and Clark, 1997; Destexhe et al., 2003; Blot et al., 2016), which led to an overestimation of the influence of evoked synaptic inputs on PC discharge. To overcome this limitation, we used a transgenic mouse expressing Channelrhodopsin2 in MFs (Thy1-ChR2-eYFP; Fig. 1B) in which background activity can be generated by an illumination of blue light. To mimic the variability of PC discharges observed in vivo (Shin et al., 2007; Jelitai et al., 2016), we illuminated the cerebellar slices from Thy1-ChR2-YFP mice in an irregular manner to increase the level of spontaneous EPSCs/IPSCs in PCs (Fig. 1B–D; see Materials and Methods). We adjusted the photostimulation parameters to obtain in vivo-like PC discharges (Fig. 1C,D; mean CV2 during illumination: 0.202 ± 0.09; control: 0.152 ± 0.09, p = 0.001; mean LvR during illumination: 0.086 ± 0.084; control: 0.050 ± 0.077, p < 0.001; mean baseline frequency during illumination: 40.1 ± 2.9 Hz; control: 35.1 ± 2.4 Hz, p = 0.0006; Wilcoxon signed rank test, n = 32). To mimic the stimulus-induced activity in vivo, in addition to this background activity, small groups of GrCs were repeatedly stimulated (min 30 trials per protocol), which changed the PC membrane potential (2–3 mV) (Jelitai et al., 2016) and the firing rate (Bower and Woolston, 1983; Jaeger and Bower, 1994; Wilms and Häusser, 2015). The mean amplitude of the direct EPSC elicited by a single stimulation of a group of GrCs was 228 ± 190 pA (at −60 mV; n = 17) and the mean disynaptic IPSC was 1178 ± 1040 pA (at 0 mV; n = 17). This suggests that the number of nonsilent GrC synapses in the stimulated groups was between 5 and 50 (Isope and Barbour, 2002; Schmidt et al., 2013). The mean latency between EPSC and IPSC was 1.91 ± 0.46 ms (n = 18) in agreement with previous observations (Brunel et al., 2004; Mittmann and Häusser, 2007).

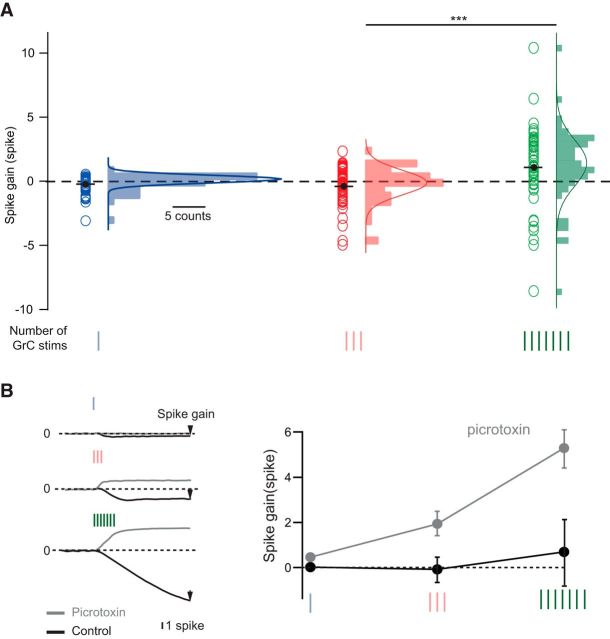
To quantify the net increase (or decrease) in the PC firing rate in response to the GrC stimulations, we defined the “spike gain.” The spike gain was calculated by integrating the mean PSTH of the PC spike train after baseline subtraction (Fig. 1E; see Materials and Methods) (Mittmann and Häusser, 2007). An increase (or decrease) in spike gain after the stimulus onset corresponds to a net increase (or decrease) in the firing rate. If PC discharge is controlled solely by the overall E/I balance, we expect that increasing the number of stimuli will only affect the magnitude of the spike gain. However, if excitatory and inhibitory synapses also exhibit STD, the sign of the spike gain may also be inverted when the number of GrC stimuli is increased. In 40 of the 51 recorded PCs, GrC stimulations elicited biphasic changes in firing rate, illustrating the E/I sequence characteristic of the FFI motif (Fig. 1E). The spike gain was found to be highly variable across PCs, from −3.09 to 0.53 spike on average for a single stimulation. This indicates that even a single stimulation of a group of GrCs can drive an overall increase (acceleration n = 21) or decrease (deceleration n = 27) in the PC discharge rate (Figs. 1E, 2A, blue circles). Increasing the duration of the GrC stimulation (3 and 7 pulses at 200 Hz) further increased the variability of the spike gain (Fig. 2A) and significantly skewed the distribution toward a positive spike gain (mean = −0.34 ± 1.46 and 1.05 ± 3 spike for 3 and 7 stimuli, respectively; Wilcoxon signed rank test, p = 2.3 × 10⁻⁶). PC discharge could be accelerated up to 138 ± 37 Hz (for 7 stimulations) or silenced (mean pause duration for 7 stimuli = 123 ± 64 ms, n = 13 of 51). To confirm that the negative part of the spike gain was mediated by the FFI, we blocked inhibition by the application of picrotoxin (100 μm), a GABA_A receptor antagonist. This led to a positive spike gain for all the cells (n = 7; Fig. 2B; mean spike gain 1 stim, control = 0.02 ± 0.11 spike, picrotoxin = 0.46 ± 0.08 spike, p = 0.015; 3 stims, control = −0.08 ± 0.42 spike, picrotoxin = 1.93 ± 0.4 spike, p = 0.016; 7 stims, control = 0.69 ± 1.62 spike, picrotoxin = 5.29 ± 1.04 spike, p = 0.016; Wilcoxon signed rank test).

Figure 2.

GrC stimulation can evoke a wide range of PC spike gains. A, Spike gain distribution in PCs (n = 51) in response to 1 (blue), 3 (red), or 7 (green) GrC stimulations at 200 Hz. ***p ≤ 0.001 Wilcoxon rank test. B, Pauses and decreases in firing rate in PC discharge are mediated by FFI. Left, Example of a PC showing a negative spike gain in response to 1, 3, or 7 stimulations of GrCs in control condition (black traces) and a positive spike gain in picrotoxin condition (100 μm; gray thick traces). Right, Averaged effect of picrotoxin application on spike gain (n = 7). Error bars indicate SEM.

Burst duration influences the sign of the spike gain

To classify the wide range of PC responses to GrC stimulations, we used PCA (Fig. 3A–C). We chose 10 parameters describing the PC spike train statistics for 3 and 7 stimuli and the evoked synaptic weights (EPSC and IPSC) for 1 stimulus (Fig. 3A; see Materials and Methods). The number of omitted spikes for 7 stimuli (Om7), the duration of PC inhibition for 7 stimuli (OmDur7; determined by the FFI), and the duration of the stimulus (Net7, Net3: the spike gain elicited by 3 and 7 GrC stimuli) emerged as key parameters (correlation coefficient > 0.8 with Dim 1; Fig. 3B) that classified different PC responses. EPSC and IPSC amplitudes were correlated only with the second dimension of the PCA (correlation coefficient_EPSC = 0.42, correlation coefficient_IPSC = 0.64 with Dim 2, Fig. 3B). Because they explain the majority of the variance (dimension 1, 52.76%; dimension 2, 15.1%), the first two dimensions of the PCA were used in a hierarchical clustering method, which identified three groups of PC responses (Fig. 3C).

The first two groups were characterized by a monotonic increase or decrease in spike gain as the stimulus duration was increased. We refer to these as accelerating (n = 22 of 51 cells, 43.1%) and decelerating (n = 8 of 51 cells, 15.7%) groups (Fig. 3D). Cells in these two groups predominantly received either excitation or inhibition (median E/I accelerating = 0.6, n = 4; median E/I decelerating = 0.18, n = 5; Fig. 3E; Table 1). The monotonic change in the PC spike gain for longer stimulation can be attributed to temporal summation of incoming inputs.

Table 1.

Summary of PC responses to GrC stimulations^a

	EPSC (pA)	IPSC (pA)	E/I	One stimulation					Three stimulation					Seven stimulation
				Add (sp)	AddDur (ms)	Om (sp)	OmDur (ms)	Spike gain (sp)	Add	AddDur	Om	OmDur	Spike gain	Add	AddDur	Om	OmDur	Spike gain
Decelerating group
Minimum	69	166	0.06	0.00	0.00	−3.09	0.00	−3.09	0.00	0.00	−5.05	10.00	−4.97	0.00	0.00	−8.58	90.00	−8.58
Maximum	163	2755	0.43	0.12	10.00	0.45	95.00	0.10	0.39	20.00	−0.10	165.00	−0.10	1.24	35.00	−2.55	235.00	−1.31
Mean	115	1121	0.18	0.04	5.00	−0.73	34.38	−0.80	0.09	6.88	−2.59	89.38	−2.51	0.17	8.75	−4.30	153.75	−4.13
SEM	20	469	0.06	0.06	1.90	0.40	12.50	0.38	0.05	2.80	0.65	19.75	0.62	0.15	5.07	0.67	21.22	0.74
Shift group
Minimum	55	54	0.05	0.00	0.00	−1.84	0.00	−1.64	−0.05	5.00	−2.56	10.00	−2.10	0.01	5.00	−1.99	0.00	−0.68
Maximum	493	3188	1.02	0.36	10.00	0.00	70.00	0.08	1.00	20.00	−0.20	85.00	0.21	2.28	50.00	0.00	115.00	2.01
Mean	253	1566	0.34	0.12	5.48	−0.63	31.90	−0.51	0.38	15.71	−1.06	44.29	−0.68	1.30	36.43	−0.77	38.33	0.52
SEM	62	373	0.14	0.03	0.90	0.12	4.95	0.11	0.07	1.25	0.14	4.15	0.15	0.13	2.05	0.13	6.37	0.15
Accelerating group
Minimum	18	0	0.37	0.01	5.00	−0.78	0.00	−0.36	0.32	10.00	−2.59	0.00	−0.27	1.20	40.00	−0.91	0.00	1.20
Maximum	617	1675	1.20	0.77	20.00	0.00	50.00	0.53	2.32	40.00	0.00	80.00	2.32	11.22	70.00	0.00	40.00	10.40
Mean	319	474	0.69	0.28	10.23	−0.16	10.68	0.12	1.14	20.68	−0.42	20.00	0.78	3.58	45.00	−0.14	8.64	3.44
SEM	145	402	0.15	0.04	0.60	0.04	2.90	0.04	0.08	1.05	0.13	4.95	0.13	0.43	1.70	0.05	2.75	0.40
p K–W test	ns	ns	ns	***	***	*	**	***	***	***	***	***	***	***	***	***	***	***
	0.43	0.12	0.1	4.01e-05	3.41e-04	0.014	0.009	3.77e-07	9.25e-12	3.17e-06	7.48e-06	9.55e-06	2.10e-12	5.34e-13	1.92e-09	1.19e-10	3.1e-09	0

^aAdd, Average number of additional spikes; AddDur, average duration of acceleration; Om, number of omitted spikes; OmDur, average duration of deceleration.

*p < 0.05;

**p < 0.01;

***p < 0.001; K–W test, Kruskal–Wallis between the three PC groups (decelerating, shift and accelerating).

The third group (n = 21 of 51 cells, 41.1%) was characterized by a significant change in the sign of the spike gain when burst duration was increased from 3 to 7 GrC stimuli (mean spike gain for 3 stimuli = −0.68 ± 0.7 spike; 7 stimuli = 0.52 ± 0.67 spike, p = 1.9 × 10⁻⁶; Wilcoxon signed rank test). In this group, the negative spike gain observed for 1 and 3 stimuli was switched to a positive spike gain for 7 stimuli in 17 of 21 cells (Fig. 3D; Table 1). We refer to these neurons as the “shift group.” The E/I balance was more variable than observed in the other two groups (mean EPSC = 253 ± 176 pA, mean IPSC = 1566 ± 1054 pA; n = 8; Fig. 3E, orange). In addition, in this group of cells, no correlation was found between either the spike gain and E/I balance (Pearson: ρ = 0.33, p = 0.42 and ρ = 0.26, p = 0.53 for 3 and 7 stimuli, respectively) or between the amplitudes of the first PSCs (IPSC₁ and EPSC₁; Pearson ρ = 0.24, p = 0.55; n = 8). These analyses show that the initial E/I balance based on postsynaptic synaptic weight is a poor predictor of the influence of GrC stimulations on PC discharge when burst duration increases, suggesting that presynaptic STD may play a major role.

STD at excitatory and inhibitory synapses account for the shift group

The fact that spike gain can be negative for bursts of 3 stimuli and positive for 7 stimuli suggests that E/I balance may shift toward more excitation as the stimulation duration increases. Such a change in the E/I balance can be attributed to synaptic facilitation and/or depression. Indeed, >10 Hz, a short-term facilitation (at the GrC-PC synapse) and a short-term depression (at the MLI-PC synapses) have been reported (Atluri and Regehr, 1996; Isope and Barbour, 2002; Bao et al., 2010; Valera et al., 2012). To test this hypothesis, we plotted the magnitude of the acceleration and deceleration phases (see Add spikes and Om spikes, respectively, Fig. 4A) of the PC discharge of the shift group. We found that the deceleration phase was significantly reduced as the number of GrC stimulations was increased from 3 to 7 (Fig. 4A; deceleration phase 3 stimuli = −1.06 ± 0.6, 7 stimuli = −0.77 ± 0.6, p = 0.02 Wilcoxon signed rank test; n = 21). Next, we measured the STD of excitatory and inhibitory synaptic inputs (Fig. 4B), which correspond to the monosynaptic GrC-PC and the disynaptic GrC-MLI-PC connections, respectively. EPSC (IPSC) amplitudes were normalized to the first EPSC at each position in a burst (ratio PSCn/PSC₁ with n = 1–7) in two sets of experiments. In a subset of the experiments, the PCs were recorded both in juxtacellular and whole-cell mode and STD measurements have been performed (n = 12; 6 shift, 3 decelerating and 3 accelerating PCs). In addition, 16 PCs were recorded only in the whole-cell mode to measure STD (n = 16; see Materials and Methods). On average, at 200 Hz, excitation facilitated during the burst (EPSC₂/EPSC₁ = 2 ± 0.62, n = 17; EPSC₇/EPSC₁ = 2.68 ± 1.46, n = 13; Fig. 4B, STD excitation, black thick line), whereas inhibition facilitated at the second stimulation (IPSC₂/IPSC₁ = 2.12 ± 1.82, n = 27) but strongly depressed thereafter (IPSC₇/IPSC₁ = 0.27 ± 0.18, n = 15; Fig. 4B, STD inhibition, black thick line), yielding a severalfold increase in the dynamic E/I ratio. In the shift group, the E/I ratio increased between 3 and 7 stimuli (median E/I ratio 1 stim = 0.15, 3 stim = 1.24, 7 stim = 5.51). However, STD were spread across PC groups (Fig. 4B, orange, green, and dark gray lines), and no correlation between STD and PC groups was observed (e.g., for 7 stimuli mean EPSC₇/EPSC₁ shift group = 1.79 ± 1.05, accelerating group = 2.57 ± 1.81, p = 0.15, Wilcoxon rank test; mean IPSC₇/IPSC₁ shift group = 0.26 ± 0.15, decelerating group = 0.9 ± 1.3, p = 0.08, Wilcoxon rank test). These findings suggest that, if an increase in the number of stimulations of a GrC cluster enhances excitation over inhibition, a complex interplay between STD and E/I balance determines PC discharge.

Interplay of STD and E/I balance determines the heterogeneity of PC responses

Next, we tested how E, I, and STD in the GrC-PC and GrC-MLI-PC pathways can explain the diversity of PC discharge patterns observed in response to GrC stimulation. E/I balance and STD are not independent synaptic parameters because pharmacological agents or calcium concentration that modify STD at the GrC-PC synapses also alter the probability of vesicular release, thereby affecting synaptic strength and E/I balance (Zucker and Regehr, 2002). Therefore, we used a computational model of the GrC-MLI-PC feedforward pathway (see Materials and Methods) to understand the interplay between E/I balance and STD and their influence on PC discharge over a wide range of conditions. STD of EPSPs and IPSPs amplitude were simulated using the deterministic model proposed by Tsodyks and Markram (1997) (Table 2) in which a single parameter (U) can be used to systematically change the nature of a synapse from a facilitating to a depressing mode. In this model, a set of four parameters described the E/I balance (EPSP and IPSP amplitudes) and the STD of excitation (U_E) and inhibition (U_I). We systematically varied U_E (0.02–0.5) and U_I (0.03–0.6) to obtain different degrees of facilitation and depression for E and I synapses (Fig. 5A). U_E ≈ 0.07 and U_I ≈ 0.3 corresponded to the average excitatory and inhibitory STD measured in our experiments (biological range: 0.02 < U_E <0.2 and 0.15 < U_I < 0.6).

Figure 5.

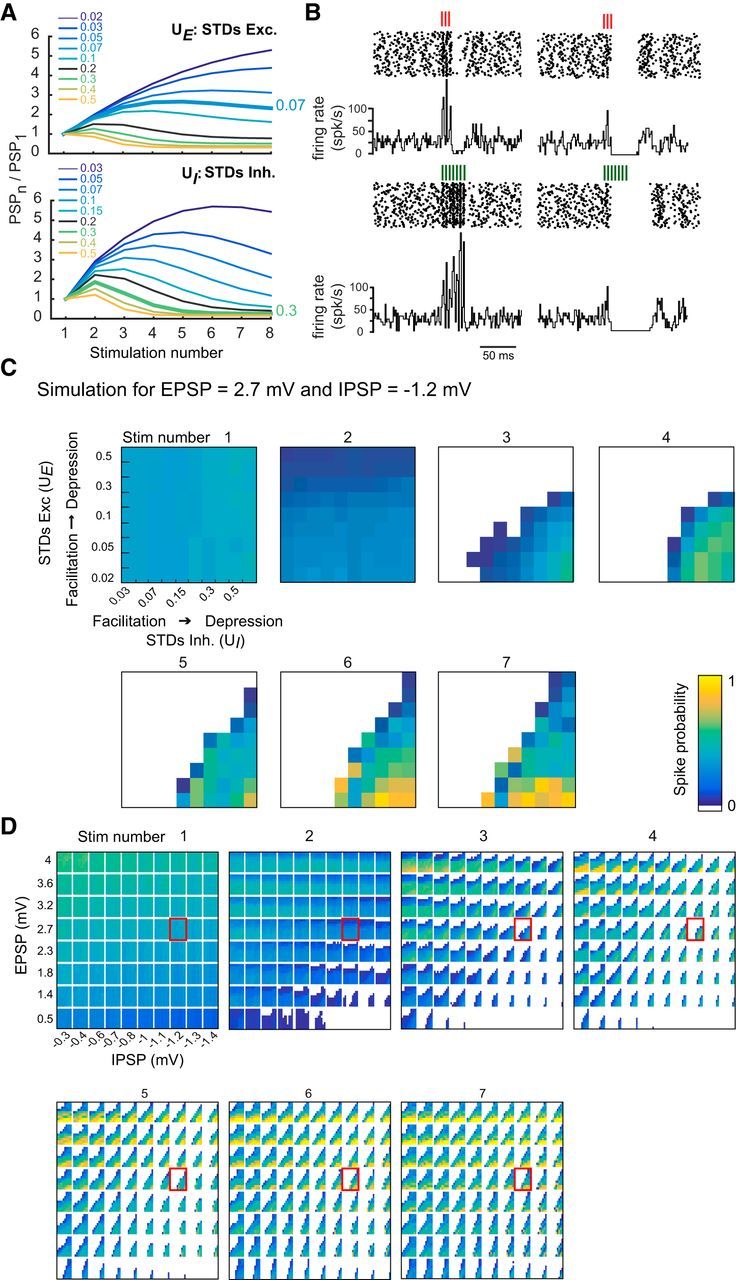
Varying E, I, and STD at the excitatory and inhibitory pathways of a simple model reproduces discharge patterns seen in vitro. A, STD of simulated EPSPs (top) and IPSPs (bottom). Ratios PSP_n/PSP₁ were determined for a range of U variables (U_E and U_I for excitation and inhibition, respectively; see Materials and Methods). Thicker lines indicate U_E and U_I values simulating the averaged experimental STD (Fig. 4). B, Examples of simulated raster plots and PSTH. Left, Response of a PC for 3 and 7 GrC stimuli at 200 Hz. Excitation is strong and facilitates, whereas inhibition is small and depresses mildly (EPSPs = 3.0 mV at −70 mV, U_E = 0.05; IPSP = −0.8 mV at −70 mV, U_I = 0.3). Right, Simulated PC response for weak depressing excitation and strong facilitating inhibition (EPSPs = 1.2 mV, U_E = 0.5; IPSP = −1.2 mV at −70 mV, U_I = 0.05). C, Reproducing PC response variability by combining E/I balance and STD. Spike probability for a given set of E/I balance (EPSP = 2.7 mV and IPSP = −1.2 mV). Inner rectangles in each subpanel represent the spike probability following a given stimulation (5 ms window) as a function of STD. Within each subpanel, EPSPs range from facilitating to depressing from bottom to top, whereas IPSPs go from facilitating to depressing from left to right. D, Spike probability following GrC stimulation (1–7) as a function of EPSP (y axis) and IPSP (x axis) amplitudes. Inner rectangles in each subpanel represent the spike probability as a function of STD as in C. Rectangles highlighted in red represent EPSP = 2.7 mV and IPSP = −1.2 mV expanded in C.

We simulated the evolution of the spike probability for the 3 GrC stimulation protocols (1, 3, and 7 stimuli at 200 Hz, 100 trials per set of parameter) and systematically varied the four model parameters (Fig. 5B–D). EPSP values ranged between 0.5 and 4 mV at −70 mV. The maximum EPSP value used in the model corresponds to a maximal EPSC of ∼500 pA (Isope and Barbour, 2002), the upper bound of our recorded dataset (Table 1). IPSPs (between −0.3 mV and −1.4 mV at −70 mV) were then constrained by matching the resulting spike output with experimental data (Fig. 5B). An example of the spike probability for every stimulation pulse (1–7) is shown in Figure 5C (extracted from the full simulation displayed in Fig. 5D). As expected, an increase in the EPSP or IPSP amplitude resulted in a corresponding increase or decrease in the probability of the PC to elicit a spike in response to a single stimulation (Fig. 5D, see first column or bottom row of the first panel stim number 1). In our simulations, we could modulate spike probability of a PC between 0.1 to 0.6 by varying the amplitude of EPSP and IPSP. When excitatory synapses are facilitating (U_E < 0.2; see Fig. 5A) and inhibitory synapses are depressing (U_I > 0.15; Fig. 5D, bottom right part of the inside rectangles; Fig. 5C, bottom right part of each stimulation panel), the spike probability increased with every stimulation in the input sequence and saturated to 1. On the other hand, when excitatory synapses are depressing (U_E > 0.2, see Fig. 5D) and inhibitory synapses are facilitating (U_I < 0.15; upper left part of the inside rectangles), spike probability decreased with stimulation number in the input sequence and can be reduced to zero. Thus, spike probability depends on E/I balance, STD of the excitation and inhibition, and the rank of stimulation in the sequence.

After estimating spike probability, we computed the spike gain for a biologically plausible range of E, I, and STD parameters. We first considered static synapses (U_E and U_I not included in the simulation) in which only E and I varied and compared the sign of the spike gain for the 3 and 7 GrC stimuli. For a wide range of E and I values (Fig. 6A, white circles), we found that the spike gain sign mostly did not depend on the E/I values (Fig. 6A, green and gray quarters). For some values of E/I synapses, spike gain changed the sign but only from positive to negative (Fig. 6A, blue region). These results show that neurons with static synapses cannot show shift cell behavior in a biologically realistic range of excitatory and inhibitory synaptic strengths. On the contrary, when synapses exhibited STD, the sign of the spike gain could be reversed (as for the shift group in the experimental dataset) between 3 and 7 stimulation cases for a wide range of E, I, and STD parameters values (Fig. 6B, orange region). Moreover, for a given E/I balance, STD can modulate how GrCs influence PC discharge (Fig. 6B, right). For fixed values of EPSP and IPSP, all 3 types of PC responses can be observed by varying the STD parameters. For instance, when EPSP = 2.3 mV and IPSP = −1 mV, by varying the facilitation (at the excitatory synapse) and depression (at the inhibitory synapse), the GrC simulation led to 44% of accelerating cells, 36% of shift cells, and 19% of decelerating cells (Fig. 6B, right, red rectangle indicates the biologically realistic range of STD parameters panel). This distribution is similar to our experimental observations (Fig. 3). By contrast, depression of excitation and facilitation of inhibition resulted in the opposite scenario for various E and I set of values (Fig. 6B, blue regions). However, when the space of parameters was restricted to the experimentally observed values of STD (0.02 < U_E < 0.2 and 0.15 < U_I < 0.6 defined by the upper and lower range of Fig. 4), the latter scenario was almost absent, and the simulation predicted the same 3 groups as in the experimental dataset (Fig. 6B, red rectangle).

Figure 6.

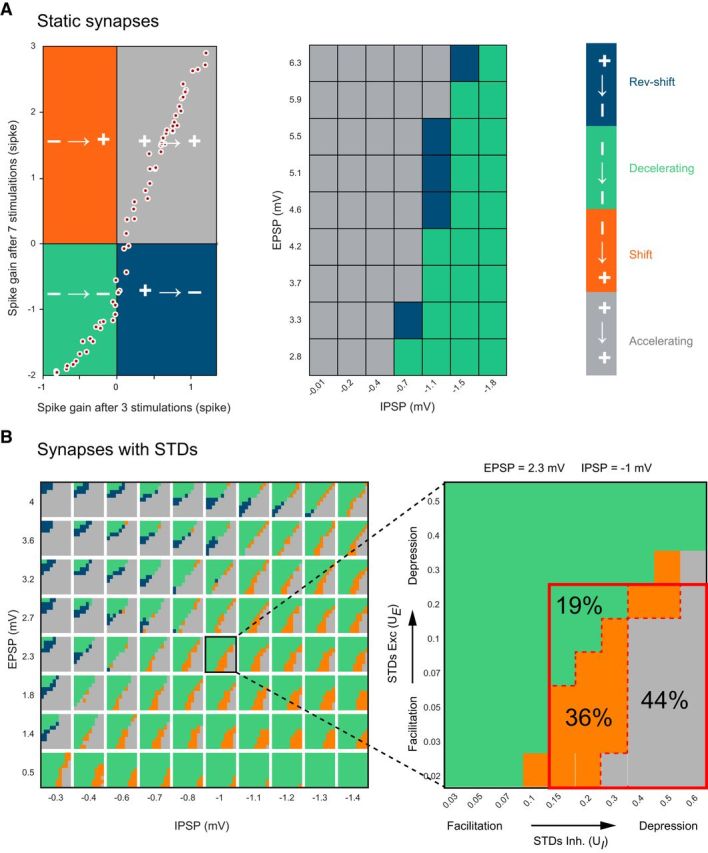
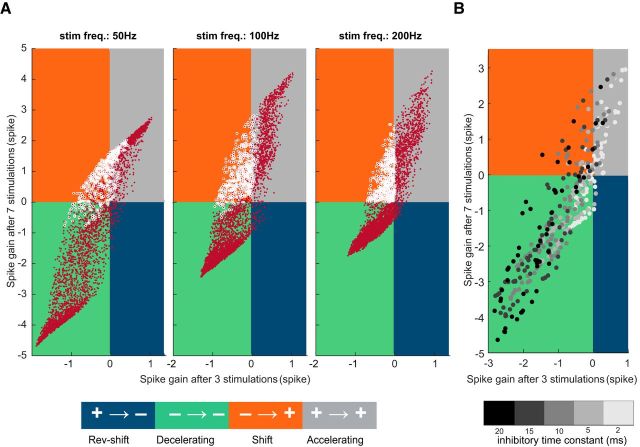
The shift group of PC responses requires STD at excitatory and inhibitory pathways. A, Left, Plot of the spike gain elicited by 7 GrC stimuli against spike gain for 3 stimuli when GrC-PC and MLI-PC synapses are static (no STD). The four possible scenarios for the spike gain are marked in different colors. Gray and green represents no change in the sign of the spike gain between 3 and 7 GrC stimuli; gray and green correspond to accelerating and decelerating PC response groups, respectively. Blue and orange represents change in the sign of the spike gain; blue and orange correspond to reverse-shift and shift PC response groups, respectively. Each white dot indicates spike gains for different combinations of E and I. The absence of any points in the orange quadrant shows that, without STD, it is not possible to observe negative spike gains for 3 GrC stimuli then positive for 7 stimuli (i.e., the shift group of PC responses is absent). Middle, PC response group as a function of E and I for static synapses. For no combination of EPSP and IPSP amplitude did we obtain a shift in the spike gain as observed in in vitro experiments. B, Evolution of the sign of the spike gain with dynamic synapses (with STD) as a function of EPSP (y axis) and IPSP (x axis) amplitudes (left) when GrC stimulations switch from 3 to 7 GrC stimulations. Inset, Inner rectangles represent excitatory STD U_E (y axis) as a function of inhibitory STD U_I (x axis). Same color code as in A. The reverse group is absent when simulations are restricted to U_E and U_I values corresponding to the physiological range observed in our recordings (red rectangle, Inset). One rectangle has been highlighted to illustrate the influence of STD of excitation (y axis) and inhibition (x axis) on the behavior of the PC response.

We then assessed whether varying other model and input parameters in addition to E/I and STD parameters affected the spike gain and the occurrence of the shift group. The accelerating, decelerating, and shift type spike gain could be observed at lower frequencies, down to 50 Hz (Fig. 7A) and for a wide range of time constants of the inhibitory synapses (Fig. 7B). These findings suggest that the shift group is a robust feature of PC integration of GrC rate code as long as the synapses are endowed with STD. Thus, the simulations confirm that the combination of E, I, and STD is necessary and sufficient for the accurate description of the PC discharge following GrC stimulation. Moreover, we confirmed that the structure of the PC spike train is strongly controlled by the number of spikes in the GrC burst. Finally, our model demonstrates that shift cell behavior requires facilitating excitation and depressing inhibition as observed in the experimental dataset.

Figure 7.

Effect of the inhibitory decay time constant and stimulus frequency on the spike gain evolution. A, Evolution of the sign of the spike gain at varying GrC input frequency (50, 100, and 200 Hz). Each panel represents spike gain for 7 GrC stimuli plotted against the spike gain for 3 stimuli. The four possible scenarios for the spike gain are marked in different colors (same color code as in Fig. 6). Each dot indicates spike gain for different combinations of E, I, and STD parameters (same range as Fig. 6). For all 3 frequencies, we observed shift behavior in PC response. White circles represent simulation parameters leading to a shift behavior at 200 Hz. B, Evolution of the sign of the spike gain at varying time constant of inhibition for a subset of E, I, and STD parameters. Each dot indicates spike gain for different combinations of E, I, STD parameters and inhibitory decay time constant (marked in different gray shaded; see color bar). Increasing the decay time constant of synaptic inhibition enhances the magnitude of the spike gain but does not affect the occurrence of the shift group. Here E, I, and STD parameters spanned the same range as in A, but we used a coarse grained sampling of these parameters so as to avoid cluttering.

Discussion

A large diversity of Purkinje cell response elicited by GrCs

In this study, we demonstrated that, although the sensorimotor MF-GrC-MLI-PC input pathway in the cerebellum is anatomically organized as a classical FFI microcircuit, specific operational rules for synaptic excitation and inhibition lead to a wide diversity in PC discharges in response to GrCs stimulation: from an increase in firing rate to a complete shutdown of the discharge. The versatility of the PC discharge was enhanced by an interplay of excitatory and inhibitory STD that regulates vesicular release at individual connections. Indeed, in the MF-GrC-PC pathway, GrCs can fire at several hundred Hz during sensorimotor processing in different areas of the cerebellar cortex (Chadderton et al., 2004; Jörntell and Ekerot, 2006; Arenz et al., 2008). As high firing rates scale up the STD (Atluri and Regehr, 1996; Pedroarena and Schwarz, 2003; Hallermann et al., 2010; Valera et al., 2012), E/I balance is highly affected by burst duration.

Several in vivo and in vitro studies (Eccles et al., 1967; Brunel et al., 2004; Mittmann et al., 2005) have previously reported a correlation between E and I synaptic weights in the MF-GrC-PC FFI pathway, suggesting that inhibition may control the temporal window of PC discharge (Mittmann et al., 2005). In our results, no correlation was observed between EPSC and IPSC amplitude elicited by GrCs, and PC discharges were not determined solely by E/I balance. This discrepancy can be explained by the use of compound parallel fiber stimulation in previous studies. Such protocols simultaneously excite thousands of fibers from multiple heterogeneous GrC-PC and GrC-MLI-PC pathways. However, in a recent study, we have demonstrated that PCs or MLIs at the same location may be driven by different clusters of GrCs. This suggests, for example, that GrC activation in a given zone of the cerebellar cortex might lead to PCs inhibition (Valera et al., 2016), questioning the basic postulate that at a population-level GrC-induced excitation and inhibition are always highly correlated. The interplay between long-term synaptic plasticity observed at the excitatory (GrC-PC and GrC-MLI) and inhibitory (MLI-PC) connections in the GrC-MLI-PC pathway lead to the description of specific and complex influence on PC discharge (Mittmann et al., 2004; Smith and Otis, 2005; Steuber et al., 2007; Wang et al., 2009; Bing et al., 2015; ten Brinke et al., 2015). Whole-cell patch-clamp in vivo recordings in awake animals confirmed both the linear relationship between PC firing rate and the independent regulation of E and I targeting PCs (Jelitai et al., 2016). These particular features of the FFI in the cerebellar cortex allow for a precise modulation of the spontaneously active PCs. When combined with high-frequency burst stimulation (from 50 to 200 Hz, as shown in Fig. 7) of GrC inputs and STD, here we have demonstrated an unexpected influence of GrC stimulation on PC discharge. Despite the heterogeneity in STD parameters of E and I synapses (Fig. 4) (Perkel et al., 1990; Llano et al., 1991; Isope and Barbour, 2002; Bao et al., 2010; Valera et al., 2012), inhibition always depresses while excitation facilitates when bursts lengthen. These STD lead to a systematic increase in E/I ratios and a switch in the sign of the overall effect on PC firing rate for a wide range of initial E/I ratio. Indeed, in 41% of the experiments (in the shift group), the sign of the spike gain switched from inhibitory to excitatory when burst duration increased from 3 to 7 stimuli. These findings strongly suggest that the interplay between E, I, and STD can encode burst duration through a nonlinear spike gain modulation, supporting the idea of a temporal-to-rate code transformation. For the accelerating and decelerating groups, a monotonic change in the spike gain was observed similar to the monotonic increase in PC discharge with GrC input strengths (Walter and Khodakhah, 2006). Moreover, our computational model revealed that all the PC discharges observed in the experimental dataset, including the switch in the spike gain, can be explained solely by the interplay between E, I, and STD parameters. The model confirmed that depression of inhibitory synapses is essential to generate output similar to the shift cells. Excitatory input to the shift cell could be of both facilitating (for weak synapses) and depressing type (for strong synapses) and PCs receiving only static synapses cannot exhibit the shift cell behavior (Fig. 6). Hence, networks endowed with synaptic STD may encode longer and shorter stimuli differently. The multiplexing of the postsynaptic weights (E and I; rate coding) with the temporal and frequency-dependent properties of STD, a presynaptic feature, at the GrC-PC and GrC-MLI-PC synapses may then extend PC encoding possibilities and information transfer to the downstream cerebellar nuclei.

Functional implications

Movement encoding by both negative and positive changes in spike gain in PC discharges have been observed in many studies (see, e.g., Thach, 1968; Armstrong and Edgley, 1984; Thier et al., 2000; Herzfeld et al., 2015; Chen et al., 2016). In primates, rapid eye movements (saccades) are coded by a dual population of PCs, with one group increasing its firing rate while the other decreases it (Herzfeld et al., 2015). Similarly, in rodents, whisker position during voluntary movements is encoded by the modulation of PCs from an acceleration to a complete shutdown (Chen et al., 2016). Then, the FFI circuit in association with the direct GrC-PC excitatory pathway of the cerebellar cortex takes over the adjustment of the set point frequency of PCs that controls the movement.

Presynaptic STD properties could also account for some features of the encoding of motor actions by PCs. Interestingly at the MF-GrC connection, pathway-specific STD allowing temporal coding of multimodal sensory inputs has been recently observed (Chabrol et al., 2015). In this study, the delay of the first spike and the frequency of discharge of GrCs encode a specific combination of MF and input frequency. Therefore, for short MF bursts (<10 spikes), GrC burst duration may also reflect MF identity. The nonlinear encoding of GrC burst duration by PCs shown in this study would then transmit MF input diversity to the output stage of the cerebellar cortex. These results were obtained for very high input firing rates as often observed in vivo (Chadderton et al., 2004; Jörntell and Ekerot, 2006; Arenz et al., 2008) for which the effect of STD is very strong. But we show that the results are qualitatively similar even when stimulation frequency is reduced down to 50 Hz (Fig. 7), a frequency observed in other cerebellar regions coding for more continuous sensorimotor stimuli (e.g., in the vestibular system). As expected, a progressive increase in the stimulation frequency from 50 to 200 Hz increases the incidence of shift behavior and variability in the spike pattern of PCs. Typically, STD is observed for frequencies >20 Hz (Valera et al., 2012), so we hypothesize that the behavior of the GrC-MLI-PC system will be akin to the static synapse case when stimulation frequency is <20 Hz.

The combination of presynaptic and postsynaptic plasticity might expand the dynamic range of the PCs by including a nonlinear dimension that would increase the number of features encoded by the cerebellar cortex. Consistent with this, in a recent study, in which PCs were recorded in vivo during locomotion (Sauerbrei et al., 2015), not only step-locked PC firing rates were observed, but also a correlation between the variability of the firing rate around the step-locked discharge and features of the behavior have been established. Concretely, the trial-by-trial jitter in the PC discharge during the step cycle carried information related to speed, roll, and tilt, and the precise pattern of discharge was found behaviorally relevant. These properties require fast modulation of PC discharge embedded in an averaged firing rate. Therefore, the combination of E/I balance and STD leading to a large diversity of PC discharges observed in our dataset might underlie this precise control of movements. In conclusion, both the experimental data and computational model described in this study suggest that the interplay between E/I balance and STD allows PCs to multiplex rate- and timing-based coding strategy.