Schaffer Collateral Inputs to CA1 Excitatory and Inhibitory Neurons Follow Different Connectivity Rules

Abstract

Neural circuits, governed by a complex interplay between excitatory and inhibitory neurons, are the substrate for information processing, and the organization of synaptic connectivity in neural network is an important determinant of circuit function. Here, we analyzed the fine structure of connectivity in hippocampal CA1 excitatory and inhibitory neurons innervated by Schaffer collaterals (SCs) using mGRASP in male mice. Our previous study revealed spatially structured synaptic connectivity between CA3 and CA1 pyramidal cells (PCs). Surprisingly, parvalbumin-positive interneurons (PVs) showed a significantly more random pattern spatial structure. Notably, application of Peters' rule for synapse prediction by random overlap between axons and dendrites enhanced structured connectivity in PCs, but, by contrast, made the connectivity pattern in PVs more random. In addition, PCs in a deep sublayer of striatum pyramidale appeared more highly structured than PCs in superficial layers, and little or no sublayer specificity was found in PVs. Our results show that CA1 excitatory PCs and inhibitory PVs innervated by the same SC inputs follow different connectivity rules. The different organizations of fine scale structured connectivity in hippocampal excitatory and inhibitory neurons provide important insights into the development and functions of neural networks.

SIGNIFICANCE STATEMENT Understanding how neural circuits generate behavior is one of the central goals of neuroscience. An important component of this endeavor is the mapping of fine-scale connection patterns that underlie, and help us infer, signal processing in the brain. Here, using our recently developed synapse detection technology (mGRASP and neuTube), we provide detailed profiles of synaptic connectivity in excitatory (CA1 pyramidal) and inhibitory (CA1 parvalbumin-positive) neurons innervated by the same presynaptic inputs (CA3 Schaffer collaterals). Our results reveal that these two types of CA1 neurons follow different connectivity patterns. Our new evidence for differently structured connectivity at a fine scale in hippocampal excitatory and inhibitory neurons provides a better understanding of hippocampal networks and will guide theoretical and experimental studies.

Introduction

Neuronal circuits exhibit multiple types of precise patterns of connectivity between specialized groups of neurons (Hofer et al., 2011; DeBello et al., 2014; Druckmann et al., 2014; Rieubland et al., 2014; Harris and Shepherd, 2015; Jiang et al., 2015; Kasthuri et al., 2015; Straub et al., 2016). Synaptic connectivity is a central element in shaping neural dynamics and the computational functions it supports. Therefore, it is imperative to map the organization of synaptic connections and the principles underlying this organization. Indeed, much progress has been made toward unveiling the organization of complex neural networks in increasing detail: different cell types, afferent and efferent projections, synaptic connections, and more have recently been assessed with new technologies (Druckmann et al., 2014; Oh et al., 2014; Zingg et al., 2014; Kasthuri et al., 2015; Bloss et al., 2016; Cadwell et al., 2016; Wallace et al., 2017). It is important to obtain quantitative descriptions of connectivity motifs and network architectures, particularly those of excitatory and inhibitory neurons innervated by the same type of cell. However, such descriptions remain elusive.

Recent studies of synaptic connectivity have focused on the spatial distribution of afferent inputs (structured vs random; Druckmann et al., 2014; J. S. Kim et al., 2014; Kasthuri et al., 2015; Bloss et al., 2016) and have attempted to elucidate basic principles of connectivity, for instance, with reference to Peters' rule. Peters' rule, a method proposed to predict synaptic connectivity on the basis of geometric overlaps between axon and dendrite, has been interpreted to provide support for random synaptic connectivity (Peters and Feldman, 1976; Braitenberg and Schüz, 1998). This idea has been extrapolated to a general principle of brain organization and has been used extensively in models of theoretical networks and theories about random connectivity at the cellular and subcellular levels (Markram, 2006). However, when recent studies have directly tested Peters' rule with advanced technologies, conclusions have been divided between confirming and refuting the concept; therefore, the debates continue (Rees et al., 2017). Previous studies, including our own, of postsynaptic dendrites and dendritic subdomains of different neuron types show structured synaptic connectivity at the cellular and branch levels in a way that is not consistent with Peters' rule (Mishchenko et al., 2010; Druckmann et al., 2014; Rieubland et al., 2014; Kasthuri et al., 2015). Additionally, recent studies with advanced technologies demonstrate that traditionally defined cell types need to be refined by additional criteria, such as topological location along principal axes, long-distance projection targets, and comprehensive transcriptomes, and that these newly defined subpopulations exhibit structural and functional differentiations, suggesting subtype-specific connectivity (S.-H. Lee et al., 2014; Valero et al., 2015; Danielson et al., 2016; Geiller et al., 2017). Despite the need for a precise description of subpopulation-specific connectivity, such information is not yet available at fine spatial scales.

Here, we contribute to this description with a comprehensive, fine-scale mapping of the spatial synaptic profiles of the main excitatory synaptic Schaffer collateral (SC) inputs onto dorsal hippocampal CA1 inhibitory neurons, parvalbumin-positive interneurons (PVs), as major target interneurons of SC inputs. To achieve this goal, we used mammalian GFP reconstitution across synaptic partners (mGRASP), as previously described (Feng et al., 2012; J. Kim et al., 2012; Druckmann et al., 2014). We found a broad range of spatial structure of synaptic connections onto PVs, from structured to random, with significantly and substantially more PVs showing nearly random connectivity than pyramidal cells (PCs). Interestingly, the selectivity of synaptic connections onto PVs seems to be consistent with Peters' rule, opposite to that onto PCs. We next examined the sublayer specificity of the spatial structure of synaptic connections of PVs and PCs and observed that deep PCs show more structured connectivity than superficial PCs. However, little or no sublayer specificity in PVs was apparent. These results demonstrate that the connectivity profiles of CA1 excitatory PCs and inhibitory PVs innervated by the same SC inputs are fundamentally different.

Materials and Methods

Animals.

The PV-Cre mouse line (B6;129P2-Pvalbtm1(cre)Arbr/J) was purchased from the The Jackson Laboratory and was backcrossed with C57BL/6J (The Jackson Laboratory) for >10 generations before use. All experiments were conducted in accordance with protocols approved by the Institutional Animal Care and Use Committee at the Korea Institute of Science and Technology (approval number 2016-076) and the National Institutes of Health guidelines for animal care and use.

mGRASP labeling and detection.

Recombinant adeno-associated viruses (rAAVs) expressing mGRASP components were produced with serotype 1 for the presynaptic mGRASP component (pre-mGRASP) and serotype 7 for the postsynaptic mGRASP component (post-mGRASP) in PVs as described previously (Feng et al., 2014). Post-mGRASP was transduced specifically in PV-positive neurons using the PV-Cre mice line.

For contralateral PV neuron (contraPV) labeling, as previously described (J. Kim et al., 2012; Druckmann et al., 2014), Cre-independent pre-mGRASP (Pre, Addgene 34910, paavCAG-pre-mGRASP-mCerulean) and Cre-dependent “switch on” post-mGRASP (JxON-post, Addgene 34913, paavCAG-Jx-rev-post-mGRASP-2A-dTomato) were injected into the left CA3 and right CA1, respectively, in PV-Cre mice (P60–P80). For ipsilateral PV neuron (ipsiPV) labeling, to avoid double injection in a single neuron, we injected Cre-dependent “switch off” pre-mGRASP (JxOFF-pre, Addgene 51900) and JxON-post into the right CA3 and CA1, respectively, in male PV-Cre mice. The stereotaxic coordinates of CA1 were anteroposterior (AP) −2.0 mm, mediolateral (ML) +1.6 mm relative to bregma, and dorsoventral (DV) 1.05–1.2 relative to the dura, and those of CA3 were AP −2.06 mm, ML ±2.4 and ±2.625 mm, and DV 1.95–2.15 mm for both contraPV and ipsiPV. Brain slices were prepared and imaged with an LSM 780 confocal microscope (Zeiss), as previously described (J. Kim et al., 2012; Druckmann et al., 2014; Feng et al., 2014).

Fluorescent immunostaining and immunoelectron microscopy.

To validate post-mGRASP component expression, we injected PV-Cre mice with JxON-post in CA1. Coronal brain slices (50∼100 μm) were prepared and stained, as previously described (Druckmann et al., 2014). The following antibodies were used: rabbit anti-GFP (Invitrogen, 1:1000; RRID:AB_221569); rabbit anti-DsRed (Clontech, 1:2000; RRID:AB_10013483); mouse anti-PV (swant Biotechnologies, 1:2000; RRID:AB_10000343); and AlexaFluor 488-, 555-, and 633-conjugated secondary antibodies (Invitrogen, 1:300∼500; RRID:AB_2534069, RRID:AB_141822, RRID:AB_141431, respectively). The post-mGRASP distribution was analyzed by calculating the correlation between the number of branch voxels and the number of post-mGRASP-positive voxels, as in our previous study (Druckmann et al., 2014).

For electron microscopic immunohistochemistry, animals were deeply anesthetized with sodium pentobarbital (80 mg/kg, i.p.) and perfused transcardially with heparinized normal saline (10 ml) followed by a freshly prepared mixture (50 ml) of 4% paraformaldehyde and 0.05% glutaraldehyde in 0.1 m phosphate buffer (PB), pH 7.4. The hippocampus was removed and postfixed in the same fixative for 2 h at 4°C. Sagittal sections were cut on a vibratome at 60 μm and were frozen on dry ice for 20 min and thawed in PBS (0.01 m, pH 7.2) to enhance penetration after cryoprotection in 30% sucrose in PB overnight at 4°C. They were pretreated with 1% sodium borohydride for 30 min to quench glutaraldehyde and then blocked with 3% H₂O₂ for 10 min to suppress endogenous peroxidases and with 10% normal donkey serum (Jackson ImmunoResearch; RRID:AB_2337254) for 30 min to mask secondary antibody binding sites. The sections were incubated overnight in rabbit anti-GFP (1:1000; A11122, Invitrogen, RRID:AB_221569) antibody, rinsed in PBS for 15 min, and incubated with an ultrasmall gold-conjugated donkey anti-rabbit (1:50; Electron Microscopy Sciences; RRID:AB_2629850) antibody for 2 h. The sections were postfixed with 1% glutaraldehyde in PB for 10 min, rinsed in PB several times, incubated for 4 min in HQ silver enhancement solution (Nanoprobes), and rinsed in 0.1 m sodium acetate and PB. Sections were further rinsed in PB, osmicated (in 0.5% osmium tetroxide in PB) for 1 h, dehydrated in a graded ethanol series, flat embedded in Durcupan ACM (Sigma) between strips of Aclar plastic film and cured for 48 h at 60°C. Chips containing prominent staining for GFP in the hippocampus were cut out of the wafers and glued onto blank resin blocks with cyanoacrylate. The 60-μm-thick sections were further cut with a diamond knife, collected on Formvar-coated single-slot nickel grids, and stained with uranyl acetate and lead citrate. Grids were examined on a Hitachi H 7500 electron microscope at an accelerating voltage of 80 kV. Images were captured with Digital Montage software driving a cooled CCD camera (SC 1000; Gatan) attached to the microscope, and the resulting data were saved as TIFF files.

Neuron reconstruction and synapse detection.

Images were obtained using the Zeiss Plan Apochromat 40× oil objective with a 1.3 numerical aperture, 559–639 nm emission wavelength, and a 1.3 Airy unit pinhole; neuronal morphologies were reconstructed with neuTube software (Feng et al., 2015) and saved in SWC format, in which each dendritic branch was represented as a series of small, connected tubes with estimated radii. On the basis of these settings and the calculated point-spread-function of our images in the x–y place, the maximum possible error in our diameter estimation is 0.12 μm (∼1 pixel), which is reasonably small considering the range of dendritic diameters (0.3∼2.7 μm) reported in a previous EM study (Gulyás et al., 1999). We confirmed that our measurements of the diameters of PV dendrites (range: 0.45∼3.4 μm, depending on proximal/distal subclasses of dendrites) matched well the range defined by the previous EM study. The surface area of each dendritic branch was estimated by adding the surface areas of its constituent tubes. Synaptic contacts were detected using the mGRASP detection package (Feng et al., 2012, 2014). We manually proofread all reconstructed neurons and all detected synapses for accuracy.

Layer segmentation and soma location.

To identify hippocampal strata, we binarized the blue channel of pre-mGRASP signals with a manually selected threshold to isolate the foreground that contained stratum oriens (SO) and stratum radiatum (SR), followed by additional image processing, i.e., a morphological opening operation on the binary image with a disk of manually determined size to separate SO and SR in case they were not separated by the thresholding step. Then, we extracted the masks of SO and SR from the binary image and collected the voxels on their top and bottom borders, corresponding to the boundary voxels between strata (e.g., voxels on the bottom border of the SO mask were the boundary voxels between SO and SP). For each boundary, we used the least absolute residual method from MATLAB to fit its boundary voxels to a set of algebraic surfaces up to order 9. The surfaces that best matched the boundaries between strata were manually selected to segment the image into alveus (alv), SO, SR, stratum pyramidale (SP), and stratum lacunosum-moleculare (SLM). For sublayer-specific pattern analyses, SP was further equally divided into deep (close to SO) and superficial (close to SR) sublayers. For PVs, given their characteristic soma positions near but not actually in SP, the borders of the deep and superficial sublayers were expanded by 15 μm. To determine the locations of somata in layers, we drew a line perpendicular to the boundary between the segmented deep and superficial sublayers passing through the soma center, and we calculated the soma's relative offset as the ratio of the distance between the nearest dorsal boundary and the soma center (L1) to the distance between the two nearest segmented (dorsal-ventral) boundaries (L2). We subclassified neurons for subpopulation analysis on the basis of their soma locations and excluded neurons whose soma centers were on the borders of layers (within 2 μm) for all sublayer-specific analyses.

Laminar correction.

neuTube-based reconstructed neurons, composed of nodes along the dendritic structure, were overlaid on the segmented layers, and their nodes in alv, SP, and SLM with few or no presynaptic CA3 inputs were subtracted, a process we term laminar correction. For branch-level analysis, branches broken by laminar correction were reconstructed by joining their remaining dendritic parts. For PCs, as previously, we excluded the main trunks.

Branch-level connectivity analysis.

After laminar correction, we calculated the average synaptic density for each neuron by dividing the total number of synapses by the total surface area of the dendritic branches. In the control model, the number of synapses is assumed to be proportional to the postsynaptic dendritic surface area. The expected number of synapses for a branch can be calculated as the product of its surface area and the average synaptic density of the neuron of origin. In our previous study (Druckmann et al., 2014), we used three statistical analyses to determine the structure of branch-level connectivity: the fraction of nonrandom branches (fraction of branches that have significantly higher or lower numbers of synapses than expected); maximum z-score (maximal difference between observed and expected number of synapses normalized to the SD); and the R² value of linear regression between number of synapses and branch surface area, which measures a neuron's degree of deviation from the control model. In this study, we mostly focused on the R² value-based analysis, which, compared with previously applied methods to measure branch-level structure of synaptic connectivity, is especially robust against changes in the numbers of synapses and dendritic branches (see Fig. 4B). Given the fidelity of R², we divided neurons into three types of structure of branch-level connectivity based on their R² values, i.e., highly structured (R² ranging from 0 to 0.33), moderately structured (R² ranging from 0.33 to 0.66), and nearly random (R² ranging from 0.66 to 1).

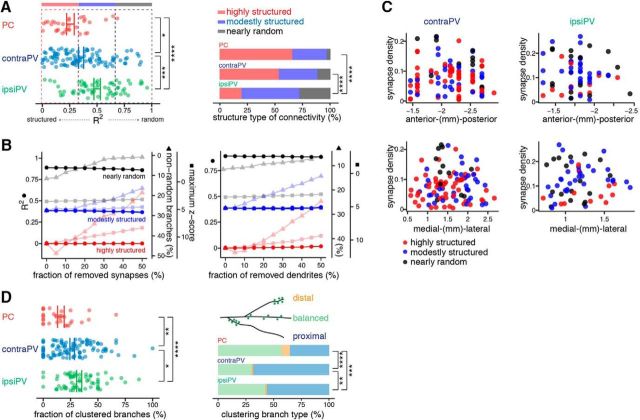
Figure 4.

Comparison of synapse distribution patterns between PVs and PCs at the dendritic branch and intra-branch levels. A, Structured versus random synaptic connectivity at the branch level in PVs and PCs. A summary of the extent of correlation between the measured and expected distributions of synapse numbers across branches (R²) indicates differential ranges of branch-level synaptic connectivity of PCs and PVs. Each dot represents an individual neuron, and lines indicate the mean ± SEM of each cell group. *p < 0.05, ***p < 0.001, ****p < 0.0001, permutation test (left). Bar plots show the percentages of highly structured, moderately structured, and nearly random neurons, defined by R² value. ****p < 0.0001, Fisher's exact test (right). B, Robustness of R² against changes in the number of synapse (left) and dendrites (right) of the representative neurons for highly structured, moderately structured, and nearly random connectivity patterns, shown in Figure 3E. The lack of substantial change in R² with random removal of synapses and dendrites demonstrates the fidelity of R²-based branch level analysis compared with that of other methods of evaluating branch-level structure, such as fraction of nonrandom dendrites (triangle marker) and maximum z-score (square marker). Because of their extremely small size, the error bars (SEM) are hardly visible. C, No clear relationship between degree of branch-level synaptic structure and topographic location in PVs. Neurons were classified as highly structured, moderately structured, or nearly random according to R² value and are shown in scatter plots of their synapse density and spatial location. D, A summary of the fractions of clustered branches for the three cell groups shows higher average degrees of clustering on PVs than on PCs. Each dot represents an individual neuron, and lines indicate the mean ± SEM of each cell group. *p < 0.05, **p < 0.01, ****p < 0.0001, permutation test (left). Stacked bar plots show the percentage of branches in each of the three clustering branch types (balanced, distal, and proximal clustering branches) for the three cell groups. **p < 0.01, ***p < 0.001, ****p < 0.0001, Fisher's exact test (right).

Clustering analysis.

For intra-branch-level analysis, we examined the distributions of synapse locations rather than intersynaptic distances as previously performed (Druckmann et al., 2014). Given the hypothesis that the occurrences of synapses on a branch follow a random Poisson process, the relative locations of synapses given by the fractional surface area distance along the entire dendritic branch (0–1) should follow a uniform distribution. For each synapse, we calculated the relative location on the branch by dividing the surface area between the start of the branch and the synapse location by the surface area of the whole branch. This yielded a collection of relative synapse locations for each branch, which should follow a uniform distribution in the interval (0,1) if the null hypothesis is true. We compared this collection for each branch with the uniform distribution using the Anderson–Darling test (Anderson and Darling, 1954). Having corrected for multiple comparisons, we collected all branches that significantly deviated from this distribution and calculated the fraction of significantly clustered branches for each neuron. To further analyze the clustering pattern of each cell group, we divided clustered branches into three types: those with a significantly greater number of synapses on the proximal half (proximal), those with a significantly greater number of synapses on the distal half (distal), and those showing equal probabilities on both halves (balanced). Then, a frequency distribution of clustering types was calculated for each cell group.

Peters' rule analysis.

To test Peters' rule, which has been proposed to describe synapse density in proportion to the postsynaptic dendritic surface area and nearby presynaptic axonal density, we determined the presynaptic axonal density by measuring the average intensity of blue signals of pre-mGRASP proximal to dendrites (within the dendritic radius plus ∼2.5 μm for PCs and ∼1.0 μm for aspiny PVs). Measuring axonal density and the number of synapses within 3∼4 extended radial shells from the dendritic radius, we found no qualitative differences in outcome. Given prior EM-based anatomical knowledge that the size of SC axons innervating CA1 is consistent (0.2 ± 0.06 μm) with very small variation compared with variations in the dendrite diameter (ranging from 0.3 to 2.7 μm) of CA1 PCs and PVs depending on subclasses of dendrites (such as distal and proximal dendrites) of each laminar stratum (Gulyás et al., 1999; Megías et al., 2001; Mishchenko et al., 2010), we focused on the dendritic surface area for our analyses. We performed the same connectivity analyses accounting for Peters' rule, as previously described (Druckmann et al., 2014).

Statistics.

All statistical tests are described in the main text or corresponding figure legends. For all statistical tests, mice and their brain sections containing traceable neurons and detectable mGRASP signals with infection and image quality, as defined by Feng et al. (2014), were randomly assigned to experimental groups. The modified signed log-likelihood ratio test (MSLRT) for equality of coefficients of variation (CVs; Krishnamoorthy and M. Lee, 2014) was used to compare the CVs of synaptic density between cell groups. The exact binomial test was used to determine whether the observed synapse numbers of neighboring neurons deviated significantly from the values expected under the assumption of equal synapse density. Normality was tested by the Shapiro–Wilk test at a significance level of 0.05. To compare the means between groups, we used Welch's t tests if all groups were normally distributed; otherwise, we used the permutation test with 100,000 permutations. Similarly, to compare means between related groups (e.g., between the dendritic-surface-only random model and Peters' rule), we used paired t tests if the differences between pairs were normally distributed; otherwise, we used the paired permutation test with 100,000 permutations. The Conover–Iman test (Conover and Iman, 1978) was used to compare the scale differences between groups. Fisher's exact test was used to compare the frequency distributions of structure types and clustering types between groups. Correlation between axonal and synaptic density was tested by Pearson's correlation test. The Benjamini–Hochberg procedure (Benjamini and Hochberg, 1995) was used to correct for multiple comparisons. All data analyses were performed with custom scripts written in MATLAB (RRID:SCR_001622) and R (RRID:SCR_001905).

Results

Moderate cellular-level variability in synaptic connectivity of SCs on CA1 PVs

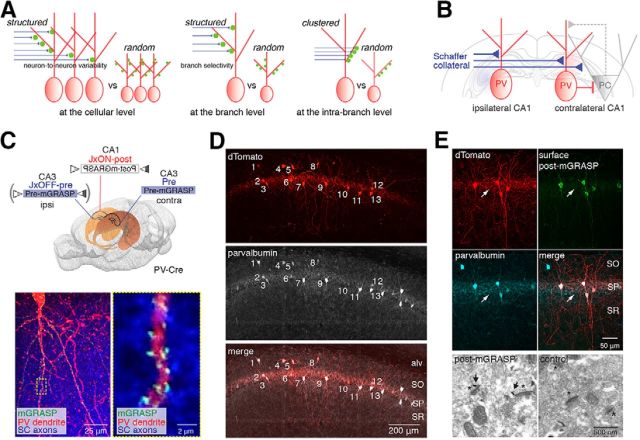
Our previous finding that synaptic connectivity of PCs in CA1 is not randomly but selectively organized (Druckmann et al., 2014) led to the question of whether hippocampal interneurons are selectively or randomly innervated by the same SC inputs at the level of individual dendritic branches, at specific subbranch sites, and at the cellular level (Fig. 1A). To examine synaptic connections between a broad presynaptic population of CA3 excitatory neurons and individual postsynaptic CA1 PVs, we contralaterally introduced an rAAV expressing pre-mGRASP into CA3 and another expressing Cre-switchable post-mGRASP into CA1 of the PV-Cre mouse line, as in our previous study (Fig. 1B,C). To further examine connections from ipsilateral inputs, we injected Cre-dependent OFF/ON switchable pre- and post-mGRASP rAAV into CA3 and CA1, respectively, of the same hemisphere. Synapses detected by mGRASP were evident throughout the dendrites of PV neurons (Figure 1C and Movie 1.) Except, as expected, for the dendrites in the alv, SP, and SLM, all of which lack SC inputs. To verify that the post-mGRASP component was correctly expressed in the postsynaptic compartments of PVs, we used immunofluorescence staining and immunogold EM labeling with a GFP antibody recognizing the split GFP 1–10 of post-mGRASP. We found that most of the post-mGRASP-labeled cells were PVs (Fig. 1D), and its expression in the PVs was tightly restricted to postsynaptic compartments, whereas no axonal expression was detected in SP of CA1 (Fig. 1E), consistent with results previously obtained in CA1 PCs.

Figure 1.

Structured synaptic connectivity patterns and expression of post-mGRASP in PVs. A, Structured versus random synaptic connectivity patterns at the cellular and (inter-)branch levels. B, Schematic illustration of circuits in hippocampal CA1 excitatory PCs and inhibitory PVs innervated by SCs. C, Strategy to label synapses on CA1 PVs innervated by SC inputs with mGRASP and example fluorescent image showing green reconstituted mGRASP signals at sites where dense CA3 blue axons expressing mCerulean-conjugated pre-mGRASP intersect with CA1 PV red dendrites coexpressing post-mGRASP and dTomato (left). The high-magnification image indicated by the dashed box (left) shows the discrete puncta of reconstituted mGRASP signals (right). D, All post-mGRASP-labeled cells coexpressing dTomato, marked by numbers, are PV+ neurons, as verified by fluorescence immunostaining with an antibody against parvalbumin. Approximately 97% of post-mGRASP-labeled cells were PV+ (n = 65 PVs). E, Top, Postsynaptic distribution of post-mGRASP in PVs was confirmed by fluorescence immunostaining. Surface post-mGRASP (visualized by anti-GFP) was expressed predominantly in postsynaptic compartments, with no detectable expression in axons of PVs in SP (visualized by coexpressed cytosolic dTomato signals; arrow). Most of the post-mGRASP-expressing cells were PV+. Bottom, An EM image shows that post-mGRASP (arrows) was specifically detected in the postsynaptic density of PVs (asterisks) in PV-Cre mice infected with Cre-dependent post-mGRASP AAV; uninfected control PV-Cre mice show no immune signal.

Movie 1.

Download video file ^{(4.5MB, mp4)}

DOI: 10.1523/JNEUROSCI.0155-18.2018.video.1

This extended data movie supports Figure 1. Confocal z-stack images show that discrete puncta of reconstituted mGRASP fluorescence are visible along dTomato-labeled dendrites of CA1 excitatory PCs (left) and inhibitory PVs (right) in locations where blue CA3 axons and red CA1 dendrites intersect.

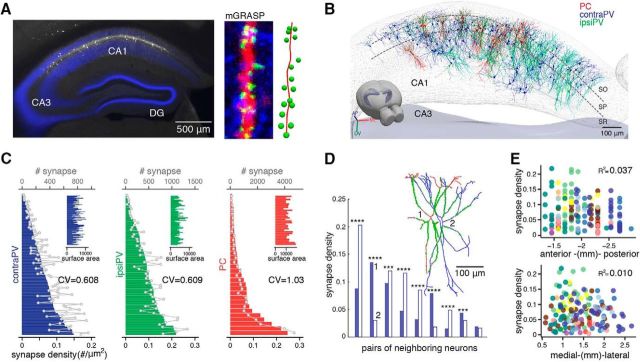
We next determined the morphologies of individual postsynaptic CA1 PVs and their synapses with ipsiPV and contraPV presynaptic CA3 inputs. For this purpose, we used neuTube-assisted tracing and mGRASP image analysis techniques, as previously described (Fig. 2A,B; 103 contraPVs from 10 mice and 61 ipsiPVs from 4 mice). We analyzed the distribution of synapses in contraPV and ipsiPV datasets to test for random versus structured synaptic connectivity, and we compared the results with those we previously obtained for CA1 PCs (n = 32). We found somewhat lower neuron-to-neuron variability in synaptic density]number of synapses per dendritic surface area (#/μm²)[ for contraPV and ipsiPV than for PC (CV of synaptic density: 0.608 in contraPV, 0.609 in ipsiPV, and 1.03 in PC; p_{contraPV-ipsiPV} = 0.93, p_contraPV-PC = 0.015, p_ipsiPV-PC = 0.028, MSLRT for equality of CVs; Fig. 2C). This variability was not due to differences between animals, as even neighboring neurons in the same animal varied considerably in synaptic density (Fig. 2D). In addition, along the anterior–posterior and medial–lateral axes, we found no topological differences in the synaptic density of PV neurons (Wilcoxon rank sum test; Fig. 2E), as opposed to moderate differences for PCs, as previously shown. In summary, we found that the SCs innervate the CA1 PVs non-uniformly, with less variability at the cellular level than in CA1 PCs.

Figure 2.

Moderate cellular-level variability in synaptic connectivity of SCs onto CA1 PVs. A, Left, An example fluorescent image shows CA1 PVs coexpressing post-mGRASP and dTomato (white) along with dense contralateral CA3 projections expressing mCerulean-conjugated pre-mGRASP (blue). Middle, An example PV dendrite showing discrete reconstituted mGRASP signals (green puncta) in sites where dense CA3 axons (blue) intersect with a PV dendrite (red). Right, Reconstruction of this dendrite with annotated synapses. B, All reconstructed neurons (contraPVs, blue; ipsiPVs, cyan; PCs, red) and detected synapses (green dots) registered to the Allen Brain Atlas 3D hippocampus mesh. C, The sorted bar plot shows variations in synapse density per neuron across the population [contraPV: 0.062 ± 0.038 (mean ± SD) synapse/μm², range 0.0034–0.15; ipsiPV: 0.092 ± 0.056 synapse/μm², range 0.0075–0.22]. Overlaid gray lines indicate numbers of synapses (contraPV: 357 ± 244 per neuron, range 24∼959; ipsiPV: 451 ± 312, range 29∼1333), and insets show the surface area of each neuron (contraPV: 5768 ± 1895 μm², range 2526∼10,354; ipsiPV: 4843 ± 1539 μm², range 1775∼9191). The degree of neuron-to-neuron variability in synaptic density, measured by CV of PVs is significantly lower than that of PCs (MSLRT_{contraPV-ipsiPV} = 0.0069, p_{contraPV-ipsiPV} = 0.93, MSLRT_contraPV-PC = 5.97, p_contraPV-PC = 0.015, MSLRT_ipsiPV-PC = 4.86, p_ipsiPV-PC = 0.028, MSLRT for equality of CVs). The cellular-level PC data are from a previous study (Druckmann et al., 2014). D, A comparison of synapse density of nearest-neighbor pairs in a single contraPV animal shows variable synaptic density. ***p < 0.001, ****p < 0.0001, exact binomial test. Inset, An example pair of reconstructed PVs marked 1 and 2, along with their synapses (green dots). E, A scatter plot of synapse density versus spatial location of PVs shows no topological pattern along the AP or the ML axis. Dots in different colors indicate individual PVs from different animals (binned from 100-μm-thick sections of contraPVs and ipsiPVs).

Synapse distribution patterns of PVs at the branch level

Next, we examined the spatial structure of synaptic connections among the different dendrites within single PVs. We had previously performed this type of analysis at the branch level in CA1 PCs. However, it became clear that we would need to adjust our previous approach in PVs, given the heterogeneity of their soma locations and the extended reach of PV branches through hippocampal strata. These extended branches in the alv and SP included abundant dendritic surface area in regions where no SC fibers exist, making it challenging to analyze the spatial structure at the branch level (Fig. 3A–D). Somata of labeled PVs expressing post-mGRASP were detected mainly in pyramidal basket cells in SP (n = 135, ∼82%) and less frequently in the SO (n = 22), and SR (n = 7; Fig. 3B).

Figure 3.

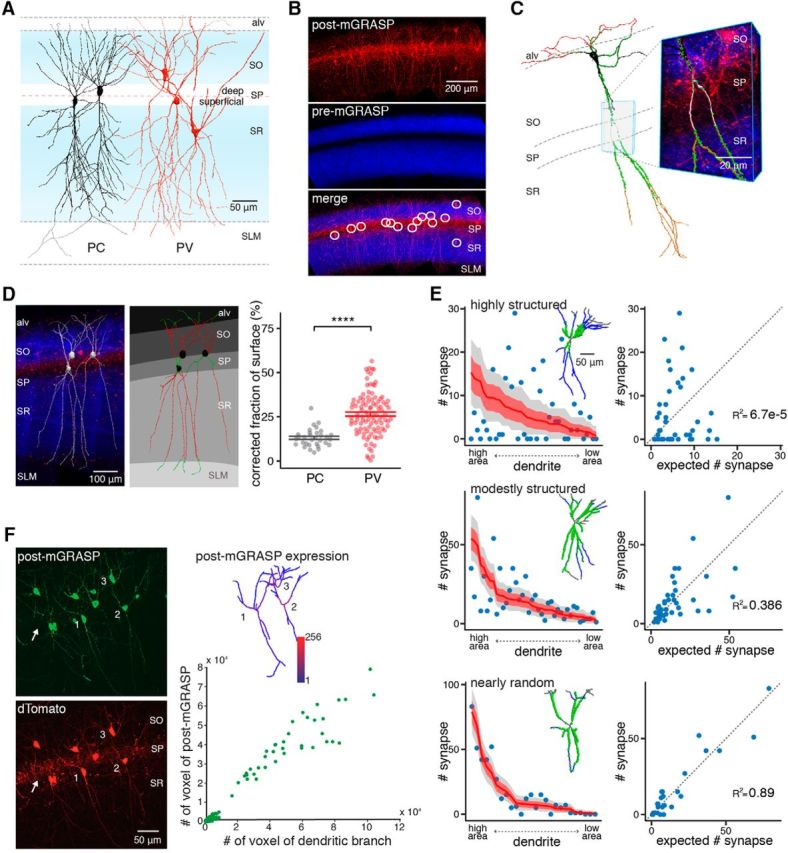
Laminar correction and the synapse distribution patterns of PVs at the dendritic branch level. A, Representative PCs and PVs with schematic broad CA3 inputs (blue) showing their soma locations and extended dendrites throughout hippocampal CA1 strata. B, The majority of post-mGRASP-expressing PVs (red) innervated by dense pre-mGRASP-expressing CA3 axons of neurons (blue) are detected in SP. C, Example reconstructed PV with detected synapses (green puncta) and zoomed-in view with overlaid fluorescent image (PV dendrites, red; CA3 axons, blue; mGRASP, green), requiring laminar correction because of the contact-free spaces along continuous dendrites. D, Laminar correction was performed on the basis of blue SC axonal signal on red PVs from fluorescent images (left). Layers are segmented, and branch portions in alv, SP, and SLM (shown in green) are determined for targets of laminar correction. The red portions of dendrites were used for further analyses (middle). A summary of the fraction of subtracted surface (FoS) by laminar correction shows significantly higher FoS in PVs than in PCs. Each dot represents an individual neuron, and lines indicate the mean ± SEM of each cell group. ****p < 0.0001, Welch's t test (right). E, Example PVs exhibiting highly structured, moderately structured, and nearly random synaptic distribution of PVs at the branch level. Left, Scatter plots show the number of synapses on each dendritic branch sorted by surface area, whereas overlaid red lines indicate the number of synapses expected from a random null model; light red regions and gray regions indicate ±1 SD and the 95% confidence interval of the expected number of synapses, respectively. Inset, Corresponding reconstructed PVs with detected synapses (green). Right, Scatter plots show the relationship between number of synapses expected in the random null model and actual number of synapses. Branch-level connectivity patterns of individual PVs are shown in Extended Table 3-1. F, The small degree of variation in the expression of post-mGRASP along PVs branch by branch was confirmed by immunostaining with anti-GFP (left) and the relationship between the numbers of branch voxels and the numbers of post-mGRASP voxels (branches from 11 cells of 2 mice, Spearman's ρ = 0.84, p = 3.4 × 10⁻⁴⁸; right). Inset, A color map of the intensity of post-mGRASP in the three reconstructed PVs. Additionally, the lack of detectable expression in axons of PVs in SP visualized by coexpressed cytosolic dTomato signals (arrow) supports predominantly postsynaptic expression.

Table 3-1

Branch-level Connectivity Patterns of Individual PVs. Download Table 3-1, XLSX file ^{(5.6MB, xlsx)}

A considerable fraction of the dendritic surface area of these post-mGRASP-expressing PVs was located in alv, SP, and SLM, in which little or no synaptic contacts from SC inputs were detected. This caused the formation of contact-free spaces along continuous dendrites (Fig. 3C), which our analysis could misinterpret as evidence for structured connectivity at the branch level. Therefore, to analyze branch-level connectivity more accurately, we first delineated hippocampal strata on the basis of SC inputs measured by presynaptic blue fluorescence signals, and we then subtracted the branch portions in alv, SP, and SLM from the three data groups (ipsiPVs, contraPVs, and PCs), a process we term laminar correction (Fig. 3D; see Materials and Methods). On the basis of these strata, we mapped each PC and PV neuron to allow further sublayer-specific branch-level analysis of synaptic connectivity (see Figs. 5 and 7).

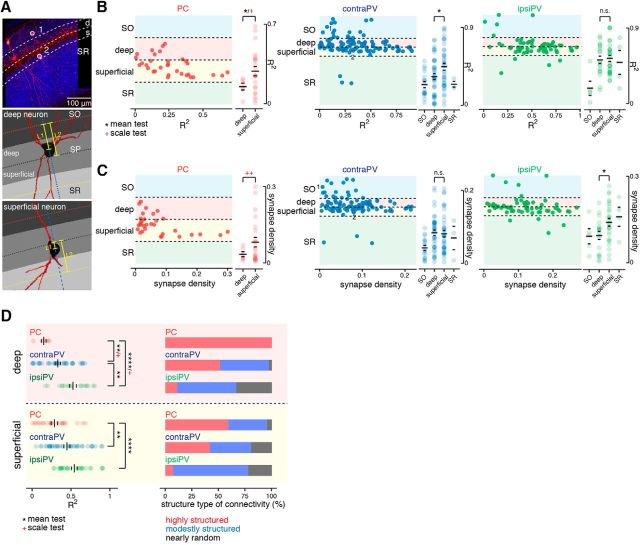
Figure 5.

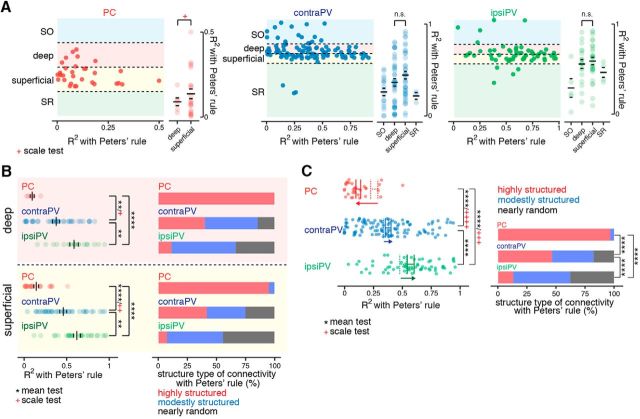
Sublayer-specific patterns of synaptic connectivity at the branch level. A, Top, An example fluorescent image of mGRASP-expressing PVs (red) and SC axonal inputs (blue) shows two different subgroups of PVs defined by somata in different hippocampal strata, in this case SO and superficial sublayer of SP, marked 1 and 2, respectively. Bottom, Deep and superficial neurons are distinguished by the ratio of L1 to L2, which measures the relative offset of the soma once layers are segmented on the basis of axonal signals (Fig. 3D). The blue dashed line is drawn to pass through the center of the soma, perpendicular to the boundary between the deep and superficial sublayers. L1 is the distance between the nearest dorsal boundary from the soma and the center of the soma along the blue dashed line, and L2 is the distance between the two nearest boundaries along the blue dashed line. B, Scatter plots (left) show the branch-level structure of connectivity (R² value) of each neuron located in the hippocampal strata. Each dot represents an individual neuron. Soma location was determined by relative offset as described in A and in Materials and Methods. A summary of R² values of individual neurons subclassified by layer and sublayer populations (right). Significant differences in the means and/or scales of R² values between deep and superficial subpopulations were observed in PCs and contraPVs but not in ipsiPVs. *p < 0.05, Welch's t test for mean; red +p < 0.05, Conover–Iman scale test for scale; n.s., not significant (right). C, Scatter plots of the synaptic density of each neuron in the hippocampal strata. Significant differences in means or scales of synaptic density between deep and superficial subpopulations were observed in PCs and ipsiPVs but not in contraPVs. *p < 0.05, permutation test for mean; red ++p < 0.01, Conover–Iman scale test for scale; n.s., not significant. D, For subpopulations of PCs and PVs in deep and superficial sublayers, a summary of degrees of correlation (R²) between the measured and expected distribution of synapse numbers across branches. **p < 0.01, ****p < 0.0001, Welch's t test for mean; red +p < 0.05, Conover–Iman scale test for scale) and stacked bar plots of the percentages of highly structured, moderately structured, and nearly random neurons as defined by their R² values.

Figure 7.

Sublayer-specific patterns of synaptic connectivity at the branch level with Peters' rule. A, Scatter plots (left) show the branch-level structure of connectivity (R² value) given Peters' rule applied to neurons located in different hippocampal strata. Dots represent individual neurons. A summary of R² values of individual neurons subclassified by layer and sublayer populations is also shown (right). Significant differences in R² values with Peters' rule between deep and superficial subpopulations were observed in PCs but not in PVs. Red +p < 0.05, Conover–Iman scale test for scale (right); n.s., not significant. B, For subpopulations of PCs and PVs in deep and superficial sublayers, a summary of R² values with Peters' rule (deep: **p < 0.01, ****p < 0.0001, permutation test for mean; red +p < 0.05, Conover–Iman scale test for scale; superficial: **p < 0.01, ****p < 0.0001, permutation test for mean; red ++p < 0.01, Conover–Iman scale test for scale) and stacked bar plots of the percentages of highly structured, moderately structured, and nearly random neurons as classified by R² value with Peters' rule. C, A Summary of opposite changes in R² with Peters' rule. Dots represent individual neurons, and solid lines indicate mean R² with Peters' rule; overlaid dashed lines indicate the mean R² with the dendritic-surface-only random model. ****p < 0.0001, permutation test; red +++p < 0.001, red ++++p < 0.0001, Conover–Iman scale test (left). Bar plots show the percentages of highly structured, moderately structured, and nearly randomly structured neurons as classified by R² value; the results show that most PCs are highly structured, whereas more PVs are nearly random, compared with the dendritic-surface-only random model shown in Figure 4A. ****p < 0.0001, Fisher's exact test (right).

After laminar correction, we analyzed the variability in the synaptic density of individual branches of a given PV neuron by comparing the measured synapse numbers with those expected by the random null model, i.e., the number of synapses that would be predicted by a Poisson process with a fixed density per unit branch area (Tab. 3-1), as previously described (Druckmann et al., 2014). We differentiated random from structured connectivity by correlating (R²) the number of synapses measured across branches in PV neurons and the number of synapses predicted by the random null model; thus, high correlations reflect random connectivity, and low correlations reflect more structured connectivity. As in our previous study of structured synaptic connectivity at the branch level between CA3-CA1 PCs, we found various degrees of correlation (R²), reflecting connectivity ranging from random to structured (Fig. 3E). We confirmed that the variability in the number of synapses on different dendrites was not driven by viability in dendritic expression of post-mGRASP (Fig. 3F).

Differential branch-level synaptic connectivity patterns between PCs and PVs

We extended our analysis to the population level, comparing the match between synapse numbers from the random null model and from our measurements across the three data groups (ipsiPVs, contraPVs, and PCs). Interestingly, we observed that the range of structure in synaptic connectivity (structured to random) in PVs was substantially broader, with more neurons showing nearly random connections, than that in PCs [ipsiPV: R² range 0.022∼0.958, average (avg)R² = 0.506 ± 0.0286; contraPV: R² range 0.00007∼0.901, avgR² = 0.361 ± 0.0231; and PC: R² range 0.005∼0.686, avgR² = 0.259 ± 0.0309; p_{contraPV-ipsiPV} = 0.00024, p_contraPV-PC = 0.025, p_ipsiPV-PC ≈ 0, permutation test; Fig. 4A]. Furthermore, we divided PVs and PCs into three groups (highly structured, moderately structured, and nearly random) on the basis of R², given the robustness of R² for measuring the branch-level structure of synapse distribution (Fig. 4B; see Materials and Methods), and we found that more PVs than PCs exhibited nearly random connectivity (ipsiPV: 27.9%, contraPV: 11.7%, and PC: 3.13%; Fig. 4A). These results indicate that the degree of branch-level structure of synaptic connectivity onto PVs is broader and more random than onto PCs. No relationship between topographic location and degree of branch-level structure was obvious (Fig. 4C).

We further examined the degree of synapse clustering within a single dendrite for intra-branch-level structure in connectivity between PVs and PCs (Figs. 4D, 1A). Interestingly, we found that PVs exhibit higher average degrees of clustering than PCs (ipsiPV: 33.8%, contraPV: 26.8%, and PC: 15.1% fraction of clustered branches, p_{contraPV-ipsiPV} = 0.027, p_contraPV-PC = 0.0055, p_ipsiPV-PC ≈ 0, permutation test). Further, a previous EM study has shown that synapses on PVs were concentrated in the perisomatic region (Gulyás et al., 1999). Thus, we tested perisomatic synapse distribution in our data, and found that clustering in PVs appears consistent with that observed in the EM study (Fig. 4D). No relationship was found between topographic location and branch-level selectivity with degree of clustering (Spearman's rank correlation test). These results clearly demonstrate differential branch-level synaptic connectivity between CA1 excitatory and inhibitory neurons innervated by the same presynaptic projections, the SCs.

Sublayer-specific patterns of synaptic connectivity innervated by SCs

Even within a particular cell-type population, recent studies have demonstrated layer- and sublayer-specific structural and functional differences as commonly classified by morphology, electrophysiological properties, and/or genetic identity (S.-H. Lee et al., 2014; Valero et al., 2015; Danielson et al., 2016; Geiller et al., 2017). To examine these differences, we subdivided PVs and PCs on the basis of their soma location along commonly described CA1 layers, including SO, SP and SR, as well as deep (soma located close to SO) and superficial (soma located close to SR) sublayers of SP (Fig. 5A; see Materials and Methods). We then focused on sublayer-specific patterns of synaptic connectivity and synaptic density in these deep and superficial subpopulations of PVs and PCs at the branch level (Fig. 5B,C). Most PVs (82.3%) were in SP, and most synapses showed nearly random connectivity appeared to originate from PVs. On the other hand, PVs in SO and SR appeared to follow more structured patterns (Fig. 5B). This trend was comparable between contraPVs and ipsiPVs. Additionally, we observed slightly distinct synaptic connectivity patterns between the deep (d) and superficial (s) sublayers in contraPVs [dR² = 0.33 ± 0.035 (n = 35), range 0.00007∼0.68, and sR² = 0.45 ± 0.039 (n = 36), range 0.048–0.90, p = 0.028, Welch's t test] but not in ipsiPVs [dR² = 0.53 ± 0.044 (n = 18), range 0.17∼0.80, and sR² = 0.54 ± 0.037 (n = 27), range 0.28∼0.91, p = 0.77, Welch's t test].

Notably, in CA1 PCs along the deep-superficial axis (dPCs and sPCs), we observed a significantly wider range of deviation (R²) and synapse density in the sPCs than in the dPCs [R² of dPCs = 0.15 ± 0.03 (n = 6), range 0.014∼0.22, and synaptic density of dPCs = 0.036 ± 0.0097, ranged 0.012∼0.072; R² of sPCs = 0.29 ± 0.041 (n = 22), range 0.0052∼0.69, and synaptic density of sPCs = 0.083 ± 0.019, range 0.0074∼0.30; p = 0.028 (R²), p = 0.0095 (synapse density), Conover–Iman scale test; Fig. 5B,C]. The sublayer-specific connectivity differences between dPCs and sPCs became more obvious when they were divided into three groups (highly structured, moderately structured, and nearly random) as in Figure 4A. All the dPCs were categorized as highly structured, whereas sPCs were spread across the three groups, with 59, 36, and 5%, respectively (Fig. 5D). In summary, the cell-type-specific general patterns of synaptic connectivity (random to structured, mean of R² of ipsiPVs > contraPVs > PCs; Fig. 4A) were consistent in each sublayer, yet, interestingly, dPCs clearly showed more structured synaptic connectivity from SCs at the branch level than sPCs did, whereas PVs showed little or moderate sublayer specificity. The sublayer-specific differences in organization of CA3 afferent connectivity support the idea that distinct functional domains exist along radial axis of the hippocampus.

Opposite effects of Peters' rule on the structure of synaptic connectivity in CA1 PCs and PVs

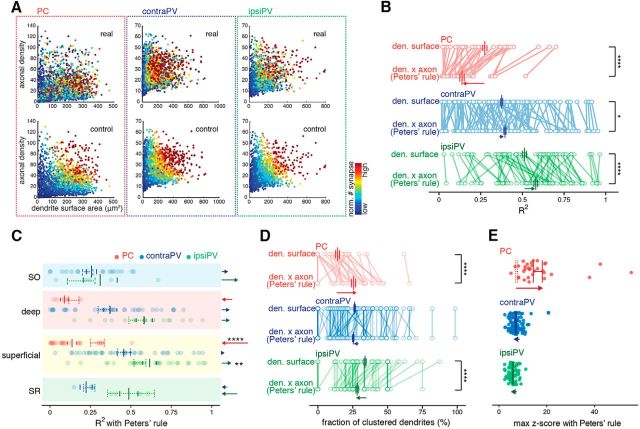
Thus far, we have considered only the amount of dendritic surface area as a predictor for synapse number, setting aside the presynaptic axonal density. We previously demonstrated that axonal density contributed little to explaining the branch-level variability we observed in synaptic connectivity between CA3 and CA1 PCs (Druckmann et al., 2014). We compared Peters' rule predictions with the numbers of synapses observed (Fig. 6A); in PVs, as predicted by Peters' rule, we observed a significant positive linear correlation between axonal and synapse density, whereas in PCs, we observed a strong disagreement with Peters' rule predictions (contraPV: 44 significant of 103, population correlation 0.18, p ≈ 0; ipsiPV: 43 significant of 61, population correlation 0.49, p ≈ 0; PC: 1 significant of 32, population correlation 0.011, p = 0.32, Pearson's correlation test). Interestingly, when comparing the contribution of axonal density to explaining variability in the synaptic structure of PCs and PVs innervated by SCs, we observed the opposite effects (Fig. 6B–E). As in our previous study, including axonal density in our model actually worsened the match between modeled and measured synapse numbers in PCs (54% decrease of average of R² in PCs, p ≈ 0, paired permutation test) but improved the match in PVs (6% increase in contraPVs, p = 0.027; 12% increase in ipsiPVs, p = 0.00007; paired permutation test; Fig. 6B). These cell-type-specific opposite effects of incorporating axonal density appeared in sublayers and layers (Fig. 6C). Consistently, additional analyses of the fraction of clustered branches and the maximal deviation from random Poisson distributions also confirmed that synaptic connectivity follows different rules in PCs and PVs (Fig. 6D,E).

Figure 6.

Results opposite to Peters' rule predictions on the structure of synaptic connectivity in PCs and PVs. A, The population-level relation of Peters' rule prediction to synapse number shows a close-to-control pattern for PVs and a highly structured pattern for PCs. The color plot shows each branch as a dot whose color corresponds to the number of synapses according to the branch surface area and the axonal density for real data (top) and for a control model in which synapse number was generated according to Peters' rule (bottom) as previously shown. The PC data were collected in our previous study (Druckmann et al., 2014) and refined with laminar correction. B, Paired dot plots of the R² value of a dendritic (den)-surface-only random model and a Peters' rule model (dendritic surface × axonal density) show opposite changes in mean R² values between PCs and PVs (a decrease in PCs and an increase in PVs). Dots represent individual neurons, and each line indicates a paired comparison within a neuron across models. *p < 0.05, ****p < 0.0001, paired permutation test. C, Dot plots show changes in R² values with Peters' rule for individual neurons subclassified into layer and sublayer populations: solid line, mean R² with Peters' rule; overlaid dashed lines, mean R² with dendritic-surface-only random model. Dots represent individual neurons. The magnitudes and directions of R² shifts from the dendritic-surface-only random model to Peters' rule in each sublayer and layer for three cell groups are shown as colored arrows. **p < 0.01, ****p < 0.0001, paired permutation test. D, Paired dot plots of the fraction of clustered branches of the dendritic-surface-only random model and Peters' rule show opposite changes in the average degree of clustering between PCs and PVs (an increase in PCs and a decrease in PVs). Each dot represents individual neurons, and each line indicates paired comparisons within a neuron across models. ****p < 0.0001, paired permutation test. E, Summary of opposite changes in the maximum z-score with Peters' rule. Each dot represents an individual neuron, and solid lines indicate the mean ± SEM of the maximum z-score with Peters' rule, whereas dashed lines indicate the mean ± SEM of maximum z-score with the dendritic-surface-only random model.

After assumptions based on Peters' rule were incorporated into our model, sublayer specificity was maintained only between dPCs and sPCs (Fig. 7A,B). On the population level, after Peters' rule was incorporated, most PCs showed highly structured connectivity, as opposed to the nearly random connectivity of the PVs (Fig. 7C). Together, these results demonstrate that the spatial organization of PC connectivity is more structured, whereas that of PVs is more random. These results demonstrate that the synaptic connectivity of CA1 PVs innervated by SCs, which is close to random, seems to be consistent with Peters' rule, whereas that of CA1 PCs shows an elevated degree of selectivity with sublayer specificity, inconsistent with Peters' rule.

Discussion

Neural circuits are the substrate for information processing. Their dynamics are governed by a complex interplay between input activity and the responses of excitatory and inhibitory neurons. Thus, the organization of patterns of synaptic connectivity is an important determinant of the dynamics, and hence, the function of circuits. We mapped the fine structure of connectivity in hippocampal CA1 excitatory and inhibitory neurons innervated by SCs using mGRASP. We found that the connectivity profiles of CA1 excitatory PCs and inhibitory PVs innervated by the same SC inputs are fundamentally different, following different connectivity rules: the synaptic connectivity profile between hippocampal CA3 and CA1 PCs strongly deviated from randomness, contrary to Peters' rule, whereas PVs showed more random connectivity, consistent with Peters' rule. In addition, deep versus superficial sublayer specificity of the structure of connectivity was found only PCs, with little or none in PVs.

The difference between the degree of structure in principal neurons and interneurons is consistent with results from conceptual models of neural processing (Maass, 2000; Douglas and Martin, 2004). In many such models, principal neurons act as sophisticated pattern detectors that are sensitive to specific correlations in their input and relay this information downstream. Such a mode of operation works especially well when the input is structured into specific branches and when nonlinear branch-level processing can amplify or suppress responses (Polsky et al., 2004). It is generally thought that interneurons, by contrast, act more generally to sharpen responses, as in winner-take-all circuit computations in which strongly activated neurons broadly suppress the responses of other neurons, yielding a simpler and more specific population response pattern (Maass, 2000; Douglas and Martin, 2004). To perform such an operation, interneurons do not require any specific spatial input structure. Similar arguments can be made for temporal structures, as when a barrage of input to principal neurons is followed by activation of inhibitory interneurons to sharpen the response in time. Here again, the inhibitory response—and, hence, perhaps the spatial structure of its input—need not be specific. However, in reality, complex networks governed by the interplay of inhibition and excitation are more complicated (S.-H. Lee et al., 2014; Cembrowski et al., 2016).

Further, it is becoming clear that traditional cell-type classification based on morphology, electrophysiological properties, and/or genetic identity is insufficient to encompass all meaningful variations among neurons. Additional criteria are needed, such as topological location along principal axes, long-distance projection targets, and comprehensive transcriptomes (S.-H. Lee et al., 2014; Cembrowski et al., 2016). Using new criteria such as these to subdivide traditionally defined populations of cell types reveals striking structural and functional specializations, apparently organized by cell-subtype-specific connectivity (S.-H. Lee et al., 2014; Valero et al., 2015; Danielson et al., 2016; Geiller et al., 2017). In fact, a recent study clearly demonstrated that hippocampal CA1 PVs can receive highly selective inputs from subpopulations of CA1 PCs, i.e., superficial/deep, at the cellular level (S.-H. Lee et al., 2014; Cembrowski et al., 2016). This might seem to contradict our finding that the connectivity of CA1 PVs innervated by CA3 PCs is more random. A possible straightforward explanation might be that feedforward- and feedback-related inputs follow different connectivity profiles onto CA1 PVs. However, in our view, our results are not necessarily inconsistent with previous studies showing selective excitatory inputs on PVs, as our assertion of more random connectivity patterns on CA1 PVs is at the branch level and relative to CA1 PCs innervated from the same SC inputs. In fact, we found neuron-to-neuron variability in the synaptic connectivity of SCs on CA1 PVs at the cellular level (Figs. 2C, 5C).

In this study, we confirmed that potential experimental and biological variability does not affect our conclusions. First, we compared synaptic densities between neighboring neurons (within ∼100 μm) in the same animal. This analysis still revealed considerable neuron-to-neuron variability (Fig. 2D; and in our previous study Druckmann et al., 2014, Fig. 1E). Further, we compared clustering analyses in the same animal and found no obvious difference in the fraction of clustered branches (0.273 ± 0.032, n = 27, range 0∼0.67 of one PV mouse compared with binned PVs, 0.268 ± 0.020, n = 103, range 0∼1; Fig. 4D). These sets of measurement rule out topographical and animal-to-animal differences as sole sources of cellular level variability. Second, our branch-level analyses were designed specifically to test for random or structured connectivity by measuring variability in synapses from branch to branch “within a single neuron”. Third, we specifically analyzed dendritic expression of post-mGRASP components and found no clear variability in their branch-by-branch expression (Fig. 3F). In addition, we note that, since pre-mGRASP tagged with mCerulean has been shown to be expressed mainly in axons, we performed immunostaining using anti-GFP that recognizes GFP variants like CFPs to visualize broad CA3 expression after mGRASPing. We did not observe any significant variations in the expression of pre-mGRASP component. Therefore, we can rule out the potential concern that experimental and biological variability might affect our conclusions of synaptic connectivity patterns.

We provided a detailed description of PV connectivity at the level of individual dendritic branches, analyzing differences between PVs and PCs. Using a PV-Cre mouse line to determine the molecular identities of the neurons did not allow us to distinguish distinct types of PVs such as basket cells, bistratified cells, and axoaxonic cells, but we were able to confidently divide PVs into groups according to the locations of their somata throughout hippocampal strata (Figs. 5, 7). We also focused mainly on PVs detected in SP (∼83%). To extend this analysis, subclassified connectivity mapping of distinct subpopulations of PVs will need to be further defined with new combinations of molecular labels and other measures of cell properties.

Interestingly, we observed that ipsiPVs and contraPVs exhibit slightly different connectivity patterns, namely, that synaptic connectivity of ipsiPVs from SCs at the branch level is more random (Figs. 4, 7). In general, similar connection patterns in ipsiPVs and contraPVs are expected, but this concept need to be tested. A previous study performed a quantitative input mapping to hippocampal CA1 neurons including PCs and PVs through Cre-dependent rabies virus tracing (Sun et al., 2014) and found that CA1 PVs receive unequal inputs from ipsilateral and contralateral CA3 PCs, suggesting differential patterns of circuit connectivity within the two hemispheres. At this stage, we cannot exclude the possibility that differences between ipsiPVs and contraPVs reflect variations in viral injections to presynaptic inputs in bilateral CA3. Nonetheless, it is true that ipsiPVs and contraPVs share general connectivity rules that are different from those of PCs.

Peters' rule provides an estimate of the number of synapses in a volume of tissue given the proportion of dendritic and axonal neurites that cross within that volume. Several researchers are currently using different approaches to investigate cell-type-specific connections in various brain areas. This work will help resolve ongoing debates about the general principles underlying the spatial profiles of synaptic connectivity and how they shape network function (Jiang et al., 2015; Markram et al., 2015; Bloss et al., 2016; Straub et al., 2016; Swanson and Lichtman, 2016). To test whether connectivity was structured or random, we compared our measured results to those from a model generated by applying the assumptions of Peters' rule to our data. In our previous study, we found that, when PCs alone were considered, adding axonal density to dendritic surface area as a predictor in the model (i.e., Peters' rule) did not improve the prediction of synapse number beyond establishing that low synaptic density was correlated with low axonal density (Druckmann et al., 2014). However, this finding was difficult to interpret, because it was consistent with two very different possibilities. First, it could mean that Peters' rule, or our ability to measure axonal density, is a poor predictor. Second, it could mean that axonal density is a useful predictor, but there is an additional fine level structure that, if not considered, reduces the utility of the predictions. Our finding here that adding axonal density improved the prediction of structure in interneurons (i.e., increased R² values more consistent with the random null model) raises the possibility that prediction failures in principal neurons (i.e., reduced R² values and more structured connectivity, less consistent with the random null model) may indeed be attributable to the existence of additional unknown structure, rather than to poor estimates of axonal density. It is also possible that once additional types of structure, such as the functional properties of neurons, are accounted for, the diverse patterns of synaptic connectivity will become clearer. Thus, Peters' rule may need to be revised rather than set aside.

Here, we presented new evidence for fine-scale differential structure in synaptic connectivity onto hippocampal CA1 excitatory and inhibitory neurons by connections originating from the same projection, the SC inputs. We found a highly selective synaptic connectivity profile (i.e., one that strongly deviates from chance) in connectivity between hippocampal CA3 and CA1 PCs at the cellular and branch levels, as well as the sublayer level. By contrast, for the CA3-PV connection, we found only little to moderate specificity. The multiple types of fine-scale structured connectivity in hippocampal excitatory and inhibitory neurons and their different organization provide important hints as to the organization, development, and function of neural circuits. Together with detailed reciprocal connectivity patterns recently revealed between subpopulations of CA1 PVs and PCs, especially those segregated along the deep and superficial sublayers of the stratum pyramidale (S.-H. Lee et al., 2014), our new evidence for differently structured connectivity at a fine scale in hippocampal excitatory and inhibitory neurons provides a better understanding of hippocampal networks and will guide theoretical and experimental studies.