Feedback and Feedforward Inhibition May Resonate Distinctly in the Ripple Symphony

Hippocampal sharp waves are transient deflections of local field potentials (LFPs) recorded in the stratum radiatum of CA1 during immobility and slow-wave sleep. Ripple oscillations are superimposed on sharp waves, but they emerge from the stratum pyramidale. These sharp-wave ripple complexes are considered a biomarker for episodic memory (Buzsáki, 2015). Data from normal (Sullivan et al., 2011) and epileptic hippocampus (Valero et al., 2017) suggest that the complex spectral structure of ripples cannot be explained by simple mechanisms. Nonetheless, a recent computational study published in The Journal of Neuroscience shed light on a microcircuit mechanism that can explain part of the spectral phenomenology of ripples (Donoso et al., 2018).

Ripples associated with sharp waves were initially identified at the high-frequency band (150–200 Hz), but subsequent data revealed a contribution at the fast gamma band (90–150 Hz) (Sullivan et al., 2011; Buzsaki, 2015). High-frequency ripples and fast gamma ripples were associated with different strengths of CA3 inputs and correlated differently with CA3 and dentate gyrus excitability, suggesting that the involvement of different circuits to generate ripples in fast gamma band or ripple band (Sullivan et al., 2011). In epileptic hippocampus, faster ripples (250–600 Hz) exhibited complex spectral properties, including harmonic oscillations (Ibarz et al., 2010; Valero et al., 2017). Furthermore, in many events, a slowdown of the oscillatory frequency (called intraripple frequency accommodation) suggests additional dynamical processes at play (Nguyen et al., 2009). Whether a single mechanism underlies this complex behavior remains unclear, but there is agreement that interaction between pyramidal cells and interneurons is critical (Aivar et al., 2014; Stark et al., 2014).

To investigate network mechanisms underlying complex ripple patterns, Donoso et al. (2018) implemented a computational model. They randomly activated a set of CA1 parvalbumin basket-cells directly (to simulate a CA3-mediated feedforward inhibition) or indirectly via initial activation of CA1 pyramidal neurons (to simulate locally mediated feedback inhibition). Through a different set of simulations, they aimed to understand how different oscillatory regimens emerge at the population level depending on network topology and dynamics of input activity. This simplified model was able to capture some basic features of sharp-wave ripple dynamics.

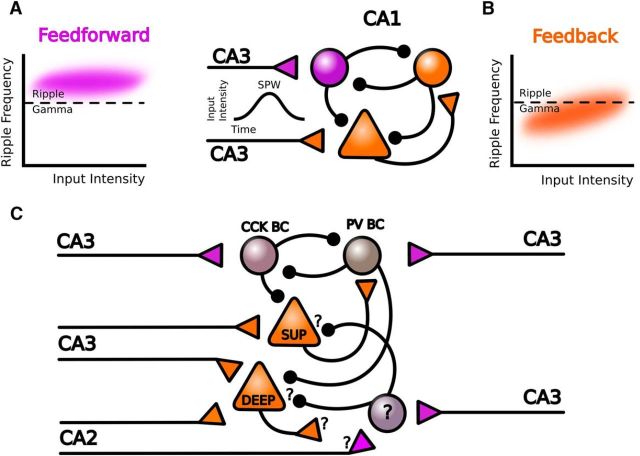
Donoso et al. (2018) simulated the arrival of transient CA3 excitatory inputs with a period in which the input rate increased from the baseline to a maximum (ascending phase), a plateau, and a period of recovery to the baseline input rate (descending phase). In the feedforward model, the network exhibited hysteresis during transient excitatory inputs mimicking sharp waves. During the initial ascending phase of the transient excitation, individual interneurons had low firing rates, but as a population they oscillated at the ripple frequency. This frequency was determined by synaptic delays between CA3 inputs and the induced action potential responses of the GABAergic inhibitory population. In such a sparsely synchronized state, cell recruitment depends on noise fluctuation around the sinusoidal response of the population to the CA3 burst. Thus, the network frequency was poorly sensitive to changes in the input rate and the ripple oscillation was relatively stable (Fig. 1A). As excitatory inputs rise, the interconnected interneuronal network became progressively more synchronized. At the sharp-wave peak, when CA3 input rate was maximal, interneurons reached a fully synchronized state. At this point, the network oscillation frequency and interneuron firing rate were similar and both could change with the input rate. Thus, during the descending phase from a saturated state, the network frequency decayed monotonically with decreasing excitation, mimicking the intraripple frequency accommodation typical of some events (Nguyen et al., 2009; Sullivan et al., 2011).

Figure 1.

Summary of model predictions. A, Schematic representation of the model described by Donoso et al. (2018). Direct feedforward activation of CA1 interneurons by CA3 inputs during sharp waves (SPW) resulted in oscillations in the ripple band that poorly correlate with input rates (purple). B, Indirect feedback activation by CA1 pyramidal cells resulted in fast gamma events with different dynamics (orange). C, Extension of the model to include a deep-superficial organization of CA1 feedforward and feedback microcircuits. Question marks indicate unknown aspects of cell types and connectivity. PV BC: parvalbumin basket cell and CCK BC: cholecystokinin basket cell.

In contrast, in the feedback model, CA3 inputs reach interneurons indirectly via local CA1 pyramidal cells. This imposes additional synaptic delays and a small depolarizing buildup to activate them synchronously. In this regimen, coordinated interneuronal firing emerged quickly, reaching a fully synchronized state earlier than in the feedforward model. Thus, in the feedback model, the network frequency was sensitive to changes in input rates. With the range of parameter values and inputs tested, the feedback model produced oscillations within the fast gamma band (Fig. 1B). Similar to the feedforward model, the oscillatory frequency accommodates during the descending phase of excitatory inputs reflecting the network hysteresis.

Equipped with these models, the authors evaluated data in vitro. They found that oscillations were confined to the ripple band. The oscillations exhibited an early peak during the ascending part of the sharp waves followed by frequency accommodation, supporting the hypothesis that, in this in vitro condition, ripples were generated by feedforward inhibition.

The paper by Donoso et al. (2018) suggests that different transient sharp-wave-associated oscillations can emerge from local circuit interneurons activated directly or indirectly by different drivers. The two oscillators may explain part of the spectral complexity underlying physiological sharp waves in vivo where both feedforward and feedback mechanisms operate (Sullivan et al., 2011). In vitro, there may be a dominance of the feedforward inhibition and ripples in CA1 (Maier et al., 2011), whereas feedback mechanisms may be at play in CA3 (Schlingloff et al., 2014), probably due to recurrent collateral system of the excitatory axons of CA3. Importantly, the model suggests that, depending on the activation regime and connectivity, interneurons may oscillate differently. Possibly, the study would have benefitted from a more rigorous parametric study (Marder and Taylor, 2011).

One problem with the work by Donoso et al. (2018) is that the ripple frequency was estimated in the model in an unrealistic way. The power spectra were calculated from population activities, but ripples are LFP phenomena. Ripples are constrained to the stratum pyramidale because inhibitory currents impinging on the somatodendritic compartments from several pyramidal cells generate a field event (Beyeler et al., 2013; Aivar et al., 2014; Bazelot et al., 2016). While the authors tried to incorporate these features indirectly, a simple LFP model confirms that both synaptic currents and morphological aspects influence extracellular fields (Chizhov et al., 2015). Thus, any interneuronal-type innervating groups of pyramidal cells in the stratum pyramidale, including parvalbumin⁺ and cholecystokinin⁺ basket cells, bistratified cells, and axo-axonic interneurons, may also contribute to shape ripple oscillations (Somogyi and Klausberger, 2005; Glickfeld et al., 2009; Hájos et al., 2013).

Importantly, different rules may operate in feedforward and feedback activation of CA1 interneurons (Fig. 1C). Lee et al. (2014) recently showed that CA1 parvalbumin⁺ basket cells are mainly driven by superficial pyramidal cells to inhibit deep pyramidal neurons. During sharp-wave ripples in vivo, superficial pyramidal neurons are typically depolarized and fire, whereas deep cells are rhythmically hyperpolarized (Valero et al., 2015). Strikingly, the power of oscillations recorded intracellularly correlated better with the extracellular ripple in deep-layer cells than in superficial cells, whereas the opposite was seen for sharp waves (Valero et al., 2015). Thus, variability of sharp-wave ripples may reflect the different composition of participating cells (Valero et al., 2017).

Another possible source of feedforward activation of local circuit interneurons is CA2. CA2 pyramidal cells have recently been gaining attention because of their preferential connectivity with the basal dendrites of deep CA1 pyramidal cells (Kohara et al., 2014). Recently, Oliva et al. (2016) showed that some CA2 neurons could fire before sharp-wave ripples detected in CA1 and therefore might play a role in their initiation. Possibly, some CA2 pyramidal cells could directly activate CA1 interneurons independently of CA3 direct inputs, providing alternative microcircuits for ripple generation (Fig. 1C).

Finally, it should be remembered that, whereas CA1 interneurons are critical for ripples, pyramidal neurons also contribute. Coherent firing of CA3 pyramidal cells and inhibitory currents control the timing of action potentials in CA1 pyramidal cells (Csicsvari et al., 2000). A realistic LFP simulation showed that coherent phasic firing in small groups of CA1 pyramidal cells can generate population spikes contributing to high-frequency oscillations (Schomburg et al., 2012). When inhibitory currents are compromised, such as in the epileptic hippocampus, CA1 pyramidal cells are dominated by excitatory drives and rhythmic bursting emerges (Aivar et al., 2014). Population spikes from cluster of cells firing in- and out-of-phase give raise to high-frequency fast ripples (Ibarz et al., 2010; Aivar et al., 2014).

The paper by Donoso et al. (2018) presents a useful model that starts to unravel the complex spectral phenomenology associated with physiological sharp-wave ripples in vivo and in vitro. This study sets the basis for new experimental studies, which will help us to better understand the role of these oscillations in health and disease.