Attractor-like Dynamics in Belief Updating in Schizophrenia

Abstract

Subjects with a diagnosis of schizophrenia (Scz) overweight unexpected evidence in probabilistic inference: such evidence becomes “aberrantly salient.” A neurobiological explanation for this effect is that diminished synaptic gain (e.g., hypofunction of cortical NMDARs) in Scz destabilizes quasi-stable neuronal network states (or “attractors”). This attractor instability account predicts that (1) Scz would overweight unexpected evidence but underweight consistent evidence, (2) belief updating would be more vulnerable to stochastic fluctuations in neural activity, and (3) these effects would correlate. Hierarchical Bayesian belief updating models were tested in two independent datasets (n = 80 male and n = 167 female) comprising human subjects with Scz, and both clinical and nonclinical controls (some tested when unwell and on recovery) performing the “probability estimates” version of the beads task (a probabilistic inference task). Models with a standard learning rate, or including a parameter increasing updating to “disconfirmatory evidence,” or a parameter encoding belief instability were formally compared. The “belief instability” model (based on the principles of attractor dynamics) had most evidence in all groups in both datasets. Two of four parameters differed between Scz and nonclinical controls in each dataset: belief instability and response stochasticity. These parameters correlated in both datasets. Furthermore, the clinical controls showed similar parameter distributions to Scz when unwell, but were no different from controls once recovered. These findings are consistent with the hypothesis that attractor network instability contributes to belief updating abnormalities in Scz, and suggest that similar changes may exist during acute illness in other psychiatric conditions.

SIGNIFICANCE STATEMENT Subjects with a diagnosis of schizophrenia (Scz) make large adjustments to their beliefs following unexpected evidence, but also smaller adjustments than controls following consistent evidence. This has previously been construed as a bias toward “disconfirmatory” information, but a more mechanistic explanation may be that in Scz, neural firing patterns (“attractor states”) are less stable and hence easily altered in response to both new evidence and stochastic neural firing. We model belief updating in Scz and controls in two independent datasets using a hierarchical Bayesian model, and show that all subjects are best fit by a model containing a belief instability parameter. Both this and a response stochasticity parameter are consistently altered in Scz, as the unstable attractor hypothesis predicts.

Introduction

Subjects with a diagnosis of schizophrenia (Scz) tend to use less evidence to make decisions in probabilistic tasks than healthy controls (Garety et al., 1991; Dudley et al., 2016). The paradigm most commonly used to demonstrate this effect is the 'beads' or 'urn' task, in which subjects are shown two urns, each containing opposite ratios of colored beads (e.g., 85% blue and 15% red and vice versa), which are then hidden. A sequence of beads is then drawn (with replacement) from one urn, and the subject either has to stop the sequence when they are sure which urn it is coming from (the 'draws to decision' task) or the subject must rate the probability of the sequence coming from either urn after seeing each bead, without having to make any decision (the 'probability estimates' task). Bayesian analysis of these tasks has indicated that Scz are more stochastic in their responding (Moutoussis et al., 2011) and that they overweight recent evidence and thus update their beliefs (in the probabilistic sense) more rapidly (Jardri et al., 2017).

Several belief-updating abnormalities have been found in Scz using the 'probability estimates' task. The most consistent finding is that Scz (or just Scz with delusions) (Moritz and Woodward, 2005) change their beliefs more than nonpsychiatric controls in response to changes in evidence (Langdon et al., 2010), particularly 'disconfirmatory' evidence (i.e., evidence contradicting a current belief) (Garety et al., 1991; Fear and Healy, 1997; Young and Bentall, 1997; Peters and Garety, 2006). Another is that probability ratings at the start of the sequence are higher in currently psychotic (but not in recovered) Scz than in both clinical and healthy controls (Peters and Garety, 2006), similar to the 'jumping to conclusions' bias in the 'draws to decision' version of the task. Others have also found that Scz update less than controls to more consistent evidence, in this (Baker et al., 2018) and other paradigms (Averbeck et al., 2011).

These findings can potentially be understood in the light of the 'unstable attractor network' hypothesis of Scz. An attractor network is a neural network that can occupy numerous stable states that are learned from experience, via adjustments to synaptic weights. It can revisit these states if presented with inputs that resemble previous patterns of synaptic weights, or through spontaneous fluctuations in neural activity: either way, the activity of all nodes is 'attracted' to a quasi-stable state because the network energy is lower at these states, and network firing patterns evolve to minimize energy. Attractor networks were originally developed to model the storage and reactivation of memories (Hopfield, 1982), but related network models also offer mechanistic explanations for working memory storage (e.g., Brunel and Wang, 2001), decision-making (Wang, 2013), and interval timing (Standage et al., 2013), as well as Bayesian belief updating (Gepperth and Lefort, 2016).

In Scz, attractor states in prefrontal cortex are thought to be less stable, so it is easier for the network to switch between them, but harder to become more confident about (i.e., increase the stability of) any particular one (Rolls et al., 2008). This loss of stable neuronal states, recently demonstrated in two animal models of Scz (Hamm et al., 2017), is thought to be due to hypofunction of NMDARs or cortical dopamine 1 receptors in Scz (Fig. 1). Interestingly, healthy volunteers given ketamine (an NMDAR antagonist) show a decrement in updating to consistent stimulus associations and an increase in decision stochasticity in this context (Vinckier et al., 2016). Attractor network perturbations have been linked to working memory problems in Scz using a bistable (i.e., a stable 'up' state corresponding to persistent neuronal activity, and a 'down' state corresponding to background activity) model (Murray et al., 2014), but not as yet to a computational understanding of belief updating.

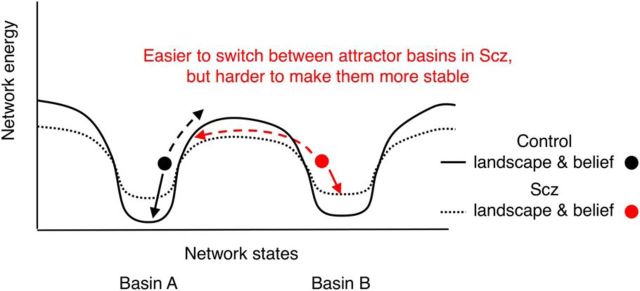
Figure 1.

Effects of attractor network dynamics on belief updating. This schematic illustrates the energy landscapes of two Hopfield-type networks each with two basins of attraction. Continuous black line indicates a normal network whose basins of attraction are relatively deep. Dotted black line indicates the effect of NMDAR (or cortical dopamine 1 receptor) (Durstewitz and Seamans, 2008; Redish et al., 2007) hypofunction (Abi-Saab et al., 1998; Javitt et al., 2012) on the energy landscape: the attractor basins become more shallow. We assume that Basins A and B correspond to different inferences about (hidden) states in the world (e.g., one jar or another being the source of beads in the beads task). Dots indicate the networks' representations of either control or Scz subjects' beliefs about these hidden states. Such networks are highly reminiscent of Hopfield networks with two stored representations; in this case, the representations correspond to inferences about hidden states, rather than memories. Arrows indicate the changes in network states resulting from sensory evidence for (solid arrows) or against (dashed arrows) the current inference. When the attractor basin is shallower, it is harder for supportive evidence to stabilize the current state much further, but it is easier for contradictory evidence, or just stochastic neuronal firing, to shift the current network state toward an alternative state. These changes in network dynamics may also be reflected in the inferences the network computes (i.e., easier switching between attractor basins may correspond to easier switching between beliefs), although this is yet to be demonstrated experimentally. NMDAR hypofunction could contribute to an increased tendency to switch between beliefs and increased stochasticity in responding in several ways (Rolls et al., 2008): (1) by reducing inhibitory interneuron activity, via weakened NMDAR synapses from pyramidal cells to interneurons, such that other attractor states are less suppressed when one is active (a spiking network model has shown that this leads to more rapid initial belief updating in perceptual tasks) (Lam et al., 2017); (2) by reducing pyramidal cell activity, via weakened recurrent NMDAR synapses on pyramidal cells, such that attractor states are harder to sustain; and (3) by reducing the NMDAR time constant, making states more vulnerable to random fluctuations in neural activity. See also similar schematics elsewhere (Durstewitz and Seamans, 2008; Rolls et al., 2008).

We analyzed belief updating in Scz using the Hierarchical Gaussian Filter (HGF) (Mathys et al., 2011), a variational Bayesian model with individual priors, in two independent 'probability estimates' beads task datasets. We asked: given the larger belief updates in Scz compared with controls, can these be explained by group differences in (1) general learning rate and/or (2) response stochasticity, or by adding parameters encoding (3) the variance (i.e., uncertainty) of beliefs at the start of the sequence, (4) a propensity to overweight disconfirmatory evidence specifically, or (5) patterns of belief updating typical of unstable attractor states in a Hopfield-type network (i.e., greater instability and stochasticity), which correlate with each other? The HGF does not contain attractor states: the model in (5) is designed to simulate the effects on inference that unstable neuronal attractors may have. Furthermore, are these findings consistent within Scz tested at different illness phases, and are they unique to Scz or also present in other nonpsychotic mood disorders?

Materials and Methods

Subject characteristics.

Dataset 1 comprised 23 patients with delusions (18 Scz), 22 patients with nonpsychotic mood disorders, and 35 nonclinical controls (overall, 50 male and 30 female; for details of the groups, see Tables 1, 2); the first two groups were selected from inpatient wards at the Maudsley and the Bethlem Royal Hospitals. All groups were tested twice (with loss of n = 25 from the groups; Tables 1, 2); the clinical groups were tested once when they were unwell ('baseline'), and again once they had recovered ('follow-up'). The mean time between testing sessions was 17.4 (range 6–41) weeks in the deluded group, 33.4 (range 4–68) weeks in the clinical control group, and 35.6 (range 27–46) weeks in the nonclinical control group. The deluded group's shorter intertest interval was due to their shorter admission period and to the prioritization of their follow-up over the nonclinical control group. Dataset 1 was described in detail previously (Peters and Garety, 2006).

Table 1.

Demographic, psychological, and behavioral details of Dataset 1^a

	Nonclinical controls t1	Nonclinical controls t2	Clinical controls t1	Clinical controls t2	Psychotic t1	Psychotic t2
N	35	20	22	18	23	17
Ageb (yr)	27.77 (6.74)	27.9 (6.37)	40.91 (13.57)	40.1 (13)	31.22 (7.28)	29.9 (7.83)
Gender	18 M, 17 F	12 M, 8 F	11 M, 11 F	8 M, 10 F	21 M, 2 F	17 M, 0 F
Cognitive measures
IQc	107.5 (11.6)	108.6 (10.3)	97.4 (13.8)	99.8 (10.2)	88.1 (12.7)	87.8 (14.2)
Delusion proneness
PDI (total)d	54.6 (43.1)	43.6 (42.5)	87.1 (55.2)	64.3 (57.3)	138.1 (74.2)	96.7 (42.6)
DSSIe	2.3 (4.9)	2.9 (5.3)	4.8 (4.5)	4.5 (5.6)	15.2 (6.3)	8.1 (6.6)
Diagnosis/symptoms
Diagnoses			16 Depression, 3 anxiety and depression, 3 SAD	12 Depression, 3 anxiety and depression, 3 SAD	18 Scz, 5 bipolar/schizo-affective	13 Scz, 4 bipolar/schizo-affective
MS affective	—	—	4.6 (1.7)	1.0 (1.2)	1.8 (1.5)	1.5 (1.3)
MS positive	—	—	0.3 (0.8)	0 (0)	6.0 (2.4)	1.4 (1.7)
MS negative	—	—	0.7 (1.6)	1.8 (3.19)	1.3 (2.0)	0.9 (1.6)
MS totalf	—	—	5.5 (2.6)	2.8 (3.39)	9.1 (3.76)	3.7 (3.9)
Beads task
Initial certainty (1 bead)g	0.58 (0.15)	0.59 (0.12)	0.68 (0.19)	0.63 (0.16)	0.76 (0.17)	0.68 (0.29)
Initial certainty (3 beads)h	0.65 (0.14)	0.67 (0.1)	0.69 (0.15)	0.64 (0.16)	0.78 (0.15)	0.74 (0.15)
Disconfirmatory updatingi	−0.06 (0.14)	−0.03 (0.13)	−0.19 (0.3)	−0.11 (0.22)	−0.29 (0.33)	−0.2 (0.3)
Final certaintyj	0.85 (0.2)	0.94 (0.11)	0.82 (0.16)	0.79 (0.23)	0.88 (0.11)	0.85 (0.23)

^aDataset 1 includes measures at both baseline (t1) and follow-up (t2). In Dataset 1, verbal IQ was estimated using the Quick Test (Ammons and Ammons, 1962) and delusion proneness using the Peters Delusion Inventory (PDI) (Peters et al., 1999) and Delusions-Symptoms-States Inventory (DSSI) (Foulds and Bedford, 1975). Symptoms were assessed using the Manchester Scale (MS) (Krawiecka et al., 1977). In the tests below, ‘Scz’ refers to the whole Psychotic group. Results are given for ‘Initial certainty’ using both the measure in the original analysis of Dataset 1 (Peters and Garety, 2006), the mean response to the first three beads (3 beads); in Dataset 2, this had to be the mean response to the first three beads in Sequences B and C and two beads in Sequences A and D (2–3 beads), and using the response to the first bead (1 bead).

^bAt t1: one-way ANOVA F_(2,77) = 13.9, p = 10⁻⁵. Tukey's HSD: Scz versus Nonclinical controls diff = 3.45, p(adj) = 0.35; Clinical versus Nonclinical controls diff = 13.1, p(adj) = 10⁻⁵; Clinical controls versus Scz diff = 9.69, p(adj) = 0.002. At t2: one-way ANOVA F_(2,52) = 8.85, p = 0.0005. Tukey's HSD: Scz versus Nonclinical controls diff = 1.98, p(adj) = 0.8; Clinical versus Nonclinical controls diff = 12.2, p(adj) = 0.0006; Clinical controls versus Scz diff = 10.2, p(adj) = 0.007.

^cAt t1: one-way ANOVA F_(2,75) = 16.2, p = 10⁻⁶; Tukey's HSD: Scz versus Nonclinical controls diff = −19.5, p(adj) = 10⁻⁶; Clinical versus Nonclinical controls diff = −10.1, p(adj) = 0.011; Clinical controls versus Scz diff = 9.36, p(adj) = 0.043. At t2: one-way ANOVA F_(2,51) = 14.5, p = 10⁻⁵; Tukey's HSD: Scz versus Nonclinical controls diff = −20.8, p(adj) = 10⁻⁵; Clinical versus Nonclinical controls diff = −8.8, p(adj) = 0.057; Clinical controls versus Scz diff = 12, p(adj) = 0.01.

^dAt t1: one-way ANOVA F_(2,68) = 12.6, p = 0.00002; Tukey's HSD: Scz versus Nonclinical controls diff = 83.5, p(adj) = 10⁻⁵; Clinical versus Nonclinical controls diff = −32.5, p(adj) = 0.094; Clinical controls versus Scz diff = −51, p(adj) = 0.016. At t2: one-way ANOVA F_(2,52) = 4, p = 0.024; Tukey's HSD: Scz versus Nonclinical controls diff = 53.1, p(adj) = 0.018; Clinical versus Nonclinical controls diff = −20.7, p(adj) = 0.5; Clinical controls versus Scz diff = −32.4, p(adj) = 0.22.

^eAt t1: one-way ANOVA F_(2,76) = 43, p = 10⁻¹³; Tukey's HSD: Scz versus Nonclinical controls diff = 12.9, p(adj) = 10⁻¹⁰; Clinical versus Nonclinical controls diff = 2.52, p(adj) = 0.19; Clinical controls versus Scz diff = −10.4, p(adj) = 10⁻⁸. At t2: one-way ANOVA F_(2,51) = 3.7, p = 0.032; Tukey's HSD: Scz versus Nonclinical controls diff = 5.2, p(adj) = 0.026; Clinical versus Nonclinical controls diff = 1.65, p(adj) = 0.66; Clinical controls versus Scz diff = −3.56, p(adj) = 0.18.

^fAt t1: Welch's t_(38.4) = −3.62, p = 0.00086, Cohen's d = 1.1. At t2: Welch's t_(17.8) = −2.55, p = 0.02, Cohen's d = 1.0.

^gAt t1: one-way ANOVA F_(2,77) = 8.7, p = 0.0004; Tukey's HSD: Scz versus Nonclinical controls diff = 0.18, p(adj) = 0.0003; Clinical versus Nonclinical controls diff = 0.11, p = 0.06; Clinical controls versus Scz diff = −0.08, p(adj) = 0.25. At t2: one-way ANOVA F_(2,52) = 0.9, p = 0.4.

^hAt t1: one-way ANOVA F_(2,77) = 6.2, p = 0.003; Tukey's HSD: Scz versus Nonclinical controls diff = −0.14, p(adj) = 0.002; Clinical versus Nonclinical controls diff = 0.04, p = 0.57; Clinical controls versus Scz diff = −0.096, p(adj) = 0.074. At t2: one-way ANOVA F_(2,52) = 2.35, p = 0.11; Tukey's HSD: Scz versus Nonclinical controls diff = 0.07, p(adj) = 0.28; Clinical versus Nonclinical controls diff = −0.03, p = 0.8; Clinical controls versus Scz diff = −0.1, p(adj) = 0.1.

ⁱAt t1: one-way ANOVA F_(2,77) = 6, p = 0.004; Tukey's HSD: Scz versus Nonclinical controls diff = −0.23, p(adj) = 0.003; Clinical versus Nonclinical controls diff = −0.14, p = 0.13; Clinical controls versus Scz diff = 0.097, p(adj) = 0.41. At t2: one-way ANOVA F_(2,52) = 2.9, p = 0.062; Tukey's HSD: Scz versus Nonclinical controls diff = −0.18, p(adj) = 0.049; Clinical versus Nonclinical controls diff = −0.08, p = 0.51; Clinical controls versus Scz diff = 0.098, p(adj) = 0.4.

^jAt t1: one-way ANOVA F_(2,77) = 0.71, p = 0.5. At t2: one-way ANOVA F_(2,52) = 2.79, p = 0.07; Tukey's HSD: Scz versus Nonclinical controls diff = −0.082, p(adj) = 0.41; Clinical versus Nonclinical controls diff = −0.15, p = 0.057; Clinical controls versus Scz diff = −0.066, p(adj) = 0.57. As reported previously, there were consistent negative correlations between initial certainty (2–3 beads) and disconfirmatory updating in the clinical controls (baseline: ρ = −0.68, p = 0.0005; follow-up: ρ = −0.75, p = 0.0003) and the nonclinical controls (baseline: ρ = −0.52, p = 0.001; follow-up: ρ = −0.43, p = 0.06), but not in the psychotic group (baseline: ρ = −0.30, p = 0.17; follow-up: ρ = 0.17, p = 0.5). There was no consistent correlation between final certainty and either of the other two measures at either time point (p ≥ 0.1 in 11 of 12 comparisons).

Table 2.

Demographic, psychological, and behavioral details of Dataset 2^a

	Controls (all)	Scz	Controls (subset)
N	111	56	60
Age (yr)	32.8 (11.5)	45.3 (8.8)	39.5 (11.4)
Gender	45 M, 66 F	38 M, 18 F	40 M, 20 F
NARTb	112 (6.9)	109 (8.2)	112 (7.5)
Working memory (LNS)c	16.2 (2.8)	10.3 (4.2)	16.4 (2.7)
Schizotypy
SPQ, cognitive	2.8 (1.9)	4.0 (2.6)	3.1 (2)
SPQ, interpers	3.2 (2.2)	5.3 (2.6)	3.2 (2.2)
SPQ, disorg	2.1 (1.7)	2.7 (1.9)	1.9 (1.8)
SPQ, totald	8.2 (1.3)	12 (5.3)	8.2 (4.4)
Diagnoses	—	56 Scz	—
PANSS, gen	—	32.6 (9.2)	—
PANSS, pos	—	15.9 (5.8)	—
PANSS, neg	—	15.9 (6.2)	—
PANSS, total	—	64.4 (17.3)	—
Initial certainty (all, 1 bead)e	0.67 (0.13)	0.71 (0.14)	0.68 (0.14)
Initial certainty (all, 2–3 beads)f	0.7 (0.12)	0.71 (0.12)	0.71 (0.13)
Disconfirmatory updating (all sequences)g	−0.16 (0.17)	−0.23 (0.22)	−0.19 (0.2)
Final certainty Sequence Ah	0.88 (0.16)	0.77 (0.25)	0.86 (0.18)
Final certainty Sequence Di	0.12 (0.18)	0.25 (0.24)	0.16 (0.2)

^aIn dataset 2, IQ was estimated using the National Adult Reading Test (NART) (Nelson, 1982) and working memory using the Letter Number Sequencing task (LNS) from the Wechsler Adult Intelligence Scale-III (Wechsler, 1997). Schizotypy was assessed using the Schizotypal Personality Questionnaire (SPQ) (Raine, 1991), and symptoms using the Positive and Negative Syndrome Scale (PANSS) (Kay et al., 1987). As can be seen in Figure 2, the Scz group showed greater initial certainty (1 bead) in Sequences A and B (Welch's t₍₉₄₎ = 2.8, p = 0.007, Cohen's d = 0.47; Welch's t₍₉₇₎ = 3, p = 0.004, Cohen's d = 0.5, respectively) but not Sequences C and D (Welch's t₍₈₇₎ = 0.5, p = 0.6, Cohen's d = 0.09; Welch's t₍₉₀₎ = −0.34, p = 0.73, Cohen's d = 0.06, respectively).

^bControls (all): Welch's t_(95.1) = 2.27, p = 0.026, Cohen's d = 0.38; Controls (subset): Welch's t₍₁₁₁₎ = 1.95, p = 0.053, Cohen's d = 0.36.

^cControls (all): Welch's t₍₈₁₎ = 9.57, p = 10⁻¹⁴, Cohen's d = 1.66; Controls (subset): Welch's t_(93.6) = 9.25, p = 10⁻¹⁵, Cohen's d = 1.73.

^dControls (all): Welch's t_(92.4) = −4.64, p = 10⁻⁵, Cohen's d = 0.78; Controls (subset): Welch'st₍₁₀₇₎ = −4.19, p = 10⁻⁵, Cohen's d = 0.78.

^eControls (all): Welch's t₍₁₁₀₎ = −1.9, p = 0.059, Cohen's d = 0.32; Controls (subset): Welch's t₍₁₁₀₎ = −1.1, p = 0.28, Cohen's d = 0.2.

^fControls (all): Welch's t_(109.1) = −0.76, p = 0.45, Cohen's d = 0.12; Controls (subset): Welch's t_(113.9) = −0.19, p = 0.85, Cohen's d = 0.03.

^gControls (all): Welch's t_(88.2) = 2.09, p = 0.04, Cohen's d = 0.36; Controls (subset): Welch's t_(110.4) = −0.94, p = 0.35, Cohen's d = 0.18.

^hControls (all): Welch's t_(80.1) = 2.99, p = 0.0038, Cohen's d = 0.56; Controls (subset): Welch's t_(98.7) = 2.18, p = 0.032, Cohen's d = 0.41.

ⁱControls (all): Welch's t_(85.5) = −3.41, p = 0.001, Cohen's d = 0.62; Controls (subset): Welch's t₍₁₀₆₎ = −2.21, p = 0.029, Cohen's d = 0.42.

Dataset 2 comprised 56 subjects with a diagnosis of Scz and 111 controls (overall, 83 male and 84 female; Tables 1, 2). All subjects provided informed, written consent, and ethical permission for the study was obtained from the local NHS Research Ethics Committee (Reference 14/LO/0532). Given the National Adult Reading Test (Nelson, 1982) was used to estimate IQ in these participants, a recruitment condition was that English was their first language.

Measures of cognitive function and delusion-proneness (or schizotypy) were collected in all subjects; clinical symptom ratings were collected in clinical subjects only (for details, see Tables 1, 2).

Experimental design.

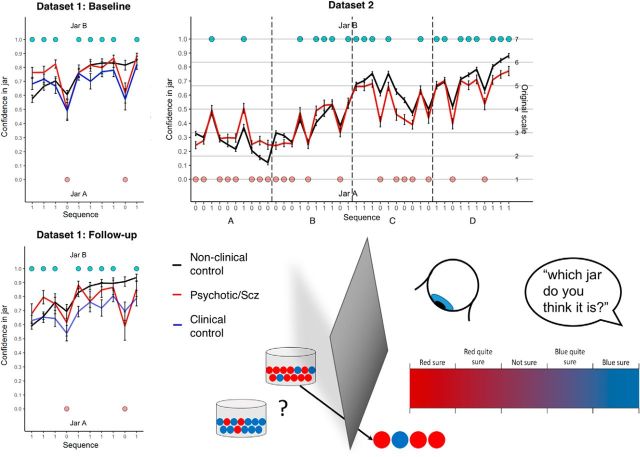
Subjects in Dataset 1 performed the 'probability estimates' beads task as used previously (Garety et al., 1991), with two urns with ratios of 85:15 and 15:85 blue and red beads, respectively, and viewing a single sequence of 10-beads (Fig. 2); after each bead, they had to mark an analog scale (from 1 to 100) denoting the probability the urn was 85% red.

Figure 2.

Beads task schematic and group average confidence ratings in Datasets 1 and 2. Bottom right, Schematic of the beads task: two jars containing opposite proportions of beads are concealed from view, and a subject is asked to rate the probability of either jar being the source of a sequence of beads he/she is viewing (after each bead in turn). Top left, Mean (± SE) confidence ratings in the blue jar over the 10-bead sequence averaged across each group at baseline in Dataset 1. Bottom left, Same quantities at follow-up in Dataset 1. Top right, Quantities in four 10-bead sequences concatenated together (they were presented to the subjects separately during testing) in Dataset 2.

Subjects in Dataset 2 performed the 'probability estimates' beads task, with two urns with ratios of 80:20 and 20:80 red and blue beads, respectively. They each viewed four separate sequences (two identical pairs of sequences with the colors swapped within each pair) of 10-beads (Fig. 2); after each bead, they had to mark a Likert scale (from 1 to 7) denoting the probability the urn was the 80% blue one. Two sequences contained an apparent change of jar. The order of the four sequences was randomized.

We used some of the behavioral measures used in the original analysis of Dataset 1 (Peters and Garety, 2006) to analyze Dataset 2. These were 'disconfirmatory updating,' the mean change in belief on seeing a bead of a different color to the ≥2 beads preceding it and 'final certainty' (the response to the last bead). We altered their 'initial certainty' measure from the mean response to the first three beads to the response to the first bead, which comes closer to capturing the classic 'jumping to conclusions' bias (in which ∼50% of Scz decide on the jar color after seeing only one bead) (Garety et al., 1991), although the results of both measures are presented below.

Computational modeling.

The optimal way to use sensory information to update one's beliefs under conditions of uncertainty is to use Bayesian inference. Neural systems are likely to approximate Bayesian inference using schemes of simple update equations (Rao and Ballard, 1999; Friston, 2005); one such model is the HGF. The HGF is a hierarchical Bayesian inference scheme that gives a principled account of how beliefs are updated on acquiring new data, using variational Bayes and individual priors. Variational Bayesian schemes (e.g., Beal, 2003) use analytic equations to derive an exact solution to an approximation of the posterior distribution over the latent variables and parameters (as opposed to sampling methods, which approximate a solution to the exact posterior). The HGF has been used as a generic state model for learning under uncertainty and has repeatedly been shown to outperform similar approaches, such as reinforcement learning models with fixed (e.g., Rescorla-Wagner) or dynamic (e.g., Sutton, 1992) learning rates (Iglesias et al., 2013; Diaconescu et al., 2014; Hauser et al., 2014; Vossel et al., 2014). One advantage of the HGF is that it contains subject-specific parameters (and prior beliefs) that can account for between-subject differences in learning while preserving the (Bayes) optimality of any individual's learning (relative to his/her model parameters and prior beliefs). These parameters may be encoded by tonic levels of neuromodulators, such as dopamine (Marshall et al., 2016), or by the intrinsic properties of neuronal networks (e.g., the ratio of excitatory to inhibitory neural activity can affect the speed of evidence accumulation) (Lam et al., 2017), analogous to the evolution rate in the HGF and also response stochasticity (Murray et al., 2014). Differences in model parameters between Scz and controls may therefore explain, in computational terms, how pathophysiology leads to abnormal inference (Adams et al., 2016).

In general, when modeling behavior under Bayesian assumptions, it is necessary to distinguish between the model of the world used by the subject (the perceptual model) and a model of how a subject's beliefs translated into observed behavior (the observation or response model). Most of the parameters pertain to the perceptual model (here, all parameters except response stochasticity ν; Table 3) and reflect (inferred) neuronal processing. In contrast, the parameters of the response model link subjective states to behavioral outcomes, and thus may reflect stochasticity in neuronal processing, measurement noise (in some paradigms), or nonrandom effects that have not been captured by the perceptual model. This and related learning models are freely available from http://www.translationalneuromodeling.org/tapas/ (version 5.1.0): this analysis used the perceptual models 'hgf_binary' or 'hgf_ar1_binary' and the response model 'beta_obs.'

Table 3.

Models, parameters, and their prior distributions

Model	Perceptual model parameters (prior mean in native space, prior variance in estimation space)				Response model parameter: response stochasticity
	Evolution rate	Initial variance of belief regarding jars	Disconfirmatory bias	Belief instability
1	ω (−2, 16)				ν (exp(4.85), 1)
2	ω (−2, 16)	σ2(0) (0.8, 0.5)			ν (exp(4.85), 1)
3	ω (−2, 16)		ϕ (0.1, 2)		ν (exp(4.85), 1)
4	ω (−2, 16)	σ2(0) (0.8, 0.5)	ϕ (0.1, 2)		ν (exp(4.85), 1)
5	ω (−2, 16)			κ1 (1, 1)	ν (exp(4.85), 1)
6	ω (−2, 16)	σ2(0) (0.8, 0.5)		κ1 (1, 1)	ν (exp(4.85), 1)

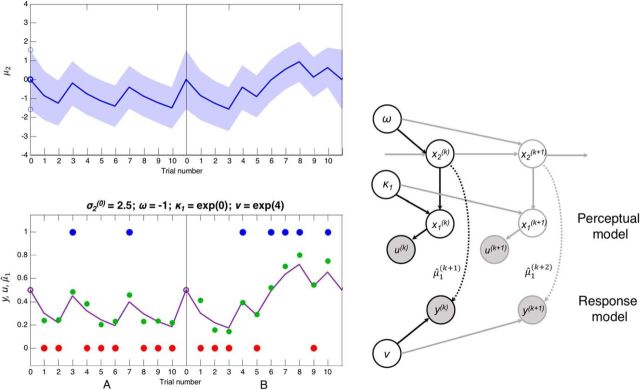
At the bottom of the model (Fig. 3 shows some simulated responses) is the bead drawn u^(k) on trial k and the probability x₁^(k) that draws are coming from the blue jar. At the level above this is x₂, the tendency toward the blue jar (a transform of the probability, bounded by ±∞); by definition, x₁ = s(x₂), where s(•) is the logistic sigmoid function. As x₂ approaches infinity, the probability of the blue jar approaches 1; as it approaches minus infinity, the probability of the blue jar approaches 0. For x₂ = 0, both jars are equally probable. This quantity is hidden from the subject and must be inferred: the subject's posterior estimate of x₂ is μ₂, and the subject's posterior estimate of the probability of the jar being blue on trial k is s(μ₂^(k)), equivalent to the prediction (denoted by ∧) on the next trial μ̂₁^(k+1).

Figure 3.

The structure of the HGF (Model 6) and some simulated data. Top left, The evolution of μ₂, the posterior estimate of tendency x₂ toward the blue (positive) or red (negative) jar, is plotted over two concatenated series of 10 trials (the first two in Dataset 2). The estimate of the tendency on trial k + 1, μ₂^(k+1), is selected from a Gaussian distribution with mean μ₂^(k) (blue line) and variance σ₂^(k) + exp(ω) (blue shading). ω is a static source of variance at this level. The initial variance σ₂⁽⁰⁾ (along with ω) affects the size of initial updates, so we estimated this parameter (which is often fixed). Bottom left, The beads seen by the subjects, u^(k) (blue and red dots) and the response model. The response model maps from μ̂₁^(k+1) (purple line), the prediction of x₁ on the next trial, which is a sigmoid function s of μ₂^(k) (or of (κ₁μ₂^(k)) in Models 5 and 6), to y^(k), the subject's indicated estimate of the probability the jar is blue (green dots). Variation in this mapping is modeled as the precision ν of a β distribution. Right, Schematic representation of the generative model in Models 5 and 6 (i.e., including κ₁). Black arrows indicate the probabilistic network on trial k. Gray arrows indicate the network at other points in time. The perceptual model lies above the dotted arrows, and the response model below them. Shaded circles represent known quantities. Unshaded circles represent estimated parameters and states. Dotted line indicates the result of an inferential process (the response model builds on a perceptual model inference). Solid lines indicate generative processes.

Before seeing any new input on trial k, the model's expected jar probability μ̂₁^(k) and precisions (inverse variances) π̂₁^(k),π̂₂^(k) of the expectations at each level are given by the following:

In Models 1–4, κ₁ is fixed to 1. A new input u^(k) ≡ μ₁^(k) generates a prediction error δ₁^(k), and the model updates and generates a new prediction as follows:

The subject's response y^(k) (i.e., where on the continuous or Likert scale they responded) is determined by μ̂₁^(k+1) and the precision of the response model's β distribution ν.

We parameterize the β distribution in terms of its mean μ and precision ν. These sufficient statistics relate to the conventional parameterization in terms of the sufficient statistics α and β by the following bijection:

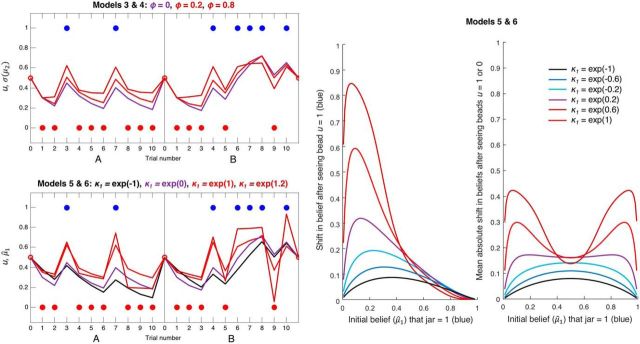
Updates to μ₂ are driven by the product of the prediction error from Bayesian updating explained above and a learning rate which, crucially, can change over time: this is an important aspect of the HGF in contrast to learning models, such as Rescorla-Wagner, which have a fixed learning rate. Parameters that affect the degree to which μ₂ can change during the experiment include ω, ϕ, κ₁, and σ₂⁽⁰⁾. The contributions of ϕ and κ₁ are illustrated in Figure 4 (left panels).

Figure 4.

Simulated data illustrating the effects of ϕ (Models 3 and 4) and κ₁ (Models 5 and 6) on inference. Both panels represent simulated perceptual model predictions in the same format as before, with σ₂⁽⁰⁾ and ω set to their previous values; hence, the purple line in these plots is identical to that in Figure 3. The second level and simulated responses y have been omitted for clarity. Top left, Simulations of a perceptual model incorporating an autoregressive order (1) process at the second level, using three different values of AR(1) parameter ϕ: 0, 0.2, and 0.8. The estimate of the tendency on trial k + 1, μ₂^(k+1), is selected from a Gaussian distribution with mean μ₂^(k) + ϕ(m − μ₂^(k)) and variance σ₂^(k) + exp(ω). Over time, μ₂ is therefore attracted toward level m (fixed to 0, i.e., at σ(μ₂) = 0.5) at a rate determined by ϕ. In effect, this gives the model a 'disconfirmatory bias,' such that as ϕ increases, σ(μ₂) is pulled further away from a belief in either jar, and toward 0.5 (maximum uncertainty about the jars). Bottom left, Simulations of a perceptual model using four different values of scaling factor κ₁, which alters the sigmoid transformation: μ̂₁^(k+1) = s(κ₁ · μ₂^(k)). When κ₁ > exp(0), updating is greater to unexpected evidence and lower to consistent evidence; when κ₁ < exp(0), the reverse is true. Red and brown lines (κ₁ > exp(0)) indicate the effects of increasingly unstable attractor networks; that is, switching between states (jars) becomes more likely (a concomitant increase in vulnerability to noise, i.e., response stochasticity, is not shown). Green line (κ₁ = exp(−1)) indicates slower updating around μ̂₁ = 0.5, as was found in controls. κ₁ permits a greater range of updating patterns than ϕ (the green and brown trajectories in the bottom cannot be produced by Model 4), which may be why Model 6 can fit both controls and Scz groups well. Middle, Plot represents the effects of κ₁ on belief updating, as a function of the initial belief μ̂₁ (σ₂⁽⁰⁾ and ω were set to 1.5 and −1, respectively, as in Fig. 5; changing these parameters does not qualitatively alter the effects of κ₁ shown here). For values of κ₁ < exp(0) = 1 (bottom three curves) and initial beliefs to the left of these curves' maxima (i.e., that the jar is probably red), relatively small increases in μ̂₁ are made if one blue bead (u = 1) is observed, such that the subject still believes the jar is most likely red. For values of κ₁ > exp(0.5) (top two curves), observing one blue bead causes such a large update for all but the most certain initial beliefs in a red jar that the subject's posterior belief is that the jar is probably blue. These subjects' beliefs are no longer stable, but neither can they reach certainty: only tiny updates toward 1 are possible for μ̂₁ > 0.8. Right, Plot represents the average absolute shifts in beliefs on observing beads of either color. This 'vulnerability to updating' is highly reminiscent of the 'energy state' of a neural network model (schematically illustrated in Fig. 1) (i.e., in low energy states); less updating is expected. The effect of increasing κ₁ is to convert confident beliefs about the jar (near 0 and 1) from low to high 'energy states' (i.e., to make them much more unstable).

The model usually has a third level, at which x₃ encodes the phasic volatility of x₂ (this determines the probability of the jar changing at any point): given the very short sequences used in our datasets, from which volatility cannot be reliably estimated, we omitted this level. In any case, volatility could not account for the rapid changes in learning rate (from trial to trial, following confirmatory vs disconfirmatory evidence) present in the Scz group in these datasets.

In Models 1 and 2, changes in x₂ from trial to trial occur only according to the evolution rate ω, the variance of the random process at the second level. These models were equivalent to the subsequent models with either ϕ (Models 3 and 4) fixed to 0 or κ₁ (Models 5 and 6) fixed to 1.

In Models 3 and 4, changes in x₂ from trial to trial occur according to an autoregressive (AR(1)) process that is controlled by three parameters: m, the level to which x₂ is attracted; ϕ, the rate of change of x₂ toward m; and ω, the variance of the random process as follows:

After inversion, the evolution of x₂ according to this equation is reflected in the prediction of μ₂ as follows:

In this study, given there was no bias toward one jar or the other, m was fixed to 0, so ϕ always acted to shift the model's beliefs back toward maximum uncertainty (i.e., disconfirm the current belief) about the jars. Figure 4 (top left) illustrates the effect of ϕ on s(μ₂^(k)) over time.

In Models 5 and 6, changes in μ₂ from trial to trial occur according to two parameters: ω, the variance of the random process; and κ₁, a scaling factor that changes the size of updates when μ̂₁ = 0.5, or maximum uncertainty, relative to when μ̂₁ is closer to 0 or 1 (i.e., when the subject is more confident about either jar). Figure 4 (bottom left) illustrates the effect of κ₁ on μ̂₁ over time. Formally, the scaling occurs as follows:

When κ₁ > 1, updating toward 1 on observing a blue bead (μ = 1) is greatest (i.e., switching between jars becomes more likely) when μ̂₁ < 0.3; when κ₁ < 1, updating is comparatively far lower when μ̂₁ < 0.3. This is illustrated in Figure 4 (middle): for high values of κ₁ (brown line), belief updates that cross the μ̂₁ = 0.5 line encounter little resistance (i.e., little evidence is required to cause a large shift), whereas approaching the extremes of μ̂₁ = 0 and μ̂₁ = 1 in response to confirmatory evidence is resisted (belief shifts are very small for μ̂₁ near 1). By contrast, for low values of κ₁ (Fig. 4 middle, black line), there is relatively less resistance against approaching the extremes while it takes more evidence for beliefs to cross the μ̂₁ = 0.5 line.

Figure 4 (right) illustrates the average absolute shifts in beliefs on observing beads of either color. This 'vulnerability to updating' is highly reminiscent of the 'energy state' of a neural network model (i.e., in low-energy states) less updating occurs. The effect of increasing κ₁ is to convert confident beliefs about the jar (near 0 and 1) from low to high 'energy states' (i.e., to make them much more unstable). This recapitulates the attractor network properties illustrated in Figure 1: an unstable network easily switches from one state to another but has difficulty stabilizing any one state, whereas a stable network requires more energy (here, information) to overcome the boundary between two states (here, beliefs). Models 5 and 6 therefore capture the effects of attractor (in)stability on belief updating, or at least the kind of updating for which (un) stable attractor states are a good analogy.

As group differences in initial updating had been observed in Dataset 1, we also estimated the SD of μ₂ before the sequence begins, σ₂⁽⁰⁾, in Models 2, 4, and 6.

NB for intermediate values of κ₁, Models 5 and 6 produce similar belief updating trajectories to Models 3 and 4 (containing the disconfirmatory updating parameter ϕ): both make greater updates following disconfirmatory evidence. For more extreme values of κ₁, however, Models 5 and 6 produce trajectories that Models 3 and 4 cannot: ϕ cannot pull beliefs far toward certainty in the opposite jar (compare Fig. 4, bottom left, brown line), and neither can it make it more difficult to update to disconfirmatory evidence (compare Fig. 4, bottom left, black line).

The parameters ω and ν ± σ₂⁽⁰⁾ ± ϕ or κ₁ were estimated individually for each subject. If estimated, the prior probability distributions for their values are given in Table 3. The means given here refer to the parameters' native space, but the variances refer not to the parameters' native space, which in many cases is bounded, but to the unbounded space they were transformed to for estimation purposes. Otherwise, they were fixed as ϕ = 0 (Models 1 and 2) and σ₂⁽⁰⁾ = 0.006 (Models 1, 3, and 5). The model's prior beliefs about the jars at the start of the sequence were fixed at μ₂⁽⁰⁾ = 0 (i.e., believing each to be equally likely). The priors were sufficiently uninformative to be easily updated by the data: all prior means are standard for the HGF, except σ₂⁽⁰⁾, which had to be increased from 0.006 to 0.8 to allow the data to change it. The latter change ensured that group differences in initial belief updating alone would cause group differences in σ₂⁽⁰⁾ rather than κ₁.

Model fitting and statistical analysis.

We tested models with different combinations of parameters ω, ν, ϕ, or κ₁ and σ₂⁽⁰⁾ (Table 3). In analyzing Dataset 2, we concatenated all four sequences for each subject to estimate the model parameters as accurately as possible (resetting the beliefs about the jars at the start of each sequence).

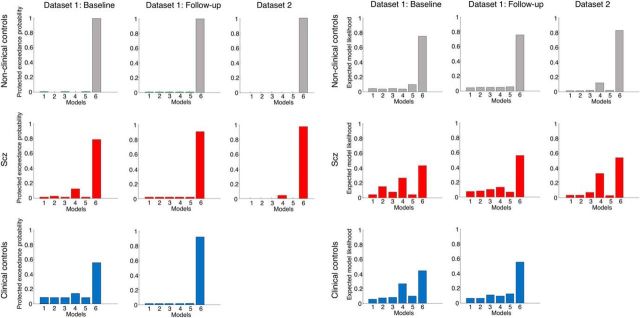
After fitting the six models to each subject's data, we performed Bayesian model selection on all groups separately in both Dataset 1 (at baseline and follow-up) and Dataset 2. This procedure weights models according to their accuracy but penalizes them for complexity (i.e., unnecessary extra parameters) to prevent overfitting (Stephan et al., 2009; Rigoux et al., 2014). The winning model in all eight groups was Model 6 (see Fig. 6), although approximately one-third of psychotic subjects and nonclinical controls in Dataset 1 (at baseline) and in Dataset 2 were better fit by Model 4. It is unclear why this change occurs; but given that Model 6 can produce very similar trajectories to Model 4 for intermediate values of κ₁ (Fig. 4), any increase in response stochasticity is likely to diminish the strength of evidence for one model over a similar one.

Figure 6.

Bayesian model selection results for both datasets. Left, Protected exceedance probabilities for the six models in each group in each dataset. The protected exceedance probability is the probability a particular model is more likely than any other tested model, above and beyond chance, given the group data (Rigoux et al., 2014). Model 6 wins in all groups in both datasets (top row, controls; middle row, Scz; bottom row, clinical controls). Right, Model likelihoods for the six models in each group in each dataset. The model likelihood is the probability of that model being the best for any randomly selected subject (Stephan et al., 2009). Model 4 is a clear runner-up in the psychotic (Scz) and clinical control groups at baseline in Dataset 1, and in the Scz group in Dataset 2.

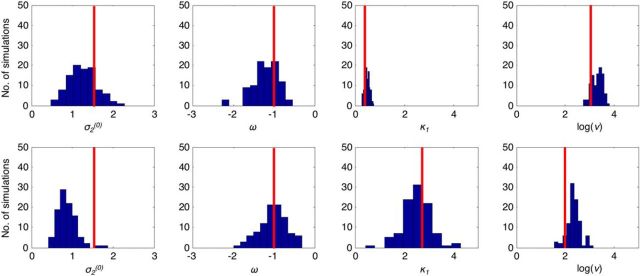
To confirm we could reliably estimate the parameters of the winning model, Model 6, we simulated 100 datasets using the modal values of the parameters for both control and Scz groups (Fig. 5, top and bottom rows, respectively; an example simulated dataset is shown in Fig. 3). We then estimated the parameters for the simulated data and showed that, in most cases, the parameters are recovered reasonably accurately. The exception was σ₂⁽⁰⁾ in the Scz group simulation, which was distributed around the prior mean of 0.8 rather than the true value of 1.5. We retained a prior mean of 0.8 for σ₂⁽⁰⁾ because using a higher prior mean led to overestimation of σ₂⁽⁰⁾ in other simulations (data not shown).

Figure 5.

Recovery of model parameters from simulated data. The 200 datasets were simulated using Model 6: 100 using modal parameter values for the control group (Dataset 2) and 100 using modal values for the Scz group (also Dataset 2). Red lines indicate the values. Both used settings of σ₂⁽⁰⁾ = 1.5, ω = −1. The control group used κ₁ = 0.37 (i.e., exp(−1)) and ν = exp(3). The Scz group used κ₁ = 2.7 (i.e., exp(1)) and ν = exp(2). Histograms represent the parameter estimates from model inversion using the same priors as were used in the main analysis shown above: the modal control and Scz simulation results are in the top and bottom rows, respectively.

Results

Behavioral results: Dataset 1

Each group's mean responses are plotted in Figure 2A, and statistical tests detailed in Tables 1 and 2 (p(adj) refer to the adjusted p value of Tukey's HSD post hoc test). As described previously (Peters and Garety, 2006), at baseline there was a significant difference in disconfirmatory updating between the groups (F_(2,77) = 6, p = 0.004, ANOVA), and the psychotic group had greater disconfirmatory updating than the nonclinical controls (p(adj) = 0.003) but not the clinical controls (p(adj) = 0.4). There was no difference between the clinical and nonclinical controls (p(adj) = 0.13). There were also significant differences in initial certainty across the three groups (F_(2,77) = 8.7, p = 0.0004, ANOVA); the psychotic group's initial certainty was higher than the nonclinical controls' (p(adj) = 0.0003) but not the clinical controls' (p(adj) = 0.25). There was not a significant difference between the clinical and nonclinical control groups (p(adj) = 0.06). There were no group differences in final certainty (F_(2,77) = 0.7, p = 0.5, ANOVA).

At follow-up, the difference in disconfirmatory updating between the groups was no longer significant (F_(2,52) = 2.9, p = 0.06, ANOVA); the psychotic group had greater disconfirmatory updating than the nonclinical controls (p(adj) = 0.049) but not the clinical controls (p(adj) = 0.4). There was no significant difference in initial certainty across the groups (F_(2,52) = 0.9, p = 0.4, ANOVA). Differences in final certainty were no longer significant (F_(2,52) = 2.8, p = 0.07, ANOVA); the biggest difference was the nonclinical controls' final certainty, which was numerically higher than the clinical controls' (p(adj) = 0.057).

There were negative correlations between initial certainty and disconfirmatory updating at both baseline (ρ = −0.41, p = 0.00015) and follow-up (ρ = −0.41, p = 0.002), but not between final certainty and the other two measures (p > 0.1 in all four comparisons).

Behavioral results: Dataset 2

The mean responses of subjects in each group are plotted in Figure 2B. There was a significant increase in disconfirmatory updating in Scz compared with controls (t_(88.6) = 2.1, p = 0.04, Welch's t test). There was mixed evidence for a difference in initial certainty between Scz and controls: Scz were more certain after the first bead in Sequences A and B but not Sequences C or D (Fig. 2; Table 3), but the difference in mean initial certainty fell short of statistical significance (t₍₁₁₀₎ = −1.9, p = 0.059, Cohen's d = 0.32, Welch's t test). Final certainty was only assessed in Sequences A and D (B and C contained two changes of color in the last three beads): in both sequences, Scz were less certain than controls (Sequence A: t_(80.1) = 3.0, p = 0.004; Sequence D: t_(85.5) = 3.4, p = 0.001, Welch's t tests).

Initial certainty and disconfirmatory updating negatively correlated within both Scz (ρ = −0.46, p = 0.0003) and control (ρ = −0.57, p = 10⁻¹¹) groups. Final certainty did not correlate with either measure in either group (p > 0.4 in four comparisons).

Modeling results: Dataset 1

Model selection results for the three groups analyzed separately at both baseline and follow-up are plotted in Figure 6 (columns 1, 2, 4, and 5); the probability of each model being best for any given subject is shown in the left panel, and the probability of each model being the best overall is shown in the right panel. Model 6 is the clear winner at each time point, although a minority of psychotic and clinical controls are best fit by Model 4.

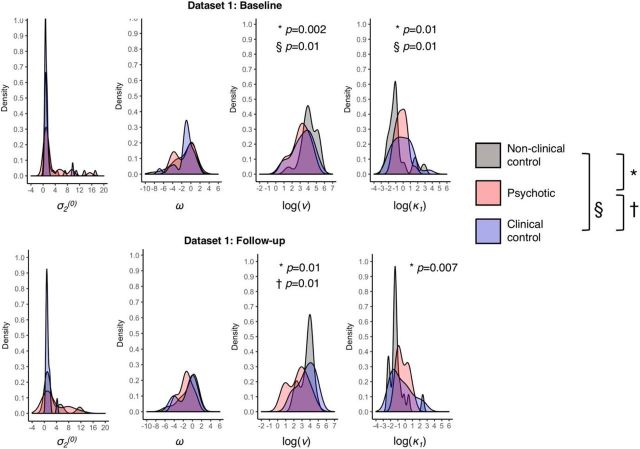
Model 6's parameter distributions are shown in Figure 7; they are skewed; hence, nonparametric tests were used to determine group differences (full details in Table 4; p(adj) refers to the adjusted p value of Dunn's post hoc test). At baseline there were large group differences in belief instability κ₁ (χ²(2, n = 80) = 9.64, p = 0.008, η² = 0.12, Kruskal–Wallis' one-way ANOVA on ranks) and response stochasticity ν (χ²(2, n = 80) = 11.9, p = 0.003, η² = 0.15) but not in σ₂⁽⁰⁾ or ω. There were statistically significant differences in κ₁ between the nonclinical controls and both the psychotic group (p(adj) = 0.01, Dunn's test) and the clinical control group (p(adj) = 0.01), but not between the latter two groups (p(adj) = 0.4). Similarly, there were statistically significant differences in ν between the nonclinical controls and both the psychotic group (p(adj) = 0.002, Dunn's test) and the clinical control group (p(adj) = 0.01), but not between the latter two groups (p(adj) = 0.3).

Figure 7.

Probability density plots for Model 6 parameters in Dataset 1. The distributions of parameter values for σ₂⁽⁰⁾, ω, log(ν), and log(κ₁) are plotted for Dataset 1 at baseline (top row) and Dataset 1 at follow-up (bottom row). Symbols represent significant group differences: §between nonclinical controls and clinical controls; *between nonclinical controls and Scz; †between Scz and clinical controls.

Table 4.

Parameter distributions and statistical tests in Datasets 1 and 2

	σ2(0)	ω	log(ν)	log(κ1)
Dataset 1 (baseline, n = 80)
Nonclinical controls: mean (SD)	2.5 (3.9)	−1.3 (2.4)	4.1 (1.0)	−0.8 (1.4)
Psychotic: mean (SD)	3.0 (3.9)	−1.4 (2.0)	3.1 (1.1)	−0.2 (0.8)
Clinical controls: mean (SD)	1.4 (1.9)	−1.2 (2.0)	3.3 (1.3)	−0.1 (1.4)
Kruskal–Wallis χ2(2,80)	2.33, p = 0.31	0.22, p = 0.9	11.9, p = 0.003	9.6, p = 0.008
	η2 = 0.02	η2 = 0.0	η2 = 0.15	η2 = 0.12
Post hoc Dunn tests
Psychotic versus nonclinical controls	p(adj) = 0.3	p(adj) = 1	p(adj) = 0.002	p(adj) = 0.01
Clinical versus nonclinical controls	p(adj) = 0.2	p(adj) = 0.7	p(adj) = 0.01	p(adj) = 0.01
Psychotic versus clinical controls	p(adj) = 0.2	p(adj) = 0.5	p(adj) = 0.3	p(adj) = 0.4
Dataset 1 (follow-up, n = 55)
Nonclinical controls: mean (SD)	2.8 (3.4)	−0.9 (2.0)	3.6 (0.8)	−1.2 (1.1)
Psychotic: mean (SD)	3.2 (3.7)	−1.4 (1.5)	2.5 (1.2)	−0.3 (0.8)
Clinical controls: mean (SD)	1.2 (0.9)	−1.1 (2.0)	3.5 (1.1)	−0.5 (1.4)
Kruskal–Wallis χ2(2,80)	2.35, p = 0.3	2.32, p = 0.3	8.5, p = 0.01	8.0, p = 0.02
	η2 = 0.04	η2 = 0.04	η2 = 0.16	η2 = 0.15
Post hoc Dunn tests
Psychotic versus nonclinical controls	p(adj) = 0.4	p(adj) = 0.2	p(adj) = 0.01	p(adj) = 0.007
Clinical versus nonclinical controls	p(adj) = 0.2	p(adj) = 0.3	p(adj) = 0.5	p(adj) = 0.1
Psychotic versus clinical controls	p(adj) = 0.3	p(adj) = 0.3	p(adj) = 0.01	p(adj) = 0.1
Dataset 2 (n = 167)
Nonclinical controls: mean (SD)	3.1 (2.6)	−2.3 (2.0)	2.8 (1.0)	−0.8 (0.9)
Scz: mean (SD)	1.9(1.5)	−2.1 (1.8)	2.1 (1.2)	0.2 (1.0)
Mann–Whitney U test	Z = 3.1, p = 0.002, r = 0.24	Z = −0.6, p = 0.6, r = 0.04	Z = 3.9, p = 0.0001, r = 0.3	Z = −5.6, p = 3 × 10−8, r = 0.43
Dataset 2 (better-matched controls, n = 116)
Nonclinical controls: mean (SD)	2.8 (2.7)	−2.2 (2.1)	2.9 (1.1)	−0.6 (1.0)
Scz: mean (SD)	1.9 (1.5)	−2.1 (1.8)	2.1 (1.2)	0.2 (1.0)
Mann–Whitney U test	Z = 1.9, p = 0.056, r = 0.18	Z = 0.12, p = 0.9, r = 0.01	Z = 3.4, p = 0.0007, r = 0.31	Z = −4.1, p = 0.00004, r = 0.38

At follow-up, there were still large group differences in κ₁ (χ²(2, n = 55) = 8.0, p = 0.02, η² = 0.15, Kruskal–Wallis' one-way ANOVA on ranks) and ν (χ²(2, n = 55) = 8.5, p = 0.01, η² = 0.16), but not in σ₂⁽⁰⁾ or ω. There was a significant difference in κ₁ between the psychotic and nonclinical control groups (p(adj) = 0.007, Dunn's test) but not the clinical and nonclinical control groups (p(adj) = 0.1); ν remained significantly different between the nonclinical controls and both the psychotic group (p(adj) = 0.01, Dunn's test) and now also between the psychotic and clinical control groups (p(adj) = 0.01), but not between the clinical and nonclinical controls (p(adj) = 0.5).

We explored whether group differences in κ₁ or ν at baseline and follow-up might be ascribable to IQ (Quick Test score) (Ammons and Ammons, 1962), as the groups' IQ scores were not equivalent (Tables 1, 2). Including both IQ and group status within one regression model is an unsound method of testing for confounding by IQ because group and IQ are clearly not independent here (Miller and Chapman, 2001), so we tested for relationships between the parameters and IQ separately within each group at each time point. No relationships reached statistical significance (all p > 0.1), the closest being a trend between κ₁ and IQ in nonclinical controls only (r = −0.30, p = 0.08); nevertheless, given the smaller group sizes and larger between- versus within-group variances, it remains plausible that IQ differences contribute to group parameter differences.

We tested whether κ₁ or ν at baseline related to delusion-proneness (Peters Delusion Inventory score [PDI]; Peters et al., 1999) across all groups, after first excluding any interaction between PDI and group; PDI significantly correlated with ν (F_(1,67) = 7.1, p = 0.01, ANCOVA) but not κ₁ (F_(1,67) = 3.2, p = 0.079, ANCOVA). We did not analyse the Delusions-Symptoms-States Inventory (Foulds and Bedford, 1975) as it is a less specific measure of delusions. We tested whether κ₁ or ν at baseline was correlated with any particular subgroup of symptoms (measured using the Manchester Scale) (Krawiecka et al., 1977) in both clinical groups only, using the regression models κ₁[or ν] ∼ const + ν₁ * MSaffective + ν₂ * MSpositive + ν₃ * MSnegative: none of the models was significant, however (all p > 0.1).

At baseline, there was no evidence of a correlation between κ₁ and antipsychotic medication dose (p = 0.3), but the correlation between ν and medication dose approached significance (ρ = −0.4, p = 0.067).

We tested for correlations between the Model 6 parameters (Spearman's ρ was used where distributions were not parametric): κ₁ and ν were negatively correlated both at baseline (ρ = −0.38, p = 0.0004) and at follow-up (ρ = −0.52, p = 0.0001), as were κ₁ and ω at baseline (ρ = −0.47, p = 10⁻⁵) and follow-up (ρ = −0.53, p = 10⁻⁵). In estimating the parameters from simulated data, the only correlation present in both simulations (indicating some consistent trading-off between these parameters during estimation) was between κ₁ and ω, with r = −0.5 in each case. This is not surprising, as both κ₁ and ω affect updating to new information throughout the sequence (unlike σ₂⁽⁰⁾) in a deterministic way (unlike ν). Nevertheless, κ₁ was estimated very reliably in the first simulation (Fig. 5, top row) and with reasonable accuracy in the second (Fig. 5, bottom row), so we are confident that the group differences in κ₁ are genuine. The correlations of ρ ≈ −0.5 between ω and κ₁ in Dataset 1 are unlikely to be reliable, however.

Modeling results: Dataset 2

We tested the same six models and performed Bayesian model selection as before. As in Dataset 1, the winning model was Model 6 overall and in each group separately (Fig. 6), although in the Scz group a minority were best captured by Model 4. Model 6's parameter distributions are shown in Figure 8; they are skewed, so nonparametric tests were used (for full details, see Table 4).

Figure 8.

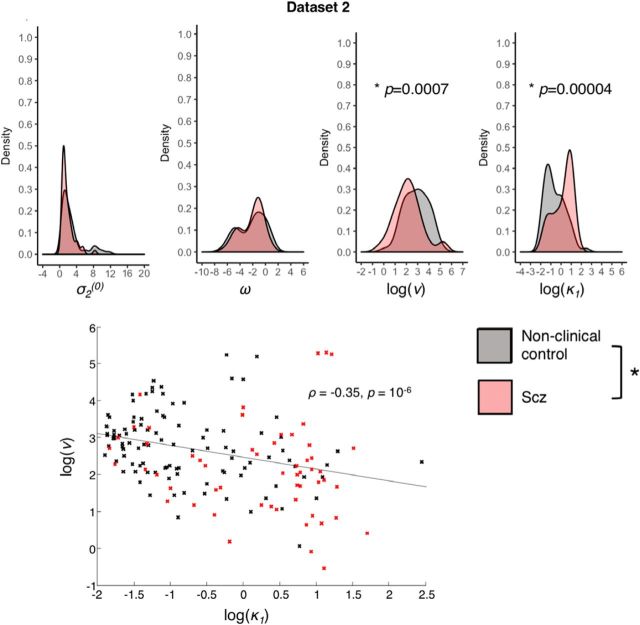
Model 6 parameters in Dataset 2: distributions and correlation. Top, The distributions of parameter values for σ₂⁽⁰⁾, ω, log(ν), and log(κ₁) are plotted for Dataset 2. *Significant group differences between the Scz group and nonclinical control subgroup (well matched in age and sex); the group difference in σ₂⁽⁰⁾ is not indicated because it was nonsignificant (p = 0.056) in the well-matched comparison. Bottom, The significant correlation between log(ν) and log(κ₁) in Dataset 2 is plotted, with controls' parameters in black and Scz in red. Similar correlations were also found in Dataset 1 at both time points.

As in Dataset 1, belief instability κ₁ was significantly higher in Scz than in controls (Z = −5.6, p = 10⁻⁸, Mann–Whitney U test) with a medium-to-large effect size (r = 0.43); also response stochasticity ν was lower in Scz than in controls (Z = 3.9, p = 0.0001, r = 0.3, Mann–Whitney U test), as was initial belief variance σ₂⁽⁰⁾ (Z = 3.1, p = 0.002, r = 0.24, Mann–Whitney U test). There were no statistically significant group differences in evolution rate ω. See Figures 6 and 7 for examples of model fits in subjects with lower κ₁ values (two controls in Fig. 9) and higher κ₁ values (2 Scz subjects in Fig. 10); each figure also illustrates the effects of lower and higher ω values (in the top and bottom rows, respectively). We repeated the analysis using a subset of the controls (n = 60) that were better matched in age and sex, as the original control group was younger and more female than the patient group (Tables 1, 2). The group differences in κ₁ and ν were unchanged in this analysis (Z = −4.1, p = 0.00004; Z = 3.4, p = 0.0007, respectively, Mann–Whitney U tests), but that in σ₂⁽⁰⁾ was no longer significant (Z = 1.9, p = 0.056, Mann–Whitney U test).

Figure 9.

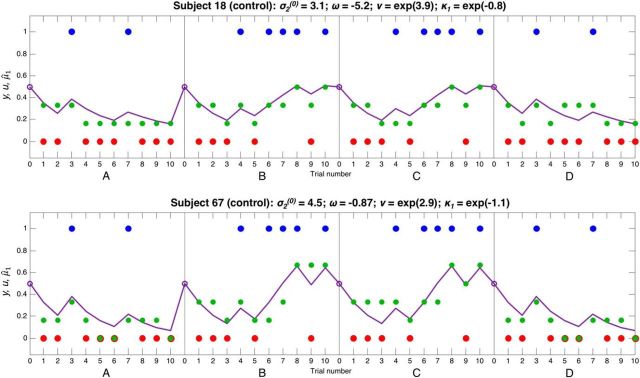
Responses and model fits for 2 control subjects. These plots show 2 control subjects' responses to four 10-bead sequences concatenated together, in the same format as Figure 3 (but without the second level, due to space constraints); in the latter two sequences, blue and red were swapped around for model-fitting purposes. Each plot shows u^(k), the beads seen by the subjects on trials k = 1,…, 10 (blue and red dots), y, the subject's (Likert scale) response about the probability the jar is blue (green dots), and μ̂₁^(k+1), the model's estimate of the subject's prediction the jar is blue (purple line). The parameter estimates for each subject are shown above their graphs. These subjects have fairly similar initial variance σ₂⁽⁰⁾, (inverse) response stochasticity ν, and instability factor κ₁. Subject 18 in the top has a much lower overall evolution rate ω than Subject 67 in the bottom; therefore, Subject 18 never reaches certainty about either jar, and makes relatively small changes to her beliefs in response to beads of varying colors. Both subjects have a low κ₁, and so they make relatively small adjustments to their beliefs following unexpected evidence (this behavior can best be captured by the models containing κ₁; see Fig. 4). Subject 18's responses are very close to those predicted by the model, and this is reflected in her relatively high value of ν.

Figure 10.

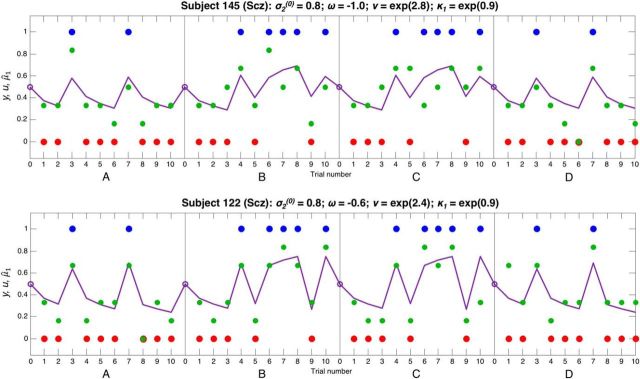
Responses and model fits for 2 Scz subjects. These plots show 2 Scz subjects' responses to four 10-bead sequences in the same format as Figure 9. These subjects have similar evolution rate ω to the control subjects in Figure 9, but they both have a much higher κ₁, meaning that they make much greater changes to their beliefs when presented with unexpected evidence, but do not reach certainty when faced with consistent evidence. Subject 122 (bottom) has a slightly higher evolution rate ω than Subject 145 (top), and so his switching between jars is even more pronounced. These subjects also have slightly lower (inverse) response stochasticity ν than the control subjects in Figure 9, and so their responses tend to be further from the model predictions.

Although IQ (National Adult Reading Test score) (Nelson, 1982) was evenly matched in these groups, working memory (Letter Number Sequencing score) (Wechsler, 1997) was lower in Scz than in controls (Tables 1, 2). We explored whether the group parameter differences might be related to working memory, by testing for correlations between κ₁ or ν and working memory in each group separately (Miller and Chapman, 2001): none was statistically significant (all p > 0.1). We also tested for relationships between κ₁ or ν and IQ (National Adult Reading Test) in each group: ν and IQ (National Adult Reading Test) were correlated in Scz (r = 0.33, p = 0.014), but no other relationships were significant (all p > 0.1).

We tested whether κ₁ or ν related to schizotypy (Schizotypal Personality Questionnaire score; Raine, 1991) across all groups, but neither did so (both p = 0.4, ANCOVA). We tested whether κ₁ or ν was predicted by any particular subgroup of symptoms (measured using the Positive and Negative Symptom Scale) (Kay et al., 1987) in the Scz group only, using the regression model κ₁ [or ν] ∼ const + ν₁ * PANSSgeneral + ν₂ * PANSSpositive + ν₃ * PANSSnegative: the κ₁ model was not significant (F = 0.9, p = 0.4), but ν was weakly predicted by negative symptoms (overall F = 2.76, p = 0.051; for ν₃, t = −2.1, p = 0.04). We had no record of medication dose in Dataset 2.

We tested for correlations between the Model 6 parameters: as in Dataset 1, κ₁ and ν were negatively correlated (Fig. 8; ρ = −0.35, p = 10⁻⁶), but unlike Dataset 1, the only other statistically significant correlation was between κ₁ and σ₂⁽⁰⁾ (ρ = −0.54, p = 10⁻¹³). There was a correlation of r = −0.2 between κ₁ and ν in the data simulated from modal Scz parameter values (Fig. 5, bottom row), but no correlation in the first. This implies that the consistent correlations between these parameters of ρ = −0.38, ρ = −0.52 (Dataset 1 baseline and follow-up) and ρ = −0.35 (Dataset 2) are unlikely to be just estimation artifacts. The only other correlation between parameters in the simulated data was between σ₂⁽⁰⁾ and κ₁, of r = −0.25, in the first simulation only. These parameters were correlated in Dataset 2 but not Dataset 1.

Discussion

Scz tend to update their beliefs more to unexpected information and less to consistent information, compared with controls. We have replicated these behavioral effects, and demonstrated a computational basis for them that is informed by the unstable attractor hypothesis of Scz. In computational models of two 'beads task' datasets, Scz had consistently greater belief instability (κ₁) and response stochasticity (ν) than controls, as the unstable attractor hypothesis predicts. Furthermore, ν correlated with κ₁ in all three experiments, supporting the idea that ν is measuring a stochasticity that is related to κ₁ by an underlying neurobiological process, rather than simply an unmodeled effect.

These findings are important because they connect numerous reasoning biases previously found in Scz (e.g., a disconfirmatory bias) (Garety et al., 1991; Fear and Healy, 1997; Young and Bentall, 1997; Peters and Garety, 2006), increased initial certainty (Peters and Garety, 2006), and decreased final certainty (Baker et al., 2018), and its associated stochasticity in responding (Moutoussis et al., 2011; Schlagenhauf et al., 2014) to model parameters that describe how belief updating in cortex could be perturbed by unstable attractor states due to NMDA (or dopamine 1) receptor hypofunction (Fig. 1).

The unique features of Model 6 that make attractor dynamics a compelling neurobiological explanation for its dominance are both Scz and controls' nonlinearities in belief updating to confirmatory versus disconfirmatory evidence. The Scz group updated its beliefs (sometimes much) more to disconfirmatory than confirmatory evidence, particularly at points of relative certainty about the jar, and the controls were the opposite. Models with uniformly high or low learning rates cannot reproduce these effects; and adding high- or low-level (sensory) uncertainty to a hierarchical model would lead to uniformly high or low learning rates, respectively. Although Models 3 and 4 do show differential updating to confirmatory versus disconfirmatory evidence, this results in beliefs in either jar hovering at ∼0.5 (as in Fig. 4, top left) rather than making large updates from belief in one jar to the other (as when κ₁ = exp(1.2): Fig. 4, bottom left). Furthermore, degraded neuronal ensemble firing (consistent with unstable attractor states) has recently been shown to be common to two different mouse models of Scz (Hamm et al., 2017).

In Dataset 1, belief instability κ₁ and response stochasticity ν were also significantly different between the clinical (mood disorder) and nonclinical control groups when the former were unwell, but not at follow-up, whereas the differences between the psychotic group and nonclinical controls persisted. This indicates that the same computational parameters can be perturbed in either a trait- or state-like manner, perhaps by different mechanisms. It seems unlikely that these parameter changes simply reflect a lack of engagement with the task in clinical groups (especially when unwell) because the consistent changes in κ₁, with which the changes in ν consistently correlate, reflect specific patterns of belief updating.

Parameter relationships with cognition and symptoms

Neither κ₁ nor ν showed significant relationships with IQ (in Dataset 1) or working memory (in Dataset 2) within the groups, giving some indication that the group differences in these cognitive measures were unlikely to be the main drivers of group differences in the parameters. Nevertheless, aside from the correlation between response stochasticity ν and IQ in Dataset 2, it is perhaps surprising that there were not more relationships between κ₁ or ν and cognitive measures in Scz, given it is likely that abnormal prefrontal dynamics have profound effects on all these variables. We may have lacked power to detect them, although Dataset 2 had 80% power to detect a correlation of 0.33, or perhaps different prefrontal regions contribute to working memory, IQ, and belief updating.

One might also question why there were no strong relationships between κ₁ or ν and positive or negative symptom domains (negative symptoms were weakly associated with ν in Dataset 2 only). Again, power may have been an issue, although across all subjects in Dataset 1, response stochasticity ν was associated with PDI score, even after including group in the model, indicating a potential relationship with delusions, but not with the broader concept of schizotypy (assessed in Dataset 2). It is also likely that other pathological factors contribute to symptoms, beyond those measured here (e.g., striatal dopamine availability and positive symptoms). Of note, two other computational studies demonstrating clear working memory parameter differences between Scz and controls also failed to detect any relationship between those parameters and symptom domains (Collins et al., 2014, 2017). Both their and our Scz groups were taking antipsychotic medication, which is also likely to weaken correlations of parameters to positive symptoms.

Although replicated numerous times in the beads task, a 'disconfirmatory bias' is perhaps surprising in Scz, given one might expect delusional subjects to show a bias against disconfirmatory evidence (as indeed they do in tasks involving scenario interpretation) (Woodward et al., 2006). Indeed, the disconfirmatory bias is misleadingly named, as Scz make large shifts in beliefs both away from and back toward the current hypothesis (there are numerous examples in both datasets in Fig. 2). This pronounced switching behavior in the beads task is likely to illustrate a more fundamental instability of cognition and prefrontal dynamics in Scz, rather than being related to delusions specifically; indeed, the latter may be an attempt to remedy the former.

It is interesting that nonclinical controls' data were also best fit by Model 6 in both datasets, implying that even healthy subjects show some asymmetry in their belief updating to expected versus unexpected evidence. Most nonclinical control subjects had κ₁ < 1 (i.e., reduced updating to changing evidence).

Related modeling studies

How do these findings relate to other computational modeling work in Scz? A study of unmedicated, mainly first-episode Scz performing a reversal learning task (Schlagenhauf et al., 2014) also demonstrated an increased tendency to switch that was not accounted for by reward sensitivity (which would be affected by more stochastic behavior), and increased switching also occurs in chronic Scz (Waltz et al., 2013), although not always (Pantelis et al., 1999).

Two recent studies of similar tasks in Scz populations have also demonstrated evidence of nonlinear belief updating. Jardri et al. (2017) showed that the Scz group on average “overcount” the likelihood in a single belief update, an effect they attribute to reverberating cortical message-passing but could also be due to the belief instability shown by Model 6. Stuke et al. (2017) showed, in a very similar task, that all subjects showed evidence of nonlinear updating, but the Scz group updated more than controls to “irrelevant information” (i.e., disconfirmatory evidence). Some differences between their model and ours are that they did not estimate response stochasticity in their subjects (neither did Jardri et al., 2017), and their 'nonlinearity' parameter was bounded by linear updating on one side, approximately equivalent to belief instability κ₁ being constrained to being <1 in our model, whereas we have shown (as in Jardri et al., 2017) that Scz belief updating is often beyond this bound (Fig. 7) and more stochastic. Conversely, Moutoussis et al. (2011) demonstrated increased response stochasticity in acutely psychotic subjects but did not test for differences in belief updating.

The extent to which a loss of belief stability in Scz is apparent depends critically on the strength (precision) of incoming sensory evidence relative to the current belief (prior): if the former is less precise, no belief switching may occur, and instead the percept may be weighted toward the prior. In the beads task, sensory evidence (i.e., the color of the bead drawn) is unambiguous, but a task using very imprecise auditory sensory evidence (Powers et al., 2017) demonstrated some interesting heterogeneity in Scz: nonhallucinating Scz showed greater belief updating relative to controls, whereas in hallucinating Scz, percepts were driven by prior expectations, leading to a reduction in the updating of their beliefs (relative to controls).

Further evidence for heterogeneity in Scz is that those with delusions have greater certainty about the hypothesis that matches the evidence at every stage (Speechley et al., 2010), unlike the reduced final certainty we observed in Scz in Dataset 2. On the other hand, Scz with high negative symptoms have difficulty choosing the most rewarding option very consistently (Gold et al., 2012), which may reflect a lack of certainty about its value. We lacked sufficient power to detect differences between Scz with exclusively high positive or negative symptoms, however.

Limitations

Each of our datasets contains some limitations of the beads task that are addressed by the other. Dataset 1 did not include a memory aid or measure working memory, but Dataset 2 did both, and Dataset 2 also matched IQ across groups much better than Dataset 1; Dataset 2 used a Likert scale for responding and so could potentially exaggerate small changes in belief updating, but Dataset 1 used a continuous measure; Dataset 2 only tested stable outpatients, but Dataset 1 tested more unwell inpatients and retested them once they were better. The main limitation common to both datasets is that all subjects with psychotic diagnoses were taking antipsychotic medication when tested. Although the correlation between ν and medication dose was almost significant in Dataset 1, this relationship seems likely to be driven by illness severity rather than medication itself. Dopamine 2 receptor antagonists seem to both reduce overconfidence in probabilistic reasoning (Andreou et al., 2014) and also reduce motor response variability (Galea et al., 2013) and so, if anything, likely reduce our group differences.

In conclusion, we have shown that Scz subjects in two independent beads task datasets have consistent differences in two parameters of a belief updating model that attempts to reproduce consequences of attractor network instability. This study was designed to link patterns of inferences to model parameters that (do or do not) mimic the effects of abnormal attractor states on belief updating. The HGF itself does not contain attractor states, and no relation between its parameters and NMDAR function has hitherto been tested. More detailed spiking network modeling, pharmacological (or other NMDAR) manipulations, and imaging are required in the future to understand how neuromodulatory function in both pyramidal cells and inhibitory interneurons contributes to real attractor dynamics and probabilistic inference, and to seek empirical evidence for a correspondence between the stability of network states and the stability of its inferences (especially in Scz). This work underscores the importance of relating psychological biases to their underlying computational mechanisms, and thence (in future) to the constraints (e.g., the hypofunction of NMDARs) that neurobiology imposes on these mechanisms.