High-speed OCT-based ocular biometer combined with an air-puff system for determination of induced retraction-free eye dynamics

Abstract

We demonstrate a swept source OCT-based ocular biometer integrated with an air-puff stimulus to study the reaction of the eye to mechanical stimulation in vivo. The system enables simultaneous measurement of the stimulus strength and high-speed imaging of the eye dynamics along the visual axis. We characterize the stimulus and perform optimization of the data acquisition for a proper interpretation of the results. Access to the dynamics of axial eye length allows for a determination of the eye retraction, which is used to correct the air-puff induced displacement of ocular structures. We define the parameters to quantify the reaction of the eye to the air puff and determine their reproducibility in a group of healthy subjects. We observe the corneal deformation process and axial wobbling of the crystalline lens. OCT biometer combined with the air puff is the first instrument with the potential to provide comprehensive information on the biomechanics of ocular components.

1. Introduction

The human eye represents a complex dynamic system whose properties can be considered from both optical and mechanical points of view [1–3]. Optics of the eye has been explored for centuries, however, the biomechanical aspects of the eye have recently caught attention as biomechanics plays a role in many physiological ocular effects and corresponding diseases, e.g. accommodation (presbyopia), development of myopia, glaucoma, keratoconus, vitreo-retinal diseases, and in the outcome of refractive surgery [4–6]. In particular, the measurement of intraocular pressure (IOP), an important diagnostic parameter, is influenced by the biomechanics, and vice versa [7].

Current measurement paradigms for the IOP and biomechanics include application of the mechanic force in a non-contact way like the air puff, and simultaneous non-invasive visualization of the tissue reaction to such a stimulus [8,9]. Generally, the air pulse directed to the eye causes an inward movement of the cornea from the normal state to slight concavity. Few milliseconds later, the cornea undergoes an outward movement from the concavity state to the normal convex curvature. Thus, there are two applanated positions of the cornea during the cycle [7,10–12]. Apart from the corneal deformation, the entire eye also retracts and rotates when the air puff is applied [10,11].

The Ocular Response Analyzer (ORA; Reichert Inc., USA) is the first clinically accepted device that determines the IOP and the corneal biomechanics using non-contact air-puff stimulus. ORA device consists of a pump to generate the air puff, and the eye dynamics is registered by detecting the light beam reflected from the corneal interface [13]. Analysis of the corneal dynamics allows to obtain different parameters associated with corneal biomechanics such as corneal hysteresis (CH), corneal resistance factor (CRF) or corneal constant factor (CCF) [13–15]. Another commercial tonometer utilizing the same corneal deformation process integrates high-speed Scheimpflug camera to image the dynamic behavior of the anterior chamber morphology (Corvis ST; OCULUS Optikgeräte GmbH, Germany). Corvis ST device is able to capture 433 frames within 100 ms period (4330 frames per second) [16,17]. Analysis of the image sequence allows to extract the parameters of corneal deformation like the highest concavity time, the highest concavity curvature or time and the length of corneal applanation etc [17,18]. Recently, additional parameters related to corneal deformation have also been reported [19,20].

A correct assessment of the deformation amplitudes of the eye components requires taking into account the movement of the eye as a whole. The eye retraction correction is implemented in the next-generation of Corvis ST instrument, in which the analysis of the displacement of periphery of the cornea represents the movement of the whole eye during air-puff stimulation [10–12].

Optical Coherence Tomography (OCT) is a non-invasive and non-contact imaging modality that enables two-dimensional cross-sectional or three-dimensional volumetric imaging at micrometer resolution [21–23]. The structural information of the eye comes from the light backscattered from the layers with different optical properties. In the last ten years, OCT with Fourier-domain detection demonstrated advantages in the anterior segment imaging [24–27]. Fourier-domain OCT instrumentation can be implemented in two ways: spectral-domain OCT (SD-OCT) with a broadband light source and a spectrometer, or swept-source OCT (SS-OCT) with a wavelength-tunable light source and a high-speed point detector [28]. SS-OCT has experienced a tremendous progress related to the coherence length of swept light sources. New light source technologies like vertical-cavity surface emitting lasers, short external cavity MEMS-tunable lasers or distributed Bragg reflector (akinetic) lasers have shown to be able to perform long-range imaging [29]. As a result, ocular biometry of the eye in vivo, i.e. to measure the intraocular distances including the axial eye length, could be realized with high accuracy and precision, which has led to the introduction of new optical biometers in clinical practice [30–34].

Both generations of Fourier-domain OCT instruments were integrated with air-puff tonometers in order to assess the biomechanical properties of the cornea. The air puff was directed collinearly with the optical beam in SS-OCT [35] or a tilted mirror was used to couple mechanical excitation and optical probing in the same direction [36]. The studies with air-puff OCT systems were conducted on ex vivo eyes of model animals or in vivo human eyes [35,37]. Biomechanics of the eye was studied with sub-microscopic air-puff stimulation to reveal corneal resonances [38,39]. In addition to that, OCT was used as a modality to map elastic properties of tissues (optical coherence elastography, OCE) [40]. OCE in ophthalmic applications was demonstrated in several configurations of mechanical excitation and optical probing, and those studies were focused on extracting biomechanics of the cornea and the crystalline lens [41–43].

In this paper, we demonstrate an original long-range SS-OCT instrument integrated with an air-puff system, which enables comprehensive measurement of the reaction of all ocular structures to mechanical stimulus. The system extends the concept of regular M-mode imaging systems with air-puff stimulus that have been developed earlier for the in vivo and ex vivo studies of corneal dynamics [35,37]. The system allows for performing ocular biometry during air puff along the visual axis of the eye. Therefore, not only the corneal response can be analyzed but also the reaction of other ocular components such as the crystalline lens or the eye globe as a whole. We also present the optimization of both imaging and air-puff subsystems to correctly determine the dynamics of the eye. We show the potential of this technology in human eyes in vivo in terms of the reproducibility of extracted parameters. In this paper, a novel method of correction of measured deformation for eye retraction (movement of the whole eye) is also presented. The SS-OCT based ocular biometer is the first instrument enabling a complete characterization of eye reaction to short mechanical stimulation, including observations of the effects such as retraction and axial lens wobbling.

2. Methods

2.1 Optical setup

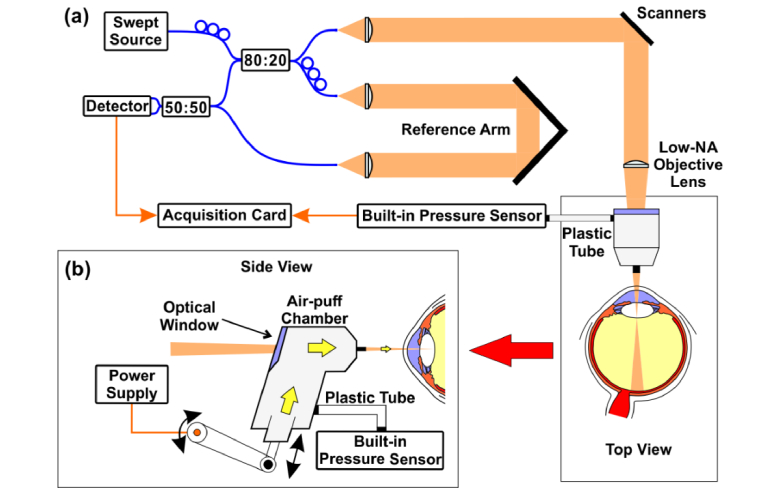
The experimental system used in this study was a long-depth range SS-OCT system integrated with an air-puff system (Fig. 1(a)). It was a fiber-optic Michelson interferometer with a 80:20 splitting ratio between the arms. The instrument operating at the sweep rate of 30 kHz utilized a short-cavity swept source laser (Axsun Technologies Inc., USA), which emitted light at the central wavelength of 1,050 nm and the optical bandwidth of 35 nm. The source had a long instantaneous coherence length (−6 dB width of coherence function was 118 mm) to enable imaging through the entire eye length and performing biometric measurements.

Fig. 1.

Prototype air-puff SS-OCT ocular biometer: (a) Schematic representation of the optical setup integrated with the air-puff system. (b) Integration of the air-puff chamber in the sample arm of the OCT system (side view).

An objective lens of f = 100 mm with low numerical aperture was selected to provide sufficiently long depth of focus of 4.1 mm, which was determined by a CMOS beam profiler (WinCamD-LCM; DataRay Inc., USA). The interferometric fringes were detected by a dual-balance detector (PDB480-AC; Thorlabs Inc., USA), and digitized by a dual-channel acquisition board at the sampling rate of 200 MS/s (Gage Compuscope 14200; Gage Applied Inc., USA). The OCT signal acquired at the first channel of the board. The measured sensitivity of the system was101 dB for the optical power of 1.9 mW incident on the eye. The axial resolution and the imaging depth range of the designed OCT system were 20 µm and 28.97 mm, respectively.

2.2 Air-puff subsystem

The sample arm of the interferometer was integrated with an air-puff chamber taken from a commercial non-contact tonometer (XPert NCT; Reichert Inc., USA). The details about the mechanical integration and the specifications of the electronic drivers were described earlier [35]. The movement of a plunger resulted in generation of the puff (duration ca. 20 ms) exiting the nozzle (3 mm in diameter), and the speed of a plunger was controlled by an external power supply (Fig. 1(b)). The optical beam was collinear with the direction of the air puff. The light passed through the air-puff chamber thanks to the optical window. The air-puff chamber was also equipped with a built-in internal pressure sensor (connected with the air-puff chamber via a plastic tube) to monitor the time-dependence of the pressure exiting the air-puff nozzle (Fig. 1(b)). The signal from the built-in pressure sensor was acquired by the second channel of the acquisition card.

The data acquisition was synchronized with start of the piston movement in the air-puff chamber. Each data set consisted of 4,000 A-scans (corresponding to the total measurement time of 132 ms) collected along the visual axis of the eye (from the anterior to posterior pole of the eye) and a corresponding time-evolution of the pressure generated in the chamber.

2.3 In vivo eye imaging and data post-processing

The study involved human subjects and it was approved by the Institutional Review Board (Bio-Ethics Committee) at the Nicolaus Copernicus University (Collegium Medicum). All procedures adhered to the tenets of the Declaration of Helsinki. Each subject was informed about the nature of the study, and the consent was obtained before scanning the eye. Five healthy subjects were recruited in this study (mean age 27.6 ± 3.5 yo; age range: 22-33 yo; mean spherical equivalent refractive error −1.25 ± 1.75 D; range: + 0.25 D to −3.75 D), and a single randomly selected eye from each subject was measured 8 times. An experienced operator precisely aligned the interface of the system using a preview mode of the instrument. A cross scan pattern was used in the preview mode so that the operator could observe both horizontal and vertical cross-sections. The eye was aligned to the optical axis of the device since the subject placed his / her head in a chinrest and was asked to look directly to the air pipe. The eye was positioned 10 mm away from the pipe end. The focal plane of the objective lens was located at the back surface of the crystalline lens. All measurements were taken in the photopic conditions to achieve small pupil sizes since the lateral scan range available in the preview mode was limited by the internal diameter of the nozzle. This solution enabled observation of the iris and precise alignment of the eye. The measurement was taken when the specular reflection was found near the center of the preview scans to avoid a total saturation of the image.

Data post-processing included the following steps: (1) segmentation of the ocular interfaces (anterior and posterior cornea, anterior and posterior lens, retina); (2) refraction correction of the image; (3) eye retraction correction; (4) measurement of deformation of cornea and crystalline lens deformation; (5) ocular biometry (measurement of intraocular distances including the axial eye length) at different observation phases such as before air-puff application and during maximum deformation; (6) measurement of the corneal hysteresis and the corneal slope; (7) determination of the moments of maximum speed and acceleration of the corneal apex during the puff. The details of the procedure along with demonstration of the extracted parameters are presented in Sections 3.3-3.5.

The statistical analysis of all data sets enabled the assessment of reproducibility of the parameters described above. The data were further analyzed using Microsoft Excel 2013 spreadsheet (Microsoft Corp., Redmond, WA). One-way analysis of variance (one-way ANOVA) with a random-effects model was used. Intraclass correlation coefficients (ICC) and 95% confidence interval (CI) of ICC were calculated. The grand mean of each defined parameter x was calculated. The standard deviation SD_x was calculated using the formula:

$$S{D}_x=\sqrt{\frac{{\displaystyle \sum _{i=1}^M{\displaystyle \sum _{j=1}^N{\left(x_{ij}-{\overline{x}}_i\right)}^2}}}{M\left(N-1\right)}},$$ (1)

where: x_ij is a j-th measurement of i-th subject, ${\overline{x}}_i$ is the mean values of the parameter for i-th subject, M = 5 is the number of subjects, and N = 8 is the number of measurements for each subject. The numerator in Eq. (1) is the sum of squares ‘within’ the subject taken from ANOVA. Finally, the coefficient of variation (CoV) was computed as the ratio of the standard deviation to the mean.

3. Results

3.1 Calibration of the force and the spatio-temporal profile of the air puff

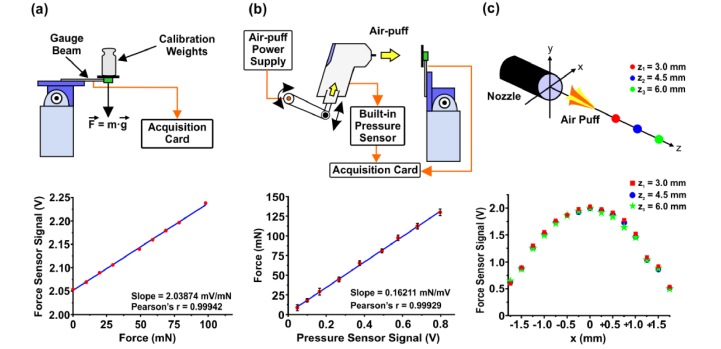
The internal (built-in) pressure sensor had to be calibrated prior to the study to reveal actual air-puff force. Accordingly, we developed a customized external force sensor that was based on a strain gauge beam of the cantilever type. The free end of the strain gauge beam was loaded by an air stream acting on the circular adapter (30 mm in diameter) in the direction normal to its surface. The fixed end of the cantilever beam was attached to the revolve arm of the external force sensor (Fig. 2(a)). The arm could be rotated relative to the sensor body associated with the housing of the OCT set-up. Two strain gauges were placed in the central part of the strain gauge beam: the first one on the tension site and the second one on compression side of the gauge beam. Therefore, the system operated as a full bridge Wheatstone circuit. Loading the free end of the strain gauge beam caused its deformation. As a consequence, this changed the resistance of the strain gauges, which generated the measurable voltage changes (signal) in the bridge Wheatstone circuit.

Fig. 2.

Determination of the spatial characteristics of the air-puff. (a) Calibration of the customized external force sensor. Relation between weight (gravitational force) and external force sensor signal. (b) Calibration of the internal pressure sensor of the air-puff system with the force sensor. Relation between pressure sensor signal and force (force sensor signal). (c) Characterization of the air-puff shape in transverse (x-axis) and axial (z-axis) directions. The spatial filter and the external force sensor have not been shown. The maximum of the force sensor signal across the nozzle diameter for different positions behind the nozzle end.

The built-in pressure sensor of the air-puff system was calibrated by the external customized force sensor to obtain the relation of the force exerted on the corneal apex with the air-puff. The entire procedure of calibration of the internal pressure sensor included two steps. Firstly, the external force sensor was calibrated in horizontal position of gauge beam by loading it with the test weights (1 g to 10 g; gravitational force). A linear relation between force acting on the sensor and the output voltage signal was obtained (Fig. 2(a)).

Secondly, the internal air-puff pressure sensor was calibrated with respect to external force sensor to find the relation between voltage signals from both sensors. The customized force sensor with vertical orientation of the gauge beam was placed in front of the instrument, at the distance of 10 mm of the air-puff nozzle, which was the same distance where the eyes were positioned in the in vivo measurements. During the test, the air-puff strength (amplitude) was controlled by a control drive supplied by an external power supply in the range between 30 V and 70 V in steps of 5 V. For each voltage level from the power supply, 5 measurements of air-puff waveforms were taken by the internal pressure sensor of the air-puff system and by the customized force sensor using the dual-channel acquisition card. Both averaged temporal profiles were calculated for each air-puff amplitude, and the maximum amplitudes were determined. Additionally, the voltage from the external force sensor was transformed into force using the relation in Fig. 2(a). A linear dependence between the signal from the internal sensor, and the force detected by the customized force sensor was found (Fig. 2(b)). During a standard operation of the air puff in subsequent in vivo measurements, the control electronics of the puff was driven at the voltage level 70 V from the power supply. This corresponded to the peak force (generated by the air-puff system) of 130 mN in the plane of the cornea (i.e. 10 mm behind the nozzle end).

Finally, the external force sensor with a spatial filter (a pinhole) of the diameter of 400 µm in front of the sensor was used to determine the spatial distribution of the air puff. We characterized the transverse profiles of the air puff by shifting the effective sensing area (the force sensor together with the pinhole) along the x-axis with the steps of 0.25 mm. The profiles were obtained for different distances away from the end of the nozzle, i.e. 3 mm, 4.5 mm and 6 mm (Fig. 2(c)). Figure 2(c) demonstrates that the profiles of the air puff behind the nozzle represent Gaussian-like shapes.

3.2 Synchronization of the optical detection and air-puff pressure sensing

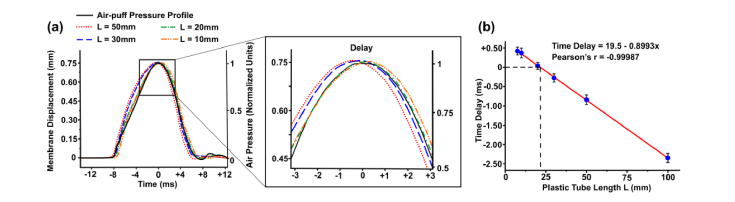
The OCT signal and the air-pulse (mechanical excitation) signal from the puff are acquired by the same acquisition card. Since our data analysis required determination of the tissue reaction to mechanical stimulus in time, it was critical to avoid any possible delay that would significantly modify the shape of hysteresis loop and consequently would impact the interpretation of the viscoelastic properties of the ocular tissues. The dynamics of the stimulus strength should be measured at the eye position (10 mm away from the nozzle end) so that one could relate the signal level from the built-in pressure sensor with the A-scan showing the eye response to the air-puff. However, the design of the air-puff chamber, which was connected with the built-in pressure sensor via the short plastic tube, introduced an unwanted time delay that could be controlled by changing the length of the tube. Therefore, we studied the impact of the length of plastic tube of the internal (built-in) pressure sensor of the air puff on the detected temporal characteristics of the pressure waveform.

The test was based on the analysis of the air-puff deformation of the latex membrane which is regarded as an elastic material that does not produce any delay between mechanical stimulation and the material reaction. The sample was located 10 mm away from the nozzle end. The light reflected from the membrane and the air-puff pressure were detected with the air-puff SS-OCT system. The time delay between the stimulus and the response of the membrane was assessed. The time evolution of the membrane displacement and the signal from the built-in pressure sensor for different lengths L of the tube are shown in Fig. 3(a), and the time delay between maximum deformation and air-puff peak is plotted in Fig. 3(b). We found out that the optimum length of the plastic tube is L = 21.7 cm, which corresponds to zero time delay between the signal from the pressure sensor and the deformation of the phantom (membrane). That length of the tube was implemented in the air-puff SS-OCT system in the next stages of our study.

Fig. 3.

Optimization of air-puff signal and optical detection of sample deformation. (a) Signal delay caused by the length L of the tube that connects the air-puff chamber and the built-in pressure sensor. Time scale is offset with respect to the selected data set. (b) Dependence of the delay between displacement and pressure temporal profiles on the length L of the tube.

3.3 Whole eye reaction to air-puff stimulus

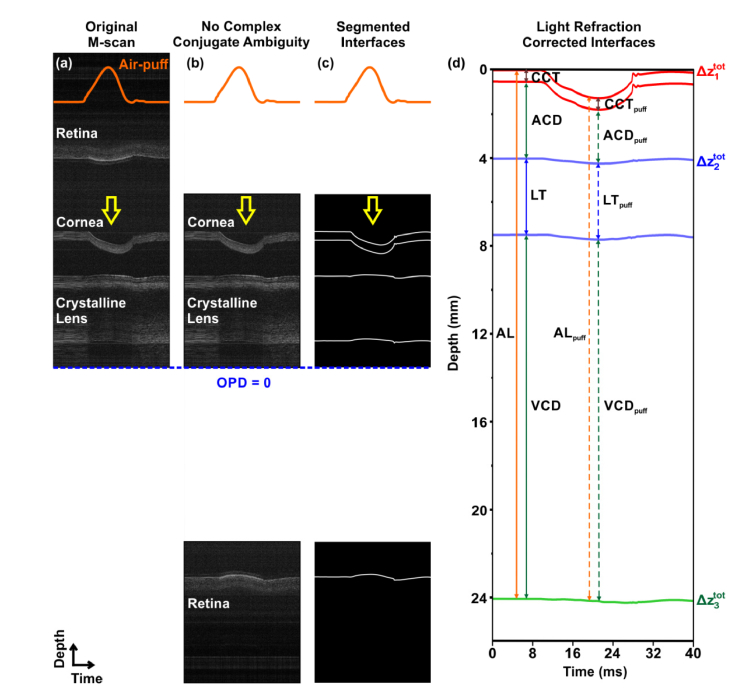
The experiments shown in previous sections made the air-puff long-range SS-OCT instrument optimized to image the temporal changes of all ocular components along the visual axis of the eye. Figure 4(a) shows an example of M-scan representing the reaction (temporal changes) of the cornea, the crystalline lens and the retina, when they were excited by the mechanical stimulus (air puff). The temporal profile of the air puff (of the length of ca. 20 ms) is also superimposed in Figs. 4(a)–4(c). The ocular components in Fig. 4(a) are not positioned in the anatomical order due to the fact that the depth range of OCT system is not long enough to perform full-eye-length imaging. The retina in the M-scan is a complex conjugate signal that does not overlap with the signal from the cornea or from the crystalline lens since the length of the reference arm of the interferometer is set appropriately. Therefore, complex conjugate ambiguity can be easily corrected by cropping a part of the image with the retina, mirroring it and positioning on the other side of the zero optical path delay (Fig. 4(b)). In the next step, the interfaces of the cornea, the crystalline lens and the retina are segmented, and a binary image is generated (Fig. 4(c)).

Fig. 4.

Eye reaction to the air puff and ocular biometry. (a) SS-OCT M-scan of the response of the ocular components to the air puff measured along the visual axis. Acquired data set. Representative M-scan of the left eye of 31-yo subject representing dynamics of the ocular components during air puff and segmented analysis. Temporal evolution of the air puff is plotted with orange line. The yellow arrow indicates the air-puff action. The blue dashed line represents zero optical path delay (OPD = 0). (b) The complex conjugate resolved M-scan. (c) Binary image showing segmentation of ocular interfaces. (d) Dynamics of the eye components after correction for light refraction. Geometrical distances correspond to ocular biometry measurements that can be performed before the air puff and at the maximum displacement. CCT – central corneal thickness, ACD – anterior chamber depth, LT – lens thickness, VCD – vitreous chamber depth, AL – axial eye length. The parameters with subscript ‘puff’ indicate the parameters measured at maximum deformation.

It has to be mentioned that the crystalline lens and the retina in Figs. 4(b) and 4(c) seem to be deformed in the direction opposite to that of the air puff. However, it is necessary to take into account that OCT maps optical distances. As a consequence, we corrected the M-scan for light refraction using the following group refractive indexes of the ocular components (calculated for 1050 nm): cornea – 1.3755, aqueous – 1.3356, crystalline lens – 1.4048 (averaged), vitreous – 1.3354 [30]. Thus, air-puff-induced dynamics of ocular structures and ocular media at the visual axis of the eye can be revealed (Fig. 4(d)). Morphologically correct data allow to perform the ocular biometry (the measurement of intraocular distances including the axial eye length) and enable extracting the deformation time-profiles (Fig. 4(d)).

3.4 Deformation correction for eye retraction

The eye reaction to the mechanical stimulus is based on the displacements of the ocular structures (e.g. cornea, crystalline lens). However, the total displacement (deformation) amplitude $\Delta z_i^{tot}$ of the particular structure (with the index i) at time t is given by the deflection amplitude $\Delta z_i$ and the movement of the eye as a whole (eye retraction) $\delta z^{retr}$:

$$\Delta z_i^{tot}\left(t\right)=\Delta z_i\left(t\right)+\delta z^{retr}\left(t\right).$$ (2)

In our case, i = 1 is the cornea, i = 2 is the crystalline lens and i = 3 stands for the retina (Fig. 4(c)). Accordingly, the deflection (retraction-free displacement) of the ocular component, which represents an effective impact of the stimulus, requires subtraction of the retraction amplitude:

$$\Delta z_i\left(t\right)=\Delta z_i^{tot}\left(t\right)-\delta z^{retr}\left(t\right).$$ (3)

Ocular biometry performed during the air puff provides information on the behavior of the cornea, the crystalline lens and the retina during the stimulus, which also enables the measurement of the intraocular distances (Fig. 5(a)). Air-puff-induced dynamics of the retina allows for the extraction of the eye retraction, as given by the formula:

$$\delta z^{retr}\left(t\right)=\Delta z_3^{tot}\left(t\right)-\Delta z_3^{tot}\left(t=0\right),$$ (4)

where t = 0 indicates any moment before the air puff. In other words, changes of the axial position of the retinal layer in the OCT M-scan relative to the pre-puff phase is the eye retraction (Fig. 5(a)).

Fig. 5.

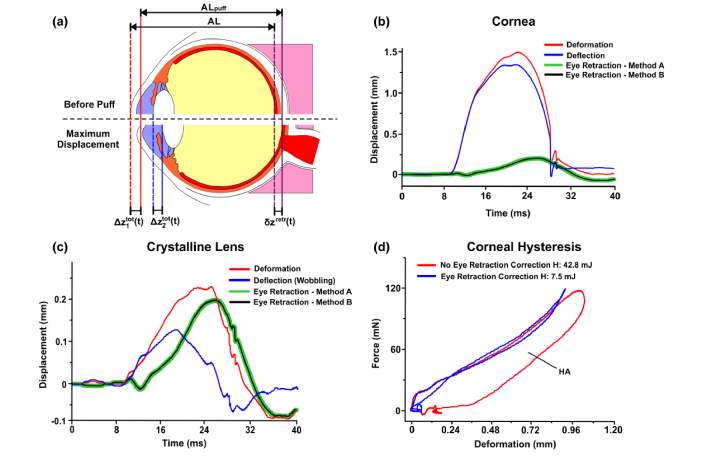
Correction of measured displacement for eye retraction. (a) Schematic of the eye retraction during air-puff stimulation. The eye before the air-puff stimulation and during maximum deformation. (b) Extracted eye retraction dynamics from full-eye-length OCT data using method A and B. Displacement of the corneal apex (anterior corneal interface) of the left eye of 28-yo subject before (red) and after (blue) eye retraction correction. (c) Extracted eye retraction dynamics from full-eye-length OCT data using method A and B. Displacement of the anterior lens surface of the same subject before (red) and after (blue) eye retraction correction. (d) Corneal hysteresis before (red) and after (blue) eye retraction correction. AL – axial eye length before the air puff application, AL_puff – axial eye length during maximum deformation, CH – corneal hysteresis.

Accordingly, the deformation of cornea or the crystalline lens can be corrected for eye-retraction with two interchangeable approaches:

• (A)directly using Eq. (3) applied to the cornea (i = 1) or the crystalline lens (i = 2) whereas the eye retraction is calculated from Eq. (4) by monitoring the retinal position during the air puff;
• (B)
  indirectly since the changes of the eye length AL during the puff relative to the initial eye length demonstrates retraction-free deflection of the cornea:

  $$\Delta z_1\left(t\right)=AL\left(t=0\right)-AL\left(t\right).$$ (5)

This observation expressed by Eq. (5) is a consequence of the definition in Eq. (2), and comes from the fact that the axial eye length is defined as the distance between the anterior and posterior pole of the eye, i.e. it is the difference between the corneal apex and the retina $(AL\equiv \Delta z_1^{tot}-\Delta z_3^{tot}).$ Therefore, no explicit calculation of the eye retraction $\delta z^{retr}$ is needed during determination of corneal deflection. Having corneal deformation $\Delta z_1^{tot}$ and corneal deflection $\Delta z_1,$ one can calculate the eye retraction $\delta z^{retr}$ (Eq. (2)). This can be further used when the correction of the lens deformation for the eye retraction is performed.

Figures 5(b) and 5(c) demonstrate the results of the impact of eye retraction correction on the measured corneal apex displacement and crystalline lens displacement. The correspondence of the above-mentioned approaches to eye retraction correction is proven. The eye retraction dynamics during the air-puff stimulation calculated from Eq. (4) (method A) overlap with that extracted from the analysis of the eye length (method B). Consequently, the maximum amplitude of retraction-free displacement of the corneal apex is lower than that before correction (red and blue curves in Fig. 5(b)). What is more, the eye retraction correction of the crystalline lens movement reveals an oscillatory movement of the lens (displacement changed from positive to negative values), which is an axial wobbling of the lens induced by the puff (Fig. 5(c)).

3.5 Extracted parameters of the dynamics of ocular structures

The reaction of the eye to the air-puff shown in Fig. 4(d) can be quantitatively described by the measurements of the intraocular distances at different observation phases such as before air-puff application and during maximum deformation. The analyzed biometric parameters include: the central corneal thickness (CCT and CCT_puff); the anterior chamber depth (ACD and ACD_puff); the lens thickness (LT and LT_puff), the vitreous chamber depth (VCD and VCD_puff), and the axial eye length (AL and AL_puff) (Fig. 4(d)). The deformation profiles also allow for the extraction of (maximum) deformation amplitudes. Next, the difference between particular distance measured before the air puff and during maximum deformation demonstrates the compression of the corresponding ocular structure or medium (i.e. the cornea, aqueous, lens, vitreous and the eyeball).

The ocular biometer developed in this study enables simultaneous measurement of the temporal evolution of the pressure (force) F(t) and the deflection of the corneal apex (after eye retraction correction) z₁(t). Those two equations can be treated as parametric equations with time t as a parameter. If the parameter t is eliminated, one can obtain a hysteresis loop F(z₁). This approach has been reported for ex vivo porcine corneas, and it provides an insight into viscoelasticity of the tissue [37]. The area of hysteresis HA can be interpreted as the energy loss due to the viscous properties of the cornea. Figure 5(d) demonstrates the example of corneal hysteresis loop showing two phases: loading and unloading. The eye retraction correction modifies the hysteresis significantly so that the HA is ca. 5-6 × lower. Elastic properties of the cornea dominate the air-puff induced reaction.

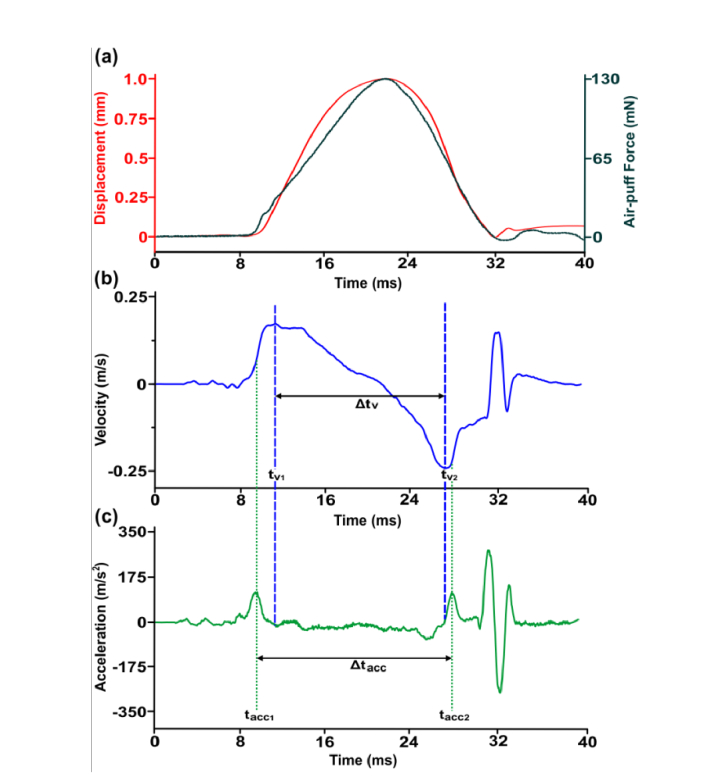
Another set of parameters can be extracted by the analysis of the temporal behavior of the displacement (deformation or deflection) of the cornea. Access to temporal profile allows calculation of the corneal apex velocity and acceleration, which directly show the dynamics of corneal apex (Fig. 6). The velocity profile represents two extrema: maximum t_v1 and minimum t_v2 corresponding to the corneal movements during inward and outward applanations. Moreover, zero velocity is related to the maximum deformation, i.e. the change of the direction of motion (Fig. 6(b)). The vibrations at the end of the air puff clearly visible in Fig. 6(b) and 6(c) have been neglected in the analysis. The acceleration profile shows also two maxima, t_acc1 and t_acc2 (Fig. 6(c)). We also calculate the time intervals between velocity extrema Δt_v and Δt_acc (Fig. 6(b) and 6(c)).

Fig. 6.

Analysis of the temporal profile of the deformation (deflection of the cornea) of the right eye of 22-yo subject. (a) Corneal deformation after eye retraction correction. Air-puff stimulus. (b) Corneal apex velocity. (c) Corneal apex acceleration.

To sum up, we defined the following parameters that describe the response of the ocular components to the air puff:

• (1) ocular biometry before the air puff (CCT, ACD, LT, VCD, AL),
• (2) ocular biometry at the maximum deformation (CCT_puff, ACD_puff, LT_puff, VCD_puff, AL_puff),
• (3) amplitudes of deformation of the cornea and the crystalline lens interfaces,
• (4) compression of ocular tissues and ocular media,
• (5) corneal hysteresis HA,
• (6) temporal characteristics of the corneal deformation (t_v1, t_v2, t_acc1, t_acc2, Δt_v and Δt_acc).

3.6 Measurement precision and reproducibility

We recruited 5 subjects to assess the reproducibility and precision. A summary of intraclass correlation coefficients (ICCs) is given in Table 1. All parameters except for CCT compression, LT compression and corneal HA show good (0.75 < ICC < 0.9) or excellent (ICC > 0.9) intersession reproducibility. The highest ICC values (reaching almost 1) are obtained for the intraocular distances (except for CCT). The eye retraction correction methodology implemented in the data post-processing does not affect reproducibility.

Table 1. Precision and reproducibility of computed parameters.

	Parameter	No Eye Retraction Correction			With Eye Retraction Correction
		ICC	Grand Mean ± SD	CoV [%]	ICC	Grand Mean ± SD	CoV [%]
Biometry before air puff [mm]	CCT	0.8797	0.567 ± 0.012	2.13	0.8796	0.567 ± 0.013	2.13
	ACD	0.9914	2.885 ± 0.079	2.72	0.9984	2.895 ± 0.035	1.19
	LT	0.9979	4.126 ± 0.041	0.98	0.9979	4.126 ± 0.041	0.98
	VCD	0.9998	17.057 ± 0.049	0.29	0.9998	17.057 ± 0.049	0.29
	AL	0.9998	24.635 ± 0.058	0.23	0.9998	24.635 ± 0.058	0.23
Biometry at maximum deformation [mm]	CCTpuff	0.8423	0.559 ± 0.012	2.13	0.8370	0.559 ± 0.012	2.06
	ACDpuff	0.9935	2.081 ± 0.076	3.62	0.9963	2.032 ± 0.055	2.67
	LTpuff	0.9979	4.167 ± 0.042	0.98	0.9977	4.106 ± 0.043	1.04
	VCDpuff	0.9998	17.057 ± 0.048	0.28	0.9998	16.951 ± 0.052	0.30
	ALpuff	0.9998	23.864 ± 0.058	0.24	0.9998	23.645 ± 0.057	0.24
Deformation [mm]	Anterior Cornea	0.9573	1.133 ± 0.060	5.3	0.9634	0.991 ± 0.054	5.4
	Posterior Cornea	0.9565	1.125 ± 0.061	5.4	0.9595	0.983 ± 0.058	5.8
	Anterior Lens	0.8707	0.320 ± 0.042	12.7	0.9595	0.126 ± 0.018	14.2
	Posterior Lens	0.8917	0.361 ± 0.041	11.2	0.9409	0.107 ± 0.022	20.3
Compression [mm]	CCT	0.3221	0.008 ± 0.014	169.5	0.3166	0.007 ± 0.013	171.2
	ACD	0.9196	0.804 ± 0.057	7.0	0.9622	0.863 ± 0.041	4.8
	LT	0.6080	−0.041 ± 0.020	47.2	0.0447	0.020 ± 0.015	70.0
	VCD	0.8189	−0.0005 ± 0.0310	5550	0.9365	0.105 ± 0.024	22.3
	AL	0.9402	0.771 ± 0.047	6.0	0.9620	0.990 ± 0.055	5.5
Hysteresis [mJ]	Cornea HA	0.6756	27.6 ± 6.7	24.2	0.5977	12.6 ± 3.6	27.9
Temporal characteristics [ms]	tv1	0.9131	10.49 ± 0.47	4.39	0.9179	11.54 ± 0.43	3.64
	tv2	0.7449	25.05 ± 0.57	2.24	0.5025	24.47 ± 0.44	1.76
	Δtv	0.8963	14.56 ± 0.81	5.55	0.8473	12.93 ± 0.45	3.43
	tacc1	0.9488	8.24 ± 0.38	4.51	0.9147	9.44 ± 0.38	3.99
	tacc2	0.8555	27.24 ± 0.56	2.03	0.9497	28.19 ± 0.43	1.50
	Δtacc	0.9398	19.01 ± 0.67	3.49	0.9536	18.75 ± 0.65	3.43

ICC – intraclass correlation coefficient, CoV – coefficient of variation

The precision of temporal profiles of the deformation of the cornea and the crystalline lens in the case of 22-yo subject is presented in Fig. 7. We also summarized the precision of the measurements of each parameter in Table 1 by calculating the standard deviation (‘within’ subject) and coefficients of variation. The largest standard deviation in ocular biometry is observed for the anterior chamber depth. The average precision of the axial length and the deformation amplitude of the cornea is ca. 60 μm. The displacement of the crystalline lens is significantly lower than the displacement of the cornea. Moreover, it is also observed that the cornea is not compressed during air-puff stimulation, whereas the crystalline lens is slightly compressed. However, the changes in vitreous depth between the pre-puff phase and the phase at maximum deformation are associated with the wobbling amplitude. In addition to that, the time interval between the acceleration maxima is larger than that between the velocity extrema.

Fig. 7.

Precision of the measurement of the reaction of ocular components to air-puff stimulation. Average retraction-corrected displacement (deflection) of the anterior surface of the cornea (a) and the crystalline lens (b) of 22-yo subject. Mean and standard deviation of temporal responses of the cornea and the crystalline lens were calculated from 8 measurements.

4. Discussion and conclusions

In this paper, we demonstrate the design details of an ocular biometer that enables the measurements of the intraocular distances during application of the air-puff stimulus. Therefore, this novel instrumentation merges two well-established technologies used in clinical ophthalmic diagnostics, namely air puff and SS-OCT ocular biometry. Although the concept of those combined technologies is known, the novelty is represented by a longer imaging range that allows for visualization of the eye dynamics along its entire axial length. Since all current techniques utilizing high-speed image technology and mechanical stimulation are confined to the analysis of corneal reaction, extending the imaging range offers new opportunities for a complete characterization of the dynamics of ocular structures.

The technical solution presented in this paper has several features that make it a unique tool for the analysis of the reaction of the eye globe to any mechanical stimulus. First, the system takes advantage of recent advances of OCT technology since it implements novel long-range OCT imaging with a wavelength-swept laser (that has to have a long instantaneous coherence length) and a wide-bandwidth acquisition card. Although the depth range of the system does not allow to image through the entire eye length, we take advantage of the complex conjugate signal in the image. The other air-puff systems combined with imaging modality like Corvis ST can visualize only the corneal reaction to air puff. The previously reported OCT imaging and air-puff mechanical stimulus was performed at the central wavelength of 1310 nm but the laser and acquisition technology allowed for the visualization of the anterior chamber or only the cornea [35,37]. Secondly, the image analysis is based on retrieving intraocular distances measured along visual axis, thus it enables to visualize the air-puff induced movement of all ocular structures and media like the cornea, the anterior chamber, the crystalline lens, the vitreous and the axial eye length. This should be regarded as comprehensive information on the whole eye morphology dynamics during external mechanical stimulus. Thirdly, the system is characterized by an axial scan rate of 30,000 axial scans per second, which is one order of magnitude higher than the imaging speed (frame rate) of the Scheimpflug camera-based air-puff tonometer (Corvis ST). However, in our case we visualize only the dynamics along a single axis, which represents limitation of this solution. No cross-sectional images are acquired since beam lateral scanning is not implemented in the current version of instrumentation. Our approach can be extended to B-scans to reveal the dynamics of the same cross-sectional plane of the eye. However, this would pose extremely high requirements on the technologies used in the system design: MHz range of laser sweeping rates (which is at least one / two orders of magnitude higher than that of current laser), along with long coherence length, extremely high-speed data acquisition, and very fast lateral beam scanning (e.g. resonance scanners).

The reproducibility study was preceded by several optimization tests and implemented data post-processing steps that allow for a proper and correct interpretation of the obtained results. We show careful calibration and determination of spatio-temporal characteristics of the air-puff stimulus. The results indicate similar air-puff features observed in other studies that are used in clinical non-contact tonometers for the measurement of the intraocular pressure and corneal biomechanics [44].

Another important issue was to correct mutual temporal relations between the acquired signals (pressure and OCT) since the delay between the signals significantly impacts the shape of the observed hysteresis loop. From the physical point of view, the hysteresis is a consequence of delayed response of the corneal tissue with respect to the stimulus. The stimulus should be measured in the plane where the air-puff is applied to the cornea, which is physically impossible. Finite propagation speed of the air pulse and the construction of the air-puff chamber made it possible to control the delay by changing the length of the plastic tube that connects the air-puff chamber with the built-in pressure sensor. The optimized length of the plastic tube allowed for appropriate interpretation of the hysteresis with no systematic error. That effect has never been considered since standard systems do not take into account temporal relations of the stimulus and the response.

Later, we introduced an original method of extracting information on the eye retraction during deformation process. Determination of the retraction-free deformation of the tissue is critical because it is directly related to the biomechanics of that tissue (e.g. the cornea). The eye retraction correction methodology developed in this study utilized the ability of the proposed system to perform ocular biometry, in particular to measure the axial eye length with high temporal resolution.

Several parameters were defined to assess the dynamics of the eye with respect to the air puff, and their reproducibility was assessed in this study. Ocular biometry with the SS-OCT system demonstrated high intersession reproducibility similar to previously reported biometers although the precision did not achieve the values reported earlier [30]. This might have been caused by a lower M-scan image quality compared to standard SS-OCT biometry devices. The statistical analysis revealed higher ICC values for all intraocular distances at the time instances before the air puff and during the maximum deformation than those in simultaneous study with IOP modulation [45]. The lowest ICC values were obtained for the CCT and LT compression. This effect along with the fact that the population-average values of those parameters are around zero indicated that the cornea and the lens are practically not compressed during the air pulse. Consequently, the interaction of the air pulse with the eye caused deformation of the corneal shape as well as the shift of the lens with no change of its thickness. Moreover, the dynamic behavior of the lens revealed a wobbling effect (damped oscillation).

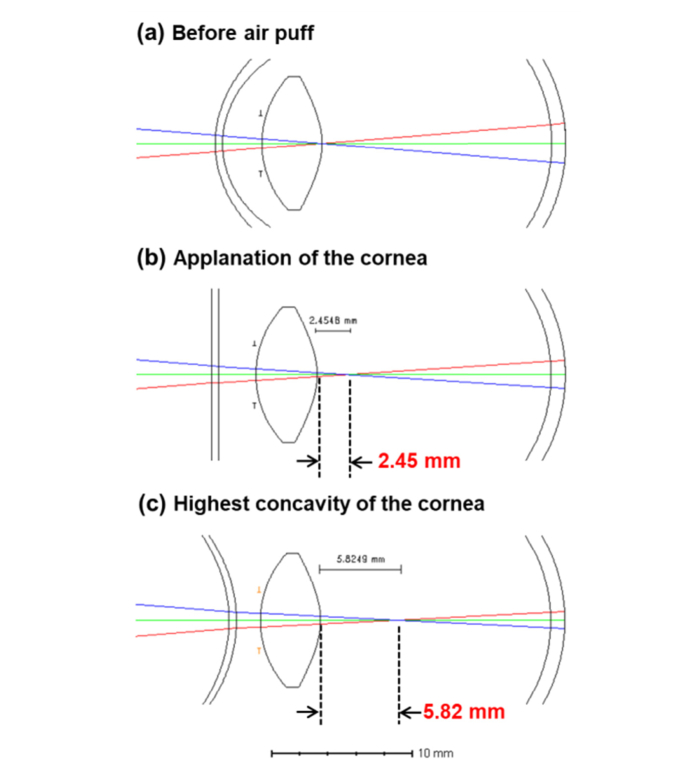
The main limitation of the presented methodology is that the cornea changes its shape from convex to concave (through two applanation states), thus modulating the instantaneous refractive status of the eye. Hence, the deformation process modifies light propagation in the eye during air-puff stimulation, which is critical if we sample the morphological response optically. The puff-induced changes in the corneal curvature cause the axial shift of the focus inside the eye. Accordingly, we performed simulation of light propagation in the eye in selected phases of air-puff deformation process using optical design software (OpticStudio; Zemax LCC, USA). The sample arm of the SS-OCT biometer was designed and a focused light beam illuminated a model eye (corneal radii of curvature: R₁ = 7.8 mm, R₂ = 6.7 mm, anterior chamber depth ACD = 2.7 mm). In the pre-puff phase, we positioned the eye so that the focus coincided with the posterior surface of the crystalline lens (Fig. 8(a)). When the cornea is applanated (R₁ = R₂ = ∞, ACD_appl = 2.5 mm), the total refractive power of the eye is lower, which results in the shift of the focal plane by 2.5 mm towards the retina (Fig. 8(b)). Furthermore, maximum deformation of the cornea corresponds also to the highest concavity phase. In the model, we used maximum deformation value observed in our experiments (ca. 1.1 mm, thus ACD_puff = 2.7-1.1 = 1.6 mm) and assumed the radius of curvature at the highest concavity phase taken from the studies with Corvis ST (ca. −10.0 mm) [7]. In that case, the focus was found 5.8 mm behind the crystalline lens (Fig. 8(c)). Therefore, the basic model might explain the effect of air-puff induced changes in eye geometry that impact also the signal from the retina in the M-scan. The retinal signal in OCT image was higher during the air-puff due to a better light collection efficiency (depth-of-focus closer to the retina).

Fig. 8.

Impact of the air-puff deformation on the light propagation in the eye. Simulations of the light propagation in the eye in the pre-puff phase (a), during corneal applanation (b) and in the highest concavity phase (c).

The effect of light propagation (focusing) in the eye imposed the requirements on the scanning procedure. We had to provide a precise axial and lateral positioning of the corneal apex with respect to the incident optical beam. Any lateral motion of the eye during air-puff application contributes to the uncertainty of the measurements since the light may not propagate using straight path to the retina. Experimentally, this effect manifests as motion artifacts in the segmented interfaces from M-scans.

Another limitation is a lower M-scan image quality compared with the SS-OCT images that we reported in previous air-puff studies at 1310 nm [35,37,46]. Although similar technology of external cavity wavelength-tunable laser was applied in the current study, the systems at 1310 nm are usually characterized by a higher sensitivity levels than systems at 1050 nm. In addition to that, the laser used in this study was a prototype light source with the instantaneous coherence adjusted for ocular biometry but the noise performance of the source still requires improvement.

In conclusion, SS-OCT-based ocular biometry integrated with air-puff stimulus allows for reproducible determination of the eye reaction to mechanical stimulation in vivo. The measurements of intraocular distances during the air-puff application enables observation of corneal and crystalline lens deformation with high temporal resolution. While the anterior chamber becomes deformed due to air-puff indentation, the crystalline lens wobbles axially. Access to the eye length dynamics enables correcting the deformation for the eye retraction (whole eye movement). OCT biometry combined with the air puff has the potential to provide comprehensive information on the biomechanics of ocular components.

Funding

Polish National Science Center (2015/18/E/NZ5/00697; 2014/14/E/ST7/00637); the European Fund within the Smart Growth Operational Programme 2014–2020 (TEAM; POIR.04.04.00-00-5C9B/17-00); the European Union's Horizon 2020 research, technological development and demonstration program (BE-OPTICAL; 675512); the European Union’s Horizon 2020 research and innovation program (CREATE; 666295); the European Union’s Horizon 2020, Information and Communication Technologies (IMCUSTOMEYE; 779960); PROM Programme ‘International scholarship exchange of PhD candidates and academic staff’ co-financed by the European Social Fund under the Knowledge Education Development Operational Programme (AJV; POWR.03.03.00-00-PN/13/18).

Disclosures

AJV, MW, BJK, IG – submitted patent application (P).