Abstract
Spatially resolved multiply excited autofluorescence spectroscopy is a valuable optical biopsy technique to investigate skin UV-visible optical properties in vivo in clinics. However, it provides bulk fluorescence signals from which the individual endogenous fluorophore contributions need to be disentangled. Skin optical clearing allows for increasing tissue transparency, thus providing access to more accurate in-depth information. The aim of the present contribution was to study the time changes in skin spatially resolved and multiply excited autofluorescence spectra during skin optical clearing. The latter spectra were acquired on an ex vivo human skin strip lying on a fluorescent gel substrate during 37 minutes of the optical clearing process of a topically applied sucrose-based solution. A Non Negative Matrix Factorization-based blind source separation approach was proposed to unmix skin tissue intrinsic fluorophore contributions and to analyze the time evolution of this mixing throughout the optical clearing process. This spectral unmixing exploited the multidimensionality of the acquired data, i.e., spectra resolved in five excitation wavelengths, four source-to-detector separations, and eight measurement times. Best fitting results between experimental and estimated spectra were obtained for optimal numbers of 3 and 4 sources. These estimated spectral sources exhibited common identifiable shapes of fluorescence emission spectra related to the fluorescent gel substrate and to known skin intrinsic fluorophores matching namely dermis collagen/elastin and epidermis flavins. The time analysis of the fluorophore contributions allowed us to highlight how the clearing process towards the deepest skin layers impacts skin autofluorescence through time, namely with a strongest contribution to the bulk autofluorescence signal of dermis collagen (respectively epidermis flavins) fluorescence at shortest (respectively longest) excitation wavelengths and longest (respectively shortest) source-to-detector separations.
1. Introduction
Multimodal fibered optical spectroscopy is a point optical biopsy technique combining Spatially Resolved (SR) diffuse reflectance and AutoFluorescence (AF) intensity spectra measurements. It is a valuable tool for in vivo non invasive investigation of skin optical properties in the UV-Visible spectral range, of particular interest for diagnosing and studying skin carcinogenesis stages [1–3].
Multiple excitation light induced AF spectroscopy applied on skin provides global information about the composition and metabolism of the cutaneous tissue in probing the intrinsic fluorophores contained in cells (keratin, reduced forms of pyridine nucleotides NAD(P)H, Flavin Adenine Dinucleotide FAD, porphyrins) and in extracellular matrix (elastin, collagen) [4,5]. Indeed, skin carcinogenesis modulates the fluorescence signals in such ways that collagen fluorescence is decreased due to enzymatic degradation, and NAD(P)H and porphyrin fluorescence are increased due to metabolic changes. It was observed that fluorescence of normal skin tissues is always (i) higher than that of basal cell carcinoma lesions and (ii) lower than fluorescence of squamous cell carcinomas [6,7]. Furthermore, epidermal and dermal fluorescence contributions are produced in distinct spectral regions [8]. Consequently, the use of several excitation wavelength sources allows one for scanning the relative contributions of various fluorophores according to their respective excitation and emission spectra. The latter are involved in the shape formation of the global AF spectra collected by spectroscopy which also depends on the penetration depths of the different excitation wavelengths and on differences in influence of pigments, especially hemoglobin [9]. The spectral shape of skin global AF signals is modified in accordance with the concentration of fluorophores, which is correlated with the biochemical activity related to skin pathological states.
Spatially Resolved (SR) point spectroscopy is based on the use of a multi-fiber optics probe displaying several Source-to-Detector Separations (SDS) i.e. several measurement distances between usually one excitation fiber and groups of detection fibers, in order to probe tissues at different depths. By providing complementary informative depth-related data, spatial resolution has proved its efficiency to improve diagnostic classification based on DR and AF spectra [2].
The sensitivity of this approach can be improved by the application on skin of Optical Clearing Agents (OCA) that increase tissue transparency by decreasing photon diffusion and absorption, thus providing access to more accurate in-depth information [10,11]. The formulation and validation of OCA for clinical use are of primary interest because of their hyperosmotic properties [10]. OCA may allow for detecting deep-seated tumours in skin by using an exogenous fluorescent marker [12,13]. Only few works have studied the changes in skin AF spectra related to the application of OCA for multiple excitation wavelengths and application times. Indeed, authors in [14] showed that for one single excitation wavelength, the AF intensity spectra decreased as the soak time of skin in OCA increased.
Because of the relatively wide excitation and emission wavelength bands of the various fluorophores naturally present in the biological tissues, AF spectra are bulk signals mixing the overlapping contribution of several single spectra emitted by these respective fluorescent molecules. Consequently, unmixing individual fluorophore contributions from bulk AF spectra is at stake especially when searching to understand how their relative contribution evolves throughout an Optical Clearing (OC) process. Source separation techniques such as Non Negative Matrix Factorization (NMF) aim at decomposing a set of non-negative signals into distinct non-negative features (so-called sources) [15] and is therefore well adapted to spectroscopic signal unmixing [16]. NMF is widely used in fluorescence microscopy image processing to eliminate tissue autofluorescence (intrinsic fluorescence) and to spectrally unmix different extrinsic fluorescent dyes in multi-labeled samples [17].
We are interested here in studying the time behaviour of skin intrinsic fluorophores during OC process based on topical application. In the present contribution, a NMF-based source separation approach was implemented to (i) unmix skin tissue intrinsic fluorophore contributions from SR multiply excited AF spectra acquired on a hybrid two-layer model of ex vivo skin lying on a fluorescent gel and to (ii) analyze the time evolution of this mixing throughout the OC process of a human skin strip under topical application of a sucrose-based OCA. In this way, the latter spectral unmixing exploits the multidimensionality of the acquired data that consist in spectra resolved in excitation wavelengths, in SDS and in time.
The present paper is organized as follows. Section 2 describes (i) the experimental data acquisition procedure including instrumentation, experimental model and protocol using OCA, and (ii) the NMF-based source separation approach applied to the latter experimental data. Results obtained with reference to SDS, fluorescence excitations, skin OC duration and for different numbers of sources are described, analyzed and discussed in sections 3 and 4 respectively.
2. Materials and methods
2.1. Experimental data
2.1.1. Instrumentation
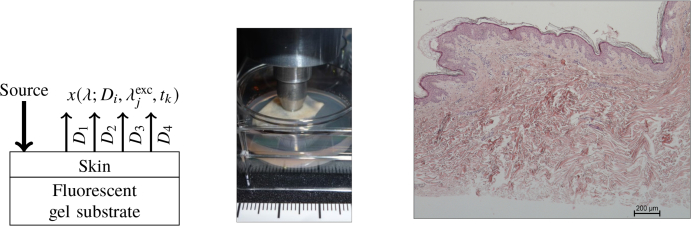
The point spectroscopy system used to acquire Spatially Resolved (SR) multiply excited fluorescence intensity spectra is described in detail in [18]. Briefly, spatial resolution is provided through the multi-fiber optics probe consisting of (i) one central 600 μm diameter excitation fiber (Numerical Aperture NA = 0.22) for delivering light onto the skin and (ii) four rings of six detection fibers each (200 μm core diameter fiber, NA = 0.22), located at SDS D1=400 μm, D2=600 μm, D3=800 μm and D4=1000 μm respectively (Fig. 1). The SR fluorescence emission spectra are measured consecutively for five bandpass filtered LED light sources (∼ 10 nm Full Width at Half-Maximum) centered at , , , and respectively.
Fig. 1.
Schematic representation (left) and picture (middle) of the experimental configuration including the hybrid two-layer model made of an ex vivo skin strip lying on a fluorescent gel substrate and the multi-fiber optics probe in contact with skin epidermis. Fluorescence spectra x(λ; Di, , tk) are collected according to four SDS Di (i ∈ {1, …, ND = 4}), five fluorescence excitation wavelengths (j ∈ {1, …, Nexc = 5}) and eight time measurement points tk (k ∈ {1, …, Nt = 8}). Right picture: Hematoxylin and Eosin stained histological slide of the skin strip tested (scale bar = 200 μm).
2.1.2. Experimental model and protocol
Measurements were performed on a hybrid two-layer experimental model consisting of an ex vivo skin strip (thskin=1143 μm average thickness) harvested on human skin wastes placed on top of a fluorescing agarose (1 % weight/vol.) gel substrate (thgel=5 mm thickness). The skin strip (see Hematoxylin and Eosin stained H&E histological slide on Fig. 1) was obtained from abdominal skin wastes of a fair-skinned (phototype 2) female aged 38 years old (protocol authorization #17–400, International Review Board #00003888). Epidermis and dermis thicknesses of the skin strip, 91 ± 27 μm and 1052 ± 195 μm respectively, were determined as average values over 18 evenly distributed points of measurement (at papilla sites and at non-papilla sites) on a H&E stained histological slide (scale bar = 200 μm). The gel absorption, scattering and fluorescence optical properties were fixed using 0.02 % (vol./vol.) indian ink, 5 % (vol./vol) Intralipids-20 % and 500 μM Chlorin e6 (Ce6), respectively.
Such skin-gel model was used in order to study the relative contributions of intrinsic and extrinsic fluorophores, located in skin and gel layers respectively, during the optical clearing of the skin strip. With reference to the five excitation wavelength peaks available on our device, skin autofluorescence contributions are expected from (i) collagen and elastin, extracellular fibrous proteins located in the dermis, featuring fluorescence emission spectra in the [420 – 510] nm spectral range when excited in the [350 – 420] nm spectral range, (ii) NAD(P)H coenzymes featuring strong fluorescence emission between 400 and 500 nm arising from epidermis when excited in between 330 and 380 nm, and (iii) FAD coenzymes with maximum absorption at and and exhibiting an emission spectrum peak at 525 nm [4, 9, 19–21]. Other main skin fluorescing compounds such as tryptophan (present in both epidermis and dermis, excitation/emission peaks 295/345 nm, [22]) and keratin (epidermis, excitation/emission peaks 277/382 nm) were not considered in the present study as their excitation bands are outside the range of our excitation source wavelengths.
The Optical Clearing Agent (OCA) was a solution made by mixing 45 % PolyEthylene Glycol 400 (PEG 400, Sigma-Aldrich ref. 88440) with 5 % Polypropylene Glycol (PG, ref. P4347) and 50 % sucrose (ref. S9378). The solution was applied on top of the skin strip itself lying on the gel substrate.
The measurement protocol consisted in collecting fluorescence spectra (skin AF and gel Ce6 fluorescence), at the four SDS and at every of the five excitation wavelengths, according to the application time of the OCA on the skin surface for eight measurement times T0 (before OCA application), T0 +7,+13,+20,+25,+29,+32,+37 minutes. Every acquisition was repeated three times on three different skin sites; these nine measurements were then averaged in order to improve the signal-to-noise ratio.
2.2. Source separation
2.2.1. Non Negative Matrix Factorization-based mixing model
Source separation [23] can be mathematically formulated as a matrix factorization problem defined as follows:
| (1) |
where matrix X gathers the experimental data, and matrices A and S are both unknown. In Non-Negative Matrix Factorization (NMF) [24,25], A and S are assumed to be non negative (that is, containing only non-negative values). This is a natural assumption is optical spectroscopy where the source signals identify with fluorophore emission spectra, and the elements of A are the weights of the sources in the observed spectra. More specifically,
is the observation matrix gathering the set of acquired data i.e. the fluorescence spectra x(λ; Di, , tk). Each row of X is a wavelength resolved vector x(λ) with λ = [451 : 1 : 730] nm, so the total number of columns of X is Nλ= 280. The number of rows in X is equal to the total number of acquired spectra NSp = ND × Nexc × Nt =160, corresponding to all measurements performed at four SDS (i ∈ {1, …, ND = 4}), five fluorescence excitation wavelengths (j ∈ {1, …, Nexc = 5}) and eight time measurements (k ∈ {1, …, Nt = 8}),
is the source matrix containing the different source signals i.e. the vectors sm(λ) of the estimated fluorescence emission spectra. The maximum number of sources NS = 3 and NS = 4 was retained after several evaluations (see Section 3 for details),
is the mixing matrix gathering the abundances i.e. the weight coefficients al,m of the spectral sources m, with al,. referring to the lth observation (the lth row of X), seen as a mixture of sources signals s1(λ), …, sNS(λ).
Each spectrum x(λ; Di, , tk) corresponds to a row vector xl(λ) of X, whose index l ∈ {1, …, ND × Nexc × Nt} matches the specific value of (i, j, k) (we set l = i + ND × (j − 1) + ND × Nexc × (k − 1)). An observed data spectrum rewrites as a linear combination of the sources sm(λ):
| (2) |
2.2.2. ALS based-NMF estimation algorithm
The underlying idea of blind source separation is that no strong prior is set on A and S matrices. Typically, no assumption is made on the wavelength peak locations in the source signals. The only (weak) requirement is the non-negativity of matrices A and S. Consequently, the matrix factorization problem (1) is addressed by minimizing the following cost function corresponding to the total squared error:
| (3) |
where ‖·‖F and (, Ŝ) denote the Frobenius matrix norm and the estimated matrices resulting from the minimization of the cost function f(A, S) respectively. In (3), the ℓ2 norm is related to the sum of squares in the λ-domain.
The NMF problem is known to be difficult because the cost function f(A, S) in (3) is non-convex with respect to matrices (A, S) jointly, therefore the solution may not be unique (usually there are many local minimizers). However, the function A ↦ f(A, S) is quadratic, hence convex for fixed S. Similarly, S ↦ f(A, S) is a quadratic functional. A natural heuristic to minimize (3) therefore consists of alternating between minimization of f with respect to A (for fixed S) and with respect to S (for fixed A). This strategy is known as Alternating Least Squares (ALS). This algorithm is stated in Algorithm 1.
Algorithm 1.
Alternating Least Squares algorithm
| 1: Inputs: X observation matrix, εstop stopping criterion |
| 2: Outputs: abundance matrix, Ŝ source matrix |
| 3: A(0) = random (NSp, NS) |
| 4: S(0) = random (NS, Nλ) |
| 5: iter = 1 |
| 6: repeat |
| 7: Solve: |
| 8: Solve: |
| 9: Calculate: ε = (f(A(iter−1), S(iter−1)) − f(A(iter), S(iter)))/f(A(iter−1), S(iter−1)) |
| 10: iter ← iter + 1 |
| 11: until ε < εstop |
| 12: , Ŝ ← S(iter) |
The resolution of each quadratic sub-problem is usually carried out in a sub-optimal way because exact non-negative least-square solvers are numerically expensive, especially for large-scale problems [26]. Therefore, the solutions of lines 7 and 8 of Algorithm 1 are approximate. We use the classical multiplicative update method of Lee and Seung [23] whose structure is rather simple. The update of matrix A reads:
| (4) |
where ⊙ and ⊘ respectively refer to element-wise multiplication and division of matrices. Similarly, the update of S reads:
| (5) |
The reader is referred to, e.g., [15,26] for further details on ALS algorithms and further discussions on alternative choices of non-negative least-square approximate solvers.
As a local optimization algorithm, ALS yields outputs that are highly dependent on the initialization of matrices A and S. The latter matrices are usually randomly drawn. In the present work, the elements of A(0) were drawn according to the uniform distribution U ([0, 1]). The initial sources in S(0) were initialized as Gaussian signals with 25 nm Full Width at Half Maximum (FWHM) and with center position (peak wavelength) uniformly drawn in the [451 – 730] nm spectral range. The latter interval covers both expected peaks of the autofluorescence emission spectrum and of the fluorescence emission spectrum of Ce6 (around 670 nm, Fig. 2 (right)). ALS being an iterative descent algorithm, we adopt a stopping rule based on the decrease of the total approximation error: ALS is stopped when the relative decrease
| (6) |
is lower than εstop = 1 %, where iter stands for the ALS iteration number.
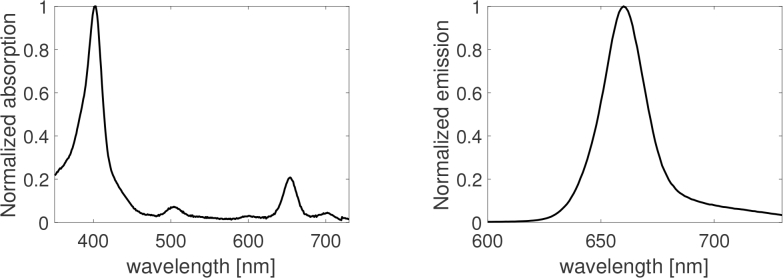
Fig. 2.
Absorption (left) and emission (right) fluorescence spectra of Chlorin e6 normalized to their respective maximum peak values. The emission spectra was obtained under 403 nm excitation wavelength (corresponding to the wavelength of maximum absorption).
As mentioned above, ALS is sensitive to the initial solution. Therefore, we choose to run repeated calls to ALS with the random initialization strategy described above for 100 trials i.e. with 100 draws of initial matrices A(0) and S(0). This yields outputs (, Ŝ(trial)) for trial = 1, …, 100. The outputs yielding the least value of f (, Ŝ(trial)) are finally selected as the source and abundance matrix estimates.
3. Results
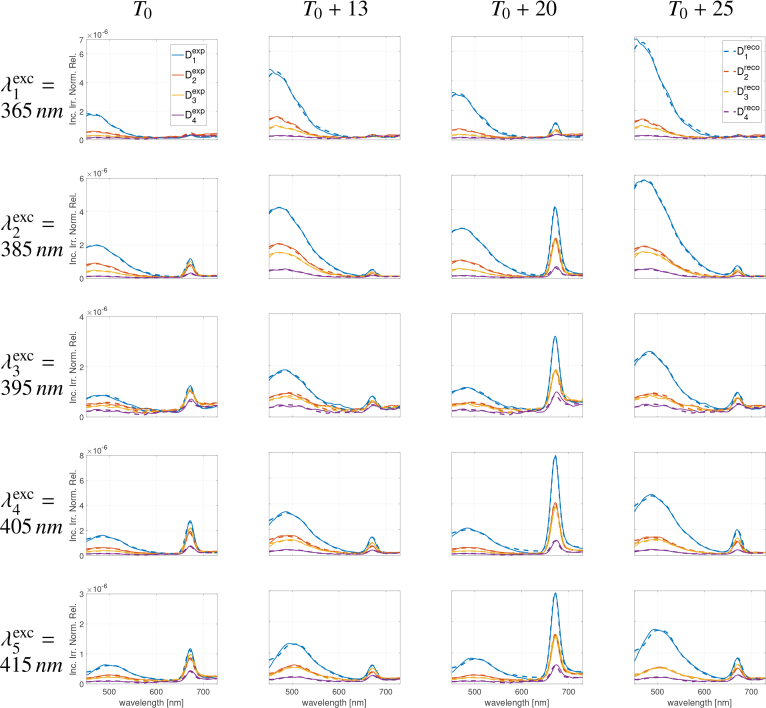
Figure 3 illustrates the very good fitting obtained between fluorescence intensity spectra (X) acquired experimentally (as a function of SDS D1:4 in colors, excitation wavelengths in rows and OC time in columns) and their corresponding recovered spectra (X̂) using the ALS-based NMF algorithm with 4 sources (NS = 4). Similar results were obtained for NS = 3 sources (not shown). Other lower and higher numbers of sources were also tested but did not bring better results in terms of fitting quality or source interpretation. In both conditions (NS = 3, 4), residual curves (differences between experimental and recovered spectra) were characterized by average absolute values less than 10 %.
Fig. 3.
Measured (continuous lines) and recovered (dashed lines) fluorescence spectra using ALS-based NMF algorithm with a fixed number of 4 sources (NS = 4). Blue, red, yellow and purple color correspond to the curves at SDS D1:4 respectively. Results are plotted (i) for the 5 fluorescence excitation wavelengths in rows from top to bottom and (ii) for 4 time points during the Optical Clearing process at T0, +13, +20 and +25 minutes respectively from left to right columns.
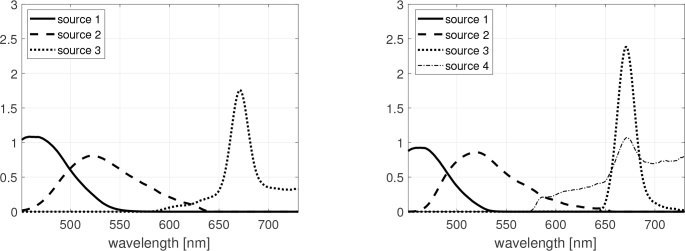
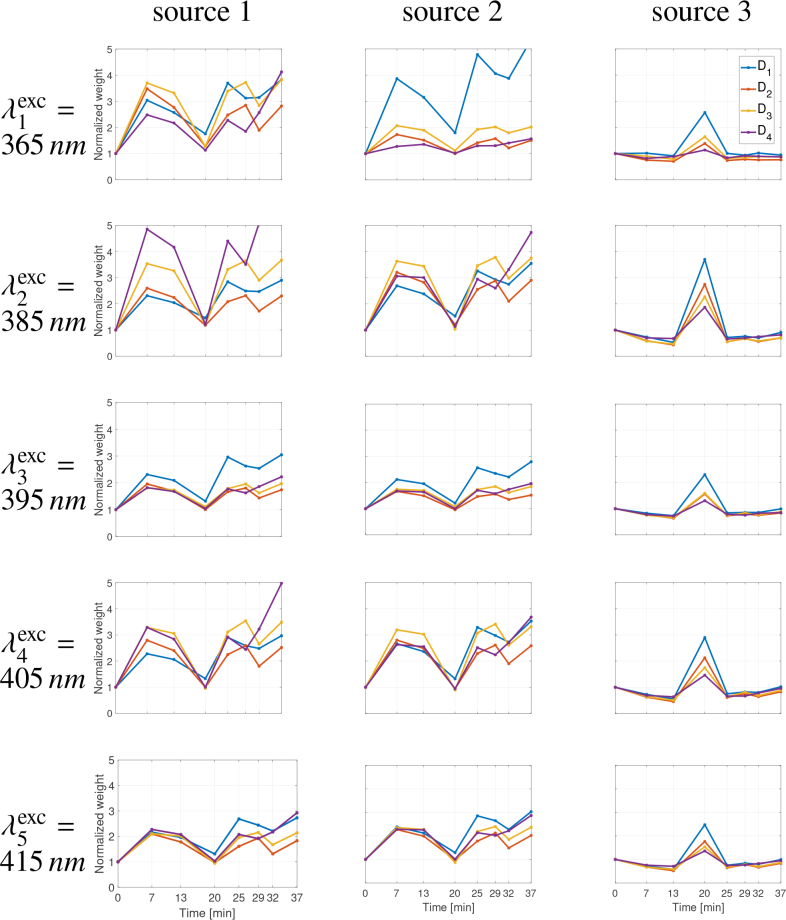
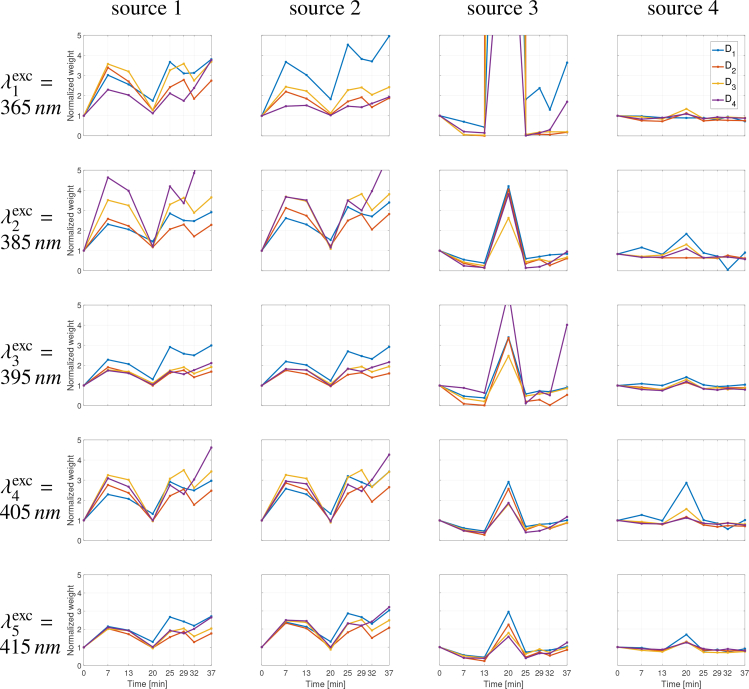
The spectral sources Ŝ estimated by the ALS-based NMF method, according to all SDS D1:4, all fluorescence excitation wavelengths and all time points during the Optical Clearing process t1:8, are shown in Fig. 4 for both numbers of sources NS = 3 and NS = 4. Sources 1, 2 and 3 can be commonly identified as skin AF (sources 1 and 2) and Ce6 fluorescence (source 3) contributions respectively, while source 4 (in the case NS = 4) does not relate to any other clearly identified contribution.
Fig. 4.
Estimated spectral sources Ŝ obtained by the ALS-based NMF method, for NS = 3 (left) and NS = 4 (right), according to all SDS D1:4, all fluorescence excitation wavelengths and all time points during the Optical Clearing process t1:8.
The time contribution of the various fluorescent compounds during the skin sample OC process can be analyzed throughout the contribution level of every estimated source in our NMF model. Figures 5 and 6 show the results obtained in terms of time evolution of the weight coefficients al,m of the estimated abundance matrix for NS = 3 and NS = 4 sources respectively (in the order of columns from left to right). Considering the abundance results on Fig. 5 for excitation wavelength , it may be noted that the contribution of source 2 (FAD in epidermis) is predominant at SDS D1 whereas the contribution of source 1 (collagen/elastin in dermis) is predominant at D2 and D3. For higher excitation wavelengths , it can be observed that the contributions of source 2 is also more significantly visible at shortest distance D1.
Fig. 5.
Time evolution of the weight coefficients in the estimated abundance matrix with a total number of sources fixed at NS = 3. Each point correspond to the value of a coefficient al,m = ai+ND×(j−1)+ND×Nexc×(k−1),m with i ∈ {1, …, ND = 4}, j ∈ {1, …, Nexc = 5}, k ∈ {1, …, Nt = 8} and m ∈ {1, …, NS = 3} the SDS, the excitation wavelength, the time point and the source numbers respectively. Results (weights normalized to their initial values at T0) are plotted in blue, red, yellow and purple colors corresponding to SDS D1:4 respectively, (i) for the 5 fluorescence excitation wavelengths in rows from top to bottom and (ii) for the 3 sources S1:3 from left to right columns.
Fig. 6.
Time evolution of the weight coefficients in the estimated abundance matrix with a total number of sources fixed at NS = 4. Each point correspond to the value of a coefficient al,m = ai+ND×(j−1)+ND×Nexc×(k−1),m with i ∈ {1, …, ND = 4}, j ∈ {1, …, Nexc = 5}, k ∈ {1, …, Nt = 8} and m ∈ {1, …, NS = 3} the SDS, the excitation wavelength, the time point and the source numbers respectively. Results (weights normalized to their initial values at T0) are plotted in blue, red, yellow and purple colors corresponding to SDS D1:4 respectively, (i) for the 5 fluorescence excitation wavelengths in rows from top to bottom and (ii) for the 4 sources S1:4 from left to right columns.
For sake of consistency, weight values were all normalized with reference to their initial values obtained at T0 i.e. at the very beginning of the OC process. The time evolution of al,m values was thus plotted with reference to a common unitary value at start time T0. Distinct behaviours can be observed between sources (1,2) and source 3, similarly for NS = 3 and NS = 4 sources. The time weight of sources 1 and 2 contributions (two first columns in Figs. 5 and 6) to the overall fluorescence signal, depending on SDS (in colors) and λexc (in rows) considered, highlights a significant two- to five-fold increase at T0 + 13 minutes followed by a strong decrease by a dividing factor of 1.5 to 1.6 at T0 + 20 minutes. After 20 minutes of OCA application, the latter sources 1 and 2 contributions were observed to rise again at equivalent (for longest SDS D2 to D4) or even higher (for shorter SDS D1) levels than values reached at T0 + 13 for the respective SDS. In contrast, the time contribution of source 3 show a rather opposite behavior with a distinct decrease down to 0.5 and less than 0.01 in NS = 3 (Fig. 5) and NS = 4 (Fig. 6) source configurations respectively, at T0 + 13 minutes. This behavior was observed similarly for all SDS and all excitation wavelengths nonetheless with a lesser importance at the shorter . At T0 + 20 minutes, for NS = 3 sources in Fig. 5, the source 3 contribution appeared to be maximum with values between 2.5 and 3.7 for D1, 1.4 and 2.7 for D2, 1.5 and 2.3 for D3, and 1.3 and 1.9 for D4, depending on λexc considered, nevertheless with highest values obtained for . For NS = 4 sources in Fig. 6, the source 3 contribution appeared to be maximum with values between 2.9 and 35 for D1, 2.2 and 628 for D2, 1.8 and 99 for D3 and 1.6 and 14 for D4, depending on λexc considered, nevertheless with highest values obtained for . The weight coefficient of source 4 are rather flat over time except for D1 and at where a peak located at T0 + 20 minutes can be observed, similarly to source 3, but with reduced magnitude.
4. Discussion
The ALS-based NMF method applied to time and spatially resolved multiply excited fluorescence spectra appears to provide very good fitting results for fixed numbers of NS = 3 and NS = 4 sources (Fig. 3) exhibiting common identifiable shapes of fluorescence emission spectra related to Ce6 in the gel substrate of our hybrid experimental model and to known skin intrinsic fluorophores matching namely dermis collagen and elastin as well as epidermis NAD(P)H and flavins [4,9]. Thus, in Fig. 4, source 1 could be related to skin collagen/elastin AF emission in the [400 – 500] nm spectral range with a known peak at [420 – 440] nm for collagenase digestible cross-links [9]. Source 2 might refer to skin flavin AF emission with a well identified peak in the [500 – 540] nm spectral range [9]. It is to be noticed that the two expected contributions of NAD(P)H and collagen/elastin cannot be unmixed in the present configuration. The contribution of NAD(P)H may be relatively lower compared to collagen and elastin with reference to their excitation wavelength ranges ([330 – 380] nm and [350 – 420] nm respectively) and our set of excitation wavelengths limited to for the shortest excitation peak. Also, a 600 μm core diameter was chosen for our excitation fiber in order to (i) optimize technical constraints to efficiently combine all light sources in one unique excitation fiber and to (ii) have a corresponding large depth probing (the latter increasing with the source spot size). This configuration leads to a shortest SDS D1 of 400 μm (center-to-center distance between the excitation fiber and the first ring of 200 μm core diameter detection fibers) that extends up to 800 μm when considering the full diameters of both fibers. Consequently, this relatively “large” size of the shortest SDS covering all distances up to 800 μm has an integrating effect of the collected photons travelling through epidermis (91 μm thick) and upper dermis layers (in the case of the current skin sample under test). However, it is possible to disentangle fluorescence contribution of dermis collagen/elastin on one side and of epidermis FAD on the other side. Indeed, it can be observed on Fig. 3 a red-shift of the left peak from 450 nm towards 500 nm as excitation wavelengths increase. The unmixing procedure allowed to identify that this shift corresponds to the change of the relative contribution of the two different sources (1 and 2) identified on Fig. 4 and related to collagen/elastin and FAD respectively.
Source 3 is clearly identified to correspond to the Ce6 fluorescence peak emitted between 650 nm and 700 nm from the gel substrate on which skin strip is lying. For this particular source 3, it can be observed that the signal is non zero after 700 nm when using NS = 3 (left Fig. 4) whereas it returns to zero when using NS = 4 (right Fig. 4) as should be expected. In this respect, it can be implied that using 4 sources provides more coherent results in terms of individual source shapes which is also true for source 2 that exhibits a more slightly curved shape between 520 nm and 650 nm for NS = 4 compared to NS = 3. In the latter 4 sources configuration, source 4 could not be linked to any known fluorophore in the present experimental model and was therefore related to a noise contribution appearing for wavelengths longer than 600 nm. However, source 4 also displayed a visible peak at the same wavelength as the one of source 3 which seems to be in favor of a residual mixing correlation. This is confirmed by looking at the time evolution of source 4 abundances in Fig. 6 (determined from estimated matrix ) that follows the same trend as for source 3. The difficulty in unmixing more drastically sources 3 and 4 may be explained by the non-linear nature of the light-tissue interactions which is not taken into account in the present linear model-based NMF method.
The presence of the gel substrate Ce6 fluorescence peak in the spectra measured at T0, despite the 1143 μm thickness of our skin strip, can be explained by a number of factors. First, although there is a strong limitation in depth penetration of light in skin below 350 nm, as shown by [27] with a 340 nm light penetration depth of 140 μm for exposed forearm skin (due to important UVB filtering from keratin and melanin), there is also a rapid exponential decay of melanin absorbance in this spectral region. Ash et al. [28] showed that a 1% fraction of a 350 nm (respectively 400 nm) - light beam may penetrate as deep as 800 μm (1100 μm respectively). Second, the skin sample used in our study was an UV-unexposed abdominal skin piece harvested from a fair-skinned (phototype 2) female aged 38 years old. This implies a very low amount of melanin in the epidermis. Third, epidermis and dermis thicknesses of the skin strip, 91 ± 27 μm and 1052 ± 195 μm respectively, were determined as average values over 18 evenly distributed points of measurement on a H&E stained histological slide. With a total thickness variability of about 30 %, skin may thus be more or less thick depending on the exact skin site. Also this thickness measured on histological slide overestimates the thickness of the skin strip during test as subjected to the pressure contact of the multi-fiber optics probe (Fig. 1). Fourth, photon collection volume is determined namely by the core dimensions and NA of the fibers and by the scattering properties of the tissue [28]. Thus, the effect of beam width is that a larger spot size (the excitation fiber core diameter is 600 μm in our case) increases penetration depth. It has also been reported [29,30] that 400 nm excitation photons can penetrate deep through skin epidermis and dermis to more than 1 mm and that using 250 μm - SDS (1/3 of our shortest SDS) allows light in the 337–400 nm wavelength range to penetrate as deep as 225–250 μm in skin tissues. Consequently, from our results on Fig. 3, it can be observed that no fluorescence from Ce6 was detected at T0 (before clearing) for the - excitation wavelength, which means that the latter does not reach the gel substrate. Weak fluorescence signal from Ce6 was detected for and excitations and stronger signal was detected for and excitations, which confirms the deeper penetration of excitation light through the skin strip down to the gel substrate as wavelength increases. At T0 + 20 minutes, the fluorescence contribution of Ce6 is significantly increased compared to T0, for all excitation wavelengths including the shortest wavelength , meaning that the latter excitation now reaches the gel substrate even at shortest SDS.
The time analysis of the abundances represented in Figs. 5 and 6 for NS = 3 and NS = 4 respectively, corresponding to the weight coefficients affected to the spectral sources, was used to study the evolution of the skin and fluorophore gel estimated fluorescence during the (topically applied) OCA in-depth penetration and propagation in skin. This analysis needs to take into account the fact that (i) the skin depth penetration of fluorescence excitation photons increases with wavelength, (ii) the intrinsic fluorophores are located at different depths in skin (e.g. collagen and elastin are mainly located in the dermis while flavins are more specifically found in the epidermis), (iii) the Ce6 fluorescence originates from the gel layer on which the skin strip lays and (iv) the spectra measured at the 4 SDS result from fluorescence photons originating from different depths throughout the skin-gel model. It can be noticed from Figs. 5 and 6 that the estimated abundances are very similar between NS = 3 and NS = 4.
The time evolution of their contributions of sources 1 and 2, relative to the very beginning of the OC process T0, was observed to be similarly highly increased by a factor of 2 to 5 at T0 + 13 minutes, which is in good agreement with fluorescence signal increase also observed by Migacheva et al. [14] between 10–15 minutes after OC process started. This observation may be correlated with the skin dehydration process initiated during the first step of the OC. Considering source 1, the time contribution of the latter appears to be more effective at shorter excitation wavelengths () and for longer SDS D2,3,4, which is in good agreement with the fluorescence contribution of skin collagen/elastin located in the dermis. Considering source 2, the time contribution of the latter appears to be (i) more prominent at shorter SDS D1 and for excitation wavelengths (), and (ii) quite similar for all SDS for longest excitation wavelengths (), which corresponds to the fluorescence contribution of skin FAD located in the epidermis.
Between T0 + 13 and T0 + 20 minutes, the weight coefficients of sources 1 and 2 exhibit similar time behaviours with a strong decrease by a factor of 35 to 40% down depending on SDS (the longest SDS the strongest decrease in AF). This observation may be correlated with the skin optical property changes, that is in-depth progressive refractive index matching and loss of scattering related to the first 20 minutes of OC action with maximum skin transparency achieved at T0 + 20 minutes [13,31]. At this time point, OCA effect may have reached lower layers of skin, including collagen cross-links in dermis, and changed its geometry (probably the last but not yet “cleared” compound). For the dermis composed of collagen, the sucrose may also cause a disorganization of the collagen structure leading to reduced optical scattering [10,32].
Following the minimum values attained at T0+20 minutes, the latter source 1 and 2 contributions (Figs. 5 and 6) were observed to rise again at equivalent and higher magnitudes, for longest SDS D2,3,4 and shortest SDS D1 respectively, compared to values reached at T0 + 13 for the corresponding SDS. The interpretation of such behavior may refer to the skin dehydration and rehydration steps occurring during the OC process, as it was also observed through 20 minutes decrease and 20 minutes increase of diffuse reflectance spectra measured on normal skin submitted to OCA [33].
Concerning source 3 as obtained in Fig. 6 (in direct relation to the fluorescence emission spectra of Ce6 located in the gel substrate), its time contributions during the OC process show a rather opposite behavior with (i) from T0 to T0 + 13 minutes, a distinct decrease down to almost zero value, that is in favor of skin optical property modifications (higher AF) leading to limited collection of Ce6 fluorescence, (ii) a sharp increase at T0 + 20 minutes, correlated with increased transparency and lowered AF of skin at this moment, and followed by (iii) another strong decrease and a progressive return to unity value (same as starting fluorescence level). As a result of strong refractive index matching and reduced scattering of cleared skin, photons might propagate into deeper layers (directly to Ce6 molecules). This may be confirmed through the behavior observed similarly for all SDS and all excitation wavelengths nonetheless with a much higher importance at the shortest excitation wavelength . The time variations observed for skin AF (sources 1 and 2) and Ce6 fluorescence (source 3) are correlated with the progressive diffusion of the topically applied OCA towards the deepest layers of the skin, including refractive index matching between tissue components and interstitial fluid, diffusion of the OCA down to the skin bottom layers with a tissue dehydration and rehydration process, and finally a return to equilibrium [31].
In the present work, a sucrose-based OCA was chosen in order to investigate the clearing effect of a biocompatible OC solution of interest for clinical trials. It was topically applied on the skin epidermis of our ex vivo sample in order to mimic clinical conditions. The relevance and potential of OC for in vivo studies is increasingly growing like in (i) the selective photothermolysis of vascular lesions where the use of glycerol pre-treatment of skin surface in vivo has led to significantly reduced radiation exposure compared to normal conditions required for photocoagulation [34], and (ii) the in vivo spectro-imaging and photodiagnosis of skin lesions using optical coherence tomography (OCT) [33,35], Surface-Enhanced Raman Spectroscopy (SERS) imaging [36] or multimodal optical biopsy (present work), where the application of OCA led to increased probing depth or improved image contrast. Indeed, the development and application of biocompatible non-toxic OCA might provide significant improvement for currently existing optical approaches for diagnosis and treatment in clinics [10,31].
The present source separation approach relies on a simple instantaneous linear mixing model (3) and was validated on experimental data related to a two-layer sample composed of an ex vivo skin strip and a homogeneous gel substrate as bottom layer substrate. But it is well-known that the propagation of light in biological tissues is highly non-linear, due to the variety of absorption, scattering and fluorescence photo-physical phenomena involved and the complex multi-scale structure of the biological tissues. Consequently, for future work, we plan to (i) investigate more complex mixing models and (ii) elaborate the potential of the source separation approach for analyzing data from ex vivo skin strips of different thicknesses and different phototypes and possibly from in vivo skin.
5. Conclusion
Spatially Resolved (SR) multiply excited AutoFluorescence (AF) spectra were acquired on an ex vivo skin strip lying on a fluorescent gel substrate. Their time changes were studied throughout the Optical Clearing (OC) process of a topically applied sucrose-based solution. An Alternating Least Squares (ALS)-based Non-negative Matrix Factorization (NMF) blind source separation method was successfully used to unmix skin tissue intrinsic fluorophore contributions from the bulk AF spectra, exploiting the multidimensionality of the acquired data i.e. spectra resolved in five excitation wavelengths, four source-to-detector separations and eight measurement times. The analysis of the estimated abundance matrix allowed us to identify the relative contributions of two sources related to the skin intrinsic fluorescence of collagen/elastin (in dermis) and flavins (in epidermis) and one source related to the Ce6 fluorescence arising from gel substrate. The time evolution of these spectral sources was further jointly studied for all distances and all fluorescence excitation wavelengths under the topical application of OCA on skin from the contributions of each fluorophore. These kinetics highlighted several distinct amplitude variation phases in good agreement with the main successive steps of the Optical Clearing diffusion process towards the deepest skin layers. Future work to improve the correspondence between the source separation model and light-tissue interactions will concern the investigation of more complex (nonlinear) mixing models.
Acknowledgement
The authors warmly thank Dr. Philippe Arnoux (LRGP, UMR 7274 UL-CNRS) for his help on acquiring reference Ce6 fluorescence excitation and emission spectra composing our experimental model.
Funding
French Région Grand-Est, CNRS and Metz-Thionville Regional Hospital (2016 clinical research Award) in the frame of SpectroLive project and Contrat de Plan Etat - Région Grand Est 2015–2020 (CPER IT2MP, plateforme IMTI) including European Regional Development Fund FEDER; French Embassy in Russia under the Vernadski international joint PhD programme (2018-2021); Russian Foundation for Basic Research (18-52-16025).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Amouroux M., Diaz-Ayil G., Blondel W., Bourg-Heckly G., Leroux A., Guillemin F., “Classification of ultraviolet irradiated mouse skin histological stages by bimodal spectroscopy: multiple excitation autofluorescence and diffuse reflectance,” J. Biomed. Opt. 14, 014011 (2009). 10.1117/1.3077194 [DOI] [PubMed] [Google Scholar]
- 2.Abdat F., Amouroux M., Guermeur Y., Blondel W., “Hybrid feature selection and svm-based classification for mouse skin precancerous stages diagnosis from bimodal spectroscopy,” Opt. Express 20, 228–244 (2012). 10.1364/OE.20.000228 [DOI] [PubMed] [Google Scholar]
- 3.Calin M., Parasca S., Savastru R., Calin R., Dontu S., “Optical techniques for the noninvasive diagnosis of skin cancer,” J. Cancer Res. Clin. Oncol. 139, 1083 (2013). 10.1007/s00432-013-1423-3 [DOI] [PubMed] [Google Scholar]
- 4.Kollias N., Zonios G., Stamatas G., “Fluorescence spectroscopy of skin,” Vib. Spectrosc. 28, 17–23 (2002). 10.1016/S0924-2031(01)00142-4 [DOI] [Google Scholar]
- 5.Borisova E., Angelova L., Pavlova E., “Endogenous and exogenous fluorescence skin cancer diagnostics for clinical applications,” IEEE J. Sel. Top. Quantum Electron. 20, 1–12 (2014). 10.1109/JSTQE.2013.2280503 [DOI] [Google Scholar]
- 6.Bratchenko I., Artemyev D., Myakinin O., Vrakova M., Shpuntenko K., Moryatov A., Kozlov S., Zakharov V., “Malignant melanoma and basal cell carcinoma detection with 457 nm laser-induced fluorescence,” J. Biomed. Photonics & Eng. 1, 180–185 (2015). 10.18287/JBPE-2015-1-3-180 [DOI] [Google Scholar]
- 7.Artemyev D., “Mathematical model of skin autofluorescence induced by 450 nm laser,” J. Biomed. Photonics & Eng. 4, 020303 (2018). 10.18287/JBPE18.04.020303 [DOI] [Google Scholar]
- 8.Borisova E., Troyanova P., Pavlova P., Avramov L., “Diagnostics of pigmented skin tumors based on laser-induced autofluorescence and diffuse reflectance spectroscopy,” Quantum Electron. 38, 597 (2008). 10.1070/QE2008v038n06ABEH013891 [DOI] [Google Scholar]
- 9.Borisova E., Pavlova P., Pavlova E., Troyanova P., Avramov L., “Optical biopsy of human skin-a tool for cutaneous tumours’ diagnosis,” Int. J. Bioautomation 16, 53–72 (2012). [Google Scholar]
- 10.Sdobnov A. Y., Darvin M. E., Genina E. A., Bashkatov A. N., Lademann J., Tuchin V. V., “Recent progress in tissue optical clearing for spectroscopic application,” Spectrochimica Acta Part A: Mol. Biomol. Spectrosc. 197, 216–229 (2018). 10.1016/j.saa.2018.01.085 [DOI] [PubMed] [Google Scholar]
- 11.Guo L., Shi R., Zhang C., Zhu D., Ding Z., Li P., “Optical coherence tomography angiography offers comprehensive evaluation of skin optical clearing in vivo by quantifying optical properties and blood flow imaging simultaneously,” J. Biomed. Opt. 21, 1–6 (2016). 10.1117/1.JBO.21.8.081202 [DOI] [PubMed] [Google Scholar]
- 12.Kozina A. M., Genina E. A., Terentyuk G. S., Terentyuk A. N., Bashkatov A. G., Tuchin V. V., Khlebtsov B. N., “The development of skin immersion clearing method for increasing of laser exposure efficiency on subcutaneous objects,” SPIE Proc. 8427, 842726 (2012). 10.1117/12.922725 [DOI] [Google Scholar]
- 13.Vargas G., Chan E. K., Barton J. K., Rylander H. G., III, Welch A. J., “Use of an agent to reduce scattering in skin,” Lasers Surg. Medicine 24, 133–141 (1999). [DOI] [PubMed] [Google Scholar]
- 14.Migacheva E., Pravdin A., Tuchin V., “Alterations in autofluorescence signal from rat skin ex vivo under optical immersion clearing,” J. Innov. Opt. Heal. Sci. 3, 147–152 (2010). 10.1142/S1793545810001027 [DOI] [Google Scholar]
- 15.Comon P., Jutten C., eds., Handbook of Blind Source Separation, Independent Component Analysis and Applications (Academic Press, 2010). [Google Scholar]
- 16.Montcuquet A., Herve L., Navarro F., Dinten J., Mars J., “In vivo fluorescence spectra unmixing and autofluorescence removal by sparse nonnegative matrix factorization,” IEEE Transactions on Biomed. Eng. 58, 2554–2565 (2011). 10.1109/TBME.2011.2159382 [DOI] [PubMed] [Google Scholar]
- 17.Pengo T., Muñoz-Barrutia A., Zudaire I., Ortiz-de Solorzano C., “Efficient blind spectral unmixing of fluorescently labeled samples using multi-layer non-negative matrix factorization,” PLoS One 8, e78504 (2013). 10.1371/journal.pone.0078504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Amouroux M., Blondel W., Delconte A., “Medical device for fibred bimodal optical spectroscopy,” Tech. Rep. WO2017093316A1, University of Lorraine; (2015). [Google Scholar]
- 19.Blacker T. S., Mann Z. F., Gale J. E., Ziegler M., Bain A. J., Szabadkai G., Duchen M. R., “Separating nadh and nadph fluorescence in live cells and tissues using flim,” Nat. Commun. 5, 3936 (2014). 10.1038/ncomms4936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Masters B., So P., Gratton E., “Optical biopsy of in vivo human skin: multi-photon excitation microscopy,” Lasers Med. Sci. 13, 196–203 (1998). 10.1007/s101030050074 [DOI] [Google Scholar]
- 21.Croce A., Bottiroli G., “Autofluorescence spectroscopy and imaging: a tool for biomedical research and diagnosis,” Eur. J. Histochem. 58, 2461 (2014). 10.4081/ejh.2014.2461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brancaleon L., Lin G., Kollias N., “The in vivo fluorescence of tryptophan moieties in human skin increases with uv exposure and is a marker for epidermal proliferation,” J. Investig. Dermatol. 113, 977–982 (1999). 10.1046/j.1523-1747.1999.00799.x [DOI] [PubMed] [Google Scholar]
- 23.Lee D. D., Seung H. S., “Learning the parts of objects by non-negative matrix factorization,” Nature 401, 788–791 (1999). 10.1038/44565 [DOI] [PubMed] [Google Scholar]
- 24.Montcuquet A.-S., Herve L., Navarro F. P., Dinten J.-M., Mars J., “Nonnegative matrix factorization: a blind spectra separation method for in vivo fluorescent optical imaging,” J. Biomed. Opt. 15, 1–14 (2010). [DOI] [PubMed] [Google Scholar]
- 25.Neher R. A., Mitkovski M., Kirchhoff F., Neher E., Theis F. J., Zeug A., “Blind source separation techniques for the decomposition of multiply labeled fluorescence images,” Biophys. J. 96, 3791–3800 (2009). 10.1016/j.bpj.2008.10.068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhou G., Cichocki A., Zhao Q., Xie S., “Nonnegative matrix and tensor factorizations: an algorithmic perspective,” IEEE Sig. Proc. Mag. 31, 54–65 (2014). 10.1109/MSP.2014.2298891 [DOI] [Google Scholar]
- 27.Meinhardt M., Krebs R., Anders A., Heinrich U., Tronnier H., “Wavelength-dependent penetration depths of ultraviolet radiation in human skin,” J. Biomed. Opt. 13, 044030 (2008). 10.1117/1.2957970 [DOI] [PubMed] [Google Scholar]
- 28.Ash C., Dubec M., Donne K., Bashford T., “Effect of wavelength and beam width on penetration in light-tissue interaction using computational methods,” Lasers Med. Sci. 32, 1909–1918 (2017). 10.1007/s10103-017-2317-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Katika K. M., Pilon L., “Steady-state directional diffuse reflectance and fluorescence of human skin,” Appl. Opt. 45, 4174–4183 (2006). 10.1364/AO.45.004174 [DOI] [PubMed] [Google Scholar]
- 30.Liu H., Gisquet H., Blondel W., Guillemin F., “Bimodal spectroscopy for in vivo characterization of hypertrophic skin tissue: pre-clinical experimentation, data selection and classification,” Biomed. Opt. Express 3, 3278–3290 (2012). 10.1364/BOE.3.003278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhu D., Larin K. V., Luo Q., Tuchin V. V., “Recent progress in tissue optical clearing,” Laser Photonics Rev. 7, 732–757 (2013). 10.1002/lpor.201200056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hirshburg J., Choi B., Nelson J. S., Yeh A. T., “Correlation between collagen solubility and skin optical clearing using sugars,” Lasers Surg. Medicine 39, 140–144 (2007). 10.1002/lsm.20417 [DOI] [PubMed] [Google Scholar]
- 33.Pires L., Demidov V., Vitkin I. A., Bagnato V. S., Kurachi C., Wilson B. C., “Optical clearing of melanoma in vivo: characterization by diffuse reflectance spectroscopy and optical coherence tomography,” J. Biomed. Opt. 21, 081210 (2016). 10.1117/1.JBO.21.8.081210 [DOI] [PubMed] [Google Scholar]
- 34.Vargas G., Barton J. K., Welch A. J., “Use of hyperosmotic chemical agent to improve the laser treatment of cutaneous vascular lesions,” J. Biomed. Opt. 13, 021114 (2008). 10.1117/1.2907327 [DOI] [PubMed] [Google Scholar]
- 35.Dolin L. S., Gelikonov G., Gelikonov V., Gladkova N. D., Iksanov R. R., Kamensky V., Kuranov R. S., Shakhova N. M., Tuchin I., Handbook of Coherent-Domain Optical Methods: Biomedical Diagnostics, Environmental Monitoring and Material Science., vol. 2 (Springer-Verlag, 2012). [Google Scholar]
- 36.Zhang Y., Liu H., Tang J., Li Z., Zhou X., Zhang R., Chen L., Mao Y., Li C., “Noninvasively imaging subcutaneous tumor xenograft by a handheld raman detector, with the assistance of an optical clearing agent,” ACS Appl. Mater. Interfaces 9, 17769–17776 (2017). 10.1021/acsami.7b04205 [DOI] [PubMed] [Google Scholar]